खेल

एक चर के कार्य की सीमा और निरंतरता - दस्तावेज़। एक सतत तर्क के एक फ़ंक्शन की सीमा एक फ़ंक्शन की निरंतरता की अवधारणा

सीमा और निरंतरता

एक चर के कार्य

3.1.1. परिभाषा। संख्या ए एक्सके लिए प्रयासरत एक्सयदि किसी संख्या के लिए 0
वहाँ एक संख्या है
(
), और शर्त पूरी हो जाएगी:

अगर
, वह
.

(प्रतीकात्मकता:
).

यदि ग्राफ इंगित करता है जीकार्य

, कब बिंदु के असीम करीब पहुंचता है (वे।
), (चित्र 3.1 देखें), तो यह परिस्थिति इस तथ्य के ज्यामितीय समकक्ष है कि फ़ंक्शन
पर
एक सीमा मान है (सीमा) ए(प्रतीकवाद:
).

फ़ंक्शन ग्राफ़,

चावल। 3.1

यह ध्यान दिया जाना चाहिए कि किसी फ़ंक्शन का सीमा मान (सीमा) निर्धारित करने में एक्सके लिए प्रयासरत एक्स 0 बिंदु पर फ़ंक्शन के व्यवहार के बारे में कुछ नहीं कहता है एक्स 0 . ठीक इसी बिंदु पर एक्स 0 फ़ंक्शन को परिभाषित नहीं किया जा सकता है, हो सकता है
, शायद
.

अगर
, तो फ़ंक्शन को इनफिनिटसिमल कहा जाता है
.

अंतराल कहा जाता है  - एक बिंदु का पड़ोस एक्स 0 एक चिपके हुए केंद्र के साथ। इस नाम का उपयोग करके, हम यह कह सकते हैं: यदि किसी संख्या के लिए एक संख्या है, और शर्त पूरी होगी: यदि
, वह
.

3.1.2. परिभाषा। , यदि किसी अभिसरण के लिए एक्स 0 क्रम
परिणाम को
में एकत्रित हो जाता है ए.

3.1.3. आइए हम अनुभाग 3.1.1 और 3.1.2 की परिभाषाओं की तुल्यता सिद्ध करें

पहले परिभाषा के अर्थ में पहले चलो और चलो
(
), फिर सभी , उनकी सीमित संख्या को छोड़कर असमानता को संतुष्ट करते हैं
, कहाँ  द्वारा चयनित  पहली परिभाषा के अर्थ में, अर्थात्
, अर्थात। पहली परिभाषा का तात्पर्य दूसरे से है। अभी रहने दो
दूसरी परिभाषा के अर्थ में और मान लीजिए कि दूसरी परिभाषा के अर्थ में
, अर्थात। कुछ के लिए मनमाने ढंग से छोटे के लिए (उदाहरण के लिए, के लिए
) अनुक्रम पाया गया
, लेकिन साथ ही
. हम एक विरोधाभास पर पहुंच गए हैं, इसलिए पहली परिभाषा दूसरी परिभाषा से आती है।

3.1.4. इन परिभाषाओं की समतुल्यता विशेष रूप से सुविधाजनक है, क्योंकि अनुक्रमों की सीमा के गुणों पर पहले से सिद्ध सभी प्रमेय लगभग स्वचालित रूप से लागू होते हैं नया केस. केवल सीमा की अवधारणा को स्पष्ट करना आवश्यक है। संबंधित प्रमेय का निम्नलिखित सूत्रीकरण है:

अगर
, तो यह बिंदु के कुछ  - पड़ोस तक सीमित है एक्स 0 एक चिपके हुए केंद्र के साथ।

3.2.1.प्रमेय. होने देना
,
,

तब,
,

3.2.2. होने देना

- मनमाना, अभिसरण एक्सफ़ंक्शन तर्क मानों का 0 अनुक्रम और
. मिलान अनुक्रम
और
इन कार्यों के मूल्यों की सीमाएँ हैं एऔर बी. लेकिन फिर, धारा 2.13.2 के प्रमेय के आधार पर, अनुक्रम
,
और
सीमाएँ संगत रूप से समान हैं ए +बी,
और
. किसी बिंदु पर किसी फ़ंक्शन की सीमा की परिभाषा के अनुसार (अनुभाग 2.5.2 देखें), इसका मतलब यह है

,
,

3.2.3. प्रमेय. अगर
,
, और कुछ आसपास के क्षेत्र में

घटित होना

3.2.4. किसी बिंदु पर किसी फ़ंक्शन की सीमा की परिभाषा के अनुसार एक्सकिसी भी क्रम के लिए 0
ऐसा है कि

फ़ंक्शन मानों के अनुक्रम की एक सीमा बराबर होती है ए. इसका मतलब यह है कि किसी के लिए भी
वहाँ एक संख्या है
प्रदर्शन किया । इसी प्रकार, अनुक्रम के लिए
वहाँ एक संख्या है
ऐसे कि किसी भी संख्या के लिए
प्रदर्शन किया । का चयन
, हम इसे हर किसी के लिए पाते हैं
प्रदर्शन किया । असमानताओं की इस श्रृंखला से हमारे पास किसी के लिए, जिसका अर्थ है
.

3.2.5. परिभाषा। संख्या एफ़ंक्शन का सीमा मान (सीमा) कहा जाता है एक्सके लिए प्रयासरत एक्सदाईं ओर 0 (प्रतीकात्मकता:
), यदि किसी संख्या के लिए कोई संख्या () है और शर्त पूरी होती है: यदि
, वह
.

समुच्चय को दाएँ  - बिंदु का पड़ोस कहा जाता है एक्स 0 . बाईं ओर सीमा मूल्य (सीमा) की अवधारणा को इसी तरह परिभाषित किया गया है (
).

3.2.6. प्रमेय. फ़ंक्शन at का एक सीमा मान (सीमा) के बराबर है एतब और केवल जब

3.3.1. परिभाषा। संख्या एफ़ंक्शन का सीमा मान (सीमा) कहा जाता है एक्सअनंत की ओर प्रवृत्त होना, यदि किसी संख्या के लिए कोई संख्या हो
(
) और निम्नलिखित शर्त पूरी होगी:

अगर
, वह ।

(प्रतीकात्मकता:
.)

गुच्छा
बुलाया डी- अनंत का पड़ोस.

3.3.2. परिभाषा। संख्या एफ़ंक्शन का सीमा मान (सीमा) कहा जाता है एक्सयदि किसी संख्या के लिए कोई संख्या हो तो धन अनंत की ओर प्रवृत्त होना डी() और शर्त पूरी होगी:

अगर
, वह ।

(प्रतीकात्मकता:
).

यदि ग्राफ इंगित करता है जीकार्य
असीमित विकास के साथ
एक क्षैतिज रेखा तक अनिश्चित काल तक पहुंचें
(चित्र 3.2 देखें), तो यह परिस्थिति इस तथ्य का ज्यामितीय समतुल्य है कि फ़ंक्शन
पर
संख्या के बराबर एक सीमा मान (सीमा) होता है ए(प्रतीकवाद:
).

किसी फ़ंक्शन का ग्राफ़
,

गुच्छा
बुलाया डी-पड़ोस प्लस अनंत.

सीमा की अवधारणा
.

व्यायाम.

मामलों पर लागू सीमाओं के बारे में सभी प्रमेय बताएं:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. परिभाषा। फ़ंक्शन को असीम रूप से कहा जाता है महान कार्य(या बस असीम रूप से बड़ा) पर, यदि किसी संख्या के लिए

, असमानता को संतुष्ट करते हुए, असमानता को संतुष्ट किया जाता है
.

(प्रतीकात्मकता:
.)

अगर पूरा हो गया
, फिर वे लिखते हैं
.

3.4.2. प्रमेय. होने देना
और
पर
.

तब
के लिए एक असीम रूप से बड़ा कार्य है।

3.4.3. इसे एक मनमाना संख्या होने दें. चूँकि संख्या के लिए एक अतिसूक्ष्म फलन है
एक नंबर ऐसा है जो हर किसी के लिए है एक्सइस प्रकार कि असमानता बनी रहे
, लेकिन फिर उसी के लिए एक्सअसमानता संतुष्ट हो जाएगी
. वे। के लिए एक असीम रूप से बड़ा कार्य है।

3.4.4.प्रमेय. आज्ञा देना के लिए और के लिए एक असीम रूप से बड़ा कार्य हो।

फिर के लिए एक अतिसूक्ष्म फलन है।

(यह प्रमेय धारा 3.8.2 में प्रमेय के समान ही सिद्ध है।)

3.4.5. समारोह
अनबाउंड कहा जाता है जब
, यदि किसी संख्या के लिए
और बिंदु का कोई δ-पड़ोस आप एक बिंदु निर्दिष्ट कर सकते हैं एक्सइस मोहल्ले से ऐसे कि
.

3.5.1. परिभाषा। फ़ंक्शन को कॉल किया जाता है निरंतरबिंदु पर , अगर
.

अंतिम शर्त इस प्रकार लिखी जा सकती है:

इस नोटेशन का मतलब है कि निरंतर कार्यों के लिए सीमा का चिह्न और फ़ंक्शन का चिह्न बदला जा सकता है

या इस तरह: . या फिर, शुरुआत की तरह.

चलो निरूपित करें
. तब
और =
और अंतिम रिकॉर्डिंग फॉर्म फॉर्म ले लेगा

सीमा चिह्न के नीचे की अभिव्यक्ति वृद्धि के कारण फ़ंक्शन बिंदु की वृद्धि को दर्शाती है
तर्क एक्सबिंदु पर, आमतौर पर इस रूप में दर्शाया जाता है
. परिणामस्वरूप, हमें एक बिंदु पर किसी फ़ंक्शन की निरंतरता के लिए शर्त लिखने का निम्नलिखित रूप प्राप्त होता है

जिसे किसी बिंदु पर किसी फ़ंक्शन की निरंतरता की "कार्यशील परिभाषा" कहा जाता है।

फ़ंक्शन को कॉल किया जाता है निरंतरबिंदु पर बाएं, अगर
.

फ़ंक्शन को कॉल किया जाता है निरंतरबिंदु पर दायी ओर, अगर
.

3.5.2. उदाहरण।
. यह फ़ंक्शन किसी के लिए भी निरंतर है। सीमाओं के गुणों पर प्रमेयों का उपयोग करते हुए, हम तुरंत प्राप्त करते हैं: कोई भी तर्कसंगत कार्य प्रत्येक बिंदु पर निरंतर होता है जिस पर इसे परिभाषित किया जाता है, अर्थात। प्रपत्र का कार्य
.

अभ्यास.

3.6.1. स्कूल की पाठ्यपुस्तक (चालू) साबित करती है उच्च स्तरकठोरता) वह
(पहली उल्लेखनीय सीमा)। दृश्य ज्यामितीय विचारों से यह तुरंत अनुसरण करता है
. ध्यान दें कि बाईं असमानता से भी यह अनुसरण होता है
, अर्थात। कार्य क्या है
शून्य पर निरंतर. यहां से सभी की निरंतरता को सिद्ध करना बिल्कुल भी कठिन नहीं है त्रिकोणमितीय कार्यउन सभी बिंदुओं पर जहां उन्हें परिभाषित किया गया है। दरअसल, जब
जैसे कोई उत्पाद अनंत है छोटा सा कार्य
पर सीमित कार्य
.

3.6.2. (दूसरी अद्भुत सीमा)। जैसा कि हम पहले से ही जानते हैं

कहाँ प्राकृतिक संख्याओं के माध्यम से चलता है। ऐसा दिखाया जा सकता है
. इसके अतिरिक्त
.

अभ्यास.

3.7.1. प्रमेय (एक जटिल कार्य की निरंतरता पर)।

यदि फ़ंक्शन
एक बिंदु पर निरंतर है और
, और फ़ंक्शन
एक बिंदु पर निरंतर , फिर एक जटिल कार्य
बिंदु पर निरंतर है.

3.7.2. इस कथन की वैधता तुरंत निरंतरता की परिभाषा से मिलती है, जिसे इस प्रकार लिखा गया है:

3.8.1. प्रमेय. समारोह हर बिंदु पर निरंतर है (
).

3.8.2. यदि हम इसे उचित मानते हैं तो फ़ंक्शन
किसी के लिए परिभाषित किया गया है और सख्ती से मोनोटोनिक है (सख्ती से घट रहा है)।
, सख्ती से बढ़ रहा है
), तो प्रमाण कठिन नहीं है।

पर
हमारे पास है:

वे। जब हम रखते है
, जिसका अर्थ है कि फ़ंक्शन पर निरंतर है.

पर
यह सब पिछले पर आ जाता है:

पर
.

पर
समारोह
सभी के लिए स्थिर है, इसलिए सतत है।

3.9.1. प्रमेय (प्रतिलोम फलन के सह-अस्तित्व और निरंतरता पर)।

मान लीजिए एक सतत फलन बिंदु के कुछ δ - पड़ोस में सख्ती से घटता (कड़ाई से बढ़ता) है,
. फिर कुछ ε में - बिंदु का पड़ोस एक व्युत्क्रम फलन है
, जो सख्ती से घटता है (सख्ती से बढ़ता है) और बिंदु के ε - पड़ोस में निरंतर होता है।

3.9.2. यहां हम केवल बिंदु पर व्युत्क्रम फलन की सातत्यता को सिद्ध करते हैं।

चलो इसे लेते हैं, अवधि यबिंदुओं के बीच स्थित है
और
, इसलिए, यदि
, वह
, कहाँ ।

3.10.1. इसलिए, निरंतर कार्यों पर कोई भी अनुमेय अंकगणितीय परिचालन फिर से निरंतर कार्यों की ओर ले जाता है। इनसे जटिल एवं व्युत्क्रम फलनों का निर्माण निरंतरता को खराब नहीं करता है। इसलिए, कुछ हद तक जिम्मेदारी के साथ, हम यह दावा कर सकते हैं कि सभी प्राथमिक कार्य तर्क के सभी स्वीकार्य मूल्यों के लिए निरंतर हैं।

व्यायाम.

साबित करें कि
पर
(दूसरी अद्भुत सीमा का दूसरा रूप)।

3.11.1. यदि हम समतुल्य अतिसूक्ष्म की अवधारणा का उपयोग करते हैं तो सीमाओं की गणना बहुत सरल हो जाती है। मनमाने कार्यों के मामले में तुल्यता की अवधारणा को सामान्य बनाना सुविधाजनक है।

परिभाषा। फ़ंक्शंस और को यदि के लिए समतुल्य कहा जाता है
(के बजाय आप लिख सकते हो
,
,
,
,
).

संकेतन का प्रयोग किया गया एफ ~ जी.

समतुल्यता में निम्नलिखित गुण होते हैं

समतुल्य अतिसूक्ष्मों की निम्नलिखित सूची को ध्यान में रखा जाना चाहिए:

~
पर
; (1)

~ पर ; (2)

~
पर ; (3)

~ पर ; (4)

~ पर ; (5)

~ पर ; (6)

~ पर ; (7)

~ पी पर ; (8)

~ पर
; (9)

~
पर । (10)

यहां स्वतंत्र चर नहीं, बल्कि कार्य हो सकते हैं
और
कुछ व्यवहार के लिए क्रमशः शून्य और एक की ओर प्रवृत्त होना एक्स. उदाहरण के लिए,

~
पर
,

~
पर
.

समतुल्यता (1) पहली उल्लेखनीय सीमा लिखने का दूसरा रूप है। समतुल्यताएं (2), (3), (6) और (7) सीधे सिद्ध की जा सकती हैं। समतुल्यता (4) समतुल्यता के (1) संपत्ति 2 को ध्यान में रखते हुए प्राप्त की जाती है:

~
.

इसी प्रकार, (2) और (6) से (5) और (7) प्राप्त होते हैं। वास्तव में

~
,

~
.

(8) की समतुल्यता (7) और (6) के क्रमिक अनुप्रयोग से सिद्ध होती है:

और (9) और (10) को (6) और (8) से प्रतिस्थापित करके प्राप्त किया जाता है
.

3.11.2. प्रमेय. किसी उत्पाद और अनुपात में सीमा की गणना करते समय, आप फ़ंक्शन को समतुल्य में बदल सकते हैं। अर्थात्, यदि ~
, तो या तो दोनों सीमाएँ एक साथ मौजूद नहीं हैं, और
, या ये दोनों सीमाएँ एक साथ मौजूद नहीं हैं।

आइए पहली समानता सिद्ध करें। चलो एक सीमा, कहते हैं,
मौजूद। तब

3.11.3. मान लीजिए ( एक संख्या या प्रतीक है,
या
). हम विभिन्न बी.एम. के व्यवहार पर विचार करेंगे। फ़ंक्शंस (इस प्रकार हम इनफिनिटसिमल शब्द को संक्षिप्त करेंगे)।

परिभाषाएँ।
और समकक्ष बी.एम. कहलाते हैं। यदि के लिए कार्य करता है
(पर )।

हम इसे बी.एम. कहेंगे. अधिक उच्च स्तरबी.एम. से समारोह
, अगर
(पर )।

3.11.4. यदि और समतुल्य बी.एम. तब कार्य करता है
वहाँ बी.एम. है से उच्च क्रम का कार्य
और क्या। - बी.एम. फ़ंक्शन पर, जिसमें सभी x के लिए और, यदि इस बिंदु पर फ़ंक्शन को हटाने योग्य असंततता बिंदु कहा जाता है। दूसरे प्रकार का असंततता है। बात स्वयं परीक्षा

संगोष्ठी के लिए. अनुभाग: " आप LIMITऔर निरंतरताकार्यवैध चर" कार्यएकचर", "अंतर कलन कार्यअनेक चर"

परीक्षण और प्रश्नों के विषय और उदाहरण (व्यक्तिगत मानक गणना बोलचाल का परीक्षण) प्रथम सेमेस्टर परीक्षण संख्या 1 खंड "वास्तविक चर के एक फ़ंक्शन की सीमा और निरंतरता"

परीक्षा

संगोष्ठी के लिए. अनुभाग: " आप LIMITऔर निरंतरताकार्यवैध चर", "अंतर कलन कार्यएकचर", "अंतर कलन कार्यअनेक चर". संख्या क्रम...

परीक्षा

परीक्षण असाइनमेंट और प्रश्नों के विषय और उदाहरण (परीक्षण कार्य व्यक्तिगत मानक गणना बोलचाल) प्रथम सेमेस्टर परीक्षण कार्य अनुभाग "वास्तविक चर के एक फ़ंक्शन की सीमा और निरंतरता"

परीक्षा

व्याख्यान 19 कई चरों वाले एक फलन की सीमा और निरंतरता

भाषण

... आप LIMITऔर निरंतरताकार्यअनेक चर. 19.1. अवधारणा कार्यअनेक चर. संशोधन करके कार्यअनेक चर... गुण कार्यएकचर, निरंतरखंड पर. गुण देखें कार्य, निरंतरपर...

कार्य की निरंतरता. ब्रेकिंग पॉइंट.

बैल चलता है, डोलता है, चलते समय आहें भरता है:
- ओह, बोर्ड ख़त्म हो रहा है, अब मैं गिरने वाला हूँ!

इस पाठ में हम किसी फ़ंक्शन की निरंतरता की अवधारणा, असंततता बिंदुओं के वर्गीकरण और सामान्य की जांच करेंगे व्यावहारिक समस्या कार्यों की निरंतरता का अध्ययन. विषय के नाम से ही, कई लोग सहजता से अनुमान लगा लेते हैं कि किस पर चर्चा की जाएगी और सोचते हैं कि सामग्री काफी सरल है। यह सच है। लेकिन यह सरल कार्य हैं जिन्हें अक्सर उपेक्षा और उन्हें हल करने के लिए सतही दृष्टिकोण के लिए दंडित किया जाता है। इसलिए, मेरा सुझाव है कि आप लेख का बहुत ध्यानपूर्वक अध्ययन करें और सभी सूक्ष्मताओं और तकनीकों को समझें।

आपको क्या जानने और करने में सक्षम होने की आवश्यकता है?बहुत ज़्यादा नहीं। पाठ को अच्छी तरह से सीखने के लिए, आपको यह समझने की आवश्यकता है कि यह क्या है किसी फ़ंक्शन की सीमा. निम्न स्तर की तैयारी वाले पाठकों के लिए, लेख को समझना ही पर्याप्त है कार्य सीमाएँ. समाधान के उदाहरणऔर देखना ज्यामितीय अर्थमैनुअल में सीमा प्राथमिक कार्यों के रेखांकन और गुण. इससे स्वयं को परिचित करने की भी सलाह दी जाती है ग्राफ़ का ज्यामितीय परिवर्तन, क्योंकि अधिकांश मामलों में अभ्यास में एक चित्र बनाना शामिल होता है। संभावनाएं हर किसी के लिए आशावादी हैं, और यहां तक कि एक पूर्ण केतली भी अगले एक या दो घंटे में अपने आप ही कार्य का सामना करने में सक्षम हो जाएगी!

कार्य की निरंतरता. ब्रेकप्वाइंट और उनका वर्गीकरण

कार्य की निरंतरता की अवधारणा

आइए कुछ फ़ंक्शन पर विचार करें जो संपूर्ण संख्या रेखा पर निरंतर है:

या, इसे और अधिक संक्षेप में कहें तो, हमारा कार्य निरंतर (सेट) पर है वास्तविक संख्या).

निरंतरता की "परोपकारी" कसौटी क्या है? जाहिर है, किसी सतत फलन का ग्राफ कागज से पेंसिल उठाए बिना भी खींचा जा सकता है।

इस मामले में, दोनों को स्पष्ट रूप से अलग करना आवश्यक है सरल अवधारणाएँ: किसी फ़ंक्शन का डोमेनऔर कार्य की निरंतरता. सामान्य रूप में यह वही बात नहीं है. उदाहरण के लिए:

यह फ़ंक्शनसंपूर्ण संख्या रेखा पर, अर्थात् के लिए परिभाषित किया गया है सब लोग"x" का अर्थ "y" का अपना अर्थ है। विशेषकर, यदि , तो . ध्यान दें कि अन्य बिंदु विराम चिह्न वाला है, क्योंकि किसी फ़ंक्शन की परिभाषा के अनुसार, तर्क का मान इसके अनुरूप होना चाहिए एकमात्र वस्तुफ़ंक्शन मान. इस प्रकार, कार्यक्षेत्रहमारा कार्य: .

तथापि यह फ़ंक्शन निरंतर चालू नहीं है!यह बिल्कुल स्पष्ट है कि इस समय वह पीड़ित है अंतर. यह शब्द वास्तव में काफी समझदार और दृश्य है, यहां पेंसिल को वैसे भी कागज से फाड़ना होगा। थोड़ी देर बाद हम ब्रेकप्वाइंट के वर्गीकरण को देखेंगे।

एक बिंदु पर और एक अंतराल पर किसी फ़ंक्शन की निरंतरता

किसी विशेष गणितीय समस्या में, हम एक बिंदु पर किसी फ़ंक्शन की निरंतरता, किसी अंतराल पर किसी फ़ंक्शन की निरंतरता, अर्ध-अंतराल, या किसी खंड पर किसी फ़ंक्शन की निरंतरता के बारे में बात कर सकते हैं। वह है, कोई "मात्र निरंतरता" नहीं है- फ़ंक्शन कहीं भी निरंतर हो सकता है। और बाकी सभी चीज़ों का मूलभूत "बिल्डिंग ब्लॉक" है कार्य की निरंतरता बिंदु पर .

गणितीय विश्लेषण का सिद्धांत "डेल्टा" और "एप्सिलॉन" पड़ोस का उपयोग करके एक बिंदु पर एक फ़ंक्शन की निरंतरता की परिभाषा देता है, लेकिन व्यवहार में उपयोग में एक अलग परिभाषा है, जिस पर हम बारीकी से ध्यान देंगे।

पहले याद कर लेते हैं एकतरफ़ा सीमाजो पहले पाठ में ही हमारे जीवन में फूट पड़े फ़ंक्शन ग्राफ़ के बारे में. रोजमर्रा की स्थिति पर विचार करें:

यदि हम अक्ष से बिंदु तक पहुंचते हैं बाएं(लाल तीर), फिर "गेम" के संबंधित मान अक्ष के साथ बिंदु (क्रिमसन तीर) तक जाएंगे। गणितीय रूप से इस तथ्य को प्रयोग करके निश्चित किया जाता है बाएँ हाथ की सीमा:

प्रविष्टि पर ध्यान दें (पढ़ें "x बाईं ओर ka की ओर जाता है")। "एडिटिव" "माइनस जीरो" का प्रतीक है , अनिवार्य रूप से इसका मतलब है कि हम बाईं ओर से संख्या के करीब पहुंच रहे हैं।

इसी तरह, यदि आप बिंदु "का" पर पहुंचते हैं दायी ओर (नीला तीर), तो "गेम" समान मान पर आ जाएंगे, लेकिन हरे तीर के साथ, और दाहिने हाथ की सीमानिम्नानुसार स्वरूपित किया जाएगा:

"एडिटिव" का प्रतीक है , और प्रविष्टि में लिखा है: "x दाईं ओर ka की ओर प्रवृत्त होता है।"

यदि एकतरफ़ा सीमाएँ परिमित और समान हैं(जैसा कि हमारे मामले में): , तो हम कहेंगे कि एक सामान्य सीमा है। यह सरल है, सामान्य सीमा हमारी "सामान्य" है किसी फ़ंक्शन की सीमा, एक परिमित संख्या के बराबर।

ध्यान दें कि यदि फ़ंक्शन को परिभाषित नहीं किया गया है (ग्राफ़ शाखा पर काले बिंदु को बाहर निकालें), तो उपरोक्त गणना मान्य रहती है। जैसा कि पहले ही कई बार उल्लेख किया जा चुका है, विशेष रूप से लेख में अतिसूक्ष्म कार्यों पर, भाव का अर्थ है कि "x" असीम रूप से करीबजबकि, बिंदु तक पहुंचता है कोई फर्क नहीं पड़ता, चाहे फ़ंक्शन स्वयं किसी दिए गए बिंदु पर परिभाषित हो या नहीं। एक अच्छा उदाहरण अगले पैराग्राफ में मिलेगा, जब फ़ंक्शन का विश्लेषण किया जाएगा।

परिभाषा: एक फ़ंक्शन एक बिंदु पर निरंतर होता है यदि किसी दिए गए बिंदु पर फ़ंक्शन की सीमा उस बिंदु पर फ़ंक्शन के मान के बराबर होती है:।

परिभाषा निम्नलिखित शब्दों में विस्तृत है:

1) फ़ंक्शन को बिंदु पर परिभाषित किया जाना चाहिए, अर्थात मान मौजूद होना चाहिए।

2)कार्य की एक सामान्य सीमा होनी चाहिए। जैसा कि ऊपर बताया गया है, इसका तात्पर्य एकतरफा सीमाओं के अस्तित्व और समानता से है: .

3) किसी दिए गए बिंदु पर फ़ंक्शन की सीमा इस बिंदु पर फ़ंक्शन के मान के बराबर होनी चाहिए:।

यदि उल्लंघन किया गया कम से कम एकतीन स्थितियों में से, तब फ़ंक्शन बिंदु पर निरंतरता की संपत्ति खो देता है।

एक अंतराल पर किसी फ़ंक्शन की निरंतरतासरलतापूर्वक और बहुत सरलता से तैयार किया गया है: एक फ़ंक्शन अंतराल पर निरंतर होता है यदि यह दिए गए अंतराल के प्रत्येक बिंदु पर निरंतर होता है।

विशेष रूप से, कई फ़ंक्शन अनंत अंतराल पर, यानी वास्तविक संख्याओं के सेट पर निरंतर होते हैं। यह एक रैखिक फलन, बहुपद, घातांक, ज्या, कोज्या आदि है। और सामान्य तौर पर, कोई भी प्राथमिक कार्यइस पर निरंतर परिभाषा का क्षेत्र, उदाहरण के लिए, लघुगणकीय कार्यअंतराल पर निरंतर है. उम्मीद है कि अब तक आपको यह अच्छी तरह से पता चल गया होगा कि बुनियादी कार्यों के ग्राफ़ कैसे दिखते हैं। अधिक विस्तार में जानकारीउनकी निरंतरता के बारे में फिचटेनहोल्ट्ज़ नामक एक दयालु व्यक्ति से प्राप्त किया जा सकता है।

एक खंड और आधे-अंतराल पर एक फ़ंक्शन की निरंतरता के साथ, सब कुछ भी मुश्किल नहीं है, लेकिन कक्षा में इस बारे में बात करना अधिक उपयुक्त है किसी खंड पर किसी फ़ंक्शन के न्यूनतम और अधिकतम मान ज्ञात करने के बारे में, लेकिन अभी इसके बारे में चिंता न करें।

ब्रेक प्वाइंट का वर्गीकरण

कार्यों का आकर्षक जीवन सभी प्रकार के विशेष बिंदुओं से समृद्ध है, और विराम बिंदु उनकी जीवनी के केवल एक पृष्ठ हैं।

टिप्पणी : बस किसी मामले में, मैं एक प्रारंभिक बिंदु पर ध्यान केंद्रित करूंगा: ब्रेकिंग पॉइंट हमेशा होता है सिंगल पॉइंट- कोई "एक पंक्ति में कई ब्रेक पॉइंट" नहीं हैं, अर्थात, "ब्रेक अंतराल" जैसी कोई चीज़ नहीं है।

बदले में, ये बिंदु दो बड़े समूहों में विभाजित हैं: पहली तरह का टूटनाऔर दूसरे प्रकार का टूटना. प्रत्येक प्रकार का अंतराल अपना-अपना होता है विशेषताएँजिसे हम अभी देखेंगे:

प्रथम प्रकार का असंततता बिंदु

यदि किसी बिंदु पर निरंतरता की स्थिति का उल्लंघन होता है और एकतरफ़ा सीमाएँ परिमित , तो इसे कहा जाता है पहली तरह का असंततता बिंदु.

आइए सबसे आशावादी मामले से शुरुआत करें। पाठ के मूल विचार के अनुसार, मैं "में" सिद्धांत बताना चाहता था सामान्य रूप से देखें”, लेकिन सामग्री की वास्तविकता प्रदर्शित करने के लिए, मैंने विशिष्ट पात्रों वाले विकल्प पर फैसला किया।

दुखद, पृष्ठभूमि में नवविवाहित जोड़े की तस्वीर की तरह अनन्त लौ, लेकिन निम्नलिखित फ्रेम आम तौर पर स्वीकार किया जाता है। आइए चित्र में फ़ंक्शन का ग्राफ़ चित्रित करें:

यह फ़ंक्शन बिंदु को छोड़कर संपूर्ण संख्या रेखा पर निरंतर होता है। और वास्तव में, हर शून्य के बराबर नहीं हो सकता। हालाँकि, सीमा के अर्थ के अनुसार, हम कर सकते हैं असीम रूप से करीबबाएँ और दाएँ दोनों ओर से "शून्य" तक पहुँचें, अर्थात, एकतरफा सीमाएँ मौजूद हैं और, जाहिर है, मेल खाती हैं:
(निरंतरता की शर्त संख्या 2 संतुष्ट है)।

लेकिन फ़ंक्शन को बिंदु पर परिभाषित नहीं किया गया है, इसलिए, निरंतरता की शर्त संख्या 1 का उल्लंघन होता है, और फ़ंक्शन इस बिंदु पर असंतोष से ग्रस्त है।

इस प्रकार का ब्रेक (मौजूदा के साथ)। सामान्य सीमा) कहा जाता है मरम्मत योग्य अंतराल. हटाने योग्य क्यों? क्योंकि फ़ंक्शन कर सकता है फिर से परिभाषितब्रेकिंग पॉइंट पर:

क्या यह अजीब लग रहा है? शायद। लेकिन ऐसा फ़ंक्शन नोटेशन किसी भी चीज़ का खंडन नहीं करता है! अब अंतर ख़त्म हो गया है और हर कोई खुश है:

आइए एक औपचारिक जाँच करें:

2) – एक सामान्य सीमा है;
3)

इस प्रकार, सभी तीन शर्तें पूरी हो जाती हैं, और एक बिंदु पर किसी फ़ंक्शन की निरंतरता की परिभाषा के अनुसार फ़ंक्शन एक बिंदु पर निरंतर होता है।

हालाँकि, उदाहरण के लिए, मटन से नफरत करने वाले फ़ंक्शन को बुरे तरीके से परिभाषित कर सकते हैं :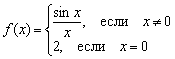

यह दिलचस्प है कि पहली दो निरंतरता शर्तें यहां संतुष्ट हैं:
1)-फ़ंक्शन को किसी दिए गए बिंदु पर परिभाषित किया गया है;
2) - एक सामान्य सीमा है.

लेकिन तीसरी सीमा पार नहीं की गई है: यानी, बिंदु पर फ़ंक्शन की सीमा सम नहीकिसी दिए गए बिंदु पर दिए गए फ़ंक्शन का मान।

इस प्रकार, एक बिंदु पर कार्य में असंततता आ जाती है।

दूसरा, दुखद मामला कहा जाता है पहली तरह का टूटना एक छलांग के साथ. और दुःख एकतरफ़ा सीमाओं से उत्पन्न होता है परिमित और भिन्न. पाठ के दूसरे चित्र में एक उदाहरण दिखाया गया है। ऐसा गैप आमतौर पर होता है टुकड़ों में परिभाषित कार्य, जिनका उल्लेख लेख में पहले ही किया जा चुका है ग्राफ़ परिवर्तनों के बारे में.

टुकड़ेवार कार्य पर विचार करें और हम इसकी ड्राइंग पूरी करेंगे. ग्राफ़ कैसे बनाएं? बहुत सरल। आधे अंतराल पर हम एक परवलय का एक टुकड़ा खींचते हैं ( हरा रंग), अंतराल पर - एक सीधी रेखा खंड (लाल) और आधे-अंतराल पर - एक सीधी रेखा (नीला)।

इसके अलावा, असमानता के कारण, मान द्विघात फ़ंक्शन (हरा बिंदु) के लिए निर्धारित किया जाता है, और असमानता के कारण, मान निर्धारित किया जाता है रैखिक प्रकार्य(नीला बिंदु):

सबसे कठिन मामले में, आपको ग्राफ़ के प्रत्येक टुकड़े के बिंदु-दर-बिंदु निर्माण का सहारा लेना चाहिए (पहला देखें)। कार्यों के ग्राफ़ के बारे में पाठ).

अब हमें सिर्फ मुद्दे में दिलचस्पी होगी. आइए निरंतरता के लिए इसकी जांच करें:

2) आइए एकतरफ़ा सीमा की गणना करें।

बाईं ओर हमारे पास एक लाल रेखा खंड है, इसलिए बाईं ओर की सीमा है:

दाईं ओर नीली सीधी रेखा है, और दाईं ओर की सीमा:

परिणामस्वरूप, हमें प्राप्त हुआ परिमित संख्या, वे और सम नही. चूँकि एकतरफ़ा सीमाएँ परिमित और भिन्न: , तो हमारा कार्य सहन करता है एक छलांग के साथ पहली तरह की असंततता.

यह तर्कसंगत है कि अंतर को समाप्त नहीं किया जा सकता है - फ़ंक्शन को वास्तव में आगे परिभाषित नहीं किया जा सकता है और पिछले उदाहरण की तरह "एक साथ चिपकाया" नहीं जा सकता है।

दूसरे प्रकार के असंततता बिंदु

आमतौर पर, टूटने के अन्य सभी मामलों को चतुराई से इस श्रेणी में वर्गीकृत किया जाता है। मैं सब कुछ सूचीबद्ध नहीं करूंगा, क्योंकि व्यवहार में, 99% समस्याओं में आपका सामना होगा अंतहीन अंतराल- जब बाएं हाथ से या दाएं हाथ से, और अधिक बार, दोनों सीमाएं अनंत होती हैं।

और, निःसंदेह, सबसे स्पष्ट चित्र बिंदु शून्य पर अतिपरवलय है। यहाँ दोनों एकतरफ़ा सीमाएँ अनंत हैं: इसलिए, फ़ंक्शन को बिंदु पर दूसरे प्रकार की असंततता का सामना करना पड़ता है।

मैं अपने लेखों को यथासंभव विविध सामग्री से भरने का प्रयास करता हूं, तो आइए एक ऐसे फ़ंक्शन के ग्राफ़ को देखें जो अभी तक नहीं देखा गया है:

मानक योजना के अनुसार:

1) इस बिंदु पर फ़ंक्शन परिभाषित नहीं है क्योंकि हर शून्य पर चला जाता है।

बेशक, हम तुरंत यह निष्कर्ष निकाल सकते हैं कि फ़ंक्शन बिंदु पर एक असंतोष से ग्रस्त है, लेकिन असंतोष की प्रकृति को वर्गीकृत करना अच्छा होगा, जो अक्सर स्थिति के लिए आवश्यक होता है। इसके लिए:

मैं आपको याद दिला दूं कि रिकॉर्डिंग से हमारा मतलब है बहुत छोता एक ऋणात्मक संख्या , और प्रविष्टि के अंतर्गत - अतिसूक्ष्म धनात्मक संख्या.

एकतरफ़ा सीमाएँ अनंत हैं, जिसका अर्थ है कि फ़ंक्शन को बिंदु पर दूसरे प्रकार की असंततता का सामना करना पड़ता है। y-अक्ष है ऊर्ध्वाधर एसिम्पटोटचार्ट के लिए.

दोनों एकतरफ़ा सीमाओं का अस्तित्व में होना असामान्य नहीं है, लेकिन उनमें से केवल एक ही अनंत है, उदाहरण के लिए:

यह फ़ंक्शन का ग्राफ़ है.

हम निरंतरता के लिए बिंदु की जांच करते हैं:

1) इस बिंदु पर फ़ंक्शन परिभाषित नहीं है।

2) आइए एकतरफ़ा सीमा की गणना करें:

हम व्याख्यान के अंतिम दो उदाहरणों में ऐसी एकतरफा सीमाओं की गणना करने की विधि के बारे में बात करेंगे, हालाँकि कई पाठक पहले ही सब कुछ देख और अनुमान लगा चुके हैं।

बाएं हाथ की सीमा परिमित है और शून्य के बराबर है (हम "बिंदु पर ही नहीं जाते"), लेकिन दाएं हाथ की सीमा अनंत है और ग्राफ़ की नारंगी शाखा इसके असीम रूप से करीब पहुंचती है ऊर्ध्वाधर एसिम्पटोट, समीकरण द्वारा दिया गया(काली बिंदीदार रेखा).

अतः कार्य प्रभावित होता है दूसरे प्रकार की असंततताबिंदु पर.

जहां तक पहली तरह की असंततता का सवाल है, फ़ंक्शन को असंततता बिंदु पर ही परिभाषित किया जा सकता है। उदाहरण के लिए, एक टुकड़े-टुकड़े फ़ंक्शन के लिए निर्देशांक के मूल में एक काला बोल्ड बिंदु लगाने के लिए स्वतंत्र महसूस करें। दाईं ओर हाइपरबोला की एक शाखा है, और दाईं ओर की सीमा अनंत है। मुझे लगता है कि लगभग हर किसी को इस बात का अंदाज़ा है कि यह ग्राफ़ कैसा दिखता है।

हर कोई किस चीज़ का इंतज़ार कर रहा था:

निरंतरता के लिए किसी फ़ंक्शन की जांच कैसे करें?

किसी बिंदु पर निरंतरता के लिए फ़ंक्शन का अध्ययन पहले से स्थापित नियमित योजना के अनुसार किया जाता है, जिसमें निरंतरता की तीन स्थितियों की जाँच होती है:

उदाहरण 1

फ़ंक्शन का अन्वेषण करें

समाधान:

1) दायरे के भीतर एकमात्र बिंदु वह है जहां फ़ंक्शन परिभाषित नहीं है।

2) आइए एकतरफ़ा सीमा की गणना करें:

एकतरफ़ा सीमाएँ परिमित और समान हैं।

इस प्रकार, इस बिंदु पर फ़ंक्शन एक हटाने योग्य असंतोष से ग्रस्त है।

इस फ़ंक्शन का ग्राफ़ कैसा दिखता है?

मैं सरलीकरण करना चाहूँगा , और ऐसा लगता है जैसे एक साधारण परवलय प्राप्त होता है। लेकिनमूल फ़ंक्शन को बिंदु पर परिभाषित नहीं किया गया है, इसलिए निम्नलिखित खंड की आवश्यकता है:

आइए चित्र बनाएं:

उत्तर: फ़ंक्शन उस बिंदु को छोड़कर संपूर्ण संख्या रेखा पर निरंतर है जिस पर यह हटाने योग्य असंततता से ग्रस्त है।

फ़ंक्शन को आगे अच्छे या बुरे तरीके से परिभाषित किया जा सकता है, लेकिन स्थिति के अनुसार इसकी आवश्यकता नहीं है।

आप कहते हैं कि यह एक दूरगामी उदाहरण है? बिल्कुल नहीं। व्यवहार में ऐसा दर्जनों बार हो चुका है. साइट के लगभग सभी कार्य वास्तविक स्वतंत्र कार्य और परीक्षणों से आते हैं।

आइए अपने पसंदीदा मॉड्यूल से छुटकारा पाएं:

उदाहरण 2

फ़ंक्शन का अन्वेषण करें निरंतरता के लिए. यदि वे मौजूद हैं, तो फ़ंक्शन असंततता की प्रकृति निर्धारित करें। ड्राइंग निष्पादित करें.

समाधान: किसी कारण से, छात्र डरते हैं और मॉड्यूल के साथ फ़ंक्शन पसंद नहीं करते हैं, हालांकि उनमें कुछ भी जटिल नहीं है। ऐसी बातों पर हम पहले ही पाठ में थोड़ा विचार कर चुके हैं। ग्राफ़ का ज्यामितीय परिवर्तन. चूंकि मॉड्यूल गैर-नकारात्मक है, इसलिए इसे निम्नानुसार विस्तारित किया गया है: , जहां "अल्फा" कुछ अभिव्यक्ति है। इस मामले में, और हमारे कार्य को टुकड़ों में लिखा जाना चाहिए:

लेकिन दोनों टुकड़ों के अंशों को कम किया जाना चाहिए। पिछले उदाहरण की तरह, कटौती बिना परिणामों के नहीं होगी। मूल फ़ंक्शन को बिंदु पर परिभाषित नहीं किया गया है क्योंकि हर शून्य पर चला जाता है। इसलिए, सिस्टम को अतिरिक्त रूप से शर्त निर्दिष्ट करनी चाहिए, और पहली असमानता को सख्त बनाना चाहिए:

अब एक बहुत ही उपयोगी निर्णय तकनीक के बारे में: ड्राफ्ट पर कार्य को अंतिम रूप देने से पहले, एक ड्राइंग बनाना फायदेमंद होता है (चाहे यह शर्तों के अनुसार आवश्यक हो या नहीं)। यह, सबसे पहले, निरंतरता के बिंदुओं और असंततता के बिंदुओं को तुरंत देखने में मदद करेगा, और दूसरी बात, यह आपको एकतरफा सीमाएं खोजने पर त्रुटियों से 100% बचाएगा।

चलो ड्राइंग बनाते हैं. हमारी गणना के अनुसार, बिंदु के बाईं ओर एक परवलय (नीला रंग) का एक टुकड़ा खींचना आवश्यक है, और दाईं ओर - एक परवलय (लाल रंग) का एक टुकड़ा, जबकि फ़ंक्शन को परिभाषित नहीं किया गया है स्वयं बिंदु:

यदि संदेह है, तो कुछ x मान लें और उन्हें फ़ंक्शन में प्लग करें (याद रखें कि मॉड्यूल संभावित ऋण चिह्न को नष्ट कर देता है) और ग्राफ़ की जाँच करें।

आइए विश्लेषणात्मक रूप से निरंतरता के लिए फ़ंक्शन की जांच करें:

1) फ़ंक्शन को बिंदु पर परिभाषित नहीं किया गया है, इसलिए हम तुरंत कह सकते हैं कि यह इस पर निरंतर नहीं है।

2) आइए असंततता की प्रकृति स्थापित करें, ऐसा करने के लिए, हम एक तरफा सीमा की गणना करते हैं:

एकतरफ़ा सीमाएँ परिमित और भिन्न हैं, जिसका अर्थ है कि फ़ंक्शन बिंदु पर छलांग के साथ पहली तरह की असंततता से ग्रस्त है। फिर से ध्यान दें कि सीमाएँ खोजते समय, इससे कोई फर्क नहीं पड़ता कि ब्रेक पॉइंट पर फ़ंक्शन परिभाषित है या नहीं।

अब जो कुछ बचा है वह ड्राइंग को ड्राफ्ट से स्थानांतरित करना है (इसे ऐसे बनाया गया था जैसे कि शोध की मदद से ;-)) और कार्य पूरा करें:

उत्तर: फ़ंक्शन उस बिंदु को छोड़कर संपूर्ण संख्या रेखा पर निरंतर होता है जिस पर छलांग के साथ यह पहली तरह की असंततता से ग्रस्त होता है।

कभी-कभी उन्हें असंततता छलांग के अतिरिक्त संकेत की आवश्यकता होती है। इसकी गणना सरलता से की जाती है - दाहिनी सीमा से आपको बाईं सीमा को घटाना होगा: यानी, ब्रेक पॉइंट पर हमारा फ़ंक्शन 2 यूनिट नीचे कूद गया (जैसा कि ऋण चिह्न हमें बताता है)।

उदाहरण 3

फ़ंक्शन का अन्वेषण करें निरंतरता के लिए. यदि वे मौजूद हैं, तो फ़ंक्शन असंततता की प्रकृति निर्धारित करें। एक चित्र बनाओ.

के लिए यह एक उदाहरण है स्वतंत्र निर्णय, पाठ के अंत में नमूना समाधान।

आइए कार्य के सबसे लोकप्रिय और व्यापक संस्करण पर चलते हैं, जब फ़ंक्शन में तीन भाग होते हैं:

उदाहरण 4

निरंतरता के लिए किसी फ़ंक्शन की जांच करें और फ़ंक्शन का एक ग्राफ बनाएं .

समाधान: यह स्पष्ट है कि फ़ंक्शन के सभी तीन भाग संबंधित अंतराल पर निरंतर हैं, इसलिए टुकड़ों के बीच "जंक्शन" के केवल दो बिंदुओं की जांच करना बाकी है। सबसे पहले, आइए एक ड्राफ्ट ड्राइंग बनाएं; मैंने लेख के पहले भाग में निर्माण तकनीक पर पर्याप्त विस्तार से टिप्पणी की है। केवल एक चीज यह है कि हमें अपने एकवचन बिंदुओं का सावधानीपूर्वक पालन करने की आवश्यकता है: असमानता के कारण, मान सीधी रेखा (हरा बिंदु) से संबंधित है, और असमानता के कारण, मान परवलय (लाल बिंदु) से संबंधित है:

खैर, सिद्धांत रूप में, सब कुछ स्पष्ट है =) जो कुछ बचा है वह निर्णय को औपचारिक बनाना है। दो "जुड़ने" बिंदुओं में से प्रत्येक के लिए, हम मानक रूप से 3 निरंतरता शर्तों की जांच करते हैं:

मैं)हम निरंतरता के लिए बिंदु की जांच करते हैं

एकतरफ़ा सीमाएँ परिमित और भिन्न हैं, जिसका अर्थ है कि फ़ंक्शन बिंदु पर छलांग के साथ पहली तरह की असंततता से ग्रस्त है।

आइए दाएं और बाएं सीमा के बीच अंतर के रूप में असंततता छलांग की गणना करें:
, यानी, ग्राफ़ एक इकाई तक ऊपर चला गया।

द्वितीय)हम निरंतरता के लिए बिंदु की जांच करते हैं

1) - फ़ंक्शन को किसी दिए गए बिंदु पर परिभाषित किया गया है।

2) एकतरफ़ा सीमाएँ खोजें:

- एकतरफ़ा सीमाएँ परिमित और समान हैं, जिसका अर्थ है कि एक सामान्य सीमा है।

3) - किसी बिंदु पर किसी फ़ंक्शन की सीमा किसी दिए गए बिंदु पर इस फ़ंक्शन के मान के बराबर होती है।

अंतिम चरण में, हम ड्राइंग को अंतिम संस्करण में स्थानांतरित करते हैं, जिसके बाद हम अंतिम राग डालते हैं:

उत्तर: फ़ंक्शन संपूर्ण संख्या रेखा पर निरंतर है, उस बिंदु को छोड़कर जिस पर यह एक छलांग के साथ पहली तरह की असंततता से ग्रस्त है।

उदाहरण 5

निरंतरता के लिए किसी फ़ंक्शन की जांच करें और उसका ग्राफ़ बनाएं .

यह पाठ के अंत में स्वतंत्र समाधान, संक्षिप्त समाधान और समस्या का अनुमानित नमूना का एक उदाहरण है।

आपको यह आभास हो सकता है कि एक बिंदु पर कार्य निरंतर होना चाहिए, और दूसरे बिंदु पर असंततता होनी चाहिए। व्यवहार में, हमेशा ऐसा नहीं होता है। शेष उदाहरणों की उपेक्षा न करने का प्रयास करें - इनमें कई दिलचस्प और महत्वपूर्ण विशेषताएं होंगी:

उदाहरण 6

एक फ़ंक्शन दिया गया . बिंदुओं पर निरंतरता के लिए फ़ंक्शन की जांच करें। एक ग्राफ बनाएं.

समाधान: और फिर से तुरंत ड्राफ्ट पर ड्राइंग निष्पादित करें:

इस ग्राफ़ की ख़ासियत यह है कि टुकड़ा-वार फ़ंक्शन एब्सिस्सा अक्ष के समीकरण द्वारा दिया गया है। यहां यह क्षेत्र हरे रंग में खींचा गया है, लेकिन नोटबुक में इसे आमतौर पर एक साधारण पेंसिल से बोल्ड में हाइलाइट किया जाता है। और, निश्चित रूप से, हमारे मेढ़ों के बारे में मत भूलिए: मान स्पर्शरेखा शाखा (लाल बिंदु) से संबंधित है, और मान सीधी रेखा से संबंधित है।

ड्राइंग से सब कुछ स्पष्ट है - फ़ंक्शन संपूर्ण संख्या रेखा के साथ निरंतर है, जो कुछ बचा है वह समाधान को औपचारिक बनाना है, जिसे 3-4 समान उदाहरणों के बाद वस्तुतः पूर्ण स्वचालन में लाया जाता है:

मैं)हम निरंतरता के लिए बिंदु की जांच करते हैं

1)-फ़ंक्शन को किसी दिए गए बिंदु पर परिभाषित किया गया है।

2) आइए एकतरफ़ा सीमा की गणना करें:

, जिसका अर्थ है कि एक सामान्य सीमा है।

बस किसी मामले में, मैं आपको एक तुच्छ तथ्य याद दिला दूं: एक स्थिरांक की सीमा स्वयं स्थिरांक के बराबर होती है। इस मामले में, शून्य की सीमा स्वयं शून्य (बाएं हाथ की सीमा) के बराबर है।

इस प्रकार, किसी बिंदु पर किसी फ़ंक्शन की निरंतरता की परिभाषा के अनुसार एक फ़ंक्शन एक बिंदु पर निरंतर होता है।

द्वितीय)हम निरंतरता के लिए बिंदु की जांच करते हैं

1)-फ़ंक्शन को किसी दिए गए बिंदु पर परिभाषित किया गया है।

2) एकतरफ़ा सीमाएँ खोजें:

और यहाँ - एक की सीमा इकाई के बराबर है।

- एक सामान्य सीमा है.

हमेशा की तरह, शोध के बाद हम अपनी ड्राइंग को अंतिम संस्करण में स्थानांतरित करते हैं।

उत्तर: फ़ंक्शन बिंदुओं पर निरंतर है।

कृपया ध्यान दें कि इस स्थिति में हमसे निरंतरता के लिए संपूर्ण फ़ंक्शन की जांच करने के बारे में कुछ नहीं पूछा गया था, और इसे तैयार करने के लिए इसे अच्छा गणितीय रूप माना जाता है सटीक और स्पष्टपूछे गए प्रश्न का उत्तर. वैसे, यदि परिस्थितियाँ आपको ग्राफ़ बनाने की आवश्यकता नहीं देती हैं, तो आपको इसे न बनाने का पूरा अधिकार है (हालाँकि बाद में शिक्षक आपको ऐसा करने के लिए मजबूर कर सकता है)।

इसे स्वयं हल करने के लिए एक छोटा गणितीय "टंग ट्विस्टर":

उदाहरण 7

एक फ़ंक्शन दिया गया 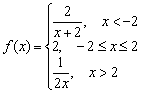. बिंदुओं पर निरंतरता के लिए फ़ंक्शन की जांच करें। ब्रेकप्वाइंट, यदि कोई हो, वर्गीकृत करें। ड्राइंग निष्पादित करें.

सभी "शब्दों" को सही ढंग से "उच्चारण" करने का प्रयास करें =) और ग्राफ को अधिक सटीक, सटीकता से बनाएं, यह हर जगह अतिश्योक्तिपूर्ण नहीं होगा;-)

जैसा कि आपको याद है, मैंने ड्राइंग को ड्राफ्ट के रूप में तुरंत पूरा करने की सिफारिश की थी, लेकिन समय-समय पर आपके सामने ऐसे उदाहरण आते हैं जहां आप तुरंत यह पता नहीं लगा सकते कि ग्राफ़ कैसा दिखता है। इसलिए, कुछ मामलों में, पहले एक तरफा सीमाएं ढूंढना फायदेमंद होता है और उसके बाद ही अध्ययन के आधार पर शाखाओं का चित्रण करना फायदेमंद होता है। अंतिम दो उदाहरणों में हम कुछ एकतरफ़ा सीमाओं की गणना करने की तकनीक भी सीखेंगे:

उदाहरण 8

निरंतरता के लिए फ़ंक्शन की जांच करें और इसका योजनाबद्ध ग्राफ़ बनाएं।

समाधान: खराब बिंदु स्पष्ट हैं: (घातक के हर को शून्य तक कम कर देता है) और (संपूर्ण भिन्न के हर को शून्य तक कम कर देता है)। यह स्पष्ट नहीं है कि इस फ़ंक्शन का ग्राफ़ कैसा दिखता है, जिसका अर्थ है कि पहले कुछ शोध करना बेहतर है।

टोपोलॉजी- गणित की एक शाखा जो कार्यों की सीमाओं और निरंतरता के अध्ययन से संबंधित है। बीजगणित के साथ संयोजन में, टोपोलॉजी गणित का सामान्य आधार बनती है।

टोपोलॉजिकल स्पेस या आकृति -हमारे सजातीय यूक्लिडियन स्थान का एक उपसमुच्चय, जिसके बिंदुओं के बीच एक निश्चित निकटता संबंध दिया गया है। यहां आकृतियों को कठोर पिंडों के रूप में नहीं, बल्कि बहुत लोचदार रबर से बनी वस्तुओं के रूप में माना जाता है, जो निरंतर विरूपण की अनुमति देता है जो उनके गुणात्मक गुणों को संरक्षित करता है।

आकृतियों का एक-से-एक सतत मानचित्रण कहलाता है होमियोमोर्फिज्म. दूसरे शब्दों में, आँकड़े होम्योमॉर्फिक, यदि निरंतर विरूपण द्वारा एक को दूसरे में स्थानांतरित किया जा सकता है।

उदाहरण। निम्नलिखित आंकड़े होमियोमॉर्फिक हैं (विभिन्न समूहों के आंकड़े होमियोमॉर्फिक नहीं हैं), चित्र में दिखाए गए हैं। 2.

1. स्व-प्रतिच्छेदन रहित एक खंड और एक वक्र।

2. वृत्त, वर्ग के अंदर, रिबन।

3. गोला, घन की सतह और चतुष्फलक।

4. वृत्त, दीर्घवृत्त और गांठदार वृत्त।

5. समतल पर एक वलय (एक छेद वाला वृत्त), अंतरिक्ष में एक वलय, दो बार मुड़ी हुई वलय, एक सिलेंडर की पार्श्व सतह।

6. मोबियस स्ट्रिप, यानी। एक बार मुड़ी हुई अंगूठी, और एक तीन बार मुड़ी हुई अंगूठी।

7. टोरस (डोनट) की सतह, एक हैंडल वाला गोला और एक गांठदार टोरस।

8. दो हैंडल वाला एक गोला और दो छेद वाला एक प्रेट्ज़ेल।

में गणितीय विश्लेषणकार्यों का अध्ययन सीमा विधि द्वारा किया जाता है। चर और सीमा बुनियादी अवधारणाएँ हैं।

विभिन्न परिघटनाओं में, कुछ मात्राएँ अपना संख्यात्मक मान बनाए रखती हैं, जबकि अन्य बदल जाती हैं। किसी वेरिएबल के सभी संख्यात्मक मानों के समुच्चय को कहा जाता है इस चर के परिवर्तन की सीमा.

एक चर के व्यवहार करने के विभिन्न तरीकों में से सबसे महत्वपूर्ण वह है जिसमें चर एक निश्चित सीमा तक प्रवृत्त होता है।

लगातार संख्या एबुलाया परिवर्तनशील सीमा, यदि अंतर का निरपेक्ष मान एक्सऔर ए() एक परिवर्तनीय मान को बदलने की प्रक्रिया में बन जाता है एक्सइच्छानुसार छोटा:

"जितना आप चाहें उतना छोटा" का क्या मतलब है? परिवर्तनीय मान एक्ससीमा तक जाता है ए, यदि किसी मनमाने ढंग से छोटी (मनमाने ढंग से छोटी) संख्या के लिए चर के परिवर्तन में ऐसा क्षण हो एक्स, जिससे असमानता कायम रहती है .

सीमा की परिभाषा का एक सरल ज्यामितीय अर्थ है: असमानता मतलब कि एक्सबिंदु के पड़ोस में है ए, वे। अंतराल में .

इस प्रकार, सीमा की परिभाषा दी जा सकती है ज्यामितीय आकार:

संख्या एचर की सीमा है एक्स, यदि किसी मनमाने ढंग से छोटे (मनमाने ढंग से छोटे) के लिए -संख्या का पड़ोस एआप वेरिएबल को बदलने में ऐसा कोई क्षण निर्दिष्ट कर सकते हैं एक्स, जिससे प्रारंभ होकर इसके सभी मान बिंदु के निर्दिष्ट -पड़ोस में आते हैं ए.

टिप्पणी. परिवर्तनीय मान एक्सविभिन्न तरीकों से अपनी सीमा तक पहुंच सकते हैं: इस सीमा से कम (बाईं ओर), अधिक (दाहिनी ओर), सीमा के मूल्य के आसपास उतार-चढ़ाव।

अनुक्रम सीमा

समारोहवह नियम (नियम) कहलाता है जिसके अनुसार प्रत्येक तत्व एक्सकुछ सेट एक्सएक तत्व से मेल खाता है यसेट वाई

फ़ंक्शन को सभी प्राकृतिक संख्याओं के सेट पर परिभाषित किया जा सकता है:। इस फ़ंक्शन को कहा जाता है प्राकृतिक तर्क समारोहया संख्यात्मक क्रम.

चूंकि अनुक्रम, किसी भी अनंत सेट की तरह, गणना द्वारा निर्दिष्ट नहीं किया जा सकता है, इसे एक सामान्य शब्द द्वारा निर्दिष्ट किया जाता है: , अनुक्रम का सामान्य पद कहां है।

असतत चर किसी अनुक्रम का एक सामान्य पद है।

निरंतरता के लिए, "किसी बिंदु पर शुरू करना" शब्द का अर्थ "किसी संख्या पर शुरू करना" है।

संख्या एअनुक्रम की सीमा कहलाती है , यदि किसी मनमाने ढंग से छोटी (मनमाने ढंग से छोटी) संख्या के लिए ऐसी कोई संख्या हो एन, जो संख्या के साथ अनुक्रम के सभी सदस्यों के लिए है एन>एनअसमानता कायम है .

या पर .

ज्यामितीय रूप से, किसी अनुक्रम की सीमा की परिभाषा का अर्थ निम्नलिखित है: किसी भी मनमाने ढंग से छोटे (मनमाने ढंग से छोटे) -संख्या के पड़ोस के लिए एएक संख्या ऐसी है जो अनुक्रम के सभी पदों से अधिक है एन, संख्याएँ, इस क्षेत्र में आती हैं। अनुक्रम के आरंभिक पदों की केवल एक सीमित संख्या पड़ोस के बाहर दिखाई देती है। प्राकृतिक संख्या एनपर निर्भर करता है : .