गणितीय विश्लेषण।

कार्यशाला।

विशेषता में विश्वविद्यालय के छात्रों के लिए:

"राज्य और नगर प्रशासन"

टी.जेड. पावलोवा

कोल्पाशेवो 2008

अध्याय 1. विश्लेषण का परिचय

1.1 कार्य। सामान्य विशेषता

1.2 सीमा का सिद्धांत

1.3 कार्य की निरंतरता

2.1 व्युत्पन्न की परिभाषा

2.4 कार्यों की खोज

2.4.1 पूर्ण कार्य अध्ययन योजना

2.4.2 कार्य अध्ययन उदाहरण

2.4.3. किसी खंड पर किसी फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान

2.5 एल'अस्पताल का नियम

3.1 अनिश्चितकालीन अभिन्न

3.1.1 परिभाषाएं और गुण

3.1.2 समाकलकों की तालिका

3.1.3 एकीकरण के बुनियादी तरीके

3.2 निश्चित समाकलन

3.2.2 निश्चित समाकल की गणना करने की विधियाँ

अध्याय 4. कई चरों के कार्य

4.1 बुनियादी अवधारणाएँ

4.2 कई चरों के कार्यों की सीमा और निरंतरता

4.3.3 कुल अंतर और अनुमानित गणना के लिए इसका अनुप्रयोग

अध्याय 5. शास्त्रीय अनुकूलन के तरीके

6.1 उपयोगिता समारोह।

6.2 उदासीनता की रेखाएं

6.3 बजट सेट

गृहकार्य कार्य

1.1 कार्य। सामान्य विशेषता

वास्तविक संख्याओं के सेट डी पर एक संख्यात्मक फ़ंक्शन परिभाषित किया जाता है यदि चर का प्रत्येक मान चर y के कुछ अच्छी तरह से परिभाषित वास्तविक मान से जुड़ा होता है, जहां डी फ़ंक्शन का डोमेन है।

फ़ंक्शन का विश्लेषणात्मक प्रतिनिधित्व:

स्पष्ट रूप से:;

परोक्ष रूप से:;

पैरामीट्रिक रूप में:

परिभाषा के क्षेत्र में विभिन्न सूत्र:

गुण।

यहां तक ​​कि समारोह:। उदाहरण के लिए, फलन सम है, क्योंकि ...

पुराना फंक्शन: ... उदाहरण के लिए, फ़ंक्शन विषम है, क्योंकि ...

आवधिक कार्य: , जहां टी समारोह की अवधि है,। उदाहरण के लिए, त्रिकोणमितीय कार्य।

मोनोटोनिक फ़ंक्शन। यदि परिभाषा के किसी भी क्षेत्र के लिए - फलन बढ़ रहा है, - घट रहा है। जैसे,-बढ़ना, और-घटाना।

सीमित कार्य। यदि ऐसी कोई संख्या M है। उदाहरण के लिए, कार्य और, चूंकि .

उदाहरण 1. फलनों की परिभाषा का क्षेत्र ज्ञात कीजिए।

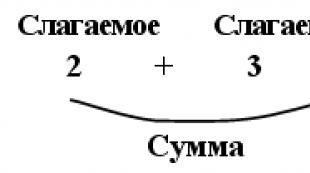
+ 2 – 3 +

1.2 सीमा का सिद्धांत

परिभाषा 1... किसी फ़ंक्शन की सीमा एक संख्या b है यदि किसी (- मनमाने ढंग से छोटी सकारात्मक संख्या) के लिए कोई तर्क का ऐसा मान प्राप्त कर सकता है, जिससे असमानता संतुष्ट हो।

पद:।

परिभाषा 2... पर एक फ़ंक्शन की सीमा एक संख्या बी है यदि किसी के लिए (एक मनमाने ढंग से छोटी सकारात्मक संख्या है) एक सकारात्मक संख्या है जैसे कि असमानता को संतुष्ट करने वाले x के सभी मूल्यों के लिए असमानता है।

पद:।

परिभाषा 3.फ़ंक्शन को या, यदि या के लिए इनफिनिटसिमल कहा जाता है।

गुण।

1. अपरिमित मात्राओं की एक परिमित संख्या का बीजगणितीय योग एक अपरिमित मात्रा होती है।

2. एक परिबद्ध फलन द्वारा एक अपरिमित रूप से छोटी मात्रा का गुणनफल (स्थिर, एक अन्य अपरिमित रूप से छोटी मात्रा) एक अपरिमित रूप से छोटी मात्रा होती है।

3. एक अपरिमित रूप से छोटी मात्रा को एक फलन से विभाजित करने का भागफल जिसकी सीमा शून्येतर है, एक अपरिमित रूप से छोटी मात्रा होती है।

परिभाषा 4.फ़ंक्शन को असीम रूप से बड़ा कहा जाता है, अगर।

गुण।

1. एक फलन द्वारा एक अपरिमित रूप से बड़ी मात्रा का गुणनफल, जिसकी सीमा अशून्य है, एक अपरिमित रूप से बड़ी मात्रा है।

2. अपरिमित रूप से बड़े मान और परिबद्ध फलन का योग अपरिमित रूप से बड़ा मान होता है।

3. एक असीम रूप से बड़ी मात्रा को एक सीमा वाले फलन से विभाजित करने का भागफल एक अपरिमित रूप से बड़ी मात्रा होती है।

प्रमेय।(अपरिमित रूप से छोटी मात्रा और अपरिमित रूप से बड़ी मात्रा के बीच संबंध।) यदि कोई फलन () पर अपरिमित है, तो फलन () पर अपरिमित रूप से बड़ी मात्रा है। और, इसके विपरीत, यदि फलन () पर अपरिमित रूप से बड़ा है, तो फलन () पर अपरिमित रूप से छोटा है।

प्रमेयों को सीमित करें।

1. एक फलन की एक से अधिक सीमा नहीं हो सकती।

2. कई फलनों के बीजीय योग की सीमा इन फलनों की सीमाओं के बीजगणितीय योग के बराबर होती है:

3. कई फलनों के गुणनफल की सीमा इन फलनों की सीमाओं के गुणनफल के बराबर होती है:

4. डिग्री सीमा सीमा की डिग्री के बराबर है:

5. भाजक सीमा मौजूद होने पर भागफल सीमा सीमा के भागफल के बराबर होती है:

.

6. पहली उल्लेखनीय सीमा।

परिणाम:

7. दूसरी उल्लेखनीय सीमा:

परिणाम:

के लिए समतुल्य अन्तर्निहित मान:

सीमा की गणना।

सीमाओं की गणना करते समय, सीमा पर मूल प्रमेय, निरंतर कार्यों के गुण और इन प्रमेयों और गुणों से उत्पन्न होने वाले नियमों का उपयोग किया जाता है।

नियम 1।इस बिंदु पर निरंतर एक फ़ंक्शन के बिंदु पर सीमा को खोजने के लिए, तर्क x के बजाय सीमा चिह्न के तहत फ़ंक्शन में इसके सीमा मान को प्रतिस्थापित करना आवश्यक है।

उदाहरण 2. खोजें

नियम 2.यदि किसी भिन्न की सीमा ज्ञात करते समय हर की सीमा शून्य हो और अंश की सीमा अशून्य हो, तो ऐसे फलन की सीमा होती है।

उदाहरण 3. खोजें

नियम 3.यदि किसी भिन्न की सीमा ज्ञात करते समय हर की सीमा समान हो और अंश की सीमा शून्य से भिन्न हो, तो ऐसे फलन की सीमा शून्य होती है।

उदाहरण 4. खोजें

अक्सर, किसी तर्क के लिए एक सीमा मान के प्रतिस्थापन के परिणामस्वरूप अपरिभाषित अभिव्यक्तियाँ होती हैं जैसे

.

इन मामलों में किसी फलन की सीमा ज्ञात करना अनिश्चितता प्रकटीकरण कहलाता है। अनिश्चितता का खुलासा करने के लिए, सीमा तक जाने से पहले इस अभिव्यक्ति को बदलना आवश्यक है। अनिश्चितताओं को प्रकट करने के लिए विभिन्न तकनीकों का उपयोग किया जाता है।

नियम 4... सबलिमिट फ़ंक्शन को बदलने से प्रकार की अनिश्चितता का पता चलता है, इस प्रकार, अंश और हर में एक कारक का चयन करने के लिए, जिसकी सीमा शून्य है, और, इसके द्वारा अंश को कम करके, भागफल की सीमा का पता लगाएं। ऐसा करने के लिए, अंश और हर को या तो गुणा किया जाता है या अंश और हर से संयुग्मित व्यंजकों से गुणा किया जाता है।

नियम 5.यदि उप-सीमा व्यंजक में त्रिकोणमितीय फलन होते हैं, तो प्रजातियों की अनिश्चितता को उजागर करने के लिए पहली उल्लेखनीय सीमा का उपयोग किया जाता है।

.

नियम 6... फॉर्म की अनिश्चितता को प्रकट करने के लिए, उप-सीमा अंश के अंश और हर को तर्क की उच्चतम डिग्री से विभाजित किया जाना चाहिए और फिर भागफल की सीमा का पता लगाना चाहिए।

संभावित परिणाम:

1) वांछित सीमा अंश और हर के तर्क की उच्चतम शक्तियों पर गुणांक के अनुपात के बराबर है, यदि ये डिग्री समान हैं;

2) सीमा अनंत के बराबर है यदि अंश के तर्क की डिग्री हर के तर्क की डिग्री से अधिक है;

3) सीमा शून्य है यदि अंश के तर्क की डिग्री हर के तर्क की डिग्री से कम है।

ए)

जबसे

डिग्री बराबर हैं, जिसका अर्थ है कि सीमा उच्च डिग्री पर गुणांक के अनुपात के बराबर है, अर्थात। ...

बी)

अंश, हर की डिग्री 1 है, जिसका अर्थ है कि सीमा है

वी)

अंश की घात 1 है, हर की घात है, इसलिए सीमा 0 है।

नियम 7... प्रपत्र की अनिश्चितता को प्रकट करने के लिए, उप-सीमा भिन्न के अंश और हर को संयुग्मी व्यंजक से गुणा किया जाना चाहिए।

उदाहरण 10.

नियम 8... प्रजातियों की अनिश्चितता को उजागर करने के लिए एक दूसरी उल्लेखनीय सीमा और उसके परिणामों का उपयोग किया जाता है।

यह साबित किया जा सकता है कि

उदाहरण 11.

उदाहरण 12.

उदाहरण 13.

नियम 9... अनिश्चितताओं का खुलासा करते समय, जिसके अचेतन कार्य में इनफिनिटिमल होता है, इन इनफिनिट्स की सीमाओं को बदलना आवश्यक है। उनके तुल्य अतिसूक्ष्म तत्वों की सीमा पर।

उदाहरण 14.

उदाहरण 15.

नियम 10. एल अस्पताल का नियम (2.6 देखें)।

1.3 कार्य की निरंतरता

एक फ़ंक्शन एक बिंदु पर निरंतर होता है यदि तर्क के रूप में फ़ंक्शन की सीमा मौजूद है, मौजूद है और इस बिंदु पर फ़ंक्शन के मान के बराबर है।

समतुल्य शर्तें:

1. ;

3.

विराम बिंदु वर्गीकरण:

पहली तरह का ब्रेक

डिस्पोजेबल - एकतरफा सीमाएं मौजूद हैं और बराबर हैं;

घातक (कूदना) - एक तरफा सीमाएँ समान नहीं हैं;

दूसरे प्रकार का असंततता: किसी बिंदु पर किसी फ़ंक्शन की सीमा मौजूद नहीं होती है।

उदाहरण 16. किसी बिंदु पर किसी फलन के असंतत होने की प्रकृति को स्थापित करें या इस बिंदु पर किसी फलन की निरंतरता को सिद्ध करें।

क्योंकि फलन परिभाषित नहीं है, इसलिए यह इस बिंदु पर सतत नहीं है। चूंकि और तदनुसार, , तो पहली तरह की एक हटाने योग्य असंततता का बिंदु है।

बी)

कार्य (ए) की तुलना में, फ़ंक्शन को एक बिंदु पर बढ़ाया जाता है ताकि इसलिए, यह फ़ंक्शन इस बिंदु पर निरंतर है।

जब फ़ंक्शन परिभाषित नहीं होता है;

.

चूंकि एक तरफा सीमाओं में से एक अनंत है, तो यह दूसरी तरह का विराम बिंदु है।

अध्याय 2. विभेदक कलन

2.1 व्युत्पन्न की परिभाषा

व्युत्पन्न परिभाषा

किसी दिए गए फ़ंक्शन का व्युत्पन्न या व्युत्पन्न फ़ंक्शन वृद्धि के अनुपात की सीमा है जब तर्क वृद्धि शून्य हो जाती है:

या .

व्युत्पन्न का यांत्रिक अर्थ किसी फ़ंक्शन के परिवर्तन की दर है। व्युत्पन्न का ज्यामितीय अर्थ फ़ंक्शन के ग्राफ़ के स्पर्शरेखा के झुकाव के कोण का स्पर्शरेखा है:

2.2 विभेदीकरण के लिए बुनियादी नियम

नाम	समारोह	यौगिक
एक स्थिर कारक से गुणा
दो कार्यों का बीजगणितीय योग
दो कार्यों का उत्पाद
निजी दो कार्य
जटिल कार्य

बुनियादी प्राथमिक कार्यों के व्युत्पन्न

पी / पी नं।	समारोह का नाम	कार्य और उसका व्युत्पन्न
1	लगातार
2	ऊर्जा समीकरण विशेष स्थितियां
3	घातांक प्रकार्य विशेष मामला
4	लॉगरिदमिक फ़ंक्शन विशेष मामला
5	त्रिकोणमितीय फलन
6	उलटना त्रिकोणमितीय

बी)

2.3 हायर ऑर्डर डेरिवेटिव्स

किसी फ़ंक्शन का द्वितीय-क्रम व्युत्पन्न

फ़ंक्शन का दूसरा क्रम व्युत्पन्न:

उदाहरण 18.

ए) फ़ंक्शन के दूसरे क्रम के व्युत्पन्न का पता लगाएं।

समाधान। आइए पहले पहले क्रम का अवकलज ज्ञात करें .

आइए हम पहले क्रम के व्युत्पन्न का व्युत्पन्न लें।

उदाहरण 19. फलन का तृतीय-क्रम अवकलज ज्ञात कीजिए।

2.4 कार्यों की खोज

2.4.1 एक पूर्ण कार्य अध्ययन के लिए योजना:

पूर्ण कार्य अध्ययन योजना:

1. प्राथमिक शोध:

डोमेन और मानों की श्रेणी का पता लगाएं;

सामान्य गुणों का पता लगाएं: समता (विषमता), आवधिकता;

निर्देशांक अक्षों के साथ प्रतिच्छेदन के बिंदु खोजें;

स्थिरता के क्षेत्रों का निर्धारण करें।

2. स्पर्शोन्मुख:

ऊर्ध्वाधर अनंतस्पर्शी खोजें यदि;

तिरछे स्पर्शोन्मुख खोजें:।

यदि कोई संख्या है, तो - क्षैतिज स्पर्शोन्मुख।

3. अनुसंधान का उपयोग कर:

महत्वपूर्ण बिंदु खोजें, वो। जिन बिंदुओं पर या मौजूद नहीं है;

वृद्धि के अंतराल को निर्धारित करें, अर्थात्। अंतराल, जिस पर और घटते कार्य -;

एक्स्ट्रेमा का निर्धारण करें: जिन बिंदुओं से गुजरते हुए वह "+" से "-" में बदलते हैं, वे अधिकतम बिंदु हैं, "-" से "+" तक - न्यूनतम।

4. अनुसंधान का उपयोग कर:

उन बिंदुओं का पता लगाएं जिन पर या मौजूद नहीं है;

उत्तलता के क्षेत्रों का पता लगाएं, अर्थात। अंतराल जिस पर अंतराल हैं;

विभक्ति बिंदु खोजें, अर्थात। बिंदु जब से गुजरते हुए संकेत बदलते हैं।

1. अध्ययन के अलग-अलग तत्वों को ग्राफ पर धीरे-धीरे प्लॉट किया जाता है, जैसा कि वे पाए जाते हैं।

2. यदि फ़ंक्शन के ग्राफ़ के निर्माण में कठिनाइयाँ आती हैं, तो फ़ंक्शन के मान कुछ अतिरिक्त बिंदुओं पर पाए जाते हैं।

3. अध्ययन का उद्देश्य कार्य के व्यवहार की प्रकृति का वर्णन करना है। इसलिए, एक सटीक ग्राफ नहीं बनाया गया है, लेकिन इसका सन्निकटन, जिस पर पाए गए तत्व स्पष्ट रूप से इंगित किए गए हैं (चरम, विभक्ति बिंदु, स्पर्शोन्मुख, आदि)।

4. उपरोक्त योजना का कड़ाई से पालन करना आवश्यक नहीं है; यह महत्वपूर्ण है कि फ़ंक्शन के व्यवहार के विशिष्ट तत्वों की अनदेखी न करें।

2.4.2 फ़ंक्शन अध्ययन के उदाहरण:

1)

2) फ़ंक्शन विषम है:

.

3) स्पर्शोन्मुख।

- लंबवत स्पर्शोन्मुख, क्योंकि

तिरछा स्पर्शोन्मुख।

5)

- संक्रमण का बिन्दु।

2) फ़ंक्शन विषम है:

3) स्पर्शोन्मुख: कोई लंबवत स्पर्शोन्मुख नहीं हैं।

झुका हुआ:

- तिरछा स्पर्शोन्मुख

4) - समारोह बढ़ता है।

- संक्रमण का बिन्दु।

इस फ़ंक्शन का योजनाबद्ध आरेख:

2) सामान्य कार्य

3) स्पर्शोन्मुख

- कोई तिरछा स्पर्शोन्मुख नहीं

- क्षैतिज स्पर्शोन्मुख at

- संक्रमण का बिन्दु

इस फ़ंक्शन का योजनाबद्ध आरेख:

2) स्पर्शोन्मुख।

- लंबवत स्पर्शोन्मुख, क्योंकि

- कोई तिरछा स्पर्शोन्मुख नहीं

, - समस्तरीय अनंतस्पर्शी रेखा

इस फ़ंक्शन का योजनाबद्ध आरेख:

2) स्पर्शोन्मुख

- लंबवत स्पर्शोन्मुख पर, चूंकि

- कोई तिरछा स्पर्शोन्मुख नहीं

, - समस्तरीय अनंतस्पर्शी रेखा

3) - प्रत्येक अंतराल पर फ़ंक्शन घटता है।

इस फ़ंक्शन का योजनाबद्ध आरेख:

किसी खंड पर किसी फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान ज्ञात करने के लिए, आप आरेख का उपयोग कर सकते हैं:

1. फलन का अवकलज ज्ञात कीजिए।

2. फलन के उन क्रांतिक बिन्दुओं को ज्ञात कीजिए जिन पर या नहीं है।

3. किसी दिए गए खंड और उसके सिरों से संबंधित महत्वपूर्ण बिंदुओं पर फ़ंक्शन का मान ज्ञात करें और उनमें से सबसे बड़ा और सबसे छोटा चुनें।

उदाहरण। किसी दिए गए खंड पर फ़ंक्शन का सबसे छोटा और सबसे बड़ा मान ज्ञात कीजिए।

25. बीच में

2) - महत्वपूर्ण बिंदु

26. बीच में।

अवकलज मौजूद नहीं है, लेकिन 1 इस अंतराल से संबंधित नहीं है। अंतराल में फ़ंक्शन घटता है, जिसका अर्थ है कि कोई सबसे बड़ा मान नहीं है, लेकिन सबसे छोटा मान है।

2.5 एल'अस्पताल का नियम

प्रमेय। दो अपरिमित या अपरिमित रूप से बड़े फलनों के अनुपात की सीमा उनके व्युत्पन्न (परिमित या अनंत) के अनुपात की सीमा के बराबर होती है, यदि उत्तरार्द्ध संकेतित अर्थ में मौजूद है।

वे। प्रकार की अनिश्चितताओं का खुलासा करते समय या, आप सूत्र का उपयोग कर सकते हैं:

.

27.

अध्याय 3. इंटीग्रल कैलकुलस

3.1 अनिश्चितकालीन अभिन्न

3.1.1 परिभाषाएं और गुण

परिभाषा 1. एक फलन को यदि के लिए प्रतिअवकलन कहते हैं।

परिभाषा 2. किसी फलन f (x) का अनिश्चित समाकल इस फलन के लिए सभी प्रतिअवकलजों का संग्रह है।

पद: , जहां c एक मनमाना स्थिरांक है।

अनिश्चितकालीन अभिन्न गुण

1. अनिश्चितकालीन अभिन्न का व्युत्पन्न:

2. अनिश्चितकालीन अभिन्न का अंतर:

3. अंतर का अनिश्चितकालीन अभिन्न:

4. दो कार्यों के योग (अंतर) का अनिश्चितकालीन अभिन्न:

5. अनिश्चितकालीन अभिन्न के संकेत से परे एक स्थिर कारक को स्थानांतरित करना:

3.1.2 समाकलकों की तालिका

.1.3 एकीकरण के बुनियादी तरीके

1. अनिश्चितकालीन अभिन्न के गुणों का उपयोग करना।

उदाहरण 29.

2. विभेदक चिन्ह के तहत लाना।

उदाहरण 30.

3. परिवर्तनीय प्रतिस्थापन विधि:

ए) इंटीग्रल में प्रतिस्थापन

कहाँ पे - एक ऐसा फ़ंक्शन जो मूल की तुलना में एकीकृत करना आसान है; - कार्य के विपरीत कार्य; फ़ंक्शन का प्रतिपक्षी है।

उदाहरण 31.

बी) फॉर्म के अभिन्न अंग में प्रतिस्थापन:

उदाहरण 32.

उदाहरण 33.

4. भागों द्वारा एकीकरण विधि:

उदाहरण 34.

उदाहरण 35.

आइए हम अभिन्न को अलग से लें

आइए अपने अभिन्न पर वापस जाएं:

3.2 निश्चित समाकलन

3.2.1 एक निश्चित समाकल की अवधारणा और उसके गुण

परिभाषा।मान लीजिए कि कुछ अंतराल पर एक सतत फलन दिया जाता है। आइए उसका ग्राफ बनाते हैं।

बिंदु a और b के बीच भुज अक्ष के एक खंड द्वारा नीचे से एक वक्र द्वारा बाईं और दाईं ओर सीधी रेखाओं से घिरी हुई आकृति को वक्र समलम्बाकार कहा जाता है।

एस - क्षेत्र - घुमावदार ट्रेपोजॉइड।

अंतराल को बिंदुओं से विभाजित करें और प्राप्त करें:

अभिन्न योग:

परिभाषा। निश्चित समाकल समाकलन योग की सीमा है।

निश्चित अभिन्न गुण:

1. अचर गुणनखंड को समाकल चिह्न से निकाला जा सकता है:

2. दो फलनों के बीजीय योग का समाकल इन फलनों के समाकलों के बीजगणितीय योग के बराबर होता है:

3. यदि एकीकरण के खंड को भागों में विभाजित किया जाता है, तो पूरे खंड पर समाकलन उत्पन्न होने वाले प्रत्येक भाग के लिए समाकलन के योग के बराबर होता है, अर्थात, किसी भी ए, बी, सी के लिए:

4. यदि एक खंड पर है, तो

5. एकीकरण की सीमाओं को आपस में बदला जा सकता है, जबकि अभिन्न परिवर्तन के संकेत:

6.

7. बिंदु पर समाकल 0 के बराबर है:

8.

9. ("माध्य के बारे में") मान लीजिए y = f (x) एक पूर्णांकीय फलन है। फिर , जहां f (c) f (x) का औसत मान है:

10. न्यूटन-लीबनिज सूत्र

,

जहां एफ (एक्स) एफ (एक्स) के लिए एंटीडेरिवेटिव है।

3.2.2 निश्चित समाकल की गणना करने की विधियाँ।

1. प्रत्यक्ष एकीकरण

उदाहरण 35.

ए)

बी)

वी)

इ)

2. निश्चित अभिन्न चिह्न के तहत चरों का परिवर्तन .

उदाहरण 36.

2. एक निश्चित अभिन्न में भागों द्वारा एकीकरण .

उदाहरण 37.

ए)

बी)

इ)

3.2.3 एक निश्चित अभिन्न के अनुप्रयोग

विशेषता	समारोह प्रकार	सूत्र
	कार्टेशियन निर्देशांक में
घुमावदार क्षेत्र क्षेत्र	ध्रुवीय निर्देशांक में
घुमावदार ट्रेपोजॉइड क्षेत्र	पैरामीट्रिक रूप में
चाप की लम्बाई	कार्टेशियन निर्देशांक में
चाप की लम्बाई	ध्रुवीय निर्देशांक में
चाप की लम्बाई	पैरामीट्रिक रूप में
शरीर की मात्रा रोटेशन	कार्टेशियन निर्देशांक में
दिए गए अनुप्रस्थ के साथ शरीर का आयतन अनुप्रस्थ काट

उदाहरण 38. रेखाओं से घिरी आकृति के क्षेत्रफल की गणना करें: तथा ।

समाधान:आइए इन कार्यों के रेखांकन के प्रतिच्छेदन बिंदु खोजें। ऐसा करने के लिए, हम कार्यों को समान करते हैं और समीकरण को हल करते हैं

तो, प्रतिच्छेदन बिंदु और।

हम सूत्र का उपयोग करके आकृति का क्षेत्रफल ज्ञात करते हैं

.

हमारे मामले में

उत्तर: क्षेत्रफल (वर्ग इकाई) के बराबर है।

4.1 बुनियादी अवधारणाएँ

परिभाषा। यदि, किसी नियम के अनुसार, एक निश्चित सेट से स्वतंत्र संख्याओं के प्रत्येक जोड़े को चर z के एक या अधिक मान निर्दिष्ट किए जाते हैं, तो चर z को दो चर का एक फ़ंक्शन कहा जाता है।

परिभाषा। फ़ंक्शन z का डोमेन युग्मों का समूह है जिसके लिए फ़ंक्शन z मौजूद है।

दो चरों के फलन का प्रांत निर्देशांक तल ऑक्सी पर बिंदुओं का समुच्चय होता है। z-निर्देशांक को एप्लिकेट कहा जाता है, और फिर फ़ंक्शन को अंतरिक्ष E 3 में किसी सतह के रूप में दर्शाया जाता है। उदाहरण के लिए:

उदाहरण 39. किसी फलन का प्रांत ज्ञात कीजिए।

ए)

दायीं ओर का व्यंजक केवल के लिए अर्थपूर्ण है। इसका मतलब यह है कि इस फ़ंक्शन का डोमेन मूल में केन्द्रित त्रिज्या R के एक वृत्त के अंदर और सीमा पर स्थित सभी बिंदुओं का संग्रह है।

इस फलन का क्षेत्र सीधी रेखाओं के बिंदुओं को छोड़कर, समतल के सभी बिंदु हैं, अर्थात्। समायोजन ध्रुव।

परिभाषा। फ़ंक्शन स्तर रेखाएं रूप के समीकरणों द्वारा वर्णित समन्वय तल पर वक्रों का एक परिवार हैं।

उदाहरण 40. फ़ंक्शन स्तर की रेखाएं खोजें .

समाधान। किसी दिए गए फ़ंक्शन की स्तर रेखाएं समीकरण द्वारा वर्णित विमान में वक्रों का एक परिवार हैं

अंतिम समीकरण त्रिज्या के बिंदु O 1 (1, 1) पर केन्द्रित वृत्तों के परिवार का वर्णन करता है। इस फ़ंक्शन द्वारा वर्णित क्रांति की सतह (पैराबोलॉइड) धुरी से दूर जाने पर "स्टीपर" हो जाती है, जो समीकरण x = 1, y = 1 द्वारा दिया जाता है। (चित्र 4)

4.2 कई चरों के कार्यों की सीमा और निरंतरता।

1. सीमाएं।

परिभाषा। एक संख्या ए को एक फ़ंक्शन की सीमा कहा जाता है क्योंकि एक बिंदु एक बिंदु पर जाता है, यदि प्रत्येक मनमाने ढंग से छोटी संख्या के लिए एक संख्या है जैसे कि किसी भी बिंदु के लिए शर्त सही है, और शर्त ... वे लिखते हैं: .

उदाहरण 41. सीमाएँ ज्ञात कीजिए:

वे। सीमा निर्भर करती है, और इसलिए, यह अस्तित्व में नहीं है।

2. निरंतरता।

परिभाषा। मान लें कि बिंदु फ़ंक्शन की परिभाषा के क्षेत्र से संबंधित है। तब एक फलन को एक बिंदु पर निरंतर कहा जाता है यदि

(1)

इसके अलावा, बिंदु मनमाने ढंग से बिंदु की ओर जाता है।

यदि किसी बिंदु पर शर्त (1) संतुष्ट नहीं होती है, तो इस बिंदु को फलन के असंततता का बिंदु कहा जाता है। यह निम्नलिखित मामलों में हो सकता है:

1) फ़ंक्शन को बिंदु पर परिभाषित नहीं किया गया है।

2) कोई सीमा नहीं है।

3) यह सीमा मौजूद है, लेकिन यह बराबर नहीं है।

उदाहरण 42. निर्धारित करें कि क्या दिया गया फलन बिंदु पर सतत है, यदि।

मिला क्या इसलिए, यह फ़ंक्शन बिंदु पर निरंतर है।

सीमा k पर निर्भर करती है, अर्थात। यह किसी दिए गए बिंदु पर मौजूद नहीं है, जिसका अर्थ है कि इस बिंदु पर फ़ंक्शन में असंतुलन है।

4.3 अनेक चरों के फलनों के अवकलज और अवकलन

4.3.1 पहले आदेश के आंशिक व्युत्पन्न

तर्क x के संबंध में किसी फ़ंक्शन का आंशिक व्युत्पन्न चर y के निश्चित मान के लिए एक चर x के फ़ंक्शन का सामान्य व्युत्पन्न है और इसे दर्शाया गया है:

तर्क y के संबंध में एक फ़ंक्शन का आंशिक व्युत्पन्न चर x के निश्चित मान पर एक चर y के फ़ंक्शन का सामान्य व्युत्पन्न है और इसे निरूपित किया जाता है:

उदाहरण 43. फलनों के आंशिक अवकलज ज्ञात कीजिए।

4.3.2 दूसरे क्रम का आंशिक व्युत्पन्न

दूसरे क्रम के आंशिक व्युत्पन्न पहले क्रम के आंशिक व्युत्पन्न के आंशिक व्युत्पन्न हैं। प्रपत्र के दो चरों के एक फलन के लिए, दूसरे क्रम के चार प्रकार के आंशिक अवकलज संभव हैं:

दूसरे क्रम के आंशिक व्युत्पन्न, जिसमें विभिन्न चरों के संबंध में विभेदन किया जाता है, मिश्रित व्युत्पन्न कहलाते हैं। दो बार अवकलनीय फलन के दूसरे क्रम के मिश्रित अवकलज बराबर होते हैं।

उदाहरण 44. द्वितीय कोटि के आंशिक अवकलज ज्ञात कीजिए।

4.3.3 कुल अंतर और अनुमानित गणना के लिए इसका अनुप्रयोग।

परिभाषा। दो चरों वाले फलन के प्रथम कोटि का अंतर सूत्र द्वारा ज्ञात किया जाता है

.

उदाहरण 45. किसी फलन का कुल अंतर ज्ञात कीजिए।

समाधान। आइए आंशिक डेरिवेटिव खोजें:

.

तर्क x और y के छोटे वेतन वृद्धि के लिए, फ़ंक्शन लगभग dz के बराबर वृद्धि प्राप्त करता है, अर्थात। ...

किसी बिंदु पर किसी फ़ंक्शन का अनुमानित मान ज्ञात करने का सूत्र, यदि किसी बिंदु पर उसका सटीक मान ज्ञात हो:

उदाहरण 46. खोजें .

समाधान। होने देना ,

फिर हम सूत्र का उपयोग करते हैं

उत्तर। .

उदाहरण 47. लगभग गणना करें।

समाधान। आइए एक समारोह पर विचार करें। हमारे पास है

उदाहरण 48. लगभग गणना करें।

समाधान। समारोह पर विचार करें ... हम पाते हैं:

उत्तर। .

4.3.4 निहित कार्य विभेदन

परिभाषा। एक फ़ंक्शन को निहित कहा जाता है यदि यह एक समीकरण द्वारा दिया जाता है जो z के संबंध में हल करने योग्य नहीं है।

ऐसे फ़ंक्शन के आंशिक व्युत्पन्न सूत्रों द्वारा पाए जाते हैं:

उदाहरण 49. समीकरण द्वारा दिए गए फलन z का आंशिक अवकलज ज्ञात कीजिए .

समाधान।

परिभाषा। एक फ़ंक्शन को निहित कहा जाता है यदि यह एक समीकरण द्वारा दिया जाता है जो y के संबंध में हल करने योग्य नहीं है।

ऐसे फ़ंक्शन का व्युत्पन्न सूत्र द्वारा पाया जाता है:

.

उदाहरण 50. इन फलनों के अवकलज ज्ञात कीजिए।

5.1 अनेक चरों वाले फलन का स्थानीय चरम सीमा

परिभाषा 1. एक फलन का एक बिंदु पर अधिकतम होता है यदि

परिभाषा 2. एक फ़ंक्शन का एक बिंदु पर न्यूनतम होता है यदि सभी बिंदुओं के लिए पर्याप्त रूप से बिंदु के करीब और उससे अलग।

एक चरम के लिए एक आवश्यक शर्त। यदि कोई फ़ंक्शन किसी बिंदु पर चरम पर पहुंच जाता है, तो फ़ंक्शन का आंशिक व्युत्पन्न गायब हो जाता है या इस बिंदु पर मौजूद नहीं होता है।

जिन बिंदुओं पर आंशिक व्युत्पन्न गायब हो जाते हैं या मौजूद नहीं होते हैं उन्हें महत्वपूर्ण कहा जाता है।

एक चरम का पर्याप्त संकेत। फ़ंक्शन को महत्वपूर्ण बिंदु के कुछ पड़ोस में परिभाषित करें और इस बिंदु पर निरंतर दूसरे क्रम के आंशिक डेरिवेटिव हैं

1) बिंदु पर एक स्थानीय अधिकतम है, यदि और;

2) बिंदु पर एक स्थानीय न्यूनतम है, यदि और;

3) यदि बिंदु पर स्थानीय चरम सीमा नहीं है;

दो चर के एक समारोह के चरम के लिए अध्ययन की योजना।

1. फ़ंक्शन के आंशिक व्युत्पन्न खोजें: और।

2. समीकरणों की प्रणाली को हल करें और फ़ंक्शन के महत्वपूर्ण बिंदु खोजें।

3. दूसरे क्रम के आंशिक व्युत्पन्न खोजें, महत्वपूर्ण बिंदुओं पर उनके मूल्यों की गणना करें और पर्याप्त स्थिति का उपयोग करके, एक्स्ट्रेमा की उपस्थिति के बारे में निष्कर्ष निकालें।

4. फलन का चरम ज्ञात कीजिए।

उदाहरण 51. किसी फलन का चरम ज्ञात कीजिए .

1) आंशिक व्युत्पन्न खोजें।

2) समीकरणों के निकाय को हल करें

4) दूसरे क्रम के आंशिक व्युत्पन्न और महत्वपूर्ण बिंदुओं पर उनके मूल्यों का पता लगाएं:। बिंदु पर हमें मिलता है:

इसलिए, बिंदु पर कोई चरम सीमा नहीं है। बिंदु पर हमें मिलता है:

इसलिए, बिंदु पर न्यूनतम है।

5.2 वैश्विक चरम सीमा (फ़ंक्शन का उच्चतम और निम्नतम मान)

कई चरों के एक फ़ंक्शन के सबसे बड़े और सबसे छोटे मान, कुछ बंद सेट पर निरंतर, चरम बिंदुओं पर या सेट की सीमा पर प्राप्त किए जाते हैं।

उच्चतम और निम्नतम मूल्यों को खोजने की योजना।

1) क्षेत्र के अंदर स्थित महत्वपूर्ण बिंदुओं का पता लगाएं, इन बिंदुओं पर फ़ंक्शन के मान की गणना करें।

2) क्षेत्र की सीमा पर कार्य का अन्वेषण करें; यदि सीमा में कई अलग-अलग रेखाएँ हैं, तो प्रत्येक साइट के लिए अलग-अलग अध्ययन किया जाना चाहिए।

3) फ़ंक्शन के प्राप्त मूल्यों की तुलना करें और सबसे बड़ा और सबसे छोटा चुनें।

उदाहरण 52. एक आयत में सबसे बड़े और सबसे छोटे फ़ंक्शन मान ज्ञात करें।

समाधान। 1) फ़ंक्शन के महत्वपूर्ण बिंदु खोजें, इसके लिए हम आंशिक व्युत्पन्न पाते हैं: और समीकरणों की प्रणाली को हल करते हैं:

महत्वपूर्ण बिंदु ए प्राप्त किया। परिणामी बिंदु निर्दिष्ट क्षेत्र के अंदर स्थित है,

क्षेत्र की सीमा चार खंडों से बनी है: और। प्रत्येक खंड पर फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान ज्ञात करें।

4) प्राप्त परिणामों की तुलना कीजिए और ज्ञात कीजिए कि बिन्दुओं पर .

अध्याय 6. उपभोक्ता विकल्प मॉडल

हम मान लेंगे कि n अलग-अलग सामान हैं। फिर माल के एक निश्चित सेट को n-आयामी वेक्टर द्वारा दर्शाया जाएगा , i-वें उत्पाद की मात्रा कहां है। वस्तु X के सभी समुच्चयों के समुच्चय को स्थान कहते हैं।

व्यक्तिगत उपभोक्ता की पसंद एक वरीयता संबंध की विशेषता है: यह माना जाता है कि उपभोक्ता किन्हीं दो सेटों के बारे में कह सकता है, जो अधिक वांछनीय है, या वह उनके बीच अंतर नहीं देखता है। वरीयता संबंध सकर्मक है: यदि एक सेट एक सेट के लिए बेहतर है, और एक सेट एक सेट के लिए बेहतर है, तो एक सेट एक सेट के लिए बेहतर है। हम मानेंगे कि उपभोक्ता व्यवहार पूरी तरह से व्यक्तिगत उपभोक्ता के स्वयंसिद्ध द्वारा वर्णित है: प्रत्येक व्यक्तिगत उपभोक्ता अपनी वरीयताओं की प्रणाली के आधार पर खपत, खरीद आदि के बारे में निर्णय लेता है।

6.1 उपयोगिता समारोह

उपभोक्ता समुच्चय X के समुच्चय पर, फलन परिभाषित होता है , जिसका उपभोक्ता सेट पर मूल्य इस सेट के लिए व्यक्ति के उपभोक्ता के अनुमान के बराबर है। फ़ंक्शन को उपभोक्ता का उपयोगिता फ़ंक्शन या उपभोक्ता का वरीयता फ़ंक्शन कहा जाता है। वे। प्रत्येक उपभोक्ता का अपना उपयोगिता कार्य होता है। लेकिन उपभोक्ताओं के पूरे समूह को उपभोक्ताओं के कुछ वर्गों (उम्र, संपत्ति की स्थिति, आदि) में विभाजित किया जा सकता है और प्रत्येक वर्ग को कुछ, शायद, औसत उपयोगिता कार्य सौंपा जा सकता है।

इस प्रकार, एक फ़ंक्शन एक उपभोक्ता अनुमान या किसी दिए गए सेट को खरीदते समय किसी व्यक्ति की जरूरतों की संतुष्टि का स्तर है। यदि एक सेट किसी दिए गए व्यक्ति के लिए एक सेट के लिए बेहतर है, तो।

उपयोगिता समारोह गुण।

1.

उपयोगिता फलन के प्रथम आंशिक अवकलज को उत्पादों की सीमांत उपयोगिता कहा जाता है। यह इस संपत्ति से निम्नानुसार है कि एक उत्पाद की खपत में वृद्धि जबकि अन्य उत्पादों की खपत अपरिवर्तित रहती है, उपभोक्ता मूल्यांकन में वृद्धि होती है। वेक्टर फ़ंक्शन का ग्रेडिएंट है, यह फ़ंक्शन की सबसे बड़ी वृद्धि की दिशा को दर्शाता है। किसी फ़ंक्शन के लिए, इसका ग्रेडिएंट उत्पादों की सीमांत उपयोगिताओं का एक सदिश है।

2.

वे। किसी भी वस्तु की सीमांत उपयोगिता बढ़ती हुई खपत के साथ घटती जाती है।

3.

वे। प्रत्येक उत्पाद की सीमांत उपयोगिता दूसरे उत्पाद की मात्रा के साथ बढ़ती है।

कुछ प्रकार के उपयोगिता कार्य।

1) नियोक्लासिकल:।

2) द्विघात: जहां मैट्रिक्स नकारात्मक निश्चित है और के लिये ।

3) लॉगरिदमिक फ़ंक्शन:।

6.2 उदासीनता की रेखाएं

अनुप्रयुक्त समस्याओं और उपभोक्ता की पसंद के मॉडल में, दो वस्तुओं के सेट के एक विशेष मामले का अक्सर उपयोग किया जाता है, अर्थात। जब उपयोगिता फलन दो चरों पर निर्भर करता है। उदासीनता की रेखा उपभोक्ता सेटों को जोड़ने वाली एक रेखा है जिसमें व्यक्ति की जरूरतों की संतुष्टि का समान स्तर होता है। संक्षेप में, उदासीनता की रेखाएँ कार्य के स्तर की रेखाएँ हैं। उदासीनता रेखा समीकरण: .

उदासीनता रेखाओं के मूल गुण।

1. उदासीनता की रेखाएं, आवश्यकताओं की संतुष्टि के विभिन्न स्तरों के अनुरूप, स्पर्श या प्रतिच्छेद नहीं करती हैं।

2. उदासीनता की रेखाएँ घटती हैं।

3. उदासीनता रेखाएँ नीचे की ओर उत्तल होती हैं।

संपत्ति 2 का तात्पर्य एक महत्वपूर्ण अनुमानित समानता से है।

यह अनुपात दर्शाता है कि व्यक्ति को अपनी आवश्यकताओं की संतुष्टि के स्तर को बदले बिना एक इकाई द्वारा पहले उत्पाद की खपत को कम (बढ़ते) करते हुए दूसरे उत्पाद की खपत में कितना वृद्धि (कमी) करनी चाहिए। अनुपात को दूसरे उत्पाद द्वारा पहले उत्पाद के प्रतिस्थापन की दर कहा जाता है, और मूल्य को दूसरे उत्पाद द्वारा पहले उत्पाद के प्रतिस्थापन की सीमांत दर कहा जाता है।

उदाहरण 53. यदि पहली वस्तु की सीमांत उपयोगिता 6 है, और दूसरी - 2, तो पहली वस्तु की खपत में एक इकाई की कमी के साथ, आपको दूसरी वस्तु की खपत में 3 इकाई की वृद्धि करने की आवश्यकता है संतुष्टि का समान स्तर।

6.3 बजट सेट

होने देना - n उत्पादों के एक सेट के लिए कीमतों का वेक्टर; I - एक व्यक्ति की आय, जिसे वह उत्पादों के एक सेट की खरीद पर खर्च करने को तैयार है। दी गई कीमतों पर I से अधिक लागत वाली वस्तुओं के सेट को बजट सेट B कहा जाता है। इसके अलावा, लागत I के सेट को बजट सेट B की सीमा G कहा जाता है। सेट बी सीमा जी और प्राकृतिक प्रतिबंधों से घिरा है।

बजट सेट को असमानताओं की एक प्रणाली द्वारा वर्णित किया गया है:

दो वस्तुओं के एक सेट के मामले में, बजट सेट बी (चित्र 1) समन्वय प्रणाली में एक त्रिकोण है, जो समन्वय अक्ष और एक सीधी रेखा से घिरा है।

6.4 उपभोक्ता मांग सिद्धांत

खपत के सिद्धांत में, यह माना जाता है कि उपभोक्ता हमेशा अपनी उपयोगिता को अधिकतम करने का प्रयास करता है और उसके लिए एकमात्र प्रतिबंध सीमित आय I है, जिसे वह माल के एक सेट की खरीद पर खर्च कर सकता है। सामान्य तौर पर, उपभोक्ता की पसंद की समस्या (बाजार में तर्कसंगत उपभोक्ता व्यवहार की समस्या) निम्नानुसार तैयार की जाती है: एक उपभोक्ता सेट खोजें , जो किसी दिए गए बजट बाधा के लिए अपने उपयोगिता कार्य को अधिकतम करता है। इस समस्या का गणितीय मॉडल:

दो उत्पादों के एक सेट के मामले में:

ज्यामितीय रूप से, इस समस्या का समाधान बजटीय सेट G की सीमा और उदासीनता की रेखा के बीच संपर्क बिंदु है।

समीकरणों की प्रणाली को हल करने के लिए इस समस्या का समाधान कम किया गया है:

(1)

इस प्रणाली का समाधान उपभोक्ता की पसंद की समस्या का समाधान है।

उपभोक्ता की पसंद की समस्या के समाधान को मांग बिंदु कहा जाता है। यह मांग बिंदु कीमतों और आय I पर निर्भर करता है। यानी। मांग बिंदु मांग का एक कार्य है। बदले में, मांग फ़ंक्शन n फ़ंक्शन का एक सेट है, जिनमें से प्रत्येक तर्क पर निर्भर करता है:

इन कार्यों को संबंधित वस्तुओं के मांग फलन कहा जाता है।

उदाहरण 54। बाजार में दो वस्तुओं के एक सेट के लिए, उनके लिए ज्ञात मूल्य और आय I, मांग कार्यों का पता लगाएं यदि उपयोगिता फ़ंक्शन का रूप है .

समाधान। आइए उपयोगिता फ़ंक्शन को अलग करें:

.

प्राप्त अभिव्यक्तियों को (1) में प्रतिस्थापित करें और समीकरणों की प्रणाली प्राप्त करें:

इस मामले में, प्रत्येक उत्पाद का खर्च उपभोक्ता की आय का आधा होगा, और खरीदे गए उत्पाद की राशि उस पर खर्च की गई राशि के बराबर होती है, जो उत्पाद की कीमत से विभाजित होती है।

उदाहरण 55। मान लीजिए कि उपयोगिता पहले अच्छे के लिए कार्य करती है, दूसरी,

पहले उत्पाद की कीमत, दूसरे की कीमत। आय। उपयोगिता को अधिकतम करने के लिए उपभोक्ता को कितना खरीदना चाहिए?

समाधान। आइए हम उपयोगिता कार्यों के व्युत्पन्न खोजें, उन्हें सिस्टम (1) में प्रतिस्थापित करें और इसे हल करें:

उपयोगिता को अधिकतम करने के मामले में माल का यह सेट उपभोक्ता के लिए इष्टतम है।

परीक्षण एक अलग नोटबुक में रिकॉर्ड बुक नंबर के अंतिम अंक द्वारा चुने गए विकल्प के अनुसार किया जाना चाहिए। प्रत्येक समस्या में एक शर्त, एक विस्तृत समाधान और एक निष्कर्ष होना चाहिए।

1. पथरी का परिचय

कार्य 1. फ़ंक्शन का डोमेन खोजें।

5.

समस्या 2. फलनों की सीमाएँ ज्ञात कीजिए।

.

कार्य 3. फ़ंक्शन के विराम बिंदु खोजें और उनके प्रकार का निर्धारण करें।

1. 2. 3.

अध्याय 2. एक चर के फलन का विभेदक कलन

कार्य 4. इन कार्यों के व्युत्पन्न खोजें।

1.ए); बी) सी) वाई =;

डी) वाई = एक्स 6 + + + 5; ई) वाई = एक्स टीजी एक्स + एलएन पाप एक्स + ई 3x;

च) y = 2 x - चाप x.

2.ए) ; बी) वाई =; सी) वाई =; डी) वाई = एक्स 2 - + 3; ई) वाई = ई कॉस; च) वाई =।

3.ए) वाई = एलएनएक्स; बी) वाई =; सी) वाई = एलएन;

4. ए) वाई =; बी) वाई = (ई 5 एक्स - 1) 6; सी) वाई =; डी) वाई =; ई) वाई = एक्स 8 ++ + 5; च) y = 3 x - चाप x.

5.ए) वाई = 2x 3 - + ई एक्स; बी) वाई =; सी) वाई =;

डी) वाई =; ई) वाई = 2 कॉस; च) वाई =।

6.ए) वाई = एलएनएक्स; बी) वाई =; सी) वाई = एलएन;

डी) वाई =; ई) वाई = एक्स 7 + + 1; च) वाई = 2.

7.ए) ; बी) वाई =; सी) वाई =; डी) वाई = एक्स 2 + xsinx +; ई) वाई = ई कॉस; च) वाई =।

8. ए) वाई =; बी) वाई = (3 एक्स - 4) 6; सी) वाई = सिंघ;

डी) वाई = 3x 4 - - 9+ 9; ई) वाई =;

च) y = x 2 + चाप x - x पर।

9.ए); बी) ; सी) वाई =; डी) वाई = 5 पाप 3 एक्स; ई) वाई = एक्स 3 - - 6+ 3; च) वाई = 4x 4 + एलएन।

10:00 पूर्वाह्न) बी) वाई =; सी) वाई = (3 एक्स - 4) 6; डी) वाई =; ई) वाई = एक्स 2 - एक्स; च) y = ई पाप 3 x + 2.

टास्क 5. फ़ंक्शन की जांच करें और उसका ग्राफ बनाएं।

1. ए) बी) सी)।

2.ए) बी) वी) ।

3.ए) बी) वी) ।

4.बी) वी)

5.ए) बी) वी) ।

6.ए) बी) वी) ।

7. ए) बी) सी)।

8. ए) बी) सी)।

9.ए) बी) सी)।

10. ए) बी) वी) ।

कार्य 6. किसी दिए गए खंड पर फ़ंक्शन का सबसे बड़ा और सबसे छोटा मान ज्ञात करें।

1. .

3. .

6. .

8. .

9. .

10. .

अध्याय 3. इंटीग्रल कैलकुलस

समस्या 7. अनिश्चितकालीन समाकल ज्ञात कीजिए।

1.ए) बी);

2.ए) ; बी) सी) डी)।

4. जी)

5.ए) ; बी); वी) ; जी)।

6.ए) ; बी); वी); जी)

7.ए) ; बी) ; वी) ; जी)

8.ए) ; बी); वी) ; जी) ।

9.ए) ; बी) सी); जी)।

10:00 पूर्वाह्न) बी) वी) ; जी) ।

समस्या 8. निश्चित समाकलों की गणना कीजिए।

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

समस्या 9. अनुचित समाकल ज्ञात कीजिए या सिद्ध कीजिए कि वे विचलन करते हैं।

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

समस्या 10. वक्रों से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए

1. .2. .

5. 6.

7. , .8..

10. , .

अध्याय 4. अनेक चरों वाले फलन का अवकलन कलन।

कार्य 11. फ़ंक्शन का डोमेन ढूंढें (ड्राइंग में दिखाएं)।

समस्या 12. के लिए फलन की निरंतरता की जाँच करें

समस्या 13. एक परोक्ष रूप से परिभाषित फलन का अवकलज ज्ञात कीजिए।

समस्या 14. लगभग गणना करें

1.ए); बी) ; वी)

2.ए) ; बी); वी) .

3.ए) ; बी) ; वी) ।

4.ए) ; बी) ; वी) ।

5. ए); बी) ; वी) ।

6. ए); बी); वी) ।

7. ए); बी) ; वी) ।

8.ए); बी) ; वी)

9.ए) ; बी); वी) .

10. ए); बी) ; वी)

समस्या 15. एक्स्ट्रेमा के लिए कार्य की जाँच करें।

7. .

8. .

9. .

10. .

समस्या 16. दिए गए बंद क्षेत्र में फलन का सबसे बड़ा और सबसे छोटा मान ज्ञात कीजिए।

1. आयत में

2.

3. आयत में

4.एक परवलय से घिरे क्षेत्र में

और एब्सिस्सा।

5.वर्ग

6. निर्देशांक अक्षों और एक सीधी रेखा से घिरे त्रिभुज में

7. निर्देशांक अक्षों और एक सीधी रेखा से घिरे त्रिभुज में

8. निर्देशांक अक्षों और एक सीधी रेखा से घिरे त्रिभुज में

9.एक परवलय से घिरे क्षेत्र में

और एब्सिस्सा।

10.एक परवलय से घिरे क्षेत्र में

और एब्सिस्सा।

मुख्य

1. एम.एस. क्रैसस, बी.पी. चुप्रिनोव। गणित के बुनियादी सिद्धांत और आर्थिक शिक्षा में इसका अनुप्रयोग: पाठ्यपुस्तक। - चौथा संस्करण।, आईएसपी। - एम।: डेलो, 2003।

2. एम.एस. क्रैसस, बी.पी. चुप्रिनोव। आर्थिक विशिष्टताओं के लिए गणित: पाठ्यपुस्तक। - चौथा संस्करण।, आईएसपी। - एम।: डेलो, 2003।

3. एम.एस. क्रैसस, बी.पी. चुप्रिनोव। अर्थशास्त्र में स्नातक की डिग्री के लिए गणित। पाठ्यपुस्तक। - चौथा संस्करण।, आईएसपी। - एम।: डेलो, 2005।

4. अर्थशास्त्रियों के लिए उच्च गणित। विश्वविद्यालयों के लिए पाठ्यपुस्तक / एन.एस. क्रेमर, बी.ए. पुटको, आई.एम. त्रिशिन, एम.एन. फ्राइडमैन; ईडी। प्रो एन.एस. क्रेमर, - दूसरा संस्करण, संशोधित। और जोड़। - एम: यूनिटी, 2003।

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman MN आर्थिक विशिष्टताओं के लिए उच्च गणित। पाठ्यपुस्तक और कार्यशाला (भाग I और II) / एड। प्रो एन.एस. क्रेमर, - दूसरा संस्करण, संशोधित। और जोड़। - एम: उच्च शिक्षा, 2007। - 893पी। - (विज्ञान की बुनियादी बातों)

6. डैंको पी.ई., पोपोव ए.जी., कोज़ेवनिकोवा टी.वाईए। अभ्यास और समस्याओं में उच्च गणित। एम. हाई स्कूल। 1999.

अतिरिक्त

1. आई.आई. बावरिन, वी.एल. नाविक। उच्च गणित। "व्लाडोस ह्यूमैनिटेरियन पब्लिशिंग सेंटर", 2002।

2. आई.ए. जैतसेव। उच्च गणित। "हाई स्कूल", 1998।

3. ए.एस. सोलोडोवनिकोव, वी.ए. बाबयत्सेव, ए.वी. ब्रायलोव, आई. जी. शंद्रा। अर्थशास्त्र में गणित / दो भागों में /। एम. वित्त और सांख्यिकी। 1999.

छात्रों के लिए चिकित्सा, बाल चिकित्सा, दंत चिकित्सा

और निवारक दवा संकाय

प्रयोगशाला के काम के लिए

"गणितीय विश्लेषण की बुनियादी अवधारणाएं"

1. विषय की वैज्ञानिक और पद्धतिगत पुष्टि:

व्युत्पन्न और विभेदक अवधारणाएँ गणितीय विश्लेषण की मूल अवधारणाओं में से एक हैं। भौतिकी और गणित (गति, त्वरण, दबाव, आदि का पता लगाना) में कई समस्याओं को हल करते समय डेरिवेटिव की गणना करना आवश्यक है। व्युत्पन्न की अवधारणा का महत्व, विशेष रूप से, इस तथ्य से निर्धारित होता है कि किसी फ़ंक्शन का व्युत्पन्न इस फ़ंक्शन के परिवर्तन की दर को दर्शाता है जब इसका तर्क बदलता है।

अंतर का उपयोग अनुमानित गणना करने के साथ-साथ त्रुटियों का अनुमान लगाने के लिए संभव बनाता है।

व्युत्पन्न और कार्यों के अंतर और उनके आवेदन खोजने के तरीके अंतर कैलकुस की मुख्य समस्या का गठन करते हैं। गति की गति की गणना करने और वक्र के स्पर्शरेखा के कोण को खोजने की समस्या के निर्माण के संबंध में व्युत्पन्न की अवधारणा की आवश्यकता उत्पन्न होती है। उलटा समस्या भी संभव है: गति द्वारा तय की गई दूरी निर्धारित करें, और स्पर्शरेखा ढलान के स्पर्शरेखा द्वारा संबंधित कार्य खोजें। यह उलटा समस्या अनिश्चितकालीन अभिन्न की अवधारणा की ओर ले जाती है।

एक निश्चित समाकलन की अवधारणा का उपयोग कई व्यावहारिक समस्याओं में किया जाता है, विशेष रूप से, समतल आकृतियों के क्षेत्रों की गणना करने, चर बल द्वारा किए गए कार्य की गणना करने और किसी फलन का औसत मान ज्ञात करने की समस्याओं में।

विभिन्न भौतिक, रासायनिक, जैविक प्रक्रियाओं और घटनाओं के गणितीय विवरण में, अक्सर ऐसे समीकरणों का उपयोग किया जाता है जिनमें न केवल अध्ययन के तहत मात्राएँ होती हैं, बल्कि इन मात्राओं के विभिन्न आदेशों के उनके व्युत्पन्न भी होते हैं। उदाहरण के लिए, बैक्टीरिया के गुणन के नियम के सरलतम संस्करण के अनुसार, प्रजनन की दर एक निश्चित समय में बैक्टीरिया की संख्या के समानुपाती होती है। यदि इस मात्रा को एन (टी) द्वारा निरूपित किया जाता है, तो व्युत्पन्न के भौतिक अर्थ के अनुसार, बैक्टीरिया के प्रजनन की दर एन (टी) का व्युत्पन्न है, और उपरोक्त कानून के आधार पर, हम लिख सकते हैं अनुपात एन "(टी) = के एन, जहां के> 0 - आनुपातिकता का गुणांक परिणामी समीकरण बीजगणितीय नहीं है, क्योंकि इसमें न केवल अज्ञात फ़ंक्शन एन (टी) शामिल है, बल्कि इसका प्रथम-क्रम व्युत्पन्न भी है।

2. संक्षिप्त सिद्धांत:

1. व्युत्पन्न की अवधारणा की ओर ले जाने वाली समस्याएं

1. किसी भौतिक बिंदु का वेग v ज्ञात करने की समस्या... मान लीजिए कि कोई भौतिक बिंदु सरल रेखीय गति करता है। एक पल में टी 1 बिंदु स्थिति में है एम 1. एक पल में टी 2 गर्भवती एम 2 . आइए हम अंतराल को निरूपित करें एम 1 , एम 2 आर - पार एस; टी 2 - टी 1 = t... मान को गति की औसत गति कहा जाता है। किसी स्थान पर किसी बिंदु की तात्क्षणिक चाल ज्ञात करने के लिए एम 1 ज़रूरी tशून्य की ओर प्रवृत्त। गणितीय रूप से, इसका अर्थ है कि

, (1)

इस प्रकार, एक भौतिक बिंदु के तात्कालिक वेग को खोजने के लिए, फ़ंक्शन के वेतन वृद्धि के अनुपात की सीमा की गणना करना आवश्यक है एसतर्क की वृद्धि के लिए बशर्ते कि t → 0.

2. किसी फ़ंक्शन के ग्राफ़ पर स्पर्शरेखा के झुकाव के कोण को खोजने की समस्या.

चित्र .1

किसी फ़ंक्शन के ग्राफ़ पर विचार करें वाई = एफ (एक्स)।झुकाव का कोण क्या है
बिंदु पर स्पर्शरेखा एम 1 ? बिंदु पर एम 1 फ़ंक्शन के ग्राफ़ के लिए एक स्पर्शरेखा बनाएं। ग्राफ पर एक मनमाना बिंदु चुनें एम 2 और एक छेदक ड्रा करें। वह अक्ष की ओर झुका हुआ है ओहएक कोण पर α 1 ... विचार करना एम 1 एम 2 ए:

, (2)

अगर बिंदु एम 1 फिक्स, और पॉइंट एम 2 के करीब ले जाएँ एम 1 , फिर secant एम 1 एम 2 बिंदु पर फ़ंक्शन के ग्राफ़ के स्पर्शरेखा पर जाएगा एम 1 और आप लिख सकते हैं:

, (3)

इस प्रकार, यदि तर्क वृद्धि शून्य हो जाती है, तो तर्क वृद्धि के लिए फ़ंक्शन वृद्धि के अनुपात की सीमा की गणना करना आवश्यक है।

फ़ंक्शन y = f (x) की वृद्धि y के अनुपात की सीमा किसी दिए गए बिंदु x पर तर्क Δx की वृद्धि के लिए है 0 जैसा कि x शून्य की ओर प्रवृत्त होता है, किसी दिए गए बिंदु पर फलन का अवकलज कहलाता है।

व्युत्पन्न संकेतन: वाई ", एफ" (एक्स), ... परिभाषा से

, (4)

जहां Δx = x 2 -x 1 तर्क की वृद्धि है (तर्क के दो बाद के पर्याप्त रूप से करीबी मूल्यों के बीच का अंतर), y = y 2 -y 1 फ़ंक्शन की वृद्धि है (मानों के बीच का अंतर तर्क के इन मूल्यों के अनुरूप कार्य)।

किसी दिए गए फलन का अवकलज ज्ञात करना उसका कहलाता है भेदभाव... मुख्य प्राथमिक कार्यों का अंतर तैयार किए गए सूत्रों (तालिका देखें) के साथ-साथ उपयोग करके किया जाता है नियमों:

एक बीजीय योग का व्युत्पन्न फ़ंक्शन इन कार्यों के डेरिवेटिव के योग के बराबर है:

(तुम+ υ )"= तुम" + υ "

2. दो कार्यों के उत्पाद का व्युत्पन्न पहले के व्युत्पन्न द्वारा दूसरे फ़ंक्शन के उत्पादों के योग के बराबर होता है और दूसरे के व्युत्पन्न द्वारा पहला कार्य:

(यूυ ) "= यू"υ + यूυ "

3. भागफल का व्युत्पन्न दो कार्यों का अंश एक अंश के बराबर होता है, जिसका अंश अंश के व्युत्पन्न द्वारा हर के उत्पादों और हर के व्युत्पन्न द्वारा अंश के बीच का अंतर होता है, और हर हर का वर्ग होता है:

व्युत्पन्न का भौतिक अर्थ. (4) और (1) की तुलना का तात्पर्य है कि किसी भौतिक बिंदु की सीधी गति का तात्कालिक वेग समय पर उसके निर्देशांक की निर्भरता के व्युत्पन्न के बराबर है।

किसी फ़ंक्शन के व्युत्पन्न का सामान्य अर्थ यह है कि यह विशेषता है कार्य परिवर्तन की दर (तीव्रता)किसी दिए गए तर्क परिवर्तन के लिए। भौतिक, रासायनिक और अन्य प्रक्रियाओं की गति, उदाहरण के लिए, शरीर के ठंडा होने की दर, रासायनिक प्रतिक्रिया की दर, बैक्टीरिया के प्रजनन की दर आदि को भी व्युत्पन्न का उपयोग करके व्यक्त किया जाता है।

व्युत्पन्न का ज्यामितीय अर्थ।फलन के ग्राफ पर खींची गई स्पर्श रेखा के झुकाव कोण के स्पर्शरेखा के परिमाण को गणित में कहा जाता है स्पर्शरेखा का ढलान।

किसी बिंदु पर अवकलनीय फलन के ग्राफ़ की स्पर्शरेखा का ढलान संख्यात्मक रूप से इस बिंदु पर फलन के अवकलज के बराबर होता है।

इस कथन को कहा जाता है व्युत्पन्न का ज्यामितीय अर्थ।

लेख की सामग्री

गणितीय विश्लेषण,गणित की एक शाखा जो परिवर्तन की विभिन्न प्रक्रियाओं के मात्रात्मक अध्ययन के लिए तरीके प्रदान करती है; परिवर्तन की दर (डिफरेंशियल कैलकुलस) के अध्ययन और वक्रों की लंबाई, क्षेत्रों और घुमावदार आकृति और सतहों (इंटीग्रल कैलकुलस) से बंधे हुए आंकड़ों के आयतन के निर्धारण से संबंधित है। गणितीय विश्लेषण की समस्याओं के लिए, यह विशेषता है कि उनका समाधान एक सीमा की अवधारणा से जुड़ा है।

गणितीय विश्लेषण 1665 में आई. न्यूटन द्वारा और (लगभग 1675) स्वतंत्र रूप से जी. लीबनिज द्वारा शुरू किया गया था, हालांकि महत्वपूर्ण प्रारंभिक कार्य आई. केपलर (1571-1630), एफ. कैवेलियरी (1598-1647), पी. फर्मा द्वारा किया गया था। (1601-1665), जे. वालिस (1616-1703) और आई. बैरो (1630-1677)।

प्रस्तुति को अधिक जीवंत बनाने के लिए हम रेखांकन की भाषा का सहारा लेंगे। इसलिए, पाठक को इस लेख को पढ़ने से पहले विश्लेषणात्मक ज्यामिति लेख पर एक नज़र डालने में मदद मिल सकती है।

अंतर कलन

स्पर्शरेखा।

अंजीर में। 1 वक्र का एक टुकड़ा दिखाता है आप = 2एक्स – एक्स 2, के बीच संपन्न हुआ एक्स= -1 और एक्स= 3. पर्याप्त रूप से इस वक्र के छोटे खंड सीधे दिखते हैं। दूसरे शब्दों में, यदि आरइस वक्र का एक मनमाना बिंदु है, तो इस बिंदु से गुजरने वाली कुछ सीधी रेखा है और बिंदु के एक छोटे से पड़ोस में वक्र का सन्निकटन है आर, और आस-पड़ोस जितना छोटा होगा, सन्निकटन उतना ही बेहतर होगा। ऐसी सीधी रेखा को बिंदु पर वक्र की स्पर्श रेखा कहा जाता है आर... डिफरेंशियल कैलकुलस का मुख्य कार्य एक सामान्य विधि का निर्माण करना है जो आपको वक्र पर किसी भी बिंदु पर स्पर्शरेखा की दिशा खोजने की अनुमति देता है जहाँ स्पर्शरेखा मौजूद है। एक तीव्र विराम के साथ वक्र की कल्पना करना कठिन नहीं है (चित्र 2)। अगर आर- इस तरह के ब्रेक के ऊपर, फिर आप एक अनुमानित सीधी रेखा बना सकते हैं पीटी 1 - बिंदु के दाईं ओर आरऔर दूसरी सन्निकटन रेखा आर टी 2 - बिंदु के बाईं ओर आर... लेकिन एक बिंदु से गुजरने वाली कोई भी सीधी रेखा नहीं है आर, जो समान रूप से बिंदु के आसपास के वक्र के करीब पहुंच गया पीदोनों दायीं और बायीं ओर, इसलिए बिंदु पर स्पर्शरेखा पीमौजूद नहीं होना।

अंजीर में। 1 स्पर्शरेखा सेमूल के माध्यम से खींचा गया हे= (0,0)। इस रेखा का ढाल 2 है, अर्थात्। जब भुज 1 से बदल जाता है, तो कोटि 2 से बढ़ जाती है। यदि एक्सतथा आप- पर एक मनमाना बिंदु के निर्देशांक से, फिर, से दूर जा रहा है हेदूरी पर एक्सइकाइयाँ दाईं ओर, हम दूर जाते हैं हे 2 . को आपइकाइयां ऊपर। इसलिये, आप/एक्स= 2, या आप = 2एक्स... यह स्पर्शरेखा समीकरण है सेवक्र के लिए आप = 2एक्स – एक्स 2 बिंदु पर हे.

अब यह स्पष्ट करना आवश्यक है कि बिन्दु से गुजरने वाली रेखाओं के समुच्चय से क्यों? हे, यह वह सीधी रेखा थी जिसे चुना गया था से... 2 की ढलान वाली सीधी रेखा और अन्य सीधी रेखाओं में क्या अंतर है? एक सरल उत्तर है, और हमें वृत्त की स्पर्शरेखा की सादृश्यता का उपयोग करने के प्रलोभन का विरोध करना कठिन लगता है: स्पर्शरेखा सेवक्र के साथ केवल एक बिंदु उभयनिष्ठ होता है, जबकि बिंदु से गुजरने वाली कोई अन्य गैर-ऊर्ध्वाधर सीधी रेखा होती है हे, वक्र को दो बार काटती है। इसे निम्नानुसार सत्यापित किया जा सकता है।

अभिव्यक्ति के बाद से आप = 2एक्स – एक्स 2 घटाकर प्राप्त किया जा सकता है एक्स 2 के आप = 2एक्स(सीधी रेखा के समीकरण से), फिर मान आपग्राफ के लिए कम ज्ञान है आपएक बिंदु को छोड़कर सभी बिंदुओं पर एक सीधी रेखा के लिए एक्स= 0. इसलिए, बिंदु को छोड़कर, ग्राफ हर जगह है हेनीचे स्थित से, और इस रेखा और आलेख में केवल एक ही बिंदु उभयनिष्ठ है। इसके अलावा, अगर आप = एमएक्स- एक बिंदु से गुजरने वाली किसी अन्य सीधी रेखा का समीकरण हे, तो निश्चित रूप से दो प्रतिच्छेदन बिंदु होंगे। सच में, एमएक्स = 2एक्स – एक्स 2 न केवल के लिए एक्स= 0, लेकिन के लिए भी एक्स = 2 – एम... और केवल जब एम= 2 दोनों प्रतिच्छेदन बिंदु संपाती हैं। अंजीर में। 3 मामला दिखाता है जब एम 2 से कम, तो . के दायीं ओर हेदूसरा चौराहा बिंदु है।

क्या से- एक बिंदु से गुजरने वाली एकमात्र गैर-ऊर्ध्वाधर सीधी रेखा हेऔर ग्राफ़ के साथ केवल एक बिंदु उभयनिष्ठ होना, न कि इसकी सबसे महत्वपूर्ण संपत्ति। वास्तव में, यदि हम अन्य रेखांकन की ओर मुड़ें, तो यह जल्द ही स्पष्ट हो जाएगा कि स्पर्शरेखा का जो गुण हमने सामान्य मामले में नोट किया है वह पूरा नहीं हुआ है। उदाहरण के लिए, अंजीर से। 4 यह देखा जा सकता है कि बिंदु (1,1) के निकट वक्र का ग्राफ आप = एक्स 3 एक सीधी रेखा द्वारा अच्छी तरह से अनुमानित है आर टी, हालांकि, इसके साथ एक से अधिक सामान्य बिंदु हैं। हालांकि, हम विचार करना चाहेंगे आर टीबिंदु पर इस ग्राफ के स्पर्शरेखा आर... इसलिए, पहले उदाहरण में हमें इतनी अच्छी तरह से सेवा देने वाले की तुलना में स्पर्शरेखा को उजागर करने के लिए कोई अन्य तरीका खोजना आवश्यक है।

मान लीजिए कि बिंदु के माध्यम से हेऔर एक मनमाना बिंदु क्यू = (एच,क) वक्र के ग्राफ पर आप = 2एक्स – एक्स 2 (चित्र 5) एक सीधी रेखा (जिसे छेदक कहा जाता है) खींची जाती है। वक्र के समीकरण में मूल्यों को प्रतिस्थापित करना एक्स = एचतथा आप = क, हमें वह मिलता है क = 2एच – एच 2, इसलिए, छेदक का ढलान है

बहुत छोटे से एचअर्थ एम 2 के करीब। इसके अलावा, चुनना एच 0 के काफी करीब हम कर सकते हैं एममनमाने ढंग से करीब 2. हम कह सकते हैं कि एम"सीमा तक जाता है" 2 के बराबर जब एचशून्य हो जाता है, या जो भी सीमा हो एम 2 के लिए बराबर एचशून्य की ओर प्रवृत्त। यह प्रतीकात्मक रूप से इस प्रकार लिखा गया है:

फिर बिंदु . पर ग्राफ की स्पर्शरेखा हेएक बिंदु से गुजरने वाली सीधी रेखा के रूप में परिभाषित हे, इस सीमा के बराबर ढलान के साथ। स्पर्शरेखा की यह परिभाषा आम तौर पर लागू होती है।

आइए इस दृष्टिकोण के फायदे एक और उदाहरण के साथ दिखाएं: वक्र के ग्राफ के स्पर्शरेखा के ढलान का पता लगाएं आप = 2एक्स – एक्स 2 एक मनमाना बिंदु पर पी = (एक्स,आप), खुद को सबसे सरल मामले तक सीमित नहीं रखते जब पी = (0,0).

होने देना क्यू = (एक्स + एच, आप + क) - दूरी पर स्थित चार्ट पर दूसरा बिंदु एचके अधिकार के लिए आर(अंजीर। 6)। ढलान का पता लगाना आवश्यक है क/एचकाटनेवाला पी क्यू... दूरसंचार विभाग क्यूदूरी पर है

अक्ष के ऊपर एक्स.

कोष्ठक का विस्तार करते हुए, हम पाते हैं:

इस समीकरण से घटाना आप = 2एक्स – एक्स 2, हम बिंदु से ऊर्ध्वाधर दूरी पाते हैं आरमुद्दे पर क्यू:

इसलिए, ढलान एमकाटनेवाला पी क्यूके बराबर है

अब वह एचशून्य हो जाता है, एम 2 - 2 . की ओर जाता है एक्स; हम अंतिम मान को स्पर्शरेखा के ढलान के रूप में लेंगे पीटी... (वही परिणाम प्राप्त होगा यदि एचनकारात्मक मान लेता है, जो बिंदु की पसंद से मेल खाता है क्यूकी बाईं ओर पी।) ध्यान दें कि के लिए एक्स= 0 परिणाम पिछले वाले जैसा ही है।

अभिव्यक्ति 2 - 2 एक्स 2 . का व्युत्पन्न कहा जाता है एक्स – एक्स 2. पुराने दिनों में, व्युत्पन्न को "अंतर अनुपात" और "अंतर गुणांक" भी कहा जाता था। यदि व्यंजक 2 एक्स – एक्स 2 मनोनीत एफ(एक्स), अर्थात।

तब व्युत्पन्न निरूपित किया जा सकता है

फलन के ग्राफ पर स्पर्श रेखा का ढाल ज्ञात करने के लिए आप = एफ(एक्स) किसी बिंदु पर, प्रतिस्थापित किया जाना चाहिए एफў ( एक्स) इस बिंदु के अनुरूप मूल्य एक्स... तो ढलान एफ(0) = 2 के लिए एक्स = 0, एफ(0) = 0 के लिए एक्स= 1 और एफ(2) = -2 के लिए एक्स = 2.

व्युत्पन्न को भी निरूपित किया जाता है परў , डीवाई/डीएक्स, डी एक्स वाईतथा ड्यू.

तथ्य यह है कि वक्र आप = 2एक्स – एक्सकिसी दिए गए बिंदु के पास 2 इस बिंदु पर अपनी स्पर्शरेखा से व्यावहारिक रूप से अप्रभेद्य है, हमें स्पर्शरेखा के ढलान को स्पर्शरेखा के बिंदु पर "वक्र की ढलान" के रूप में बोलने की अनुमति देता है। इस प्रकार, हम यह दावा कर सकते हैं कि विचाराधीन वक्र की ढलान बिंदु (0,0) पर 2 की ढलान है। यह भी कहा जा सकता है कि एक्स= 0 परिवर्तन की दर आपअपेक्षाकृत एक्स 2 है। बिंदु (2,0) पर, स्पर्शरेखा (और वक्र) का ढलान -2 है। (ऋण चिह्न का अर्थ है कि जैसे एक्सचर आपघटता है।) बिंदु (1,1) पर, स्पर्शरेखा क्षैतिज होती है। हम कहते हैं वक्र आप = 2एक्स – एक्सइस बिंदु पर 2 का स्थिर मान है।

उतार - चढ़ाव।

हमने अभी दिखाया है कि वक्र एफ(एक्स) = 2एक्स – एक्स 2 बिंदु (1,1) पर स्थिर है। चूंकि एफў ( एक्स) = 2 – 2एक्स = 2(1 – एक्स), यह स्पष्ट है कि एक्स 1 से कम, एफў ( एक्स) सकारात्मक है, और इसलिए आपबढ़ती है; पर एक्स, बड़ा 1, एफў ( एक्स) नकारात्मक है, और इसलिए आपघटता है। इस प्रकार, अंजीर में दर्शाए गए बिंदु (1,1) के आसपास के क्षेत्र में। 6 अक्षर एम, अर्थ परएक बिंदु तक बढ़ता है एम, बिंदु पर स्थिर एमऔर बिंदु के बाद घटता है एम... इस बिंदु को "अधिकतम" कहा जाता है क्योंकि मान परइस बिंदु पर इसके पर्याप्त रूप से छोटे पड़ोस में इसके किसी भी मूल्य से अधिक है। इसी तरह, "न्यूनतम" को उस बिंदु के रूप में परिभाषित किया जाता है जिसके आसपास के सभी मूल्य आपसंख्या से बढ़ना परइसी बिंदु पर। ऐसा भी हो सकता है कि यद्यपि का व्युत्पन्न एफ(एक्स) किसी बिंदु पर और गायब हो जाता है, इस बिंदु के आसपास के क्षेत्र में इसका चिन्ह नहीं बदलता है। ऐसा बिंदु, जो न तो अधिकतम और न ही न्यूनतम हो, विभक्ति बिंदु कहलाता है।

एक उदाहरण के रूप में, आइए हम वक्र का स्थिर बिंदु ज्ञात करें

इस फ़ंक्शन का व्युत्पन्न है

और गायब हो जाता है एक्स = 0, एक्स= 1 और एक्स= -1; वे। बिंदुओं (0,0), (1, -2/15) और (-1, 2/15) पर। अगर एक्स-1 से थोड़ा कम, तो एफў ( एक्स) नकारात्मक है; अगर एक्स-1 से थोड़ा अधिक, तो एफў ( एक्स) सकारात्मक है। इसलिए, बिंदु (-1, 2/15) अधिकतम है। इसी तरह, यह दिखाया जा सकता है कि बिंदु (1, -2/15) एक न्यूनतम है। लेकिन व्युत्पन्न एफў ( एक्स) बिंदु (0,0) के पहले और बाद में ऋणात्मक है। इसलिए, (0,0) विभक्ति बिंदु है।

वक्र के आकार के साथ-साथ इस तथ्य का अध्ययन किया गया कि वक्र अक्ष को काटता है एक्सपर एफ(एक्स) = 0 (यानी, के लिए एक्स= 0 या) आपको इसके ग्राफ को लगभग चित्र में दर्शाए अनुसार निरूपित करने की अनुमति देता है। 7.

सामान्य तौर पर, यदि हम असामान्य मामलों (सीधी रेखा खंडों वाले वक्र या अनंत संख्या में मोड़) को बाहर करते हैं, तो वक्र की सापेक्ष स्थिति और स्पर्शरेखा बिंदु के आसपास स्पर्शरेखा के लिए चार विकल्प होते हैं। आर. (सेमी... चावल। 8 जहाँ स्पर्श रेखा का ढाल धनात्मक है।)

1) बिंदु के दोनों ओर आरवक्र स्पर्शरेखा के ऊपर स्थित है (चित्र 8, ए) इस मामले में, वे कहते हैं कि बिंदु पर वक्र आरउत्तल नीचे या अवतल।

2) बिंदु के दोनों ओर आरवक्र स्पर्शरेखा के नीचे स्थित है (चित्र 8, बी) इस मामले में, वक्र को उत्तल ऊपर की ओर या केवल उत्तल कहा जाता है।

3) और 4) वक्र बिंदु के एक तरफ स्पर्शरेखा के ऊपर स्थित होता है आरऔर नीचे - दूसरे पर। इस मामले में आर- संक्रमण का बिन्दु।

मूल्यों की तुलना एफў ( एक्स) के दोनों किनारों पर आरबिंदु पर इसके मूल्य के साथ आर, यह निर्धारित करना संभव है कि किसी विशेष समस्या में इन चार मामलों में से किससे निपटा जाना है।

अनुप्रयोग।

उपरोक्त सभी विभिन्न क्षेत्रों में महत्वपूर्ण अनुप्रयोग पाते हैं। उदाहरण के लिए, यदि शरीर को 200 फीट प्रति सेकंड की प्रारंभिक गति से लंबवत ऊपर की ओर फेंका जाता है, तो ऊंचाई एसजिस पर वे स्थित होंगे टीप्रारंभिक बिंदु की तुलना में सेकंड होगा

जिस तरह से हमने उदाहरणों पर विचार किया है, उसी तरह से कार्य करते हुए, हम पाते हैं

यह मान c पर गायब हो जाता है। यौगिक एफў ( एक्स) c के मान तक धनात्मक है और इस समय के बाद ऋणात्मक है। इसलिये, एसतक बढ़ता है, फिर स्थिर हो जाता है, और फिर घट जाता है। यह ऊपर की ओर फेंके गए पिंड की गति का एक सामान्य विवरण है। इससे हमें पता चलता है कि शरीर अपने उच्चतम बिंदु पर कब पहुंचता है। इसके अलावा, प्रतिस्थापन टी= 25/4 इंच एफ(टी), हमें 625 फीट, अधिकतम लिफ्ट मिलती है। इस कार्य में एफў ( टी) का भौतिक अर्थ है। यह व्युत्पन्न उस गति को दर्शाता है जिसके साथ शरीर समय के क्षण में आगे बढ़ रहा है टी.

आइए अब हम एक अन्य प्रकार के अनुप्रयोग पर विचार करें (चित्र 9)। 75 सेमी 2 के क्षेत्र के साथ कार्डबोर्ड की शीट से एक चौकोर तल के साथ एक बॉक्स बनाना आवश्यक है। अधिकतम आयतन प्राप्त करने के लिए इस बॉक्स को कितना बड़ा होना चाहिए? अगर एक्स- बॉक्स के आधार की तरफ और एच- इसकी ऊँचाई, तो डिब्बे का आयतन है वी = एक्स 2 एच, और सतह का क्षेत्रफल 75 = . है एक्स 2 + 4xh... समीकरण को बदलने पर, हम प्राप्त करते हैं:

से व्युत्पन्न वीबराबर हो जाता है

और गायब हो जाता है एक्स= 5. तब

तथा वी= 125/2। फंक्शन ग्राफ वी = (75एक्स – एक्स 3) / 4 अंजीर में दिखाया गया है। 10 (ऋणात्मक मान एक्सइस समस्या में कोई भौतिक अर्थ नहीं होने के कारण छोड़ा गया है)।

संजात।

डिफरेंशियल कैलकुलस का एक महत्वपूर्ण कार्य उन तरीकों का निर्माण है जो आपको जल्दी और आसानी से डेरिवेटिव खोजने की अनुमति देते हैं। उदाहरण के लिए, यह गणना करना आसान है कि

(स्थिरांक का व्युत्पन्न, निश्चित रूप से, शून्य है।) सामान्य नियम को निकालना मुश्किल नहीं है:

कहाँ पे एन- कोई पूर्णांक या भिन्न। उदाहरण के लिए,

(यह उदाहरण दिखाता है कि भिन्नात्मक घातांक कितने उपयोगी हैं।)

यहाँ कुछ सबसे महत्वपूर्ण सूत्र दिए गए हैं:

निम्नलिखित नियम भी हैं: 1) यदि दोनों में से प्रत्येक कार्य करता है जी(एक्स) तथा एफ(एक्स) में डेरिवेटिव हैं, तो उनके योग का व्युत्पन्न इन कार्यों के डेरिवेटिव के योग के बराबर है, और अंतर का व्युत्पन्न डेरिवेटिव के अंतर के बराबर है, अर्थात।

2) दो कार्यों के उत्पाद के व्युत्पन्न की गणना सूत्र द्वारा की जाती है:

3) दो कार्यों के अनुपात के व्युत्पन्न का रूप है

4) किसी फलन के अवकलज को एक अचर से गुणा करने पर, इस फलन के अवकलज से गुणित स्थिरांक के बराबर होता है, अर्थात्।

अक्सर ऐसा होता है कि किसी फ़ंक्शन के मानों की गणना चरणों में करनी पड़ती है। उदाहरण के लिए, पाप की गणना करने के लिए एक्स 2, हमें पहले खोजने की जरूरत है तुम = एक्स 2, और फिर संख्या की ज्या की गणना करें तुम... हम तथाकथित "श्रृंखला नियम" का उपयोग करके ऐसे जटिल कार्यों का व्युत्पन्न पाते हैं:

हमारे उदाहरण में एफ(तुम) = पाप तुम, एफў ( तुम) = कोस तुम, इसलिए,

ये और इसी तरह के अन्य नियम कई कार्यों के डेरिवेटिव को तुरंत लिखने की अनुमति देते हैं।

रैखिक सन्निकटन।

तथ्य यह है कि, व्युत्पन्न जानने के बाद, हम कई मामलों में इस बिंदु पर अपने स्पर्शरेखा के कुछ बिंदु के पास एक फ़ंक्शन के ग्राफ को बदल सकते हैं, यह बहुत महत्वपूर्ण है, क्योंकि सीधी रेखाओं के साथ काम करना आसान होता है।

यह विचार कार्यों के अनुमानित मूल्यों की गणना में प्रत्यक्ष आवेदन पाता है। उदाहरण के लिए, जब मूल्य की गणना करना मुश्किल होता है एक्स= 1.033। लेकिन आप इस बात का फायदा उठा सकते हैं कि 1.033 नंबर 1 के करीब है और वो भी। बंद करे एक्स= 1 हम बिना कोई गंभीर गलती किए स्पर्शरेखा वक्र के ग्राफ को बदल सकते हैं। ऐसी स्पर्शरेखा का ढलान व्युत्पन्न के मान के बराबर होता है ( एक्स 1/3) = (1/3) एक्स-2/3 x = 1 पर, अर्थात 1/3. चूंकि बिंदु (1,1) वक्र पर स्थित है और इस बिंदु पर वक्र के स्पर्शरेखा का ढलान 1/3 है, स्पर्शरेखा के समीकरण का रूप है

इस लाइन पर एक्स = 1,033

परिणामी मूल्य आपसही मूल्य के बहुत करीब होना चाहिए आप; और, वास्तव में, यह सत्य से केवल 0.00012 अधिक है। गणितीय विश्लेषण में, इस तरह के रैखिक सन्निकटन की सटीकता में सुधार के लिए तरीके विकसित किए गए हैं। ये विधियां हमारी अनुमानित गणनाओं की विश्वसनीयता सुनिश्चित करती हैं।

अभी वर्णित प्रक्रिया एक उपयोगी संकेतन का सुझाव देती है। होने देना पी- फ़ंक्शन के ग्राफ़ पर संगत बिंदु एफचर एक्सऔर समारोह चलो एफ(एक्स) भिन्न है। वक्र के ग्राफ को बिंदु के पास बदलें आरइसकी स्पर्शरेखा, इस बिंदु पर खींची गई। अगर एक्सराशि के अनुसार बदलें एच, तो स्पर्शरेखा की कोटि मान से बदल जाएगी एचएच एफ ў ( एक्स) अगर एचबहुत छोटा है, तो बाद वाला मान कोटि में सही परिवर्तन के लिए एक अच्छा सन्निकटन है आपग्राफिक्स। अगर के बजाय एचहम प्रतीक लिखेंगे डीएक्स(यह एक उत्पाद नहीं है!), लेकिन कोटि में बदलाव आपनिरूपित डीवाई, तो हमें मिलता है डीवाई = एफ ў ( एक्स)डीएक्स, या डीवाई/डीएक्स = एफ ў ( एक्स) (सेमी... चावल। ग्यारह)। इसलिए, के बजाय डीवाईया एफ ў ( एक्स) प्रतीक का उपयोग अक्सर व्युत्पन्न को दर्शाने के लिए किया जाता है डीवाई/डीएक्स... इस संकेतन की सुविधा मुख्य रूप से श्रृंखला नियम (एक जटिल कार्य का अंतर) की स्पष्ट उपस्थिति पर निर्भर करती है; नए नोटेशन में, यह सूत्र इस तरह दिखता है:

जहां यह निहित है कि परनिर्भर करता है तुम, ए तुमबदले में निर्भर करता है एक्स.

महत्व डीवाईअंतर कहा जाता है पर; वास्तव में यह इस पर निर्भर करता है दोचर, अर्थात्: से एक्सऔर वेतन वृद्धि डीएक्स... जब वेतन वृद्धि डीएक्सबहुत छोटा, परिमाण डीवाईमूल्य में संबंधित परिवर्तन के करीब है आप... लेकिन मान लें कि वेतन वृद्धि डीएक्सथोड़ा, कोई ज़रूरत नहीं।

व्युत्पन्न कार्य आप = एफ(एक्स) हमने निरूपित किया एफ ў ( एक्स) या डीवाई/डीएक्स... व्युत्पन्न के व्युत्पन्न को लेना अक्सर संभव होता है। परिणाम को का दूसरा व्युत्पन्न कहा जाता है एफ (एक्स) और निरूपित एफ ўў ( एक्स) या डी 2 आप/डीएक्स 2. उदाहरण के लिए, यदि एफ(एक्स) = एक्स 3 – 3एक्स 2, तब एफ ў ( एक्स) = 3एक्स 2 – 6एक्सतथा एफ ўў ( एक्स) = 6एक्स- 6. उच्च क्रम के डेरिवेटिव के लिए समान पदनामों का उपयोग किया जाता है। हालांकि, बड़ी संख्या में डैश (व्युत्पन्न के क्रम के बराबर) से बचने के लिए, चौथा व्युत्पन्न (उदाहरण के लिए) के रूप में लिखा जा सकता है एफ (4) (एक्स), और व्युत्पन्न एन-वें क्रम के रूप में एफ (एन) (एक्स).

यह दिखाया जा सकता है कि एक बिंदु पर वक्र नीचे की ओर उत्तल होता है यदि दूसरा अवकलज धनात्मक है, और यदि दूसरा अवकलज ऋणात्मक है तो उत्तल ऊपर की ओर है।

यदि फ़ंक्शन का दूसरा व्युत्पन्न है, तो मात्रा में परिवर्तन आपवृद्धि के अनुरूप डीएक्सचर एक्स, लगभग सूत्र द्वारा गणना की जा सकती है

यह सन्निकटन आम तौर पर अंतर द्वारा दिए गए अनुमान से बेहतर होता है एफў ( एक्स)डीएक्स... यह वक्र के एक भाग को एक सीधी रेखा के बजाय एक परवलय से बदलने के अनुरूप है।

यदि समारोह एफ(एक्स) उच्च आदेशों के डेरिवेटिव हैं, फिर

शेष है

कहाँ पे एक्स- के बीच कुछ संख्या एक्सतथा एक्स + डीएक्स... उपरोक्त परिणाम को शेष टेलर सूत्र कहा जाता है। अगर एफ(एक्स) सभी ऑर्डर के डेरिवेटिव हैं, तो आमतौर पर आर नहीं® 0 के लिए एन ® Ґ .

समाकलन गणित

वर्ग।

वक्रीय समतल आकृतियों के क्षेत्रों का अध्ययन करने पर गणितीय विश्लेषण के नए पहलू सामने आते हैं। यहां तक ​​​​कि प्राचीन यूनानियों ने भी ऐसी समस्याओं को हल करने की कोशिश की, जिनके लिए, उदाहरण के लिए, एक सर्कल के क्षेत्र का निर्धारण सबसे कठिन कार्यों में से एक था। आर्किमिडीज ने इस समस्या को हल करने में बड़ी सफलता हासिल की, जो एक परवलयिक खंड (चित्र 12) के क्षेत्र को खोजने में भी कामयाब रहे। बहुत जटिल तर्क की सहायता से, आर्किमिडीज ने सिद्ध किया कि एक परवलयिक खंड का क्षेत्रफल वर्णित आयत के क्षेत्रफल का 2/3 है और इसलिए, इस मामले में (2/3) (16) के बराबर है = 32/3। जैसा कि हम बाद में देखेंगे, यह परिणाम गणितीय विश्लेषण की विधियों द्वारा आसानी से प्राप्त किया जा सकता है।

न्यूटन और लाइबनिज़ के पूर्ववर्तियों, मुख्य रूप से केप्लर और कैवेलियरी ने वक्रतापूर्ण आंकड़ों के क्षेत्रों की गणना की समस्या को एक ऐसी विधि का उपयोग करके हल किया जिसे शायद ही तार्किक कहा जा सकता है, लेकिन जो बेहद उपयोगी साबित हुआ। जब वालिस ने 1655 में केप्लर और कैवेलियरी की विधियों को डेसकार्टेस (विश्लेषणात्मक ज्यामिति) के तरीकों के साथ जोड़ा और नवजात बीजगणित का उपयोग किया, तो न्यूटन के प्रकट होने का मंच पूरी तरह से तैयार हो गया।

वालिस ने उस आकृति को विभाजित किया, जिसके क्षेत्र की गणना करने की आवश्यकता थी, बहुत संकीर्ण पट्टियों में, जिनमें से प्रत्येक को लगभग एक आयत माना जाता था। फिर उन्होंने सन्निकटन आयतों के क्षेत्रफलों को जोड़ा और, सरलतम मामलों में, वह मान प्राप्त किया जिससे आयतों के क्षेत्रफलों का योग तब होता है जब धारियों की संख्या अनंत हो जाती है। अंजीर में। 13 वक्र के नीचे के क्षेत्र की पट्टियों में कुछ विभाजन के अनुरूप आयतों को दिखाता है आप = एक्स 2 .

मुख्य प्रमेय।

न्यूटन और लाइबनिज की महान खोज ने क्षेत्रों के योग की सीमा तक जाने की श्रमसाध्य प्रक्रिया को बाहर करना संभव बना दिया। यह वर्ग की अवधारणा पर एक नए रूप के लिए धन्यवाद किया गया था। मुद्दा यह है कि हमें वक्र के नीचे के क्षेत्र की कल्पना करनी होगी जैसा कि बाएं से दाएं जाने वाले कोर्डिन द्वारा उत्पन्न होता है और यह पूछना है कि निर्देशांक द्वारा क्षेत्र कितनी तेजी से बहता है। हमें इस प्रश्न के उत्तर की कुंजी तब मिलेगी जब हम दो विशेष मामलों पर विचार करें जिनमें क्षेत्र पहले से जाना जाता है।

आइए रेखीय फलन के ग्राफ के अंतर्गत क्षेत्रफल से प्रारंभ करें आप = 1 + एक्सक्योंकि इस मामले में क्षेत्र की गणना प्राथमिक ज्यामिति का उपयोग करके की जा सकती है।

होने देना ए(एक्स) क्या समतल का वह भाग जो सीधी रेखा के बीच घिरा होता है आप = 1 + एक्सऔर एक खंड ओक्यू(अंजीर। 14)। जब ड्राइविंग करें क्यूपीसही क्षेत्र ए(एक्स) बढ़ती है। कितना तेज? इस प्रश्न का उत्तर देना कठिन नहीं है, क्योंकि हम जानते हैं कि एक समलम्ब चतुर्भुज का क्षेत्रफल उसके आधारों के आधे योग से उसकी ऊँचाई के गुणनफल के बराबर होता है। इसलिये,

क्षेत्र परिवर्तन दर ए(एक्स) इसके व्युत्पन्न द्वारा निर्धारित किया जाता है

हम देखते है कि एў ( एक्स) निर्देशांक के साथ मेल खाता है परअंक आर... क्या यह संयोग है? आइए अंजीर में दिखाए गए परवलय को जांचने का प्रयास करें। 15. स्क्वायर ए (एक्स) परवलय के तहत पर = एक्स 2 0 से . की सीमा में एक्सके बराबर है ए(एक्स) = (1 / 3)(एक्स)(एक्स 2) = एक्स 3/3। इस क्षेत्र के परिवर्तन की दर अभिव्यक्ति द्वारा निर्धारित की जाती है

जो बिल्कुल निर्देशांक के साथ मेल खाता है परगतिमान बिंदु आर.

यदि हम यह मान लें कि यह नियम सामान्यतः इस प्रकार पूरा होता है कि

फ़ंक्शन के ग्राफ़ के अंतर्गत क्षेत्र के परिवर्तन की दर है आप = एफ(एक्स), तो इसका उपयोग गणना और अन्य क्षेत्रों के लिए किया जा सकता है। वास्तव में, अनुपात एў ( एक्स) = एफ(एक्स) एक मौलिक प्रमेय व्यक्त करता है, जिसे निम्नानुसार तैयार किया जा सकता है: व्युत्पन्न, या क्षेत्र के परिवर्तन की दर के एक समारोह के रूप में एक्स, फ़ंक्शन के मान के बराबर है एफ (एक्स) बिंदु पर एक्स.

उदाहरण के लिए, किसी फ़ंक्शन के ग्राफ़ के अंतर्गत क्षेत्रफल ज्ञात करने के लिए आप = एक्स 3 से 0 तक एक्स(चित्र 16), हम डालते हैं

एक संभावित उत्तर है:

के व्युत्पन्न के बाद से एक्स 4/4 वास्तव में के बराबर है एक्स 3. इसके अलावा, ए(एक्स) के लिए शून्य के बराबर है एक्स= 0, जैसा कि होना चाहिए अगर ए(एक्स) वास्तव में एक क्षेत्र है।

गणितीय विश्लेषण साबित करता है कि उपरोक्त अभिव्यक्ति के अलावा एक और उत्तर ए(एक्स), मौजूद नहीं होना। आइए हम दिखाते हैं कि यह कथन निम्नलिखित अनुमानी (गैर-कठोर) तर्क का उपयोग करके प्रशंसनीय है। मान लीजिए कोई दूसरा उपाय है वी(एक्स) अगर ए(एक्स) तथा वी(एक्स) शून्य मान से एक साथ "प्रारंभ" पर एक्स= 0 और हर समय एक ही दर से बदलते रहते हैं, तो उनका मान no . पर होता है एक्सअलग नहीं हो सकता। वे हर जगह एक जैसे होने चाहिए; इसलिए, केवल एक ही समाधान है।

अनुपात को कैसे उचित ठहराया जा सकता है? एў ( एक्स) = एफ(एक्स) सामान्य रूप में? इस प्रश्न का उत्तर केवल के फलन के रूप में क्षेत्र के परिवर्तन की दर का अध्ययन करके ही दिया जा सकता है एक्ससामान्य रूप में। होने देना एम- फ़ंक्शन का सबसे छोटा मान एफ (एक्स) की सीमा में एक्सइससे पहले ( एक्स + एच), ए एम- एक ही अंतराल में इस फ़ंक्शन का सबसे बड़ा मान। फिर से जाने पर क्षेत्रफल की वृद्धि एक्सप्रति ( एक्स + एच) दो आयतों के क्षेत्रफलों के बीच संलग्न होना चाहिए (चित्र 17)। दोनों आयतों के आधार बराबर हैं एच... छोटे आयत की ऊँचाई होती है एमऔर क्षेत्र महाराष्ट्र, बड़ा, क्रमशः, एमतथा महाराष्ट्र... क्षेत्र बनाम के भूखंड पर एक्स(चित्र 18) यह देखा जा सकता है कि जब भुज बदल जाता है एच, कोटि (अर्थात क्षेत्रफल) का मान के बीच संलग्न राशि से बढ़ जाता है महाराष्ट्रतथा महाराष्ट्र... इस ग्राफ में छेदक ढलान के बीच है एमतथा एम... क्या होता है जब एचशून्य हो जाता है? यदि फ़ंक्शन का ग्राफ आप = एफ(एक्स) निरंतर है (अर्थात, इसमें असंततता नहीं है), तो एम, तथा एमप्रवृत्त एफ(एक्स) इसलिए, ढलान एў ( एक्स) के एक समारोह के रूप में क्षेत्र की साजिश एक्सके बराबर है एफ(एक्स) यह ठीक इसी निष्कर्ष पर था कि किसी को आना ही था।

लाइबनिज ने वक्र के तहत क्षेत्र के लिए प्रस्तावित किया आप = एफ(एक्स) 0 से . तक एपद

एक कठोर दृष्टिकोण के साथ, इस तथाकथित निश्चित अभिन्न को वालिस के तरीके में कुछ राशियों की सीमा के रूप में परिभाषित किया जाना चाहिए। उपरोक्त परिणाम को देखते हुए, यह स्पष्ट है कि इस अभिन्न की गणना की जाती है, बशर्ते कि हम ऐसा फ़ंक्शन पा सकें ए(एक्स), जो गायब हो जाता है एक्स= 0 और एक व्युत्पन्न है एў ( एक्स) के बराबर एफ (एक्स) इस तरह के एक फ़ंक्शन को खोजने को आमतौर पर एकीकरण कहा जाता है, हालांकि इस ऑपरेशन को एंटीडिफेनरेशन कहना अधिक उपयुक्त होगा, जिसका अर्थ है कि यह एक तरह से भेदभाव के विपरीत है। बहुपद के मामले में, एकीकरण सीधा है। उदाहरण के लिए, यदि

जिसे विभेदित करके सत्यापित करना आसान है ए(एक्स).

क्षेत्रफल की गणना करने के लिए ए 1 वक्र के नीचे आप = 1 + एक्स + एक्स 2/2, कोटि 0 और 1 के बीच संलग्न है, हम बस लिखते हैं

और प्रतिस्थापन एक्स= 1, हमें मिलता है ए 1 = 1 + 1/2 + 1/6 = 5/3। वर्ग ए(एक्स) 0 से 2 तक बराबर है ए 2 = 2 + 4/2 + 8/6 = 16/3। जैसा कि अंजीर से देखा गया है। 19, कोटि 1 और 2 के बीच का क्षेत्रफल है ए 2 – ए 1 = 11/3। यह आमतौर पर एक निश्चित अभिन्न के रूप में लिखा जाता है

वॉल्यूम।

इसी तरह का तर्क क्रांति के निकायों की मात्रा की गणना करने के लिए आश्चर्यजनक रूप से सरल बनाता है। आइए इसे एक गेंद के आयतन की गणना के उदाहरण से प्रदर्शित करें, एक और शास्त्रीय समस्या जिसे प्राचीन यूनानियों ने ज्ञात विधियों का उपयोग करके बड़ी कठिनाई से हल करने में कामयाबी हासिल की।

त्रिज्या के एक वृत्त के एक चौथाई के भीतर संलग्न विमान के भाग को घुमाएँ आर, अक्ष के चारों ओर 360 ° के कोण पर एक्स... नतीजतन, हमें एक गोलार्द्ध (चित्र 20) मिलता है, जिसका आयतन हम निरूपित करते हैं वी(एक्स) उस दर को निर्धारित करना आवश्यक है जिस पर वी(एक्स) बढ़ते हुए एक्स... से आगे बढ़ रहा है एक्सप्रति एक्स + एच, यह सत्यापित करना आसान है कि वॉल्यूम वृद्धि वॉल्यूम से कम है पी(आर 2 – एक्स 2)एचगोलाकार सिलेंडर त्रिज्या और ऊंचाई एच, और मात्रा से अधिक पी[आर 2 – (एक्स + एच) 2 ]एचसिलेंडर त्रिज्या और ऊंचाई एच... इसलिए, फ़ंक्शन के ग्राफ पर वी(एक्स) छेदक का ढाल के बीच है पी(आर 2 – एक्स 2) और पी[आर 2 – (एक्स + एच) 2]। कब एचशून्य की ओर जाता है, ढलान की ओर जाता है

पर एक्स = आरहम पाते हैं

गोलार्ध के आयतन के लिए, और इसलिए 4 पी आरपूरी गेंद के आयतन के लिए 3/3।

इसी तरह की एक विधि आपको वक्रों की लंबाई और घुमावदार सतहों के क्षेत्रों को खोजने की अनुमति देती है। उदाहरण के लिए, यदि ए(एक्स) - चाप की लम्बाई जनसंपर्कअंजीर में। 21, तो हमारा काम गणना करना है एў( एक्स) अनुमानी स्तर पर, हम एक ऐसी चाल का उपयोग करते हैं जो हमें उस सीमा तक सामान्य मार्ग का सहारा नहीं लेने देती है, जो परिणाम के कठोर प्रमाण के लिए आवश्यक है। मान लीजिए कि फ़ंक्शन के परिवर्तन की दर ए(एक्स) बिंदु पर आरयह वैसा ही है जैसा कि वक्र को उसकी स्पर्शरेखा से बदल दिया जाता है पीटीबिंदु पर पी... लेकिन अंजीर से। 21 कदम रखते समय सीधे देखा जा सकता है एचबिंदु के दायीं या बायीं ओर एक्ससाथ में आर टीअर्थ ए(एक्स) में परिवर्तन

इसलिए, फ़ंक्शन के परिवर्तन की दर ए(एक्स) है

फ़ंक्शन को स्वयं खोजने के लिए ए(एक्स), केवल समानता के दाहिने हाथ की अभिव्यक्ति को एकीकृत करना आवश्यक है। यह पता चला है कि अधिकांश कार्यों को एकीकृत करना मुश्किल है। इसलिए, अभिन्न कलन विधियों का विकास गणितीय विश्लेषण का एक बड़ा हिस्सा है।

एंटिडेरिवेटिव्स।

प्रत्येक फ़ंक्शन जिसका व्युत्पन्न किसी दिए गए फ़ंक्शन के बराबर होता है एफ(एक्स), के लिए व्युत्पन्न (या आदिम) कहा जाता है एफ(एक्स) उदाहरण के लिए, एक्स 3/3 फलन के लिए प्रतिअवकलन है एक्स 2, चूंकि ( एक्स 3/3) = एक्स 2. बेशक एक्स 3/3 किसी फलन का एकमात्र अवकलज नहीं है एक्स 2 से एक्स 3 /3 + सीके लिए व्युत्पन्न भी है एक्स 2 किसी भी स्थिरांक के लिए साथ... हालांकि, निम्नलिखित में हम ऐसे योगात्मक स्थिरांक को छोड़ने के लिए सहमत होंगे। सामान्य रूप में

कहाँ पे एनएक धनात्मक पूर्णांक है, क्योंकि ( एक्स एन + 1/(एन+ 1)) = एक्स एन... संबंध (1) और भी अधिक सामान्य अर्थों में धारण करता है यदि एनकिसी भी परिमेय संख्या से बदलें क-1 को छोड़कर।

किसी दिए गए फ़ंक्शन के लिए मनमाना एंटीडेरिवेटिव फ़ंक्शन एफ(एक्स) को आमतौर पर का अनिश्चितकालीन समाकल कहा जाता है एफ(एक्स) और इसे के रूप में निरूपित करें

उदाहरण के लिए, चूंकि (sin एक्स) = cos एक्स, सूत्र मान्य है

कई मामलों में, जब किसी दिए गए फ़ंक्शन के अनिश्चितकालीन अभिन्न के लिए एक सूत्र होता है, तो यह अनिश्चितकालीन अभिन्न के कई व्यापक रूप से प्रकाशित तालिकाओं में पाया जा सकता है। प्राथमिक कार्यों के समाकलन सारणीबद्ध होते हैं (इनमें शक्तियाँ, लघुगणक, घातांक फलन, त्रिकोणमितीय फलन, व्युत्क्रम त्रिकोणमितीय फलन, साथ ही जोड़, घटाव, गुणा और भाग के संक्रियाओं का उपयोग करके प्राप्त उनके परिमित संयोजन शामिल हैं)। सारणीबद्ध समाकलों का उपयोग करके, आप अधिक जटिल फलनों के समाकलनों की गणना कर सकते हैं। अनिश्चितकालीन समाकलों की गणना करने के कई तरीके हैं; इनमें से सबसे आम चर प्रतिस्थापन या प्रतिस्थापन विधि है। यह इस तथ्य में निहित है कि यदि हम अनिश्चितकालीन अभिन्न (2) में बदलना चाहते हैं एक्सकुछ अलग-अलग कार्यों पर एक्स = जी(तुम), ताकि अभिन्न न बदले, यह आवश्यक है एक्सद्वारा प्रतिस्थापित जीў ( तुम)ड्यू... दूसरे शब्दों में, समानता

(प्रतिस्थापन 2 एक्स = तुम, जहां से 2 डीएक्स = ड्यू).

यहाँ एक और एकीकरण विधि है - भागों द्वारा एकीकरण की विधि। यह पहले से ही ज्ञात सूत्र पर आधारित है

बाएँ और दाएँ पक्षों को एकीकृत करके, और इसे ध्यान में रखते हुए

इस सूत्र को भागों द्वारा समाकलन का सूत्र कहते हैं।

उदाहरण 2. इसे खोजना आवश्यक है। चूँकि cos एक्स= (पाप एक्स) , हम लिख सकते हैं कि

से (5), सेटिंग तुम = एक्सतथा वी= पाप एक्स, हम पाते हैं

और चूंकि (-cos एक्स) = पाप एक्सहम पाते हैं कि और

इस बात पर जोर दिया जाना चाहिए कि हमने अपने आप को एक बहुत व्यापक विषय के बहुत संक्षिप्त परिचय तक ही सीमित रखा है, जिसमें कई मजाकिया तकनीकें जमा की गई हैं।

दो चर के कार्य।

वक्र के कारण आप = एफ(एक्स) हमने दो कार्यों पर विचार किया है।

1) किसी दिए गए बिंदु पर वक्र की स्पर्श रेखा की प्रवणता ज्ञात कीजिए। व्युत्पन्न के मूल्य की गणना करके इस समस्या को हल किया जाता है एफў ( एक्स) निर्दिष्ट बिंदु पर।

2) अक्ष खंड के ऊपर वक्र के नीचे का क्षेत्र खोजें एक्सखड़ी रेखाओं से घिरा एक्स = एतथा एक्स = बी... एक निश्चित समाकल की गणना करके इस समस्या का समाधान किया जाता है।

इनमें से प्रत्येक समस्या का सतह के मामले में एक एनालॉग है जेड = एफ(एक्स,आप).

1) किसी दिए गए बिंदु पर सतह पर स्पर्शरेखा तल का पता लगाएं।

2) समतल के भाग के ऊपर की सतह के नीचे का आयतन ज्ञात कीजिए हूवक्र से घिरा साथ, और पक्ष से - विमान के लंबवत xyसीमा वक्र के बिंदुओं से गुजरना साथ (सेमी... चावल। 22)।

निम्नलिखित उदाहरण दिखाते हैं कि इन कार्यों को कैसे पूरा किया जाता है।

उदाहरण 4. सतह पर स्पर्शरेखा विमान खोजें

बिंदु पर (0,0,2)।

एक समतल को परिभाषित किया जाता है यदि उसमें पड़ी दो प्रतिच्छेदी रेखाएँ दी गई हों। इन पंक्तियों में से एक ( मैं 1) हम विमान में पहुँचते हैं xz (पर= 0), दूसरा ( मैं 2) - विमान में यज़ी (एक्स = 0) (सेमी... चावल। 23)।

सबसे पहले, अगर पर= 0, तब जेड = एफ(एक्स,0) = 2 – 2एक्स – 3एक्स 2. के संबंध में व्युत्पन्न एक्सद्वारा चिह्नित एफў एक्स(एक्स,0) = –2 – 6एक्स, पर एक्स= 0 का मान -2 है। सीधा मैं 1 समीकरणों द्वारा दिया गया जेड = 2 – 2एक्स, पर= 0 - स्पर्शरेखा to साथ 1, समतल के साथ सतह के प्रतिच्छेदन की रेखाएं पर= 0. इसी प्रकार, यदि एक्स= 0, तब एफ(0,आप) = 2 – आप – आप 2, और व्युत्पन्न के संबंध में पररूप है

चूंकि एफў आप(0,0) = -1, वक्र साथ 2 - समतल के साथ सतह के प्रतिच्छेदन की रेखा यज़ी- एक स्पर्शरेखा है मैं 2 समीकरणों द्वारा दिया गया जेड = 2 – आप, एक्स= 0. वांछित स्पर्शरेखा तल में दोनों सीधी रेखाएँ होती हैं मैं 1 और मैं 2 और समीकरण द्वारा लिखा गया है

यह विमान का समीकरण है। इसके अलावा, हमें सीधी रेखाएँ मिलती हैं मैं 1 और मैं 2, सेटिंग, क्रमशः, पर= 0 और एक्स = 0.

तथ्य यह है कि समीकरण (7) वास्तव में स्पर्शरेखा विमान को परिभाषित करता है, अनुमानी स्तर पर सत्यापित किया जा सकता है यदि हम देखते हैं कि इस समीकरण में समीकरण (6) में शामिल प्रथम-क्रम की शर्तें शामिल हैं, और यह कि दूसरे क्रम के शब्दों का प्रतिनिधित्व किया जा सकता है प्रपत्र -। चूँकि यह व्यंजक सभी मानों के लिए ऋणात्मक है एक्सतथा पर, के अतिरिक्त एक्स = पर= 0, सतह (6) बिंदु . को छोड़कर, तल (7) के नीचे हर जगह स्थित है आर= (0,0,0)। हम कह सकते हैं कि पृष्ठ (6) बिंदु पर ऊपर की ओर उत्तल है आर.

उदाहरण 5. सतह पर स्पर्शरेखा तल ज्ञात कीजिए जेड = एफ(एक्स,आप) = एक्स 2 – आप 2 मूल 0.

सतह पर पर= 0 हमारे पास है: जेड = एफ(एक्स,0) = एक्स 2 और एफў एक्स(एक्स,0) = 2एक्स... पर साथ 1, चौराहे की रेखाएं, जेड = एक्स 2. बिंदु पर हेढलान है एफў एक्स(0,0) = 0. समतल पर एक्स= 0 हमारे पास है: जेड = एफ(0,आप) = –आप 2 और एफў आप(0,आप) = –2आप... पर साथ 2, चौराहे की रेखाएं, जेड = –आप 2. बिंदु पर हेएक वक्र की ढलान साथ 2 बराबर है एफў आप(0,0) = 0. चूँकि की स्पर्श रेखाएँ साथ 1 और साथ 2 कुल्हाड़ी हैं एक्सतथा पर, स्पर्शरेखा विमान जिसमें वे शामिल हैं, वह तल है जेड = 0.

हालांकि, मूल के आसपास के क्षेत्र में, हमारी सतह स्पर्शरेखा तल के एक तरफ नहीं है। दरअसल, वक्र साथ 1 हर जगह, बिंदु 0 को छोड़कर, स्पर्शरेखा तल और वक्र के ऊपर स्थित है साथ 2 - क्रमशः इसके नीचे। सतह स्पर्शरेखा तल को काटती है जेड= 0 सीधी रेखाओं में पर = एक्सतथा पर = –एक्स... ऐसी सतह को मूल बिंदु पर एक काठी बिंदु कहा जाता है (चित्र 24)।

आंशिक अवकलज।

पिछले उदाहरणों में, हमने से व्युत्पन्नों का उपयोग किया था एफ (एक्स,आप) पर एक्सऔर तक पर... आइए अब हम ऐसे डेरिवेटिव पर अधिक सामान्य रूप से विचार करें। यदि हमारे पास दो चर का एक कार्य है, उदाहरण के लिए, एफ(एक्स,आप) = एक्स 2 – xy, तो हम प्रत्येक बिंदु पर इसके "आंशिक डेरिवेटिव" के दो को परिभाषित कर सकते हैं, एक के संबंध में फ़ंक्शन को अलग करके एक्सऔर फिक्सिंग पर, दूसरे के संबंध में अंतर करके परऔर फिक्सिंग एक्स... इनमें से पहला डेरिवेटिव के रूप में दर्शाया गया है एफў एक्स(एक्स,आप) या ¶ एफ/¶ एक्स; दूसरा - कैसे एफच आप... यदि दोनों मिश्रित व्युत्पन्न (द्वारा एक्सतथा पर, पर परतथा एक्स) निरंतर हैं, तो ¶ 2 एफ/¶ एक्स¶ आप= 2 एफ/¶ आप¶ एक्स; हमारे उदाहरण में 2 एफ/¶ एक्स¶ आप= 2 एफ/¶ आप¶ एक्स = –1.

आंशिक व्युत्पन्न एफў एक्स(एक्स,आप) फ़ंक्शन के परिवर्तन की दर को इंगित करता है एफबिंदु पर ( एक्स,आप) बढ़ाने की दिशा में एक्स, ए एफў आप(एक्स,आप) फलन के परिवर्तन की दर है एफआरोही दिशा पर... समारोह परिवर्तन दर एफबिंदु पर ( एक्स,पर) कोण बनाने वाली एक सीधी रेखा की दिशा में क्यूअक्ष की सकारात्मक दिशा के साथ एक्स, फ़ंक्शन का व्युत्पन्न कहा जाता है एफकी ओर; इसका मान फ़ंक्शन के दो आंशिक व्युत्पन्नों का एक संयोजन है f स्पर्शरेखा तल में लगभग बराबर है (छोटे के लिए डीएक्सतथा डीवाई) सच परिवर्तन जेडसतह पर, लेकिन अंतर की गणना करना आमतौर पर आसान होता है।

एक-आयामी मामले में, एक जटिल फ़ंक्शन या चेन नियम के व्युत्पन्न के रूप में ज्ञात चर परिवर्तन विधि से हमने पहले ही सूत्र पर विचार किया है। परनिर्भर करता है एक्स, ए एक्सनिर्भर करता है टी, का रूप है:

दो चर के कार्यों के लिए, एक समान सूत्र है:

आंशिक विभेदीकरण की अवधारणाओं और पदनामों को उच्च आयामों में सामान्य बनाना आसान है। विशेष रूप से, यदि सतह परोक्ष रूप से समीकरण द्वारा दी गई है एफ(एक्स,आप,जेड) = 0, सतह पर स्पर्शरेखा तल के समीकरण को अधिक सममित रूप दिया जा सकता है: बिंदु पर स्पर्शरेखा तल का समीकरण ( एक्स (एक्स 2/4)], फिर इसे एकीकृत किया जाता है एक्स 0 से 1. अंतिम परिणाम 3/4 है।

फॉर्मूला (10) की व्याख्या तथाकथित डबल इंटीग्रल के रूप में भी की जा सकती है, यानी। प्राथमिक "कोशिकाओं" की मात्रा के योग की सीमा के रूप में। ऐसी प्रत्येक कोशिका का आधार D होता है एक्सडी आपऔर आयताकार आधार के किसी बिंदु से ऊपर की सतह की ऊंचाई के बराबर ऊंचाई ( सेमी... चावल। 26)। यह दिखाया जा सकता है कि सूत्र (10) पर दोनों दृष्टिकोण समान हैं। गुरुत्वाकर्षण के केंद्रों और यांत्रिकी में पाए जाने वाले कई क्षणों को खोजने के लिए डबल इंटीग्रल का उपयोग किया जाता है।

गणितीय तंत्र की अधिक कठोर पुष्टि।

अब तक, हमने सहज ज्ञान युक्त स्तर पर पथरी की अवधारणाओं और विधियों को प्रस्तुत किया है और ज्यामितीय आकृतियों का सहारा लेने में संकोच नहीं किया है। 19वीं और 20वीं शताब्दी में सामने आए अधिक कठोर तरीकों पर संक्षेप में विचार करना हमारे लिए बाकी है।

19वीं शताब्दी के प्रारंभ में जब "गणितीय विश्लेषण के निर्माण" में हमले और हमले का युग समाप्त हुआ, तो इसके औचित्य के प्रश्न सामने आए। हाबिल, कॉची और कई अन्य उत्कृष्ट गणितज्ञों के कार्यों में, "सीमा", "निरंतर कार्य", "अभिसरण श्रृंखला" की अवधारणाओं को सटीक रूप से परिभाषित किया गया था। यह एक विश्वसनीय शोध उपकरण बनाने के लिए गणितीय विश्लेषण के आधार पर तार्किक क्रम लाने के लिए आवश्यक था। 1872 में वीयरस्ट्रैस द्वारा हर जगह निरंतर की खोज के बाद पूरी तरह से औचित्य की आवश्यकता और भी स्पष्ट हो गई, लेकिन कहीं भी अलग-अलग कार्य नहीं हैं (ऐसे कार्यों के ग्राफ में प्रत्येक बिंदु पर एक विराम होता है)। इस परिणाम ने गणितज्ञों पर भारी प्रभाव डाला, क्योंकि यह स्पष्ट रूप से उनके ज्यामितीय अंतर्ज्ञान का खंडन करता था। ज्यामितीय अंतर्ज्ञान की अविश्वसनीयता का एक और भी अधिक आकर्षक उदाहरण डी। पीनो द्वारा निर्मित निरंतर वक्र था, जो पूरी तरह से एक निश्चित वर्ग को भरता है, अर्थात। अपने सभी बिंदुओं से गुजर रहा है। इन और अन्य खोजों ने गणित के "अंकगणितीकरण" के कार्यक्रम को जन्म दिया, अर्थात्। संख्या की अवधारणा का उपयोग करके सभी गणितीय अवधारणाओं की पुष्टि करके इसे और अधिक विश्वसनीय बनाना। गणित की नींव पर कार्यों में स्पष्टता से लगभग शुद्धतावादी संयम का ऐतिहासिक औचित्य था।

तार्किक कठोरता के आधुनिक सिद्धांतों के अनुसार, वक्र के नीचे के क्षेत्र के बारे में बात करना अस्वीकार्य है। आप = एफ(एक्स) और अक्ष खंड के ऊपर एक्स, यहाँ तक की एफ- एक निरंतर कार्य, पहले "क्षेत्र" शब्द के सटीक अर्थ को परिभाषित किए बिना और यह स्थापित किए बिना कि इस तरह से निर्धारित क्षेत्र वास्तव में मौजूद है। इस समस्या को 1854 में बी. रीमैन द्वारा सफलतापूर्वक हल किया गया था, जिन्होंने एक निश्चित अभिन्न की अवधारणा की एक सटीक परिभाषा दी थी। तब से, एक निश्चित अभिन्न की धारणा के पीछे योग का विचार कई गहन अध्ययन और सामान्यीकरण का विषय रहा है। परिणामस्वरूप, आज एक निश्चित अभिन्न को अर्थ देना संभव है, भले ही अभिन्न हर जगह असंतत हो। एकीकरण की नई अवधारणाएं, जिसके निर्माण में ए. लेब्सग (1875-1941) और अन्य गणितज्ञों ने एक महान योगदान दिया, ने आधुनिक गणितीय विश्लेषण की शक्ति और सुंदरता को बढ़ाया।

इन सभी और अन्य अवधारणाओं के विवरण में जाना शायद ही उचित होगा। हम स्वयं को केवल सीमा और निश्चित समाकलन की कठोर परिभाषा देने तक ही सीमित रखेंगे।

निष्कर्ष के तौर पर, हम कह सकते हैं कि गणितीय विश्लेषण, एक वैज्ञानिक और एक इंजीनियर के हाथों में एक अत्यंत मूल्यवान उपकरण होने के कारण, आज भी गणितज्ञों का ध्यान फलदायी विचारों के स्रोत के रूप में आकर्षित करता है। साथ ही, आधुनिक विकास यह इंगित करता प्रतीत होता है कि 20वीं शताब्दी में गणितीय विश्लेषण इस तरह के प्रभावशाली लोगों द्वारा तेजी से अवशोषित किया जा रहा है। गणित की शाखाएँ जैसे अमूर्त बीजगणित और टोपोलॉजी।

गणित में भौतिक समस्याओं या उदाहरणों को व्युत्पन्न और इसकी गणना के तरीकों के ज्ञान के बिना हल करना बिल्कुल असंभव है। व्युत्पन्न गणितीय विश्लेषण की सबसे महत्वपूर्ण अवधारणाओं में से एक है। हमने आज के लेख को इस मौलिक विषय पर समर्पित करने का निर्णय लिया। व्युत्पन्न क्या है, इसका भौतिक और ज्यामितीय अर्थ क्या है, किसी फ़ंक्शन के व्युत्पन्न की गणना कैसे करें? इन सभी प्रश्नों को एक में जोड़ा जा सकता है: व्युत्पन्न को कैसे समझें?

व्युत्पन्न का ज्यामितीय और भौतिक अर्थ

एक समारोह होने दें च (एक्स) कुछ अंतराल में दिया गया (ए, बी) ... अंक х और х0 इसी अंतराल के हैं। जब x बदलता है, तो फ़ंक्शन स्वयं बदल जाता है। तर्क बदलना - इसके मूल्यों के बीच का अंतर x-x0 ... यह अंतर इस प्रकार लिखा जाता है डेल्टा x और तर्क वृद्धि कहा जाता है। किसी फ़ंक्शन का परिवर्तन या वृद्धि दो बिंदुओं पर फ़ंक्शन के मानों में अंतर है। व्युत्पन्न परिभाषा:

एक बिंदु पर एक फ़ंक्शन का व्युत्पन्न किसी दिए गए बिंदु पर फ़ंक्शन की वृद्धि के अनुपात की सीमा है जब तर्क की वृद्धि शून्य हो जाती है।

अन्यथा, इसे इस प्रकार लिखा जा सकता है:

ऐसी सीमा खोजने का क्या मतलब है? और यहाँ क्या है:

किसी बिंदु पर फलन का अवकलज OX अक्ष के बीच के कोण की स्पर्शरेखा और इस बिंदु पर फलन के ग्राफ की स्पर्शरेखा के बराबर होता है।

व्युत्पन्न का भौतिक अर्थ: समय के सापेक्ष पथ का अवकलज सरल रेखीय गति की गति के बराबर होता है।

दरअसल, स्कूल के समय से ही सभी जानते हैं कि गति एक निजी रास्ता है। एक्स = एफ (टी) और समय टी ... समय की अवधि में औसत गति:

एक बार में गति की गति का पता लगाने के लिए टी0 आपको सीमा की गणना करने की आवश्यकता है:

नियम एक: एक स्थिरांक निकालें

स्थिरांक को व्युत्पन्न के चिह्न के बाहर ले जाया जा सकता है। इसके अलावा, यह किया जाना चाहिए। गणित में उदाहरण हल करते समय, एक नियम के रूप में लें - यदि आप व्यंजक को सरल बना सकते हैं, तो सरल करना सुनिश्चित करें .

उदाहरण। आइए व्युत्पन्न की गणना करें:

नियम दो: कार्यों के योग का व्युत्पन्न

दो कार्यों के योग का व्युत्पन्न इन कार्यों के व्युत्पन्न के योग के बराबर है। कार्यों के अंतर के व्युत्पन्न के लिए भी यही सच है।

हम इस प्रमेय का प्रमाण नहीं देंगे, बल्कि एक व्यावहारिक उदाहरण पर विचार करेंगे।

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं:

नियम तीन: कार्यों के उत्पाद का व्युत्पन्न

दो अलग-अलग कार्यों के उत्पाद के व्युत्पन्न की गणना सूत्र द्वारा की जाती है:

उदाहरण: किसी फ़ंक्शन का व्युत्पन्न खोजें:

समाधान:

यहां जटिल कार्यों के डेरिवेटिव की गणना के बारे में कहना महत्वपूर्ण है। स्वतंत्र चर के संबंध में मध्यवर्ती तर्क के व्युत्पन्न द्वारा मध्यवर्ती तर्क के संबंध में एक जटिल फ़ंक्शन का व्युत्पन्न इस फ़ंक्शन के व्युत्पन्न के उत्पाद के बराबर है।

उपरोक्त उदाहरण में, हम अभिव्यक्ति से मिलते हैं:

इस मामले में, मध्यवर्ती तर्क पांचवीं शक्ति के लिए 8x है। इस तरह की अभिव्यक्ति के व्युत्पन्न की गणना करने के लिए, हम पहले मध्यवर्ती तर्क के संबंध में बाहरी फ़ंक्शन के व्युत्पन्न की गणना करते हैं, और फिर स्वतंत्र चर के संबंध में तत्काल मध्यवर्ती तर्क के व्युत्पन्न से गुणा करते हैं।

नियम चार: दो कार्यों का भागफल व्युत्पन्न

दो कार्यों के भागफल के व्युत्पन्न को निर्धारित करने का सूत्र:

हमने आपको शुरुआत से ही डमी के डेरिवेटिव के बारे में बताने की कोशिश की। यह विषय जितना आसान लगता है उतना आसान नहीं है, इसलिए सावधान रहें: उदाहरणों में अक्सर नुकसान होते हैं, इसलिए डेरिवेटिव की गणना करते समय सावधान रहें।

इस और अन्य विषयों पर किसी भी प्रश्न के लिए, आप छात्र सेवा से संपर्क कर सकते हैं। थोड़े समय में, हम आपको सबसे कठिन परीक्षा को हल करने और कार्यों से निपटने में मदद करेंगे, भले ही आपने पहले कभी डेरिवेटिव की गणना नहीं की हो।

जिस पर हमने सरलतम अवकलजों का विश्लेषण किया और विभेदीकरण के नियमों तथा अवकलजों को खोजने की कुछ तकनीकों से भी परिचित हुए। इस प्रकार, यदि आप कार्यों के व्युत्पन्न के साथ बहुत अधिक नहीं हैं, या इस लेख के कुछ बिंदु पूरी तरह से स्पष्ट नहीं हैं, तो पहले उपरोक्त पाठ को पढ़ें। कृपया, एक गंभीर मूड में ट्यून करें - सामग्री आसान नहीं है, लेकिन फिर भी मैं इसे सरल और सुलभ तरीके से प्रस्तुत करने का प्रयास करूंगा।

व्यवहार में, आपको एक जटिल फलन के अवकलज से बहुत बार निपटना पड़ता है, मैं यह भी कहूंगा, लगभग हमेशा, जब आपको व्युत्पन्न खोजने के लिए कार्य दिए जाते हैं।

हम एक जटिल फलन में अंतर करने के लिए नियम (संख्या 5) की तालिका में देखते हैं:

सहमति। सबसे पहले, आइए रिकॉर्डिंग पर ध्यान दें। यहां हमारे दो कार्य हैं - और, इसके अलावा, फ़ंक्शन, आलंकारिक रूप से बोलना, फ़ंक्शन में अंतर्निहित है। इस तरह के एक फंक्शन (जब एक फंक्शन दूसरे के भीतर नेस्ट किया जाता है) को कॉम्प्लेक्स फंक्शन कहा जाता है।

मैं समारोह को बुलाऊंगा बाहरी कार्यऔर समारोह - एक आंतरिक (या नेस्टेड) ​​फ़ंक्शन.

! ये परिभाषाएं सैद्धांतिक नहीं हैं और इन्हें सत्रीय कार्यों के अंतिम डिजाइन में नहीं दिखना चाहिए। मैं अनौपचारिक अभिव्यक्तियों "बाहरी कार्य", "आंतरिक" फ़ंक्शन का उपयोग केवल आपके लिए सामग्री को समझना आसान बनाने के लिए करता हूं।

स्थिति को स्पष्ट करने के लिए, विचार करें:

उदाहरण 1

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

साइन के तहत, हमारे पास केवल "X" अक्षर नहीं है, बल्कि एक पूर्णांक अभिव्यक्ति है, इसलिए तालिका से तुरंत व्युत्पन्न खोजना संभव नहीं होगा। हम यह भी देखते हैं कि यहां पहले चार नियमों को लागू करना असंभव है, एक अंतर प्रतीत होता है, लेकिन तथ्य यह है कि आप एक साइन को "फाड़" नहीं सकते:

इस उदाहरण में, पहले से ही मेरे स्पष्टीकरण से, यह सहज रूप से स्पष्ट है कि एक फ़ंक्शन एक जटिल कार्य है, और बहुपद एक आंतरिक फ़ंक्शन (घोंसला) और एक बाहरी फ़ंक्शन है।

पहला कदम, जो एक जटिल कार्य के व्युत्पन्न को खोजने के दौरान किया जाना चाहिए, वह है पता लगाएं कि कौन सा कार्य आंतरिक है और कौन सा बाहरी है.

सरल उदाहरणों के मामले में, यह स्पष्ट प्रतीत होता है कि एक बहुपद ज्या के नीचे स्थित है। लेकिन क्या होगा अगर सब कुछ स्पष्ट नहीं है? कैसे निर्धारित करें कि कौन सा फ़ंक्शन बाहरी है और कौन सा आंतरिक है? ऐसा करने के लिए, मैं निम्नलिखित तकनीक का उपयोग करने का सुझाव देता हूं, जो मानसिक रूप से या मसौदे पर किया जा सकता है।

कल्पना कीजिए कि हमें कैलकुलेटर पर एक अभिव्यक्ति के मूल्य की गणना करने की आवश्यकता है (एक के बजाय, कोई भी संख्या हो सकती है)।

हम पहले क्या गणना करेंगे? सबसे पहलेआपको निम्नलिखित क्रिया करने की आवश्यकता होगी:, इसलिए बहुपद एक आंतरिक कार्य होगा:

दूसरेखोजने की आवश्यकता होगी, इसलिए साइन एक बाहरी कार्य होगा:

हमारे बाद पता लगायाआंतरिक और बाहरी कार्यों के साथ, यह एक जटिल कार्य के भेदभाव के नियम को लागू करने का समय है .

हम फैसला करना शुरू करते हैं। पाठ से मैं व्युत्पन्न कैसे ढूंढूं?हमें याद है कि किसी भी व्युत्पन्न के समाधान का डिज़ाइन हमेशा इस तरह से शुरू होता है - हम अभिव्यक्ति को कोष्ठक में संलग्न करते हैं और ऊपर दाईं ओर एक स्ट्रोक लगाते हैं:

प्रथमबाह्य फलन (साइन) का अवकलज ज्ञात कीजिए, प्राथमिक फलनों के अवकलजों की तालिका देखिए और ध्यान दीजिए। सभी सारणीबद्ध सूत्र लागू होते हैं भले ही "x" को एक जटिल व्यंजक से बदल दिया जाए, इस मामले में:

ध्यान दें कि आंतरिक कार्य नहीं बदला है, हम इसे छूते नहीं हैं.

खैर, यह बिल्कुल स्पष्ट है कि

सूत्र लागू करने का परिणाम अंतिम डिजाइन में यह इस तरह दिखता है:

एक स्थिर कारक आमतौर पर एक अभिव्यक्ति की शुरुआत में रखा जाता है:

यदि कोई भ्रम है, तो समाधान लिखें और स्पष्टीकरण दोबारा पढ़ें।

उदाहरण 2

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

उदाहरण 3

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

हमेशा की तरह, हम लिखते हैं:

आइए जानें कि हमारे पास बाहरी कार्य कहां है, और हमारे पास आंतरिक कहां है। ऐसा करने के लिए, अभिव्यक्ति के मूल्य की गणना करने के लिए (मानसिक रूप से या मसौदे पर) प्रयास करें। पहले क्या किया जाना चाहिए? सबसे पहले, आपको गणना करने की आवश्यकता है कि आधार किसके बराबर है: जिसका अर्थ है कि बहुपद आंतरिक कार्य है:

और, तभी घातांक किया जाता है, इसलिए, शक्ति कार्य एक बाहरी कार्य है:

सूत्र के अनुसार , पहले आपको बाहरी फ़ंक्शन के व्युत्पन्न को खोजने की आवश्यकता है, इस मामले में, डिग्री। हम तालिका में आवश्यक सूत्र की तलाश कर रहे हैं:। हम फिर दोहराते हैं: कोई भी सारणीबद्ध सूत्र न केवल "x" के लिए, बल्कि एक जटिल व्यंजक के लिए भी मान्य है... इस प्रकार, एक जटिल कार्य के भेदभाव के नियम को लागू करने का परिणाम अगला:

मैं फिर से जोर देता हूं कि जब हम बाहरी फ़ंक्शन का व्युत्पन्न लेते हैं, तो आंतरिक कार्य हमारे लिए नहीं बदलता है:

अब यह आंतरिक फ़ंक्शन का एक बहुत ही सरल व्युत्पन्न खोजने और परिणाम को "कंघी" करने के लिए बनी हुई है:

उदाहरण 4

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

यह एक स्वतंत्र समाधान के लिए एक उदाहरण है (ट्यूटोरियल के अंत में उत्तर)।

एक जटिल फ़ंक्शन के व्युत्पन्न की समझ को मजबूत करने के लिए, मैं टिप्पणियों के बिना एक उदाहरण दूंगा, इसे स्वयं समझने का प्रयास करें, अनुमान लगाएं कि बाहरी कहां है और आंतरिक कार्य कहां है, कार्यों को इस तरह क्यों हल किया गया था?

उदाहरण 5

ए) फ़ंक्शन के व्युत्पन्न का पता लगाएं

बी) फ़ंक्शन का व्युत्पन्न खोजें

उदाहरण 6

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

यहां हमारे पास एक जड़ है, और जड़ को अलग करने के लिए, इसे एक डिग्री के रूप में दर्शाया जाना चाहिए। इस प्रकार, पहले हम फ़ंक्शन को भेदभाव के लिए उपयुक्त रूप में लाते हैं:

फलन का विश्लेषण करते हुए, हम इस निष्कर्ष पर पहुँचते हैं कि तीन पदों का योग एक आंतरिक फलन है, और घातांक एक बाहरी फलन है। हम एक जटिल फलन के विभेदीकरण का नियम लागू करते हैं :

डिग्री को फिर से एक कट्टरपंथी (रूट) के रूप में दर्शाया जाता है, और आंतरिक फ़ंक्शन के व्युत्पन्न के लिए हम योग को अलग करने के लिए एक सरल नियम लागू करते हैं:

तैयार। आप व्यंजक को कोष्ठकों में एक सामान्य हर में भी ला सकते हैं और सब कुछ एक भिन्न में लिख सकते हैं। अच्छा, निश्चित रूप से, लेकिन जब बोझिल लंबे डेरिवेटिव प्राप्त होते हैं, तो ऐसा न करना बेहतर होता है (भ्रमित होना आसान है, एक अनावश्यक गलती करें, और शिक्षक के लिए जांचना असुविधाजनक होगा)।

उदाहरण 7

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

यह एक स्वतंत्र समाधान के लिए एक उदाहरण है (ट्यूटोरियल के अंत में उत्तर)।

यह ध्यान रखना दिलचस्प है कि कभी-कभी, एक जटिल फ़ंक्शन को अलग करने के नियम के बजाय, कोई व्यक्ति भागफल को अलग करने के लिए नियम का उपयोग कर सकता है , लेकिन ऐसा समाधान विकृति के रूप में असामान्य लगेगा। यहाँ एक विशिष्ट उदाहरण है:

उदाहरण 8

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

यहां आप भागफल को अलग करने के लिए नियम का उपयोग कर सकते हैं , लेकिन एक जटिल फ़ंक्शन के भेदभाव के नियम के माध्यम से व्युत्पन्न खोजना अधिक लाभदायक है:

हम विभेदन के लिए फ़ंक्शन तैयार करते हैं - हम ऋण को व्युत्पन्न के चिह्न के बाहर ले जाते हैं, और कोसाइन को अंश तक बढ़ाते हैं:

कोसाइन एक आंतरिक कार्य है, घातांक एक बाहरी कार्य है।
हम अपने नियम का उपयोग करते हैं :

आंतरिक फ़ंक्शन के व्युत्पन्न का पता लगाएं, कोसाइन को वापस नीचे रीसेट करें:

तैयार। विचार किए गए उदाहरण में, यह महत्वपूर्ण है कि संकेतों में भ्रमित न हों। वैसे, इसे नियम से हल करने का प्रयास करें , उत्तरों का मिलान होना चाहिए।

उदाहरण 9

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

यह एक स्वतंत्र समाधान के लिए एक उदाहरण है (ट्यूटोरियल के अंत में उत्तर)।

अब तक, हमने उन मामलों पर ध्यान दिया है जहां एक जटिल फ़ंक्शन में हमारा केवल एक अटैचमेंट था। व्यावहारिक कार्यों में, आप अक्सर व्युत्पन्न पा सकते हैं, जहां, घोंसले के शिकार गुड़िया की तरह, एक दूसरे के अंदर, 3 या यहां तक ​​​​कि 4-5 फ़ंक्शन एक ही बार में नेस्टेड होते हैं।

उदाहरण 10

किसी फ़ंक्शन के व्युत्पन्न का पता लगाएं

आइए इस फ़ंक्शन के अनुलग्नकों को समझते हैं। परीक्षण मान का उपयोग करके व्यंजक का मूल्यांकन करने का प्रयास कर रहा है। हम कैलकुलेटर पर कैसे भरोसा करेंगे?

पहले आपको खोजने की जरूरत है, जिसका अर्थ है कि आर्क्सिन सबसे गहरा घोंसला है:

फिर एक के इस आर्क्साइन को चुकता किया जाना चाहिए:

और अंत में, 7 को घात में बढ़ाएं:

यही है, इस उदाहरण में हमारे पास तीन अलग-अलग कार्य और दो अनुलग्नक हैं, जबकि अंतरतम कार्य आर्क्सिन है, और सबसे बाहरी कार्य घातीय कार्य है।

हम हल करना शुरू करते हैं

नियम के अनुसार सबसे पहले आपको बाहरी फ़ंक्शन का व्युत्पन्न लेना होगा। हम डेरिवेटिव की तालिका को देखते हैं और घातीय फ़ंक्शन का व्युत्पन्न पाते हैं: केवल अंतर यह है कि "x" के बजाय हमारे पास एक जटिल अभिव्यक्ति है, जो इस सूत्र की वैधता को नकारती नहीं है। तो, एक जटिल कार्य के भेदभाव के नियम को लागू करने का परिणाम अगला।