मॉड्यूल उदाहरणों के साथ किसी फ़ंक्शन का ग्राफ़ बनाएं। मॉड्यूल के साथ एक रैखिक फ़ंक्शन के ग्राफ़। दायीं ओर के चर का मामला

एर्डनिगोरीएवा मरीना

यह कार्य आठवीं कक्षा में एक विषय को वैकल्पिक के रूप में अध्ययन करने का परिणाम है। ग्राफ़ के ज्यामितीय परिवर्तन और मॉड्यूल के साथ ग्राफ़ के निर्माण में उनके अनुप्रयोग को यहां दिखाया गया है। एक मॉड्यूल की अवधारणा और उसके गुणों का परिचय दिया गया है। यह दिखाया गया है कि विभिन्न तरीकों से मॉड्यूल के साथ ग्राफ़ कैसे बनाएं: परिवर्तनों का उपयोग करके और मॉड्यूल की अवधारणा के आधार पर। परियोजना का विषय गणित पाठ्यक्रम में सबसे कठिन में से एक है, यह ऐच्छिक में विचार किए गए मुद्दों से संबंधित है, और है उन्नत गणित वाली कक्षाओं में अध्ययन किया गया। हालाँकि, ऐसे कार्य एकीकृत राज्य परीक्षा में जीआईए के दूसरे भाग में दिए गए हैं। यह कार्य आपको यह समझने में मदद करेगा कि न केवल रैखिक, बल्कि अन्य कार्यों (द्विघात, व्युत्क्रमानुपाती, आदि) के मॉड्यूल के साथ ग्राफ़ कैसे बनाएं। यह कार्य राज्य परीक्षा और एकीकृत राज्य परीक्षा की तैयारी में मदद करेगा।

डाउनलोड करना:

पूर्व दर्शन:

प्रस्तुति पूर्वावलोकन का उपयोग करने के लिए, एक Google खाता बनाएं और उसमें लॉग इन करें: https://accounts.google.com

स्लाइड कैप्शन:

मॉड्यूल के साथ एक रेखीय फ़ंक्शन के ग्राफ़ एर्डनिगोरीवा मरीना द्वारा काम, एमसीओयू "कामिशोव्स्काया ओओएसएच" के 8 वीं कक्षा के छात्र पर्यवेक्षक गोरियाएवा ज़ोया एर्डनिगोरीवना, गणित शिक्षक एमसीओयू "कामिशोव्स्काया ओओएसएच" पी। कामिशेवो, 2013

परियोजना का लक्ष्य: मॉड्यूल के साथ रैखिक कार्यों के ग्राफ़ कैसे बनाएं, इस प्रश्न का उत्तर देना। परियोजना के उद्देश्य: इस मुद्दे पर साहित्य का अध्ययन करें। ग्राफ़ के ज्यामितीय परिवर्तनों और मॉड्यूल के साथ ग्राफ़ के निर्माण में उनके अनुप्रयोग का अध्ययन करें। एक मॉड्यूल की अवधारणा और उसके गुणों का अध्ययन करें। विभिन्न तरीकों से मॉड्यूल के साथ ग्राफ़ बनाना सीखें।

प्रत्यक्ष आनुपातिकता प्रत्यक्ष आनुपातिकता एक फ़ंक्शन है जिसे फॉर्म y=kx के सूत्र द्वारा निर्दिष्ट किया जा सकता है, जहां x एक स्वतंत्र चर है, k एक गैर-शून्य संख्या है।

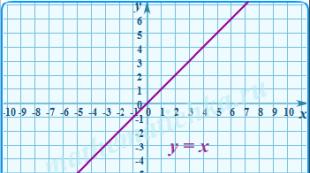
आइए फलन y = x x 0 2 y 0 2 आलेखित करें

ग्राफ़ का ज्यामितीय परिवर्तन नियम संख्या 1 फ़ंक्शन y = f (x) + k - एक रैखिक फ़ंक्शन का ग्राफ़ - फ़ंक्शन y = f (x) के ग्राफ़ को O से ऊपर + k इकाइयों के समानांतर स्थानांतरण द्वारा प्राप्त किया जाता है। k> 0 या |- k| के लिए y अक्ष O y अक्ष के नीचे k पर इकाइयाँ

आइए ग्राफ़ बनाएं y=x+3 y=x-2

नियम संख्या 2 फ़ंक्शन y=kf(x) का ग्राफ़ फ़ंक्शन y = f (x) के ग्राफ़ को O y अक्ष a के साथ a>1 पर कई बार खींचकर और इसे O y अक्ष a के साथ संपीड़ित करके प्राप्त किया जाता है। 0स्लाइड 9 पर कई बार

आइए एक ग्राफ बनाएं y=x y= 2 x

नियम संख्या 3 फ़ंक्शन y = - f (x) का ग्राफ O x अक्ष के सापेक्ष ग्राफ y = f (x) को सममित रूप से प्रदर्शित करके प्राप्त किया जाता है

नियम संख्या 4 फ़ंक्शन y = f (- x) का ग्राफ O y अक्ष के सापेक्ष फ़ंक्शन y = f (x) के ग्राफ को सममित रूप से प्रदर्शित करके प्राप्त किया जाता है

नियम संख्या 5 फ़ंक्शन y=f(x+c) का ग्राफ़ फ़ंक्शन y=f(x) के ग्राफ़ को O x अक्ष के साथ दाईं ओर समानांतर स्थानांतरण द्वारा प्राप्त किया जाता है, यदि c 0।

आइए ग्राफ बनाएं y=f(x) y=f(x+2)

मापांक की परिभाषा एक गैर-ऋणात्मक संख्या a का मापांक स्वयं संख्या a के बराबर होता है; किसी ऋणात्मक संख्या a का मापांक उसके विपरीत धनात्मक संख्या -a के बराबर होता है। या, |a|=a, यदि a ≥0 |a|=-a, यदि a

मॉड्यूल के साथ रैखिक कार्यों के ग्राफ़ का निर्माण किया जाता है: मॉड्यूल की परिभाषा का विस्तार करके ज्यामितीय परिवर्तनों का उपयोग करना।

नियम संख्या 6 फ़ंक्शन का ग्राफ़ y=|f(x)| निम्नानुसार प्राप्त किया जाता है: ग्राफ y=f(x) का भाग O x अक्ष के ऊपर स्थित संरक्षित है; O x अक्ष के नीचे स्थित भाग O x अक्ष के सापेक्ष सममित रूप से प्रदर्शित होता है।

फ़ंक्शन y=-2| को ग्राफ़ करें x-3|+4 y ₁=| की रचना कीजिए एक्स | हम y₂= |x - 3 | बनाते हैं → ऑक्स अक्ष के साथ +3 इकाइयों द्वारा समानांतर अनुवाद (दाईं ओर शिफ्ट) हम y ₃ =+2|x-3| → O अक्ष के अनुदिश y को 2 बार फैलाएं = 2 y₂ हम y बनाते हैं ₄ =-2|x-3| → x-अक्ष के बारे में समरूपता = - y₃ हम y₅ =-2|x-3|+4 बनाते हैं → O अक्ष के साथ +4 इकाइयों द्वारा समानांतर अनुवाद y (ऊपर की ओर बदलाव) = y ₄ +4

फ़ंक्शन का ग्राफ़ y =-2|x-3|+4

फ़ंक्शन का ग्राफ़ y= 3|x|+2 y₁=|x| y₂=3|x|= 3 y₁ → 3 गुना खींचकर y₃=3|x| +2= y₄+2 → 2 इकाई ऊपर शिफ्ट करें

नियम संख्या 7 फ़ंक्शन का ग्राफ y=f(| x |) फ़ंक्शन y=f(x) के ग्राफ से निम्नानुसार प्राप्त किया जाता है: x > 0 के लिए, फ़ंक्शन का ग्राफ संरक्षित है, और वही ग्राफ़ का भाग O y अक्ष के सापेक्ष सममित रूप से प्रदर्शित होता है

फ़ंक्शन y = || का ग्राफ़ बनाएं एक्स-1 | -2 |

Y₁= |x| y₂=|x-1| y₃= y₂-2 y₄= |y₃| Y=||x-1|-2|

फ़ंक्शन का ग्राफ़ बनाने के लिए एल्गोरिदम y=│f(│x│)│ फ़ंक्शन का ग्राफ़ बनाएं y=f(│x│) । फिर निर्मित ग्राफ़ के सभी हिस्सों को अपरिवर्तित छोड़ दें जो x अक्ष के ऊपर स्थित हैं। x-अक्ष के नीचे स्थित भाग इस अक्ष के बारे में सममित रूप से प्रदर्शित होते हैं।

Y=|2|x|-3| निर्माण: a) x>0 के लिए y=2x-3, b) x स्लाइड 26 के लिए y=-2x-3

नियम #8 निर्भरता ग्राफ़ | y|=f(x) फ़ंक्शन y=f(x) के ग्राफ से प्राप्त किया जाता है यदि सभी बिंदु जिनके लिए f(x) > 0 संरक्षित हैं और वे एब्सिस्सा अक्ष के सापेक्ष सममित रूप से स्थानांतरित भी हैं।

समतल पर बिंदुओं का एक समूह बनाएं जिसके कार्टेशियन निर्देशांक x और y समीकरण को संतुष्ट करते हैं |y|=||x-1|-1|

| y|=||x-1| -1| हम दो ग्राफ बनाते हैं 1) y=||x-1|-1| और 2) y =-|| x-1|-1| y₁=|x| y₂=| एक्स-1 | → ऑक्स अक्ष के अनुदिश दायीं ओर 1 इकाई y₃ = | शिफ्ट करें x -1 |- 1= → 1 इकाई नीचे शिफ्ट करें y ₄ = || x-1|- 1| → ग्राफ़ बिंदुओं की समरूपता जिसके लिए O x के सापेक्ष y₃ 0 है

समीकरण का ग्राफ |y|=||x-1|-1| हम इस प्रकार प्राप्त करते हैं: 1) फ़ंक्शन y=f(x) का एक ग्राफ़ बनाएं और इसके उस हिस्से को अपरिवर्तित छोड़ दें जहां y≥0 2) ऑक्स अक्ष के बारे में समरूपता का उपयोग करते हुए, y के अनुरूप ग्राफ़ का एक और भाग बनाएं।

फ़ंक्शन y =|x | को ग्राफ़ करें − | 2 - एक्स | . समाधान। यहां मापांक चिह्न दो अलग-अलग शब्दों में दिखाई देता है और इसे हटाया जाना चाहिए। 1) सबमॉड्यूलर अभिव्यक्तियों की जड़ें खोजें: x=0, 2-x=0, x=2 2) अंतरालों पर चिह्न सेट करें:

किसी फ़ंक्शन का ग्राफ़

निष्कर्ष परियोजना का विषय गणित पाठ्यक्रम में कठिन विषयों में से एक है, यह ऐच्छिक में विचार किए जाने वाले मुद्दों से संबंधित है, और गणित पाठ्यक्रम के गहन अध्ययन के लिए कक्षाओं में इसका अध्ययन किया जाता है। फिर भी, ऐसे कार्य GIA के दूसरे भाग में दिए गए हैं। यह कार्य आपको यह समझने में मदद करेगा कि न केवल रैखिक कार्यों, बल्कि अन्य कार्यों (द्विघात, व्युत्क्रमानुपाती, आदि) के मॉड्यूल के साथ ग्राफ़ कैसे बनाया जाए। यह कार्य राज्य परीक्षा और एकीकृत राज्य परीक्षा की तैयारी में मदद करेगा और आपको गणित में उच्च अंक प्राप्त करने की अनुमति देगा।

साहित्य विलेनकिन एन.वाई.ए. , झोखोव वी.आई.. गणित।" पाठ्यपुस्तक छठी कक्षा मास्को। पब्लिशिंग हाउस "मेनेमोसिन", 2010 विलेनकिन एन.वाई.ए., विलेनकिन एल.एन., सर्विलो जी.एस. और अन्य। बीजगणित। आठवीं कक्षा: शैक्षणिक। गणित के उन्नत अध्ययन वाले छात्रों और कक्षाओं के लिए एक मैनुअल। - मास्को। ज्ञानोदय, 2009 गेडुकोव आई.आई. "निरपेक्ष मूल्य।" मास्को. ज्ञानोदय, 1968. गुरस्की आई.पी. "कार्य और रेखांकन।" मास्को. ज्ञानोदय, 1968. यशचिना एन.वी. मॉड्यूल युक्त ग्राफ़ बनाने की तकनीकें। जर्नल "स्कूल में गणित", नंबर 3, 1994 बच्चों का विश्वकोश। मास्को. "शिक्षाशास्त्र", 1990. डायनकिन ई.बी., मोलचानोवा एस.ए. गणित की समस्याओं। एम., "विज्ञान", 1993. पेट्राकोव आई.एस. कक्षा 8-10 में गणित क्लब। एम., "ज्ञानोदय", 1987। गैलिट्स्की एम.एल. और अन्य। ग्रेड 8-9 के लिए बीजगणित में समस्याओं का संग्रह: गणित के उन्नत अध्ययन वाले छात्रों और कक्षाओं के लिए एक पाठ्यपुस्तक। - 12वां संस्करण. - एम.: शिक्षा, 2006. - 301 पी. मकरिचेव यू.एन., मिंड्युक एन.जी. बीजगणित: 9वीं कक्षा की स्कूली पाठ्यपुस्तक के लिए अतिरिक्त अध्याय: गणित के गहन अध्ययन के साथ स्कूलों और कक्षाओं के छात्रों के लिए एक पाठ्यपुस्तक / जी.वी. डोरोफीव द्वारा संपादित। - एम.: शिक्षा, 1997. - 224 पी. सादिकिना एन. मापांक चिह्न/गणित युक्त ग्राफ़ और निर्भरता का निर्माण। - क्रमांक 33. - 2004. - पी.19-21 .. कोस्ट्रिकिना एन.पी. "ग्रेड 7-9 के लिए बीजगणित पाठ्यक्रम में बढ़ी हुई कठिनाई की समस्याएं"... मॉस्को: शिक्षा, 2008।

प्रतिलिपि

ग्रेड 6-11 में छात्रों के शैक्षिक और अनुसंधान कार्यों का 1 क्षेत्रीय वैज्ञानिक और व्यावहारिक सम्मेलन "गणित के अनुप्रयुक्त और मौलिक मुद्दे" गणित के अध्ययन के पद्धतिगत पहलू मॉड्यूल गैबोवा एंजेला युरेविना, 10 वीं कक्षा, एमओबीयू "जिम्नैजियम 3" युक्त कार्यों के ग्राफ का निर्माण ” कुडिमकर, पिकुलेवा नादेज़्दा इवानोव्ना, नगरपालिका शैक्षणिक संस्थान "जिमनैजियम 3", कुडिमकर पर्म, 2016 के गणित शिक्षक

2 सामग्री: परिचय...3 पृष्ठ I. मुख्य भाग...6 पृष्ठ 1.1ऐतिहासिक पृष्ठभूमि..6 पृष्ठ 2.कार्यों की मूल परिभाषाएँ और गुण पृष्ठ 2.1 द्विघात फलन..7 पृष्ठ 2.2 रैखिक फलन.. .8 पृष्ठ। 2.3 भिन्नात्मक-तर्कसंगत फ़ंक्शन 8 पी. 3. मापांक 9 पी. 3.1 मॉड्यूल का निर्धारण.. 9 पी. 3.2 मापांक के साथ रैखिक कार्यों के ग्राफ़ बनाने के लिए एल्गोरिदम...9 पी. 3.3 कार्यों के ग्राफ़ का निर्माण "नेस्टेड मॉड्यूल" सूत्र में शामिल। 10 पी। 3.4 फॉर्म के कार्यों के ग्राफ़ बनाने के लिए एल्गोरिदम वाई = ए 1 एक्स एक्स 1 + ए 2 एक्स एक्स ए एन एक्स एक्स एन + एक्स + बी...13 पी। 3.5 द्विघात के ग्राफ़ बनाने के लिए एल्गोरिदम मापांक के साथ फलन.14 पी. 3.6 एल्गोरिथ्म मापांक के साथ एक भिन्नात्मक तर्कसंगत फलन की साजिश रच रहा है। 15पीपी. 4. निरपेक्ष मान के चिह्न के स्थान के आधार पर द्विघात फलन के ग्राफ़ में परिवर्तन..17p. द्वितीय. निष्कर्ष...26 पृष्ठ III. सन्दर्भों और स्रोतों की सूची...27 पृष्ठ IV. परिशिष्ट....28पृ. 2

3 परिचय फ़ंक्शंस के ग्राफ़ का निर्माण स्कूली गणित में सबसे दिलचस्प विषयों में से एक है। हमारे समय के महानतम गणितज्ञ, इज़राइल मोइसेविच गेलफैंड ने लिखा: “ग्राफ़ बनाने की प्रक्रिया सूत्रों और विवरणों को ज्यामितीय छवियों में बदलने का एक तरीका है। यह ग्राफ़िंग सूत्रों और फ़ंक्शंस को देखने और यह देखने का एक साधन है कि वे फ़ंक्शंस कैसे बदलते हैं। उदाहरण के लिए, यदि लिखा है y =x 2, तो आपको तुरंत एक परवलय दिखाई देता है; यदि y = x 2-4, तो आप एक परवलय को चार इकाइयों से नीचे देखते हैं; यदि y = -(x 2 4), तो आप देखेंगे कि पिछला परवलय ठुकरा दिया गया है। किसी सूत्र को तुरंत देखने और उसकी ज्यामितीय व्याख्या करने की यह क्षमता न केवल गणित के अध्ययन के लिए, बल्कि अन्य विषयों के लिए भी महत्वपूर्ण है। यह एक ऐसा कौशल है जो जीवन भर आपके साथ रहता है, जैसे बाइक चलाना, टाइपिंग करना या कार चलाना। मॉड्यूल के साथ समीकरणों को हल करने की मूल बातें छठी-सातवीं कक्षा में प्राप्त की गईं। मैंने इस विशेष विषय को इसलिए चुना क्योंकि मेरा मानना ​​है कि इसके लिए गहन और अधिक गहन शोध की आवश्यकता है। मैं संख्याओं के मापांक, निरपेक्ष मान के चिह्न वाले ग्राफ़ बनाने के विभिन्न तरीकों के बारे में अधिक ज्ञान प्राप्त करना चाहता हूँ। जब मापांक चिह्न को रेखाओं, परवलय और अतिपरवलय के "मानक" समीकरणों में शामिल किया जाता है, तो उनके ग्राफ़ असामान्य और सुंदर भी हो जाते हैं। ऐसे ग्राफ़ बनाने का तरीका सीखने के लिए, आपको बुनियादी आंकड़े बनाने की तकनीक में महारत हासिल करने की ज़रूरत है, साथ ही किसी संख्या के मापांक की परिभाषा को दृढ़ता से जानने और समझने की ज़रूरत है। स्कूली गणित पाठ्यक्रम में, मॉड्यूल के साथ ग्राफ़ पर पर्याप्त गहराई से चर्चा नहीं की जाती है, यही कारण है कि मैं इस विषय पर अपने ज्ञान का विस्तार करना चाहता था और अपना शोध करना चाहता था। मापांक की परिभाषा को जाने बिना, निरपेक्ष मान वाले सबसे सरल ग्राफ का निर्माण करना भी असंभव है। मापांक चिह्न वाले भावों वाले फ़ंक्शन ग्राफ़ की एक विशिष्ट विशेषता 3 है

4 उन बिंदुओं पर किंक की उपस्थिति है जहां मापांक चिह्न के तहत अभिव्यक्ति चिह्न बदलती है। कार्य का उद्देश्य: मापांक चिह्न के अंतर्गत एक चर वाले रैखिक, द्विघात और आंशिक रूप से तर्कसंगत कार्यों के ग्राफ के निर्माण पर विचार करना। उद्देश्य: 1) रैखिक, द्विघात और भिन्नात्मक तर्कसंगत कार्यों के निरपेक्ष मान के गुणों पर साहित्य का अध्ययन करें। 2) निरपेक्ष मान के चिह्न के स्थान के आधार पर फ़ंक्शन ग्राफ़ में परिवर्तनों की जांच करें। 3) समीकरणों को रेखांकन करना सीखें। अध्ययन का उद्देश्य: रैखिक, द्विघात और भिन्नात्मक तर्कसंगत कार्यों के ग्राफ़। शोध का विषय: निरपेक्ष मान के चिह्न के स्थान के आधार पर रैखिक, द्विघात और भिन्नात्मक तर्कसंगत कार्यों के ग्राफ में परिवर्तन। मेरे काम का व्यावहारिक महत्व इसमें निहित है: 1) इस विषय पर अर्जित ज्ञान का उपयोग करना, साथ ही इसे गहरा करना और इसे अन्य कार्यों और समीकरणों पर लागू करना; 2) आगे की शैक्षिक गतिविधियों में अनुसंधान कौशल का उपयोग करना। प्रासंगिकता: रेखांकन कार्य परंपरागत रूप से गणित में सबसे कठिन विषयों में से एक है। हमारे स्नातकों को राज्य परीक्षा और एकीकृत राज्य परीक्षा को सफलतापूर्वक उत्तीर्ण करने की समस्या का सामना करना पड़ता है। अनुसंधान समस्या: जीआईए के दूसरे भाग से मापांक चिह्न वाले कार्यों के ग्राफ़ का निर्माण। अनुसंधान परिकल्पना: जीआईए के दूसरे भाग में कार्यों को हल करने के लिए एक पद्धति का उपयोग, मापांक चिह्न वाले कार्यों के ग्राफ़ बनाने के सामान्य तरीकों के आधार पर विकसित किया गया है, जो छात्रों को इन कार्यों को हल करने की अनुमति देगा 4

5 सचेतन आधार पर, समाधान का सबसे तर्कसंगत तरीका चुनें, समाधान के विभिन्न तरीकों को लागू करें और राज्य परीक्षा को अधिक सफलतापूर्वक पास करें। कार्य में प्रयुक्त अनुसंधान विधियाँ: 1. इस विषय पर गणितीय साहित्य और इंटरनेट संसाधनों का विश्लेषण। 2. अध्ययन की गई सामग्री का पुनरुत्पादन। 3. संज्ञानात्मक और खोज गतिविधि। 4.समस्याओं के समाधान की खोज में डेटा का विश्लेषण और तुलना। 5. परिकल्पनाओं का कथन एवं उनका सत्यापन। 6. गणितीय तथ्यों की तुलना एवं सामान्यीकरण। 7. प्राप्त परिणामों का विश्लेषण. इस कार्य को लिखते समय निम्नलिखित स्रोतों का उपयोग किया गया: इंटरनेट संसाधन, ओजीई परीक्षण, गणितीय साहित्य। 5

6 I. मुख्य भाग 1.1 ऐतिहासिक पृष्ठभूमि। 17वीं शताब्दी के पूर्वार्ध में, एक चर की दूसरे पर निर्भरता के रूप में कार्य का विचार उभरने लगा। इस प्रकार, फ्रांसीसी गणितज्ञ पियरे फ़र्मेट () और रेने डेसकार्टेस () ने एक फ़ंक्शन की कल्पना उसके भुज पर एक वक्र पर एक बिंदु की कोटि की निर्भरता के रूप में की। और अंग्रेजी वैज्ञानिक आइजैक न्यूटन () ने एक फ़ंक्शन को समय के आधार पर बदलते हुए एक गतिशील बिंदु के समन्वय के रूप में समझा। शब्द "फ़ंक्शन" (लैटिन फ़ंक्शन निष्पादन, उपलब्धि से) पहली बार जर्मन गणितज्ञ गॉटफ्राइड लीबनिज़ () द्वारा पेश किया गया था। उन्होंने एक फ़ंक्शन को एक ज्यामितीय छवि (फ़ंक्शन का ग्राफ़) के साथ जोड़ा। इसके बाद, स्विस गणितज्ञ जोहान बर्नौली () और सेंट पीटर्सबर्ग एकेडमी ऑफ साइंसेज के सदस्य, 18 वीं शताब्दी के प्रसिद्ध गणितज्ञ लियोनार्ड यूलर () ने फ़ंक्शन को एक विश्लेषणात्मक अभिव्यक्ति के रूप में माना। यूलर के पास एक फ़ंक्शन की सामान्य समझ एक चर की दूसरे पर निर्भरता के रूप में भी है। शब्द "मॉड्यूल" लैटिन शब्द "मॉड्यूलस" से आया है, जिसका अर्थ है "माप"। यह एक बहुअर्थी शब्द (समानार्थी शब्द) है, जिसके कई अर्थ हैं और इसका उपयोग न केवल गणित में, बल्कि वास्तुकला, भौतिकी, प्रौद्योगिकी, प्रोग्रामिंग और अन्य सटीक विज्ञानों में भी किया जाता है। वास्तुकला में, यह किसी दिए गए वास्तुशिल्प ढांचे के लिए स्थापित माप की प्रारंभिक इकाई है और इसका उपयोग इसके घटक तत्वों के कई अनुपातों को व्यक्त करने के लिए किया जाता है। प्रौद्योगिकी में, यह प्रौद्योगिकी के विभिन्न क्षेत्रों में उपयोग किया जाने वाला एक शब्द है, जिसका कोई सार्वभौमिक अर्थ नहीं है और यह विभिन्न गुणांकों और मात्राओं को निर्दिष्ट करने के लिए कार्य करता है, उदाहरण के लिए, जुड़ाव मापांक, लोचदार मापांक, आदि। 6

7 बल्क मापांक (भौतिकी में) किसी सामग्री में सामान्य तनाव और सापेक्ष बढ़ाव का अनुपात है। 2. फ़ंक्शन की मूल परिभाषाएँ और गुण फ़ंक्शन सबसे महत्वपूर्ण गणितीय अवधारणाओं में से एक है। एक फ़ंक्शन वेरिएबल y की वेरिएबल x पर निर्भरता है जैसे कि वेरिएबल x का प्रत्येक मान वेरिएबल y के एकल मान से मेल खाता है। किसी फ़ंक्शन को निर्दिष्ट करने के तरीके: 1) विश्लेषणात्मक विधि (फ़ंक्शन को गणितीय सूत्र का उपयोग करके निर्दिष्ट किया जाता है); 2) सारणीबद्ध विधि (फ़ंक्शन तालिका का उपयोग करके निर्दिष्ट किया गया है); 3) वर्णनात्मक विधि (फ़ंक्शन मौखिक विवरण द्वारा निर्दिष्ट है); 4) ग्राफ़िकल विधि (फ़ंक्शन एक ग्राफ़ का उपयोग करके निर्दिष्ट किया गया है)। किसी फ़ंक्शन का ग्राफ़ निर्देशांक तल के सभी बिंदुओं का समुच्चय है, जिसके भुज तर्क के मान के बराबर होते हैं, और निर्देशांक फ़ंक्शन के संगत मान के बराबर होते हैं। 2.1 द्विघात फलन सूत्र y = ax 2 + in + c द्वारा परिभाषित एक फलन, जहां x और y चर हैं, और पैरामीटर a, b और c कोई वास्तविक संख्याएं हैं, और a = 0, द्विघात कहलाता है। फलन y=ax 2 +in+c का ग्राफ एक परवलय है; परवलय y=ax 2 +in+c की समरूपता की धुरी एक सीधी रेखा है, a>0 के लिए परवलय की "शाखाएँ" ऊपर की ओर निर्देशित होती हैं, a के लिए<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (एक चर के कार्यों के लिए)। रैखिक कार्यों की मुख्य संपत्ति: फ़ंक्शन की वृद्धि तर्क की वृद्धि के समानुपाती होती है। अर्थात्, फ़ंक्शन प्रत्यक्ष आनुपातिकता का सामान्यीकरण है। एक रैखिक फ़ंक्शन का ग्राफ़ एक सीधी रेखा है, जहां से इसका नाम आता है। यह एक वास्तविक चर के वास्तविक कार्य से संबंधित है। 1) जब, सीधी रेखा भुज अक्ष की धनात्मक दिशा के साथ एक न्यून कोण बनाती है। 2) जब, सीधी रेखा x-अक्ष की धनात्मक दिशा के साथ एक अधिक कोण बनाती है। 3) कोटि अक्ष के साथ रेखा के प्रतिच्छेदन बिंदु का कोटि सूचक है। 4) जब, सीधी रेखा मूल बिंदु से होकर गुजरती है। , 2.3 एक भिन्नात्मक-तर्कसंगत फलन एक भिन्न है जिसका अंश और हर बहुपद हैं। इसका वह रूप है, जहां किसी भी संख्या में चर में बहुपद होते हैं। एक विशेष मामला एक चर के तर्कसंगत कार्य है:, जहां और बहुपद हैं। 1) कोई भी अभिव्यक्ति जो चार अंकगणितीय संक्रियाओं का उपयोग करके चर से प्राप्त की जा सकती है, एक तर्कसंगत कार्य है। 8

9 2) तर्कसंगत कार्यों का सेट अंकगणितीय संचालन और संरचना संचालन के तहत बंद है। 3) किसी भी तर्कसंगत फ़ंक्शन को सरल अंशों के योग के रूप में दर्शाया जा सकता है - इसका उपयोग विश्लेषणात्मक एकीकरण में किया जाता है। यह गैर-ऋणात्मक है, और यदि a ऋणात्मक है तो इसके विपरीत संख्या। a = 3.2 मापांक के साथ एक रैखिक फ़ंक्शन का ग्राफ़ बनाने के लिए एल्गोरिदम y = x फ़ंक्शंस के ग्राफ़ बनाने के लिए आपको यह जानना होगा कि सकारात्मक x के लिए हमारे पास x = x है। इसका मतलब यह है कि तर्क के सकारात्मक मूल्यों के लिए, ग्राफ़ y= x ग्राफ़ y=x के साथ मेल खाता है, अर्थात ग्राफ़ का यह भाग मूल बिंदु से भुज अक्ष पर 45 डिग्री के कोण पर निकलने वाली एक किरण है . एक्स पर< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 निर्माण के लिए, हम अंक (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2) लेते हैं। आइए अब एक ग्राफ y= x-1 बनाएं। यदि A, निर्देशांक (a; a) के साथ ग्राफ y= x पर एक बिंदु है, तो Y कोटि के समान मान के साथ ग्राफ y= x-1 पर बिंदु होगा बिंदु A1(a+1; a) हो। दूसरे ग्राफ़ का यह बिंदु पहले ग्राफ़ के बिंदु A(a; a) से ऑक्स अक्ष के समानांतर दाईं ओर स्थानांतरित करके प्राप्त किया जा सकता है। इसका मतलब यह है कि फ़ंक्शन y= x-1 का पूरा ग्राफ़ ऑक्स अक्ष के समानांतर दाईं ओर 1 स्थानांतरित करके फ़ंक्शन y= x के ग्राफ़ से प्राप्त किया जाता है। आइए ग्राफ़ बनाएं: y= x-1 बनाने के लिए , अंक लें (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1)। 3.3 सूत्र में "नेस्टेड मॉड्यूल" वाले फ़ंक्शन के ग्राफ़ का निर्माण आइए एक विशिष्ट उदाहरण का उपयोग करके निर्माण एल्गोरिदम पर विचार करें एक फ़ंक्शन का ग्राफ़ बनाएं: 10

11 y=i-2-ix+5ii 1. फ़ंक्शन का एक ग्राफ़ बनाएं। 2. हम निचले आधे तल के ग्राफ़ को OX अक्ष के सापेक्ष सममित रूप से ऊपर की ओर प्रदर्शित करते हैं और फ़ंक्शन का ग्राफ़ प्राप्त करते हैं। ग्यारह

12 3. हम फ़ंक्शन के ग्राफ़ को OX अक्ष के सापेक्ष सममित रूप से नीचे की ओर प्रदर्शित करते हैं और फ़ंक्शन का ग्राफ़ प्राप्त करते हैं। 4. हम फ़ंक्शन के ग्राफ़ को OX अक्ष के सापेक्ष सममित रूप से नीचे की ओर प्रदर्शित करते हैं और फ़ंक्शन का एक ग्राफ़ प्राप्त करते हैं। हम OX अक्ष के सापेक्ष फ़ंक्शन के ग्राफ़ को प्रदर्शित करते हैं और एक ग्राफ़ प्राप्त करते हैं। 12

13 6. परिणामस्वरूप, फ़ंक्शन का ग्राफ़ इस 3.4 जैसा दिखता है। फॉर्म y = a 1 x x 1 + a 2 x x a n x x n + ax + b के कार्यों के ग्राफ बनाने के लिए एल्गोरिदम। पिछले उदाहरण में, मापांक चिह्नों को प्रकट करना काफी आसान था। यदि मॉड्यूल के योग अधिक हैं, तो सबमॉड्यूलर अभिव्यक्तियों के संकेतों के सभी संभावित संयोजनों पर विचार करना समस्याग्रस्त है। इस मामले में, फ़ंक्शन का ग्राफ़ कैसे बनाएं? ध्यान दें कि ग्राफ़ एक टूटी हुई रेखा है, जिसके शीर्षों पर भुज -1 और 2 हैं। x = -1 और x = 2 पर, सबमॉड्यूलर अभिव्यक्ति शून्य के बराबर हैं। व्यवहार में, हम ऐसे ग्राफ़ बनाने के नियम के करीब आ गए हैं: फॉर्म y = a 1 x x 1 + a 2 x x a n x x n + ax + b के फ़ंक्शन का ग्राफ़ अनंत चरम लिंक वाली एक टूटी हुई रेखा है। ऐसी टूटी हुई रेखा का निर्माण करने के लिए, इसके सभी शीर्षों (शीर्षों के भुज सबमॉड्यूलर अभिव्यक्तियों के शून्य हैं) और बाएँ और दाएँ अनंत लिंक पर एक नियंत्रण बिंदु जानना पर्याप्त है। 13

14 समस्या. फ़ंक्शन y = x + x 1 + x + 1 को ग्राफ़ करें और इसका सबसे छोटा मान ज्ञात करें। समाधान: 1. सबमॉड्यूलर अभिव्यक्तियों के शून्य: 0; -1; पॉलीलाइन के शीर्ष (0; 2); (-13); (1; 3)। (हम समीकरण में सबमॉड्यूलर अभिव्यक्तियों के शून्य को प्रतिस्थापित करते हैं) 3 दाईं ओर जांच बिंदु (2; 6), बाईं ओर (-2; 6)। हम एक ग्राफ़ बनाते हैं (चित्र 7), फ़ंक्शन का सबसे छोटा मान मॉड्यूल के साथ एक द्विघात फ़ंक्शन का ग्राफ़ बनाने के लिए एल्गोरिदम है, फ़ंक्शन ग्राफ़ को परिवर्तित करने के लिए एल्गोरिदम तैयार करना। 1. फ़ंक्शन y= f(x) का ग्राफ़ प्लॉट करना। मॉड्यूल की परिभाषा के अनुसार, इस फ़ंक्शन को दो फ़ंक्शन के सेट में विभाजित किया गया है। नतीजतन, फ़ंक्शन के ग्राफ़ y= f(x) में दो ग्राफ़ होते हैं: y= f(x) दाएँ आधे तल में, y= f(-x) बाएँ आधे तल में। इसके आधार पर एक नियम (एल्गोरिदम) तैयार किया जा सकता है। फ़ंक्शन y= f(x) का ग्राफ़ फ़ंक्शन y= f(x) के ग्राफ़ से निम्नानुसार प्राप्त किया जाता है: x 0 पर ग्राफ़ संरक्षित है, और x पर< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. फ़ंक्शन y= f(x) का ग्राफ़ बनाने के लिए, आपको पहले x> 0 के लिए फ़ंक्शन y= f(x) का ग्राफ़ बनाना होगा, फिर x के लिए< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 इस ग्राफ़ को प्राप्त करने के लिए, आपको बस पहले प्राप्त ग्राफ़ को तीन इकाइयों को दाईं ओर स्थानांतरित करना होगा। ध्यान दें कि यदि भिन्न के हर में अभिव्यक्ति x + 3 है, तो हम ग्राफ़ को बाईं ओर स्थानांतरित कर देंगे: अब हमें फ़ंक्शन का ग्राफ़ प्राप्त करने के लिए सभी कोटिओं को दो से गुणा करना होगा। अंत में, हम ग्राफ़ को ऊपर की ओर स्थानांतरित करते हैं दो इकाइयाँ: आखिरी चीज़ जो हमें करनी है, वह है किसी दिए गए फ़ंक्शन का ग्राफ़ बनाना, यदि वह मापांक चिह्न के नीचे संलग्न है। ऐसा करने के लिए, हम ग्राफ़ के पूरे भाग को सममित रूप से ऊपर की ओर दर्शाते हैं जिसके निर्देशांक ऋणात्मक हैं (वह भाग जो x-अक्ष के नीचे स्थित है): चित्र 4 16

17 4. निरपेक्ष मान के चिन्ह के स्थान के आधार पर द्विघात फलन के ग्राफ में परिवर्तन। फ़ंक्शन y = x 2 - x -3 1 का एक ग्राफ़ बनाएं) चूंकि x 0 पर x = x है, इसलिए आवश्यक ग्राफ़ परवलय y = 0.25 x 2 - x - 3 के साथ मेल खाता है।<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. बी) इसलिए, मैं x के लिए निर्माण पूरा करता हूं<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 चित्र. 4 फ़ंक्शन y = f (x) का ग्राफ़ तर्क के गैर-नकारात्मक मानों के सेट पर फ़ंक्शन y = f (x) के ग्राफ़ के साथ मेल खाता है और अक्ष के संबंध में इसके सममित है तर्क के नकारात्मक मानों के सेट पर OU. प्रमाण: यदि x 0, तो f (x) = f (x), अर्थात। तर्क के गैर-नकारात्मक मानों के सेट पर, फ़ंक्शन y = f (x) और y = f (x) के ग्राफ़ मेल खाते हैं। चूँकि y = f (x) एक सम फलन है, इसका ग्राफ op-amp के संबंध में सममित है। इस प्रकार, फ़ंक्शन y = f (x) का ग्राफ़ फ़ंक्शन y = f (x) के ग्राफ़ से निम्नानुसार प्राप्त किया जा सकता है: 1. x>0 के लिए फ़ंक्शन y = f (x) का ग्राफ़ बनाएं; 2. एक्स के लिए<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. एक्स के लिए<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 यदि x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 और y पर सममित रूप से प्रतिबिंबित भाग y = f(x)।<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, तो f (x) = f (x), जिसका अर्थ है कि इस भाग में फ़ंक्शन y = f (x) का ग्राफ़ स्वयं फ़ंक्शन y = f (x) के ग्राफ़ के साथ मेल खाता है। यदि f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 चित्र.5 निष्कर्ष: फ़ंक्शन y= f(x) का ग्राफ़ बनाने के लिए 1. फ़ंक्शन y=f(x) का ग्राफ़ बनाएं; 2. उन क्षेत्रों में जहां ग्राफ़ निचले आधे तल में स्थित है, यानी, जहां f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 फ़ंक्शन y = f (x) के ग्राफ़ बनाने पर शोध कार्य, निरपेक्ष मान की परिभाषा और पहले चर्चा किए गए उदाहरणों का उपयोग करके, हम फ़ंक्शन के ग्राफ़ बनाएंगे: y = 2 x - 3 y = x 2-5 x y = x 2 -2 और निष्कर्ष निकालें। फ़ंक्शन y = f (x) का ग्राफ़ बनाने के लिए आपको यह करना होगा: 1. x>0 के लिए फ़ंक्शन y = f (x) का ग्राफ़ बनाएं। 2. ग्राफ़ के दूसरे भाग का निर्माण करें, अर्थात निर्मित ग्राफ़ को ऑप-एम्प के सापेक्ष सममित रूप से प्रतिबिंबित करें, क्योंकि यह फ़ंक्शन सम है. 3. निचले आधे तल में स्थित परिणामी ग्राफ़ के अनुभागों को ऊपरी आधे तल में सममित रूप से OX अक्ष में परिवर्तित करें। फ़ंक्शन y = 2 x - 3 का एक ग्राफ़ बनाएं (मापांक निर्धारित करने की पहली विधि) 1. 2 x - 3 > 0, x >1.5 यानी के लिए y = 2 x - 3 का निर्माण करें। एक्स< -1,5 и х>1.5 a) y = 2x - 3, x>0 के लिए b) x के लिए<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 बी) एक्स के लिए<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) हम एक सीधी रेखा बनाते हैं, जो ऑप-एम्प की धुरी के सापेक्ष निर्मित रेखा के सममित होती है। 3) मैं OX अक्ष के सापेक्ष निचले आधे तल में स्थित ग्राफ के अनुभागों को सममित रूप से प्रदर्शित करता हूं। दोनों ग्राफ़ की तुलना करने पर, हम देखते हैं कि वे समान हैं। 21

22 समस्याओं के उदाहरण उदाहरण 1. फ़ंक्शन y = x 2 6x +5 के ग्राफ़ पर विचार करें। चूँकि x का वर्ग किया जाता है, संख्या x के चिह्न की परवाह किए बिना, वर्ग करने के बाद यह धनात्मक होगा। इससे यह निष्कर्ष निकलता है कि फ़ंक्शन y = x 2-6x +5 का ग्राफ़ फ़ंक्शन y = x 2-6x +5 के ग्राफ़ के समान होगा, अर्थात। किसी फ़ंक्शन का ग्राफ़ जिसमें निरपेक्ष मान चिह्न नहीं है (चित्र 2)। चित्र 2 उदाहरण 2. फ़ंक्शन y = x 2 6 x +5 के ग्राफ़ पर विचार करें। किसी संख्या के मापांक की परिभाषा का उपयोग करते हुए, हम सूत्र y = x 2 6 x +5 को प्रतिस्थापित करते हैं। अब हम टुकड़े-टुकड़े निर्भरता असाइनमेंट से निपट रहे हैं जो हमारे लिए परिचित है। हम इस प्रकार एक ग्राफ़ बनाएंगे: 1) एक परवलय y = x 2-6x +5 बनाएं और 22 वाले भाग पर गोला बनाएं।

23 x के गैर-नकारात्मक मानों से मेल खाता है, अर्थात। ओय अक्ष के दाईं ओर स्थित भाग। 2) उसी निर्देशांक तल में, एक परवलय y = x 2 +6x +5 का निर्माण करें और उस भाग पर गोला बनाएं जो x के नकारात्मक मानों से मेल खाता हो, अर्थात। ओय अक्ष के बाईं ओर स्थित भाग। परवलय के वृत्ताकार भाग मिलकर फलन y = x 2-6 x +5 का ग्राफ बनाते हैं (चित्र 3)। चित्र 3 उदाहरण 3. फ़ंक्शन y = x 2-6 x +5 के ग्राफ़ पर विचार करें। क्योंकि समीकरण y = x 2 6x +5 का ग्राफ़ मापांक चिह्न के बिना फ़ंक्शन के ग्राफ़ के समान है (उदाहरण 2 में चर्चा की गई है), यह इस प्रकार है कि फ़ंक्शन y = x 2 6 x +5 का ग्राफ़ समान है फ़ंक्शन y = x 2 6 x +5 के ग्राफ़ पर, उदाहरण 2 में माना गया है (चित्र 3)। उदाहरण 4. आइए फ़ंक्शन y = x 2 6x +5 का एक ग्राफ़ बनाएं। ऐसा करने के लिए, आइए फ़ंक्शन y = x 2-6x का एक ग्राफ बनाएं। इससे फ़ंक्शन y = x 2-6x का एक ग्राफ़ प्राप्त करने के लिए, आपको परवलय के प्रत्येक बिंदु को एक नकारात्मक कोटि के साथ समान भुज वाले एक बिंदु से, लेकिन विपरीत (सकारात्मक) कोटि के साथ प्रतिस्थापित करने की आवश्यकता है। दूसरे शब्दों में, x-अक्ष के नीचे स्थित परवलय के भाग को x-अक्ष के सापेक्ष उसके सममित रेखा से प्रतिस्थापित किया जाना चाहिए। क्योंकि हमें फ़ंक्शन y = x 2-6x +5 का एक ग्राफ़ बनाने की आवश्यकता है, फिर जिस फ़ंक्शन का ग्राफ़ हमने y = x 2-6x माना है उसे y-अक्ष के साथ 5 इकाइयों तक ऊपर उठाने की आवश्यकता है (चित्र 4) ). 23

24 चित्र.4 उदाहरण 5. आइए फ़ंक्शन y = x 2-6x+5 का एक ग्राफ़ बनाएं। ऐसा करने के लिए, हम सुप्रसिद्ध टुकड़ेवार फ़ंक्शन का उपयोग करेंगे। आइए फलन y = 6x +5 6x + 5 = 0 पर शून्य ज्ञात करें। आइए दो मामलों पर विचार करें: 1) यदि, तो समीकरण y = x 2 6x -5 का रूप लेगा। आइए इस परवलय का निर्माण करें और उस भाग पर गोला बनाएं। 2) यदि, तो समीकरण y = x 2 + 6x +5 का रूप लेता है। आइए इस परवलय को खड़ा करें और इसके उस हिस्से पर गोला बनाएं जो निर्देशांक वाले बिंदु के बाईं ओर स्थित है (चित्र 5)। 24

25 चित्र.5 उदाहरण6. आइए फ़ंक्शन y = x 2 6 x +5 का एक ग्राफ़ बनाएं। ऐसा करने के लिए, हम फ़ंक्शन y = x 2-6 x +5 का एक ग्राफ़ बनाएंगे। हमने यह ग्राफ़ उदाहरण 3 में बनाया है। चूँकि हमारा फ़ंक्शन पूरी तरह से मापांक चिह्न के अंतर्गत है, फ़ंक्शन y = x 2 6 x +5 का ग्राफ़ बनाने के लिए, हमें फ़ंक्शन y = x 2 के ग्राफ़ के प्रत्येक बिंदु की आवश्यकता है। ऋणात्मक कोटि वाले 6 x + 5 को समान भुज वाले, लेकिन विपरीत (सकारात्मक) कोटि वाले एक बिंदु से प्रतिस्थापित किया जाना चाहिए, अर्थात। ऑक्स अक्ष के नीचे स्थित परवलय के भाग को ऑक्स अक्ष के सापेक्ष इसके सममित रेखा से प्रतिस्थापित किया जाना चाहिए (चित्र 6)। चित्र 6 25

26 II. निष्कर्ष "गणितीय जानकारी का उपयोग कुशलतापूर्वक और उपयोगी रूप से तभी किया जा सकता है जब इसे रचनात्मक रूप से महारत हासिल हो, ताकि छात्र स्वयं देख सके कि वह अपने दम पर इस तक कैसे पहुंच सकता है।" एक। कोलमोगोरोव। ये समस्याएँ नौवीं कक्षा के छात्रों के लिए बहुत रुचिकर हैं, क्योंकि ये OGE परीक्षाओं में बहुत आम हैं। फ़ंक्शंस के डेटा ग्राफ़ बनाने की क्षमता आपको परीक्षा को अधिक सफलतापूर्वक उत्तीर्ण करने की अनुमति देगी। फ्रांसीसी गणितज्ञ पियरे फ़र्मेट () और रेने डेसकार्टेस () ने एक फ़ंक्शन की कल्पना उसके भुज पर एक वक्र पर एक बिंदु की कोटि की निर्भरता के रूप में की। और अंग्रेजी वैज्ञानिक आइजैक न्यूटन () ने एक फ़ंक्शन को समय के आधार पर बदलते हुए एक गतिशील बिंदु के समन्वय के रूप में समझा। 26

27 III. संदर्भों और स्रोतों की सूची 1. गैलिट्स्की एम.एल., गोल्डमैन ए.एम., ज़वाविच एल.आई. ग्रेड 8-9 के लिए बीजगणित में समस्याओं का संग्रह: पाठ्यपुस्तक। स्कूली छात्रों के लिए मैनुअल। और उन्नत कक्षाएं अध्ययन गणित द्वितीय संस्करण. एम.: ज्ञानोदय, डोरोफीव जी.वी. गणित। बीजगणित. कार्य. डेटा विश्लेषण। 9वीं कक्षा: एम34 शैक्षिक। सामान्य शिक्षा अध्ययन के लिए. स्थापना द्वितीय संस्करण, स्टीरियोटाइप। एम.: बस्टर्ड, सोलोमोनिक वी.एस. गणित में प्रश्नों और समस्याओं का संग्रह एम.: "हायर स्कूल", यशचेंको आई.वी. जीआईए. गणित: मानक परीक्षा विकल्प: विकल्पों के बारे में.एम.: "राष्ट्रीय शिक्षा", पी. 5. यशचेंको आई.वी. OGE. गणित: मानक परीक्षा विकल्प: विकल्पों के बारे में.एम.: "राष्ट्रीय शिक्षा", पी. 6. यशचेंको आई.वी. OGE. गणित: मानक परीक्षा विकल्प: विकल्पों के बारे में.एम.: "राष्ट्रीय शिक्षा", के साथ

28 परिशिष्ट 28

29 उदाहरण 1. फ़ंक्शन y = x 2 8 x समाधान का ग्राफ़ बनाएं। आइए फ़ंक्शन की समता निर्धारित करें। y(-x) का मान y(x) के मान के समान है, इसलिए यह फ़ंक्शन सम है। तब इसका ग्राफ ओय अक्ष के प्रति सममित होता है। हम x 0 के लिए फ़ंक्शन y = x 2 8x + 12 प्लॉट करते हैं और नकारात्मक x के लिए Oy के संबंध में ग्राफ को सममित रूप से प्रदर्शित करते हैं (चित्र 1)। उदाहरण 2. फॉर्म y = x 2 8x का निम्नलिखित ग्राफ़ इसका मतलब है कि फ़ंक्शन का ग्राफ़ निम्नानुसार प्राप्त किया जाता है: फ़ंक्शन y = x 2 8x + 12 का एक ग्राफ़ बनाएं, ग्राफ़ का वह भाग छोड़ दें जो ऊपर है ऑक्स अक्ष अपरिवर्तित है, और ग्राफ़ का वह भाग जो एब्सिस्सा अक्ष के नीचे स्थित है और ऑक्स अक्ष के सापेक्ष सममित रूप से प्रदर्शित होता है (चित्र 2)। उदाहरण 3. फ़ंक्शन y = x 2 8 x + 12 का ग्राफ बनाने के लिए, परिवर्तनों का एक संयोजन किया जाता है: y = x 2 8x + 12 y = x 2 8 x + 12 y = x 2 8 x उत्तर: चित्र 3. उदाहरण 4 मापांक चिह्न के अंतर्गत अभिव्यक्ति, बिंदु x=2/3 पर चिह्न बदलता है। एक्स पर<2/3 функция запишется так: 29

30 x>2/3 के लिए फ़ंक्शन इस प्रकार लिखा जाएगा: यानी, बिंदु x=2/3 हमारे समन्वय विमान को दो क्षेत्रों में विभाजित करता है, जिनमें से एक में (दाईं ओर) हम एक फ़ंक्शन बनाते हैं और दूसरे में (बाईं ओर) हम फ़ंक्शन का एक ग्राफ़ बनाते हैं: उदाहरण 5 अगला ग्राफ़ भी टूटा हुआ है, लेकिन इसमें दो ब्रेक पॉइंट हैं, क्योंकि इसमें मापांक चिह्नों के अंतर्गत दो अभिव्यक्तियाँ हैं: आइए देखें कि किन बिंदुओं पर सबमॉड्यूलर अभिव्यक्तियाँ चिह्न बदलती हैं: आइए देखें समन्वय रेखा पर सबमॉड्यूलर अभिव्यक्तियों के लिए चिह्नों को व्यवस्थित करें: 30

31 हम पहले अंतराल पर मॉड्यूल का विस्तार करते हैं: दूसरे अंतराल पर: तीसरे अंतराल पर: इस प्रकार, अंतराल (- ; 1.5] पर हमारे पास पहले समीकरण द्वारा लिखा गया एक ग्राफ होता है, अंतराल पर दूसरे समीकरण द्वारा लिखा गया एक ग्राफ होता है , और अंतराल पर)