Jocuri

Limita și continuitatea unei funcții a unei variabile - document. Limita unei funcţii a unui argument continuu Conceptul de continuitate a unei funcţii

Limită și continuitate

funcţiile unei variabile

3.1.1. Definiție. Număr A X lupta pentru X 0 dacă pentru orice număr
există un număr
(
), iar condiția va fi îndeplinită:

Dacă
, Acea
.

(Simbolism:
).

Dacă graficul indică G funcții

, Când se apropie de punctul infinit de aproape (acestea.
), (vezi Fig. 3.1), atunci această împrejurare este echivalentul geometric al faptului că funcția
la
are o valoare limită (limită) A(simbolism:
).

Graficul funcției,

Orez. 3.1

De remarcat că la determinarea valorii limită (limită) a unei funcții la X lupta pentru X 0 nu spune nimic despre comportamentul funcției la punctul X 0 . Chiar la punctul X Funcția 0 poate să nu fie definită, poate fi
, pot fi
.

Dacă
, atunci funcția se numește infinitezimal pentru
.

Se numește intervalul  - vecinătatea unui punct X 0 cu un centru ciobit. Folosind acest nume, putem spune astfel: dacă pentru orice număr există un număr, iar condiția va fi îndeplinită: dacă
, Acea
.

3.1.2. Definiție. , dacă pentru orice convergent către X 0 secvențe
ulterior
converge spre A.

3.1.3. Să demonstrăm echivalența definițiilor secțiunilor 3.1.1 și 3.1.2

Fie mai întâi în sensul primei definiții și fie
(
), apoi toate , cu excepția numărului lor finit, satisfac inegalitatea
, Unde  selectat de  în sensul primei definiții, i.e.
, adică prima definiţie o implică pe a doua. Lasă-l acum
în sensul celei de-a doua definiţii şi să presupunem că în sensul celei de-a doua definiţii
, adică pentru unii pentru arbitrar mic (de exemplu, pentru
) a fost găsită secvența
, dar in acelasi timp
. Am ajuns la o contradicție, așadar, prima decurge din a doua definiție.

3.1.4. Echivalența acestor definiții este deosebit de convenabilă, deoarece toate teoremele demonstrate anterior privind proprietățile limitelor pentru secvențe se transferă aproape automat la caz nou. Este necesar doar să clarificăm conceptul de limitare. Teorema corespunzătoare are următoarea formulă:

Dacă
, atunci se limitează la oarecare  - vecinătate a punctului X 0 cu un centru ciobit.

3.2.1.Teorema. Lăsa
,
,

Apoi,
,

3.2.2. Lăsa

- arbitrar, convergent către X 0 secvență de valori ale argumentelor funcției și
. Secvențe de potrivire
Și
valorile acestor funcții au limite AȘi B. Dar apoi, în virtutea teoremei din Secțiunea 2.13.2, secvențele
,
Și
au limite egale în mod corespunzător A +B,
Și
. Conform definiției limitei unei funcții la un punct (vezi secțiunea 2.5.2), aceasta înseamnă că

,
,

3.2.3. Teorema. Dacă
,
, și în oarecare vecinătate

apare

3.2.4. Prin definiția limitei unei funcții într-un punct X 0 pentru orice secvență
astfel încât

succesiunea valorilor funcției are o limită egală cu A. Asta înseamnă că pentru oricine
există un număr
efectuat . La fel, pentru secvență
există un număr
astfel încât pentru orice număr
efectuat . Alegerea
, găsim asta pentru toată lumea
efectuat . Din acest lanț de inegalități avem pentru orice , ceea ce înseamnă că
.

3.2.5. Definiție. Număr A se numește valoarea limită (limită) a funcției la X lupta pentru X 0 în dreapta (simbolism:
), dacă pentru orice număr există un număr () și este îndeplinită condiția: dacă
, Acea
.

Mulțimea se numește dreapta  - vecinătatea punctului X 0 . Conceptul de valoare limită (limită) din stânga este definit în mod similar (
).

3.2.6. Teorema. Funcția la are o valoare limită (limită) egală cu A atunci și numai când

3.3.1. Definiție. Număr A se numește valoarea limită (limită) a funcției la X tinzând spre infinit, dacă pentru orice număr există un număr
(
) și va fi îndeplinită următoarea condiție:

Dacă
, Acea .

(Simbolism:
.)

O multime de
numit D- vecinătatea infinitului.

3.3.2. Definiție. Număr A se numește valoarea limită (limită) a funcției la X tinzând spre plus infinit, dacă pentru orice număr există un număr D() și va fi îndeplinită condiția:

Dacă
, Acea .

(Simbolism:
).

Dacă graficul indică G funcții
cu creștere nelimitată
se apropie la infinit de o singură linie orizontală
(vezi Fig. 3.2), atunci această împrejurare este echivalentul geometric al faptului că funcția
la
are o valoare limită (limită) egală cu numărul A(simbolism:
).

Graficul unei funcții
,

O multime de
numit D-cartier plus infinit.

Conceptul de limită la
.

Exerciții.

Prezentați toate teoremele despre limite aplicate cazurilor:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. Definiție. Funcția este numită la infinit mare functie(sau pur și simplu infinit de mare) la , dacă pentru orice număr

, satisfacerea inegalității, inegalitatea este satisfăcută
.

(Simbolism:
.)

Dacă este îndeplinită
, apoi scriu
.

3.4.2. Teorema. Lăsa
Și
la
.

Apoi
este o funcție infinit de mare pentru .

3.4.3. Să fie un număr arbitrar. Deoarece este o funcție infinitezimală pentru , atunci pentru număr
există un număr astfel încât pentru toată lumea X astfel încât inegalitatea este valabilă
, dar apoi pentru același lucru X inegalitatea va fi satisfăcută
. Acestea. este o funcție infinit de mare pentru .

3.4.4.Teorema. Fie o funcție infinit de mare pentru și pentru .

Atunci este o funcție infinitezimală pentru .

(Această teoremă este demonstrată într-un mod similar cu teorema din Secțiunea 3.8.2.)

3.4.5. Funcţie
se numeşte nemărginit când
, dacă pentru orice număr
și orice vecinătate δ a punctului puteți specifica un punct X din acest cartier astfel încât
.

3.5.1. DEFINIȚIE. Funcția este numită continuu la punct , Dacă
.

Ultima condiție poate fi scrisă astfel:

Această notație înseamnă că pentru funcțiile continue semnul limitei și semnul funcției pot fi schimbate

Sau cam asa: . Sau din nou, ca la început.

Să notăm
. Apoi
și =
iar ultima formă de înregistrare va lua forma

Expresia de sub semnul limită reprezintă incrementul punctului funcției cauzat de increment
argument X la punctul, de obicei notat ca
. Ca rezultat, obținem următoarea formă de scriere a condiției pentru continuitatea unei funcții într-un punct

care se numește „definiția de lucru” a continuității unei funcții într-un punct.

Funcția este numită continuu la punct stânga, Dacă
.

Funcția este numită continuu la punct pe dreapta, Dacă
.

3.5.2. Exemplu.
. Această funcție este continuă pentru orice . Folosind teoreme privind proprietățile limitelor, obținem imediat: orice funcție rațională este continuă în fiecare punct în care este definită, adică. functia formei
.

EXERCIȚII.

3.6.1. Manualul școlar dovedește (la nivel inalt rigoare) că
(prima limită remarcabilă). Din considerente geometrice vizuale rezultă imediat că
. Rețineți că din inegalitatea din stânga rezultă și că
, adică care este functia
este continuă la zero. De aici nu este deloc greu de demonstrat continuitatea tuturor funcții trigonometriceîn toate punctele în care sunt definite. De fapt, când
ca un produs este infinit funcție mică
pe funcție limitată
.

3.6.2. (a doua limită minunată). După cum știm deja

Unde trece prin numere naturale. Se poate arăta că
. în plus
.

EXERCIȚII.

3.7.1. TEOREMA (asupra continuitatii unei functii complexe).

Dacă funcţia
este continuă într-un punct şi
, și funcția
continuu la un punct , apoi o funcție complexă
este continuu la punct.

3.7.2. Valabilitatea acestei afirmații decurge imediat din definiția continuității, scrisă astfel:

3.8.1. TEOREMA. Funcţie este continuă în fiecare punct (
).

3.8.2. Dacă considerăm rezonabil ca funcţia
este definită pentru orice și este strict monotonă (strict descrescătoare pentru
, crescând strict cu
), atunci dovada nu este dificilă.

La
avem:

acestea. când avem
, ceea ce înseamnă funcția este continuă la .

La
totul se reduce la precedentul:

La
.

La
funcţie
este constantă pentru toți, deci continuă.

3.9.1. TEOREMA (despre coexistența și continuitatea funcției inverse).

Fie ca o funcție continuă să scadă strict (strict să crească) într-o zonă δ - a punctului,
. Apoi, în unele ε - vecinătate a punctului există o funcție inversă
, care scade strict (crește strict) și este continuă în ε - vecinătatea punctului.

3.9.2. Aici demonstrăm doar continuitatea funcției inverse în punctul .

Să luăm, punct y situat între puncte
Și
, prin urmare, dacă
, Acea
, Unde .

3.10.1. Deci, orice operații aritmetice permise pe funcții continue conduc din nou la funcții continue. Formarea de funcții complexe și inverse din ele nu strica continuitatea. Prin urmare, cu un anumit grad de responsabilitate, putem afirma că toate funcțiile elementare sunt continue pentru toate valorile admisibile ale argumentului.

EXERCIȚIU.

Demonstrează asta
la
(o altă formă a celei de-a doua limite minunate).

3.11.1. Calculul limitelor este mult simplificat dacă folosim conceptul de infinitezimale echivalente. Este convenabil să se generalizeze conceptul de echivalență în cazul funcțiilor arbitrare.

Definiție. Se spune că funcțiile și sunt echivalente pentru dacă
(în loc de poti sa scrii
,
,
,
,
).

Notația folosită f ~ g.

Echivalența are următoarele proprietăți

Următoarea listă de infinitezimale echivalente trebuie reținută:

~
la
; (1)

~ la ; (2)

~
la ; (3)

~ la ; (4)

~ la ; (5)

~ la ; (6)

~ la ; (7)

~ p la ; (8)

~ la
; (9)

~
la . (10)

Aici și nu pot fi variabile independente, ci funcții
Și
tinzând spre zero și, respectiv, unu sub un anumit comportament X. De exemplu,

~
la
,

~
la
.

Echivalența (1) este o altă formă de scriere a primei limite remarcabile. Echivalențele (2), (3), (6) și (7) pot fi dovedite direct. Echivalența (4) se obține din (1) luând în considerare proprietatea 2) a echivalențelor:

~
.

În mod similar, (5) și (7) sunt obținute din (2) și (6). Într-adevăr

~
,

~
.

Echivalența lui (8) este dovedită prin aplicarea succesivă a (7) și (6):

și (9) și (10) sunt obținute din (6) și (8) prin înlocuire
.

3.11.2. Teorema. Când calculați limite într-un produs și raport, puteți schimba funcțiile cu unele echivalente. Și anume, dacă ~
, atunci fie ambele limite nu există simultan și
, sau ambele aceste limite nu există simultan.

Să demonstrăm prima egalitate. Lasă una dintre limite, să zicem,
există. Apoi

3.11.3. Fie ( să fie un număr sau un simbol,
sau
). Vom lua în considerare comportamentul diferitelor b.m. funcții (așa vom prescurta termenul infinitezimal).

DEFINIȚII.
și se numesc echivalent b.m. funcții pentru , dacă
(la ).

o vom numi b.m. Mai mult ordin înalt decât b.m. funcţie
, Dacă
(la ).

3.11.4. Dacă și echivalentul b.m. funcții, atunci
există b.m. funcţie de ordin mai mare decât
si ce. - h.m. funcția la, în care pentru tot x și, dacă în acest punct funcția se numește punct de discontinuitate amovibil. are o discontinuitate de al doilea fel. Punctul în sine Test

La colocviu. Secțiuni: " LimităȘi continuitatefuncții valabil variabil" funcțiiunuvariabil", „Calcul diferențial funcții mai multe variabile"

Subiecte și exemple de teste și întrebări (teste colocviu calcule standard individuale) Testul semestrului I nr.1 secțiunea „limita și continuitatea unei funcții a unei variabile reale”

Test

La colocviu. Secțiuni: " LimităȘi continuitatefuncții valabil variabil", „Calcul diferențial funcțiiunuvariabil", „Calcul diferențial funcții mai multe variabile". Succesiunea de numere...

Test

Subiecte și exemple de teme și întrebări de testare (lucrări de testare colocvii de calcule standard individuale) Semestrul I secțiune de lucru „limita și continuitatea unei funcții a unei variabile reale”

Test

Cursul 19 limita și continuitatea unei funcții a mai multor variabile

Lectura

... LimităȘi continuitatefuncții mai multe variabile. 19.1. Concept funcții mai multe variabile. Prin revizuire funcții mai multe variabile... proprietăți funcțiiunuvariabil, continuu pe segment. Consultați Proprietăți funcții, continuu pe...

Continuitatea funcției. Puncte de rupere.

Taurul merge, se leagănă, suspină în timp ce merge:
- Oh, se epuizează tabla, acum o să cad!

În această lecție vom examina conceptul de continuitate a unei funcții, clasificarea punctelor de discontinuitate și comunitatea problema practica studii de continuitate a funcţiilor. Din chiar numele subiectului, mulți ghicesc intuitiv despre ce se va discuta și cred că materialul este destul de simplu. Asta este adevărat. Dar sarcinile simple sunt cel mai adesea pedepsite pentru neglijență și pentru o abordare superficială a rezolvării lor. Prin urmare, vă recomand să studiați articolul cu mare atenție și să surprindeți toate subtilitățile și tehnicile.

Ce trebuie să știi și să poți face? Nu prea mult. Pentru a învăța bine lecția, trebuie să înțelegeți ce este limita unei funcții. Pentru cititorii cu un nivel scăzut de pregătire, este suficient să înțeleagă articolul Limitele funcțiilor. Exemple de soluțiiși să privească sens geometric limită în manual Grafice și proprietăți ale funcțiilor elementare. De asemenea, este recomandabil să vă familiarizați cu transformări geometrice ale graficelor, deoarece practica în majoritatea cazurilor presupune construirea unui desen. Perspectivele sunt optimiste pentru toată lumea și chiar și un fierbător plin va putea face față singur sarcinii în următoarea oră sau două!

Continuitatea funcției. Puncte de întrerupere și clasificarea lor

Conceptul de continuitate a funcției

Să luăm în considerare o funcție care este continuă pe întreaga linie numerică:

Sau, pentru a spune mai succint, funcția noastră este continuă (setul numere reale).

Care este criteriul „filistin” al continuității? Evident, graficul unei funcții continue poate fi desenat fără a ridica creionul de pe hârtie.

În acest caz, este necesar să le distingem clar pe cele două concepte simple: domeniul unei funcțiiȘi continuitatea functiei. În general nu e acelasi lucru. De exemplu:

Această funcție definit pe întreaga linie numerică, adică pt toata lumea Semnificația lui „x” are propriul său sens de „y”. În special, dacă , atunci . Rețineți că celălalt punct este punctat, deoarece prin definiția unei funcții, valoarea argumentului trebuie să corespundă singurul lucru valoarea functiei. Prin urmare, domeniu funcția noastră: .

in orice caz această funcție nu este continuă! Este destul de evident că în acel moment ea suferă decalaj. Termenul este, de asemenea, destul de inteligibil și vizual, aici creionul va trebui oricum rupt de pe hârtie. Puțin mai târziu ne vom uita la clasificarea punctelor de întrerupere.

Continuitatea unei funcții într-un punct și pe un interval

Într-o anumită problemă de matematică, putem vorbi despre continuitatea unei funcții într-un punct, continuitatea unei funcții pe un interval, un semi-interval sau continuitatea unei funcții pe un segment. Acesta este, nu există „simple continuitate”– funcția poate fi continuă UNEDE. Și „bloca de bază” fundamentală a tuturor celorlalte este continuitatea functiei la punct .

Teoria analizei matematice oferă o definiție a continuității unei funcții într-un punct folosind vecinătăți „delta” și „epsilon”, dar în practică există o definiție diferită în uz, căreia îi vom acorda o atenție deosebită.

Mai întâi să ne amintim limite unilaterale care a izbucnit în viața noastră în prima lecție despre graficele de funcții. Luați în considerare o situație de zi cu zi:

Dacă ne apropiem de axă până la punct stânga(săgeată roșie), atunci valorile corespunzătoare ale „jocurilor” vor merge de-a lungul axei până la punct (săgeata purpurie). Din punct de vedere matematic, acest fapt este fixat folosind limita din stanga:

Fiți atenți la intrare (se citește „x tinde spre ka în stânga”). „Aditivul” „minus zero” simbolizează , în esență asta înseamnă că ne apropiem de numărul din partea stângă.

În mod similar, dacă te apropii de punctul „ka” pe dreapta (săgeată albastră), atunci „jocurile” vor ajunge la aceeași valoare, dar de-a lungul săgeții verzi și limita dreapta va fi formatat după cum urmează:

„Aditiv” simbolizează , iar intrarea spune: „x tinde spre ka pe dreapta”.

Dacă limitele unilaterale sunt finite și egale(ca și în cazul nostru): , atunci vom spune că există o limită GENERALĂ. Este simplu, limita generală este „obișnuită” noastră limita unei funcții, egal cu un număr finit.

Rețineți că dacă funcția nu este definită la (scoateți punctul negru de pe ramura graficului), atunci calculele de mai sus rămân valabile. După cum sa menționat deja de mai multe ori, în special în articol asupra funcţiilor infinitezimale, expresiile înseamnă că „x” infinit de aproape se apropie de subiect, în timp ce NU CONTEAZĂ, indiferent dacă funcția în sine este definită la un punct dat sau nu. Un bun exemplu îl vom găsi în paragraful următor, când se analizează funcția.

Definiție: o funcție este continuă într-un punct dacă limita funcției într-un punct dat este egală cu valoarea funcției în acel punct: .

Definiția este detaliată în următorii termeni:

1) Funcția trebuie definită la punctul, adică valoarea trebuie să existe.

2) Trebuie să existe o limită generală a funcției. După cum sa menționat mai sus, aceasta implică existența și egalitatea limitelor unilaterale: .

3) Limita funcției într-un punct dat trebuie să fie egală cu valoarea funcției în acest punct: .

Dacă este încălcat cel puțin unul dintre cele trei condiții, atunci funcția își pierde proprietatea de continuitate în punctul .

Continuitatea unei funcții pe un interval este formulată ingenios și foarte simplu: o funcție este continuă pe interval dacă este continuă în fiecare punct al intervalului dat.

În special, multe funcții sunt continue pe un interval infinit, adică pe mulțimea numerelor reale. Aceasta este o funcție liniară, polinoame, exponențială, sinus, cosinus etc. Și, în general, orice funcţie elementară continuă pe ea domeniul definirii, de exemplu, funcţie logaritmică este continuă pe interval. Sperăm că până acum aveți o idee destul de bună despre cum arată graficele funcțiilor de bază. Mai mult informatii detaliate despre continuitatea lor poate fi cules de la un om bun pe nume Fichtenholtz.

Cu continuitatea unei funcții pe un segment și semiintervale, totul nu este, de asemenea, dificil, dar este mai potrivit să vorbim despre asta în clasă despre găsirea valorilor minime și maxime ale unei funcții pe un segment, dar deocamdată să nu ne facem griji.

Clasificarea punctelor de întrerupere

Viața fascinantă a funcțiilor este bogată în tot felul de puncte speciale, iar punctele de întrerupere sunt doar una dintre paginile biografiei lor.

Notă : pentru orice eventualitate, mă voi opri asupra unui punct elementar: punctul de rupere este întotdeauna un singur punct– nu există „mai multe puncte de pauză la rând”, adică nu există un „interval de pauză”.

Aceste puncte, la rândul lor, sunt împărțite în două grupuri mari: rupturi de primul felȘi rupturi de al doilea fel. Fiecare tip de decalaj are propriul său caracteristici la care ne vom uita chiar acum:

Punct de discontinuitate de primul fel

Dacă condiția de continuitate este încălcată la un punct și limite unilaterale finit , atunci se numește punct de discontinuitate de primul fel.

Să începem cu cel mai optimist caz. Conform ideii originale a lecției, am vrut să spun teoria „în vedere generala”, dar pentru a demonstra realitatea materialului, am optat pentru varianta cu personaje specifice.

Trist, ca o fotografie cu tineri căsătoriți în fundal Flacara vesnica, dar următorul cadru este în general acceptat. Să reprezentăm graficul funcției din desen:

Această funcție este continuă pe întreaga linie numerică, cu excepția punctului. Și de fapt, numitorul nu poate fi egal cu zero. Cu toate acestea, în conformitate cu sensul limitei, putem infinit de aproape abordați „zero” atât din stânga, cât și din dreapta, adică există limite unilaterale și, evident, coincid:
(Condiția nr. 2 de continuitate este îndeplinită).

Dar funcția nu este definită în acest punct, prin urmare, Condiția nr. 1 de continuitate este încălcată, iar funcția suferă o discontinuitate în acest punct.

O pauză de acest tip (cu cea existentă limita generala) sunt numite gol reparabil. De ce detașabil? Pentru că funcția poate redefiniți la punctul de rupere:

Pare ciudat? Pot fi. Dar o astfel de notație a funcției nu contrazice nimic! Acum decalajul este închis și toată lumea este fericită:

Să efectuăm o verificare formală:

2) – există o limită generală;
3)

Astfel, toate cele trei condiții sunt îndeplinite, iar funcția este continuă într-un punct prin definiția continuității unei funcții într-un punct.

Cu toate acestea, cei care urăsc matan pot defini funcția într-un mod prost, de exemplu :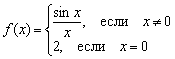

Este interesant că aici sunt îndeplinite primele două condiții de continuitate:
1) – funcția este definită la un punct dat;
2) – există o limită generală.

Dar a treia graniță nu a fost depășită: , adică limita funcției în punct nu este egal valoarea unei funcții date într-un punct dat.

Astfel, la un moment dat funcția suferă o discontinuitate.

Al doilea caz, mai trist, este numit ruptura de primul fel cu un salt. Iar tristețea este evocată de limitele unilaterale care finită și diferită. Un exemplu este prezentat în al doilea desen al lecției. Un astfel de decalaj apare de obicei când funcții definite pe bucăți, care au fost deja menționate în articol despre transformările grafice.

Luați în considerare funcția pe bucăți și îi vom finaliza desenul. Cum se construiește un grafic? Foarte simplu. Pe o jumătate de interval desenăm un fragment de parabolă ( Culoarea verde), pe interval – un segment de linie dreaptă (roșu) și pe un semiinterval – o linie dreaptă (albastru).

Mai mult, din cauza inegalității, valoarea este determinată pentru funcția pătratică (punctul verde), iar din cauza inegalității, valoarea este determinată pentru funcție liniară(punct albastru):

În cel mai dificil caz, ar trebui să recurgeți la construcția punct cu punct a fiecărei piese din grafic (vezi prima lecție despre graficele funcțiilor).

Acum ne va interesa doar subiectul. Să-l examinăm pentru continuitate:

2) Să calculăm limite unilaterale.

În stânga avem un segment de linie roșie, deci limita din stânga este:

În dreapta este linia dreaptă albastră, iar limita din dreapta:

Drept urmare, am primit numere finite, si ei nu este egal. Din moment ce limite unilaterale finită și diferită: , atunci funcția noastră tolerează discontinuitate de primul fel cu un salt.

Este logic că decalajul nu poate fi eliminat - funcția într-adevăr nu poate fi definită și „lipită împreună”, ca în exemplul anterior.

Puncte de discontinuitate de al doilea fel

De obicei, toate celelalte cazuri de ruptură sunt clasificate inteligent în această categorie. Nu voi enumera totul, pentru că în practică, în 99% dintre problemele veți întâmpina decalaj nesfârșit– când este stângaci sau dreptaci și, mai des, ambele limite sunt infinite.

Și, desigur, cea mai evidentă imagine este hiperbola din punctul zero. Aici ambele limite unilaterale sunt infinite: , prin urmare, funcția suferă o discontinuitate de al doilea fel în punctul .

Încerc să-mi umplu articolele cu un conținut cât mai divers posibil, așa că să ne uităm la graficul unei funcții care nu a fost încă întâlnită:

conform schemei standard:

1) Funcția nu este definită în acest moment deoarece numitorul ajunge la zero.

Desigur, putem concluziona imediat că funcția suferă o discontinuitate la punctul , dar ar fi bine să clasificăm natura discontinuității, care este adesea cerută de condiție. Pentru aceasta:

Permiteți-mi să vă reamintesc că prin înregistrare ne referim infinitezimal un număr negativ , iar sub intrarea - număr pozitiv infinitezimal.

Limitele unilaterale sunt infinite, ceea ce înseamnă că funcția suferă o discontinuitate de al 2-lea fel în punctul . Axa y este asimptotă verticală pentru diagramă.

Nu este neobișnuit ca ambele limite unilaterale să existe, dar numai una dintre ele este infinită, de exemplu:

Acesta este graficul funcției.

Examinăm punctul de continuitate:

1) Funcția nu este definită în acest moment.

2) Să calculăm limitele unilaterale:

Vom vorbi despre metoda de calcul a unor astfel de limite unilaterale în ultimele două exemple ale prelegerii, deși mulți cititori au văzut deja și au ghicit totul.

Limita din stânga este finită și egală cu zero (noi „nu mergem la punctul în sine”), dar limita din dreapta este infinită și ramura portocalie a graficului se apropie infinit de aproape de ea. asimptotă verticală, dat de ecuaţie(linie punctată neagră).

Deci funcția are de suferit discontinuitate de al doilea tip la punctul .

În ceea ce privește o discontinuitate de primul fel, funcția poate fi definită chiar în punctul de discontinuitate. De exemplu, pentru o funcție pe bucăți Simțiți-vă liber să puneți un punct negru aldine la originea coordonatelor. În dreapta este o ramură a unei hiperbole, iar limita din dreapta este infinită. Cred că aproape toată lumea are o idee despre cum arată acest grafic.

Ceea ce toată lumea aștepta cu nerăbdare:

Cum se examinează o funcție pentru continuitate?

Studiul unei funcții pentru continuitate într-un punct se realizează după o schemă de rutină deja stabilită, care constă în verificarea a trei condiții de continuitate:

Exemplul 1

Explorați funcția

Soluţie:

1) Singurul punct din domeniul de aplicare este locul în care funcția nu este definită.

2) Să calculăm limitele unilaterale:

Limitele unilaterale sunt finite și egale.

Astfel, la punctul în care funcția suferă o discontinuitate detașabilă.

Cum arată graficul acestei funcții?

As dori sa simplific , și se pare că se obține o parabolă obișnuită. DAR funcția originală nu este definită la punctul , deci este necesară următoarea clauză:

Să facem desenul:

Răspuns: funcția este continuă pe întreaga dreaptă numerică cu excepția punctului în care suferă o discontinuitate amovibilă.

Funcția poate fi definită în continuare într-un mod bun sau nu atât de bun, dar în funcție de condiție acest lucru nu este necesar.

Spui că acesta este un exemplu exagerat? Deloc. Acest lucru s-a întâmplat de zeci de ori în practică. Aproape toate sarcinile site-ului provin din lucrări și teste reale independente.

Să scăpăm de modulele noastre preferate:

Exemplul 2

Explorați funcția pentru continuitate. Determinați natura discontinuităților funcției, dacă acestea există. Executați desenul.

Soluţie: Din anumite motive, studenților le este frică și nu le plac funcțiile cu un modul, deși nu este nimic complicat la ele. Am atins deja puțin despre astfel de lucruri în lecție. Transformări geometrice ale graficelor. Deoarece modulul nu este negativ, acesta este extins după cum urmează: , unde „alfa” este o expresie. În acest caz, iar funcția noastră ar trebui scrisă pe bucăți:

Dar fracțiile ambelor piese trebuie reduse cu . Reducerea, ca în exemplul precedent, nu va avea loc fără consecințe. Funcția originală nu este definită la punctul, deoarece numitorul ajunge la zero. Prin urmare, sistemul ar trebui să specifice în plus condiția și să facă prima inegalitate strictă:

Acum despre o tehnică de decizie FOARTE UTILĂ: inainte de a finaliza sarcina pe o schita, este avantajos sa se realizeze un desen (indiferent daca este cerut de conditii sau nu). Acest lucru vă va ajuta, în primul rând, să vedeți imediat punctele de continuitate și punctele de discontinuitate și, în al doilea rând, vă va proteja 100% de erori atunci când găsiți limite unilaterale.

Hai să facem desenul. În conformitate cu calculele noastre, în stânga punctului este necesar să se deseneze un fragment de parabolă (culoare albastră), iar la dreapta - o bucată de parabolă (culoare roșie), în timp ce funcția nu este definită la punctul în sine:

Dacă aveți îndoieli, luați câteva valori x și conectați-le la funcție (amintindu-ne ca modulul distruge posibilul semn minus) si verificati graficul.

Să examinăm funcția pentru continuitate analitic:

1) Funcția nu este definită la punct, așa că putem spune imediat că nu este continuă la ea.

2) Să stabilim natura discontinuității pentru a face acest lucru, calculăm limite unilaterale:

Limitele unilaterale sunt finite și diferite, ceea ce înseamnă că funcția suferă o discontinuitate de primul fel cu un salt în punctul . Rețineți din nou că atunci când găsiți limite, nu contează dacă funcția la punctul de întrerupere este definită sau nu.

Acum, tot ce rămâne este să transferați desenul din schiță (a fost făcut ca cu ajutorul cercetării ;-)) și să finalizați sarcina:

Răspuns: functia este continua pe toata dreapta numerica cu exceptia punctului in care sufera o discontinuitate de primul fel cu un salt.

Uneori ele necesită o indicație suplimentară a saltului de discontinuitate. Se calculează simplu - din limita din dreapta trebuie să scădeți limita din stânga: , adică la punctul de întrerupere funcția noastră a sărit cu 2 unități în jos (după cum ne spune semnul minus).

Exemplul 3

Explorați funcția pentru continuitate. Determinați natura discontinuităților funcției, dacă acestea există. Faceți un desen.

Acesta este un exemplu pentru decizie independentă, probă de soluție la sfârșitul lecției.

Să trecem la cea mai populară și răspândită versiune a sarcinii, când funcția constă din trei părți:

Exemplul 4

Examinați o funcție pentru continuitate și trasați graficul funcției .

Soluţie: Este evident că toate cele trei părți ale funcției sunt continue pe intervalele corespunzătoare, așa că rămâne de verificat doar două puncte de „joncțiune” între piese. Mai întâi, să facem o schiță de desen am comentat suficient de detaliat tehnica de construcție în prima parte a articolului. Singurul lucru este că trebuie să urmărim cu atenție punctele noastre singulare: din cauza inegalității, valoarea aparține liniei drepte (punct verde), iar din cauza inegalității, valoarea aparține parabolei (punct roșu):

Ei bine, în principiu, totul este clar =) Mai rămâne doar să oficializezi decizia. Pentru fiecare dintre cele două puncte de „unire”, verificăm în mod standard 3 condiții de continuitate:

eu) Examinăm punctul de continuitate

Limitele unilaterale sunt finite și diferite, ceea ce înseamnă că funcția suferă o discontinuitate de primul fel cu un salt în punctul .

Să calculăm saltul de discontinuitate ca diferență între limitele din dreapta și din stânga:
, adică graficul a crescut cu o unitate.

II) Examinăm punctul de continuitate

1) – funcția este definită la un punct dat.

2) Găsiți limite unilaterale:

– limitele unilaterale sunt finite și egale, ceea ce înseamnă că există o limită generală.

3) – limita unei funcții într-un punct este egală cu valoarea acestei funcții într-un punct dat.

În etapa finală, transferăm desenul în versiunea finală, după care punem acordul final:

Răspuns: functia este continua pe toata dreapta numerica, cu exceptia punctului in care sufera o discontinuitate de primul fel cu un salt.

Exemplul 5

Examinați o funcție pentru continuitate și construiți graficul acesteia .

Acesta este un exemplu de soluție independentă, o soluție scurtă și un eșantion aproximativ al problemei la sfârșitul lecției.

Poti avea impresia ca la un moment dat functia trebuie sa fie continua, iar la altul trebuie sa existe o discontinuitate. În practică, acest lucru nu este întotdeauna cazul. Încercați să nu neglijați exemplele rămase - vor exista câteva caracteristici interesante și importante:

Exemplul 6

Dată o funcție . Investigați funcția pentru continuitate în puncte. Construiți un grafic.

Soluţie: și din nou executați imediat desenul pe proiect:

Particularitatea acestui grafic este că funcția pe bucăți este dată de ecuația axei absciselor. Aici această zonă este desenată cu verde, dar într-un caiet este de obicei evidențiată cu caractere aldine cu un simplu creion. Și, desigur, nu uitați de berbecii noștri: valoarea aparține ramurii tangente (punct roșu), iar valoarea aparține liniei drepte.

Totul este clar din desen - funcția este continuă de-a lungul întregii linii numerice, tot ce rămâne este să oficializezi soluția, care este adusă la o automatizare completă literalmente după 3-4 exemple similare:

eu) Examinăm punctul de continuitate

1) – funcția este definită la un punct dat.

2) Să calculăm limitele unilaterale:

, ceea ce înseamnă că există o limită generală.

Pentru orice eventualitate, permiteți-mi să vă reamintesc un fapt banal: limita unei constante este egală cu constanta în sine. În acest caz, limita lui zero este egală cu zero în sine (limită pentru stânga).

3) – limita unei funcții într-un punct este egală cu valoarea acestei funcții într-un punct dat.

Astfel, o funcție este continuă într-un punct prin definiția continuității unei funcții într-un punct.

II) Examinăm punctul de continuitate

1) – funcția este definită la un punct dat.

2) Găsiți limite unilaterale:

Și aici – limita unuia este egală cu unitatea în sine.

– există o limită generală.

3) – limita unei funcții într-un punct este egală cu valoarea acestei funcții într-un punct dat.

Astfel, o funcție este continuă într-un punct prin definiția continuității unei funcții într-un punct.

Ca de obicei, după cercetări ne transferăm desenul în versiunea finală.

Răspuns: functia este continua la puncte.

Vă rugăm să rețineți că în condiția nu am fost întrebați nimic despre examinarea întregii funcții pentru continuitate și este considerată o formă matematică bună de a formula precisă și clară răspunsul la întrebarea pusă. Apropo, dacă condițiile nu vă cer să construiți un grafic, atunci aveți tot dreptul să nu îl construiți (deși mai târziu profesorul vă poate obliga să faceți acest lucru).

Un mic „învârtitor de limbă” matematic pentru a o rezolva singur:

Exemplul 7

Dată o funcție 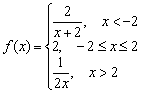. Investigați funcția pentru continuitate în puncte. Clasificați punctele de întrerupere, dacă există. Executați desenul.

Încercați să „pronunțați” toate „cuvintele” corect =) Și desenați graficul mai precis, acuratețe, nu va fi de prisos peste tot;-)

După cum vă amintiți, am recomandat să completați imediat desenul ca schiță, dar din când în când întâlniți exemple în care nu vă puteți da seama imediat cum arată graficul. Prin urmare, în unele cazuri, este avantajos să găsiți mai întâi limite unilaterale și abia apoi, pe baza studiului, să descrieți ramurile. În ultimele două exemple vom învăța și o tehnică pentru calcularea unor limite unilaterale:

Exemplul 8

Examinați funcția pentru continuitate și construiți graficul ei schematic.

Soluţie: punctele rele sunt evidente: (reduce numitorul exponentului la zero) și (reduce numitorul întregii fracții la zero). Nu este clar cum arată graficul acestei funcții, ceea ce înseamnă că este mai bine să faceți mai întâi câteva cercetări.

Topologie– o ramură a matematicii care se ocupă cu studiul limitelor și continuității funcțiilor. În combinație cu algebra, topologia constituie baza generală a matematicii.

Spațiu sau figură topologică - o submulțime a spațiului nostru euclidian omogen, între punctele căruia este dată o anumită relație de proximitate. Aici figurile sunt considerate nu corpuri rigide, ci obiecte realizate parcă din cauciuc foarte elastic, permițând o deformare continuă care le păstrează proprietățile calitative.

Se numește o mapare continuă unu-la-unu a cifrelor homeomorfism. Cu alte cuvinte, cifrele homeomorf, dacă unul poate fi transferat la altul prin deformare continuă.

Exemple. Următoarele figuri sunt homeomorfe (figurele din diferite grupuri nu sunt homeomorfe), prezentate în Fig. 2.

1. Un segment și o curbă fără autointersecții.

2. Cerc, în interiorul pătratului, panglică.

3. Sfera, suprafața cubului și tetraedrul.

4. Cercul, elipsa și cercul înnodat.

5. Un inel pe un plan (un cerc cu o gaură), un inel în spațiu, un inel răsucit de două ori, suprafața laterală a unui cilindru.

6. Banda Möbius, i.e. un inel o dată răsucit și un inel de trei ori răsucit.

7. Suprafața unui tor (goasă), a unei sfere cu mâner și a unui tor înnodat.

8. O sferă cu două mânere și un covrig cu două găuri.

ÎN analiză matematică funcţiile sunt studiate prin metoda limitelor. Variabila și limita sunt concepte de bază.

În diverse fenomene, unele cantități își păstrează valoarea numerică, altele se modifică. Se numește setul tuturor valorilor numerice ale unei variabile zona de modificare a acestei variabile.

Dintre diferitele moduri în care se comportă o variabilă, cel mai important este cel în care variabila tinde către o anumită limită.

Număr constant A numit limită variabilă, dacă valoarea absolută a diferenței dintre XȘi A() devine în proces de modificare a unei valori variabile X cât de mic se dorește:

Ce înseamnă „oricât de mic vrei”? Valoare variabilă X tinde spre limită A, dacă pentru orice număr arbitrar mic (arbitrar mic) există un astfel de moment în schimbarea variabilei X, pornind de la care inegalitatea este valabilă .

Definiția limitei are un sens geometric simplu: inegalitatea înseamnă că X este în vecinătatea punctului A, acestea. în interval .

Astfel, definiția limitei poate fi dată în formă geometrică:

Număr A este limita variabilei X, dacă pentru orice arbitrar mic (arbitrar mic) - vecinătate a numărului A puteți specifica un astfel de moment în schimbarea variabilei X, începând de la care toate valorile sale se încadrează în vecinătatea specificată a punctului A.

cometariu. Valoare variabilă X se poate apropia de limita sa in diferite moduri: ramanand sub aceasta limita (pe stanga), mai mult (pe dreapta), fluctuand in jurul valorii limitei.

Limită de secvență

Funcţie numită legea (regula) conform căreia fiecare element X unele set X se potrivește cu un singur element y seturi Y.

Funcția poate fi definită pe mulțimea tuturor numerelor naturale: . Această funcție este numită funcția argument natural sau succesiune numerică.

Deoarece o secvență, ca orice mulțime infinită, nu poate fi specificată prin enumerare, este specificată printr-un termen comun: , unde este termenul general al secvenței.

O variabilă discretă este un termen comun al unei secvențe.

Pentru coerență, cuvintele „începând la un moment dat” înseamnă cuvintele „începând de la un anumit număr”.

Număr A numită limita secvenței , dacă pentru orice număr arbitrar mic (arbitrar mic) există un astfel de număr N, care pentru toți membrii secvenței cu număr n>N inegalitatea este valabilă .

sau la .

Din punct de vedere geometric, definiția limitei unei secvențe înseamnă următoarele: pentru orice vecinătate arbitrar de mică (arbitrar de mică) a numărului A există un număr astfel încât toți termenii șirului cu mai mare decât N, cifre, se încadrează în această vecinătate. Doar un număr finit de termeni inițiali ai secvenței apar în afara vecinătății. Numar natural N depinde de : .