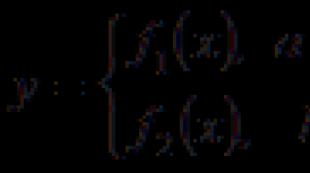Analiza matematică.

Atelier.

Pentru studenții de specialitate:

„Administrația de stat și municipală”

T.Z. Pavlova

Kolpașevo 2008

Capitolul 1. Introducere în analiză

1.1 Funcții. Proprietăți generale

1.2 Teoria limitelor

1.3 Continuitatea funcției

2.1 Definiția derivatei

2.4 Explorarea funcțiilor

2.4.1 Planul de studiu complet al funcției

2.4.2 Exemple de studiu al funcției

2.4.3. Cea mai mare și cea mai mică valoare a unei funcții pe un segment

2.5 Regula lui L'Hôpital

3.1 Integrală nedefinită

3.1.1 Definiții și proprietăți

3.1.2 Tabelul integralelor

3.1.3 Metode de bază de integrare

3.2 Integrala definită

3.2.2 Metode de calcul a integralei definite

Capitolul 4. Funcţiile mai multor variabile

4.1 Concepte de bază

4.2 Limitele și continuitatea funcțiilor mai multor variabile

4.3.3 Diferenţialul total şi aplicarea acestuia la calcule aproximative

Capitolul 5. Metode clasice de optimizare

6.1 Funcția de utilitate.

6.2 Linii de indiferență

6.3 Stabilirea bugetului

Teme pentru acasă

1.1 Funcții. Proprietăți generale

O funcție numerică este definită pe mulțimea D de numere reale dacă fiecare valoare a variabilei este asociată cu o valoare reală bine definită a variabilei y, unde D este domeniul funcției.

Reprezentarea analitică a funcției:

explicit:;

implicit:;

sub forma parametrica:

diferite formule în domeniul definirii:

Proprietăți.

Funcția chiar:. De exemplu, funcția este pară, deoarece ...

Funcție impară: ... De exemplu, funcția este impară, deoarece ...

Funcția periodică: , unde T este perioada funcției,. De exemplu, funcțiile trigonometrice.

Funcția monotonă. Dacă pentru oricare dintre domeniile de definiție - funcția este în creștere, - în scădere. De exemplu, - în creștere și - în scădere.

Funcție limitată. Dacă există un număr M astfel încât. De exemplu, funcții și, din moment ce .

Exemplul 1. Găsiți domeniul de definire a funcțiilor.

+ 2 – 3 +

1.2 Teoria limitelor

Definiția 1... Limita unei funcții la este un număr b dacă pentru orice (- număr pozitiv arbitrar mic) se poate găsi o astfel de valoare a argumentului, pornind de la care inegalitatea este satisfăcută.

Desemnare:.

Definiția 2... Limita unei funcții la este un număr b dacă pentru oricare (este un număr pozitiv arbitrar mic) există un număr pozitiv astfel încât pentru toate valorile lui x care satisfac inegalitatea inegalității să fie valabilă.

Desemnare:.

Definiția 3. Funcția se numește infinitezimal pentru sau, dacă sau.

Proprietăți.

1. Suma algebrică a unui număr finit de mărimi infinitezimale este o mărime infinitezimală.

2. Produsul unei cantități infinit de mici de o funcție mărginită (constantă, o altă cantitate infinit de mică) este o cantitate infinit de mică.

3. Cât de împărțire a unei cantități infinit de mici la o funcție a cărei limită este diferită de zero este o cantitate infinit de mică.

Definiția 4. Funcția se numește infinit mare la, dacă.

Proprietăți.

1. Produsul unei cantități infinit de mare de o funcție, a cărei limită este nenulă, este o cantitate infinit de mare.

2. Suma unei valori infinit de mare și a unei funcții mărginite este o valoare infinit de mare.

3. Cât de împărțire a unei cantități infinit de mare la o funcție care are o limită este o cantitate infinit de mare.

Teorema.(Relația dintre o cantitate infinit de mică și o cantitate infinit de mare.) Dacă o funcție este infinitezimală la (), atunci funcția este o cantitate infinit de mare la (). Și, invers, dacă funcția este infinit de mare la (), atunci funcția este infinit de mică la ().

Teoreme limită.

1. O funcție nu poate avea mai mult de o limită.

2. Limita sumei algebrice a mai multor funcții este egală cu suma algebrică a limitelor acestor funcții:

3. Limita produsului mai multor funcții este egală cu produsul limitelor acestor funcții:

4. Limita gradului este egală cu gradul limitei:

5. Limita câtului este egală cu câtul limitelor dacă există limita divizorului:

.

6. Prima limită remarcabilă.

Consecințe:

7. A doua limită remarcabilă:

Consecințe:

Valori infinitezimale echivalente pentru:

Calculul limitelor.

La calcularea limitelor se folosesc teoremele de bază privind limitele, proprietățile funcțiilor continue și regulile care decurg din aceste teoreme și proprietăți.

Regula 1. Pentru a găsi limita într-un punct al unei funcții care este continuă în acest punct, este necesar să înlocuiți valoarea limită a acesteia în funcția de sub semnul limită în loc de argumentul x.

Exemplul 2. Găsiți

Regula 2. Dacă, la găsirea limitei unei fracții, limita numitorului este zero, iar limita numărătorului este diferită de zero, atunci limita unei astfel de funcții este.

Exemplul 3. Găsiți

Regula 3. Dacă, la găsirea limitei unei fracții, limita numitorului este egală, iar limita numărătorului este diferită de zero, atunci limita unei astfel de funcții este zero.

Exemplul 4. Găsiți

Adesea, înlocuirea unei valori limită pentru un argument are ca rezultat expresii nedefinite, cum ar fi

.

Găsirea limitei unei funcții în aceste cazuri se numește divulgare de incertitudine. Pentru a dezvălui incertitudinea, este necesar să se transforme această expresie înainte de a trece la limită. Sunt folosite diferite tehnici pentru a dezvălui incertitudinile.

Regula 4... Incertitudinea tipului este relevată prin transformarea funcției sublimită, astfel, pentru a selecta un factor la numărător și numitor, a cărui limită este zero, și, prin reducerea fracției cu aceasta, să se afle limita coeficientului. Pentru a face acest lucru, numărătorul și numitorul sunt fie înmulțiți, fie înmulțiți cu expresiile conjugate la numărător și numitor.

Regula 5. Dacă expresia sublimită conține funcții trigonometrice, atunci prima limită remarcabilă este folosită pentru a expune incertitudinea speciei.

.

Regula 6... Pentru a dezvălui incertitudinea formei la, numărătorul și numitorul fracției sublimită trebuie împărțite la gradul cel mai înalt al argumentului și apoi trebuie găsită limita coeficientului.

Rezultate posibile:

1) limita dorită este egală cu raportul dintre coeficienții la cele mai mari puteri ale argumentului numărătorului și numitorului, dacă aceste grade sunt aceleași;

2) limita este egală cu infinit dacă gradul argumentului numărătorului este mai mare decât gradul argumentului numitorului;

3) limita este zero dacă gradul argumentului numărătorului este mai mic decât gradul argumentului numitorului.

A)

de cand

Gradele sunt egale, ceea ce înseamnă că limita este egală cu raportul coeficienților la gradele superioare, adică. ...

b)

Gradul numărătorului, numitorul este 1, ceea ce înseamnă că limita este

v)

Gradul numărătorului este 1, gradul numitorului este, deci limita este 0.

Regula 7... Pentru a dezvălui incertitudinea formei, numărătorul și numitorul fracției sublimită trebuie înmulțite cu expresia conjugată.

Exemplul 10.

Regula 8... O a doua limită remarcabilă și consecințele ei sunt folosite pentru a descoperi incertitudinea speciei.

Se poate dovedi că

Exemplul 11.

Exemplul 12.

Exemplul 13.

Regula 9... La dezvăluirea incertitudinilor, a căror funcție subliminală conține infinitezimalul, este necesară înlocuirea limitelor acestor infinite. pe limitele elementelor infinitezimale echivalente cu acestea.

Exemplul 14.

Exemplul 15.

Regula 10. Regula lui L'Hôpital (vezi 2.6).

1.3 Continuitatea funcției

O funcție este continuă într-un punct dacă limita funcției, așa cum argumentul tinde spre a, există și este egală cu valoarea funcției în acest punct.

Conditii echivalente:

1. ;

3.

Clasificarea punctului de rupere:

pauză de primul fel

De unică folosință - limitele unilaterale există și sunt egale;

Fatal (săritură) - limitele unilaterale nu sunt egale;

discontinuitate de al doilea fel: limita unei funcţii într-un punct nu există.

Exemplul 16. Stabiliți natura discontinuității unei funcții într-un punct sau demonstrați continuitatea unei funcții în acest punct.

deoarece funcția nu este definită, prin urmare, nu este continuă în acest punct. pentru că și în mod corespunzător, , atunci este punctul unei discontinuități detașabile de primul fel.

b)

în comparaţie cu sarcina (a), funcţia este extinsă într-un punct astfel încât , prin urmare, această funcție este continuă în acest punct.

Când funcția nu este definită;

.

pentru că una dintre limitele unilaterale este infinită, atunci este un punct de rupere de al doilea fel.

Capitolul 2. Calcul diferenţial

2.1 Definiția derivatei

Definiție derivată

Derivata sau a unei funcții date este limita raportului dintre incrementul funcției și incrementul corespondent al argumentului atunci când incrementul argumentului tinde spre zero:

Sau .

Semnificația mecanică a unei derivate este rata de schimbare a unei funcții. Semnificația geometrică a derivatei este tangenta unghiului de înclinare a tangentei la graficul funcției:

2.2 Reguli de bază pentru diferențiere

Nume	Funcţie	Derivat
Înmulțirea cu un factor constant
Suma algebrică a două funcții
Produsul a două funcții
Două funcții private
Funcție complexă

Derivate ale funcţiilor elementare de bază

P/p nr.	Numele funcției	Funcția și derivata ei
1	constant
2	functie de putere cazuri speciale
3	functie exponentiala caz special
4	funcţie logaritmică caz special
5	funcții trigonometrice
6	verso trigonometric

b)

2.3 Derivate de ordin superior

Derivată de ordinul doi a unei funcții

Derivata de ordinul doi a functiei:

Exemplul 18.

a) Aflați derivata de ordinul doi a funcției.

Soluţie. Să găsim mai întâi derivata de ordinul întâi .

Să luăm derivata derivatei de ordinul întâi.

Exemplul 19. Găsiți derivata de ordinul trei a funcției.

2.4 Explorarea funcțiilor

2.4.1 Planificarea unui studiu complet al funcției:

Plan de studiu complet al funcției:

1. Cercetare elementară:

Găsiți domeniul și intervalul de valori;

Aflați proprietățile generale: paritate (ciudățenie), periodicitate;

Aflați punctele de intersecție cu axele de coordonate;

Determinați zonele de constanță.

2. Asimptote:

Găsiți asimptote verticale dacă;

Găsiți asimptote oblice:.

Dacă există un număr, atunci - asimptote orizontale.

3. Cercetare folosind:

Găsiți punctele critice, acelea. puncte în care există sau nu;

Determinați intervalele de creștere, acelea. intervale, la care și funcții descrescătoare -;

Determinați extrema: punctele, la trecere prin care își schimbă semnul de la „+” la „-”, sunt puncte maxime, de la „-” la „+” - minim.

4. Cercetare folosind:

Găsiți puncte în care există sau nu;

Găsiți zone de convexitate, de ex. intervalele la care sunt concavitățile;

Găsiți punctele de inflexiune, de ex. puncte la trecere prin care se schimbă semnul.

1. Elementele individuale ale studiului sunt trasate pe grafic treptat, pe măsură ce sunt găsite.

2. Dacă există dificultăți în construirea graficului funcției, atunci valorile funcției se găsesc în unele puncte suplimentare.

3. Scopul studiului este de a descrie natura comportamentului funcției. Prin urmare, nu se construiește un grafic exact, ci o aproximare a acestuia, pe care sunt indicate clar elementele găsite (extreme, puncte de inflexiune, asimptote etc.).

4. Nu este necesar să respectați cu strictețe planul de mai sus; este important să nu trecem cu vederea elementele caracteristice ale comportamentului funcţiei.

2.4.2 Exemple de studiu de funcții:

1)

2) Funcția este impară:

.

3) Asimptote.

- asimptote verticale, deoarece

Asimptotă oblică.

5)

- punct de inflexiune.

2) Funcția este impară:

3) Asimptote: Nu există asimptote verticale.

Înclinat:

- asimptote oblice

4) - functia creste.

- punct de inflexiune.

Schema schematică a acestei funcții:

2) Funcția generală

3) Asimptote

- fără asimptote oblice

- asimptotă orizontală la

- punct de inflexiune

Schema schematică a acestei funcții:

2) Asimptote.

- asimptotă verticală, deoarece

- fără asimptote oblice

, - asimptotă orizontală

Schema schematică a acestei funcții:

2) Asimptote

- asimptotă verticală la, din moment ce

- fără asimptote oblice

, - asimptotă orizontală

3) - funcţia scade la fiecare dintre intervale.

Schema schematică a acestei funcții:

Pentru a găsi cea mai mare și cea mai mică valoare a unei funcții pe un segment, puteți utiliza diagrama:

1. Aflați derivata funcției.

2. Aflați punctele critice ale funcției, la care există sau nu.

3. Aflați valoarea funcției în punctele critice aparținând unui segment dat și la capetele acestuia și alegeți cel mai mare și cel mai mic dintre ele.

Exemplu. Găsiți cea mai mică și cea mai mare valoare a funcției pe un anumit segment.

25. intre

2) - puncte critice

26. între.

Derivata nu există la, dar 1 nu aparține acestui interval. Funcția scade în interval, ceea ce înseamnă că nu există cea mai mare valoare, ci cea mai mică valoare.

2.5 Regula lui L'Hôpital

Teorema. Limita raportului a două funcții infinitezimale sau infinit de mari este egală cu limita raportului derivatelor lor (finite sau infinite), dacă aceasta din urmă există în sensul indicat.

Acestea. atunci când dezvăluiți incertitudini de tip sau, puteți utiliza formula:

.

27.

Capitolul 3. Calcul integral

3.1 Integrală nedefinită

3.1.1 Definiții și proprietăți

Definiție 1. O funcție se numește antiderivată pentru dacă.

Definiția 2. O integrală nedefinită a unei funcții f (x) este colecția tuturor antiderivate pentru această funcție.

Desemnare: , unde c este o constantă arbitrară.

Proprietăți integrale nedefinite

1. Derivată a integralei nedefinite:

2. Diferenţialul integralei nedefinite:

3. Integrală nedefinită a diferenţialului:

4. Integrală nedefinită a sumei (diferenței) a două funcții:

5. Deplasarea unui factor constant dincolo de semnul integralei nedefinite:

3.1.2 Tabelul integralelor

.1.3 Metode de bază de integrare

1. Folosind proprietățile integralei nedefinite.

Exemplul 29.

2. Aducerea sub semnul diferenţial.

Exemplul 30.

3. Metoda de înlocuire variabilă:

a) înlocuire în integrală

Unde - o functie mai usor de integrat decat cea originala; - functie inversa functiei; este antiderivată a funcției.

Exemplul 31.

b) înlocuire în integrala formei:

Exemplul 32.

Exemplul 33.

4. Metoda de integrare pe părți:

Exemplul 34.

Exemplul 35.

Să luăm separat integrala

Să revenim la integrala noastră:

3.2 Integrala definită

3.2.1 Conceptul de integrală definită și proprietățile acesteia

Definiție. Să fie dată o funcție continuă pe un anumit interval. Să construim graficul ei.

O figură delimitată deasupra printr-o curbă, la stânga și la dreapta prin linii drepte și de jos de un segment al axei absciselor între punctele a și b, se numește trapez curbat.

S - zona - trapez curbat.

Împărțiți intervalul cu puncte și obțineți:

Suma integrală:

Definiție. Integrala definită este limita sumei integrale.

Proprietăți integrale definite:

1. Factorul constant poate fi scos din semnul integral:

2. Integrala sumei algebrice a două funcții este egală cu suma algebrică a integralelor acestor funcții:

3. Dacă segmentul de integrare este împărțit în părți, atunci integrala pe întregul segment este egală cu suma integralelor pentru fiecare dintre părțile care au apărut, adică pentru orice a, b, c:

4. Dacă pe un segment, atunci

5. Limitele integrării pot fi interschimbate, în timp ce semnul integralei se schimbă:

6.

7. Integrala în punct este egală cu 0:

8.

9. („despre medie”) Fie y = f (x) o funcție integrabilă pe. Atunci , unde, f (c) este valoarea medie a lui f (x) pe:

10. Formula Newton-Leibniz

,

unde F (x) este antiderivată pentru f (x).

3.2.2 Metode de calcul a integralei definite.

1. Integrare directă

Exemplul 35.

A)

b)

v)

e)

2. Schimbarea variabilelor sub semnul integral definit .

Exemplul 36.

2. Integrarea pe părți într-o integrală definită .

Exemplul 37.

A)

b)

e)

3.2.3 Aplicații ale unei integrale definite

Caracteristică	Tipul funcției	Formulă
	în coordonate carteziene
zona sectorului curbat	în coordonate polare
zona trapezoidală curbată	în formă parametrică
lungimea arcului	în coordonate carteziene
lungimea arcului	în coordonate polare
lungimea arcului	în formă parametrică
volumul corpului rotație	în coordonate carteziene
volumul corpului cu o transversală dată secțiune transversală

Exemplul 38. Calculați aria unei forme delimitate de linii: și .

Soluţie: Să găsim punctele de intersecție ale graficelor acestor funcții. Pentru a face acest lucru, echivalăm funcțiile și rezolvăm ecuația

Deci, punctele de intersecție și.

Găsim aria figurii folosind formula

.

În cazul nostru

Răspuns: aria este egală cu (unități pătrate).

4.1 Concepte de bază

Definiție. Dacă, conform unei reguli, una sau mai multe valori ale variabilei z sunt atribuite fiecărei perechi de numere independente dintr-o anumită mulțime, atunci variabila z se numește funcție a două variabile.

Definiție. Domeniul funcției z este mulțimea de perechi pentru care există funcția z.

Domeniul unei funcții a două variabile este un set de puncte pe planul de coordonate Oxy. Coordonata z se numește aplicat, iar apoi funcția în sine este descrisă ca o suprafață în spațiul E 3. De exemplu:

Exemplul 39. Găsiți domeniul unei funcții.

A)

Expresia din partea dreaptă are sens numai pentru. Aceasta înseamnă că domeniul acestei funcții este colecția tuturor punctelor aflate în interiorul și la marginea unui cerc de rază R centrat la origine.

Domeniul acestei funcții sunt toate punctele planului, cu excepția punctelor dreptelor, adică axele de coordonate.

Definiție. Liniile de nivel de funcție sunt o familie de curbe pe planul de coordonate descris de ecuații de formă.

Exemplul 40. Găsiți linii de nivel de funcție .

Soluţie. Liniile de nivel ale unei funcții date sunt o familie de curbe în planul descris de ecuație

Ultima ecuație descrie o familie de cercuri centrate în punctul O 1 (1, 1) al razei. Suprafața de revoluție (paraboloid) descrisă de această funcție devine mai „abruptă” pe măsură ce se îndepărtează de axă, care este dată de ecuațiile x = 1, y = 1. (Fig. 4)

4.2 Limitele și continuitatea funcțiilor mai multor variabile.

1. Limite.

Definiție. Un număr A se numește limita unei funcții, deoarece un punct tinde către un punct, dacă pentru fiecare număr arbitrar mic există un număr astfel încât condiția să fie adevărată pentru orice punct și condiția ... Ei notează: .

Exemplul 41. Găsiți limitele:

acestea. limita depinde de, și, prin urmare, nu există.

2. Continuitate.

Definiție. Fie punctul aparține domeniului de definire a funcției. Atunci o funcție se numește continuă într-un punct dacă

(1)

în plus, punctul tinde spre punct într-un mod arbitrar.

Dacă în orice punct condiția (1) nu este îndeplinită, atunci acest punct se numește punct de discontinuitate a funcției. Acest lucru poate fi în următoarele cazuri:

1) Funcția nu este definită în acest punct.

2) Nu există limită.

3) Această limită există, dar nu este egală.

Exemplul 42. Stabiliți dacă funcția dată este continuă în punctul, dacă.

Am inteles prin urmare, această funcție este continuă în punct.

limita depinde de k, i.e. nu există într-un punct dat, ceea ce înseamnă că funcția are o discontinuitate în acest punct.

4.3 Derivate și diferențiale ale funcțiilor mai multor variabile

4.3.1 Derivate parțiale de ordinul întâi

Derivata parțială a unei funcții în raport cu argumentul x este derivata obișnuită a unei funcții a unei variabile x pentru o valoare fixă ​​a variabilei y și se notează:

Derivata parțială a unei funcții în raport cu argumentul y este derivata obișnuită a unei funcții a unei variabile y la o valoare fixă ​​a variabilei x și se notează:

Exemplul 43. Găsiți derivate parțiale ale funcțiilor.

4.3.2 Derivate parțiale de ordinul doi

Derivatele parțiale de ordinul doi sunt derivate parțiale ale derivatelor parțiale de ordinul întâi. Pentru o funcție a două variabile de formă, sunt posibile patru tipuri de derivate parțiale de ordinul doi:

Derivatele parțiale de ordinul doi, în care diferențierea se realizează față de diferite variabile, se numesc derivate mixte. Derivatele mixte de ordinul doi ale unei funcții de două ori diferențiabile sunt egale.

Exemplul 44. Aflați derivatele parțiale de ordinul doi.

4.3.3 Diferenţialul total şi aplicarea acestuia la calcule aproximative.

Definiție. Diferenţialul de ordinul întâi al unei funcţii a două variabile se găseşte prin formula

.

Exemplul 45. Aflați diferența totală pentru o funcție.

Soluţie. Să găsim derivatele parțiale:

.

Pentru incremente mici ale argumentelor x și y, funcția câștigă un increment aproximativ egal cu dz, adică. ...

Formula pentru găsirea valorii aproximative a unei funcții într-un punct, dacă valoarea ei exactă într-un punct este cunoscută:

Exemplul 46. Găsiți .

Soluţie. Lăsa ,

Apoi folosim formula

Răspuns. .

Exemplul 47. Calculați aproximativ.

Soluţie. Să luăm în considerare o funcție. Noi avem

Exemplul 48. Calculați aproximativ.

Soluţie. Luați în considerare funcția ... Primim:

Răspuns. .

4.3.4 Diferențierea funcției implicite

Definiție. O funcție se numește implicită dacă este dată de o ecuație care nu este rezolvabilă față de z.

Derivatele parțiale ale unei astfel de funcții se găsesc prin formulele:

Exemplul 49. Aflați derivatele parțiale ale funcției z date de ecuație .

Soluţie.

Definiție. O funcție se numește implicită dacă este dată de o ecuație care nu este rezolvabilă în raport cu y.

Derivata unei astfel de functii se gaseste prin formula:

.

Exemplul 50. Găsiți derivate ale acestor funcții.

5.1 Extremul local al unei funcții a mai multor variabile

Definiţie 1. O funcţie are un maxim într-un punct dacă

Definiţia 2. O funcţie are un minim într-un punct dacă pentru toate punctele suficient de apropiate de punct și diferite de acesta.

O condiție necesară pentru un extremum. Dacă o funcție atinge un extremum într-un punct, atunci derivatele parțiale ale funcției dispar sau nu există în acest punct.

Punctele în care derivatele parțiale dispar sau nu există sunt numite critice.

Un semn suficient de extremum. Fie ca funcția să fie definită într-o vecinătate a punctului critic și să aibă derivate parțiale continue de ordinul doi în acest punct

1) are un maxim local la punctul, dacă și;

2) are un minim local la punctul, dacă și;

3) nu are un extremum local în punctul dacă;

Schema studiului pentru extremul unei funcții a două variabile.

1. Aflați derivatele parțiale ale funcției: și.

2. Rezolvați sistemul de ecuații și găsiți punctele critice ale funcției.

3. Găsiți derivatele parțiale de ordinul doi, calculați valorile lor în punctele critice și, folosind condiția suficientă, trageți o concluzie despre prezența extremelor.

4. Aflați extremele funcției.

Exemplul 51. Găsiți extremele unei funcții .

1) Aflați derivatele parțiale.

2) Rezolvați sistemul de ecuații

4) Aflați derivatele parțiale de ordinul doi și valorile lor în punctele critice:. În momentul în care obținem:

prin urmare, nu există niciun extremum în acest punct. În momentul în care obținem:

prin urmare, în acel punct există un minim.

5.2 Extremum global (valoarea cea mai mare și cea mai mică a unei funcții)

Cele mai mari și cele mai mici valori ale unei funcție a mai multor variabile, continue pe o mulțime închisă, se realizează fie la punctele extreme, fie la limita mulțimii.

Schema de găsire a valorilor cele mai mari și cele mai mici.

1) Găsiți punctele critice aflate în interiorul regiunii, calculați valoarea funcției în aceste puncte.

2) Explorează funcția la limita zonei; dacă granița constă din mai multe linii diferite, atunci studiul trebuie efectuat pentru fiecare sit separat.

3) Comparați valorile obținute ale funcției și alegeți cel mai mare și cel mai mic.

Exemplul 52. Găsiți cele mai mari și cele mai mici valori ale funcției dintr-un dreptunghi.

Soluţie. 1) Aflați punctele critice ale funcției, pentru aceasta găsim derivatele parțiale: și rezolvăm sistemul de ecuații:

A primit punctul critic A. Punctul rezultat se află în interiorul zonei specificate,

Granița zonei este alcătuită din patru segmente: și. găsiți cea mai mare și cea mai mică valoare a funcției pe fiecare segment.

4) Comparați rezultatele obținute și găsiți că la puncte .

Capitolul 6. Modelul alegerii consumatorului

Vom presupune că există n bunuri diferite. Atunci un anumit set de bunuri va fi notat cu vectorul n-dimensional , unde este cantitatea produsului i-lea. Mulțimea tuturor mulțimilor de bunuri X se numește spațiu.

Alegerea consumatorului individual se caracterizează printr-o relație de preferință: se crede că consumatorul poate spune despre oricare două seturi, ceea ce este mai de dorit, sau nu vede diferența dintre ele. Relația de preferință este tranzitivă: dacă o mulțime este de preferat unei mulțimi și o mulțime este de preferat unei mulțimi, atunci o mulțime este de preferat unei mulțimi. Vom presupune că comportamentul consumatorului este pe deplin descris de axioma consumatorului individual: fiecare consumator individual ia o decizie cu privire la consum, cumpărături etc., pe baza sistemului său de preferințe.

6.1 Funcția de utilitate

Pe setul de seturi de consumatori X, funcția este definită , a cărui valoare pe setul de consumator este egală cu estimarea consumatorului asupra individului pentru acest set. Funcția se numește funcția de utilitate a consumatorului sau funcția de preferință a consumatorului. Acestea. fiecare consumator are propria sa funcţie de utilitate. Dar întregul set de consumatori poate fi împărțit în anumite clase de consumatori (după vârstă, starea proprietății etc.) și fiecărei clase i se poate atribui o funcție de utilitate medie, poate.

Astfel, o funcție este o estimare a consumatorului sau nivelul de satisfacție al nevoilor unui individ atunci când cumpără un anumit set. Dacă un set este de preferat unui set pentru un anumit individ, atunci.

Proprietățile funcției de utilitate.

1.

Primele derivate parțiale ale funcției de utilitate se numesc utilități marginale ale produselor. Din această proprietate rezultă că o creștere a consumului unui produs în timp ce consumul altor produse rămâne neschimbat duce la o creștere a evaluării consumatorului. Vector este gradientul funcției, arată direcția de creștere cea mai mare a funcției. Pentru o funcție, gradientul acesteia este un vector de utilități marginale ale produselor.

2.

Acestea. utilitatea marginală a oricărei mărfuri scade odată cu creșterea consumului.

3.

Acestea. utilitatea marginală a fiecărui produs crește odată cu cantitatea celuilalt produs.

Unele tipuri de funcții utilitare.

1) Neoclasic:.

2) Cvadratic: unde matricea este definită negativă și pentru .

3) Funcția logaritmică:.

6.2 Linii de indiferență

În problemele aplicate și modelele de alegere a consumatorului, este adesea folosit un caz particular al unui set de două bunuri, de ex. când funcţia de utilitate depinde de două variabile. Linia indiferenței este o linie care leagă seturi de consumatori care au același nivel de satisfacție a nevoilor individului. În esență, liniile indiferenței sunt liniile nivelului de funcție. Ecuații ale liniilor de indiferență: .

Proprietățile de bază ale liniilor de indiferență.

1. Liniile de indiferență, corespunzătoare diferitelor niveluri de satisfacere a nevoilor, nu se ating și nu se intersectează.

2. Liniile de indiferență scad.

3. Liniile de indiferență sunt convexe în jos.

Proprietatea 2 implică o egalitate aproximativă importantă.

Acest raport arată cât de mult ar trebui individul să crească (scădeze) consumul celui de-al doilea produs în timp ce scade (mărește) consumul primului produs cu o unitate fără a modifica nivelul de satisfacție al nevoilor sale. Raportul se numește rata de înlocuire a primului produs cu al doilea, iar valoarea se numește rata marginală de înlocuire a primului produs cu al doilea.

Exemplul 53. Dacă utilitatea marginală a primului bun este 6, iar a doua - 2, atunci cu o scădere a consumului primului bun cu o unitate, este necesară creșterea consumului celui de-al doilea bun cu 3 unități cu acelaşi nivel de satisfacere a nevoilor.

6.3 Stabilirea bugetului

Lăsa - vector de preţuri pentru o mulţime de n produse; I - venitul unei persoane, pe care este dispus să-l cheltuiască pentru achiziționarea unui set de produse. Setul de seturi de bunuri care costă nu mai mult decât I la prețuri date se numește mulțime bugetară B. Mai mult, setul de seturi de bunuri care costă I se numește granița G a mulțimii bugetare B. mulţimea B este mărginită de graniţa G şi de restricţii naturale.

Setul de buget este descris printr-un sistem de inegalități:

Pentru cazul unei multimi de doua bunuri, setul bugetar B (Fig. 1) este un triunghi in sistemul de coordonate, delimitat de axele de coordonate si o dreapta.

6.4 Teoria cererii consumatorilor

În teoria consumului, se presupune că consumatorul se străduiește întotdeauna să-și maximizeze utilitatea și singura restricție pentru el este venitul limitat I, pe care îl poate cheltui pentru achiziționarea unui set de bunuri. În general, problema alegerii consumatorului (problema comportamentului rațional al consumatorului pe piață) este formulată astfel: găsiți un set de consumator , care își maximizează funcția de utilitate pentru o constrângere bugetară dată. Modelul matematic al acestei probleme:

În cazul unui set de două produse:

Din punct de vedere geometric, soluția acestei probleme este punctul de contact dintre limita mulțimii bugetare G și linia indiferenței.

Soluția acestei probleme se reduce la rezolvarea sistemului de ecuații:

(1)

Soluția acestui sistem este soluția la problema alegerii consumatorului.

Soluția la problema alegerii consumatorului se numește punctul de cerere. Acest punct de cerere depinde de prețuri și venit I. Adică. punctul de cerere este o funcție a cererii. La rândul său, funcția de cerere este un set de n funcții, fiecare dintre ele depinde de argument:

Aceste funcții se numesc funcții de cerere ale bunurilor corespunzătoare.

Exemplul 54. Pentru o mulțime de două bunuri de pe piață, prețurile cunoscute pentru acestea și venitul I, găsiți funcțiile cererii dacă funcția de utilitate are forma .

Soluţie. Să diferențiem funcția de utilitate:

.

Înlocuiți expresiile obținute în (1) și obțineți sistemul de ecuații:

În acest caz, cheltuiala pentru fiecare produs va fi jumătate din venitul consumatorului, iar valoarea produsului achiziționat este egală cu suma cheltuită pe acesta, împărțită la prețul produsului.

Exemplul 55. Fie funcția de utilitate pentru primul bun, al doilea,

prețul primului produs, prețul celui de-al doilea. Sursa de venit . Cât de mult ar trebui să cumpere consumatorul pentru a maximiza utilitatea?

Soluţie. Să găsim derivatele funcțiilor de utilitate, să le substituim în sistemul (1) și să o rezolvăm:

Acest set de bunuri este optim pentru consumator in ceea ce priveste maximizarea utilitatii.

Testul trebuie efectuat în conformitate cu opțiunea selectată de ultima cifră a numărului cărții de înregistrare într-un caiet separat. Fiecare problemă trebuie să conțină o condiție, o soluție detaliată și o concluzie.

1. Introducere în calcul

Sarcina 1. Găsiți domeniul funcției.

5.

Problema 2. Aflați limitele funcțiilor.

.

Sarcina 3. Găsiți punctele de întrerupere ale funcției și determinați tipul acestora.

1. 2. 3.

Capitolul 2. Calculul diferenţial al unei funcţii a unei variabile

Sarcina 4. Găsiți derivate ale acestor funcții.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - arcsin x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e 5 x - 1) 6; c) y =; d) y =; e) y = x 8 ++ + 5; f) y = 3 x - arcsin x.

5.a) y = 2x 3 - + e x; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sing;

d) y = 3x 4 - - 9+ 9; e) y =;

f) y = x 2 + arcsin x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4x 4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x 2 - x; f) y = e sin 3 x + 2.

Sarcina 5. Investigați funcția și construiți graficul acesteia.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9.a) b) c).

10. a) b) v) .

Sarcina 6. Găsiți cea mai mare și cea mai mică valoare a funcției pe un segment dat.

1. .

3. .

6. .

8. .

9. .

10. .

Capitolul 3. Calcul integral

Problema 7. Aflați integrale nedefinite.

1.a) b);

2.a) ; b) c) d).

4. G)

5.a) ; b); v) ; G).

6.a) ; b); v); G)

7.a) ; b) ; v) ; G)

8.a) ; b); v) ; G).

9.a) ; b) c); G).

10.a) b) v) ; G).

Problema 8. Calculați integrale definite.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Problema 9. Găsiți integrale improprii sau demonstrați că acestea diverg.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Problema 10. Aflați aria ariei delimitate de curbe

1. .2. .

5. 6.

7. , .8..

10. , .

Capitolul 4. Calculul diferenţial al unei funcţii a mai multor variabile.

Sarcina 11. Găsiți domeniul funcției (arată în desen).

Problema 12. Investigați continuitatea funcției pt

Problema 13. Aflați derivata unei funcții definite implicit.

Problema 14. Calculați aproximativ

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

Problema 15. Investigați funcția pentru extrema.

7. .

8. .

9. .

10. .

Problema 16. Aflați cea mai mare și cea mai mică valoare a funcției într-o zonă închisă dată.

1.în dreptunghi

2.

3.în dreptunghi

4.în regiunea mărginită de o parabolă

Și abscisa.

5.pătrat

6.într-un triunghi mărginit de axele de coordonate și de o dreaptă

7.într-un triunghi mărginit de axele de coordonate și de o dreaptă

8. într-un triunghi mărginit de axele de coordonate și de o dreaptă

9.în regiunea delimitată de o parabolă

Și abscisa.

10.în regiunea delimitată de o parabolă

Și abscisa.

Principalul

1. M.S. Crassus, B.P. Chuprynov. Fundamentele matematicii și aplicarea ei în educația economică: manual. - Ed. a IV-a, Isp. - M .: Delo, 2003.

2. M.S. Crassus, B.P. Chuprynov. Matematică pentru specialitățile economice: Manual. - Ed. a IV-a, Isp. - M .: Delo, 2003.

3. M.S. Crassus, B.P. Chuprynov. Matematică pentru o diplomă de licență în economie. Manual. - Ed. a IV-a, Isp. - M .: Delo, 2005.

4. Matematică superioară pentru economiști. Manual pentru universități / N.Sh. Kremer, B.A. Putko, I.M. Trishin, M.N. Friedman; Ed. prof. N.Sh. Kremer, - ed. a 2-a, revizuită. si adauga. - M: UNITATE, 2003.

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman MN Matematică superioară pentru specialitățile economice. Manual și Atelier (părțile I și II) / Ed. prof. N.Sh. Kremer, - ed. a 2-a, revizuită. si adauga. - M: Învățământ superior, 2007. - 893p. - (Fundamentele științelor)

6. Danko P.E., Popov A.G., Kozhevnikova T.Ya. Matematică superioară în exerciții și probleme. M. liceu. 1999.

Adiţional

1. I.I. Bavrin, V.L. Marinarii. Matematică superioară. „Centrul de editură umanitară Vlados”, 2002.

2. I.A. Zaitsev. Matematică superioară. „Liceu”, 1998.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, I.G. Shandra. Matematică în economie / în două părți /. M. Finanţe şi statistică. 1999.

pentru studenti medical, pediatric, stomatologic

și facultăți de medicină preventivă

la munca de laborator

„Concepte de bază ale analizei matematice”

1. Fundamentarea științifică și metodologică a temei:

Conceptele derivate și diferențiale sunt unul dintre conceptele de bază ale analizei matematice. Calcularea derivatelor este necesară atunci când se rezolvă multe probleme de fizică și matematică (găsirea vitezei, accelerației, presiunii etc.). Importanța conceptului de derivată, în special, este determinată de faptul că derivata unei funcții caracterizează rata de modificare a acestei funcții atunci când argumentul ei se schimbă.

Utilizarea diferenţialului face posibilă efectuarea de calcule aproximative, precum şi estimarea erorilor.

Metodele de găsire a derivatelor și diferențialelor de funcții și aplicarea lor constituie principala problemă a calculului diferențial. Necesitatea conceptului de derivată apare în legătură cu formularea problemei calculării vitezei de mișcare și găsirii unghiului tangentei la curbă. Problema inversă este de asemenea posibilă: determinați distanța parcursă de viteză și găsiți funcția corespunzătoare prin tangentei pantei tangentei. Această problemă inversă duce la conceptul de integrală nedefinită.

Conceptul de integrală definită este utilizat într-o serie de probleme practice, în special în problemele de calculare a ariilor figurilor plane, calculul muncii efectuate de o forță variabilă și găsirea valorii medii a unei funcții.

În descrierea matematică a diferitelor procese și fenomene fizice, chimice, biologice, sunt adesea folosite ecuații care conțin nu numai mărimile studiate, ci și derivatele lor din diferite ordine ale acestor mărimi. De exemplu, conform celei mai simple versiuni a legii înmulțirii bacteriilor, rata de reproducere este proporțională cu numărul de bacterii la un moment dat. Dacă această cantitate este notată cu N (t), atunci, în conformitate cu semnificația fizică a derivatului, rata de reproducere a bacteriilor este un derivat al lui N (t), iar pe baza legii de mai sus, putem scrie: raportul N „(t) = k ∙ N, unde k> 0 - coeficient de proporționalitate Ecuația rezultată nu este algebrică, deoarece conține nu numai funcția necunoscută N (t), ci și derivata ei de ordinul întâi.

2. Scurtă teorie:

1. Probleme care duc la conceptul de derivată

1. Problema găsirii vitezei v a unui punct material... Lasă un punct material să efectueze mișcare rectilinie. La un moment dat t 1 punctul este în poziție M 1. La un moment dat t 2 gravidă M 2 . Să notăm intervalul M 1 , M 2 peste ΔS; t 2 - t 1 = Δt... Valoarea se numește viteza medie de mișcare. Pentru a afla viteza instantanee a unui punct într-o poziție M 1 necesar Δt tind spre zero. Din punct de vedere matematic, asta înseamnă că

, (1)

Astfel, pentru a găsi viteza instantanee a unui punct material, este necesar să se calculeze limita raportului de creștere a funcției ΔS la incrementul argumentului Δt cu condiţia ca Δt → 0.

2. Problema găsirii unghiului de înclinare al tangentei la graficul unei funcții.

Fig. 1

Luați în considerare graficul unei funcții y = f (x). Care este unghiul de înclinare
tangentă în punct M 1 ? La punctul M 1 trageți o tangentă la graficul funcției. Selectați un punct arbitrar pe grafic M 2 si trage o secanta. Ea este înclinată spre axă OH la un unghi α 1 ... Considera ΔM 1 M 2 A:

, (2)

Dacă punct M 1 fixează și punctează M 2 se apropie de M 1 , apoi secant M 1 M 2 va merge la tangenta la graficul funcției în punctul M 1 si poti scrie:

, (3)

Astfel, este necesar să se calculeze limita raportului dintre incrementul funcției și incrementul argumentului dacă incrementul argumentului tinde spre zero.

Limita raportului dintre incrementul Δy al funcției y = f (x) și incrementul argumentului Δx la un punct dat x 0 întrucât Δx tinde spre zero, se numește derivată a funcției într-un punct dat.

Notație derivată: y ", f" (x), ... Prin definitie

, (4)

unde Δx = x 2 -x 1 este incrementul argumentului (diferența dintre două valori ulterioare suficient de apropiate ale argumentului), Δy = y 2 -y 1 este incrementul funcției (diferența dintre valori ​a funcției corespunzătoare acestor valori ale argumentului).

Găsirea derivatei unei funcții date se numește ea diferenţiere... Diferențierea principalelor funcții elementare se realizează în funcție de formule gata făcute (vezi tabel), precum și folosind reguli:

Derivată a unei sume algebrice funcții este egală cu suma derivatelor acestor funcții:

(u+ υ )"= u" + υ "

2. Derivata produsului a doua functii este egala cu suma produselor celei de-a doua functii prin derivata primei si prima functie prin derivata celei de-a doua:

(u ∙υ ) "= u"υ + uυ "

3. Derivată a coeficientului a două funcții este egal cu o fracție, al cărei numărător este diferența dintre produsele numitorului prin derivata numărătorului și numărătorul prin derivata numitorului, iar numitorul este pătratul numitorului:

Sensul fizic al derivatului. Comparația dintre (4) și (1) implică faptul că viteza instantanee a mișcării rectilinie a unui punct material este egală cu derivata dependenței coordonatei sale de timp.

Sensul general al derivatei unei funcții este că ea caracterizează rata (rapiditatea) schimbării funcției pentru o anumită schimbare de argument. Viteza proceselor fizice, chimice și a altor procese, de exemplu, viteza de răcire a corpului, viteza reacției chimice, rata de reproducere a bacteriilor etc., este, de asemenea, exprimată folosind un derivat.

Sensul geometric al derivatului. Mărimea tangentei unghiului de înclinare a tangentei trasate la graficul funcției se numește în matematică panta tangentei.

Panta tangentei la graficul funcției diferențiabile într-un anumit punct este numeric egală cu derivata funcției în acest punct.

Această afirmație se numește sensul geometric al derivatului.

Conținutul articolului

ANALIZA MATEMATICĂ, o ramură a matematicii care oferă metode pentru studiul cantitativ al diferitelor procese de schimbare; se ocupă cu studiul vitezei de schimbare (calcul diferențial) și determinarea lungimilor curbelor, ariilor și volumelor figurilor delimitate de contururi și suprafețe curbe (calcul integral). Pentru problemele de analiză matematică, este caracteristic ca soluția lor să fie asociată cu conceptul de limită.

Analiza matematică a fost inițiată în 1665 de I. Newton și (aproximativ 1675) independent de G. Leibniz, deși lucrări pregătitoare importante au fost efectuate de I. Kepler (1571–1630), F. Cavalieri (1598–1647), P. Ferma (1601– 1665), J. Wallis (1616-1703) și I. Barrow (1630-1677).

Pentru a face prezentarea mai vie, vom recurge la limbajul graficelor. Prin urmare, cititorul poate considera util să arunce o privire la articolul GEOMETRIE ANALITĂ înainte de a citi acest articol.

CALCUL DIFERENȚIAL

Tangente.

În fig. 1 prezintă un fragment al curbei y = 2X – X 2, încheiat între X= –1 și X= 3. Segmentele suficient de mici ale acestei curbe par drepte. Cu alte cuvinte, dacă R Este un punct arbitrar al acestei curbe, atunci există o linie dreaptă care trece prin acest punct și este o aproximare a curbei într-o mică vecinătate a punctului R, iar cu cât cartierul este mai mic, cu atât este mai bună aproximarea. O astfel de dreaptă se numește tangentă la curba în punctul respectiv R... Sarcina principală a calculului diferențial este de a construi o metodă generală care vă permite să găsiți direcția unei tangente în orice punct al unei curbe în care există tangenta. Nu este greu să ne imaginăm o curbă cu o rupere ascuțită (Fig. 2). Dacă R- vârful unei astfel de pauze, atunci puteți construi o linie dreaptă aproximativă PT 1 - în dreapta punctului Rși o altă linie de aproximare RT 2 - la stânga punctului R... Dar nu există o singură linie dreaptă care să treacă printr-un punct R, care s-a apropiat la fel de bine de curba din vecinătatea punctului P atat la dreapta cat si la stanga, de unde tangenta in punct P nu exista.

În fig. 1 tangentă DIN trasate prin origine O= (0,0). Panta acestei drepte este 2, i.e. cand abscisa se modifica cu 1, ordonata creste cu 2. Daca Xși y- coordonatele unui punct arbitrar pe DIN, apoi, îndepărtându-se de O de la distanță X unități la dreapta, ne îndepărtăm de O pe 2 y unități în sus. Prin urmare, y/X= 2 sau y = 2X... Aceasta este ecuația tangentei DIN la curbă y = 2X – X 2 la punct O.

Acum este necesar să explicăm de ce din setul de drepte care trec prin punct O, a fost linia dreaptă cea care a fost aleasă DIN... Care este diferența dintre o linie dreaptă cu o pantă de 2 și alte drepte? Există un răspuns simplu și ne este greu să rezistam tentației de a folosi analogia tangentei la cerc: tangenta. DIN are un singur punct în comun cu curba, în timp ce orice altă linie dreaptă neverticală care trece prin punct O, intersectează curba de două ori. Acest lucru poate fi verificat după cum urmează.

Din moment ce expresia y = 2X – X 2 se poate obține prin scădere X 2 din y = 2X(ecuațiile dreptei DIN), apoi valorile y există mai puține cunoștințe pentru grafic y pentru o linie dreaptă în toate punctele, cu excepția unui punct X= 0. Prin urmare, graficul este peste tot, cu excepția punctului O situat mai jos DIN, iar această linie și graficul au un singur punct în comun. Mai mult, dacă y = mx- ecuația unei alte drepte care trece printr-un punct O, atunci cu siguranță vor fi două puncte de intersecție. Într-adevăr, mx = 2X – X 2 nu numai pentru X= 0, dar și pentru X = 2 – m... Și numai când m= 2 ambele puncte de intersecție coincid. În fig. 3 arată cazul când m mai putin de 2, deci la dreapta de O există un al doilea punct de intersecție.

Ce DIN- singura dreaptă neverticală care trece printr-un punct Oși având un singur punct în comun cu graficul, nu proprietatea sa cea mai importantă. Într-adevăr, dacă ne întoarcem la alte grafice, va deveni în curând clar că proprietatea tangentei pe care am observat-o în cazul general nu este îndeplinită. De exemplu, din fig. 4 se poate observa că în apropierea punctului (1,1) graficul curbei y = X 3 este bine aproximat printr-o linie dreaptă RT, care, însă, are mai mult de un punct comun cu el. Cu toate acestea, am dori să luăm în considerare RT tangentă la acest grafic în punct R... Prin urmare, este necesar să găsim o altă modalitate de a evidenția tangenta decât cea care ne-a servit atât de bine în primul exemplu.

Să presupunem că până la capăt Oși un punct arbitrar Q = (h,k) pe graficul curbei y = 2X – X 2 (Fig. 5) este trasată o linie dreaptă (numită secantă). Substituind în ecuația curbei valorile X = hși y = k, înțelegem asta k = 2h – h 2, prin urmare, panta secantei este

Cu foarte mici h sens m aproape de 2. Mai mult, alegerea h destul de aproape de 0 putem face mîn mod arbitrar aproape de 2. Putem spune că m„Tind la limită” egal cu 2 când h tinde spre zero, sau oricare ar fi limita m este egal cu 2 pentru h tinde spre zero. Aceasta este scrisă simbolic după cum urmează:

Apoi tangenta la grafic în punct O definită ca o dreaptă care trece printr-un punct O, cu o pantă egală cu această limită. Această definiție a unei tangente este aplicabilă în general.

Să arătăm avantajele acestei abordări cu un alt exemplu: găsiți panta tangentei la graficul curbei y = 2X – X 2 într-un punct arbitrar P = (X,y), nelimitându-ne la cel mai simplu caz când P = (0,0).

Lăsa Q = (X + h, y + k) - al doilea punct de pe diagramă, situat la distanță h la dreapta de R(fig. 6). Este necesar să găsiți panta k/h secantă PQ... Punct Q se afla la distanta

deasupra axei X.

Extindem parantezele, găsim:

Scăzând din această ecuație y = 2X – X 2, găsim distanța verticală de la punct R până la punctul Q:

Prin urmare, panta m secantă PQ este egal cu

Acum că h tinde spre zero, m tinde spre 2 - 2 X; vom lua ultima valoare ca panta tangentei PT... (Se va obține același rezultat dacă h ia valori negative, ceea ce corespunde alegerii punctului Qîn partea stângă a P.) Rețineți că pentru X= 0 rezultatul este același cu cel precedent.

Expresia 2 - 2 X se numeste derivata lui 2 X – X 2. Pe vremuri, derivatul era numit și „raport diferențial” și „coeficient diferențial”. Dacă expresia 2 X – X 2 desemnează f(X), adică

atunci derivata poate fi notata

Pentru a afla panta tangentei la graficul functiei y = f(X) la un moment dat, trebuie înlocuit în fў ( X) valoarea corespunzătoare acestui punct X... Deci panta fў (0) = 2 pentru X = 0, fў (0) = 0 pentru X= 1 și fў (2) = –2 pentru X = 2.

Derivatul este de asemenea notat laў , dy/dx, D x yși Du.

Faptul că curba y = 2X – X 2 în apropierea unui punct dat este practic imposibil de distins de tangenta lui în acest punct, ne permite să vorbim despre panta tangentei ca pe o „pantă a curbei” în punctul de tangență. Astfel, putem afirma că panta curbei luate în considerare are în punctul (0,0) o pantă de 2. Se mai poate spune că la X= 0 rata de schimbare y relativ X este 2. În punctul (2,0), panta tangentei (și curbei) este –2. (Semnul minus înseamnă că ca X variabil y scade.) În punctul (1,1), tangenta este orizontală. Noi spunem curba y = 2X – X 2 are o valoare staționară în acest punct.

Maxime și minime.

Tocmai am arătat că curba f(X) = 2X – X 2 este staționar în punctul (1,1). pentru că fў ( X) = 2 – 2X = 2(1 – X), este clar că pt X mai putin de 1, fў ( X) este pozitivă și, prin urmare y crește; la X, mare 1, fў ( X) este negativă și, prin urmare y scade. Astfel, în vecinătatea punctului (1,1) indicat în Fig. 6 lit M, sens la crește până la un punct M, staționar la punct Mși scade după punct M... Acest punct se numește „maximum” deoarece valoarea laîn acest moment depășește oricare dintre valorile sale într-o vecinătate suficient de mică a acestuia. În mod similar, „minimul” este definit ca un punct în apropierea căruia toate valorile y depășesc numeric la chiar în acest moment. Se mai poate întâmpla ca deși derivatul lui f(X) la un moment dat și dispare, semnul său nu se schimbă în vecinătatea acestui punct. Un astfel de punct, care nu este nici maxim, nici minim, se numește punct de inflexiune.

De exemplu, să găsim punctul staționar al curbei

Derivata acestei functii este

și dispare la X = 0, X= 1 și X= –1; acestea. la punctele (0,0), (1, –2/15) și (–1, 2/15). Dacă X puțin mai puțin decât -1, atunci fў ( X) este negativ; dacă X puțin mai mult de -1, atunci fў ( X) este pozitivă. Prin urmare, punctul (–1, 2/15) este maximul. În mod similar, se poate demonstra că punctul (1, –2/15) este un minim. Dar derivatul fў ( X) este negativ atât înainte, cât și după punctul (0,0). Prin urmare, (0,0) este punctul de inflexiune.

Studiul efectuat al formei curbei, precum și al faptului că curba intersectează axa X la f(X) = 0 (adică pentru X= 0 sau) vă permit să reprezentați graficul său aproximativ așa cum se arată în Fig. 7.

În general, dacă excludem cazuri neobișnuite (curbe care conțin segmente de linie dreaptă sau un număr infinit de coturi), există patru opțiuni pentru poziția relativă a curbei și a tangentei în vecinătatea punctului tangentei. R. (Cm... orez. 8 unde tangenta are o pantă pozitivă.)

1) Pe ambele părți ale punctului R curba se află deasupra tangentei (Fig. 8, A). În acest caz, ei spun că curba la punctul R convex în jos sau concav.

2) Pe ambele părți ale punctului R curba este situată sub tangentă (Fig. 8, b). În acest caz, se spune că curba este convexă în sus sau pur și simplu convexă.

3) și 4) Curba este situată deasupra tangentei pe o parte a punctului R iar mai jos – pe de altă parte. În acest caz R- punct de inflexiune.

Compararea valorilor fў ( X) pe ambele părți ale R cu valoarea ei la punct R, este posibil să se determine care dintre aceste patru cazuri trebuie tratată într-o anumită problemă.

Aplicații.

Toate cele de mai sus găsesc aplicații importante în diverse domenii. De exemplu, dacă corpul este aruncat vertical în sus cu o viteză inițială de 200 de picioare pe secundă, atunci înălțimea s pe care vor fi amplasate prin t secunde comparativ cu punctul de plecare vor fi

Acționând în același mod ca în exemplele pe care le-am luat în considerare, găsim

această valoare dispare la c. Derivat fў ( X) este pozitivă până la valoarea lui c și negativă după acest timp. Prin urmare, s crește la, apoi devine staționar și apoi scade. Aceasta este o descriere generală a mișcării unui corp aruncat în sus. Din ea știm când corpul atinge punctul cel mai înalt. Mai departe, înlocuind t= 25/4 in f(t), obținem 625 de picioare, ridicarea maximă. În această sarcină fў ( t) are un sens fizic. Această derivată arată viteza cu care corpul se mișcă în momentul de timp t.

Să luăm acum în considerare un alt tip de aplicație (Fig. 9). Este necesar să se facă o cutie cu fundul pătrat dintr-o foaie de carton cu o suprafață de 75 cm 2. Cât de mare trebuie să fie această cutie pentru a avea volumul maxim? Dacă X- laterala bazei cutiei si h- înălțimea sa, atunci volumul cutiei este V = X 2 h, iar aria suprafeței este 75 = X 2 + 4xh... Transformând ecuația, obținem:

Derivat de la V se dovedește a fi egal

și dispare la X= 5. Apoi

și V= 125/2. Graficul funcției V = (75X – X 3) / 4 este prezentat în Fig. 10 (valori negative X omisă ca neavând sens fizic în această problemă).

Derivate.

O sarcină importantă a calculului diferențial este crearea de metode care vă permit să găsiți rapid și convenabil derivate. De exemplu, este ușor să calculezi asta

(Derivata constantei este, desigur, zero.) Nu este greu de dedus regula generală:

Unde n- orice număr întreg sau fracție. De exemplu,

(Acest exemplu arată cât de utili sunt exponenții fracționali.)

Iată câteva dintre cele mai importante formule:

Există şi următoarele reguli: 1) dacă fiecare dintre cele două funcţii g(X) și f(X) are derivate, atunci derivata sumei lor este egală cu suma derivatelor acestor funcții, iar derivata diferenței este egală cu diferența derivatelor, i.e.

2) derivata produsului a două funcții se calculează cu formula:

3) derivata raportului celor două funcții are forma

4) derivata unei funcții înmulțită cu o constantă este egală cu o constantă înmulțită cu derivata acestei funcții, i.e.

Se întâmplă adesea ca valorile unei funcții să fie calculate în etape. De exemplu, pentru a calcula păcatul X 2, mai întâi trebuie să găsim u = X 2, apoi calculați sinusul numărului u... Găsim derivata unor astfel de funcții complexe folosind așa-numita „regula lanțului”:

În exemplul nostru f(u) = păcat u, fў ( u) = cos u, prin urmare,

Acestea și alte reguli similare permit să scrieți imediat derivatele multor funcții.

Aproximații liniare.

Faptul că, cunoscând derivata, în multe cazuri putem înlocui graficul unei funcții în apropierea unui punct al tangentei sale în acest punct este de mare importanță, deoarece liniile drepte sunt mai ușor de lucrat.

Această idee își găsește aplicare directă în calculul valorilor aproximative ale funcțiilor. De exemplu, este destul de dificil să calculezi valoarea când X= 1,033. Dar poți profita de faptul că numărul 1.033 este aproape de 1 și asta. Închide X= 1 putem înlocui graficul curbei tangentei fără a face vreo greșeală gravă. Panta unei astfel de tangente este egală cu valoarea derivatei ( X 1/3) ў = (1/3) X–2/3 la x = 1, adică 1/3. Deoarece punctul (1,1) se află pe curbă și panta tangentei la curbă în acest punct este 1/3, ecuația tangentei are forma

Pe această linie la X = 1,033

Valoarea rezultată y ar trebui să fie foarte aproape de valoarea adevărată y; și, într-adevăr, este doar cu 0,00012 mai mult decât cel adevărat. În analiza matematică, au fost dezvoltate metode pentru a îmbunătăți acuratețea acestui tip de aproximare liniară. Aceste metode asigură fiabilitatea calculelor noastre aproximative.

Procedura descrisă tocmai sugerează o notație utilă. Lăsa P- punctul corespunzător pe graficul funcţiei f variabil Xși lăsați funcția f(X) este diferențiabilă. Înlocuiți graficul curbei în apropierea punctului R tangentă la ea, desenată în acest punct. Dacă X modificarea sumei h, atunci ordonata tangentei se va schimba cu valoarea h H f ў ( X). Dacă h este foarte mică, atunci cea din urmă valoare este o bună aproximare a schimbării adevărate a ordonatei y grafică. Dacă în loc de h vom scrie simbolul dx(asta nu este un produs!), ci o schimbare a ordonatei y denota dy, apoi primim dy = f ў ( X)dx, sau dy/dx = f ў ( X) (cm... orez. unsprezece). Prin urmare, în loc de Dy sau f ў ( X) simbolul este adesea folosit pentru a desemna o derivată dy/dx... Comoditatea acestei notații depinde în principal de aspectul explicit al regulii lanțului (diferențierea unei funcții complexe); în noua notație, această formulă arată astfel:

unde se presupune că la depinde de u, A u la rândul său depinde de X.

Magnitudinea dy numit diferenţial la; de fapt depinde de Două variabile si anume: din Xși creșteri dx... Când incrementul dx foarte mic, magnitudine dy este aproape de modificarea corespunzătoare a valorii y... Dar să presupunem că creșterea dx putin, nu e nevoie.

Funcția derivată y = f(X) am notat f ў ( X) sau dy/dx... Este adesea posibil să se ia derivata derivatei. Rezultatul se numește derivata a doua a f (X) și notat f ўў ( X) sau d 2 y/dx 2. De exemplu, dacă f(X) = X 3 – 3X 2, atunci f ў ( X) = 3X 2 – 6Xși f ўў ( X) = 6X- 6. Denumiri similare sunt folosite pentru derivatele de ordin superior. Cu toate acestea, pentru a evita un număr mare de liniuțe (egal cu ordinea derivatei), derivata a patra (de exemplu) poate fi scrisă ca f (4) (X), și derivata n-a comanda ca f (n) (X).

Se poate demonstra că curba într-un punct este convexă în jos dacă derivata a doua este pozitivă și convexă în sus dacă derivata a doua este negativă.

Dacă funcția are o derivată a doua, atunci modificarea cantității y corespunzătoare incrementului dx variabil X, poate fi calculat aproximativ prin formula

Această aproximare este în general mai bună decât cea dată de diferenţial fў ( X)dx... Ea corespunde înlocuirii unei părți a curbei cu o parabolă și nu cu o linie dreaptă.

Dacă funcţia f(X) sunt derivate de ordin superior, atunci

Restul este

Unde X- un număr între Xși X + dx... Rezultatul de mai sus se numește formula Taylor de rest. Dacă f(X) are derivate de toate ordinele, atunci de obicei R n® 0 pentru n ® Ґ .

CALCUL INTEGRAL

Pătrate.

Când se studiază ariile figurilor plane curbilinii, sunt relevate noi aspecte ale analizei matematice. Chiar și grecii antici au încercat să rezolve astfel de probleme, pentru care determinarea, de exemplu, a zonei unui cerc a fost una dintre cele mai dificile sarcini. Arhimede a obținut un mare succes în rezolvarea acestei probleme, care a reușit să găsească și aria unui segment parabolic (Fig. 12). Cu ajutorul unui raționament foarte complicat, Arhimede a demonstrat că aria unui segment parabolic este 2/3 din aria dreptunghiului descris și, prin urmare, în acest caz este egală cu (2/3) (16) = 32/3. După cum vom vedea mai târziu, acest rezultat poate fi obținut cu ușurință prin metode de analiză matematică.

Predecesorii lui Newton și Leibniz, în principal Kepler și Cavalieri, au rezolvat problema calculării ariilor figurilor curbilinii folosind o metodă care cu greu poate fi numită logică, dar care s-a dovedit a fi extrem de fructuoasă. Când Wallis în 1655 a combinat metodele lui Kepler și Cavalieri cu metodele lui Descartes (geometria analitică) și a folosit algebra nou născută, scena pentru apariția lui Newton a fost complet pregătită.

Wallis a împărțit figura, a cărei zonă trebuia calculată, în benzi foarte înguste, fiecare fiind considerată aproximativ dreptunghi. Apoi a adunat ariile dreptunghiurilor de aproximare si, in cazurile cele mai simple, a obtinut valoarea la care tinde suma ariilor dreptunghiurilor atunci cand numarul dungilor tinde spre infinit. În fig. 13 prezintă dreptunghiuri corespunzătoare unei anumite diviziuni în benzi ale zonei de sub curbă y = X 2 .

Teorema principală.

Marea descoperire a lui Newton și Leibniz a făcut posibilă excluderea procesului laborios de trecere la limita sumei zonelor. Acest lucru a fost realizat datorită unei noi imagini asupra conceptului de pătrat. Ideea este că trebuie să ne imaginăm aria de sub curbă generată de ordonata care se mișcă de la stânga la dreapta și să întrebăm cât de repede se modifică aria măturată de ordonate. Vom obține cheia răspunsului la această întrebare dacă luăm în considerare două cazuri speciale în care zona este cunoscută dinainte.

Să începem cu aria de sub graficul funcției liniare y = 1 + X deoarece în acest caz aria poate fi calculată folosind geometria elementară.

Lăsa A(X) Este partea de plan cuprinsă între linia dreaptă y = 1 + Xși un segment OQ(fig. 14). Când conduceți QP zona dreapta A(X) crește. Cât de repede? Nu este dificil să răspundem la această întrebare, deoarece știm că aria unui trapez este egală cu produsul înălțimii sale cu jumătatea sumei bazelor sale. Prin urmare,

Rata de schimbare a zonei A(X) este determinată de derivata sa

Vedem asta Aў ( X) coincide cu ordonata la puncte R... Este aceasta o coincidență? Să încercăm să verificăm parabola prezentată în Fig. 15. Pătrat A (X) sub parabolă la = X 2 în intervalul de la 0 la X este egal cu A(X) = (1 / 3)(X)(X 2) = X 3/3. Rata de modificare a acestei zone este determinată de expresie

care coincide exact cu ordonata la punct de mișcare R.

Dacă presupunem că această regulă este în general îndeplinită în aşa fel încât

este rata de schimbare a ariei de sub graficul funcției y = f(X), atunci aceasta poate fi folosită pentru calcule și alte domenii. De fapt, raportul Aў ( X) = f(X) exprimă o teoremă fundamentală, care ar putea fi formulată astfel: derivata, sau rata de modificare a ariei în funcție de X, este egal cu valoarea funcției f (X) la punct X.

De exemplu, pentru a găsi aria de sub graficul unei funcții y = X 3 de la 0 la X(Fig. 16), punem

Un posibil răspuns este:

din moment ce derivatul lui X 4/4 este într-adevăr egal cu X 3. În plus, A(X) este egal cu zero pentru X= 0, așa cum ar trebui să fie dacă A(X) este într-adevăr o zonă.

Analiza matematică demonstrează că un alt răspuns pe lângă expresia de mai sus pentru A(X), nu exista. Să arătăm că această afirmație este plauzibilă utilizând următorul raționament euristic (neriguros). Să presupunem că există o a doua soluție V(X). Dacă A(X) și V(X) „Start” simultan de la valoarea zero la X= 0 și tot timpul se schimbă în aceeași rată, apoi valorile lor la nr X nu poate deveni diferit. Ele trebuie să fie la fel peste tot; prin urmare, există o singură soluție.

Cum poate fi justificat raportul? Aў ( X) = f(X) în general? La această întrebare se poate răspunde doar studiind rata de schimbare a zonei în funcție de Xîn general. Lăsa m- cea mai mică valoare a funcției f (X) în intervalul de la X inainte de ( X + h), A M- cea mai mare valoare a acestei functii in acelasi interval. Apoi, creșterea zonei în pornire de la X La ( X + h) trebuie să fie cuprinse între zonele a două dreptunghiuri (Fig. 17). Bazele ambelor dreptunghiuri sunt egale h... Dreptunghiul mai mic are o înălțime m si zona mh, mai mare, respectiv, Mși Mh... Pe parcela de suprafata versus X(Fig. 18) se poate observa că atunci când abscisa se modifică de h, valoarea ordonatei (adică, suprafața) este mărită cu suma cuprinsă între mhși Mh... Panta secantă din acest grafic este între mși M... ce se intampla cand h tinde spre zero? Dacă graficul funcţiei y = f(X) este continuă (adică nu conține discontinuități), atunci M, și m tind să f(X). Prin urmare, panta Aў ( X) parcela de suprafață în funcție de X este egal cu f(X). Tocmai la o astfel de concluzie trebuia să se ajungă.

Leibniz a propus pentru zona de sub curbă y = f(X) de la 0 la A desemnare

Cu o abordare riguroasă, această așa-numită integrală definită trebuie definită ca limită a anumitor sume în maniera lui Wallis. Având în vedere rezultatul de mai sus, este clar că această integrală este calculată cu condiția să găsim o astfel de funcție A(X), care dispare la X= 0 și are o derivată Aў ( X) egal cu f (X). Găsirea unei astfel de funcții se numește de obicei integrare, deși ar fi mai potrivit să numim această operație antidiferențiere, adică este, într-un sens, inversă diferențierii. În cazul unui polinom, integrarea este simplă. De exemplu, dacă

care este uşor de verificat prin diferenţiere A(X).

Pentru a calcula suprafața A 1 sub curbă y = 1 + X + X 2/2, cuprins între ordonatele 0 și 1, scriem pur și simplu

și înlocuirea X= 1, obținem A 1 = 1 + 1/2 + 1/6 = 5/3. Pătrat A(X) de la 0 la 2 este egal cu A 2 = 2 + 4/2 + 8/6 = 16/3. După cum se vede din fig. 19, aria cuprinsă între ordonatele 1 și 2 este A 2 – A 1 = 11/3. De obicei este scrisă ca o integrală definită

Volumele.

Un raționament similar face să fie surprinzător de simplu să se calculeze volumele corpurilor de revoluție. Să demonstrăm acest lucru prin exemplul de calcul al volumului unei mingi, o altă problemă clasică pe care grecii antici, folosind metodele cunoscute de ei, au reușit să o rezolve cu mare dificultate.

Rotiți partea din plan închisă într-un sfert de cerc de rază r, la un unghi de 360 ​​° în jurul axei X... Ca urmare, obținem o emisferă (Fig. 20), al cărei volum îl notăm V(X). Este necesar să se determine rata la care V(X) cu creşterea X... Trecând de la X La X + h, este ușor să verificați dacă creșterea volumului este mai mică decât volumul p(r 2 – X 2)h raza și înălțimea cilindrului circular h, și mai mult decât volum p[r 2 – (X + h) 2 ]h raza și înălțimea cilindrului h... Prin urmare, pe graficul funcției V(X) panta secantei este între p(r 2 – X 2) și p[r 2 – (X + h) 2]. Când h tinde spre zero, panta tinde spre

La X = r primim

pentru volumul emisferei și, prin urmare, 4 relatii cu publicul 3/3 pentru volumul întregii mingi.

O metodă similară vă permite să găsiți lungimile curbelor și zonele suprafețelor curbate. De exemplu, dacă A(X) - lungimea arcului relatii cu publiculîn fig. 21, atunci sarcina noastră este să calculăm Aў( X). La nivel euristic, folosim un truc care ne permite să nu apelăm la trecerea obișnuită la limită, necesară pentru o demonstrație riguroasă a rezultatului. Să presupunem că rata de modificare a funcției A(X) la punct R este la fel ca în cazul în care curba ar fi înlocuită cu tangenta ei PT la punct P... Dar din fig. 21 poate fi văzut direct când pășiți h la dreapta sau la stânga punctului X de-a lungul RT sens A(X) schimbări la

Prin urmare, rata de schimbare a funcției A(X) este

Pentru a găsi funcția în sine A(X), este necesar doar să se integreze expresia din partea dreaptă a egalității. Se dovedește că majoritatea funcțiilor sunt greu de integrat. Prin urmare, dezvoltarea metodelor de calcul integral constituie o mare parte a analizei matematice.

Antiderivate.

Fiecare funcție a cărei derivată este egală cu o funcție dată f(X), se numește antiderivată (sau primitivă) pentru f(X). De exemplu, X 3/3 este antiderivată pentru funcție X 2, deoarece ( X 3/3) ў = X 2. Desigur X 3/3 nu este singura antiderivată a unei funcții X 2 din moment ce X 3 /3 + C este, de asemenea, un derivat pentru X 2 pentru orice constantă CU... Cu toate acestea, în cele ce urmează vom fi de acord să omitem astfel de constante aditive. În general

Unde n Este un număr întreg pozitiv, deoarece ( x n + 1/(n+ 1)) ў = x n... Relația (1) este valabilă într-un sens și mai general dacă nînlocuiți cu orice număr rațional k cu excepția lui -1.

Funcție antiderivată arbitrară pentru o funcție dată f(X) se numește de obicei integrala nedefinită a f(X) și notează-l ca

De exemplu, din moment ce (păcat X) ў = cos X, formula este valabilă

În multe cazuri, când există o formulă pentru o integrală nedefinită a unei funcții date, aceasta poate fi găsită în numeroase tabele de integrale nedefinite publicate pe scară largă. Integralele funcțiilor elementare sunt tabulare (acestea includ puteri, logaritmi, funcții exponențiale, funcții trigonometrice, funcții trigonometrice inverse, precum și combinațiile finite ale acestora obținute cu ajutorul operațiilor de adunare, scădere, înmulțire și împărțire). Folosind integrale tabulare, puteți calcula integrale ale funcțiilor mai complexe. Există multe moduri de a calcula integrale nedefinite; cea mai comună dintre acestea este metoda de substituție sau substituție variabilă. Constă în faptul că dacă dorim să înlocuim în integrala nedeterminată (2) X pe o funcție diferențiabilă X = g(u), pentru ca integrala să nu se modifice, este necesar X inlocuit de gў ( u)du... Cu alte cuvinte, egalitatea

(înlocuirea 2 X = u, de unde 2 dx = du).

Iată o altă metodă de integrare - metoda integrării pe părți. Se bazează pe formula deja cunoscută

După ce au integrat părțile din stânga și din dreapta și ținând cont de asta

Această formulă se numește formula de integrare pe părți.

Exemplu 2. Se cere să se găsească. Din moment ce cos X= (păcat X) ў, putem scrie că

De la (5), setare u = Xși v= păcat X, primim

Și din moment ce (–cos X) ў = sin X găsim că şi

Trebuie subliniat că ne-am limitat doar la o foarte scurtă introducere a unui subiect foarte amplu, în care s-au acumulat numeroase tehnici duhovnicești.

Funcțiile a două variabile.

Datorită curbei y = f(X) am luat în considerare două sarcini.

1) Aflați panta tangentei la curbă într-un punct dat. Această problemă se rezolvă prin calcularea valorii derivatei fў ( X) în punctul specificat.

2) Găsiți aria de sub curba deasupra segmentului axei X delimitate de linii verticale X = Ași X = b... Această problemă se rezolvă prin calculul unei integrale definite.

Fiecare dintre aceste probleme are un analog în cazul suprafeței z = f(X,y).

1) Aflați planul tangent la suprafață într-un punct dat.

2) Aflați volumul de sub suprafața deasupra părții planului hu delimitată de curbă CU, iar din lateral - perpendiculare pe plan X y trecând prin punctele curbei limită CU (cm... orez. 22).

Următoarele exemple arată cum sunt îndeplinite aceste sarcini.

Exemplu 4. Găsiți planul tangent la suprafață

în punctul (0,0,2).

Un plan este definit dacă sunt date două drepte care se intersectează în el. Una dintre aceste rânduri ( l 1) ne urcăm în avion xz (la= 0), al doilea ( l 2) - în avion yz (X = 0) (cm... orez. 23).

În primul rând, dacă la= 0, atunci z = f(X,0) = 2 – 2X – 3X 2. Derivată cu privire la X notat cu fў X(X,0) = –2 – 6X, la X= 0 are valoarea –2. Drept l 1 dat de ecuații z = 2 – 2X, la= 0 - tangentă la CU 1, liniile de intersecție a suprafeței cu planul la= 0. În mod similar, dacă X= 0, atunci f(0,y) = 2 – y – y 2, iar derivata cu privire la la are forma

pentru că fў y(0,0) = –1, curbă CU 2 - linia de intersecție a suprafeței cu planul yz- are o tangentă l 2 dat de ecuații z = 2 – y, X= 0. Planul tangent dorit conține ambele drepte l 1 și l 2 și se scrie prin ecuație

Aceasta este ecuația planului. În plus, obținem linii drepte l 1 și l 2, stabilirea, respectiv, la= 0 și X = 0.

Faptul că ecuația (7) definește cu adevărat planul tangent poate fi verificat la nivel euristic dacă observăm că această ecuație conține termenii de ordinul întâi incluși în ecuația (6) și că termenii de ordinul doi pot fi reprezentați în forma -. Deoarece această expresie este negativă pentru toate valorile Xși la, În afară de X = la= 0, suprafața (6) se află peste tot sub planul (7), cu excepția punctului R= (0,0,0). Putem spune că suprafața (6) este convexă în sus în punctul respectiv R.

Exemplu 5. Găsiți planul tangent la suprafață z = f(X,y) = X 2 – y 2 la origine 0.

La suprafata la= 0 avem: z = f(X,0) = X 2 și fў X(X,0) = 2X... Pe CU 1, linii de intersecție, z = X 2. La punctul O panta este fў X(0,0) = 0. În avion X= 0 avem: z = f(0,y) = –y 2 și fў y(0,y) = –2y... Pe CU 2, linii de intersecție, z = –y 2. La punctul O panta unei curbe CU 2 este egal fў y(0,0) = 0. Deoarece tangentele la CU 1 și CU 2 sunt axe Xși la, planul tangent care le conține este planul z = 0.

Cu toate acestea, în vecinătatea originii, suprafața noastră nu se află pe o parte a planului tangent. Într-adevăr, curba CU 1 peste tot, cu excepția punctului 0, se află deasupra planului tangent și a curbei CU 2 - respectiv sub ea. Suprafața intersectează planul tangent z= 0 în linii drepte la = Xși la = –X... Se spune că o astfel de suprafață are un punct de șa la origine (Fig. 24).

Derivate parțiale.

În exemplele anterioare, am folosit derivate din f (X,y) pe Xși prin la... Să luăm acum în considerare astfel de derivate mai general. Dacă avem o funcție a două variabile, de exemplu, F(X,y) = X 2 – X y, atunci putem defini în fiecare punct două dintre „derivatele parțiale” ale sale, una prin diferențierea funcției în raport cu X si fixare la, celălalt prin diferențierea față de la si fixare X... Prima dintre aceste derivate se notează ca fў X(X,y) sau ¶ f/¶ X; al doilea - cum f f ў y... Dacă ambele derivate mixte (prin Xși la, pe lași X) sunt continue, atunci ¶ 2 f/¶ X¶ y= ¶ 2 f/¶ y¶ X; în exemplul nostru ¶ 2 f/¶ X¶ y= ¶ 2 f/¶ y¶ X = –1.

Derivată parțială fў X(X,y) indică rata de modificare a funcției f la un moment dat ( X,y) în direcţia creşterii X, A fў y(X,y) Este rata de modificare a funcției f sens ascendent la... Rata de schimbare a funcției f la un moment dat ( X,la) în direcția unei drepte făcând un unghi q cu direcția pozitivă a axei X, se numește derivata funcției f către; valoarea sa este o combinație a două derivate parțiale ale funcției f în planul tangent este aproape egală (pentru mic dxși dy) schimbarea adevărată z la suprafață, dar calcularea diferenţialului este de obicei mai ușoară.

Formula pe care am considerat-o deja din metoda schimbării variabilei, cunoscută sub numele de derivată a unei funcții complexe sau a unei reguli de lanț, în cazul unidimensional când la depinde de X, A X depinde de t, are forma:

Pentru funcțiile a două variabile, o formulă similară este:

Este ușor să generalizezi conceptele și denumirile de diferențiere parțială la dimensiuni superioare. În special, dacă suprafața este dată implicit de ecuație f(X,y,z) = 0, ecuației planului tangent la suprafață i se poate da o formă mai simetrică: ecuația planului tangent în punctul ( x (x 2/4)], apoi se integrează peste X 0 la 1. Rezultatul final este 3/4.

Formula (10) poate fi interpretată și ca așa-numita integrală dublă, i.e. ca limită a sumei volumelor de „celule” elementare. Fiecare astfel de celulă are o bază D X D yși o înălțime egală cu înălțimea suprafeței deasupra unui punct al bazei dreptunghiulare ( cm... orez. 26). Se poate arăta că ambele puncte de vedere ale formulei (10) sunt echivalente. Integrale duble sunt folosite pentru a găsi centrele de greutate și numeroasele momente găsite în mecanică.

Fundamentarea mai riguroasă a aparatului matematic.

Până acum, am prezentat concepte și metode de calcul la nivel intuitiv și nu am ezitat să apelăm la forme geometrice. Rămâne să luăm în considerare pe scurt metodele mai riguroase care au apărut în secolele al XIX-lea și al XX-lea.

La începutul secolului al XIX-lea, când s-a încheiat era asaltului și atacului în „crearea analizei matematice”, întrebările privind justificarea acesteia au ieșit în prim-plan. În lucrările lui Abel, Cauchy și al unui număr de alți matematicieni remarcabili, conceptele de „limită”, „funcție continuă”, „serie convergentă” au fost definite cu precizie. Acest lucru a fost necesar pentru a aduce o ordine logică la baza analizei matematice pentru a face din aceasta un instrument de cercetare de încredere. Necesitatea unei justificări amănunțite a devenit și mai evidentă după descoperirea în 1872 de către Weierstrass a funcțiilor continue, dar nicăieri diferențiabile (graficul unor astfel de funcții are o pauză în fiecare punct). Acest rezultat a făcut o impresie copleșitoare asupra matematicienilor, deoarece a contrazis în mod clar intuiția lor geometrică. Un exemplu și mai izbitor al nesiguranței intuiției geometrice a fost curba continuă construită de D. Peano, care umple complet un anumit pătrat, adică. trecând prin toate punctele sale. Aceste și alte descoperiri au dat naștere programului de „aritmetizare” a matematicii, adică. făcându-l mai fiabil prin fundamentarea tuturor conceptelor matematice folosind conceptul de număr. Abstinența aproape puritană de la claritate în lucrările pe bazele matematicii și-a avut justificarea istorică.

Conform canoanelor moderne de rigoare logică, este inadmisibil să vorbim despre zona de sub curbă. y = f(X) și deasupra segmentului de axă X, chiar f- o funcție continuă, fără a defini mai întâi sensul exact al termenului „zonă” și fără a stabili că zona astfel determinată există cu adevărat. Această problemă a fost rezolvată cu succes în 1854 de către B. Riemann, care a dat o definiție precisă a conceptului de integrală definită. De atunci, ideea de însumare din spatele noțiunii de integrală definită a făcut obiectul multor studii profunde și generalizări. Drept urmare, astăzi este posibil să se dea sens unei integrale definite, chiar dacă integrandul este discontinuu peste tot. Noile concepte de integrare, la crearea cărora A. Lebesgue (1875–1941) și alți matematicieni au avut o mare contribuție, au sporit puterea și frumusețea analizei matematice moderne.

Cu greu ar fi potrivit să intrăm în detaliile tuturor acestor și altor concepte. Ne vom restrânge doar la a da definiții riguroase ale limitei și integralei definite.

În concluzie, să spunem că analiza matematică, fiind un instrument extrem de valoros în mâinile unui om de știință și al unui inginer, atrage și astăzi atenția matematicienilor ca sursă de idei fructuoase. În același timp, dezvoltarea modernă pare să indice că analiza matematică este din ce în ce mai absorbită de astfel de dominante în secolul al XX-lea. ramuri ale matematicii precum algebra abstractă și topologia.

Este absolut imposibil să rezolvi probleme fizice sau exemple de matematică fără cunoașterea derivatei și a metodelor de calcul al acesteia. Derivata este unul dintre cele mai importante concepte ale analizei matematice. Am decis să dedicăm articolul de astăzi acestui subiect fundamental. Ce este o derivată, care este semnificația sa fizică și geometrică, cum se calculează derivata unei funcții? Toate aceste întrebări pot fi combinate într-una singură: cum să înțelegeți derivatul?

Sensul geometric și fizic al derivatului

Să existe o funcție f (x) dat într-un anumit interval (a, b) ... Punctele х și х0 aparțin acestui interval. Când x se schimbă, funcția în sine se schimbă. Schimbarea unui argument - diferența dintre valorile acestuia x-x0 ... Această diferență este scrisă ca delta x și se numește increment de argument. O modificare sau o creștere a unei funcții este diferența dintre valorile unei funcții în două puncte. Definiție derivată:

Derivata unei funcții într-un punct este limita raportului dintre incrementul funcției la un punct dat și incrementul argumentului atunci când acesta din urmă tinde spre zero.

În caz contrar, se poate scrie astfel:

Ce rost are să găsești o astfel de limită? Și iată ce:

derivata funcției într-un punct este egală cu tangentei unghiului dintre axa OX și tangentei la graficul funcției în acest punct.

Semnificația fizică a derivatului: derivata traseului în raport cu timpul este egală cu viteza mișcării rectilinie.

Într-adevăr, încă de pe vremea școlii, toată lumea știe că viteza este o cale privată. x = f (t) si timpul t ... Viteza medie pe o perioadă de timp:

Pentru a afla viteza de mișcare la un moment dat t0 trebuie să calculați limita:

Regula unu: scoateți o constantă

Constanta poate fi mutată în afara semnului derivatei. Mai mult, trebuie făcut. Când rezolvați exemple la matematică, luați ca regulă - dacă puteți simplifica expresia, asigurați-vă că simplificați .

Exemplu. Să calculăm derivata:

Regula a doua: derivata sumei functiilor

Derivata sumei a doua functii este egala cu suma derivatelor acestor functii. Același lucru este valabil și pentru derivata diferenței de funcții.

Nu vom da o demonstrație a acestei teoreme, ci mai degrabă vom lua în considerare un exemplu practic.

Aflați derivata unei funcții:

Regula trei: derivata produsului de funcții

Derivata produsului a doua functii diferentiabile se calculeaza prin formula:

Exemplu: găsiți derivata unei funcții:

Soluţie:

Este important să spunem aici despre calculul derivatelor funcțiilor complexe. Derivata unei functii complexe este egala cu produsul derivatei acestei functii fata de argumentul intermediar cu derivata argumentului intermediar fata de variabila independenta.

În exemplul de mai sus întâlnim expresia:

În acest caz, argumentul intermediar este de 8x față de a cincea putere. Pentru a calcula derivata unei astfel de expresii, mai întâi calculăm derivata funcției externe față de argumentul intermediar, apoi înmulțim cu derivata argumentului intermediar imediat față de variabila independentă.

Regula a patra: derivata coeficientului a două funcții

Formula pentru determinarea derivatei coeficientului a două funcții:

Am încercat să vă spunem despre derivate pentru manechine de la zero. Acest subiect nu este atât de simplu pe cât pare, așa că fiți atenți: există adesea capcane în exemple, așa că aveți grijă când calculați derivatele.

Pentru orice întrebare pe aceasta și alte subiecte, puteți contacta serviciul studenți. În scurt timp, vă vom ajuta să rezolvați cel mai dificil test și să vă ocupați de sarcini, chiar dacă nu ați mai făcut niciodată calculul derivatelor.

Pe care am analizat cele mai simple derivate, și, de asemenea, ne-am familiarizat cu regulile de diferențiere și unele tehnici de găsire a derivatelor. Astfel, dacă nu sunteți prea mult cu derivatele funcțiilor sau unele puncte din acest articol nu sunt în totalitate clare, atunci citiți mai întâi lecția de mai sus. Vă rog, acordați-vă o dispoziție serioasă - materialul nu este unul ușor, dar voi încerca totuși să îl prezint într-un mod simplu și accesibil.

În practică, trebuie să te ocupi de derivata unei funcții complexe foarte des, chiar aș spune, aproape întotdeauna, când ți se dau sarcini să găsești derivate.

Ne uităm în tabel la regula (nr. 5) pentru diferențierea unei funcții complexe:

Înţelegere. În primul rând, să fim atenți la înregistrare. Aici avem două funcții - și, în plus, funcția, la figurat vorbind, este încorporată în funcție. O funcție de acest fel (când o funcție este imbricată în alta) se numește funcție complexă.

Voi apela funcția functie externa si functia - o funcție interioară (sau imbricată)..

! Aceste definiții nu sunt teoretice și nu ar trebui să apară în proiectarea finală a sarcinilor. Folosesc expresii informale „funcție externă”, funcție „internă” doar pentru a vă facilita înțelegerea materialului.

Pentru a clarifica situația, luați în considerare:

Exemplul 1

Aflați derivata unei funcții

Sub sinus, nu avem doar litera „X”, ci o expresie întreagă, deci nu va fi posibil să găsim derivata imediat din tabel. De asemenea, observăm că este imposibil să aplici primele patru reguli aici, pare să existe o diferență, dar adevărul este că nu poți „srupe” un sinus:

În acest exemplu, deja din explicațiile mele, este intuitiv clar că o funcție este o funcție complexă, iar polinomul este o funcție internă (imbricare) și o funcție externă.

Primul pas, care trebuie efectuată la găsirea derivatei unei funcții complexe, este că aflați ce funcție este internă și care este externă.

În cazul exemplelor simple, pare clar că un polinom este imbricat sub sinus. Dar dacă totul nu este evident? Cum să determinați exact ce funcție este externă și care este internă? Pentru a face acest lucru, vă sugerez să utilizați următoarea tehnică, care poate fi făcută mental sau pe ciornă.

Imaginează-ți că trebuie să calculăm valoarea unei expresii la pe un calculator (în loc de unul, poate exista orice număr).

Ce vom calcula mai întâi? Pentru inceput va trebui să efectuați următoarea acțiune:, deci polinomul va fi o funcție internă:

În al doilea rând va trebui găsit, deci sine va fi o funcție externă:

După ce noi Înțeles cu funcții interne și externe, este timpul să aplici regula de diferențiere a unei funcții complexe .

Începem să decidem. De la lecție Cum găsesc derivatul? ne amintim că proiectarea soluției oricărei derivate începe întotdeauna astfel - închidem expresia în paranteze și punem o contur în dreapta sus:

Primul găsiți derivata funcției externe (sinus), uitați-vă la tabelul derivatelor funcțiilor elementare și observați că. Toate formulele tabelare sunt aplicabile chiar dacă „x” este înlocuit cu o expresie complexă, în acest caz:

Rețineți că funcția interioară nu s-a schimbat, nu o atingem.

Ei bine, este destul de evident că

Rezultatul aplicării formulei în designul final arată astfel:

Un factor constant este de obicei plasat la începutul unei expresii:

Dacă există vreo confuzie, notează soluția și citește din nou explicațiile.

Exemplul 2

Aflați derivata unei funcții

Exemplul 3

Aflați derivata unei funcții

Ca întotdeauna, notăm:

Să ne dăm seama unde avem o funcție externă și unde avem una internă. Pentru a face acest lucru, încercați (mental sau pe o schiță) să calculați valoarea expresiei la. Ce ar trebui făcut mai întâi? În primul rând, trebuie să calculați cu ce este egală baza: ceea ce înseamnă că polinomul este funcția internă:

Și, abia atunci se realizează exponențiarea, prin urmare, funcția de putere este o funcție externă:

Conform formulei , mai întâi trebuie să găsiți derivata funcției externe, în acest caz, gradul. Căutăm formula necesară în tabel:. Repetăm ​​din nou: orice formulă tabelară este valabilă nu numai pentru „x”, ci și pentru o expresie complexă... Astfel, rezultatul aplicării regulii de diferențiere a unei funcții complexe Următorul:

Subliniez din nou că atunci când luăm derivata funcției exterioare, funcția interioară nu se schimbă pentru noi:

Acum rămâne să găsiți o derivată foarte simplă a funcției interioare și să „pieptănați” puțin rezultatul:

Exemplul 4

Aflați derivata unei funcții

Acesta este un exemplu pentru o soluție independentă (răspunsul la sfârșitul tutorialului).

Pentru a consolida înțelegerea derivatei unei funcții complexe, voi da un exemplu fără comentarii, încercați să vă dați seama singur, speculați unde este funcția externă și unde este funcția internă, de ce sarcinile au fost rezolvate astfel?

Exemplul 5

a) Aflați derivata funcției

b) Aflați derivata funcției

Exemplul 6

Aflați derivata unei funcții

Aici avem o rădăcină, iar pentru a diferenția rădăcina, aceasta trebuie reprezentată ca un grad. Astfel, mai întâi aducem funcția într-o formă adecvată pentru diferențiere:

Analizând funcția, ajungem la concluzia că suma a trei termeni este o funcție internă, iar exponențiația este o funcție externă. Aplicam regula de diferentiere a unei functii complexe :

Gradul este din nou reprezentat ca un radical (rădăcină), iar pentru derivata funcției interne aplicăm o regulă simplă de diferențiere a sumei:

Gata. De asemenea, puteți aduce expresia la un numitor comun între paranteze și scrieți totul într-o fracție. Frumos, desigur, dar atunci când se obțin derivate lungi greoaie, este mai bine să nu faci acest lucru (este ușor să te confuzi, să faci o greșeală inutilă și profesorul va fi incomod să verifice).

Exemplul 7

Aflați derivata unei funcții

Acesta este un exemplu pentru o soluție independentă (răspunsul la sfârșitul tutorialului).

Este interesant de observat că uneori, în locul regulii de diferențiere a unei funcții complexe, se poate folosi regula de diferențiere a coeficientului. , dar o astfel de soluție va părea neobișnuită ca o perversie. Iată un exemplu tipic:

Exemplul 8

Aflați derivata unei funcții

Aici puteți folosi regula pentru diferențierea coeficientului , dar este mult mai profitabil să găsim derivata prin regula de diferențiere a unei funcții complexe:

Pregătim funcția pentru diferențiere - mutăm minusul în afara semnului derivatei și ridicăm cosinusul la numărător:

Cosinusul este o funcție internă, exponențiația este o funcție externă.
Ne folosim regula :

Găsiți derivata funcției interne, resetați cosinusul înapoi în jos:

Gata. În exemplul luat în considerare, este important să nu vă confundați în semne. Apropo, încercați să o rezolvați cu regula , răspunsurile trebuie să se potrivească.

Exemplul 9

Aflați derivata unei funcții

Acesta este un exemplu pentru o soluție independentă (răspunsul la sfârșitul tutorialului).

Până acum, am analizat cazurile în care am avut un singur atașament într-o funcție complexă. În sarcinile practice, puteți găsi adesea derivate, în care, precum păpușile de cuibărit, una în cealaltă, 3 sau chiar 4-5 funcții sunt imbricate deodată.

Exemplul 10

Aflați derivata unei funcții

Să înțelegem atașamentele acestei funcții. Încercarea de a evalua expresia folosind valoarea de test. Cum am conta pe un calculator?

Mai întâi trebuie să găsiți, ceea ce înseamnă că arcsinusul este cel mai adânc cuib:

Atunci acest arcsinus al lui unu ar trebui să fie pătrat:

Și, în sfârșit, ridicați 7 la putere:

Adică, în acest exemplu avem trei funcții diferite și două atașamente, în timp ce funcția cea mai interioară este arcsinus, iar funcția cea mai exterioară este funcția exponențială.

Începem să rezolvăm

Conform regulii mai întâi trebuie să luați derivata funcției externe. Ne uităm la tabelul de derivate și aflăm derivata funcției exponențiale: Singura diferență este că în loc de „x” avem o expresie complexă, care nu anulează validitatea acestei formule. Deci, rezultatul aplicării regulii de diferențiere a unei funcții complexe Următorul.