Piir ja järjepidevus

ühe muutuja funktsioonid

3.1.1. Definitsioon. Number A x poole püüdlemas x 0 kui suvalise numbri puhul
on number
(
) ja tingimus on täidetud:

Kui
, See
.

(Sümbolism:
).

Kui graafik osutab G funktsioonid

, Millal läheneb punktile lõpmatult lähedale (need.
), (vt joonis 3.1), siis on see asjaolu geomeetriline vaste asjaolule, et funktsioon
juures
omab piirväärtust (limiit) A(sümboolika:
).

Funktsioonigraafik,

Riis. 3.1

Tuleb märkida, et funktsiooni piirväärtuse (limiidi) määramisel at x poole püüdlemas x 0 ei ütle midagi funktsiooni käitumise kohta punktis x 0 . Kohapeal x 0 funktsioon ei pruugi olla määratletud, võib olla
, võib olla
.

Kui
, siis nimetatakse funktsiooni infinitesimaalseks
.

Intervalli nimetatakse  - punkti naabruskond x 0 killustunud keskpunktiga. Seda nime kasutades saame öelda järgmist: kui mis tahes arvu jaoks on arv ja tingimus on täidetud: kui
, See
.

3.1.2. Definitsioon. , kui mis tahes koonduv x 0 järjestust
järeljada
koondub A.

3.1.3. Tõestame punktide 3.1.1 ja 3.1.2 määratluste samaväärsust

Las kõigepealt esimese definitsiooni tähenduses ja lase
(
), siis kõik , välja arvatud nende lõplik arv, rahuldavad ebavõrdsust
, Kus  poolt valitud  esimese definitsiooni mõttes, s.o.
, st. esimene määratlus eeldab teist. Las see nüüd
teise definitsiooni tähenduses ja oletame, et teise definitsiooni tähenduses
, st. mõne jaoks suvaliselt väikeste jaoks (näiteks jaoks
) jada leiti
, kuid samal ajal
. Seetõttu oleme jõudnud vastuoluni, esimene tuleneb teisest definitsioonist.

3.1.4. Nende definitsioonide samaväärsus on eriti mugav, kuna kõik eelnevalt tõestatud teoreemid jadade piirväärtuste omaduste kohta kanduvad peaaegu automaatselt üle uus juhtum. On vaja ainult selgitada piirangu mõistet. Vastaval teoreemil on järgmine sõnastus:

Kui
, siis on see piiratud mõne  - punkti naabruskonnaga x 0 killustunud keskpunktiga.

3.2.1.Teoreem. Lase
,
,

Siis
,

,

.

3.2.2. Lase

- meelevaldne, lähenev x 0 funktsiooni argumendi väärtuste jada ja
. Sobivad järjestused
Ja
nende funktsioonide väärtustel on piirid A Ja B. Siis aga vastavalt jaotise 2.13.2 teoreemile jadad
,
Ja
piirid on vastavalt võrdsed A +B,
Ja
. Funktsiooni piiri definitsiooni kohaselt punktis (vt punkt 2.5.2) tähendab see seda

,
,

.

3.2.3. Teoreem. Kui
,
, ja mõnes läheduses

esineb

.

3.2.4. Funktsiooni piiri määratluse järgi punktis x 0 mis tahes järjestuse jaoks
selline, et

funktsiooni väärtuste jada piirang on võrdne A. See tähendab, et igaühe jaoks
on number
sooritatud . Samamoodi jada jaoks
on number
nii et mis tahes numbri jaoks
sooritatud . Valimine
, leiame selle kõigile
sooritatud . Sellest ebavõrdsuse ahelast on meil mis tahes , mis tähendab seda
.

3.2.5. Definitsioon. Number A nimetatakse funktsiooni piirväärtuseks (limiidiks) at x poole püüdlemas x 0 paremal (sümboolika:
), kui mis tahes arvu puhul on arv () ja tingimus on täidetud: kui
, See
.

Hulka nimetatakse parempoolseks  - punkti naabruskonnaks x 0 . Vasakpoolse piirväärtuse (limiidi) mõiste on defineeritud sarnaselt (
).

3.2.6. Teoreem. Funktsioonil on piirväärtus (limiit), mis on võrdne A siis ja ainult siis

,

3.3.1. Definitsioon. Number A nimetatakse funktsiooni piirväärtuseks (limiidiks) at x kaldub lõpmatuseni, kui mis tahes arvu jaoks on arv
(
) ja järgmine tingimus on täidetud:

Kui
, See.

(Sümbolism:
.)

Trobikond
helistas D- lõpmatuse naabrus.

3.3.2. Definitsioon. Number A nimetatakse funktsiooni piirväärtuseks (limiidiks) at x kaldub pluss lõpmatuseni, kui mis tahes arvu jaoks on arv D() ja tingimus on täidetud:

Kui
, See.

(Sümbolism:
).

Kui graafik osutab G funktsioonid
piiramatu kasvuga
piiramatult läheneda ühele horisontaaljoonele
(vt joon. 3.2), siis on see asjaolu geomeetriline vaste tõsiasjale, et funktsioon
juures
on arvuga võrdne piirväärtus (limiit). A(sümboolika:
).

Funktsiooni graafik
,

Trobikond
helistas D-naabruskond pluss lõpmatus.

Piiri mõiste at
.

Harjutused.

Esitage kõik teoreemid piiride kohta, nagu neid juhtudel rakendatakse:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. Definitsioon. Funktsiooni nimetatakse lõpmatuks suurepärane funktsioon(või lihtsalt lõpmatult suur) juures , kui suvalise arvu puhul

, rahuldades ebavõrdsust, on ebavõrdsus rahuldatud
.

(Sümbolism:
.)

Kui täidetakse
, siis nad kirjutavad
.

Kui täidetakse
, siis nad kirjutavad
.

3.4.2. Teoreem. Lase
Ja
juures
.

Siis
on lõpmatult suur funktsioon .

3.4.3. Olgu see suvaline arv. Kuna on lõpmatult väike funktsioon , siis arvu jaoks
igaühe jaoks on selline number x nii, et ebavõrdsus kehtib
, aga siis sama eest x ebavõrdsus rahuldatakse
. Need. on lõpmatult suur funktsioon .

3.4.4.Teoreem. Laskma olema lõpmatult suur funktsioon ja jaoks .

Siis on lõpmatult väike funktsioon .

(See teoreem on tõestatud sarnaselt punktis 3.8.2 toodud teoreemiga.)

3.4.5. Funktsioon
nimetatakse piiramatuks millal
, kui mõne numbri puhul
ja punkti mis tahes δ-naabruskond saate määrata punkti x sellest naabruskonnast selline, et
.

3.5.1. MÄÄRATLUS. Funktsiooni kutsutakse pidev punktis , Kui
.

Viimase tingimuse saab kirjutada järgmiselt:

.

See märge tähendab, et pidevate funktsioonide puhul saab piiri ja funktsiooni märki vahetada

Või nii: . Või jälle, nagu alguses.

Tähistame
. Siis
ja =
ja viimane salvestusvorm võtab vormi

.

Piirmärgi all olev avaldis tähistab inkremendist põhjustatud funktsioonipunkti juurdekasvu
argument x punktis, mida tavaliselt tähistatakse kui
. Selle tulemusena saame funktsiooni punktis pidevuse tingimuse kirjutamiseks järgmise vormi

,

mida nimetatakse funktsiooni pidevuse punktis "töödefinitsiooniks".

Funktsiooni kutsutakse pidev punktis vasakule, Kui
.

Funktsiooni kutsutakse pidev punktis paremal, Kui
.

3.5.2. Näide.
. See funktsioon on pidev mis tahes . Kasutades teoreeme piirväärtuste omaduste kohta, saame kohe: iga ratsionaalne funktsioon on pidev igas punktis, kus ta on defineeritud, s.t. vormi funktsioon
.

HARJUTUSED.

3.6.1. Kooliõpik tõestab (edas kõrge tase rangus) seda
(esimene tähelepanuväärne piir). Visuaalsetest geomeetrilistest kaalutlustest järeldub see kohe
. Pange tähele, et vasakpoolsest ebavõrdsusest järeldub ka see
, st. mis on funktsioon
on pidev nullis. Siit edasi pole sugugi raske tõestada kõigi järjepidevust trigonomeetrilised funktsioonid kõigis punktides, kus need on määratletud. Tegelikult, millal
nagu toode on lõpmatu väike funktsioon
peal piiratud funktsioon
.

3.6.2. (2. imeline piir). Nagu me juba teame

,

Kus jookseb läbi naturaalarvude. Seda saab näidata
. enamgi veel
.

HARJUTUSED.

3.7.1. TEOREEM (keerulise funktsiooni pidevuse kohta).

Kui funktsioon
on pidev punktis ja
ja funktsioon
pidev mingis punktis , siis kompleksfunktsioon
on punktis pidev.

3.7.2. Selle väite kehtivus tuleneb kohe järjepidevuse definitsioonist, mis on kirjutatud järgmiselt:

3.8.1. TEOREEM. Funktsioon on pidev igas punktis (
).

3.8.2. Kui peame mõistlikuks, et funktsioon
on määratletud mis tahes jaoks ja on rangelt monotoonne (rangelt kahanev
, suurendades rangelt
), siis pole tõestamine keeruline.

Kell
meil on:

need. kui meil on
, mis tähendab, et funktsioon on pidev kell .

Kell
kõik taandub eelmisele:

Kell
.

Kell
funktsiooni
on kõigi jaoks konstantne, seega pidev.

3.9.1. TEOREEM (pöördfunktsiooni kooseksisteerimise ja pidevuse kohta).

Laske pideval funktsioonil rangelt väheneda (suureneda) mõnes δ - punkti läheduses,
. Siis mõnes ε - punkti naabruses on pöördfunktsioon
, mis rangelt väheneb (rangelt suureneb) ja on pidev punkti ε - naabruses.

3.9.2. Siin tõestame ainult pöördfunktsiooni pidevust punktis .

Võtame selle, punkt y asub punktide vahel
Ja
Seega, kui
, See
, Kus.

3.10.1. Seega viivad pidevate funktsioonide lubatud aritmeetilised toimingud taas pidevate funktsioonideni. Nendest keerukate ja pöördfunktsioonide moodustamine ei riku järjepidevust. Seetõttu võime teatud vastutustundega kinnitada, et kõik elementaarfunktsioonid on argumendi kõigi lubatud väärtuste puhul pidevad.

HARJUTUS.

Tõesta seda
juures
(teise imelise piiri teine ​​vorm).

3.11.1. Piirmäärade arvutamine on oluliselt lihtsustatud, kui kasutada samaväärsete lõpmatute suuruste mõistet. Samaväärsuse mõistet on mugav üldistada suvaliste funktsioonide puhul.

Definitsioon. Funktsioonid ja on samaväärsed kui
(selle asemel sa võid kirjutada
,
,
,
,
).

Kasutatud märge f ~ g.

Ekvivalentsusel on järgmised omadused

Tuleb meeles pidada järgmist samaväärsete lõpmatute suuruste loendit:

~
juures
; (1)

~ kell ; (2)

~
kell ; (3)

~ kell ; (4)

~ kell ; (5)

~ kell ; (6)

~ kell ; (7)

~ lk kell ; (8)

~ juures
; (9)

~
aadressil . (10)

Siin ja ei pruugi olla sõltumatud muutujad, vaid funktsioonid
Ja
teatud käitumise korral kaldudes vastavalt nullile ja ühele x. Näiteks,

~
juures
,

~
juures
.

Ekvivalentsus (1) on veel üks esimese märkimisväärse piiri kirjutamise vorm. Ekvivalentse (2), (3), (6) ja (7) saab otse tõestada. Ekvivalents (4) saadakse punktist (1), võttes arvesse ekvivalentide omadust 2:

~
.

Sarnaselt (5) ja (7) saadakse punktidest (2) ja (6). Tõepoolest

~
,

~
.

(8) samaväärsust tõestatakse punktide (7) ja (6) järjestikuse rakendamisega:

ja (9) ja (10) saadakse punktidest (6) ja (8) asendades
.

3.11.2. Teoreem. Korrutise ja suhte piirmäärade arvutamisel saate funktsioone muuta samaväärseteks. Nimelt kui ~
, siis kas mõlemad piirid ei eksisteeri samaaegselt ja
, või mõlemad piirangud ei eksisteeri korraga.

Tõestame esimest võrdsust. Olgu üks piirangutest, ütleme
on olemas. Siis

.

3.11.3. Olgu ( number või sümbol,
või
). Vaatleme erinevate b.m. funktsioonid (nii lühendame terminit infinitesimal).

MÕISTED.
ja neid nimetatakse samaväärseteks b.m. funktsioonid , kui jaoks
(at ).

me nimetame seda b.m. rohkem kõrge järjekord kui b.m. funktsiooni
, Kui
(at ).

3.11.4. Kui ja samaväärne b.m. funktsioonid siis
seal on b.m. funktsioon kõrgemat järku kui
ja mida. - b.m. funktsioon at, milles kõigi x ja, kui selles punktis funktsiooni nimetatakse eemaldatavaks katkestuspunktiks. on teist tüüpi katkestus. Punkt ise Test

Kollokviumile. Sektsioonid: " Piirang Ja järjepidevusfunktsioonid kehtiv muutuja" funktsioonidüksmuutuja", “Diferentsiaalarvutus funktsioonid mitu muutujad"

Kontrolltööde ja küsimuste teemad ja näited (testide individuaalne standardarvutuste kollokvium) 1. semestri kontrolltöö nr 1 jagu “Reaalmuutuja funktsiooni piir ja pidevus”

Test

Kollokviumile. Sektsioonid: " Piirang Ja järjepidevusfunktsioonid kehtiv muutuja", “Diferentsiaalarvutus funktsioonidüksmuutuja", “Diferentsiaalarvutus funktsioonid mitu muutujad". Numbrite jada...

Test

Kollokviumile. Sektsioonid: " Piirang Ja järjepidevusfunktsioonid kehtiv muutuja", “Diferentsiaalarvutus funktsioonidüksmuutuja", “Diferentsiaalarvutus funktsioonid mitu muutujad". Numbrite jada...

Kontrolltööde ja küsimuste teemad ja näited (kontrolltöö individuaalsed standardarvutuste kollokviumid) 1. semestri kontrolltöö osa “Reaalmuutuja funktsiooni piir ja pidevus”

Test

Kollokviumile. Sektsioonid: " Piirang Ja järjepidevusfunktsioonid kehtiv muutuja", “Diferentsiaalarvutus funktsioonidüksmuutuja", “Diferentsiaalarvutus funktsioonid mitu muutujad". Numbrite jada...

Loeng 19 mitme muutuja funktsiooni piir ja pidevus

Loeng

... Piirang Ja järjepidevusfunktsioonid mitu muutujad. 19.1. Kontseptsioon funktsioonid mitu muutujad. Revideerides funktsioonid mitu muutujad... omadused funktsioonidüksmuutuv, pidev segmendil. Vaadake Atribuudid funktsioonid, pidev peal...

Funktsiooni järjepidevus. Murdepunktid.

Sõnn kõnnib, kõigub, ohkab minnes:
- Oh, laud hakkab otsa saama, nüüd ma kukun!

Selles õppetükis uurime funktsiooni pidevuse kontseptsiooni, katkestuspunktide klassifikatsiooni ja ühist praktiline probleem funktsioonide järjepidevusuuringud. Juba teema nime järgi arvavad paljud intuitiivselt, mida arutatakse, ja arvavad, et materjal on üsna lihtne. See on tõsi. Kuid hooletusse jätmise ja pealiskaudse lähenemise eest karistatakse kõige sagedamini just lihtsaid ülesandeid. Seetõttu soovitan teil artiklit väga hoolikalt uurida ja mõista kõiki peensusi ja tehnikaid.

Mida pead teadma ja oskama? Mitte väga. Et õppetund hästi õppida, peate mõistma, mis see on funktsiooni piir. Madala ettevalmistustasemega lugejatele piisab artiklist aru saamisest Funktsioonide piirangud. Näited lahendustest ja vaatama geomeetriline tähendus limiit juhendis Elementaarfunktsioonide graafikud ja omadused. Samuti on soovitatav end kurssi viia graafikute geomeetrilised teisendused, kuna praktika hõlmab enamikul juhtudel joonise koostamist. Väljavaated on kõigi jaoks optimistlikud ja isegi täis veekeetja saab järgmise tunni või paari jooksul ülesandega iseseisvalt hakkama!

Funktsiooni järjepidevus. Katkestuspunktid ja nende klassifikatsioon

Funktsiooni järjepidevuse mõiste

Vaatleme mõnda funktsiooni, mis on pidev kogu arvureal:

Või lühidalt öeldes on meie funktsioon pidevalt sees (komplekt reaalarvud).

Mis on järjepidevuse "filisti" kriteerium? Ilmselgelt saab pideva funktsiooni graafiku joonistada ilma pliiatsit paberilt tõstmata.

Sel juhul on vaja neid kahte selgelt eristada lihtsad mõisted: funktsiooni domeen Ja funktsiooni järjepidevus. Üldiselt see pole sama asi. Näiteks:

See funktsioon defineeritud tervel arvureal, st jaoks kõik"X" tähendusel on "y" oma tähendus. Eelkõige, kui , siis . Pange tähele, et teine ​​punkt on kirjavahemärgiga, sest funktsiooni definitsiooni järgi peab argumendi väärtus vastama sellele ainuke asi funktsiooni väärtus. Seega domeeni meie funktsioon: .

Kuid see funktsioon ei ole pidevalt sisse lülitatud! On üsna ilmne, et hetkel ta kannatab lõhe. Mõiste on ka üsna arusaadav ja visuaalne, siin tuleb pliiats nagunii paberilt maha rebida. Veidi hiljem vaatame murdepunktide klassifikatsiooni.

Funktsiooni pidevus punktis ja intervallil

Konkreetse matemaatilise ülesande puhul saame rääkida funktsiooni pidevusest punktis, funktsiooni pidevusest intervallil, poolintervallist või funktsiooni pidevusest segmendil. See on, pole olemas "lihtsat järjepidevust"– funktsioon võib KUSALIKULT olla pidev. Ja kõige muu põhiline "ehituskivi" on funktsiooni järjepidevus punktis .

Matemaatilise analüüsi teooria annab funktsiooni pidevuse definitsiooni punktis, kasutades “delta” ja “epsilon” naabrusi, kuid praktikas on kasutusel erinev definitsioon, millele pöörame suurt tähelepanu.

Kõigepealt meenutame ühepoolsed piirid kes tungisid meie ellu esimeses õppetunnis funktsioonigraafikute kohta. Mõelge igapäevasele olukorrale:

Kui läheneme teljele punktile vasakule(punane nool), siis lähevad "mängude" vastavad väärtused piki telge punktini (karmiinpunane nool). Matemaatiliselt fikseeritakse see fakt kasutades vasakpoolne piirang:

Pöörake tähelepanu kirjele (vasakul on "x kipub ka"). "Lisand" "miinus null" sümboliseerib , sisuliselt tähendab see seda, et läheneme numbrile vasakult poolt.

Samamoodi, kui lähenete punktile "ka" paremal (sinine nool), siis on „mängud” sama väärtusega, kuid mööda rohelist noolt ja parema käe piir vormindatakse järgmiselt:

"Lisaaine" sümboliseerib , ja kirje on järgmine: "x kipub paremal pool ka".

Kui ühepoolsed piirid on lõplikud ja võrdsed(nagu meie puhul): , siis me ütleme, et on ÜLDpiirang. See on lihtne, üldine piir on meie "tavaline" funktsiooni piir, võrdne lõpliku arvuga.

Pange tähele, et kui funktsioon pole defineeritud (torkake graafiku harul must täpp välja), jäävad ülaltoodud arvutused kehtima. Nagu on juba mitu korda märgitud, eriti artiklis lõpmata väikeste funktsioonide kohta, väljendid tähendavad, et "x" lõpmatult lähedal läheneb punktile, samas EI OLE TÄHTIS, kas funktsioon ise on antud punktis defineeritud või mitte. Hea näide on järgmises lõigus, kui funktsiooni analüüsitakse.

Definitsioon: funktsioon on punktis pidev, kui funktsiooni piir antud punktis on võrdne funktsiooni väärtusega selles punktis: .

Määratlus on üksikasjalikult kirjeldatud järgmistes mõistetes:

1) Funktsioon peab olema punktis defineeritud, st väärtus peab olemas olema.

2) Funktsioonil peab olema üldine piirmäär. Nagu eespool märgitud, tähendab see ühepoolsete piiride olemasolu ja võrdsust: .

3) Funktsiooni piirväärtus antud punktis peab olema võrdne funktsiooni väärtusega selles punktis: .

Kui rikutakse vähemalt üks kolmest tingimusest, siis funktsioon kaotab pidevuse omaduse punktis .

Funktsiooni järjepidevus üle intervalli on sõnastatud leidlikult ja väga lihtsalt: funktsioon on intervallil pidev, kui ta on pidev antud intervalli igas punktis.

Eelkõige on paljud funktsioonid pidevad lõpmatul intervallil, st reaalarvude hulgal. See on lineaarne funktsioon, polünoomid, eksponentsiaal, siinus, koosinus jne. Ja üldiselt mis tahes elementaarne funktsioon pidev selle peal määratluspiirkond, näiteks, logaritmiline funktsioon on intervallil pidev. Loodetavasti on teil praeguseks üsna hea ettekujutus sellest, millised põhifunktsioonide graafikud välja näevad. Rohkem detailne info nende järjepidevuse kohta saab aru ühelt lahkelt mehelt nimega Fichtenholtz.

Funktsiooni järjepidevuse segmendil ja poolintervallidel pole ka kõik keeruline, kuid sellest on õigem rääkida tunnis funktsiooni minimaalse ja maksimaalse väärtuse leidmise kohta segmendis, kuid ärgem praegu selle pärast muretsege.

Murdepunktide klassifikatsioon

Funktsioonide põnev elukäik on rikas kõikvõimalike eripunktide poolest ja murdepunktid on vaid üks nende eluloo lehekülg.

Märge : igaks juhuks peatun ühel elementaarsel punktil: murdepunkt on alati üks punkt– pole olemas “mitu vaheajapunkti järjest”, st ei ole olemas sellist asja nagu “vaheajavahemik”.

Need punktid jagunevad omakorda kahte suurde rühma: esimest tüüpi rebendid Ja teist tüüpi rebendid. Igal lõhe tüübil on oma omadused mida me praegu vaatame:

Esimest tüüpi katkestuspunkt

Kui järjepidevuse tingimust mingis punktis rikutakse ja ühepoolsed piirid lõplik , siis nimetatakse seda esimest tüüpi katkestuspunkt.

Alustame kõige optimistlikuma juhtumiga. Tunni algse idee järgi tahtsin rääkida teooriast "in üldine vaade”, kuid materjali reaalsuse demonstreerimiseks otsustasin konkreetsete tegelastega variandiga.

Kurb, nagu taustal foto noorpaaridest Igavene leek, kuid üldiselt aktsepteeritakse järgmist raami. Kujutame joonisel funktsiooni graafikut:


See funktsioon on pidev kogu arvureal, välja arvatud punkt. Ja tegelikult ei saa nimetaja olla võrdne nulliga. Kuid vastavalt piiri tähendusele saame lõpmatult lähedal läheneda nullile nii vasakult kui ka paremalt, see tähendab, et ühepoolsed piirid on olemas ja ilmselgelt langevad kokku:
(Järjepidevuse tingimus nr 2 on täidetud).

Kuid funktsioon ei ole selles punktis määratletud, seetõttu rikutakse järjepidevuse tingimust nr 1 ja funktsioon kannatab selles punktis katkestuse all.

Seda tüüpi paus (koos olemasoleva üldine piirmäär) kutsutakse parandatav vahe. Miks eemaldatav? Kuna funktsioon saab uuesti määratleda murdepunktis:

Kas see tundub imelik? Võib olla. Aga selline funktsiooni tähistus ei räägi millegi vastu! Nüüd on vahe kinni ja kõik on rahul:


Teeme ametliku kontrolli:

2) – on olemas üldine piirmäär;
3)

Seega on kõik kolm tingimust täidetud ja funktsioon on punktis pidev funktsiooni punktis pidevuse definitsiooni järgi.

Kuid matani vihkajad võivad funktsiooni näiteks halvasti määratleda :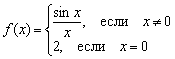


Huvitav on see, et siin on täidetud kaks esimest järjepidevuse tingimust:
1) – funktsioon on defineeritud antud punktis;
2) – on üldine piirmäär.

Kuid kolmas piir ei ole ületatud: st funktsiooni piir punktis pole võrdne antud funktsiooni väärtus antud punktis.

Seega esineb teatud hetkel funktsiooni katkestus.

Teist, kurvemat juhtumit nimetatakse esimest tüüpi rebend hüppega. Ja kurbust kutsuvad esile ühekülgsed piirid, mis piiratud ja erinev. Näide on toodud õppetunni teisel joonisel. Selline lõhe tekib tavaliselt siis, kui tükkhaaval määratletud funktsioonid, mida on artiklis juba mainitud graafiteisenduste kohta.

Mõelge tükipõhisele funktsioonile ja me lõpetame selle joonise. Kuidas graafikut koostada? Väga lihtne. Poolintervallil joonistame parabooli fragmendi ( roheline värv), intervallil – sirge lõik (punane) ja poolintervallil – sirge (sinine).

Veelgi enam, ebavõrdsuse tõttu määratakse ruutfunktsiooni väärtus (roheline punkt) ja ebavõrdsuse tõttu määratakse väärtus lineaarne funktsioon(sinine täpp):

Kõige keerulisemal juhul peaksite kasutama iga graafiku osa punkt-punkti konstrueerimist (vt esimest õppetund funktsioonide graafikute kohta).

Nüüd huvitab meid ainult punkt. Uurime seda järjepidevuse tagamiseks:

2) Arvutame ühepoolsed piirid.

Vasakul on punane joon, nii et vasakpoolne piirang on:

Paremal on sinine sirgjoon ja parempoolne piir:

Selle tulemusena saime lõplikud arvud, ja nemad pole võrdne. Kuna ühepoolsed piirid piiratud ja erinev: , siis meie funktsioon talub esimest tüüpi katkestus hüppega.

On loogiline, et tühimikku ei saa kõrvaldada - funktsiooni ei saa tõesti täpsemalt määratleda ja "kokku liimida", nagu eelmises näites.

Teist tüüpi katkestuspunktid

Tavaliselt liigitatakse kõik muud rebenemise juhtumid nutikalt sellesse kategooriasse. Ma ei loetle kõike, sest praktikas tekib 99% probleemidest lõputu vahe– kui olete vasaku- või paremakäeline, ja sagedamini, on mõlemad piirid lõpmatud.

Ja muidugi kõige ilmsem pilt on hüperbool punktis null. Siin on mõlemad ühepoolsed piirid lõpmatud: , seetõttu kannatab funktsioon punktis teist tüüpi katkestus.

Püüan täita oma artikleid võimalikult mitmekesise sisuga, seega vaatame veel nägemata funktsiooni graafikut:

vastavalt standardskeemile:

1) Funktsioon pole praegu määratletud, kuna nimetaja läheb nulli.

Muidugi võime kohe järeldada, et funktsioon kannatab punktis katkestuse, kuid hea oleks liigitada katkestuse olemust, mida tingimus sageli nõuab. Selle jaoks:

Lubage mul teile meelde tuletada, et salvestamise all peame silmas lõpmatult väike negatiivne arv ja kirje all - lõpmata väike positiivne arv.

Ühepoolsed piirid on lõpmatud, mis tähendab, et funktsioonil esineb punktis 2. tüüpi katkestus. Y-telg on vertikaalne asümptoot graafiku jaoks.

Pole haruldane, et eksisteerivad mõlemad ühepoolsed piirid, kuid ainult üks neist on lõpmatu, näiteks:

See on funktsiooni graafik.

Uurime järjepidevuse punkti:

1) Funktsioon pole praegu määratletud.

2) Arvutame ühepoolsed piirid:

Selliste ühekülgsete piiride arvutamise meetodist räägime loengu kahes viimases näites, kuigi paljud lugejad on kõike juba näinud ja ära arvanud.

Vasakpoolne piir on lõplik ja võrdne nulliga (me “ei lähe punkti enda juurde”), aga parempoolne piir on lõpmatu ja graafiku oranž haru läheneb lõpmatult lähedale. vertikaalne asümptoot, võrrandiga antud(must punktiirjoon).

Nii et funktsioon kannatab teist tüüpi katkestus punktis .

Mis puutub 1. tüüpi katkestustesse, siis funktsiooni saab määratleda katkestuspunktis endas. Näiteks tükipõhise funktsiooni jaoks Võid julgelt panna koordinaatide alguspunkti musta paksu täpi. Paremal on hüperbooli haru ja parempoolne piir on lõpmatu. Ma arvan, et peaaegu kõigil on aimu, milline see graafik välja näeb.

Mida kõik ootasid:

Kuidas kontrollida funktsiooni järjepidevust?

Funktsiooni järjepidevuse uurimine punktis viiakse läbi juba kehtestatud rutiinskeemi järgi, mis koosneb kolme pidevuse tingimuse kontrollimisest:

Näide 1

Uurige funktsiooni

Lahendus:

1) Ainus punkt ulatuses on see, kus funktsioon pole määratletud.

2) Arvutame ühepoolsed piirid:

Ühepoolsed piirid on lõplikud ja võrdsed.

Seega esineb funktsioonil eemaldatav katkestus.

Kuidas selle funktsiooni graafik välja näeb?

Ma tahaksin lihtsustada , ja tundub, et saadakse tavaline parabool. AGA algne funktsioon ei ole punktis määratletud, seega on vajalik järgmine klausel:

Teeme joonise:

Vastus: funktsioon on pidev kogu arvureal, välja arvatud punkt, kus tal on eemaldatav katkestus.

Funktsiooni saab edasi defineerida nii hästi kui ka mitte nii hästi, kuid vastavalt tingimusele pole see vajalik.

Ütlete, et see on kaugeleulatuv näide? Üldse mitte. Praktikas on seda juhtunud kümneid kordi. Peaaegu kõik saidi ülesanded pärinevad reaalsest iseseisvast tööst ja testidest.

Vabaneme oma lemmikmoodulitest:

Näide 2

Uurige funktsiooni järjepidevuse nimel. Määrake funktsiooni katkestuste olemus, kui need on olemas. Teostage joonis.

Lahendus: Mingil põhjusel õpilased kardavad ja neile ei meeldi mooduli funktsioonid, kuigi neis pole midagi keerulist. Selliseid asju oleme tunnis juba veidi puudutanud. Graafikute geomeetrilised teisendused. Kuna moodul ei ole negatiivne, laiendatakse seda järgmiselt: , kus "alfa" on mingi väljend. Sel juhul tuleks meie funktsioon kirjutada tükkhaaval:

Kuid mõlema tüki murde tuleb vähendada . Vähendamine, nagu eelmises näites, ei toimu ilma tagajärgedeta. Algfunktsioon ei ole selles punktis määratletud, kuna nimetaja läheb nulli. Seetõttu peaks süsteem täiendavalt täpsustama tingimust ja muutma esimese ebavõrdsuse rangeks:

Nüüd VÄGA KASULIKust otsustustehnikast: enne ülesande viimistlemist mustandil on kasulik teha joonis (olenemata sellest, kas tingimused seda nõuavad või mitte). See aitab esiteks kohe näha järjepidevuse ja katkestuspunkte ning teiseks kaitseb teid 100% vigade eest ühepoolsete piiride leidmisel.

Teeme joonistamise. Vastavalt meie arvutustele on punktist vasakule vaja joonistada parabooli fragment (sinine värv) ja paremale parabooli tükk (punane värv), samas kui funktsioon pole punktis määratletud. punkt ise:

Kui kahtlete, võtke paar x väärtust ja ühendage need funktsiooniga (pidage meeles, et moodul hävitab võimaliku miinusmärgi) ja kontrollige graafikut.

Uurime järjepidevuse funktsiooni analüütiliselt:

1) Funktsioon ei ole punktis määratletud, seega võime kohe öelda, et see ei ole selles pidev.

2) Teeme kindlaks katkestuse olemuse, arvutame ühepoolsed piirid:

Ühepoolsed piirid on lõplikud ja erinevad, mis tähendab, et funktsioon kannatab 1. tüüpi katkestuse ja hüppega punktis . Jällegi pange tähele, et piiride leidmisel pole vahet, kas murdepunktis olev funktsioon on defineeritud või mitte.

Nüüd jääb üle vaid mustandist joonis üle kanda (see on tehtud justkui uurimistöö abil ;-)) ja ülesanne täita:

Vastus: funktsioon on pidev kogu arvureal, välja arvatud punkt, kus tal esineb hüppega esimest tüüpi katkestus.

Mõnikord nõuavad nad katkestushüppe täiendavat märki. See arvutatakse lihtsalt - parempoolsest piirist peate lahutama vasakpoolse piiri: , see tähendab, et murdepunktis hüppas meie funktsioon 2 ühikut allapoole (nagu miinusmärk ütleb).

Näide 3

Uurige funktsiooni järjepidevuse nimel. Määrake funktsiooni katkestuste olemus, kui need on olemas. Tee joonis.

See on näide sõltumatu otsus, tunni lõpus näidislahendus.

Liigume edasi ülesande kõige populaarsema ja levinuma versiooni juurde, kui funktsioon koosneb kolmest osast:

Näide 4

Uurige funktsiooni pidevust ja joonistage funktsiooni graafik .

Lahendus: on ilmselge, et funktsiooni kõik kolm osa on vastavatel intervallidel pidevad, seega jääb üle kontrollida vaid kahte tükkide vahelist “ristumispunkti”. Esmalt teeme mustandjoonise Ma kommenteerisin artikli esimeses osas piisavalt üksikasjalikult ehitustehnikat. Ainus asi on see, et peame hoolikalt järgima meie ainsuse punkte: ebavõrdsuse tõttu kuulub väärtus sirgele (roheline punkt) ja ebavõrdsuse tõttu kuulub väärtus paraboolile (punane punkt):


Noh, põhimõtteliselt on kõik selge =) Jääb vaid otsus vormistada. Iga kahe "liitumispunkti" puhul kontrollime tavaliselt kolme järjepidevuse tingimust:

ma) Uurime järjepidevuse punkti

1)

Ühepoolsed piirid on lõplikud ja erinevad, mis tähendab, et funktsioon kannatab 1. tüüpi katkestuse ja hüppega punktis .

Arvutame katkestushüppe parempoolse ja vasakpoolse piiri erinevusena:
, see tähendab, et graafik tõusis ühe ühiku võrra ülespoole.

II) Uurime järjepidevuse punkti

1) – funktsioon on defineeritud antud punktis.

2) Leidke ühepoolsed piirid:

– ühepoolsed piirid on lõplikud ja võrdsed, mis tähendab, et on olemas üldine piir.

3) – funktsiooni piirväärtus punktis on võrdne selle funktsiooni väärtusega antud punktis.

Viimases etapis kanname joonise üle lõppversiooni, mille järel paneme viimase akordi:

Vastus: funktsioon on pidev kogu arvureal, välja arvatud punkt, kus tal esineb hüppega esimest tüüpi katkestus.

Näide 5

Uurige funktsiooni pidevust ja koostage selle graafik .

See on näide iseseisvaks lahendamiseks, lühilahendus ja ülesande ligikaudne näidis õppetunni lõpus.

Võib jääda mulje, et ühel hetkel peab funktsioon olema pidev, teises aga katkestus. Praktikas see alati nii ei ole. Püüdke mitte jätta tähelepanuta ülejäänud näiteid - seal on mitmeid huvitavaid ja olulisi funktsioone:

Näide 6

Antud funktsioon . Uurige punktide pidevuse funktsiooni. Koostage graafik.

Lahendus: ja uuesti viivitamatult teostada mustandil olev joonis:

Selle graafiku eripära on see, et tükipõhine funktsioon on antud abstsisstelje võrrandiga. Siin on see ala joonistatud rohelisega, kuid märkmikus on see tavaliselt lihtsa pliiatsiga paksus kirjas esile tõstetud. Ja muidugi ärge unustage meie jäärasid: väärtus kuulub puutuja harule (punane punkt) ja väärtus sirgjoonele.

Jooniselt on kõik selge - funktsioon on pidev kogu arvujoonel, jääb üle vaid vormistada lahendus, mis viiakse täieliku automatiseerimiseni sõna otseses mõttes pärast 3-4 sarnast näidet:

ma) Uurime järjepidevuse punkti

1) – funktsioon on defineeritud antud punktis.

2) Arvutame ühepoolsed piirid:

, mis tähendab, et on olemas üldine limiit.

Igaks juhuks tuletan meelde triviaalset tõsiasja: konstandi piir on võrdne konstandi endaga. Sel juhul on nulli piirmäär võrdne nulliga endaga (vasakukäeline piir).

3) – funktsiooni piirväärtus punktis on võrdne selle funktsiooni väärtusega antud punktis.

Seega on funktsioon punktis pidev funktsiooni punktis pidevuse definitsiooni järgi.

II) Uurime järjepidevuse punkti

1) – funktsioon on defineeritud antud punktis.

2) Leidke ühepoolsed piirid:

Ja siin – ühe piir on võrdne ühiku endaga.

– on üldine piirmäär.

3) – funktsiooni piirväärtus punktis on võrdne selle funktsiooni väärtusega antud punktis.

Seega on funktsioon punktis pidev funktsiooni punktis pidevuse definitsiooni järgi.

Nagu tavaliselt, kanname pärast uurimistööd oma joonise lõplikku versiooni.

Vastus: funktsioon on punktides pidev.

Pange tähele, et tingimusel, et meilt ei küsitud midagi järjepidevuse kogu funktsiooni uurimise kohta ja seda peetakse heaks matemaatiliseks vormiks sõnastada täpne ja selge vastus esitatud küsimusele. Muide, kui tingimused ei nõua graafiku koostamist, siis on teil täielik õigus seda mitte ehitada (kuigi hiljem võib õpetaja teid sundida seda tegema).

Väike matemaatiline “keelekeeraja” selle ise lahendamiseks:

Näide 7

Antud funktsioon 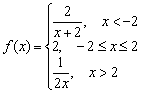. Uurige punktide pidevuse funktsiooni. Klassifitseerige katkestuspunktid, kui neid on. Teostage joonis.

Proovige kõiki "sõnu" õigesti "hääldada" =) Ja joonistage graafik täpsemalt, täpsus, see pole kõikjal üleliigne;-)

Nagu mäletate, soovitasin joonise kohe mustandina valmis teha, kuid aeg-ajalt tuleb ette näiteid, kus ei saa kohe aru, milline graafik välja näeb. Seetõttu on paljudel juhtudel soodne esmalt leida ühekülgsed piirid ja alles seejärel uuringu põhjal oksad kujutada. Kahes viimases näites õpime ka mõne ühepoolse piirmäära arvutamise tehnikat:

Näide 8

Uurige funktsiooni pidevust ja koostage selle skemaatiline graafik.

Lahendus: halvad punktid on ilmsed: (vähendab astendaja nimetaja nulli) ja (taandab kogu murdosa nimetaja nulliks). Ei ole selge, kuidas selle funktsiooni graafik välja näeb, mis tähendab, et parem on esmalt veidi uurimistööd teha.

Topoloogia– matemaatika haru, mis tegeleb funktsioonide piiride ja pidevuse uurimisega. Koos algebraga moodustab topoloogia matemaatika üldise aluse.

Topoloogiline ruum või kujund – meie homogeense eukleidilise ruumi alamhulk, mille punktide vahel on antud teatav lähedusseos. Siin käsitletakse figuure mitte jäikade kehadena, vaid justkui väga elastsest kummist valmistatud esemetena, mis võimaldavad pidevat deformatsiooni, mis säilitab nende kvalitatiivsed omadused.

Kujundite üks-ühele pidevat kaardistamist nimetatakse homöomorfism. Teisisõnu, arvud homöomorfne, kui üht saab pideva deformatsiooni teel üle kanda teisele.

Näited. Järgmised joonised on homöomorfsed (erinevate rühmade arvud ei ole homöomorfsed), näidatud joonisel fig. 2.

1. Lõik ja kõver ilma iselõikusteta.

2. Ring, ruudu sisemus, lint.

3. Kera, kuubi ja tetraeedri pind.

4. Ring, ellips ja sõlmeline ring.

5. Rõngas tasapinnal (auguga ring), rõngas ruumis, kaks korda keerdunud rõngas, silindri külgpind.

6. Möbiuse riba, s.o. üks kord keerutatud sõrmus ja kolm korda keerutatud sõrmus.

7. Toruse pind (sõõrik), käepidemega kera ja sõlmeline toru.

8. Kahe sangaga kera ja kahe auguga kringel.

IN matemaatiline analüüs funktsioone uuritakse piiride meetodil. Muutuja ja piirmäär on põhimõisted.

Erinevate nähtuste puhul säilitavad ühed suurused oma arvulise väärtuse, teised muutuvad. Kutsutakse muutuja kõigi arvväärtuste kogumit selle muutuja muutuste vahemik.

Erinevatest viisidest, kuidas muutuja käitub, on kõige olulisem see, kuidas muutuja kaldub teatud piirini.

Püsiv number a helistas muutuv piirmäär, kui absoluutväärtus vahe x Ja a() muutub muutuva väärtuse muutmise protsessis x nii väike kui soovite:

Mida tähendab “nii väike, kui sulle meeldib”? Muutuv väärtus X kipub piirini A, kui suvaliselt väikese (suvaliselt väikese) arvu korral on muutuja muutumises selline moment X, millest alates kehtib ebavõrdsus .

Piirmäära määratlusel on lihtne geomeetriline tähendus: ebavõrdsus tähendab seda X on punkti -naabruses a, need. intervallis .

Seega saab piiri määratluse anda sisse geomeetriline kuju:

Number A on muutuja piir X, kui mõne suvaliselt väikese (suvaliselt väikese) -arvu naabruskonna jaoks A muutuja muutmisel saate määrata sellise hetke X, millest alates kõik selle väärtused langevad punkti määratud naabrusesse A.

Kommenteeri. Muutuv väärtus X võib läheneda oma piirile erineval viisil: jäädes sellest piirist alla (vasakul), rohkem (paremal), kõikudes limiidi väärtuse ümber.

Järjestuse piirang

Funktsioon nimetatakse seaduseks (reegliks), mille kohaselt iga element x mingi komplekt X sobib ühele elemendile y komplektid Y.

Funktsiooni saab defineerida kõigi naturaalarvude hulgal: . Seda funktsiooni nimetatakse loomulik argument funktsioon või numbriline jada.

Kuna jada, nagu iga lõpmatu hulk, ei saa loendamisega täpsustada, määratakse see ühise terminiga: , kus on jada üldtermin.

Diskreetne muutuja on jada tavaline termin.

Järjepidevuse huvides tähendavad sõnad "alates mingil hetkel" sõnu "alates teatud arvust".

Number A nimetatakse jada piiriks , kui suvaliselt väikese (suvaliselt väikese) arvu korral on selline arv olemas N, mis kõigile numbriga jada liikmetele n>N ebavõrdsus kehtib .

või juures .

Geomeetriliselt tähendab jada piiri määratlus järgmist: suvaliselt väikese (suvaliselt väikese) arvu naabruskonna jaoks A on selline arv, et kõik jada liikmed on suuremad kui N, numbrid, satuvad sellesse lähedusse. Väljaspool naabrust ilmub ainult piiratud arv jada algliikmeid. Naturaalarv N sõltub : .