თამაშები

ერთი ცვლადის - დოკუმენტის ფუნქციის ლიმიტი და უწყვეტობა. უწყვეტი არგუმენტის ფუნქციის ლიმიტი ფუნქციის უწყვეტობის ცნება

ლიმიტი და უწყვეტობა

ერთი ცვლადის ფუნქციები

3.1.1. განმარტება. ნომერი ა xმიისწრაფვის x 0 თუ რომელიმე რიცხვისთვის
არის ნომერი
(
), და დაკმაყოფილდება პირობა:

თუ
, ეს
.

(სიმბოლიზმი:
).

თუ გრაფიკი მიუთითებს გფუნქციები

, Როდესაც უახლოვდება წერტილს უსასრულოდ ახლოს (ისინი.
), (იხ. სურ. 3.1), მაშინ ეს გარემოება არის გეომეტრიული ეკვივალენტი იმისა, რომ ფუნქცია
ზე
აქვს ზღვრული მნიშვნელობა (ლიმიტი) ა(სიმბოლიზმი:
).

ფუნქციის გრაფიკი,

ბრინჯი. 3.1

უნდა აღინიშნოს, რომ ფუნქციის ზღვრული მნიშვნელობის (ლიმიტის) განსაზღვრისას at xმიისწრაფვის x 0 არაფერს ამბობს წერტილის ფუნქციის ქცევაზე x 0 . იმ მომენტში x 0 ფუნქცია შეიძლება არ იყოს განსაზღვრული, შეიძლება იყოს
, შესაძლოა
.

თუ
, მაშინ ფუნქციას ეწოდება უსასრულო მცირე for
.

ინტერვალი ე.წ  - წერტილის მეზობლობა x 0 ჩიპიანი ცენტრით. ამ სახელის გამოყენებით შეგვიძლია ვთქვათ: თუ რომელიმე რიცხვისთვის არის რიცხვი და დაკმაყოფილდება პირობა: თუ
, ეს
.

3.1.2. განმარტება. , თუ რაიმე კონვერგენტისთვის x 0 თანმიმდევრობა
შემდგომი მიმდევრობა
ემთხვევა ა.

3.1.3. მოდით დავამტკიცოთ 3.1.1 და 3.1.2 სექციების განმარტებების ეკვივალენტობა.

მოდით პირველი პირველი განმარტების მნიშვნელობით და მოდით
(
), შემდეგ ყველა , გარდა მათი სასრული რიცხვისა, აკმაყოფილებენ უტოლობას
, სად  მიერ შერჩეული  პირველი განმარტების მნიშვნელობით, ე.ი.
, ე.ი. პირველი განმარტება გულისხმობს მეორეს. დაე ახლა
მეორე განმარტების მნიშვნელობით და დავუშვათ, რომ მეორე განმარტების გაგებით
, ე.ი. ზოგიერთი თვითნებურად მცირე (მაგალითად, ამისთვის
) მოიძებნა თანმიმდევრობა
, მაგრამ ამავდროულად
. ჩვენ მივედით წინააღმდეგობაში, ამიტომ პირველი გამომდინარეობს მეორე განმარტებიდან.

3.1.4. ამ განმარტებების ეკვივალენტობა განსაკუთრებით მოსახერხებელია, რადგან ყველა ადრე დადასტურებული თეორემა მიმდევრობის ზღვრების თვისებებზე თითქმის ავტომატურად გადადის ახალი საქმე. საჭიროა მხოლოდ შეზღუდვის ცნების გარკვევა. შესაბამის თეორემას აქვს შემდეგი ფორმულირება:

თუ
, მაშინ ის შემოიფარგლება წერტილის რაღაც  - მეზობლობით x 0 ჩიპიანი ცენტრით.

3.2.1.თეორემა. დაე
,
,

შემდეგ,
,

3.2.2. დაე

- თვითნებური, თანხვედრა xფუნქციის არგუმენტების მნიშვნელობების 0 თანმიმდევრობა და
. თანმიმდევრობის შესატყვისი
და
ამ ფუნქციების მნიშვნელობებს აქვთ საზღვრები ადა ბ. მაგრამ შემდეგ, 2.13.2 ნაწილის თეორემის ძალით, მიმდევრობები
,
და
აქვს ლიმიტები შესაბამისად თანაბარი ა +ბ,
და
. ფუნქციის ლიმიტის განსაზღვრის მიხედვით წერტილში (იხ. ნაწილი 2.5.2), ეს ნიშნავს, რომ

,
,

3.2.3. თეორემა. თუ
,
და ზოგიერთ მიმდებარედ

ხდება

3.2.4. ფუნქციის ლიმიტის განსაზღვრით წერტილში x 0 ნებისმიერი თანმიმდევრობისთვის
ისეთივე როგორც

ფუნქციის მნიშვნელობების თანმიმდევრობას აქვს ლიმიტი ტოლი ა. ეს ნიშნავს, რომ ვინმესთვის
არის ნომერი
შესრულებული . ანალოგიურად, თანმიმდევრობისთვის
არის ნომერი
ისეთი, რომ ნებისმიერი რიცხვისთვის
შესრულებული . Არჩევა
, ჩვენ ამას ყველასთვის ვპოულობთ
შესრულებული . ამ უტოლობათა ჯაჭვიდან გვაქვს ნებისმიერი , რაც იმას ნიშნავს
.

3.2.5. განმარტება. ნომერი აეწოდება ფუნქციის ზღვრული მნიშვნელობა (ლიმიტი) at xმიისწრაფვის x 0 მარჯვნივ (სიმბოლიზმი:
), თუ რომელიმე რიცხვისთვის არის რიცხვი () და დაკმაყოფილებულია პირობა: თუ
, ეს
.

სიმრავლეს ეწოდება მარჯვენა  - წერტილის მეზობლობა x 0 . მარცხნივ ზღვრული მნიშვნელობის (ლიმიტის) კონცეფცია ანალოგიურად არის განსაზღვრული (
).

3.2.6. თეორემა. ფუნქციას აქვს ზღვრული მნიშვნელობა (ლიმიტი) ტოლი ამაშინ და მხოლოდ მაშინ

3.3.1. განმარტება. ნომერი აეწოდება ფუნქციის ზღვრული მნიშვნელობა (ლიმიტი) at xუსასრულობისკენ მიდრეკილება, თუ რომელიმე რიცხვისთვის არის რიცხვი
(
) და დაკმაყოფილდება შემდეგი პირობა:

თუ
, რომ .

(სიმბოლიზმი:
.)

Რამოდენიმე
დაურეკა დ- უსასრულობის სამეზობლო.

3.3.2. განმარტება. ნომერი აეწოდება ფუნქციის ზღვრული მნიშვნელობა (ლიმიტი) at xმიდრეკილია პლუს უსასრულობისკენ, თუ რომელიმე რიცხვისთვის არის რიცხვი დ() და დაკმაყოფილდება პირობა:

თუ
, რომ .

(სიმბოლიზმი:
).

თუ გრაფიკი მიუთითებს გფუნქციები
შეუზღუდავი ზრდით
განუსაზღვრელი ვადით მიუახლოვდით ერთ ჰორიზონტალურ ხაზს
(იხ. სურ. 3.2), მაშინ ეს გარემოება არის გეომეტრიული ეკვივალენტი იმისა, რომ ფუნქცია
ზე
აქვს ზღვრული მნიშვნელობა (ლიმიტი) რიცხვის ტოლი ა(სიმბოლიზმი:
).

ფუნქციის გრაფიკი
,

Რამოდენიმე
დაურეკა დ-მეზობლობა პლუს უსასრულობა.

ლიმიტის კონცეფცია ზე
.

Სავარჯიშოები.

ჩამოთვალეთ ყველა თეორემა ლიმიტების შესახებ, რომლებიც გამოიყენება შემთხვევებზე:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. განმარტება. ფუნქციას უწოდებენ უსასრულოდ დიდი ფუნქცია(ან უბრალოდ უსასრულოდ დიდი) ზე, თუ რომელიმე რიცხვისთვის

, უთანასწორობის დაკმაყოფილება, უთანასწორობა დაკმაყოფილებულია
.

(სიმბოლიზმი:
.)

თუ შესრულდა
, მერე წერენ
.

3.4.2. თეორემა. დაე
და
ზე
.

მერე
არის უსასრულოდ დიდი ფუნქცია .

3.4.3. დაე ეს იყოს თვითნებური რიცხვი. რადგან არის უსასრულოდ მცირე ფუნქცია , შემდეგ რიცხვისთვის
არის ისეთი რიცხვი, რომელიც ყველასთვის xისეთი, რომ უთანასწორობა ინარჩუნებს
, მაგრამ შემდეგ იგივე xუთანასწორობა დაკმაყოფილდება
. იმათ. არის უსასრულოდ დიდი ფუნქცია .

3.4.4.თეორემა. მოდით იყოს უსასრულოდ დიდი ფუნქცია და for .

მაშინ არის უსასრულოდ მცირე ფუნქცია .

(ეს თეორემა დადასტურებულია 3.8.2 ნაწილის თეორემის ანალოგიურად.)

3.4.5. ფუნქცია
შეუზღუდავი ეწოდება როცა
, თუ რომელიმე ნომრისთვის
და წერტილის ნებისმიერი δ-მეზობლობა შეგიძლიათ მიუთითოთ წერტილი xამ უბნიდან ისეთი რომ
.

3.5.1. განმარტება. ფუნქციას ეძახიან უწყვეტიწერტილში , თუ
.

ბოლო პირობა შეიძლება ჩაიწეროს ასე:

ეს აღნიშვნა ნიშნავს, რომ უწყვეტი ფუნქციებისთვის ლიმიტის ნიშანი და ფუნქციის ნიშანი შეიძლება შეიცვალოს

ან ასე: . ან ისევ, როგორც თავიდან.

აღვნიშნოთ
. მერე
და =
და ბოლო ჩაწერის ფორმა მიიღებს ფორმას

ლიმიტის ნიშნის ქვეშ გამოხატული გამოხატულება წარმოადგენს ნაზრდით გამოწვეულ ფუნქციის წერტილის ზრდას
არგუმენტი xწერტილში, ჩვეულებრივ აღინიშნება როგორც
. შედეგად, ვიღებთ ფუნქციის უწყვეტობის პირობის ჩაწერის შემდეგ ფორმას წერტილში

რომელსაც ეწოდება ფუნქციის უწყვეტობის „სამუშაო განსაზღვრება“ წერტილში.

ფუნქციას ეძახიან უწყვეტიწერტილში დატოვა, თუ
.

ფუნქციას ეძახიან უწყვეტიწერტილში მარჯვნივ, თუ
.

3.5.2. მაგალითი.
. ეს ფუნქცია უწყვეტია ნებისმიერისთვის. ზღვრების თვისებებზე თეორემების გამოყენებით, ჩვენ დაუყოვნებლივ ვიღებთ: ნებისმიერი რაციონალური ფუნქცია უწყვეტია ყველა წერტილში, სადაც ის განისაზღვრება, ე.ი. ფორმის ფუნქცია
.

ᲡᲐᲕᲐᲠᲯᲘᲨᲝᲔᲑᲘ.

3.6.1. სკოლის სახელმძღვანელო ადასტურებს (ზე მაღალი დონესიმკაცრე) რომ
(პირველი ღირსშესანიშნავი ზღვარი). ვიზუალური გეომეტრიული მოსაზრებებიდან დაუყოვნებლივ გამომდინარეობს, რომ
. გაითვალისწინეთ, რომ მარცხენა უტოლობიდან ეს ასევე გამომდინარეობს
, ე.ი. რა არის ფუნქცია
უწყვეტი ნულზე. აქედან სულაც არ არის რთული ყველაფრის უწყვეტობის დამტკიცება ტრიგონომეტრიული ფუნქციებიყველა წერტილში, სადაც ისინი განსაზღვრულია. ფაქტობრივად, როცა
როგორც პროდუქტი უსასრულოა მცირე ფუნქცია
on შეზღუდული ფუნქცია
.

3.6.2. (მე-2 მშვენიერი ლიმიტი). როგორც უკვე ვიცით

სად გადის ნატურალურ რიცხვებში. ამის ჩვენება შეიძლება
. მეტიც
.

ᲡᲐᲕᲐᲠᲯᲘᲨᲝᲔᲑᲘ.

3.7.1. თეორემა (კომპლექსური ფუნქციის უწყვეტობაზე).

თუ ფუნქცია
არის უწყვეტი წერტილი და
და ფუნქცია
უწყვეტი წერტილში , შემდეგ რთული ფუნქცია
უწყვეტია წერტილში.

3.7.2. ამ განცხადების მართებულობა დაუყოვნებლივ გამომდინარეობს უწყვეტობის განმარტებიდან, რომელიც დაწერილია შემდეგნაირად:

3.8.1. თეორემა. ფუნქცია უწყვეტია ყველა წერტილში (
).

3.8.2. თუ გონივრულად ჩავთვლით, რომ ფუნქცია
განსაზღვრულია ნებისმიერისთვის და მკაცრად მონოტონურია (მკაცრად კლებადი
, მკაცრად იზრდება ერთად
), მაშინ მტკიცებულება არ არის რთული.

ზე
ჩვენ გვაქვს:

იმათ. როცა გვაქვს
, რაც ნიშნავს, რომ ფუნქცია არის უწყვეტი ზე.

ზე
ყველაფერი წინაზე მოდის:

ზე
.

ზე
ფუნქცია
მუდმივია ყველასთვის, შესაბამისად, უწყვეტი.

3.9.1. თეორემა (შებრუნებული ფუნქციის თანაარსებობისა და უწყვეტობის შესახებ).

მოდით, უწყვეტი ფუნქცია მკაცრად შემცირდეს (მკაცრად გაიზარდოს) წერტილის ზოგიერთ δ - სამეზობლოში,
. შემდეგ ზოგიერთ ε - წერტილის სამეზობლოში არის შებრუნებული ფუნქცია
, რომელიც მკაცრად მცირდება (მკაცრად მატულობს) და უწყვეტია წერტილის ε - მეზობლად.

3.9.2. აქ ჩვენ ვამტკიცებთ მხოლოდ შებრუნებული ფუნქციის უწყვეტობას წერტილში.

ავიღოთ წერტილი წმდებარეობს წერტილებს შორის
და
მაშასადამე, თუ
, ეს
, სად .

3.10.1. ასე რომ, ნებისმიერი დასაშვები არითმეტიკული მოქმედებები უწყვეტ ფუნქციებზე კვლავ იწვევს უწყვეტ ფუნქციებს. მათგან რთული და ინვერსიული ფუნქციების ფორმირება არ აფუჭებს უწყვეტობას. ამიტომ, გარკვეული პასუხისმგებლობით, შეგვიძლია ვამტკიცოთ, რომ ყველა ელემენტარული ფუნქცია უწყვეტია არგუმენტის ყველა დასაშვები მნიშვნელობისთვის.

ვარჯიში.

დაამტკიცე რომ
ზე
(მეორე მშვენიერი ლიმიტის სხვა ფორმა).

3.11.1. ლიმიტების გამოთვლა მნიშვნელოვნად გამარტივდება, თუ გამოვიყენებთ ეკვივალენტური უსასრულოების ცნებას. მოსახერხებელია ეკვივალენტობის ცნების განზოგადება თვითნებური ფუნქციების შემთხვევაში.

განმარტება. ფუნქციები და ნათქვამია, რომ ექვივალენტურია თუ
(იმის მაგივრად შეგიძლიათ დაწეროთ
,
,
,
,
).

გამოყენებული აღნიშვნა ვ ~ გ.

ეკვივალენტობას აქვს შემდეგი თვისებები

გასათვალისწინებელია ეკვივალენტური უსასრულოების შემდეგი სია:

~
ზე
; (1)

~ ზე ; (2)

~
ზე ; (3)

~ ზე ; (4)

~ ზე ; (5)

~ ზე ; (6)

~ ზე ; (7)

~ გვ ზე ; (8)

~ ზე
; (9)

~
ზე. (10)

აქ და შეიძლება იყოს არა დამოუკიდებელი ცვლადები, არამედ ფუნქციები
და
მიდრეკილია ნულისკენ და ერთისკენ, შესაბამისად, გარკვეული ქცევისთვის x. Მაგალითად,

~
ზე
,

~
ზე
.

ეკვივალენტობა (1) არის პირველი მნიშვნელოვანი ლიმიტის ჩაწერის კიდევ ერთი ფორმა. ეკვივალენტები (2), (3), (6) და (7) შეიძლება პირდაპირ დადასტურდეს. ეკვივალენტობა (4) მიიღება (1) ეკვივალენტობის თვისების 2) გათვალისწინებით:

~
.

ანალოგიურად, (5) და (7) მიიღება (2) და (6)-დან. Ნამდვილად

~
,

~
.

(8)-ის ეკვივალენტობა დასტურდება (7) და (6) თანმიმდევრული გამოყენებით:

და (9) და (10) მიიღება (6) და (8)-დან ჩანაცვლებით
.

3.11.2. თეორემა. პროდუქტისა და თანაფარდობის ლიმიტების გაანგარიშებისას, შეგიძლიათ შეცვალოთ ფუნქციები ეკვივალენტურად. კერძოდ, თუ ~
, მაშინ ან ორივე ლიმიტი არ არსებობს ერთდროულად და
, ან ორივე ეს ლიმიტი ერთდროულად არ არსებობს.

დავამტკიცოთ პირველი თანასწორობა. დაე, ერთ-ერთი ლიმიტი, თქვას,
არსებობს. მერე

3.11.3. მოდით ( იყოს რიცხვი ან სიმბოლო,
ან
). განვიხილავთ ქცევას სხვადასხვა ბ.მ. ფუნქციები (ასე მოვაკლებთ ტერმინს უსასრულოდ მცირე).

განმარტებები.
და ეკვივალენტური ბ.მ. ფუნქციები, თუ
(ზე).

დავარქმევთ ბ.მ. მეტი მაღალი შეკვეთავიდრე ბ.მ. ფუნქცია
, თუ
(ზე).

3.11.4. თუ და ექვივალენტი ბ.მ. ფუნქციები, მაშინ
არის ბ.მ. უფრო მაღალი რიგის ფუნქცია ვიდრე
და რა. - ბ.მ. ფუნქცია at, რომელშიც ყველა x და, თუ ამ მომენტში ფუნქციას ეწოდება მოხსნადი შეწყვეტის წერტილი. აქვს მეორე სახის შეწყვეტა. წერტილი თავად ტესტი

კოლოკვიუმამდე. სექციები: " Ზღვარიდა უწყვეტობაფუნქციებიმოქმედებს ცვლადი" ფუნქციებიერთიცვლადი", „დიფერენციალური გაანგარიშება ფუნქციებირამდენიმე ცვლადები"

ტესტებისა და კითხვების თემები და მაგალითები (ტესტები ინდივიდუალური სტანდარტული გამოთვლების კოლოკვიუმი) 1-ლი სემესტრის ტესტი No1 განყოფილება „რეალური ცვლადის ფუნქციის ზღვარი და უწყვეტობა“

ტესტი

კოლოკვიუმამდე. სექციები: " Ზღვარიდა უწყვეტობაფუნქციებიმოქმედებს ცვლადი", „დიფერენციალური გაანგარიშება ფუნქციებიერთიცვლადი", „დიფერენციალური გაანგარიშება ფუნქციებირამდენიმე ცვლადები". რიცხვების თანმიმდევრობა...

ტესტი

ტესტური დავალებების და კითხვების თემები და მაგალითები (სატესტო სამუშაოები ინდივიდუალური სტანდარტული გამოთვლების კოლოკვიუმები) 1-ლი სემესტრის ტესტის სამუშაო განყოფილება „რეალური ცვლადის ფუნქციის ზღვარი და უწყვეტობა“

ტესტი

ლექცია 19 რამდენიმე ცვლადის ფუნქციის ლიმიტი და უწყვეტობა

ლექცია

... Ზღვარიდა უწყვეტობაფუნქციებირამდენიმე ცვლადები. 19.1. Შინაარსი ფუნქციებირამდენიმე ცვლადები. გადახედვით ფუნქციებირამდენიმე ცვლადები... თვისებები ფუნქციებიერთიცვლადი, უწყვეტისეგმენტზე. იხილეთ თვისებები ფუნქციები, უწყვეტიზე...

ფუნქციის უწყვეტობა. დარღვევის წერტილები.

ხარი დადის, ქანაობს, კვნესის, როცა მიდის:
- ოჰ, დაფა იწურება, ახლა ვაპირებ ჩავარდნას!

ამ გაკვეთილზე განვიხილავთ ფუნქციის უწყვეტობის ცნებას, შეწყვეტის წერტილების კლასიფიკაციას და საერთო პრაქტიკული პრობლემა ფუნქციების უწყვეტობის შესწავლა. თემის სახელიდან ბევრი ინტუიციურად გამოიცნობს რაზე იქნება საუბარი და ფიქრობს, რომ მასალა საკმაოდ მარტივია. Ეს მართალია. მაგრამ ეს არის მარტივი ამოცანები, რომლებიც ყველაზე ხშირად ისჯება უგულებელყოფისა და მათი გადაჭრის ზედაპირული მიდგომისთვის. ამიტომ, გირჩევთ, რომ ძალიან ფრთხილად შეისწავლოთ სტატია და დაიჭიროთ ყველა დახვეწილობა და ტექნიკა.

რა უნდა იცოდეთ და შეგეძლოთ?Არც ისე ბევრი. იმისათვის, რომ კარგად ისწავლოთ გაკვეთილი, უნდა გესმოდეთ, რა არის ეს ფუნქციის ლიმიტი. მომზადების დაბალი დონის მკითხველისთვის საკმარისია სტატიის გააზრება ფუნქციის შეზღუდვები. გადაწყვეტილებების მაგალითებიდა ყურება გეომეტრიული მნიშვნელობალიმიტი სახელმძღვანელოში ელემენტარული ფუნქციების გრაფიკები და თვისებები. ასევე სასურველია გაეცნოთ გრაფიკების გეომეტრიული გარდაქმნები, ვინაიდან პრაქტიკა უმეტეს შემთხვევაში გულისხმობს ნახატის აგებას. პერსპექტივები ყველასთვის ოპტიმისტურია და სავსე ქვაბიც კი შეძლებს დამოუკიდებლად გაუმკლავდეს დავალებას მომდევნო საათში ან ორ საათში!

ფუნქციის უწყვეტობა. წყვეტების წერტილები და მათი კლასიფიკაცია

ფუნქციის უწყვეტობის კონცეფცია

განვიხილოთ რამდენიმე ფუნქცია, რომელიც უწყვეტია მთელ რიცხვით წრფეზე:

ან, უფრო მოკლედ რომ ვთქვათ, ჩვენი ფუნქცია უწყვეტია (კომპლექტში რეალური რიცხვები).

რა არის უწყვეტობის „ფილისტური“ კრიტერიუმი? ცხადია, უწყვეტი ფუნქციის გრაფიკის დახატვა შესაძლებელია ფურცლიდან ფანქრის აწევის გარეშე.

ამ შემთხვევაში, აუცილებელია ნათლად განვასხვავოთ ეს ორი მარტივი ცნებები: ფუნქციის დომენიდა ფუნქციის უწყვეტობა. Ზოგადად ეს არ არის იგივე. Მაგალითად:

ეს ფუნქციაგანსაზღვრულია მთელ რიცხვთა წრფეზე, ანუ for ყველას"x"-ის მნიშვნელობას აქვს "y"-ის საკუთარი მნიშვნელობა. კერძოდ, თუ, მაშინ. გაითვალისწინეთ, რომ სხვა წერტილი პუნქტუირებულია, რადგან ფუნქციის განმარტებით, არგუმენტის მნიშვნელობა უნდა შეესაბამებოდეს ერთადერთი რამფუნქციის მნიშვნელობა. ამრიგად, დომენიჩვენი ფუნქცია:.

თუმცა ეს ფუნქცია არ არის უწყვეტი ჩართული!აშკარაა, რომ ამ ეტაპზე ის იტანჯება უფსკრული. ტერმინი ასევე საკმაოდ გასაგები და ვიზუალურია, აქ ფანქარი მაინც უნდა მოიგლიჯოს. ცოტა მოგვიანებით განვიხილავთ წყვეტის წერტილების კლასიფიკაციას.

ფუნქციის უწყვეტობა წერტილში და ინტერვალზე

კონკრეტულ მათემატიკურ ამოცანაში შეიძლება ვისაუბროთ ფუნქციის უწყვეტობაზე წერტილში, ფუნქციის უწყვეტობაზე ინტერვალზე, ნახევარინტერვალზე ან ფუნქციის უწყვეტობაზე სეგმენტზე. ანუ არ არსებობს "უბრალო უწყვეტობა"– ფუნქცია შეიძლება იყოს უწყვეტი სადღაც. და ყველაფრის ფუნდამენტური "სამშენებლო ბლოკი" არის ფუნქციის უწყვეტობა წერტილში .

მათემატიკური ანალიზის თეორია იძლევა ფუნქციის უწყვეტობის განმარტებას წერტილში „დელტას“ და „ეპსილონის“ სამეზობლოების გამოყენებით, მაგრამ პრაქტიკაში გამოიყენება სხვა განმარტება, რომელსაც ჩვენ დიდ ყურადღებას მივაქცევთ.

ჯერ გავიხსენოთ ცალმხრივი საზღვრებივინც პირველ გაკვეთილზე შემოიჭრა ჩვენს ცხოვრებაში ფუნქციების გრაფიკების შესახებ. განვიხილოთ ყოველდღიური სიტუაცია:

თუ ღერძს მივუახლოვდებით წერტილს დატოვა(წითელი ისარი), შემდეგ "თამაშების" შესაბამისი მნიშვნელობები მიდის ღერძის გასწვრივ წერტილამდე (ჟოლოსფერი ისარი). მათემატიკურად, ეს ფაქტი ფიქსირდება გამოყენებით მარცხენა ლიმიტი:

ყურადღება მიაქციეთ ჩანაწერს (წაკითხულია "x tends to ka მარცხნივ"). "დანამატი" "მინუს ნული" სიმბოლოა არსებითად ეს ნიშნავს, რომ ჩვენ ვუახლოვდებით რიცხვს მარცხენა მხრიდან.

ანალოგიურად, თუ მიუახლოვდებით წერტილს "ka" მარჯვნივ (ლურჯი ისარი), შემდეგ "თამაშები" მივა იმავე მნიშვნელობამდე, მაგრამ მწვანე ისრის გასწვრივ და მარჯვენა ლიმიტიფორმატირებული იქნება შემდეგნაირად:

„დანამატი“ სიმბოლოა , და ჩანაწერში ნათქვამია: „x მიდრეკილია ka-სკენ მარჯვნივ“.

თუ ცალმხრივი ზღვრები სასრული და ტოლია(როგორც ჩვენს შემთხვევაში): , მაშინ ვიტყვით, რომ არსებობს ზოგადი ლიმიტი. ეს მარტივია, ზოგადი ზღვარი არის ჩვენი "ჩვეულებრივი" ფუნქციის ლიმიტი, სასრულ რიცხვის ტოლია.

გაითვალისწინეთ, რომ თუ ფუნქცია არ არის განსაზღვრული (გამოიღეთ შავი წერტილი გრაფიკის ტოტზე), მაშინ ზემოაღნიშნული გამოთვლები ძალაში რჩება. როგორც უკვე არაერთხელ აღინიშნა, კერძოდ სტატიაში უსასრულოდ მცირე ფუნქციებზე, გამონათქვამები ნიშნავს, რომ "x" უსასრულოდ ახლოსუახლოვდება პუნქტს, ხოლო არ აქვს მნიშვნელობა, განსაზღვრულია თუ არა თავად ფუნქცია მოცემულ წერტილში. კარგი მაგალითი ნახავთ შემდეგ აბზაცში, როდესაც მოხდება ფუნქციის ანალიზი.

განმარტება: ფუნქცია უწყვეტია წერტილში, თუ ფუნქციის ზღვარი მოცემულ წერტილში უდრის ფუნქციის მნიშვნელობას ამ წერტილში: .

განმარტება დეტალურად არის აღწერილი შემდეგ ტერმინებში:

1) ფუნქცია უნდა განისაზღვროს წერტილში, ანუ მნიშვნელობა უნდა არსებობდეს.

2) უნდა არსებობდეს ფუნქციის ზოგადი ლიმიტი. როგორც ზემოთ აღინიშნა, ეს გულისხმობს ცალმხრივი საზღვრების არსებობას და თანასწორობას: .

3) ფუნქციის ზღვარი მოცემულ წერტილში უნდა იყოს ფუნქციის მნიშვნელობის ტოლი ამ წერტილში: .

თუ დაირღვა ერთი მაინცსამი პირობიდან, მაშინ ფუნქცია კარგავს უწყვეტობის თვისებას წერტილში.

ფუნქციის უწყვეტობა ინტერვალზეფორმულირებულია გენიალურად და ძალიან მარტივად: ფუნქცია უწყვეტია ინტერვალზე, თუ ის უწყვეტია მოცემული ინტერვალის ყველა წერტილში.

კერძოდ, ბევრი ფუნქცია უწყვეტია უსასრულო ინტერვალზე, ანუ რეალური რიცხვების სიმრავლეზე. ეს არის წრფივი ფუნქცია, პოლინომები, ექსპონენციალური, სინუსი, კოსინუსი და ა.შ. და ზოგადად, ნებისმიერი ელემენტარული ფუნქციაუწყვეტი მასზე განმარტების სფერო, მაგალითად, ლოგარითმული ფუნქციაუწყვეტია ინტერვალზე. ვიმედოვნებთ, რომ ახლა თქვენ გაქვთ საკმაოდ კარგი წარმოდგენა იმის შესახებ, თუ როგორ გამოიყურება ძირითადი ფუნქციების გრაფიკები. მეტი დეტალური ინფორმაციამათი უწყვეტობის შესახებ შეიძლება მივიღოთ კეთილი ადამიანი, სახელად ფიხტენჰოლცი.

სეგმენტზე ფუნქციის უწყვეტობით და ნახევრად ინტერვალებით, ყველაფერი ასევე არ არის რთული, მაგრამ ამაზე საუბარი უფრო მიზანშეწონილია კლასში სეგმენტზე ფუნქციის მინიმალური და მაქსიმალური მნიშვნელობების პოვნის შესახებ, მაგრამ ახლა ამაზე არ ინერვიულოთ.

შესვენების წერტილების კლასიფიკაცია

ფუნქციების მომხიბლავი ცხოვრება მდიდარია ყველა სახის განსაკუთრებული წერტილით და შესვენების წერტილები მათი ბიოგრაფიის მხოლოდ ერთ-ერთი გვერდია.

შენიშვნა : ყოველი შემთხვევისთვის, ელემენტარულ პუნქტზე შევჩერდები: წყვეტის წერტილი ყოველთვის არის ერთი წერტილი– არ არსებობს „რამდენიმე შესვენების წერტილი ზედიზედ“, ანუ არ არსებობს „შესვენების ინტერვალი“.

ეს პუნქტები, თავის მხრივ, იყოფა ორ დიდ ჯგუფად: პირველი სახის რღვევებიდა მეორე სახის რღვევები. თითოეული ტიპის უფსკრული აქვს საკუთარი მახასიათებლებირომელსაც ახლავე განვიხილავთ:

პირველი ტიპის შეწყვეტის წერტილი

თუ უწყვეტობის პირობა ირღვევა წერტილში და ცალმხრივი საზღვრები სასრული , მაშინ ე.წ პირველი ტიპის შეწყვეტის წერტილი.

დავიწყოთ ყველაზე ოპტიმისტური შემთხვევით. გაკვეთილის თავდაპირველი იდეის მიხედვით, მინდოდა მეთქვა თეორია „ში ზოგადი ხედი”, მაგრამ მასალის რეალობის დემონსტრირების მიზნით, მე გადავწყვიტე ვარიანტი კონკრეტული სიმბოლოებით.

სევდიანი, როგორც ფონზე ახალდაქორწინებულთა ფოტო მარადიული ალი, მაგრამ შემდეგი ჩარჩო ზოგადად მიღებულია. მოდით გამოვსახოთ ნახაზზე ფუნქციის გრაფიკი:

ეს ფუნქცია უწყვეტია მთელ რიცხვით წრფეზე, წერტილის გარდა. და ფაქტობრივად, მნიშვნელი არ შეიძლება იყოს ნულის ტოლი. თუმცა, ლიმიტის მნიშვნელობის შესაბამისად, შეგვიძლია უსასრულოდ ახლოსმიუახლოვდით "ნულს" როგორც მარცხნიდან, ასევე მარჯვნიდან, ანუ არსებობს ცალმხრივი საზღვრები და, ცხადია, ემთხვევა:
(უწყვეტობის No2 პირობა დაკმაყოფილებულია).

მაგრამ ფუნქცია არ არის განსაზღვრული წერტილში, შესაბამისად, დარღვეულია უწყვეტობის No1 პირობა და ფუნქცია განიცდის წყვეტას ამ ეტაპზე.

ამ ტიპის შესვენება (არსებულთან ზოგადი ლიმიტი) უწოდებენ შესაკეთებელი უფსკრული. რატომ მოსახსნელი? რადგან ფუნქციას შეუძლია ხელახლა განსაზღვრაგატეხვის წერტილში:

უცნაურად გამოიყურება? Შესაძლოა. მაგრამ ასეთი ფუნქციის აღნიშვნა არაფერს ეწინააღმდეგება! ახლა უფსკრული დაიხურა და ყველა ბედნიერია:

მოდით შევასრულოთ ოფიციალური შემოწმება:

2) - არსებობს ზოგადი ლიმიტი;
3)

ამრიგად, სამივე პირობა დაკმაყოფილებულია და ფუნქცია არის უწყვეტი წერტილში ფუნქციის უწყვეტობის განსაზღვრით.

თუმცა, მატანის მოძულეებს შეუძლიათ, მაგალითად, ფუნქცია ცუდად განსაზღვრონ :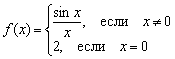

საინტერესოა, რომ პირველი ორი უწყვეტობის პირობა დაკმაყოფილებულია აქ:
1) – ფუნქცია განისაზღვრება მოცემულ წერტილში;
2) - არსებობს ზოგადი ზღვარი.

მაგრამ მესამე საზღვარი არ არის გავლილი: , ანუ ფუნქციის ზღვარი წერტილში არ უდრისმოცემული ფუნქციის მნიშვნელობა მოცემულ წერტილში.

ამრიგად, ერთ მომენტში ფუნქცია განიცდის შეწყვეტას.

მეორე, უფრო სევდიანი შემთხვევა ჰქვია პირველი სახის რღვევა ნახტომით. და სევდა გამოწვეულია ცალმხრივი საზღვრებით სასრული და განსხვავებული. მაგალითი ნაჩვენებია გაკვეთილის მეორე ნახატში. ასეთი უფსკრული ჩვეულებრივ ხდება ნაწილებად განსაზღვრული ფუნქციები, რომლებიც უკვე აღინიშნა სტატიაში გრაფიკის გარდაქმნების შესახებ.

განვიხილოთ ცალმხრივი ფუნქცია და ჩვენ დავასრულებთ მის ნახატს. როგორ ავაშენოთ გრაფიკი? Ძალიან მარტივი. ნახევარი ინტერვალით ვხატავთ პარაბოლას ფრაგმენტს ( მწვანე ფერი), ინტერვალზე – სწორი ხაზის სეგმენტი (წითელი) და ნახევარინტერვალზე – სწორი ხაზი (ლურჯი).

უფრო მეტიც, უტოლობის გამო, მნიშვნელობა განისაზღვრება კვადრატული ფუნქციისთვის (მწვანე წერტილი), ხოლო უტოლობის გამო, მნიშვნელობა განისაზღვრება ხაზოვანი ფუნქცია(ლურჯი წერტილი):

ყველაზე რთულ შემთხვევაში, თქვენ უნდა მიმართოთ გრაფიკის თითოეული ნაწილის პუნქტ-ქულის აგებას (იხ. პირველი გაკვეთილი ფუნქციების გრაფიკების შესახებ).

ახლა ჩვენ მხოლოდ საკითხი გვაინტერესებს. მოდით შევამოწმოთ იგი უწყვეტობისთვის:

2) გამოვთვალოთ ცალმხრივი ლიმიტები.

მარცხნივ გვაქვს წითელი ხაზის სეგმენტი, ამიტომ მარცხნივ ზღვარი არის:

მარჯვნივ არის ლურჯი სწორი ხაზი და მარჯვენა ზღვარი:

შედეგად მივიღეთ სასრული რიცხვები, და ისინი არ უდრის. ვინაიდან ცალმხრივი ლიმიტები სასრული და განსხვავებული: , მაშინ ჩვენი ფუნქცია მოითმენს პირველი სახის შეწყვეტა ნახტომით.

ლოგიკურია, რომ ხარვეზის აღმოფხვრა შეუძლებელია - ფუნქციის შემდგომი განსაზღვრა და "ერთად დამაგრება" ნამდვილად შეუძლებელია, როგორც წინა მაგალითში.

მეორე სახის შეწყვეტის წერტილები

ჩვეულებრივ, რღვევის ყველა სხვა შემთხვევა ჭკვიანურად კლასიფიცირდება ამ კატეგორიაში. ყველაფერს არ ჩამოვთვლი, რადგან პრაქტიკაში პრობლემების 99%-ში შეგხვდებათ გაუთავებელი უფსკრული- როდესაც მემარცხენეა ან მემარჯვენე და უფრო ხშირად, ორივე ზღვარი უსასრულოა.

და, რა თქმა უნდა, ყველაზე თვალსაჩინო სურათი არის ჰიპერბოლა ნულოვან წერტილში. აქ ორივე ცალმხრივი ზღვარი უსასრულოა: მაშასადამე, ფუნქცია განიცდის მეორე სახის შეწყვეტას წერტილში.

ვცდილობ ჩემი სტატიები შევავსო რაც შეიძლება მრავალფეროვანი შინაარსით, ასე რომ, მოდით გადავხედოთ ფუნქციის გრაფიკს, რომელიც ჯერ არ არის ნანახი:

სტანდარტული სქემის მიხედვით:

1) ფუნქცია არ არის განსაზღვრული ამ ეტაპზე, რადგან მნიშვნელი მიდის ნულზე.

რა თქმა უნდა, დაუყოვნებლივ შეგვიძლია დავასკვნათ, რომ ფუნქცია განიცდის წყვეტას წერტილში, მაგრამ კარგი იქნება, რომ კლასიფიცირდეს შეწყვეტის ბუნება, რაც ხშირად მოითხოვს მდგომარეობას. Ამისთვის:

შეგახსენებთ, რომ ჩაწერაში ვგულისხმობთ უსასრულოდ მცირე უარყოფითი რიცხვი და ჩანაწერის ქვეშ - უსასრულოდ მცირე დადებითი რიცხვი.

ცალმხრივი საზღვრები უსასრულოა, რაც ნიშნავს, რომ ფუნქცია განიცდის მე-2 ტიპის შეწყვეტას წერტილში. y-ღერძი არის ვერტიკალური ასიმპტოტისქემისთვის.

არც ისე იშვიათია ორივე ცალმხრივი საზღვრების არსებობა, მაგრამ მხოლოდ ერთი მათგანია უსასრულო, მაგალითად:

ეს არის ფუნქციის გრაფიკი.

ჩვენ განვიხილავთ პუნქტს უწყვეტობისთვის:

1) ფუნქცია ამ ეტაპზე არ არის განსაზღვრული.

2) გამოვთვალოთ ცალმხრივი ლიმიტები:

ასეთი ცალმხრივი ლიმიტების გამოთვლის მეთოდზე ვისაუბრებთ ლექციის ბოლო ორ მაგალითში, თუმცა ბევრმა მკითხველმა უკვე ნახა და გამოიცნო ყველაფერი.

მარცხენა ზღვარი არის სასრული და ნულის ტოლი (ჩვენ „თვითონ წერტილამდე არ მივდივართ“), მაგრამ მარჯვენა ზღვარი უსასრულოა და გრაფიკის ნარინჯისფერი ტოტი უსასრულოდ უახლოვდება მას. ვერტიკალური ასიმპტოტი, მოცემული განტოლებით(შავი წერტილოვანი ხაზი).

ასე რომ, ფუნქცია ზარალდება მეორე სახის შეწყვეტაწერტილში.

რაც შეეხება 1-ლი ტიპის წყვეტას, ფუნქცია შეიძლება განისაზღვროს თავად შეწყვეტის წერტილში. მაგალითად, ცალი ფუნქციისთვის თავისუფლად დააყენეთ შავი სქელი წერტილი კოორდინატების სათავეში. მარჯვნივ არის ჰიპერბოლის ტოტი, ხოლო მარჯვენა ზღვარი უსასრულოა. ვფიქრობ, თითქმის ყველას აქვს წარმოდგენა იმის შესახებ, თუ როგორ გამოიყურება ეს გრაფიკი.

რასაც ყველა მოუთმენლად ელოდა:

როგორ გამოვიკვლიოთ ფუნქცია უწყვეტობისთვის?

უწყვეტობის ფუნქციის შესწავლა წერტილში ხორციელდება უკვე დადგენილი რუტინული სქემის მიხედვით, რომელიც შედგება უწყვეტობის სამი პირობის შემოწმებისგან:

მაგალითი 1

შეისწავლეთ ფუნქცია

გამოსავალი:

1) მოქმედების ფარგლებში ერთადერთი წერტილია, სადაც ფუნქცია არ არის განსაზღვრული.

2) გამოვთვალოთ ცალმხრივი ლიმიტები:

ცალმხრივი საზღვრები სასრული და თანაბარია.

ამრიგად, იმ მომენტში ფუნქცია განიცდის მოსახსნელ შეწყვეტას.

როგორ გამოიყურება ამ ფუნქციის გრაფიკი?

გამარტივება მინდა და, როგორც ჩანს, ჩვეულებრივი პარაბოლა არის მიღებული. მაგრამთავდაპირველი ფუნქცია არ არის განსაზღვრული წერტილში, ამიტომ საჭიროა შემდეგი პუნქტი:

მოდით გავაკეთოთ ნახატი:

უპასუხე: ფუნქცია უწყვეტია მთელ რიცხვით წრფეზე, გარდა იმ წერტილისა, სადაც ის განიცდის მოსახსნელ წყვეტას.

ფუნქცია შეიძლება შემდგომ განისაზღვროს კარგი ან არც ისე კარგი გზით, მაგრამ პირობის მიხედვით ეს არ არის საჭირო.

თქვენ ამბობთ, რომ ეს შორეული მაგალითია? Არაფერს. ეს პრაქტიკაში ათჯერ მოხდა. საიტის თითქმის ყველა დავალება მოდის რეალური დამოუკიდებელი სამუშაოდან და ტესტებიდან.

მოვიშოროთ ჩვენი საყვარელი მოდულები:

მაგალითი 2

შეისწავლეთ ფუნქცია უწყვეტობისთვის. განსაზღვრეთ ფუნქციის უწყვეტობის ბუნება, თუ ისინი არსებობს. შეასრულეთ ნახაზი.

გამოსავალი: რატომღაც სტუდენტებს ეშინიათ და არ მოსწონთ ფუნქციები მოდულით, თუმცა მათში არაფერია რთული. ასეთ რამეებს გაკვეთილზე უკვე ცოტა შევეხეთ. გრაფიკების გეომეტრიული გარდაქმნები. ვინაიდან მოდული არანეგატიურია, ის გაფართოვდა შემდეგნაირად: , სადაც "ალფა" არის რაღაც გამოთქმა. ამ შემთხვევაში და ჩვენი ფუნქცია ნაწილ-ნაწილ უნდა დაიწეროს:

მაგრამ ორივე ნაწილის წილადები უნდა შემცირდეს . შემცირება, როგორც წინა მაგალითში, არ მოხდება შედეგების გარეშე. თავდაპირველი ფუნქცია არ არის განსაზღვრული წერტილში, რადგან მნიშვნელი მიდის ნულზე. ამიტომ სისტემამ დამატებით უნდა მიუთითოს პირობა და პირველი უტოლობა მკაცრი გახადოს:

ახლა ძალიან სასარგებლო გადაწყვეტილების ტექნიკის შესახებ: პროექტზე დავალების დასრულებამდე მიზანშეწონილია ნახაზის გაკეთება (მიუხედავად იმისა, ამას მოითხოვს პირობები თუ არა). ეს დაგეხმარებათ, პირველ რიგში, დაუყოვნებლივ დაინახოთ უწყვეტობის წერტილები და შეწყვეტის წერტილები და, მეორეც, ის 100%-ით დაგიცავთ შეცდომებისგან ცალმხრივი საზღვრების პოვნისას.

მოდით დავხატოთ. ჩვენი გამოთვლების შესაბამისად, წერტილიდან მარცხნივ აუცილებელია პარაბოლის ფრაგმენტის დახატვა (ლურჯი ფერი), ხოლო მარჯვნივ - პარაბოლის ცალი (წითელი ფერი), ხოლო ფუნქცია არ არის განსაზღვრული თავად მიუთითეთ:

თუ ეჭვი გეპარებათ, აიღეთ რამდენიმე x მნიშვნელობა და შეაერთეთ ისინი ფუნქციაში (გახსოვდეთ, რომ მოდული ანადგურებს შესაძლო მინუს ნიშანს) და შეამოწმეთ გრაფიკი.

მოდით განვიხილოთ ფუნქცია უწყვეტობისთვის ანალიტიკურად:

1) ფუნქცია არ არის განსაზღვრული წერტილში, ამიტომ დაუყოვნებლივ შეგვიძლია ვთქვათ, რომ ის არ არის უწყვეტი მასში.

2) დავადგინოთ შეწყვეტის ბუნება, რომ გავაკეთოთ, გამოვთვალოთ ცალმხრივი ლიმიტები:

ცალმხრივი საზღვრები სასრული და განსხვავებულია, რაც ნიშნავს, რომ ფუნქცია განიცდის 1-ლი სახის შეწყვეტას წერტილში ნახტომით. კიდევ ერთხელ გაითვალისწინეთ, რომ ლიმიტების პოვნისას არ აქვს მნიშვნელობა განსაზღვრულია თუ არა ფუნქცია შესვენების წერტილში.

ახლა რჩება მხოლოდ ნახატის გადატანა მონახაზიდან (ის გაკეთდა თითქოს კვლევის დახმარებით ;-)) და დაასრულეთ დავალება:

უპასუხე: ფუნქცია უწყვეტია მთელ რიცხვით წრფეზე, გარდა იმ წერტილისა, სადაც ის განიცდის პირველი სახის წყვეტას ნახტომით.

ზოგჯერ ისინი საჭიროებენ უწყვეტი ნახტომის დამატებით მითითებას. იგი გამოითვლება უბრალოდ - მარჯვენა ზღვრიდან უნდა გამოკლოთ მარცხენა ლიმიტი: , ანუ შესვენების დროს ჩვენი ფუნქცია 2 ერთეულით ქვემოთ გადახტა (როგორც მინუს ნიშანი გვეუბნება).

მაგალითი 3

შეისწავლეთ ფუნქცია უწყვეტობისთვის. განსაზღვრეთ ფუნქციის უწყვეტობის ბუნება, თუ ისინი არსებობს. გააკეთე ნახატი.

ეს არის მაგალითი დამოუკიდებელი გადაწყვეტილება, ხსნარის ნიმუში გაკვეთილის ბოლოს.

მოდით გადავიდეთ ამოცანის ყველაზე პოპულარულ და გავრცელებულ ვერსიაზე, როდესაც ფუნქცია შედგება სამი ნაწილისგან:

მაგალითი 4

შეისწავლეთ ფუნქცია უწყვეტობისთვის და დახაზეთ ფუნქციის გრაფიკი .

გამოსავალი: აშკარაა, რომ ფუნქციის სამივე ნაწილი უწყვეტია შესაბამის ინტერვალებზე, ამიტომ რჩება მხოლოდ ნაწილებს შორის „შეერთების“ ორი წერტილის შემოწმება. პირველ რიგში, მოდით გავაკეთოთ ნახაზის პროექტი, სტატიის პირველ ნაწილში საკმარისად დეტალურად გამოვთქვი კომენტარი მშენებლობის ტექნიკაზე. ერთადერთი ის არის, რომ ყურადღებით უნდა მივყვეთ ჩვენს სინგულარულ წერტილებს: უტოლობის გამო, მნიშვნელობა მიეკუთვნება სწორ ხაზს (მწვანე წერტილი), ხოლო უტოლობის გამო, მნიშვნელობა ეკუთვნის პარაბოლას (წითელი წერტილი):

ისე, პრინციპში, ყველაფერი ნათელია =) რჩება მხოლოდ გადაწყვეტილების გაფორმება. თითოეული ორი „შეერთების“ წერტილისთვის ჩვენ სტანდარტულად ვამოწმებთ 3 უწყვეტობის პირობას:

ᲛᲔ)ჩვენ განვიხილავთ პუნქტს უწყვეტობისთვის

ცალმხრივი საზღვრები სასრული და განსხვავებულია, რაც ნიშნავს, რომ ფუნქცია განიცდის 1-ლი ტიპის შეწყვეტას წერტილში ნახტომით.

მოდით გამოვთვალოთ უწყვეტობის ნახტომი, როგორც განსხვავება მარჯვენა და მარცხენა ზღვრებს შორის:
ანუ, გრაფიკმა ერთი ერთეული აიწია.

II)ჩვენ განვიხილავთ პუნქტს უწყვეტობისთვის

1) – ფუნქცია განსაზღვრულია მოცემულ წერტილში.

2) იპოვეთ ცალმხრივი საზღვრები:

- ცალმხრივი საზღვრები სასრული და თანაბარია, რაც ნიშნავს, რომ არსებობს ზოგადი ზღვარი.

3) – ფუნქციის ზღვარი წერტილში უდრის ამ ფუნქციის მნიშვნელობას მოცემულ წერტილში.

ფინალურ ეტაპზე ნახატს გადავიტანთ საბოლოო ვერსიაზე, რის შემდეგაც ვათავსებთ საბოლოო აკორდს:

უპასუხე: ფუნქცია უწყვეტია მთელ რიცხვთა წრფეზე, გარდა იმ წერტილისა, სადაც ის განიცდის პირველი სახის წყვეტას ნახტომით.

მაგალითი 5

შეისწავლეთ ფუნქცია უწყვეტობისთვის და შექმენით მისი გრაფიკი .

ეს არის მაგალითი დამოუკიდებელი გადაწყვეტისთვის, მოკლე ამოხსნისა და პრობლემის სავარაუდო ნიმუში გაკვეთილის ბოლოს.

შეიძლება გქონდეთ შთაბეჭდილება, რომ ერთ მომენტში ფუნქცია უნდა იყოს უწყვეტი, ხოლო მეორეში უნდა იყოს შეწყვეტა. პრაქტიკაში, ეს ყოველთვის ასე არ არის. შეეცადეთ არ უგულებელყოთ დარჩენილი მაგალითები - იქნება რამდენიმე საინტერესო და მნიშვნელოვანი თვისება:

მაგალითი 6

მოცემული ფუნქცია . გამოიკვლიეთ ფუნქცია წერტილებში უწყვეტობისთვის. შექმენით გრაფიკი.

გამოსავალი: და ისევ დაუყოვნებლივ შეასრულეთ ნახატი ნახატზე:

ამ გრაფიკის თავისებურება ის არის, რომ ცალი ფუნქცია მოცემულია აბსცისის ღერძის განტოლებით. აქ ეს უბანი დახატულია მწვანეში, მაგრამ რვეულში ის ჩვეულებრივ ხაზგასმულია თამამად მარტივი ფანქრით. და, რა თქმა უნდა, არ დაივიწყოთ ჩვენი ვერძები: მნიშვნელობა ეკუთვნის ტანგენტის ტოტს (წითელი წერტილი), ხოლო მნიშვნელობა ეკუთვნის სწორ ხაზს.

ნახაზიდან ყველაფერი ნათელია - ფუნქცია უწყვეტია მთელი რიცხვითი ხაზის გასწვრივ, რჩება მხოლოდ გადაწყვეტის ფორმალიზება, რომელიც სრულ ავტომატიზაციამდე მიდის სიტყვასიტყვით 3-4 მსგავსი მაგალითის შემდეგ:

ᲛᲔ)ჩვენ განვიხილავთ პუნქტს უწყვეტობისთვის

1) – ფუნქცია განისაზღვრება მოცემულ წერტილში.

2) გამოვთვალოთ ცალმხრივი ლიმიტები:

, რაც ნიშნავს, რომ არსებობს ზოგადი ლიმიტი.

ყოველი შემთხვევისთვის შეგახსენებთ ტრივიალურ ფაქტს: მუდმივის ზღვარი უდრის თავად მუდმივას. ამ შემთხვევაში ნულის ზღვარი უდრის თავად ნულს (მარცხენა ლიმიტი).

ამრიგად, ფუნქცია უწყვეტია წერტილში ფუნქციის უწყვეტობის განსაზღვრით წერტილში.

II)ჩვენ განვიხილავთ პუნქტს უწყვეტობისთვის

1) – ფუნქცია განისაზღვრება მოცემულ წერტილში.

2) იპოვეთ ცალმხრივი საზღვრები:

და აქ - ერთის ზღვარი უდრის თავად ერთეულს.

- არსებობს ზოგადი ზღვარი.

ჩვეულებისამებრ, კვლევის შემდეგ გადავიტანთ ჩვენს ნახატს საბოლოო ვერსიაზე.

უპასუხე: ფუნქცია უწყვეტია წერტილებში.

გთხოვთ გაითვალისწინოთ, რომ იმ პირობით, რომ ჩვენ არაფერი გვკითხეს მთელი ფუნქციის უწყვეტობის შესწავლის შესახებ და ითვლება კარგ მათემატიკური ფორმად ჩამოყალიბება ზუსტი და ნათელიპასუხი დასმულ კითხვაზე. სხვათა შორის, თუ პირობები არ მოითხოვს გრაფიკის შექმნას, მაშინ თქვენ გაქვთ სრული უფლება არ ააწყოთ იგი (თუმცა მოგვიანებით მასწავლებელს შეუძლია ამის გაკეთება გაიძულებთ).

პატარა მათემატიკური „ენის ტრიალი“ საკუთარი თავის გადასაჭრელად:

მაგალითი 7

მოცემული ფუნქცია 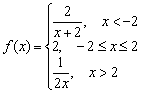. გამოიკვლიეთ ფუნქცია წერტილებში უწყვეტობისთვის. წყვეტის წერტილების კლასიფიკაცია, ასეთის არსებობის შემთხვევაში. შეასრულეთ ნახაზი.

სცადეთ ყველა „სიტყვის“ სწორად „გამოთქმა“ =) და უფრო ზუსტად დახაზეთ გრაფიკი, სიზუსტე, ყველგან ზედმეტი არ იქნება;-)

როგორც გახსოვთ, მე გირჩევდი ნახატის დაუყონებლივ დასრულებას მონახაზის სახით, მაგრამ დროდადრო ხვდები მაგალითებს, სადაც მაშინვე ვერ ხვდები, როგორ გამოიყურება გრაფიკი. ამიტომ, ზოგიერთ შემთხვევაში, ხელსაყრელია ჯერ ცალმხრივი საზღვრების პოვნა და მხოლოდ ამის შემდეგ, კვლევის საფუძველზე, ტოტების გამოსახვა. ბოლო ორ მაგალითში ჩვენ ასევე ვისწავლით რამდენიმე ცალმხრივი ლიმიტების გამოთვლის ტექნიკას:

მაგალითი 8

შეისწავლეთ ფუნქცია უწყვეტობისთვის და შექმენით მისი სქემატური გრაფიკი.

გამოსავალი: ცუდი წერტილები აშკარაა: (ამცირებს მაჩვენებლის მნიშვნელს ნულამდე) და (ამცირებს მთელი წილადის მნიშვნელს ნულამდე). გაურკვეველია, როგორ გამოიყურება ამ ფუნქციის გრაფიკი, რაც იმას ნიშნავს, რომ ჯობია ჯერ ჩაატაროთ კვლევა.

ტოპოლოგია– მათემატიკის დარგი, რომელიც სწავლობს ფუნქციების საზღვრებსა და უწყვეტობას. ალგებრასთან ერთად ტოპოლოგია წარმოადგენს მათემატიკის ზოგად საფუძველს.

ტოპოლოგიური სივრცე ან ფიგურა -ჩვენი ერთგვაროვანი ევკლიდური სივრცის ქვესიმრავლე, რომლის წერტილებს შორის მოცემულია გარკვეული სიახლოვის მიმართება. აქ ფიგურები განიხილება არა როგორც ხისტი სხეულები, არამედ როგორც საგნები, რომლებიც დამზადებულია თითქოს ძალიან ელასტიური რეზინისგან, რაც იძლევა უწყვეტ დეფორმაციას, რაც ინარჩუნებს მათ ხარისხობრივ თვისებებს.

ფიგურების ერთი-ერთზე უწყვეტი გამოსახვა ეწოდება ჰომეომორფიზმი. სხვა სიტყვებით რომ ვთქვათ, ფიგურები ჰომეომორფულითუ ერთი შეიძლება გადავიდეს მეორეზე უწყვეტი დეფორმაციით.

მაგალითები. შემდეგი ფიგურები ჰომეომორფულია (სხვადასხვა ჯგუფის ფიგურები ჰომეომორფული არ არის), ნაჩვენებია ნახ. 2.

1. სეგმენტი და მრუდი თვითგადაკვეთის გარეშე.

2. წრე, კვადრატის შიგნით, ლენტი.

3. სფერო, კუბის ზედაპირი და ტეტრაედონი.

4. წრე, ელიფსი და კვანძოვანი წრე.

5. რგოლი სიბრტყეზე (წრე ნახვრეტით), რგოლი სივრცეში, ორჯერ დაგრეხილი რგოლი, ცილინდრის გვერდითი ზედაპირი.

6. მობიუსის ზოლი, ე.ი. ერთხელ გრეხილი ბეჭედი და სამჯერ დაგრეხილი ბეჭედი.

7. ტორუსის (დონატის) ზედაპირი, სახელურიანი სფერო და კვანძოვანი ტორსი.

8. სფერო ორი სახელურით და პრეცელი ორი ნახვრეტით.

IN მათემატიკური ანალიზიფუნქციები შესწავლილია ლიმიტების მეთოდით. ცვლადი და ლიმიტი ძირითადი ცნებებია.

სხვადასხვა ფენომენში, ზოგიერთი სიდიდე ინარჩუნებს რიცხობრივ მნიშვნელობას, ზოგი იცვლება. ცვლადის ყველა რიცხვითი მნიშვნელობის სიმრავლე ეწოდება ამ ცვლადის ცვლილების დიაპაზონი.

ცვლადის ქცევის სხვადასხვა გზებიდან ყველაზე მნიშვნელოვანია ის, რომლითაც ცვლადი მიდრეკილია გარკვეულ ზღვარზე.

მუდმივი რიცხვი ადაურეკა ცვლადი ლიმიტი, თუ შორის სხვაობის აბსოლუტური მნიშვნელობა xდა ა() ხდება ცვლადის მნიშვნელობის შეცვლის პროცესში xსურვილისამებრ პატარა:

რას ნიშნავს "რაც გინდა პატარა"? ცვლადი მნიშვნელობა Xმიდრეკილია ზღვრამდე ა, თუ რაიმე თვითნებურად მცირე (თვითნებურად მცირე) რიცხვისთვის არის ასეთი მომენტი ცვლადის ცვლილებაში X, საიდანაც იწყება უთანასწორობა .

ლიმიტის განსაზღვრას აქვს მარტივი გეომეტრიული მნიშვნელობა: უტოლობა ნიშნავს რომ Xარის წერტილის მიმდებარედ ა, იმათ. ინტერვალში .

ამრიგად, ლიმიტის განმარტება შეიძლება იყოს მოცემული გეომეტრიული ფორმა:

ნომერი აარის ცვლადის ზღვარი X, თუ რომელიმე თვითნებურად მცირე (თვითნებურად მცირე) - რიცხვის სამეზობლო ათქვენ შეგიძლიათ მიუთითოთ ასეთი მომენტი ცვლადის შეცვლაში X, საიდანაც მისი ყველა მნიშვნელობა ხვდება წერტილის მითითებულ სამეზობლოში ა.

კომენტარი. ცვლადი მნიშვნელობა Xშეუძლია მიუახლოვდეს მის ზღვარს სხვადასხვა გზით: დარჩეს ამ ზღვარზე ნაკლები (მარცხნივ), მეტი (მარჯვნივ), მერყეობდეს ლიმიტის მნიშვნელობის გარშემო.

თანმიმდევრობის ლიმიტი

ფუნქციაკანონს (წესს) უწოდებენ, რომლის მიხედვითაც ყოველი ელემენტი xგარკვეული ნაკრები Xშეესაბამება ერთ ელემენტს წკომპლექტი ი.

ფუნქცია შეიძლება განისაზღვროს ყველა ნატურალური რიცხვის სიმრავლეზე: . ეს ფუნქცია ე.წ ბუნებრივი არგუმენტის ფუნქციაან რიცხვითი თანმიმდევრობა.

ვინაიდან მიმდევრობა, ისევე როგორც ნებისმიერი უსასრულო სიმრავლე, არ შეიძლება განისაზღვროს ჩამოთვლით, იგი მითითებულია საერთო ტერმინით: , სადაც არის მიმდევრობის ზოგადი ტერმინი.

დისკრეტული ცვლადი არის მიმდევრობის საერთო ტერმინი.

თანმიმდევრულობისთვის, სიტყვები "დაწყებული რაღაც მომენტიდან" ნიშნავს სიტყვებს "დაწყებული რაღაც რიცხვიდან".

ნომერი ათანმიმდევრობის ლიმიტს უწოდებენ , თუ რომელიმე თვითნებურად მცირე (თვითნებურად მცირე) რიცხვისთვის არის ასეთი რიცხვი ნ, რომელიც რიცხვით მიმდევრობის ყველა წევრისთვის ნ>ნუთანასწორობა მოქმედებს .

ან ზე .

გეომეტრიულად, მიმდევრობის ზღვრის განსაზღვრა ნიშნავს შემდეგს: ნებისმიერი თვითნებურად მცირე (თვითნებურად მცირე) - რიცხვის სამეზობლო. აარის ისეთი რიცხვი, რომ მიმდევრობის ყველა ტერმინი მეტია ნ, ნომრები, მოხვდება ამ სიახლოვეს. მიმდევრობის საწყისი ტერმინების მხოლოდ სასრული რაოდენობა ჩნდება მიმდებარედ. ბუნებრივი რიცხვი ნდამოკიდებულია : .