ააგეთ ფუნქციის გრაფიკი მოდულის მაგალითებით. ხაზოვანი ფუნქციის გრაფიკები მოდულებით. მარჯვენა მხარის ცვლადის შემთხვევა

ერდნიგორიაევა მარინა

ეს ნაშრომი მე-8 კლასში არჩევით თემის შესწავლის შედეგია. აქ ნაჩვენებია გრაფიკების გეომეტრიული გარდაქმნები და მათი გამოყენება მოდულებით გრაფიკების აგებაში. წარმოდგენილია მოდულის კონცეფცია და მისი თვისებები. ნაჩვენებია, თუ როგორ ავაშენოთ გრაფიკები მოდულებით სხვადასხვა გზით: გარდაქმნების გამოყენებით და მოდულის კონცეფციაზე დაყრდნობით.პროექტის თემა ერთ-ერთი ყველაზე რთულია მათემატიკის კურსში, ეხება არჩევით საგანში განხილულ საკითხებს და არის სწავლობდა მოწინავე მათემატიკის კლასებში. თუმცა, ასეთი დავალებები მოცემულია GIA-ს მეორე ნაწილში, ერთიან სახელმწიფო გამოცდაში. ეს ნამუშევარი დაგეხმარებათ გაიგოთ, თუ როგორ უნდა ააგოთ გრაფიკები არა მხოლოდ წრფივი, არამედ სხვა ფუნქციების მოდულებით (კვადრატული, უკუპროპორციული და ა.შ.) ნაშრომი დაგეხმარებათ მოემზადოთ სახელმწიფო გამოცდისთვის და ერთიანი სახელმწიფო გამოცდისთვის.

ჩამოტვირთვა:

გადახედვა:

პრეზენტაციის გადახედვის გამოსაყენებლად შექმენით Google ანგარიში და შედით მასში: https://accounts.google.com

სლაიდის წარწერები:

წრფივი ფუნქციის გრაფიკები მოდულებით ნამუშევარი ერდნიგორიაევა მარინა, MCOU "Kamyshovskaya OOSH" მე -8 კლასის მოსწავლე ხელმძღვანელი გორიაევა ზოია ერდნიგორიაევნა, მათემატიკის მასწავლებელი MCOU "Kamyshovskaya OOSH" გვ. კამიშევო, 2013 წ

პროექტის მიზანი: პასუხის გაცემა კითხვაზე, თუ როგორ ავაშენოთ ხაზოვანი ფუნქციების გრაფიკები მოდულებით. პროექტის მიზნები: ამ საკითხზე ლიტერატურის შესწავლა. გრაფიკების გეომეტრიული გარდაქმნების შესწავლა და მათი გამოყენება მოდულებით გრაფიკების აგებაში. შეისწავლეთ მოდულის კონცეფცია და მისი თვისებები. ისწავლეთ გრაფიკების აგება მოდულებით სხვადასხვა გზით.

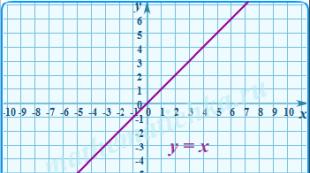
პირდაპირი პროპორციულობა პირდაპირი პროპორციულობა არის ფუნქცია, რომელიც შეიძლება განისაზღვროს y=kx ფორმის ფორმულით, სადაც x დამოუკიდებელი ცვლადია, k არის არანულოვანი რიცხვი.

დავხატოთ ფუნქცია y = x x 0 2 y 0 2

გრაფიკების გეომეტრიული ტრანსფორმაცია წესი No1 y = f (x) + k ფუნქციის გრაფიკი - წრფივი ფუნქცია - მიიღება y = f (x) ფუნქციის გრაფიკის პარალელური გადაცემით + k ერთეულით O-ზე. y ღერძი k> 0-ისთვის ან |- k| ერთეული O y ღერძის ქვემოთ k-ზე

ავაშენოთ გრაფიკები y=x+3 y=x-2

წესი No2 y=kf(x) ფუნქციის გრაფიკი მიიღება y = f (x) ფუნქციის გრაფიკის გაჭიმვით O y ღერძის გასწვრივ a>1-ზე და შეკუმშვით O y ღერძზე a. ჯერ 0Slide 9-ზე

ავაშენოთ გრაფიკი y=x y= 2 x

წესი No3 y = - f (x) ფუნქციის გრაფიკი მიიღება O x ღერძის მიმართ y = f (x) გრაფიკის სიმეტრიულად ჩვენებით.

წესი No4 y = f (- x) ფუნქციის გრაფიკი მიიღება y = f (x) ფუნქციის გრაფიკის სიმეტრიულად ჩვენებით O y ღერძის მიმართ.

წესი No5 y=f(x+c) ფუნქციის გრაფიკი მიიღება y=f(x) ფუნქციის გრაფიკის პარალელური გადატანით O x ღერძის გასწვრივ მარჯვნივ, თუ c 0.

მოდით ავაშენოთ გრაფიკები y=f(x) y=f(x+2)

მოდულის განმარტება არაუარყოფითი a რიცხვის მოდული უდრის თავად a რიცხვს; უარყოფითი რიცხვის a მოდული უდრის მის საპირისპირო პოზიტიურ რიცხვს -a. ან, |a|=a, თუ a ≥0 |a|=-a, თუ a

აგებულია ხაზოვანი ფუნქციების გრაფიკები მოდულებით: გეომეტრიული გარდაქმნების გამოყენებით მოდულის განმარტების გაფართოებით.

წესი No6 y=|f(x)| ფუნქციის გრაფიკი მიიღება შემდეგნაირად: შენარჩუნებულია გრაფიკის y=f(x) ნაწილი, რომელიც მდებარეობს O x ღერძის ზემოთ; O x ღერძის ქვეშ მდებარე ნაწილი ნაჩვენებია სიმეტრიულად O x ღერძის მიმართ.

დახატეთ ფუნქცია y=-2| x-3|+4 აგება y 1=| x | ჩვენ ვაშენებთ y₂= |x - 3 | → პარალელური გადათარგმნა +3 ერთეულით Ox ღერძის გასწვრივ (გადაადგილება მარჯვნივ) ვაშენებთ y ₃ =+2|x-3| → გაჭიმვა O ღერძის გასწვრივ y 2-ჯერ = 2 y₂ ვაშენებთ y ₄ =-2|x-3| → სიმეტრია x ღერძის მიმართ = - y₃ ჩვენ ვაშენებთ y₅ =-2|x-3|+4 → პარალელური გადაყვანა +4 ერთეულით O ღერძის გასწვრივ y (ზედა ცვლა) = y ₄ +4

y ფუნქციის გრაფიკი =-2|x-3|+4

ფუნქციის გრაფიკი y= 3|x|+2 y₁=|x| y₂=3|x|= 3 y₁ → გაჭიმვა 3-ჯერ y₃=3|x| +2= y₄+2 → 2 ერთეულით ზევით ცვლა

წესი No7 y=f(| x |) ფუნქციის გრაფიკი მიღებულია y=f(x) ფუნქციის გრაფიკიდან შემდეგნაირად: x > 0-ისთვის შენარჩუნებულია ფუნქციის გრაფიკი და იგივე. გრაფიკის ნაწილი სიმეტრიულად არის ნაჩვენები O y ღერძის მიმართ

y = || ფუნქცია გრაფიკის მიხედვით x-1 | -2 |

Y₁= |x| y₂=|x-1| y₃= y2-2 y₄= |y₃| Y=||x-1|-2|

y=│f(│x│)│ ფუნქციის გრაფიკის აგების ალგორითმი y=f(│x│) ფუნქციის გრაფიკის აგება. შემდეგ უცვლელად დატოვეთ აგებული გრაფიკის ყველა ნაწილი, რომელიც მდებარეობს x ღერძის ზემოთ. x ღერძის ქვემოთ მდებარე ნაწილები ნაჩვენებია სიმეტრიულად ამ ღერძის მიმართ.

Y=|2|x|-3| კონსტრუქცია: ა) y=2x-3 x>0-სთვის, ბ) y=-2x-3 x სლაიდ 26-ისთვის

წესი #8 დამოკიდებულების გრაფიკი | y|=f(x) მიიღება y=f(x) ფუნქციის გრაფიკიდან, თუ დაცულია ყველა წერტილი, რომლისთვისაც f(x) > 0 და ისინი ასევე სიმეტრიულად არიან გადატანილი აბსცისის ღერძის მიმართ.

ააგეთ წერტილთა სიმრავლე სიბრტყეზე, რომლის დეკარტიული კოორდინატები x და y აკმაყოფილებს განტოლებას |y|=||x-1|-1|.

| y|=||x-1| -1| ვაშენებთ ორ გრაფიკს 1) y=||x-1|-1| და 2) y =-|| x-1|-1| y₁=|x| y₂=| x-1 | → Ox ღერძის გასწვრივ მარჯვნივ გადაწევა 1 ერთეულით y₃ = | x -1 |- 1= → გადაწევა 1 ერთეულით y ₄ = || x-1|- 1| → გრაფიკის წერტილების სიმეტრია, რომლებისთვისაც y₃ 0 O x-ის მიმართ

განტოლების გრაფიკი |y|=||x-1|-1| ვიღებთ შემდეგნაირად: 1) ააგეთ y=f(x) ფუნქციის გრაფიკი და უცვლელად დავტოვოთ მისი ის ნაწილი, სადაც y≥0 2) Ox ღერძის მიმართ სიმეტრიის გამოყენებით, ააგეთ y-ის შესაბამისი გრაფიკის მეორე ნაწილი.

y =|x | − | 2 − x | . გამოსავალი. აქ მოდულის ნიშანი ჩნდება ორი განსხვავებული ტერმინით და უნდა მოიხსნას. 1) იპოვეთ სუბმოდულური გამონათქვამების ფესვები: x=0, 2-x=0, x=2 2) დააყენეთ ნიშნები ინტერვალებზე:

ფუნქციის გრაფიკი

დასკვნა პროექტის თემა ერთ-ერთი რთულია მათემატიკის კურსში, ის ეხება არჩევით საგანში განხილულ საკითხებს და ისწავლება მათემატიკის კურსის სიღრმისეული შესწავლის კლასებში. მიუხედავად ამისა, ასეთი დავალებები მოცემულია GIA-ს მეორე ნაწილში. ეს ნამუშევარი დაგეხმარებათ გაიგოთ, თუ როგორ უნდა ააწყოთ გრაფიკები არა მხოლოდ წრფივი ფუნქციების, არამედ სხვა ფუნქციების მოდულებით (კვადრატული, უკუპროპორციული და ა.შ.). ნამუშევარი ხელს შეუწყობს სახელმწიფო გამოცდისა და ერთიანი სახელმწიფო გამოცდისთვის მომზადებას და საშუალებას მოგცემთ მიიღოთ მაღალი ქულები მათემატიკაში.

ლიტერატურა Vilenkin N.Ya. , ჟოხოვი V.I.. მათემატიკა“. სახელმძღვანელო მოსკოვი მე-6 კლასი. გამომცემლობა "Mnemosyne", 2010 Vilenkin N.Ya., Vilenkin L.N., Survillo G.S. და სხვა.ალგებრა. მე-8 კლასი: საგანმანათლებლო. სახელმძღვანელო სტუდენტებისა და კლასებისთვის მათემატიკის გაღრმავებული შესწავლით. - მოსკოვი. განმანათლებლობა, 2009 გაიდუკოვი ი.ი. "აბსოლუტური ღირებულება." მოსკოვი. განმანათლებლობა, 1968. გურსკი ი.პ. "ფუნქციები და გრაფიკა." მოსკოვი. განმანათლებლობა, 1968. იაშჩინა ნ.ვ. მოდულების შემცველი გრაფიკების აგების ტექნიკა. ჟურნალი „მათემატიკა სკოლაში“, No3, 1994წ საბავშვო ენციკლოპედია. მოსკოვი. "პედაგოგია", 1990. Dynkin E.B., Molchanova S.A. მათემატიკის ამოცანები. მ., „მეცნიერება“, 1993. პეტრაკოვი ი.ს. მათემატიკის კლუბები 8-10 კლასებში. მ., „განმანათლებლობა“, 1987 წ. გალიცკი მ.ლ. და სხვა.. ალგებრაში ამოცანების კრებული 8-9 კლასებისთვის: სახელმძღვანელო მოსწავლეებისთვის და მათემატიკის გაღრმავებული შესწავლით კლასებისთვის. - მე-12 გამოცემა. – მ.: განათლება, 2006. – 301გვ. მაკრიჩევი იუ.ნ., მინდიუკ ნ.გ. ალგებრა: დამატებითი თავები მე-9 კლასის სასკოლო სახელმძღვანელოსთვის: სახელმძღვანელო სკოლებისა და კლასების მოსწავლეებისთვის მათემატიკის სიღრმისეული შესწავლით / რედაქტორი გ.ვ. დოროფეევი. – მ.: განათლება, 1997. – 224გვ. Sadykina N. მოდულის ნიშნის შემცველი გრაფიკების და დამოკიდებულებების აგება / მათემატიკა. - No33. – 2004. – გვ.19-21 .. კოსტრიკინა ნ.პ. „გაზრდილი სირთულის პრობლემები ალგებრის კურსში 7-9 კლასებისთვის“... მოსკოვი: განათლება, 2008 წ.

Ტრანსკრიფცია

1 მე-6-11 კლასების მოსწავლეთა საგანმანათლებლო და კვლევითი სამუშაოების რეგიონალური სამეცნიერო და პრაქტიკული კონფერენცია „მათემატიკის გამოყენებითი და ფუნდამენტური საკითხები“ მათემატიკის შესწავლის მეთოდოლოგიური ასპექტები გაბოვა ანგელა იურიევნა მოდულის შემცველი ფუნქციების გრაფიკების აგება, მე-10 კლასი, MOBU „გიმნაზია 3“. ” კუდიმკარი, პიკულევა ნადეჟდა ივანოვნა, მუნიციპალური საგანმანათლებლო დაწესებულების მათემატიკის მასწავლებელი ”გიმნაზია 3”, კუდიმკარ პერმი, 2016 წ.

2 სარჩევი: შესავალი...3 გვერდი I. მთავარი ნაწილი...6 გვერდი 1.1ისტორიული ფონი..6 გვერდი 2.ფუნქციების ძირითადი განმარტებები და თვისებები გვერდი 2.1 კვადრატული ფუნქცია..7 გვერდი 2.2 წრფივი ფუნქცია.. .8 გვ. 2.3 წილად-რაციონალური ფუნქცია 8 გვ 3. გრაფიკების აგების ალგორითმები მოდულით 9 გვ 3.1 მოდულის განსაზღვრა.. 9 გვ 3.2 წრფივი ფუნქციების გრაფიკების აგების ალგორითმი მოდულით...9 გვ 3.3 ფუნქციების გრაფიკების აგება ფორმულაში შემავალი „ჩასმული მოდულები“.10 გვ 3.4 y = a 1 x x 1 + a 2 x x a n x x n + ax + b...13 გვ. 3.5 ალგორითმი კვადრატის გრაფიკების აგების ალგორითმი ფუნქცია მოდულით.14 გვ 3.6 ალგორითმი წილადი რაციონალური ფუნქციის მოდულით გამოსახვა. 15 გვ. 4. კვადრატული ფუნქციის გრაფიკის ცვლილებები აბსოლუტური მნიშვნელობის ნიშნის მდებარეობიდან გამომდინარე..17გვ. II. დასკვნა...26 გვ III. ცნობათა და წყაროების ნუსხა...27 გვ IV. დანართი....28გვ. 2

3 შესავალი ფუნქციათა გრაფიკების აგება ერთ-ერთი ყველაზე საინტერესო თემაა სასკოლო მათემატიკაში. ჩვენი დროის უდიდესი მათემატიკოსი ისრაელ მოისეევიჩ გელფანდი წერდა: „გრაფების აგების პროცესი არის ფორმულებისა და აღწერილობების გეომეტრიულ გამოსახულებებად გადაქცევის გზა. ეს გრაფიკა არის ფორმულების და ფუნქციების დანახვის საშუალება და იმის დანახვა, თუ როგორ იცვლება ეს ფუნქციები. მაგალითად, თუ დაიწერება y =x 2, მაშინვე ხედავთ პარაბოლას; თუ y = x 2-4, ხედავთ პარაბოლას დაბლა ოთხი ერთეულით; თუ y = -(x 2 4), მაშინ ხედავთ წინა პარაბოლას გადაბრუნებულს. ფორმულის დაუყოვნებლივ დანახვის ეს უნარი და მისი გეომეტრიული ინტერპრეტაცია მნიშვნელოვანია არა მხოლოდ მათემატიკის შესასწავლად, არამედ სხვა საგნებისთვისაც. ეს არის უნარი, რომელიც დარჩება შენთან მთელი ცხოვრება, როგორიცაა ველოსიპედის ტარება, აკრეფა ან მანქანის მართვა. მოდულებით განტოლებების ამოხსნის საფუძვლები მიიღეს მე-6-7 კლასებში. ეს კონკრეტული თემა ავირჩიე, რადგან მიმაჩნია, რომ ის უფრო ღრმა და საფუძვლიან კვლევას მოითხოვს. მინდა მივიღო მეტი ცოდნა რიცხვების მოდულის, აბსოლუტური მნიშვნელობის ნიშნის შემცველი გრაფიკების აგების სხვადასხვა ხერხების შესახებ. როდესაც მოდულის ნიშანი შედის ხაზების, პარაბოლების და ჰიპერბოლების „სტანდარტულ“ განტოლებებში, მათი გრაფიკები უჩვეულო და ლამაზიც კი ხდება. იმისათვის, რომ გაიგოთ, თუ როგორ უნდა შექმნათ ასეთი გრაფიკები, თქვენ უნდა დაეუფლოთ ძირითადი ფიგურების აგების ტექნიკას, ასევე მტკიცედ იცოდეთ და გესმოდეთ რიცხვის მოდულის განმარტება. სასკოლო მათემატიკის კურსში მოდულით გრაფიკები საკმარისად სიღრმისეულად არ არის განხილული, რის გამოც მინდოდა ამ თემაზე ცოდნის გაფართოება და საკუთარი კვლევის ჩატარება. მოდულის განმარტების ცოდნის გარეშე, შეუძლებელია აბსოლუტური მნიშვნელობის შემცველი უმარტივესი გრაფიკის აგებაც კი. მოდულის ნიშნით გამოსახულებების შემცველი ფუნქციის გრაფიკების დამახასიათებელი თვისებაა 3

4 არის დახრილობის არსებობა იმ წერტილებში, რომლებზეც მოდულის ნიშნის ქვეშ გამოხატული ნიშანს ცვლის. სამუშაოს მიზანი: მოდულის ნიშნით ცვლადის შემცველი წრფივი, კვადრატული და წილადი რაციონალური ფუნქციების გრაფიკის აგების განხილვა. მიზნები: 1) ლიტერატურის შესწავლა წრფივი, კვადრატული და წილადი რაციონალური ფუნქციების აბსოლუტური მნიშვნელობის თვისებების შესახებ. 2) შეისწავლეთ ცვლილებები ფუნქციის გრაფიკებში აბსოლუტური მნიშვნელობის ნიშნის მდებარეობის მიხედვით. 3) ისწავლეთ განტოლებების გრაფიკი. კვლევის ობიექტი: წრფივი, კვადრატული და წილადი რაციონალური ფუნქციების გრაფიკები. კვლევის საგანი: წრფივი, კვადრატული და წილადი რაციონალური ფუნქციების გრაფიკის ცვლილებები აბსოლუტური მნიშვნელობის ნიშნის მდებარეობის მიხედვით. ჩემი ნაშრომის პრაქტიკული მნიშვნელობა მდგომარეობს იმაში, რომ: 1) ამ თემაზე მიღებული ცოდნის გამოყენება, ასევე მისი გაღრმავება და სხვა ფუნქციებისა და განტოლებების გამოყენება; 2) კვლევის უნარების გამოყენებაში შემდგომ საგანმანათლებლო საქმიანობაში. აქტუალობა: გრაფიკული ამოცანები ტრადიციულად ერთ-ერთი ყველაზე რთული თემაა მათემატიკაში. ჩვენი კურსდამთავრებულები სახელმწიფო გამოცდისა და ერთიანი სახელმწიფო გამოცდის წარმატებით ჩაბარების პრობლემის წინაშე დგანან. საკვლევი პრობლემა: GIA-ს მეორე ნაწილიდან მოდულის ნიშნის შემცველი ფუნქციების გრაფიკების აგება. კვლევის ჰიპოთეზა: GIA-ს მეორე ნაწილში ამოცანების ამოხსნის მეთოდოლოგიის გამოყენება, რომელიც შემუშავებულია მოდულის ნიშნის შემცველი ფუნქციების გრაფიკების აგების ზოგადი მეთოდების საფუძველზე, საშუალებას მისცემს სტუდენტებს გადაჭრას ეს ამოცანები 4

5 შეგნებულად აირჩიე გადაწყვეტის ყველაზე რაციონალური მეთოდი, გამოიყენე გადაწყვეტის სხვადასხვა მეთოდი და უფრო წარმატებულად ჩააბარე სახელმწიფო გამოცდა. ნაშრომში გამოყენებული კვლევის მეთოდები: 1. ამ თემაზე მათემატიკური ლიტერატურისა და ინტერნეტ რესურსების ანალიზი. 2. შესწავლილი მასალის რეპროდუქციული რეპროდუქცია. 3. შემეცნებითი და საძიებო აქტივობები. 4.მონაცემების ანალიზი და შედარება პრობლემების გადაწყვეტის ძიებაში. 5. ჰიპოთეზების გამოთქმა და მათი გადამოწმება. 6. მათემატიკური ფაქტების შედარება და განზოგადება. 7. მიღებული შედეგების ანალიზი. ამ ნაწარმოების დაწერისას გამოყენებული იქნა შემდეგი წყაროები: ინტერნეტ რესურსები, OGE ტესტები, მათემატიკური ლიტერატურა. 5

6 I. ძირითადი ნაწილი 1.1 ისტორიული ფონი. XVII საუკუნის პირველ ნახევარში გაჩნდა იდეა ფუნქციის, როგორც ერთი ცვლადის მეორეზე დამოკიდებულების შესახებ. ამრიგად, ფრანგმა მათემატიკოსებმა პიერ ფერმამ () და რენე დეკარტმა () წარმოიდგინეს ფუნქცია, როგორც წერტილის ორდინატის დამოკიდებულება მრუდზე მის აბსცისაზე. და ინგლისელმა მეცნიერმა ისააკ ნიუტონმა () გააცნობიერა ფუნქცია, როგორც მოძრავი წერტილის კოორდინატი, რომელიც იცვლება დროის მიხედვით. ტერმინი „ფუნქცია“ (ლათინური ფუნქციის შესრულება, შესრულება) პირველად შემოიღო გერმანელმა მათემატიკოსმა გოტფრიდ ლაიბნიცმა(). მან ფუნქცია დააკავშირა გეომეტრიულ სურათთან (ფუნქციის გრაფიკი). შემდგომში შვეიცარიელმა მათემატიკოსმა იოჰან ბერნულიმ() და სანქტ-პეტერბურგის მეცნიერებათა აკადემიის წევრმა, მე-18 საუკუნის ცნობილმა მათემატიკოსმა ლეონარდ ეულერმა(), ეს ფუნქცია ანალიტიკურ გამოხატულებად მიიჩნიეს. ეილერს ასევე აქვს ზოგადი გაგება ფუნქციის, როგორც ერთი ცვლადის მეორეზე დამოკიდებულების შესახებ. სიტყვა "მოდული" მომდინარეობს ლათინური სიტყვიდან "modulus", რაც ნიშნავს "ზომას". ეს არის პოლისემანტიკური სიტყვა (ჰომონიმი), რომელსაც აქვს მრავალი მნიშვნელობა და გამოიყენება არა მხოლოდ მათემატიკაში, არამედ არქიტექტურაში, ფიზიკაში, ტექნოლოგიაში, პროგრამირებაში და სხვა ზუსტ მეცნიერებებში. არქიტექტურაში, ეს არის გაზომვის საწყისი ერთეული, რომელიც დადგენილია მოცემული არქიტექტურული სტრუქტურისთვის და გამოიყენება მისი შემადგენელი ელემენტების მრავალჯერადი შეფარდების გამოსახატავად. ტექნოლოგიაში ეს არის ტერმინი, რომელიც გამოიყენება ტექნოლოგიის სხვადასხვა დარგში, რომელსაც არ აქვს უნივერსალური მნიშვნელობა და ემსახურება სხვადასხვა კოეფიციენტებისა და რაოდენობის აღნიშვნას, მაგალითად, ჩართულობის მოდულს, ელასტიურ მოდულს და ა.შ. 6

7 ნაყარი მოდული (ფიზიკაში) არის ნორმალური სტრესის თანაფარდობა მატერიაში შედარებით დრეკადობასთან. 2. ფუნქციების ძირითადი განმარტებები და თვისებები ფუნქცია ერთ-ერთი ყველაზე მნიშვნელოვანი მათემატიკური ცნებაა. ფუნქცია არის y ცვლადის დამოკიდებულება x ცვლადზე ისე, რომ x ცვლადის თითოეული მნიშვნელობა შეესაბამება y ცვლადის ერთ მნიშვნელობას. ფუნქციის დაზუსტების მეთოდები: 1) ანალიტიკური მეთოდი (ფუნქცია მითითებულია მათემატიკური ფორმულით); 2) ტაბულური მეთოდი (ფუნქცია მითითებულია ცხრილის გამოყენებით); 3) აღწერითი მეთოდი (ფუნქცია მითითებულია სიტყვიერი აღწერით); 4) გრაფიკული მეთოდი (ფუნქცია მითითებულია გრაფიკის გამოყენებით). ფუნქციის გრაფიკი არის კოორდინატთა სიბრტყის ყველა წერტილის ერთობლიობა, რომელთა აბსციები უდრის არგუმენტის მნიშვნელობას, ხოლო ორდინატები ტოლია ფუნქციის შესაბამისი მნიშვნელობების. 2.1 კვადრატული ფუნქცია ფუნქციას, რომელიც განსაზღვრულია ფორმულით y = ax 2 + in + c, სადაც x და y არის ცვლადები, ხოლო პარამეტრები a, b და c არის ნებისმიერი რეალური რიცხვი და a = 0, ეწოდება კვადრატული. y=ax 2 +in+c ფუნქციის გრაფიკი პარაბოლაა; პარაბოლის სიმეტრიის ღერძი y=ax 2 +in+c არის სწორი ხაზი, a>0-სთვის პარაბოლის „ტოტები“ მიმართულია ზემოთ, ამისთვის a<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (ერთი ცვლადის ფუნქციებისთვის). წრფივი ფუნქციების ძირითადი თვისება: ფუნქციის ზრდა პროპორციულია არგუმენტის ზრდისა. ანუ ფუნქცია არის პირდაპირი პროპორციულობის განზოგადება. წრფივი ფუნქციის გრაფიკი არის სწორი ხაზი, საიდანაც მოდის მისი სახელი. ეს ეხება ერთი რეალური ცვლადის რეალურ ფუნქციას. 1) როდესაც სწორი ხაზი ქმნის მახვილ კუთხეს აბსცისის ღერძის დადებითი მიმართულებით. 2) როდესაც სწორი ხაზი ქმნის ბლაგვ კუთხეს x-ღერძის დადებითი მიმართულებით. 3) არის ორდინატთა ღერძთან წრფის გადაკვეთის წერტილის ორდინატიანი მაჩვენებელი. 4) როდესაც სწორი ხაზი გადის საწყისზე. , 2.3 წილად-რაციონალური ფუნქცია არის წილადი, რომლის მრიცხველი და მნიშვნელი მრავალწევრია. მას აქვს ფორმა, სადაც, პოლინომები ცვლადების ნებისმიერ რაოდენობაში. განსაკუთრებული შემთხვევაა ერთი ცვლადის რაციონალური ფუნქციები:, სადაც და არიან პოლინომები. 1) ნებისმიერი გამოხატულება, რომელიც შეიძლება მივიღოთ ცვლადებიდან ოთხი არითმეტიკული მოქმედების გამოყენებით, არის რაციონალური ფუნქცია. 8

9 2) რაციონალური ფუნქციების სიმრავლე დახურულია არითმეტიკული მოქმედებების და შემადგენლობის მოქმედების დროს. 3) ნებისმიერი რაციონალური ფუნქცია შეიძლება წარმოდგენილი იყოს როგორც მარტივი წილადების ჯამი - ეს გამოიყენება ანალიტიკურ ინტეგრაციაში.. , 3. გრაფიკების აგების ალგორითმები მოდულით 3.1 მოდულის განმარტება რეალური რიცხვის a მოდული არის თავად რიცხვი a, თუ ის არაუარყოფითია და a-ს საპირისპირო რიცხვი, თუ a უარყოფითია. a = 3.2 ალგორითმი წრფივი ფუნქციის გრაფიკის ასაგებად მოდულით y = x ფუნქციების გრაფიკების ასაგებად, უნდა იცოდეთ, რომ x დადებითი x გვაქვს x = x. ეს ნიშნავს, რომ არგუმენტის დადებითი მნიშვნელობებისთვის, გრაფიკი y= x ემთხვევა გრაფიკს y=x, ანუ გრაფიკის ეს ნაწილი არის სხივი, რომელიც წარმოიქმნება საწყისიდან 45 გრადუსიანი კუთხით აბსცისის ღერძთან. . x-ზე< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 ასაგებად ვიღებთ ქულებს (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2). ახლა ავაშენოთ გრაფიკი y= x-1. თუ A არის წერტილი გრაფიკზე y= x კოორდინატებით (a; a), მაშინ წერტილი გრაფიკზე y= x-1 Y ორდინატის იგივე მნიშვნელობით იქნება. იყოს წერტილი A1(a+1; a). მეორე გრაფიკის ეს წერტილი შეიძლება მივიღოთ პირველი გრაფიკის A(a; a) წერტილიდან Ox ღერძის მარჯვნივ გადაადგილებით. ეს ნიშნავს, რომ y= x-1 ფუნქციის მთელი გრაფიკი მიღებულია y= x ფუნქციის გრაფიკიდან Ox ღერძის პარალელურად მარჯვნივ 1-ით გადანაცვლებით. ავაშენოთ გრაფიკები: y= x-1 ასაგებად. აიღეთ ქულები (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1). 3.3 ფორმულაში „ბუდებული მოდულების“ შემცველი ფუნქციების გრაფიკების აგება განვიხილოთ კონსტრუქციის ალგორითმი კონკრეტული მაგალითის გამოყენებით ააგეთ ფუნქციის გრაფიკი: 10

11 y=i-2-ix+5ii 1. ფუნქციის გრაფიკის აგება. 2. ქვედა ნახევრად სიბრტყის გრაფიკს ვაჩვენებთ სიმეტრიულად OX ღერძის მიმართ და ვიღებთ ფუნქციის გრაფიკს. თერთმეტი

12 3. ფუნქციის გრაფიკს ვაჩვენებთ ქვემოთ სიმეტრიულად OX ღერძის მიმართ და ვიღებთ ფუნქციის გრაფიკს. 4. ფუნქციის გრაფიკს ვაჩვენებთ ქვემოთ სიმეტრიულად OX ღერძის მიმართ და ვიღებთ 5 ფუნქციის გრაფიკს. ვაჩვენებთ ფუნქციის გრაფიკს OX ღერძის მიმართ და ვიღებთ გრაფიკს. 12

13 6. შედეგად, ფუნქციის გრაფიკი ასე გამოიყურება 3.4. y = a 1 x x 1 + a 2 x x a n x x n + ax + b ფორმის ფუნქციების გრაფიკების აგების ალგორითმი. წინა მაგალითში საკმაოდ მარტივი იყო მოდულის ნიშნების გამოვლენა. თუ მოდულების მეტი ჯამია, მაშინ პრობლემურია სუბმოდულური გამონათქვამების ნიშნების ყველა შესაძლო კომბინაციის განხილვა. როგორ ავაშენოთ ამ შემთხვევაში ფუნქციის გრაფიკი? გაითვალისწინეთ, რომ გრაფიკი არის გატეხილი ხაზი, წერტილებში წვეროებით, რომლებსაც აქვთ აბსცისები -1 და 2. x = -1 და x = 2-ზე, სუბმოდულური გამოსახულებები ნულის ტოლია. პრაქტიკაში ჩვენ მივუახლოვდით ასეთი გრაფიკების აგების წესს: y = a 1 x x 1 + a 2 x x a n x x n + ax + b ფორმის ფუნქციის გრაფიკი არის გატეხილი ხაზი უსასრულო უკიდურესი ბმულებით. ასეთი გატეხილი ხაზის ასაგებად საკმარისია ვიცოდეთ მისი ყველა წვერო (წვეროების აბსციები არის სუბმოდულური გამონათქვამების ნულები) და ერთი საკონტროლო წერტილი მარცხენა და მარჯვენა უსასრულო ბმულებზე. 13

14 პრობლემა. დახატეთ ფუნქცია y = x + x 1 + x + 1 და იპოვეთ მისი უმცირესი მნიშვნელობა. ამოხსნა: 1. სუბმოდულური გამოსახულებების ნულები: 0; -1; პოლიხაზის წვეროები (0; 2); (-13); (1; 3) (ჩვენ ვცვლით სუბმოდულური გამოსახულებების ნულებს განტოლებაში) 3 გამშვები წერტილი მარჯვნივ (2; 6), მარცხნივ (-2; 6). ვაშენებთ გრაფიკს (ნახ. 7), ფუნქციის უმცირესი მნიშვნელობა არის ალგორითმი კვადრატული ფუნქციის გრაფიკის ასაგებად მოდულით ფუნქციის გრაფიკების გარდაქმნის ალგორითმების შედგენა. 1. y= f(x) ფუნქციის გრაფიკის დახატვა. მოდულის განმარტებით, ეს ფუნქცია დაყოფილია ორ ფუნქციად. შესაბამისად, y= f(x) ფუნქციის გრაფიკი შედგება ორი გრაფიკისგან: y= f(x) მარჯვენა ნახევარსიბრტყეში, y= f(-x) მარცხენა ნახევარსიბრტყეში. ამის საფუძველზე შეიძლება ჩამოყალიბდეს წესი (ალგორითმი). y= f(x) ფუნქციის გრაფიკი მიღებულია y= f(x) ფუნქციის გრაფიკიდან შემდეგნაირად: x 0-ზე გრაფიკი შენარჩუნებულია, ხოლო x-ზე.< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. y= f(x) ფუნქციის გრაფიკის ასაგებად ჯერ უნდა ააგოთ y= f(x) ფუნქციის გრაფიკი x> 0-ისთვის, შემდეგ x-ისთვის.< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 ამ გრაფიკის მისაღებად, თქვენ უბრალოდ უნდა გადაიტანოთ ადრე მიღებული გრაფიკი სამი ერთეულით მარჯვნივ. გაითვალისწინეთ, რომ თუ წილადის მნიშვნელი შეიცავდა გამონათქვამს x + 3, მაშინ გრაფიკს გადავიტანთ მარცხნივ: ახლა ყველა ორდინატი უნდა გავამრავლოთ ორზე, რომ მივიღოთ ფუნქციის გრაფიკი, ბოლოს კი დიაგრამა ზევით გადავწიოთ. ორი ერთეული: ბოლო რაც უნდა გავაკეთოთ არის , ეს არის მოცემული ფუნქციის გრაფიკის გამოსახვა, თუ ის მოდულის ნიშნის ქვეშ არის ჩასმული. ამისათვის სიმეტრიულად ზევით ასახავს გრაფიკის მთელ ნაწილს, რომლის ორდინატებიც უარყოფითია (ის ნაწილი, რომელიც მდებარეობს x ღერძის ქვემოთ): სურ. 4 16

17 4. კვადრატული ფუნქციის გრაფიკის ცვლილებები აბსოლუტური მნიშვნელობის ნიშნის მდებარეობის მიხედვით. ააგეთ y = x 2 - x -3 ფუნქციის გრაფიკი 1) ვინაიდან x = x x 0-ზე, საჭირო გრაფიკი ემთხვევა პარაბოლას y = 0,25 x 2 - x - 3. თუ x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. ბ) მაშასადამე ვასრულებ x-ის კონსტრუქციას<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 ნახ. 4 y = f (x) ფუნქციის გრაფიკი ემთხვევა y = f (x) ფუნქციის გრაფიკს არგუმენტის არაუარყოფითი მნიშვნელობების სიმრავლეზე და სიმეტრიულია მის ღერძთან მიმართებაში. OU არგუმენტის უარყოფითი მნიშვნელობების სიმრავლეზე. დადასტურება: თუ x 0, მაშინ f (x) = f (x), ე.ი. არგუმენტის არაუარყოფითი მნიშვნელობების სიმრავლეში, y = f (x) და y = f (x) ფუნქციების გრაფიკები ემთხვევა. ვინაიდან y = f (x) არის ლუწი ფუნქცია, მისი გრაფიკი სიმეტრიულია op-amp-ის მიმართ. ამრიგად, y = f (x) ფუნქციის გრაფიკი შეიძლება მივიღოთ y = f (x) ფუნქციის გრაფიკიდან შემდეგნაირად: 1. ააგეთ y = f (x) ფუნქციის გრაფიკი x>0-ისთვის; 2. x-სთვის<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. x-სთვის<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 თუ x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 და სიმეტრიულად ასახული ნაწილი y = f(x) y-ზე<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, შემდეგ f (x) = f (x), რაც ნიშნავს, რომ ამ ნაწილში ფუნქციის გრაფიკი y = f (x) ემთხვევა თავად ფუნქციის y = f (x) გრაფიკს. თუ f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 სურ.5 დასკვნა: y= f(x) ფუნქციის გრაფიკის ასაგებად 1. ააგეთ y=f(x) ფუნქციის გრაფიკი; 2. იმ ადგილებში, სადაც გრაფიკი მდებარეობს ქვედა ნახევარ სიბრტყეში, ანუ სადაც f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 კვლევითი სამუშაო y = f (x) ფუნქციის გრაფიკების აგებაზე აბსოლუტური მნიშვნელობის განმარტებისა და ადრე განხილული მაგალითების გამოყენებით ავაშენებთ ფუნქციის გრაფიკებს: y = 2 x - 3 y = x 2-5 x y = x 2. -2 და გამოიტანე დასკვნები. y = f (x) ფუნქციის გრაფიკის ასაგებად საჭიროა: 1. ააგოთ y = f (x) ფუნქციის გრაფიკი x>0-სთვის. 2. ააგეთ გრაფიკის მეორე ნაწილი, ანუ ასახეთ აგებული გრაფიკი სიმეტრიულად op-amp-თან მიმართებაში, რადგან ეს ფუნქცია თანაბარია. 3. ქვედა ნახევარსიბრტყეში მდებარე მიღებული გრაფის მონაკვეთები გადააქციეთ ზედა ნახევარსიბრტყეზე სიმეტრიულად OX ღერძზე. ააგეთ y = 2 x - 3 ფუნქციის გრაფიკი (მოდულის განსაზღვრის 1 მეთოდი) 1. ააგეთ y = 2 x - 3, 2 x - 3 > 0, x >1,5 ე.ი. X< -1,5 и х>1.5 ა) y = 2x - 3, x>0-ისთვის ბ) x-სთვის<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 ბ) x-სთვის<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) ვაშენებთ სწორ ხაზს, სიმეტრიულს, რომელიც აგებულია op-amp-ის ღერძის მიმართ. 3) ვაჩვენებ ქვედა ნახევარ სიბრტყეში მდებარე გრაფიკის მონაკვეთებს სიმეტრიულად OX ღერძის მიმართ. ორივე გრაფიკის შედარება, ჩვენ ვხედავთ, რომ ისინი ერთნაირია. 21

22 ამოცანების მაგალითები მაგალითი 1. განვიხილოთ y = x 2 6x +5 ფუნქციის გრაფიკი. ვინაიდან x კვადრატია, x რიცხვის ნიშნის მიუხედავად, კვადრატის შემდეგ ის დადებითი იქნება. აქედან გამომდინარეობს, რომ y = x 2-6x +5 ფუნქციის გრაფიკი იდენტური იქნება y = x 2-6x +5 ფუნქციის გრაფიკისა, ე.ი. ფუნქციის გრაფიკი, რომელიც არ შეიცავს აბსოლუტური მნიშვნელობის ნიშანს (ნახ. 2). ნახ.2 მაგალითი 2. განვიხილოთ y = x 2 6 x +5 ფუნქციის გრაფიკი. რიცხვის მოდულის განმარტების გამოყენებით, ჩვენ ვცვლით ფორმულას y = x 2 6 x +5 ახლა საქმე გვაქვს ჩვენთვის ნაცნობ ცალმხრივ დამოკიდებულების დავალებასთან. ჩვენ ავაშენებთ გრაფიკს შემდეგნაირად: 1) ავაშენებთ პარაბოლას y = x 2-6x +5 და შემოხაზეთ ის ნაწილი, რომელიც არის 22.

23 შეესაბამება x-ის არაუარყოფით მნიშვნელობებს, ე.ი. ნაწილი, რომელიც მდებარეობს Oy ღერძის მარჯვნივ. 2) იმავე კოორდინატულ სიბრტყეში ააგეთ პარაბოლა y = x 2 +6x +5 და შემოხაზეთ ის ნაწილი, რომელიც შეესაბამება x-ის უარყოფით მნიშვნელობებს, ე.ი. ნაწილი, რომელიც მდებარეობს Oy ღერძის მარცხნივ. პარაბოლების წრიული ნაწილები ერთად ქმნიან y = x 2-6 x +5 ფუნქციის გრაფიკს (ნახ. 3). ნახ.3 მაგალითი 3. განვიხილოთ y = x 2-6 x +5 ფუნქციის გრაფიკი. იმიტომ რომ y = x 2 6x +5 განტოლების გრაფიკი იგივეა, რაც ფუნქციის გრაფიკი მოდულის ნიშნის გარეშე (განხილულია მაგალით 2-ში), აქედან გამომდინარეობს, რომ y = x 2 6 x +5 ფუნქციის გრაფიკი იდენტურია. y = x 2 6 x +5 ფუნქციის გრაფიკზე, განხილული მაგალით 2-ში (ნახ. 3). მაგალითი 4. ავაშენოთ y = x 2 6x +5 ფუნქციის გრაფიკი. ამისათვის ავაშენოთ ფუნქციის გრაფიკი y = x 2-6x. მისგან y = x 2-6x ფუნქციის გრაფიკის მისაღებად, თქვენ უნდა შეცვალოთ პარაბოლის თითოეული წერტილი უარყოფითი ორდინატით იმავე აბსცისის წერტილით, მაგრამ საპირისპირო (დადებითი) ორდინატით. სხვა სიტყვებით რომ ვთქვათ, პარაბოლის ნაწილი, რომელიც მდებარეობს x ღერძის ქვემოთ, უნდა შეიცვალოს x ღერძის მიმართ მის მიმართ სიმეტრიული ხაზით. იმიტომ რომ ჩვენ უნდა ავაშენოთ y = x 2-6x +5 ფუნქციის გრაფიკი, შემდეგ ფუნქციის გრაფიკი, რომელიც ჩვენ მივიჩნიეთ y = x 2-6x, უბრალოდ y-ღერძის გასწვრივ 5 ერთეულით ზემოთ უნდა იყოს ამაღლებული (ნახ. 4. ). 23

24 ნახ.4 მაგალითი 5. ავაშენოთ y = x 2-6x+5 ფუნქციის გრაფიკი. ამისათვის ჩვენ გამოვიყენებთ ცნობილ ნაწილებად ფუნქციას. ვიპოვოთ y = 6x +5 6x + 5 = 0 ფუნქციის ნულები. განვიხილოთ ორი შემთხვევა: 1) თუ, მაშინ განტოლება მიიღებს y = x 2 6x -5 ფორმას. ავაშენოთ ეს პარაბოლა და შემოვხაზოთ ის ნაწილი, სადაც. 2) თუ, მაშინ განტოლება იღებს y = x 2 + 6x +5 ფორმას. დავდგეთ ეს პარაბოლა და შემოვხაზოთ მისი ის ნაწილი, რომელიც წერტილიდან მარცხნივ მდებარეობს კოორდინატებით (სურ. 5). 24

25 ნახ.5 მაგალითი6. ავაშენოთ y = x 2 6 x +5 ფუნქციის გრაფიკი. ამისათვის ჩვენ ავაშენებთ y = x 2-6 x +5 ფუნქციის გრაფიკს. ჩვენ ავაშენეთ ეს გრაფიკი მაგალითში 3. ვინაიდან ჩვენი ფუნქცია მთლიანად მოდულის ნიშნის ქვეშაა, y = x 2 6 x +5 ფუნქციის გრაფიკის ასაგებად, გვჭირდება y = x 2 ფუნქციის გრაფიკის თითოეული წერტილი. 6 x + 5 უარყოფითი ორდინატით უნდა შეიცვალოს წერტილით იგივე აბსცისით, მაგრამ საპირისპირო (დადებითი) ორდინატით, ე.ი. პარაბოლის ნაწილი, რომელიც მდებარეობს Ox ღერძის ქვემოთ, უნდა შეიცვალოს Ox ღერძის მიმართ მის მიმართ სიმეტრიული ხაზით (ნახ. 6). სურ.6 25

26 II. დასკვნა ,,მათემატიკური ინფორმაციის ოსტატურად და სასარგებლოდ გამოყენება შესაძლებელია მხოლოდ შემოქმედებითად ათვისების შემთხვევაში, რათა მოსწავლემ თავად ნახოს, როგორ შეეძლო მასზე დამოუკიდებლად მისვლა“. ა.ნ. კოლმოგოროვი. ეს პრობლემები დიდ ინტერესს იწვევს მეცხრე კლასის მოსწავლეებისთვის, რადგან ისინი ძალიან ხშირია OGE ტესტებში. ფუნქციების მონაცემთა გრაფიკების აგების შესაძლებლობა საშუალებას მოგცემთ უფრო წარმატებით ჩააბაროთ გამოცდა. ფრანგმა მათემატიკოსებმა პიერ ფერმამ () და რენე დეკარტმა () წარმოიდგინეს ფუნქცია, როგორც წერტილის ორდინატის დამოკიდებულება მრუდზე მის აბსცისაზე. და ინგლისელმა მეცნიერმა ისააკ ნიუტონმა () გააცნობიერა ფუნქცია, როგორც მოძრავი წერტილის კოორდინატი, რომელიც იცვლება დროის მიხედვით. 26

27 III ცნობათა და წყაროების სია 1. Galitsky M. L., Goldman A. M., Zvavich L. I. ამოცანების კრებული ალგებრაში 8-9 კლასებისთვის: სახელმძღვანელო. სახელმძღვანელო სკოლის მოსწავლეებისთვის. და მოწინავე კლასები შეისწავლა მათემატიკა მე-2 გამოცემა. მ.: განმანათლებლობა, დოროფეევი გ.ვ. მათემატიკა. Ალგებრა. ფუნქციები. Მონაცემთა ანალიზი. მე-9 კლასი: m34 სასწავლო. ზოგადსაგანმანათლებლო სწავლებისთვის. დაწესებულება მე-2 გამოცემა, სტერეოტიპი. M.: Bustard, Solomonik V.S. მათემატიკაში კითხვებისა და ამოცანების კრებული M.: ”უმაღლესი სკოლა”, Yashchenko I.V. GIA. მათემატიკა: სტანდარტული გამოცდის ვარიანტები: ვარიანტების შესახებ.მ.: „ეროვნული განათლება“, გვ. 5. იაშჩენკო ი.ვ. OGE. მათემატიკა: სტანდარტული გამოცდის ვარიანტები: ვარიანტების შესახებ.მ.: „ეროვნული განათლება“, გვ. 6. იაშჩენკო ი.ვ. OGE. მათემატიკა: სტანდარტული გამოცდის ვარიანტები: ვარიანტების შესახებ.მ.: „ეროვნული განათლება“, თან

28 დანართი 28

29 მაგალითი 1. ასახეთ ფუნქცია y = x 2 8 x ამოხსნა. განვსაზღვროთ ფუნქციის პარიტეტი. y(-x)-ის მნიშვნელობა იგივეა რაც y(x-ის მნიშვნელობა), ამიტომ ეს ფუნქცია ლუწია. მაშინ მისი გრაფიკი სიმეტრიულია Oy ღერძის მიმართ. ჩვენ გამოვსახავთ ფუნქციას y = x 2 8x + 12 x 0-ზე და სიმეტრიულად ვაჩვენებთ გრაფიკს Oy-ის მიმართ უარყოფითი x-ისთვის (ნახ. 1). მაგალითი 2. y = x 2 8x ფორმის შემდეგი გრაფიკი ეს ნიშნავს, რომ ფუნქციის გრაფიკი მიიღება შემდეგნაირად: ააგეთ ფუნქციის გრაფიკი y = x 2 8x + 12, დატოვეთ გრაფიკის ის ნაწილი, რომელიც დევს ზემოთ. Ox ღერძი უცვლელი და გრაფიკის ნაწილი, რომელიც დევს აბსცისის ღერძის ქვეშ და სიმეტრიულად არის გამოსახული Ox ღერძის მიმართ (ნახ. 2). მაგალითი 3. y = x 2 8 x + 12 ფუნქციის გრაფიკის გამოსახატავად ტარდება გარდაქმნების კომბინაცია: y = x 2 8x + 12 y = x 2 8 x + 12 y = x 2 8 x პასუხი: სურათი 3. მაგალითი 4 გამოხატვა მოდულის ნიშნის ქვეშ, ცვლის ნიშანს x=2/3 წერტილში. x-ზე<2/3 функция запишется так: 29

30 x>2/3-ისთვის ფუნქცია ასე დაიწერება: ანუ წერტილი x=2/3 ყოფს ჩვენს კოორდინატულ სიბრტყეს ორ ზონად, რომელთაგან ერთში (მარჯვნივ) ვაშენებთ ფუნქციას, ხოლო მეორეში. (მარცხნივ) ვაშენებთ ფუნქციის გრაფიკს: მაგალითი 5 შემდეგი გრაფიკი ასევე გატეხილია, მაგრამ აქვს ორი წყვეტის წერტილი, რადგან შეიცავს ორ გამოსახულებას მოდულის ნიშნების ქვეშ: ვნახოთ, რომელ წერტილებში ცვლის სუბმოდულური გამონათქვამები: მოდით დაალაგეთ ნიშნები სუბმოდულური გამოსახულებების კოორდინატთა ხაზზე: 30

31 ჩვენ ვაფართოებთ მოდულებს პირველ ინტერვალზე: მეორე ინტერვალზე: მესამე ინტერვალზე: ამრიგად, ინტერვალზე (- ; 1.5] გვაქვს პირველი განტოლებით დაწერილი გრაფიკი, ინტერვალზე მეორე განტოლებით დაწერილი გრაფიკი. და ინტერვალით)