ដែនកំណត់និងភាពបន្ត

មុខងារនៃអថេរមួយ។

៣.១.១. និយមន័យ។ ចំនួន ក xខិតខំសម្រាប់ x 0 ប្រសិនបើសម្រាប់លេខណាមួយ។
មានលេខមួយ។
(
) ហើយលក្ខខណ្ឌនឹងពេញចិត្ត៖

ប្រសិនបើ
, នោះ។
.

(និមិត្តសញ្ញា៖
).

ប្រសិនបើក្រាហ្វចង្អុលបង្ហាញ ជីមុខងារ

, ពេលណា​ ខិត​ជិត​ចំណុច​ជិត​គ្មាន​កំណត់ (ទាំងនោះ។
), (សូមមើលរូប 3.1) បន្ទាប់មកកាលៈទេសៈនេះគឺសមមូលធរណីមាត្រនៃការពិតដែលថាមុខងារ
នៅ
មានតម្លៃកំណត់ (ដែនកំណត់) ក(និមិត្តសញ្ញា៖
).

ក្រាហ្វមុខងារ,

អង្ករ។ ៣.១

វាគួរតែត្រូវបានកត់សម្គាល់ថាក្នុងការកំណត់តម្លៃដែនកំណត់ (ដែនកំណត់) នៃអនុគមន៍នៅ xខិតខំសម្រាប់ x 0 មិន​និយាយ​អ្វី​អំពី​ឥរិយាបទ​នៃ​មុខងារ​នៅ​ចំណុច​នោះ​ទេ។ x 0. នៅចំណុចខ្លាំងណាស់ xមុខងារ 0 ប្រហែលជាមិនត្រូវបានកំណត់ទេ អាចជា
, ប្រហែល
.

ប្រសិនបើ
បន្ទាប់មកមុខងារត្រូវបានគេហៅថា infinitesimal សម្រាប់
.

ចន្លោះពេលត្រូវបានគេហៅថា  - សង្កាត់នៃចំណុចមួយ។ x 0 ជាមួយនឹងមជ្ឈមណ្ឌលកាត់។ ដោយប្រើឈ្មោះនេះយើងអាចនិយាយបានថា: ប្រសិនបើសម្រាប់លេខណាមួយមានលេខហើយលក្ខខណ្ឌនឹងពេញចិត្ត: ប្រសិនបើ
, នោះ។
.

៣.១.២. និយមន័យ។ ប្រសិនបើសម្រាប់ convergent ណាមួយ។ x 0 លំដាប់
បន្តបន្ទាប់
បង្រួបបង្រួម ក.

៣.១.៣. ចូរយើងបញ្ជាក់អំពីសមមូលនៃនិយមន័យនៃផ្នែក 3.1.1 និង 3.1.2

អនុញ្ញាតឱ្យដំបូងនៅក្នុងន័យនៃនិយមន័យដំបូងនិងអនុញ្ញាតឱ្យ
(
) បន្ទាប់មកទាំងអស់។ លើកលែងតែចំនួនកំណត់របស់ពួកគេ បំពេញវិសមភាព
, កន្លែងណា  ជ្រើសរើសដោយ  នៅក្នុងន័យនៃនិយមន័យដំបូង, i.e.
, i.e. និយមន័យទីមួយមានន័យថាទីពីរ។ អនុញ្ញាតឱ្យវាឥឡូវនេះ
នៅក្នុងន័យនៃនិយមន័យទីពីរ ហើយអនុញ្ញាតឱ្យយើងសន្មតថានៅក្នុងន័យនៃនិយមន័យទីពីរ
, i.e. សម្រាប់មួយចំនួន សម្រាប់តូចតាមអំពើចិត្ត (ឧទាហរណ៍សម្រាប់
) បានរកឃើញលំដាប់
ប៉ុន្តែនៅពេលជាមួយគ្នា
. យើងបានមកដល់ភាពផ្ទុយគ្នា ដូច្នេះហើយ ទីមួយគឺមកពីនិយមន័យទីពីរ។

៣.១.៤. សមមូលនៃនិយមន័យទាំងនេះគឺងាយស្រួលជាពិសេស ដោយសារទ្រឹស្តីបទដែលបានបញ្ជាក់ពីមុនទាំងអស់លើលក្ខណៈសម្បត្តិនៃដែនកំណត់សម្រាប់លំដាប់បន្តស្ទើរតែដោយស្វ័យប្រវត្តិទៅ ករណីថ្មី។. វាគ្រាន់តែជាការចាំបាច់ដើម្បីបញ្ជាក់គោលគំនិតនៃការកំណត់។ ទ្រឹស្តីបទដែលត្រូវគ្នាមានទម្រង់ដូចខាងក្រោមៈ

ប្រសិនបើ
បន្ទាប់មកវាត្រូវបានកំណត់ទៅ  មួយចំនួន - សង្កាត់នៃចំណុច x 0 ជាមួយនឹងមជ្ឈមណ្ឌលកាត់។

៣.២.១.ទ្រឹស្តីបទ។ អនុញ្ញាតឱ្យ
,
,

បន្ទាប់មក
,

,

.

៣.២.២. អនុញ្ញាតឱ្យ

- បំពាន, បង្រួបបង្រួម x 0 លំដាប់នៃតម្លៃអាគុយម៉ង់មុខងារ និង
. លំដាប់ដែលត្រូវគ្នា។
និង
តម្លៃនៃមុខងារទាំងនេះមានដែនកំណត់ កនិង ខ. ប៉ុន្តែ​បន្ទាប់​មក តាម​ទ្រឹស្ដី​នៃ​ផ្នែក ២.១៣.២ លំដាប់
,
និង
មានដែនកំណត់ស្មើគ្នា ក +ខ,
និង
. យោងតាមនិយមន័យនៃដែនកំណត់នៃមុខងារនៅចំណុចមួយ (សូមមើលផ្នែក 2.5.2) នេះមានន័យថា

,
,

.

៣.២.៣. ទ្រឹស្តីបទ។ ប្រសិនបើ
,
និងនៅតំបន់ជុំវិញមួយចំនួន

កើតឡើង

.

៣.២.៤. តាមនិយមន័យនៃដែនកំណត់នៃអនុគមន៍នៅចំណុចមួយ។ x 0 សម្រាប់លំដាប់ណាមួយ។
បែបនោះ។

លំដាប់នៃតម្លៃមុខងារមានដែនកំណត់ស្មើនឹង ក. នេះមានន័យថាសម្រាប់នរណាម្នាក់
មានលេខមួយ។
បានសម្តែង។ ដូចគ្នានេះដែរសម្រាប់លំដាប់
មានលេខមួយ។
ដូច្នេះសម្រាប់លេខណាមួយ។
បានសម្តែង។ ការជ្រើសរើស
យើងរកឃើញថាសម្រាប់អ្នករាល់គ្នា
បានសម្តែង។ ពីខ្សែសង្វាក់នៃវិសមភាពនេះ យើងមានសម្រាប់ណាមួយ ដែលមានន័យថា
.

៣.២.៥. និយមន័យ។ ចំនួន កត្រូវបានគេហៅថាតម្លៃដែនកំណត់ (ដែនកំណត់) នៃអនុគមន៍នៅ xខិតខំសម្រាប់ x 0 នៅខាងស្តាំ (និមិត្តសញ្ញា៖
)ប្រសិនបើសម្រាប់លេខណាមួយមានលេខ () ហើយលក្ខខណ្ឌគឺពេញចិត្ត: ប្រសិនបើ
, នោះ។
.

សំណុំត្រូវបានគេហៅថាខាងស្តាំ  - សង្កាត់នៃចំណុច x 0. គោលគំនិតនៃតម្លៃដែនកំណត់ (ដែនកំណត់) នៅខាងឆ្វេងត្រូវបានកំណត់ស្រដៀងគ្នា (
).

៣.២.៦. ទ្រឹស្តីបទ។ អនុគមន៍នៅមានតម្លៃកំណត់ (limit) ស្មើនឹង កពេល​នោះ​ហើយ​តែ​ពេល​ណា

,

៣.៣.១. និយមន័យ។ ចំនួន កត្រូវបានគេហៅថាតម្លៃដែនកំណត់ (ដែនកំណត់) នៃអនុគមន៍នៅ xទំនោរទៅរកភាពគ្មានទីបញ្ចប់ ប្រសិនបើលេខណាមួយមានលេខ
(
) ហើយលក្ខខណ្ឌខាងក្រោមនឹងពេញចិត្ត៖

ប្រសិនបើ
, នោះ។

(និមិត្តសញ្ញា៖
.)

មួយ​បាច់
ហៅ ឃ- សង្កាត់នៃភាពគ្មានទីបញ្ចប់។

៣.៣.២. និយមន័យ។ ចំនួន កត្រូវបានគេហៅថាតម្លៃដែនកំណត់ (ដែនកំណត់) នៃអនុគមន៍នៅ xទំនោរទៅបូកនឹងភាពគ្មានទីបញ្ចប់ ប្រសិនបើលេខណាមួយមានលេខ ឃ() ហើយលក្ខខណ្ឌនឹងត្រូវបានបំពេញ៖

ប្រសិនបើ
, នោះ។

(និមិត្តសញ្ញា៖
).

ប្រសិនបើក្រាហ្វចង្អុលបង្ហាញ ជីមុខងារ
ជាមួយនឹងកំណើនគ្មានដែនកំណត់
ខិតទៅជិតបន្ទាត់ផ្តេកតែមួយដោយមិនកំណត់
(សូមមើលរូប 3.2) បន្ទាប់មកកាលៈទេសៈនេះគឺសមមូលធរណីមាត្រនៃការពិតដែលថាមុខងារ
នៅ
មានតម្លៃកំណត់ (limit) ស្មើនឹងចំនួន ក(និមិត្តសញ្ញា៖
).

ក្រាហ្វនៃមុខងារមួយ។
,

មួយ​បាច់
ហៅ ឃ- អ្នកជិតខាងបូកនឹងភាពគ្មានទីបញ្ចប់។

គំនិតនៃដែនកំណត់នៅ
.

លំហាត់។

បញ្ជាក់ទ្រឹស្តីបទទាំងអស់អំពីដែនកំណត់ដូចដែលបានអនុវត្តចំពោះករណី៖

1)
, 2)
, 3)
, 4)
, 5)
.

៣.៤.១. និយមន័យ។ មុខងារត្រូវបានគេហៅថាគ្មានកំណត់ មុខងារដ៏អស្ចារ្យ(ឬជាធម្មតាមានទំហំធំគ្មានកំណត់) នៅ ប្រសិនបើសម្រាប់លេខណាមួយ។

បំពេញវិសមភាព វិសមភាពគឺពេញចិត្ត
.

(និមិត្តសញ្ញា៖
.)

ប្រសិនបើបានបំពេញ
បន្ទាប់មកពួកគេសរសេរ
.

ប្រសិនបើបានបំពេញ
បន្ទាប់មកពួកគេសរសេរ
.

៣.៤.២. ទ្រឹស្តីបទ។ អនុញ្ញាតឱ្យ
និង
នៅ
.

បន្ទាប់មក
គឺជាមុខងារដ៏ធំគ្មានកំណត់សម្រាប់ .

៣.៤.៣. សូមឱ្យវាជាលេខដែលបំពាន។ ចាប់តាំងពីគឺជាអនុគមន៍គ្មានកំណត់សម្រាប់ , បន្ទាប់មកសម្រាប់លេខ
មានលេខបែបនេះសម្រាប់មនុស្សគ្រប់គ្នា xដែលវិសមភាពមាន
ប៉ុន្តែបន្ទាប់មកសម្រាប់ដូចគ្នា។ xវិសមភាពនឹងពេញចិត្ត
. ទាំងនោះ។ គឺជាមុខងារដ៏ធំគ្មានកំណត់សម្រាប់ .

៣.៤.៤.ទ្រឹស្តីបទ។ អនុញ្ញាតឱ្យមានមុខងារដ៏ធំគ្មានកំណត់សម្រាប់ និងសម្រាប់ .

បន្ទាប់មកគឺជាមុខងារគ្មានកំណត់សម្រាប់ .

(ទ្រឹស្តីបទនេះត្រូវបានបញ្ជាក់តាមរបៀបស្រដៀងគ្នាទៅនឹងទ្រឹស្តីបទនៅក្នុងផ្នែកទី 3.8.2 ។ )

៣.៤.៥. មុខងារ
ត្រូវបានគេហៅថាគ្មានដែនកំណត់នៅពេលដែល
ប្រសិនបើសម្រាប់លេខណាមួយ។
និង δ-សង្កាត់ណាមួយនៃចំណុច អ្នកអាចបញ្ជាក់ចំណុចមួយ។ xពីសង្កាត់បែបនេះ
.

៣.៥.១. និយមន័យ។ មុខងារត្រូវបានគេហៅថា បន្តនៅចំណុច , ប្រសិនបើ
.

លក្ខខណ្ឌចុងក្រោយអាចត្រូវបានសរសេរដូចនេះ៖

.

សញ្ញាណនេះមានន័យថាសម្រាប់មុខងារបន្ត សញ្ញានៃដែនកំណត់ និងសញ្ញានៃមុខងារអាចត្រូវបានផ្លាស់ប្តូរ

ឬដូចនេះ៖ . ឬម្តងទៀតដូចជានៅដើមដំបូង។

ចូរយើងសម្គាល់
. បន្ទាប់មក
និង =
ហើយទម្រង់ថតចុងក្រោយនឹងយកទម្រង់

.

កន្សោមនៅក្រោមសញ្ញាកំណត់តំណាងឱ្យការបង្កើនចំណុចមុខងារដែលបណ្តាលមកពីការបង្កើន
អាគុយម៉ង់ xនៅចំណុច, ជាធម្មតាត្រូវបានតំណាងថាជា
. ជាលទ្ធផល យើងទទួលបានទម្រង់ខាងក្រោមនៃការសរសេរលក្ខខណ្ឌសម្រាប់ការបន្តនៃអនុគមន៍នៅចំណុចមួយ។

,

ដែលត្រូវបានគេហៅថា "និយមន័យការងារ" នៃការបន្តនៃមុខងារនៅចំណុចមួយ។

មុខងារត្រូវបានគេហៅថា បន្តនៅចំណុច ឆ្វេង, ប្រសិនបើ
.

មុខងារត្រូវបានគេហៅថា បន្តនៅចំណុច នៅខាងស្ដាំ, ប្រសិនបើ
.

៣.៥.២. ឧទាហរណ៍។
. មុខងារនេះគឺបន្តសម្រាប់ណាមួយ។ ដោយប្រើទ្រឹស្ដីអំពីលក្ខណៈសម្បត្តិនៃដែនកំណត់ យើងទទួលបានភ្លាមៗ៖ មុខងារសនិទានភាពគឺបន្តនៅគ្រប់ចំណុចដែលវាត្រូវបានកំណត់ ពោលគឺឧ។ មុខងារនៃទម្រង់
.

លំហាត់.

៣.៦.១. សៀវភៅសិក្សារបស់សាលាបញ្ជាក់ (នៅលើ កម្រិតខ្ពស់រឹង) នោះ។
(ដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង) ។ ពីការពិចារណាធរណីមាត្រដែលមើលឃើញវាភ្លាមៗធ្វើតាមនោះ។
. ចំណាំថាពីវិសមភាពខាងឆ្វេង វាក៏ធ្វើតាមនោះដែរ
, i.e. តើអ្វីទៅជាមុខងារ
គឺបន្តនៅសូន្យ។ ពីទីនេះ វាមិនពិបាកទាល់តែសោះ ដើម្បីបញ្ជាក់ពីភាពបន្តនៃទាំងអស់គ្នា អនុគមន៍ត្រីកោណមាត្រនៅគ្រប់ចំណុចទាំងអស់ដែលពួកគេត្រូវបានកំណត់។ តាមពិតពេលណា
ដូចជាផលិតផលគ្មានកំណត់ មុខងារតូច
នៅលើ មុខងារមានកំណត់
.

៣.៦.២. (ដែនកំណត់ដ៏អស្ចារ្យទី ២) ។ ដូចដែលយើងដឹងរួចមកហើយ

,

កន្លែងណា រត់តាមលេខធម្មជាតិ។ វាអាចត្រូវបានបង្ហាញថា
. ជាងនេះ។
.

លំហាត់.

៣.៧.១. ទ្រឹស្តីបទ (នៅលើការបន្តនៃមុខងារស្មុគស្មាញ) ។

ប្រសិនបើមុខងារ
គឺបន្តនៅចំណុចមួយ និង
និងមុខងារ
បន្តនៅចំណុចមួយ។ បន្ទាប់មកមុខងារស្មុគស្មាញ
គឺបន្តនៅចំណុច។

៣.៧.២. សុពលភាពនៃសេចក្តីថ្លែងការណ៍នេះ កើតឡើងភ្លាមៗពីនិយមន័យនៃការបន្ត ដែលសរសេរជា៖

៣.៨.១. ទ្រឹស្តីបទ។ មុខងារ គឺបន្តនៅគ្រប់ចំណុច (
).

៣.៨.២. ប្រសិនបើយើងពិចារណាវាសមហេតុផលដែលមុខងារ
ត្រូវបានកំណត់សម្រាប់ណាមួយ និងជា monotonic យ៉ាងតឹងរឹង (កាត់បន្ថយយ៉ាងតឹងរ៉ឹងសម្រាប់
កើនឡើងយ៉ាងតឹងរ៉ឹងជាមួយ
) បន្ទាប់មកភស្តុតាងមិនពិបាកទេ។

នៅ
យើង​មាន:

ទាំងនោះ។ នៅពេលដែលយើងមាន
ដែលមានន័យថាមុខងារ គឺបន្តនៅ។

នៅ
វាទាំងអស់ចុះមកមុន:

នៅ
.

នៅ
មុខងារ
គឺថេរសម្រាប់ទាំងអស់គ្នា ដូច្នេះបន្ត។

៣.៩.១. ទ្រឹស្តីបទ (នៅលើការរួមរស់ និងបន្តនៃមុខងារបញ្ច្រាស)។

អនុញ្ញាតឱ្យមុខងារបន្តថយចុះយ៉ាងតឹងរ៉ឹង (កើនឡើងយ៉ាងតឹងរ៉ឹង) នៅក្នុង δ មួយចំនួន - សង្កាត់នៃចំណុច,
. បន្ទាប់មកនៅក្នុង ε មួយចំនួន - សង្កាត់នៃចំណុច មានមុខងារបញ្ច្រាស
ដែលថយចុះយ៉ាងតឹងរ៉ឹង (កើនឡើងយ៉ាងតឹងរ៉ឹង) និងបន្តនៅក្នុង ε - សង្កាត់នៃចំណុច។

៣.៩.២. នៅទីនេះយើងបង្ហាញតែការបន្តនៃមុខងារបញ្ច្រាសនៅចំណុច។

ចូរយើងទទួលយកវា, រយៈពេល yស្ថិតនៅចន្លោះចំណុច
និង
ដូច្នេះប្រសិនបើ
, នោះ។
, កន្លែងណា .

៣.១០.១. ដូច្នេះ រាល់ប្រតិបត្តិការនព្វន្ធដែលអាចអនុញ្ញាតបានលើអនុគមន៍បន្តម្តងទៀតនាំឱ្យមុខងារបន្ត។ ការបង្កើតមុខងារស្មុគ្រស្មាញនិងច្រាសពីពួកវាមិនធ្វើឱ្យខូចការបន្តទេ។ ដូច្នេះ ជាមួយនឹងកម្រិតនៃទំនួលខុសត្រូវមួយចំនួន យើងអាចអះអាងថាមុខងារបឋមទាំងអស់គឺបន្តសម្រាប់តម្លៃដែលអាចទទួលយកបានទាំងអស់នៃអាគុយម៉ង់។

លំហាត់ប្រាណ.

បញ្ជាក់
នៅ
(ទម្រង់មួយផ្សេងទៀតនៃដែនកំណត់ដ៏អស្ចារ្យទីពីរ) ។

៣.១១.១. ការគណនាដែនកំណត់គឺសាមញ្ញណាស់ ប្រសិនបើយើងប្រើគោលគំនិតនៃសមមូលគ្មានកំណត់។ វាមានភាពងាយស្រួលក្នុងការធ្វើទូទៅនូវគោលគំនិតនៃសមមូលទៅនឹងករណីនៃមុខងារបំពាន។

និយមន័យ។ មុខងារ និងត្រូវបានគេនិយាយថាស្មើនឹង if
(ជំនួស​អោយ អ្នកអាចសរសេរបាន។
,
,
,
,
).

កំណត់ចំណាំបានប្រើ f ~ g.

សមមូលមានលក្ខណៈសម្បត្តិដូចខាងក្រោម

បញ្ជីរាយនាមដែលសមមូលខាងក្រោមត្រូវរក្សាទុកក្នុងចិត្ត៖

~
នៅ
; (1)

~ នៅ ; (2)

~
នៅ ; (3)

~ នៅ ; (4)

~ នៅ ; (5)

~ នៅ ; (6)

~ នៅ ; (7)

~ ទំ នៅ ; (8)

~ នៅ
; (9)

~
នៅ។ (10)

នៅទីនេះ និងអាចមិនមែនជាអថេរឯករាជ្យ ប៉ុន្តែមុខងារ
និង
ទំនោរទៅសូន្យ និងមួយ រៀងគ្នា សម្រាប់ឥរិយាបថមួយចំនួន x. ឧទាហរណ៍,

~
នៅ
,

~
នៅ
.

សមមូល (1) គឺជាទម្រង់មួយផ្សេងទៀតនៃការសរសេរដែនកំណត់គួរឱ្យកត់សម្គាល់ដំបូង។ សមមូល (2), (3), (6) និង (7) អាចបញ្ជាក់ដោយផ្ទាល់។ សមមូល (៤) ទទួលបានពី (១) គិតដល់ទ្រព្យសម្បត្តិ ២) សមមូល៖

~
.

ដូចគ្នានេះដែរ (5) និង (7) ត្រូវបានទទួលពី (2) និង (6) ។ ជា​ការ​ពិត

~
,

~
.

សមមូលនៃ (8) ត្រូវបានបញ្ជាក់ដោយការអនុវត្តតាមលំដាប់នៃ (7) និង (6)៖

និង (9) និង (10) ត្រូវបានទទួលពី (6) និង (8) ដោយជំនួស
.

៣.១១.២. ទ្រឹស្តីបទ។ នៅពេលគណនាដែនកំណត់ក្នុងផលិតផល និងសមាមាត្រ អ្នកអាចប្តូរមុខងារទៅជាសមមូល។ ពោលគឺប្រសិនបើ ~
បន្ទាប់មកដែនកំណត់ទាំងពីរមិនមានក្នុងពេលដំណាលគ្នា និង
ឬដែនកំណត់ទាំងពីរនេះមិនមានក្នុងពេលដំណាលគ្នាទេ។

ចូរយើងបង្ហាញពីសមភាពដំបូង។ អនុញ្ញាតឱ្យមានដែនកំណត់មួយនិយាយថា
មាន។ បន្ទាប់មក

.

៣.១១.៣. អនុញ្ញាតឱ្យ (ជាលេខឬនិមិត្តសញ្ញា,
ឬ
) យើងនឹងពិចារណាអំពីអាកប្បកិរិយារបស់ b.m. ផ្សេងៗ។ អនុគមន៍ (នេះ​ជា​របៀប​ដែល​យើង​នឹង​កាត់​ពាក្យ​ថា infinitesimal)។

និយមន័យ។
ហើយត្រូវបានគេហៅថាសមមូល b.m. មុខងារសម្រាប់, ប្រសិនបើ
(នៅ)

យើងនឹងហៅវាថា b.m. ច្រើនទៀត លំដាប់ខ្ពស់។ជាង b.m. មុខងារ
, ប្រសិនបើ
(នៅ)

៣.១១.៤. ប្រសិនបើ និងសមមូល b.m. មុខងារបន្ទាប់មក
មាន b.m. មុខងារនៃលំដាប់ខ្ពស់ជាង
និងអ្វី។ - ខ.ម. មុខងារនៅ ដែលក្នុងនោះសម្រាប់ x ទាំងអស់ ហើយប្រសិនបើនៅចំណុចនេះ មុខងារត្រូវបានគេហៅថា ចំណុចដាច់ដែលអាចដកចេញបាន។ មានការដាច់នៃប្រភេទទីពីរ។ ចំណុចខ្លួនឯង សាកល្បង

ទៅ កូឡុំកូ។ ផ្នែក៖ " ដែនកំណត់និង ការបន្តមុខងារត្រឹមត្រូវ។ អថេរ" មុខងារមួយ។អថេរ"" ការគណនាឌីផេរ៉ង់ស្យែល មុខងារជាច្រើន អថេរ"

ប្រធានបទ និងឧទាហរណ៍នៃការធ្វើតេស្ត និងសំណួរ (សាកល្បងការគណនាស្តង់ដារបុគ្គល) ការធ្វើតេស្តឆមាសទី 1 លេខ 1 ផ្នែក "ដែនកំណត់និងភាពបន្តនៃមុខងារនៃអថេរពិតប្រាកដ"

សាកល្បង

ទៅ កូឡុំកូ។ ផ្នែក៖ " ដែនកំណត់និង ការបន្តមុខងារត្រឹមត្រូវ។ អថេរ"" ការគណនាឌីផេរ៉ង់ស្យែល មុខងារមួយ។អថេរ"" ការគណនាឌីផេរ៉ង់ស្យែល មុខងារជាច្រើន អថេរ". លំដាប់លេខ...

សាកល្បង

ទៅ កូឡុំកូ។ ផ្នែក៖ " ដែនកំណត់និង ការបន្តមុខងារត្រឹមត្រូវ។ អថេរ"" ការគណនាឌីផេរ៉ង់ស្យែល មុខងារមួយ។អថេរ"" ការគណនាឌីផេរ៉ង់ស្យែល មុខងារជាច្រើន អថេរ". លំដាប់លេខ...

ប្រធានបទ និងឧទាហរណ៍នៃកិច្ចការសាកល្បង និងសំណួរ (ការងារសាកល្បង ការគណនាស្តង់ដារបុគ្គល) ផ្នែកការងារសាកល្បងឆមាសទី១ “ដែនកំណត់ និងបន្តនៃមុខងារនៃអថេរពិតប្រាកដ”

សាកល្បង

ទៅ កូឡុំកូ។ ផ្នែក៖ " ដែនកំណត់និង ការបន្តមុខងារត្រឹមត្រូវ។ អថេរ"" ការគណនាឌីផេរ៉ង់ស្យែល មុខងារមួយ។អថេរ"" ការគណនាឌីផេរ៉ង់ស្យែល មុខងារជាច្រើន អថេរ". លំដាប់លេខ...

មេរៀនទី 19 ដែនកំណត់ និងការបន្តនៃមុខងារនៃអថេរជាច្រើន។

ការបង្រៀន

... ដែនកំណត់និង ការបន្តមុខងារជាច្រើន អថេរ. ១៩.១. គំនិត មុខងារជាច្រើន អថេរ. ដោយការពិនិត្យឡើងវិញ មុខងារជាច្រើន អថេរ... លក្ខណៈសម្បត្តិ មុខងារមួយ។អថេរ, បន្តនៅលើផ្នែក។ មើលលក្ខណសម្បត្តិ មុខងារ, បន្តនៅ​លើ...

ការបន្តនៃមុខងារ។ ចំណុចបំបែក។

គោ​ដើរ​ហើរ ដកដង្ហើម​ធំ​ពេល​ទៅ៖
- អូ ក្តារអស់ហើយ ពេលនេះខ្ញុំនឹងដួលហើយ!

នៅក្នុងមេរៀននេះ យើងនឹងពិនិត្យមើលគោលគំនិតនៃការបន្តនៃមុខងារមួយ ការចាត់ថ្នាក់នៃចំនុចមិនបន្ត និងទូទៅ បញ្ហាជាក់ស្តែង ការសិក្សាបន្តនៃមុខងារ. តាមឈ្មោះនៃប្រធានបទ មនុស្សជាច្រើនទាយដោយវិចារណញាណអំពីអ្វីដែលនឹងត្រូវបានពិភាក្សា ហើយគិតថាសម្ភារៈនេះគឺសាមញ្ញណាស់។ វា​ជា​ការពិត។ ប៉ុន្តែ​វា​ជា​កិច្ចការ​សាមញ្ញ​ដែល​ច្រើន​តែ​ត្រូវ​ទទួល​ទោស​ចំពោះ​ការ​ធ្វេសប្រហែស និង​ជា​វិធីសាស្ត្រ​ដ៏​វិសេស​ដើម្បី​ដោះស្រាយ​ពួកគេ។ ដូច្នេះ ខ្ញុំ​សូម​ណែនាំ​ឱ្យ​អ្នក​សិក្សា​អត្ថបទ​ឱ្យ​បាន​ហ្មត់ចត់ ហើយ​ចាប់​យក​នូវ​រាល់​ការ​ពន្យល់ និង​បច្ចេកទេស។

តើអ្នកត្រូវដឹង និងអាចធ្វើអ្វីបាន?មិនច្រើនទេ។ ដើម្បីរៀនមេរៀនបានល្អ អ្នកត្រូវយល់ថាវាជាអ្វី ដែនកំណត់នៃមុខងារមួយ។. សម្រាប់​អ្នក​អាន​ដែល​មាន​កម្រិត​ទាប​នៃ​ការ​រៀបចំ​វា​គ្រប់គ្រាន់​ដើម្បី​យល់​អត្ថបទ ដែនកំណត់មុខងារ។ ឧទាហរណ៍នៃដំណោះស្រាយនិងដើម្បីមើល អត្ថន័យធរណីមាត្រដែនកំណត់នៅក្នុងសៀវភៅណែនាំ ក្រាហ្វនិងលក្ខណៈសម្បត្តិនៃអនុគមន៍បឋម. វាត្រូវបានណែនាំឱ្យស្គាល់ខ្លួនឯងផងដែរ។ ការផ្លាស់ប្តូរធរណីមាត្រនៃក្រាហ្វចាប់តាំងពីការអនុវត្តក្នុងករណីភាគច្រើនពាក់ព័ន្ធនឹងការសាងសង់គំនូរ។ ការរំពឹងទុកមានសុទិដ្ឋិនិយមសម្រាប់មនុស្សគ្រប់គ្នា ហើយសូម្បីតែកំសៀវពេញមួយនឹងអាចទប់ទល់នឹងកិច្ចការដោយខ្លួនឯងបានក្នុងរយៈពេលមួយម៉ោង ឬពីរម៉ោងបន្ទាប់!

ការបន្តនៃមុខងារ។ ចំណុចបំបែកនិងចំណាត់ថ្នាក់របស់ពួកគេ។

គំនិតនៃការបន្តនៃមុខងារមួយ។

តោះពិចារណាមុខងារមួយចំនួនដែលបន្តនៅលើបន្ទាត់លេខទាំងមូល៖

ឬដើម្បីដាក់វាឱ្យកាន់តែខ្លី មុខងាររបស់យើងគឺបន្ត (សំណុំ ចំនួនពិត).

តើអ្វីជាលក្ខណៈវិនិច្ឆ័យ "ភីលីស្ទីន" នៃការបន្ត? ជាក់ស្តែង ក្រាហ្វនៃមុខងារបន្តអាចត្រូវបានគូរដោយមិនចាំបាច់លើកខ្មៅដៃចេញពីក្រដាស។

ក្នុងករណីនេះចាំបាច់ត្រូវបែងចែកឱ្យច្បាស់នូវទាំងពីរ គំនិតសាមញ្ញ: ដែននៃមុខងារមួយ។និង ភាពបន្តនៃមុខងារ. ជាទូទៅ វាមិនមែនជារឿងដូចគ្នាទេ។. ឧទាហរណ៍:

មុខងារនេះ។កំណត់នៅលើបន្ទាត់លេខទាំងមូល នោះគឺសម្រាប់ គ្រប់គ្នាអត្ថន័យនៃ "x" មានអត្ថន័យផ្ទាល់ខ្លួននៃ "y" ។ ជាពិសេសប្រសិនបើ . ចំណាំថាចំណុចផ្សេងទៀតត្រូវបានដាក់សញ្ញាវណ្ណយុត្តិ ពីព្រោះតាមនិយមន័យនៃអនុគមន៍ តម្លៃនៃអាគុយម៉ង់ត្រូវតែឆ្លើយតបទៅនឹង រឿង​តែ​មួយ​គត់តម្លៃមុខងារ។ ដូច្នេះ ដែនមុខងាររបស់យើង: .

ទោះយ៉ាងណាក៏ដោយ មុខងារនេះមិនបន្តទេ!វាច្បាស់ណាស់ថានៅចំណុចដែលនាងកំពុងរងទុក្ខ គម្លាត. ពាក្យនេះក៏អាចយល់បាន និងមើលឃើញច្បាស់ នៅទីនេះ ខ្មៅដៃនឹងត្រូវរហែកចេញពីក្រដាស។ បន្តិចទៀតយើងនឹងពិនិត្យមើលចំណាត់ថ្នាក់នៃចំណុចឈប់។

ការបន្តនៃអនុគមន៍នៅចំណុចមួយ និងនៅលើចន្លោះពេលមួយ។

នៅក្នុងបញ្ហាគណិតវិទ្យាជាក់លាក់មួយ យើងអាចនិយាយអំពីការបន្តនៃអនុគមន៍នៅចំណុចមួយ ការបន្តនៃអនុគមន៍នៅលើចន្លោះពេល ចន្លោះពេលពាក់កណ្តាល ឬការបន្តនៃអនុគមន៍នៅលើផ្នែកមួយ។ នោះគឺ មិនមាន "ការបន្ត" ទេ- មុខងារអាចបន្តទៅកន្លែងណាមួយ។ ហើយ "ប្លុកអគារ" ជាមូលដ្ឋាននៃអ្វីផ្សេងទៀតគឺ ភាពបន្តនៃមុខងារ នៅចំណុច .

ទ្រឹស្តីនៃការវិភាគគណិតវិទ្យាផ្តល់និយមន័យនៃការបន្តនៃអនុគមន៍នៅចំណុចមួយដោយប្រើសង្កាត់ "ដីសណ្ត" និង "epsilon" ប៉ុន្តែនៅក្នុងការអនុវត្តមាននិយមន័យផ្សេងគ្នានៅក្នុងការប្រើប្រាស់ ដែលយើងនឹងយកចិត្តទុកដាក់។

ជាដំបូង ចូរយើងចងចាំ ដែនកំណត់ម្ខាងដែលបានចូលមកក្នុងជីវិតរបស់យើងនៅក្នុងមេរៀនដំបូង អំពីក្រាហ្វិកមុខងារ. ពិចារណាស្ថានភាពប្រចាំថ្ងៃ៖

ប្រសិនបើយើងចូលទៅជិតអ័ក្សទៅចំណុច ឆ្វេង(ព្រួញក្រហម) បន្ទាប់មកតម្លៃដែលត្រូវគ្នានៃ "ហ្គេម" នឹងដើរតាមអ័ក្សទៅចំណុច (ព្រួញពណ៌ក្រហម)។ តាមគណិតវិទ្យា ការពិតនេះត្រូវបានជួសជុលដោយប្រើ ដែនកំណត់ខាងឆ្វេង:

យកចិត្តទុកដាក់លើធាតុ (អាន "x ទំនោរទៅកានៅខាងឆ្វេង") ។ "ការបន្ថែម" "ដកសូន្យ" តំណាងឱ្យ សំខាន់នេះមានន័យថាយើងកំពុងខិតជិតលេខពីផ្នែកខាងឆ្វេង។

ស្រដៀងគ្នានេះដែរ ប្រសិនបើអ្នកចូលទៅជិតចំណុច "កា" នៅខាងស្ដាំ (ព្រួញពណ៌ខៀវ) បន្ទាប់មក "ហ្គេម" នឹងមានតម្លៃដូចគ្នា ប៉ុន្តែតាមព្រួញពណ៌បៃតង និង ដែនកំណត់ខាងស្តាំនឹង​ត្រូវ​បាន​ធ្វើ​ទ្រង់ទ្រាយ​ដូច​ខាង​ក្រោម​:

"សារធាតុបន្ថែម" តំណាងឱ្យ ហើយធាតុសរសេរថា "x ទំនោរទៅកានៅខាងស្តាំ" ។

ប្រសិនបើដែនកំណត់ម្ខាងមានកំណត់ និងស្មើគ្នា(ដូចករណីរបស់យើង)៖ បន្ទាប់មកយើងនឹងនិយាយថាមានដែនកំណត់ទូទៅ។ វាសាមញ្ញ ដែនកំណត់ទូទៅគឺ "ធម្មតា" របស់យើង ដែនកំណត់នៃមុខងារមួយ។ស្មើនឹងចំនួនកំណត់។

ចំណាំថាប្រសិនបើមុខងារមិនត្រូវបានកំណត់នៅ (បញ្ចេញចំណុចខ្មៅនៅលើសាខាក្រាហ្វ) នោះការគណនាខាងលើនៅតែមានសុពលភាព។ ដូចដែលត្រូវបានកត់សម្គាល់ជាច្រើនដងរួចមកហើយជាពិសេសនៅក្នុងអត្ថបទ នៅលើមុខងារគ្មានកំណត់កន្សោមមានន័យថា "x" ជិតស្និទ្ធគ្មានកំណត់ខិតជិតដល់ចំណុច ខណៈពេលដែល មិនសំខាន់ទេ។ថាតើមុខងារខ្លួនវាត្រូវបានកំណត់នៅចំណុចដែលបានផ្តល់ឱ្យឬអត់។ ឧទាហរណ៍ដ៏ល្អមួយនឹងត្រូវបានរកឃើញនៅក្នុងកថាខណ្ឌបន្ទាប់ នៅពេលដែលមុខងារត្រូវបានវិភាគ។

និយមន័យ៖ អនុគមន៍​មួយ​គឺ​បន្ត​នៅ​ចំណុច​មួយ ប្រសិន​បើ​ដែនកំណត់​នៃ​អនុគមន៍​នៅ​ចំណុច​ដែល​បាន​ផ្ដល់​គឺ​ស្មើ​នឹង​តម្លៃ​នៃ​អនុគមន៍​នៅ​ចំណុច​នោះ ៖ .

និយមន័យ​មាន​លម្អិត​ក្នុង​លក្ខខណ្ឌ​ដូច​ខាង​ក្រោម​៖

1) មុខងារត្រូវតែកំណត់នៅចំណុច ពោលគឺតម្លៃត្រូវតែមាន។

2) ត្រូវតែមានដែនកំណត់ទូទៅនៃមុខងារ។ ដូចដែលបានកត់សម្គាល់ខាងលើ នេះបង្កប់ន័យអត្ថិភាព និងសមភាពនៃដែនកំណត់ម្ខាង៖ .

3) ដែនកំណត់នៃអនុគមន៍នៅចំណុចដែលបានផ្តល់ឱ្យត្រូវតែស្មើនឹងតម្លៃនៃអនុគមន៍នៅចំណុចនេះ: .

បើបំពាន យ៉ាងហោចណាស់​មួយនៃលក្ខខណ្ឌចំនួនបី បន្ទាប់មកមុខងារបាត់បង់ទ្រព្យសម្បត្តិនៃការបន្តនៅចំណុច .

ការបន្តនៃអនុគមន៍មួយនៅលើចន្លោះពេលមួយ។ត្រូវបានបង្កើតយ៉ាងប៉ិនប្រសប់ និងសាមញ្ញបំផុត៖ មុខងារមួយគឺបន្តនៅលើចន្លោះពេលប្រសិនបើវាបន្តនៅគ្រប់ចំណុចនៃចន្លោះពេលដែលបានផ្តល់ឱ្យ។

ជាពិសេស មុខងារជាច្រើនគឺបន្តនៅលើចន្លោះពេលគ្មានកំណត់ ពោលគឺនៅលើសំណុំនៃចំនួនពិត។ នេះគឺជាអនុគមន៍លីនេអ៊ែរ ពហុនាម អិចស្ប៉ូណង់ស្យែល ស៊ីនុស កូស៊ីនុស។ល។ ហើយជាទូទៅ ណាមួយ មុខងារបឋមបន្តលើរបស់វា។ ដែននៃនិយមន័យ, ឧទាហរណ៍, មុខងារលោការីតគឺបន្តនៅចន្លោះពេល។ សង្ឃឹមថាឥឡូវនេះអ្នកមានគំនិតល្អអំពីអ្វីដែលក្រាហ្វនៃមុខងារមូលដ្ឋានមើលទៅដូច។ ច្រើនទៀត ព​ត៌​មាន​លំអិតអំពីការបន្តរបស់ពួកគេអាចត្រូវបានប្រមូលពីបុរសចិត្តល្អម្នាក់ឈ្មោះ Fichtenholtz ។

ជាមួយនឹងការបន្តនៃមុខងារនៅលើផ្នែកមួយ និងពាក់កណ្តាលចន្លោះ អ្វីគ្រប់យ៉ាងក៏មិនពិបាកដែរ ប៉ុន្តែវាជាការសមស្របជាងក្នុងការនិយាយអំពីរឿងនេះនៅក្នុងថ្នាក់។ អំពីការស្វែងរកតម្លៃអប្បបរមា និងអតិបរមានៃអនុគមន៍នៅលើផ្នែកមួយ។ប៉ុន្តែសម្រាប់ពេលនេះ ចូរយើងកុំបារម្ភអំពីវា

ចំណាត់ថ្នាក់នៃចំណុចបំបែក

ជីវិតគួរឱ្យចាប់អារម្មណ៍នៃមុខងារគឺសំបូរទៅដោយចំណុចពិសេសគ្រប់ប្រភេទ ហើយចំនុចបំបែកគឺគ្រាន់តែជាទំព័រមួយនៃទំព័រជីវប្រវត្តិរបស់ពួកគេ។

ចំណាំ ៖ គ្រាន់តែក្នុងករណី ខ្ញុំនឹងរស់នៅលើចំណុចបឋមមួយ៖ ចំណុចបំបែកគឺតែងតែ ចំណុចតែមួយ- មិនមាន "ចំណុចសម្រាកជាច្រើនក្នុងមួយជួរ" នោះគឺមិនមានអ្វីដូចជា "ចន្លោះពេលសម្រាក" ទេ។

ចំនុចទាំងនេះ ចែកចេញជាពីរក្រុមធំៗ៖ ការបែកបាក់នៃប្រភេទទីមួយនិង ការដាច់នៃប្រភេទទីពីរ. ប្រភេទនៃគម្លាតនីមួយៗមានរបស់វា។ ច​រិ​ក​លក្ខណៈដែលយើងនឹងពិនិត្យមើលឥឡូវនេះ៖

ចំណុចដាច់នៃប្រភេទទីមួយ

ប្រសិនបើលក្ខខណ្ឌបន្តត្រូវបានបំពាននៅចំណុចមួយ។ និងដែនកំណត់ម្ខាង កំណត់ បន្ទាប់មកវាត្រូវបានគេហៅថា ចំណុចដាច់នៃប្រភេទទីមួយ.

ចូរចាប់ផ្តើមជាមួយនឹងករណីសុទិដ្ឋិនិយមបំផុត។ យោងតាមគំនិតដើមនៃមេរៀន ខ្ញុំចង់ប្រាប់ទ្រឹស្តី “in ទិដ្ឋភាពទូទៅ” ប៉ុន្តែដើម្បីបង្ហាញពីការពិតនៃសម្ភារៈ ខ្ញុំបានសម្រេចចិត្តលើជម្រើសជាមួយនឹងតួអក្សរជាក់លាក់។

សោកសៅ ដូចជារូបថតគូស្នេហ៍ថ្មីថ្មោងនៅផ្ទៃខាងក្រោយ អណ្តាតភ្លើងដ៏អស់កល្បប៉ុន្តែស៊ុមខាងក្រោមត្រូវបានទទួលយកជាទូទៅ។ ចូរយើងពណ៌នាក្រាហ្វនៃមុខងារក្នុងគំនូរ៖


មុខងារនេះបន្តនៅលើបន្ទាត់លេខទាំងមូល លើកលែងតែចំណុច។ ហើយតាមពិត ភាគបែងមិនអាចស្មើនឹងសូន្យទេ។ ទោះជាយ៉ាងណាក៏ដោយស្របតាមអត្ថន័យនៃដែនកំណត់យើងអាចធ្វើបាន ជិតស្និទ្ធគ្មានកំណត់ខិតទៅជិត "សូន្យ" ទាំងពីឆ្វេង និងពីស្តាំ ពោលគឺដែនកំណត់ម្ខាងមាន ហើយជាក់ស្តែងស្របគ្នា៖
(លក្ខខណ្ឌទី 2 នៃការបន្តគឺពេញចិត្ត) ។

ប៉ុន្តែមុខងារមិនត្រូវបានកំណត់នៅចំណុចនោះទេ ដូច្នេះលក្ខខណ្ឌលេខ 1 នៃការបន្តត្រូវបានរំលោភបំពាន ហើយមុខងារនេះទទួលរងការមិនដំណើរការនៅចំណុចនេះ។

ការសម្រាកនៃប្រភេទនេះ (ជាមួយដែលមានស្រាប់ ដែនកំណត់ទូទៅ) ត្រូវបានគេហៅថា គម្លាតដែលអាចជួសជុលបាន។. ហេតុអ្វីបានជាអាចដកចេញបាន? ដោយសារតែមុខងារអាច កំណត់ឡើងវិញនៅចំណុចបំបែក៖

មើលទៅប្លែកទេ? ប្រហែល។ ប៉ុន្តែ​ការ​កំណត់​មុខងារ​បែប​នេះ​មិន​ផ្ទុយ​ពី​អ្វី​នោះ​ទេ! ឥឡូវនេះគម្លាតត្រូវបានបិទ ហើយគ្រប់គ្នាសប្បាយចិត្ត៖


ចូរយើងធ្វើការត្រួតពិនិត្យជាផ្លូវការ៖

2) - មានដែនកំណត់ទូទៅ;
3)

ដូច្នេះលក្ខខណ្ឌទាំងបីគឺពេញចិត្ត ហើយមុខងារគឺបន្តនៅចំណុចមួយដោយនិយមន័យនៃការបន្តនៃអនុគមន៍នៅចំណុចមួយ។

ទោះជាយ៉ាងណាក៏ដោយ អ្នកស្អប់ matan អាចកំណត់មុខងារនៅក្នុងវិធីអាក្រក់ :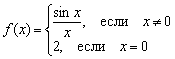


វាគួរឱ្យចាប់អារម្មណ៍ដែលលក្ខខណ្ឌបន្តពីរដំបូងត្រូវបានពេញចិត្តនៅទីនេះ:
1) - មុខងារត្រូវបានកំណត់នៅចំណុចដែលបានផ្តល់ឱ្យ;
2) - មានដែនកំណត់ទូទៅ។

ប៉ុន្តែព្រំដែនទីបីមិនត្រូវបានឆ្លងកាត់ទេ: នោះគឺដែនកំណត់នៃមុខងារនៅចំណុច មិនស្មើគ្នាតម្លៃនៃមុខងារដែលបានផ្តល់ឱ្យនៅចំណុចដែលបានផ្តល់ឱ្យ។

ដូច្នេះ នៅចំណុចមួយ មុខងារទទួលរងការមិនដំណើរការ។

ករណីទីពីរ សោកសៅត្រូវបានគេហៅថា ការបែកបាក់នៃប្រភេទទីមួយ ជាមួយនឹងការលោតមួយ។. ហើយ​ភាព​សោកសៅ​គឺ​កើត​ឡើង​ដោយ​ការ​កំណត់​តែ​ម្ខាង កំណត់និងខុសគ្នា. ឧទាហរណ៍មួយត្រូវបានបង្ហាញនៅក្នុងគំនូរទីពីរនៃមេរៀន។ គម្លាតបែបនេះជាធម្មតាកើតឡើងនៅពេល មុខងារដែលបានកំណត់ដោយផ្នែកដែលត្រូវបានរៀបរាប់រួចហើយនៅក្នុងអត្ថបទ អំពីការផ្លាស់ប្តូរក្រាហ្វ.

ពិចារណាមុខងារជាផ្នែក ហើយយើងនឹងបញ្ចប់គំនូររបស់វា។ របៀបបង្កើតក្រាហ្វ? សាមញ្ញ​ណាស់។ នៅពាក់កណ្តាលចន្លោះពេលយើងគូរបំណែកនៃប៉ារ៉ាបូឡាមួយ ( ពណ៌បៃតង) នៅចន្លោះពេល - ផ្នែកបន្ទាត់ត្រង់ (ក្រហម) និងពាក់កណ្តាលចន្លោះ - បន្ទាត់ត្រង់ (ពណ៌ខៀវ) ។

លើសពីនេះទៅទៀត ដោយសារវិសមភាព តម្លៃត្រូវបានកំណត់សម្រាប់អនុគមន៍បួនជ្រុង (ចំណុចពណ៌បៃតង) ហើយដោយសារវិសមភាព តម្លៃត្រូវបានកំណត់សម្រាប់ មុខងារលីនេអ៊ែរ(ចំណុចពណ៌ខៀវ)៖

ក្នុង​ករណី​លំបាក​បំផុត អ្នក​គួរ​ងាក​ទៅ​រក​ការ​ស្ថាបនា​ចំណុច​ដោយ​ចំណុច​នៃ​បំណែក​នីមួយៗ​នៃ​ក្រាហ្វ (មើល​ទីមួយ មេរៀនអំពីក្រាហ្វនៃមុខងារ).

ឥឡូវនេះយើងនឹងចាប់អារម្មណ៍តែលើចំណុចប៉ុណ្ណោះ។ ចូរ​យើង​ពិនិត្យ​មើល​វា​ជា​បន្តបន្ទាប់៖

2) ចូរយើងគណនាដែនកំណត់ម្ខាង។

នៅខាងឆ្វេងយើងមានផ្នែកបន្ទាត់ក្រហម ដូច្នេះដែនកំណត់ខាងឆ្វេងគឺ៖

នៅខាងស្តាំគឺជាបន្ទាត់ត្រង់ពណ៌ខៀវ ហើយដែនកំណត់ខាងស្តាំ៖

ជាលទ្ធផលយើងទទួលបាន ចំនួនកំណត់, ហើយ​ពួក​គេ មិនស្មើគ្នា. ចាប់តាំងពីដែនកំណត់ម្ខាង កំណត់និងខុសគ្នា: បន្ទាប់មកមុខងាររបស់យើងអត់ធ្មត់ ភាពមិនដំណើរការនៃប្រភេទទីមួយជាមួយនឹងការលោត.

វាជាឡូជីខលដែលគម្លាតមិនអាចត្រូវបានលុបចោល - មុខងារពិតជាមិនអាចត្រូវបានកំណត់បន្ថែមទៀតនិង "ស្អិតជាប់ជាមួយគ្នា" ដូចនៅក្នុងឧទាហរណ៍មុន។

ចំណុចដាច់នៃប្រភេទទីពីរ

ជាធម្មតា ករណីផ្សេងទៀតនៃការប្រេះឆាត្រូវបានចាត់ថ្នាក់យ៉ាងឆ្លាតវៃទៅក្នុងប្រភេទនេះ។ ខ្ញុំនឹងមិនរាយបញ្ជីអ្វីគ្រប់យ៉ាងទេព្រោះនៅក្នុងការអនុវត្តជាក់ស្តែងក្នុង 99% នៃបញ្ហាដែលអ្នកនឹងជួបប្រទះ គម្លាតគ្មានទីបញ្ចប់- នៅពេលដែលដៃឆ្វេង ឬដៃស្តាំ ហើយច្រើនដង ដែនកំណត់ទាំងពីរគឺគ្មានកំណត់។

ហើយជាការពិតណាស់ រូបភាពច្បាស់បំផុតគឺអ៊ីពែបូឡានៅចំណុចសូន្យ។ នៅទីនេះដែនកំណត់ទាំងសងខាងគឺគ្មានដែនកំណត់៖ ដូច្នេះ មុខងារទទួលរងការដាច់នៃប្រភេទទីពីរនៅចំណុច .

ខ្ញុំព្យាយាមបំពេញអត្ថបទរបស់ខ្ញុំជាមួយនឹងមាតិកាចម្រុះតាមដែលអាចធ្វើទៅបាន ដូច្នេះសូមមើលក្រាហ្វនៃមុខងារដែលមិនទាន់បានឃើញ៖

យោងតាមគ្រោងការណ៍ស្តង់ដារ៖

1) អនុគមន៍មិនត្រូវបានកំណត់នៅចំណុចនេះទេ ព្រោះភាគបែងទៅសូន្យ។

ជាការពិតណាស់ យើងអាចសន្និដ្ឋានបានភ្លាមៗថា មុខងារនេះទទួលរងនូវភាពមិនដំណើរការនៅចំណុច ប៉ុន្តែវាជាការល្អក្នុងការបែងចែកលក្ខណៈនៃភាពមិនដំណើរការ ដែលជារឿយៗត្រូវបានទាមទារដោយលក្ខខណ្ឌ។ សម្រាប់​ការ​នេះ:

ខ្ញុំសូមរំលឹកអ្នកថា តាមរយៈការថត យើងមានន័យ គ្មានដែនកំណត់ លេខអវិជ្ជមាន និងនៅក្រោមធាតុ - ចំនួនវិជ្ជមានគ្មានកំណត់.

ដែនកំណត់ម្ខាងគឺគ្មានកំណត់ ដែលមានន័យថាមុខងារទទួលរងការមិនបន្តនៃប្រភេទទី 2 នៅចំណុច។ អ័ក្ស y គឺ asymptote បញ្ឈរសម្រាប់ក្រាហ្វ។

វាមិនមែនជារឿងចម្លែកទេដែលដែនកំណត់ទាំងសងខាងមាន ប៉ុន្តែមានតែមួយក្នុងចំនោមពួកគេគឺគ្មានដែនកំណត់ ឧទាហរណ៍៖

នេះគឺជាក្រាហ្វនៃមុខងារ។

យើងពិនិត្យមើលចំណុចសម្រាប់បន្ត៖

1) មុខងារមិនត្រូវបានកំណត់នៅចំណុចនេះទេ។

២) ចូរយើងគណនាដែនកំណត់ម្ខាង៖

យើងនឹងនិយាយអំពីវិធីសាស្រ្តនៃការគណនាដែនកំណត់ម្ខាងបែបនេះនៅក្នុងឧទាហរណ៍ពីរចុងក្រោយនៃការបង្រៀន ទោះបីជាអ្នកអានជាច្រើនបានឃើញ និងទាយអ្វីៗគ្រប់យ៉ាងរួចហើយក៏ដោយ។

ដែនកំណត់ខាងឆ្វេងគឺកំណត់ និងស្មើសូន្យ (យើង "មិនទៅចំណុចខ្លួនឯងទេ") ប៉ុន្តែដែនកំណត់ខាងស្តាំគឺគ្មានដែនកំណត់ ហើយសាខាពណ៌ទឹកក្រូចនៃក្រាហ្វខិតជិតគ្មានដែនកំណត់ទៅនឹងរបស់វា។ asymptote បញ្ឈរ, ផ្តល់ដោយសមីការ(បន្ទាត់ចំនុចខ្មៅ) ។

ដូច្នេះមុខងារទទួលរង ភាពមិនទៀងទាត់នៃប្រភេទទីពីរនៅចំណុច។

ចំពោះភាពមិនដំណើរការនៃប្រភេទទី 1 មុខងារអាចត្រូវបានកំណត់នៅចំណុចដាច់ដោយខ្លួនវាផ្ទាល់។ ឧទាហរណ៍សម្រាប់មុខងារមួយដុំ មានអារម្មណ៍ថាមានសេរីភាពក្នុងការដាក់ចំណុចដិតខ្មៅនៅប្រភពដើមនៃកូអរដោនេ។ នៅខាងស្តាំគឺជាសាខានៃអ៊ីពែបូឡា ហើយដែនកំណត់ខាងស្តាំគឺគ្មានកំណត់។ ខ្ញុំគិតថាស្ទើរតែគ្រប់គ្នាមានគំនិតអំពីអ្វីដែលក្រាហ្វនេះមើលទៅ។

អ្វីដែលគ្រប់គ្នាទន្ទឹងរង់ចាំ៖

តើធ្វើដូចម្តេចដើម្បីពិនិត្យមើលមុខងារសម្រាប់ការបន្ត?

ការសិក្សាអំពីមុខងារសម្រាប់ការបន្តនៅចំណុចមួយត្រូវបានអនុវត្តតាមគ្រោងការណ៍ទម្លាប់ដែលបានបង្កើតឡើងរួចហើយ ដែលរួមមានការត្រួតពិនិត្យលក្ខខណ្ឌបីនៃការបន្ត៖

ឧទាហរណ៍ ១

មុខងាររុករក

ដំណោះស្រាយ:

1) ចំណុចតែមួយគត់នៅក្នុងវិសាលភាពគឺកន្លែងដែលមុខងារមិនត្រូវបានកំណត់។

២) ចូរយើងគណនាដែនកំណត់ម្ខាង៖

ដែនកំណត់ម្ខាងគឺកំណត់ និងស្មើគ្នា។

ដូច្នេះ នៅចំណុចនេះ មុខងារទទួលរងនូវការដាច់ដែលអាចដកចេញបាន។

តើក្រាហ្វនៃមុខងារនេះមើលទៅដូចអ្វី?

ខ្ញុំចង់ធ្វើឱ្យសាមញ្ញ ហើយវាហាក់ដូចជាប៉ារ៉ាបូឡាធម្មតាត្រូវបានទទួល។ ប៉ុន្តែមុខងារដើមមិនត្រូវបានកំណត់នៅចំណុចទេ ដូច្នេះឃ្លាខាងក្រោមត្រូវបានទាមទារ៖

តោះធ្វើគំនូរ៖

ចម្លើយ៖ មុខងារគឺបន្តនៅលើបន្ទាត់លេខទាំងមូល លើកលែងតែចំណុចដែលវាទទួលរងនូវការដាច់ដែលអាចដកចេញបាន។

មុខងារអាចត្រូវបានកំណត់បន្ថែមទៀតនៅក្នុងវិធីល្អ ឬមិនល្អ ប៉ុន្តែយោងទៅតាមលក្ខខណ្ឌនេះមិនត្រូវបានទាមទារទេ។

អ្នកនិយាយថានេះជាឧទាហរណ៍ឆ្ងាយ? មិនមែនទាល់តែសោះ។ រឿងនេះបានកើតឡើងរាប់សិបដងក្នុងការអនុវត្ត។ ស្ទើរតែទាំងអស់នៃភារកិច្ចរបស់គេហទំព័របានមកពីការងារឯករាជ្យពិតប្រាកដ និងការសាកល្បង។

តោះកម្ចាត់ម៉ូឌុលដែលយើងចូលចិត្ត៖

ឧទាហរណ៍ ២

មុខងាររុករក សម្រាប់ការបន្ត។ កំណត់លក្ខណៈនៃការឈប់ដំណើរការមុខងារ ប្រសិនបើវាមាន។ អនុវត្តគំនូរ។

ដំណោះស្រាយ៖ សម្រាប់ហេតុផលមួយចំនួន សិស្សមានការភ័យខ្លាច និងមិនចូលចិត្តមុខងារដែលមានម៉ូឌុល ទោះបីជាមិនមានអ្វីស្មុគស្មាញអំពីពួកវាក៏ដោយ។ យើង​បាន​ប៉ះ​រឿង​បែប​នេះ​បន្តិច​រួច​ហើយ​ក្នុង​មេរៀន។ ការបំប្លែងធរណីមាត្រនៃក្រាហ្វ. ដោយសារម៉ូឌុលមិនអវិជ្ជមាន វាត្រូវបានពង្រីកដូចខាងក្រោម៖ ដែលជាកន្លែងដែល "អាល់ហ្វា" គឺជាកន្សោមមួយចំនួន។ ក្នុងករណីនេះ ហើយមុខងាររបស់យើងគួរតែត្រូវបានសរសេរជាផ្នែកៗ៖

ប៉ុន្តែប្រភាគនៃបំណែកទាំងពីរត្រូវតែកាត់បន្ថយដោយ . ការកាត់បន្ថយដូចក្នុងឧទាហរណ៍មុននឹងមិនកើតឡើងដោយគ្មានផលវិបាកទេ។ អនុគមន៍ដើមមិនត្រូវបានកំណត់នៅចំណុចនោះទេ ចាប់តាំងពីភាគបែងទៅសូន្យ។ ដូច្នេះ ប្រព័ន្ធគួរតែបញ្ជាក់បន្ថែមពីលក្ខខណ្ឌ និងធ្វើឱ្យវិសមភាពទីមួយមានភាពតឹងរ៉ឹង៖

ឥឡូវនេះអំពីបច្ចេកទេសការសម្រេចចិត្តដ៏មានប្រយោជន៍៖ មុននឹងបញ្ចប់កិច្ចការលើសេចក្តីព្រាង វាមានអត្ថប្រយោជន៍ក្នុងការធ្វើគំនូរមួយ (មិនថាវាត្រូវបានទាមទារដោយលក្ខខណ្ឌ ឬអត់)។ ទីមួយ វានឹងជួយឱ្យឃើញភ្លាមៗនូវចំណុចនៃការបន្ត និងចំណុចនៃការមិនបន្ត ហើយទីពីរ វានឹងការពារអ្នក 100% ពីកំហុសនៅពេលរកឃើញដែនកំណត់ម្ខាង។

តោះធ្វើគំនូរ។ យោងទៅតាមការគណនារបស់យើងនៅខាងឆ្វេងនៃចំណុចវាចាំបាច់ត្រូវគូរបំណែកនៃប៉ារ៉ាបូឡា (ពណ៌ខៀវ) និងទៅខាងស្តាំ - បំណែកនៃប៉ារ៉ាបូល (ពណ៌ក្រហម) ខណៈពេលដែលមុខងារមិនត្រូវបានកំណត់នៅ ចង្អុលខ្លួនវា៖

ប្រសិនបើមានការសង្ស័យ ចូរយកតម្លៃ x ពីរបី ហើយដោតវាទៅក្នុងមុខងារ (ចងចាំថាម៉ូឌុលបំផ្លាញសញ្ញាដកដែលអាចកើតមាន) ហើយពិនិត្យមើលក្រាហ្វ។

ចូរយើងពិនិត្យមើលមុខងារសម្រាប់ការវិភាគបន្ត៖

1) មុខងារមិនត្រូវបានកំណត់នៅចំណុចនោះទេ ដូច្នេះយើងអាចនិយាយបានភ្លាមៗថាវាមិនបន្តនៅវាទេ។

2) ចូរបង្កើតលក្ខណៈនៃភាពមិនស៊ីសង្វាក់គ្នា ដើម្បីធ្វើវា យើងគណនាដែនកំណត់ម្ខាង៖

ដែនកំណត់ម្ខាងគឺកំណត់ និងខុសគ្នា ដែលមានន័យថា មុខងារទទួលរងការមិនបន្តនៃប្រភេទទី 1 ជាមួយនឹងការលោតនៅចំណុច។ ចំណាំម្តងទៀតថានៅពេលស្វែងរកដែនកំណត់ វាមិនមានបញ្ហាថាតើមុខងារនៅចំណុចបំបែកត្រូវបានកំណត់ឬអត់នោះទេ។

ឥឡូវនេះអ្វីៗដែលនៅសល់គឺត្រូវផ្ទេរគំនូរពីសេចក្តីព្រាង (វាត្រូវបានធ្វើឡើងដូចជាដោយមានជំនួយពីការស្រាវជ្រាវ ;-)) ហើយបំពេញភារកិច្ច៖

ចម្លើយ៖ អនុគមន៍​គឺ​បន្ត​នៅ​លើ​បន្ទាត់​លេខ​ទាំង​មូល លើក​លែង​តែ​ចំណុច​ដែល​វា​ទទួល​រង​ការ​ដាច់​នៃ​ប្រភេទ​ទី​មួយ​ដោយ​ការ​លោត។

ពេលខ្លះពួកគេទាមទារការចង្អុលបង្ហាញបន្ថែមអំពីការលោតមិនបន្ត។ វាត្រូវបានគណនាយ៉ាងសាមញ្ញ - ពីដែនកំណត់ខាងស្តាំអ្នកត្រូវដកដែនកំណត់ខាងឆ្វេង: នោះគឺនៅចំណុចបំបែកមុខងាររបស់យើងលោត 2 ឯកតាចុះ (ដូចសញ្ញាដកប្រាប់យើង) ។

ឧទាហរណ៍ ៣

មុខងាររុករក សម្រាប់ការបន្ត។ កំណត់លក្ខណៈនៃការឈប់ដំណើរការមុខងារ ប្រសិនបើវាមាន។ ធ្វើគំនូរ។

នេះគឺជាឧទាហរណ៍សម្រាប់ ការសម្រេចចិត្តឯករាជ្យដំណោះស្រាយគំរូនៅចុងបញ្ចប់នៃមេរៀន។

ចូរបន្តទៅកំណែដែលពេញនិយម និងរីករាលដាលបំផុតនៃភារកិច្ច នៅពេលដែលមុខងារមានបីផ្នែក៖

ឧទាហរណ៍ 4

ពិនិត្យមុខងារមួយសម្រាប់ភាពបន្ត និងគ្រោងក្រាហ្វនៃអនុគមន៍ .

ដំណោះស្រាយ៖ វាច្បាស់ណាស់ថាផ្នែកទាំងបីនៃមុខងារបន្តនៅចន្លោះពេលដែលត្រូវគ្នា ដូច្នេះវានៅតែត្រូវពិនិត្យមើលតែពីរចំណុចនៃ "ប្រសព្វ" រវាងបំណែក។ ជាដំបូង ចូរយើងបង្កើតគំនូរព្រាងមួយ ខ្ញុំបានធ្វើអត្ថាធិប្បាយលើបច្ចេកទេសសាងសង់ដោយលម្អិតគ្រប់គ្រាន់នៅក្នុងផ្នែកដំបូងនៃអត្ថបទ។ រឿងតែមួយគត់គឺថាយើងត្រូវអនុវត្តតាមចំណុចឯកវចនៈរបស់យើងដោយប្រុងប្រយ័ត្ន៖ ដោយសារវិសមភាព តម្លៃជារបស់បន្ទាត់ត្រង់ (ចំណុចពណ៌បៃតង) ហើយដោយសារវិសមភាព តម្លៃជាកម្មសិទ្ធិរបស់ប៉ារ៉ាបូឡា (ចំណុចក្រហម)៖


ជាការប្រសើរណាស់ ជាគោលការណ៍ អ្វីគ្រប់យ៉ាងគឺច្បាស់ =) អ្វីទាំងអស់ដែលនៅសេសសល់គឺដើម្បីធ្វើការសម្រេចចិត្តជាផ្លូវការ។ សម្រាប់ចំណុច "ចូលរួម" នីមួយៗ យើងពិនិត្យមើលលក្ខខណ្ឌបន្តចំនួន 3 តាមស្តង់ដារ៖

ខ្ញុំ)យើងពិនិត្យមើលចំណុចដើម្បីបន្ត

1)

ដែនកំណត់ម្ខាងគឺកំណត់ និងខុសគ្នា ដែលមានន័យថា មុខងារទទួលរងការមិនបន្តនៃប្រភេទទី 1 ជាមួយនឹងការលោតនៅចំណុច។

ចូរ​យើង​គណនា​ការ​លោត​មិន​ជាប់​គ្នា​ជា​ភាព​ខុស​គ្នា​រវាង​ដែន​កំណត់​ខាង​ស្ដាំ និង​ឆ្វេង៖
នោះ​គឺ​ថា​ក្រាហ្វ​បាន​លោត​ឡើង​មួយ​ឯកតា។

II)យើងពិនិត្យមើលចំណុចដើម្បីបន្ត

1) - មុខងារត្រូវបានកំណត់នៅចំណុចជាក់លាក់មួយ។

២) ស្វែងរកដែនកំណត់ម្ខាង៖

- ដែនកំណត់ម្ខាងគឺកំណត់ និងស្មើគ្នា ដែលមានន័យថាមានដែនកំណត់ទូទៅ។

3) - ដែនកំណត់នៃអនុគមន៍នៅចំណុចមួយគឺស្មើនឹងតម្លៃនៃអនុគមន៍នេះនៅចំណុចដែលបានផ្តល់ឱ្យ។

នៅដំណាក់កាលចុងក្រោយ យើងផ្ទេរគំនូរទៅកំណែចុងក្រោយ បន្ទាប់មកយើងដាក់អង្កត់ធ្នូចុងក្រោយ៖

ចម្លើយ៖ អនុគមន៍​គឺ​បន្ត​នៅ​តាម​បន្ទាត់​លេខ​ទាំង​មូល លើក​លែង​តែ​ចំណុច​ដែល​វា​រង​ការ​ដាច់​នៃ​ប្រភេទ​ទី​មួយ​ដោយ​លោត។

ឧទាហរណ៍ 5

ពិនិត្យមុខងារមួយសម្រាប់ការបន្ត និងបង្កើតក្រាហ្វរបស់វា។ .

នេះគឺជាឧទាហរណ៍សម្រាប់ដំណោះស្រាយឯករាជ្យ ដំណោះស្រាយខ្លីៗ និងគំរូប្រហាក់ប្រហែលនៃបញ្ហានៅចុងបញ្ចប់នៃមេរៀន។

អ្នកអាចទទួលបានការចាប់អារម្មណ៍ថា នៅចំណុចមួយ មុខងារត្រូវតែបន្ត ហើយនៅពេលមួយទៀត ត្រូវតែមានការឈប់ដំណើរការ។ នៅក្នុងការអនុវត្តនេះមិនតែងតែជាករណីនោះទេ។ ព្យាយាមមិនឱ្យធ្វេសប្រហែសឧទាហរណ៍ដែលនៅសល់ - វានឹងមានលក្ខណៈពិសេសគួរឱ្យចាប់អារម្មណ៍និងសំខាន់មួយចំនួន:

ឧទាហរណ៍ ៦

បានផ្តល់មុខងារមួយ។ . ស៊ើបអង្កេតមុខងារសម្រាប់បន្តនៅចំណុច។ បង្កើតក្រាហ្វ។

ដំណោះស្រាយ៖ ហើយ​អនុវត្ត​គំនូរ​លើ​សេចក្តី​ព្រាង​ជា​ថ្មី​ម្តង​ទៀត​ភ្លាមៗ៖

ភាពប្លែកនៃក្រាហ្វនេះគឺថា អនុគមន៍ដុំត្រូវបានផ្តល់ដោយសមីការនៃអ័ក្ស abscissa ។ នៅទីនេះតំបន់នេះត្រូវបានគូរជាពណ៌បៃតង ប៉ុន្តែនៅក្នុងសៀវភៅកត់ត្រា ជាធម្មតាវាត្រូវបានគូសជាដិតដោយប្រើខ្មៅដៃសាមញ្ញ។ ហើយជាការពិតណាស់ កុំភ្លេចអំពីចៀមឈ្មោលរបស់យើង៖ តម្លៃជាកម្មសិទ្ធិរបស់សាខាតង់សង់ (ចំណុចក្រហម) ហើយតម្លៃជាកម្មសិទ្ធិរបស់បន្ទាត់ត្រង់។

អ្វីគ្រប់យ៉ាងគឺច្បាស់លាស់ពីគំនូរ - មុខងារគឺបន្តតាមបណ្តោយបន្ទាត់លេខទាំងមូលដែលអ្វីទាំងអស់ដែលនៅសល់គឺការរៀបចំដំណោះស្រាយជាផ្លូវការដែលត្រូវបាននាំយកទៅស្វ័យប្រវត្តិកម្មពេញលេញតាមព្យញ្ជនៈបន្ទាប់ពីឧទាហរណ៍ 3-4 ស្រដៀងគ្នា:

ខ្ញុំ)យើងពិនិត្យមើលចំណុចដើម្បីបន្ត

1) - មុខងារត្រូវបានកំណត់នៅចំណុចដែលបានផ្តល់ឱ្យ។

២) ចូរយើងគណនាដែនកំណត់ម្ខាង៖

ដែលមានន័យថាមានដែនកំណត់ទូទៅ។

ក្នុង​ករណី​នេះ ខ្ញុំ​សូម​រំលឹក​អ្នក​ពី​ការ​ពិត​មួយ​ចំនួន៖ កម្រិត​នៃ​ថេរ​គឺ​ស្មើ​នឹង​ថេរ​ខ្លួន​វា។ ក្នុងករណីនេះដែនកំណត់នៃសូន្យគឺស្មើនឹងសូន្យខ្លួនឯង (ដែនកំណត់នៃដៃឆ្វេង) ។

3) - ដែនកំណត់នៃអនុគមន៍នៅចំណុចមួយគឺស្មើនឹងតម្លៃនៃអនុគមន៍នេះនៅចំណុចដែលបានផ្តល់ឱ្យ។

ដូច្នេះ អនុគមន៍មួយគឺបន្តនៅចំណុចមួយដោយនិយមន័យនៃការបន្តនៃអនុគមន៍នៅចំណុចមួយ។

II)យើងពិនិត្យមើលចំណុចដើម្បីបន្ត

1) - មុខងារត្រូវបានកំណត់នៅចំណុចដែលបានផ្តល់ឱ្យ។

២) ស្វែងរកដែនកំណត់ម្ខាង៖

ហើយនៅទីនេះ - ដែនកំណត់នៃមួយគឺស្មើនឹងឯកតាខ្លួនឯង។

- មានដែនកំណត់ទូទៅ។

3) - ដែនកំណត់នៃអនុគមន៍នៅចំណុចមួយគឺស្មើនឹងតម្លៃនៃអនុគមន៍នេះនៅចំណុចដែលបានផ្តល់ឱ្យ។

ដូច្នេះ អនុគមន៍មួយគឺបន្តនៅចំណុចមួយដោយនិយមន័យនៃការបន្តនៃអនុគមន៍នៅចំណុចមួយ។

ដូចធម្មតា បន្ទាប់ពីការស្រាវជ្រាវ យើងផ្ទេរគំនូររបស់យើងទៅកំណែចុងក្រោយ។

ចម្លើយ៖ មុខងារគឺបន្តនៅចំណុច។

សូមចំណាំថានៅក្នុងលក្ខខណ្ឌយើងមិនត្រូវបានសួរអ្វីទាំងអស់អំពីការសិក្សាមុខងារទាំងមូលសម្រាប់ការបន្ត ហើយវាត្រូវបានចាត់ទុកថាជាទម្រង់គណិតវិទ្យាដ៏ល្អសម្រាប់បង្កើត ច្បាស់លាស់ និងច្បាស់លាស់ចម្លើយចំពោះសំណួរដែលបានដាក់។ និយាយអីញ្ចឹង ប្រសិនបើលក្ខខណ្ឌមិនតម្រូវឱ្យអ្នកបង្កើតក្រាហ្វទេ នោះអ្នកមានសិទ្ធិទាំងអស់មិនបង្កើតវាទេ (ទោះបីជាគ្រូអាចបង្ខំអ្នកឱ្យធ្វើវានៅពេលក្រោយក៏ដោយ) ។

គណិតវិទ្យាតូចមួយ "អណ្តាតរុញ" សម្រាប់ដោះស្រាយវាដោយខ្លួនឯង៖

ឧទាហរណ៍ ៧

បានផ្តល់មុខងារមួយ។ 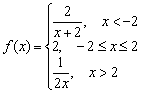. ស៊ើបអង្កេតមុខងារសម្រាប់បន្តនៅចំណុច។ ចាត់ថ្នាក់ចំណុចឈប់ប្រសិនបើមាន។ អនុវត្តគំនូរ។

ព្យាយាម "បញ្ចេញ" "ពាក្យ" ទាំងអស់ឱ្យបានត្រឹមត្រូវ =) ហើយគូរក្រាហ្វឱ្យកាន់តែច្បាស់ ភាពត្រឹមត្រូវ វានឹងមិននាំអោយមានគ្រប់ទីកន្លែង ;-)

ដូចដែលអ្នកចងចាំ ខ្ញុំបានណែនាំឱ្យបំពេញគំនូរភ្លាមៗជាសេចក្តីព្រាង ប៉ុន្តែយូរៗម្តងអ្នកឃើញឧទាហរណ៍ ដែលអ្នកមិនអាចដឹងភ្លាមៗថាតើក្រាហ្វមើលទៅដូចអ្វី។ ហេតុដូច្នេះហើយ ក្នុងករណីខ្លះ វាជាការប្រសើរក្នុងការស្វែងរកដែនកំណត់ម្ខាងៗជាមុនសិន ហើយមានតែបន្ទាប់មកដោយផ្អែកលើការសិក្សា ពិពណ៌នាអំពីសាខា។ នៅក្នុងឧទាហរណ៍ពីរចុងក្រោយ យើងក៏នឹងរៀនពីបច្ចេកទេសសម្រាប់គណនាដែនកំណត់ម្ខាងៗមួយចំនួនផងដែរ៖

ឧទាហរណ៍ ៨

ពិនិត្យមុខងារសម្រាប់ភាពបន្ត និងបង្កើតក្រាហ្វគ្រោងការណ៍របស់វា។

ដំណោះស្រាយ៖ ចំណុចអាក្រក់គឺជាក់ស្តែង៖ (កាត់បន្ថយភាគបែងនៃនិទស្សន្តទៅជាសូន្យ) និង (កាត់បន្ថយភាគបែងនៃប្រភាគទាំងមូលទៅសូន្យ)។ វាមិនច្បាស់ថាក្រាហ្វនៃមុខងារនេះមើលទៅដូចអ្វី ដែលមានន័យថា វាជាការប្រសើរជាងមុនក្នុងការស្រាវជ្រាវមួយចំនួន។

តូប៉ូឡូញ- សាខានៃគណិតវិទ្យាដែលទាក់ទងនឹងការសិក្សាអំពីដែនកំណត់ និងការបន្តនៃអនុគមន៍។ នៅក្នុងការរួមបញ្ចូលគ្នាជាមួយពិជគណិត, topology បង្កើតជាមូលដ្ឋានទូទៅនៃគណិតវិទ្យា។

លំហ topological ឬតួលេខ -សំណុំរងនៃលំហ Euclidean ដូចគ្នារបស់យើង រវាងចំនុចដែលទំនាក់ទំនងជិតស្និទ្ធជាក់លាក់មួយត្រូវបានផ្តល់ឱ្យ។ នៅទីនេះ តួរលេខត្រូវបានចាត់ទុកថាមិនរឹងដូចវត្ថុរឹង ប៉ុន្តែជាវត្ថុដែលធ្វើពីកៅស៊ូយឺត ដែលអនុញ្ញាតឱ្យមានការខូចទ្រង់ទ្រាយជាបន្តបន្ទាប់ ដែលរក្សាបាននូវលក្ខណៈគុណភាពរបស់វា។

ការគូសផែនទីបន្តពីមួយទៅមួយត្រូវបានគេហៅថា homeomorphism. នៅក្នុងពាក្យផ្សេងទៀតតួលេខ homeomorphicប្រសិនបើមួយអាចត្រូវបានផ្ទេរទៅមួយផ្សេងទៀតដោយការខូចទ្រង់ទ្រាយជាបន្តបន្ទាប់។

ឧទាហរណ៍។ តួលេខខាងក្រោមគឺជា homeomorphic (តួលេខពីក្រុមផ្សេងៗគ្នាមិនមែនជា homeomorphic) បង្ហាញក្នុងរូប។ ២.

1. ចម្រៀក និងខ្សែកោងដោយគ្មានប្រសព្វដោយខ្លួនឯង។

2. រង្វង់, ខាងក្នុងនៃការ៉េ, ខ្សែបូ។

3. ស្វ៊ែរ ផ្ទៃនៃគូប និង tetrahedron ។

4. រង្វង់រាងពងក្រពើនិងរង្វង់ knotted ។

5. ចិញ្ចៀនមួយនៅលើយន្តហោះ (រង្វង់មួយដែលមានរន្ធ) ចិញ្ចៀននៅក្នុងលំហ, ចិញ្ចៀន twisted ពីរដង, ផ្ទៃចំហៀងនៃស៊ីឡាំងមួយ។

6. បន្ទះ Möbius, i.e. ចិញ្ចៀន​បង្វិល​មួយ​ដង និង​ចិញ្ចៀន​បង្វិល​បី​ដង។

7. ផ្ទៃនៃ torus (donut) រាងស្វ៊ែរជាមួយនឹងចំណុចទាញមួយនិង knotted torus មួយ។

8. ស្វ៊ែរដែលមានចំណុចទាញពីរនិង pretzel ដែលមានរន្ធពីរ។

IN ការវិភាគគណិតវិទ្យាមុខងារត្រូវបានសិក្សាដោយវិធីសាស្ត្រកំណត់។ អថេរ និងដែនកំណត់គឺជាគោលគំនិតជាមូលដ្ឋាន។

នៅក្នុងបាតុភូតផ្សេងៗ បរិមាណមួយចំនួនរក្សាតម្លៃជាលេខរបស់ពួកគេ ខ្លះទៀតផ្លាស់ប្តូរ។ សំណុំនៃតម្លៃលេខទាំងអស់នៃអថេរមួយត្រូវបានហៅ ជួរនៃការផ្លាស់ប្តូរនៃអថេរនេះ។.

ក្នុង​ចំណោម​វិធី​ផ្សេងៗ​ដែល​អថេរ​មាន​ឥរិយា​បទ សារៈសំខាន់​បំផុត​គឺ​វិធី​ដែល​អថេរ​មាន​ទំនោរ​ទៅ​នឹង​កម្រិត​ជាក់លាក់។

លេខថេរ កហៅ ដែនកំណត់អថេរប្រសិនបើតម្លៃដាច់ខាតនៃភាពខុសគ្នារវាង xនិង ក() ក្លាយជានៅក្នុងដំណើរការនៃការផ្លាស់ប្តូរតម្លៃអថេរ xតូចតាមការចង់បាន៖

តើ "តូចតាមចិត្ត" មានន័យដូចម្តេច? បរិមាណអថេរ Xទំនោរទៅដែនកំណត់ កប្រសិនបើសម្រាប់ចំនួនតូចតាមអំពើចិត្ត (តូចតាមអំពើចិត្ត) មានពេលបែបនេះនៅក្នុងការផ្លាស់ប្តូរនៃអថេរ Xចាប់ផ្តើមពីវិសមភាពដែលកាន់កាប់ .

និយមន័យនៃដែនកំណត់មានអត្ថន័យធរណីមាត្រសាមញ្ញ: វិសមភាព មានន័យថា Xស្ថិតនៅក្នុងសង្កាត់នៃចំណុច ក, ទាំងនោះ។ ក្នុងចន្លោះពេល .

ដូច្នេះនិយមន័យនៃដែនកំណត់អាចត្រូវបានផ្តល់ឱ្យ រាងធរណីមាត្រ:

ចំនួន កគឺជាដែនកំណត់នៃអថេរ Xប្រសិនបើសម្រាប់តូចតាមអំពើចិត្ត (តូចតាមអំពើចិត្ត) - អ្នកជិតខាងនៃលេខ កអ្នកអាចបញ្ជាក់ពេលវេលាបែបនេះក្នុងការផ្លាស់ប្តូរអថេរ Xចាប់ផ្តើមពីតម្លៃរបស់វាទាំងអស់ធ្លាក់ចូលទៅក្នុងតំបន់ដែលបានបញ្ជាក់ -neighborhood នៃចំណុច ក.

មតិយោបល់. បរិមាណអថេរ Xអាចចូលទៅដល់ដែនកំណត់របស់វាតាមវិធីផ្សេងៗគ្នា៖ នៅសល់តិចជាងដែនកំណត់នេះ (នៅខាងឆ្វេង) ច្រើនទៀត (នៅខាងស្តាំ) ប្រែប្រួលជុំវិញតម្លៃនៃដែនកំណត់។

ដែនកំណត់លំដាប់

មុខងារហៅថាច្បាប់ (ច្បាប់) តាមធាតុនីមួយៗ xសំណុំមួយចំនួន Xផ្គូផ្គងធាតុតែមួយ yសំណុំ យ.

មុខងារអាចត្រូវបានកំណត់លើសំណុំនៃលេខធម្មជាតិទាំងអស់៖ . មុខងារនេះត្រូវបានគេហៅថា មុខងារអាគុយម៉ង់ធម្មជាតិឬ លំដាប់លេខ.

ចាប់តាំងពីលំដាប់មួយ ដូចជាសំណុំគ្មានកំណត់ណាមួយ មិនអាចបញ្ជាក់ដោយការរាប់បញ្ចូលទេ វាត្រូវបានបញ្ជាក់ដោយពាក្យទូទៅ តើពាក្យទូទៅនៃលំដាប់នៅឯណា។

អថេរដាច់ពីគ្នា គឺជាពាក្យទូទៅនៃលំដាប់មួយ។

សម្រាប់ភាពស៊ីសង្វាក់គ្នា ពាក្យថា "ចាប់ផ្តើមនៅចំណុចខ្លះ" មានន័យថា "ចាប់ផ្តើមពីលេខមួយចំនួន"។

ចំនួន កហៅថាដែនកំណត់នៃលំដាប់ ប្រសិនបើលេខតូច (តូចតាមអំពើចិត្ត) មានលេខបែបនេះ នដែលសម្រាប់សមាជិកទាំងអស់នៃលំដាប់ដែលមានលេខ ន>នភាពមិនស្មើភាពកាន់កាប់ .

ឬ នៅ .

តាមធរណីមាត្រ និយមន័យនៃដែនកំណត់នៃលំដាប់មានអត្ថន័យដូចខាងក្រោម៖ សម្រាប់តូចតាមអំពើចិត្ត (តូចតាមអំពើចិត្ត) - អ្នកជិតខាងនៃចំនួន កមាន​ចំនួន​ដូច​ដែល​ពាក្យ​ទាំងអស់​នៃ​លំដាប់​ដែល​មាន​ធំ​ជាង នលេខ ធ្លាក់ចូលទៅក្នុងបរិវេណនេះ។ មានតែចំនួនកំណត់នៃលក្ខខណ្ឌដំបូងនៃលំដាប់ប៉ុណ្ណោះដែលលេចឡើងនៅខាងក្រៅសង្កាត់។ លេខធម្មជាតិ នអាស្រ័យ​លើ : .