បង្កើតក្រាហ្វនៃអនុគមន៍ជាមួយឧទាហរណ៍ម៉ូឌុល។ ក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរជាមួយម៉ូឌុល។ ករណីនៃអថេរផ្នែកខាងស្តាំ

Erdnigoryaeva ម៉ារីណា

ការងារ​នេះ​គឺ​ជា​លទ្ធផល​នៃ​ការ​សិក្សា​ប្រធានបទ​ជា​ការ​ជ្រើសរើស​នៅ​ថ្នាក់​ទី​៨។ ការបំប្លែងធរណីមាត្រនៃក្រាហ្វ និងការអនុវត្តរបស់ពួកគេចំពោះការសាងសង់ក្រាហ្វជាមួយម៉ូឌុលត្រូវបានបង្ហាញនៅទីនេះ។ គំនិតនៃម៉ូឌុល និងលក្ខណៈសម្បត្តិរបស់វាត្រូវបានណែនាំ។ វាត្រូវបានបង្ហាញពីរបៀបបង្កើតក្រាហ្វជាមួយម៉ូឌុលតាមវិធីផ្សេងៗ៖ ការប្រើប្រាស់ការបំប្លែង និងផ្អែកលើគោលគំនិតនៃម៉ូឌុល។ ប្រធានបទនៃគម្រោងគឺជាផ្នែកមួយនៃការពិបាកបំផុតក្នុងវគ្គសិក្សាគណិតវិទ្យា វាទាក់ទងនឹងបញ្ហាដែលត្រូវបានពិចារណាក្នុងការជ្រើសរើស និងជា បានសិក្សាក្នុងថ្នាក់ជាមួយគណិតវិទ្យាកម្រិតខ្ពស់។ ទោះជាយ៉ាងណាក៏ដោយភារកិច្ចបែបនេះត្រូវបានផ្តល់ឱ្យនៅក្នុងផ្នែកទីពីរនៃ GIA នៅក្នុងការប្រឡងរដ្ឋបង្រួបបង្រួម។ ការងារនេះនឹងជួយអ្នកឱ្យយល់ពីរបៀបបង្កើតក្រាហ្វជាមួយម៉ូឌុលមិនត្រឹមតែលីនេអ៊ែរប៉ុណ្ណោះទេ ប៉ុន្តែក៏មានមុខងារផ្សេងទៀតផងដែរ (ការ៉េ សមាមាត្រច្រាស។

ទាញយក៖

មើលជាមុន៖

ដើម្បីប្រើការមើលការបង្ហាញជាមុន បង្កើតគណនី Google ហើយចូលទៅវា៖ https://accounts.google.com

ចំណងជើងស្លាយ៖

ក្រាហ្វនៃមុខងារលីនេអ៊ែរជាមួយម៉ូឌុល ការងារដោយ Erdnigoryaeva Marina សិស្សថ្នាក់ទី 8 នៃ MCOU "Kamyshovskaya OOSH" អ្នកគ្រប់គ្រង Goryaeva Zoya Erdnigoryaevna គ្រូបង្រៀនគណិតវិទ្យា MCOU "Kamyshovskaya OOSH" ទំ។ Kamyshevo, 2013

គោលដៅគម្រោង៖ ដើម្បីឆ្លើយសំណួរអំពីរបៀបបង្កើតក្រាហ្វនៃមុខងារលីនេអ៊ែរជាមួយម៉ូឌុល។ គោលបំណងនៃគម្រោង៖ សិក្សាអក្សរសិល្ប៍លើបញ្ហានេះ។ សិក្សាការបំប្លែងធរណីមាត្រនៃក្រាហ្វ និងការអនុវត្តរបស់ពួកគេចំពោះការសាងសង់ក្រាហ្វជាមួយម៉ូឌុល។ សិក្សាគោលគំនិតនៃម៉ូឌុល និងលក្ខណៈសម្បត្តិរបស់វា។ រៀនបង្កើតក្រាហ្វជាមួយម៉ូឌុលតាមវិធីផ្សេងៗ។

Direct proportionality សមាមាត្រដោយផ្ទាល់គឺជាអនុគមន៍ដែលអាចត្រូវបានបញ្ជាក់ដោយរូបមន្តនៃទម្រង់ y=kx ដែល x ជាអថេរឯករាជ្យ k ជាចំនួនមិនមែនសូន្យ។

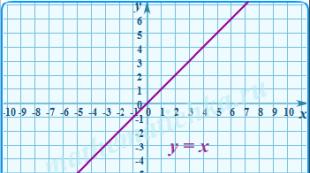
ចូរយើងរៀបចំអនុគមន៍ y = x x 0 2 y 0 2

ការបំប្លែងធរណីមាត្រនៃក្រាហ្វ ក្បួនលេខ 1 ក្រាហ្វនៃអនុគមន៍ y = f (x) + k - អនុគមន៍លីនេអ៊ែរ - ត្រូវបានទទួលដោយការផ្ទេរប៉ារ៉ាឡែលនៃក្រាហ្វនៃអនុគមន៍ y = f (x) ដោយ + k ឡើងលើ O y axis សម្រាប់ k> 0 ឬ |- k| ឯកតាចុះក្រោមអ័ក្ស O y នៅ k

ចូរយើងបង្កើតក្រាហ្វ y=x+3 y=x-2

ច្បាប់លេខ 2 ក្រាហ្វនៃអនុគមន៍ y=kf(x) ត្រូវបានទទួលដោយការលាតសន្ធឹងក្រាហ្វនៃអនុគមន៍ y = f (x) តាមអ័ក្ស O y a ដងនៅ a> 1 ហើយបង្ហាប់វាតាមអ័ក្ស O y a ដងនៅ 0 ស្លាយទី 9

ចូរយើងបង្កើតក្រាហ្វ y = x y = 2 x

ច្បាប់លេខ 3 ក្រាហ្វនៃអនុគមន៍ y = - f (x) ត្រូវបានទទួលដោយការបង្ហាញស៊ីមេទ្រីនៃក្រាហ្វ y = f (x) ទាក់ទងទៅនឹងអ័ក្ស O x

ច្បាប់លេខ 4 ក្រាហ្វនៃអនុគមន៍ y = f (- x) ត្រូវបានទទួលដោយការបង្ហាញស៊ីមេទ្រីនៃក្រាហ្វនៃអនុគមន៍ y = f (x) ទាក់ទងទៅនឹងអ័ក្ស O y

ក្បួនលេខ 5 ក្រាហ្វនៃអនុគមន៍ y=f(x+c) ត្រូវបានទទួលដោយការផ្ទេរប៉ារ៉ាឡែលនៃក្រាហ្វនៃអនុគមន៍ y=f(x) តាមអ័ក្ស O x ទៅខាងស្តាំ ប្រសិនបើ c 0 ។

តោះបង្កើតក្រាហ្វ y=f(x) y=f(x+2)

និយមន័យនៃម៉ូឌុល ម៉ូឌុលនៃចំនួនមិនអវិជ្ជមាន a គឺស្មើនឹងចំនួន a ខ្លួនវា; ម៉ូឌុលនៃចំនួនអវិជ្ជមាន a គឺស្មើនឹងចំនួនវិជ្ជមានផ្ទុយរបស់វា -a ។ ឬ |a|=a ប្រសិនបើ a ≥0 |a|=-a ប្រសិនបើ a

ក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរជាមួយម៉ូឌុលត្រូវបានសាងសង់៖ ដោយប្រើការបំប្លែងធរណីមាត្រដោយពង្រីកនិយមន័យនៃម៉ូឌុល។

ក្បួនលេខ 6 ក្រាហ្វនៃអនុគមន៍ y=|f(x)| ត្រូវបានទទួលដូចខាងក្រោមៈ ផ្នែកនៃក្រាហ្វ y = f (x) ដែលស្ថិតនៅខាងលើអ័ក្ស O x ត្រូវបានបម្រុងទុក។ ផ្នែកដែលស្ថិតនៅក្រោមអ័ក្ស O x ត្រូវបានបង្ហាញស៊ីមេទ្រីទាក់ទងទៅនឹងអ័ក្ស O x ។

ក្រាហ្វនៃអនុគមន៍ y=-2| x-3|+4 ស្ថាបនា y ₁=| x | យើងបង្កើត y₂= |x − 3 | → ការបកប្រែស្របគ្នាដោយ +3 ឯកតាតាមអ័ក្សអុក (ប្តូរទៅខាងស្តាំ) យើងសង់ y ₃ =+2|x-3| → លាតសន្ធឹងតាមអ័ក្ស O y 2 ដង = 2 y₂ យើងបង្កើត y ₄ =-2|x-3| → ស៊ីមេទ្រីអំពីអ័ក្ស x = - y₃ យើងបង្កើត y₅ =-2|x-3|+4 → ការបកប្រែប៉ារ៉ាឡែលដោយ +4 ឯកតាតាមអ័ក្ស O y (ការផ្លាស់ប្តូរឡើងលើ) = y ₄ +4

ក្រាហ្វនៃអនុគមន៍ y =-2|x-3|+4

ក្រាហ្វនៃអនុគមន៍ y= 3|x|+2 y₁=|x| y₂=3|x|= 3 y₁ → លាតសន្ធឹង 3 ដង y₃=3|x| +2= y₄+2 → ផ្លាស់ប្តូរឡើង 2 ឯកតា

ច្បាប់លេខ 7 ក្រាហ្វនៃអនុគមន៍ y=f(| x |) ត្រូវបានទទួលពីក្រាហ្វនៃអនុគមន៍ y=f(x) ដូចតទៅ៖ សម្រាប់ x > 0 ក្រាហ្វនៃអនុគមន៍ត្រូវបានរក្សាទុក ហើយដូចគ្នា ផ្នែកនៃក្រាហ្វត្រូវបានបង្ហាញស៊ីមេទ្រីទាក់ទងទៅនឹងអ័ក្ស O y

ក្រាហ្វនៃអនុគមន៍ y = || x-1 | -២ |

Y₁= |x| y₂=|x-1| y₃= y₂-2 y₄= |y₃| Y=||x-1|-2|

ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វនៃអនុគមន៍ y=│f(│x│)│ បង្កើតក្រាហ្វនៃអនុគមន៍ y=f(│x│) ។ បន្ទាប់មកទុកផ្នែកទាំងអស់នៃក្រាហ្វដែលបានសាងសង់មិនផ្លាស់ប្តូរដែលស្ថិតនៅខាងលើអ័ក្ស x ។ ផ្នែកដែលមានទីតាំងនៅខាងក្រោមអ័ក្ស x ត្រូវបានបង្ហាញស៊ីមេទ្រីអំពីអ័ក្សនេះ។

យ=|2|x|-3| សំណង់៖ ក) y=2x-3 សម្រាប់ x>0, b) y=-2x-3 សម្រាប់ x ស្លាយ 26

វិធាន #8 ក្រាហ្វភាពអាស្រ័យ | y|=f(x) ត្រូវបានទទួលពីក្រាហ្វនៃអនុគមន៍ y=f(x) ប្រសិនបើចំណុចទាំងអស់ដែល f(x) > 0 ត្រូវបានរក្សា ហើយពួកវាក៏ត្រូវបានផ្ទេរដោយស៊ីមេទ្រីទាក់ទងទៅនឹងអ័ក្ស abscissa ផងដែរ។

បង្កើតសំណុំនៃចំណុចនៅលើយន្តហោះដែល Cartesian សំរបសំរួល x និង y បំពេញសមីការ |y|=||x-1|-1| ។

| y|=||x-1| -1| យើងបង្កើតក្រាហ្វពីរ 1) y=||x-1|-1| និង 2) y =-|| x-1|-1| y₁=|x| y₂=| x-1 | → ប្តូរតាមអ័ក្សអុកទៅខាងស្តាំដោយ 1 ឯកតា y₃ = | x −1 |- 1= → ប្តូរចុះក្រោម 1 ឯកតា y ₄ = || x-1|- 1| → ស៊ីមេទ្រីនៃចំណុចក្រាហ្វដែល y₃ 0 ទាក់ទងទៅនឹង O x

ក្រាហ្វនៃសមីការ |y|=||x-1|-1| យើងទទួលបានដូចខាងក្រោម៖ 1) បង្កើតក្រាហ្វនៃអនុគមន៍ y=f(x) ហើយទុកផ្នែកនោះមិនផ្លាស់ប្តូរដែល y≥0 2) ដោយប្រើស៊ីមេទ្រីអំពីអ័ក្សអុក បង្កើតផ្នែកផ្សេងទៀតនៃក្រាហ្វដែលត្រូវនឹង y

ក្រាហ្វនៃអនុគមន៍ y =|x| − | 2 − x | . ដំណោះស្រាយ។ នៅទីនេះសញ្ញាម៉ូឌុលលេចឡើងក្នុងលក្ខខណ្ឌពីរផ្សេងគ្នា ហើយត្រូវតែដកចេញ។ 1) ស្វែងរកឫសនៃកន្សោមម៉ូឌុល៖ x=0, 2-x=0, x=2 2) កំណត់សញ្ញានៅលើចន្លោះពេល៖

ក្រាហ្វនៃមុខងារមួយ។

សេចក្តីសន្និដ្ឋាន ប្រធានបទនៃគម្រោងគឺជាបញ្ហាលំបាកមួយនៅក្នុងវគ្គសិក្សាគណិតវិទ្យា វាទាក់ទងទៅនឹងបញ្ហាដែលត្រូវបានពិចារណាក្នុងការជ្រើសរើស និងត្រូវបានសិក្សានៅក្នុងថ្នាក់សម្រាប់ការសិក្សាស៊ីជម្រៅនៃមុខវិជ្ជាគណិតវិទ្យា។ ទោះជាយ៉ាងណាក៏ដោយភារកិច្ចបែបនេះត្រូវបានផ្តល់ឱ្យនៅក្នុងផ្នែកទីពីរនៃ GIA ។ ការងារនេះនឹងជួយអ្នកឱ្យយល់ពីរបៀបបង្កើតក្រាហ្វដោយប្រើម៉ូឌុលមិនត្រឹមតែមុខងារលីនេអ៊ែរប៉ុណ្ណោះទេ ប៉ុន្តែក៏មានមុខងារផ្សេងទៀតផងដែរ (ចតុកោណ សមាមាត្រច្រាស។ ល។ )។ ការងារនេះនឹងជួយក្នុងការរៀបចំសម្រាប់ការប្រឡងថ្នាក់រដ្ឋ និងការប្រឡងបង្រួបបង្រួមរដ្ឋ ហើយនឹងអនុញ្ញាតឱ្យអ្នកទទួលបានពិន្ទុខ្ពស់ក្នុងគណិតវិទ្យា។

អក្សរសិល្ប៍ Vilenkin N.Ya. Zhokhov V.I.. គណិតវិទ្យា។ សៀវភៅសិក្សាថ្នាក់ទី ៦ ទីក្រុងម៉ូស្គូ។ គ្រឹះស្ថានបោះពុម្ពផ្សាយ "Mnemosyne" ឆ្នាំ 2010 Vilenkin N.Ya., Vilenkin L.N., Survillo G.S. និងផ្សេងៗទៀត។ ពិជគណិត។ ថ្នាក់ទី ៨៖ ការអប់រំ។ សៀវភៅណែនាំសម្រាប់សិស្ស និងថ្នាក់ដែលមានការសិក្សាគណិតវិទ្យាកម្រិតខ្ពស់។ - ទីក្រុងម៉ូស្គូ។ ការត្រាស់ដឹង ឆ្នាំ ២០០៩ Gaidukov I.I. "តម្លៃ​ដាច់ខាត។" ទីក្រុងម៉ូស្គូ។ ការត្រាស់ដឹង, 1968. Gursky I.P. "មុខងារ និងក្រាហ្វិក។" ទីក្រុងម៉ូស្គូ។ ការត្រាស់ដឹង, ឆ្នាំ 1968. Yashchina N.V. បច្ចេកទេសសាងសង់ក្រាហ្វដែលមានម៉ូឌុល។ ទិនានុប្បវត្តិ "គណិតវិទ្យានៅសាលារៀន", លេខ 3, 1994 សព្វវចនាធិប្បាយកុមារ។ ទីក្រុងម៉ូស្គូ។ "គរុកោសល្យ", ឆ្នាំ 1990 ។ Dynkin E.B., Molchanova S.A. បញ្ហាគណិតវិទ្យា។ M. , "វិទ្យាសាស្រ្ត", ឆ្នាំ 1993. Petrakov I.S. ក្លឹបគណិតវិទ្យានៅថ្នាក់ទី 8-10 ។ M., "ការត្រាស់ដឹង", ឆ្នាំ 1987 ។ Galitsky M.L. និងផ្សេងៗទៀត ការប្រមូលបញ្ហាក្នុងពិជគណិតសម្រាប់ថ្នាក់ទី 8-9៖ សៀវភៅសិក្សាសម្រាប់សិស្ស និងថ្នាក់ដែលមានការសិក្សាគណិតវិទ្យាកម្រិតខ្ពស់។ - ទី 12 ed ។ – អិមៈ ការអប់រំ ២០០៦ – ៣០១ ទំ។ Makrychev Yu.N., Mindyuk N.G. ពិជគណិត៖ ជំពូកបន្ថែមសម្រាប់សៀវភៅសិក្សាថ្នាក់ទី៩៖ សៀវភៅសិក្សាសម្រាប់សិស្សសាលា និងថ្នាក់រៀនគណិតវិទ្យាស៊ីជម្រៅ / កែសម្រួលដោយ G.V. Dorofeev ។ - អិមៈ ការអប់រំ ឆ្នាំ ១៩៩៧ - ២២៤ ទំ។ Sadykina N. ការស្ថាបនាក្រាហ្វ និងភាពអាស្រ័យដែលមានសញ្ញាម៉ូឌុល / គណិតវិទ្យា។ - លេខ 33 ។ - ឆ្នាំ 2004. – p.19-21.. Kostrikina N.P. "បញ្ហានៃការកើនឡើងនៃការលំបាកក្នុងវគ្គសិក្សាពិជគណិតសម្រាប់ថ្នាក់ទី 7-9"... Moscow: Education, 2008 ។

ប្រតិចារិក

1 សន្និសីទវិទ្យាសាស្ត្រ និងជាក់ស្តែងក្នុងតំបន់នៃការងារអប់រំ និងស្រាវជ្រាវរបស់សិស្សថ្នាក់ទី 6-11 "បញ្ហាអនុវត្ត និងមូលដ្ឋានគ្រឹះនៃគណិតវិទ្យា" ទិដ្ឋភាពវិធីសាស្រ្តនៃការសិក្សាគណិតវិទ្យា ការសាងសង់ក្រាហ្វនៃមុខងារដែលមានម៉ូឌុល Gabova Angela Yuryevna ថ្នាក់ទី 10 MOBU " Gymnasium 3 ” Kudymkar, Pikuleva Nadezhda Ivanovna, គ្រូបង្រៀនគណិតវិទ្យានៃស្ថាប័នអប់រំក្រុង “Gymnasium 3”, Kudymkar Perm, 2016

2 Contents: Introduction...3 pages I. Main part...6 pages 1.1Historical background..6 pages 2.Basic definitions and properties of functions page 2.1 Quadratic function..7 pages 2.2 Linear function..8 p. 2.3 អនុគមន៍ប្រភាគ 8 ទំ 3. ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វជាមួយម៉ូឌុល 9 ទំ 3.1 ការកំណត់ម៉ូឌុល.. 9 ទំ. 3.2 ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរជាមួយម៉ូឌុល...9 ទំ 3.3 ការបង្កើតក្រាហ្វនៃអនុគមន៍ ដែលមាននៅក្នុងរូបមន្ត "ម៉ូឌុលដែលដាក់ជាប់គ្នា"។ 10 ទំ។ 3.4 ក្បួនដោះស្រាយសម្រាប់ការសាងសង់ក្រាហ្វនៃមុខងារនៃទម្រង់ y = a 1 x x 1 + a 2 x x a n x x n + ax + b...13 p. 3.5 ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វនៃការ៉េ function with modulus.14 p. 3.6 Algorithm ធ្វើផែនការអនុគមន៍ប្រភាគប្រភាគជាមួយម៉ូឌុល។ 15 ទំ។ 4. ការផ្លាស់ប្តូរក្រាហ្វនៃអនុគមន៍ quadratic អាស្រ័យលើទីតាំងនៃសញ្ញានៃតម្លៃដាច់ខាត..17p ។ II. សេចក្តីសន្និដ្ឋាន ... 26 ទំព័រ III ។ បញ្ជីឯកសារយោង និងប្រភព...27 ទំព័រ IV. ឧបសម្ព័ន្ធ .... 28 ទំ។ ២

3 សេចក្តីផ្តើម ការសាងសង់ក្រាហ្វនៃអនុគមន៍គឺជាប្រធានបទដ៏គួរឱ្យចាប់អារម្មណ៍បំផុតមួយនៅក្នុងគណិតវិទ្យាសាលា។ គណិតវិទូដ៏អស្ចារ្យបំផុតនៃសម័យកាលរបស់យើងគឺ Israel Moiseevich Gelfand បានសរសេរថា “ដំណើរការនៃការបង្កើតក្រាហ្វគឺជាវិធីនៃការបំប្លែងរូបមន្ត និងការពិពណ៌នាទៅជារូបភាពធរណីមាត្រ។ ក្រាហ្វនេះគឺជាមធ្យោបាយនៃការមើលឃើញរូបមន្ត និងមុខងារ និងមើលពីរបៀបដែលមុខងារទាំងនោះផ្លាស់ប្តូរ។ ឧទាហរណ៍ ប្រសិនបើវាត្រូវបានសរសេរ y =x 2 នោះអ្នកឃើញប៉ារ៉ាបូឡាភ្លាមៗ។ ប្រសិនបើ y = x 2-4 អ្នកឃើញប៉ារ៉ាបូឡាបន្ទាបដោយបួនឯកតា។ ប្រសិនបើ y = -(x 2 4) នោះអ្នកឃើញប៉ារ៉ាបូឡាមុនបានបដិសេធ។ សមត្ថភាពក្នុងការមើលរូបមន្តភ្លាមៗ និងការបកស្រាយធរណីមាត្ររបស់វាមានសារៈសំខាន់មិនត្រឹមតែសម្រាប់ការសិក្សាគណិតវិទ្យាប៉ុណ្ណោះទេ ប៉ុន្តែសម្រាប់មុខវិជ្ជាផ្សេងទៀតផងដែរ។ វា​ជា​ជំនាញ​ដែល​នៅ​ជាមួយ​អ្នក​អស់​មួយ​ជីវិត ដូចជា​ការ​ជិះ​កង់ វាយ​អក្សរ ឬ​បើក​ឡាន​ជាដើម»។ មូលដ្ឋានគ្រឹះនៃការដោះស្រាយសមីការជាមួយម៉ូឌុលត្រូវបានទទួលនៅថ្នាក់ទី 6 ដល់ទី 7 ។ ខ្ញុំបានជ្រើសរើសប្រធានបទពិសេសនេះ ពីព្រោះខ្ញុំជឿថា វាទាមទារការស្រាវជ្រាវឱ្យកាន់តែស៊ីជម្រៅ និងហ្មត់ចត់ជាងនេះ។ ខ្ញុំចង់ទទួលបានចំណេះដឹងបន្ថែមអំពីម៉ូឌុលនៃលេខ វិធីផ្សេងគ្នានៃការបង្កើតក្រាហ្វដែលមានសញ្ញានៃតម្លៃដាច់ខាត។ នៅពេលដែលសញ្ញាម៉ូឌុលត្រូវបានរួមបញ្ចូលនៅក្នុងសមីការ "ស្តង់ដារ" នៃបន្ទាត់ ប៉ារ៉ាបូឡា និងអ៊ីពែបូឡា ក្រាហ្វរបស់ពួកគេក្លាយទៅជាមិនធម្មតា ហើយថែមទាំងស្រស់ស្អាតទៀតផង។ ដើម្បីរៀនពីរបៀបបង្កើតក្រាហ្វបែបនេះ អ្នកត្រូវធ្វើជាម្ចាស់នៃបច្ចេកទេសនៃការសាងសង់តួរលេខជាមូលដ្ឋាន ក៏ដូចជាដឹងច្បាស់ និងយល់ច្បាស់អំពីនិយមន័យនៃម៉ូឌុលនៃលេខមួយ។ នៅក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា ក្រាហ្វជាមួយម៉ូឌុលមិនត្រូវបានពិភាក្សាឱ្យស៊ីជម្រៅគ្រប់គ្រាន់ទេ ដែលជាមូលហេតុដែលខ្ញុំចង់ពង្រីកចំណេះដឹងរបស់ខ្ញុំលើប្រធានបទនេះ និងធ្វើការស្រាវជ្រាវផ្ទាល់ខ្លួនរបស់ខ្ញុំ។ ដោយមិនដឹងពីនិយមន័យនៃម៉ូឌុល វាមិនអាចទៅរួចទេក្នុងការសាងសង់សូម្បីតែក្រាហ្វដ៏សាមញ្ញបំផុតដែលមានតម្លៃដាច់ខាត។ លក្ខណៈលក្ខណៈនៃក្រាហ្វមុខងារដែលមានកន្សោមដែលមានសញ្ញាម៉ូឌុលគឺ 3

4 គឺជាវត្តមាននៃ kinks នៅចំណុចទាំងនោះដែលកន្សោមនៅក្រោមសញ្ញាម៉ូឌុលផ្លាស់ប្តូរសញ្ញា។ គោលបំណងនៃការងារ៖ ដើម្បីពិចារណាលើការស្ថាបនាក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរ ចតុកោណ និងប្រភាគដែលមានអថេរនៅក្រោមសញ្ញាម៉ូឌុល។ គោលបំណង៖ ១) សិក្សាអក្សរសិល្ប៍អំពីលក្ខណៈសម្បត្តិនៃតម្លៃដាច់ខាតនៃអនុគមន៍លីនេអ៊ែរ ចតុកោណ និងប្រភាគ។ 2) ស៊ើបអង្កេតការផ្លាស់ប្តូរនៅក្នុងក្រាហ្វមុខងារអាស្រ័យលើទីតាំងនៃសញ្ញានៃតម្លៃដាច់ខាត។ 3) រៀនក្រាហ្វសមីការ។ កម្មវត្ថុនៃការសិក្សា៖ ក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរ ចតុកោណ និងប្រភាគប្រភាគ។ ប្រធានបទនៃការស្រាវជ្រាវ៖ ការផ្លាស់ប្តូរក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរ ចតុកោណ និងប្រភាគ អាស្រ័យលើទីតាំងនៃសញ្ញានៃតម្លៃដាច់ខាត។ សារៈសំខាន់ជាក់ស្តែងនៃការងាររបស់ខ្ញុំស្ថិតនៅក្នុង៖ 1) ការប្រើប្រាស់ចំណេះដឹងដែលទទួលបានលើប្រធានបទនេះ ក៏ដូចជាការធ្វើឱ្យស៊ីជម្រៅ និងអនុវត្តវាទៅមុខងារ និងសមីការផ្សេងទៀត; 2) ក្នុងការប្រើប្រាស់ជំនាញស្រាវជ្រាវក្នុងសកម្មភាពអប់រំបន្ថែម។ ភាពពាក់ព័ន្ធ៖ កិច្ចការក្រាហ្វិចជាប្រពៃណីមួយនៃប្រធានបទពិបាកបំផុតក្នុងគណិតវិទ្យា។ និស្សិតបញ្ចប់ការសិក្សារបស់យើងត្រូវប្រឈមមុខនឹងបញ្ហានៃការឆ្លងកាត់ការប្រឡងរដ្ឋដោយជោគជ័យ និងការប្រឡងរដ្ឋបង្រួបបង្រួម។ បញ្ហាស្រាវជ្រាវ៖ ការបង្កើតក្រាហ្វនៃមុខងារដែលមានសញ្ញាម៉ូឌុលពីផ្នែកទីពីរនៃ GIA ។ សម្មតិកម្មស្រាវជ្រាវ៖ ការប្រើប្រាស់វិធីសាស្រ្តសម្រាប់ដោះស្រាយកិច្ចការនៅក្នុងផ្នែកទីពីរនៃ GIA ដែលត្រូវបានបង្កើតឡើងដោយផ្អែកលើវិធីសាស្រ្តទូទៅសម្រាប់ការសាងសង់ក្រាហ្វនៃមុខងារដែលមានសញ្ញាម៉ូឌុលនឹងអនុញ្ញាតឱ្យសិស្សដោះស្រាយកិច្ចការទាំងនេះ 4

5 នៅលើមូលដ្ឋានមនសិការ ជ្រើសរើសវិធីសាស្រ្តសមហេតុផលបំផុតនៃដំណោះស្រាយ អនុវត្តវិធីសាស្រ្តផ្សេងគ្នានៃដំណោះស្រាយ និងឆ្លងកាត់ការប្រឡងរដ្ឋកាន់តែជោគជ័យ។ វិធីសាស្រ្តស្រាវជ្រាវដែលប្រើក្នុងការងារ៖ 1. ការវិភាគអក្សរសិល្ប៍គណិតវិទ្យា និងធនធានអ៊ីនធឺណិតលើប្រធានបទនេះ។ 2. ការបន្តពូជនៃសម្ភារៈដែលបានសិក្សា។ 3. សកម្មភាពយល់ដឹង និងស្វែងរក។ 4. ការវិភាគ និងការប្រៀបធៀបទិន្នន័យក្នុងការស្វែងរកដំណោះស្រាយចំពោះបញ្ហា។ 5. សេចក្តីថ្លែងការណ៍នៃសម្មតិកម្ម និងការផ្ទៀងផ្ទាត់របស់ពួកគេ។ 6. ការប្រៀបធៀបនិងទូទៅនៃការពិតគណិតវិទ្យា។ 7. ការវិភាគលទ្ធផលដែលទទួលបាន។ នៅពេលសរសេរការងារនេះ ប្រភពខាងក្រោមត្រូវបានប្រើប្រាស់៖ ធនធានអ៊ីនធឺណិត ការធ្វើតេស្ត OGE អក្សរសិល្ប៍គណិតវិទ្យា។ ៥

6 I. ផ្នែកសំខាន់ 1.1 ប្រវត្តិប្រវត្តិសាស្ត្រ។ នៅពាក់កណ្តាលទីមួយនៃសតវត្សទី 17 គំនិតនៃមុខងារដូចជាការពឹងផ្អែកនៃអថេរមួយទៅមួយទៀតបានចាប់ផ្តើមលេចឡើង។ ដូច្នេះ គណិតវិទូជនជាតិបារាំង Pierre Fermat () និង Rene Descartes () បានស្រមៃមើលមុខងារមួយដែលជាការពឹងផ្អែកនៃការចាត់តាំងនៃចំនុចមួយនៅលើខ្សែកោងនៅលើ abscissa របស់វា។ ហើយអ្នកវិទ្យាសាស្ត្រអង់គ្លេស Isaac Newton () បានយល់ពីមុខងារមួយដែលជាកូអរដោណេនៃចំណុចផ្លាស់ទីដែលផ្លាស់ប្តូរអាស្រ័យលើពេលវេលា។ ពាក្យ "មុខងារ" (មកពីពាក្យឡាតាំង ការអនុវត្តមុខងារ ការសម្រេច) ត្រូវបានណែនាំជាលើកដំបូងដោយគណិតវិទូអាល្លឺម៉ង់ Gottfried Leibniz () ។ គាត់បានភ្ជាប់មុខងារជាមួយរូបភាពធរណីមាត្រ (ក្រាហ្វនៃអនុគមន៍)។ ក្រោយមក គណិតវិទូជនជាតិស្វីស Johann Bernoulli() និងជាសមាជិកនៃបណ្ឌិតសភាវិទ្យាសាស្ត្រ St. Petersburg ដែលជាគណិតវិទូដ៏ល្បីល្បាញនៅសតវត្សរ៍ទី 18 លោក Leonard Euler() បានចាត់ទុកមុខងារនេះថាជាការបញ្ចេញមតិវិភាគ។ អយល័រ​ក៏​មាន​ការ​យល់​ដឹង​ទូទៅ​អំពី​អនុគមន៍​មួយ​ដែល​ជា​ការ​ពឹង​ផ្អែក​នៃ​អថេរ​មួយ​ទៅ​លើ​អថេរ​មួយ​ទៀត។ ពាក្យ "ម៉ូឌុល" មកពីពាក្យឡាតាំង "ម៉ូឌុល" ដែលមានន័យថា "រង្វាស់" ។ នេះគឺជាពាក្យ polysemantic ( homonym ) ដែលមានអត្ថន័យជាច្រើន ហើយត្រូវបានគេប្រើមិនត្រឹមតែនៅក្នុងគណិតវិទ្យាប៉ុណ្ណោះទេ ប៉ុន្តែក៏មាននៅក្នុងស្ថាបត្យកម្ម រូបវិទ្យា បច្ចេកវិទ្យា ការសរសេរកម្មវិធី និងវិទ្យាសាស្ត្រពិតប្រាកដផ្សេងទៀត។ នៅក្នុងស្ថាបត្យកម្ម នេះគឺជាឯកតារង្វាស់ដំបូងដែលបង្កើតឡើងសម្រាប់រចនាសម្ព័ន្ធស្ថាបត្យកម្មដែលបានផ្តល់ឱ្យ ហើយប្រើដើម្បីបង្ហាញពីសមាមាត្រជាច្រើននៃធាតុផ្សំរបស់វា។ នៅក្នុងបច្ចេកវិទ្យា នេះគឺជាពាក្យដែលប្រើក្នុងវិស័យផ្សេងៗនៃបច្ចេកវិទ្យា ដែលមិនមានអត្ថន័យជាសកល និងបម្រើដើម្បីកំណត់មេគុណ និងបរិមាណផ្សេងៗ ឧទាហរណ៍ ម៉ូឌុលភ្ជាប់ ម៉ូឌុលយឺត ជាដើម។ ៦

7 ម៉ូឌុលភាគច្រើន (នៅក្នុងរូបវិទ្យា) គឺជាសមាមាត្រនៃភាពតានតឹងធម្មតានៅក្នុងសម្ភារៈទៅនឹងការពន្លូតដែលទាក់ទង។ 2. និយមន័យជាមូលដ្ឋាន និងលក្ខណៈសម្បត្តិនៃអនុគមន៍ មុខងារគឺជាគោលគំនិតគណិតវិទ្យាដ៏សំខាន់បំផុតមួយ។ អនុគមន៍គឺជាការពឹងផ្អែកនៃអថេរ y លើអថេរ x ដែលតម្លៃនីមួយៗនៃអថេរ x ត្រូវគ្នាទៅនឹងតម្លៃតែមួយនៃអថេរ y ។ វិធីសាស្រ្តបញ្ជាក់មុខងារ៖ 1) វិធីសាស្ត្រវិភាគ (មុខងារត្រូវបានបញ្ជាក់ដោយប្រើរូបមន្តគណិតវិទ្យា); 2) វិធីសាស្រ្តតារាង (មុខងារត្រូវបានបញ្ជាក់ដោយប្រើតារាង); 3) វិធីសាស្រ្តពិពណ៌នា (មុខងារត្រូវបានបញ្ជាក់ដោយការពិពណ៌នាពាក្យសំដី); 4) វិធីសាស្រ្តក្រាហ្វិក (មុខងារត្រូវបានបញ្ជាក់ដោយប្រើក្រាហ្វ) ។ ក្រាហ្វនៃអនុគមន៍គឺជាសំណុំនៃចំណុចទាំងអស់នៃប្លង់កូអរដោនេ អេស៊ីសស៊ីស ដែលស្មើនឹងតម្លៃនៃអាគុយម៉ង់ ហើយការចាត់តាំងគឺស្មើនឹងតម្លៃដែលត្រូវគ្នានៃអនុគមន៍។ 2.1 អនុគមន៍ Quadratic អនុគមន៍ A ដែលកំណត់ដោយរូបមន្ត y = ax 2 + in + c ដែល x និង y ជាអថេរ ហើយប៉ារ៉ាម៉ែត្រ a, b និង c គឺជាចំនួនពិតណាមួយ ហើយ a = 0 ត្រូវបានគេហៅថា quadratic ។ ក្រាហ្វនៃអនុគមន៍ y=ax 2 +in+c គឺជាប៉ារ៉ាបូឡា។ អ័ក្សនៃស៊ីមេទ្រីនៃប៉ារ៉ាបូឡា y=ax 2 +in+c គឺជាបន្ទាត់ត្រង់សម្រាប់ a>0 “សាខា” នៃប៉ារ៉ាបូឡាត្រូវបានតម្រង់ឡើងលើសម្រាប់<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (សម្រាប់មុខងារនៃអថេរមួយ) ។ ទ្រព្យសម្បត្តិសំខាន់នៃអនុគមន៍លីនេអ៊ែរ៖ ការកើនឡើងនៃអនុគមន៍គឺសមាមាត្រទៅនឹងការបង្កើនអាគុយម៉ង់។ នោះ​គឺ​មុខងារ​គឺ​ជា​ទូទៅ​នៃ​សមាមាត្រ​ផ្ទាល់។ ក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរគឺជាបន្ទាត់ត្រង់ដែលជាឈ្មោះរបស់វាមកពី។ វាទាក់ទងនឹងមុខងារពិតនៃអថេរពិតប្រាកដមួយ។ 1) នៅពេល បន្ទាត់ត្រង់បង្កើតជាមុំស្រួចជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្ស abscissa ។ 2) នៅពេល បន្ទាត់ត្រង់បង្កើតជាមុំ obtuse ជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្ស x ។ 3) គឺជាសូចនាករកំណត់នៃចំណុចប្រសព្វនៃបន្ទាត់ជាមួយអ័ក្សតម្រៀប។ 4) នៅពេលដែលបន្ទាត់ត្រង់ឆ្លងកាត់ប្រភពដើម។ , 2.3 អនុគមន៍ប្រភាគ-សនិទានកម្ម គឺជាប្រភាគដែលភាគបែង និងភាគបែងជាពហុនាម។ វា​មាន​ទម្រង់​ដែល​ពហុធា​ក្នុង​ចំនួន​អថេរ​ណាមួយ។ ករណីពិសេសមួយគឺជាមុខងារសនិទានភាពនៃអថេរមួយ៖ កន្លែង និងពហុនាម។ 1) កន្សោមណាមួយដែលអាចទទួលបានពីអថេរដោយប្រើប្រតិបត្តិការនព្វន្ធចំនួនបួនគឺជាអនុគមន៍សនិទាន។ ៨

9 2) សំណុំនៃអនុគមន៍សនិទានត្រូវបានបិទនៅក្រោមប្រតិបត្តិការនព្វន្ធ និងប្រតិបត្តិការសមាសភាព។ 3) អនុគមន៍សនិទានណាមួយអាចត្រូវបានតំណាងថាជាផលបូកនៃប្រភាគសាមញ្ញ - នេះត្រូវបានប្រើក្នុងការរួមបញ្ចូលការវិភាគ.. , 3. ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វជាមួយម៉ូឌុល 3.1 និយមន័យនៃម៉ូឌុល ម៉ូឌុលនៃចំនួនពិត a គឺជាលេខដោយខ្លួនឯង ប្រសិនបើ វាមិនអវិជ្ជមានទេ ហើយលេខទល់មុខ a ប្រសិនបើ a ជាអវិជ្ជមាន។ a = 3.2 ក្បួនដោះស្រាយសម្រាប់សង់ក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរជាមួយម៉ូឌុល ដើម្បីបង្កើតក្រាហ្វនៃអនុគមន៍ y = x អ្នកត្រូវដឹងថាសម្រាប់ x វិជ្ជមាន យើងមាន x = x ។ នេះមានន័យថាសម្រាប់តម្លៃវិជ្ជមាននៃអាគុយម៉ង់ ក្រាហ្វ y = x ស្របគ្នានឹងក្រាហ្វ y = x នោះគឺជាផ្នែកនៃក្រាហ្វនេះគឺជាកាំរស្មីដែលផុសចេញពីប្រភពដើមនៅមុំ 45 ដឺក្រេទៅអ័ក្ស abscissa ។ . នៅ x< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 ដើម្បីសាងសង់ យើងយកចំណុច (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2) ។ ឥឡូវ​យើង​បង្កើត​ក្រាហ្វ y=x-1 បើ A ជា​ចំណុច​មួយ​នៅ​លើ​ក្រាហ្វ y=x ជាមួយ​កូអរដោណេ (a; a) នោះ​ចំណុច​នៅ​លើ​ក្រាហ្វ y=x-1 ដែល​មាន​តម្លៃ​ដូចគ្នា​នៃ​ការ​ចាត់តាំង Y នឹង ជាចំណុច A1(a+1; a)។ ចំណុចនៃក្រាហ្វទីពីរនេះ អាចទទួលបានពីចំណុច A(a; a) នៃក្រាហ្វទីមួយ ដោយផ្លាស់ទីស្របទៅនឹងអ័ក្សអុកទៅខាងស្តាំ។ នេះមានន័យថាក្រាហ្វទាំងមូលនៃអនុគមន៍ y= x-1 គឺទទួលបានពីក្រាហ្វនៃអនុគមន៍ y= x ដោយផ្លាស់ទីស្របទៅនឹងអ័ក្សអុកទៅខាងស្តាំដោយ 1។ ចូរយើងបង្កើតក្រាហ្វៈ y= x-1 ដើម្បីស្ថាបនា , យកពិន្ទុ (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1) ។ 3.3 ការបង្កើតក្រាហ្វនៃអនុគមន៍ដែលមាន "ម៉ូឌុលដែលបានដាក់" ក្នុងរូបមន្ត ចូរយើងពិចារណាអំពីក្បួនដោះស្រាយការសាងសង់ដោយប្រើឧទាហរណ៍ជាក់លាក់ សាងសង់ក្រាហ្វនៃអនុគមន៍មួយ៖ 10

11 y=i-2-ix+5ii 1. បង្កើតក្រាហ្វនៃអនុគមន៍។ 2. យើងបង្ហាញក្រាហ្វនៃផ្នែកខាងក្រោមនៃយន្តហោះពាក់កណ្តាលចុះឡើងដោយស៊ីមេទ្រីទាក់ទងទៅនឹងអ័ក្ស OX និងទទួលបានក្រាហ្វនៃមុខងារ។ ដប់មួយ

12 3. យើងបង្ហាញក្រាហ្វនៃអនុគមន៍ចុះក្រោមដោយស៊ីមេទ្រីទាក់ទងទៅនឹងអ័ក្ស OX និងទទួលបានក្រាហ្វនៃអនុគមន៍។ 4. យើងបង្ហាញក្រាហ្វនៃអនុគមន៍ចុះក្រោមដោយស៊ីមេទ្រីទាក់ទងទៅនឹងអ័ក្ស OX និងទទួលបានក្រាហ្វនៃអនុគមន៍ 5. យើងបង្ហាញក្រាហ្វនៃអនុគមន៍ទាក់ទងទៅនឹងអ័ក្ស OX និងទទួលបានក្រាហ្វ។ ១២

13 6. ជាលទ្ធផលក្រាហ្វនៃអនុគមន៍មើលទៅដូចនេះ 3.4 ។ ក្បួនដោះស្រាយសម្រាប់សាងសង់ក្រាហ្វនៃមុខងារនៃទម្រង់ y = a 1 x x 1 + a 2 x x a n x x n + ax + b ។ នៅក្នុងឧទាហរណ៍មុន វាពិតជាងាយស្រួលក្នុងការបង្ហាញសញ្ញាម៉ូឌុល។ ប្រសិនបើមានផលបូកនៃម៉ូឌុលច្រើន នោះវាមានបញ្ហាក្នុងការពិចារណាបន្សំដែលអាចធ្វើបានទាំងអស់នៃសញ្ញានៃកន្សោមម៉ូឌុល។ ក្នុងករណីនេះ តើត្រូវបង្កើតក្រាហ្វនៃអនុគមន៍ដោយរបៀបណា? ចំណាំថាក្រាហ្វគឺជាបន្ទាត់ដែលខូច ដោយបញ្ឈរនៅចំណុចមាន abscissas -1 និង 2 ។ នៅ x = -1 និង x = 2 កន្សោម submodular គឺស្មើនឹងសូន្យ។ នៅក្នុងការអនុវត្ត យើងបានខិតទៅជិតច្បាប់សម្រាប់ការសាងសង់ក្រាហ្វបែបនេះ៖ ក្រាហ្វនៃមុខងារនៃទម្រង់ y = a 1 x x 1 + a 2 x x a n x x n + ax + b គឺជាបន្ទាត់ខូចដែលមានតំណភ្ជាប់ខ្លាំងគ្មានកំណត់។ ដើម្បីបង្កើតបន្ទាត់ដែលខូចបែបនេះ វាគ្រប់គ្រាន់ដើម្បីដឹងពីចំនុចកំពូលរបស់វាទាំងអស់ ( abscissas នៃ vertices គឺជាសូន្យនៃកន្សោម submodular ) និងចំណុចត្រួតពិនិត្យមួយនៅខាងឆ្វេង និងខាងស្តាំ តំណភ្ជាប់គ្មានកំណត់។ ១៣

14 បញ្ហា។ ក្រាហ្វនៃអនុគមន៍ y = x + x 1 + x + 1 ហើយស្វែងរកតម្លៃតូចបំផុតរបស់វា។ ដំណោះស្រាយ: 1. សូន្យនៃកន្សោម submodular: 0; -1; ចំនុចកំពូលនៃប៉ូលីលីន (0; 2); (-១៣); (1; 3) ។ យើងបង្កើតក្រាហ្វ (រូបភាពទី 7) តម្លៃតូចបំផុតនៃអនុគមន៍គឺ Algorithm សម្រាប់សាងសង់ក្រាហ្វនៃអនុគមន៍ quadratic ជាមួយនឹងម៉ូឌុល គូរឡើងនូវក្បួនដោះស្រាយសម្រាប់បំប្លែងក្រាហ្វមុខងារ។ 1. គូរក្រាហ្វនៃអនុគមន៍ y=f(x)។ តាមនិយមន័យនៃម៉ូឌុល មុខងារនេះត្រូវបានបែងចែកទៅជាសំណុំនៃមុខងារពីរ។ ដូច្នេះ ក្រាហ្វនៃអនុគមន៍ y=f(x) មានក្រាហ្វពីរ៖ y=f(x) ក្នុងយន្តហោះពាក់កណ្តាលខាងស្តាំ y=f(-x) ក្នុងយន្តហោះពាក់កណ្តាលខាងឆ្វេង។ ដោយផ្អែកលើនេះ ក្បួន (ក្បួនដោះស្រាយ) អាចត្រូវបានបង្កើត។ ក្រាហ្វនៃអនុគមន៍ y= f(x) ទទួលបានពីក្រាហ្វនៃអនុគមន៍ y= f(x) ដូចតទៅ៖ នៅ x 0 ក្រាហ្វត្រូវបានរក្សាទុក ហើយនៅ x< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. ដើម្បីបង្កើតក្រាហ្វនៃអនុគមន៍ y=f(x) ដំបូងអ្នកត្រូវតែបង្កើតក្រាហ្វនៃអនុគមន៍ y=f(x) សម្រាប់ x> 0 បន្ទាប់មកសម្រាប់ x< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 ដើម្បីទទួលបានក្រាហ្វនេះ អ្នកគ្រាន់តែត្រូវប្តូរក្រាហ្វដែលទទួលបានពីមុនបីឯកតាទៅខាងស្តាំ។ ចំណាំថាប្រសិនបើភាគបែងនៃប្រភាគមានកន្សោម x + 3 នោះយើងនឹងប្តូរក្រាហ្វទៅខាងឆ្វេង៖ ឥឡូវនេះយើងត្រូវគុណលេខរៀងទាំងអស់ដោយពីរដើម្បីទទួលបានក្រាហ្វនៃអនុគមន៍។ ចុងក្រោយយើងប្តូរក្រាហ្វឡើងដោយ ឯកតាពីរ៖ រឿងចុងក្រោយដែលយើងត្រូវធ្វើគឺ នេះគឺដើម្បីគូសក្រាហ្វនៃអនុគមន៍ដែលបានផ្តល់ឱ្យប្រសិនបើវាត្រូវបានរុំព័ទ្ធនៅក្រោមសញ្ញាម៉ូឌុល។ ដើម្បីធ្វើដូច្នេះបាន យើងឆ្លុះបញ្ចាំងស៊ីមេទ្រីឡើងលើផ្នែកទាំងមូលនៃក្រាហ្វដែលការចាត់តាំងគឺអវិជ្ជមាន (ផ្នែកនោះដែលស្ថិតនៅក្រោមអ័ក្ស x)៖ រូបទី 4 16

17 4. ការផ្លាស់ប្តូរនៅក្នុងក្រាហ្វនៃអនុគមន៍ quadratic អាស្រ័យលើទីតាំងនៃសញ្ញានៃតម្លៃដាច់ខាត។ សង់ក្រាហ្វនៃអនុគមន៍ y = x 2 − x −3 1) ចាប់តាំងពី x = x នៅ x 0 ក្រាហ្វដែលត្រូវការស្របគ្នានឹងប៉ារ៉ាបូឡា y = 0.25 x 2 − x − 3. ប្រសិនបើ x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. ខ) ដូេចនះ ខ្ញំុ បញ្ចប់ការសាងសងស ប់ x<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 រូបភព។ 4 ក្រាហ្វនៃអនុគមន៍ y = f (x) ស្របគ្នានឹងក្រាហ្វនៃអនុគមន៍ y = f (x) លើសំណុំនៃតម្លៃមិនអវិជ្ជមាននៃអាគុយម៉ង់ ហើយស៊ីមេទ្រីទៅវាដោយគោរពតាមអ័ក្សនៃ OU នៅលើសំណុំនៃតម្លៃអវិជ្ជមាននៃអាគុយម៉ង់។ ភស្តុតាង៖ ប្រសិនបើ x 0 នោះ f (x) = f (x), i.e. នៅលើសំណុំនៃតម្លៃមិនអវិជ្ជមាននៃអាគុយម៉ង់ ក្រាហ្វនៃអនុគមន៍ y = f (x) និង y = f (x) ស្របគ្នា។ ដោយសារ y = f (x) គឺជាអនុគមន៍គូ ក្រាហ្វរបស់វាគឺស៊ីមេទ្រីទាក់ទងទៅនឹង op-amp ។ ដូចនេះក្រាហ្វនៃអនុគមន៍ y = f (x) អាចទទួលបានពីក្រាហ្វនៃអនុគមន៍ y = f (x) ដូចតទៅ៖ 1. សង់ក្រាហ្វនៃអនុគមន៍ y = f (x) សម្រាប់ x> 0; 2. សម្រាប់ x<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. សម្រាប់ x<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 ប្រសិនបើ x 2 − x −6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 និងឆ្លុះបញ្ចាំងដោយស៊ីមេទ្រីផ្នែក y = f(x) នៅ y<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0 បន្ទាប់មក f (x) = f (x) ដែលមានន័យថានៅក្នុងផ្នែកនេះ ក្រាហ្វនៃអនុគមន៍ y = f (x) ស្របគ្នានឹងក្រាហ្វនៃអនុគមន៍ខ្លួនវា y = f (x) ។ ប្រសិនបើ f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 Fig.5 សេចក្តីសន្និដ្ឋាន៖ ដើម្បីបង្កើតក្រាហ្វនៃអនុគមន៍ y=f(x) 1. បង្កើតក្រាហ្វនៃអនុគមន៍ y=f(x); 2. នៅតំបន់ដែលក្រាហ្វស្ថិតនៅផ្នែកខាងក្រោមនៃយន្តហោះពាក់កណ្តាល ឧ. ដែល f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 ការងារស្រាវជ្រាវលើការសាងសង់ក្រាហ្វនៃអនុគមន៍ y = f (x) ដោយប្រើនិយមន័យនៃតម្លៃដាច់ខាត និងឧទាហរណ៍ដែលបានពិភាក្សាពីមុន យើងនឹងសាងសង់ក្រាហ្វនៃអនុគមន៍៖ y = 2 x − 3 y = x 2-5 x y = x 2 -២ និង​ធ្វើការ​សន្និដ្ឋាន។ ដើម្បីបង្កើតក្រាហ្វនៃអនុគមន៍ y = f (x) អ្នកត្រូវ៖ 1. បង្កើតក្រាហ្វនៃអនុគមន៍ y = f (x) សម្រាប់ x> 0 ។ 2. សាងសង់ផ្នែកទីពីរនៃក្រាហ្វ ពោលគឺឆ្លុះបញ្ចាំងពីក្រាហ្វដែលបានសាងសង់ដោយស៊ីមេទ្រីទាក់ទងទៅនឹង op-amp ពីព្រោះ មុខងារនេះគឺសូម្បីតែ។ 3. បម្លែងផ្នែកនៃក្រាហ្វលទ្ធផលដែលមានទីតាំងនៅពាក់កណ្តាលយន្តហោះទាបទៅពាក់កណ្តាលយន្តហោះខាងលើដោយស៊ីមេទ្រីទៅអ័ក្ស OX ។ សង់ក្រាហ្វនៃអនុគមន៍ y = 2 x − 3 (វិធីសាស្ត្រទី 1 សម្រាប់កំណត់ម៉ូឌុល) 1. សង់ y = 2 x − 3 សម្រាប់ 2 x − 3 > 0, x >1.5 i.e. X< -1,5 и х>1.5 ក) y = 2x − 3 សម្រាប់ x> 0 ខ) សម្រាប់ x<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 ខ) សម្រាប់ x<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) យើងសាងសង់បន្ទាត់ត្រង់មួយស៊ីមេទ្រីទៅនឹងសំណង់ដែលទាក់ទងទៅនឹងអ័ក្សនៃ op-amp ។ 3) ខ្ញុំ​បង្ហាញ​ផ្នែក​នៃ​ក្រាហ្វ​ដែល​មាន​ទីតាំង​នៅ​ផ្នែក​ខាងក្រោម​នៃ​យន្តហោះ​ពាក់កណ្តាល​ស៊ីមេទ្រី​ទាក់ទង​នឹង​អ័ក្ស OX ។ ប្រៀបធៀបក្រាហ្វទាំងពីរ យើងឃើញថាវាដូចគ្នា ២១

22 ឧទាហរណ៍នៃបញ្ហា ឧទាហរណ៍ 1. ពិចារណាក្រាហ្វនៃអនុគមន៍ y = x 2 6x +5 ។ ដោយសារ x ជាការ៉េ ដោយមិនគិតពីសញ្ញានៃលេខ x នោះបន្ទាប់ពីការ៉េវានឹងជាវិជ្ជមាន។ វាធ្វើតាមថាក្រាហ្វនៃអនុគមន៍ y = x 2-6x +5 នឹងដូចគ្នាបេះបិទទៅនឹងក្រាហ្វនៃអនុគមន៍ y = x 2-6x +5, i.e. ក្រាហ្វនៃមុខងារដែលមិនមានសញ្ញាតម្លៃដាច់ខាត (រូបភាពទី 2) ។ Fig.2 ឧទាហរណ៍ 2. ពិចារណាក្រាហ្វនៃអនុគមន៍ y = x 2 6 x +5 ។ ដោយប្រើនិយមន័យនៃម៉ូឌុលនៃចំនួនមួយ យើងជំនួសរូបមន្ត y = x 2 6 x +5 ឥឡូវនេះយើងកំពុងដោះស្រាយជាមួយនឹងកិច្ចការពឹងផ្អែកជាបំណែកដែលស៊ាំនឹងយើង។ យើងនឹងបង្កើតក្រាហ្វដូចនេះ៖ ១) បង្កើតប៉ារ៉ាបូឡា y = x ២-៦x +៥ ហើយគូសរង្វង់ផ្នែកដែលមាន ២២

23 ត្រូវ​នឹង​តម្លៃ​មិន​អវិជ្ជមាន​នៃ x, i.e. ផ្នែកដែលស្ថិតនៅខាងស្តាំនៃអ័ក្សអូយ។ 2) នៅក្នុងយន្តហោះកូអរដោនេដូចគ្នា សង់ប៉ារ៉ាបូឡា y = x 2 +6x +5 ហើយគូសរង្វង់ផ្នែកដែលត្រូវគ្នានឹងតម្លៃអវិជ្ជមាននៃ x, i.e. ផ្នែកដែលមានទីតាំងនៅខាងឆ្វេងនៃអ័ក្សអូយ។ ផ្នែកដែលគូសរង្វង់នៃប៉ារ៉ាបូឡារួមគ្នាបង្កើតជាក្រាហ្វនៃអនុគមន៍ y = x 2-6 x +5 (រូបភាព 3) ។ Fig.3 ឧទាហរណ៍ 3. ពិចារណាក្រាហ្វនៃអនុគមន៍ y = x 2-6 x +5 ។ ដោយសារតែ ក្រាហ្វនៃសមីការ y = x 2 6x +5 គឺដូចគ្នានឹងក្រាហ្វនៃអនុគមន៍ដោយគ្មានសញ្ញាម៉ូឌុល (ពិភាក្សាក្នុងឧទាហរណ៍ទី 2) វាដូចខាងក្រោមថាក្រាហ្វនៃអនុគមន៍ y = x 2 6 x +5 គឺដូចគ្នាបេះបិទ ទៅក្រាហ្វនៃអនុគមន៍ y = x 2 6 x +5 ពិចារណាក្នុងឧទាហរណ៍ 2 (រូបភាព 3) ។ ឧទាហរណ៍ 4. ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y = x 2 6x +5 ។ ដើម្បីធ្វើដូច្នេះ ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y = x 2-6x ។ ដើម្បីទទួលបានក្រាហ្វនៃអនុគមន៍ y = x 2-6x ពីវា អ្នកត្រូវជំនួសចំណុចនីមួយៗនៃប៉ារ៉ាបូឡាជាមួយនឹងចំនុចអវិជ្ជមានដែលមានចំនុចដែលមាន abscissa ដូចគ្នា ប៉ុន្តែជាមួយនឹងការបញ្ជាផ្ទុយ (វិជ្ជមាន) ។ ម្យ៉ាងវិញទៀត ផ្នែកនៃប៉ារ៉ាបូឡាដែលមានទីតាំងនៅខាងក្រោមអ័ក្ស x ត្រូវតែត្រូវបានជំនួសដោយបន្ទាត់ស៊ីមេទ្រីទៅវាទាក់ទងទៅនឹងអ័ក្ស x ។ ដោយសារតែ យើងត្រូវបង្កើតក្រាហ្វនៃអនុគមន៍ y = x 2-6x +5 បន្ទាប់មកក្រាហ្វនៃអនុគមន៍ដែលយើងចាត់ទុកថា y = x 2-6x គ្រាន់តែត្រូវលើកតាមអ័ក្ស y ដោយ 5 ឯកតាឡើង (រូបភាព 4 ។ ) ២៣

24 Fig.4 ឧទាហរណ៍ 5. ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y = x 2-6x+5 ។ ដើម្បីធ្វើដូចនេះយើងនឹងប្រើមុខងារ piecewise ល្បី។ ចូររកលេខសូន្យនៃអនុគមន៍ y = 6x +5 6x + 5 = 0 នៅ។ ចូរយើងពិចារណាករណីពីរ៖ 1) ប្រសិនបើ នោះសមីការនឹងយកទម្រង់ y = x 2 6x −5 ។ ចូរយើងសាងសង់ប៉ារ៉ាបូឡានេះ ហើយគូសរង្វង់ផ្នែកណា។ 2) ប្រសិនបើ នោះសមីការយកទម្រង់ y = x 2 + 6x +5 ។ ចូរយើងឈរប៉ារ៉ាបូឡានេះ ហើយគូសរង្វង់ផ្នែកនោះដែលមានទីតាំងនៅខាងឆ្វេងនៃចំណុចជាមួយនឹងកូអរដោនេ (រូបភាពទី 5)។ ២៤

25 Fig.5 ឧទាហរណ៍6. ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y = x 2 6 x +5 ។ ដើម្បីធ្វើដូចនេះយើងនឹងបង្កើតក្រាហ្វនៃអនុគមន៍ y = x 2-6 x +5 ។ យើងបង្កើតក្រាហ្វនេះក្នុងឧទាហរណ៍ 3 6 x + 5 ជាមួយនឹង ordinate អវិជ្ជមាន គួរតែត្រូវបានជំនួសដោយចំនុចដែលមាន abscissa ដូចគ្នា ប៉ុន្តែជាមួយនឹង ordinate ផ្ទុយ (វិជ្ជមាន) i.e. ផ្នែកនៃប៉ារ៉ាបូឡាដែលមានទីតាំងនៅខាងក្រោមអ័ក្សអុកត្រូវតែត្រូវបានជំនួសដោយបន្ទាត់ស៊ីមេទ្រីទៅវាទាក់ទងទៅនឹងអ័ក្សអុក (រូបភាព 6) ។ រូប ៦ ២៥

26 II. សេចក្តីសន្និដ្ឋាន “ព័ត៌មានគណិតវិទ្យាអាចប្រើប្រាស់យ៉ាងប៉ិនប្រសប់ និងមានប្រយោជន៍ លុះត្រាតែវាត្រូវបានស្ទាត់ជំនាញប្រកបដោយភាពច្នៃប្រឌិត ដើម្បីឱ្យសិស្សឃើញដោយខ្លួនឯងពីរបៀបដែលគាត់អាចមករកវាបានដោយខ្លួនឯង”។ A.N. Kolmogorov ។ បញ្ហាទាំងនេះមានការចាប់អារម្មណ៍យ៉ាងខ្លាំងចំពោះសិស្សថ្នាក់ទីប្រាំបួនព្រោះវាជារឿងធម្មតាណាស់នៅក្នុងការធ្វើតេស្ត OGE ។ សមត្ថភាពក្នុងការបង្កើតក្រាហ្វទិន្នន័យនៃមុខងារនឹងអនុញ្ញាតឱ្យអ្នកឆ្លងកាត់ការប្រឡងកាន់តែជោគជ័យ។ គណិតវិទូជនជាតិបារាំង Pierre Fermat () និង Rene Descartes () បានស្រមៃមើលមុខងារមួយដែលជាការពឹងផ្អែកនៃការចាត់តាំងនៃចំណុចនៅលើខ្សែកោងនៅលើ abscissa របស់វា។ ហើយអ្នកវិទ្យាសាស្ត្រអង់គ្លេស Isaac Newton () បានយល់ពីមុខងារមួយដែលជាកូអរដោណេនៃចំណុចផ្លាស់ទីដែលផ្លាស់ប្តូរអាស្រ័យលើពេលវេលា។ ២៦

27 III. បញ្ជីឯកសារយោង និងប្រភព 1. Galitsky M. L., Goldman A. M., Zvavich L. I. ការប្រមូលបញ្ហាក្នុងពិជគណិតសម្រាប់ថ្នាក់ទី 8-9៖ សៀវភៅសិក្សា។ សៀវភៅណែនាំសម្រាប់សិស្សសាលា។ និងថ្នាក់កម្រិតខ្ពស់ បានសិក្សា គណិតវិទ្យាទី ២ អេដ។ M.: ការត្រាស់ដឹង, Dorofeev G.V. គណិតវិទ្យា។ ពិជគណិត។ មុខងារ។ ការវិភាគ​ទិន្នន័យ។ ថ្នាក់ទី 9: m34 ការអប់រំ។ សម្រាប់ការសិក្សាអប់រំទូទៅ។ ការបង្កើតទី 2 ed., stereotype ។ M.: Bustard, Solomonik V.S. ការប្រមូលសំណួរ និងបញ្ហាក្នុងគណិតវិទ្យា M.: "វិទ្យាល័យ" Yashchenko I.V. GIA គណិតវិទ្យា៖ ជម្រើសប្រឡងស្តង់ដារ៖ អំពីជម្រើស៖ “ការអប់រំជាតិ”, ទំ. 5. Yashchenko I.V. OGE ។ គណិតវិទ្យា៖ ជម្រើសប្រឡងស្តង់ដារ៖ អំពីជម្រើស៖ “ការអប់រំជាតិ”, ទំ. 6. Yashchenko I.V. OGE ។ គណិតវិទ្យា៖ ជម្រើសប្រឡងស្តង់ដារ៖ អំពីជម្រើស៖ “ការអប់រំជាតិ” ជាមួយ

28 ឧបសម្ព័ន្ធ 28

29 ឧទាហរណ៍ 1. ក្រាបអនុគមន៍ y = x 2 8 x ដំណោះស្រាយ។ ចូរកំណត់ភាពស្មើគ្នានៃមុខងារ។ តម្លៃសម្រាប់ y(-x) គឺដូចគ្នាទៅនឹងតម្លៃសម្រាប់ y(x) ដូច្នេះមុខងារនេះគឺស្មើ។ បន្ទាប់មកក្រាហ្វរបស់វាគឺស៊ីមេទ្រីអំពីអ័ក្ស Oy ។ យើងកំណត់មុខងារ y = x 2 8x + 12 សម្រាប់ x 0 ហើយបង្ហាញក្រាហ្វដោយស៊ីមេទ្រីដោយគោរពតាម Oy សម្រាប់ x អវិជ្ជមាន (រូបភាព 1) ។ ឧទាហរណ៍ 2. ក្រាហ្វខាងក្រោមនៃទម្រង់ y = x 2 8x មានន័យថាក្រាហ្វនៃអនុគមន៍ត្រូវបានទទួលដូចខាងក្រោម៖ បង្កើតក្រាហ្វនៃអនុគមន៍ y = x 2 8x + 12 ទុកផ្នែកនៃក្រាហ្វដែលស្ថិតនៅខាងលើ អ័ក្សអុកមិនផ្លាស់ប្តូរ ហើយផ្នែកនៃក្រាហ្វដែលស្ថិតនៅក្រោមអ័ក្ស abscissa និងត្រូវបានបង្ហាញស៊ីមេទ្រីទាក់ទងទៅនឹងអ័ក្សអុក (រូបភាព 2) ។ ឧទាហរណ៍ 3. ដើម្បីគូរក្រាហ្វនៃអនុគមន៍ y = x 2 8 x + 12 ការរួមបញ្ចូលគ្នានៃការបំប្លែងត្រូវបានអនុវត្ត៖ y = x 2 8x + 12 y = x 2 8 x + 12 y = x 2 8 x ចម្លើយ៖ រូបភាពទី 3. ឧទាហរណ៍ទី 4 កន្សោមនៅក្រោមសញ្ញាម៉ូឌុល ការផ្លាស់ប្តូរសញ្ញានៅចំណុច x=2/3 ។ នៅ x<2/3 функция запишется так: 29

30 សម្រាប់ x> 2/3 មុខងារនឹងត្រូវបានសរសេរដូចនេះ៖ នោះគឺចំនុច x=2/3 បែងចែកប្លង់កូអរដោនេរបស់យើងជាពីរផ្នែក ដែលក្នុងនោះមួយ (ទៅខាងស្តាំ) យើងបង្កើតមុខងារមួយ និងមួយទៀត។ (ទៅខាងឆ្វេង) យើងបង្កើតក្រាហ្វនៃអនុគមន៍៖ ឧទាហរណ៍ទី 5 បន្ទាប់ ក្រាហ្វក៏ខូចដែរ ប៉ុន្តែមានចំណុចបំបែកពីរ ដោយសារវាមានកន្សោមពីរនៅក្រោមសញ្ញាម៉ូឌុល៖ តោះមើលចំណុចណាខ្លះដែលកន្សោមម៉ូឌុលប្តូរសញ្ញា៖ តោះ រៀបចំសញ្ញាសម្រាប់កន្សោមម៉ូឌុលនៅលើបន្ទាត់កូអរដោនេ៖ ៣០

31 យើងពង្រីកម៉ូឌុលនៅចន្លោះពេលទីមួយ៖ នៅចន្លោះពេលទីពីរ៖ នៅចន្លោះពេលទីបី៖ ដូច្នេះនៅចន្លោះពេល (-; 1.5] យើងមានក្រាហ្វដែលសរសេរដោយសមីការទីមួយ នៅចន្លោះពេលក្រាហ្វដែលសរសេរដោយសមីការទីពីរ។ និងនៅចន្លោះពេល)