MBOU gymnasieskola nr 17, Ivanovo

« Ekvationer med modul"
Metodutveckling

Sammanställt

mattelärare

Lebedeva N.V.

20010

Förklarande anteckning

Kapitel 1 Inledning

Avsnitt 2. Grundegenskaper Avsnitt 3. Geometrisk tolkning av begreppet modul för ett tal Avsnitt 4. Graf över funktionen y = |x| Avsnitt 5. Konventioner

Kapitel 2. Lösa ekvationer som innehåller en modul

Avsnitt 1. Ekvationer av formen |F(x)| = m (enklast) Avsnitt 2. Ekvationer av formen F(|x|) = m Avsnitt 3. Ekvationer av formen |F(x)| = G(x) Avsnitt 4. Ekvationer av formen |F(x)| = ± F(x) (snyggast) Avsnitt 5. Ekvationer av formen |F(x)| = |G(x)| Avsnitt 6. Exempel på att lösa icke-standardiserade ekvationer Avsnitt 7. Ekvationer av formen |F(x)| + |G(x)| = 0 Avsnitt 8. Ekvationer av formen |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± i n | = m Avsnitt 9. Ekvationer som innehåller flera moduler

Kapitel 3. Exempel på att lösa olika ekvationer med modul.

Sektion 1. Trigonometriska ekvationer Avsnitt 2. Exponentiella ekvationer Avsnitt 3. Logaritmiska ekvationer Avsnitt 4. Irrationella ekvationer Avsnitt 5. Avancerade uppgifter Svar på övningarna Bibliografi

Förklarande anteckning.

Begreppet absolutvärde (modul) för ett reellt tal är en av dess väsentliga egenskaper. Detta koncept är utbrett inom olika delar av fysikaliska, matematiska och tekniska vetenskaper. I praktiken att undervisa i matematikkurser i gymnasium i enlighet med programmet för Ryska federationens försvarsministerium förekommer begreppet "absolut värde av ett nummer" upprepade gånger: i 6:e klass introduceras definitionen av en modul, dess geometrisk betydelse; i 8:e klass bildas begreppet absolut fel, lösningen av de enklaste ekvationerna och olikheterna innehållande en modul övervägs och den aritmetiska kvadratrotens egenskaper studeras; i 11:e klass finns konceptet i avsnittet ”Root n-e graden." Undervisningserfarenhet visar att elever ofta stöter på svårigheter att lösa uppgifter som kräver kunskap om detta material, och ofta hoppar över dem utan att börja slutföra dem. Även texterna till tentamensuppgifter för årskurs 9 och 11 innehåller liknande uppgifter. Dessutom skiljer sig de krav som universiteten ställer på skolutexaminerade, nämligen mer hög nivåän kraven i skolans läroplan. För livet i det moderna samhället är bildandet av en matematisk tankestil, manifesterad i vissa mentala färdigheter, mycket viktig. I processen att lösa problem med moduler krävs förmåga att använda tekniker som generalisering och specifikation, analys, klassificering och systematisering samt analogi. Genom att lösa sådana uppgifter kan du testa dina kunskaper om huvuddelarna i skolkursen, nivån logiskt tänkande, inledande forskningsfärdigheter. Detta arbete ägnas åt ett av avsnitten - att lösa ekvationer som innehåller en modul. Den består av tre kapitel. Det första kapitlet introducerar grundläggande begrepp och de viktigaste teoretiska övervägandena. Det andra kapitlet föreslår nio huvudtyper av ekvationer som innehåller en modul, diskuterar metoder för att lösa dem och undersöker exempel på olika nivåer av komplexitet. Det tredje kapitlet erbjuder mer komplexa och icke-standardiserade ekvationer (trigonometriska, exponentiella, logaritmiska och irrationella). För varje typ av ekvation finns övningar för oberoende beslut(svar och instruktioner bifogas). Huvudsyftet med detta arbete är att ge metodologisk hjälp till lärare med att förbereda lektioner och anordna valbara kurser. Materialet kan även användas som läromedel för gymnasieelever. De uppgifter som föreslås i arbetet är intressanta och inte alltid lätta att lösa, vilket gör det möjligt att göra elevernas pedagogiska motivation mer medveten, testa deras förmågor och öka förberedelsenivån för akademiker för att komma in på universitet. Ett differentierat urval av de föreslagna övningarna innebär en övergång från den reproduktiva nivån av att bemästra materialet till den kreativa, såväl som möjligheten att lära ut hur du tillämpar dina kunskaper när du löser icke-standardiserade problem.

Kapitel 1 Inledning.

Avsnitt 1. Bestämning av absolut värde .

Definition : Det absoluta värdet (modulen) för ett reellt tal A ringde inte ett negativt tal: A eller -A. Beteckning: │ A │ Posten lyder som följer: "modul för talet a" eller "absolut värde för talet a"

│ a, om a > 0

│a│ = │ 0, om a = 0 (1)

│ - och, om a
Exempel: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Expandera uttrycksmodul:

a) │x - 8│, om x > 12 b) │2x + 3│, om x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Avsnitt 2. Grundegenskaper.

Låt oss överväga de grundläggande egenskaperna för absolut värde. Egendom #1: Motsatta tal har lika moduler, d.v.s. │а│=│- а│ Låt oss visa att jämställdheten är korrekt. Låt oss skriva ner definitionen av numret -A : │- a│= (2) Låt oss jämföra set (1) och (2). Uppenbarligen definitionerna av de absoluta värdena av siffror A Och -A passa ihop. Därav, │а│=│- а│
När vi överväger följande egenskaper kommer vi att begränsa oss till deras formulering, eftersom deras bevis ges in Egendom #2: Absolutvärdet av summan av ett ändligt tal riktiga nummer inte överstiger summan av de absoluta värdena av termerna: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │ Egendom #3: Det absoluta värdet av skillnaden mellan två reella tal överstiger inte summan av deras absoluta värden: │а - в│ ≤│а│+│в│ Egendom #4: Det absoluta värdet av produkten av ett ändligt antal reella tal är lika med produkten av de absoluta värdena av faktorerna: │а·в│=│а│·│в│ Egendom #5: Det absoluta värdet av kvoten av reella tal är lika med kvoten av deras absoluta värden:

Avsnitt 3. Geometrisk tolkning av begreppet modul för ett tal.

Varje reellt tal kan associeras med en punkt på tallinjen, som blir en geometrisk bild av detta reella tal. Varje punkt på tallinjen motsvarar dess avstånd från origo, d.v.s. längden på segmentet från origo till en given punkt. Detta avstånd betraktas alltid som ett icke-negativt värde. Därför kommer längden på motsvarande segment att vara geometrisk tolkning absolutvärdet av ett givet reellt tal

Den presenterade geometriska illustrationen bekräftar tydligt egenskap nr 1, d.v.s. modulerna för motsatta tal är lika. Härifrån är giltigheten av likheten lätt att förstå: │х – а│= │а – x│. Lösningen till ekvationen │х│= m, där m ≥ 0, nämligen x 1,2 = ± m, blir också mer uppenbar. Exempel: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Avsnitt 4. Graf över funktionen y = │х│

Domänen för denna funktion är alla reella tal.

Avsnitt 5. Konventioner.

I framtiden, när man överväger exempel på att lösa ekvationer, kommer följande konventioner att användas: ( - tecken på systemet [ - tecken på helheten När man löser ett ekvationssystem (ojämlikheter) hittas skärningspunkten av lösningar för de ekvationer (ojämlikheter) som ingår i systemet. När man löser en uppsättning ekvationer (olikheter), hittas föreningen av lösningar som ingår i ekvationsuppsättningen (olikheter).

Kapitel 2. Lösa ekvationer som innehåller en modul.

I det här kapitlet kommer vi att titta på algebraiska metoder för att lösa ekvationer som innehåller en eller flera moduler.

Avsnitt 1. Ekvationer av formen │F (x)│= m

En ekvation av denna typ kallas den enklaste. Den har en lösning om och bara om m ≥ 0. Per definition av modulen är den ursprungliga ekvationen ekvivalent med en uppsättning av två ekvationer: │ F(x)│=m
Exempel:
№1. Lös ekvationen: │7х - 2│= 9


Svar: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Svar: summan av rötterna är -2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 betecknar x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5 m + 4 = 0 m = 1; 4 – båda värdena uppfyller villkoret m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Svar: antalet rötter i ekvation 7. Övningar:
№1. Lös ekvationen och ange summan av rötterna: │х - 5│= 3 №2 . Lös ekvationen och ange den mindre roten: │x 2 + x│= 0 №3 . Lös ekvationen och ange den större roten: │x 2 – 5x + 4│= 4 №4 .Lös ekvationen och ange hela roten: │2x 2 – 7x + 6│= 1 №5 .Lös ekvationen och ange antalet rötter: │x 4 – 13x 2 + 50│= 14

Avsnitt 2. Ekvationer av formen F(│х│) = m

Funktionsargumentet på vänster sida är under modultecknet och höger del beror inte på variabeln. Låt oss överväga två sätt att lösa ekvationer av denna typ. 1 sätt: Per definition av absolut värde är den ursprungliga ekvationen ekvivalent med kombinationen av två system. I var och en av dessa ställs ett villkor på ett submodulärt uttryck. F(│х│) =m
Eftersom funktionen F(│x│) är jämn genom hela definitionsdomänen, är rötterna till ekvationerna F(x) = m och F(- x) = m par av motsatta tal. Därför räcker det med att lösa ett av systemen (när man överväger exempel på detta sätt kommer lösningen till ett system att ges). Metod 2: Tillämpning av metoden för att introducera en ny variabel. I detta fall införs beteckningen │x│= a, där a ≥ 0. Denna metod är mindre voluminös till sin design.
Exempel: №1 . Lös ekvationen: 3x 2 – 4│x│= - 1 Låt oss använda introduktionen av en ny variabel. Låt oss beteckna │x│= a, där a ≥ 0. Vi får ekvationen 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Återgå till den ursprungliga variabeln: │ x│=1 och │х│= 1/3. Varje ekvation har två rötter. Svar: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Lös ekvationen: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2
Låt oss hitta lösningen på det första systemet i populationen: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Observera att x 2 inte uppfyller villkoret x ≥ 0. Lösning det andra systemet blir talet motsatt värdet x 1. Svar: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Lös ekvationen: x 4 – │х│= 0 Låt oss beteckna │х│= a, där a ≥ 0. Vi får ekvationen a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Återgå till den ursprungliga variabeln: │х│=0 och │х│= 1 x = 0; ± 1 Svar: x 1 = 0; X 2 = 1; X 3 = - 1.
Övningar: №6. Lös ekvationen: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Lös ekvationen, ange antalet rötter i ditt svar: 3x 2 - 7│x│ + 2 = 0 №8 . Lös ekvationen, ange heltalslösningar i ditt svar: x 4 + │x│ - 2 = 0

Avsnitt 3. Ekvationer av formen │F(x)│ = G(x)

Den högra sidan av en ekvation av denna typ beror på en variabel och har därför en lösning om och endast om den högra sidan är en funktion G(x) ≥ 0. Den ursprungliga ekvationen kan lösas på två sätt : 1 sätt: Standard, baserad på avslöjandet av en modul baserad på dess definition och består av en likvärdig övergång till en kombination av två system. │ F(x)│ =G(X)

Denna metod kan rationellt användas i fallet med ett komplext uttryck för funktionen G(x) och ett mindre komplext för funktionen F(x), eftersom det antas att olikheter med funktionen F(x) kommer att lösas. Metod 2: Består i övergången till ett likvärdigt system där ett villkor ställs på höger sida. │ F(x)│= G(x)

Denna metod är bekvämare att använda om uttrycket för funktionen G(x) är mindre komplext än för funktionen F(x), eftersom lösningen på olikheten G(x) ≥ 0 antas av flera moduler, rekommenderas att använda det andra alternativet. Exempel: №1. Lös ekvationen: │x + 2│= 6 -2x
(en väg) Svar: x = 1 1 / 3 №2.
│x 2 – 2x - 1│= 2 (x + 1)
(2-vägs) Svar: Produkten av rötter är 3.
№3. Lös ekvationen och ange summan av rötterna i ditt svar:
│x - 6│= x 2 - 5x + 9

Svar: summan av rötterna är 4.
Övningar: №9. │x + 4│= - 3x №10. Lös ekvationen, ange antalet lösningar i ditt svar:│x 2 + x - 1│= 2x – 1 №11 . Lös ekvationen, ange produkten av rötterna i ditt svar:│x + 3│= x 2 + x – 6

Avsnitt 4. Ekvationer med formen │F(x)│= F(x) och │F(x)│= - F(x)

Ekvationer av denna typ kallas ibland "den vackraste". Eftersom den högra sidan av ekvationerna beror på variabeln, finns lösningar om och endast om den högra sidan är icke-negativ. Därför är de ursprungliga ekvationerna ekvivalenta med ojämlikheterna:
│F(x)│= F(x) F(x) ≥ 0 och │F(x)│= - F(x) F(x) Exempel: №1 . Lös ekvationen, ange den mindre heltalsroten i ditt svar: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Svar: x = 1№2. Lös ekvationen, ange längden på intervallet i ditt svar: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Svar: längden på gapet är 6.№3 . Lös ekvationen och ange antalet heltalslösningar i ditt svar: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Svar: 4 hela lösningar.№4 . Lös ekvationen och ange den största roten i ditt svar:
│4 – x –
│= 4 – x –
x 2 – 5x + 5 = 0 D = 5 x 1,2 =
≈ 1,4

Svar: x = 3.

Övningar: №12. Lös ekvationen, ange hela roten i svaret: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Lös ekvationen, ange antalet heltalslösningar i ditt svar: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Lös ekvationen i ditt svar, ange ett heltal som inte är roten till ekvationen:

Avsnitt 5. Ekvationer av formen │F(x)│= │G(x)│

Eftersom båda sidor av ekvationen är icke-negativa, innebär lösningen att överväga två fall: submodulära uttryck är lika eller motsatta i tecken. Därför är den ursprungliga ekvationen ekvivalent med kombinationen av två ekvationer: │ F(x)│= │ G(x)│
Exempel: №1. Lös ekvationen, ange hela roten i ditt svar: │x + 3│=│2x - 1│
Svar: hel rot x = 4.№2. Lös ekvationen: │ x – x 2 - 1│=│2x – 3 – x 2 │
Svar: x = 2.№3 . Lös ekvationen och ange produkten av rötterna i ditt svar:




Rotekvationer 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Svar: produkten av rötterna är – 0,25. Övningar: №15 . Lös ekvationen och ange hela lösningen i ditt svar: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Lös ekvationen, ange den mindre roten i ditt svar:│5x - 3│=│7 - x│ №17 . Lös ekvationen och ange summan av rötterna i ditt svar:

Avsnitt 6. Exempel på att lösa icke-standardiserade ekvationer

I det här avsnittet kommer vi att titta på exempel på icke-standardiserade ekvationer, när vi löser vilka det absoluta värdet av uttrycket avslöjas per definition. Exempel:

№1. Lös ekvationen, ange summan av rötterna i ditt svar: x · │x│- 5x – 6 = 0
Svar: summan av rötterna är 1 №2. . Lös ekvationen, ange den mindre roten i ditt svar: x 2 - 4x ·
- 5 = 0
Svar: mindre rot x = -5. №3. Lös ekvationen:

Svar: x = -1. Övningar: №18. Lös ekvationen och ange summan av rötterna: x · │3x + 5│= 3x 2 + 4x + 3
№19. Lös ekvationen: x 2 – 3x =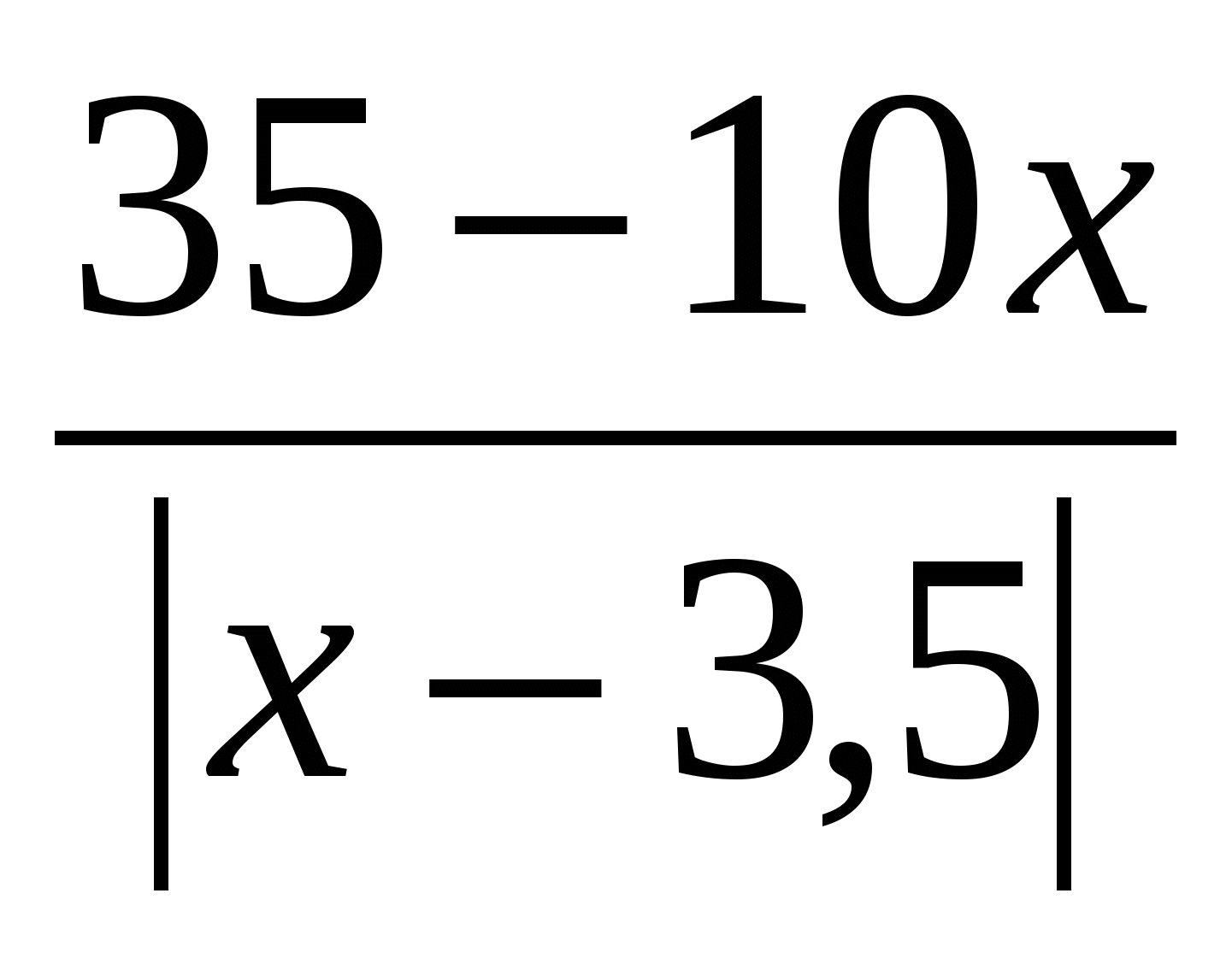

№20. Lös ekvationen:

Avsnitt 7. Ekvationer av formen │F(x)│+│G(x)│=0

Det är lätt att märka att på vänster sida av ekvationen av denna typ finns summan av icke-negativa storheter. Därför har den ursprungliga ekvationen en lösning om och bara om båda termerna är lika med noll samtidigt. Ekvationen är ekvivalent med ekvationssystemet: │ F(x)│+│ G(x)│=0
Exempel: №1 . Lös ekvationen:
Svar: x = 2. №2. Lös ekvationen: Svar: x = 1. Övningar: №21. Lös ekvationen: №22 . Lös ekvationen och ange summan av rötterna i ditt svar: №23 . Lös ekvationen och ange antalet lösningar i ditt svar:

Avsnitt 8. Ekvationer av formen │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

För att lösa ekvationer av denna typ används intervallmetoden. Om vi ​​löser det genom sekventiell expansion av moduler får vi n uppsättningar av system, vilket är mycket besvärligt och obekvämt. Låt oss överväga intervallmetodens algoritm: 1). Hitta variabelvärden X, för vilken varje modul är lika med noll (nollor av submodulära uttryck):
2). Markera de hittade värdena på en tallinje, som är uppdelad i intervall (antalet intervall är respektive lika med n+1 ) 3). Bestäm med vilket tecken varje modul avslöjas vid vart och ett av de erhållna intervallen (när du gör en lösning kan du använda en tallinje, markera tecknen på den) 4). Den ursprungliga ekvationen är ekvivalent med aggregatet n+1 system, i vilka variabelns medlemskap anges X ett av intervallen. Exempel: №1 . Lös ekvationen och ange den största roten i ditt svar:
1). Låt oss hitta nollorna för de submodulära uttrycken: x = 2; x = -3 2). Låt oss markera de hittade värdena på tallinjen och bestämma med vilket tecken varje modul avslöjas på de erhållna intervallen:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- inga lösningar Ekvationen har två rötter. Svar: den största roten x = 2. №2. Lös ekvationen och ange hela roten i ditt svar:
1). Låt oss hitta nollorna för de submodulära uttrycken: x = 1,5; x = -12). Låt oss markera de hittade värdena på tallinjen och bestämma med vilket tecken varje modul avslöjas på de resulterande intervallen: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).
Det sista systemet har inga lösningar, därför har ekvationen två rötter. När du löser ekvationen bör du vara uppmärksam på "-"-tecknet framför den andra modulen. Svar: hel rot x = 7. №3. Lös ekvationen, ange summan av rötterna i ditt svar: 1). Låt oss hitta nollorna för de submodulära uttrycken: x = 5; x = 1; x = -2 2). Låt oss markera de hittade värdena på tallinjen och bestämma med vilket tecken varje modul avslöjas med de resulterande intervallen: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Ekvationen har två rötter x = 0 och 2. Svar: summan av rötterna är 2. №4 . Lös ekvationen: 1). Låt oss hitta nollorna för de submodulära uttrycken: x = 1; x = 2; x = 3,2). Låt oss bestämma med vilket tecken varje modul avslöjas på de resulterande intervallen. 3).
Låt oss kombinera lösningarna för de tre första systemen. Svar: ; x = 5.
Övningar: №24. Lös ekvationen:
№25. Lös ekvationen och ange summan av rötterna i ditt svar: №26. Lös ekvationen och ange den mindre roten i ditt svar: №27. Lös ekvationen och ange den större roten i ditt svar:

Avsnitt 9. Ekvationer som innehåller flera moduler

Ekvationer som innehåller flera moduler antar närvaron av absoluta värden i submodulära uttryck. Grundprincipen för att lösa ekvationer av denna typ är den sekventiella redovisningen av moduler, som börjar med den "externa". Under lösningen används de tekniker som diskuteras i avsnitt nr 1, nr 3.

Exempel: №1. Lös ekvationen:
Svar: x = 1; - elva. №2. Lös ekvationen:
Svar: x = 0; 4; - 4. №3. Lös ekvationen och ange produkten av rötterna i ditt svar:
Svar: produkten av rötterna är – 8. №4. Lös ekvationen:
Låt oss beteckna befolkningens ekvationer (1) Och (2) och överväg lösningen för var och en av dem separat för enkel design. Eftersom båda ekvationerna innehåller mer än en modul är det bekvämare att utföra en ekvivalent övergång till uppsättningar av system. (1)

(2)


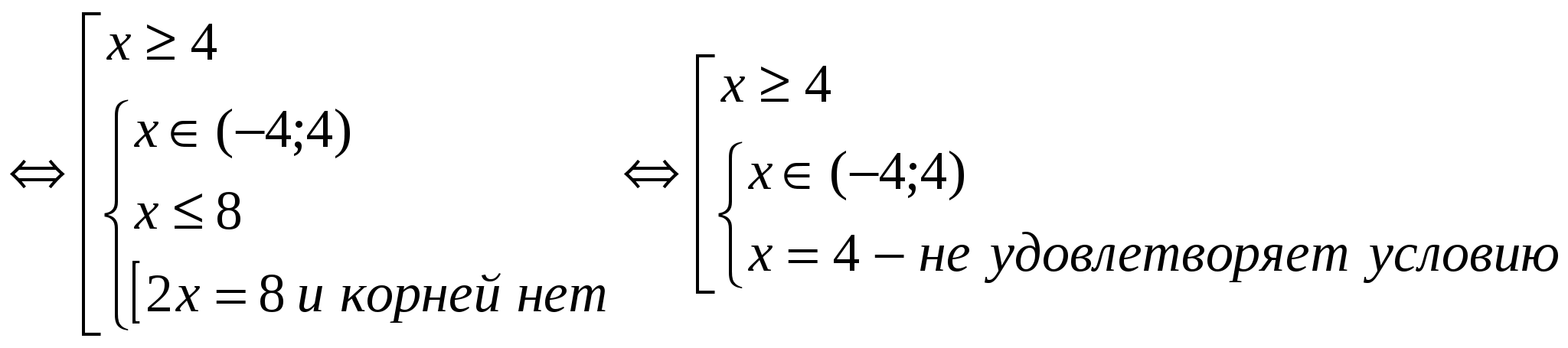Svar:
Övningar: №36. Lös ekvationen, ange summan av rötterna i ditt svar: 5 │3x-5│ = 25 x №37. Lös ekvationen, om det finns mer än en rot, ange summan av rötterna i ditt svar: │x + 2│ x – 3x – 10 = 1 №38. Lös ekvationen: 3 │2х -4│ = 9 │х│ №39. Lös ekvationen, i ditt svar ange antalet rötter per: 2 │ sin x│ = √2 №40 . Lös ekvationen och ange antalet rötter i ditt svar:

Avsnitt 3. Logaritmiska ekvationer.

Innan du löser följande ekvationer är det nödvändigt att se över egenskaperna hos logaritmer och logaritmisk funktion. Exempel: №1. Lös ekvationen, ange produkten av rötterna i ditt svar: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Fall 1: om x ≥ - 1, då log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – uppfyller villkoret x ≥ - 1 2 fall: om x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – uppfyller skick x - 1
Svar: produkten av rötterna är – 15.
№2. Lös ekvationen, ange summan av rötterna i ditt svar: lg
O.D.Z.

Svar: summan av rötterna är 0,5.
№3. Lös ekvationen: log 5
O.D.Z.

Svar: x = 9. №4. Lös ekvationen: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Låt oss använda formeln för att flytta till en annan bas. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Låt oss hitta nollorna för de submodulära uttrycken: x = 25; x = Dessa siffror delar upp området för acceptabla värden i tre intervall, så ekvationen är ekvivalent kombination av tre system.
Svar:)