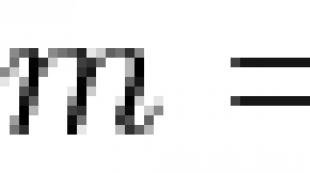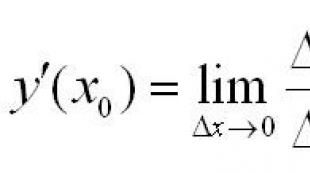Vem introducerade derivatan? Vad är en derivata Definition och betydelse av en derivata funktion. Geometrisk betydelse av derivatan av en funktion vid en punkt
Uppgift B9 ger en graf över en funktion eller derivata från vilken du behöver bestämma en av följande storheter:
- Värdet av derivatan vid någon punkt x 0,
- Högsta eller lägsta poäng (extrempoäng),
- Intervaller av ökande och minskande funktioner (intervall av monotoni).
Funktionerna och derivatorna som presenteras i detta problem är alltid kontinuerliga, vilket gör lösningen mycket enklare. Trots att uppgiften tillhör sektionen matematisk analys, det är helt inom förmågan för även de svagaste eleverna, eftersom inga djupa teoretiska kunskaper krävs här.
För att hitta värdet av derivatan, extrema punkter och monotonisitetsintervall finns det enkla och universella algoritmer - alla kommer att diskuteras nedan.
Läs villkoren för problem B9 noggrant för att undvika att göra dumma misstag: ibland stöter du på ganska långa texter, men det finns få viktiga förhållanden som påverkar lösningens gång.
Beräkning av derivatvärdet. Tvåpunktsmetod
Om problemet ges en graf av en funktion f(x), som tangerar denna graf vid någon punkt x 0, och det krävs för att hitta värdet på derivatan vid denna punkt, tillämpas följande algoritm:
- Hitta två "tillräckliga" punkter på tangentgrafen: deras koordinater måste vara heltal. Låt oss beteckna dessa punkter A (x 1 ; y 1) och B (x 2 ; y 2). Skriv ner koordinaterna korrekt - detta är en nyckelpunkt i lösningen, och alla misstag här kommer att leda till ett felaktigt svar.
- Genom att känna till koordinaterna är det lätt att beräkna ökningen av argumentet Δx = x 2 − x 1 och ökningen av funktionen Δy = y 2 − y 1 .
- Slutligen finner vi värdet av derivatan D = Δy/Δx. Med andra ord måste du dividera ökningen av funktionen med ökningen av argumentet - och detta kommer att vara svaret.
Låt oss återigen notera: punkterna A och B måste letas efter exakt på tangenten, och inte på grafen för funktionen f(x), som ofta händer. Tangentlinjen kommer nödvändigtvis att innehålla minst två sådana punkter - annars kommer problemet inte att formuleras korrekt.
Betrakta punkterna A (−3; 2) och B (−1; 6) och hitta stegen:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Låt oss hitta värdet på derivatan: D = Δy/Δx = 4/2 = 2.
Uppgift. Figuren visar en graf över funktionen y = f(x) och en tangent till den i punkten med abskissan x 0. Hitta värdet på derivatan av funktionen f(x) i punkten x 0 .
Tänk på punkterna A (0; 3) och B (3; 0), hitta stegen:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Nu hittar vi värdet på derivatan: D = Δy/Δx = −3/3 = −1.
Uppgift. Figuren visar en graf över funktionen y = f(x) och en tangent till den i punkten med abskissan x 0. Hitta värdet på derivatan av funktionen f(x) i punkten x 0 .
Betrakta punkterna A (0; 2) och B (5; 2) och hitta stegen:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Det återstår att hitta värdet på derivatan: D = Δy/Δx = 0/5 = 0.
Från det sista exemplet kan vi formulera en regel: om tangenten är parallell med OX-axeln är derivatan av funktionen i tangentpunkten noll. I det här fallet behöver du inte ens räkna någonting - titta bara på grafen.
Beräkning av högsta och lägsta poäng
Ibland, istället för en graf för en funktion, ger uppgift B9 en graf över derivatan och kräver att man hittar funktionens max- eller minimumpunkt. I den här situationen är tvåpunktsmetoden värdelös, men det finns en annan, ännu enklare algoritm. Låt oss först definiera terminologin:
- Punkten x 0 kallas maximipunkten för funktionen f(x) om följande olikhet gäller i någon omgivning till denna punkt: f(x 0) ≥ f(x).
- Punkten x 0 kallas minimipunkten för funktionen f(x) om i någon grannskap av denna punkt följande olikhet gäller: f(x 0) ≤ f(x).
För att hitta högsta och lägsta poäng från derivatdiagrammet, följ bara dessa steg:
- Rita om derivatagrafen och ta bort all onödig information. Som praxis visar stör onödiga uppgifter bara beslutet. Därför markerar vi nollorna för derivatan på koordinataxeln - och det är det.
- Ta reda på tecknen för derivatan på intervallen mellan nollor. Om det för någon punkt x 0 är känt att f'(x 0) ≠ 0, så är bara två alternativ möjliga: f'(x 0) ≥ 0 eller f'(x 0) ≤ 0. Tecknet för derivatan är lätt att avgöra från originalritningen: om derivatagrafen ligger ovanför OX-axeln, då f'(x) ≥ 0. Och vice versa, om derivatagrafen ligger under OX-axeln, då f'(x) ≤ 0.
- Återigen kontrollerar vi nollorna och tecknen för derivatan. Där tecknet ändras från minus till plus är minimipunkten. Omvänt, om tecknet för derivatan ändras från plus till minus, är detta maxpunkten. Räkningen görs alltid från vänster till höger.
Detta schema fungerar bara för kontinuerliga funktioner - det finns inga andra i problem B9.
Uppgift. Figuren visar en graf av derivatan av funktionen f(x) definierad på intervallet [−5; 5]. Hitta minimipunkten för funktionen f(x) på detta segment.
Låt oss bli av med onödig information och lämna bara gränserna [−5; 5] och nollor av derivatan x = −3 och x = 2,5. Vi noterar också tecknen:
Uppenbarligen ändras derivatans tecken från minus till plus vid punkten x = −3. Detta är minimipunkten.
Uppgift. Figuren visar en graf av derivatan av funktionen f(x) definierad på intervallet [−3; 7]. Hitta maxpunkten för funktionen f(x) på detta segment.
Låt oss rita om grafen och lämna bara gränserna [−3; 7] och nollor för derivatan x = −1,7 och x = 5. Låt oss notera derivatans tecken på den resulterande grafen. Vi har:
![]()
Uppenbarligen, vid punkten x = 5 ändras tecknet för derivatan från plus till minus - detta är maxpunkten.
Uppgift. Figuren visar en graf av derivatan av funktionen f(x) definierad på intervallet [−6; 4]. Hitta antalet maxpunkter för funktionen f(x) som hör till segmentet [−4; 3].
Av villkoren för problemet följer att det är tillräckligt att endast beakta den del av grafen som begränsas av segmentet [−4; 3]. Därför bygger vi en ny graf där vi bara markerar gränserna [−4; 3] och nollor av derivatan inuti den. Nämligen punkterna x = −3,5 och x = 2. Vi får:
![]()
På denna graf finns bara en maxpunkt x = 2. Det är vid denna punkt som derivatans tecken ändras från plus till minus.
En liten anteckning om punkter med icke-heltalskoordinater. Till exempel, i det sista problemet övervägdes punkten x = −3,5, men med samma framgång kan vi ta x = −3,4. Om problemet är korrekt sammanställt bör sådana ändringar inte påverka svaret, eftersom punkterna ”utan fast bostadsort” inte direkt deltar i att lösa problemet. Naturligtvis kommer det här tricket inte att fungera med heltalspunkter.
Hitta intervall av ökande och minskande funktioner
I ett sådant problem, som punkterna för maximum och minimum, föreslås det att använda grafen för derivatan för att hitta områden där själva funktionen ökar eller minskar. Låt oss först definiera vad ökande och minskande är:
- En funktion f(x) sägs öka på ett segment om följande påstående är sant för två punkter x 1 och x 2 från detta segment: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Med andra ord, ju större argumentvärde, desto större funktionsvärde.
- En funktion f(x) kallas minskande på ett segment om för två punkter x 1 och x 2 från detta segment följande påstående är sant: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). De där. Ett större argumentvärde motsvarar ett mindre funktionsvärde.
Låt oss formulera tillräckliga förutsättningar för att öka och minska:
- För att kontinuerlig funktion f(x) ökar på segmentet , det räcker att dess derivata inuti segmentet är positiv, d.v.s. f’(x) ≥ 0.
- För att en kontinuerlig funktion f(x) ska minska på segmentet räcker det att dess derivata inuti segmentet är negativ, d.v.s. f’(x) ≤ 0.
Låt oss acceptera dessa uttalanden utan bevis. Således får vi ett schema för att hitta intervall av ökande och minskande, som på många sätt liknar algoritmen för att beräkna extremumpunkter:
- Ta bort all onödig information. I den ursprungliga grafen för derivatan är vi främst intresserade av funktionens nollor, så vi lämnar bara dem.
- Markera derivatans tecken med intervallen mellan nollor. Där f’(x) ≥ 0 ökar funktionen och där f’(x) ≤ 0 minskar den. Om problemet sätter begränsningar för variabeln x, markerar vi dem dessutom på en ny graf.
- Nu när vi känner till funktionens beteende och begränsningarna återstår det att beräkna den kvantitet som krävs i problemet.
Uppgift. Figuren visar en graf över derivatan av funktionen f(x) definierad på intervallet [−3; 7,5]. Hitta minskningsintervallen för funktionen f(x). I ditt svar, ange summan av de heltal som ingår i dessa intervall.
Låt oss som vanligt rita om grafen och markera gränserna [−3; 7,5], samt nollor av derivatan x = −1,5 och x = 5,3. Sedan noterar vi derivatans tecken. Vi har:
![]()
Eftersom derivatan är negativ på intervallet (− 1,5), är detta intervallet för minskande funktion. Det återstår att summera alla heltal som finns inom detta intervall:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Uppgift. Figuren visar en graf av derivatan av funktionen f(x), definierad på intervallet [−10; 4]. Hitta ökningsintervallen för funktionen f(x). I ditt svar, ange längden på den största av dem.
Låt oss bli av med onödig information. Låt oss bara lämna gränserna [−10; 4] och nollor av derivatan, av vilka det var fyra denna gång: x = −8, x = −6, x = −3 och x = 2. Låt oss markera tecknen för derivatan och få följande bild:
Vi är intresserade av intervallerna för ökande funktion, d.v.s. sådan där f’(x) ≥ 0. Det finns två sådana intervall på grafen: (−8; −6) och (−3; 2). Låt oss beräkna deras längder:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Eftersom vi behöver hitta längden på det största av intervallen skriver vi ner värdet l 2 = 5 som svar.
Låt funktionen definieras vid en punkt och en del av dess grannskap. Låt oss ge argumentet ett steg så att punkten faller inom definitionsdomänen för funktionen. Funktionen kommer då att ökas.
DEFINITION. Derivata av en funktion vid en punkt kallas gränsen för förhållandet mellan ökningen av funktionen vid denna punkt till ökningen av argumentet, vid (om denna gräns finns och är finit), dvs.
Beteckna: ,,,.
Derivat av en funktion vid en punkt till höger (vänster) kallad
(om denna gräns finns och är ändlig).
Betecknad av: , – derivata vid punkten till höger,
, är derivatan vid punkten till vänster.
Uppenbarligen är följande teorem sann.
SATS. En funktion har en derivata vid en punkt om och bara om vid denna punkt derivatorna av funktionen till höger och vänster existerar och är lika med varandra. Dessutom
Följande sats etablerar ett samband mellan förekomsten av en derivata av en funktion vid en punkt och kontinuiteten för funktionen vid den punkten.
SAT (ett nödvändigt villkor för att det ska finnas en derivata av en funktion i en punkt). Om en funktion har en derivata vid en punkt, är funktionen vid den punkten kontinuerlig.
BEVIS
Låt det existera. Sedan
![]() ,
,
var är oändligt liten vid.
Kommentar
derivata av en funktion och beteckna
differentiering av funktion .
GEOMETRISK OCH FYSISK BETYDELSE
1) Fysisk betydelse av derivatan. Om en funktion och dess argument är fysiska kvantiteter, då är derivatan förändringshastigheten för en variabel i förhållande till variabeln vid en punkt. Om till exempel är det avstånd som en tidpunkt täcker, är dess derivata hastigheten vid tidpunkten. Om är mängden elektricitet som strömmar genom ledarens tvärsnitt vid ett ögonblick, då är förändringshastigheten i mängden elektricitet vid ett ögonblick, dvs. nuvarande styrka vid ett ögonblick i tiden.
2) Geometrisk betydelse av derivata.
Låt vara en kurva, vara en punkt på kurvan. 
Varje rät linje som skär minst två punkter kallas sekant .
Tangent till en kurva vid en punkt Gränsläget för en sekant kallas om punkten tenderar att när den rör sig längs en kurva.
Av definitionen är det uppenbart att om en tangent till en kurva finns vid en punkt, så är den den enda
Betrakta en kurva (dvs. en graf över en funktion). Låt den ha en icke-vertikal tangent i en punkt. Dess ekvation: (ekvation för en rät linje som går genom en punkt och har en vinkelkoefficient). 
Per definition av lutningen
var är den räta linjens lutningsvinkel mot axeln.
Låta vara lutningsvinkeln för sekanten till axeln, där. Sedan är en tangent, då när
Därav,
Därmed fick vi det – vinkelkoefficient för tangenten till grafen för funktionen i punkten(geometrisk betydelse av derivatan av en funktion vid en punkt). Därför kan ekvationen för tangenten till kurvan i en punkt skrivas i formen
Kommentar . En rät linje som går genom en punkt vinkelrät mot tangenten som dras till kurvan i punkten kallas vinkelrät mot kurvan vid punkten . Eftersom vinkelkoefficienterna för vinkelräta räta linjer är relaterade av relationen, kommer ekvationen för normalen till kurvan vid en punkt att ha formen
![]() , Om .
, Om .
Om , då kommer tangenten till kurvan vid punkten att ha formen
och normalt.
TANGENT OCH NORMALA EKVATIONER
Tangentekvation
Låt funktionen ges av ekvationen y=f(x), måste du skriva ekvationen tangent vid punkten x 0. Från definitionen av derivat:
y/(x)=limA x→0Δ yΔ x
Δ y=f(x+Δ x)−f(x).
Ekvationen tangent till grafen för funktionen: y=kx+b (k,b=konst). Från den geometriska betydelsen av derivatan: f/(x 0)=tgα= k Därför att x 0 och f(x 0)∈ rät linje, sedan ekvationen tangent skrivs som: y−f(x 0)=f/(x 0)(x−x 0), eller
y=f/(x 0)· x+f(x 0)−f/(x 0)· x 0.

Normal ekvation
Vanligt- är vinkelrät mot tangent(se bild). Baserat på det här:
tgβ= tg(2π−α)= ctg a=1 tg a=1 f/(x 0)
Därför att lutningsvinkeln för normalen är vinkeln β1, då har vi:
tgβ1= tg(π−β)=− tgβ=−1 f/(x).
Punkt ( x 0,f(x 0))∈ normal, ekvationen har formen:
y−f(x 0)=−1f/(x 0)(x−x 0).
BEVIS
Låt det existera. Sedan
![]() ,
,
var är oändligt liten vid.
Men det betyder att den är kontinuerlig vid en punkt (se den geometriska definitionen av kontinuitet). ∎
Kommentar . Kontinuiteten för en funktion vid en punkt är inte ett tillräckligt villkor för att det ska finnas en derivata av denna funktion vid en punkt. Till exempel är en funktion kontinuerlig, men har ingen derivata vid en punkt. Verkligen,
och därför inte existerar.
Uppenbarligen är korrespondens en funktion definierad på någon uppsättning. De ringer henne derivata av en funktion och beteckna
Operationen att hitta för en funktion dess derivata funktion kallas differentiering av funktion .
Derivat av summa och skillnad
Låt funktionerna f(x) och g(x) ges vars derivator är kända för oss. Till exempel kan du ta de elementära funktionerna som diskuterats ovan. Sedan kan du hitta derivatan av summan och skillnaden av dessa funktioner:
(f + g)' = f ' + g '
(f − g)' = f ' − g '
Så derivatan av summan (skillnaden) av två funktioner är lika med summan (skillnaden) av derivatorna. Det kan finnas fler termer. Till exempel, (f + g + h)' = f' + g' + h'.
Strängt taget finns det inget koncept för "subtraktion" i algebra. Det finns ett koncept av "negativt element". Därför kan skillnaden f − g skrivas om till summan f + (−1) g, och då återstår bara en formel - derivatan av summan.
Innehållet i artikeln
DERIVAT– derivata av funktionen y = f(x), ges på ett visst intervall ( a, b) vid punkt x av detta intervall kallas gränsen till vilken förhållandet mellan funktionens inkrement tenderar f vid denna punkt till motsvarande ökning av argumentet när ökningen av argumentet tenderar till noll.
Derivaten betecknas vanligtvis enligt följande:
Andra beteckningar används också ofta:
Omedelbar hastighet.
Låt poängen M rör sig i en rak linje. Distans s rörlig punkt, räknat från någon utgångsposition M 0 , beror på tid t, dvs. s det finns en funktion av tiden t: s= f(t). Låt någon gång i tiden t rörlig punkt M var på avstånd s från startpositionen M 0, och i nästa ögonblick t+D t befann sig i en position M 1 - på distans s+D s från utgångsläget ( se bild.).
Alltså, under en tidsperiod D t distans sändras med beloppet D s. I det här fallet säger de att under tidsintervallet D t magnitud s fick inkrement D s.
Medelhastigheten kan inte i alla fall exakt karakterisera en punkts rörelsehastighet M vid en tidpunkt t. Om till exempel kroppen i början av intervallet D t flyttas mycket snabbt, och i slutet mycket långsamt, då kommer medelhastigheten inte att kunna återspegla de angivna egenskaperna hos punktens rörelse och ge en uppfattning om den verkliga hastigheten för dess rörelse för tillfället t. För att mer exakt uttrycka den verkliga hastigheten med medelhastigheten måste du ta en kortare tid D t. Karakteriserar till fullo rörelsehastigheten för en punkt för tillfället t gränsen till vilken medelhastigheten tenderar vid D t® 0. Denna gräns kallas den aktuella hastigheten:
Således kallas rörelsehastigheten vid ett givet ögonblick gränsen för banökningsförhållandet D s till tidsökning D t, när tidsstegringen tenderar till noll. Därför att
Geometrisk betydelse av derivatan. Tangent till grafen för en funktion.
Konstruktionen av tangenter är ett av de problem som ledde till födelsen av differentialkalkyl. Det första publicerade arbetet relaterade till differentialkalkyl, skrivet av Leibniz, hade titeln En ny metod för maxima och minima, såväl som tangenter, för vilka varken bråktal eller irrationella storheter är ett hinder, och en speciell typ av kalkyl för detta.
Låt kurvan vara grafen för funktionen y =f(x) i ett rektangulärt koordinatsystem ( centimeter. ris.).
Till något värde x funktion har betydelse y =f(x). Dessa värden x Och y punkten på kurvan motsvarar M 0(x, y). Om argumentet x ge öka D x, sedan det nya värdet för argumentet x+D x motsvarar det nya funktionsvärdet y+ D y = f(x + D x). Motsvarande punkt på kurvan kommer att vara punkten M 1(x+D x,y+D y). Om du ritar en sekant M 0M 1 och betecknad med j vinkeln som bildas av en tvärgående med axelns positiva riktning Oxe, av figuren är det omedelbart tydligt att .
Om nu D x tenderar till noll, sedan punkten M 1 rör sig längs kurvan och närmar sig punkten M 0 och vinkel j ändras med D x. På Dx® 0 vinkeln j tenderar till en viss gräns a och den räta linjen som går genom punkten M 0 och komponenten med x-axelns positiva riktning, vinkel a, blir den önskade tangenten. Dess lutning är:
Därav, f´( x) = tga
de där. derivatvärde f´( x) för ett givet argumentvärde xär lika med tangenten för vinkeln som bildas av tangenten till grafen för funktionen f(x) vid motsvarande punkt M 0(x,y) med positiv axelriktning Oxe.
Funktioners differentierbarhet.
Definition. Om funktionen y = f(x) har en derivata vid punkten x = x 0, då är funktionen differentierbar vid denna punkt.
Kontinuitet för en funktion som har en derivata. Sats.
Om funktionen y = f(x) är differentierbar någon gång x = x 0, då är den kontinuerlig vid denna punkt.
Funktionen kan alltså inte ha en derivata vid diskontinuitetspunkter. Den motsatta slutsatsen är felaktig, d.v.s. från det faktum att någon gång x = x 0 funktion y = f(x) är kontinuerlig betyder inte att den är differentierbar vid denna tidpunkt. Till exempel funktionen y = |x| kontinuerligt för alla x(–Ґ x x = 0 har ingen derivata. Vid denna punkt finns det ingen tangent till grafen. Det finns en höger tangent och en vänster, men de sammanfaller inte.
Några satser om differentierbara funktioner. Sats om rötterna till derivatan (Rolles sats). Om funktionen f(x) är kontinuerlig på segmentet [a,b], är differentierbar vid alla inre punkter i detta segment och i ändarna x = a Och x = b går till noll ( f(a) = f(b) = 0), sedan inuti segmentet [ a,b] finns det minst en punkt x= Med, a c b, där derivatan fў( x) går till noll, dvs. fў( c) = 0.
Finita inkrementsats (Lagranges sats). Om funktionen f(x) är kontinuerlig på intervallet [ a, b] och är differentierbar vid alla inre punkter i detta segment, sedan inuti segmentet [ a, b] finns det minst en punkt Med, a c b det
f(b) – f(a) = fў( c)(b– a).
Sats om förhållandet mellan inkrementen av två funktioner (Cauchys sats). Om f(x) Och g(x) – två kontinuerliga funktioner på segmentet [a, b] och differentierbar vid alla inre punkter i detta segment, och gў( x) försvinner inte någonstans i detta segment, sedan inuti segmentet [ a, b] det finns en sådan poäng x = Med, a c b det
Derivat av olika beställningar.
Låt funktionen y =f(x) är differentierbar på något intervall [ a, b]. Derivatvärden f ў( x), generellt sett beror på x, dvs. derivat f ў( x) är också en funktion av x. När vi differentierar denna funktion får vi den så kallade andraderivatan av funktionen f(x), som betecknas f ўў ( x).
Derivat n- funktionsordningen f(x) kallas (första ordningens) derivatan av derivatan n- 1- th och betecknas med symbolen y(n) = (y(n– 1))ў.
Differentialer av olika ordning.
Funktionsdifferential y = f(x), Var x– oberoende variabel, ja dy = f ў( x)dx, någon funktion från x, men från x endast den första faktorn kan bero f ў( x), den andra faktorn ( dx) är ökningen av den oberoende variabeln x och beror inte på värdet på denna variabel. Därför att dy det finns en funktion från x, då kan vi bestämma differentialen för denna funktion. Differentialen för differentialen för en funktion kallas den andra differentialen eller andra ordningens differential för denna funktion och betecknas d 2y:
d(dx) = d 2y = f ўў( x)(dx) 2 .
Differentiell n- av första ordningen kallas differentialens första differential n- 1- ordning:
d n y = d(d n–1y) = f(n)(x)dx(n).
Partiell derivat.
Om en funktion inte beror på ett, utan på flera argument x i(i varierar från 1 till n,i= 1, 2,… n),f(x 1,x 2,… x n), så introduceras i differentialkalkyl begreppet partiell derivata, som kännetecknar förändringshastigheten för en funktion av flera variabler när endast ett argument ändras, till exempel, x i. Partiell derivata av 1:a ordningen med avseende på x i definieras som en vanlig derivata, och det antas att alla argument utom x i, håll konstanta värden. För partiella derivator införs notationen
1:a ordningens partiella derivator definierade på detta sätt (som funktioner av samma argument) kan i sin tur också ha partiella derivator, dessa är andra ordningens partiella derivator osv. Sådana derivator hämtade från olika argument kallas blandade. Kontinuerliga blandade derivator av samma ordning beror inte på differentieringsordningen och är lika med varandra.
Anna Chugainova
(\large\bf Derivata av en funktion)
Tänk på funktionen y=f(x), specificerad på intervallet (a, b). Låta x- valfri fast punkt i intervallet (a, b), A Δx- ett godtyckligt tal så att värdet x+Δx hör också till intervallet (a, b). Detta nummer Δx kallas argumentökning.
Definition. Funktionsökning y=f(x) vid punkten x, motsvarande argumentökningen Δx, låt oss ringa numret
Δy = f(x+Δx) - f(x).
vi tror att Δx ≠ 0. Överväg vid en given fast punkt x förhållandet mellan funktionen ökning vid denna punkt och motsvarande argumentökning Δx
Vi kommer att kalla detta förhållande för skillnadsrelationen. Eftersom värdet x vi anser vara fixerade, skillnadsförhållandet är en funktion av argumentet Δx. Denna funktion är definierad för alla argumentvärden Δx, tillhörande något tillräckligt litet område av punkten Δx=0, förutom själva punkten Δx=0. Vi har således rätt att pröva frågan om förekomsten av en gräns för den angivna funktionen vid Δx → 0.
Definition. Derivata av en funktion y=f(x) vid en given fast punkt x kallas gränsen kl Δx → 0 skillnadsförhållande, det vill säga
Förutsatt att denna gräns finns.
Beteckning. y′(x) eller f′(x).
Geometrisk betydelse av derivata: Derivata av en funktion f(x) vid denna tidpunkt x lika med tangenten för vinkeln mellan axeln Oxe och en tangent till grafen för denna funktion vid motsvarande punkt:
f′(x 0) = \tgα.
Mekanisk betydelse av derivata: Banans derivata med avseende på tid är lika med hastigheten för punktens rätlinjiga rörelse:
Ekvation för en tangent till en linje y=f(x) vid punkten M 0 (x 0 ,y 0) tar formen
y-y 0 = f′(x 0) (x-x 0).
Normalen till en kurva vid någon punkt är vinkelrät mot tangenten vid samma punkt. Om f′(x 0)≠ 0, sedan ekvationen för normalen till linjen y=f(x) vid punkten M 0 (x 0 ,y 0)är skrivet så här:

Begreppet differentierbarhet för en funktion
Låt funktionen y=f(x) definieras över ett visst intervall (a, b), x- något fast argumentvärde från detta intervall, Δx- varje ökning av argumentet så att värdet av argumentet x+Δx ∈ (a, b).
Definition. Fungera y=f(x) kallas differentierbar vid en given punkt x, om ökning Δy denna funktion vid punkten x, motsvarande argumentökningen Δx, kan representeras i formen
Δy = A Δx + αΔx,
Var A- något antal oberoende av Δx, A α - argument funktion Δx, vilket är oändligt vid Δx→ 0.
Eftersom produkten av två infinitesimala funktioner αΔxär oändligt lite mer hög order, hur Δx(egenskap för 3 infinitesimala funktioner), då kan vi skriva:
Δy = A Δx +o(Δx).
Sats. För funktionen y=f(x) var differentierbar vid en given punkt x, är det nödvändigt och tillräckligt att den har en finit derivata vid denna punkt. Vart i A=f′(x), det är
Δy = f′(x) Δx +o(Δx).
Operationen att hitta derivatan brukar kallas differentiering.
Sats. Om funktionen y=f(x) x, då är den kontinuerlig vid denna punkt.
Kommentar. Från kontinuiteten i funktionen y=f(x) vid denna tidpunkt x, generellt sett följer inte funktionens differentierbarhet f(x) vid denna tidpunkt. Till exempel funktionen y=|x|- kontinuerlig vid en punkt x=0, men har ingen derivata.
Begreppet differentialfunktion
Definition. Funktionsdifferential y=f(x) produkten av derivatan av denna funktion och ökningen av den oberoende variabeln kallas x:
dy = y′ Δx, df(x) = f′(x) Δx.
För funktion y=x vi får dy=dx=x′Δx = 1· Δx= Δx, det är dx=Δx- differentialen för en oberoende variabel är lika med ökningen av denna variabel.
Så vi kan skriva
dy = y′ dx, df(x) = f′(x) dx
![]()
Differentiell dy och öka Δy funktioner y=f(x) vid denna tidpunkt x, båda motsvarar samma argumentökning Δx, generellt sett inte är lika med varandra.
Geometrisk betydelse av differential: Differentialen för en funktion är lika med ökningen av ordinatan för tangenten till grafen för denna funktion när argumentet inkrementeras Δx.
Regler för differentiering
Sats. Om var och en av funktionerna u(x) Och v(x) differentierbar vid en given punkt x, sedan summan, skillnaden, produkten och kvoten av dessa funktioner (kvoten förutsatt att v(x)≠ 0) är också differentierbara vid denna tidpunkt, och formlerna håller:

Tänk på den komplexa funktionen y=f(φ(x))≡ F(x), Var y=f(u), u=φ(x). I detta fall u kallad mellanargument, x - oberoende variabel.
Sats. Om y=f(u) Och u=φ(x)är differentierbara funktioner av sina argument, sedan derivatan av en komplex funktion y=f(φ(x)) existerar och är lika med produkten av denna funktion med avseende på det mellanliggande argumentet och derivatan av det mellanliggande argumentet med avseende på den oberoende variabeln, dvs.
![]()
Kommentar. För en komplex funktion som är en överlagring av tre funktioner y=F(f(φ(x))), differentieringsregeln har formen
y′ x = y′ u u′ v v′ x,
var finns funktionerna v=φ(x), u=f(v) Och y=F(u)- differentierbara funktioner för deras argument.
Sats. Låt funktionen y=f(x)ökar (eller minskar) och är kontinuerlig i någon del av punkten x 0. Låt dessutom denna funktion vara differentierbar vid den angivna punkten x 0 och dess derivata vid denna tidpunkt f′(x 0) ≠ 0. Sedan i något grannskap av motsvarande punkt y 0 =f(x 0) inversen definieras för y=f(x) fungera x=f -1 (y), och den indikerade inversa funktionen är differentierbar vid motsvarande punkt y 0 =f(x 0) och för dess derivat vid denna tidpunkt y formeln är giltig

Derivattabell

Invarians av formen av den första differentialen
Låt oss överväga differentialen för en komplex funktion. Om y=f(x), x=φ(t)- funktioner av deras argument är differentierbara, sedan derivatan av funktionen y=f(φ(t)) uttrycks med formeln
y′ t = y′ x x′ t.
A-priory dy=y′ t dt, då får vi
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,
dy = y′ x dx.
Så det har vi bevisat
Egenskapen för invarians av formen av den första differentialen för en funktion: som i fallet när argumentet xär en oberoende variabel, och i fallet när argumentet x i sig är en differentierbar funktion av den nya variabeln, differentialen dy funktioner y=f(x)är lika med derivatan av denna funktion multiplicerat med argumentets differential dx.
Tillämpning av differential i ungefärliga beräkningar
Vi har visat att skillnaden dy funktioner y=f(x), generellt sett är inte lika med ökningen Δy denna funktion. Dock med en noggrannhet upp till oändligheten liten funktion högre ordning av litenhet än Δx, är den ungefärliga jämlikheten giltig
Δy ≈ dy.
Förhållandet kallas det relativa felet för denna likhets likhet. Därför att Δy-dy=o(Δx), då blir det relativa felet för denna jämlikhet så litet som önskat med minskande |Δх|.
Med tanke på att Δy=f(x+δ x)-f(x), dy=f'(x)Δx, vi får f(x+δ x)-f(x) ≈ f'(x)Δx eller
f(x+δ x) ≈ f(x) + f′(x)Δx.
Denna ungefärliga likhet tillåter med fel o(Δx) byt ut funktion f(x) i ett litet område av punkten x(dvs för små värden Δx) linjär funktion av argumentet Δx, stående på höger sida.
Derivat av högre ordning
Definition. Andra derivata (eller andra ordningens derivata) av en funktion y=f(x) kallas derivatan av dess första derivata.
Notation för andraderivatan av en funktion y=f(x):
Mekanisk betydelse av den andra derivatan. Om funktionen y=f(x) beskriver rörelselagen för en materiell punkt i en rät linje, sedan andraderivatan f″(x) lika med accelerationen av en rörlig punkt vid tidpunkten x.
Tredje och fjärde derivatan bestäms på liknande sätt.
Definition. n derivatan (eller derivatan n-th order) funktioner y=f(x) kallas derivatan av det n-1 derivatan:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.
Beteckningar: y″′, y IV, y V etc.
Geometrisk betydelse av derivata
|
DEFINITION AV TANGENT TILL EN KURVA Tangent till en kurva y=ƒ(x) vid punkten M kallas gränsläget för en sekant som dras genom en punkt M och punkten intill den M 1 kurva, förutsatt att punkten M 1 närmar sig oändligt längs kurvan till punkten M. GEOMETRISK BETYDELSE AV DERIVAT Derivata av en funktion y=ƒ(x) vid punkten X 0 är numeriskt lika med tangenten för lutningsvinkeln mot axeln Åh tangent till kurvan y=ƒ(x) vid punkten M (x 0; ƒ(x 0)). |
VARIATION DOTIC TILL KURVA Prickad till kurvan y=ƒ(x) exakt M kallas gränsläget för den linje som dras genom punkten M och en poäng med henne M 1 snett, för sinnet, vad är poängen M 1 kurvan närmar sig oundvikligen punkten M. GEOMETRISK ZMIST POKHIDNOI Liknande funktioner y=ƒ(x) exakt x 0 numeriskt lika med tangenten för lutningen till axeln Åh decimal, utförs till kurvan y=ƒ(x) exakt M (x 0; ƒ(x 0)). |
Praktisk betydelse av derivata
Låt oss överväga vad kvantiteten vi hittade som en derivata av en viss funktion praktiskt taget betyder.
För det första, derivat- detta är det grundläggande konceptet för differentialkalkyl, som karakteriserar förändringshastigheten för en funktion vid en given punkt.
Vad är "förändringshastighet"? Låt oss föreställa oss funktionen f(x) = 5. Oavsett värdet på argumentet (x), ändras inte dess värde på något sätt. Det vill säga, takten för dess förändring är noll.
Tänk nu på funktionen f(x) = x. Derivatan av x är lika med ett. Det är faktiskt lätt att lägga märke till att för varje förändring av argumentet (x) med en, ökar värdet på funktionen också med en.
Med tanke på den mottagna informationen, låt oss nu titta på tabellen över derivator av enkla funktioner. Utifrån detta blir det direkt klart fysisk mening hitta derivatan av en funktion. Denna förståelse ska göra det lättare att lösa praktiska problem.
Följaktligen, om derivatan visar förändringshastigheten för en funktion, visar dubbelderivatan acceleration.
2080.1947