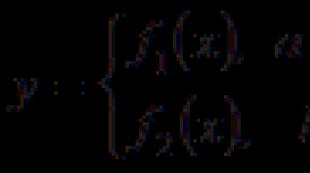Matematisk analys.

Verkstad.

För universitetsstudenter inom specialiteten:

"Statlig och kommunal förvaltning"

T.Z. Pavlova

Kolpashevo 2008

Kapitel 1. Introduktion till analys

1.1 Funktioner. Generella egenskaper

1.2 Teori om gränser

1.3 Funktionens kontinuitet

2.1 Definition av derivatan

2.4 Utforska funktioner

2.4.1 Fullständig studieplan

2.4.2 Exempel på funktionsstudier

2.4.3. Största och minsta värdet av en funktion på ett segment

2.5 L'Hôpitals regel

3.1 Obestämd integral

3.1.1 Definitioner och egenskaper

3.1.2 Tabell över integraler

3.1.3 Grundläggande metoder för integration

3.2 Den bestämda integralen

3.2.2 Metoder för att beräkna den bestämda integralen

Kapitel 4. Flera variablers funktioner

4.1 Grundbegrepp

4.2 Gränser och kontinuitet för funktioner för flera variabler

4.3.3 Total differential och dess tillämpning på approximativa beräkningar

Kapitel 5. Klassiska optimeringsmetoder

6.1 Verktygsfunktion.

6.2 Linjer av likgiltighet

6.3 Budgetuppsättning

Hemuppgifter

1.1 Funktioner. Generella egenskaper

En numerisk funktion definieras på uppsättningen D av reella tal om varje värde på variabeln är associerat med något väldefinierat reellt värde av variabeln y, där D är funktionens domän.

Analytisk representation av funktionen:

uttryckligen:;

implicit:;

i parametrisk form:

olika formler inom definitionsområdet:

Egenskaper.

Jämn funktion:. Till exempel är funktionen jämn, eftersom ...

Udda funktion: ... Funktionen är till exempel udda, eftersom ...

Periodisk funktion: , där T är perioden för funktionen,. Till exempel trigonometriska funktioner.

Monoton funktion. Om för någon av definitionsdomänerna - funktionen ökar, - minskar. Till exempel - ökar och - minskar.

Begränsad funktion. Om det finns ett nummer M så att. Till exempel funktioner och sedan .

Exempel 1. Hitta domänen för definition av funktioner.

+ 2 – 3 +

1.2 Teori om gränser

Definition 1... Gränsen för en funktion vid är ett tal b om man för något (- godtyckligt litet positivt tal) kan hitta ett sådant värde på argumentet, med utgångspunkt från vilket olikheten är uppfylld.

Beteckning:.

Definition 2... Gränsen för en funktion vid är ett tal b om det för något (är ett godtyckligt litet positivt tal) finns ett positivt tal så att för alla värden på x som uppfyller olikheten olikheten gäller.

Beteckning:.

Definition 3. Funktionen kallas infinitesimal för eller, om eller.

Egenskaper.

1. Den algebraiska summan av ett ändligt antal infinitesimala storheter är en infinitesimal storhet.

2. Produkten av en oändligt liten kvantitet av en begränsad funktion (konstant, en annan oändligt liten kvantitet) är en oändligt liten storhet.

3. Kvoten för att dividera en oändligt liten kvantitet med en funktion vars gräns inte är noll är en oändligt liten kvantitet.

Definition 4. Funktionen kallas oändligt stor vid, if.

Egenskaper.

1. Produkten av en oändligt stor kvantitet av en funktion, vars gräns är icke-noll, är en oändligt stor kvantitet.

2. Summan av ett oändligt stort värde och en begränsad funktion är ett oändligt stort värde.

3. Kvoten för att dividera en oändligt stor kvantitet med en funktion som har en gräns är en oändligt stor kvantitet.

Sats.(Släktskapet mellan en oändligt liten kvantitet och en oändligt stor kvantitet.) Om en funktion är oändligt liten vid (), så är funktionen en oändligt stor kvantitet vid (). Och omvänt, om funktionen är oändligt stor vid (), så är funktionen oändligt liten vid ().

Gränssatser.

1. En funktion kan inte ha mer än en gräns.

2. Gränsen för den algebraiska summan av flera funktioner är lika med den algebraiska summan av gränserna för dessa funktioner:

3. Gränsen för produkten av flera funktioner är lika med produkten av gränserna för dessa funktioner:

4. Gradgränsen är lika med graden av gränsen:

5. Kvotgränsen är lika med kvoten av gränserna om divisorgränsen finns:

.

6. Den första anmärkningsvärda gränsen.

Konsekvenser:

7. Andra anmärkningsvärda gränsen:

Konsekvenser:

Motsvarande infinitesimala värden för:

Beräkning av gränser.

Vid beräkning av gränsvärden används de grundläggande satserna om gränser, egenskaper hos kontinuerliga funktioner och regler som härrör från dessa satser och egenskaper.

Regel 1. För att hitta gränsen vid en punkt i en funktion som är kontinuerlig vid denna punkt, är det nödvändigt att ersätta dess gränsvärde i funktionen under gränstecknet istället för argumentet x.

Exempel 2. Hitta

Regel 2. Om, när man hittar gränsen för ett bråk, gränsen för nämnaren är noll, och gränsen för täljaren är icke-noll, då är gränsen för en sådan funktion.

Exempel 3. Hitta

Regel 3. Om, när man hittar gränsen för ett bråk, gränsen för nämnaren är lika, och gränsen för täljaren skiljer sig från noll, är gränsen för en sådan funktion noll.

Exempel 4. Hitta

Ofta resulterar ersättning av ett gränsvärde för ett argument i odefinierade uttryck som

.

Att hitta gränsen för en funktion i dessa fall kallas osäkerhetsupplysning. För att avslöja osäkerhet är det nödvändigt att omvandla detta uttryck innan man går till gränsen. Olika tekniker används för att avslöja osäkerheter.

Regel 4... Osäkerheten för typen avslöjas genom att transformera sublimit-funktionen, så att man, för att välja en faktor i täljaren och nämnaren, vars gräns är noll, och, efter att ha reducerat bråket med det, hitta gränsen för kvoten. För att göra detta, multipliceras täljaren och nämnaren antingen eller multipliceras med uttrycken konjugerat med täljaren och nämnaren.

Regel 5. Om sublimit-uttrycket innehåller trigonometriska funktioner, används den första anmärkningsvärda gränsen för att exponera artens osäkerhet.

.

Regel 6... För att avslöja osäkerheten i formen vid måste täljaren och nämnaren för delgränsbråket divideras med den högsta graden av argumentet och sedan måste gränsen för kvoten hittas.

Möjliga resultat:

1) den önskade gränsen är lika med förhållandet mellan koefficienterna vid de högsta potenserna av argumentet för täljaren och nämnaren, om dessa grader är desamma;

2) gränsen är lika med oändlighet om graden av argumentet för täljaren är högre än graden av argumentet för nämnaren;

3) gränsen är noll om graden av argumentet för täljaren är lägre än graden av argumentet för nämnaren.

a)

eftersom

Graderna är lika, vilket innebär att gränsen är lika med förhållandet mellan koefficienterna vid de högre graderna, d.v.s. ...

b)

Graden av täljaren, nämnaren är 1, vilket betyder att gränsen är

v)

Graden av täljaren är 1, graden av nämnaren är, så gränsen är 0.

Regel 7... För att avslöja osäkerheten i formen måste täljaren och nämnaren för delgränsfraktionen multipliceras med det konjugerade uttrycket.

Exempel 10.

Regel 8... En andra anmärkningsvärd gräns och dess konsekvenser används för att avslöja artens osäkerhet.

Det kan bevisas

Exempel 11.

Exempel 12.

Exempel 13.

Regel 9... När man avslöjar osäkerheterna, vars subliminal funktion innehåller det oändliga, är det nödvändigt att ersätta gränserna för dessa oändligheter. på gränserna för infinitesimala element motsvarande dem.

Exempel 14.

Exempel 15.

Regel 10. L'Hôpitals regel (se 2.6).

1.3 Funktionens kontinuitet

En funktion är kontinuerlig vid en punkt om gränsen för funktionen som argument tenderar till a, finns och är lika med värdet på funktionen vid denna punkt.

Motsvarande villkor:

1. ;

3.

Brytpunktsklassificering:

paus av den första sorten

Disponibel - ensidiga gränser finns och är lika;

Fatal (hopp) - ensidiga gränser är inte lika;

diskontinuitet av det andra slaget: gränsen för en funktion vid en punkt existerar inte.

Exempel 16. Fastställ arten av diskontinuiteten för en funktion vid en punkt eller bevisa kontinuiteten för en funktion vid denna punkt.

för funktionen är inte definierad, därför är den inte kontinuerlig vid denna tidpunkt. Eftersom och på motsvarande sätt, , då är poängen med en borttagbar diskontinuitet av det första slaget.

b)

i jämförelse med uppgift (a) utökas funktionen vid en punkt så att , därför är denna funktion kontinuerlig vid denna tidpunkt.

När funktionen inte är definierad;

.

Eftersom en av de ensidiga gränserna är oändlig, sedan är det en brytpunkt av det andra slaget.

Kapitel 2. Differentialkalkyl

2.1 Definition av derivatan

Derivatdefinition

Den eller derivatan av en given funktion är gränsen för förhållandet mellan funktionsökningen och motsvarande argumentökning när argumentökningen tenderar mot noll:

Eller .

Den mekaniska betydelsen av en derivata är förändringshastigheten för en funktion. Den geometriska betydelsen av derivatan är tangenten för lutningsvinkeln för tangenten till grafen för funktionen:

2.2 Grundläggande regler för differentiering

namn	Fungera	Derivat
Multiplikation med en konstant faktor
Algebraisk summa av två funktioner
Produkt av två funktioner
Privata två funktioner
Komplex funktion

Derivater av grundläggande elementära funktioner

P/p nr.	Funktionsnamn	Funktion och dess derivata
1	konstant
2	kraftfunktion speciella fall
3	exponentiell funktion specialfall
4	logaritmisk funktion specialfall
5	trigonometriska funktioner
6	omvänd trigonometrisk

b)

2.3 Högre ordningsderivat

Andra ordningens derivata av en funktion

Den andra ordningens derivata av funktionen:

Exempel 18.

a) Hitta andra ordningens derivata av funktionen.

Lösning. Låt oss först hitta derivatan av första ordningen .

Låt oss ta derivatan av första ordningens derivata.

Exempel 19. Hitta tredje ordningens derivata av funktionen.

2.4 Utforska funktioner

2.4.1 Planera för en komplett funktionsstudie:

Fullständig studieplan:

1. Elementär forskning:

Hitta domänen och värdeintervallet;

Ta reda på de allmänna egenskaperna: paritet (udda), periodicitet;

Hitta skärningspunkterna med koordinataxlarna;

Bestäm områden med beständighet.

2. Asymptoter:

Hitta vertikala asymptoter om;

Hitta sneda asymptoter:.

Om något nummer, då - horisontella asymptoter.

3. Forskning med:

Hitta de kritiska punkterna, de. punkter där eller inte finns;

Bestäm intervallen för att öka, de. intervaller, vid vilka och minskande funktioner -;

Bestäm extrema: punkterna, när de passerar genom vilka den ändrar tecken från "+" till "-", är maxpunkter, från "-" till "+" - minimum.

4. Forskning med:

Hitta punkter där eller inte finns;

Hitta konvexitetsområden, dvs. de intervall med vilka konkaviteterna är;

Hitta böjningspunkterna, d.v.s. punkter när man passerar som byter tecken.

1. Individuella delar av studien ritas upp på grafen gradvis, allt eftersom de hittas.

2. Om det finns svårigheter med konstruktionen av grafen för funktionen, så hittas funktionens värden på några ytterligare punkter.

3. Syftet med studien är att beskriva arten av funktionens beteende. Därför byggs inte en exakt graf, utan dess approximation, på vilken de hittade elementen (extrema, böjningspunkter, asymptoter, etc.) tydligt anges.

4. Det är inte nödvändigt att strikt följa planen ovan; det är viktigt att inte förbise de karakteristiska delarna av funktionens beteende.

2.4.2 Exempel på en funktionsstudie:

1)

2) Funktionen är udda:

.

3) Asymptoter.

- vertikala asymptoter, eftersom

Sned asymptot.

5)

- böjningspunkt.

2) Funktionen är udda:

3) Asymptoter: Det finns inga vertikala asymptoter.

Lutande:

- sneda asymptoter

4) - funktionen ökar.

- böjningspunkt.

Schematiskt diagram över denna funktion:

2) Allmän funktion

3) Asymptoter

- inga sneda asymptoter

- horisontell asymptot vid

- böjningspunkt

Schematiskt diagram över denna funktion:

2) Asymptoter.

- vertikal asymptot, eftersom

- inga sneda asymptoter

, - horisontell asymptot

Schematiskt diagram över denna funktion:

2) Asymptoter

- vertikal asymptot vid, sedan

- inga sneda asymptoter

, - horisontell asymptot

3) - funktionen minskar vid vart och ett av intervallen.

Schematiskt diagram över denna funktion:

För att hitta det största och minsta värdet av en funktion på ett segment kan du använda diagrammet:

1. Hitta derivatan av funktionen.

2. Hitta de kritiska punkterna för funktionen, vid vilka eller inte finns.

3. Hitta värdet på funktionen vid kritiska punkter som hör till ett givet segment och i dess ändar och välj den största och den minsta av dem.

Exempel. Hitta det minsta och största värdet av funktionen på ett givet segment.

25. mellan

2) - kritiska punkter

26. emellan.

Derivatan finns inte vid, men 1 hör inte till detta intervall. Funktionen minskar i intervallet, vilket innebär att det inte finns något största värde utan det minsta värdet.

2.5 L'Hôpitals regel

Sats. Gränsen för förhållandet mellan två infinitesimala eller oändligt stora funktioner är lika med gränsen för förhållandet mellan deras derivator (finita eller oändlig), om den senare existerar i den angivna meningen.

De där. när du avslöjar osäkerheter av typen eller kan du använda formeln:

.

27.

Kapitel 3. Integralkalkyl

3.1 Obestämd integral

3.1.1 Definitioner och egenskaper

Definition 1. En funktion kallas antiderivata för if.

Definition 2. En obestämd integral av en funktion f (x) är samlingen av alla antiderivator för denna funktion.

Beteckning: , där c är en godtycklig konstant.

Obestämda integralegenskaper

1. Derivata av den obestämda integralen:

2. Differentialen för den obestämda integralen:

3. Obestämd integral av differentialen:

4. Obestämd integral av summan (skillnaden) av två funktioner:

5. Flytta en konstant faktor bortom tecknet för den obestämda integralen:

3.1.2 Tabell över integraler

.1.3 Grundläggande metoder för integration

1. Använda egenskaperna hos den obestämda integralen.

Exempel 29.

2. Föra under differentialtecknet.

Exempel 30.

3. Variabel ersättningsmetod:

a) utbyte i integralen

var - en funktion som är lättare att integrera än den ursprungliga; - funktion invers till funktion; är funktionens antiderivata.

Exempel 31.

b) ersättning i integralen av formen:

Exempel 32.

Exempel 33.

4. Integrationsmetod efter delar:

Exempel 34.

Exempel 35.

Låt oss ta integralen separat

Låt oss gå tillbaka till vår integral:

3.2 Den bestämda integralen

3.2.1 Begreppet en bestämd integral och dess egenskaper

Definition. Låt en kontinuerlig funktion ges på något intervall. Låt oss bygga hennes graf.

En figur som ovanför avgränsas av en kurva, till vänster och till höger av räta linjer och underifrån av ett segment av abskissaxeln mellan punkterna a och b, kallas en krökt trapets.

S - area - böjd trapets.

Dela intervallet med prickar och få:

Integral summa:

Definition. Den bestämda integralen är gränsen för integralsumman.

Bestämda integralegenskaper:

1. Konstantfaktorn kan tas ur heltaltecknet:

2. Integralen av den algebraiska summan av två funktioner är lika med den algebraiska summan av integralerna för dessa funktioner:

3. Om integrationssegmentet är uppdelat i delar, så är integralen över hela segmentet lika med summan av integraler för var och en av de delar som har uppstått, dvs. för alla a, b, c:

4. Om på ett segment, då

5. Integrationens gränser kan bytas ut, medan integralens tecken ändras:

6.

7. Integralen vid punkten är lika med 0:

8.

9. (“om medelvärde”) Låt y = f (x) vara en funktion som kan integreras på. Sedan , där f (c) är medelvärdet av f (x) på:

10. Newton-Leibniz formel

,

där F (x) är antiderivatan för f (x).

3.2.2 Metoder för att beräkna den bestämda integralen.

1. Direkt integration

Exempel 35.

a)

b)

v)

e)

2. Ändring av variabler under det bestämda heltecknet .

Exempel 36.

2. Integrering av delar i en bestämd integral .

Exempel 37.

a)

b)

e)

3.2.3 Tillämpningar av en bestämd integral

Karakteristisk	Funktionstyp	Formel
	i kartesiska koordinater
krökt sektorområde	i polära koordinater
krökt trapetsformad yta	i parametrisk form
båglängd	i kartesiska koordinater
båglängd	i polära koordinater
båglängd	i parametrisk form
kroppsvolym rotation	i kartesiska koordinater
kroppsvolym med en given tvärgående tvärsnitt

Exempel 38. Beräkna arean av en form avgränsad av linjer: och .

Lösning: Låt oss hitta skärningspunkterna för graferna för dessa funktioner. För att göra detta likställer vi funktionerna och löser ekvationen

Så skärningspunkterna och.

Vi hittar arean av figuren med hjälp av formeln

.

I vårat fall

Svar: arean är lika med (kvadratenheter).

4.1 Grundbegrepp

Definition. Om, enligt någon regel, ett eller flera värden av variabeln z tilldelas varje par oberoende tal från en viss uppsättning, så kallas variabeln z en funktion av två variabler.

Definition. Domänen för funktionen z är uppsättningen av par för vilka funktionen z existerar.

Domänen för en funktion av två variabler är en uppsättning punkter på koordinatplanet Oxy. Z-koordinaten kallas applikatet, och då avbildas själva funktionen som någon yta i utrymmet E 3. Till exempel:

Exempel 39. Hitta domänen för en funktion.

a)

Uttrycket på höger sida är meningsfullt endast för. Detta betyder att domänen för denna funktion är samlingen av alla punkter som ligger inuti och på gränsen till en cirkel med radien R centrerad vid origo.

Domänen för denna funktion är alla punkter i planet, förutom punkter med räta linjer, dvs. koordinataxlar.

Definition. Funktionsnivålinjer är en familj av kurvor på koordinatplanet som beskrivs av formekvationer.

Exempel 40. Hitta funktionsnivålinjer .

Lösning. Nivålinjerna för en given funktion är en familj av kurvor i det plan som beskrivs av ekvationen

Den sista ekvationen beskriver en familj av cirklar centrerad vid punkten O 1 (1, 1) med radie. Rotationsytan (paraboloid) som beskrivs av denna funktion blir "brantare" när den rör sig bort från axeln, vilket ges av ekvationerna x = 1, y = 1. (Fig. 4)

4.2 Gränser och kontinuitet för funktioner för flera variabler.

1. Gränser.

Definition. Ett tal A kallas gränsen för en funktion eftersom en punkt tenderar till en punkt, om det för varje godtyckligt litet tal finns ett tal så att villkoret är sant för vilken punkt som helst, och villkoret ... De skriver ner: .

Exempel 41. Hitta gränserna:

de där. gränsen beror på, och därför finns den inte.

2. Kontinuitet.

Definition. Låt punkten tillhöra definitionsdomänen för funktionen. Då kallas en funktion kontinuerlig vid en punkt if

(1)

dessutom tenderar punkten till punkten på ett godtyckligt sätt.

Om vid någon punkt villkor (1) inte är uppfyllt, kallas denna punkt för en diskontinuitetspunkt för funktionen. Detta kan vara i följande fall:

1) Funktionen är inte definierad vid punkten.

2) Det finns ingen gräns.

3) Denna gräns finns, men den är inte lika.

Exempel 42. Bestäm om den givna funktionen är kontinuerlig vid punkten if.

Förstod det därför är denna funktion kontinuerlig vid punkten.

gränsen beror på k, dvs. den existerar inte vid en given punkt, vilket betyder att funktionen har en diskontinuitet vid denna punkt.

4.3 Derivater och differentialer av funktioner för flera variabler

4.3.1 Partiella derivator av första ordningen

Den partiella derivatan av en funktion med avseende på argumentet x är den vanliga derivatan av en funktion av en variabel x för ett fast värde av variabeln y och betecknas:

Den partiella derivatan av en funktion med avseende på argumentet y är den vanliga derivatan av en funktion av en variabel y vid ett fast värde av variabeln x och betecknas:

Exempel 43. Hitta partiella derivator av funktioner.

4.3.2 Partiella derivator av andra ordningen

Partiella derivator av andra ordningen är partiella derivator av partiella derivator av första ordningen. För en funktion av två variabler i formen är fyra typer av partiella derivator av andra ordningen möjliga:

Partiella derivator av andra ordningen, där differentiering utförs med avseende på olika variabler, kallas blandade derivator. De blandade derivatorna av andra ordningen av en två gånger differentierbar funktion är lika.

Exempel 44. Hitta de partiella derivatorna av andra ordningen.

4.3.3 Total differential och dess tillämpning på approximativa beräkningar.

Definition. Differentialen av den första ordningen av en funktion av två variabler hittas av formeln

.

Exempel 45. Hitta den totala differentialen för en funktion.

Lösning. Låt oss hitta de partiella derivatorna:

.

För små inkrement av argumenten x och y får funktionen ett inkrement ungefär lika med dz, dvs. ...

Formeln för att hitta det ungefärliga värdet av en funktion vid en punkt, om dess exakta värde vid en punkt är känt:

Exempel 46. Hitta .

Lösning. Låt,

Sedan använder vi formeln

Svar. .

Exempel 47. Räkna ungefär.

Lösning. Låt oss överväga en funktion. Vi har

Exempel 48. Räkna ungefär.

Lösning. Tänk på funktionen ... Vi får:

Svar. .

4.3.4 Implicit funktionsdifferentiering

Definition. En funktion kallas implicit om den ges av en ekvation som inte är lösbar med avseende på z.

De partiella derivatorna av en sådan funktion hittas av formlerna:

Exempel 49. Hitta de partiella derivatorna av funktionen z som ges av ekvationen .

Lösning.

Definition. En funktion kallas implicit om den ges av en ekvation som inte är lösbar med avseende på y.

Derivaten av en sådan funktion hittas av formeln:

.

Exempel 50. Hitta derivator av dessa funktioner.

5.1 Lokalt extremum av en funktion av flera variabler

Definition 1. En funktion har ett maximum vid en punkt if

Definition 2. En funktion har ett minimum vid en punkt if för alla punkter tillräckligt nära punkten och olika från den.

En nödvändig förutsättning för ett extremum. Om en funktion når ett extremum vid en punkt, försvinner de partiella derivatorna av funktionen eller existerar inte vid denna punkt.

Punkterna där partiella derivator försvinner eller inte existerar kallas kritiska.

Ett tillräckligt tecken på ett extremum. Låt funktionen definieras i något område av den kritiska punkten och ha kontinuerliga andra ordningens partiella derivator vid denna punkt

1) har ett lokalt maximum vid punkten, om och;

2) har ett lokalt minimum vid punkten, om och;

3) inte har ett lokalt extremum vid punkten om;

Schema för studien för extremumet av en funktion av två variabler.

1. Hitta de partiella derivatorna av funktionen: och.

2. Lös ekvationssystemet och hitta de kritiska punkterna för funktionen.

3. Hitta de partiella derivatorna av den andra ordningen, beräkna deras värden vid kritiska punkter och dra en slutsats om närvaron av extrema, med hjälp av det tillräckliga villkoret.

4. Hitta extrema för funktionen.

Exempel 51. Hitta extrema för en funktion .

1) Hitta de partiella derivatorna.

2) Lös ekvationssystemet

4) Hitta de partiella derivatorna av andra ordningen och deras värden vid kritiska punkter:. Vid punkten får vi:

därför finns det inget extremum vid punkten. Vid punkten får vi:

därför finns det ett minimum.

5.2 Globalt extremum (högsta och lägsta värdet för en funktion)

De största och minsta värdena av en funktion av flera variabler, kontinuerliga på någon sluten uppsättning, uppnås antingen vid ytterpunkterna eller på mängdens gräns.

Schemat för att hitta de högsta och lägsta värdena.

1) Hitta de kritiska punkterna som ligger inom området, beräkna värdet på funktionen vid dessa punkter.

2) Utforska funktionen på områdets gräns; om gränsen består av flera olika linjer, så måste undersökningen utföras för varje plats separat.

3) Jämför de erhållna värdena för funktionen och välj den största och den minsta.

Exempel 52. Hitta de största och minsta funktionsvärdena i en rektangel.

Lösning. 1) Hitta de kritiska punkterna för funktionen, för detta hittar vi de partiella derivatorna:, och lös ekvationssystemet:

Mottog den kritiska punkten A. Den resulterande punkten ligger inom det angivna området,

Områdesgränsen består av fyra segment: och. hitta det största och minsta värdet av funktionen på varje segment.

4) Jämför de erhållna resultaten och hitta det vid punkterna .

Kapitel 6. Konsumentvalsmodellen

Vi kommer att anta att det finns n olika varor. Då kommer en viss uppsättning varor att betecknas med den n-dimensionella vektorn , var är kvantiteten av den i:te produkten. Mängden av alla uppsättningar av varor X kallas rymd.

Valet av den individuella konsumenten kännetecknas av en preferensrelation: man tror att konsumenten kan säga om vilka två uppsättningar som helst, vilket är mer önskvärt, eller så ser han inte skillnaden mellan dem. Preferensrelationen är transitiv: om en mängd är att föredra framför en mängd och en mängd är att föredra framför en mängd, då är en mängd att föredra framför en mängd. Vi kommer att anta att konsumentbeteendet är fullt beskrivet av den individuella konsumentens axiom: varje enskild konsument fattar ett beslut om konsumtion, inköp etc., baserat på sitt system av preferenser.

6.1 Verktygsfunktion

På uppsättningen konsumentuppsättningar X är funktionen definierad , vars värde på konsumentuppsättningen är lika med konsumentens uppskattning av individen för denna uppsättning. Funktionen kallas för konsumentens nyttofunktion eller konsumentens preferensfunktion. De där. varje konsument har sin egen nyttofunktion. Men hela uppsättningen konsumenter kan delas in i vissa klasser av konsumenter (efter ålder, fastighetsstatus, etc.) och varje klass kan tilldelas någon, kanske, genomsnittlig nyttofunktion.

Således är en funktion en konsumentuppskattning eller graden av tillfredsställelse av en individs behov vid köp av en given uppsättning. Om en uppsättning är att föredra framför en uppsättning för en given individ, då.

Verktygsfunktionsegenskaper.

1.

De första partiella derivatorna av nyttofunktionen kallas produkters marginalnytta. Av denna egenskap följer att en ökning av konsumtionen av en produkt medan konsumtionen av andra produkter förblir oförändrad leder till en ökning av konsumenternas bedömning. Vektor är funktionens gradient, den visar riktningen för den största tillväxten av funktionen. För en funktion är dess gradient en vektor för produkters marginella nytta.

2.

De där. marginalnyttan av varje vara minskar med ökande konsumtion.

3.

De där. marginalnyttan för varje produkt ökar med mängden av den andra produkten.

Vissa typer av hjälpfunktioner.

1) Neoklassisk:.

2) Kvadratisk: där matrisen är negativ bestämd och för .

3) Logaritmisk funktion:.

6.2 Linjer av likgiltighet

I tillämpade problem och modeller för konsumentval används ofta ett särskilt fall av en uppsättning av två varor, dvs. när nyttofunktionen beror på två variabler. Linjen av likgiltighet är en linje som förbinder konsumentuppsättningar som har samma nivå av tillfredsställelse av individens behov. I huvudsak är likgiltighetslinjerna funktionsnivåns linjer. Indifferenslinjeekvationer: .

Grundläggande egenskaper hos likgiltighetslinjer.

1. Linjer av likgiltighet, som motsvarar olika nivåer av behovstillfredsställelse, berör inte eller skär varandra.

2. Linjer av likgiltighet minskar.

3. Linjer av likgiltighet är konvexa nedåt.

Fastighet 2 innebär en viktig ungefärlig jämlikhet.

Detta förhållande visar hur mycket individen bör öka (minska) konsumtionen av den andra produkten samtidigt som den minskar (öker) konsumtionen av den första produkten med en enhet utan att ändra graden av tillfredsställelse av hans behov. Förhållandet kallas graden av utbyte av den första produkten med den andra, och värdet kallas marginalhastigheten för utbyte av den första produkten med den andra.

Exempel 53. Om marginalnyttan för den första varan är 6 och den andra - 2, då med en minskning av konsumtionen av den första varan med en enhet, måste du öka konsumtionen av den andra varan med 3 enheter med samma nivå av tillfredsställelse.

6.3 Budgetuppsättning

Låta - vektor av priser för en uppsättning av n produkter; I - inkomst för en individ, som han är villig att spendera på köp av en uppsättning produkter. Uppsättningen av uppsättningar varor som inte kostar mer än I till givna priser kallas budgetuppsättning B. Dessutom kallas uppsättningen av uppsättningar av kostnader I gränsen G för budgetuppsättning B. mängden B begränsas av gränsen G och naturliga restriktioner.

Budgetuppsättningen beskrivs av ett system av ojämlikheter:

För fallet med en uppsättning av två varor är budgetmängden B (Fig. 1) en triangel i koordinatsystemet, avgränsad av koordinataxlarna och en rät linje.

6.4 Konsumentefterfrågansteori

I teorin om konsumtion antas det att konsumenten alltid strävar efter att maximera sin användbarhet och den enda begränsningen för honom är den begränsade inkomst I, som han kan spendera på att köpa en uppsättning varor. I allmänhet formuleras konsumentvalsproblemet (problemet med rationellt konsumentbeteende på marknaden) på följande sätt: hitta en konsumentuppsättning , som maximerar dess nyttofunktion för en given budgetbegränsning. Matematisk modell för detta problem:

I fallet med en uppsättning av två produkter:

Geometriskt är lösningen på detta problem kontaktpunkten mellan gränsen för budgetmängden G och likgiltighetslinjen.

Lösningen på detta problem reduceras till att lösa ekvationssystemet:

(1)

Lösningen på detta system är lösningen på konsumenternas valproblem.

Lösningen på konsumentvalsproblemet kallas efterfrågepunkten. Denna efterfrågepunkt beror på priser och inkomst I. Det vill säga. efterfrågepunkten är en funktion av efterfrågan. I sin tur är efterfrågefunktionen en uppsättning av n funktioner, som var och en beror på argumentet:

Dessa funktioner kallas efterfrågefunktioner för motsvarande varor.

Exempel 54. För en uppsättning av två varor på marknaden, kända priser för dem och och inkomst I, hitta efterfrågefunktionerna om nyttofunktionen har formen .

Lösning. Låt oss skilja på verktygsfunktionen:

.

Ersätt de erhållna uttrycken i (1) och få ekvationssystemet:

I det här fallet kommer kostnaden för varje produkt att vara hälften av konsumentens inkomst, och mängden av den köpta produkten är lika med det belopp som spenderas på den, dividerat med priset på produkten.

Exempel 55. Låt verktyget fungera för den första varan, den andra,

priset på den första produkten, priset på den andra. Inkomst . Hur mycket bör konsumenten köpa för att maximera användbarheten?

Lösning. Låt oss hitta derivatorna av nyttofunktionerna, ersätta dem med system (1) och lösa det:

Denna uppsättning varor är optimal för konsumenten när det gäller att maximera användbarheten.

Testet bör utföras i enlighet med det alternativ som valts av den sista siffran i registernumret i en separat anteckningsbok. Varje problem bör innehålla ett villkor, en detaljerad lösning och en slutsats.

1. Introduktion till kalkyl

Uppgift 1. Hitta funktionens domän.

5.

Uppgift 2. Hitta gränserna för funktioner.

.

Uppgift 3. Hitta brytpunkterna för funktionen och bestäm deras typ.

1. 2. 3.

Kapitel 2. Differentialkalkyl för en funktion av en variabel

Uppgift 4. Hitta derivator av dessa funktioner.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - båge x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e 5 x - 1) 6; c) y =; d) y =; e) y = x 8 ++ + 5; f) y = 3 x - båge x.

5.a) y = 2x3- + ex; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sintg;

d) y = 3x4--9+9; e) y =;

f) y = x 2 + båge x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4x4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x 2 - x; f) y = e sin 3 x + 2.

Uppgift 5. Undersök funktionen och bygg dess graf.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9.a) b) c).

10. a) b) v) .

Uppgift 6. Hitta det största och minsta värdet på funktionen på ett givet segment.

1. .

3. .

6. .

8. .

9. .

10. .

Kapitel 3. Integralkalkyl

Uppgift 7. Hitta obestämda integraler.

1.a) b);

2.a) b) c) d).

4. G)

5.a) ; b); v); G).

6.a) ; b); v); G)

7.a) ; b) ; v); G)

8.a) ; b); v) ; G) .

9.a) ; före Kristus); G).

10.a) b) v); G) .

Uppgift 8. Beräkna bestämda integraler.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Uppgift 9. Hitta felaktiga integraler eller bevisa att de divergerar.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Uppgift 10. Hitta arean av området som begränsas av kurvor

1. .2. .

5. 6.

7. , .8..

10. , .

Kapitel 4. Differentialkalkyl av en funktion av flera variabler.

Uppgift 11. Hitta funktionens domän (visa på ritningen).

Uppgift 12. Undersök kontinuiteten i funktionen för

Uppgift 13. Hitta derivatan av en implicit definierad funktion.

Uppgift 14. Räkna ungefär

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

Uppgift 15. Undersök funktionen för extrema.

7. .

8. .

9. .

10. .

Uppgift 16. Hitta det största och minsta värdet på funktionen i ett givet slutet område.

1.i rektangeln

2.

3.i rektangeln

4.i regionen som avgränsas av en parabel

Och abskissan.

5. kvadrat

6.i en triangel som begränsas av koordinataxlarna och en rät linje

7.i en triangel som begränsas av koordinataxlarna och en rät linje

8. i en triangel som begränsas av koordinataxlarna och en rät linje

9.i regionen som avgränsas av en parabel

Och abskissan.

10.i regionen som avgränsas av en parabel

Och abskissan.

Den huvudsakliga

1. M.S. Crassus, B.P. Chuprynov. Grunderna i matematik och dess tillämpning i ekonomisk utbildning: lärobok. - 4:e uppl., Isp. - M .: Delo, 2003.

2. M.S. Crassus, B.P. Chuprynov. Matematik för ekonomiska specialiteter: Lärobok. - 4:e uppl., Isp. - M .: Delo, 2003.

3. M.S. Crassus, B.P. Chuprynov. Matematik för en grundexamen i nationalekonomi. Lärobok. - 4:e uppl., Isp. - M .: Delo, 2005.

4. Högre matematik för ekonomer. Lärobok för universitet / N.Sh. Kremer, B.A. Putko, I.M. Trishin, M.N. Friedman; Ed. prof. N.Sh. Kremer, - 2:a uppl., Reviderad. och lägg till. - M: UNITY, 2003.

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman MN Högre matematik för ekonomiska specialiteter. Lärobok och verkstad (del I och II) / Ed. prof. N.Sh. Kremer, - 2:a uppl., Reviderad. och lägg till. - M: Högre utbildning, 2007. - 893s. - (Fundamentals of Sciences)

6. Danko P.E., Popov A.G., Kozhevnikova T.Ya. Högre matematik i övningar och problem. M. gymnasiet. 1999.

Ytterligare

1. I.I. Bavrin, V.L. Sjömän. Högre matematik. "Vlados Humanitarian Publishing Center", 2002.

2. I.A. Zaitsev. Högre matematik. "Högstadiet", 1998.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, I.G. Shandra. Matematik i ekonomi / i två delar /. M. Finans och statistik. 1999.

för studenter medicinsk, pediatrisk, dental

och förebyggande medicinska fakulteter

till laboratoriearbete

"Grundläggande begrepp för matematisk analys"

1. Vetenskapliga och metodologiska belägg för ämnet:

Derivat- och differentialbegrepp är ett av de grundläggande begreppen inom matematisk analys. Att beräkna derivator är nödvändigt när man löser många problem inom fysik och matematik (att hitta hastighet, acceleration, tryck, etc.). Betydelsen av begreppet en derivata, i synnerhet, bestäms av det faktum att derivatan av en funktion kännetecknar förändringshastigheten för denna funktion när dess argument ändras.

Användningen av differentialen gör det möjligt att utföra ungefärliga beräkningar, samt att uppskatta felen.

Metoder för att hitta derivator och differentialer av funktioner och deras tillämpning utgör differentialkalkylens huvudproblem. Behovet av begreppet derivata uppstår i samband med formuleringen av problemet med att beräkna rörelsehastigheten och hitta tangentens vinkel till kurvan. Det omvända problemet är också möjligt: ​​bestäm den tillryggalagda sträckan med hastighet och hitta motsvarande funktion genom tangenten till tangentlutningen. Detta omvända problem leder till begreppet en obestämd integral.

Begreppet en bestämd integral används i ett antal praktiska problem, särskilt i problem med att beräkna arean av platta figurer, beräkna arbetet som utförs av en variabel kraft och att hitta medelvärdet för en funktion.

I den matematiska beskrivningen av olika fysikaliska, kemiska, biologiska processer och fenomen används ofta ekvationer som innehåller inte bara de kvantiteter som studeras, utan också deras derivator av olika ordningsföljder av dessa kvantiteter. Till exempel, enligt den enklaste versionen av lagen om bakteriers multiplikation, är reproduktionshastigheten proportionell mot antalet bakterier vid en given tidpunkt. Om denna kvantitet betecknas med N (t), så är, i enlighet med den fysiska betydelsen av derivatet, bakteriernas reproduktionshastighet ett derivat av N (t), och på grundval av ovanstående lag kan vi skriva förhållande N "(t) = k ∙ N, där k> 0 - proportionalitetskoefficient Den resulterande ekvationen är inte algebraisk, eftersom den innehåller inte bara den okända funktionen N (t), utan också dess första ordningens derivata.

2. Kort teori:

1. Problem som leder till begreppet derivat

1. Problemet med att hitta hastigheten v för en materialpunkt... Låt någon materialpunkt utföra rätlinjig rörelse. Vid ett ögonblick i tiden t 1 punkten är i position M 1. Vid ett ögonblick i tiden t 2 gravid M 2 . Låt oss beteckna intervallet M 1 , M 2 tvärs över ΔS; t 2 - t 1 = Δt... Värdet kallas för den genomsnittliga rörelsehastigheten. För att hitta den momentana hastigheten för en punkt vid en position M 1 nödvändig Δt tenderar till noll. Matematiskt betyder det det

, (1)

Sålunda, för att hitta den momentana hastigheten för en materialpunkt, är det nödvändigt att beräkna gränsen för förhållandet mellan ökningen av funktionen ΔS till ökningen av argumentet Δt förutsatt att Δt → 0.

2. Problemet med att hitta lutningsvinkeln för tangenten till grafen för en funktion.

figur 1

Betrakta grafen för någon funktion y = f (x). Vad är lutningsvinkeln
tangent vid punkt M 1 ? Vid punkten M 1 rita en tangent till grafen för funktionen. Välj en godtycklig punkt på grafen M 2 och rita en sekant. Hon lutar mot axeln ÅH i vinkel α 1 ... Överväga ΔM 1 M 2 A:

, (2)

Om punkt M 1 fixa och peka M 2 flytta närmare M 1 , sedan sekant M 1 M 2 kommer att gå till tangenten till grafen för funktionen vid punkten M 1 och du kan skriva:

, (3)

Därför är det nödvändigt att beräkna gränsen för förhållandet mellan funktionsökningen och argumentökningen om argumentökningen tenderar mot noll.

Gränsen för förhållandet mellan ökningen Δy för funktionen y = f (x) till ökningen av argumentet Δx vid en given punkt x 0 eftersom Δx tenderar mot noll, kallas derivatan av funktionen vid en given punkt.

Derivatnotation: y ", f" (x), ... Per definition

, (4)

där Δx = x 2 -x 1 är ökningen av argumentet (skillnaden mellan två efterföljande tillräckligt nära värden av argumentet), Δy = y 2 -y 1 är ökningen av funktionen (skillnaden mellan värdena ​​för funktionen som motsvarar dessa värden i argumentet).

Att hitta derivatan av en given funktion kallas dess differentiering... Differentiering av de viktigaste elementära funktionerna utförs enligt färdiga formler (se tabell), samt med hjälp av regler:

Derivat av en algebraisk summa funktioner är lika med summan av derivatorna av dessa funktioner:

(u+ υ )"= u" + υ "

2. Derivatan av produkten av två funktioner är lika med summan av produkterna av den andra funktionen med derivatan av den första och den första funktionen med derivatan av den andra:

(u ∙υ ) "= u"υ + uυ "

3. Derivat av kvoten av två funktioner är lika med en bråkdel, vars täljare är skillnaden mellan produkterna av nämnaren med derivatan av täljaren och täljaren med derivatan av nämnaren, och nämnaren är kvadraten på nämnaren:

Den fysiska betydelsen av derivatan. Jämförelse av (4) och (1) innebär att den momentana hastigheten för den rätlinjiga rörelsen av en materialpunkt är lika med derivatan av dess koordinats beroende av tiden.

Den allmänna innebörden av derivatan av en funktion är att den karaktäriserar hastighet (snabbhet) av funktionsändring för en given argumentändring. Hastigheten för fysikaliska, kemiska och andra processer, till exempel hastigheten för kroppskylning, hastigheten för kemisk reaktion, hastigheten för bakteriers reproduktion, etc., uttrycks också med hjälp av ett derivat.

Den geometriska betydelsen av derivatan. Storleken på tangenten för lutningsvinkeln för tangenten ritad till grafen för funktionen kallas i matematik tangentens lutning.

Lutningen för tangenten till grafen för den differentierbara funktionen vid någon punkt är numeriskt lika med derivatan av funktionen vid denna punkt.

Detta uttalande kallas den geometriska betydelsen av derivatan.

Innehållet i artikeln

MATEMATISK ANALYS, en gren av matematiken som tillhandahåller metoder för kvantitativ studie av olika förändringsprocesser; behandlar studiet av förändringshastigheten (differentialkalkyl) och bestämning av längderna på kurvor, ytor och volymer av figurer avgränsade av krökta konturer och ytor (integralkalkyl). För problem med matematisk analys är det karakteristiskt att deras lösning är förknippad med begreppet en gräns.

Matematisk analys initierades 1665 av I. Newton och (cirka 1675) oberoende av G. Leibniz, även om viktiga förberedande arbeten utfördes av I. Kepler (1571–1630), F. Cavalieri (1598–1647), P. Ferma (1601– 1665), J. Wallis (1616-1703) och I. Barrow (1630-1677).

För att göra presentationen mer livlig kommer vi att tillgripa grafernas språk. Därför kan det vara till hjälp för läsaren att ta en titt på artikeln ANALYTISK GEOMETRI innan du läser den här artikeln.

DIFFERENTIALKalkyl

Tangenter.

I fig. 1 visar ett fragment av kurvan y = 2x – x 2, slutit mellan x= –1 och x= 3. Tillräckligt små segment av denna kurva ser raka ut. Med andra ord, om RÄr en godtycklig punkt i denna kurva, så finns det någon rät linje som går genom denna punkt och är en approximation av kurvan i ett litet område av punkten R, och ju mindre grannskap, desto bättre approximation. En sådan rät linje kallas tangenten till kurvan i punkten R... Huvuduppgiften för differentialkalkyl är att bygga en generell metod som låter dig hitta riktningen för en tangent vid vilken punkt som helst på en kurva där tangenten finns. Det är inte svårt att föreställa sig en kurva med ett skarpt brott (Fig. 2). Om R- toppen av en sådan brytning, då kan du bygga en ungefärlig rät linje PT 1 - till höger om punkten R och ytterligare en ungefärlig linje RT 2 - till vänster om punkten R... Men det finns ingen rät linje som går genom en punkt R, som lika väl närmade sig kurvan i närheten av punkten P både till höger och till vänster, därav tangenten vid punkten P existerar inte.

I fig. 1 tangent FRÅN dras genom ursprunget O= (0,0). Lutningen på denna linje är 2, dvs. när abskissan ändras med 1, ökar ordinatan med 2. If x och y- koordinater för en godtycklig punkt på FRÅN, sedan flytta ifrån O på ett avstånd X enheter till höger, går vi bort från O på 2 y enheter upp. Därmed, y/x= 2, eller y = 2x... Detta är tangentekvationen FRÅN till kurvan y = 2x – x 2 vid punkten O.

Det är nu nödvändigt att förklara varför från uppsättningen linjer som passerar genom punkten O, det var den raka linjen som valdes FRÅN... Vad är skillnaden mellan en rät linje med en lutning på 2 och andra räta linjer? Det finns ett enkelt svar, och vi har svårt att motstå frestelsen att använda analogin med tangenten till cirkeln: tangenten FRÅN har bara en punkt gemensam med kurvan, medan varje annan icke-vertikal rät linje som går genom punkten O, skär kurvan två gånger. Detta kan verifieras enligt följande.

Sedan uttrycket y = 2x – x 2 kan erhållas genom att subtrahera X 2 av y = 2x(den räta linjens ekvationer FRÅN), sedan värdena y det finns mindre kunskap för grafen y för en rät linje i alla punkter, utom för en punkt x= 0. Därför är grafen överallt, förutom punkten O finns nedan FRÅN, och denna linje och grafen har bara en punkt gemensamt. Dessutom, om y = mx- ekvationen för någon annan rät linje som går genom en punkt O, då finns det säkert två skärningspunkter. Verkligen, mx = 2x – x 2 inte bara för x= 0, men också för x = 2 – m... Och bara när m= 2 båda skärningspunkterna sammanfaller. I fig. 3 visar fallet när m mindre än 2, alltså till höger om O det finns en andra skärningspunkt.

Vad FRÅN- den enda icke-vertikala räta linjen som går genom en punkt O och har bara en punkt gemensam med grafen, inte dess viktigaste egenskap. I själva verket, om vi vänder oss till andra grafer, kommer det snart att stå klart att egenskapen för tangenten som vi har noterat i det allmänna fallet inte är uppfylld. Till exempel, från fig. 4 kan man se att nära punkten (1,1) kurvans graf y = x 3 är väl approximerad av en rät linje RT, som dock har mer än en gemensam poäng med sig. Vi skulle dock vilja överväga RT tangent till denna graf vid punkten R... Därför är det nödvändigt att hitta något annat sätt att lyfta fram tangenten än det som tjänade oss så väl i det första exemplet.

Antag att genom poängen O och en godtycklig poäng F = (h,k) på kurvans graf y = 2x – x 2 (Fig. 5) dras en rät linje (kallad sekant). Ersätter värdena i kurvans ekvation x = h och y = k, det förstår vi k = 2h – h 2 är därför sekantens lutning

Med mycket liten h menande m nära 2. Dessutom att välja h nära nog 0 vi kan göra m godtyckligt nära 2. Det kan vi säga m"Tender to the limit" lika med 2 när h tenderar till noll, eller vilken gräns som helst mär lika med 2 för h tenderar mot noll. Detta är symboliskt skrivet så här:

Sedan tangenten till grafen vid punkten O definieras som en rät linje som går genom en punkt O, med en lutning lika med denna gräns. Denna definition av en tangent är allmänt tillämplig.

Låt oss visa fördelarna med detta tillvägagångssätt med ett annat exempel: hitta lutningen på tangenten till kurvans graf y = 2x – x 2 vid en godtycklig punkt P = (x,y), inte begränsa oss till det enklaste fallet när P = (0,0).

Låta F = (x + h, y + k) - den andra punkten på diagrammet, som ligger på avstånd h till höger om R(fig. 6). Det krävs för att hitta lutningen k/h sekant PQ... Punkt Fär på avstånd

ovanför axeln X.

När vi utökar parenteserna finner vi:

Subtrahera från denna ekvation y = 2x – x 2, finner vi det vertikala avståndet från punkten R till poängen F:

Därför lutningen m sekant PQär lika med

Nu när h tenderar till noll, m tenderar till 2-2 x; vi tar det sista värdet som tangentens lutning PT... (Samma resultat kommer att erhållas om h tar negativa värden, vilket motsvarar valet av punkten F till vänster om P.) Observera att för x= 0 resultatet är detsamma som det föregående.

Uttryck 2 - 2 x kallas derivatan av 2 x – x 2. Förr i tiden kallades derivatan även "differentialkvot" och "differentialkoefficient". Om uttryck 2 x – x 2 beteckna f(x), dvs.

då kan derivatan betecknas

För att ta reda på lutningen av tangenten till grafen för funktionen y = f(x) någon gång måste ersättas i fў ( x) värdet som motsvarar denna punkt X... Alltså lutningen fў (0) = 2 för X = 0, fў (0) = 0 för X= 1 och fў (2) = –2 för X = 2.

Derivaten betecknas också påў , dy/dx, D x y och Du.

Det faktum att kurvan y = 2x – x 2 nära en given punkt är praktiskt taget omöjlig att skilja från sin tangent vid denna punkt, gör det möjligt för oss att tala om tangentens lutning som en "kurvans lutning" vid tangenspunkten. Således kan vi hävda att lutningen på kurvan i fråga har en lutning på 2 vid punkten (0,0). Det kan också sägas att vid punkten (0,0) x= 0 förändringshastighet y relativt xär 2. Vid punkt (2,0) är lutningen för tangenten (och kurvan) –2. (Minustecknet betyder att som x variabel y minskar.) Vid punkten (1,1) är tangenten horisontell. Vi säger kurvan y = 2x – x 2 har ett stationärt värde vid denna punkt.

Toppar och dalar.

Vi har precis visat att kurvan f(x) = 2x – x 2 är stationär vid punkten (1,1). Eftersom fў ( x) = 2 – 2x = 2(1 – x), är det tydligt att för x mindre än 1, fў ( x) är positivt, och därför yökar; på x, stor 1, fў ( x) är negativ, och därför y minskar. Således, i närheten av punkten (1,1) som anges i fig. 6 bokstäver M, betydelse på växer till en punkt M, stationär vid punkten M och minskar efter punkten M... Denna punkt kallas "maximum" eftersom värdet på vid denna tidpunkt överstiger något av dess värden i ett tillräckligt litet område av det. På liknande sätt definieras "minimum" som en punkt i närheten av vilken alla värden y fler på just vid denna tidpunkt. Det kan också hända att även om derivatet av f(x) vid något tillfälle och försvinner, ändras dess tecken inte i närheten av denna punkt. En sådan punkt, som varken är ett maximum eller ett minimum, kallas en böjningspunkt.

Låt oss som ett exempel hitta kurvans stationära punkt

Derivatan av denna funktion är

och försvinner kl x = 0, X= 1 och X= –1; de där. vid punkterna (0,0), (1, –2/15) och (–1, 2/15). Om X något mindre än -1 alltså fў ( x) är negativ; om X något mer än -1 alltså fў ( x) är positivt. Därför är poängen (–1, 2/15) max. På samma sätt kan det visas att punkten (1, –2/15) är ett minimum. Men derivatan fў ( x) är negativ både före och efter punkten (0,0). Därför är (0,0) böjningspunkten.

Den genomförda studien av kurvans form, liksom det faktum att kurvan skär axeln X på f(x) = 0 (dvs. för X= 0 eller) låter dig representera dess graf ungefär som visas i fig. 7.

I allmänhet, om vi utesluter ovanliga fall (kurvor som innehåller räta linjesegment eller ett oändligt antal böjar), finns det fyra alternativ för kurvans relativa position och tangenten i närheten av tangentpunkten R. (Centimeter... ris. 8 där tangenten har en positiv lutning.)

1) På båda sidor om spetsen R kurvan ligger ovanför tangenten (fig. 8, a). I det här fallet säger de att kurvan vid punkten R konvex nedåt eller konkav.

2) På båda sidor om spetsen R kurvan ligger under tangenten (fig. 8, b). I detta fall sägs kurvan vara konvex uppåt eller helt enkelt konvex.

3) och 4) Kurvan är placerad ovanför tangenten på ena sidan av punkten R och under - på den andra. I detta fall R- böjningspunkt.

Jämföra värden fў ( x) på båda sidor av R med dess värde vid punkten R, är det möjligt att avgöra vilket av dessa fyra fall som måste hanteras i ett särskilt problem.

Ansökningar.

Allt ovanstående har viktiga tillämpningar inom olika områden. Till exempel, om kroppen kastas vertikalt uppåt med en initial hastighet på 200 fot per sekund, då höjden s där de kommer att placeras genom t sekunder jämfört med startpunkten kommer att vara

Att agera på samma sätt som i de exempel vi har övervägt finner vi

detta värde försvinner vid c. Derivat fў ( x) är positiv upp till värdet av c och negativ efter denna tid. Därmed, sökar till, blir sedan stationär och minskar sedan. Detta är en allmän beskrivning av rörelsen av en kropp som kastas uppåt. Av den vet vi när kroppen når sin högsta punkt. Vidare, ersätta t= 25/4 tum f(t), får vi 625 fot, det maximala lyftet. I denna uppgift fў ( t) har en fysisk betydelse. Denna derivata visar hastigheten med vilken kroppen rör sig vid tidpunkten t.

Låt oss nu överväga en annan typ av applikation (fig. 9). Det krävs att du gör en låda med fyrkantig botten av ett kartongark med en yta på 75 cm 2. Hur stor måste den här lådan vara för att den ska ha maximal volym? Om X- sidan av lådans bas och h- dess höjd, då är lådans volym V = x 2 h, och ytarean är 75 = x 2 + 4xh... Om vi ​​transformerar ekvationen får vi:

Härrörande från V visar sig vara lika

och försvinner kl X= 5. Sedan

och V= 125/2. Funktionsdiagram V = (75x – x 3) / 4 visas i fig. 10 (negativa värden X utelämnas eftersom det inte har någon fysisk betydelse i detta problem).

Derivat.

En viktig uppgift för differentialkalkyl är att skapa metoder som gör att du snabbt och bekvämt kan hitta derivator. Det är till exempel lätt att räkna ut det

(Konstantens derivata är naturligtvis noll.) Det är inte svårt att härleda den allmänna regeln:

var n- vilket heltal eller bråk som helst. Till exempel,

(Detta exempel visar hur användbara bråkexponenter är.)

Här är några av de viktigaste formlerna:

Det finns också följande regler: 1) om var och en av de två funktionerna g(x) och f(x) har derivator, då är derivatan av deras summa lika med summan av derivatorna av dessa funktioner, och derivatan av skillnaden är lika med skillnaden mellan derivatorna, d.v.s.

2) derivatan av produkten av två funktioner beräknas med formeln:

3) derivatan av förhållandet mellan de två funktionerna har formen

4) derivatan av en funktion multiplicerad med en konstant är lika med en konstant multiplicerad med derivatan av denna funktion, dvs.

Det händer ofta att värdena för en funktion måste beräknas stegvis. Till exempel för att beräkna synd x 2 måste vi först hitta u = x 2, och beräkna sedan sinus för talet u... Vi hittar derivatan av sådana komplexa funktioner med den så kallade "kedjeregeln":

I vårt exempel f(u) = synd u, fў ( u) = cos u, därmed,

Dessa och andra liknande regler tillåter en att omedelbart skriva ut derivatan av många funktioner.

Linjära approximationer.

Det faktum att vi, genom att känna till derivatan, i många fall kan ersätta grafen för en funktion nära någon punkt av dess tangent vid denna punkt, är av stor betydelse, eftersom räta linjer är lättare att arbeta med.

Denna idé finner direkt tillämpning vid beräkning av ungefärliga värden på funktioner. Till exempel är det ganska svårt att beräkna värdet när x= 1,033. Men du kan dra fördel av att siffran 1.033 är nära 1 och det. Stänga x= 1 kan vi ersätta grafen för tangentkurvan utan att göra något allvarligt misstag. Lutningen för en sådan tangent är lika med värdet på derivatan ( x 1/3) ў = (1/3) x–2/3 vid x = 1, dvs 1/3. Eftersom punkten (1,1) ligger på kurvan och lutningen för tangenten till kurvan vid denna punkt är 1/3, har tangentens ekvation formen

På denna linje kl X = 1,033

Det resulterande värdet y bör vara mycket nära det verkliga värdet y; och det är faktiskt bara 0,00012 mer än sant. Inom matematisk analys har metoder utvecklats för att förbättra noggrannheten hos denna typ av linjär approximation. Dessa metoder säkerställer tillförlitligheten av våra ungefärliga beräkningar.

Proceduren som just beskrivits föreslår en användbar notation. Låta P- den punkt som motsvarar funktionens graf f variabel X och låt funktionen f(x) är differentierbar. Byt ut kurvans graf nära punkten R tangent till den, ritad vid denna punkt. Om Xändras med belopp h, då kommer tangentens ordinata att ändras med värdet h H f ў ( x). Om här mycket liten, då är det senare värdet en bra approximation till den sanna förändringen i ordinatan y grafik. Om istället för h vi kommer att skriva symbolen dx(detta är inte en produkt!), utan en förändring i ordinatan y beteckna dy, då får vi dy = f ў ( x)dx, eller dy/dx = f ў ( x) (centimeter... ris. elva). Därför istället för Dy eller f ў ( x) används symbolen ofta för att beteckna en derivata dy/dx... Bekvämligheten med denna notation beror huvudsakligen på kedjeregelns explicita utseende (differentiering av en komplex funktion); i den nya notationen ser denna formel ut så här:

där det antyds att på beror på u, a u i sin tur beror på X.

Magnituden dy kallas differential på; i själva verket beror det på två variabler, nämligen: från X och inkrement dx... När ökningen dx mycket liten, magnitud dyär nära motsvarande förändring i värdet y... Men att anta att ökningen dx lite, inget behov.

Derivatfunktion y = f(x) betecknade vi f ў ( x) eller dy/dx... Det är ofta möjligt att ta derivatan av derivatan. Resultatet kallas andraderivatan av f (x) och betecknas f ўў ( x) eller d 2 y/dx 2. Till exempel om f(x) = x 3 – 3x 2, då f ў ( x) = 3x 2 – 6x och f ўў ( x) = 6x- 6. Liknande beteckningar används för högre ordningsderivat. Men för att undvika ett stort antal bindestreck (lika med ordningen på derivatan), kan den fjärde derivatan (till exempel) skrivas som f (4) (x), och derivatan n-th order as f (n) (x).

Det kan visas att kurvan vid en punkt är konvex nedåt om andraderivatan är positiv och konvex uppåt om andraderivatan är negativ.

Om funktionen har en andraderivata, då förändringen i kvantiteten y motsvarande ökningen dx variabel X, kan beräknas ungefär med formeln

Denna approximation är i allmänhet bättre än den som ges av differentialen fў ( x)dx... Det motsvarar att ersätta en del av kurvan med en parabel snarare än en rät linje.

Om funktionen f(x) det finns derivator av högre ordning, alltså

Resten är

var x- något nummer mellan x och x + dx... Ovanstående resultat kallas resten av Taylor-formeln. Om f(x) har derivator av alla ordningar, då vanligtvis R n® 0 för n ® Ґ .

INTEGRAL BERÄKNING

Rutor.

När man studerar områdena för kurvlinjära planfigurer avslöjas nya aspekter av matematisk analys. Till och med de antika grekerna försökte lösa sådana problem, för vilka bestämningen av till exempel cirkelområdet var en av de svåraste uppgifterna. Arkimedes uppnådde stor framgång med att lösa detta problem, som också lyckades hitta området för ett paraboliskt segment (fig. 12). Med hjälp av mycket komplicerade resonemang bevisade Archimedes att arean av ett paraboliskt segment är 2/3 av arean av den beskrivna rektangeln och därför i detta fall är lika med (2/3) (16) = 32/3. Som vi kommer att se senare kan detta resultat lätt erhållas med metoder för matematisk analys.

Föregångarna till Newton och Leibniz, främst Kepler och Cavalieri, löste problemet med att beräkna arean av kurvlinjiga figurer med hjälp av en metod som knappast kan kallas logisk, men som visade sig vara extremt fruktbar. När Wallis 1655 kombinerade Keplers och Cavalieris metoder med Descartes metoder (analytisk geometri) och använde den nyfödda algebra, var scenen för Newtons framträdande helt förberedd.

Wallis delade figuren, vars yta krävdes för att beräknas, i mycket smala remsor, som var och en ungefär betraktades som en rektangel. Sedan adderade han de ungefärliga rektanglarnas area och fick i de enklaste fallen det värde som summan av rektanglarnas area tenderar mot när antalet ränder tenderar mot oändligheten. I fig. Figur 13 visar rektanglar som motsvarar en viss uppdelning i remsor av området under kurvan y = x 2 .

Huvudsatsen.

Den stora upptäckten av Newton och Leibniz gjorde det möjligt att utesluta den mödosamma processen att gå över till gränsen för summan av områden. Detta gjordes tack vare en ny titt på konceptet kvadrat. Poängen är att vi måste föreställa oss området under kurvan som genereras av ordinatan som rör sig från vänster till höger och fråga hur snabbt området som svepas ut av ordinatan ändras. Nyckeln till svaret på denna fråga får vi om vi överväger två specialfall där området är känt i förväg.

Låt oss börja med arean under grafen för den linjära funktionen y = 1 + x eftersom området i detta fall kan beräknas med hjälp av elementär geometri.

Låta A(x) Är den del av planet som är innesluten mellan den räta linjen y = 1 + x och ett segment O Q(fig. 14). När du kör QP rätt område A(x) ökar. Hur snabbt? Det är inte svårt att svara på denna fråga, eftersom vi vet att arean av en trapets är lika med produkten av dess höjd med halvsumman av dess baser. Därmed,

Områdesförändringshastighet A(x) bestäms av dess derivata

Vi ser det Aў ( x) sammanfaller med ordinatan på poäng R... Är detta en slump? Låt oss försöka kontrollera parabeln som visas i fig. 15. Fyrkant A (x) under parabeln på = X 2 i intervallet från 0 till Xär lika med A(x) = (1 / 3)(x)(x 2) = x 3/3. Förändringshastigheten för detta område bestäms av uttrycket

som exakt sammanfaller med ordinatan på rörlig punkt R.

Om vi ​​antar att denna regel i allmänhet är uppfylld på ett sådant sätt att

är förändringshastigheten för området under funktionens graf y = f(x), då kan detta användas för beräkningar och andra områden. Faktum är att förhållandet Aў ( x) = f(x) uttrycker en fundamental sats, som skulle kunna formuleras enligt följande: derivatan, eller areans förändringshastighet som funktion av X, är lika med värdet på funktionen f (x) vid punkten X.

Till exempel för att hitta arean under grafen för en funktion y = x 3 från 0 till X(Fig. 16), sätter vi

Ett möjligt svar är:

sedan derivatan av X 4/4 är verkligen lika med X 3. Dessutom, A(x) är lika med noll för X= 0, som det borde vara om A(x) är verkligen ett område.

Matematisk analys bevisar att ett annat svar förutom ovanstående uttryck för A(x), existerar inte. Låt oss visa att detta påstående är rimligt med hjälp av följande heuristiska (icke rigorösa) resonemang. Anta att det finns någon annan lösning V(x). Om A(x) och V(x) "Starta" samtidigt från nollvärde vid X= 0 och hela tiden ändras i samma takt, då deras värden vid no X kan inte bli annorlunda. De måste vara lika överallt; därför finns det bara en lösning.

Hur kan förhållandet motiveras? Aў ( x) = f(x) i allmänhet? Denna fråga kan endast besvaras genom att studera områdets förändringstakt som funktion av X i allmänhet. Låta m- Funktionens minsta värde f (x) i intervallet från X innan ( x + h), a M- det största värdet av denna funktion i samma intervall. Sedan ökningen av området på att gå från X till ( x + h) måste omslutas mellan områdena för två rektanglar (Fig. 17). Baserna för båda rektanglarna är lika h... Den mindre rektangeln har en höjd m och område mh, större, respektive, M och Mh... På tomten av område kontra X(Fig. 18) kan man se att när abskissan ändras med h, värdet på ordinatan (d.v.s. arean) ökas med det belopp som ingår mellan mh och Mh... Sekantlutningen i denna graf är mellan m och M... vad händer när h tenderar till noll? Om grafen för funktionen y = f(x) är kontinuerlig (d.v.s. innehåller inte diskontinuiteter), alltså M, och m brukar f(x). Därför lutningen Aў ( x) yta som funktion av Xär lika med f(x). Det var just till en sådan slutsats man måste komma.

Leibniz föreslog för området under kurvan y = f(x) från 0 till a beteckning

Med ett rigoröst tillvägagångssätt måste denna så kallade bestämda integral definieras som gränsen för vissa summor på Wallis sätt. Givet ovanstående resultat är det tydligt att denna integral beräknas förutsatt att vi kan hitta en sådan funktion A(x), som försvinner kl X= 0 och har en derivata Aў ( x) lika med f (x). Att hitta en sådan funktion kallas vanligtvis integration, även om det skulle vara lämpligare att kalla denna operation för antidifferentiering, vilket betyder att den på sätt och vis är omvänd till differentiering. I fallet med ett polynom är integrationen enkel. Till exempel om

som är lätt att verifiera genom att särskilja A(x).

För att beräkna arean A 1 under kurvan y = 1 + x + x 2/2, innesluten mellan ordinatan 0 och 1, skriver vi helt enkelt

och ersätta X= 1, vi får A 1 = 1 + 1/2 + 1/6 = 5/3. Fyrkant A(x) från 0 till 2 är lika med A 2 = 2 + 4/2 + 8/6 = 16/3. Som framgår av fig. 19 är området mellan ordinatan 1 och 2 A 2 – A 1 = 11/3. Det skrivs vanligtvis som en bestämd integral

Volymer.

Liknande resonemang gör det förvånansvärt enkelt att beräkna volymerna av rotationskroppar. Låt oss demonstrera detta genom exemplet att beräkna volymen av en boll, ett annat klassiskt problem som de gamla grekerna, med de metoder som de kände till, lyckades lösa med stor svårighet.

Rotera den del av planet som är innesluten inom en fjärdedel av en cirkel med radie r, i en vinkel på 360 ° runt axeln X... Som ett resultat får vi en halvklot (fig. 20), vars volym vi betecknar V(x). Det är nödvändigt att bestämma den takt med vilken V(x) med ökande x... Går vidare från X Till X + h, är det lätt att verifiera att volymökningen är mindre än volymen sid(r 2 – x 2)h cirkulär cylinderradie och höjd h, och mer än volym sid[r 2 – (x + h) 2 ]h cylinderradie och höjd h... Därför på grafen för funktionen V(x) sekantens lutning är mellan sid(r 2 – x 2) och sid[r 2 – (x + h) 2]. När h tenderar till noll, lutningen tenderar att

På x = r vi får

för volymen av halvklotet och därför 4 p r 3/3 för volymen av hela bollen.

En liknande metod låter dig hitta längderna på kurvorna och områdena på krökta ytor. Till exempel om a(x) - båglängd PR i fig. 21, då är vår uppgift att beräkna aў( x). På den heuristiska nivån använder vi ett trick som gör att vi inte kan ta till den vanliga passagen till gränsen, vilket är nödvändigt för ett noggrant bevis på resultatet. Antag att förändringshastigheten för funktionen a(x) vid punkten Rär detsamma som det skulle vara om kurvan ersattes av sin tangent PT vid punkten P... Men från fig. 21 kan ses direkt när man kliver h till höger eller vänster om punkten X längs RT menande a(x) ändras till

Därför förändringshastigheten för funktionen a(x) är

För att hitta själva funktionen a(x), är det bara nödvändigt att integrera uttrycket på höger sida av jämlikheten. Det visar sig att de flesta funktioner är svåra att integrera. Därför utgör utvecklingen av integralkalkylmetoder en stor del av matematisk analys.

Antiderivat.

Varje funktion vars derivata är lika med en given funktion f(x), kallas antiderivatet (eller primitivt) för f(x). Till exempel, X 3/3 är antiderivatan för funktionen X 2, sedan ( x 3/3) ў = x 2. Självklart X 3/3 är inte den enda antiderivatan av en funktion X 2 sedan x 3 /3 + Cär också en derivata för X 2 för varje konstant MED... I det följande kommer vi dock att komma överens om att utelämna sådana additiva konstanter. I allmänhet

var nÄr ett positivt heltal, eftersom ( x n + 1/(n+ 1)) ў = x n... Relation (1) gäller i ännu mer allmän mening om n ersätt med valfritt rationellt tal k förutom -1.

Godtycklig antiderivatfunktion för en given funktion f(x) brukar kallas den obestämda integralen av f(x) och beteckna det som

Till exempel, eftersom (synd x) ў = cos x, formeln är giltig

I många fall, när det finns en formel för en obestämd integral av en given funktion, kan den hittas i många allmänt publicerade tabeller över obestämda integraler. Integraler av elementära funktioner är tabellformade (dessa inkluderar potenser, logaritmer, exponentialfunktioner, trigonometriska funktioner, inversa trigonometriska funktioner, såväl som deras finita kombinationer som erhålls med hjälp av addition, subtraktion, multiplikation och division). Med hjälp av tabellintegraler kan du beräkna integraler för mer komplexa funktioner. Det finns många sätt att beräkna obestämda integraler; den vanligaste av dessa är den variabla substitutionen eller substitutionsmetoden. Den består i det faktum att om vi vill ersätta i den obestämda integralen (2) x på någon differentierbar funktion x = g(u), så att integralen inte ändras är det nödvändigt x ersatt av gў ( u)du... Med andra ord, jämställdheten

(ersättning 2 x = u, varifrån 2 dx = du).

Här är en annan integrationsmetod - metoden för integration av delar. Den är baserad på den redan kända formeln

Att ha integrerat vänster och höger sida, och ta hänsyn till det

Denna formel kallas formeln för integrering av delar.

Exempel 2. Det krävs för att hitta. Sedan cos x= (synd x) ў, det kan vi skriva

Från (5), inställning u = x och v= synd x, vi får

Och eftersom (–cos x) ў = synd x vi hittar det och

Det bör betonas att vi har begränsat oss till endast en mycket kort introduktion till ett mycket omfattande ämne, i vilket många kvicka tekniker har samlats.

Funktioner av två variabler.

På grund av kurvan y = f(x) har vi övervägt två uppgifter.

1) Hitta lutningen för tangenten till kurvan vid en given punkt. Detta problem löses genom att beräkna värdet på derivatan fў ( x) vid den angivna punkten.

2) Hitta arean under kurvan ovanför axelsegmentet X begränsas av vertikala linjer X = a och X = b... Detta problem löses genom att beräkna en bestämd integral.

Vart och ett av dessa problem har en analog när det gäller ytan z = f(x,y).

1) Hitta tangentplanet till ytan vid en given punkt.

2) Hitta volymen under ytan ovanför delen av planet hu begränsas av kurvan MED, och från sidan - vinkelräta mot planet xy passerar genom punkterna i gränskurvan MED (centimeter... ris. 22).

Följande exempel visar hur dessa uppgifter utförs.

Exempel 4. Hitta tangentplanet till ytan

vid punkten (0,0,2).

Ett plan definieras om två skärande linjer som ligger i det ges. En av dessa rader ( l 1) vi sätter oss i planet xz (på= 0), den andra ( l 2) - i planet yz (x = 0) (centimeter... ris. 23).

Först av allt, om på= 0, alltså z = f(x,0) = 2 – 2x – 3x 2. Derivat med avseende på X betecknas med fў x(x,0) = –2 – 6x, kl X= 0 har värdet –2. Hetero l 1 ges av ekvationer z = 2 – 2x, på= 0 - tangent till MED 1, skärningslinjerna mellan ytan och planet på= 0. På liknande sätt, om X= 0, alltså f(0,y) = 2 – y – y 2, och derivatan med avseende på på har formen

Eftersom fў y(0,0) = –1, kurva MED 2 - skärningslinjen mellan ytan och planet yz- har en tangent l 2 ges av ekvationerna z = 2 – y, X= 0. Det önskade tangentplanet innehåller båda räta linjerna l 1 och l 2 och skrivs av ekvationen

Detta är ekvationen för planet. Dessutom får vi raka linjer l 1 och l 2, inställning, respektive, på= 0 och X = 0.

Det faktum att ekvation (7) verkligen definierar tangentplanet kan verifieras på heuristisk nivå om vi märker att denna ekvation innehåller första ordningens termer som ingår i ekvation (6), och att andra ordningens termer kan representeras i form -. Eftersom detta uttryck är negativt för alla värden X och på, Förutom X = på= 0, ytan (6) ligger överallt under planet (7), förutom punkten R= (0,0,0). Vi kan säga att ytan (6) är konvex uppåt vid punkten R.

Exempel 5. Hitta tangentplanet till ytan z = f(x,y) = x 2 – y 2 vid ursprung 0.

På ytan på= 0 vi har: z = f(x,0) = x 2 och fў x(x,0) = 2x... På MED 1, skärningslinjer, z = x 2. Vid punkten O lutningen är fў x(0,0) = 0. På planet X= 0 vi har: z = f(0,y) = –y 2 och fў y(0,y) = –2y... På MED 2, skärningslinjer, z = –y 2. Vid punkten O lutningen av en kurva MED 2 är lika fў y(0,0) = 0. Eftersom tangenterna till MED 1 och MED 2 är axlar X och på, tangentplanet som innehåller dem är planet z = 0.

Men i närheten av ursprunget är vår yta inte på ena sidan av tangentplanet. Ja, kurvan MED 1 överallt, förutom punkt 0, ligger ovanför tangentplanet och kurvan MED 2 - respektive under den. Ytan skär tangentplanet z= 0 i raka linjer på = X och på = –X... En sådan yta sägs ha en sadelpunkt vid origo (bild 24).

Partiella derivat.

I de tidigare exemplen använde vi derivator från f (x,y) på X och genom att på... Låt oss nu överväga sådana derivat mer generellt. Om vi ​​har en funktion av två variabler, till exempel, F(x,y) = x 2 – xy, då kan vi vid varje punkt definiera två av dess "partiella derivator", en genom att differentiera funktionen med avseende på X och fixa på, den andra genom att särskilja med avseende på på och fixa X... Den första av dessa derivat betecknas som fў x(x,y) eller ¶ f/¶ x; andra - hur f f ў y... Om båda blandade derivaten (av X och på, på på och X) är kontinuerliga, sedan ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x; i vårt exempel ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x = –1.

Partiell derivat fў x(x,y) indikerar funktionens förändringshastighet f vid punkt ( x,y) i riktning mot att öka X, a fў y(x,y) Är funktionens förändringshastighet f stigande riktning på... Funktionsändringshastighet f vid punkt ( X,på) i riktning mot en rät linje som bildar en vinkel q med positiv riktning på axeln X, kallas derivatan av funktionen f mot; dess värde är en kombination av två partiella derivator av funktionen f i tangentplanet är nästan lika (för liten dx och dy) verklig förändring z på ytan, men att beräkna differentialen är vanligtvis lättare.

Formeln som vi redan har övervägt från variabeländringsmetoden, känd som derivatan av en komplex funktion eller kedjeregel, i det endimensionella fallet när på beror på X, a X beror på t, har formen:

För funktioner av två variabler är en liknande formel:

Det är lätt att generalisera begreppen och beteckningarna för partiell differentiering till högre dimensioner. I synnerhet om ytan implicit ges av ekvationen f(x,y,z) = 0, ekvationen för tangentplanet till ytan kan ges en mer symmetrisk form: ekvationen för tangentplanet vid punkten ( x (x 2/4)], sedan integreras den över X 0 till 1. Slutresultatet är 3/4.

Formel (10) kan också tolkas som den så kallade dubbelintegralen, dvs. som gränsen för summan av volymer av elementära "celler". Varje sådan cell har en bas D x D y och en höjd lika med höjden på ytan ovanför någon punkt på den rektangulära basen ( centimeter... ris. 26). Det kan visas att båda synpunkterna på formel (10) är likvärdiga. Dubbla integraler används för att hitta tyngdpunkterna och många moment som finns inom mekaniken.

Noggrannare underbyggande av den matematiska apparaten.

Hittills har vi presenterat begrepp och metoder för kalkylering på en intuitiv nivå och har inte tvekat att tillgripa geometriska former. Det återstår för oss att kort överväga de mer rigorösa metoderna som dök upp på 1800- och 1900-talen.

I början av 1800-talet, när angreppens och angreppens era i "skapandet av matematisk analys" upphörde, kom frågorna om dess berättigande i förgrunden. I verk av Abel, Cauchy och ett antal andra framstående matematiker var begreppen "gräns", "kontinuerlig funktion", "konvergerande serier" exakt definierade. Detta var nödvändigt för att få en logisk ordning till grunden för matematisk analys för att göra den till ett tillförlitligt forskningsverktyg. Behovet av en grundlig motivering blev ännu mer uppenbart efter upptäckten 1872 av Weierstrass av överallt kontinuerliga, men ingenstans differentierbara funktioner (grafen över sådana funktioner har ett brott vid varje punkt). Detta resultat gjorde ett överväldigande intryck på matematiker, eftersom det tydligt stred mot deras geometriska intuition. Ett ännu mer slående exempel på den geometriska intuitionens opålitlighet var den av D. Peano konstruerade kontinuerliga kurvan, som helt fyller en viss kvadrat, d.v.s. passerar genom alla dess punkter. Dessa och andra upptäckter gav upphov till programmet för "aritmetisering" av matematiken, d.v.s. göra det mer tillförlitligt genom att underbygga alla matematiska begrepp med begreppet tal. Den nästan puritanska avhållsamheten från klarhet i arbeten om matematikens grunder hade sitt historiska berättigande.

Enligt moderna kanoner av logisk rigor är det otillåtet att tala om området under kurvan. y = f(x) och ovanför axelsegmentet X, även f- en kontinuerlig funktion, utan att först definiera den exakta innebörden av begreppet "område" och inte fastställa att det på detta sätt bestämda området verkligen existerar. Detta problem löstes framgångsrikt 1854 av B. Riemann, som gav en exakt definition av begreppet en bestämd integral. Sedan dess har idén om summering bakom begreppet en bestämd integral varit föremål för många djupa studier och generaliseringar. Som ett resultat är det idag möjligt att ge mening åt en bestämd integral, även om integranden är diskontinuerlig överallt. Nya integrationsbegrepp, till vilka A. Lebesgue (1875–1941) och andra matematiker gjorde ett stort bidrag, ökade kraften och skönheten i modern matematisk analys.

Det vore knappast lämpligt att gå in på detaljerna i alla dessa och andra begrepp. Vi kommer bara att begränsa oss till att ge rigorösa definitioner av gränsen och den definitiva integralen.

Sammanfattningsvis, låt oss säga att matematisk analys, som är ett extremt värdefullt verktyg i händerna på en vetenskapsman och en ingenjör, även idag drar till sig matematikers uppmärksamhet som en källa till fruktbara idéer. Samtidigt tycks den moderna utvecklingen tyda på att matematisk analys i allt högre grad absorberas av sådana dominerande under 1900-talet. grenar av matematik som abstrakt algebra och topologi.

Det är absolut omöjligt att lösa fysiska problem eller exempel i matematik utan kunskap om derivatan och metoderna för att beräkna den. Derivat är ett av de viktigaste begreppen inom matematisk analys. Vi bestämde oss för att ägna dagens artikel åt detta grundläggande ämne. Vad är en derivata, vad är dess fysiska och geometriska betydelse, hur beräknar man derivatan av en funktion? Alla dessa frågor kan kombineras till en: hur förstår man derivatan?

Geometrisk och fysisk betydelse av derivatan

Låt det finnas en funktion f (x) ges i något intervall (a, b) ... Punkterna х och х0 hör till detta intervall. När x ändras ändras själva funktionen. Ändra ett argument - skillnaden mellan dess värden x-x0 ... Denna skillnad skrivs som delta x och kallas argumentökning. En förändring eller ökning av en funktion är skillnaden i värdena för en funktion vid två punkter. Derivatdefinition:

Derivatan av en funktion vid en punkt är gränsen för förhållandet mellan ökningen av funktionen vid en given punkt och ökningen av argumentet när det senare tenderar till noll.

Annars kan det skrivas så här:

Vad är poängen med att hitta en sådan gräns? Och här är vad:

derivatan av funktionen i en punkt är lika med tangenten för vinkeln mellan OX-axeln och tangenten till grafen för funktionen vid denna punkt.

Den fysiska betydelsen av derivatan: derivatan av banan med avseende på tid är lika med hastigheten för den rätlinjiga rörelsen.

Sedan skoltiden vet alla att hastighet är en privat väg. x = f (t) och tid t ... Medelhastighet över en tidsperiod:

För att ta reda på rörelsehastigheten åt gången t0 du måste beräkna gränsen:

Regel ett: ta ut en konstant

Konstanten kan flyttas utanför derivatans tecken. Dessutom måste det göras. När du löser exempel i matematik, ta som regel - om du kan förenkla uttrycket, se till att förenkla .

Exempel. Låt oss beräkna derivatan:

Regel två: derivata av summan av funktioner

Derivatan av summan av två funktioner är lika med summan av derivatan av dessa funktioner. Detsamma gäller för derivatan av skillnaden mellan funktioner.

Vi kommer inte att ge ett bevis för denna sats, utan snarare överväga ett praktiskt exempel.

Hitta derivatan av en funktion:

Regel tre: derivata av produkten av funktioner

Derivatan av produkten av två differentierbara funktioner beräknas med formeln:

Exempel: hitta derivatan av en funktion:

Lösning:

Det är viktigt att säga här om beräkningen av derivator av komplexa funktioner. Derivatan av en komplex funktion är lika med produkten av derivatan av denna funktion med avseende på det mellanliggande argumentet med derivatan av det mellanliggande argumentet med avseende på den oberoende variabeln.

I exemplet ovan möter vi uttrycket:

I det här fallet är det mellanliggande argumentet 8x i femte potensen. För att beräkna derivatan av ett sådant uttryck, beräknar vi först derivatan av den externa funktionen med avseende på det mellanliggande argumentet och multiplicerar sedan med derivatan av det omedelbara mellanargumentet med avseende på den oberoende variabeln.

Regel fyra: kvotderivatan av två funktioner

Formel för att bestämma derivatan av kvoten av två funktioner:

Vi försökte berätta om derivat för dummies från grunden. Det här ämnet är inte så enkelt som det låter, så var varning: det finns ofta fallgropar i exemplen, så var försiktig när du beräknar derivator.

För frågor om detta och andra ämnen kan du kontakta studenttjänsten. På kort tid hjälper vi dig att lösa det svåraste testet och ta itu med uppgifter, även om du aldrig har räknat med derivator tidigare.

På vilken vi analyserade de enklaste derivaten och bekantade oss med reglerna för differentiering och några tekniker för att hitta derivat. Således, om du inte är så mycket med derivator av funktioner, eller om vissa punkter i den här artikeln inte är helt klara, läs först ovanstående lektion. Snälla, ställ in dig på en seriös stämning - materialet är inte lätt, men jag kommer ändå att försöka presentera det på ett enkelt och lättillgängligt sätt.

I praktiken måste man hantera derivatan av en komplex funktion väldigt ofta, skulle jag till och med säga, nästan alltid, när man får uppgifter att hitta derivator.

Vi tittar i tabellen på regeln (nr 5) för att differentiera en komplex funktion:

Förståelse. Först och främst, låt oss uppmärksamma inspelningen. Här har vi två funktioner – och dessutom är funktionen bildligt talat inbäddad i funktionen. En funktion av detta slag (när en funktion är kapslad i en annan) kallas en komplex funktion.

Jag ringer funktionen extern funktion och funktionen - en inre (eller kapslad) funktion.

! Dessa definitioner är inte teoretiska och bör inte förekomma i den slutliga utformningen av uppdragen. Jag använder informella uttryck "extern funktion", "intern" funktion endast för att göra det lättare för dig att förstå materialet.

För att klargöra situationen, överväg:

Exempel 1

Hitta derivatan av en funktion

Under sinus har vi inte bara bokstaven "X", utan ett heltalsuttryck, så det kommer inte att vara möjligt att hitta derivatan direkt från tabellen. Vi märker också att det är omöjligt att tillämpa de fyra första reglerna här, det verkar finnas en skillnad, men faktum är att du inte kan "riva isär" en sinus:

I detta exempel, redan från mina förklaringar, är det intuitivt tydligt att en funktion är en komplex funktion, och polynomet är en intern funktion (kapsling) och en extern funktion.

Första steget, som måste utföras när man hittar derivatan av en komplex funktion, är det ta reda på vilken funktion som är intern och vilken som är extern.

När det gäller enkla exempel verkar det tydligt att ett polynom är kapslat under sinus. Men tänk om allt inte är självklart? Hur avgör man exakt vilken funktion som är extern och vilken som är intern? För att göra detta föreslår jag att du använder följande teknik, som kan göras mentalt eller på ett utkast.

Föreställ dig att vi behöver beräkna värdet av ett uttryck på en miniräknare (istället för ett kan det finnas valfritt tal).

Vad ska vi beräkna först? För det första du måste utföra följande åtgärd: så polynomet kommer att vara en intern funktion:

För det andra måste hittas, så sinus kommer att vara en extern funktion:

Efter att vi Räknat ut med interna och externa funktioner är det dags att tillämpa regeln om differentiering av en komplex funktion .

Vi börjar bestämma oss. Från lektionen Hur hittar jag derivatan? vi kommer ihåg att utformningen av lösningen av en derivata alltid börjar så här - vi omger uttrycket inom parentes och sätter ett streck längst upp till höger:

Först hitta derivatan av den yttre funktionen (sinus), titta på tabellen över derivator av elementära funktioner och lägg märke till det. Alla tabellformler är tillämpliga även om "x" ersätts med ett komplext uttryck, I detta fall:

Observera att den inre funktionen har inte förändrats, vi rör det inte.

Tja, det är ganska uppenbart

Resultatet av att tillämpa formeln i den slutliga designen ser det ut så här:

En konstant faktor placeras vanligtvis i början av ett uttryck:

Om det finns någon förvirring, skriv ner lösningen och läs förklaringarna igen.

Exempel 2

Hitta derivatan av en funktion

Exempel 3

Hitta derivatan av en funktion

Som alltid skriver vi ner:

Låt oss ta reda på var vi har en extern funktion, och var vi har en intern. För att göra detta, försök (mentalt eller på ett utkast) att beräkna värdet på uttrycket vid. Vad bör göras först? Först och främst måste du beräkna vad basen är lika med: vilket betyder att polynomet är den interna funktionen:

Och först då utförs exponentieringen, därför är effektfunktionen en extern funktion:

Enligt formeln , först måste du hitta derivatan av den externa funktionen, i det här fallet graden. Vi letar efter formeln som krävs i tabellen:. Vi upprepar igen: vilken tabellformel som helst är giltig inte bara för "x", utan också för ett komplext uttryck... Alltså resultatet av att tillämpa regeln om differentiering av en komplex funktion Nästa:

Jag betonar igen att när vi tar derivatan av den yttre funktionen så förändras inte den inre funktionen för oss:

Nu återstår det att hitta en mycket enkel derivata av den inre funktionen och "kamma" resultatet lite:

Exempel 4

Hitta derivatan av en funktion

Detta är ett exempel på en oberoende lösning (svar i slutet av handledningen).

För att konsolidera förståelsen av derivatan av en komplex funktion kommer jag att ge ett exempel utan kommentarer, försöka lista ut det på egen hand, spekulera var är den externa och var är den interna funktionen, varför löstes uppgifterna på detta sätt?

Exempel 5

a) Hitta derivatan av funktionen

b) Hitta derivatan av funktionen

Exempel 6

Hitta derivatan av en funktion

Här har vi en rot, och för att kunna särskilja roten måste den representeras som en grad. Därför tar vi först funktionen till en form som är lämplig för differentiering:

Genom att analysera funktionen kommer vi till slutsatsen att summan av tre termer är en intern funktion och exponentiering är en extern funktion. Vi tillämpar differentieringsregeln för en komplex funktion :

Graden representeras återigen som en radikal (rot), och för derivatan av den interna funktionen tillämpar vi en enkel regel för att differentiera summan:

Redo. Du kan också föra uttrycket till en gemensam nämnare inom parentes och skriva ner allt i ett bråk. Trevligt förstås, men när besvärliga långa derivat erhålls är det bättre att inte göra detta (det är lätt att bli förvirrad, göra ett onödigt misstag och det kommer att vara obekvämt för läraren att kontrollera).

Exempel 7

Hitta derivatan av en funktion

Detta är ett exempel på en oberoende lösning (svar i slutet av handledningen).

Det är intressant att notera att ibland, istället för regeln för att differentiera en komplex funktion, kan man använda regeln för att differentiera kvoten , men en sådan lösning kommer att se ovanlig ut som en perversion. Här är ett typiskt exempel:

Exempel 8

Hitta derivatan av en funktion

Här kan du använda regeln för att differentiera kvoten , men det är mycket mer lönsamt att hitta derivatan genom regeln om differentiering av en komplex funktion:

Vi förbereder funktionen för differentiering - vi flyttar minus utanför tecknet för derivatan och höjer cosinus till täljaren:

Cosinus är en intern funktion, exponentiering är en extern funktion.
Vi använder vår regel :

Hitta derivatan av den interna funktionen, återställ cosinus tillbaka:

Redo. I det övervägda exemplet är det viktigt att inte bli förvirrad i skyltarna. Försök förresten att lösa det med regeln , måste svaren matcha.

Exempel 9

Hitta derivatan av en funktion

Detta är ett exempel på en oberoende lösning (svar i slutet av handledningen).

Hittills har vi tittat på fall där vi bara hade en bilaga i en komplex funktion. I praktiska uppgifter kan du ofta hitta derivator, där, som häckande dockor, den ena inuti den andra, 3 eller till och med 4-5 funktioner är kapslade på en gång.

Exempel 10

Hitta derivatan av en funktion

Låt oss förstå bilagorna till denna funktion. Försöker utvärdera uttrycket med hjälp av testvärdet. Hur skulle vi räkna med en miniräknare?

Först måste du hitta, vilket betyder att bågen är den djupaste häckningen:

Då ska denna arcsine av en kvadratiseras:

Och slutligen, höj 7:an till makten:

Det vill säga, i det här exemplet har vi tre olika funktioner och två fästen, medan den innersta funktionen är arcsinus och den yttersta funktionen är exponentialfunktionen.

Vi börjar lösa

Enligt regeln först måste du ta derivatan av den externa funktionen. Vi tittar på tabellen över derivator och hittar derivatan av exponentialfunktionen: Den enda skillnaden är att istället för "x" har vi ett komplext uttryck, som inte förnekar giltigheten av denna formel. Så resultatet av att tillämpa regeln om differentiering av en komplex funktion Nästa.