Limita a spojitosť funkcie jednej premennej - dokumentu. Limita funkcie spojitého argumentu Pojem spojitosti funkcie

Limit a spojitosť

funkcie jednej premennej

3.1.1. Definícia. číslo A X usilovať sa o X 0 pre akékoľvek číslo
je tam číslo
(
), a podmienka bude splnená:

Ak
, To
.

(Symbolizmus:
).

Ak graf ukazuje G funkcie

, Kedy približuje sa k bodu nekonečne blízko (tie.
), (pozri obr. 3.1), potom je táto okolnosť geometrickým ekvivalentom skutočnosti, že funkcia
pri
má hraničnú hodnotu (limit) A(symbolizmus:
).

Funkčný graf,

Ryža. 3.1

Treba si uvedomiť, že pri určovaní limitnej hodnoty (limity) funkcie pri X usilovať sa o X 0 nehovorí nič o správaní funkcie v bode X 0 Na samom mieste X Funkcia 0 nemusí byť definovaná, môže byť
, možno
.

Ak
, potom sa funkcia nazýva infinitezimálna pre
.

Interval sa nazýva  - okolie bodu X 0 s vyštiepeným stredom. Pomocou tohto názvu môžeme povedať toto: ak pre akékoľvek číslo existuje číslo a podmienka bude splnená: ak
, To
.

3.1.2. Definícia. , ak pre nejaké konverguje k X 0 sekvencií
podsekvencia
konverguje k A.

3.1.3. Dokážme rovnocennosť definícií oddielov 3.1.1 a 3.1.2

Nech najprv v zmysle prvej definície a nech
(
), potom všetky , okrem ich konečného počtu vyhovujú nerovnosti
, Kde  vybrané používateľom  v zmysle prvej definície, t.j.
, t.j. prvá definícia implikuje druhú. Nechaj to teraz
v zmysle druhej definície a predpokladajme, že v zmysle druhej definície
, t.j. pre niektoré pre ľubovoľne malé (napr
) sekvencia bola nájdená
, ale v rovnakom čase
. Dospeli sme k rozporu, preto prvá vyplýva z druhej definície.

3.1.4. Ekvivalencia týchto definícií je obzvlášť výhodná, pretože všetky predtým overené vety o vlastnostiach limit pre postupnosti sa prenášajú takmer automaticky do nový prípad. Je potrebné len objasniť pojem premlčania. Zodpovedajúca veta má nasledujúcu formuláciu:

Ak
, potom je obmedzený na nejaké  - okolie bodu X 0 s vyštiepeným stredom.

3.2.1.Veta. Nechaj
,
,

potom
,

3.2.2. Nechaj

- ľubovoľný, zbiehajúci sa k X 0 postupnosť hodnôt argumentov funkcií a
. Zodpovedajúce sekvencie
A
hodnoty týchto funkcií majú limity A A B. Ale potom, na základe vety v sekcii 2.13.2, postupnosti
,
A
majú limity zodpovedajúco rovnaké A +B,
A
. Podľa definície limity funkcie v bode (pozri časť 2.5.2) to znamená, že

,
,

3.2.3. Veta. Ak
,
a v určitom okolí

vyskytuje

3.2.4. Podľa definície limity funkcie v bode X 0 pre akúkoľvek sekvenciu
také že

postupnosť funkčných hodnôt má limit rovný A. To znamená, že pre kohokoľvek
je tam číslo
vykonané . Rovnako tak pre postupnosť
je tam číslo
tak, že pre ľubovoľné číslo
vykonané . Výber
, zistíme, že pre každého
vykonané . Z tohto reťazca nerovností máme pre akékoľvek , čo znamená, že
.

3.2.5. Definícia. číslo A sa nazýva hraničná hodnota (limita) funkcie pri X usilovať sa o X 0 vpravo (symbol:
), ak pre ľubovoľné číslo existuje číslo () a je splnená podmienka: ak
, To
.

Množina sa nazýva pravé  - okolie bodu X 0 Pojem limitná hodnota (limit) vľavo je definovaný podobne (
).

3.2.6. Veta. Funkcia at má limitnú hodnotu (limitu) rovnú A vtedy a len vtedy

3.3.1. Definícia. číslo A sa nazýva hraničná hodnota (limita) funkcie pri X tendenciu k nekonečnu, ak pre nejaké číslo existuje číslo
(
) a bude splnená nasledujúca podmienka:

Ak
, To .

(Symbolizmus:
.)

Kopa
volal D- okolie nekonečna.

3.3.2. Definícia. číslo A sa nazýva hraničná hodnota (limita) funkcie pri X sklon k plus nekonečnu, ak pre akékoľvek číslo existuje číslo D() a bude splnená podmienka:

Ak
, To .

(Symbolizmus:
).

Ak graf ukazuje G funkcie
s neobmedzeným rastom
neobmedzene sa približovať k jedinej vodorovnej čiare
(pozri obr. 3.2), potom je táto okolnosť geometrickým ekvivalentom skutočnosti, že funkcia
pri
má hraničnú hodnotu (limit) rovnajúcu sa číslu A(symbolizmus:
).

Graf funkcie
,

Kopa
volal D- susedstvo plus nekonečno.

Pojem limit at
.

Cvičenia.

Uveďte všetky teorémy o limitách, ktoré sa aplikujú na prípady:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. Definícia. Funkcia sa volá nekonečne skvelá funkcia(alebo jednoducho nekonečne veľké) pri , ak je akékoľvek číslo

, uspokojenie nerovnosti, nerovnosť je uspokojená
.

(Symbolizmus:
.)

Ak sa splní
, potom píšu
.

3.4.2. Veta. Nechaj
A
pri
.

Potom
je nekonečne veľká funkcia pre .

3.4.3. Nech je to ľubovoľné číslo. Pretože je nekonečne malá funkcia pre , potom pre číslo
existuje taký počet, že pre každého X tak, aby nerovnosť platila
, ale potom za to isté X nerovnosť bude uspokojená
. Tie. je nekonečne veľká funkcia pre .

3.4.4.Veta. Dovoliť byť nekonečne veľká funkcia pre a pre .

Potom je nekonečne malá funkcia pre .

(Táto veta je dokázaná podobným spôsobom ako veta v časti 3.8.2.)

3.4.5. Funkcia
sa nazýva neohraničený, keď
, ak pre akékoľvek číslo
a akékoľvek δ-okolie bodu môžete určiť bod X z tejto štvrte tak, že
.

3.5.1. DEFINÍCIA. Funkcia sa volá nepretržitý v bode , Ak
.

Posledná podmienka môže byť napísaná takto:

Tento zápis znamená, že pre spojité funkcie možno zameniť znamienko limity a znamienko funkcie

Alebo takto: . Alebo znova, ako na začiatku.

Označme
. Potom
a =
a posledný záznamový formulár prevezme formulár

Výraz pod medzným znakom predstavuje prírastok funkčného bodu spôsobený prírastkom
argument X v bode, zvyčajne označovaný ako
. Výsledkom je nasledujúca forma zápisu podmienky spojitosti funkcie v bode

ktorá sa nazýva „pracovná definícia“ spojitosti funkcie v bode.

Funkcia sa volá nepretržitý v bode vľavo, Ak
.

Funkcia sa volá nepretržitý v bode napravo, Ak
.

3.5.2. Príklad.
. Táto funkcia je nepretržitá pre všetky . Pomocou viet o vlastnostiach limít okamžite dostaneme: akákoľvek racionálna funkcia je spojitá v každom bode, v ktorom je definovaná, t.j. funkcia formulára
.

CVIČENIA.

3.6.1. Školská učebnica dokazuje (na vysoký stupeň prísnosť), že
(prvá pozoruhodná hranica). Z vizuálnych geometrických úvah to okamžite vyplýva
. Všimnite si, že z ľavej nerovnosti to tiež vyplýva
, t.j. aká je funkcia
kontinuálne na nule. Odtiaľto nie je vôbec ťažké dokázať kontinuitu všetkých goniometrické funkcie vo všetkých bodoch, kde sú definované. V skutočnosti, kedy
ako produkt je nekonečný malá funkcia
na obmedzená funkcia
.

3.6.2. (2. úžasná hranica). Ako už vieme

Kde prechádza prirodzenými číslami. Dá sa to ukázať
. Navyše
.

CVIČENIA.

3.7.1. TEOREM (o spojitosti komplexnej funkcie).

Ak funkcia
je spojitá v bode a
a funkciu
súvislý v bode , teda komplexná funkcia
je v bode spojitá.

3.7.2. Platnosť tohto vyhlásenia bezprostredne vyplýva z definície kontinuity, ktorá je napísaná takto:

3.8.1. TEOREM. Funkcia je nepretržitý v každom bode (
).

3.8.2. Ak považujeme za rozumné, že funkcia
je definovaný pre akékoľvek a je prísne monotónny (prísne klesajúci pre
, prísne sa zvyšuje s
), potom dôkaz nie je náročný.

O
máme:

tie. keď máme
, čo znamená, že funkcia je nepretržitý o .

O
všetko prichádza k predchádzajúcemu:

O
.

O
funkciu
je konštantná pre všetkých, teda spojitá.

3.9.1. TEOREM (o koexistencii a spojitosti inverznej funkcie).

Nech spojitá funkcia striktne klesá (striktne rastie) v nejakom δ - okolí bodu,
. Potom v nejakom ε - okolí bodu existuje inverzná funkcia
, ktorá striktne klesá (striktne rastie) a je spojitá v ε - okolí bodu.

3.9.2. Tu dokážeme iba spojitosť inverznej funkcie v bode .

Zoberme si to, bodka r umiestnené medzi bodmi
A
, teda ak
, To
, Kde .

3.10.1. Akékoľvek prípustné aritmetické operácie so spojitými funkciami teda opäť vedú k spojitým funkciám. Vytváranie komplexných a inverzných funkcií z nich nenarúša kontinuitu. Preto s určitou mierou zodpovednosti môžeme tvrdiť, že všetky elementárne funkcie sú spojité pre všetky prípustné hodnoty argumentu.

CVIČENIE.

Dokáž to
pri
(ďalšia forma druhej nádhernej limitky).

3.11.1. Výpočet limitov sa značne zjednoduší, ak použijeme koncept ekvivalentných infinitezimálov. Koncept ekvivalencie je vhodné zovšeobecniť na prípad ľubovoľných funkcií.

Definícia. Hovorí sa, že funkcie a sú ekvivalentné pre if
(namiesto môžeš písať
,
,
,
,
).

Použitý zápis f ~ g.

Ekvivalencia má nasledujúce vlastnosti

Je potrebné mať na pamäti nasledujúci zoznam ekvivalentných infinitezimálov:

~
pri
; (1)

~ v ; (2)

~
v ; (3)

~ v ; (4)

~ v ; (5)

~ v ; (6)

~ v ; (7)

~ p v ; (8)

~ pri
; (9)

~
v . (10)

Tu a nemusia byť nezávislé premenné, ale funkcie
A
sklon k nule a jednotke pre niektoré správanie X. Napríklad,

~
pri
,

~
pri
.

Ekvivalencia (1) je ďalšou formou zápisu prvej pozoruhodnej limity. Ekvivalencie (2), (3), (6) a (7) možno dokázať priamo. Ekvivalencia (4) sa získa z (1) s prihliadnutím na vlastnosť 2) ekvivalencií:

~
.

Podobne (5) a (7) sa získajú z (2) a (6). Naozaj

~
,

~
.

Ekvivalencia (8) je dokázaná postupnou aplikáciou (7) a (6):

a (9) a (10) sa získajú z (6) a (8) nahradením
.

3.11.2. Veta. Pri výpočte limitov v súčine a pomere môžete zmeniť funkcie na ekvivalentné. Totiž, ak ~
, potom buď obidve limity neexistujú súčasne, a
alebo obe tieto limity neexistujú súčasne.

Dokážme prvú rovnosť. Nech jeden z limitov povie,
existuje. Potom

3.11.3. Nech ( je číslo alebo symbol,
alebo
). Budeme uvažovať o správaní rôznych b.m. funkcie (takto budeme skracovať výraz infinitezimálne).

DEFINÍCIE.
a nazývajú sa ekvivalentné b.m. funkcie pre , ak
(na ).

budeme to nazývať b.m. viac vysoký poriadok než b.m. funkciu
, Ak
(na ).

3.11.4. Ak a ekvivalentné b.m. funkcie teda
je tam b.m. funkcia vyššieho rádu ako
a čo. - b.m. funkcia at, v ktorej sa pre všetky x a ak v tomto bode funkcia nazýva odstrániteľný bod diskontinuity. má diskontinuitu druhého druhu. Samotná pointa Test

Na kolokvium. Sekcie: " Limit A kontinuitafunkcie platné premenná" funkciejedenpremenná", „Diferenciálny počet funkcie niekoľko premenné"

Témy a príklady testov a otázok (testy kolokvium individuálnych štandardných výpočtov) 1. semestrálny test č. 1 časť „limita a spojitosť funkcie reálnej premennej“

Test

Na kolokvium. Sekcie: " Limit A kontinuitafunkcie platné premenná", „Diferenciálny počet funkciejedenpremenná", „Diferenciálny počet funkcie niekoľko premenné". Poradie čísel...

Test

Témy a príklady testových zadaní a otázok (testové práce individuálne kolokvium štandardných výpočtov) 1. semestr testová práca časť „limita a spojitosť funkcie reálnej premennej“

Test

Prednáška 19 limita a spojitosť funkcie viacerých premenných

Prednáška

... Limit A kontinuitafunkcie niekoľko premenné. 19.1. koncepcia funkcie niekoľko premenné. Revíziou funkcie niekoľko premenné... vlastnosti funkciejedenpremenlivý, nepretržitý na segmente. Pozri Vlastnosti funkcie, nepretržitý na...

Kontinuita funkcie. Body zlomu.

Býk kráča, kolíše, vzdychá, keď ide:
- Oh, doska sa míňa, teraz spadnem!

V tejto lekcii budeme skúmať koncept spojitosti funkcie, klasifikáciu bodov diskontinuity a spoločného praktický problém štúdie kontinuity funkcií. Už zo samotného názvu témy mnohí intuitívne hádajú, o čom sa bude diskutovať, a myslia si, že materiál je celkom jednoduchý. Toto je pravda. No práve jednoduché úlohy sú najčastejšie trestané za zanedbanie a povrchný prístup k ich riešeniu. Preto vám odporúčam, aby ste si článok veľmi pozorne preštudovali a pochytili všetky jemnosti a techniky.

Čo potrebujete vedieť a vedieť? Nie veľmi. Aby ste sa dobre naučili lekciu, musíte pochopiť, čo to je limit funkcie. Pre čitateľov s nízkou úrovňou prípravy stačí článok pochopiť Funkčné limity. Príklady riešení a pozerať sa geometrický význam limit v príručke Grafy a vlastnosti elementárnych funkcií. Je tiež vhodné zoznámiť sa s geometrické transformácie grafov, pretože prax vo väčšine prípadov zahŕňa konštrukciu výkresu. Vyhliadky sú pre každého optimistické a aj plná kanvica si s úlohou poradí sama za hodinu či dve!

Kontinuita funkcie. Hraničné body a ich klasifikácia

Koncept kontinuity funkcie

Zoberme si nejakú funkciu, ktorá je spojitá na celej číselnej osi:

Alebo, aby sme to povedali stručnejšie, naša funkcia je nepretržite zapnutá (set reálne čísla).

Aké je „filistínske“ kritérium kontinuity? Je zrejmé, že graf spojitej funkcie možno nakresliť bez toho, aby sme zdvihli ceruzku z papiera.

V tomto prípade je potrebné tieto dve veci jasne odlíšiť jednoduché koncepty: doména funkcie A kontinuita funkcie. Všeobecne nie je to to isté. Napríklad:

Táto funkcia definované na celom číselnom rade, teda pre každý Význam „x“ má svoj vlastný význam „y“. Najmä ak , tak . Všimnite si, že druhý bod je interpunkčný, pretože podľa definície funkcie musí hodnota argumentu zodpovedať jediná vec funkčná hodnota. teda doména naša funkcia: .

Avšak táto funkcia nie je nepretržite zapnutá! Je celkom zrejmé, že v tejto chvíli trpí medzera. Výraz je tiež celkom zrozumiteľný a vizuálny, tu bude treba ceruzku odtrhnúť z papiera. O niečo neskôr sa pozrieme na klasifikáciu bodov zlomu.

Spojitosť funkcie v bode a na intervale

V konkrétnom matematickom probléme môžeme hovoriť o spojitosti funkcie v bode, o spojitosti funkcie na intervale, polovičnom intervale alebo o spojitosti funkcie na segmente. teda neexistuje žiadna „len kontinuita“– funkcia môže byť NIEKDE nepretržitá. A základným „stavebným kameňom“ všetkého ostatného je kontinuita funkcie v bode .

Teória matematickej analýzy poskytuje definíciu kontinuity funkcie v bode pomocou susedstiev „delta“ a „epsilon“, ale v praxi sa používa iná definícia, ktorej budeme venovať veľkú pozornosť.

Najprv si spomeňme jednostranné limity ktorí nám vtrhli do života na prvej lekcii o funkčných grafoch. Zvážte každodennú situáciu:

Ak sa priblížime k osi k bodu vľavo(červená šípka), potom zodpovedajúce hodnoty „hier“ prejdú pozdĺž osi k bodu (karmínová šípka). Matematicky je táto skutočnosť fixná pomocou ľavý limit:

Venujte pozornosť zadávaniu (číta sa „x inklinuje ku ka vľavo“). Symbol „aditívum“ „mínus nula“. , v podstate to znamená, že sa k číslu blížime z ľavej strany.

Podobne, ak sa priblížite k bodu „ka“ napravo (modrá šípka), potom „hry“ dosiahnu rovnakú hodnotu, ale pozdĺž zelenej šípky a pravostranný limit bude formátovaný nasledovne:

Symbolizuje „aditívum“. a záznam znie: „x má tendenciu ku ka vpravo.“

Ak sú jednostranné limity konečné a rovné(ako v našom prípade): , potom povieme, že existuje VŠEOBECNÝ limit. Je to jednoduché, všeobecný limit je náš „obvyklý“ limit funkcie, rovná sa konečnému číslu.

Všimnite si, že ak funkcia nie je definovaná v (vyčnievať čiernu bodku na vetve grafu), vyššie uvedené výpočty zostávajú v platnosti. Ako už bolo niekoľkokrát uvedené, najmä v článku na infinitezimálnych funkciách, výrazy znamenajú, že "x" nekonečne blízko sa približuje k bodu, pričom NEZÁLEŽÍ, či je samotná funkcia definovaná v danom bode alebo nie. Dobrý príklad nájdete v nasledujúcom odseku, keď je funkcia analyzovaná.

Definícia: funkcia je spojitá v bode, ak sa limita funkcie v danom bode rovná hodnote funkcie v tomto bode: .

Definícia je podrobne uvedená v nasledujúcich pojmoch:

1) Funkcia musí byť definovaná v bode, to znamená, že hodnota musí existovať.

2) Musí existovať všeobecný limit funkcie. Ako je uvedené vyššie, znamená to existenciu a rovnosť jednostranných limitov: .

3) Limita funkcie v danom bode sa musí rovnať hodnote funkcie v tomto bode: .

Ak dôjde k porušeniu aspoň jeden z troch podmienok, potom funkcia stráca vlastnosť spojitosti v bode .

Spojitosť funkcie v intervale je formulovaná dômyselne a veľmi jednoducho: funkcia je spojitá na intervale, ak je spojitá v každom bode daného intervalu.

Najmä mnohé funkcie sú spojité na nekonečnom intervale, teda na množine reálnych čísel. Toto je lineárna funkcia, polynómy, exponenciála, sínus, kosínus atď. A vo všeobecnosti elementárna funkcia nepretržite na svojom doména definície, napríklad, logaritmická funkcia je spojitá na intervale . Dúfajme, že už máte celkom dobrú predstavu o tom, ako vyzerajú grafy základných funkcií. Viac detailné informácie o ich kontinuite sa môžeme dozvedieť od láskavého muža menom Fichtenholtz.

Pri kontinuite funkcie na segmente a polovičných intervaloch tiež nie je všetko ťažké, ale je vhodnejšie o tom hovoriť v triede o nájdení minimálnych a maximálnych hodnôt funkcie na segmente, ale zatiaľ sa tým netrápme.

Klasifikácia bodov zlomu

Fascinujúci život funkcií je bohatý na všemožné špeciálne body a body zlomu sú len jednou zo stránok ich biografie.

Poznámka : pre každý prípad sa zastavím pri elementárnom bode: bod zlomu je vždy jediný bod– neexistuje „niekoľko bodov prerušenia za sebou“, to znamená, že neexistuje nič také ako „interval prestávky“.

Tieto body sú zase rozdelené do dvoch veľkých skupín: prietrže prvého druhu A prietrže druhého druhu. Každý typ medzery má svoje vlastné vlastnosti na ktoré sa teraz pozrieme:

Bod diskontinuity prvého druhu

Ak je v určitom bode porušená podmienka kontinuity a jednostranné limity konečný , potom sa volá bod diskontinuity prvého druhu.

Začnime tým najoptimistickejším prípadom. Podľa pôvodnej myšlienky lekcie som chcel povedať teóriu „v všeobecný pohľad“, ale aby som demonštroval reálnosť materiálu, rozhodol som sa pre možnosť s konkrétnymi postavami.

Smutné, ako fotka novomanželov v pozadí Večný plameň, ale nasledujúci rámec je všeobecne akceptovaný. Znázornime graf funkcie na výkrese:

Táto funkcia je súvislá na celej číselnej osi okrem bodky. A v skutočnosti sa menovateľ nemôže rovnať nule. V súlade s významom limitu však môžeme nekonečne blízko priblížiť sa k „nule“ zľava aj sprava, to znamená, že existujú jednostranné limity a samozrejme sa zhodujú:
(Podmienka č. 2 kontinuity je splnená).

Funkcia však nie je v bode definovaná, preto je porušená podmienka č. 1 spojitosti a funkcia v tomto bode trpí diskontinuitou.

Prestávka tohto typu (s existujúcim všeobecný limit) sa volajú opraviteľná medzera. Prečo odnímateľné? Pretože funkcia môže predefinovať v bode zlomu:

Vyzerá to zvláštne? Možno. Ale takýto zápis funkcie ničomu neodporuje! Teraz je medzera uzavretá a všetci sú šťastní:

Vykonajte formálnu kontrolu:

2) – existuje všeobecný limit;
3)

Všetky tri podmienky sú teda splnené a funkcia je spojitá v bode podľa definície spojitosti funkcie v bode.

Neprajníci matanov však môžu funkciu definovať napríklad zle :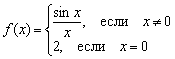

Je zaujímavé, že prvé dve podmienky kontinuity sú tu splnené:
1) – funkcia je definovaná v danom bode;
2) – existuje všeobecný limit.

Tretia hranica však neprešla: , čiže limita funkcie v bode nerovná sa hodnota danej funkcie v danom bode.

V určitom bode teda funkcia trpí diskontinuitou.

Druhý, smutnejší prípad je tzv prasknutie prvého druhu s výskokom. A smútok vyvolávajú jednostranné limity, ktoré konečný a odlišný. Príklad je uvedený na druhom výkrese lekcie. Takáto medzera sa zvyčajne vyskytuje v po častiach definované funkcie, ktoré už boli v článku spomenuté o grafových transformáciách.

Zvážte funkciu po častiach a dokreslíme jej kresbu. Ako zostaviť graf? Veľmi jednoduché. V polovičnom intervale nakreslíme fragment paraboly ( zelená farba), na intervale – priamka (červená) a na polovičnom intervale – priamka (modrá).

Navyše kvôli nerovnosti je hodnota určená pre kvadratickú funkciu (zelená bodka) a kvôli nerovnosti je hodnota určená pre lineárna funkcia(modrá bodka):

V najťažšom prípade by ste sa mali uchýliť k bodovej konštrukcii každej časti grafu (pozri prvý lekciu o grafoch funkcií).

Teraz nás bude zaujímať len pointa. Pozrime sa na kontinuitu:

2) Vypočítajme jednostranné limity.

Na ľavej strane máme segment červenej čiary, takže ľavostranný limit je:

Vpravo je modrá priamka a pravý limit:

V dôsledku toho sme dostali konečné čísla, a oni nerovná sa. Od jednostranných limitov konečný a odlišný: , potom naša funkcia toleruje diskontinuita prvého druhu so skokom.

Je logické, že medzeru nie je možné odstrániť – funkciu naozaj nemožno ďalej definovať a „zlepiť“, ako v predchádzajúcom príklade.

Body diskontinuity druhého druhu

Zvyčajne sú všetky ostatné prípady prasknutia šikovne zaradené do tejto kategórie. Nebudem uvádzať všetko, pretože v praxi sa stretnete s 99% problémov nekonečná medzera– keď je ľavák alebo pravák, a častejšie, obe hranice sú nekonečné.

A, samozrejme, najzrejmejším obrazom je hyperbola v bode nula. Tu sú obe jednostranné limity nekonečné: , preto funkcia trpí diskontinuitou druhého druhu v bode .

Svoje články sa snažím napĺňať čo najrozmanitejším obsahom, preto sa pozrime na graf funkcie, s ktorou sa ešte nestretla:

podľa štandardnej schémy:

1) Funkcia nie je v tomto bode definovaná, pretože menovateľ je nulový.

Samozrejme, okamžite môžeme konštatovať, že funkcia trpí diskontinuitou v bode , ale bolo by dobré klasifikovať povahu diskontinuity, ktorú si podmienka často vyžaduje. Pre to:

Dovoľte mi pripomenúť, že nahrávaním myslíme nekonečne malý záporné číslo a pod položkou - nekonečne malé kladné číslo.

Jednostranné limity sú nekonečné, čo znamená, že funkcia trpí diskontinuitou 2. druhu v bode . Os y je vertikálna asymptota pre graf.

Nie je nezvyčajné, že existujú obe jednostranné limity, ale iba jedna z nich je nekonečná, napríklad:

Toto je graf funkcie.

Skúmame bod kontinuity:

1) Funkcia nie je v tomto bode definovaná.

2) Vypočítajme jednostranné limity:

O spôsobe výpočtu takýchto jednostranných limitov si povieme v posledných dvoch príkladoch prednášky, hoci mnohí čitatelia už všetko videli a uhádli.

Ľavá limita je konečná a rovná sa nule („neideme k samotnému bodu“), ale pravá limita je nekonečná a oranžová vetva grafu sa nekonečne blíži k jej vertikálna asymptota, daný rovnicou(čierna bodkovaná čiara).

Takže funkcia trpí nespojitosť druhého druhu v bode .

Pokiaľ ide o diskontinuitu 1. druhu, funkcia môže byť definovaná v samotnom bode diskontinuity. Napríklad pre funkciu po častiach Neváhajte a umiestnite čiernu tučnú bodku na začiatok súradníc. Vpravo je vetva hyperboly a pravá hranica je nekonečná. Myslím, že takmer každý má predstavu o tom, ako tento graf vyzerá.

Na čo sa všetci tešili:

Ako skúmať spojitosť funkcie?

Štúdium funkcie kontinuity v bode sa vykonáva podľa už zavedenej rutinnej schémy, ktorá pozostáva z kontroly troch podmienok kontinuity:

Príklad 1

Funkcia Preskúmať

Riešenie:

1) Jediným bodom v rozsahu je, kde funkcia nie je definovaná.

2) Vypočítajme jednostranné limity:

Jednostranné limity sú konečné a rovnaké.

V tomto bode teda funkcia trpí odstrániteľnou diskontinuitou.

Ako vyzerá graf tejto funkcie?

Chcel by som to zjednodušiť a zdá sa, že sa získa obyčajná parabola. ALE pôvodná funkcia nie je definovaná v bode , preto sa vyžaduje nasledujúca klauzula:

Urobme výkres:

Odpoveď: funkcia je spojitá na celej číselnej osi okrem bodu, v ktorom trpí odstrániteľnou diskontinuitou.

Funkcia môže byť ďalej definovaná dobre alebo nie tak dobre, ale podľa podmienky to nie je potrebné.

Hovoríte, že toto je pritiahnutý príklad? Vôbec nie. V praxi sa to stalo desiatky krát. Takmer všetky úlohy stránky pochádzajú zo skutočnej nezávislej práce a testov.

Poďme sa zbaviť našich obľúbených modulov:

Príklad 2

Funkcia Preskúmať pre kontinuitu. Určte povahu diskontinuít funkcií, ak existujú. Vykonajte výkres.

Riešenie: Študenti sa z nejakého dôvodu boja a nemajú radi funkcie s modulom, hoci na nich nie je nič zložité. Takýchto vecí sme sa už v lekcii trochu dotkli. Geometrické transformácie grafov. Keďže modul nie je záporný, rozširuje sa takto: , kde „alfa“ je nejaký výraz. V tomto prípade a naša funkcia by mala byť napísaná po častiach:

Ale zlomky oboch kusov musia byť znížené o . Zníženie, ako v predchádzajúcom príklade, sa nezaobíde bez následkov. Pôvodná funkcia nie je v bode definovaná, pretože menovateľ je nulový. Preto by mal systém dodatočne špecifikovať podmienku a sprísniť prvú nerovnosť:

Teraz o VEĽMI UŽITOČNEJ technike rozhodovania: pred finalizáciou úlohy na návrhu je výhodné urobiť výkres (bez ohľadu na to, či to vyžadujú podmienky alebo nie). To vám po prvé pomôže okamžite vidieť body kontinuity a body diskontinuity a po druhé vás to 100% ochráni pred chybami pri hľadaní jednostranných limitov.

Urobme kresbu. V súlade s našimi výpočtami je vľavo od bodu potrebné nakresliť fragment paraboly (modrá farba) a vpravo - kúsok paraboly (červená farba), pričom funkcia nie je definovaná na bod sám o sebe:

Ak máte pochybnosti, zoberte niekoľko hodnôt x a zapojte ich do funkcie (pamätajte na to, že modul zničí možné znamienko mínus) a skontrolujte graf.

Analyticky preskúmame funkciu spojitosti:

1) Funkcia nie je v bode definovaná, takže môžeme hneď povedať, že v ňom nie je spojitá.

2) Stanovme povahu diskontinuity, aby sme to urobili, vypočítame jednostranné limity:

Jednostranné limity sú konečné a rôzne, čo znamená, že funkcia trpí diskontinuitou 1. druhu so skokom v bode . Opäť si všimnite, že pri hľadaní limity nezáleží na tom, či je funkcia v bode zlomu definovaná alebo nie.

Teraz už len ostáva preniesť kresbu z predlohy (bola urobená akoby pomocou výskumu ;-)) a dokončiť úlohu:

Odpoveď: funkcia je spojitá na celej číselnej osi okrem bodu, v ktorom trpí diskontinuitou prvého druhu so skokom.

Niekedy vyžadujú dodatočnú indikáciu skoku diskontinuity. Vypočítava sa jednoducho - od pravej limity treba odčítať ľavú limitu: , čiže v bode zlomu naša funkcia skočila o 2 jednotky dole (ako nám hovorí znamienko mínus).

Príklad 3

Funkcia Preskúmať pre kontinuitu. Určte povahu diskontinuít funkcií, ak existujú. Urobte si kresbu.

Toto je príklad pre nezávislé rozhodnutie, vzorové riešenie na konci lekcie.

Prejdime k najobľúbenejšej a najrozšírenejšej verzii úlohy, keď sa funkcia skladá z troch častí:

Príklad 4

Preskúmajte spojitosť funkcie a nakreslite graf funkcie .

Riešenie: je zrejmé, že všetky tri časti funkcie sú spojité na zodpovedajúcich intervaloch, takže zostáva skontrolovať iba dva body „spojnice“ medzi dielikmi. Najprv si urobme návrh výkresu, ktorý som dostatočne podrobne komentoval v prvej časti článku. Jediná vec je, že musíme starostlivo sledovať naše singulárne body: kvôli nerovnosti patrí hodnota do priamky (zelená bodka) a kvôli nerovnosti hodnota patrí do paraboly (červená bodka):

V zásade je všetko jasné =) Zostáva len formalizovať rozhodnutie. Pre každý z dvoch „spojovacích“ bodov štandardne kontrolujeme 3 podmienky kontinuity:

ja) Skúmame bod kontinuity

Jednostranné limity sú konečné a rôzne, čo znamená, že funkcia trpí diskontinuitou 1. druhu so skokom v bode .

Vypočítajme skok diskontinuity ako rozdiel medzi pravou a ľavou hranicou:
, to znamená, že sa graf trhol o jednu jednotku nahor.

II) Skúmame bod kontinuity

1) – funkcia je definovaná v danom bode.

2) Nájdite jednostranné limity:

– jednostranné limity sú konečné a rovnaké, čo znamená, že existuje všeobecný limit.

3) – limita funkcie v bode sa rovná hodnote tejto funkcie v danom bode.

V záverečnej fáze prenesieme kresbu do konečnej verzie, po ktorej vložíme posledný akord:

Odpoveď: funkcia je spojitá na celej číselnej osi, okrem bodu, v ktorom trpí nespojitosťou prvého druhu so skokom.

Príklad 5

Preskúmajte spojitosť funkcie a zostrojte jej graf .

Toto je príklad na samostatné riešenie, krátke riešenie a približná ukážka úlohy na konci hodiny.

Môžete nadobudnúť dojem, že v jednom bode musí byť funkcia spojitá a v inom musí existovať diskontinuita. V praxi to tak nie je vždy. Pokúste sa nezanedbávať zostávajúce príklady - bude tu niekoľko zaujímavých a dôležitých funkcií:

Príklad 6

Daná funkcia . Preskúmajte funkciu spojitosti v bodoch. Zostavte graf.

Riešenie: a znova okamžite vykonajte kreslenie na koncepte:

Zvláštnosťou tohto grafu je, že po častiach je funkcia daná rovnicou osi x. Tu je táto oblasť nakreslená zelenou farbou, ale v poznámkovom bloku je zvyčajne zvýraznená tučným písmom jednoduchou ceruzkou. A, samozrejme, nezabudnite na naše barany: hodnota patrí do tangentnej vetvy (červená bodka) a hodnota patrí do priamky.

Z nákresu je všetko jasné - funkcia je súvislá pozdĺž celej číselnej línie, zostáva len formalizovať riešenie, ktoré sa do plnej automatizácie dostane doslova po 3-4 podobných príkladoch:

ja) Skúmame bod kontinuity

1) – funkcia je definovaná v danom bode.

2) Vypočítajme jednostranné limity:

, čo znamená, že existuje všeobecný limit.

Pre každý prípad mi dovoľte pripomenúť triviálny fakt: limita konštanty sa rovná samotnej konštante. V tomto prípade sa hranica nuly rovná samotnej nule (limit pre ľavákov).

3) – limita funkcie v bode sa rovná hodnote tejto funkcie v danom bode.

Funkcia je teda spojitá v bode podľa definície spojitosti funkcie v bode.

II) Skúmame bod kontinuity

1) – funkcia je definovaná v danom bode.

2) Nájdite jednostranné limity:

A tu – hranica jedna sa rovná samotnej jednotke.

– existuje všeobecný limit.

3) – limita funkcie v bode sa rovná hodnote tejto funkcie v danom bode.

Funkcia je teda spojitá v bode podľa definície spojitosti funkcie v bode.

Ako obvykle, po výskume prenášame náš výkres do konečnej verzie.

Odpoveď: funkcia je v bodoch spojitá.

Upozorňujeme, že za podmienky, že sme sa nič nepýtali na štúdium celej funkcie pre spojitosť, a považuje sa to za dobrú matematickú formu na formulovanie presné a jasné odpoveď na položenú otázku. Mimochodom, ak podmienky nevyžadujú, aby ste vytvorili graf, potom máte plné právo ho nezostaviť (hoci vás k tomu môže neskôr učiteľ prinútiť).

Malý matematický „prekrúcač jazyka“, aby ste to vyriešili sami:

Príklad 7

Daná funkcia 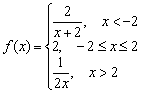. Preskúmajte funkciu spojitosti v bodoch. Klasifikujte body prerušenia, ak existujú. Vykonajte výkres.

Pokúste sa správne „vysloviť“ všetky „slová“ =) A nakreslite graf presnejšie, presnosť, nebude to všade zbytočné;-)

Ako si pamätáte, odporučil som okamžite dokončiť kresbu ako návrh, ale z času na čas narazíte na príklady, kde nemôžete okamžite zistiť, ako graf vyzerá. Preto je v mnohých prípadoch výhodné najskôr nájsť jednostranné limity a až potom na základe štúdie vetvy znázorniť. V posledných dvoch príkladoch sa tiež naučíme techniku výpočtu niektorých jednostranných limitov:

Príklad 8

Preskúmajte spojitosť funkcie a zostrojte jej schematický graf.

Riešenie: zlé body sú zrejmé: (zmenšuje menovateľa exponentu na nulu) a (zmenšuje menovateľa celého zlomku na nulu). Nie je jasné, ako vyzerá graf tejto funkcie, čo znamená, že je lepšie najprv urobiť prieskum.

Topológia– odvetvie matematiky, ktoré sa zaoberá štúdiom limity a spojitosti funkcií. V kombinácii s algebrou tvorí topológia všeobecný základ matematiky.

Topologický priestor alebo obrazec – podmnožina nášho homogénneho euklidovského priestoru, medzi bodmi ktorého je daný určitý vzťah blízkosti. Postavy tu nie sú považované za tuhé telesá, ale za predmety vyrobené akoby z veľmi elastickej gumy, umožňujúcej nepretržitú deformáciu, ktorá zachováva ich kvalitatívne vlastnosti.

Nazýva sa spojité mapovanie obrazcov jedna ku jednej homeomorfizmus. Inými slovami, čísla homeomorfný, ak je možné jednu preniesť na druhú kontinuálnou deformáciou.

Príklady. Nasledujúce obrázky sú homeomorfné (postavy z rôznych skupín nie sú homeomorfné), znázornené na obr. 2.

1. Segment a krivka bez vlastných priesečníkov.

2. Kruh, vnútro štvorca, stuha.

3. Guľa, povrch kocky a štvorstenu.

4. Kruh, elipsa a zauzlený kruh.

5. Krúžok na rovine (kruh s otvorom), krúžok v priestore, dvakrát skrútený krúžok, bočná plocha valca.

6. Möbiov pás, t.j. raz skrútený prsteň a trikrát skrútený prsteň.

7. Povrch torusu (donut), guľa s rúčkou a zauzlený torus.

8. Guľa s dvoma rúčkami a praclík s dvoma otvormi.

IN matematická analýza funkcie sa študujú metódou limít. Premenná a limit sú základné pojmy.

Pri rôznych javoch si niektoré veličiny zachovávajú svoju číselnú hodnotu, iné sa menia. Volá sa množina všetkých číselných hodnôt premennej oblasť zmeny tejto premennej.

Z rôznych spôsobov, ako sa premenná správa, je najdôležitejší ten, pri ktorom premenná smeruje k určitej hranici.

Konštantné číslo a volal variabilný limit, ak absolútna hodnota rozdielu medzi X A a() sa stáva v procese zmeny premennej hodnoty X podľa želania malé:

Čo znamená „tak malý, ako sa vám páči“? Variabilná hodnota X inklinuje k limitu A, ak pre ľubovoľne malé (ľubovoľne malé) číslo existuje taký moment pri zmene premennej X, od ktorej nerovnosť platí .

Definícia limity má jednoduchý geometrický význam: nerovnosť znamená to X je v susedstve bodu a, tie. v intervale .

Definícia limitu teda môže byť uvedená v geometrický tvar:

číslo A je limit premennej X, ak pre ľubovoľne malé (ľubovoľne malé) -okolie čísla A môžete určiť taký moment pri zmene premennej X, od ktorého všetky jeho hodnoty spadajú do určeného susedstva bodu A.

Komentujte. Variabilná hodnota X sa môže priblížiť k svojej hranici rôznymi spôsobmi: zostať pod touto hranicou (vľavo), viac (vpravo), kolísať okolo hodnoty hranice.

Limit sekvencie

Funkcia nazývaný zákon (pravidlo), podľa ktorého každý prvok X nejaká sada X zhoduje sa s jedným prvkom r súpravy Y.

Funkciu možno definovať na množine všetkých prirodzených čísel: . Táto funkcia sa nazýva funkcia prirodzeného argumentu alebo číselná postupnosť.

Keďže postupnosť, ako každá nekonečná množina, nemôže byť špecifikovaná enumeráciou, je špecifikovaná spoločným výrazom: , kde je všeobecný člen postupnosti.

Diskrétna premenná je bežným pojmom sekvencie.

Kvôli konzistencii slová „začínajúce v určitom bode“ znamenajú slová „začínajúce v určitom čísle“.

číslo A nazývaná limita postupnosti , ak pre ľubovoľne malé (ľubovoľne malé) číslo také číslo existuje N, ktorá pre všetky členy postupnosti s číslom n>N nerovnosť platí .

alebo pri .

Geometricky znamená definícia limity postupnosti toto: pre ľubovoľne malé (ľubovoľne malé) - susedstvo čísla A existuje číslo také, že všetky členy postupnosti s väčším ako N, čísla, spadajú do tejto blízkosti. Mimo susedstva sa objavuje len konečný počet počiatočných členov postupnosti. Prirodzené číslo N záleží na : .