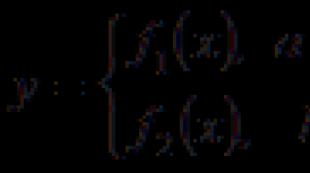Matematická analýza.

Dielňa.

Pre študentov vysokých škôl v odbore:

"Štátna a mestská správa"

T.Z. Pavlova

Kolpaševo 2008

Kapitola 1. Úvod do analýzy

1.1 Funkcie. Všeobecné vlastnosti

1.2 Teória limitov

1.3 Kontinuita funkcie

2.1 Definícia derivátu

2.4 Skúmanie funkcií

2.4.1 Plne funkčný študijný plán

2.4.2 Príklady štúdie funkcií

2.4.3. Najväčšia a najmenšia hodnota funkcie na segmente

2.5 L'Hôpitalovo pravidlo

3.1 Neurčitý integrál

3.1.1 Definície a vlastnosti

3.1.2 Tabuľka integrálov

3.1.3 Základné metódy integrácie

3.2 Určitý integrál

3.2.2 Metódy výpočtu určitého integrálu

Kapitola 4. Funkcie viacerých premenných

4.1 Základné pojmy

4.2 Limity a spojitosť funkcií viacerých premenných

4.3.3 Celkový diferenciál a jeho aplikácia na približné výpočty

Kapitola 5. Klasické optimalizačné metódy

6.1 Užitočná funkcia.

6.2 Línie ľahostajnosti

6.3 Stanovený rozpočet

Domáce úlohy

1.1 Funkcie. Všeobecné vlastnosti

Numerická funkcia je definovaná na množine D reálnych čísel, ak každá hodnota premennej je spojená s nejakou dobre definovanou reálnou hodnotou premennej y, kde D je definičný obor funkcie.

Analytické znázornenie funkcie:

výslovne:;

implicitne:;

v parametrickej forme:

rôzne vzorce v oblasti definície:

Vlastnosti.

Rovnomerná funkcia:. Napríklad funkcia je párna, od r ...

Neobvyklá funkcia: ... Napríklad funkcia je nepárna, pretože ...

Periodická funkcia: , kde T je perióda funkcie,. Napríklad goniometrické funkcie.

Monotónna funkcia. Ak pre niektorú z definičných domén - funkcia je rastúca, - klesajúca. Napríklad - zvýšenie a - zníženie.

Obmedzená funkcia. Ak existuje číslo M také, že. Napríklad funkcie a od r .

Príklad 1. Nájdite definičný obor funkcií.

+ 2 – 3 +

1.2 Teória limitov

Definícia 1... Limita funkcie at je číslo b, ak pre ľubovoľné (- ľubovoľne malé kladné číslo) možno nájsť takú hodnotu argumentu, od ktorej je nerovnosť splnená.

Označenie:.

Definícia 2... Limita funkcie v je číslo b, ak pre ľubovoľné (je ľubovoľne malé kladné číslo) existuje kladné číslo také, že pre všetky hodnoty x spĺňajúce nerovnosť platí nerovnosť.

Označenie:.

Definícia 3. Funkcia sa nazýva infinitezimálna pre alebo, ak alebo.

Vlastnosti.

1. Algebraický súčet konečného počtu nekonečne malých veličín je nekonečne malá veličina.

2. Súčin nekonečne malej veličiny ohraničenou funkciou (konštanta, iná nekonečne malá veličina) je nekonečne malá veličina.

3. Podiel delenia nekonečne malej veličiny funkciou, ktorej limita je nenulová, je nekonečne malá veličina.

Definícia 4. Funkcia sa nazýva nekonečne veľká v, ak.

Vlastnosti.

1. Súčin nekonečne veľkej veličiny funkciou, ktorej limita je nenulová, je nekonečne veľká veličina.

2. Súčet nekonečne veľkej hodnoty a ohraničenej funkcie je nekonečne veľká hodnota.

3. Podiel delenia nekonečne veľkej veličiny funkciou, ktorá má limitu, je nekonečne veľká veličina.

Veta.(Vzťah medzi nekonečne malým množstvom a nekonečne veľkým množstvom.) Ak je funkcia nekonečne malá v (), potom je funkcia nekonečne veľká veličina v (). A naopak, ak je funkcia nekonečne veľká v (), potom je funkcia nekonečne malá v ().

Limitné vety.

1. Funkcia nemôže mať viac ako jednu hranicu.

2. Limita algebraického súčtu viacerých funkcií sa rovná algebraickému súčtu limitov týchto funkcií:

3. Limita súčinu viacerých funkcií sa rovná súčinu limity týchto funkcií:

4. Hranica stupňa sa rovná stupňu hranice:

5. Podielová limita sa rovná podielu limitov, ak existuje limita deliteľa:

.

6. Prvá pozoruhodná hranica.

Dôsledky:

7. Druhý pozoruhodný limit:

Dôsledky:

Ekvivalentné nekonečne malé hodnoty pre:

Výpočet limitov.

Pri výpočte limity sa využívajú základné vety o limitách, vlastnosti spojitých funkcií a pravidlá vyplývajúce z týchto viet a vlastností.

Pravidlo 1. Na nájdenie limity v bode funkcie, ktorá je v tomto bode spojitá, je potrebné namiesto argumentu x dosadiť jej limitnú hodnotu vo funkcii pod znamienkom limity.

Príklad 2. Nájdite

Pravidlo 2. Ak je pri hľadaní limity zlomku limita menovateľa nula a limita čitateľa nenulová, potom limita takejto funkcie je.

Príklad 3. Nájdite

Pravidlo 3. Ak sa pri hľadaní limity zlomku limita menovateľa rovná a limita čitateľa je iná ako nula, potom je limita takejto funkcie nula.

Príklad 4. Nájdite

Nahradenie argumentu limitnou hodnotou často vedie k nedefinovaným výrazom ako

.

Nájdenie limity funkcie sa v týchto prípadoch nazýva zverejnenie neistoty. Na odhalenie neistoty je potrebné tento výraz pred prechodom na limit transformovať. Na odhalenie neistôt sa používajú rôzne techniky.

Pravidlo 4... Neistotu typu odhalíme transformáciou podlimitnej funkcie, teda za účelom výberu činiteľa v čitateli a menovateli, ktorého limita je nula, a zmenšením zlomku o ňu nájsť limitu kvocientu. Na tento účel sa čitateľ a menovateľ buď vynásobia alebo vynásobia výrazmi spojenými s čitateľom a menovateľom.

Pravidlo 5. Ak podlimitný výraz obsahuje goniometrické funkcie, potom sa prvý pozoruhodný limit použije na odhalenie neistoty druhu.

.

Pravidlo 6... Na odhalenie neurčitosti tvaru at je potrebné vydeliť čitateľa a menovateľa podlimitného zlomku najvyšším stupňom argumentu a následne nájsť limitu kvocientu.

Možné výsledky:

1) požadovaná hranica sa rovná pomeru koeficientov pri najvyšších mocninách argumentu čitateľa a menovateľa, ak sú tieto stupne rovnaké;

2) limita sa rovná nekonečnu, ak je stupeň argumentu čitateľa vyšší ako stupeň argumentu menovateľa;

3) limit je nula, ak je stupeň argumentu čitateľa nižší ako stupeň argumentu menovateľa.

a)

odkedy

Stupne sú rovnaké, čo znamená, že hranica sa rovná pomeru koeficientov na vyšších stupňoch, t.j. ...

b)

Stupeň čitateľa, menovateľ je 1, čo znamená, že limit je

v)

Stupeň čitateľa je 1, stupeň menovateľa je, takže limit je 0.

Pravidlo 7... Na odhalenie neurčitosti tvaru treba čitateľa a menovateľa podlimitného zlomku vynásobiť konjugovaným výrazom.

Príklad 10.

Pravidlo 8... Druhý pozoruhodný limit a jeho dôsledky sa používajú na odhalenie neistoty druhu.

Dá sa to dokázať

Príklad 11.

Príklad 12.

Príklad 13.

Pravidlo 9... Pri odhaľovaní neistôt, ktorých podprahová funkcia obsahuje infinitezimálu, je potrebné nahradiť limity týchto nekonečna. na hraniciach im ekvivalentných nekonečne malých prvkov.

Príklad 14.

Príklad 15.

Pravidlo 10. L'Hôpitalovo pravidlo (pozri 2.6).

1.3 Kontinuita funkcie

Funkcia je spojitá v bode, ak limita funkcie ako argument smeruje k a, existuje a rovná sa hodnote funkcie v tomto bode.

Ekvivalentné podmienky:

1. ;

3.

Klasifikácia bodov zlomu:

prestávka prvého druhu

Jednorazové - jednostranné limity existujú a sú rovnaké;

Fatálny (skok) - jednostranné limity nie sú rovnaké;

diskontinuita druhého druhu: limita funkcie v bode neexistuje.

Príklad 16. Stanovte povahu diskontinuity funkcie v bode alebo dokážte spojitosť funkcie v tomto bode.

pretože funkcia nie je definovaná, preto v tomto bode nie je spojitá. Pretože a zodpovedajúcim spôsobom, , potom je bodom odstrániteľnej diskontinuity prvého druhu.

b)

v porovnaní s úlohou (a) je funkcia rozšírená v bode tak, že , preto je táto funkcia v tomto bode spojitá.

Keď funkcia nie je definovaná;

.

Pretože jedna z jednostranných limitov je nekonečná, potom je to bod zlomu druhého druhu.

Kapitola 2. Diferenciálny počet

2.1 Definícia derivátu

Definícia derivátu

Derivácia alebo derivácia danej funkcie je limit pomeru prírastku funkcie k prírastku zodpovedajúceho argumentu, keď má prírastok argumentu tendenciu k nule:

Alebo .

Mechanický význam derivácie je rýchlosť zmeny funkcie. Geometrický význam derivácie je tangens uhla sklonu dotyčnice ku grafu funkcie:

2.2 Základné pravidlá pre rozlišovanie

názov	Funkcia	Derivát
Násobenie konštantným faktorom
Algebraický súčet dvoch funkcií
Produkt dvoch funkcií
Súkromné ​​dve funkcie
Komplexná funkcia

Deriváty základných elementárnych funkcií

P / p č.	Názov funkcie	Funkcia a jej derivácia
1	konštantný
2	výkonová funkcia špeciálne prípady
3	exponenciálna funkcia špeciálny prípad
4	logaritmická funkcia špeciálny prípad
5	goniometrické funkcie
6	obrátene trigonometrické

b)

2.3 Deriváty vyššieho rádu

Derivácia funkcie druhého rádu

Derivácia funkcie druhého rádu:

Príklad 18.

a) Nájdite deriváciu druhého rádu funkcie.

Riešenie. Najprv nájdime deriváciu prvého rádu .

Zoberme si derivát derivátu prvého rádu.

Príklad 19. Nájdite deriváciu tretieho rádu funkcie.

2.4 Skúmanie funkcií

2.4.1 Plán kompletnej funkčnej štúdie:

Plne funkčný študijný plán:

1. Základný výskum:

Nájdite doménu a rozsah hodnôt;

Zistite všeobecné vlastnosti: parita (nepárnosť), periodicita;

Nájdite priesečníky so súradnicovými osami;

Určite oblasti stálosti.

2. Asymptoty:

Nájdite vertikálne asymptoty if;

Nájdite šikmé asymptoty:.

Ak nejaké číslo, potom - horizontálne asymptoty.

3. Výskum pomocou:

Nájdite kritické body, tie. body, v ktorých alebo neexistujú;

Určte intervaly zvyšovania, tie. intervaly, v ktorých a klesajúce funkcie -;

Určte extrémy: body, pri ktorých prechádza, mení znamienko z „+“ na „-“, sú maximálne body, od „-“ do „+“ - minimum.

4. Výskum pomocou:

Nájdite body, v ktorých alebo neexistujú;

Nájdite oblasti konvexnosti, t.j. intervaly, v ktorých sú konkávnosti;

Nájdite inflexné body, t.j. bodov pri prechode cez ktoré sa mení znamienko.

1. Jednotlivé prvky štúdie sa do grafu vykresľujú postupne tak, ako sa nachádzajú.

2. Ak sa vyskytnú problémy s konštrukciou grafu funkcie, potom sa hodnoty funkcie nachádzajú v niektorých ďalších bodoch.

3. Účelom štúdie je opísať charakter správania sa funkcie. Preto nie je zostavený presný graf, ale jeho aproximácia, na ktorej sú jasne naznačené nájdené prvky (extrémy, inflexné body, asymptoty atď.).

4. Nie je potrebné striktne dodržiavať vyššie uvedený plán; je dôležité neprehliadnuť charakteristické prvky správania funkcie.

2.4.2 Príklady funkčnej štúdie:

1)

2) Funkcia je nepárna:

.

3) Asymptoty.

- vertikálne asymptoty, pretože

Šikmá asymptota.

5)

- inflexný bod.

2) Funkcia je nepárna:

3) Asymptoty: Neexistujú žiadne vertikálne asymptoty.

Naklonený:

- šikmé asymptoty

4) - funkcia sa zvyšuje.

- inflexný bod.

Schematický diagram tejto funkcie:

2) Všeobecná funkcia

3) Asymptoty

- žiadne šikmé asymptoty

- horizontálna asymptota pri

- inflexný bod

Schematický diagram tejto funkcie:

2) Asymptoty.

- vertikálna asymptota, pretože

- žiadne šikmé asymptoty

, - horizontálna asymptota

Schematický diagram tejto funkcie:

2) Asymptoty

- vertikálna asymptota pri, od r

- žiadne šikmé asymptoty

, - horizontálna asymptota

3) - funkcia klesá v každom z intervalov.

Schematický diagram tejto funkcie:

Ak chcete nájsť najväčšiu a najmenšiu hodnotu funkcie v segmente, môžete použiť diagram:

1. Nájdite deriváciu funkcie.

2. Nájdite kritické body funkcie, v ktorých alebo neexistujú.

3. Nájdite hodnotu funkcie v kritických bodoch patriacich do daného segmentu a na jeho koncoch a vyberte najväčší a najmenší z nich.

Príklad. Nájdite najmenšiu a najväčšiu hodnotu funkcie na danom segmente.

25. medzi

2) - kritické body

26. medzi.

Derivácia neexistuje, ale 1 do tohto intervalu nepatrí. Funkcia v intervale klesá, čo znamená, že neexistuje najväčšia hodnota, ale najmenšia hodnota.

2.5 L'Hôpitalovo pravidlo

Veta. Limita pomeru dvoch nekonečne malých alebo nekonečne veľkých funkcií sa rovná limite pomeru ich derivácií (konečných alebo nekonečných), ak tieto v naznačenom zmysle existujú.

Tie. pri zverejňovaní neistôt typu alebo môžete použiť vzorec:

.

27.

Kapitola 3. Integrálny počet

3.1 Neurčitý integrál

3.1.1 Definície a vlastnosti

Definícia 1. Funkcia sa nazýva primitívna pre ak.

Definícia 2. Neurčitý integrál funkcie f (x) je súborom všetkých primitívnych prvkov pre túto funkciu.

Označenie: , kde c je ľubovoľná konštanta.

Neurčité integrálne vlastnosti

1. Derivácia neurčitého integrálu:

2. Diferenciál neurčitého integrálu:

3. Neurčitý integrál diferenciálu:

4. Neurčitý integrál súčtu (rozdielu) dvoch funkcií:

5. Posunutie konštantného činiteľa za znamienko neurčitého integrálu:

3.1.2 Tabuľka integrálov

.1.3 Základné metódy integrácie

1. Použitie vlastností neurčitého integrálu.

Príklad 29.

2. Prinášanie pod diferenciálnym znakom.

Príklad 30.

3. Variabilný spôsob výmeny:

a) náhrada v integráli

kde - funkcia, ktorá sa ľahšie integruje ako pôvodná; - funkcia inverzná k funkcii; je primitívnym derivátom funkcie.

Príklad 31.

b) nahradenie v integráli v tvare:

Príklad 32.

Príklad 33.

4. Metóda integrácie po častiach:

Príklad 34.

Príklad 35.

Zoberme si integrál oddelene

Vráťme sa k nášmu integrálu:

3.2 Určitý integrál

3.2.1 Pojem určitého integrálu a jeho vlastnosti

Definícia. Nech je na nejakom intervale daná spojitá funkcia. Zostavme jej graf.

Obrazec ohraničený zhora krivkou, vľavo a vpravo rovnými čiarami a zdola úsečkou osi x medzi bodmi a a b sa nazýva zakrivený lichobežník.

S - plocha - zakrivený lichobežník.

Rozdeľte interval bodkami a získajte:

Integrálny súčet:

Definícia. Určitý integrál je limita integrálneho súčtu.

Jednoznačné integrálne vlastnosti:

1. Konštantný faktor je možné vyňať zo znamienka integrálu:

2. Integrál algebraického súčtu dvoch funkcií sa rovná algebraickému súčtu integrálov týchto funkcií:

3. Ak je segment integrácie rozdelený na časti, potom sa integrál v celom segmente rovná súčtu integrálov pre každú z častí, ktoré vznikli, tj. pre ľubovoľné a, b, c:

4. Ak na segmente, potom

5. Hranice integrácie sa môžu zamieňať, pričom znamienko integrálu sa mení:

6.

7. Integrál v bode sa rovná 0:

8.

9. („o priemere“) Nech y = f (x) je funkcia integrovateľná na. Potom , kde f (c) je priemerná hodnota f (x) na:

10. Newtonov-Leibnizov vzorec

,

kde F (x) je primitívna derivácia pre f (x).

3.2.2 Metódy výpočtu určitého integrálu.

1. Priama integrácia

Príklad 35.

a)

b)

v)

e)

2. Zmena premenných pod znamienkom určitého integrálu .

Príklad 36.

2. Integrácia po častiach v určitom integráli .

Príklad 37.

a)

b)

e)

3.2.3 Aplikácie určitého integrálu

Charakteristický	Typ funkcie	Vzorec
	v karteziánskych súradniciach
zakrivená sektorová oblasť	v polárnych súradniciach
zakrivená lichobežníková oblasť	v parametrickej forme
dĺžka oblúka	v karteziánskych súradniciach
dĺžka oblúka	v polárnych súradniciach
dĺžka oblúka	v parametrickej forme
telesný objem rotácia	v karteziánskych súradniciach
telesný objem s daným priečnym prierez

Príklad 38. Vypočítajte plochu tvaru ohraničenú čiarami: a .

Riešenie: Nájdite priesečníky grafov týchto funkcií. Aby sme to dosiahli, porovnávame funkcie a riešime rovnicu

Takže body priesečníka a.

Pomocou vzorca nájdeme oblasť obrázku

.

V našom prípade

Odpoveď: plocha sa rovná (štvorcové jednotky).

4.1 Základné pojmy

Definícia. Ak je podľa nejakého pravidla jedna alebo viac hodnôt premennej z priradená ku každému páru nezávislých čísel z určitej množiny, potom sa premenná z nazýva funkcia dvoch premenných.

Definícia. Definičný obor funkcie z je množina párov, pre ktoré funkcia z existuje.

Definičný obor funkcie dvoch premenných je množina bodov v súradnicovej rovine Oxy. Súradnica z sa nazýva aplikácia a samotná funkcia je potom znázornená ako nejaký povrch v priestore E 3. Napríklad:

Príklad 39. Nájdite definičný obor funkcie.

a)

Výraz na pravej strane má význam iba pre. To znamená, že doménou tejto funkcie je súbor všetkých bodov ležiacich vo vnútri a na hranici kružnice s polomerom R so stredom v počiatku.

Definičným oborom tejto funkcie sú všetky body roviny, okrem bodov priamok, t.j. súradnicové osi.

Definícia. Čiary na úrovni funkcií sú skupinou kriviek na rovine súradníc opísaných rovnicami formulára.

Príklad 40. Nájdite riadky na úrovni funkcií .

Riešenie. Úrovňové čiary danej funkcie sú rodinou kriviek v rovine opísanej rovnicou

Posledná rovnica popisuje skupinu kružníc so stredom v bode O 1 (1, 1) polomeru. Otočná plocha (paraboloid) opísaná touto funkciou sa pri vzďaľovaní od osi stáva "strmšia", čo je dané rovnicami x = 1, y = 1. (obr. 4)

4.2 Limity a spojitosť funkcií viacerých premenných.

1. Limity.

Definícia. Číslo A sa nazýva limita funkcie, pretože bod smeruje k bodu, ak pre každé ľubovoľne malé číslo existuje číslo také, že podmienka platí pre ľubovoľný bod, a podmienka ... Zapisujú si: .

Príklad 41. Nájdite limity:

tie. limit závisí od, a preto neexistuje.

2. Kontinuita.

Definícia. Nech bod patrí do oblasti definície funkcie. Potom sa funkcia nazýva spojitá v bode, ak

(1)

navyše pointa smeruje k veci svojvoľným spôsobom.

Ak v niektorom bode nie je splnená podmienka (1), potom sa tento bod nazýva bodom diskontinuity funkcie. Môže to byť v nasledujúcich prípadoch:

1) Funkcia nie je v bode definovaná.

2) Neexistuje žiadny limit.

3) Táto hranica existuje, ale nie je rovnaká.

Príklad 42. Určte, či je daná funkcia v bode spojitá, ak.

Mám to preto je táto funkcia v bode spojitá.

limit závisí od k, t.j. v danom bode neexistuje, čo znamená, že funkcia má v tomto bode diskontinuitu.

4.3 Derivácie a diferenciály funkcií viacerých premenných

4.3.1 Parciálne derivácie prvého rádu

Čiastočná derivácia funkcie vzhľadom na argument x je obyčajná derivácia funkcie jednej premennej x pre pevnú hodnotu premennej y a označuje sa:

Čiastočná derivácia funkcie vzhľadom na argument y je obyčajná derivácia funkcie jednej premennej y pri pevnej hodnote premennej x a označuje sa:

Príklad 43. Nájdite parciálne derivácie funkcií.

4.3.2 Parciálne derivácie druhého rádu

Parciálne derivácie druhého rádu sú parciálne derivácie parciálnych derivácií prvého rádu. Pre funkciu dvoch premenných tvaru sú možné štyri typy parciálnych derivácií druhého rádu:

Parciálne deriváty druhého rádu, v ktorých sa diferenciácia vykonáva vzhľadom na rôzne premenné, sa nazývajú zmiešané deriváty. Zmiešané derivácie druhého rádu dvakrát diferencovateľnej funkcie sú rovnaké.

Príklad 44. Nájdite parciálne derivácie druhého rádu.

4.3.3 Celkový diferenciál a jeho aplikácia na približné výpočty.

Definícia. Diferenciál prvého rádu funkcie dvoch premenných nájdeme pomocou vzorca

.

Príklad 45. Nájdite celkový diferenciál funkcie.

Riešenie. Poďme nájsť parciálne derivácie:

.

Pre malé prírastky argumentov x a y získava funkcia prírastok približne rovný dz, t.j. ...

Vzorec na nájdenie približnej hodnoty funkcie v bode, ak je známa jej presná hodnota v bode:

Príklad 46. Nájdi .

Riešenie. nechaj,

Potom použijeme vzorec

Odpoveď. .

Príklad 47. Vypočítajte približne.

Riešenie. Uvažujme o funkcii. Máme

Príklad 48. Vypočítajte približne.

Riešenie. Zvážte funkciu ... Dostaneme:

Odpoveď. .

4.3.4 Implicitná diferenciácia funkcií

Definícia. Funkcia sa nazýva implicitná, ak je daná rovnicou, ktorá nie je riešiteľná vzhľadom na z.

Parciálne derivácie takejto funkcie sa nachádzajú podľa vzorcov:

Príklad 49. Nájdite parciálne derivácie funkcie z danej rovnicou .

Riešenie.

Definícia. Funkcia sa nazýva implicitná, ak je daná rovnicou, ktorá nie je riešiteľná vzhľadom na y.

Deriváciu takejto funkcie nájdeme podľa vzorca:

.

Príklad 50. Nájdite derivácie týchto funkcií.

5.1 Lokálny extrém funkcie viacerých premenných

Definícia 1. Funkcia má maximum v bode, ak

Definícia 2. Funkcia má minimum v bode, ak pre všetky body dostatočne blízko k bodu a odlišné od neho.

Nevyhnutná podmienka pre extrém. Ak funkcia dosiahne extrém v bode, potom parciálne derivácie funkcie zaniknú alebo v tomto bode neexistujú.

Body, v ktorých parciálne derivácie miznú alebo neexistujú, sa nazývajú kritické.

Dostatočný znak extrému. Nech je funkcia definovaná v nejakom okolí kritického bodu a má v tomto bode spojité parciálne derivácie druhého rádu

1) má lokálne maximum v bode, ak a;

2) má lokálne minimum v bode, ak a;

3) nemá lokálny extrém v bode ak;

Schéma štúdie pre extrém funkcie dvoch premenných.

1. Nájdite parciálne derivácie funkcie: a.

2. Vyriešte sústavu rovníc a nájdite kritické body funkcie.

3. Nájdite parciálne derivácie druhého rádu, vypočítajte ich hodnoty v kritických bodoch a pomocou dostatočnej podmienky urobte záver o prítomnosti extrémov.

4. Nájdite extrémy funkcie.

Príklad 51. Nájdite extrémy funkcie .

1) Nájdite parciálne derivácie.

2) Vyriešte sústavu rovníc

4) Nájdite parciálne derivácie druhého rádu a ich hodnoty v kritických bodoch:. V bode dostaneme:

preto v bode neexistuje žiadny extrém. V bode dostaneme:

preto je v tomto bode minimum.

5.2 Globálny extrém (najvyššia a najnižšia hodnota funkcie)

Najväčšie a najmenšie hodnoty funkcie viacerých premenných, spojitých na nejakej uzavretej množine, sa dosahujú buď v extrémnych bodoch, alebo na hranici množiny.

Schéma na nájdenie najvyšších a najnižších hodnôt.

1) Nájdite kritické body ležiace vo vnútri oblasti, vypočítajte hodnotu funkcie v týchto bodoch.

2) Preskúmajte funkciu na hranici územia; ak hranica pozostáva z niekoľkých rôznych línií, potom sa štúdia musí vykonať pre každú lokalitu samostatne.

3) Porovnajte získané hodnoty funkcie a vyberte najväčšiu a najmenšiu.

Príklad 52. Nájdite najväčšiu a najmenšiu hodnotu funkcie v obdĺžniku.

Riešenie. 1) Nájdite kritické body funkcie, na to nájdeme parciálne derivácie: a vyriešte sústavu rovníc:

Prijal kritický bod A. Výsledný bod leží vo vnútri špecifikovanej oblasti,

Hranicu oblasti tvoria štyri segmenty: a. nájsť najväčšiu a najmenšiu hodnotu funkcie na každom segmente.

4) Porovnajte získané výsledky a zistite, že v bodoch .

Kapitola 6. Model spotrebiteľskej voľby

Budeme predpokladať, že existuje n rôznych tovarov. Potom bude určitá množina tovarov označená n-rozmerným vektorom , kde je množstvo i-tého produktu. Množina všetkých množín statkov X sa nazýva priestor.

Voľba individuálneho spotrebiteľa je charakterizovaná preferenčným vzťahom: predpokladá sa, že spotrebiteľ môže povedať o akýchkoľvek dvoch súboroch, čo je viac žiaduce, alebo medzi nimi nevidí rozdiel. Preferenčný vzťah je tranzitívny: ak je množina výhodnejšia ako množina a množina je výhodnejšia ako množina, potom je množina výhodnejšia ako množina. Budeme predpokladať, že spotrebiteľské správanie plne vystihuje axióma individuálneho spotrebiteľa: každý jednotlivý spotrebiteľ sa rozhoduje o spotrebe, nákupoch atď., na základe svojho systému preferencií.

6.1 Užitočná funkcia

Na množine spotrebných množín X je funkcia definovaná , ktorej hodnota na spotrebiteľskom súbore sa rovná spotrebiteľskému odhadu jednotlivca pre tento súbor. Funkcia sa nazýva úžitková funkcia spotrebiteľa alebo preferenčná funkcia spotrebiteľa. Tie. každý spotrebiteľ má svoju úžitkovú funkciu. Ale celú množinu spotrebiteľov možno rozdeliť do určitých tried spotrebiteľov (podľa veku, majetkového stavu atď.) a každej triede možno priradiť nejakú, možno, spriemerovanú úžitkovú funkciu.

Funkcia je teda spotrebiteľský odhad alebo úroveň uspokojenia potrieb jednotlivca pri kúpe daného setu. Ak je pre daného jedinca výhodnejší súbor ako súbor, potom.

Vlastnosti úžitkovej funkcie.

1.

Prvé parciálne derivácie funkcie užitočnosti sa nazývajú hraničné užitočnosti produktov. Z tejto vlastnosti vyplýva, že zvýšenie spotreby jedného produktu, zatiaľ čo spotreba ostatných produktov zostane nezmenená, vedie k zvýšeniu spotrebiteľského hodnotenia. Vektor je gradient funkcie, ukazuje smer najväčšieho rastu funkcie. Pre funkciu je jej gradient vektorom okrajových úžitkov produktov.

2.

Tie. hraničná užitočnosť akejkoľvek komodity klesá s rastúcou spotrebou.

3.

Tie. hraničná užitočnosť každého produktu rastie s množstvom iného produktu.

Niektoré druhy úžitkových funkcií.

1) Neoklasicistický:.

2) Kvadratické: kde matica je záporne jednoznačná a pre .

3) Logaritmická funkcia:.

6.2 Línie ľahostajnosti

V aplikovaných problémoch a modeloch spotrebiteľskej voľby sa často používa konkrétny prípad súboru dvoch tovarov, t.j. keď funkcia užitočnosti závisí od dvoch premenných. Čiara ľahostajnosti je čiara spájajúca spotrebiteľské množiny, ktoré majú rovnakú úroveň uspokojenia potrieb jednotlivca. V podstate sú čiary ľahostajnosti čiarami úrovne funkcie. Rovnice indiferenčných čiar: .

Základné vlastnosti indiferenčných čiar.

1. Línie ľahostajnosti, zodpovedajúce rôznym úrovniam uspokojovania potrieb, sa nedotýkajú ani nepretínajú.

2. Čiary ľahostajnosti sa znižujú.

3. Línie ľahostajnosti sú konvexné smerom nadol.

Vlastnosť 2 implikuje dôležitú približnú rovnosť.

Tento pomer ukazuje, o koľko by mal jednotlivec zvýšiť (znížiť) spotrebu druhého produktu a zároveň znížiť (zvýšiť) spotrebu prvého produktu o jednu jednotku bez toho, aby sa zmenila úroveň uspokojenia jeho potrieb. Pomer sa nazýva miera nahradenia prvého produktu druhým a hodnota sa nazýva hraničná miera nahradenia prvého produktu druhým.

Príklad 53. Ak je hraničná užitočnosť prvého tovaru 6 a druhého - 2, potom pri znížení spotreby prvého tovaru o jednu jednotku je potrebné zvýšiť spotrebu druhého tovaru o 3 jednotky s rovnakú úroveň uspokojenia potrieb.

6.3 Stanovený rozpočet

Nechaj - vektor cien pre množinu n produktov; I - príjem jednotlivca, ktorý je ochotný minúť na nákup súboru produktov. Súbor množín tovarov, ktoré pri daných cenách nestoja viac ako I, sa nazýva rozpočtový súbor B. Súbor množín tovarov v cene I sa navyše nazýva hranica G rozpočtového súboru B. množina B je ohraničená hranicou G a prirodzenými obmedzeniami.

Sada rozpočtu je opísaná systémom nerovností:

Pre prípad množiny dvoch tovarov je rozpočtovou množinou B (obr. 1) trojuholník v súradnicovej sústave, ohraničený súradnicovými osami a priamkou.

6.4 Teória spotrebiteľského dopytu

V teórii spotreby sa predpokladá, že spotrebiteľ sa vždy snaží maximalizovať svoj úžitok a jediným obmedzením je pre neho obmedzený príjem I, ktorý môže minúť na nákup súboru tovarov. Vo všeobecnosti je problém spotrebiteľskej voľby (problém racionálneho spotrebiteľského správania na trhu) formulovaný nasledovne: nájsť spotrebiteľskú množinu , ktorý maximalizuje svoju úžitkovú funkciu pre dané rozpočtové obmedzenie. Matematický model tohto problému:

V prípade sady dvoch produktov:

Geometricky je riešením tohto problému styčný bod medzi hranicou rozpočtového súboru G a čiarou ľahostajnosti.

Riešenie tohto problému sa redukuje na riešenie systému rovníc:

(1)

Riešenie tohto systému je riešením problému výberu spotrebiteľa.

Riešenie problému výberu spotrebiteľa sa nazýva bod dopytu. Tento bod dopytu závisí od cien a príjmu I. To znamená. bod dopytu je funkciou dopytu. Funkcia dopytu je zase množina n funkcií, z ktorých každá závisí od argumentu:

Tieto funkcie sa nazývajú dopytové funkcie zodpovedajúceho tovaru.

Príklad 54. Pre množinu dvoch tovarov na trhu, známych cien za ne a dôchodku I nájdite funkcie dopytu, ak funkcia užitočnosti má tvar .

Riešenie. Rozlišujme užitočnú funkciu:

.

Dosaďte získané výrazy v (1) a získajte sústavu rovníc:

V tomto prípade budú náklady na každý produkt predstavovať polovicu príjmu spotrebiteľa a množstvo zakúpeného produktu sa rovná sume vynaloženej naň, vydelenej cenou produktu.

Príklad 55. Nech funguje užitočnosť pre prvý tovar, druhý,

cena prvého produktu, cena druhého. príjem . Koľko by mal spotrebiteľ kúpiť, aby maximalizoval užitočnosť?

Riešenie. Nájdite derivácie funkcií užitočnosti, dosaďte ich do systému (1) a vyriešte to:

Tento súbor tovarov je pre spotrebiteľa optimálny z hľadiska maximalizácie úžitku.

Test by sa mal vykonať v súlade s možnosťou zvolenou poslednou číslicou čísla knihy záznamov v samostatnom zošite. Každý problém by mal obsahovať podmienku, podrobné riešenie a záver.

1. Úvod do kalkulu

Úloha 1. Nájdite doménu funkcie.

5.

Úloha 2. Nájdite limity funkcií.

.

Úloha 3. Nájdite body prerušenia funkcie a určte ich typ.

1. 2. 3.

Kapitola 2. Diferenciálny počet funkcie jednej premennej

Úloha 4. Nájdite derivácie týchto funkcií.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - arcsin x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e5 x - 1) 6; c) y =; d) y =; e) y = x 8++ + 5; f) y = 3 x - arcsin x.

5.a) y = 2 x 3 - + e x; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sintg;

d) y = 3 x 4 - - 9 + 9; e) y =;

f) y = x 2 + arcsin x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4 x 4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x2-x; f) y = e sin 3 x + 2.

Úloha 5. Preskúmajte funkciu a zostavte jej graf.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9 písm. a) b) c).

10. a) b) v) .

Úloha 6. Nájdite najväčšiu a najmenšiu hodnotu funkcie na danom segmente.

1. .

3. .

6. .

8. .

9. .

10. .

Kapitola 3. Integrálny počet

Úloha 7. Nájdite neurčité integrály.

1.a) b);

2.a) b) c) d).

4. G)

5.a) ; b); v) ; G).

6.a) ; b); v); G)

7.a) ; b) ; v) ; G)

8.a) ; b); v) ; G).

9.a) ; b) c); G).

10.a) b) v) ; G).

Úloha 8. Vypočítajte určité integrály.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Úloha 9. Nájdite nevlastné integrály alebo dokážte, že divergujú.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Úloha 10. Nájdite oblasť oblasti ohraničenej krivkami

1. .2. .

5. 6.

7. , .8..

10. , .

Kapitola 4. Diferenciálny počet funkcie viacerých premenných.

Úloha 11. Nájdite doménu funkcie (zobrazte na výkrese).

Úloha 12. Preskúmajte spojitosť funkcie pre

Úloha 13. Nájdite deriváciu implicitne definovanej funkcie.

Úloha 14. Vypočítajte približne

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

Úloha 15. Preskúmajte funkciu pre extrémy.

7. .

8. .

9. .

10. .

Úloha 16. Nájdite najväčšiu a najmenšiu hodnotu funkcie v danej uzavretej oblasti.

1.v obdĺžniku

2.

3.v obdĺžniku

4.v oblasti ohraničenej parabolou

A abscisa.

5.štvorcový

6.v trojuholníku ohraničenom súradnicovými osami a priamkou

7.v trojuholníku ohraničenom súradnicovými osami a priamkou

8. v trojuholníku ohraničenom súradnicovými osami a priamkou

9.v oblasti ohraničenej parabolou

A abscisa.

10.v oblasti ohraničenej parabolou

A abscisa.

Hlavný

1. M.S. Crassus, B.P. Chuprynov. Základy matematiky a jej aplikácia v ekonomickom vzdelávaní: učebnica. - 4. vydanie, Isp. - M.: Delo, 2003.

2. M.S. Crassus, B.P. Chuprynov. Matematika pre ekonomické odbory: Učebnica. - 4. vydanie, Isp. - M.: Delo, 2003.

3. M.S. Crassus, B.P. Chuprynov. Matematika pre bakalárske štúdium ekonómie. Učebnica. - 4. vydanie, Isp. - M.: Delo, 2005.

4. Vyššia matematika pre ekonómov. Učebnica pre vysoké školy / N.Sh. Kremer, B.A. Putko, I.M. Trishin, M.N. Friedman; Ed. Prednášal prof. N.Sh. Kremer, - 2. vyd., Prepracované. a pridať. - M: UNITY, 2003.

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman MN Vyššia matematika pre ekonomické odbory. Učebnica a workshop (I. a II. časť) / Ed. Prednášal prof. N.Sh. Kremer, - 2. vyd., Prepracované. a pridať. - M: Vysokoškolské vzdelanie, 2007. - 893s. - (Základy vied)

6. Danko P.E., Popov A.G., Koževniková T.Ya. Vyššia matematika v cvičeniach a úlohách. M. stredná škola. 1999.

Dodatočné

1. I.I. Bavrin, V.L. Námorníci. Vyššia matematika. "Humanitárne vydavateľské centrum Vlados", 2002.

2. I.A. Zajcev. Vyššia matematika. "Stredná škola", 1998.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, I.G. Shandra. Matematika v ekonómii / v dvoch častiach /. M. Financie a štatistika. 1999.

pre študentov lekárske, detské, zubné

a fakultách preventívneho lekárstva

na laboratórnu prácu

"Základné pojmy matematickej analýzy"

1. Vedecké a metodologické zdôvodnenie témy:

Derivačné a diferenciálne pojmy sú jedným zo základných pojmov matematickej analýzy. Výpočet derivácií je nevyhnutný pri riešení mnohých problémov vo fyzike a matematike (hľadanie rýchlosti, zrýchlenia, tlaku atď.). Dôležitosť pojmu derivácia je daná najmä skutočnosťou, že derivácia funkcie charakterizuje rýchlosť zmeny tejto funkcie pri zmene jej argumentu.

Použitie diferenciálu umožňuje vykonávať približné výpočty, ako aj odhadnúť chyby.

Metódy hľadania derivácií a diferenciálov funkcií a ich aplikácia predstavujú hlavný problém diferenciálneho počtu. Potreba pojmu derivácia vzniká v súvislosti s formuláciou problému výpočtu rýchlosti pohybu a nájdenia uhla dotyčnice ku krivke. Je možný aj inverzný problém: určte prejdenú vzdialenosť rýchlosťou a nájdite zodpovedajúcu funkciu podľa dotyčnice sklonu dotyčnice. Tento inverzný problém vedie ku konceptu neurčitého integrálu.

Pojem určitého integrálu sa používa v mnohých praktických problémoch, najmä pri problémoch s výpočtom plôch rovinných útvarov, výpočtom práce vykonanej premennou silou a nájdením priemernej hodnoty funkcie.

Pri matematickom popise rôznych fyzikálnych, chemických, biologických procesov a javov sa často používajú rovnice, ktoré obsahujú nielen skúmané veličiny, ale aj ich deriváty rôznych rádov týchto veličín. Napríklad podľa najjednoduchšej verzie zákona o množení baktérií je rýchlosť rozmnožovania úmerná počtu baktérií v danom čase. Ak túto veličinu označíme N (t), potom v súlade s fyzikálnym významom derivátu je rýchlosť rozmnožovania baktérií derivátom N (t) a na základe vyššie uvedeného zákona môžeme zapísať pomer N "(t) = k ∙ N, kde k> 0 - koeficient úmernosti Výsledná rovnica nie je algebraická, pretože obsahuje nielen neznámu funkciu N (t), ale aj jej deriváciu prvého rádu.

2. Stručná teória:

1. Problémy vedúce k pojmu derivát

1. Problém nájdenia rýchlosti v hmotného bodu... Nech nejaký hmotný bod vykoná priamočiary pohyb. V určitom okamihu t 1 bod je na pozícii M 1. V určitom okamihu t 2 tehotná M 2 . Označme interval M 1 , M 2 naprieč ΔS; t 2 - t 1 = Δt... Hodnota sa nazýva priemerná rýchlosť pohybu. Ak chcete zistiť okamžitú rýchlosť bodu v určitej polohe M 1 nevyhnutné Δt majú tendenciu k nule. Matematicky to znamená

, (1)

Aby sme teda našli okamžitú rýchlosť hmotného bodu, je potrebné vypočítať hranicu pomeru prírastku funkcie ΔS na prírastok argumentu Δt za predpokladu, že Δt → 0.

2. Problém nájdenia uhla sklonu dotyčnice ku grafu funkcie.

Obr

Zvážte graf nejakej funkcie y = f (x). Aký je uhol sklonu
dotyčnica v bode M 1 ? V bode M 1 nakreslite dotyčnicu ku grafu funkcie. Vyberte ľubovoľný bod na grafe M 2 a nakreslite sečnicu. Je naklonená smerom k osi OH pod uhlom α 1 ... Zvážte ΔM 1 M 2 A:

, (2)

Ak bod M 1 opraviť, a bod M 2 priblížiť sa M 1 , potom seč M 1 M 2 prejde na dotyčnicu ku grafu funkcie v bode M 1 a môžeš napísať:

, (3)

Preto je potrebné vypočítať limit pomeru prírastku funkcie k prírastku argumentu, ak prírastok argumentu smeruje k nule.

Limit pomeru prírastku Δy funkcie y = f (x) k prírastku argumentu Δx v danom bode x 0 keďže Δx smeruje k nule, nazýva sa derivácia funkcie v danom bode.

Odvodená notácia: y ", f" (x), ... Podľa definície

, (4)

kde Δx = x 2 -x 1 je prírastok argumentu (rozdiel medzi dvoma nasledujúcimi dostatočne blízkymi hodnotami argumentu), Δy = y 2 -y 1 je prírastok funkcie (rozdiel medzi hodnotami funkcie zodpovedajúcej týmto hodnotám argumentu).

Nájdenie derivácie danej funkcie sa nazýva jej diferenciácia... Diferenciácia hlavných elementárnych funkcií sa vykonáva podľa hotových vzorcov (pozri tabuľku), ako aj pomocou pravidlá:

Derivácia algebraického súčtu funkcií sa rovná súčtu derivácií týchto funkcií:

(u+ υ )"= u" + υ "

2. Derivácia súčinu dvoch funkcií sa rovná súčtu súčinov druhej funkcie deriváciou prvej a prvej funkcie deriváciou druhej:

(ty ∙υ ) "= u"υ + uυ "

3. Derivácia kvocientu dvoch funkcií sa rovná zlomku, ktorého čitateľ je rozdielom medzi súčinmi menovateľa deriváciou čitateľa a čitateľa deriváciou menovateľa a menovateľ je druhá mocnina menovateľa:

Fyzikálny význam derivátu. Z porovnania (4) a (1) vyplýva, že okamžitá rýchlosť priamočiareho pohybu hmotného bodu sa rovná derivácii závislosti jeho súradnice od času.

Všeobecný význam derivácie funkcie je, že charakterizuje rýchlosť (rýchlosť) zmeny funkcie pre danú zmenu argumentu. Rýchlosť fyzikálnych, chemických a iných procesov, napríklad rýchlosť ochladzovania tela, rýchlosť chemickej reakcie, rýchlosť rozmnožovania baktérií atď., sa tiež vyjadruje pomocou derivátu.

Geometrický význam derivátu. Veľkosť dotyčnice uhla sklonu dotyčnice nakreslenej ku grafu funkcie sa v matematike nazýva sklon dotyčnice.

Sklon dotyčnice ku grafu diferencovateľnej funkcie v určitom bode sa numericky rovná derivácii funkcie v tomto bode.

Toto vyhlásenie sa nazýva geometrický význam derivátu.

Obsah článku

MATEMATICKÁ ANALÝZA, odvetvie matematiky, ktoré poskytuje metódy na kvantitatívne štúdium rôznych procesov zmien; sa zaoberá štúdiom rýchlosti zmeny (diferenciálny počet) a určovaním dĺžok kriviek, plôch a objemov útvarov ohraničených zakrivenými obrysmi a plochami (integrálny počet). Pre problémy matematickej analýzy je charakteristické, že ich riešenie je spojené s pojmom limita.

Matematickú analýzu iniciovali v roku 1665 I. Newton a (asi 1675) nezávisle G. Leibniz, hoci dôležité prípravné práce vykonali I. Kepler (1571 – 1630), F. Cavalieri (1598 – 1647), P. Ferma (1601– 1665), J. Wallis (1616-1703) a I. Barrow (1630-1677).

Aby bola prezentácia živšia, uchýlime sa k jazyku grafov. Preto môže byť pre čitateľa užitočné pozrieť si článok ANALYTICKÁ GEOMETRIA pred prečítaním tohto článku.

DIFERENCIÁLNY POČET

Tangenty.

Na obr. 1 znázorňuje časť krivky r = 2X – X 2, uzatvorenej medzi X= –1 a X= 3. Dostatočne malé segmenty tejto krivky vyzerajú rovno. Inými slovami, ak R Je ľubovoľný bod tejto krivky, potom týmto bodom prechádza nejaká priamka a je aproximáciou krivky v malom okolí bodu R a čím menšie okolie, tým lepšia aproximácia. Takáto priamka sa nazýva dotyčnica ku krivke v bode R... Hlavnou úlohou diferenciálneho počtu je vytvoriť všeobecnú metódu, ktorá vám umožní nájsť smer dotyčnice v akomkoľvek bode krivky, kde dotyčnica existuje. Nie je ťažké si predstaviť krivku s ostrým zlomom (obr. 2). Ak R- vrchol takejto prestávky, potom môžete postaviť približnú priamku PT 1 - vpravo od bodu R a ďalšia približná čiara RT 2 - vľavo od bodu R... Ale bodom neprechádza jediná priamka R, ktorá sa rovnako dobre priblížila ku krivke v blízkosti bodu P aj vpravo aj vľavo, teda dotyčnica v bode P neexistuje.

Na obr. 1 dotyčnica ODťahaný cez pôvod O= (0,0). Sklon tejto čiary je 2, t.j. keď sa úsečka zmení o 1, ordináta sa zväčší o 2. Ak X a r- súradnice ľubovoľného bodu na OD, potom sa vzdialiť od O na diaľku X jednotiek doprava, vzďaľujeme sa od O dňa 2 r jednotky hore. teda r/X= 2, príp r = 2X... Toto je tangentová rovnica OD do zákruty r = 2X – X 2 v bode O.

Teraz je potrebné vysvetliť prečo z množiny priamok prechádzajúcich bodom O, bola zvolená priamka OD... Aký je rozdiel medzi priamkou so sklonom 2 a inými priamkami? Existuje jedna jednoduchá odpoveď a je pre nás ťažké odolať pokušeniu použiť analógiu dotyčnice ku kruhu: dotyčnica OD má s krivkou spoločný iba jeden bod, zatiaľ čo akákoľvek iná nevertikálna priamka prechádzajúca bodom O, pretína krivku dvakrát. Dá sa to overiť nasledovne.

Od výrazu r = 2X – X 2 možno získať odčítaním X 2 z r = 2X(rovnice priamky OD), potom hodnoty r pre graf je menej vedomostí r pre priamku vo všetkých bodoch okrem bodu X= 0. Preto je graf všade, okrem bodu O umiestnený nižšie OD a táto čiara a graf majú spoločný iba jeden bod. Navyše, ak r = mx- rovnica nejakej inej priamky prechádzajúcej bodom O, potom určite existujú dva priesečníky. naozaj, mx = 2X – X 2 nielen pre X= 0, ale aj pre X = 2 – m... A len kedy m= 2 oba priesečníky sa zhodujú. Na obr. 3 znázorňuje prípad, kedy m menej ako 2, teda napravo od O je tu druhý priesečník.

Čo OD- jediná nevertikálna priamka prechádzajúca bodom O a majúci s grafom spoločný iba jeden bod, nie jeho najdôležitejšiu vlastnosť. Ak sa totiž obrátime na iné grafy, čoskoro sa ukáže, že vlastnosť dotyčnice, ktorú sme zaznamenali vo všeobecnom prípade, nie je splnená. Napríklad z obr. 4 je vidieť, že v blízkosti bodu (1,1) je graf krivky r = X 3 je dobre aproximovaná priamkou RT, ktorá však má s ňou viacero spoločných bodov. Chceli by sme však zvážiť RT dotyčnica k tomuto grafu v bode R... Preto je potrebné nájsť nejaký iný spôsob zvýraznenia dotyčnice ako ten, ktorý nám tak dobre poslúžil v prvom príklade.

Predpokladajme, že cez bod O a ľubovoľný bod Q = (h,k) na grafe krivky r = 2X – X 2 (obr. 5) je nakreslená priamka (nazývaná sečna). Dosadenie hodnôt do rovnice krivky X = h a r = k, chápeme to k = 2h – h 2 je teda sklon sečnice

S veľmi malým h význam m blízko k 2. Navyše, výber h dostatočne blízko k 0, čo môžeme urobiť mľubovoľne blízko k 2. Môžeme povedať, že m"Tends to the limit" rovný 2, keď h má tendenciu k nule, alebo akémukoľvek limitu m rovná sa 2 pre h sklon k nule. Toto je symbolicky napísané takto:

Potom dotyčnica ku grafu v bode O definovaná ako priamka prechádzajúca bodom O, so sklonom rovným tejto hranici. Táto definícia dotyčnice je všeobecne použiteľná.

Ukážme si výhody tohto prístupu na ďalšom príklade: nájdite sklon dotyčnice ku grafu krivky r = 2X – X 2 v ľubovoľnom bode P = (X,r), pričom sa neobmedzujeme na najjednoduchší prípad, kedy P = (0,0).

Nechaj Q = (X + h, r + k) - druhý bod na mape, umiestnený vo vzdialenosti h napravo od R(obr. 6). Je potrebné nájsť svah k/h sekanta PQ... Bodka Q je na diaľku

nad osou X.

Rozbalením zátvoriek nájdeme:

Odčítaním z tejto rovnice r = 2X – X 2 zistíme vertikálnu vzdialenosť od bodu R k veci Q:

Preto svah m sekanta PQ rovná sa

Teraz to h má tendenciu k nule, m má tendenciu 2-2 X; budeme brať poslednú hodnotu ako sklon dotyčnice PT... (Rovnaký výsledok získate, ak h nadobúda záporné hodnoty, čo zodpovedá výberu bodu Q na ľavej strane P.) Všimnite si, že pre X= 0 výsledok je rovnaký ako predchádzajúci.

Výraz 2 – 2 X sa nazýva derivát 2 X – X 2. Za starých čias sa derivát nazýval aj „diferenciálny pomer“ a „diferenciálny koeficient“. Ak výraz 2 X – X 2 určiť f(X), t.j.

potom môže byť derivát označený

Aby sme zistili sklon dotyčnice ku grafu funkcie r = f(X) v určitom bode musí byť nahradený v fў ( X) hodnotu zodpovedajúcu tomuto bodu X... Takže sklon fў (0) = 2 pre X = 0, fў (0) = 0 pre X= 1 a fў (2) = –2 pre X = 2.

Označuje sa aj derivát priў , D Y/dx, D x y a Du.

Skutočnosť, že krivka r = 2X – X 2 v blízkosti daného bodu je v tomto bode prakticky nerozoznateľný od jeho dotyčnice, umožňuje hovoriť o sklone dotyčnice ako o "sklone krivky" v bode dotyku. Môžeme teda tvrdiť, že sklon uvažovanej krivky má v bode (0,0) sklon 2. Dá sa tiež povedať, že pri X= 0 miera zmeny r pomerne X je 2. V bode (2,0) je sklon dotyčnice (a krivky) –2. (Znamienko mínus znamená, že ako X premenlivý r klesá.) V bode (1,1) je dotyčnica vodorovná. Hovoríme krivka r = 2X – X 2 má v tomto bode stacionárnu hodnotu.

Najvyššie a najnižšie hodnoty.

Práve sme ukázali, že krivka f(X) = 2X – X 2 je stacionárny v bode (1,1). Pretože fў ( X) = 2 – 2X = 2(1 – X), je jasné, že pre X menej ako 1, fў ( X) je pozitívny, a preto r zvyšuje; pri X, veľký 1, fў ( X) je negatívny, a preto r klesá. Teda v blízkosti bodu (1,1) naznačeného na obr. 6 písm M, čo znamená pri rastie do bodu M, stacionárny v bode M a klesá po bode M... Tento bod sa nazýva „maximum“, pretože hodnota pri v tomto bode prekračuje ktorúkoľvek zo svojich hodnôt v dostatočne malom susedstve. Podobne je „minimum“ definované ako bod, v blízkosti ktorého sú všetky hodnoty r prevyšovať počet pri práve v tomto bode. Môže sa tiež stať, že hoci derivát z f(X) v určitom bode a zmizne, jeho znamienko sa v blízkosti tohto bodu nemení. Takýto bod, ktorý nie je maximom ani minimom, sa nazýva inflexný bod.

Ako príklad nájdime stacionárny bod krivky

Deriváciou tejto funkcie je

a zmizne pri X = 0, X= 1 a X= -1; tie. v bodoch (0,0), (1, –2/15) a (–1, 2/15). Ak X o niečo menej ako -1 fў ( X) je negatívny; ak X o niečo viac ako -1 fў ( X) je pozitívny. Preto je bod (–1, 2/15) maximum. Podobne sa dá ukázať, že bod (1, –2/15) je minimum. Ale ten derivát fў ( X) je záporné pred bodom aj za bodom (0,0). Preto (0,0) je inflexný bod.

Vykonaná štúdia tvaru krivky, ako aj skutočnosti, že krivka pretína os X pri f(X) = 0 (t.j. pre X= 0 alebo) vám umožňujú znázorniť jeho graf približne tak, ako je znázornené na obr. 7.

Vo všeobecnosti, ak vylúčime nezvyčajné prípady (krivky obsahujúce priame úsečky alebo nekonečný počet ohybov), existujú štyri možnosti pre relatívnu polohu krivky a dotyčnice v blízkosti bodu dotyčnice. R. (Cm... ryža. 8, kde dotyčnica má kladný sklon.)

1) Na oboch stranách bodu R krivka leží nad dotyčnicou (obr. 8, a). V tomto prípade hovoria, že krivka v bode R konvexné smerom nadol alebo konkávne.

2) Na oboch stranách bodu R krivka sa nachádza pod dotyčnicou (obr. 8, b). V tomto prípade sa o krivke hovorí, že je konvexná smerom nahor alebo jednoducho konvexná.

3) a 4) Krivka sa nachádza nad dotyčnicou na jednej strane bodu R a nižšie - na druhej strane. V tomto prípade R- inflexný bod.

Porovnávanie hodnôt fў ( X) na oboch stranách R s jeho hodnotou v bode R, je možné určiť, ktorý z týchto štyroch prípadov je potrebné riešiť v konkrétnom probléme.

Aplikácie.

Všetky vyššie uvedené nachádzajú dôležité aplikácie v rôznych oblastiach. Napríklad, ak je telo vrhnuté vertikálne nahor počiatočnou rýchlosťou 200 stôp za sekundu, potom výška s na ktorých budú umiestnené cez t sekúnd v porovnaní s počiatočným bodom bude

Zistili sme, že konáme rovnakým spôsobom ako v príkladoch, ktoré sme zvážili

táto hodnota mizne pri c. Derivát fў ( X) je kladný až do hodnoty c a po tomto čase záporný. teda s zvyšuje sa na, potom sa stáva stacionárnym a potom klesá. Toto je všeobecný popis pohybu tela hodeného nahor. Z nej vieme, kedy telo dosiahne svoj najvyšší bod. Ďalej nahrádzanie t= 25/4 palca f(t), dostaneme 625 stôp, maximálny zdvih. V tejto úlohe fў ( t) má fyzický význam. Táto derivácia ukazuje rýchlosť, ktorou sa teleso pohybuje v danom okamihu t.

Uvažujme teraz o inom type aplikácie (obr. 9). Je potrebné vyrobiť krabicu so štvorcovým dnom z kartónu s plochou 75 cm 2. Aký veľký musí byť tento box, aby mal maximálny objem? Ak X- strana základne krabice a h- jeho výška, potom je objem škatule V = X 2 h a povrchová plocha je 75 = X 2 + 4xh... Transformáciou rovnice dostaneme:

Odvodené od V sa ukazuje ako rovnocenné

a zmizne pri X= 5. Potom

a V= 125/2. Funkčný graf V = (75X – X 3) / 4 je znázornená na obr. 10 (záporné hodnoty X vynechané, pretože v tomto probléme nemajú žiadny fyzický význam).

Deriváty.

Dôležitou úlohou diferenciálneho počtu je vytváranie metód, ktoré umožňujú rýchlo a pohodlne nájsť deriváty. Napríklad je ľahké to vypočítať

(Derivácia konštanty je, samozrejme, nula.) Nie je ťažké odvodiť všeobecné pravidlo:

kde n- akékoľvek celé číslo alebo zlomok. napr.

(Tento príklad ukazuje, aké užitočné sú zlomkové exponenty.)

Tu sú niektoré z najdôležitejších vzorcov:

Existujú aj nasledujúce pravidlá: 1) ak každá z týchto dvoch funkcií g(X) a f(X) má derivácie, potom sa derivácia ich súčtu rovná súčtu derivácií týchto funkcií a derivácia rozdielu sa rovná rozdielu derivácií, t.j.

2) derivácia súčinu dvoch funkcií sa vypočíta podľa vzorca:

3) derivácia pomeru dvoch funkcií má tvar

4) derivácia funkcie vynásobená konštantou sa rovná konštante vynásobenej deriváciou tejto funkcie, t.j.

Často sa stáva, že hodnoty funkcie sa musia počítať postupne. Napríklad na výpočet hriechu X 2, najprv musíme nájsť u = X 2 a potom vypočítajte sínus čísla u... Deriváciu takýchto zložitých funkcií nájdeme pomocou takzvaného „reťazového pravidla“:

V našom príklade f(u) = hriech u, fў ( u) = cos u, teda,

Tieto a ďalšie podobné pravidlá umožňujú okamžite vypísať deriváty mnohých funkcií.

Lineárne aproximácie.

Skutočnosť, že pri znalosti derivácie môžeme v mnohých prípadoch nahradiť graf funkcie v blízkosti niektorého bodu jej dotyčnice v tomto bode, je veľmi dôležitá, pretože s priamkami sa ľahšie pracuje.

Táto myšlienka nachádza priame uplatnenie pri výpočte približných hodnôt funkcií. Napríklad je dosť ťažké vypočítať hodnotu kedy X= 1,033. Ale môžete využiť skutočnosť, že číslo 1,033 je blízko 1 a to. Zavrieť X= 1 môžeme nahradiť graf tangens krivky bez toho, aby sme urobili nejakú závažnejšiu chybu. Sklon takejto dotyčnice sa rovná hodnote derivácie ( X 1/3) ў = (1/3) X–2/3 pri x = 1, tj 1/3. Keďže bod (1,1) leží na krivke a sklon dotyčnice ku krivke je v tomto bode 1/3, rovnica dotyčnice má tvar

Na tejto linke na X = 1,033

Výsledná hodnota r by mala byť veľmi blízko skutočnej hodnote r; a v skutočnosti je to len o 0,00012 viac ako v skutočnosti. V matematickej analýze boli vyvinuté metódy na zlepšenie presnosti tohto druhu lineárnej aproximácie. Tieto metódy zabezpečujú spoľahlivosť našich približných výpočtov.

Práve opísaný postup naznačuje užitočnú notáciu. Nechaj P- bod zodpovedajúci na grafe funkcie f premenlivý X a nechajte funkciu f(X) je rozlíšiteľné. Nahraďte graf krivky blízko bodu R dotyčnica k nej, nakreslená v tomto bode. Ak X meniť podľa sumy h, potom sa ordináta dotyčnice zmení o hodnotu h H f ў ( X). Ak h je veľmi malá, potom posledná hodnota je dobrou aproximáciou skutočnej zmeny na ordináte r grafika. Ak namiesto toho h napíšeme symbol dx(toto nie je produkt!), ale zmena súradnice r označovať D Y, potom dostaneme D Y = f ў ( X)dx, alebo D Y/dx = f ў ( X) (cm... ryža. jedenásť). Preto namiesto toho D Y alebo f ў ( X) symbol sa často používa na označenie derivátu D Y/dx... Pohodlie tohto zápisu závisí hlavne od explicitného vzhľadu reťazového pravidla (diferenciácia komplexnej funkcie); v novom zápise tento vzorec vyzerá takto:

kde sa to naznačuje pri záleží na u, a u zase závisí od X.

Veľkosť D Y nazývaný diferenciál pri; v skutočnosti to závisí od dva premenných, a to: od X a prírastky dx... Pri prírastku dx veľmi malý, veľký D Y sa blíži zodpovedajúcej zmene hodnoty r... Ale predpokladať, že prírastok dx málo, netreba.

Derivačná funkcia r = f(X) sme označili f ў ( X) alebo D Y/dx... Často je možné použiť derivát derivátu. Výsledok sa nazýva druhá derivácia f (X) a označené f ўў ( X) alebo d 2 r/dx 2. Napríklad ak f(X) = X 3 – 3X 2, potom f ў ( X) = 3X 2 – 6X a f ўў ( X) = 6X- 6. Podobné označenia sa používajú pre deriváty vyššieho rádu. Aby sme sa však vyhli veľkému počtu pomlčiek (rovnajúcich sa poradiu derivátu), štvrtý derivát (napríklad) možno zapísať ako f (4) (X) a derivát n-tého rádu ako f (n) (X).

Dá sa ukázať, že krivka v bode je konvexná smerom nadol, ak je druhá derivácia kladná, a konvexná smerom nahor, ak je druhá derivácia záporná.

Ak má funkcia druhú deriváciu, potom ide o zmenu množstva r zodpovedajúce prírastku dx premenlivý X, možno približne vypočítať podľa vzorca

Táto aproximácia je vo všeobecnosti lepšia ako aproximácia daná diferenciálom fў ( X)dx... Zodpovedá nahradeniu časti krivky skôr parabolou ako priamkou.

Ak je funkcia f(X) existujú deriváty vyšších rádov, teda

Zvyšok je

kde X- nejaké číslo medzi X a X + dx... Vyššie uvedený výsledok sa nazýva zvyšok Taylorov vzorec. Ak f(X) má deriváty všetkých rádov, potom zvyčajne R n® 0 pre n ® Ґ .

INTEGRÁLNY POČET

Štvorce.

Pri štúdiu oblastí krivočiarych rovinných útvarov sa odhaľujú nové aspekty matematickej analýzy. Takéto problémy sa pokúšali vyriešiť aj starí Gréci, pre ktorých bolo určenie napríklad oblasti kruhu jednou z najťažších úloh. Veľký úspech pri riešení tohto problému dosiahol Archimedes, ktorému sa podarilo nájsť aj oblasť parabolického segmentu (obr. 12). Pomocou veľmi komplikovaného uvažovania Archimedes dokázal, že plocha parabolického segmentu je 2/3 plochy opísaného obdĺžnika, a preto sa v tomto prípade rovná (2/3) (16) = 32/3. Ako uvidíme neskôr, tento výsledok možno ľahko získať metódami matematickej analýzy.

Predchodcovia Newtona a Leibniza, hlavne Kepler a Cavalieri, vyriešili problém výpočtu plôch krivočiarych útvarov metódou, ktorú možno len ťažko nazvať logickou, ale ktorá sa ukázala ako mimoriadne plodná. Keď Wallis v roku 1655 spojil metódy Keplera a Cavalieriho s metódami Descartesa (analytická geometria) a použil novozrodenú algebru, javisko pre objavenie sa Newtona bolo úplne pripravené.

Wallis rozdelil postavu, ktorej plochu bolo potrebné vypočítať, na veľmi úzke pásy, z ktorých každý bol približne považovaný za obdĺžnik. Potom sčítal plochy aproximačných obdĺžnikov a v najjednoduchších prípadoch dostal hodnotu, ku ktorej smeruje súčet plôch obdĺžnikov, keď sa počet pruhov blíži k nekonečnu. Na obr. 13 znázorňuje obdĺžniky zodpovedajúce určitému rozdeleniu na pásy oblasti pod krivkou r = X 2 .

Hlavná veta.

Veľký objav Newtona a Leibniza umožnil vylúčiť namáhavý proces prechodu na hranicu súčtu plôch. Stalo sa tak vďaka novému pohľadu na koncept námestia. Ide o to, že si musíme predstaviť oblasť pod krivkou, ako ju vygeneruje ordináta pohybujúca sa zľava doprava, a opýtať sa, ako rýchlo sa mení oblasť vytiahnutá osi. Kľúč k odpovedi na túto otázku dostaneme, ak zvážime dva špeciálne prípady, v ktorých je oblasť vopred známa.

Začnime s oblasťou pod grafom lineárnej funkcie r = 1 + X pretože v tomto prípade možno plochu vypočítať pomocou elementárnej geometrie.

Nechaj A(X) Je časť roviny uzavretá medzi priamkou r = 1 + X a segment OQ(obr. 14). Pri jazde QP pravá oblasť A(X) zvyšuje. Ako rýchlo? Nie je ťažké odpovedať na túto otázku, pretože vieme, že plocha lichobežníka sa rovná súčinu jeho výšky a polovičného súčtu jeho základov. teda

Miera zmeny oblasti A(X) je určená jeho deriváciou

To vidíme Aў ( X) sa zhoduje s ordinátom pri bodov R... Je to náhoda? Skúsme skontrolovať parabolu znázornenú na obr. 15. Štvorec A (X) pod parabolou pri = X 2 v rozsahu od 0 do X rovná sa A(X) = (1 / 3)(X)(X 2) = X 3/3. Rýchlosť zmeny tejto oblasti je určená výrazom

ktorá sa presne zhoduje s ordinátom pri pohyblivý bod R.

Ak predpokladáme, že toto pravidlo sa vo všeobecnosti napĺňa tak, že

je rýchlosť zmeny plochy pod grafom funkcie r = f(X), potom to možno použiť na výpočty a iné oblasti. V skutočnosti pomer Aў ( X) = f(X) vyjadruje základnú vetu, ktorá by mohla byť formulovaná takto: derivácia alebo rýchlosť zmeny plochy ako funkcia X, sa rovná hodnote funkcie f (X) v bode X.

Napríklad na nájdenie oblasti pod grafom funkcie r = X 3 od 0 do X(obr. 16), dáme

Možná odpoveď je:

od derivátu X 4/4 sa skutočne rovná X 3. navyše A(X) sa rovná nule pre X= 0, ako by malo byť, keby A(X) je skutočne oblasť.

Matematická analýza dokazuje, že ďalšia odpoveď okrem vyššie uvedeného výrazu pre A(X), neexistuje. Ukážme, že toto tvrdenie je prijateľné pomocou nasledujúceho heuristického (nerigorózneho) uvažovania. Predpokladajme, že existuje nejaké druhé riešenie V(X). Ak A(X) a V(X) "Štart" súčasne od nulovej hodnoty pri X= 0 a po celú dobu sa menia rovnakou rýchlosťou, potom ich hodnoty pri č X nemôže byť iný. Musia byť všade rovnaké; preto je len jedno riešenie.

Ako možno zdôvodniť pomer? Aў ( X) = f(X) všeobecne? Na túto otázku možno odpovedať iba štúdiom rýchlosti zmeny oblasti ako funkcie X všeobecne. Nechaj m- najmenšia hodnota funkcie f (X) v rozsahu od X predtým ( X + h), a M- najväčšia hodnota tejto funkcie v rovnakom intervale. Potom prírastok oblasti na ceste z X Komu ( X + h) musia byť uzavreté medzi oblasťami dvoch obdĺžnikov (obr. 17). Základy oboch obdĺžnikov sú rovnaké h... Menší obdĺžnik má výšku m a oblasť mh, väčšie, resp. M a Mh... Na pozemku plocha vs X(obr. 18) je vidieť, že keď sa úsečka zmení o h, hodnota ordináta (t. j. plochy) sa zvýši o čiastku uzavretú medzi mh a Mh... Sklon sečnice v tomto grafe je medzi m a M... čo sa stane keď h má tendenciu k nule? Ak je graf funkcie r = f(X) je spojitý (t.j. neobsahuje diskontinuity), potom M a m mať tendenciu f(X). Preto svah Aў ( X) pozemok plochy ako funkcia X rovná sa f(X). Presne k takémuto záveru človek musel dospieť.

Leibniz navrhol pre oblasť pod krivkou r = f(X) od 0 do a označenie

Pri rigoróznom prístupe musí byť tento takzvaný určitý integrál definovaný ako hranica určitých súčtov na Wallisov spôsob. Vzhľadom na vyššie uvedený výsledok je zrejmé, že tento integrál sa vypočíta za predpokladu, že takúto funkciu nájdeme A(X), ktorý zaniká pri X= 0 a má deriváciu Aў ( X) rovná f (X). Nájdenie takejto funkcie sa zvyčajne nazýva integrácia, aj keď by bolo vhodnejšie nazvať túto operáciu antidiferenciáciou, čo znamená, že je v istom zmysle inverzná k diferenciácii. V prípade polynómu je integrácia jednoduchá. Napríklad ak

čo sa dá ľahko overiť diferenciáciou A(X).

Na výpočet plochy A 1 pod krivkou r = 1 + X + X 2/2, uzavreté medzi súradnicami 0 a 1, jednoducho napíšeme

a nahrádzanie X= 1, dostaneme A 1 = 1 + 1/2 + 1/6 = 5/3. Námestie A(X) od 0 do 2 sa rovná A 2 = 2 + 4/2 + 8/6 = 16/3. Ako je vidieť z obr. 19 je oblasť medzi súradnicami 1 a 2 A 2 – A 1 = 11/3. Zvyčajne sa píše ako určitý integrál

Objemy.

Podobné úvahy umožňujú prekvapivo jednoducho vypočítať objemy rotačných telies. Ukážme si to na príklade výpočtu objemu lopty, ďalšieho klasického problému, ktorý starí Gréci pomocou metód, ktoré poznali, dokázali vyriešiť len veľmi ťažko.

Otočte časť roviny ohraničenú štvrtinou kruhu s polomerom r, v uhle 360° okolo osi X... V dôsledku toho dostaneme hemisféru (obr. 20), ktorej objem označíme V(X). Je potrebné určiť mieru, ktorou sa V(X) s rastúcim X... Pokračujeme z X Komu X + h, je ľahké overiť, že prírastok objemu je menší ako objem p(r 2 – X 2)h polomer a výška kruhového valca h a viac ako objem p[r 2 – (X + h) 2 ]h polomer a výška valca h... Preto na grafe funkcie V(X) sklon sečnice je medzi p(r 2 – X 2) a p[r 2 – (X + h) 2]. Kedy h má tendenciu k nule, sklon má tendenciu

o X = r dostaneme

pre objem hemisféry, a preto 4 p r 3/3 na objem celej gule.

Podobná metóda umožňuje nájsť dĺžky kriviek a plochy zakrivených plôch. Napríklad ak a(X) - dĺžka oblúka PR na obr. 21, potom je našou úlohou vypočítať aў( X). Na heuristickej úrovni používame trik, ktorý nám umožňuje neuchýliť sa k obvyklému prechodu na limit, ktorý je potrebný na rigorózny dôkaz výsledku. Predpokladajme, že rýchlosť zmeny funkcie a(X) v bode R je rovnaký, ako by bol, keby krivku nahradila jej dotyčnica PT v bode P... Ale z obr. 21 je priamo vidieť pri šliapaní h napravo alebo naľavo od bodu X pozdĺž RT význam a(X) sa zmení na

Preto rýchlosť zmeny funkcie a(X) je

Na nájdenie samotnej funkcie a(X), je potrebné integrovať iba výraz na pravej strane rovnosti. Ukazuje sa, že väčšinu funkcií je ťažké integrovať. Preto vývoj metód integrálneho počtu tvorí veľkú časť matematickej analýzy.

Primitívne deriváty.

Každá funkcia, ktorej derivácia sa rovná danej funkcii f(X), sa nazýva primitívne (alebo primitívne) pre f(X). napr. X 3/3 je primitívna derivácia funkcie X 2, keďže ( X 3/3) ў = X 2. Samozrejme X 3/3 nie je jediným priradením funkcie X 2 odvtedy X 3 /3 + C je tiež derivátom pre X 2 pre akúkoľvek konštantu S... V nasledujúcom texte sa však dohodneme na vynechaní takýchto aditívnych konštánt. Všeobecne

kde n je kladné celé číslo, pretože ( x n + 1/(n+ 1)) ў = x n... Vzťah (1) platí v ešte všeobecnejšom zmysle, ak n nahradiť ľubovoľným racionálnym číslom k okrem -1.

Ľubovoľná priraďovacia funkcia pre danú funkciu f(X) sa zvyčajne nazýva neurčitý integrál z f(X) a označte ho ako

Napríklad, keďže (sin X) ў = cos X, vzorec je platný

V mnohých prípadoch, keď existuje vzorec pre neurčitý integrál danej funkcie, možno ho nájsť v mnohých široko publikovaných tabuľkách neurčitých integrálov. Integrály elementárnych funkcií sú tabuľkové (patria sem mocniny, logaritmy, exponenciálna funkcia, goniometrické funkcie, inverzné goniometrické funkcie, ako aj ich konečné kombinácie získané pomocou operácií sčítania, odčítania, násobenia a delenia). Pomocou tabuľkových integrálov môžete vypočítať integrály zložitejších funkcií. Existuje mnoho spôsobov, ako vypočítať neurčité integrály; najbežnejšou z nich je variabilná substitúcia alebo substitučná metóda. Spočíva v tom, že ak chceme nahradiť v neurčitom integráli (2) X na nejakej diferencovateľnej funkcii X = g(u), aby sa integrál nezmenil, je potrebné X nahradené gў ( u)du... Inými slovami, rovnosť

(náhrada 2 X = u, odkiaľ 2 dx = du).

Tu je ďalšia metóda integrácie - metóda integrácie po častiach. Vychádza z už známeho vzorca

Po integrácii ľavej a pravej strany a s prihliadnutím na to

Tento vzorec sa nazýva vzorec pre integráciu po častiach.

Príklad 2. Vyžaduje sa nájsť. Keďže čos X= (hriech X) ў, môžeme to napísať

Od (5), nastavenie u = X a v= hriech X, dostaneme

A keďže (–cos X) ў = hriech X nájdeme to a

Treba zdôrazniť, že sme sa obmedzili len na veľmi stručný úvod k veľmi rozsiahlej téme, v ktorej sa nahromadilo množstvo vtipných techník.

Funkcie dvoch premenných.

Kvôli krivke r = f(X) sme zvážili dve úlohy.

1) Nájdite sklon dotyčnice ku krivke v danom bode. Tento problém je vyriešený výpočtom hodnoty derivátu fў ( X) v určenom bode.

2) Nájdite oblasť pod krivkou nad segmentom osi X ohraničené zvislými čiarami X = a a X = b... Tento problém sa rieši výpočtom určitého integrálu.

Každý z týchto problémov má analóg v prípade povrchu z = f(X,r).

1) Nájdite dotykovú rovinu k povrchu v danom bode.

2) Nájdite objem pod povrchom nad časťou roviny hu ohraničený krivkou S, a zo strany - kolmice na rovinu xy prechádzajúci bodmi hraničnej krivky S (cm... ryža. 22).

Nasledujúce príklady ukazujú, ako sa tieto úlohy vykonávajú.

Príklad 4. Nájdite dotykovú rovinu k povrchu

v bode (0,0,2).

Rovina je definovaná, ak sú dané dve pretínajúce sa priamky v nej ležiace. Jeden z týchto riadkov ( l 1) nastúpime do lietadla xz (pri= 0), druhý ( l 2) - v lietadle yz (X = 0) (cm... ryža. 23).

V prvom rade ak pri= 0 teda z = f(X,0) = 2 – 2X – 3X 2. Derivát vzhľadom na X označené fў X(X,0) = –2 – 6X, o X= 0 má hodnotu –2. Rovno l 1 daný rovnicami z = 2 – 2X, pri= 0 - dotyčnica k S 1, priesečníky povrchu s rovinou pri= 0. Podobne ak X= 0 teda f(0,r) = 2 – r – r 2 a derivát vzhľadom na pri má formu

Pretože fў r(0,0) = –1, krivka S 2 - priesečník povrchu s rovinou yz- má dotyčnicu l 2 daný rovnicami z = 2 – r, X= 0. Požadovaná dotyková rovina obsahuje obe priamky l 1 a l 2 a je zapísaná rovnicou

Toto je rovnica roviny. Okrem toho dostaneme rovné čiary l 1 a l 2, nastavenie, resp. pri= 0 a X = 0.

Skutočnosť, že rovnica (7) skutočne definuje dotykovú rovinu, možno overiť na heuristickej úrovni, ak si všimneme, že táto rovnica obsahuje členy prvého rádu zahrnuté v rovnici (6) a že členy druhého rádu môžu byť reprezentované v forma -. Pretože tento výraz je záporný pre všetky hodnoty X a pri, Okrem toho X = pri= 0, plocha (6) leží všade pod rovinou (7), okrem bodu R= (0,0,0). Môžeme povedať, že plocha (6) je v bode konvexná smerom nahor R.

Príklad 5. Nájdite dotykovú rovinu k povrchu z = f(X,r) = X 2 – r 2 na začiatku 0.

Na povrchu pri= 0 máme: z = f(X,0) = X 2 a fў X(X,0) = 2X... Na S 1, priesečníky, z = X 2. V bode O sklon je fў X(0,0) = 0. Na rovine X= 0 máme: z = f(0,r) = –r 2 a fў r(0,r) = –2r... Na S 2, priesečníky, z = –r 2. V bode O sklon krivky S 2 sa rovná fў r(0,0) = 0. Keďže dotyčnice k S 1 a S 2 sú osi X a pri, dotyčnicová rovina, ktorá ich obsahuje, je rovina z = 0.

V blízkosti počiatku však náš povrch nie je na jednej strane dotyčnicovej roviny. Naozaj, krivka S 1 všade, okrem bodu 0, leží nad dotykovou rovinou a krivkou S 2 - respektíve pod ním. Plocha pretína dotykovú rovinu z= 0 v priamych čiarach pri = X a pri = –X... O takomto povrchu sa hovorí, že má na začiatku sedlový bod (obr. 24).

Parciálne deriváty.

V predchádzajúcich príkladoch sme použili deriváty z f (X,r) zapnuté X a podľa pri... Uvažujme teraz o takýchto derivátoch všeobecnejšie. Ak máme funkciu dvoch premenných, napr. F(X,r) = X 2 – xy, potom môžeme v každom bode definovať dve jeho „parciálne derivácie“, jednu derivovaním funkcie vzhľadom na X a upevnenie pri, druhý diferencovaním vzhľadom na pri a upevnenie X... Prvý z týchto derivátov je označený ako fў X(X,r) alebo ¶ f/¶ X; druhá - ako f f ў r... Ak oba zmiešané deriváty (podľa X a pri, na pri a X) sú spojité, potom ¶ 2 f/¶ X¶ r= ¶ 2 f/¶ r¶ X; v našom príklade ¶ 2 f/¶ X¶ r= ¶ 2 f/¶ r¶ X = –1.

Čiastočná derivácia fў X(X,r) udáva rýchlosť zmeny funkcie f v bode ( X,r) v smere zvyšovania X, a fў r(X,r) Je rýchlosť zmeny funkcie f vzostupný smer pri... Rýchlosť zmeny funkcie f v bode ( X,pri) v smere priamky zvierajúcej uhol q s kladným smerom osi X, sa nazýva derivácia funkcie f smerom k; jeho hodnota je kombináciou dvoch parciálnych derivácií funkcie f v dotyčnicovej rovine je takmer rovnaké (pre malé dx a D Y) skutočná zmena z na povrchu, ale výpočet diferenciálu je zvyčajne jednoduchší.

Vzorec, ktorý sme už zvážili z metódy premennej zmeny, známej ako derivácia komplexnej funkcie alebo reťazové pravidlo, v jednorozmernom prípade, keď pri záleží na X, a X záleží na t, má tvar:

Pre funkcie dvoch premenných je podobný vzorec:

Pojmy a označenia čiastočnej diferenciácie je ľahké zovšeobecniť do vyšších dimenzií. Najmä ak je povrch implicitne daný rovnicou f(X,r,z) = 0, rovnica dotykovej roviny k povrchu môže mať symetrickejší tvar: rovnica dotykovej roviny v bode ( x (x 2/4)], potom sa integruje X 0 ku 1. Konečný výsledok je 3/4.

Vzorec (10) možno interpretovať aj ako takzvaný dvojitý integrál, t.j. ako hranica súčtu objemov elementárnych „buniek“. Každá takáto bunka má základ D X D r a výška rovnajúca sa výške povrchu nad niektorým bodom obdĺžnikovej základne ( cm... ryža. 26). Dá sa ukázať, že oba pohľady na vzorec (10) sú ekvivalentné. Dvojité integrály sa používajú na nájdenie ťažísk a početných momentov nájdených v mechanike.

Dôslednejšie zdôvodňovanie matematického aparátu.

Doteraz sme koncepty a metódy kalkulu prezentovali na intuitívnej úrovni a neváhali sme siahnuť po geometrických tvaroch. Zostáva nám krátko zvážiť prísnejšie metódy, ktoré sa objavili v 19. a 20. storočí.

Začiatkom 19. storočia, keď sa skončila éra útokov a náporov v „tvorbe matematickej analýzy“, sa do popredia dostali otázky jej opodstatnenosti. V prácach Abela, Cauchyho a mnohých ďalších vynikajúcich matematikov boli pojmy „limita“, „spojitá funkcia“, „konvergujúce rady“ presne definované. Bolo to nevyhnutné na to, aby sa základ matematickej analýzy dostal do logického poriadku, aby sa z nej stal spoľahlivý výskumný nástroj. Potreba dôkladného zdôvodnenia sa stala ešte zrejmejšou po tom, čo Weierstrass v roku 1872 objavil všade spojité, ale nikde nediferencovateľné funkcie (graf takýchto funkcií má v každom bode zlom). Tento výsledok urobil na matematikov ohromujúci dojem, pretože jasne odporoval ich geometrickej intuícii. Ešte nápadnejším príkladom nespoľahlivosti geometrickej intuície bola súvislá krivka skonštruovaná D. Peanom, ktorá úplne vypĺňa určitý štvorec, t.j. prechádza všetkými jeho bodmi. Tieto a ďalšie objavy dali podnet k programu „aritmetizácie“ matematiky, t.j. čím sa stáva spoľahlivejším zdôvodňovaním všetkých matematických pojmov pomocou pojmu číslo. Takmer puritánska abstinencia od jasnosti v prácach o základoch matematiky mala svoje historické opodstatnenie.

Podľa moderných kánonov logickej prísnosti je neprípustné hovoriť o ploche pod krivkou. r = f(X) a nad segmentom osi X, dokonca f- súvislá funkcia bez toho, aby sa najprv definoval presný význam pojmu "plocha" a nezistilo sa, že takto určená plocha skutočne existuje. Tento problém úspešne vyriešil v roku 1854 B. Riemann, ktorý presne definoval pojem určitého integrálu. Odvtedy sa myšlienka zhrnutia za pojmom určitého integrálu stala predmetom mnohých hlbokých štúdií a zovšeobecnení. Výsledkom je, že dnes je možné dať význam určitému integrálu, aj keď je integrand všade nespojitý. Nové koncepcie integrácie, ku vzniku ktorých veľkou mierou prispel A. Lebesgue (1875–1941) a ďalší matematici, zvýšili silu a krásu modernej matematickej analýzy.

Sotva by bolo vhodné zachádzať do detailov všetkých týchto a iných pojmov. Obmedzíme sa len na presné definície limity a určitého integrálu.

Na záver povedzme, že matematická analýza, ktorá je mimoriadne cenným nástrojom v rukách vedca a inžiniera, aj dnes priťahuje pozornosť matematikov ako zdroj plodných myšlienok. Zároveň sa zdá, že moderný vývoj naznačuje, že matematická analýza je v 20. storočí čoraz viac pohltená takýmito dominantami. odbory matematiky ako abstraktná algebra a topológia.

Bez znalosti derivácie a metód jej výpočtu je absolútne nemožné riešiť fyzikálne problémy alebo príklady v matematike. Derivácia je jedným z najdôležitejších konceptov matematickej analýzy. Tejto zásadnej téme sme sa rozhodli venovať dnešný článok. Čo je to derivácia, aký je jej fyzikálny a geometrický význam, ako vypočítať deriváciu funkcie? Všetky tieto otázky možno spojiť do jednej: ako porozumieť derivátu?

Geometrický a fyzikálny význam derivácie

Nech existuje funkcia f (x) uvedené v nejakom intervale (a, b) ... Do tohto intervalu patria body х a х0. Keď sa zmení x, zmení sa aj samotná funkcia. Zmena argumentu - rozdiel medzi jeho hodnotami x-x0 ... Tento rozdiel je napísaný ako delta x a nazýva sa prírastok argumentov. Zmena alebo prírastok funkcie je rozdiel v hodnotách funkcie v dvoch bodoch. Definícia derivátu:

Derivácia funkcie v bode je limitom pomeru prírastku funkcie v danom bode k prírastku argumentu, keď ten má tendenciu k nule.

Inak sa to dá napísať aj takto:

Aký zmysel má nájsť takúto hranicu? A tu je čo:

derivácia funkcie v bode sa rovná dotyčnici uhla medzi osou OX a dotyčnici ku grafu funkcie v tomto bode.

Fyzikálny význam derivátu: derivácia dráhy vzhľadom na čas sa rovná rýchlosti priamočiareho pohybu.

V skutočnosti už od školských čias každý vie, že rýchlosť je súkromná cesta. x = f (t) a čas t ... Priemerná rýchlosť za určité obdobie:

Ak chcete zistiť rýchlosť pohybu v čase t0 musíte vypočítať limit:

Pravidlo jedna: vyberte konštantu

Konštantu možno presunúť mimo znamienka derivácie. Navyše sa to musí urobiť. Pri riešení príkladov v matematike berte ako pravidlo - ak môžete zjednodušiť výraz, určite zjednodušte .

Príklad. Vypočítajme deriváciu:

Pravidlo dva: derivácia súčtu funkcií

Derivácia súčtu dvoch funkcií sa rovná súčtu derivácií týchto funkcií. To isté platí pre deriváciu rozdielu funkcií.

Nebudeme dávať dôkazy o tejto vete, ale uvažujme skôr o praktickom príklade.

Nájdite deriváciu funkcie:

Pravidlo tri: derivácia súčinu funkcií

Derivácia súčinu dvoch diferencovateľných funkcií sa vypočíta podľa vzorca:

Príklad: nájdite deriváciu funkcie:

Riešenie:

Tu je dôležité povedať o výpočte derivácií komplexných funkcií. Derivácia komplexnej funkcie sa rovná súčinu derivácie tejto funkcie vzhľadom na stredný argument deriváciou stredného argumentu vzhľadom na nezávislú premennú.

Vo vyššie uvedenom príklade sa stretneme s výrazom:

V tomto prípade je stredný argument 8-násobok k piatej mocnine. Aby sme mohli vypočítať deriváciu takéhoto výrazu, najprv vypočítame deriváciu externej funkcie vzhľadom na stredný argument a potom vynásobíme deriváciou bezprostredného stredného argumentu vzhľadom na nezávislú premennú.

Pravidlo štyri: kvocientová derivácia dvoch funkcií

Vzorec na určenie derivácie podielu dvoch funkcií:

Snažili sme sa vám povedať o derivátoch pre figuríny od začiatku. Táto téma nie je taká jednoduchá, ako to znie, takže buďte upozornení: v príkladoch sa často vyskytujú úskalia, preto buďte opatrní pri výpočte derivátov.

V prípade akýchkoľvek otázok na túto a iné témy sa môžete obrátiť na študentský servis. V krátkom čase vám pomôžeme vyriešiť najťažší test a vysporiadať sa s úlohami, aj keď ste ešte nikdy nerobili počítanie derivácií.

Na ktorom sme analyzovali najjednoduchšie deriváty a tiež sme sa oboznámili s pravidlami diferenciácie a niektorými technikami na hľadanie derivátov. Ak teda nie ste veľmi v derivátoch funkcií alebo vám niektoré body tohto článku nie sú úplne jasné, prečítajte si najprv vyššie uvedenú lekciu. Prosím, nalaďte sa na vážnu náladu - materiál nie je ľahký, ale aj tak sa ho pokúsim podať jednoduchým a prístupným spôsobom.

V praxi sa musíte veľmi často zaoberať deriváciou komplexnej funkcie, dokonca by som povedal, že takmer vždy, keď dostanete úlohy na nájdenie derivácií.

V tabuľke sa pozrieme na pravidlo (č. 5) na diferenciáciu komplexnej funkcie:

Porozumenie. V prvom rade sa venujme nahrávke. Tu máme dve funkcie – a navyše funkcia je, obrazne povedané, do funkcie zakomponovaná. Funkcia tohto druhu (keď je jedna funkcia vnorená do inej) sa nazýva komplexná funkcia.

Zavolám funkciu vonkajšia funkcia a funkciu - vnútorná (alebo vnorená) funkcia.

! Tieto definície nie sú teoretické a nemali by sa objaviť v konečnom návrhu zadaní. Neformálne výrazy „vonkajšia funkcia“, „vnútorná“ funkcia používam len preto, aby som vám uľahčil pochopenie látky.

Ak chcete objasniť situáciu, zvážte:

Príklad 1

Nájdite deriváciu funkcie

Pod sínusom nemáme len písmeno "X", ale celočíselný výraz, takže deriváciu nebude možné okamžite nájsť z tabuľky. Všimli sme si tiež, že tu nie je možné použiť prvé štyri pravidlá, zdá sa, že existuje rozdiel, ale faktom je, že sínus nemôžete „roztrhnúť“:

V tomto príklade, už z mojich vysvetlení, je intuitívne jasné, že funkcia je komplexná funkcia a polynóm je vnútorná funkcia (vnorenie) a vonkajšia funkcia.

Prvý krok, ktorý je potrebné vykonať pri hľadaní derivácie komplexnej funkcie, je to zistiť, ktorá funkcia je vnútorná a ktorá vonkajšia.

V prípade jednoduchých príkladov sa zdá jasné, že polynóm je vnorený pod sínus. Ale čo ak všetko nie je zrejmé? Ako presne určiť, ktorá funkcia je vonkajšia a ktorá vnútorná? Na tento účel navrhujem použiť nasledujúcu techniku, ktorú je možné vykonať mentálne alebo na návrhu.

Predstavte si, že potrebujeme vypočítať hodnotu výrazu at na kalkulačke (namiesto jedného môže byť ľubovoľné číslo).

Čo vypočítame ako prvé? Po prvé budete musieť vykonať nasledujúcu akciu:, takže polynóm bude internou funkciou:

Po druhé bude potrebné nájsť, takže sínus bude externá funkcia:

Po nás Zistil s vnútornými a vonkajšími funkciami je čas uplatniť pravidlo diferenciácie komplexnej funkcie .

Začíname sa rozhodovať. Z lekcie Ako nájdem derivát? pamätáme si, že návrh riešenia akejkoľvek derivácie vždy začína takto - výraz uzavrieme do zátvoriek a vpravo hore umiestnime ťah:

najprv nájdite deriváciu vonkajšej funkcie (sínus), pozrite si tabuľku derivácií elementárnych funkcií a všimnite si to. Všetky tabuľkové vzorce sú použiteľné aj vtedy, ak je „x“ nahradené zložitým výrazom, v tomto prípade:

Všimnite si, že vnútorná funkcia sa nezmenil, nedotýkame sa ho.

No to je celkom zrejmé

Výsledok použitia vzorca vo finálnom dizajne to vyzerá takto:

Konštantný faktor je zvyčajne umiestnený na začiatku výrazu:

Ak dôjde k nejasnostiam, zapíšte si riešenie a znova si prečítajte vysvetlenia.

Príklad 2

Nájdite deriváciu funkcie

Príklad 3

Nájdite deriváciu funkcie

Ako vždy píšeme:

Poďme zistiť, kde máme vonkajšiu funkciu a kde máme vnútornú. Ak to chcete urobiť, skúste (mentálne alebo na koncepte) vypočítať hodnotu výrazu at. Čo treba urobiť ako prvé? Najprv musíte vypočítať, čomu sa rovná základňa: čo znamená, že polynóm je vnútorná funkcia:

A až potom sa vykoná umocnenie, preto je výkonová funkcia vonkajšou funkciou:

Podľa vzorca , najprv musíte nájsť deriváciu vonkajšej funkcie, v tomto prípade stupeň. Požadovaný vzorec hľadáme v tabuľke:. Znova opakujeme: akýkoľvek tabuľkový vzorec platí nielen pre "x", ale aj pre komplexný výraz... Teda výsledok uplatnenia pravidla diferenciácie komplexnej funkcie Ďalšie:

Opäť zdôrazňujem, že keď vezmeme deriváciu vonkajšej funkcie, vnútorná funkcia sa nám nezmení:

Teraz zostáva nájsť veľmi jednoduchú deriváciu vnútornej funkcie a výsledok trochu „učesať“:

Príklad 4

Nájdite deriváciu funkcie

Toto je príklad nezávislého riešenia (odpoveď na konci tutoriálu).

Pre upevnenie pochopenia derivácie komplexnej funkcie uvediem príklad bez komentárov, skúste si na to prísť sami, špekulujte, kde je vonkajšia a kde vnútorná funkcia, prečo sa úlohy riešili takto?

Príklad 5

a) Nájdite deriváciu funkcie

b) Nájdite deriváciu funkcie

Príklad 6

Nájdite deriváciu funkcie

Tu máme koreň a na rozlíšenie koreňa musí byť reprezentovaný ako stupeň. Najprv teda uvedieme funkciu do formy vhodnej na diferenciáciu:

Pri analýze funkcie dospejeme k záveru, že súčet troch členov je vnútorná funkcia a umocňovanie je vonkajšia funkcia. Uplatňujeme pravidlo diferenciácie komplexnej funkcie :

Stupeň je opäť reprezentovaný ako radikál (odmocnina) a pre deriváciu vnútornej funkcie aplikujeme jednoduché pravidlo na derivovanie súčtu:

Pripravený. Môžete tiež uviesť výraz do spoločného menovateľa v zátvorkách a všetko zapísať do jedného zlomku. Pekné, samozrejme, ale keď sa získajú ťažkopádne dlhé deriváty, je lepšie to nerobiť (je ľahké sa zmiasť, urobiť zbytočnú chybu a pre učiteľa bude nepohodlná kontrola).

Príklad 7

Nájdite deriváciu funkcie

Toto je príklad nezávislého riešenia (odpoveď na konci tutoriálu).

Je zaujímavé poznamenať, že niekedy namiesto pravidla na diferenciáciu komplexnej funkcie možno použiť pravidlo na diferenciáciu kvocientu , ale takéto riešenie bude vyzerať neobvykle ako zvrátenosť. Tu je typický príklad:

Príklad 8

Nájdite deriváciu funkcie

Tu môžete použiť pravidlo na diferenciáciu kvocientu , ale je oveľa výnosnejšie nájsť deriváciu pomocou pravidla diferenciácie komplexnej funkcie:

Pripravíme funkciu na diferenciáciu - posunieme mínus mimo znamienka derivácie a zvýšime kosínus do čitateľa:

Kosínus je vnútorná funkcia, umocňovanie je vonkajšia funkcia.
Používame naše pravidlo :

Nájdite deriváciu vnútornej funkcie, resetujte kosínus späť:

Pripravený. V uvažovanom príklade je dôležité nenechať sa zmiasť v znameniach. Mimochodom, skúste to vyriešiť pravidlom , odpovede sa musia zhodovať.

Príklad 9

Nájdite deriváciu funkcie

Toto je príklad nezávislého riešenia (odpoveď na konci tutoriálu).

Doteraz sme sa zaoberali prípadmi, keď sme mali v komplexnej funkcii iba jednu prílohu. V praktických úlohách sa často dajú nájsť odvodeniny, kde sa ako hniezdiace bábiky jedna do druhej vnorí 3 alebo aj 4-5 funkcií naraz.

Príklad 10

Nájdite deriváciu funkcie

Poďme pochopiť prílohy tejto funkcie. Pokúšame sa vyhodnotiť výraz pomocou testovacej hodnoty. Ako by sme rátali s kalkulačkou?

Najprv musíte nájsť, čo znamená, že arcsínus je najhlbšie hniezdenie:

Potom by mal byť tento arcsínus jedna odmocnený:

A nakoniec zdvihnite 7 na silu:

To znamená, že v tomto príklade máme tri rôzne funkcie a dve prílohy, pričom najvnútornejšia funkcia je arkussínus a vonkajšia funkcia je exponenciálna funkcia.

Začíname riešiť

Podľa pravidla najprv musíte vziať deriváciu vonkajšej funkcie. Pozrieme sa na tabuľku derivácií a nájdeme deriváciu exponenciálnej funkcie: Jediný rozdiel je v tom, že namiesto „x“ máme komplexný výraz, ktorý nepopiera platnosť tohto vzorca. Takže výsledok uplatnenia pravidla diferenciácie komplexnej funkcie Ďalšie.