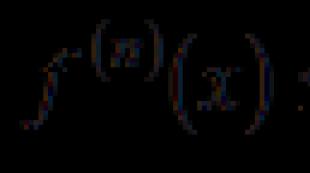Kto zaviedol derivát? Čo je to derivácia Definícia a význam derivačnej funkcie. Geometrický význam derivácie funkcie v bode
Úloha B9 poskytuje graf funkcie alebo derivácie, z ktorej musíte určiť jednu z nasledujúcich veličín:
- Hodnota derivátu v určitom bode x 0,
- Maximálny alebo minimálny počet bodov (extrémne body),
- Intervaly rastúcich a klesajúcich funkcií (intervaly monotónnosti).
Funkcie a derivácie uvedené v tomto probléme sú vždy spojité, čo značne uľahčuje riešenie. Napriek tomu, že úloha patrí do časti matematickej analýzy, zvládnu ju aj najslabší študenti, keďže tu nie sú potrebné žiadne hlboké teoretické znalosti.
Na nájdenie hodnoty derivácie, extrémnych bodov a intervalov monotónnosti existujú jednoduché a univerzálne algoritmy – o všetkých sa bude diskutovať nižšie.
Pozorne si prečítajte podmienky úlohy B9, aby ste sa vyhli hlúpym chybám: niekedy narazíte na dosť zdĺhavé texty, ale dôležitých podmienok, ktoré ovplyvňujú priebeh riešenia, je málo.
Výpočet hodnoty derivátu. Dvojbodová metóda
Ak je problému daný graf funkcie f(x), dotyčnica k tomuto grafu v určitom bode x 0, a je potrebné nájsť hodnotu derivácie v tomto bode, použije sa nasledujúci algoritmus:
- Nájdite dva „adekvátne“ body na dotyčnicovom grafe: ich súradnice musia byť celé číslo. Označme tieto body ako A (x 1 ; y 1) a B (x 2 ; y 2). Zapíšte si súradnice správne – ide o kľúčový bod riešenia a akákoľvek chyba tu povedie k nesprávnej odpovedi.
- Keď poznáme súradnice, je ľahké vypočítať prírastok argumentu Δx = x 2 − x 1 a prírastok funkcie Δy = y 2 − y 1 .
- Nakoniec nájdeme hodnotu derivácie D = Δy/Δx. Inými slovami, musíte vydeliť prírastok funkcie prírastkom argumentu – a toto bude odpoveď.
Ešte raz si všimnime: body A a B treba hľadať presne na dotyčnici, a nie na grafe funkcie f(x), ako sa to často stáva. Dotyková čiara bude nevyhnutne obsahovať aspoň dva takéto body - inak nebude problém správne formulovaný.
Zvážte body A (−3; 2) a B (−1; 6) a nájdite prírastky:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Zistime hodnotu derivácie: D = Δy/Δx = 4/2 = 2.
Úloha. Na obrázku je znázornený graf funkcie y = f(x) a dotyčnica k nej v bode s os x 0. Nájdite hodnotu derivácie funkcie f(x) v bode x 0 .
Zvážte body A (0; 3) a B (3; 0), nájdite prírastky:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Teraz nájdeme hodnotu derivácie: D = Δy/Δx = −3/3 = −1.
Úloha. Na obrázku je znázornený graf funkcie y = f(x) a dotyčnica k nej v bode s os x 0. Nájdite hodnotu derivácie funkcie f(x) v bode x 0 .
Zvážte body A (0; 2) a B (5; 2) a nájdite prírastky:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Zostáva nájsť hodnotu derivácie: D = Δy/Δx = 0/5 = 0.
Z posledného príkladu môžeme sformulovať pravidlo: ak je dotyčnica rovnobežná s osou OX, derivácia funkcie v bode dotyku je nulová. V tomto prípade nemusíte ani nič počítať - stačí sa pozrieť na graf.
Výpočet maximálneho a minimálneho počtu bodov
Niekedy namiesto grafu funkcie dáva úloha B9 graf derivácie a vyžaduje nájdenie maximálneho alebo minimálneho bodu funkcie. V tejto situácii je dvojbodová metóda zbytočná, ale existuje iný, ešte jednoduchší algoritmus. Najprv si definujme terminológiu:
- Bod x 0 sa nazýva maximálny bod funkcie f(x), ak v niektorom okolí tohto bodu platí nerovnosť: f(x 0) ≥ f(x).
- Bod x 0 sa nazýva minimálny bod funkcie f(x), ak v niektorom okolí tohto bodu platí nerovnosť: f(x 0) ≤ f(x).
Ak chcete nájsť maximum a minimum bodov z derivačného grafu, postupujte podľa týchto krokov:
- Prekreslite derivačný graf a odstráňte všetky nepotrebné informácie. Ako ukazuje prax, nepotrebné údaje len zasahujú do rozhodnutia. Preto na súradnicovej osi označíme nuly derivácie - a je to.
- Zistite znamienka derivácie na intervaloch medzi nulami. Ak je pre nejaký bod x 0 známe, že f'(x 0) ≠ 0, potom sú možné len dve možnosti: f'(x 0) ≥ 0 alebo f'(x 0) ≤ 0. Znamienko derivácie je ľahko určiť z pôvodného nákresu: ak derivačný graf leží nad osou OX, potom f'(x) ≥ 0. A naopak, ak derivačný graf leží pod osou OX, potom f'(x) ≤ 0.
- Opäť skontrolujeme nuly a znamienka derivácie. Tam, kde sa znamienko zmení z mínus na plus, je minimálny bod. Naopak, ak sa znamienko derivácie zmení z plus na mínus, ide o maximálny bod. Počítanie sa vždy vykonáva zľava doprava.
Táto schéma funguje len pre spojité funkcie - v úlohe B9 nie sú žiadne iné.
Úloha. Na obrázku je znázornený graf derivácie funkcie f(x) definovanej na intervale [−5; 5]. Nájdite minimálny bod funkcie f(x) na tomto segmente.
Zbavme sa nepotrebných informácií a ponechajme len hranice [−5; 5] a nuly derivácie x = −3 a x = 2,5. Všímame si aj tieto znaky:
Je zrejmé, že v bode x = −3 sa znamienko derivácie zmení z mínus na plus. Toto je minimálny bod.
Úloha. Na obrázku je znázornený graf derivácie funkcie f(x) definovanej na intervale [−3; 7]. Nájdite maximálny bod funkcie f(x) na tomto segmente.
Prekreslíme graf a ponecháme len hranice [−3; 7] a nuly derivácie x = −1,7 a x = 5. Všimnime si znamienka derivácie na výslednom grafe. Máme:
![]()
Je zrejmé, že v bode x = 5 sa znamienko derivácie zmení z plus na mínus - to je maximálny bod.
Úloha. Na obrázku je znázornený graf derivácie funkcie f(x), definovanej na intervale [−6; 4]. Nájdite maximálny počet bodov funkcie f(x) patriacich segmentu [−4; 3].
Z podmienok úlohy vyplýva, že stačí uvažovať len časť grafu obmedzenú úsečkou [−4; 3]. Zostavíme preto nový graf, na ktorom vyznačíme len hranice [−4; 3] a nuly derivácie v ňom. Konkrétne body x = −3,5 a x = 2. Dostaneme:
![]()
Na tomto grafe je len jeden maximálny bod x = 2. Práve v tomto bode sa mení znamienko derivácie z plus na mínus.
Malá poznámka o bodoch s neceločíselnými súradnicami. Napríklad v poslednej úlohe bol uvažovaný bod x = −3,5, ale s rovnakým úspechom môžeme vziať x = −3,4. Ak je problém zostavený správne, takéto zmeny by nemali ovplyvniť odpoveď, pretože body „bez trvalého bydliska“ sa priamo nezúčastňujú na riešení problému. Samozrejme, tento trik nebude fungovať s celočíselnými bodmi.
Hľadanie intervalov rastúcich a klesajúcich funkcií
V takom probléme, ako je maximálny a minimálny bod, sa navrhuje použiť derivačný graf na nájdenie oblastí, v ktorých sa samotná funkcia zvyšuje alebo znižuje. Najprv si definujme, čo je zvyšovanie a znižovanie:
- O funkcii f(x) sa hovorí, že je rastúca na segmente, ak pre ľubovoľné dva body x 1 a x 2 z tohto segmentu platí nasledujúce tvrdenie: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Inými slovami, čím väčšia je hodnota argumentu, tým väčšia je hodnota funkcie.
- O funkcii f(x) sa hovorí, že je na úsečke klesajúca, ak pre ľubovoľné dva body x 1 a x 2 z tejto úsečky platí nasledujúce tvrdenie: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . Tie. Väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.
Formulujme dostatočné podmienky na zvýšenie a zníženie:
- Aby spojitá funkcia f(x) na segmente vzrástla, stačí, aby jej derivácia vo vnútri segmentu bola kladná, t.j. f'(x) ≥ 0.
- Aby sa spojitá funkcia f(x) na segmente zmenšila, stačí, aby jej derivácia vo vnútri segmentu bola záporná, t.j. f'(x) ≤ 0.
Prijmime tieto vyhlásenia bez dôkazov. Získame tak schému na nájdenie intervalov zvyšovania a znižovania, ktorá je v mnohom podobná algoritmu na výpočet extrémnych bodov:
- Odstráňte všetky nepotrebné informácie. V pôvodnom grafe derivácie nás primárne zaujímajú nuly funkcie, preto necháme len tie.
- Označte znamienka derivácie v intervaloch medzi nulami. Kde f'(x) ≥ 0, funkcia sa zvyšuje a kde f'(x) ≤ 0 sa znižuje. Ak problém nastavuje obmedzenia na premennú x, dodatočne ich označíme na novom grafe.
- Teraz, keď poznáme správanie funkcie a obmedzenia, zostáva vypočítať množstvo požadované v úlohe.
Úloha. Na obrázku je znázornený graf derivácie funkcie f(x) definovanej na intervale [−3; 7,5]. Nájdite intervaly poklesu funkcie f(x). Vo svojej odpovedi uveďte súčet celých čísel zahrnutých v týchto intervaloch.
Ako obvykle, prekreslíme graf a označíme hranice [−3; 7,5], ako aj nuly derivácie x = −1,5 a x = 5,3. Potom si všimneme znaky derivácie. Máme:
![]()
Keďže derivácia je záporná na intervale (− 1,5), ide o interval klesajúcej funkcie. Zostáva sčítať všetky celé čísla, ktoré sú v tomto intervale:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Úloha. Na obrázku je znázornený graf derivácie funkcie f(x), definovanej na intervale [−10; 4]. Nájdite intervaly nárastu funkcie f(x). Vo svojej odpovedi uveďte dĺžku najväčšieho z nich.
Zbavme sa nepotrebných informácií. Ponechajme len hranice [−10; 4] a nuly derivácie, ktoré boli tentokrát štyri: x = −8, x = −6, x = −3 a x = 2. Označme znamienka derivácie a získame nasledujúci obrázok:
Zaujímajú nás intervaly rastúcej funkcie, t.j. také, kde f’(x) ≥ 0. Na grafe sú dva takéto intervaly: (−8; −6) a (−3; 2). Vypočítajme ich dĺžku:
l 1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.
Keďže potrebujeme nájsť dĺžku najväčšieho z intervalov, zapíšeme si ako odpoveď hodnotu l 2 = 5.
Nech je funkcia definovaná v bode a nejakom jeho okolí. Dajme argumentu taký prírastok, aby bod spadal do oblasti definície funkcie. Funkcia sa potom zvýši.
DEFINÍCIA. Derivácia funkcie v bode sa nazýva limita pomeru prírastku funkcie v tomto bode k prírastku argumentu, at (ak táto limita existuje a je konečná), t.j.
Označte: ,,,.
Derivácia funkcie v bode vpravo (vľavo) volal
(ak táto hranica existuje a je konečná).
Označené: , – derivácia v bode vpravo,
, je derivácia v bode vľavo.
Je zrejmé, že nasledujúca veta je pravdivá.
TEOREM. Funkcia má deriváciu v bode vtedy a len vtedy, ak v tomto bode existujú derivácie funkcie vpravo a vľavo a sú si navzájom rovné. Navyše
Nasledujúca veta vytvára spojenie medzi existenciou derivácie funkcie v bode a kontinuitou funkcie v tomto bode.
VETA (nevyhnutná podmienka existencie derivácie funkcie v bode). Ak má funkcia v bode deriváciu, potom je funkcia v tomto bode spojitá.
DÔKAZ
Nech to existuje. Potom
![]() ,
,
kde je nekonečne malé.
Komentujte
derivácia funkcie a označujú
diferenciácia funkcie .
GEOMETRICKÝ A FYZIKÁLNY VÝZNAM
1) Fyzikálny význam derivátu. Ak funkcia a jej argument sú fyzikálne veličiny, potom derivácia je rýchlosť zmeny premennej vzhľadom na premennú v bode. Napríklad, ak je vzdialenosť prejdená bodom v čase, potom jeho deriváciou je rýchlosť v danom čase. Ak je množstvo elektriny pretekajúcej prierezom vodiča v určitom časovom okamihu, potom je miera zmeny množstva elektriny v určitom časovom okamihu, t.j. sila prúdu v danom okamihu.
2) Geometrický význam derivácie.
Nech je nejaká krivka, buď bod na krivke. 
Nazýva sa akákoľvek priamka pretínajúca aspoň dva body sekanta .
Tangenta ku krivke v bode nazývaná hraničná poloha sečny, ak má bod tendenciu sa pohybovať po krivke.
Z definície je zrejmé, že ak v bode existuje dotyčnica ku krivke, potom je jediný
Uvažujme krivku (t. j. graf funkcie). Nech má v bode nevertikálnu dotyčnicu. Jeho rovnica: (rovnica priamky prechádzajúcej bodom a majúcej uhlový koeficient). 
Podľa definície svahu
kde je uhol sklonu priamky k osi.
Nech je uhol sklonu sečnice k osi, kde. Od je tangens, tak kedy
teda
Tak sme to dostali – uhlový koeficient dotyčnice ku grafu funkcie v bode(geometrický význam derivácie funkcie v bode). Preto rovnica dotyčnice ku krivke v bode môže byť zapísaná v tvare
Komentujte . Nazýva sa priamka prechádzajúca bodom kolmým na dotyčnicu vedenú ku krivke v bode kolmá na krivku v bode . Keďže uhlové koeficienty kolmých priamok sú spojené vzťahom, rovnica normály ku krivke v bode bude mať tvar
![]() , Ak .
, Ak .
Ak , potom dotyčnica ku krivke v bode bude mať tvar
a normálne.
TANGENTNÉ A NORMÁLNE ROVNICE
Tangentová rovnica
Nech je funkcia daná rovnicou r=f(X), musíte napísať rovnicu dotyčnica v bode X 0. Z definície derivátu:
r/(X)=limΔ X→0Δ rΔ X
Δ r=f(X+Δ X)−f(X).
Rovnica dotyčnica do funkčného grafu: r=kx+b (k,b=konšt). Z geometrického významu derivátu: f/(X 0)=tgα= k Pretože X 0 a f(X 0)∈ priamka, potom rovnica dotyčnica sa píše ako: r−f(X 0)=f/(X 0)(X−X 0) alebo
r=f/(X 0)· X+f(X 0)−f/(X 0)· X 0.

Normálna rovnica
Normálne- je kolmá na dotyčnica(pozri obrázok). Na základe toho:
tgβ= tg(2π−α)= ctg a=1 tg a=1 f/(X 0)
Pretože uhol sklonu normály je uhol β1, potom máme:
tg p1= tg(π−β)=− tgβ=-1 f/(X).
Bodka ( X 0,f(X 0))∈ normálne, rovnica má tvar:
r−f(X 0)=−1f/(X 0)(X−X 0).
DÔKAZ
Nech to existuje. Potom
![]() ,
,
kde je nekonečne malé.
Ale to znamená, že je spojitá v bode (pozri geometrickú definíciu spojitosti). ∎
Komentujte . Spojitosť funkcie v bode nie je dostatočnou podmienkou existencie derivácie tejto funkcie v bode. Napríklad funkcia je spojitá, ale nemá deriváciu v bode. naozaj,
a preto neexistuje.
Je zrejmé, že korešpondencia je funkcia definovaná na nejakej množine. Volajú ju derivácia funkcie a označujú
Operácia hľadania derivačnej funkcie funkcie sa nazýva diferenciácia funkcie .
Derivácia súčtu a rozdielu
Nech sú dané funkcie f(x) a g(x), ktorých derivácie sú nám známe. Môžete si napríklad vziať základné funkcie diskutované vyššie. Potom môžete nájsť deriváciu súčtu a rozdielu týchto funkcií:
(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’
Takže derivácia súčtu (rozdielu) dvoch funkcií sa rovná súčtu (rozdielu) derivácií. Termínov môže byť viac. Napríklad (f + g + h)’ = f’ + g’ + h’.
Presne povedané, v algebre neexistuje koncept „odčítania“. Existuje pojem „negatívny prvok“. Preto rozdiel f − g možno prepísať ako súčet f + (−1) g a potom zostane iba jeden vzorec - derivácia súčtu.
Obsah článku
DERIVÁT– derivácia funkcie r = f(X), daný v určitom intervale ( a, b) v bode X tohto intervalu sa nazýva hranica, ku ktorej smeruje pomer prírastku funkcie f v tomto bode na zodpovedajúci prírastok argumentu, keď má prírastok argumentu tendenciu k nule.
Derivát sa zvyčajne označuje takto:
Iné označenia sú tiež široko používané:
Okamžitá rýchlosť.
Nechajte bod M sa pohybuje v priamom smere. Vzdialenosť s pohyblivý bod, počítaný od nejakej počiatočnej polohy M 0 , závisí od času t, t.j. s existuje funkcia času t: s= f(t). Nech v určitom okamihu t pohyblivý bod M bol na diaľku s z východiskovej pozície M 0 a v ďalšom okamihu t+D t sa ocitla v pozícii M 1 - na diaľku s+D s z počiatočnej polohy ( pozri obr.).
Takže v priebehu času D t vzdialenosť s zmenené o sumu D s. V tomto prípade hovoria, že počas časového intervalu D t rozsah s dostal prírastok D s.
Priemerná rýchlosť nemôže vo všetkých prípadoch presne charakterizovať rýchlosť pohybu bodu M v určitom časovom bode t. Ak napríklad teleso na začiatku intervalu D t pohyboval sa veľmi rýchlo a na konci veľmi pomaly, potom priemerná rýchlosť nebude schopná odrážať naznačené vlastnosti pohybu bodu a poskytnúť predstavu o skutočnej rýchlosti jeho pohybu v súčasnosti t. Ak chcete presnejšie vyjadriť skutočnú rýchlosť pomocou priemernej rýchlosti, musíte použiť kratší časový úsek D t. Väčšina plne charakterizuje rýchlosť pohybu bodu v súčasnosti t limit, ku ktorému sa priemerná rýchlosť približuje pri D t® 0. Tento limit sa nazýva aktuálna rýchlosť:
Rýchlosť pohybu v danom momente sa teda nazýva hranica pomeru prírastku dráhy D s do časového prírastku D t, kedy má časový prírastok tendenciu k nule. Pretože
Geometrický význam derivácie. Tangenta ku grafu funkcie.
Konštrukcia dotyčníc je jedným z problémov, ktoré viedli k zrodu diferenciálneho počtu. Prvá publikovaná práca týkajúca sa diferenciálneho počtu, ktorú napísal Leibniz, mala názov Nová metóda maxím a miním, ako aj tangens, pre ktoré nie sú prekážkou ani zlomkové ani iracionálne veličiny, a na to špeciálny typ kalkulu.
Nech krivka je grafom funkcie r =f(X) v pravouhlom súradnicovom systéme ( cm. ryža.).
V nejakej hodnote X na funkcii záleží r =f(X). Tieto hodnoty X A r bod na krivke zodpovedá M 0(X, r). Ak argument X dať prírastok D X, potom nová hodnota argumentu X+D X zodpovedá novej hodnote funkcie y+ D r = f(X + D X). Zodpovedajúci bod krivky bude bod M 1(X+D X,r+D r). Ak nakreslíte seč M 0M 1 a označené j uhol tvorený priečkou s kladným smerom osi Vôl, z obrázku je hneď zrejmé, že .
Ak teraz D X má tendenciu k nule, potom bod M 1 sa pohybuje po krivke a približuje sa k bodu M 0 a uhol j zmeny s D X. O Dx® 0 uhol j smeruje k určitej hranici a a priamka prechádzajúca bodom M 0 a komponent s kladným smerom osi x, uhol a, bude požadovaná dotyčnica. Jeho sklon je:
teda f´( X) = tga
tie. derivátová hodnota f´( X) pre danú hodnotu argumentu X sa rovná dotyčnici uhla, ktorý tvorí dotyčnica ku grafu funkcie f(X) v príslušnom bode M 0(X,r) s kladným smerom osi Vôl.
Diferencovateľnosť funkcií.
Definícia. Ak funkcia r = f(X) má v bode deriváciu X = X 0, potom je funkcia v tomto bode diferencovateľná.
Spojitosť funkcie s deriváciou. Veta.
Ak funkcia r = f(X) je v určitom bode rozlíšiteľné X = X 0, potom je v tomto bode spojitá.
Funkcia teda nemôže mať deriváciu v bodoch diskontinuity. Nesprávny je opačný záver, t.j. zo skutočnosti, že v určitom okamihu X = X 0 funkcia r = f(X) je spojitý neznamená, že je v tomto bode diferencovateľný. Napríklad funkcia r = |X| nepretržite pre všetkých X(–Ґ x x = 0 nemá žiadnu deriváciu. V tomto bode neexistuje dotyčnica ku grafu. Existuje pravá a ľavá dotyčnica, ale nezhodujú sa.
Niektoré vety o diferencovateľných funkciách. Veta o koreňoch derivácie (Rolleova veta). Ak funkcia f(X) je na segmente súvislá [a,b], je diferencovateľná vo všetkých vnútorných bodoch tohto segmentu a na koncoch X = a A X = b ide na nulu ( f(a) = f(b) = 0), potom vnútri segmentu [ a,b] je tam aspoň jeden bod X= s, a c b, v ktorom je derivát fў( X) ide na nulu, t.j. fў( c) = 0.
Veta o konečnom prírastku (Lagrangeova veta). Ak funkcia f(X) je spojitý na intervale [ a, b] a je diferencovateľná vo všetkých vnútorných bodoch tohto segmentu, potom vo vnútri segmentu [ a, b] je tam aspoň jeden bod s, a c b to
f(b) – f(a) = fў( c)(b– a).
Veta o pomere prírastkov dvoch funkcií (Cauchyho veta). Ak f(X) A g(X) – dve funkcie súvislé na segmente [a, b] a diferencovateľné vo všetkých vnútorných bodoch tohto segmentu, a gў( X) nezmizne nikde v tomto segmente, potom vo vnútri segmentu [ a, b] je taký bod X = s, a c b to
Deriváty rôznych rádov.
Nechajte funkciu r =f(X) je diferencovateľný na určitom intervale [ a, b]. Odvodené hodnoty f ў( X), všeobecne povedané, závisí od X, t.j. derivát f ў( X) je tiež funkciou X. Pri derivovaní tejto funkcie získame takzvanú druhú deriváciu funkcie f(X), ktorý je označený f ўў ( X).
Derivát n- funkčného rádu f(X) sa nazýva derivát (prvého rádu) derivátu n- 1- a je označený symbolom r(n) = (r(n– 1))ў.
Diferenciály rôznych rádov.
Funkčný diferenciál r = f(X), Kde X– nezávislá premenná, áno D Y = f ў( X)dx, nejaká funkcia z X, ale od X môže závisieť iba prvý faktor f ў( X), druhý faktor ( dx) je prírastok nezávislej premennej X a nezávisí od hodnoty tejto premennej. Pretože D Y existuje funkcia od X, potom môžeme určiť diferenciál tejto funkcie. Diferenciál diferenciálu funkcie sa nazýva druhý diferenciál alebo diferenciál druhého rádu tejto funkcie a označuje sa d 2r:
d(dx) = d 2r = f ўў( X)(dx) 2 .
Diferenciál n- prvého rádu sa nazýva prvý diferenciál diferenciálu n- 1- poradie:
d n y = d(d n–1r) = f(n)(X)dx(n).
Čiastočná derivácia.
Ak funkcia nezávisí od jedného, ale od viacerých argumentov x i(i sa pohybuje od 1 do n,i= 1, 2,… n),f(X 1,X 2,… x n), potom sa v diferenciálnom počte zavedie pojem parciálna derivácia, ktorá charakterizuje rýchlosť zmeny funkcie viacerých premenných, keď sa zmení len jeden argument, napr. x i. Čiastočná derivácia 1. rádu vzhľadom na x i je definovaný ako obyčajný derivát a predpokladá sa, že všetky argumenty okrem x i, udržujte konštantné hodnoty. Pre parciálne derivácie sa zavádza zápis
Takto definované parciálne derivácie 1. rádu (ako funkcie tých istých argumentov) môžu mať zasa aj parciálne derivácie, ide o parciálne derivácie 2. rádu atď. Takéto deriváty prevzaté z rôznych argumentov sa nazývajú zmiešané. Spojité zmiešané deriváty rovnakého rádu nezávisia od rádu diferenciácie a sú si navzájom rovné.
Anna Chugainová
(\large\bf Derivácia funkcie)
Zvážte funkciu y=f(x), uvedený na intervale (a, b). Nechaj X- akýkoľvek pevný bod intervalu (a, b), A Δx- ľubovoľné číslo také, že hodnota x+Δx patrí tiež medzi interval (a, b). Toto číslo Δx nazývaný prírastok argumentov.
Definícia. Prírastok funkcie y=f(x) v bode X, zodpovedajúci prírastku argumentu Δx, zavoláme na číslo
Δy = f(x+Δx) - f(x).
Tomu veríme Δx ≠ 0. Zvážte v danom pevnom bode X pomer prírastku funkcie v tomto bode k prírastku zodpovedajúceho argumentu Δx
Tento vzťah budeme nazývať rozdielový vzťah. Od hodnoty X považujeme za pevný, rozdielový pomer je funkciou argumentu Δx. Táto funkcia je definovaná pre všetky hodnoty argumentov Δx, patriace do nejakého dostatočne malého okolia bodu Δx=0, okrem samotného bodu Δx=0. Máme teda právo zvážiť otázku existencie limity zadanej funkcie at Δx → 0.
Definícia. Derivácia funkcie y=f(x) v danom pevnom bode X s názvom limit at Δx → 0 rozdielový pomer, tzn
Za predpokladu, že tento limit existuje.
Označenie. y′(x) alebo f′(x).
Geometrický význam derivácie: Derivácia funkcie f(x) v tomto bode X rovná dotyčnici uhla medzi osou Vôl a dotyčnica ku grafu tejto funkcie v zodpovedajúcom bode:
f'(x 0) = \tgα.
Mechanický význam derivátu: Derivácia dráhy vzhľadom na čas sa rovná rýchlosti priamočiareho pohybu bodu:
Rovnica dotyčnice k priamke y=f(x) v bode M 0 (x 0, y 0) má formu
y-y 0 = f′(x 0) (x-x 0).
Normálou na krivku v určitom bode je kolmica na dotyčnicu v tom istom bode. Ak f′(x 0)≠ 0, potom rovnica normály k priamke y=f(x) v bode M 0 (x 0, y 0) sa píše takto:

Pojem diferencovateľnosti funkcie
Nechajte funkciu y=f(x) definované v určitom intervale (a, b), X- nejaká pevná hodnota argumentu z tohto intervalu, Δx- akýkoľvek prírastok argumentu tak, že hodnota argumentu x+Δx ∈ (a, b).
Definícia. Funkcia y=f(x) nazývané diferencovateľné v danom bode X, ak prírastok Δy túto funkciu v bode X, zodpovedajúci prírastku argumentu Δx, môžu byť zastúpené vo forme
Δy = A Δx + αΔx,
Kde A- nejaký počet nezávislý od Δx, A α - argumentačná funkcia Δx, ktorý je nekonečne malý Δx→ 0.
Keďže súčin dvoch nekonečne malých funkcií αΔx je infinitezimálom vyššieho rádu ako Δx(vlastnosť 3 infinitezimálnych funkcií), potom môžeme napísať:
Δy = A Δx + o (Δx).
Veta. Aby bola funkcia y=f(x) bol v danom bode diferencovateľný X, je potrebné a postačujúce, aby mal v tomto bode konečnú deriváciu. V čom A=f′(x), teda
Δy = f′(x) Δx +o(Δx).
Operácia nájdenia derivátu sa zvyčajne nazýva diferenciácia.
Veta. Ak funkcia y=f(x) X, potom je v tomto bode spojitá.
Komentujte. Z kontinuity funkcie y=f(x) v tomto bode X, vo všeobecnosti diferencovateľnosť funkcie nenasleduje f(x) v tomto bode. Napríklad funkcia y=|x|- súvislý v bode x=0, ale nemá žiadny derivát.
Pojem diferenciálnej funkcie
Definícia. Funkčný diferenciál y=f(x) volá sa súčin derivácie tejto funkcie a prírastku nezávislej premennej X:
dy = y′ Δx, df(x) = f′(x) Δx.
Pre funkciu y=x dostaneme dy=dx=x′Δx = 1· Δx= Δx, teda dx=Δx- diferenciál nezávislej premennej sa rovná prírastku tejto premennej.
Môžeme teda písať
dy = y′ dx, df(x) = f′(x) dx
![]()
Diferenciál D Y a prírastok Δy funkcie y=f(x) v tomto bode X, obe zodpovedajú rovnakému prírastku argumentu Δx, všeobecne povedané, nie sú si navzájom rovné.
Geometrický význam diferenciálu: Diferenciál funkcie sa rovná prírastku ordináty dotyčnice ku grafu tejto funkcie, keď sa argument zvyšuje Δx.
Pravidlá diferenciácie
Veta. Ak každá z funkcií u(x) A v(x) diferencovateľné v danom bode X, potom súčet, rozdiel, súčin a kvocient týchto funkcií (podiel za predpokladu, že v(x)≠ 0) sú v tomto bode tiež diferencovateľné a vzorce platia:

Zvážte komplexnú funkciu y=f(φ(x))≡ F(x), Kde y=f(u), u=φ(x). V tomto prípade u volal stredný argument, X - nezávislá premenná.
Veta. Ak y=f(u) A u=φ(x) sú diferencovateľné funkcie ich argumentov, potom derivácia komplexnej funkcie y=f(φ(x)) existuje a rovná sa súčinu tejto funkcie vzhľadom na medziargument a derivátu medziargumentu vzhľadom na nezávisle premennú, t.j.
![]()
Komentujte. Pre komplexnú funkciu, ktorá je superpozíciou troch funkcií y=F(f(φ(x))), diferenciačné pravidlo má podobu
y′ x = y′ u u′ v v′ x,
kde su funkcie v=φ(x), u=f(v) A y=F(u)- diferencovateľné funkcie ich argumentov.
Veta. Nechajte funkciu y=f(x) sa zväčšuje (alebo zmenšuje) a je súvislý v niektorom okolí bodu x 0. Nech je navyše táto funkcia v označenom bode diferencovateľná x 0 a jeho derivát v tomto bode f′(x 0) ≠ 0. Potom v nejakom okolí príslušného bodu y 0 = f (x 0) inverzná je definovaná pre y=f(x) funkciu x=f -1 (y) a uvedená inverzná funkcia je diferencovateľná v príslušnom bode y 0 = f (x 0) a pre jeho derivát v tomto bode r vzorec je platný

Tabuľka derivátov

Invariantnosť tvaru prvého diferenciálu
Zoberme si diferenciál komplexnej funkcie. Ak y=f(x), x=φ(t)- funkcie ich argumentov sú diferencovateľné, potom derivácia funkcie y=f(φ(t)) vyjadrené vzorcom
y' t = y' x x' t.
A-priorstvo dy=y′t dt, potom dostaneme
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,
dy = y′ x dx.
Takže máme dokázané
Vlastnosť invariantnosti tvaru prvého diferenciálu funkcie: ako v prípade, keď argument X je nezávislá premenná av prípade, že argument X sám je diferencovateľnou funkciou novej premennej, diferenciálu D Y funkcie y=f(x) sa rovná derivácii tejto funkcie vynásobenej diferenciálom argumentu dx.
Aplikácia diferenciálu v približných výpočtoch
Ukázali sme, že diferenciál D Y funkcie y=f(x), vo všeobecnosti sa nerovná prírastku Δy túto funkciu. Avšak až do infinitezimálnej funkcie vyššieho rádu malosti ako Δx, platí približná rovnosť
Δy ≈ dy.
Pomer sa nazýva relatívna chyba rovnosti tejto rovnosti. Pretože Δy-dy=o(Δx), potom sa relatívna chyba tejto rovnosti s klesaním stane taká malá, ako si želáte |Δх|.
Zvažujem to Δy=f(x+δ x)-f(x), dy=f'(x)Ax, dostaneme f(x+δ x)-f(x) ≈ f′(x)Δx alebo
f(x+δ x) ≈ f(x) + f′(x)Δx.
Táto približná rovnosť umožňuje s chybou o (Δx) nahradiť funkciu f(x) v malom okolí bodu X(t.j. pre malé hodnoty Δx) lineárna funkcia argumentu Δx, stojaci na pravej strane.
Deriváty vyššieho rádu
Definícia. Druhá derivácia (alebo derivácia druhého rádu) funkcie y=f(x) sa nazýva derivát svojej prvej derivácie.
Zápis druhej derivácie funkcie y=f(x):
Mechanický význam druhej derivácie. Ak funkcia y=f(x) opisuje zákon pohybu hmotného bodu po priamke, potom druhá derivácia f″(x) rovná zrýchleniu pohybujúceho sa bodu v danom čase X.
Tretí a štvrtý derivát sa určujú podobne.
Definícia. n derivát (alebo derivát n-tého rádu) funkcie y=f(x) sa nazýva jeho derivát n-1 derivát:
y (n) = (y (n-1))′, f (n) (x)=(f (n-1) (x))′.
Označenia: y″′, y IV, y V atď.
Geometrický význam derivácie
|
DEFINÍCIA TANGENTY KU KRIVKE Tangenta ku krivke y=ƒ(x) v bode M sa nazýva hraničná poloha sečnice vedenej cez bod M a bod, ktorý k nemu prilieha M 1 krivka za predpokladu, že bod M 1 sa približuje nekonečne pozdĺž krivky k bodu M. GEOMETRICKÝ VÝZNAM DERIVÁTU Derivácia funkcie y=ƒ(x) v bode X 0 sa číselne rovná dotyčnici uhla sklonu k osi Oh dotyčnica ku krivke y=ƒ(x) v bode M (x 0; ƒ(x 0)). |
VARIÁCIA DO KRIVKY Bodkované do krivky y=ƒ(x) presne tak M sa nazýva hraničná poloha čiary vedenej cez bod M a ďalší bod s ňou M 1 pokrivený, za hranicou mysle, aká pointa M 1 krivka sa nevyhnutne blíži k bodu M. GEOMETRICKÉ ZMIST POKHIDNOI Podobné funkcie y=ƒ(x) presne tak x 0číselne sa rovná dotyčnici sklonu k osi Oh dotický, vyvedený do krivky y=ƒ(x) presne tak M (x 0; ƒ(x 0)). |
Praktický význam derivátu
Uvažujme, čo prakticky znamená veličina, ktorú sme našli ako deriváciu určitej funkcie.
Po prvé, derivát- toto je základný pojem diferenciálneho počtu, charakterizujúci rýchlosť zmeny funkcie v danom bode.
Čo je to „miera zmeny“? Predstavme si funkciu f(x) = 5. Bez ohľadu na hodnotu argumentu (x) sa jeho hodnota nijako nemení. To znamená, že rýchlosť jeho zmeny je nulová.
Teraz zvážte funkciu f(x) = x. Derivácia x sa rovná jednej. V skutočnosti je ľahké si všimnúť, že pri každej zmene argumentu (x) o jednotku sa hodnota funkcie tiež zvýši o jednotku.
Z pohľadu prijatých informácií sa teraz pozrime na tabuľku derivácií jednoduchých funkcií. Na základe toho sa okamžite vyjasní fyzikálny význam hľadania derivácie funkcie. Toto pochopenie by malo uľahčiť riešenie praktických problémov.
Ak teda derivácia ukazuje rýchlosť zmeny funkcie, potom dvojitá derivácia ukazuje zrýchlenie.
2080.1947