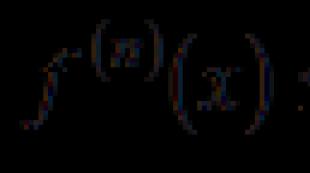Korene rovnice 2. rádu. Lineárne homogénne diferenciálne rovnice. Konštrukcia všeobecného riešenia k lineárnemu homogénnemu

Homogénne lineárne diferenciálne rovnice druhého rádu s konštantnými koeficientmi majú tvar

kde p a q sú reálne čísla. Pozrime sa na príklady, ako sa riešia homogénne diferenciálne rovnice druhého rádu s konštantnými koeficientmi.

Riešenie lineárnej homogénnej diferenciálnej rovnice druhého rádu závisí od koreňov charakteristickej rovnice. Charakteristickou rovnicou je rovnica k²+pk+q=0.

1) Ak sú koreňmi charakteristickej rovnice rôzne reálne čísla:

potom má všeobecné riešenie lineárnej homogénnej diferenciálnej rovnice druhého rádu s konštantnými koeficientmi tvar

2) Ak sa korene charakteristickej rovnice rovnajú reálnym číslam

(napríklad s diskriminantom rovným nule), potom je všeobecné riešenie homogénnej diferenciálnej rovnice druhého rádu

3) Ak sú koreňmi charakteristickej rovnice komplexné čísla

(napríklad s diskriminantom rovným zápornému číslu), potom sa všeobecné riešenie homogénnej diferenciálnej rovnice druhého rádu zapíše v tvare

Príklady riešenia lineárnych homogénnych diferenciálnych rovníc druhého rádu s konštantnými koeficientmi

Nájdite všeobecné riešenia homogénnych diferenciálnych rovníc druhého rádu:

Zostavíme charakteristickú rovnicu: k²-7k+12=0. Jeho diskriminant je D=b²-4ac=1>0, takže korene sú odlišné reálne čísla.

Všeobecné riešenie tohto homogénneho DE 2. rádu je teda

Poďme zostaviť a vyriešiť charakteristickú rovnicu:

Korene sú skutočné a zreteľné. Preto máme všeobecné riešenie tejto homogénnej diferenciálnej rovnice:

V tomto prípade charakteristická rovnica

Korene sú rôzne a platné. Preto je tu všeobecné riešenie homogénnej diferenciálnej rovnice 2. rádu

Charakteristická rovnica

Keďže korene sú skutočné a rovnaké, pre túto diferenciálnu rovnicu zapíšeme všeobecné riešenie ako

Charakteristická rovnica je tu

Keďže diskriminant je záporné číslo, korene charakteristickej rovnice sú komplexné čísla.

Všeobecné riešenie tejto homogénnej diferenciálnej rovnice druhého rádu má tvar

Charakteristická rovnica

Odtiaľ nájdeme všeobecné riešenie tohto diferenciálu. rovnice:

Príklady pre autotest.

§ 9. Lineárne homogénne diferenciálne rovnice druhého rádu s konštantnými koeficientmi

Definícia LODE druhého rádu s konštantnými koeficientmi

Charakteristická rovnica:

Prípad 1. Diskriminácia väčšia ako nula

Prípad 2 Diskriminácia je nulová

Prípad 3 Diskriminačný menej ako nula

Algoritmus na nájdenie všeobecného riešenia LODE druhého rádu s konštantnými koeficientmi

§ 10. Lineárne nehomogénne diferenciálne rovnice druhého rádu s konštantnými koeficientmi

Stanovenie LPDE druhého rádu s konštantnými koeficientmi

Metóda variácie konštánt

Metóda riešenia LNDDE so špeciálnou pravou stranou

Veta o štruktúre všeobecného riešenia LNDE

1. Funkcia r (X) – polynóm stupňa T

2. Funkcia r (X) – súčin čísla a exponenciálnej funkcie

3. Funkcia r (X) – súčet goniometrických funkcií

Algoritmus na nájdenie všeobecného riešenia LPDE so špeciálnou pravou stranou

Aplikácia

§ 9. Lineárne homogénne diferenciálne rovnice druhého rádu s konštantnými koeficientmi

Diferenciálna rovnica druhého rádu sa nazýva lineárna homogénna diferenciálna rovnica (LODE) s konštantnými koeficientmi, ak to vyzerá takto:

Kde p A q

Na nájdenie všeobecného riešenia LODE stačí nájsť jeho dve rôzne čiastkové riešenia a . Potom bude mať všeobecné riešenie LODE formu

Kde S 1 a S

Leonard Euler navrhol hľadať konkrétne riešenia LDE vo forme

Kde k- určitý počet.

Dvakrát diferencovať túto funkciu a nahradiť výrazy za pri, y" A y" do rovnice dostaneme:

Výsledná rovnica sa nazýva charakteristická rovnica LODU. Na jej zostavenie stačí nahradiť v pôvodnej rovnici y", y" A pri podľa toho k 2 , k a 1:

Po vyriešení charakteristickej rovnice, t.j. po nájdení koreňov k 1 a k 2, nájdeme aj konkrétne riešenia pôvodného LODE.

Charakteristická rovnica je kvadratická rovnica, jej korene sa nachádzajú cez diskriminant

V tomto prípade sú možné nasledujúce tri prípady.

Prípad 1. Diskriminácia väčšia ako nula , teda korene k 1 a k 2 platné a zreteľné:

k 1¹ k 2

Kde S 1 a S 2 – ľubovoľné nezávislé konštanty.

Prípad 2. Diskriminácia je nulová , teda korene k 1 a k 2 skutočné a rovnaké:

k 1 = k 2 = k

V tomto prípade má všeobecné riešenie LODE formu

Kde S 1 a S 2 – ľubovoľné nezávislé konštanty.

Prípad 3. Diskriminačný menej ako nula . V tomto prípade rovnica nemá žiadne skutočné korene:

Nie sú tam žiadne korene.

V tomto prípade má všeobecné riešenie LODE formu

Kde S 1 a S 2 – ľubovoľné nezávislé konštanty,

Nájdenie všeobecného riešenia LODE druhého rádu s konštantnými koeficientmi teda vedie k nájdeniu koreňov charakteristickej rovnice a použitiu vzorcov na všeobecné riešenie rovnice (bez použitia výpočtu integrálov).

Algoritmus na nájdenie všeobecného riešenia LODE druhého rádu s konštantnými koeficientmi:

1. Zredukujte rovnicu do tvaru kde p A q– nejaké reálne čísla.

2. Vytvorte charakteristickú rovnicu.

3. Nájdite diskriminant charakteristickej rovnice.

4. Pomocou vzorcov (pozri tabuľku 1) v závislosti od znamienka diskriminantu zapíšte všeobecné riešenie.

stôl 1

Tabuľka možných všeobecných riešení

V tomto článku preskúmame princípy riešenia lineárnych homogénnych diferenciálnych rovníc druhého rádu s konštantnými koeficientmi, kde p a q sú ľubovoľné reálne čísla. Najprv sa venujme teórii, potom získané výsledky aplikujme pri riešení príkladov a úloh.

Ak narazíte na neznáme pojmy, pozrite si časť o definíciách a konceptoch teórie diferenciálnych rovníc.

Sformulujme vetu, ktorá naznačuje, v akej forme nájsť všeobecné riešenie LOD.

Veta.

Všeobecné riešenie lineárnej homogénnej diferenciálnej rovnice s koeficientmi spojitými na integračnom intervale X je určené lineárnou kombináciou , Kde sú lineárne nezávislé parciálne riešenia LDE na X a sú to ľubovoľné konštanty.

Všeobecné riešenie lineárnej homogénnej diferenciálnej rovnice druhého rádu s konštantnými koeficientmi má teda tvar y 0 =C 1 ⋅y 1 +C 2 ⋅y 2, kde y 1 a y 2 sú čiastočné lineárne nezávislé riešenia a C 1 a C2 sú ľubovoľné konštanty. Zostáva naučiť sa nájsť čiastkové riešenia y 1 a y 2.

Euler navrhol hľadať konkrétne riešenia vo formulári.

Ak vezmeme čiastočné riešenie LODE druhého rádu s konštantnými koeficientmi, potom pri dosadení tohto riešenia do rovnice by sme mali získať identitu:

Tak sme dostali tzv charakteristická rovnica lineárna homogénna diferenciálna rovnica druhého rádu s konštantnými koeficientmi. Riešenia k 1 a k 2 tejto charakteristickej rovnice určujú parciálne riešenia našej LODE druhého rádu s konštantnými koeficientmi.

V závislosti od koeficientov p a q môžu byť korene charakteristickej rovnice:

V prvom prípade lineárne nezávislé parciálne riešenia pôvodnej diferenciálnej rovnice sú a , všeobecné riešenie LODE druhého rádu s konštantnými koeficientmi je .

Funkcie a sú skutočne lineárne nezávislé, pretože Wronského determinant je nenulový pre akékoľvek reálne x pre .

V druhom prípade jedným konkrétnym riešením je funkcia . Ako druhé konkrétne riešenie berieme . Ukážme, čo je v skutočnosti konkrétnym riešením LODE druhého rádu s konštantnými koeficientmi a dokážme lineárnu nezávislosť y 1 a y 2.

Pretože k 1 = k 0 a k 2 = k 0 sú rovnaké korene charakteristickej rovnice, má tvar . Preto je pôvodná lineárna homogénna diferenciálna rovnica. Dosaďte to do nej a uistite sa, že rovnica sa stane identitou:

Ide teda o čiastočné riešenie pôvodnej rovnice.

Ukážme lineárnu nezávislosť funkcií a . Aby sme to urobili, vypočítajme Wronského determinant a uistite sa, že je odlišný od nuly.

Záver: lineárne nezávislé parciálne riešenia LODE druhého rádu s konštantnými koeficientmi sú a , a všeobecné riešenie existuje pre .

V treťom prípade máme dvojicu komplexných čiastkových riešení LDE a . Všeobecné riešenie bude napísané ako . Tieto konkrétne riešenia môžu byť nahradené dvoma skutočnými funkciami a , ktoré zodpovedajú skutočným a imaginárnym častiam. To možno jasne vidieť, ak premeníme všeobecné riešenie pomocou vzorcov z teória funkcie komplexnej premennej typ:


kde C3 a C4 sú ľubovoľné konštanty.

Poďme si teda zhrnúť teóriu.

Algoritmus na nájdenie všeobecného riešenia lineárnej homogénnej diferenciálnej rovnice druhého rádu s konštantnými koeficientmi.

Pozrime sa na príklady pre každý prípad.

Príklad.

Nájdite všeobecné riešenie lineárnej homogénnej diferenciálnej rovnice druhého rádu s konštantnými koeficientmi .

Lineárna diferenciálna rovnica 2. rádu (LDE) má nasledujúci tvar:

kde , , a sú dané funkcie, ktoré sú spojité na intervale, na ktorom sa hľadá riešenie. Za predpokladu, že a 0 (x) ≠ 0, vydelíme (2.1) a po zavedení nových označení pre koeficienty zapíšeme rovnicu v tvare:

Pripusťme bez dôkazu, že (2.2) má na nejakom intervale jedinečné riešenie, ktoré spĺňa všetky počiatočné podmienky , , ak na uvažovanom intervale funkcie , a sú spojité. Ak , potom sa rovnica (2.2) nazýva homogénna a rovnica (2.2) sa inak nazýva nehomogénna.

Uvažujme o vlastnostiach roztokov 2. rádu.

Definícia. Lineárna kombinácia funkcií je výraz , kde sú ľubovoľné čísla.

Veta. Ak a – riešenie

potom ich lineárna kombinácia bude tiež riešením tejto rovnice.

Dôkaz.

Dajme výraz do (2.3) a ukážme, že výsledkom je identita:

Preusporiadame si pojmy:

Keďže funkcie sú riešením rovnice (2.3), potom každá zo zátvoriek v poslednej rovnici je zhodne rovná nule, čo bolo potrebné dokázať.

Dôsledok 1. Z dokázanej vety vyplýva, že ak je riešením rovnica (2.3), potom existuje aj riešenie tejto rovnice.

Dôsledok 2. Za predpokladu, že vidíme, že súčet dvoch riešení Lod je tiež riešením tejto rovnice.

Komentujte. Vlastnosť riešení dokázaná vo vete zostáva platná pre problémy akéhokoľvek poradia.

§3. Vronského determinant.

Definícia. O systéme funkcií sa hovorí, že je lineárne nezávislý na určitom intervale, ak žiadna z týchto funkcií nemôže byť reprezentovaná ako lineárna kombinácia všetkých ostatných.

V prípade dvoch funkcií to znamená , t.j. . Posledná podmienka môže byť prepísaná ako alebo . Determinant v čitateli tohto výrazu je sa nazýva Wronského determinant pre funkcie a . Wronského determinant pre dve lineárne nezávislé funkcie teda nemôže byť zhodne rovný nule.

Nechaj je Wronského determinant pre lineárne nezávislé riešenia a rovnicu (2.3). Substitúciou sa presvedčíme, že funkcia spĺňa rovnicu. (3.1)

Naozaj,. Keďže funkcie a spĺňajú rovnicu (2.3), potom, t.j. – riešenie rovnice (3.1). Nájdime toto riešenie: ; . Kde , . , , .

Na pravej strane tohto vzorca musíte vziať znamienko plus, pretože iba v tomto prípade sa získa identita. teda

(3.2)

Tento vzorec sa nazýva Liouvilleho vzorec. Vyššie bolo ukázané, že Wronského determinant pre lineárne nezávislé funkcie nemôže byť identicky rovný nule. V dôsledku toho existuje bod, v ktorom je determinant pre lineárne nezávislé riešenia rovnice (2.3) odlišný od nuly. Z Liouvilleovho vzorca potom vyplýva, že funkcia bude nenulová pre všetky hodnoty v uvažovanom intervale, keďže pre akúkoľvek hodnotu sú oba faktory na pravej strane vzorca (3.2) nenulové.

§4. Štruktúra celkového riešenia lode 2. rádu.

Veta. Ak a sú lineárne nezávislé riešenia rovnice (2.3), potom ich lineárna kombinácia , kde a sú ľubovoľné konštanty, bude všeobecným riešením tejto rovnice.

Dôkaz.

Čo je riešením rovnice (2.3), vyplýva z vety o vlastnostiach riešení 2. rádu Lodo. Musíme len ukázať, že riešenie bude všeobecný, t.j. je potrebné ukázať, že pre akékoľvek počiatočné podmienky je možné zvoliť ľubovoľné konštanty tak, aby tieto podmienky spĺňali. Zapíšme si počiatočné podmienky vo forme:

Konštanty a z tohto systému lineárnych algebraických rovníc sú určené jednoznačne, pretože determinantom tohto systému je hodnota Wronského determinantu pre lineárne nezávislé riešenia Lodu pri:

,

a takýto determinant, ako sme videli v predchádzajúcom odseku, je nenulový. Veta bola dokázaná.

Príklad. Dokážte, že funkcia , kde a sú ľubovoľné konštanty, je všeobecným riešením Lod.

Riešenie.

Je ľahké overiť substitúciou, že funkcie a spĺňajú túto rovnicu. Tieto funkcie sú lineárne nezávislé, od r . Preto, podľa vety o štruktúre všeobecného riešenia, lode 2. rádu je všeobecným riešením tejto rovnice.

Diferenciálne rovnice 2. rádu

§1. Metódy redukcie rádu rovnice.

Diferenciálna rovnica 2. rádu má tvar:

https://pandia.ru/text/78/516/images/image002_107.gif" width="19" height="25 src=">.gif" width="119" height="25 src="> ( alebo Diferenciálna" href="/text/category/differentcial/" rel="bookmark">Diferenciálna rovnica 2. rádu). Cauchyho úloha pre diferenciálnu rovnicu 2. rádu (1..gif" width="85" height= "25 src =">.gif" width="85" height="25 src=">.gif" height="25 src=">.

Nech má diferenciálna rovnica 2. rádu tvar: https://pandia.ru/text/78/516/images/image009_41.gif" height="25 src=">..gif" width="39" height=" 25 src=">.gif" width="265" height="28 src=">.

Teda rovnica 2. rádu https://pandia.ru/text/78/516/images/image015_28.gif" width="34" height="25 src=">.gif" width="118" height =" 25 src=">.gif" width="117" height="25 src=">.gif" width="34" height="25 src=">. Jeho vyriešením dostaneme všeobecný integrál pôvodnej diferenciálnej rovnice v závislosti od dvoch ľubovoľných konštánt: DIV_ADBLOCK219">

Príklad 1 Vyriešte diferenciálnu rovnicu https://pandia.ru/text/78/516/images/image021_18.gif" width="70" height="25 src=">.gif" height="25 src=">.gif " width="39" height="25 src=">.gif" width="157" height="25 src=">.gif" width="112" height="25 src=">.

Toto je diferenciálna rovnica s oddeliteľnými premennými: https://pandia.ru/text/78/516/images/image026_19.gif" width="99" height="41 src=">, t.j.gif" width= " 96" height="25 src=">.gif" width="53" height="25 src=">.gif" width="48" height="38 src=">..gif" width=" 99 " height="38 src=">..gif" width="95" height="25 src=">.

2..gif" width="117" height="25 src=">, t.j.gif" width="102" height="25 src=">..gif" width="117" height= "25 src =">.gif" width="106" height="25 src=">.gif" width="34" height="25 src=">.gif" width="117" height="25 src=" >.gif" width="111" height="27 src=">

Riešenie.

Táto rovnica 2. rádu zjavne neobsahuje požadovanú funkciu https://pandia.ru/text/78/516/images/image043_16.gif" width="98" height="25 src=">.gif" width= " 33" height="25 src=">.gif" width="105" height="36 src=">, čo je lineárna rovnica..gif" width="109" height="36 src=">. . gif" width="144" height="36 src=">.gif" height="25 src="> z niektorých funkcií..gif" width="25" height="25 src=">.gif " width="127" height="25 src=">.gif" width="60" height="25 src="> – poradie rovnice sa zníži.

§2. Lineárna diferenciálna rovnica 2. rádu.

Lineárna diferenciálna rovnica 2. rádu (LDE) má nasledujúci tvar:

https://pandia.ru/text/78/516/images/image059_12.gif" width="42" height="25 src=">.gif" width="42" height="25 src=">. gif" width="42" height="25 src="> a po zavedení nových zápisov pre koeficienty zapíšeme rovnicu v tvare:

https://pandia.ru/text/78/516/images/image064_12.gif" width="76" height="25 src=">.gif" width="35" height="25 src=">. gif" width="30" height="25 src="> súvislé..gif" width="165" height="25 src=">.gif" width="95" height="25 src="> – ľubovoľné čísla.

Veta. Ak https://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> - riešením je

https://pandia.ru/text/78/516/images/image076_10.gif" width="182" height="25 src="> bude tiež riešením tejto rovnice.

Dôkaz.

Dajme výraz https://pandia.ru/text/78/516/images/image077_11.gif" width="420" height="25 src=">.

Preusporiadame si pojmy:

https://pandia.ru/text/78/516/images/image073_10.gif" width="42" height="25 src=">.gif" width="54" height="25 src=">. gif" width="94" height="25 src="> je tiež riešením tejto rovnice.

Dôsledok 2. Za predpokladu, že https://pandia.ru/text/78/516/images/image083_11.gif" width="58" height="25 src="> je tiež riešením tejto rovnice.

Komentujte. Vlastnosť riešení dokázaná vo vete zostáva platná pre problémy akéhokoľvek poradia.

§3. Vronského determinant.

Definícia. Systém funkcií https://pandia.ru/text/78/516/images/image084_10.gif" width="61" height="25 src=">.gif" width="110" height="47 src= " >..gif" width="106" height="42 src=">..gif" width="42" height="25 src=">.gif" width="181" height="47 src= " >.gif" width="42" height="25 src="> rovnice (2.3)..gif" width="182" height="25 src=">. (3.1)

..gif" width="18" height="25 src="> rovnicu spĺňa (2..gif" width="42" height="25 src="> je riešením rovnice (3.1). .gif" width="87" height="28 src=">..gif" width="182" height="34 src=">..gif" width="162" height="42 src="> .gif" width="51" height="25 src="> získa sa identita.

https://pandia.ru/text/78/516/images/image107_7.gif" width="18" height="25 src=">, v ktorom je determinant pre lineárne nezávislé riešenia rovnice (2..gif " width= "42" height="25 src=">.gif" height="25 src="> oba faktory na pravej strane vzorca (3.2) sú nenulové.

§4. Štruktúra celkového riešenia lode 2. rádu.

Veta. Ak https://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> sú lineárne nezávislé riešenia rovnice (2..gif" width=" 19" height="25 src=">.gif" width="129" height="25 src=">je riešením rovnice (2.3), vyplýva z vety o vlastnostiach riešení 2. rádu. gif" width="85 " height="25 src=">.gif" width="19" height="25 src=">.gif" width="220" height="47">

Konštanty https://pandia.ru/text/78/516/images/image003_79.gif" width="19" height="25 src="> z tohto systému lineárnych algebraických rovníc sú určené jednoznačne, pretože determinant tento systém https: //pandia.ru/text/78/516/images/image006_56.gif" width="51" height="25 src=">:

https://pandia.ru/text/78/516/images/image116_7.gif" width="138" height="25 src=">.gif" width="19" height="25 src=">. gif" width="69" height="25 src=">.gif" width="235" height="48 src=">..gif" width="143" height="25 src="> (5 ..gif" width="77" height="25 src=">. Podľa predchádzajúceho odseku sa všeobecné riešenie Lod 2. rádu ľahko určí, ak sú známe dve lineárne nezávislé parciálne riešenia tejto rovnice. Jednoduchá metóda na nájdenie čiastočných riešení rovnice s konštantnými koeficientmi, ktorú navrhol L. Euler..gif" width="25" height="26 src=">, dostaneme algebraickú rovnicu, ktorá sa nazýva charakteristika:

https://pandia.ru/text/78/516/images/image124_5.gif" width="59" height="26 src="> bude riešením rovnice (5.1) len pre tie hodnoty k to sú korene charakteristickej rovnice (5.2)..gif" width="49" height="25 src=">..gif" width="76" height="28 src=">.gif" width= "205" height="47 src ="> a všeobecné riešenie (5..gif" width="45" height="25 src=">..gif" width="74" height="26 src=" >..gif" width="83 " height="26 src=">. Skontrolujte, či táto funkcia spĺňa rovnicu (5.1)..gif" width="190" height="26 src=">. Nahradenie týchto výrazov do rovnice (5.1), dostaneme

https://pandia.ru/text/78/516/images/image141_6.gif" width="328" height="26 src=">, pretože..gif" width="137" height="26 src= ">.

Konkrétne riešenia https://pandia.ru/text/78/516/images/image145_6.gif" width="86" height="28 src="> sú lineárne nezávislé, pretože..gif" width="166" height ="26 src=">.gif" width="45" height="25 src=">..gif" width="65" height="33 src=">.gif" width="134" height = "25 src=">.gif" width="267" height="25 src=">.gif" width="474" height="25 src=">.

Obe zátvorky na ľavej strane tejto rovnosti sú zhodne rovné nule..gif" width="174" height="25 src=">..gif" width="132" height="25 src="> je riešenie rovnice (5.1) ..gif" width="129" height="25 src="> bude vyzerať takto:

https://pandia.ru/text/78/516/images/image162_6.gif" width="179" height="25 src="> f(x) (6.1)

je prezentovaný ako súčet všeobecného riešenia https://pandia.ru/text/78/516/images/image164_6.gif" width="195" height="25 src="> (6.2)

a akékoľvek konkrétne riešenie https://pandia.ru/text/78/516/images/image166_6.gif" width="87" height="25 src="> bude riešením rovnice (6.1)..gif" width=" 272" height="25 src="> f(x). Táto rovnosť je identita, pretože..gif" width="128" height="25 src="> f(x). Preto.gif" width="85" height="25 src=">.gif" šírka ="138" height="25 src=">.gif" width="18" height="25 src="> sú lineárne nezávislé riešenia tejto rovnice. Takto:

https://pandia.ru/text/78/516/images/image173_5.gif" width="289" height="48 src=">

https://pandia.ru/text/78/516/images/image002_107.gif" width="19" height="25 src=">.gif" width="11" height="25 src=">. gif" width="51" height="25 src="> a takýto determinant, ako sme videli vyššie, je nenulový..gif" width="19" height="25 src="> zo systému rovníc (6 ..gif" width="76" height="25 src=">.gif" width="76" height="25 src=">.gif" width="140" height="25 src ="> vyrieši rovnicu

https://pandia.ru/text/78/516/images/image179_5.gif" width="91" height="25 src="> do rovnice (6.5), dostaneme

https://pandia.ru/text/78/516/images/image181_5.gif" width="140" height="25 src=">.gif" width="128" height="25 src="> f (x) (7,1)

kde https://pandia.ru/text/78/516/images/image185_5.gif" width="34" height="25 src="> rovnica (7.1) v prípade, že pravá strana f(x ) má špeciálny tvar. Táto metóda sa nazýva metóda neurčitých koeficientov a spočíva vo výbere konkrétneho riešenia v závislosti od typu pravej strany f(x). Uvažujme pravé strany nasledujúceho tvaru:

1..gif" width="282" height="25 src=">.gif" width="53" height="25 src=">, môže byť nula. Uveďme, v akej forme je v tomto prípade potrebné prijať konkrétne riešenie.

a) Ak je číslo https://pandia.ru/text/78/516/images/image191_5.gif" width="393" height="25 src=">.gif" width="157" height="25 src =>>.

Riešenie.

Pre rovnicu https://pandia.ru/text/78/516/images/image195_4.gif" width="86" height="25 src=">..gif" width="62" height="25 src = ">..gif" width="101" height="25 src=">.gif" width="153" height="25 src=">.gif" width="383" height="25 src= " >.

Obe časti zredukujeme na https://pandia.ru/text/78/516/images/image009_41.gif" height="25 src="> na ľavej a pravej strane rovnosti

https://pandia.ru/text/78/516/images/image206_5.gif" width="111" height="40 src=">

Z výsledného systému rovníc nájdeme: https://pandia.ru/text/78/516/images/image208_5.gif" width="189" height="25 src="> a všeobecné riešenie daného rovnica je:

https://pandia.ru/text/78/516/images/image190_5.gif" width="11" height="25 src=">.gif" width="423" height="25 src=">,

kde https://pandia.ru/text/78/516/images/image212_5.gif" width="158" height="25 src=">.

Riešenie.

Zodpovedajúca charakteristická rovnica má tvar:

https://pandia.ru/text/78/516/images/image214_6.gif" width="53" height="25 src=">.gif" width="85" height="25 src=">. gif" width="45" height="25 src=">.gif" width="219" height="25 src=">..gif" width="184" height="35 src=">. Konečné pre všeobecné riešenie máme nasledujúci výraz:

https://pandia.ru/text/78/516/images/image223_4.gif" width="170" height="25 src=">.gif" width="13" height="25 src="> výborné od nuly. Označme typ konkrétneho riešenia v tomto prípade.

a) Ak je číslo https://pandia.ru/text/78/516/images/image227_5.gif" width="204" height="25 src=">,

kde https://pandia.ru/text/78/516/images/image226_5.gif" width="16" height="25 src="> je koreň charakteristickej rovnice pre rovnicu (5..gif" width="229" height="25 src=">,

kde https://pandia.ru/text/78/516/images/image229_5.gif" width="147" height="25 src=">.

Riešenie.

Korene charakteristickej rovnice pre rovnicu https://pandia.ru/text/78/516/images/image231_4.gif" width="58" height="25 src=">.gif" width="203" height ="25 src=">.

Pravá strana rovnice uvedenej v príklade 3 má špeciálny tvar: f(x) https://pandia.ru/text/78/516/images/image235_3.gif" width="50" height="25 src= ">.gif " width="55" height="25 src=">.gif" width="229" height="25 src=">.

Na určenie https://pandia.ru/text/78/516/images/image240_2.gif" width="11" height="25 src=">.gif" width="43" height="25 src=" > a dosaďte ho do danej rovnice:

Citujúc podobné výrazy, porovnávanie koeficientov na https://pandia.ru/text/78/516/images/image245_2.gif" width="46" height="25 src=">.gif" width="100" height = "25 src=">.

Konečné všeobecné riešenie danej rovnice je: https://pandia.ru/text/78/516/images/image249_2.gif" width="281" height="25 src=">.gif" width="47 " height ="25 src=">.gif" width="10" height="25 src="> a jeden z týchto polynómov sa môže rovnať nule. Označme typ konkrétneho riešenia v tomto všeobecnom prípade .

a) Ak je číslo https://pandia.ru/text/78/516/images/image255_2.gif" width="605" height="51">, (7.2)

kde https://pandia.ru/text/78/516/images/image257_2.gif" width="121" height="25 src=">.

b) Ak je číslo https://pandia.ru/text/78/516/images/image210_5.gif" width="80" height="25 src=">, potom konkrétne riešenie lndu bude vyzerať takto:

https://pandia.ru/text/78/516/images/image259_2.gif" width="17" height="25 src=">. Vo výraze (7..gif" width="121" height= " 25 src=">.

Príklad 4. Označte typ konkrétneho riešenia rovnice

https://pandia.ru/text/78/516/images/image262_2.gif" width="129" height="25 src=">..gif" width="95" height="25 src="> . Všeobecné riešenie Lodu má tvar:

https://pandia.ru/text/78/516/images/image266_2.gif" width="183" height="25 src=">..gif" width="42" height="25 src="> ..gif" width="36" height="25 src=">.gif" width="351" height="25 src=">.

Ďalšie koeficienty https://pandia.ru/text/78/516/images/image273_2.gif" width="34" height="25 src=">.gif" width="42" height="28 src=" > existuje konkrétne riešenie pre rovnicu s pravou stranou f1(x) a Variácie" href="/text/category/variatciya/" rel="bookmark">variácie ľubovoľných konštánt (Lagrangeova metóda).

Priame nájdenie konkrétneho riešenia rovnice, okrem prípadu rovnice s konštantnými koeficientmi a so špeciálnymi voľnými členmi, je veľmi ťažké. Preto sa na nájdenie všeobecného riešenia rovnice zvyčajne používa metóda variácie ľubovoľných konštánt, ktorá vždy umožňuje nájsť všeobecné riešenie rovnice v kvadratúre, ak je známy základný systém riešení zodpovedajúcej homogénnej rovnice. . Táto metóda je nasledovná.

Podľa vyššie uvedeného je všeobecným riešením lineárnej homogénnej rovnice:

https://pandia.ru/text/78/516/images/image278_2.gif" width="46" height="25 src=">.gif" width="51" height="25 src="> – nie konštanty, ale niektoré, zatiaľ neznáme funkcie f(x). . treba brať z intervalu. V skutočnosti je v tomto prípade Wronského determinant nenulový vo všetkých bodoch intervalu, t.j. v celom priestore - komplexný koreň charakteristickej rovnice..gif" width="20" height="25 src="> lineárne nezávislé čiastkové riešenia tvaru:

Vo všeobecnom vzorci riešenia tento koreň zodpovedá vyjadreniu tvaru.