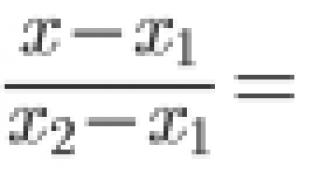
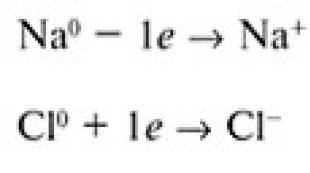Remeslá

Rovnica roviny je vzdialenosť od bodu k rovine. Vzdialenosť od bodu k rovine. spôsobom. Vektorová metóda

Zachovanie vášho súkromia je pre nás dôležité. Z tohto dôvodu sme vyvinuli Zásady ochrany osobných údajov, ktoré popisujú, ako používame a uchovávame vaše informácie. Prečítajte si naše postupy ochrany osobných údajov a ak máte nejaké otázky, dajte nám vedieť.

Zhromažďovanie a používanie osobných údajov

Osobné údaje sú údaje, ktoré možno použiť na identifikáciu alebo kontaktovanie konkrétnej osoby.

Keď nás budete kontaktovať, môžete byť kedykoľvek požiadaní o poskytnutie svojich osobných údajov.

Nižšie sú uvedené niektoré príklady typov osobných údajov, ktoré môžeme zhromažďovať, a ako môžeme tieto informácie použiť.

Aké osobné údaje zhromažďujeme:

Keď odošlete žiadosť na stránke, môžeme zhromažďovať rôzne informácie vrátane vášho mena, telefónneho čísla, e-mailovej adresy atď.

Ako používame vaše osobné údaje:

Osobné údaje, ktoré zhromažďujeme, nám umožňujú kontaktovať vás s jedinečnými ponukami, propagačnými akciami a inými udalosťami a pripravovanými udalosťami.
Z času na čas môžeme použiť vaše osobné údaje na zasielanie dôležitých upozornení a komunikácie.
Osobné údaje môžeme použiť aj na interné účely, ako je vykonávanie auditov, analýza údajov a rôzne výskumy, aby sme zlepšili služby, ktoré poskytujeme, a poskytli vám odporúčania týkajúce sa našich služieb.
Ak sa zúčastníte žrebovania o ceny, súťaže alebo podobnej propagačnej akcie, môžeme použiť informácie, ktoré nám poskytnete, na správu takýchto programov.

Sprístupnenie informácií tretím stranám

Informácie, ktoré od vás dostaneme, nezverejňujeme tretím stranám.

Výnimky:

V prípade potreby – v súlade so zákonom, súdnym konaním, v súdnom konaní a/alebo na základe verejných žiadostí alebo žiadostí vládnych orgánov v Ruskej federácii – sprístupniť vaše osobné údaje. Môžeme tiež zverejniť informácie o vás, ak zistíme, že takéto zverejnenie je potrebné alebo vhodné na účely bezpečnosti, presadzovania práva alebo na iné účely verejného významu.
V prípade reorganizácie, zlúčenia alebo predaja môžeme osobné údaje, ktoré zhromažďujeme, preniesť na príslušnú nástupnícku tretiu stranu.

Ochrana osobných údajov

Prijímame opatrenia – vrátane administratívnych, technických a fyzických – na ochranu vašich osobných údajov pred stratou, krádežou a zneužitím, ako aj neoprávneným prístupom, zverejnením, zmenou a zničením.

Rešpektovanie vášho súkromia na úrovni spoločnosti

Aby sme zaistili bezpečnosť vašich osobných údajov, informujeme našich zamestnancov o štandardoch ochrany osobných údajov a bezpečnosti a prísne presadzujeme postupy ochrany osobných údajov.

Určenie vzdialenosti medzi: 1 - bodom a rovinou; 2 - rovné a ploché; 3 - lietadlá; 4 - križujúce sa priamky sú posudzované spoločne, pretože algoritmus riešenia všetkých týchto úloh je v podstate rovnaký a pozostáva z geometrických konštrukcií, ktoré je potrebné vykonať na určenie vzdialenosti medzi daným bodom A a rovinou α. Ak existuje nejaký rozdiel, spočíva iba v tom, že v prípadoch 2 a 3 by ste pred začatím riešenia problému mali označiť ľubovoľný bod A na priamke m (prípad 2) alebo rovine β (prípad 3). vzdialenosti medzi pretínajúcimi sa čiarami, najprv ich uzavrieme do rovnobežných rovín α a β a potom určíme vzdialenosť medzi týmito rovinami.

Pozrime sa na každý z uvedených prípadov riešenia problému.

1. Určenie vzdialenosti medzi bodom a rovinou.

Vzdialenosť od bodu k rovine je určená dĺžkou kolmého segmentu vedeného z bodu do roviny.

Preto riešenie tohto problému spočíva v postupnom vykonávaní nasledujúcich grafických operácií:

1) z bodu A spustíme kolmicu na rovinu α (obr. 269);

2) nájdite priesečník M tejto kolmice s rovinou M = a ∩ α;

3) určiť dĺžku segmentu.

Ak je rovina α vo všeobecnej polohe, potom na spustenie kolmice na túto rovinu je potrebné najprv určiť smer horizontálneho a čelného priemetu tejto roviny. Nájdenie bodu stretnutia tejto kolmice s rovinou si tiež vyžaduje dodatočné geometrické konštrukcie.

Riešenie problému je zjednodušené, ak rovina α zaujíma určitú polohu vzhľadom na premietacie roviny. V tomto prípade sa premietanie kolmice aj nájdenie bodu jej stretu s rovinou vykonáva bez ďalších pomocných konštrukcií.

PRÍKLAD 1. Určte vzdialenosť bodu A k čelne vyčnievajúcej rovine α (obr. 270).

RIEŠENIE. Cez A" nakreslíme vodorovný priemet kolmice l" ⊥ h 0α a cez A" - jej čelný priemet l" ⊥ f 0α. Označíme bod M" = l" ∩ f 0α . Od AM || π 2, potom [A" M"] == |AM| = d.

Z uvažovaného príkladu je zrejmé, ako jednoducho je problém vyriešený, keď rovina zaujíma vyčnievajúcu polohu. Preto, ak je v zdrojových údajoch špecifikovaná všeobecná rovina polohy, potom pred pokračovaním v riešení by sa rovina mala presunúť do polohy kolmej na akúkoľvek projekčnú rovinu.

PRÍKLAD 2. Určte vzdialenosť od bodu K k rovine určenej ΔАВС (obr. 271).

1. Prenesieme rovinu ΔАВС do projekčnej polohy *. Aby sme to dosiahli, prejdeme zo systému xπ 2 /π 1 na x 1 π 3 /π 1: smer novej osi x 1 zvolíme kolmo na vodorovný priemet vodorovnej roviny trojuholníka.

2. Premietnite ΔABC na novú rovinu π 3 (rovina ΔABC sa premietne na π 3 v [ C " 1 B " 1 ]).

3. Premietnite bod K na rovnakú rovinu (K" → K" 1).

4. Cez bod K" 1 nakreslíme (K" 1 M" 1)⊥ segment [C" 1 B" 1]. Požadovaná vzdialenosť d = |K" 1 M" 1 |

Riešenie problému je zjednodušené, ak je rovina definovaná stopami, pretože nie je potrebné kresliť projekcie nivelačných čiar.

PRÍKLAD 3. Určte vzdialenosť od bodu K k rovine α, určenú stopami (obr. 272).

* Najracionálnejším spôsobom, ako preniesť rovinu trojuholníka do premietacej polohy, je nahradiť projekčné roviny, keďže v tomto prípade stačí zostrojiť len jednu pomocnú projekciu.

RIEŠENIE. Rovinu π 1 nahradíme rovinou π 3, preto nakreslíme novú os x 1 ⊥ f 0α. Na h 0α označíme ľubovoľný bod 1" a určíme jeho nový vodorovný priemet do roviny π 3 (1" 1). Cez body X α 1 (X α 1 = h 0α 1 ∩ x 1) a 1" 1 nakreslíme h 0α 1. Určíme nový vodorovný priemet bodu K → K" 1. Z bodu K" 1 spustíme kolmicu na h 0α 1 a bod jej priesečníka označíme h 0α 1 - M" 1. Dĺžka segmentu K" 1 M" 1 bude udávať požadovanú vzdialenosť.

2. Určenie vzdialenosti medzi priamkou a rovinou.

Vzdialenosť medzi priamkou a rovinou je určená dĺžkou kolmého segmentu spusteného z ľubovoľného bodu na priamke k rovine (pozri obr. 248).

Preto sa riešenie problému určenia vzdialenosti medzi priamkou m a rovinou α nelíši od príkladov diskutovaných v odseku 1 na určenie vzdialenosti medzi bodom a rovinou (pozri obr. 270 ... 272). Ako bod môžete vziať ľubovoľný bod patriaci do priamky m.

3. Určenie vzdialenosti medzi rovinami.

Vzdialenosť medzi rovinami je určená veľkosťou kolmého segmentu spadnutého z bodu v jednej rovine do inej roviny.

Z tejto definície vyplýva, že algoritmus na riešenie úlohy určenia vzdialenosti medzi rovinami α a β sa líši od podobného algoritmu na riešenie úlohy určenia vzdialenosti medzi priamkou m a rovinou α len tým, že priamka m musí patriť do roviny α. , t. j. na určenie vzdialenosti medzi rovinami α a β:

1) vezmite priamku m v rovine α;

2) vyberte ľubovoľný bod A na priamke m;

3) z bodu A spustite kolmicu l na rovinu β;

4) určte bod M - bod stretnutia kolmice l s rovinou β;

5) určiť veľkosť segmentu.

V praxi je vhodné použiť iný algoritmus riešenia, ktorý sa bude líšiť od uvedeného len tým, že pred prvým krokom by sa roviny mali preniesť do projekčnej polohy.

Zahrnutie tejto dodatočnej operácie do algoritmu zjednodušuje vykonávanie všetkých ostatných bodov bez výnimky, čo v konečnom dôsledku vedie k jednoduchšiemu riešeniu.

PRÍKLAD 1. Určte vzdialenosť medzi rovinami α a β (obr. 273).

RIEŠENIE. Prejdeme zo systému xπ 2 /π 1 do x 1 π 1 /π 3. Vzhľadom na novú rovinu π 3 roviny α a β zaujímajú vyčnievajúcu polohu, preto je vzdialenosť medzi novými čelnými stopami f 0α 1 a f 0 β 1 požadovaná.

V inžinierskej praxi je často potrebné riešiť problém zostrojenia roviny rovnobežnej s danou rovinou a od nej odstránenej v danej vzdialenosti. Príklad 2 nižšie ilustruje riešenie takéhoto problému.

PRÍKLAD 2. Je potrebné zostrojiť priemety roviny β rovnobežnej s danou rovinou α (m || n), ak je známe, že vzdialenosť medzi nimi je d (obr. 274).

1. V rovine α nakreslite ľubovoľné vodorovné čiary h (1, 3) a predné čiary f (1,2).

2. Z bodu 1 obnovíme kolmicu l na rovinu α(l" ⊥ h", l" ⊥ f").

3. Na kolmici l označíme ľubovoľný bod A.

4. Určte dĺžku úsečky - (poloha udáva na diagrame metricky neskreslený smer priamky l).

5. Položte segment = d na priamku (1"A 0) z bodu 1".

6. Vyznačte na výbežkoch l" a l" body B" a B", zodpovedajúce bodu B 0.

7. Bodom B vedieme rovinu β (h 1 ∩ f 1). Do β || α, je potrebné dodržať podmienku h 1 || h a f 1 || f.

4. Určenie vzdialenosti medzi pretínajúcimi sa čiarami.

Vzdialenosť medzi pretínajúcimi sa čiarami je určená dĺžkou kolmice obsiahnutej medzi rovnobežnými rovinami, ku ktorým patria pretínajúce sa čiary.

Na nakreslenie vzájomne rovnobežných rovín α a β cez pretínajúce sa priamky m a f stačí nakresliť cez bod A (A ∈ m) priamku p rovnobežnú s priamkou f a cez bod B (B ∈ f) priamka k rovnobežná s priamou m . Priesečníky m a p, f a k vymedzujú vzájomne rovnobežné roviny α a β (pozri obr. 248, e). Vzdialenosť medzi rovinami α a β sa rovná požadovanej vzdialenosti medzi čiarami kríženia m a f.

Na určenie vzdialenosti medzi pretínajúcimi sa čiarami možno navrhnúť iný spôsob, ktorý spočíva v tom, že pomocou nejakého spôsobu transformácie kolmých priemetov sa jedna z priesečníkov prenesie do priemetne. V tomto prípade sa jedna projekcia priamky zvrhne do bodu. Vzdialenosť medzi novými priemetmi krížiacich sa čiar (bod A" 2 a segment C" 2 D" 2) je požadovaná.

Na obr. 275 ukazuje riešenie problému určenia vzdialenosti medzi pretínajúcimi sa čiarami a a b, danými segmentmi [AB] a [CD]. Riešenie sa vykonáva v nasledujúcom poradí:

1. Presuňte jednu z pretínajúcich sa čiar (a) do polohy rovnobežnej s rovinou π 3; Za týmto účelom prejdite zo sústavy rovín premietania xπ 2 /π 1 do nového x 1 π 1 /π 3, pričom os x 1 je rovnobežná s horizontálnym priemetom priamky a. Určite a" 1 [A" 1 B" 1 ] a b" 1.

2. Nahradením roviny π 1 rovinou π 4 preložíme priamku

a do polohy a" 2, kolmo na rovinu π 4 (nová os x 2 je nakreslená kolmo na a" 1).

3. Zostrojte nový horizontálny priemet priamky b" 2 - [ C" 2 D" 2 ].

4. Vzdialenosť od bodu A" 2 k priamke C" 2 D" 2 (segment (A" 2 M" 2 ] (je požadovaná.

Treba mať na pamäti, že premiestnenie jednej z pretínajúcich sa čiar do vyčnievajúcej polohy nie je nič iné ako presunutie rovín rovnobežnosti, v ktorých môžu byť priamky a a b uzavreté, tiež do vyčnievajúcej polohy.

V skutočnosti posunutím priamky a do polohy kolmej na rovinu π 4 zabezpečíme, aby každá rovina obsahujúca priamku a bola kolmá na rovinu π 4, vrátane roviny α definovanej priamkami a a m (a ∩ m, m | | b). Ak teraz nakreslíme priamku n, rovnobežnú s a a pretínajúcu sa s priamkou b, potom dostaneme rovinu β, čo je druhá rovina rovnobežnosti, ktorá obsahuje priesečníky a a b. Od β || α, potom β ⊥ π 4 .

Nájdenie vzdialenosti od bodu k rovine je bežným problémom, ktorý vzniká pri riešení rôznych problémov analytickej geometrie; napríklad tento problém možno zredukovať na nájdenie vzdialenosti medzi dvoma pretínajúcimi sa priamkami alebo medzi priamkou a rovinou rovnobežnou s to.

Uvažujme rovinu $β$ a bod $M_0$ so súradnicami $(x_0;y_0; z_0)$, ktorý nepatrí do roviny $β$.

Definícia 1

Najkratšia vzdialenosť medzi bodom a rovinou bude kolmica vedená z bodu $M_0$ k rovine $β$.

Obrázok 1. Vzdialenosť od bodu k rovine. Author24 - online výmena študentských prác

Nižšie diskutujeme o tom, ako nájsť vzdialenosť od bodu k rovine pomocou metódy súradníc.

Odvodenie vzorca pre súradnicovú metódu zisťovania vzdialenosti od bodu k rovine v priestore

Kolmica z bodu $M_0$ pretínajúca rovinu $β$ v bode $M_1$ so súradnicami $(x_1;y_1; z_1)$ leží na priamke, ktorej smerový vektor je normálový vektor roviny $β$. V tomto prípade je dĺžka jednotkového vektora $n$ rovná jednej. Podľa toho bude vzdialenosť od $β$ k bodu $M_0$:

$ρ= |\vec(n) \cdot \vec(M_1M_0)|\left(1\right)$, kde $\vec(M_1M_0)$ je normálny vektor roviny $β$ a $\vec( n)$ je jednotkový normálový vektor uvažovanej roviny.

V prípade, že rovnica roviny je daná vo všeobecnom tvare $Ax+ By + Cz + D=0$, súradnicami normálového vektora roviny sú koeficienty rovnice $\(A;B;C\ )$ a jednotkový normálny vektor má v tomto prípade súradnice vypočítané pomocou nasledujúcej rovnice:

$\vec(n)= \frac($A;B;C$)(\sqrt(A^2 + B^2 + C^2))\left(2\right)$.

Teraz môžeme nájsť súradnice normálneho vektora $\vec(M_1M_0)$:

$\vec(M_0M_1)= $x_0 – x_1;y_0-y_1;z_0-z_1$\vľavo(3\vpravo)$.

Koeficient $D$ vyjadríme aj pomocou súradníc bodu ležiaceho v rovine $β$:

$D= Ax_1+By_1+Cz_1$

Súradnice jednotkového normálového vektora z rovnosti $(2)$ môžeme dosadiť do rovnice roviny $β$, potom máme:

$ρ= \frac(|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|)(\sqrt(A^2+B^2+C^2))= \frac( |Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|)(\sqrt(A^2+B^2+C^2)) = \frac(Ax_0+ By_0 + Cz_0 + D)(\sqrt(A^2) +B^2+C^2))\vľavo(4\vpravo)$

Rovnosť $(4)$ je vzorec na zistenie vzdialenosti od bodu k rovine v priestore.

Všeobecný algoritmus na nájdenie vzdialenosti od bodu $M_0$ k rovine

Ak rovnica roviny nie je daná vo všeobecnom tvare, najprv ju musíte zredukovať na všeobecnú formu.
Potom je potrebné zo všeobecnej rovnice roviny vyjadriť normálový vektor danej roviny cez bod $M_0$ a bod patriaci do danej roviny, na to musíme použiť rovnosť $(3)$ .
Ďalšou fázou je hľadanie súradníc jednotkového normálového vektora roviny pomocou vzorca $(2)$.
Nakoniec môžete začať zisťovať vzdialenosť od bodu k rovine, to sa vykonáva výpočtom skalárneho súčinu vektorov $\vec(n)$ a $\vec(M_1M_0)$.

Podmienky rovnobežnosti a kolmosti

1°. Podmienka pre koplanaritu dvoch rovín

Nech sú dané dve roviny:

A 1 X + B 1 r + C 1 z + D 1 = 0, n 1 = {A 1 ; B 1 ; C 1 } ≠ 0 ;(1)

A 2 X + B 2 r + C 2 z + D 2 = 0, n 2 = {A 2 ; B 2 ; C 2 } ≠ 0 .(2)

Kedy sú koplanárne (t. j. paralelné alebo zhodné)? Je zrejmé, že to tak bude vtedy a len vtedy, ak sú ich normálne vektory kolineárne. Aplikovaním kritéria koplanarity získame

veta 1. Dve roviny sú koplanárne vtedy a len vtedy, ak sa krížový súčin ich normálových vektorov rovná nulovému vektoru:

[n 1 , n 2 ] = 0 .

2°. Podmienka zhody dvoch rovín

Návrh 2. Roviny (1) a (2) sa zhodujú vtedy a len vtedy, ak sú všetky štyri ich koeficienty úmerné, t. j. existuje číslo λ také, že

A 2 = λ A 1 , B 2 = λ B 1 , C 2 = λ C 1 , D 2 = λ D 1 . (3)

Dôkaz. Nech sú splnené podmienky (3). Potom rovnicu druhej roviny môžeme zapísať takto:

λ A 1 X + λ B 1 r + λ C 1 z + λ D 1 = 0.

λ ≠ 0, inak by to bolo A 2 = B 2 = C 2 = D 2 = 0, čo je v rozpore s podmienkou n 2 ≠ 0 . Preto je posledná rovnica ekvivalentná rovnici (1), čo znamená, že tieto dve roviny sa zhodujú.

Teraz, naopak, vedzme, že tieto roviny sa zhodujú. Potom sú ich normálové vektory kolineárne, t.j. existuje číslo λ také, že

A 2 = λ A 1 , B 2 = λ B 1 , C 2 = λ C 1 .

Rovnicu (2) je teraz možné prepísať takto:

λ A 1 X + λ B 1 r + λ C 1 z + D 2 = 0.

Vynásobením rovnice (1) λ dostaneme ekvivalentnú rovnicu prvej roviny (keďže λ ≠ 0):

λ A 1 X + λ B 1 r + λ C 1 z + λ D 1 = 0.

Vezmime si nejaký bod ( X 0 , r 0 , z 0) z prvej (a teda aj druhej) roviny a dosaďte jej súradnice do posledných dvoch rovníc; dostaneme správne rovnosti:

λ A 1 X 0 + λ B 1 r 0 + λ C 1 z 0 + D 2 = 0 ;

λ A 1 X 0 + λ B 1 r 0 + λ C 1 z 0 + λ D 1 = 0.

Odčítaním spodného od horného dostaneme D 2 - λ D 1 = 0, t.j. D 2 = λ D 1,QED.

3°. Podmienka pre kolmosť dvoch rovín

Je zrejmé, že na to je potrebné a postačujúce, aby normálové vektory boli kolmé.

Návrh 3. Dve roviny sú kolmé práve vtedy, ak je skalárny súčin normálových vektorov nulový:

(n 1 , n 2) = 0 .

Nech je daná rovinná rovnica

Ax + Autor: + Cz + D = 0, n = {A; B; C} ≠ 0 ,

a bodka M 0 = (X 0 , r 0 , z 0). Odvoďme vzorec pre vzdialenosť od bodu k rovine:

Zoberme si ľubovoľný bod Q = (X 1 , r 1 , z 1), ležiace v tejto rovine. Jeho súradnice spĺňajú rovinnú rovnicu:

Ax 1 + Autor: 1 + Cz 1 + D = 0.

Poznamenajme teraz, že požadovaná vzdialenosť d rovná absolútnej hodnote vektorovej projekcie do smeru vektora n (tu berieme projekciu ako číselnú veličinu a nie ako vektor). Ďalej použijeme vzorec na výpočet projekcie:

Podobný vzorec platí pre vzdialenosť d z bodu M 0 = (X 0 , r 0) rovina na priamku danú všeobecnou rovnicou Ax + Autor: + C = 0.

Nech je tam lietadlo . Nakreslíme normálne
cez počiatok súradníc O. Nech je daný
– uhly zvierané normálou so súradnicovými osami.
. Nechaj – dĺžka normálneho segmentu
kým sa nepretne s rovinou. Za predpokladu, že sú známe smerové kosínusy normály , odvodíme rovnicu roviny .

Nechaj
) je ľubovoľný bod na rovine. Jednotkový normálový vektor má súradnice. Nájdeme projekciu vektora
do normálu.

Od veci M patrí teda do lietadla

Ide o rovnicu danej roviny, tzv normálne .

Vzdialenosť od bodu k rovine

Nech je dané lietadlo ,M*
- bod v priestore, d – jeho vzdialenosť od roviny.

Definícia. Odchýlka bodov M* z lietadla sa nazýva číslo ( + d), Ak M* leží na druhej strane roviny, kde smeruje kladný smer normály a číslo (- d), ak sa bod nachádza na druhej strane roviny:

Veta. Nechajte lietadlo s normálnou jednotkou je dané normálnou rovnicou:

Nechaj M*
– bod v priestore Odchýlka t. M* z roviny je dané výrazom

Dôkaz. Projekcia t.
* označujeme ako normálne Q. Bodová odchýlka M* z roviny sa rovná

Pravidlo. Nájsť odchýlka T. M* z roviny je potrebné dosadiť súradnice t do normálnej rovnice roviny. M* . Vzdialenosť od bodu k rovine je .

Redukcia všeobecnej rovinnej rovnice na normálnu formu

Nech je tá istá rovina definovaná dvoma rovnicami:

Všeobecná rovnica

Normálna rovnica.

Keďže obe rovnice definujú rovnakú rovinu, ich koeficienty sú úmerné:

Odmocnime prvé tri rovnosti a spočítajme ich:

Odtiaľto nájdeme - normalizačný faktor:

. (10)

Vynásobením všeobecnej rovnice roviny normalizačným faktorom dostaneme normálnu rovnicu roviny:

Príklady problémov na tému „Rovina“.

Príklad 1 Vytvorte rovnicu roviny prechádza cez daný bod
(2,1,-1) a rovnobežne s rovinou.

Riešenie. Normálne do lietadla :
. Keďže roviny sú rovnobežné, potom normálna je tiež normálna k požadovanej rovine . Pomocou rovnice roviny prechádzajúcej daným bodom (3) dostaneme pre rovinu rovnica:

odpoveď:

Príklad 2 Základňa kolmice klesla z počiatku do roviny , je pointa
. Nájdite rovnicu roviny .

Riešenie. Vektor
je normálne pre lietadlo . Bodka M 0 patrí do lietadla. Môžete použiť rovnicu roviny prechádzajúcej daným bodom (3):

odpoveď:

Príklad 3 Konštruovať rovinu , prechádzajúci cez body

a kolmo na rovinu :.

Preto do určitého bodu M (X, r, z) patril lietadlu , je potrebné, aby tri vektory
boli koplanárne:

=0.

Zostáva odhaliť determinant a výsledný výraz uviesť do podoby všeobecnej rovnice (1).

Príklad 4. Lietadlo je dané všeobecnou rovnicou:

Nájdite odchýlku bodu
z danej roviny.

Riešenie. Uveďme rovnicu roviny do normálneho tvaru.

Dosaďte súradnice bodu do výslednej normálovej rovnice M*.

odpoveď:
.

Príklad 5. Pretína rovina segment?

Riešenie. Rezať AB prekročil rovinu, odchýlky A z lietadla musí mať rôzne znaky:

Príklad 6. Priesečník troch rovín v jednom bode.

Systém má unikátne riešenie, preto majú tri roviny jeden spoločný bod.

Príklad 7. Nájdenie osí dihedrálneho uhla, ktorý tvoria dve dané roviny.

Nechaj A - odchýlka nejakého bodu
z prvej a druhej roviny.

Na jednej z rovín osy (zodpovedajúcej uhlu, v ktorom leží počiatok súradníc) sú tieto odchýlky rovnaké vo veľkosti a znamienku a na druhej sú rovnaké vo veľkosti a v opačnom znamienku.

Toto je rovnica prvej osovej roviny.

Toto je rovnica druhej osovej roviny.

Príklad 8. Určenie polohy dvoch daných bodov A vzhľadom k dihedrálnym uhlom tvoreným týmito rovinami.