Формула за определяне на сумата от аритметична прогресия. Сума от аритметична прогресия. Връзка между аритметична и геометрична прогресии

внимание!
Има допълнителни
материали в специален раздел 555.
За тези, които са много "не много..."
И за тези, които „много...“)

Аритметичната прогресия е поредица от числа, в която всяко число е по-голямо (или по-малко) от предишното с еднаква стойност.

Тази тема често изглежда сложна и неразбираема. Буквени индекси n-ти членпрогресии, разлики в прогресията - всичко това е някак объркващо, да... Нека разберем значението на аритметичната прогресия и всичко ще се оправи веднага.)

Концепцията за аритметична прогресия.

Аритметичната прогресия е много проста и ясна концепция. Имате ли съмнения? Напразно.) Вижте сами.

Ще напиша незавършена поредица от числа:

1, 2, 3, 4, 5, ...

Можете ли да разширите тази серия? Кои числа ще дойдат следващите след петицата? Всички... ъъъ..., накратко, всички ще разберат, че следват числата 6, 7, 8, 9 и т.н.

Нека да усложним задачата. Давам ви незавършена поредица от числа:

2, 5, 8, 11, 14, ...

Ще можете да уловите модела, да разширите серията и да дадете име седмономер на ред?

Ако сте разбрали, че това число е 20, поздравления! Не само се чувствахте ключови точки на аритметичната прогресия,но и успешно ги използва в бизнеса! Ако не сте го разбрали, прочетете нататък.

Сега нека преведем ключовите точки от усещанията в математика.)

Първата ключова точка.

Аритметичната прогресия работи с серии от числа.Това е объркващо в началото. Свикнали сме да решаваме уравнения, да чертаем графики и всичко това... Но тук разширяваме серията, намираме номера на серията...

Всичко е наред. Просто прогресиите са първото запознанство с нов клон на математиката. Разделът се нарича "Поредици" и работи специално с серии от числа и изрази. Свиквай.)

Втора ключова точка.

В аритметичната прогресия всяко число е различно от предишното със същата сума.

В първия пример тази разлика е една. Което и число да вземете, то е с едно повече от предишното. Във втория - три. Всяко число е с три повече от предишното. Всъщност именно този момент ни дава възможност да схванем модела и да изчислим следващите числа.

Трети ключов момент.

Този момент не е фрапантен, да... Но е много, много важен. Ето го: Всяко число на прогресията е на мястото си.Има първото число, има седмото, има четиридесет и петото и т.н. Ако ги смесите на случаен принцип, моделът ще изчезне. Ще изчезне и аритметична прогресия. Това, което остава, е просто поредица от числа.

Това е целият смисъл.

Разбира се, в нова темапоявяват се нови термини и обозначения. Трябва да ги познавате. В противен случай няма да разберете задачата. Например, ще трябва да решите нещо като:

Запишете първите шест члена на аритметичната прогресия (a n), ако a 2 = 5, d = -2,5.

Вдъхновяващо?) Букви, малко индекси... И задачата, между другото, не може да бъде по-проста. Просто трябва да разберете значението на термините и обозначенията. Сега ще овладеем този въпрос и ще се върнем към задачата.

Термини и обозначения.

Аритметична прогресияе поредица от числа, в която всяко число е различно от предишното със същата сума.

Това количество се нарича . Нека разгледаме тази концепция по-подробно.

Разлика в аритметична прогресия.

Разлика в аритметична прогресияе сумата, с която всяко число на прогресия Повече ▼предишното.

Един важен момент. Моля, обърнете внимание на думата "Повече ▼".Математически това означава, че всяко число на прогресията е добавяйкиразлика в аритметичната прогресия спрямо предходното число.

Да изчислим, да речем второномера на серията, трябва да първиномер добавететочно тази разлика на аритметична прогресия. За изчисление пети- разликата е необходима добаветеДа се четвърто,добре и т.н.

Разлика в аритметична прогресияМоже би положителен,тогава всяко число от поредицата ще се окаже истинско повече от предишния.Тази прогресия се нарича повишаване на.Например:

8; 13; 18; 23; 28; .....

Тук се получава всяко число добавяйкиположително число, +5 към предишното.

Разликата може да е отрицателен,тогава всяко число в серията ще бъде по-малко от предишния.Тази прогресия се нарича (няма да повярвате!) намаляващи.

Например:

8; 3; -2; -7; -12; .....

Тук също се получава всяко число добавяйкикъм предишния, но вече отрицателно число, -5.

Между другото, когато работите с прогресия, е много полезно веднага да определите нейния характер - дали е нарастваща или намаляваща. Това помага много да се ориентирате във вземането на решение, да забележите грешките си и да ги коригирате, преди да е станало твърде късно.

Разлика в аритметична прогресияобикновено се обозначава с буквата д.

Как да намеря д? Много просто. Необходимо е да се извади от всяко число в серията предишенномер. Извадете. Между другото, резултатът от изваждането се нарича "разлика".)

Нека дефинираме напр. дза увеличаване на аритметичната прогресия:

2, 5, 8, 11, 14, ...

Взимаме произволно число от серията, което искаме, например 11. Изваждаме от него предишен номертези. 8:

Това е правилният отговор. За тази аритметична прогресия разликата е три.

Можете да го вземете всяко число на прогресията,защото за конкретна прогресия д-винаги същото.Поне някъде в началото на редицата, поне в средата, поне навсякъде. Не можете да вземете само първото число. Просто защото първото число няма предишен.)

Между другото, знаейки това d=3, намирането на седмото число от тази прогресия е много лесно. Да добавим 3 към петото число – получаваме шестото, то ще бъде 17. Да добавим три към шестото число, получаваме седмото число – двадесет.

Да дефинираме дза низходяща аритметична прогресия:

8; 3; -2; -7; -12; .....

Напомням ви, че независимо от знаците, за да определите днужда от произволен номер отнеме предишния.Изберете произволно число на прогресията, например -7. Предишното му число е -2. Тогава:

d = -7 - (-2) = -7 + 2 = -5

Разликата на аритметичната прогресия може да бъде произволно число: цяло число, дробна, ирационална, всяко число.

Други термини и обозначения.

Всяко число от серията се нарича член на аритметична прогресия.

Всеки член на прогресията има собствен номер.Цифрите са строго подредени, без уловки. Първо, второ, трето, четвърто и т.н. Например, в прогресията 2, 5, 8, 11, 14, ... две е първият член, пет е вторият, единадесет е четвъртият, добре, разбирате...) Моля, разберете ясно - самите числаможе да бъде абсолютно всичко, цяло, дробно, отрицателно, каквото и да е, но номерация на числата- строго по ред!

Как да напиша прогресия в общ вид? Няма проблем! Всяко число в серия се изписва като буква. За означаване на аритметична прогресия обикновено се използва буквата а. Членският номер се обозначава с индекс долу вдясно. Пишем термини, разделени със запетаи (или точка и запетая), както следва:

1, 2, 3, 4, 5, .....

а 1- това е първото число, а 3- трети и т.н. Нищо изискано. Тази серия може да бъде написана накратко така: (a n).

Случват се прогресии крайно и безкрайно.

Ultimateпрогресията има ограничен брой членове. Пет, тридесет и осем, каквото и да е. Но това е краен брой.

Безкраенпрогресия - има безкраен брой членове, както можете да предположите.)

Можете да напишете крайната прогресия през поредица като тази, всички термини и точка в края:

1, 2, 3, 4, 5.

Или така, ако има много членове:

1, 2, ... 14, 15.

В краткия запис ще трябва допълнително да посочите броя на членовете. Например (за двадесет членове), така:

(a n), n = 20

Една безкрайна прогресия може да бъде разпозната по многоточието в края на реда, както в примерите в този урок.

Сега можете да решите задачите. Задачите са прости, чисто за разбиране на значението на аритметична прогресия.

Примери за задачи за аритметична прогресия.

Нека разгледаме дадената по-горе задача в детайли:

1. Напишете първите шест члена на аритметичната прогресия (a n), ако a 2 = 5, d = -2,5.

Превеждаме задачата на разбираем език. Дадена е безкрайна аритметична прогресия. Второто число на тази прогресия е известно: а 2 = 5.Разликата в прогресията е известна: d = -2,5.Трябва да намерим първия, третия, четвъртия, петия и шестия член на тази прогресия.

За по-голяма яснота ще запиша серия според условията на задачата. Първите шест термина, където вторият член е пет:

1, 5, 3, 4, 5, 6,...

а 3 = а 2 + д

Заместете в израз а 2 = 5И d = -2,5. Не забравяйте за минуса!

а 3=5+(-2,5)=5 - 2,5 = 2,5

Третият член се оказа по-малък от втория. Всичко е логично. Ако числото е по-голямо от предишното отрицателенстойност, което означава, че самото число ще бъде по-малко от предишното. Прогресията намалява. Добре, нека го вземем предвид.) Отчитаме четвъртия член от нашата серия:

а 4 = а 3 + д

а 4=2,5+(-2,5)=2,5 - 2,5 = 0

а 5 = а 4 + д

а 5=0+(-2,5)= - 2,5

а 6 = а 5 + д

а 6=-2,5+(-2,5)=-2,5 - 2,5 = -5

Така бяха изчислени термини от трети до шести. Резултатът е следната серия:

a 1, 5, 2,5, 0, -2,5, -5, ....

Остава да намерим първия член а 1според известното второ. Това е стъпка в другата посока, наляво.) И така, разликата в аритметичната прогресия дне трябва да се добавя към а 2, А за вкъщи:

а 1 = а 2 - д

а 1=5-(-2,5)=5 + 2,5=7,5

Това е. Отговор на задачата:

7,5, 5, 2,5, 0, -2,5, -5, ...

Между другото бих искал да отбележа, че решихме тази задача рецидивиращначин. Това страшна думапросто означава търсене на член на прогресията според предходния (съседен) номер.По-долу ще разгледаме други начини за работа с прогресия.

От тази проста задача може да се направи един важен извод.

Помня:

Ако знаем поне един член и разликата на аритметична прогресия, можем да намерим всеки член на тази прогресия.

Помниш ли? Това просто заключение ви позволява да разрешите повечето от проблемите на училищния курс по тази тема. Всички задачи се въртят около три основни параметъра: член на аритметична прогресия, разлика на прогресия, номер на член на прогресия.Всичко.

Разбира се, цялата предишна алгебра не е отменена.) Неравенствата, уравненията и други неща са свързани с прогресията. Но според самата прогресия- всичко се върти около три параметъра.

Като пример, нека разгледаме някои популярни задачи по тази тема.

2. Запишете крайната аритметична прогресия като серия, ако n=5, d = 0,4 и a 1 = 3,6.

Тук всичко е просто. Всичко вече е дадено. Трябва да запомните как се броят членовете на една аритметична прогресия, да ги преброите и да ги запишете. Препоръчително е да не пропускате думите в условията на задачата: „окончателен“ и „ n=5". За да не броите, докато не сте напълно посинели.) Има само 5 (пет) члена в тази прогресия:

a 2 = a 1 + d = 3,6 + 0,4 = 4

a 3 = a 2 + d = 4 + 0,4 = 4,4

а 4 = а 3 + d = 4,4 + 0,4 = 4,8

а 5 = а 4 + d = 4,8 + 0,4 = 5,2

Остава да напиша отговора:

3,6; 4; 4,4; 4,8; 5,2.

Друга задача:

3. Определете дали числото 7 ще бъде член на аритметичната прогресия (a n), ако a 1 = 4,1; d = 1,2.

Хм... Кой знае? Как да определим нещо?

Как-как... Запишете прогресията под формата на серия и вижте дали там ще има седем или не! Ние броим:

a 2 = a 1 + d = 4,1 + 1,2 = 5,3

a 3 = a 2 + d = 5,3 + 1,2 = 6,5

а 4 = а 3 + d = 6,5 + 1,2 = 7,7

4,1; 5,3; 6,5; 7,7; ...

Сега ясно се вижда, че сме само седем се промъкнамежду 6.5 и 7.7! Седем не попада в нашата серия от числа и следователно седем няма да бъде член на дадената прогресия.

Отговор: не.

И ето проблем, базиран на реална версия на GIA:

4. Изписани са няколко последователни членове на аритметичната прогресия:

...; 15; Х; 9; 6; ...

Ето една поредица, написана без край и начало. Няма номера на членове, няма разлика д. Всичко е наред. За да разрешите проблема, е достатъчно да разберете значението на аритметичната прогресия. Нека да погледнем и да видим какво е възможно да знамот този сериал? Кои са трите основни параметъра?

Членски номера? Тук няма нито едно число.

Но има три числа и - внимание! - дума "последователен"в състояние. Това означава, че числата са строго подредени, без пропуски. Има ли двама в този ред? съседниизвестни числа? Да, имам! Това са 9 и 6. Следователно можем да изчислим разликата на аритметичната прогресия! Извадете от шест предишенномер, т.е. девет:

Остават само дреболии. Кое число ще бъде предишното за X? Петнадесет. Това означава, че X може лесно да се намери чрез просто събиране. Добавете разликата на аритметичната прогресия към 15:

Това е всичко. Отговор: х=12

Ние решаваме следните проблеми сами. Забележка: тези проблеми не се основават на формули. Чисто, за да разберем значението на аритметичната прогресия.) Просто записваме поредица от цифри и букви, гледаме и я намираме.

5. Намерете първия положителен член от аритметичната прогресия, ако a 5 = -3; d = 1,1.

6. Известно е, че числото 5,5 е член на аритметичната прогресия (a n), където a 1 = 1,6; d = 1,3. Определете числото n на този член.

7. Известно е, че в аритметичната прогресия a 2 = 4; а 5 = 15,1. Намерете 3.

8. Изписани са няколко последователни членове на аритметичната прогресия:

...; 15,6; Х; 3.4; ...

Намерете члена на прогресията, обозначен с буквата x.

9. Влакът започна да се движи от гарата, като равномерно увеличаваше скоростта си с 30 метра в минута. Каква ще бъде скоростта на влака след пет минути? Дайте своя отговор в км/час.

10. Известно е, че в аритметичната прогресия a 2 = 5; а 6 = -5. Намерете 1.

Отговори (в безпорядък): 7,7; 7,5; 9,5; 9; 0,3; 4.

Всичко се получи? невероятно! Можете да овладеете аритметичната прогресия за повече високо ниво, в следващите уроци.

Не се ли получи всичко? Няма проблем. В специален раздел 555 всички тези проблеми са подредени част по част.) И, разбира се, е описана проста практическа техника, която веднага подчертава решението на такива задачи ясно, ясно, с един поглед!

Между другото, в пъзела с влака има два проблема, в които хората често се спъват. Единият е само по отношение на прогресията, а вторият е общ за всякакви задачи по математика, а също и по физика. Това е превод на измеренията от едно в друго. Показва как трябва да се решават тези проблеми.

В този урок разгледахме елементарното значение на аритметична прогресия и нейните основни параметри. Това е достатъчно за решаване на почти всички проблеми по тази тема. Добавете дкъм числата, напишете серия, всичко ще бъде решено.

Решението с пръст работи добре за много къси части от ред, както в примерите в този урок. Ако серията е по-дълга, изчисленията стават по-сложни. Например, ако в задача 9 във въпроса сменим "пет минути"На "тридесет и пет минути"проблемът ще се влоши значително.)

А има и задачи, които са прости по същество, но абсурдни по отношение на изчисленията, например:

Дадена е аритметична прогресия (a n). Намерете 121, ако a 1 =3 и d=1/6.

И какво, ще добавяме 1/6 много, много пъти?! Можеш да се самоубиеш!?

Можете.) Ако не знаете проста формула, чрез която можете да решите такива задачи за минута. Тази формула ще бъде в следващия урок. И този проблем там е решен. След минутка.)

Ако харесвате този сайт...

Между другото, имам още няколко интересни сайта за вас.)

Можете да практикувате решаване на примери и да разберете вашето ниво. Тестване с незабавна проверка. Да учим - с интерес!)

Можете да се запознаете с функции и производни.

Задачи за аритметична прогресия са съществували още в древността. Те се появиха и поискаха решение, защото имаха практическа нужда.

И така, в един от папирусите Древен Египет“, който има математическо съдържание – папирусът на Райнд (19 в. пр. н. е.) – съдържа следната задача: разделете десет мерки хляб между десет души, при условие че разликата между всеки от тях е една осма от мярката.“

И в математическите трудове на древните гърци има елегантни теореми, свързани с аритметичната прогресия. Така Хипсикъл от Александрия (2 век, който съставя много интересни проблеми и добавя четиринадесетата книга към Елементите на Евклид), формулира мисълта: „В една аритметична прогресия, която има четен бройчленове, сумата от членовете на 2-то полувреме е по-голяма от сумата на условията на 1-вото полувреме на квадрат от 1/2 от броя на условията.“

Последователността е означена с an. Номерата на последователност се наричат ​​нейни членове и обикновено се обозначават с букви с индекси, които показват поредния номер на този член (a1, a2, a3 ... чете се: „a 1st“, „a 2nd“, „a 3rd“ и така нататък ).

Последователността може да бъде безкрайна или крайна.

Какво е аритметична прогресия? Под него имаме предвид този, получен чрез добавяне на предишния член (n) със същото число d, което е разликата на прогресията.

Ако d<0, то мы имеем убывающую прогрессию. Если d>0, тогава тази прогресия се счита за нарастваща.

Една аритметична прогресия се нарича крайна, ако се вземат предвид само нейните първи членове. С много голям брой членове това вече е безкрайна прогресия.

Всяка аритметична прогресия се определя от следната формула:

an =kn+b, докато b и k са някои числа.

Обратното твърдение е абсолютно вярно: ако една последователност е дадена с подобна формула, тогава тя е точно аритметична прогресия, която има свойствата:

1. Всеки член на прогресията е средноаритметичното на предходния член и следващия.
2. Обратно: ако, започвайки от 2-ро, всеки член е средноаритметично на предходния член и следващия, т.е. ако условието е изпълнено, тогава тази последователност е аритметична прогресия. Това равенство също е признак за прогресия, поради което обикновено се нарича характерно свойство на прогресията.
   По същия начин теоремата, която отразява това свойство, е вярна: редицата е аритметична прогресия само ако това равенство е вярно за който и да е от членовете на редицата, започвайки с 2-ри.

Характеристичното свойство за всеки четири числа от аритметична прогресия може да се изрази с формулата an + am = ak + al, ако n + m = k + l (m, n, k са числата на прогресията).

В аритметична прогресия всеки необходим (N-ти) член може да бъде намерен с помощта на следната формула:

Например: първият член (a1) в аритметична прогресия е даден и равен на три, а разликата (d) е равна на четири. Трябва да намерите четиридесет и петия член на тази прогресия. a45 = 1+4(45-1)=177

Формулата an = ak + d(n - k) ви позволява да определите n-тия член на аритметична прогресия чрез всеки от неговите k-ти членове, при условие че е известен.

Сумата от членовете на една аритметична прогресия (което означава първите n членове на крайна прогресия) се изчислява, както следва:

Sn = (a1+an) n/2.

Ако първият член също е известен, тогава друга формула е удобна за изчисление:

Sn = ((2a1+d(n-1))/2)*n.

Сумата от аритметична прогресия, която съдържа n члена, се изчислява, както следва:

Изборът на формули за изчисления зависи от условията на задачите и изходните данни.

Естествен ред от произволни числа, като 1,2,3,...,n,...- най-прост примераритметична прогресия.

В допълнение към аритметичната прогресия съществува и геометрична прогресия, която има свои собствени свойства и характеристики.

И. В. Яковлев | Материали по математика | MathUs.ru

Аритметична прогресия

Аритметичната прогресия е специален вид последователност. Следователно, преди да дефинираме аритметичната (и след това геометричната) прогресия, трябва накратко да обсъдим важната концепция за числовата последователност.

Последователност

Представете си устройство, на екрана на което едно след друго се показват определени числа. Да кажем 2; 7; 13; 1; 6; 0; 3; : : : Този набор от числа е точно пример за последователност.

Определение. Числовата последователност е набор от числа, в който на всяко число може да бъде присвоено уникално число (т.е. свързано с едно естествено число)1. Числото с номер n се нарича n-ти членпоследователности.

И така, в горния пример първото число е 2, това е първият член на редицата, който може да бъде означен с a1; номер пет има номер 6 е петият член на редицата, който може да бъде означен с a5. Като цяло, n-тият член на последователност се означава с an (или bn, cn и т.н.).

Много удобна ситуация е, когато n-тият член на редицата може да бъде определен с някаква формула. Например формулата an = 2n 3 определя последователността: 1; 1; 3; 5; 7; : : : Формулата an = (1)n определя последователността: 1; 1; 1; 1; : : :

Не всеки набор от числа е последователност. Следователно сегментът не е последователност; съдържа „твърде много“ числа за преномериране. Множеството R на всички реални числа също не е последователност. Тези факти се доказват в хода на математически анализ.

Аритметична прогресия: основни определения

Сега сме готови да дефинираме аритметична прогресия.

Определение. Аритметичната прогресия е последователност, в която всеки член (започвайки от втория) е равен на сбора от предходния член и някакво фиксирано число (наречено разлика на аритметичната прогресия).

Например последователност 2; 5; 8; единадесет; : : : е аритметична прогресия с първи член 2 и разлика 3. Последователност 7; 2; 3; 8; : : : е аритметична прогресия с първи член 7 и разлика 5. Последователност 3; 3; 3; : : : е аритметична прогресия с разлика равна на нула.

Еквивалентна дефиниция: последователността an се нарича аритметична прогресия, ако разликата an+1 an е постоянна стойност (независима от n).

Аритметичната прогресия се нарича нарастваща, ако нейната разлика е положителна, и намаляваща, ако нейната разлика е отрицателна.

1 Ето едно по-кратко определение: последователност е функция, дефинирана в набор естествени числа. Например, поредица от реални числа е функция f: N ! Р.

По подразбиране последователностите се считат за безкрайни, т.е. съдържащи безкраен брой числа. Но никой не ни притеснява да разглеждаме крайни последователности; всъщност всеки краен набор от числа може да се нарече крайна последователност. Например, крайната последователност е 1; 2; 3; 4; 5 се състои от пет числа.

Формула за n-тия член на аритметична прогресия

Лесно е да се разбере, че една аритметична прогресия се определя изцяло от две числа: първият член и разликата. Следователно възниква въпросът: как, знаейки първия член и разликата, да намерим произволен член на аритметична прогресия?

Не е трудно да се получи необходимата формула за n-тия член на аритметичната прогресия. Нека един

аритметична прогресия с разлика d. Ние имаме:
an+1 = an + d (n = 1; 2; : : :):
По-специално, ние пишем:
a2 = a1 + d;
a3 = a2 + d = (a1 + d) + d = a1 + 2d;
a4 = a3 + d = (a1 + 2d) + d = a1 + 3d;
и сега става ясно, че формулата за е:
an = a1 + (n 1)d:

Задача 1. В аритметична прогресия 2; 5; 8; единадесет; : : : намерете формулата за n-тия член и изчислете стотния член.

Решение. Според формула (1) имаме:

an = 2 + 3(n 1) = 3n 1:

a100 = 3 100 1 = 299:

Свойство и знак на аритметичната прогресия

Свойство на аритметичната прогресия. В аритметична прогресия за всяко

С други думи, всеки член на аритметична прогресия (започвайки от втория) е средноаритметичното на съседните членове.

	Доказателство. Ние имаме:
	a n 1 + a n+1		(an d) + (an + d)

което се изискваше.

По-общо казано, аритметичната прогресия an удовлетворява равенството

a n = a n k + a n+k

за всяко n > 2 и всяко естествено k< n. Попробуйте самостоятельно доказать эту формулу тем же самым приёмом, что и формулу (2 ).

Оказва се, че формула (2) служи не само като необходимо, но и като достатъчно условие редицата да бъде аритметична прогресия.

Знак за аритметична прогресия. Ако равенството (2) е в сила за всички n > 2, тогава последователността an е аритметична прогресия.

Доказателство. Нека пренапишем формула (2), както следва:

a n a n 1 = a n+1 a n:

От това можем да видим, че разликата an+1 an не зависи от n и това точно означава, че редицата an е аритметична прогресия.

Свойството и знакът на аритметичната прогресия могат да бъдат формулирани под формата на едно твърдение; За удобство ще направим това за три числа (това е ситуацията, която често се среща при проблеми).

Характеризиране на аритметична прогресия. Три числа a, b, c образуват аритметична прогресия тогава и само ако 2b = a + c.

Задача 2. (MSU, Стопански факултет, 2007) Три числа 8x, 3 x2 и 4 в посочения ред образуват намаляваща аритметична прогресия. Намерете x и посочете разликата на тази прогресия.

Решение. По свойството на аритметичната прогресия имаме:

2(3 x2) = 8x 4, 2x2 + 8x 10 = 0, x2 + 4x 5 = 0, x = 1; x = 5:

Ако x = 1, тогава получаваме намаляваща прогресия от 8, 2, 4 с разлика от 6. Ако x = 5, тогава получаваме нарастваща прогресия от 40, 22, 4; този случай не е подходящ.

Отговор: x = 1, разликата е 6.

Сумата от първите n члена на аритметична прогресия

Легендата разказва, че един ден учителят казал на децата да намерят сбора на числата от 1 до 100 и седнал тихо да чете вестника. След няколко минути обаче едно момче каза, че е решило проблема. Това беше 9-годишният Карл Фридрих Гаус, по-късно един от най-великите математици в историята.

Идеята на малкия Гаус беше следната. Позволявам

S = 1 + 2 + 3 + : : : + 98 + 99 + 100:

Нека запишем тази сума в обратен ред:

S = 100 + 99 + 98 + : : : + 3 + 2 + 1;

и добавете тези две формули:

2S = (1 + 100) + (2 + 99) + (3 + 98) + : : : + (98 + 3) + (99 + 2) + (100 + 1):

Всеки член в скоби е равен на 101 и има общо 100 такива члена

2S = 101 100 = 10100;

Използваме тази идея, за да изведем формулата за сумата

S = a1 + a2 + : : : + an + a n n: (3)

Полезна модификация на формула (3) се получава, ако заместим формулата на n-тия член an = a1 + (n 1)d в нея:

		2a1 + (n 1)d

Задача 3. Намерете сбора на всички положителни трицифрени числа, делими на 13.

Решение. Трицифрените числа, кратни на 13, образуват аритметична прогресия, като първият член е 104, а разликата е 13; N-тият член на тази прогресия има формата:

an = 104 + 13(n 1) = 91 + 13n:

Нека разберем колко члена съдържа нашата прогресия. За да направим това, решаваме неравенството:

6 999; 91 + 13n 6 999;

n 6 908 13 = 6911 13 ; n 6 69:

И така, има 69 членове в нашата прогресия. Използвайки формула (4), намираме необходимото количество:

S = 2 104 + 68 13 69 = 37674: 2

Някои хора третират думата „прогресия“ с повишено внимание, като много сложен термин от разделите висша математика. Междувременно най-простата аритметична прогресия е работата на таксиметъра (където все още съществуват). И разбирането на същността (и в математиката няма нищо по-важно от „разбирането на същността“) на една аритметична последователност не е толкова трудно, след като анализирате няколко елементарни понятия.

Математическа числова последователност

Цифровата последователност обикновено се нарича поредица от числа, всяко от които има свой номер.

a 1 е първият член на последователността;

и 2 е вторият член на последователността;

и 7 е седмият член на редицата;

и n е n-тият член на последователността;

Въпреки това не всеки произволен набор от числа и числа ни интересува. Ще съсредоточим вниманието си върху числова последователност, в която стойността на n-тия член е свързана с неговия пореден номер чрез връзка, която може да бъде ясно формулирана математически. С други думи: числовата стойност на n-то число е някаква функция на n.

a е стойността на член на числова редица;

n е неговият сериен номер;

f(n) е функция, където поредният номер в числовата последователност n е аргумент.

Определение

Аритметична прогресия обикновено се нарича числова последователност, в която всеки следващ член е по-голям (по-малък) от предходния със същото число. Формулата за n-тия член на аритметична последователност е следната:

a n - стойността на текущия член на аритметичната прогресия;

a n+1 - формула на следващото число;

d - разлика (определено число).

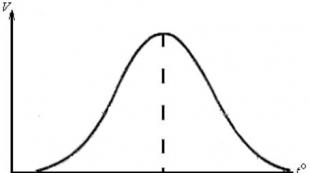
Лесно е да се определи, че ако разликата е положителна (d>0), тогава всеки следващ член на разглежданата серия ще бъде по-голям от предишния и такава аритметична прогресия ще нараства.

На графиката по-долу е лесно да се види защо числовата последователност се нарича „нарастваща“.

В случаите, когато разликата е отрицателна (d<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

Посочена стойност на член

Понякога е необходимо да се определи стойността на произволен член a n от аритметична прогресия. Това може да стане чрез последователно изчисляване на стойностите на всички членове на аритметичната прогресия, като се започне от първия до желания. Този път обаче не винаги е приемлив, ако например е необходимо да се намери стойността на петхилядната или осеммилионната дума. Традиционните изчисления ще отнемат много време. Въпреки това, специфична аритметична прогресия може да бъде изследвана с помощта на определени формули. Има и формула за n-тия член: стойността на всеки член на аритметична прогресия може да се определи като сбор от първия член на прогресията с разликата на прогресията, умножена по номера на желания член, намалена с един.

Формулата е универсална за увеличаване и намаляване на прогресията.

Пример за изчисляване на стойността на даден термин

Нека решим следната задача за намиране на стойността на n-тия член на аритметична прогресия.

Условие: има аритметична прогресия с параметри:

Първият член на редицата е 3;

Разликата в числовата серия е 1,2.

Задача: трябва да намерите стойността на 214 члена

Решение: за да определим стойността на даден член, използваме формулата:

a(n) = a1 + d(n-1)

Замествайки данните от формулировката на проблема в израза, имаме:

a(214) = a1 + d(n-1)

а(214) = 3 + 1,2 (214-1) = 258,6

Отговор: 214-ият член на редицата е равен на 258,6.

Предимствата на този метод на изчисление са очевидни - цялото решение отнема не повече от 2 реда.

Сума от даден брой членове

Много често в дадена аритметична серия е необходимо да се определи сумата от стойностите на някои от нейните сегменти. За да направите това, също няма нужда да изчислявате стойностите на всеки член и след това да ги събирате. Този метод е приложим, ако броят на членовете, чиято сума трябва да се намери, е малък. В други случаи е по-удобно да използвате следната формула.

Сумата от членовете на аритметичната прогресия от 1 до n е равна на сумата от първия и n-тия член, умножена по номера на члена n и разделена на две. Ако във формулата стойността на n-тия термин се замени с израза от предходния параграф на статията, получаваме:

Пример за изчисление

Например, нека решим задача със следните условия:

Първият член на редицата е нула;

Разликата е 0,5.

Задачата изисква да се определи сумата от членовете на редицата от 56 до 101.

Решение. Нека използваме формулата за определяне на степента на прогресия:

s(n) = (2∙a1 + d∙(n-1))∙n/2

Първо, ние определяме сумата от стойностите на 101 членове на прогресията, като заместваме дадените условия на нашия проблем във формулата:

s 101 = (2∙0 + 0,5∙(101-1))∙101/2 = 2,525

Очевидно, за да се намери сумата от членовете на прогресията от 56-то до 101-во, е необходимо да се извади S 55 от S 101.

s 55 = (2∙0 + 0,5∙(55-1))∙55/2 = 742,5

Така сумата от аритметичната прогресия за този пример е:

s 101 - s 55 = 2525 - 742,5 = 1782,5

Пример за практическо приложение на аритметичната прогресия

В края на статията нека се върнем към примера за аритметична последователност, дадена в първия параграф - таксиметър (таксиметров автомобил). Нека разгледаме този пример.

Качването на такси (което включва 3 км пътуване) струва 50 рубли. Всеки следващ километър се заплаща в размер на 22 рубли/км. Разстоянието за пътуване е 30 км. Изчислете цената на пътуването.

1. Да изхвърлим първите 3 км, чиято цена е включена в цената на кацането.

30 - 3 = 27 км.

2. По-нататъшното изчисление не е нищо повече от анализиране на аритметична числова серия.

Номер на член - броят на изминатите километри (минус първите три).

Стойността на члена е сумата.

Първият член в тази задача ще бъде равен на 1 = 50 рубли.

Разлика в прогресията d = 22 r.

числото, което ни интересува, е стойността на (27+1)-ия член от аритметичната прогресия - показанието на измервателния уред в края на 27-ия километър е 27,999... = 28 км.

a 28 = 50 + 22 ∙ (28 - 1) = 644

Изчисленията на календарните данни за произволно дълъг период се основават на формули, описващи определени числови последователности. В астрономията дължината на орбитата е геометрично зависима от разстоянието на небесното тяло до звездата. В допълнение, различни числови серии се използват успешно в статистиката и други приложни области на математиката.

Друг вид числова последователност е геометричната

Геометричната прогресия се характеризира с по-големи темпове на промяна в сравнение с аритметичната прогресия. Неслучайно в политиката, социологията и медицината, за да покажат високата скорост на разпространение на определено явление, например заболяване по време на епидемия, казват, че процесът се развива в геометрична прогресия.

N-тият член на редицата от геометрични числа се различава от предишния по това, че се умножава по някакво постоянно число - знаменателят, например, първият член е 1, знаменателят съответно е равен на 2, тогава:

n=1: 1 ∙ 2 = 2

n=2: 2 ∙ 2 = 4

n=3: 4 ∙ 2 = 8

n=4: 8 ∙ 2 = 16

n=5: 16 ∙ 2 = 32,

b n - стойността на текущия член на геометричната прогресия;

b n+1 - формула на следващия член на геометричната прогресия;

q е знаменателят на геометричната прогресия (постоянно число).

Ако графиката на аритметичната прогресия е права линия, тогава геометричната прогресия рисува малко по-различна картина:

Както в случая с аритметиката, геометричната прогресия има формула за стойността на произволен член. Всеки n-ти член от геометрична прогресия е равен на произведението от първия член и знаменателя на прогресията на степен n, намален с единица:

Пример. Имаме геометрична прогресия, като първият член е равен на 3 и знаменателят на прогресията е равен на 1,5. Нека намерим 5-ия член на прогресията

b 5 = b 1 ∙ q (5-1) = 3 ∙ 1,5 4 = 15,1875

Сумата от даден брой членове също се изчислява по специална формула. Сумата от първите n члена на геометрична прогресия е равна на разликата между произведението на n-тия член на прогресията и неговия знаменател и първия член на прогресията, разделено на знаменателя, намален с единица:

Ако b n се замени с формулата, обсъдена по-горе, стойността на сумата от първите n членове на разглежданата числова серия ще приеме формата:

Пример. Геометричната прогресия започва с първия член, равен на 1. Знаменателят е настроен на 3. Нека намерим сбора на първите осем члена.

s8 = 1 ∙ (3 8 -1) / (3-1) = 3 280