طرق التطوير

وظيفة موبيوس. صيغة انعكاس موبيوس. شريط موبيوس - اكتشاف مذهل لشريط موبيوس "السحر".

مؤسسة تعليمية تابعة للميزانية البلدية مدرسة ثانوية مع دراسة متعمقة للفرد

العناصر مع. تيربوني

شريط موبيوس

أكملتها: تشيبورينا آنا فيتاليفنا،

طالب في الصف العاشر

رئيس: كيريكوفا م.أ.

مدرس الرياضيات الأول

فئة التأهيل

قرية تيربوني

2015

مقدمة …………………………………………………………………………………………………..3

الخلفية التاريخية ………………………………………………………………………………………………………………………………… 4

شريط موبيوس – بداية علم جديد للطوبولوجيا................................................5

صنع شريط موبيوس …………………………………..6

تجارب مع شريط موبيوس ........................................... ...... .................9

الخصائص الطوبولوجية لشريط موبيوس ...........................11

نظريات على شريط موبيوس ……………………………….12

الحيل مع شريط موبيوس ........................................ 15

تطبيق شريط موبيوس ……………………………..16

خاتمة................................................. ........................................ 23

قائمة الأدبيات المستخدمة ........................................... ........... .25

طلب

مقدمة

في الوقت الحاضر، من المهم دراسة الخصائص المختلفة والتطبيقات غير القياسية للأشكال غير العادية.

هل سمعت من قبل عن شريط موبيوس؟ كيف يمكن صنعه، وما علاقته بالرياضيات، وأين يتم استخدامه في الحياة.

أثناء قيامي بهذا العمل، توصلت إلى استنتاج مفاده أنه على الرغم من اكتشاف شريط موبيوس في القرن التاسع عشر، إلا أنه كان ذا أهمية في القرنين العشرين والعشرين. لقد تم استخدام الخصائص المذهلة لشريط موبيوس في الطبخ والتكنولوجيا والفيزياء والرسم والهندسة المعمارية وفي تصميم المجوهرات والمجوهرات. ألهم إبداع العديد من الكتاب والفنانين.

لم يتلاشى الاهتمام بشريط موبيوس حتى يومنا هذا. في موسكو، في سبتمبر 2006، عقد مهرجان الرياضيات الفنية. وقد لقيت كلمة أستاذ من طوكيو نجاحا كبيرا.

لقد كنت مهتمًا جدًا ومهتمًا بهذا الموضوع. لقد درست الأدب، ثم صنعت شريط موبيوس بنفسي، ثم أجريت بحثًا وأجريت تجارب ودرست خصائصه السحرية وغير العادية.

شريط موبيوس عبارة عن شريط من الورق ذو طرف واحد يدور نصف دورة (أي 180 درجة) ويتم لصقه على الطرف الآخر. الملايين من الناس في جميع أنحاء العالم لا يدركون أنهم يستخدمون شريط موبيوس كل يوم.

هدف : أخبر زملائك وأظهر لهم أن الشريط الذي يبدو بسيطًا قد تم قلبه

نصف دورة مع نهايات ملتصقة، يمكن أن تحتوي على الكثير

مفاجآت.

موضوع الدراسة: شريط موبيوس.

مهام: تحديد المصادر والأدبيات حول هذا الموضوع وتحليلها؛

تعرف على تاريخ قطاع موبيوس؛

تعلم كيفية صنع شريط موبيوس؛

دراسة الخصائص المختلفة لشريط موبيوس؛

أثناء العمل على الموضوع، استخدمت ما يلي طُرق: التحليل والتوليف،

الملاحظة والتجربة والمقارنة والمسح الاجتماعي.

الفصل أنا

"شريط موبيوس - بداية علم جديد"

1. 1. الخلفية التاريخية

تم اختراع شريط موبيوس الغامض والمشهور في عام 1858 بواسطة مقياس هندسي ألمانيأغسطس فرديناند موبيوس . يقولون أن موبيوس ساعده في فتح "ورقته" خادمة قامت بخياطة أطراف شريط طويل بشكل غير صحيح. وانتظر سبع سنوات حتى تتم مراجعة عمله، ودون انتظار، نشر نتائجه.

في نفس الوقت الذي قام فيه موبيوس، اخترع طالب آخر من K. F. Gauss هذه الورقة -قائمة يوهان بنديكت, أستاذ بجامعة غوتنغن. وقد نشر عمله قبل موبيوس بثلاث سنوات، في عام 1862. ولد A. F. Mobius في مدينة شولبفورتي. لبعض الوقت، تحت إشراف K. Gauss، درس علم الفلك. بدأ بإجراء ملاحظات فلكية مستقلة في مرصد بليسينبورغ في عام 1818. أصبح مديرها. في تلك الأيام، لم تكن الرياضيات مدعومة، وكان علم الفلك يوفر ما يكفي من المال لعدم التفكير فيها، ويترك الوقت لأفكار المرء الخاصة. أصبح موبيوس أستاذًا في جامعة لايبزيغ في عام 1816، حيث قدم لأول مرة الهندسة الإسقاطية ونظام الإحداثيات والأساليب التحليلية للبحث. أثبتت وجود أسطح أحادية الجانب (شرائط موبيوس)، ومتعددات الوجوه، والتي لا ينطبق عليها "قانون الحواف" والتي ليس لها حجم. يعد موبيوس أحد مؤسسي نظرية التحولات الهندسية، وكذلك الطوبولوجيا. حصل على نتائج مهمة في نظرية الأعداد (دالة موبيوس) وأصبح أحد علماء الهندسة الرائدين في عصره.

1.2. شريط موبيوس - بداية علم جديد للطوبولوجيا

منذ اللحظة التي اكتشف فيها عالم الرياضيات الألماني أ. ف. موبيوس وجود ورقة مذهلة من جانب واحد، بدأ فرع جديد تمامًا من الرياضيات في التطور، يسمى الطوبولوجيا. يمكن أن يعزى مصطلح "الطوبولوجيا" إلى فرعين من الرياضيات. إحدى الطوبولوجيا، التي كان مؤسسها بوانكاريه، كانت تسمى الاندماجية لفترة طويلة. والآخر، الذي تعود أصوله إلى العالم الألماني جورج كانتور، أُعطي الاسم العام أو النظري.

الطوبولوجيا التوافقية هي فرع من فروع الهندسة. "الهندسة" هي كلمة يونانية، تُترجم إلى اللغة الروسية وتعني "مسح الأراضي" ("geo" تعني الأرض باليونانية، و"metreo" تعني القياس) تدرس خصائص الأشكال. مثل أي علم، تنقسم الهندسة إلى أقسام.

1. قياس المستوي (كلمة لاتينية، "planum" - سطح + هندسة)، قسم من الهندسة يدرس خصائص الأشكال على المستوى (مثلث، مربع، دائرة، دائرة، إلخ.)

2. القياس المجسم (باليونانية، "ستيريو" - الفضاء + الهندسة) - قسم من الهندسة يدرس خصائص الأشكال في الفضاء (الكرة، المكعب، متوازي السطوح، إلخ.)

H. الطوبولوجيا ("topos" اليونانية - المكان والتضاريس + المنطق) هي واحدة من "أصغر" أقسام الهندسة الحديثة التي تدرس خصائص هذه الأشكال التي لا تتغير إذا تم ثنيها أو تمديدها أو ضغطها أو لصقها ولا تمزق، أي لا تتغير عند التشوه. ومن أمثلة الكائنات الطوبولوجية: الحرفان I وH، والبالونات الطويلة الرفيعة.

تدرس الطوبولوجيا التوافقية خصائص الأشكال الهندسية التي تظل دون تغيير في ظل التعيينات الفردية والمستمرة. لفترة طويلة، كان يُنظر إلى الطوبولوجيا على أنها علم بعيد عن الحياة، يهدف فقط إلى "تمجيد العقل البشري". لكن في عصرنا أصبح من الواضح أن الأمر يتعلق بشكل مباشر بتفسير بنية الكون.

الطوبولوجيا العامة مجاورة لنظرية المجموعات وتكمن في أساس الرياضيات. هذه نظرية بديهية مصممة لاستكشاف مفاهيم مثل "الحد" و"التقارب" و"الاستمرارية" وما إلى ذلك. وقد وضع فيليكس هاوسدورف أسس البديهيات للفضاء الطوبولوجي، وأكملها عالم الرياضيات الروسي بافيل سيرجيفيتش ألكسندروف.

1.3. كيفية صنع شريط موبيوس

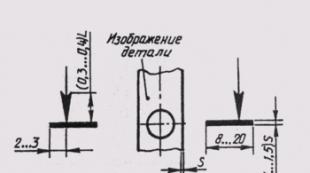
● شريط موبيوس هو أحد ( المفاجآت الرياضية ) ولصنع شريط موبيوس خذ شريط مستطيل ABقرص مضغوطقم بلفها بزاوية 180 درجة وألصق الجوانب المقابلة AB وقرص مضغوط، أي. لذلك فإن النقاط A سوف تتزامنجوالنقاط دو V.

انظر الصفة. أحد عشر.

● أشكال وأحجام شرائط الورق لقطاع موبيوس.

يجب أن يكون الشريط ضيقًا وطويلًا، مع أكبر نسبة ممكنة من الطول إلى العرض. لا يمكنك عمل شريط موبيوس من ورقة مربعة. هذا صحيح، ولكن لا ينبغي التقليل من أهمية قيود الحجم عندما لا يُسمح للورق بالتجعد. إذا لم يكن تجعد الورق محظورًا، فيمكن لصق شريط موبيوس ليس فقط من مربع، ولكن من مستطيل من أي حجم - يمكن أن تكون الجوانب الملصقة أطول بأي عدد من المرات من الجوانب غير الملصقة.

● سطح التنمية.

وبما أن شرط عدم تجعد الورق مهم، دعونا نرى ما هو معناه الرياضي.

من السهل أن نفهم أن الحظر المفروض على تجعيد الورق يحد بشكل كبير

القدرة على التعامل مع ورقة. على سبيل المثال، يمكن لف ورقة من الورق في أنبوب أو طيها من المنتصف دون تجعد، لكن لا يمكن طيها إلى أربعة. يمكنك صنع مخروط من ورقة دون تجعيدها، لكن لا يمكنك صنع كرة أو حتى قطعة منها: اضغط على ورقة الورق على الكرة الأرضية، وستظهر الطيات بالتأكيد. كما ترون، لا يمكن إعطاء ورقة أي شكل. انظر الصفة. 2.

الأسطح التي يمكن صنعها من ورقة عن طريق ثنيها دون سحقها يطلق عليها علماء الرياضيات اسم الأسطح القابلة للتطوير. في الرياضيات، يتم تعريف الأسطح القابلة للتطوير بشكل مختلف: في لغة ما وراء الرياضيات لا توجد كلمات "ورقة"، "تجعد"، "تصنع". هناك نظرية كاملة عن الأسطح القابلة للتطوير، ومن بين إنجازاتها الإجابة المرضية على سؤال ما يمكن أن تكون عليه؛ يسمي علماء الرياضيات هذا "التصنيف" (الإجابة تعود إلى ليوناردو أويلر). دعونا نقدم فقط بعض خصائص الأسطح القابلة للتطوير كحقائق تجريبية.

انظر الصفة. 3

1. من خلال كل نقطة A من سطح قابل للتطوير لا تقع على حدوده، يمر جزء يقع على السطح ولا ينتهي عند A. وبعبارة أخرى، إلى كل نقطة على سطح قابل للتطوير (منحني ولكن غير مجعد) ورقة) يمكن ربط إبرة الحياكة بحيث تكون متاخمة للسطح إلى حد ما على جانبي النقطة المأخوذة. يُطلق على هذا الجزء اسم مولد السطح (دعونا نتفق على أن هذا الاسم ينطبق فقط على الأجزاء ذات الطول الأقصى التي تقع بالكامل على السطح، أي على المقاطع غير الموجودة في أجزاء كبيرة بهذه الخاصية).

2. إذا مر مولدان مختلفان عبر نقطة A التي لا تقع على حدود السطح، و A ليست نهاية أي منهما، فإن قطعة صغيرة بما فيه الكفاية من السطح المحيط بـ A تكون مسطحة. في هذه الحالة، سنسمي النقطة A مسطحة.

3. إذا كانت النقطة A، التي لا تقع على حدود السطح، هي نهاية أحد المولدات، على سبيل المثال:أ ، فإن جوار النقطة A يتم تنظيمه على النحو التالي: من خلال النقطة A تمر المولدات الوحيدة التي لا تنتهي عند هذا الحد، دعنا نقولب . يقسم هذا المولد السطح إلى قسمين. على الجانب الآخر من المولدب ، الذي يوجد به المولدأ ، للمولد ب قطعة مسطحة مجاورة، على الجانب الآخر منب ، بشكل تعسفي من النقطة أ، هناك نقاط غير مسطحة. في هذه الحالة سوف نسمي النقطة A شبه مسطحة.

ونؤكد على أنه إذا كانت نقطة على سطح ما ليست حدًا ولا مسطحًا، فإنه يمر بها مولد واحد لا ينتهي عندها، ونهايات هذا المولد تقع على حد السطح.

●أمثلة: لا تحتوي ورقة ملفوفة في أسطوانة أو مخروط على نقاط مسطحة (أو شبه مسطحة). بالنسبة للأسطوانة، تشكل المولدات عائلة من القطع المتوازية، أما بالنسبة للمخروط، فإنها تشكل عائلة من القطع المنتشرة من نقطة واحدة. من الممكن إجراء ترتيبات أكثر تعقيدًا للمولدات.

انظر الصفة. 4 .

على سبيل المثال، تظهر المولدات والنقاط المسطحة لسطح متطور في الشكل (حيث يتم فرد السطح إلى ورقة مسطحة): الخطوط الرفيعة هي المولدات، والمناطق المظللة تتكون من نقاط مسطحة.

النقاط الواقعة على حدود منطقة من النقاط المسطحة هي إما نقاط حدودية للسطح بأكمله أو شبه مسطحة. إذا كان السطح مصنوعًا من مضلع ورقي (على سبيل المثال، مستطيل)، فإن النقاط المستوية تشكل واحدًا أو أكثر من المضلعات المستوية، ولكل من هذه المضلعات رؤوس تقع على حدود السطح وجوانب إما تقع على الحدود أو تتكون من من النقاط شبه المستوية.

الفصل 2

2.1. تجارب مع شريط موبيوس

كل واحد منا لديه فكرة بديهية عن ماهية "السطح". سطح الورقة، سطح جدران الفصل الدراسي، سطح الكرة الأرضية معروف للجميع. هل يمكن أن يكون هناك أي شيء غامض في مثل هذا المفهوم العادي؟ نعم، ربما يكون شريط موبيوس مثالاً على ذلك. لدراسة خصائصه، قمت بإجراء عدة تجارب (تقسيمها إلى مجموعتين) بمفردي.

أنا مجموعة من التجارب

التجربة رقم 1. لقد اعتدنا على ذلك على أي سطح

نحن نتعامل (ورقة أو دراجة أو أنبوب كرة طائرة) –

جانبين.

لقد بدأت في رسم شريط Mobius دون قلبه.

نتيجة . تم طلاء شريط موبيوس بالكامل.

"إذا قرر أي شخص تلوين جانب واحد فقط

سطح شريط موبيوس، دعه يغمره على الفور في دلو من الطلاء. - يكتب ريتشارد كورانت وهربرت روبينز بشكل ممتاز

كتاب "ما هي الرياضيات؟"

الخبرة رقم 2. لقد صنعت عنكبوتًا وذبابة من الورق وأرسلتهما "في نزهة على الأقدام".

حلقة عادية، ولكن منعهم من عبور الحدود.

نتيجة. العنكبوت لم يتمكن من الوصول إلى الذبابة.

التجربة رقم 3. لقد أرسلت هذا العنكبوت وأطير فقط على طول شريط موبيوس. و

منعتهم من الزحف عبر الحدود.

نتيجة.سيتم أكل الذبابة المسكينة إذا كان العنكبوت يركض بالطبع

أسرع!

الخبرة رقم 4. لقد صنعت رجلاً صغيرًا من الورق وأرسلته للسفر عبر شريط موبيوس.

نتيجة. سيعود الرجل الصغير إلى نقطة الانطلاق، حيث سيلتقي بصورته في المرآة.

ثانيامجموعة من التجارب

المرتبطة بقطع شريط موبيوس، يتم سرد النتائج في الجدول

خبرة

وصف التجربة

نتيجة

لقد قطعت حلقة بسيطة بالطول في المنتصف.

حصلت على حلقتين بسيطتين، بنفس الطول، وعرضهما مضاعف، ولهما حدان.

تم قطع شريط موبيوس بالطول من المنتصف.

لقد تلقيت حلقة واحدة يبلغ طولها ضعف طولها وعرضها ضيقًا وملتويًا بدورة واحدة كاملة وبحدود واحدة.

عرض شريط موبيوس

قطع 5 سم بالطول على مسافة 1 سم من الحافة.

حصلت على حلقتين مرتبطتين ببعضهما البعض: 1) شريط موبيوس - الطول = طول الحلقة الأصلية، العرض 3 سم؛ 2) العرض 1 سم، الطول ضعف الأصل، ملتوي دورتين كاملتين، مع حدين.

عرض شريط موبيوس

قطع 5 سم بالطول على مسافة 2 سم من الحافة.

تلقيت حلقتين مرتبطتين ببعضهما البعض: 1) الحلقة عبارة عن شريط موبيوس بعرض 1 سم، الطول = طول الحلقة الأصلية؛ 2) حلقة - عرضها 2 سم، ضعف طول الحلقة الأصلية، ملتوية بحلقتين كاملتين، مع حدين.

شريط موبيوس بعرض 5 سم، مقطع بالطول على مسافة 3 سم من الحافة.

حصلت على حلقتين مرتبطتين ببعضهما البعض: 1) الحلقة عبارة عن شريط موبيوس بالعرض

1 سم من نفس الطول؛ 2) حلقة – عرض 2 سم، طولها ضعف الأصل، ملتوية دورتين كاملتين.

نتائج المسح الاجتماعي مع طلاب الصف العاشر.

أسئلة

نعم

لا

هل سمعت

1- هل تعرف ما هي الطوبولوجيا؟

2. هل تعرف ما هو شريط موبيوس؟

3. هل تعلم خصائص شريط موبيوس؟

5% فقط من طلاب الصف العاشر يعرفون ما هي الطوبولوجيا. 30% من الطلاب يعرفون ما هو شريط موبيوس، و20% سمعوا عنه. 50% ليس لديهم أي فكرة عن شريط موبيوس. 25% من الطلاب يعرفون خصائص الشريط، و10% سمعوا عنها، و65% لا يعرفون شيئًا عن خصائص شريط موبيوس.

2.2 الخصائص الطوبولوجية لشريط موبيوس

استنادا إلى نتائج التجارب، يمكننا صياغة الخصائص الطوبولوجية التالية لشريط موبيوس المتعلقة بالمفاجآت الرياضية.

أحادية الجانب هي خاصية طوبولوجية لشريط موبيوس، وهي مميزة له فقط.

الاستمرارية - على شريط موبيوس، يمكن توصيل أي نقطة

مع أي نقطة أخرى. لا توجد فواصل - استمرارية كاملة.

من وجهة نظر طوبولوجية، لا يمكن تمييز الدائرة عن المربع،

لأنها سهلة التحول واحدة إلى أخرى دون أن تنكسر

استمرارية.

الاتصال - ستكون هناك حاجة إلى قطعتين لخفض الحلقة إلى النصف. أما بالنسبة لشريط موبيوس، فيتم استبدال عدد الوصلات اعتمادًا على التغير في عدد لفات الشريط: إذا كانت هناك لفة واحدة متصلة بشكل مزدوج، إذا كانت لفتان متصلتان ببساطة، إذا كانت ثلاث لفات متصلة بشكل مزدوج، وما إلى ذلك. نقسم المربع إلى قسمين، نحتاج إلى قطع واحد فقط. يتم تقييم الاتصال عادة من خلال رقم بيتي، أو في بعض الأحيان يتم استخدام خاصية أويلر.

4. التوجه خاصية غائبة في شريط موبيوس. لذلك، إذا تمكن الشخص من السفر على طول جميع منحنيات شريط موبيوس، فسوف يعود إلى نقطة البداية، لكنه سيتحول إلى صورته المرآة.

5. "الرقم اللوني" هو الحد الأقصى لعدد المناطق التي يمكن رسمها على السطح بحيث يكون لكل منها حدود مشتركة مع جميع المناطق الأخرى. العدد اللوني لشريط موبيوس هو ستة.

6. نظريات على شريط موبيوس

النظرية 1: ≥ ≥ π/2

ونظراً لتعقيد الإثبات، فإنني لا أعتبره في عملي.

النظرية 2: π ≥ √3

هذه النظرية أبسط من السابقة: لإثبات ذلك، يكفي شرح كيفية لصق شريط موبيوس من شريط طوله أكبر من √3. لنفترض أولًا أن طوله يساوي √3 بالضبط. ثم يمكنك وضع مثلثين منتظمين على هذا الشريط. دعونا نطوي الشريط على طول جوانب هذه المثلثات، بالتناوب في اتجاهات الطي. ستتم محاذاة الحواف AB وCD للشريط، وستتم محاذاة النقطة A مع النقطة D، والنقطة B مع النقطة C. وستكون النتيجة شريط Möbius، حيث يتم وضع حوافه من طرف إلى طرف (انظر الملحق 1.2) )

في هذا البناء، تم انتهاك القاعدة الرئيسية - لا تجعد الورق. ولكن من السهل أن نفهم أنه إذا كان طول الشريط يزيد قليلاً عن √3 على الأقل، فيمكن استبدال الكسر على طول المولد بالانحناء الذي يتم إجراؤه في قسم ضيق. باختصار، نحن لسنا خائفين من الالتواء على طول الجزء المستقيم: يمكن استبداله بانحناء قريب منه. (يحدث تجعيد الورق الذي لا يمكن إصلاحه عندما يتقاطع خطان مطويان، أي عندما يتم طي الورقة مثل المنديل - كل هذا معروف لنا من خلال التجربة اليومية.) يمكن تخيل هيكلها على النحو التالي: ثلاثة مثلثات منتظمة متطابقة ABC، A"B"C، A"B"C" تقع بالتوازي مع بعضها البعض، والقمم المقابلة فوق القمم المقابلة؛ يتم توصيل الجوانب AB وA"B" وB"C" وB"C" وC"A" وCA بواسطة وصلات العبور. يمتد خط اللصق على طول متوسط أحد المثلثات.

لماذا لا نستطيع إيجاد π بشكل أكثر دقة؟

وإلى أن يتم حل المشكلة، من الصعب أن نقول لماذا لم يتم حلها. ومع ذلك، في بعض الأحيان، في العديد من المشكلات التي لم يتم حلها، من الممكن تتبع الصعوبات الشائعة، لوضع علامة، إذا جاز التعبير، على الأماكن الصعبة على الخريطة الرياضية، مما يجعل من الممكن في بعض الأحيان التنبؤ بالنجاح أو الفشل في حل مهمة معينة

النظرية 3. يمكن لصق شريط موبيوس ذو تقاطعات ذاتية معًا من شريط بأي طول أكبر من π/2.

يتم ذلك على هذا النحو. لنأخذ n فرديًا كبيرًا بدرجة كافية ونبني n-gon منتظمًا منقوشًا في دائرة قطرها 1. خذ بعين الاعتبار أيضًا المثلثات n التي تحتوي على مركز الدائرة، كل منها محدود بجانب وقطرين من n- غون (ن = 7). تغطي هذه المثلثات بعض أماكنها عدة مرات. دعونا الآن نطبق هذه المثلثات n على بعضها البعض، وبعد ذلك نقطع نصف المثلث الموجود في أقصى اليسار على طول الوسيط الطويل ونطبقه على المثلث الموجود في أقصى اليمين. والنتيجة هي شريط مستطيل بنسبة طول إلى عرض أكبر من π/2 ويميل إلى π/2 مثل n، ويميل إلى ∞ (عرض الشريط يميل إلى 1، والطول إلى π/2). قم بطي هذا الشريط باستمرار على طول جميع الخطوط المرسومة عليه، بالتناوب في اتجاهات الطي. سوف تتطابق المقاطع AB وCD تقريبًا - لن يكون هناك سوى بضع طبقات من الورق المطوي بينهما. في هذه "المحاذاة تقريبًا"، ستتم محاذاة النقطة A مع D، وستتم محاذاة النقطة B مع C، لذلك إذا تمكنا من "تمرير الشريط من خلاله" والغراء |AB| مع |قرص مضغوط|، فإن النتيجة ستكون شريط موبيوس. إذا أخذت الشريط لفترة أطول قليلاً، فيمكنك تجنب الطيات، تمامًا كما فعلنا في إثبات النظرية 2. لقد حصلنا على شريط موبيوس، يتم فصل حوافه بعدة طبقات من الورق، انظر الملحق 1.3. لكن دعنا نعود إلى شريط موبيوس. النظرية 1، كما رأينا، تنطبق فعليًا على النطاقات المتقاطعة ذاتيًا. من غير المحتمل ألا يكون لشرط عدم التقاطع الذاتي أي تأثير على π؛ ومع ذلك، لا يمكن أخذ هذا التأثير بعين الاعتبار، إذ لا تمتلك الرياضيات الوسائل التقنية الكافية لدراسة التقاطعات الذاتية في الفضاء ثلاثي الأبعاد. على العكس من ذلك، فمن المحتمل جدًا أنه لا يمكن تحسين النظرية الثانية. بعد كل شيء، تحسينه يعني الخروج بتصميم جديد للشريط. تظهر التجربة أن الإنشاءات المثالية بسيطة ومتناغمة، وهذا هو البناء من إثبات النظرية 2. ومن الطبيعي أن نفترض أنه لو كان البناء الأفضل موجودًا، لكان قد تم العثور عليه - بعد سنوات عديدة!

ولهذا السبب يمكننا أن نتوقع π = √3.

حيل موبيوس للتعري

مشكلة في ربط العقد

كيف تربط عقدة في الوشاح دون أن تترك أطرافها؟ يمكن القيام به على هذا النحو. ضع الوشاح على الطاولة. اعبر ذراعيك على صدرك. مع الاستمرار في الاحتفاظ بهم في هذا الوضع، انحنى على الطاولة وخذ أحد طرفي الوشاح بكل يد على حدة. بعد تباعد الذراعين، ستتشكل عقدة تلقائيًا في منتصف الوشاح. باستخدام المصطلحات الطوبولوجية، يمكننا القول أن يدي المشاهد وجسده ووشاحه تشكل منحنى مغلقًا على شكل عقدة "ثلاث أوراق". عند فرد الذراعين، تنتقل العقدة فقط من اليدين إلى الوشاح.

اربطي عقدة في الوشاح بيد واحدة، دون أن تتركي نهاية الوشاح من يدك. يمكن العثور على إجابة هذا اللغز في كتاب "عجائب وأسرار الرياضيات" للكاتب إم. جاردنر.

من الناحية الطوبولوجية، يمكن اعتبار السترة بمثابة سطح ذو وجهين مع ثلاث حواف غير متشابكة، كل منها عبارة عن منحنى مغلق عادي. السترة ذات الأزرار عبارة عن سطح مزدوج الجوانب بأربعة حواف.

حلقة غامضة.

المتفرج الذي يرتدي السترة لديه حلقة موضوعة على يده ثم يُطلب منه وضع إبهامه في الجيب السفلي للسترة. يمكنك الآن دعوة الحاضرين لإزالة الحلقة من يدك دون إزالة إصبعك من جيب سترتك. الحل هو كما يلي: يجب سحب الحلقة في فتحة السترة الخاصة بالكم، وإلقائها فوق رأس المشاهد، وسحبها من خلال الفتحة الثانية للكم وتحريكها أسفل الذراع الثانية. نتيجة لهذه الإجراءات، ستكون الحلقة تحت السترة، المحيطة بالصدر. اخفضيه حتى يظهر من تحت السترة، ثم اتركيه يسقط على الأرض.

قلب السترة من الداخل إلى الخارج دون إزالتها من الشخص.

يجب على صاحب السترة أن يشبك أصابعه خلف ظهره. يجب على من حولك قلب السترة من الداخل إلى الخارج دون فصل يدي المالك. لإثبات هذه التجربة، من الضروري فك السترة وسحبها فوق اليدين خلف ظهر مرتديها. سوف تتدلى السترة في الهواء، لكنها لن تنخلع بالطبع، لأن اليدين مشبوكتان. أنت الآن بحاجة إلى أخذ الحاشية اليسرى للسترة ومحاولة عدم تجعد السترة ودفعها قدر الإمكان إلى فتحة الذراع اليمنى. ثم خذ فتحة الذراع اليمنى وأدخلها في نفس فتحة الذراع وفي نفس الاتجاه. كل ما تبقى هو تصويب السترة وسحبها على المالك. سيتم قلب السترة من الداخل إلى الخارج. لقد قمنا بهذه الخدعة وقمنا بتصويرها مع زملائنا في الفصل. وهو موجود في العرض التقديمي "Mobius Strip".

2.3. تطبيق شريط موبيوس

∞ عند مدخل متحف التاريخ والتكنولوجيا في واشنطن، يدور شريط فولاذي ملتوي نصف دورة ببطء على قاعدة. في عام 1967، عندما انعقد المؤتمر الدولي للرياضيات في البرازيل، أصدر منظموه طابعًا تذكاريًا من فئة خمسة سنتافوس. لقد صورت شريط موبيوس. يعد كل من النصب التذكاري، الذي يبلغ ارتفاعه أكثر من مترين، والختم الصغير من المعالم الأثرية الفريدة لعالم الرياضيات والفلكي الألماني أوغست فرديناند موبيوس.

انظر الملحق 5.

سجلت خدمة براءات الاختراع العديد من الاختراعات المستندة إلى نفس السطح أحادي الجانب.

∞ يُستخدم شريط موبيوس في العديد من الاختراعات المستوحاة من الدراسة الدقيقة لخصائص السطح أحادي الجانب. إن شريط الحزام الناقل، المصنوع على شكل شريط Möbius، يسمح له بالعمل مرتين لأن سطح الورقة بالكامل يتآكل بالتساوي. وفي عام 1923، صدرت براءة اختراع للمخترع لي دي فورس، الذي اقترح تسجيل الصوت على الفيلم دون تغيير البكرات على كلا الجانبين في وقت واحد. تم اختراع أشرطة الكاسيت الخاصة بمسجلات الأشرطة، حيث يتم لف الشريط ولصقه في حلقة، مما يجعل من الممكن تسجيل أو قراءة المعلومات من كلا الجانبين في وقت واحد، مما يضاعف سعة الكاسيت، وبالتالي وقت التشغيل. في الطابعات النقطية، كان شريط الحبر على شكل شريط موبيوس لزيادة مدة الصلاحية. وهذا يوفر وفورات كبيرة. يُستخدم شريط Möbius في ركوب الدراجات وأنابيب الكرة الطائرة.

∞ وفي الآونة الأخيرة، وجدوا استخدامًا آخر له - فقد بدأ يلعب دور الزنبرك، فقط زنبرك خاص. كما تعلم، ينطلق زنبرك مشحون في الاتجاه المعاكس. شريط موبيوس، خلافا لجميع القوانين، لا يغير اتجاه العمل، مثل الآليات ذات الموقعين المستقرين. يمكن أن يصبح مثل هذا الزنبرك لا يقدر بثمن في ألعاب اللف - لا يمكن لفه مثل الزنبرك العادي - وهو نوع من آلات الحركة الدائمة.

انظر الصفة. 6.

∞ في عام 1971، مخترع من جبال الأورال P. N. تشيسنوكوف. طبق مرشحًا على شكل شريط Mobius.

∞ تُستخدم ورقة Mobius في الطهي لإضفاء مظهر مثير للاهتمام وشهي للكعك والبسكويت وخشب الفرشاة. وكذلك في صناعة أدوات تحضير وتزيين الأطباق المختلفة وهياكل الطاقة (النمام).

انظر الصفة. 7.

∞ بمساعدة شريط موبيوس، يتم إنشاء روائع كاملة.

كان شريط Möbius بمثابة مصدر إلهام للمنحوتات والفنون التصويرية. كان إيشر أحد الفنانين الذين أحبوه بشكل خاص وخصص العديد من مطبوعاته الحجرية لهذا الكائن الرياضي. تُظهر إحدى الصور الشهيرة النمل يزحف عبر سطح شريط موبيوس.

انظر الملحق 9.

∞ يظهر شريط موبيوس أيضًا بانتظام في الخيال العلمي، كما هو الحال في قصة آرثر سي كلارك "جدار الظلام". تشير قصص الخيال العلمي في بعض الأحيان إلى أن كوننا قد يكون نوعًا من شريط موبيوس المعمم. في القصة للمؤلف أ.ج. Deitch، يقوم مترو أنفاق بوسطن ببناء خط جديد، يصبح مساره مربكًا للغاية لدرجة أنه يتحول إلى شريط موبيوس، وبعد ذلك تبدأ القطارات في الاختفاء على هذا الخط.

∞ هناك فرضية مفادها أن دوامة الحمض النووي نفسها هي أيضًا جزء من شريط موبيوس، وهذا هو السبب الوحيد وراء صعوبة فك الشفرة الجينية وإدراكها. علاوة على ذلك، فإن مثل هذا الهيكل يفسر بشكل منطقي تماما سبب بداية الموت البيولوجي: يغلق اللولب على نفسه، ويحدث التدمير الذاتي.

الملحق 10.

∞ لم يكن شريط موبيوس محبوبًا من قبل علماء الرياضيات فحسب، بل أيضًا من قبل السحرة

منذ أكثر من 100 عام، تم استخدام شريط موبيوس لأداء العديد من الحيل السحرية والترفيهية. تم عرض الخصائص المذهلة للورقة حتى في السيرك، حيث تم تعليق شرائط لامعة ملتصقة ببعضها البعض على شكل شرائح موبيوس. أشعل الساحر سيجارة ولمس الطرف المحترق الخط الأوسط من كل شريط مصنوع من نترات البوتاسيوم. حول المسار الناري الشريط الأول إلى شريط أطول والثاني إلى شريطين متصلين أحدهما بالآخر. (في هذه الحالة، يقطع الساحر شريط موبيوس ليس من المنتصف، بل على مسافة ثلث عرضه).

∞ يدعي الفيزيائيون أن جميع القوانين البصرية تعتمد على خصائص شريط موبيوس، وعلى وجه الخصوص، الانعكاس في المرآة هو نوع من النقل في الزمن، قصير المدى، يدوم أجزاء من مئات من الثانية، لأننا نرى أمامنا.. هذا صحيح، مرآتنا مزدوجة.

∞هناك فرضية مفادها أنه من المحتمل جدًا أن يكون كوننا مغلقًا في نفس شريط موبيوس، ووفقًا للنظرية النسبية، كلما زادت الكتلة، زاد انحناء الفضاء. تؤكد هذه النظرية تمامًا الافتراض القائل بأن سفينة الفضاء، التي تطير بشكل مستقيم طوال الوقت، يمكنها العودة إلى نقطة البداية، وهذا يؤكد عدم محدودية الكون ومحدوديته.

انظر الصفة. أحد عشر.

∞ لم يتلاشى الاهتمام بشريط موبيوس حتى يومنا هذا. أقيم مهرجان الرياضيات الفنية في موسكو في سبتمبر 2006. وقد لاقت كلمة الأستاذ من طوكيو جين أكياما نجاحا كبيرا. كان أدائه يذكرنا بعرض المخادع، حيث كان هناك مكان لشريط موبيوس (العمل باستخدام ورق "شريط موبيوس وتعديلاته").

رياضة

الموسع اليدوي "Robur"

انظر الصفة. 12 .

واحد منالأشياء المفضلة لجميع معلمي التربية البدنية في المدارس، والتي وفقا لهمعلى حد تعبيره، “القطارات لافقط عضلات اليد ولكنوعضلة الدماغ." موسع الرسغ منيكرر استوديو Artemy Lebedev شكل شريط Möbius. علاج ممتاز لتخفيف التوتر والتفكير فيهاللانهاية ومجرد وسيلة مفيدة لإبقاء يديك مشغولة.

عطر

عطر بوجاتي

انظر الصفة. 13

شركةبوجاتيبدأت في إنتاج ليس فقط السيارات باهظة الثمن (طرازفيرونيكلف 1.3 مليون يورو)، ولكن أيضًا... عطر. تم تصميم كل زجاجة، مصنوعة من الكريستال ومغطاة بالذهب الحقيقي، على شكل شريط موبيوس غير عادي، وله جانب واحد فقط. سعر العطربوجاتيهو 3500 يورو.

عطر لوي كوزا، كويزا، كويزا

انظر الصفة. 14 .

في خريف عام 2011، تم إصدار نسخة قرمزية من العطر، الزجاجة ملفوفة بشريط موبيوس - رمز لدورة المشاعر في الطبيعة. يتكون ثراء التركيبة من نضارة البرتقال الآسيوي والبرغموت والتوت الأحمر، ويستمر مع قلب زهري من الماغنوليا والفريزيا وبتلات البرتقال، وينتهي بأثر حسي من خشب الكشمير والعنبر الذهبي ونجيل الهند.

عطر UFO إصدار محدود من كينزو

انظر الصفة. 15 .

عرض العطركينزوأقيم في عام 2009 في معرض استعادي لأعمال رون أراد (روناراد) في مركز بومبيدو في باريس. كان هذا الفنان والمهندس المعماري هو الذي توصل إلى التصميم الكوني للزجاجة على شكل شريط موبيوس. وهي مصممة لتناسب راحة يدك تمامًا.مجهولة الهويةالعطرهدف، أو "كائن عطري غير محدد"، يقتصر على 180 قطعة فقط ويتم بيعه بالتجزئة مقابل 188 دولارًا.

أثاث

جدول موبيوس

انظر الصفة. 16

طاولة ذات سطح واحد يمكنك الوقوف والجلوس والاستلقاء عليها بشكل مريح.

رف الكتب إنفينيتي

انظر الصفة. 17.

كسر المصمم Job Kelevius القالب عندما صمم خزانة كتبه Infinity. باستخدام المفهوم الرياضي لـ Lemniscate، وشيء مشابه لشريط Möbius، جسد المصمم المفهوم المادي لللانهاية في Infinity Shelf. هذا يعني أنه إذا كنت قد قرأت جميع الكتب الموجودة على هذا الرف، فاعتبر أنك قد فهمت اللانهاية الكاملة للأدب.

أريكة موبيوس

انظر الصفة. 18.

ولد تحت شعار "كرسي مزدوج - متعة مزدوجة"، كرسي الأريكةموبيوسمزدوجكرسي ذو ذراعينتم إنشاؤها بواسطة المصممجاهتانسيارة نقلديوايرمن بلجيكا ويجلب رؤية جديدة للأثاث للعشاق.

الشعارات

شعار شركة وولمارك

انظر الصفة. 19.

تم إنشاء الشعار عام 1964 نتيجة لمسابقة تصميم. عضو لجنة التحكيمفرانكوجرينيانيلم يستطع المقاومة وعرض نسخته الخاصة مختبئًا تحت اسم مستعارفرانشيسكوسيراجليو. يشبه هذا الشعار شريط Mobius وهو رمز لخلود الشركة ومرونتها.

رمز إعادة التدوير

انظر الصفة. 20.

الرمز الدولي لإعادة التدوير هو شريط موبيوس.إعادة التدوير (مصطلحات أخرى: إعادة التدوير، إعادة تدوير النفايات،إعادة التدوير و إعادة التدوير)- إعادة الاستخدام أو العودة للتداول للمخلفات الصناعية أو القمامة. الأكثر شيوعا هي الثانوية والثالثية وت. هـ - إعادة التدوير بشكل أو بآخر للمواد مثل الزجاج والورق والألومنيوم والإسفلت والحديد والأقمشة ومختلف أنواع البلاستيك. كما تم استخدام النفايات الزراعية والمنزلية العضوية في الزراعة منذ العصور القديمة.

رمز الرياضيات

انظر الصفة. 21.

يعتبر شريط موبيوس رمزا للرياضيات الحديثة، لأنه هو الذي أعطى زخما للبحث الرياضي الجديد.

الملابس والأحذية

أحذية

انظر الصفة. 22.

تأسست في عام 2003 من قبل المهندس المعماري رام دي كولهاسي وصانع الأحذية جالاهاد كلاركمتحدناقصمتخصصة في إنتاج الأحذية ذات التصميم المبتكر. واحدة من أنجح التطورات للشركة هي الأحذيةموبيوس ، سمي على اسم عالم الهندسة أغسطس موبيوس وفكرته عن سطح أحادي الجانب. فكرة الحذاء هي كما يلي: الجزء العلوي من الجلد والنعل عبارة عن شريط واحد ملتوي بطريقة معينة.

وشاح موبيوس

انظر الصفة. 23.

الشيء المثير للاهتمام هو وشاح Möbius الذي يظهر في خزائن القرن الحادي والعشرين. يمكنك صنع وشاح Möbius بنفسك عن طريق ربط أطراف الوشاح ولفه دورة واحدة.

تلوين

الكتابة على الجدران

انظر الصفة. 24.

تم رسم شريط موبيوس الحديث على جدار في براغ، جمهورية التشيك.   يتحرك على طول الشريط نوعان من المركبات: الدبابات ومعدات بناء الطرق رمز الحضارة الحديثة: تدمير - بناء - تدمير - بناء..

بنيان

مبنى المكتبة

انظر الصفة. 25.

ويجري حالياً النظر في مشروع بناء مكتبة على شكل شريط موبيوس في كازاخستان.

تشكل منحنيات المبنى شريط موبيوس، وبالتالي يتدفق الفضاء الداخلي إلى الخارج والعكس. وبطريقة مماثلة، تتحول الجدران إلى سقف، ويتحول السقف مرة أخرى إلى جدران. ويدخل الضوء الطبيعي إلى الممرات الداخلية من خلال فتحات هندسية في الغلاف الخارجي، مما يخلق مساحات مضاءة بشكل جميل ومثالية للقراءة.

عوامل الجذب

انظر الصفة. 26.

تشبه رحلة السفينة الدوارة شكل شريط موبيوس. يوجد في موسكو أكبر أفعوانية مقلوبة في العالم، حيث يجلس الشخص على كرسي معلق وساقاه في الهواء. السرعة - 81 كم / ساعة، الارتفاع 30 م، الارتفاع صغير بالمقارنة مع نظائره الأجنبية، لكنه يؤتي ثماره مع وفرة اللوالب والخواتم والحلقات.

بكرة الفيلم

انظر الصفة. 27.

وفي عام 1923، صدرت براءة اختراع للمخترع لي دي فورس، الذي اقترح تسجيل الصوت على الفيلم دون تغيير البكرات، من كلا الجانبين في وقت واحد.

كاسيت

انظر الصفة. 28.

تم اختراع أشرطة الكاسيت لأجهزة تسجيل الأشرطة، حيث يتم لف الشريط ولصقه في حلقة، مما يجعل من الممكن تسجيل أو قراءة المعلومات من كلا الجانبين في وقت واحد، مما يزيد من سعة الكاسيت، وبالتالي وقت التشغيل.

سيارة تويوتا موب

انظر الصفة. 29.

تم تصميم شريط Möbius من قبل المصمم الإسباني Jorge Marti Vidal ويجمع بين جمال وغموض شريط Möbius. يوفر شكل الجسم الفريد لسيارة السباق ديناميكيات هوائية جيدة

طابعة مصفوفة

انظر الصفة. ثلاثين.

في العديد من الطابعات المصفوفية، يكون لشريط الحبر أيضًا شكل شريط Mobius لزيادة موارده.

المقاوم موبيوس

انظر الصفة. 31.

هذا عنصر إلكتروني تم اختراعه حديثًا وليس له محاثة خاصة به.

حزام الصنفرة

انظر الصفة. 32.

في عام 1969، اقترح المخترع السوفيتي جبيدولين حزام صنفرة لا نهاية له على شكل شريط موبيوس.

خاتمة

شريط موبيوس هو أول سطح أحادي الجانب اكتشفه أحد العلماء. وفي وقت لاحق، اكتشف علماء الرياضيات سلسلة كاملة من الأسطح أحادية الجانب. لكن

هذا، الأول، الذي وضع الأساس لاتجاه كامل في الهندسة، لا يزال يجذب انتباه العلماء والمخترعين والفنانين وطلابنا. لقد كنت مهتمًا جدًا بالخصائص المفتوحة لشريط موبيوس:

يحتوي شريط Mobius على حافة واحدة وجانب واحد

شريط موبيوس هو كائن طوبولوجي. مثل أي شكل طوبولوجي، فهو لا يغير خصائصه حتى يتم قطعه أو تمزيقه أو لصق قطعه الفردية معًا.

حافة واحدة وجانب واحد من شريط موبيوس لا يرتبطان بموقعهما في الفضاء، ولا يرتبطان بمفاهيم المسافة.

يجد شريط موبيوس العديد من التطبيقات في الطبخ والتكنولوجيا والفيزياء والرسم والهندسة المعمارية وتصميم المجوهرات ودراسة خصائص الكون. ألهم إبداع العديد من الكتاب والفنانين.

μ( ن) يتم تعريفه لجميع الأعداد الطبيعية نويأخذ قيما حسب طبيعة توسع العدد نلعوامل بسيطة:

μ( ن) = 1 إذا نخالية من المربعات (أي لا يوجد عدد أولي يقبل القسمة على المربع) والتحلل نعدد زوجي من العوامل؛
μ( ن) = − 1 إذا نخالية من المربعات والتحلل نإلى عوامل أولية يتكون من عدد فردي من العوامل؛
μ( ن) = 0 إذا نليست خالية من المربعات.

بحكم التعريف، نفترض أيضًا أن μ(1) = 1.

الخصائص والتطبيقات

دالة موبيوس مضاعفة: لأية أعداد أولية أو بالمساواة تحمل μ( أب) = μ( أ)μ( ب) .

مجموع قيم دالة موبيوس على جميع مقسومات العدد الصحيح ن، لا يساوي واحدًا، يساوي صفرًا

النمط = "الحد الأقصى للعرض: 98%؛ الارتفاع: تلقائي؛ العرض: تلقائي؛" src="/pictures/wiki/files/49/1bee8d0f6bd91176912a8cedc63e174b.png" border="0">

من هنا، على وجه الخصوص، يترتب على ذلك أنه بالنسبة لأي مجموعة محدودة غير فارغة، فإن عدد المجموعات الفرعية المختلفة التي تتكون من عدد فردي من العناصر يساوي عدد المجموعات الفرعية المختلفة التي تتكون من عدد زوجي من العناصر - وهي حقيقة مستخدمة في دليل.

ترتبط دالة موبيوس بدالة ميرتنز بالعلاقة

وترتبط دالة ميرتنز بدورها ارتباطًا وثيقًا بمشكلة الأصفار في دالة زيتا لريمان، راجع مقالة فرضية ميرتنز.

انقلاب موبيوس

أول صيغة انعكاس موبيوس

للوظائف الحسابية Fو ز ,

ز(ن) =	∑	F(د)
	د \| ن

ثم وفقط عندما

صيغة انعكاس موبيوس الثانية

للوظائف ذات القيمة الحقيقية F(س) و ز(س) محددة في ،

ثم وفقط عندما

هنا يتم تفسير المبلغ على أنه .

مؤسسة ويكيميديا. 2010.

تعرف على وظيفة "Mobius" في القواميس الأخرى:

دالة موبيوس μ(ن) هي دالة حسابية ضربية تستخدم في نظرية الأعداد والتوافقيات، سميت على اسم عالم الرياضيات الألماني موبيوس، الذي فكر فيها لأول مرة في عام 1831. المحتويات 1 التعريف 2 الخصائص والتطبيقات ... ويكيبيديا

نوع التحولات على المستوى المركب (الرمادي) ومجال ريمان (الأسود) المحتويات 1 التعريف 2 الخصائص الجبرية ... ويكيبيديا

الدالة الخطية الكسرية هي دالة بالشكل حيث z = (z1,...,zn) هي متغيرات معقدة أو حقيقية، ai,b,ci,d معاملات معقدة أو حقيقية. في كثير من الأحيان يتم استخدام مصطلح "الدالة الخطية الكسرية" لحالة التحول الخاصة بها ... ... ويكيبيديا

متسلسلة موبيوس هي متسلسلة وظيفية من الشكل تمت دراسة هذه المتسلسلة بواسطة موبيوس، الذي وجد صيغة انعكاس لهذه المتسلسلة: حيث μ(s) هي دالة موبيوس... ويكيبيديا

طرق البحث الطبي- أنا. المبادئ العامة للبحث الطبي. نمو وتعميق معرفتنا، والمزيد والمزيد من المعدات التقنية للعيادة، بناءً على استخدام أحدث إنجازات الفيزياء والكيمياء والتكنولوجيا، وما يرتبط بها من تعقيد الأساليب... ... الموسوعة الطبية الكبرى

حالة مرضية تتطور أثناء الولادة وتتميز بتلف أنسجة وأعضاء الطفل، ويصاحبها، كقاعدة عامة، اضطراب في وظائفها. العوامل المؤهبة لتطور R. ما يسمى غير صحيحة... ... الموسوعة الطبية

ليما.

دليل. البيان واضح. اسمحوا و يكون التوسع الكنسي للعدد . ثم مع الأخذ في الاعتبار أن المقسومات لها الشكل حيث ، ،…، ؛ ، نحن نحصل

بسبب ال

نظرية. (صيغة انعكاس موبيوس المضافة.) واسمحوا وتكون وظائف الحجة الطبيعية . ثم إذا

دليل. لدينا

يترك . ثم يمر الثابت عبر جميع قيم قواسم الرقم. وهذا يعني أن علامات الجمع في المجموع المزدوج الأخير يمكن عكسها، أي.

الآن، نظرا لذلك

نحن نحصل

هناك شكل آخر من النظرية المثبتة:

نظرية. (صيغة انعكاس موبيوس المضاعفة.) يترك

حيث يشير الرمز إلى حاصل الضرب الممتد إلى جميع قواسم الرقم.

دليل:

أمثلة على استخدام صيغة انعكاس موبيوس:

مشكلة في عدد تسلسلات الرنين. انظر: القاعة م. التوافقيات. م.: مير، § .

عدد كثيرات الحدود غير القابلة للاختزال بدرجة معينة في مجال محدود من العناصر. انظر: Berlekamp E. نظرية الترميز الجبرية. - م: مير، 1970، الفصل. 3.

Glukhov M. M.، Elizarov V. P.، Nechaev A. A. Algebra. في ت.م: هيليوس، . ت , § .

للدراسة الذاتية:

انعكاس موبيوس على مجموعات مرتبة جزئيًا. مبدأ التضمين والاستبعاد كحالة خاصة من صيغة موبيوس الانعكاسية. انظر: القاعة م. التوافقيات. م: مير،، §؛ Bender E.، Goldman J. On تطبيقات انعكاس موبيوس في التحليل التوافقي. وفي كتاب: المسائل العددية للتحليل التوافقي. م: مير، 1971. س. - .

مقارنات لمجموعات الأرقام

اسمحوا أن يكون عددا أوليا.

ليما.

دليل. عندما يكون البسط في الصيغة

عاقبة.

دليل.

ليما.دع ، ، ، تكون أعدادًا صحيحة غير سالبة ، ودع ، . ثم

دليل. لدينا

على الجانب الآخر،

وبمقارنة المعاملات بنفس الدرجات نحصل على النتيجة المطلوبة. ∎

- تمثيلات الأعداد الصحيحة والجذور غير السالبة. (هنا أي عدد صحيح له، ). في مجموعة الأعداد الصحيحة غير السالبة نحدد علاقة الترتيب الجزئي (العلاقة الأولوية) ، على افتراض، إذا وفقط إذا

نظرية لوكاس ( ).

دليل. وفقا لليما السابقة،

أين ، . وبتكرار الليما بالعدد المناسب من المرات نحصل على النتيجة المطلوبة. ∎

تعليق.النظرية ليست صحيحة بالنسبة لتلك غير الأولية. على سبيل المثال (انظر بيرليكامب، ص.)،

عاقبة.

ثانيا . الهياكل الجبرية

ثانيا. 1. مجموعات مع العمليات الثنائية. المجموعات، شبه المجموعات، monoids

العمليات الجبرية الثنائية(أو قانون التكوين) على مجموعة غير فارغة سيسمى رسم الخرائط : ، مطابقة زوج من العناصر لعنصر محدد بشكل فريد. يمكن تحديد العديد من العمليات على مجموعة. (إذا، على سبيل المثال، بالطبع، فإن عدد الطرق يساوي، أين هو عدد العناصر في .) إذا كنت تريد تسليط الضوء على واحد منهم، على سبيل المثال، اكتب، . يسمى مثل هذا الكائن الجبر الثنائي، أو com.groupoid. بدلاً من ذلك، غالبًا ما يكتبون، ويُشار إلى العملية نفسها برمز ما (،،،، وما إلى ذلك).

تعليق.جنبا إلى جنب مع العمليات الثنائية، يتم النظر في عمليات أكثر عمومية (أحادي في، ثلاثي في، وما إلى ذلك). تشكل الهياكل (الأنظمة) الجبرية المرتبطة بها موضوع بحث ما يسمى. الجبر العالمي.

تسمى العملية الثنائية على المجموعة ترابطي، لو

، لأي ، ، .

يُطلق على المجموعة ذات العملية الترابطية اسم المجموعة com.semigroup.

مثال على المجموعة غير النقابية.في المجموعة نحدد العملية على أنها . العملية غير ترابطية: ولكن .

نظرية.إذا كانت العملية الثنائية على مجموعة ترابطية، فإن قيمة التعبير لا تعتمد على موضع الأقواس فيها.

دليل.مع، أو البيان واضح. لأنه يكفي أن نبين ذلك بالاستقراء

لأي ، . من خلال الفرضية الاستقراءية، يتم وضع الأقواس في

ليست مهمة؛ بخاصة، .

اذا ثم.

اذا ثم

كما يتم أيضًا تقليل الجانب الأيمن من المساواة التي تم إثباتها (1) إلى نفس الصورة. ∎

يسمى العنصر حياديفيما يتعلق بالعملية، إذا

لأي احد .

تسمى نصف المجموعة التي تحتوي على عنصر monoid(أو شبه المجموعة مع الهوية) وتدل على , .

يمكن أن تحتوي المجموعة شبه المجموعة (groupoid) على عنصر محايد واحد على الأكثر: if

، هي عناصر محايدة، إذن

يسمى المجموعة (شبه المجموعة). مجموعة فرعية (مجموعة فرعية) المجموعة (شبه المجموعة)، ، إذا

وعن أي، .

في هذه الحالة يقولون أن المجموعة الفرعية مغلق تحت التشغيل. يسمى مونويد submonoidمونويد،،، إذا و.

يسمى عنصر المونويد تفريغ، إذا كان هناك عنصر من هذا القبيل (من الواضح أننا سنعكسه). إذا كان العنصر له نفس الخاصية، أي. ، فمن التساويات يترتب على ذلك أن العنصر فريد بالفعل (بالنسبة لـ). هذا يسمح لنا بالحديث عنه يعكسعنصر إلى عنصر (عكس) مع الخصائص:، .

إذا كانت عناصر قابلة للعكس في المونويد، ، فإن منتجها هو أيضًا عنصر قابل للعكس، نظرًا لأن , . من الواضح أنه عنصر قابل للعكس. لذلك، هناك

نظرية.يتم إغلاق مجموعة جميع العناصر القابلة للعكس للمونويد ، ، تحت العملية ∗ وتشكل شكلًا فرعيًا في ، ، .

مجموعات

تعريف المجموعة.يسمى المونويد , , , الذي جميع عناصره قابلة للعكس مجموعة.

بمعنى آخر، المجموعة عبارة عن مجموعة ذات عملية ثنائية تتضمن البديهيات التالية:

. (عملية مغلقة.) , .

. (ترابط العملية.) ,

. (وجود عنصر محايد.) ∃ .

. (وجود عنصر معكوس.) .

تعليق.وبالعودة إلى الهياكل الجبرية المقدمة أعلاه، نلاحظ التسلسل الهرمي التالي فيما بينها: الزوج، هو com.groupoid، إذا كانت البديهية راضية؛ com.semigroup, إذا البديهيات و ; monoid, إذا البديهيات , و ; مجموعة، إذا كانت البديهيات ، و .

يتم تحديد درجات العناصر ذات الخصائص الواضحة بطريقة طبيعية:

( مرة واحدة)،

; , ( , , .

بشكل عام، من المستحيل إعادة ترتيب العناصر في التعبير (أي: ). لو ، ثم يتم استدعاء العناصر قابل للتبديل، أو التنقل. إذا قام أي عنصرين من المجموعة بالتنقل، فسيتم استدعاء المجموعة تبادلي، أو أبيليان(تكريما لعالم الرياضيات النرويجي ريهل هنريك أبيل ( - )).

غالبًا ما تتم الإشارة إلى العملية في المجموعة إما برمز (إضافة) أو برمز (ضرب). وفي هذه الحالة، يتم استدعاء المجموعة وفقًا لذلك المضافةأو مضاعف، عنصرها المحايد على التوالي صفر() أو وحدة(). في المجموعة المضافة، يسمى العنصر، وهو عكس العنصر عكسويتم تعيينه، ولكن بدلا من ذلك يكتبون. في المجموعة الضربية، عادةً ما يكتبون بدلاً من ذلك، مع حذف رمز العملية.

أمثلة على المجموعات المضافة. 1) , , , , , , , - المجموعات المضافة للحلقة والحقول , , . إنهم ببساطة يكتبون , , . 2) أي حلقة بالجمع هي مجموعة أبيلية. على وجه الخصوص، حلقة كثيرات الحدود،…, ] وحلقة مصفوفات الترتيب فوق الحقل هي مجموعات أبيلية. 3) أي مساحة متجهة فوق حقل فيما يتعلق بالجمع هي مجموعة أبيلية. 4) , 1,…, – نظام كامل لمعامل المخلفات الأقل سلبية مع تشغيل معامل الإضافة .

أمثلة على المجموعات الضربية 1) , , هي مجموعات ضربية من الحقول , , . 2) هي مجموعة العناصر القابلة للعكس لأي حلقة مع الوحدة تحت الضرب. على وجه الخصوص، = ; ، هي مجموعة المصفوفات القابلة للعكس من . 3) - جميع الجذور (الحقيقية والمعقدة).

, , 1,…, , − وحدة خيالية,

المعادلة هي مجموعة أبيلية مضاعفة. 4) - مجموعة دورات المضلع المنتظم في المستوى وفي الفضاء - مجموعة غير تبادلية (ل).

علاوة على ذلك، يتم استخدام الشكل المضاعف لتسجيل العملية في كثير من الأحيان. وعادة ما يتم تحديد المجموعة بحرف واحد دون تحديد العملية. تسمى مجموعة جميع عناصر المجموعة المجموعة الرئيسية للمجموعةويشار إليه بنفس الحرف. إذا كانت المجموعة الأساسية محدودة، فسيتم استدعاء المجموعة ذروة; وإلا فإنه يسمى بلا نهاية. يسمى العنصر العددي للمجموعة المحدودة به مرتب. يتم استدعاء مجموعة من الترتيب 1 أعزب، أو ت منافس. يقال أن هناك مجموعة لا نهائية ترتيب لا نهائي. للإشارة إلى ترتيب المجموعة (الرقم الأساسي للمجموعة الرئيسية)، يتم استخدام الرموز المتساوية Card (الرقم الأصلي) و ().

إذا كانت مجموعات فرعية (من المجموعة الرئيسية) للمجموعة، فإننا نضعها

, , .

مجموعة فرعية of a group هي مجموعة فرعية تكون في حد ذاتها مجموعة فيما يتعلق بنفس العملية كما في . بمعنى آخر، المجموعة الفرعية هي مجموعة فرعية إذا وفقط إذا (واحد في) وتكون مغلقة تحت الضرب والمقلوب، أي. ، (في الواقع هناك مساواة هنا). إذا كانت هناك مجموعة فرعية، فاكتب؛ إذا كان في نفس الوقت، ثم يطلق عليه ملكمجموعة فرعية ويشار إليها باسم .

وظيفة موبيوس  (ن)، أين ن- عدد طبيعي يأخذ القيم التالية:

تتيح لك دالة Möbius كتابة دالة أويلر كمجموع:

يتم الجمع على جميع مقسومات n (وليس فقط على المقسومات الأولية).

مثال.دعونا نحسب φ (100) باستخدام وظيفة موبيوس.

جميع قواسم العدد 100 هي (1، 2، 4، 5، 10، 20، 25، 50، 100).

(2) = (-1) 1 = -1 (اثنان لهما مقسوم أولي واحد - 2)

(4) = 0 (4 مقسومة على مربع اثنين)

(5) = (-1) 1 = -1 (5 له مقسوم أولي واحد - 5)

(10) = (-1) 2 = 1 (10 لها عاملان أوليان – 2 و5)

(20) = 0 (20 مقسومًا على مربع اثنين)

(25) = 0 (25 مقسومًا على مربع الخمسة)

(50) = 0 (50 يقبل القسمة على 2 2 و5 5)

(100) = 0 (100 يقبل القسمة على 2 2 و5 5)

هكذا،

خاصية وظيفة موبيوس:.

على سبيل المثال، ن=100, {1, 2, 4, 5, 10, 20, 25, 50, 100}.

16 نظرية حول عدد الطرق لاختيار عناصر k، التي لا يوجد بينها عنصرين متجاورين، من عناصر n مرتبة في صف واحد. اثبات عن طريق الحصول على صيغة التكرار.

17 عدد المجموعات مع التكرارات

رقم ص-مجموعات مع التكرار من ن-المجموعات متساوية

– إثبات باستخدام صيغة التكرار.

تعتمد الطريقة على الحصول على صيغة تسمح لك بحساب قيم الكمية المطلوبة خطوة بخطوة، بناء على القيم الأولية المعروفة والقيم المحسوبة في الخطوات السابقة.

صيغة التكرارص - الترتيب– صيغة النموذج

أ ن = F(ن, أ ن- 1 , أ ن- 2 , … , أ ن-ر).

تعبر الصيغة في ن>صكل عضو في التسلسل ( أ أنا) من خلال السابقة صأعضاء. يتكون بناء الصيغة المتكررة من الخطوات التالية.

1. تطوير الظروف الأوليةعلى أساس أي علاقات واضحة.

دعونا نشير بواسطة F(ن، ص). من الواضح أن

2. التفكير المنطقي.دعونا إصلاح بعض العناصر في المجموعة س. ثم نسبة إلى أي ص- مجموعات مع التكرار من ن-مجموعات سيمكننا معرفة ما إذا كان يحتوي على عنصر ثابت معين أم لا.

لو يتضمنثم الباقي ( ص-1) يمكن تحديد العنصر F(ن,ص-1) الطرق.

لو لا يحتوي(هذا العنصر ليس في التحديد)، ثم ص- مجموعة مكونة من العناصر ( ن-1)-مجموعات (مجموعة سباستثناء هذا العنصر الثابت). عدد هذه المجموعات F(ن-1,ص).

لأن هذه الحالات متنافية، إذن حسب قاعدة المجموع

3. التحقق من الصيغة على بعض القيم واستنتاج النمط العام.

1) دعونا نحسب F (ن ,0) . ويأتي من (٢)

ثم F(ن,0)=F(ن,1)-F(ن-1،1). من 1) F(ن,1)=ن،و(ن-1,1)=ن-1.

لذلك، F(ن,0)=ن-(ن-1)=1=.

2) F (ن ,1) =F(ن,0)+F(ن-1,1) = 1+ن- 1 =ن==.

3) F (ن ,2) =F(ن,1)+F(ن-1,2) =ن+F(ن-1,1)+F(ن-2,2) =ن+(ن-1)+F(ن-2,1)+F(ن-3,2) = … =

= ن+(ن-1)+…+2+1 =.

(مجموع التقدم الحسابي)

4) F (ن ,3) =F(ن,2)+F(ن-1,3) =+F(ن-1,2)+F(ن-2,3) =++F(ن-2,2)+F(ن-3,3) = … =

(مجموع التقدم الهندسي)

5) F (ن ,4) =

بناءً على حالات معينة، يمكن افتراض ذلك

4. التحقق من الشروط الأولية باستخدام الصيغة الناتجة.

وهو ما يتفق مع (1) #

19، 20) عدد الأشجار الثنائية ذات الرؤوس n يساوي C(n)، حيث C(n) هو الرقم الكتالوني التاسع.

يُطلق على عدد الأشجار الثنائية ذات الرؤوس n العدد الكاتالوني، والذي يتمتع بالعديد من الخصائص المثيرة للاهتمام. يتم حساب الرقم الكاتالوني N باستخدام الصيغة (2n)! / (ن+1)!ن!، والذي ينمو بشكل كبير. (تقدم ويكيبيديا عدة أدلة على أن هذا شكل من أشكال الرقم الكاتالوني.) عدد الأشجار الثنائية ذات حجم معين 0 1 1 1 2 2 4 14 8 1430 12 208012 16 35357670

الاستبدال

اذهب إلى: ملاحة, يبحث

هذه مقالة عن الاستبدال كعملية نحويةثيرمس . كنت قد تكون مهتمة فيإعادة ترتيب .

في الرياضياتو علوم الكمبيوتر الاستبدال- هذه عملية نحوياستبدال المصطلحات الفرعية لمعطى termaشروط أخرى، وفقا لقواعد معينة. عادة ما نتحدث عن استبدال مصطلح بدلاً من عامل.

التعاريف والرموز

لا يوجد تدوين عالمي متفق عليه للاستبدال، ولا يوجد تعريف موحد. ويختلف مفهوم الاستبدال ليس فقط داخل الأقسام، ولكن أيضًا على مستوى المنشورات الفردية. بشكل عام، يمكننا تسليط الضوء استبدال السياقو استبدال "بدلا من". في الحالة الأولى، يتم تحديد المكان في المصطلح الذي يحدث فيه الاستبدال سياقأي جزء من مصطلح "المحيط" بهذا المكان. على وجه الخصوص، يتم استخدام مفهوم الاستبدال هذا في إعادة الكتابة. الخيار الثاني هو أكثر شيوعا. في هذه الحالة، عادة ما يتم تحديد الاستبدال بواسطة وظيفة ما من مجموعة من المتغيرات إلى مجموعة من المصطلحات. للإشارة إجراءات الاستبدالكقاعدة عامة، استخدم تدوين ما بعد الإصلاح. على سبيل المثال، يعني نتيجة إجراء استبدال على مصطلح ما.

في الغالبية العظمى من الحالات، يشترط أن يكون للاستبدال حامل محدود، أي المجموعة كان محدودا. في هذه الحالة، يمكن تحديده ببساطة عن طريق سرد الأزواج "قيمة متغيرة". وبما أن كل استبدال من هذا القبيل يمكن اختزاله إلى سلسلة من البدائل التي تحل محل متغير واحد فقط لكل منها، دون فقدان العمومية يمكننا أن نفترض أن الاستبدال يتم من خلال زوج واحد "قيمة متغيرة"، وهو ما يتم عادة.

ربما يكون التعريف الأخير للاستبدال هو الأكثر شيوعًا والأكثر استخدامًا. ومع ذلك، لا يوجد تدوين واحد مقبول بشكل عام لها أيضًا. غالبا ما تستخدم للإشارة إلى الاستبدال أبدلاً من سالخامس ريتم استخدام التسجيل ر[أ/س], ر[س:=أ] أو ر[س←أ].

استبدال متغير فيα-حساب التفاضل والتكامل

في حساب التفاضل والتكامل، يتم تحديد الاستبدال عن طريق الحث الهيكلي. بالنسبة للكائنات التعسفية والمتغير التعسفي، يتم حساب نتيجة استبدال حدث حر تعسفي الاستبدالويتم تحديده عن طريق الحث على البناء:

(ط) الأساس:: الكائن يطابق المتغير. ثم؛

(ثانيا) الأساس:: الكائن يطابق الثابت. ثم لتلك الذرية التعسفية؛

(ثالثًا) الخطوة: : الكائن غير ذري وله مظهر التطبيق. ثم؛

(رابعا) الخطوة:: الكائن غير ذري وهو تجريد. ثم [؛

(ت) الخطوة:: الكائن غير ذري وهو تجريد علاوة على ذلك. ثم:

لأندور.

الاستبدال المتغير في البرمجة

الاستبدالعامل ( إنجليزي الاستبدال) الخامس البرمجة التطبيقيةيفهم على النحو التالي. لحساب قيمة الدالة Fعلى الحجة الخامسيتم تطبيق الإدخال و(ت))، أين Fيحددها التصميم و(خ) = ه. سِجِلّ و(ت)في هذه الحالة يعني ذلك في التعبير هيحدث الاستبدالأو استبدال متغير سعلى الخامس. يتم تنفيذ الاستبدال وفقا ل دلالات الحسابات.

الاستبدالعامل ( إنجليزي تكليف) الخامس برمجةيفهم على أنه تكليف. عامل المهمة هو مظهر من مظاهر تأثير عنق الزجاجة فون نيومان للغات البرمجة التقليدية . خالية من هذا أنظمة الحوسبة التطبيقية.

http://math.nsc.ru/LBRT/u3/bard/fails/Brenner_Evans.pdf

21 وظائف التوليد.دالة التوليد (البسط) وتعداد دالة التوليد للمجموعات دون تكرار.

وظائف التوليد: 1) تحويلات Z 2) المولد 3) وظيفة التوليد 4) وظيفة التوليد للتسلسل (a r ) على الأساس (g r ) - الوظيفة f ، عند توسيعها إلى سلسلة من الوظائف ذات أساس ثابت (g r )، يتم تشكيل هذا التسلسل من المعاملات (a r ). …………*)

هذه السلسلة رسمية. الاسم الرسمي يعني أننا نتعامل مع الصيغة *) كتدوين مناسب لتسلسلنا - في هذه الحالة لا يهم القيم (الإجراءات والمعقدة) التي تتقارب فيها. ويتلخص دور t في تمييز معاملات التسلسل A0، A1،…Ar….لذلك في نظرية توليد الدوال، لا يتم حساب قيم هذه السلسلة أبدا لقيمة محددة للمتغير t. يتم إجراء بعض العمليات فقط على هذه المتسلسلات، وبعد ذلك يتم تحديد بعض العمليات فقط على هذه المتسلسلات، ومن ثم يتم تحديد المعاملات للقوى الفردية للمتغير t.

عادة كما

22 وظيفة توليد. دالة التوليد (البسط) وتعداد دالة التوليد للمجموعات ذات التكرارات.

منشأة التصنيع ل:

حكم البناء

1) إذا كان من الممكن تضمين عنصر من النوع i في مجموعات K 1 أو K 2 أو... K i مرات، فإنه يحتوي على مضاعف مناظر

3) يبقى العثور على المعامل. في

وظيفة توليد الأسي لقاعدة بناء المواضع

25) تشمل الأرقام التوافقية أيضًا أرقام ستيرلينغمن النوع الأول والثاني . يتم تعريف هذه الأرقام على أنها معاملات في المساواة

ولها معنى اندماجي بسيط - يساوي عدد عناصر مجموعة التقليب التي هي منتجات بالضبط كدورات مفككة، وتساوي عدد الأقسام ن-تم تعيين العنصر على كمجموعات فرعية غير فارغة. من الواضح أن. يسمى مجموع مماثل من أرقام ستيرلنغ من النوع الثاني ن- رقم الجرس ويساوي عدد جميع الأقسام ن- مجموعة العناصر. صيغة التكرار صالحة لأرقام الجرس.

عند حل المشكلات التوافقية، غالبًا ما يكون ذلك مفيدًا صيغة الإدراج والاستبعاد

والذي يسمح للمرء بإيجاد أصل اتحاد المجموعات إذا كان عدد تقاطعاتها معروفًا. دعونا نستخدم صيغة التضمين والاستبعاد للحصول على صيغة صريحة لأرقام ستيرلينغ من النوع الثاني.

أرقام ستيرلينغ من النوع الأول

مادة من ويكيبيديا – الموسوعة الحرة

اذهب إلى: ملاحة, يبحث

أرقام ستيرلينغ من النوع الأول(غير موقعة) - الكمية التباديلطلب نمع ك دورات.

تعريف

أرقام ستيرلينغ من النوع الأول(مع علامة) الصورة (ن، ك)تسمى المعاملات متعدد الحدود:

أين ( س) ن - رمز بوشهامر (تناقص مضروب):

كما يتبين من التعريف، فإن الأرقام لها علامة متناوبة. تحدد قيمها المطلقة الرقم التباديلمجموعة تتكون من نالعناصر مع ك دورات.

علاقة تكرارية

يتم إعطاء أرقام ستيرلينغ من النوع الأول متكررنسبة:

س(ن,ن) = 1، لـ n ≥ 0،

س(ن,0) = 0، لـ n > 0،

ل 0< ك < ن.

دليل.

ل ن=1 يتم التحقق من هذه المساواة مباشرة. دع التقليب ( ن-1) يتحلل الترتيب إلى كدورات. رقم نيمكن إضافتها بعد أي رقم في الحلقة المناسبة. جميع التباديل الناتجة مختلفة وتحتوي على دورات k وعددها ( ن-1)· س(ن-1, ك). من أي التقليب ( ن-1)الترتيب المحتوي على ك-1 دورة، يمكن تشكيل التقليب واحد نيحتوي على النظام كدورات عن طريق إضافة دورة مكونة من رقم مفرد ن. من الواضح أن هذا البناء يصف جميع التباديل ن-الأمر الذي يحتوي على كدورات. وهكذا تثبت المساواة.

مثال

الصفوف الأولى:

في التوافقيات رقم ستيرلينغ من النوع الثانيمن نبواسطة ك، يُشار إليه بـ أو، هو عدد غير مرتب أقسام ن-عنصري مجموعاتعلى كمجموعات فرعية غير فارغة.

صيغة التكرار

أرقام ستيرلينغ من النوع الثاني ترضي متكررنسبة:

ل ن ≥ 0،

من أجل ن > 0،

صيغة صريحة

مثال

القيم الأولية لأرقام ستيرلينغ من النوع الثاني موضحة في الجدول:

ملكيات

موضوعيرسم الخرائط هو رسم خرائط له خصائص الحقن والشمول في نفس الوقت.

1. دعونا نتذكر أولاً تعريف دالة موبيو ذات الأهمية النظرية للأرقام

1 إذا ن = 1

μ (n)=0، إذا كان هناك عدد أولي p، p2 n (-1)k، إذا كان n = p1 ... pk هو حاصل ضرب عوامل أولية مختلفة k.

دعونا نثبت الخاصية الرئيسية لوظيفة موبيوس:

النظرية 1.

♦ إذا كان n = 1، فإن المقسوم عليه الوحيد هو d = 1 و(1) صحيح، لأن μ (1) = 1. والآن لنفترض أن n > 1. فلنمثلها في الصورة

ن = p1 ق 1 بس 2 2 ك بس ك ك ,

حيث pi، i 1، k هي أعداد أولية، وsi هي قواها. إذا كان d مقسومًا على n، فإن d = p1 d 1 pd 2 2 K pd k k ,

حيث 0 ≥ di ≥ si، i 1، k. إذا كان di > 1 لبعض i 1, k، إذن μ (d) = 0. وهذا يعني أنه في (1) نحتاج فقط إلى النظر في تلك d التي يكون di ≥ 1, i 1, k لها. كل مقسوم من هذا القبيل

يتكون من منتج r أعداد أولية مختلفة، حيث r 1، k، ومساهمته في المجموع

(1) يساوي (-1)r وهناك k في المجموع. وهكذا نحصل


	μ (د) = 1 -	ك + (− 1) ك	0. ♦



	النظرية 2. (صيغة انعكاس موبيوس). دع f(n) وg(n) يكونان دالتين طبيعيتين
حجة رال. ثم المساواة
			∑و(د)

صحيح إذا وفقط إذا كانت المساواة صحيحة
			∑ μ (د)ز(
			∑ μ (د)ز(

♦ ليكن (2) صحيحا لأي ن. ثم

ز(د ن ) = ∑ و(د′ )

د ′ د ن

بالتعويض في الجانب الأيمن من (3) نحصل على

∑ μ (د)ز(	) = ∑ μ (د) ∑ f(d′ )

		د'

يتم إجراء الجمع المزدوج على اليمين على جميع الأزواج d، d′ بحيث d d′ n. إذا اخترت d ′ ، فسيتم تشغيل d عبر جميع المقسومات d n ′ . هكذا

∑ μ (د)ز(

) = ∑ و(د′ ) ∑ μ (د′ )

د'

ن > د'

لكن وفقًا لـ (1) لدينا ∑

μ (د') =

ن = د'

د'

وهذا يعني أن المساواة (3) ثابتة. الآن دع (3) يكون صحيحا لأي ن. ثم

∑ و(د) =

∑ ∑ μ (د′ )ز(

) , d'' = d d ′ - هو مقسوم على n ويمكن للمجموع المزدوج

د'

اختصار الثاني'

إعادة كتابتها كما

∑ μ (د′ )ز(د′′ ) =

∑ ز(د ′ ′ )

∑ μ(د′)

د''

اختصار الثاني '

د''

د'

د''

وبحسب (1) فإن المجموع الأخير يتحول إلى الوحدة في الحالة d′′ = n، وفي حالات أخرى

وفي كل الأحوال فهو صفر. هذا يثبت (٢). 2. خذ بعين الاعتبار تطبيق انعكاس موبيوس.

دع الأبجدية A من حروف s تعطى. توجد كلمات sn بطول n في أبجدية معينة. لكل كلمة w0 = a1 a2 … يمكن تعريف n - 1 كلمة

w1 = a2 a3 … a1 , w2 = a3 a4 … a1 a2 , … , wk-1 = a1 … an-1 , تم الحصول عليها من بعضها البعض عن طريق التحولات الدورية. في مجموعة جميع الكلمات sn، نقدم علاقة تكافؤ: نعلن أن كلمتين متكافئتين إذا تم الحصول على إحداهما من الأخرى عن طريق التحول الدوري. سنكون مهتمين بعدد الفئات التي تحتوي بالضبط على عدد n من الكلمات. تنشأ هذه المشكلة في نظرية مزامنة الرموز.

سوف نسمي الكلمة w منحلة إذا كانت فئة التكافؤ التي تحتوي على w تتكون من أقل من n من الكلمات. دعونا نسمي w دوريًا إذا كان هناك كلمة u وعدد طبيعي m بحيث w = u u … u (m مرات).

النظرية 3. الكلمة w تكون دورية إذا وفقط إذا كانت متدهورة.

كما يمكنك أن تأخذ 1 أ 2 … أ ع و ك م =

♦ ومن الواضح أنه إذا كان w دوريا فهو منحط. دعونا نكون منحطين. اجعل p هو العدد الصحيح الأدنى بحيث يكون w = wp. ثم إذا

w = a1 a2 … an، ثم wp = a1+p a2+p … an+p (مؤشرات modulo n). من هنا نحصل على ذلك في n p . (ومن السهل أن نرى ذلك ع ن). ♦ ورق الجدران

مهم من خلال M(d) - عدد المربعات التي تحتوي على كلمات d. من السابق لدينا

د ن. وبالتالي، فإن الصيغة صالحة∑ dM(d) = s n . د ن

دعونا نطبق صيغة انعكاس موبيوس للحالة g(n) = sn , f(d) = dM(d). ثم نحصل

nM(n) = ∑ μ (d)s n d d n

∑ μ (د)sn د

وبالتالي، M(n) هو الرقم الذي يهمنا. إذا كان n = p عدد أولي، إذن

- س)

هناك نسخة مضاعفة من انعكاس موبيوس. عدل

النظرية 4. اجعل f(n) وg(n) دالتين لحجة طبيعية مرتبطة وفقًا لذلك

يلبس

و(ن) = ∏ز(د)

μ(ن

ز(ن) = ∏و(د)

و وعلى العكس من (5) يتبع (4).

باستخدام صيغة موبيوس الانعكاسية، يمكن للمرء حل المشكلة المهمة عمليًا المتمثلة في عدد كثيرات الحدود غير القابلة للاختزال ذات درجة ثابتة في مجال محدود. دع GF(q) يكون مجالًا لعناصر q ويكون m عددًا طبيعيًا. ثم بالنسبة للرقم

Φ m (q) من كثيرات الحدود غير القابلة للاختزال فوق المجال GF(q) تحمل الصيغة التالية:

دعونا نقدم جدولاً بالقيم القليلة الأولى للدالة Φ m (2)


Φ م (2)

§ 5. الدائمون وتطبيقهم على العدديين

1. تستخدم الصيغ الدائمة لحل العديد من المسائل التوافقية. النظر في المصفوفة الرقمية

أ = (آي، ي)، ط = 1، ن، ي = 1، م، ن ≥ م

يتم تحديد المصفوفة الدائمة A (التعيين - لكل A) بالمساواة

لكل أ = ∑			أ 2 ي ل ن ج
(ي1،ك،جن)
(ي1،ك،جن)

حيث يتم إجراء الجمع على جميع التباديل n للعناصر m 1، 2، m. بمعنى آخر، دائم المصفوفة يساوي مجموع منتجات العناصر المأخوذة واحدًا من كل صف وأعمدة مختلفة.

من الصيغة (1) تظهر بعض الخصائص الواضحة للتابع الدائم، المشابهة لخصائص محدد المصفوفات المربعة.

1. إذا كان أحد الخطوط(n× m) المصفوفة A (n ≥ m) تتكون من أصفار، ثم لكل A = 0. بالنسبة لـ n = m ينطبق الأمر نفسه على الأعمدة.

2. عندما يتم ضرب جميع عناصر أحد صفوف المصفوفة A في عدد معين، يتم ضرب قيمة A الدائمة في نفس الرقم.

3. لا يتغير الدائم عند إعادة ترتيب صفوفه وأعمدته.

دعونا نشير بـ Aij إلى المصفوفة التي تم الحصول عليها من A عن طريق حذف الصف i والعمود j.

4. صيغة تحلل الدائم في الصف الأول صالحة: لكل A = ai1 لكل Ai1 + ai2 لكل Ai2 + ... + هدف لكل هدف (2)

وبالتالي، فإن العديد من خصائص العناصر الدائمة تشبه خصائص المحددات.

ومع ذلك، فإن الخاصية الرئيسية للمحددات det(AB) = detA detB غير راضية عن الدائمين، وهذا الظرف يجعل حسابهم صعبًا للغاية.


على سبيل المثال،


	2 لكل


ومع ذلك، 4 = لكل		≠ لكل

دعونا نفكر في أحد أهم تطبيقات مفهوم الدائم في المسائل التوافقية.

منازل ريفية اجعل X = (x1, xm) مجموعة محدودة، وX1, …, Xn يكون نظامًا من مجموعات فرعية

في هذه الحالة، يقال أن العنصر xi يمثل المجموعة Xi. تنشأ الحاجة إلى إيجاد نظام من الممثلين المختلفين عند حل العديد من المشكلات التطبيقية. النظر في مشكلة الترميز التالية. يجب أن يكون هناك بعض الاقتراحات، أي. مجموعة مرتبة من الكلمات في بعض الحروف الأبجدية. ويشترط ترميز هذه الجملة بحيث يخصص لكل كلمة حرف واحد، ويجب أن يكون هذا الحرف جزءا من هذه الكلمة، ويجب أن تتوافق الحروف المختلفة مع كلمات مختلفة.

مثال: الجملة a bc ab d abe c de cd e يمكن ترميزها كـ abecd. في الوقت نفسه، لا يمكن ترميز الجملة ab ab bc abc bcd بهذه الطريقة، لأن الكلمات الأربع الأولى معًا تحتوي على ثلاثة أحرف فقط.

بالنسبة لنظام المجموعات X1، …، Xn نحدد مصفوفة الإصابةا = (إيج)، ط = 1، ن،


	1 إذا الحادي عشر
ا ج =
	0 غير ذلك.
عدل
النظرية 1. دع A = (aij)، i =		(ن ≥ م) مصفوفة الإصابة
النظرية 1. دع A = (aij)، i =		(ن ≥ م) مصفوفة الإصابة

مجموعات X1، …، Xn، حيث Xi X، i = 1، n، X = (x1، …، xm). ثم بالنسبة لعدد الأنظمة

الممثلين الشخصيين R(X1 , … , Xn ) من المجموعات X1 , … , Xn تحمل المساواة التالية:

R(X1، …، Xn) = لكل A

♦ في الواقع، بما أن العنصر aij في المصفوفة A = 1، إذا كان xj Xi وaij = 0،

إذا xj

ك، الحادي عشر

) العناصر X هو نظام من مختلف ما قبل

Xi، ثم المجموعة (xi

اللواحق لـ X1، …، Xn

إذا وفقط إذا a1i

ك، ني

رجال شرطة a1i

ك، ني

موجودة في أعمدة مختلفة من المصفوفة A. دعونا نجمع الأرقام

a1i، ك، ني

على جميع التباديل n للعناصر 1، 2، ...، م. ثم نحصل على من مائة

rons، عدد الأنظمة ذات الممثلين المختلفين لـ X1، ...، Xn، ومن ناحية أخرى، قيمة per-

مصفوفة مانينتا أ

أ 1i 1 أ 2i 2 L a ni n

عاقبة. يوجد نظام من ممثلين مختلفين لـ X1، ...، Xn إذا وفقط إذا تم استيفاء حادثة المصفوفة المقابلة A:

نظرًا لوجود حدود m(m - 1) ... (m - n +1) في الصيغة (1)، فإن حساب الدائم بناءً على التعريف أمر صعب. دعونا نقدم صيغة عامة لهذا الغرض.

2. دعونا نقتصر على النظر في المصفوفات العددية المربعة A = (aij)، i، j = 1، n.

ثم لكل A = ∑

(i1، ك، في)

حيث يمتد المجموع على جميع التباديل i1، ... ، في العناصر

1، 2، …، ن. دعونا نطبق صيغة التضمين والاستبعاد لحساب الدائم للمصفوفة A. نخصص لكل مجموعة i1, ..., بوزن يساوي a1i 1,K,a ni n.

وهذا يعني أن A الدائم هو مجموع أوزان تلك المجموعات التي تتوافق مع التباديل. دعونا نقدم خصائص n P1 , … , Pn على مجموعة جميع المجموعات i1 , i2 , … , في 1, 2, … , n حيث الخاصية Pi تعني عدم وجود عنصر i في المجموعة i1 , … , في. وبالتالي، فإن A الدائم هو مجموع أوزان المجموعات i1، ...، التي لا تحتوي على أي من الخصائص P1، ...، Pn. يبقى تحديد مجموع الأوزان W(Pi 1 ,K , Pi k ) للمجموعات التي لها خصائص k

بي 1، ك، بي ك. لدينا مجموع الأوزان W(0) لجميع المجموعات i1 , ... , ik .
ث(0) = ∑		ك، آني	= (أ 11 + ل + أ 1ن )(أ 21 + ل + أ 2ن ) إل (أ ن1 + ل + أ ن )
i1، ك، في
i1، ك، في

ث(ن(بي)) =		a1i، ك، ني		= (أ 11 + ل + أ 1ط	L + a1n )L (a n1 + L a ni + L + a nn ) (9)

	≠ط

حيث تعني علامة ^ الموجودة أعلى أحد عناصر المصفوفة A أنه يجب حذف هذا العنصر. وبالمثل بالنسبة لـ sij (i< j) имеем


W(N(Pi , Pj )) = (a11 + L + a1i	ل+أ 1ي	L + a1n )L (a n1 + L a ni + L + a nj + L + a nn ) (10)

الآن، باستخدام صيغة التضمين والاستبعاد، نحصل على صيغة Raiser للدائم A:


لكل A = ∏ i n = 1 (ai1 + L + ain ) − ∑∏ k n = 1 (a k1 + L + a ki + L + a kn )+ L +

+ (− 1)ق	∑∏ن
+ (− 1)ق	∑∏ن	(أ ك1 + ل + أ كي1	ل + كي	ل +أ كن) +ل
	1

يمكن تنظيم حساب الدائم باستخدام صيغة Raiser بالطريقة التي تتطلبها

(2ن - 1)(ن - 4) الضرب و (2ن - 2)(ن + 1) الجمع. على الرغم من أن هذه القيمة تنمو بسرعة مع زيادة n، إلا أن هذه الصيغة توفر الطريقة الأكثر فعالية لحساب القيم الدائمة.

3. دعونا نوضح الآن مسألة شروط أن تكون المصفوفة الدائمة (0، 1) مساوية للصفر. دعونا نقتصر على حالة المصفوفة المربعة.

النظرية 2. دع A = (aij )، i، j = 1، n تكون مصفوفة (0، 1) من الرتبة n. ثم

لكل A= 0 إذا وفقط إذا كانت A تحتوي على مصفوفة فرعية من الأصفار بالحجم s × t، حيث s + t = n + 1.

♦ دع مثل هذه المصفوفة الفرعية الصفرية موجودة في A. وبما أن الدائم لا يتغير بسبب تباديل الصفوف والأعمدة، يمكننا أن نفترض أن هذه المصفوفة الفرعية تقع في الزاوية اليسرى السفلى، أي.

حيث O - (s × t) عبارة عن مصفوفة من الأصفار، والمصفوفة الفرعية B لها حجم (n - s) × t. يجب أن يحتوي كل عضو في A الدائم على عنصر واحد من الأعمدة t الأولى. لذلك، إذا بحثنا عن حد موجب للثابت، فيجب أن تنتمي عناصر هذه الأعمدة إلى صفوف مختلفة زوجية بأرقام 1، 2، ...، n - s. ومع ذلك ن - ق = ر - 1< t и поэтому данное условие выполнить нельзя, т.е. per A = 0.

دعونا الآن لكل A = 0. نثبت النظرية عن طريق الحث على n. بالنسبة لـ n = 1 تكون العبارة واضحة (A = (0)). فليكن صحيحًا بالنسبة لجميع الطلبات الأقل من n. إذا كانت A عبارة عن مصفوفة صفرية من الرتبة n، فإن العبارة واضحة. إذا لم تكن A مصفوفة صفرية، فلنفترض أن aij = 1. فلنكتب تحليل A على طول الصف i:

لكل A = ai1 Ai1 + … + عين عين

بما أن per A = 0، إذن لكل Aij = 0. لكن Aij له حجم (n - 1) × (n - 1) وبواسطة فرضية الاستقراء هناك مصفوفة فرعية من أصفار الحجم

s1 × t1، حيث s1 + t1 = n - 1 + 1 = n. دعونا نعيد ترتيب الصفوف والأعمدة بحيث تكون هذه المصفوفة الفرعية الصفرية في الزاوية اليسرى السفلية:


أ → ب =

حيث O هي المصفوفة الفرعية الصفرية ذات الحجم s1 × t1، s1 + t1 = n، C - لها حجم (n - s1) × t1، D -

حجمه s1 × (n - t) . هذا يعني أن المصفوفتين C و D مربعتان ولهما الترتيب (t1 × t1) و (s1 × s1) على التوالي. وفقًا لتعريف الدائم، لدينا لكل B = لكل A و،

لكل B = لكل C لكل D وبالتالي من لكل A = 0 يترتب على ذلك إما لكل C = 0 أو لكل D = 0.

دع لكل C = 0. حسب الفرضية الاستقراءية، هناك مصفوفة فرعية صفرية للحجم

u × v، حيث u + v = t1 + 1. دعها تكون موجودة في صفوف ذات أرقام i1، ...، iu وأعمدة ذات أرقام j1، ...، jv. خذ بعين الاعتبار مصفوفة فرعية B تتكون من صفوف

i1، …، iu، t1 + 1، …، n والأعمدة j1، …، jv. هذه مصفوفة فرعية صفرية الحجم (u + n - t1) × v،

حيث u + n - t1 + v = n + +1. لذا، تحتوي المصفوفة B على مصفوفة فرعية صفرية بحجم s × t، حيث s + t = n + 1. وبما أن المصفوفتين A وB تختلفان في تبديل الصفوف والأعمدة، فقد تم إثبات النظرية. ♦

دعونا الآن نفكر في حالة خاصة مهمة للمصفوفة A. دعونا نشير بواسطة A(k, n) إلى مصفوفة مكونة من 0.1 عنصر بالحجم n × n مع عناصر k لكل صف وكل عمود (k > 0).

النظرية 3. لأي مصفوفة A(k, n) لكل A(k, n) > 0.

♦ لنفترض العكس، أنه لكل A(k, n) = 0. ثم، حسب النظرية 2، يوجد صفر

مصفوفة فرعية بالحجم s × t، حيث s + t = n + 1. ثم، بإعادة ترتيب صفوف وأعمدة المصفوفة A(k, n) نحصل على المصفوفة

حيث O هي المصفوفة الصفرية (s × t).

دعونا نحسب عدد الآحاد في المصفوفتين B وD. بما أن A(k, n) بها k من الآحاد في كل صف وكل عمود، إذن يوجد بالضبط k من الآحاد في كل عمود من B وكل صف من D

وحدات. هناك وحدات n k إجمالاً في A(k, n)، لذا nk ≥ tk + sk = (t + s)n. من هنا

سوم، n ≥ t + s، وهو أمر مستحيل، لأن s + t = n + 1 ومن هذا التناقض ينتج ذلك

صحة البيان. ♦ وقد ثبت بطريقة مماثلة

نظرية 3 أ. لتكن A مصفوفة (0,1) بحجم n× m (n≥ m). ثم perA = 0 إذا وفقط إذا كان يحتوي على مصفوفة فرعية صفرية بحجم s×t، حيث s+t=m+1.

4. دعونا الآن ننظر في تطبيق القضايا قيد النظر في بناء la-

مربعات تينا. اللاتينية (ن × م)-المستطيلعلى المجموعة X=(x1 ,…,xm )

يُسمى (n× m) - مصفوفة العناصر X، حيث يكون كل صف عبارة عن تبديل n لـ X، وكل عمود عبارة عن تبديل m للمجموعة X. بالنسبة إلى n=m، يُسمى المستطيل اللاتيني الساحة اللاتينية.

من الواضح أنه بالنسبة لـ n=1 فإن عدد المستطيلات اللاتينية 1×m يساوي m!. عندما يكون n=2، بعد تحديد الصف الأول، يمكن اعتبار أي تبديل كالصف الثاني.

منتج جديد يتعارض مع المنتج المختار. عدد هذه التباديل هو Dm، وبالتالي فإن الرقم 2×m هو

من المستطيلات اللاتينية يساوي م! مارك ألماني.

يطرح سؤال طبيعي فيما يتعلق بالبناء الاستقرائي للمربعات اللاتينية. دعونا نبني مستطيلًا لاتينيًا (n×m) (n< m). Можно ли его расширить до ((n+1)× m) -прямоугольника добавлением (n+1)-й строки?

عدل

نظرية 4. كل لاتيني (ن×م)-مستطيل ن

♦ لنفترض أن X=(x1,...,xm) ومستطيل L-لاتيني (n×m) يحتوي على عناصر من X. فكر في مجموعة من المجموعات A1,...,Am حيث Ai هي عناصر العمود i من المستطيل اللاتيني L. لتكن A مصفوفة حدوث لنظام المجموعة A1 ,… ,Am . حجمها m×m، وكل صف من المصفوفة A يحتوي بالضبط على n منها، حيث Ai = n، i = 1، m. يمكن أن يظهر كل عنصر xi X في أعمدة L بما لا يزيد عن m مرات، وإلا سيكون هناك صف يظهر فيه هذا العنصر مرتين. العدد الإجمالي للعناصر

L يساوي m n، لذلك يظهر كل عنصر xi X بالضبط n مرات في الأعمدة. ويترتب على ذلك أن كل عمود في المصفوفة A يحتوي بالضبط على عدد n منها. دعونا الآن نفكر في المصفوفة A التي تم الحصول عليها عن طريق استبدال كل واحد بصفر وكل صفر بواحد.

المصفوفة A هي مصفوفة حدوث نظام المجموعات X1، …، Xn، حيث Xi = X\Ai،

ط = 1، م. يحتوي على وحدات m - n في كل صف وفي كل عمود. حسب النظرية

> 0. دع ai1

... ميل

≠ 0 . ثم لدينا xi X1 ,K ,xi

Xm وجميع العناصر

الحادي عشر، ك، الحادي عشر

زوجية مختلفة. خط

الحادي عشر، ك، الحادي عشر

يمكن أن تؤخذ على أنها (ن + 1).

للمستطيل اللاتيني (n × m) L. وباستمرار هذا الإجراء، نحصل على اللاتينية

ساحة السماء. ♦

دعونا نشير إلى l n - عدد المربعات اللاتينية بالترتيب n، مع عناصر من المجموعة X = (1، 2، ...، n)، حيث تكون عناصر العمود الأول والصف الأول بالترتيب الطبيعي. فيما يلي جدول يضم العديد من القيم المعروفة للرقم l n:

5. تسمى مصفوفة A = (aij) بحجم n × n وبها عناصر حقيقية غير سالبة العشوائية مرتين، لو