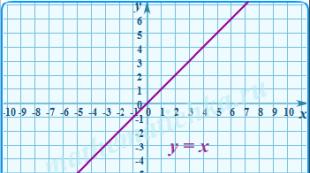
الفضاء المتجه الخطي وخصائصه البديهية. الفضاء المتجه الخطي: التعريف والخصائص. ما هو مزيج خطي من المتجهات؟
مادة من ويكيبيديا – الموسوعة الحرة
المتجه(أو خطي) فضاء- البنية الرياضية، وهي عبارة عن مجموعة من العناصر تسمى المتجهات، والتي يتم من خلالها تحديد عمليات الجمع مع بعضها البعض والضرب في عدد - العددية. تخضع هذه العمليات لثمانية بديهيات. يمكن أن تكون الكميات القياسية عناصر من حقل الأرقام الحقيقي أو المعقد أو أي حقل رقم آخر. حالة خاصة لمثل هذا الفضاء هو الفضاء الإقليدي المعتاد ثلاثي الأبعاد، والذي تستخدم ناقلاته، على سبيل المثال، لتمثيل القوى الفيزيائية. تجدر الإشارة إلى أن المتجه كعنصر من عناصر الفضاء المتجه لا يلزم بالضرورة تحديده في شكل مقطع موجه. إن تعميم مفهوم "المتجه" على عنصر الفضاء المتجه من أي طبيعة لا يؤدي فقط إلى ارتباك في المصطلحات، ولكنه يجعل من الممكن أيضًا فهم أو حتى التنبؤ بعدد من النتائج الصالحة للمساحات ذات الطبيعة التعسفية.
الفضاءات المتجهة هي موضوع الجبر الخطي. إحدى الخصائص الرئيسية للفضاء المتجه هي أبعاده. يمثل البعد الحد الأقصى لعدد عناصر الفضاء المستقلة خطيًا، أي باللجوء إلى وصف هندسي تقريبي، وهو عدد الاتجاهات التي لا يمكن التعبير عنها من خلال بعضها البعض من خلال عمليات الجمع والضرب فقط بواسطة سلم. يمكن منح مساحة المتجه بهياكل إضافية، مثل القاعدة أو المنتج الداخلي. تظهر مثل هذه الفضاءات بشكل طبيعي في التحليل الرياضي، وبشكل أساسي في شكل فضاءات دالة لا نهائية الأبعاد ( إنجليزي)، حيث الوظائف . تتطلب العديد من مشكلات التحليل معرفة ما إذا كانت سلسلة من المتجهات تتقارب مع متجه معين. يمكن النظر في مثل هذه الأسئلة في الفضاءات المتجهة ذات البنية الإضافية، وفي معظم الحالات طوبولوجيا مناسبة، مما يسمح لنا بتحديد مفهومي القرب والاستمرارية. تسمح مثل هذه الفضاءات المتجهة الطوبولوجية، وخاصة فضاءات باناخ وهيلبيرت، بدراسة أعمق.
بالإضافة إلى المتجهات، يدرس الجبر الخطي أيضًا الموترات ذات الرتبة الأعلى (يعتبر العدد العددي موترًا من الرتبة 0، ويعتبر المتجه موترًا من الرتبة 1).
تعود الأعمال الأولى التي تنبأت بإدخال مفهوم الفضاء المتجه إلى القرن السابع عشر. عندها بدأت الهندسة التحليلية وعقيدة المصفوفات وأنظمة المعادلات الخطية والمتجهات الإقليدية في التطور.
تعريف
خطي، أو مساحة المتجهات فوق الميدان - هذا أمر أربعة ، أين
- - مجموعة غير فارغة من العناصر ذات الطبيعة التعسفية، والتي تسمى ثلاثة أبعاد;
- - الحقل (الجبري) الذي تسمى عناصره العددية;
- عملية محددة إضافةثلاثة أبعاد الذي يربط كل زوج من العناصر مجموعات ناديتهم كميةوالمعينة ;
- عملية محددة ضرب المتجهات بالكميات القياسية ، مطابقة كل عنصر مجالات وكل عنصر مجموعات العنصر الوحيد في المجموعة ، يعني أو ;
ستكون المساحات المتجهة المحددة في نفس مجموعة العناصر، ولكن في مجالات مختلفة، بمثابة مساحات متجهة مختلفة (على سبيل المثال، مجموعة أزواج الأعداد الحقيقية يمكن أن تكون مساحة متجهة ثنائية الأبعاد فوق مجال الأعداد الحقيقية أو أحادية البعد - فوق مجال الأعداد المركبة).
أبسط الخصائص
- الفضاء المتجه هو مجموعة أبيلية قيد الإضافة.
- عنصر محايد
- لأي احد .
- لأي احد العنصر المعاكس هو الشيء الوحيد الذي يتبع من خصائص المجموعة.
- لأي احد .
- لأي و .
- لأي احد .
التعاريف والخصائص ذات الصلة
الفضاء الجزئي
التعريف الجبري: الفضاء الجزئي الخطيأو الفضاء الفرعي المتجه- مجموعة فرعية غير فارغة الفضاء الخطي مثل ذلك هو في حد ذاته مساحة خطية فيما يتعلق بتلك المحددة في عمليات الجمع والضرب بالعدد. عادةً ما يُشار إلى مجموعة جميع المساحات الفرعية بـ . لكي تكون المجموعة الفرعية فضاءً فرعيًا، فمن الضروري والكافي أن يكون ذلك
- لأي ناقل ، المتجه ينتمي أيضا ، لأي ;
- لجميع المتجهات ، المتجه ينتمي أيضا .
العبارتان الأخيرتان مكافئتان لما يلي:
لجميع المتجهات ، المتجه ينتمي أيضا لأي .
على وجه الخصوص، الفضاء المتجه الذي يتكون من متجه صفري واحد فقط هو فضاء فرعي لأي فضاء؛ كل مساحة هي مساحة فرعية من نفسها. تسمى الفضاءات الجزئية التي لا تتطابق مع هذين الاثنين ملكأو غير تافهة.
خصائص الفضاءات الجزئية
- تقاطع أي عائلة من الفضاءات الجزئية هو مرة أخرى فضاء جزئي؛
- مجموع المساحات الجزئية يتم تعريفه على أنه مجموعة تحتوي على جميع المجاميع الممكنة للعناصر :
.
- مجموع عائلة محدودة من الفضاءات الجزئية هو مرة أخرى فضاء جزئي.
مجموعات خطية
المجموع النهائي للنموذج
تسمى المجموعة الخطية:
أساس. البعد
ثلاثة أبعاد وتسمى تعتمد خطيا، إذا كان هناك مجموعة خطية غير بديهية منها تساوي الصفر:
وإلا تسمى هذه النواقل مستقل خطيا.
يسمح هذا التعريف بالتعميم التالي: مجموعة لا حصر لها من المتجهات من مُسَمًّى تعتمد خطيا، إذا كان البعض يعتمد خطيا أخيرمجموعة فرعية منه، و مستقل خطيا، إذا كان أي منها أخيرالمجموعة الفرعية مستقلة خطيا.
خصائص الأساس:
- أي عناصر مستقلة خطيا -شكل الفضاء الأبعاد أساسهذه المساحة.
- أي ناقل يمكن تمثيلها (بشكل فريد) كمجموعة خطية محدودة من العناصر الأساسية:
قذيفة خطية
قذيفة خطية مجموعات فرعية الفضاء الخطي - تقاطع جميع الفضاءات الجزئية تحتوي .
المدى الخطي هو مساحة فرعية .
وتسمى أيضًا الصدفة الخطية تم إنشاء الفضاء الفرعي . ويقال أيضًا أن القشرة الخطية - فضاء، امتدتمجموعة من .
قذيفة خطية يتكون من جميع المجموعات الخطية الممكنة لمختلف الأنظمة الفرعية المحدودة للعناصر من . على وجه الخصوص، إذا هي مجموعة محدودة، إذن يتكون من جميع المجموعات الخطية من العناصر . وبالتالي، فإن المتجه الصفري ينتمي دائمًا إلى الهيكل الخطي.
لو هي مجموعة مستقلة خطيا، فهي الأساس ومن ثم يحدد أبعاده.
أمثلة
- مساحة فارغة عنصرها الوحيد هو صفر.
- مساحة لجميع الوظائف مع الدعم المحدود يشكل مساحة متجهة ذات بعد مساوي للأصل .
- يمكن اعتبار مجال الأعداد الحقيقية بمثابة مساحة متجهة ذات أبعاد متواصلة فوق مجال الأعداد النسبية.
- أي حقل هو فضاء أحادي البعد فوق نفسه.
هياكل إضافية
أنظر أيضا
اكتب مراجعة عن مقالة "مساحة المتجهات"
ملحوظات
الأدب
- جلفاند آي إم.محاضرات في الجبر الخطي. - الخامس. - م: دوبروسفيت، إم تي إس إن إم أو، 1998. - 319 ص. - ردمك 5-7913-0015-8.
- جلفاند آي إم.محاضرات في الجبر الخطي. الطبعة الخامسة. - م: دوبروسفيت، إم تي إس إن إم أو، 1998. - 320 ص. - ردمك 5-7913-0016-6.
- كوستريكين إيه آي، مانين يو آي.الجبر الخطي والهندسة. الطبعة الثانية. - م: نوكا، 1986. - 304 ص.
- كوستريكين أ.مقدمة في الجبر. الجزء الثاني: الجبر الخطي. - الثالث. - م: نوكا، 2004. - 368 ص. - (كتاب الجامعة).
- مالتسيف أ.أساسيات الجبر الخطي. - الثالث. - م: نوكا، 1970. - 400 ص.
- بوستنيكوف م.الجبر الخطي (محاضرات في الهندسة. الفصل الثاني). - الثاني. - م: نوكا، 1986. - 400 ص.
- سترانج جي.الجبر الخطي و تطبيقاته. - م: مير، 1980. - 454 ص.
- إيلين في.أ.، بوزنياك إي.جي.الجبر الخطي. الطبعة السادسة. - م: فيزماتليت، 2010. - 280 ص. - ردمك 978-5-9221-0481-4.
- هالموس ص.الفضاءات المتجهة ذات الأبعاد المحدودة. - م: فيزماتجيز، 1963. - 263 ص.
- فاديف د.ك.محاضرات في الجبر. - الخامس. - سان بطرسبرج. : لان، 2007. - 416 ص.
- شافاريفيتش آي آر، ريميزوف إيه أو.الجبر الخطي والهندسة. - الأول. - م: فيزماتليت، 2009. - 511 ص.
- شراير أو.، سبيرنر جي.مقدمة للجبر الخطي في العرض الهندسي = Einfuhrung in die analytische Geometrie und Algebra / Olshansky G. (ترجمة من الألمانية). - م.-ل.: أونتي، 1934. - 210 ص.
|
||||||||||||||||||||||||||||||||||||||
مقتطف يميز الفضاء المتجه
كان كوتوزوف يمشي عبر الرتب، ويتوقف أحيانًا ويتحدث ببعض الكلمات الطيبة إلى الضباط الذين عرفهم من الحرب التركية، وأحيانًا إلى الجنود. عند النظر إلى الحذاء، هز رأسه للأسف عدة مرات وأشار إلى الجنرال النمساوي بتعبير يبدو أنه لا يلوم أي شخص على ذلك، لكنه لم يستطع إلا أن يرى مدى سوء الأمر. في كل مرة يتقدم فيها قائد الفوج خوفًا من تفويت كلمة القائد الأعلى فيما يتعلق بالفوج. خلف كوتوزوف، على مسافة يمكن سماع أي كلمة منطوقة ضعيفة، سار حوالي 20 شخصًا في حاشيته. كان السادة الحاشية يتحدثون فيما بينهم ويضحكون أحيانًا. سار المساعد الوسيم بالقرب من القائد الأعلى. كان الأمير بولكونسكي. كان يسير بجانبه رفيقه نيسفيتسكي، وهو ضابط أركان طويل القامة، سمين للغاية، ذو وجه وسيم لطيف ومبتسم وعينان رطبتان؛ لم يستطع نيسفيتسكي أن يمنع نفسه من الضحك، متحمسًا لضابط الحصار الأسود الذي يسير بجواره. ضابط الحصار، دون أن يبتسم، دون أن يغير تعبير عينيه الثابتتين، نظر بوجه جدي إلى مؤخرة قائد الفوج وقام بتقليد كل حركاته. في كل مرة يجفل فيها قائد الفوج وينحني للأمام، بنفس الطريقة تمامًا، بنفس الطريقة تمامًا، كان ضابط الحصار يجفل وينحني للأمام. ضحك نسفيتسكي ودفع الآخرين للنظر إلى الرجل المضحك.مشى كوتوزوف ببطء وبطء أمام آلاف العيون التي خرجت من مآخذها، وهي تراقب رئيسهم. بعد اللحاق بالشركة الثالثة، توقف فجأة. الحاشية، التي لم تتوقع هذا التوقف، تحركت نحوه قسراً.
- آه تيموخين! - قال القائد الأعلى معترفًا بالقبطان ذي الأنف الأحمر الذي عانى من معطفه الأزرق.
يبدو أنه كان من المستحيل التمدد أكثر من تمدد تيموخين، بينما وبخه قائد الفوج. لكن في تلك اللحظة خاطبه القائد العام، وقف القبطان منتصبًا بحيث بدا أنه لو نظر إليه القائد العام لفترة أطول قليلاً، لما تمكن القبطان من الوقوف؛ وبالتالي فإن كوتوزوف، على ما يبدو، يفهم موقفه ويتمنى، على العكس من ذلك، كل التوفيق للقبطان، ابتعد على عجل. ارتسمت ابتسامة بالكاد ملحوظة على وجه كوتوزوف الممتلئ والمشوه بالجرح.
قال: "رفيق إسماعيلوف آخر". - ضابط شجاع! هل أنت سعيد به؟ – سأل كوتوزوف قائد الفوج.
وقائد الفوج، الذي انعكس كما في المرآة، غير مرئي لنفسه، في ضابط هوسار، ارتجف، وتقدم وأجاب:
- أنا سعيد جدًا يا صاحب السعادة.
قال كوتوزوف وهو يبتسم ويبتعد عنه: "نحن جميعًا لا نخلو من نقاط الضعف". "كان لديه إخلاص لباخوس.
كان قائد الفوج خائفا من إلقاء اللوم عليه، ولم يجيب على أي شيء. لاحظ الضابط في تلك اللحظة وجه القبطان بأنف أحمر وبطن مطوية وقلد وجهه ووقف بشكل قريب جدًا لدرجة أن نيسفيتسكي لم يستطع التوقف عن الضحك.
استدار كوتوزوف. كان من الواضح أن الضابط يمكنه التحكم في وجهه كما يريد: في اللحظة التي استدار فيها كوتوزوف، تمكن الضابط من التجهم، وبعد ذلك اتخذ التعبير الأكثر جدية واحترامًا وبريئًا.
كانت الشركة الثالثة هي الأخيرة، وفكر كوتوزوف في الأمر، على ما يبدو، تذكر شيئا ما. خرج الأمير أندريه من حاشيته وقال بهدوء بالفرنسية:
– لقد أمرت بتذكير دولوخوف الذي تم تخفيض رتبته في هذا الفوج.
-أين دولوخوف؟ - سأل كوتوزوف.
لم ينتظر دولوخوف، الذي كان يرتدي معطف الجندي الرمادي، حتى يتم استدعاؤه. خرج الشكل النحيف لجندي أشقر بعيون زرقاء صافية من الأمام. اقترب من القائد الأعلى ووضعه على أهبة الاستعداد.
- مطالبة؟ - سأل كوتوزوف، عابسًا قليلاً.
قال الأمير أندريه: "هذا دولوخوف".
- أ! - قال كوتوزوف. "آمل أن يصحح لك هذا الدرس، وأن تخدم جيدًا." الرب رحيم. ولن أنساك إذا كنت تستحق ذلك.
نظرت العيون الزرقاء الواضحة إلى القائد الأعلى بتحدٍ كما نظرت إلى قائد الفوج، كما لو كانت بتعبيرها تمزق حجاب الاتفاقية التي كانت تفصل حتى الآن بين القائد الأعلى والجندي.
قال بصوته الرنان الثابت غير المتسرع: "أطلب شيئًا واحدًا يا صاحب السعادة". "من فضلك أعطني فرصة للتكفير عن ذنبي وإثبات إخلاصي للإمبراطور وروسيا."
ابتعد كوتوزوف. تومض نفس الابتسامة في عينيه كما كانت عندما ابتعد عن الكابتن تيموخين. لقد استدار وجفل، كما لو كان يريد التعبير عن أن كل ما أخبره به دولوخوف، وكل ما يمكن أن يخبره به، كان يعرفه منذ وقت طويل، أن كل هذا قد سئمه بالفعل وأن كل هذا لم يكن كذلك على الإطلاق ما يحتاج إليه. استدار واتجه نحو عربة الأطفال.
تم حل الفوج في مجموعات وتوجهوا إلى أماكن مخصصة ليست بعيدة عن براوناو، حيث كانوا يأملون في ارتداء الأحذية والملابس والراحة بعد المسيرات الصعبة.
- ألا تطالبني يا بروخور إغناتيتش؟ - قال قائد الفوج وهو يتجول حول السرية الثالثة ويتحرك نحو المكان ويقترب من النقيب تيموخين الذي كان يسير أمامها. أعرب وجه قائد الفوج عن فرحة لا يمكن السيطرة عليها بعد المراجعة المكتملة بسعادة. - الخدمة الملكية... مستحيل... مرة أخرى ستنهيها في المقدمة... سأعتذر أولاً، أنت تعرفني... أشكرك كثيراً! - ومد يده لقائد السرية .
- من أجل الرحمة، أيها الجنرال، هل أجرؤ! - أجاب القبطان وقد احمر أنفه وهو يبتسم ويكشف بابتسامة عن عدم وجود أسنان أمامية مكسورة من مؤخرته تحت إسماعيل.
- نعم، أخبر السيد دولوخوف أنني لن أنساه، حتى يهدأ. نعم، من فضلك أخبرني، ظللت أرغب في السؤال عن حاله، وكيف يتصرف؟ و هذا كل شيء...
قال تيموخين: "إنه مفيد للغاية في خدمته، يا صاحب السعادة... لكن المستأجر...".
- ماذا، ما هي الشخصية؟ - سأل قائد الفوج.
قال القبطان: «لقد اكتشف سعادتك لعدة أيام أنه ذكي ومتعلم ولطيف.» إنه وحش. لقد قتل يهودياً في بولندا، إذا سمحت...
قال قائد الفوج: "حسنًا، نعم، حسنًا، ما زلنا بحاجة إلى الأسف على الشاب الذي يعاني من سوء الحظ". بعد كل شيء، اتصالات رائعة... إذن أنت...
"أنا أستمع يا صاحب السعادة"، قال تيموخين مبتسمًا، مما جعله يشعر وكأنه يفهم رغبات رئيسه.
- نعم نعم.
وجد قائد الفوج دولوخوف في الرتب وكبح جماح حصانه.
قال له: "قبل المهمة الأولى، الكتفيات".
نظر دولوخوف حوله ولم يقل شيئًا ولم يغير تعبير فمه المبتسم ساخرًا.
وتابع قائد الفوج: "حسنًا، هذا جيد". وأضاف: "كل من الناس لديه كأس من الفودكا مني"، حتى يتمكن الجنود من سماعهم. - شكرا لكل شخص! الله يبارك! - وتجاوز الشركة وتوجه إلى أخرى.
«حسنًا، إنه رجل طيب حقًا؛ قال التابع تيموخين للضابط الذي كان يسير بجواره: "يمكنك أن تخدم معه".
"كلمة واحدة، ملك القلوب!... (كان قائد الفوج يلقب بملك القلوب)"، قال الضابط التابع ضاحكًا.
وامتد المزاج السعيد للسلطات بعد المراجعة إلى الجنود. سارت الشركة بمرح. وكانت أصوات الجنود تتحدث من كل جانب.
- ماذا قالوا أيها الملتوي كوتوزوف عن عين واحدة؟
- بخلاف ذلك لا! ملتوية تماما.
- لا... يا أخي، لديه عيون أكبر منك. الأحذية والثنيات - نظرت إلى كل شيء...
- كيف له يا أخي أن ينظر إلى قدمي... حسناً! يفكر…
- والنمساوي الآخر معه كأنه ملطخ بالطباشير. مثل الدقيق الأبيض. أنا الشاي، وكيف تنظيف الذخيرة!
- ماذا يا فيديشو!... هل قال أنه عندما بدأ القتال وقفت أقرب؟ قالوا جميعا أن بونابرت نفسه يقف في برونوفو.
- بونابرت يستحق ذلك! إنه يكذب أيها الأحمق! ما لا يعرفه! الآن البروسي يتمرد. لذلك قام النمساوي بتهدئته. بمجرد أن يصنع السلام، ستفتح الحرب مع بونابرت. وإلا، كما يقول، فإن بونابرت يقف في برونوفو! وهذا ما يدل على أنه أحمق. استمع أكثر.
- انظروا، اللعنة على المستأجرين! الشركة الخامسة، انظر، تتحول بالفعل إلى القرية، وسوف يطبخون العصيدة، وما زلنا لا نستطيع الوصول إلى المكان.
- أعطني قطعة من البسكويت، اللعنة.
- هل أعطيتني التبغ أمس؟ هذا كل شيء يا أخي. حسنًا، ها نحن ذا، الله معك.
"على الأقل توقفوا، وإلا فلن نأكل لخمسة أميال أخرى."
- كان جميلاً كيف قدم لنا الألمان عربات الأطفال. عندما تذهب، اعرف: أنه مهم!
«وهنا يا أخي أصبح الناس مسعورين تمامًا». بدا أن كل شيء هناك كان بولنديًا، وكان كل شيء من التاج الروسي؛ والآن يا أخي، أصبح ألمانيًا تمامًا.
- كتاب الأغاني إلى الأمام! - سمع صرخة القبطان.
وركض عشرين شخصا من صفوف مختلفة أمام الشركة. بدأ عازف الدرامز في الغناء والتفت لمواجهة مؤلفي الأغاني، ولوح بيده، وبدأ أغنية جندي طويلة، والتي بدأت: "أليس الفجر، لقد طلعت الشمس..." وانتهت بالكلمات: "ثم أيها الإخوة، سيكون هناك مجد لنا ولوالد كامينسكي..." تم تأليف هذه الأغنية في تركيا ويتم غنائها الآن في النمسا، فقط مع التغيير الذي تم إدراج الكلمات فيه بدلاً من "والد كامينسكي": "كوتوزوف" أب."
بعد أن مزق هذه الكلمات الأخيرة كجندي ولوح بيديه، كما لو كان يرمي شيئًا على الأرض، نظر عازف الدرامز، وهو جندي جاف ووسيم يبلغ من العمر حوالي أربعين عامًا، بصرامة إلى مؤلفي الأغاني الجندي وأغمض عينيه. بعد ذلك، بعد أن تأكد من أن كل العيون كانت مثبتة عليه، بدا وكأنه يرفع بكلتا يديه شيئًا ثمينًا غير مرئي فوق رأسه، وأمسكه بهذه الطريقة لعدة ثوانٍ ثم رماه فجأة:
أوه، أنت، مظلتي، مظلتي!
«مظلتي الجديدة...»، ترددت عشرين صوتًا، وسرعان ما قفز حامل الملعقة، رغم ثقل ذخيرته، إلى الأمام ومشى إلى الخلف أمام الشركة، وهو يحرك كتفيه ويهدد أحدهم بملاعقه. ولوح الجنود بأذرعهم على إيقاع الأغنية، وساروا بخطوات طويلة، وضربوا أقدامهم بشكل لا إرادي. من خلف الشركة سمعت أصوات العجلات وطحن النوابض ودوس الخيول.
كان كوتوزوف وحاشيته عائدين إلى المدينة. وأشار القائد العام للشعب أن يواصل المشي بحرية، وظهرت السعادة على وجهه وعلى كل وجوه حاشيته عند أصوات الأغنية، وعلى مرأى من الجندي الراقص وجنود الجيش. تسير الشركة بمرح ونشاط. في الصف الثاني، من الجهة اليمنى، حيث تجاوزت العربة الشركات، لفت أحدهم قسراً عين الجندي ذو العيون الزرقاء، دولوخوف، الذي سار بخفة ورشاقة بشكل خاص على إيقاع الأغنية ونظر إلى وجوه أولئك الذين يمرون بمثل هذا التعبير وكأنه يشعر بالأسف على كل من لم يذهب مع الشركة في هذا الوقت. سقط كورنيت هوسار من حاشية كوتوزوف، مقلدًا قائد الفوج، خلف العربة وتوجه إلى دولوخوف.
كان هوسار كورنيت زيركوف في وقت ما في سانت بطرسبرغ ينتمي إلى ذلك المجتمع العنيف بقيادة دولوخوف. في الخارج، التقى زيركوف مع دولوخوف كجندي، لكنه لم يعتبر أنه من الضروري التعرف عليه. الآن، بعد محادثة كوتوزوف مع الرجل الذي تم تخفيض رتبته، التفت إليه بفرحة صديق قديم:
- صديقي العزيز، كيف حالك؟ - قال على صوت الأغنية مطابقا خطوة حصانه مع خطوة الشركة.
- أنا مثل؟ - أجاب دولوخوف ببرود - كما ترى.
أعطت الأغنية المفعمة بالحيوية أهمية خاصة لنبرة البهجة الوقحة التي تحدث بها زيركوف والبرودة المتعمدة في إجابات دولوخوف.
- حسنًا، كيف تتعامل مع رئيسك في العمل؟ - سأل زيركوف.
- لا شيء يا أهل الخير. كيف دخلت إلى المقر؟
- معار، في الخدمة.
كانوا صامتين.
وقالت الأغنية: "لقد أطلقت صقرًا من كمها الأيمن"، مما أثار بشكل لا إرادي شعورًا بالبهجة والبهجة. ربما كان من الممكن أن تكون محادثتهم مختلفة لو لم يتحدثوا على صوت الأغنية.
– هل صحيح أن النمساويين تعرضوا للضرب؟ - سأل دولوخوف.
ويقولون: "الشيطان يعرفهم".
"أنا سعيد"، أجاب دولوخوف لفترة وجيزة وبشكل واضح، كما تتطلب الأغنية.
قال زيركوف: "حسنًا، تعال إلينا في المساء، وسوف ترهن الفرعون".
- أو هل لديك الكثير من المال؟
- يأتي.
- ممنوع. لقد قطعت نذرا. أنا لا أشرب الخمر أو المقامرة حتى يتمكنوا من ذلك.
- حسنًا، إلى أول شيء..
- سنرى هناك.
مرة أخرى كانوا صامتين.
قال زيركوف: "تأتي إذا كنت بحاجة إلى أي شيء، وسيساعدك الجميع في المقر الرئيسي...".
ابتسم دولوخوف.
- من الأفضل أن لا تقلق. لن أطلب أي شيء أحتاجه، سأأخذه بنفسي.
- حسنا أنا كذلك...
- حسنا، أنا كذلك.
- مع السلامة.
- كن بصحة جيدة…
...وعالية وبعيدة،
ومن ناحية الوطن...
لمس زيركوف مهمازه للحصان، الذي كان متحمسًا، وركل ثلاث مرات، دون أن يعرف أيهما يبدأ، وتمكن وركض متجاوزًا الشركة ولحق بالعربة، أيضًا على إيقاع الأغنية.
عند عودته من المراجعة، ذهب كوتوزوف، برفقة الجنرال النمساوي، إلى مكتبه، واستدعاء المساعد، وأمر بإعطائه بعض الأوراق المتعلقة بحالة القوات القادمة، والرسائل الواردة من الأرشيدوق فرديناند، الذي قاد الجيش المتقدم . دخل الأمير أندريه بولكونسكي إلى مكتب القائد الأعلى بالأوراق المطلوبة. جلس كوتوزوف وعضو نمساوي في Gofkriegsrat أمام الخطة المطروحة على الطاولة.
"آه..." قال كوتوزوف، وهو ينظر إلى بولكونسكي، كما لو كان بهذه الكلمة يدعو المساعد إلى الانتظار، وواصل المحادثة التي بدأها باللغة الفرنسية.
قال كوتوزوف بنعمة لطيفة في التعبير والتجويد، "أنا أقول شيئًا واحدًا فقط، أيها الجنرال"، مما أجبرك على الاستماع بعناية إلى كل كلمة منطوقة على مهل. كان من الواضح أن كوتوزوف نفسه استمتع بالاستماع إلى نفسه. "أقول شيئًا واحدًا فقط، أيها الجنرال، أنه إذا كان الأمر يعتمد على رغبتي الشخصية، لكانت إرادة صاحب الجلالة الإمبراطور فرانز قد تحققت منذ فترة طويلة." كنت سأنضم إلى الأرشيدوق منذ فترة طويلة. وصدقني شرفًا لي أن نقل القيادة العليا للجيش إلى جنرال أكثر دراية ومهارة مني، والذي تزخر به النمسا كثيرًا، والتخلي عن كل هذه المسؤولية الثقيلة سيكون بمثابة فرحة لي شخصيًا. لكن الظروف أقوى منا أيها الجنرال.
وابتسم كوتوزوف بتعبير وكأنه يقول: "لديك كل الحق في ألا تصدقني، وحتى أنا لا يهمني على الإطلاق ما إذا كنت تصدقني أم لا، لكن ليس لديك سبب لتخبرني بذلك. وهذا هو بيت القصيد.
بدا الجنرال النمساوي غير راض، لكنه لم يستطع الرد على كوتوزوف بنفس النغمة.
"على العكس من ذلك،" قال بنبرة غاضبة ومتذمرة، على عكس المعنى الممتع للكلمات التي قالها، "على العكس من ذلك، فإن مشاركة صاحب السعادة في القضية المشتركة تحظى بتقدير كبير من قبل جلالة الملك؛ لكننا نعتقد أن التباطؤ الحالي يحرم القوات الروسية المجيدة وقادتها الأعلى من الغار الذي اعتادوا على حصده في المعارك.
انحنى كوتوزوف دون أن يغير ابتسامته.
"وأنا مقتنع جدًا، واستنادًا إلى الرسالة الأخيرة التي شرفني بها صاحب السمو الأرشيدوق فرديناند، أفترض أن القوات النمساوية، تحت قيادة مساعد ماهر مثل الجنرال ماك، حققت الآن نصرًا حاسمًا ولم تعد كذلك. قال كوتوزوف: "بحاجة إلى مساعدتنا".
عبس الجنرال. على الرغم من عدم وجود أخبار إيجابية عن هزيمة النمساويين، إلا أن هناك الكثير من الظروف التي أكدت الشائعات غير المواتية العامة؛ وبالتالي فإن افتراض كوتوزوف بشأن انتصار النمساويين كان مشابهًا جدًا للسخرية. لكن كوتوزوف ابتسم بخنوع، ولا يزال بنفس التعبير، الذي قال إن له الحق في افتراض ذلك. وبالفعل، فإن الرسالة الأخيرة التي تلقاها من جيش ماك أبلغته بالنصر والموقع الاستراتيجي الأكثر فائدة للجيش.
قال كوتوزوف متوجهاً إلى الأمير أندريه: "أعطني هذه الرسالة هنا". - إذا كنت ترى من فضلك. - وقرأ كوتوزوف، بابتسامة ساخرة في أطراف شفتيه، باللغة الألمانية للجنرال النمساوي المقطع التالي من رسالة من الأرشيدوق فرديناند: "Wir haben vollkommen zusammengehaltene Krafte, nahe an 70,000 Mann, um den Feind, wenn er" den Lech passirte, angreifen und schlagen zu konnen. Wir konnen، da wir Meister von Ulm sind، den Vortheil، auch von beiden Uferien der Donau Meister zu bleiben، nicht verlieren؛ مع كل ذلك من Augenblick، عندما لا يمر أي شيء، يتم تشغيل Donau، على خط اتصالات واحد، يتم إعادة تشغيل Donau وإرجاعها، عندما لا يكون هناك أي شيء حقيقي مع ganzer Macht Wenden Wollte، Seine Absicht alabald vereitelien. نحن نسير على الطريق الصحيح في يومنا هذا، ويعزز الجيش الروسي القيصري كل شيء، ويكتشف الكثير من الناس، ويجدون ملاذًا آمنًا في شيكسال، لذلك فهو صحيح. [لدينا قوات مركزة للغاية، حوالي 70 ألف فرد، حتى نتمكن من مهاجمة العدو وهزيمته إذا عبر ليخ. نظرًا لأننا نمتلك بالفعل مدينة أولم، يمكننا الاحتفاظ بميزة السيطرة على ضفتي نهر الدانوب، لذلك، في كل دقيقة، إذا لم يعبر العدو نهر ليخ، نعبر نهر الدانوب، ونندفع إلى خط الاتصال الخاص به، ثم نعبر نهر الدانوب للخلف للعدو، إذا قرر تحويل كل قوته إلى حلفائنا المخلصين، فإنه يمنع تحقيق نيته. وهكذا، سننتظر بكل سرور الوقت الذي يكون فيه الجيش الإمبراطوري الروسي جاهزًا تمامًا، وبعد ذلك سنجد معًا بسهولة الفرصة لإعداد المصير الذي يستحقه للعدو.
VECTOR SPACE، وهي مساحة خطية فوق الحقل K، هي مجموعة أبيلية مكتوبة بشكل إضافي E، حيث يتم تعريف مضاعفة العناصر بواسطة الكميات القياسية، أي التعيين
ك × ه → ه: (φ، x) → lectx،
تحقق البديهيات التالية (x، y ∈ E، lect، μ، 1 ∈ K):
1) (س + ص) = س + y،
2) ( + μ)x = x + μx,
3) (μ)س = μ(μx)،
4) 1 ⋅ س = س.
الخصائص المهمة التالية لمساحة المتجه (0 ∈ E) تتبع من البديهيات 1)-4):
5) lect ⋅ 0 = 0,
6) 0 ⋅ س = 0،
عناصر V. ص تسمى. نقاط VP، أو المتجهات، وعناصر المجال K عبارة عن أعداد قياسية.
أعظم تطبيق في الرياضيات والتطبيقات يتم إجراؤه على الحقل ℂ للأعداد المركبة أو على الحقل ℝ للأعداد الحقيقية؛ يطلق عليهم على التوالي، معقدة v. p. أو حقيقي v. p.
بديهيات v. p. تكشف عن بعض الجبر. خصائص العديد من فئات الوظائف التي غالبًا ما تتم مواجهتها في التحليل. من بين أمثلة الفضاء الرأسي، فإن أبسط وأقدم الأمثلة هي الفضاءات الإقليدية ذات الأبعاد n. هناك أمثلة على نفس القدر من الأهمية تقريبًا وهي العديد من مساحات الوظائف: مساحة الوظائف المستمرة، مساحة الوظائف القابلة للقياس، مساحة الوظائف القابلة للجمع، مساحة الوظائف التحليلية. الوظائف، مساحة الوظائف ذات التباين المحدود.
يعد مفهوم الفضاء v حالة خاصة لمفهوم الوحدة فوق الحلقة، أي أن الفضاء v عبارة عن وحدة وحدوية فوق الحقل. تسمى أيضًا الوحدة الوحدوية فوق حقل انحراف غير تبادلي. الفضاء المتجه على الجسم؛ تعتبر نظرية أشكال الموجات هذه أكثر تعقيدًا من نواحٍ عديدة من نظرية أشكال الموجات عبر المجال.
من المسائل المهمة المرتبطة بالفضاءات المتجهة هي دراسة هندسة الفضاءات المتجهة، أي دراسة الخطوط في الفضاءات المتجهة، والمجموعات المسطحة والمحدبة في الفضاءات المتجهة، والفضاءات الجزئية في الفضاءات المتجهة، والقواعد في الفضاءات المتجهة. .ص.
يُطلق على الفضاء الفرعي المتجه، أو ببساطة الفضاء الفرعي، V. p. E فوق الحقل K. مجموعة فرعية F ⊂ E مغلقة تحت إجراءات الجمع والضرب بواسطة العددية. المساحة الجزئية، التي يتم النظر إليها بشكل منفصل عن المساحة التي تحتوي عليها، هي مساحة فوق نفس الحقل.
يسمى الخط المستقيم الذي يمر بالنقطتين x و y B. p. E . مجموعة العناصر z ∈ E من الصيغة z = lectx + (1 - lect)y, lect ∈ K. تسمى المجموعة G ∈ E. مجموعة مسطحة إذا كانت تحتوي مع أي نقطتين على خط يمر عبر هاتين النقطتين. يتم الحصول على كل مجموعة مسطحة من مساحة فرعية معينة باستخدام التحول (الترجمة الموازية): G = x + F; هذا يعني أن كل عنصر z ∈ G يمكن تمثيله بشكل فريد في النموذج z = x + y, y ∈ F، وهذه المساواة توفر مراسلات فردية بين F وG.
مجموعة جميع التحولات F x = x + F لمسافة فرعية معينة F تشكل مساحة V على K، تسمى. مساحة العامل E/F، إذا عرفنا العمليات على النحو التالي:
و س و ذ = و س+ص ; F x = F x , ∈ K.
دع M = (x α) α∈A تكون مجموعة عشوائية من المتجهات من E؛ يسمى الجمع الخطي للمتجهات x α ∈ E. المتجه x المحدد بالصيغة
س = ∑ α α α س α , α α ∈ ك,
حيث يكون عدد محدود من المعاملات غير صفر. مجموعة جميع المجموعات الخطية لمتجهات مجموعة معينة M هي أصغر مساحة فرعية تحتوي على M، وتسمى. الامتداد الخطي للمجموعة M. يسمى الجمع الخطي. تافهة إذا كانت جميع المعاملات α تساوي الصفر. تسمى المجموعة M . مجموعة مستقلة خطيًا إذا كانت جميع المجموعات الخطية غير البديهية للمتجهات من M غير صفرية.
يتم تضمين أي مجموعة مستقلة خطيًا في مجموعة أقصى مستقلة خطيًا M0، أي في مجموعة تتوقف عن أن تكون مستقلة خطيًا بعد إضافة أي عنصر من E إليها.
يمكن تمثيل كل عنصر x ∈ E بشكل فريد كمجموعة خطية من عناصر مجموعة مستقلة خطيًا قصوى:
x = ∑ α lect α x α , x α ∈ M 0 .
في هذا الصدد، يتم استدعاء الحد الأقصى للمجموعة المستقلة خطيا. أساس V. ص (أساس جبري). جميع قواعد نائب معين لها نفس العلاقة الأساسية، ما يسمى. البعد V. ص إذا كانت هذه القوة محدودة، يسمى الفضاء. محدود الأبعاد V. ص؛ وإلا فإنه يسمى لانهائي الأبعاد V. ص.
يمكن اعتبار الحقل K بمثابة مساحة رأسية أحادية البعد فوق المجال K؛ أساس هذا العنصر V. يتكون من عنصر واحد؛ يمكن أن يكون أي عنصر آخر غير الصفر. يسمى المتجه محدود الأبعاد الذي أساسه عدد n من العناصر. الفضاء ذو الأبعاد n.
في نظرية المجموعات المحدبة الحقيقية والمعقدة، تلعب نظرية المجموعات المحدبة دورًا مهمًا. المجموعة M في V.p الحقيقي تسمى. هي مجموعة محدبة إذا كانت القطعة tx + (1 - t)y, t ∈ تنتمي أيضًا إلى M مع أي نقطتين منها x, y.
تشغل نظرية الوظائف الخطية على الفضاءات الرأسية ونظرية الازدواجية ذات الصلة مكانًا كبيرًا في نظرية الفضاءات الرأسية. دع E يكون سيرة ذاتية فوق الحقل K. يتم استدعاء دالة خطية على E. رسم الخرائط المضافة والمتجانسة f: E → K:
f(x + y) = f(x) + f(y), f(x) = f(x).
تشكل المجموعة E* لجميع الوظائف الخطية على E مكانًا شاغرًا في الحقل K فيما يتعلق بالعمليات
(f 1 + f 2)(x) = f 1 (x) + f 2 (x), (lectf)(x) = lectf(x), x ∈ E, X ∈ K, f 1, f 2, f ∈ ه*.
هذا هو V. P. يسمى. الفضاء المترافق (أو المزدوج) (إلى E). يرتبط عدد من النظريات الهندسية بمفهوم الفضاء المترافق. شروط. دع D ⊂ E (على التوالي Г ⊂ E *) ؛ يُطلق على مُدمر المجموعة D، أو المكمل المتعامد للمجموعة D (على التوالي المجموعة Г). مجموعة من
د ⊥ = (f ∈ E*: f(x) = 0 للكل x ∈ D)
(على التوالي Г ⊥ = (x ∈ E: f(x) = 0 للجميع f ∈ Г)); هنا D ⊥ و Г ⊥ هي مساحات فرعية للمسافات E* و E، على التوالي، إذا كان f عنصرًا غير صفري لـ E*، فإن (f) هو أقصى مسافة فرعية خطية مناسبة لـ E، تسمى. في بعض الأحيان الفضاء الفائق؛ يسمى تحول مثل هذا الفضاء الفرعي. الطائرة الفائقة في E؛ كل طائرة مفرطة لها الشكل
(x: f(x) = α)، حيث f ≠ 0، f ∈ E*، lect ∈ K.
إذا كان F عبارة عن فضاء جزئي لـ B. p. E، فهناك تماثلات طبيعية بين F* و
E*/F ⊥ وبين (E/F)* و F ⊥ .
المجموعة الفرعية Г ⊂ E* تسمى مجموعة فرعية إجمالية على E إذا كان المدمر الخاص بها يحتوي فقط على عنصر الصفر: Г ⊥ = (0).
يمكن ربط كل مجموعة مستقلة خطيًا (x α ) α∈A ⊂ E بمجموعة مترافقة (f α ) α∈A ⊂ E*، أي. مثل هذه المجموعة التي f α (x β) = δ αβ (رمز كرونيكر) لجميع α، β ∈ A. تسمى مجموعة الأزواج (x α، f α). مع نظام متعامد. إذا كانت المجموعة (x α) أساسًا في E، فإن (f α) تكون فوق E تمامًا.
تحتل نظرية التحولات الخطية للتحولات الخطية مكانة هامة في نظرية التحولات الخطية، فلتكن E 1 و E 2 تحويلين خطيين على نفس المجال K. رسم خريطة خطية، أو عامل خطي، T، رسم خريطة خطية تحويل E 1 في V. p. E 2 (أو العامل الخطي من E 1 إلى E 2)، يسمى. رسم الخرائط المضافة والمتجانسة للمساحة E 1 إلى E 2:
T(x + y) = Tx + Ty; Т(ω) = (Т); س، ص ∈ ه 1.
هناك حالة خاصة لهذا المفهوم هي دالة خطية، أو عامل خطي من E 1 إلى K. التخطيط الخطي، على سبيل المثال، هو رسم تخطيطي طبيعي لـ B. p. E على مساحة الحاصل E/F، التي ترتبط بـ كل عنصر x ∈ E مجموعة مسطحة F x ∈ E/ F. المجموعة ℒ(E 1, E 2) لجميع العوامل الخطية T: E 1 → E 2 تشكل V. p. فيما يتعلق بالعمليات
(ت 1 + ت 2)س = ت 1 س + ت 2 س؛ (π)x = Ảx; س ∈ ه 1؛ ∈ ك؛ تي 1، تي 2، تي ∈ ℒ(ه 1، ه 2).
تم استدعاء عنصرين V. E 1 و E 2. تكون متماثلة بالنسبة للعناصر إذا كان هناك عامل خطي ("التماثل") ينفذ مراسلات فردية بين عناصرها. يكون E 1 و E 2 متماثلين إذا وفقط إذا كانت قاعدتيهما لها نفس الأصل.
دع T يكون عامل خطي يرسم E 1 إلى E 2 . يُطلق على العامل الخطي المترافق، أو العامل الخطي المزدوج، بالنسبة إلى T. العامل الخطي T* من E* 2 إلى E* 1، محدد بالمساواة
(T*φ)x = φ(Tx) للجميع x ∈ E 1, φ ∈ E* 2.
العلاقات T* -1 (0) = ⊥, T*(E* 2) = [T -1 (0)] ⊥ عقد، مما يعني أن T* هو تشابه إذا وفقط إذا كان T هو تشابه.
ترتبط نظرية التعيينات الخطية الثنائية والتعيينات المتعددة الخطوط للمساحات الرأسية ارتباطًا وثيقًا بنظرية التعيينات الخطية للمساحات الرأسية.
تتشكل مجموعة مهمة من المشكلات في نظرية التعيينات الخطية من خلال مشكلات استمرار التعيينات الخطية. دع F يكون مساحة فرعية لـ V. p. E 1، E 2 يكون فضاء خطيًا على نفس المجال مثل E 1، ودع T 0 يكون تعيينًا خطيًا لـ F إلى E 2؛ من الضروري العثور على امتداد T للخريطة T 0، المحددة على كامل E 1 والتي هي خريطة خطية من E 1 إلى E 2. يوجد مثل هذا الاستمرار دائمًا، ولكن القيود الإضافية على الوظائف (المرتبطة بهياكل إضافية في VP، على سبيل المثال، الهيكل أو علاقات النظام) يمكن أن تجعل المشكلة غير قابلة للحل. من أمثلة حل مسألة الاستمرارية نظرية هان باناخ ونظريات استمرارية الدوال الإيجابية في الفضاءات ذات المخروط.
قسم مهم من نظرية العمليات الافتراضية هو نظرية العمليات على المتجهات، أي طرق بناء ناقلات جديدة باستخدام ناقلات معروفة. ومن أمثلة هذه العمليات العمليات المعروفة المتمثلة في أخذ فضاء فرعي وتكوين فضاء خارج القسمة من فضاء فرعي. العمليات الهامة الأخرى هي بناء مجموع مباشر، منتج مباشر ومنتج موتر لـ VP.
دع (E α ) α∈I تكون عائلة من المساحات المتغيرة فوق الحقل K. يمكن تحويل المجموعة E - منتج المجموعات E α - إلى عائلة من المساحات الرأسية فوق الحقل K عن طريق إدخال العمليات
(س α) + (ص α) = (س α + ص α)؛ χ(س α) = (×× α); ∈ ك؛ س α , ص α ∈ E α , α ∈ أنا;
تلقى V. p. E يسمى. المنتج المباشر لـ V. p. E α ويشار إليه بـ P α∈I E α. يُطلق على الفضاء الجزئي لـ V. p. E، الذي يتكون من كل تلك المجموعات (x α)، التي تكون كل مجموعة منها (α: x α ≠ 0) محدودة. المجموع المباشر لـ V. p. E α ويشار إليه بـ Σ α E α أو Σ α + E α ; بالنسبة لعدد محدود من المصطلحات، تتطابق هذه التعريفات؛ في هذه الحالة يتم استخدام الترميز التالي:
دع E 1، E 2 يكونان موقعين V. فوق الحقل K؛ E" 1, E" 2 هي إجمالي المساحات الجزئية لـ V. p. E* 1, E* 2, و E 1 □ E 2 -B. ن.، والتي تعتمد على مجموع جميع عناصر الفضاء E 1 × E 2. يرتبط كل عنصر x □ y ∈ E 1 □ E 2 بوظيفة ثنائية الخط b = T(x, y) على E" 1 × E 2 وفقًا للصيغة b(f, g) = f(x)g(y) ), f ∈ E " 1 , g ∈ E" 2. يمكن توسيع هذا التعيين للمتجهات الأساسية x □ y ∈ E 1 □ E 2 إلى تعيين خطي T B. p. E 1 □ E 2 إلى B. p. لجميع الوظائف الثنائية الخطية على E" 1 × E" 2. دع E 0 = T -1 (0). المنتج الموتر للمساحة V. E 1 و E 2 يسمى فضاء العامل E 1 ○ E 2 = (E 1 □ E 2)/E 0؛ صورة العنصر x □ y يُشار إليها بـ x ○ y. الفضاء المتجه E 1 ○ E 2 متماثل للفضاء المتجه للوظائف الثنائية الخطية على E 1 × E 2 (انظر منتج Tensor من مساحات المتجهات).
مضاءة: بورباكي ن.، الجبر. الهياكل الجبرية. الجبر الخطي والمتعدد الخطوط، العابرة. من الفرنسية، م.، 1962؛ Raikov D. A.، Vector Spaces، M.، 1962؛ يوم M. M.، المساحات الخطية الطبيعية، العابرة. من الإنجليزية، م.، 1961؛ ، إدوارد ر.، التحليل الوظيفي، عبر. من الإنجليزية، م.، 1969؛ هالموس P.، الفضاءات المتجهة ذات الأبعاد المحدودة، العابرة. من الإنجليزية، م.، 1963؛ Glazman I.M.، Lyubich Yu.I.، التحليل الخطي محدود الأبعاد في المشكلات، M.، 1969.
M. I. الكاديت.
مصادر:
- الموسوعة الرياضية. ت1 (أ - د). إد. مجلس الإدارة: آي إم فينوغرادوف (رئيس التحرير) [وآخرون] - م.، "الموسوعة السوفيتية"، 1977، 1152 ستب. من الوهم.
دع P يكون حقلاً. العناصر أ، ب، ... أو رسوف نتصل العددية.
التعريف 1.فصل الخامسيتم استدعاء الكائنات (العناصر) ، ، ، ... ذات الطبيعة التعسفية مساحة المتجه فوق الحقل P، وتسمى عناصر الفئة V ثلاثة أبعاد، إذا تم إغلاق V تحت عملية "+" وعملية الضرب بالأرقام القياسية من P (أي لأي، ОV +О الخامس;"aО Р aОV)، مع استيفاء الشروط التالية:
ج1: الجبر
ج2: بالنسبة لأي a، bОР، لأي ОV، a(b)=(ab) هو قانون ترابطي معمم؛
أ 3: لأي a، bОР، لأي ОV، (a+b)= a+ b؛
A 4: لأي a من P، لأي، من V، a(+)=a+a (قوانين التوزيع المعممة)؛
ج5: لأي من V، 1 = مكتمل، حيث 1 هي وحدة المجال P - خاصية الوحدوية.
سوف نسمي عناصر المجال P العددية، وعناصر المجموعة V المتجهات.
تعليق.لا يعد ضرب المتجه بكمية قياسية عملية ثنائية على المجموعة V، نظرًا لأنه عبارة عن تعيين P´V®V.
دعونا نلقي نظرة على أمثلة للمساحات المتجهة.
مثال 1.مساحة متجهة صفرية (صفرية الأبعاد) - المساحة V 0 =() - تتكون من متجه صفري واحد.
ولأي aОР a=. دعونا نتحقق من مدى استيفاء بديهيات الفضاء المتجه.
لاحظ أن الفضاء المتجه الصفري يعتمد بشكل أساسي على المجال P. وبالتالي، تعتبر المسافات ذات الأبعاد الصفرية فوق مجال الأعداد النسبية وعلى مجال الأعداد الحقيقية مختلفة، على الرغم من أنها تتكون من متجه صفري واحد.
مثال 2.الحقل P هو في حد ذاته مساحة متجهة فوق المجال P. دع V=P. دعونا نتحقق من مدى استيفاء بديهيات الفضاء المتجه. بما أن P عبارة عن حقل، فإن P عبارة عن مجموعة أبيلية مضافة ويحمل A 1. نظرًا لإرضاء الضرب في P، فإن A2 يكون راضيًا. يتم استيفاء البديهيات أ 3 وأ 4 نظرًا لإمكانية توزيع الضرب بالنسبة إلى الجمع في P. وبما أن هناك عنصر الوحدة 1 في المجال P، فإن خاصية الوحدة A 5 تكون مستوفاة. وبالتالي، فإن المجال P هو مساحة متجهة فوق المجال P.
مثال 3.الفضاء المتجه الحسابي ذو الأبعاد n.
دع P يكون حقلاً. خذ بعين الاعتبار المجموعة V= P n =((a 1 , a 2 , … , a n) ½ a i О P, i=1,…, n). دعونا ندخل على المجموعة V عمليات جمع المتجهات وضرب المتجه بكمية قياسية وفقا للقواعد التالية:
"= (أ 1 , أ 2 , … , أ ن), = (ب 1 , ب 2 , … , ب ن) О V, "aО P += (أ 1 + ب 1 , أ 2 + ب 2 , … , أ ن + مليار) (1)
أ=(أأ 1، أأ 2، …، أأ ن) (2)
سيتم استدعاء عناصر المجموعة V ناقلات الأبعاد ن. يقال أن المتجهات ذات الأبعاد n متساوية إذا كانت مكوناتها المقابلة (الإحداثيات) متساوية. دعونا نبين أن V عبارة عن مساحة متجهة فوق الحقل P. ومن تعريف عمليات جمع المتجهات وضرب المتجه بواسطة عددي، يتبع ذلك أن V مغلقة تحت هذه العمليات. بما أن إضافة عناصر V تقلل من إضافة عناصر المجال P، و P هي مجموعة أبيلية مضافة، فإن V هي مجموعة أبيلية مضافة. علاوة على ذلك، =، حيث 0 هو صفر الحقل P، -= (-a 1، -a 2، ...، -a n). وبذلك يكون A 1 راضيًا. بما أن ضرب عنصر من V بعنصر من P يقلل من ضرب عناصر الحقل P، إذن:
يتم تحقيق A 2 بسبب ترابط الضرب بـ P؛
A 3 و A 4 محققان بسبب توزيع الضرب بالنسبة إلى الجمع بـ P؛
يتم تحقيق A 5، نظرًا لأن 1 Î P عنصر محايد فيما يتعلق بالضرب في P.
التعريف 2.تسمى المجموعة V= P n مع العمليات المحددة بواسطة الصيغتين (1) و (2) بمساحة متجهة حسابية ذات أبعاد n فوق المجال P.
المحاضرة 6. الفضاء المتجه.
الأسئلة الرئيسية.
1. الفضاء الخطي المتجه.
2. أساس وأبعاد الفضاء.
3. التوجه الفضائي.
4. تحلل المتجه حسب الأساس.
5. إحداثيات المتجهات.
1. الفضاء الخطي المتجه.
مجموعة تتكون من عناصر من أي طبيعة يتم فيها تعريف العمليات الخطية: تسمى إضافة عنصرين وضرب عنصر في رقم المساحات، وعناصرها ثلاثة أبعادهذه المساحة ويتم الإشارة إليها بنفس طريقة الكميات المتجهة في الهندسة: . ثلاثة أبعادكقاعدة عامة، ليس لهذه المساحات المجردة أي شيء مشترك مع المتجهات الهندسية العادية. يمكن أن تكون عناصر المساحات المجردة وظائف، ونظام أرقام، ومصفوفات، وما إلى ذلك، وفي حالة معينة، ناقلات عادية. لذلك، عادة ما تسمى هذه المساحات مساحات المتجهات .
مساحات المتجهات هي، على سبيل المثال، مجموعة من المتجهات الخطية، يشار إليها الخامس1 مجموعة من المتجهات متحدة المستوى الخامس2 , مجموعة من المتجهات العادية (الفضاء الحقيقي) الخامس3 .
في هذه الحالة تحديدًا، يمكننا تقديم التعريف التالي للفضاء المتجه.
التعريف 1.مجموعة المتجهات تسمى مساحة المتجهات، إذا كان الجمع الخطي لأي من متجهات المجموعة هو أيضًا متجه لهذه المجموعة. تسمى المتجهات نفسها عناصرمساحة المتجهات.
والأهم من ذلك، من الناحية النظرية والتطبيقية، هو المفهوم العام (المجرد) للفضاء المتجه.
التعريف 2.مجموعة من رالعناصر التي يتم فيها تحديد المجموع لأي عنصرين ولأي عنصر https://pandia.ru/text/80/142/images/image006_75.gif" width="68" height="20"> يسمى المتجه(أو خطي) فضاء، وعناصره متجهات، إذا كانت عمليات جمع المتجهات وضرب المتجه بعدد تحقق الشروط التالية ( البديهيات) :
1) الجمع تبادلي، على سبيل المثال..gif" width="184" height="25">;
3) يوجد مثل هذا العنصر (متجه صفر) لأي https://pandia.ru/text/80/142/images/image003_99.gif" width="45" height="20">.gif" width= " 99" ارتفاع = "27">;
5) لأي متجهات وأي رقم تساوي المساواة؛
6) لأية ناقلات وأي أرقام λ
و µ
المساواة صحيحة: https://pandia.ru/text/80/142/images/image003_99.gif" width="45 height=20" height="20"> وأي أرقام λ
و µ
عدل ![]() ;
;
8) https://pandia.ru/text/80/142/images/image003_99.gif" width="45" height="20">.
أبسط البديهيات التي تحدد الفضاء المتجه هي التالية: عواقب :
1. في الفضاء المتجه يوجد صفر واحد فقط - العنصر - المتجه الصفري.
2. في الفضاء المتجه، يكون لكل متجه متجه واحد معاكس.
3. يتم تحقيق المساواة لكل عنصر.
4. لأي عدد حقيقي λ والمتجه صفر https://pandia.ru/text/80/142/images/image017_45.gif" width="68" height="25">.
5..gif" width="145" height="28">
6..gif" width = "15" height = "19 src = ">.gif" width = "71" height = "24 src = "> هو متجه يرضي المساواة https://pandia.ru/text /80 /142/images/image026_26.gif" width="73" height="24">.
لذلك، في الواقع، مجموعة جميع المتجهات الهندسية هي مساحة خطية (متجهة)، لأنه بالنسبة لعناصر هذه المجموعة، يتم تحديد إجراءات الجمع والضرب برقم تلبي البديهيات المصاغة.
2. أساس وأبعاد الفضاء.
المفاهيم الأساسية للفضاء المتجه هي مفاهيم الأساس والبعد.
تعريف.تسمى مجموعة من المتجهات المستقلة خطيًا، مأخوذة بترتيب معين، والتي يمكن من خلالها التعبير خطيًا عن أي متجه للفضاء أساسهذه المساحة. ثلاثة أبعاد. تسمى مكونات أساس الفضاء أساسي .
يمكن اعتبار أساس مجموعة المتجهات الموجودة على خط تعسفي متجهًا خطيًا واحدًا لهذا الخط.
أساس على متن الطائرةلنستدعي متجهين غير خطيين على هذا المستوى، تم التقاطهما بترتيب معين https://pandia.ru/text/80/142/images/image029_29.gif" width="61" height="24">.
إذا كانت المتجهات الأساسية متعامدة بشكل زوجي (متعامدة)، فيسمى الأساس متعامدوإذا كان طول هذه المتجهات يساوي واحدًا، فسيتم استدعاء الأساس متعامد .
يسمى أكبر عدد من المتجهات المستقلة خطياً في الفضاء البعدلهذا الفضاء، أي أن بعد الفضاء يتطابق مع عدد المتجهات الأساسية لهذا الفضاء.
لذلك، وفقا لهذه التعريفات:
1. الفضاء أحادي البعد الخامس1 هو خط مستقيم، وأساسه يتكون من خطية واحدةالمتجه https://pandia.ru/text/80/142/images/image028_22.gif" width="39" height="23 src="> .
3. الفضاء العادي هو الفضاء ثلاثي الأبعاد الخامس3 والتي يتكون أساسها من ثلاثة غير متحد المستوىثلاثة أبعاد
من هنا نرى أن عدد المتجهات الأساسية على خط ما، على مستوى، في الفضاء الحقيقي يتطابق مع ما يسمى في الهندسة عادة بعدد الأبعاد (البعد) للخط أو المستوى أو الفضاء. ولذلك، فمن الطبيعي تقديم تعريف أكثر عمومية.
تعريف.مساحة المتجهات رمُسَمًّى ن- الأبعاد إذا لم يكن هناك أكثر من نناقلات مستقلة خطيا ويشار إليها ر ن. رقم نمُسَمًّى البعدفضاء.
وفقا لبعد الفضاء يتم تقسيمها إلى محدودة الأبعادو لانهائي الأبعاد. يعتبر بُعد المساحة الفارغة مساويًا للصفر بحكم التعريف.
ملاحظة 1.في كل مساحة يمكنك تحديد أي عدد تريده من القواعد، لكن جميع قواعد مساحة معينة تتكون من نفس عدد المتجهات.
ملاحظة 2.في ن– في الفضاء المتجه الأبعاد، الأساس هو أي مجموعة مرتبة نناقلات مستقلة خطيا.
3. التوجه الفضائي.
دع المتجهات الأساسية في الفضاء الخامس3 يملك بداية عامةو أمرأي أنه يشار إلى المتجه الذي يعتبر الأول والذي يعتبر الثاني والذي يعتبر الثالث. على سبيل المثال، في الأساس يتم ترتيب المتجهات وفقًا للفهرسة. |
|
من أجل هذا لتوجيه الفضاء، من الضروري وضع أساس ما وإعلانه إيجابيًا .
يمكن إثبات أن مجموعة جميع قواعد الفضاء تنقسم إلى فئتين، أي إلى مجموعتين فرعيتين منفصلتين.
أ) جميع القواعد التي تنتمي إلى مجموعة فرعية واحدة (فئة) لها نفس الشيءالاتجاه (قواعد تحمل نفس الاسم) ؛
ب) أي قاعدتين تنتميان إلى متنوعمجموعات فرعية (فئات)، لديك المقابلتوجيه، ( أسماء مختلفةقواعد).
إذا أعلن أن إحدى فئتي قواعد الفضاء موجبة والأخرى سلبية، فيقال أن هذا الفضاء الموجهة .
في كثير من الأحيان، عند توجيه الفضاء، يتم استدعاء بعض القواعد يمين، و اخرين - غادر .
https://pandia.ru/text/80/142/images/image029_29.gif" width="61" height="24 src="> يتم استدعاؤها يمين، إذا، عند المراقبة من نهاية المتجه الثالث، أقصر دوران للمتجه الأول https://pandia.ru/text/80/142/images/image033_23.gif" width="16" height="23" > يتم عكس عقارب الساعه(الشكل 1.8، أ).
https://pandia.ru/text/80/142/images/image036_22.gif" width="16" height="24">
https://pandia.ru/text/80/142/images/image037_23.gif" width="15" height="23">
https://pandia.ru/text/80/142/images/image039_23.gif" width="13" height="19">
https://pandia.ru/text/80/142/images/image033_23.gif" width="16" height="23">
أرز. 1.8. الأساس الأيمن (أ) والأساس الأيسر (ب)
عادةً ما يتم الإعلان عن الأساس الصحيح للمساحة على أنه أساس إيجابي
يمكن أيضًا تحديد الأساس الأيمن (الأيسر) للمساحة باستخدام قاعدة المسمار أو المثقاب "الأيمن" ("الأيسر").
وقياسا على ذلك، يتم تقديم مفهوم اليمين واليسار الثلاثاتالمتجهات غير المستوية التي يجب ترتيبها (الشكل 1.8).
وبالتالي، في الحالة العامة، يكون هناك ثلاثة توائم مرتبة من المتجهات غير المستوية لها نفس الاتجاه (نفس الاسم) في الفضاء الخامس3 إذا كانا كلاهما يمينًا أو كلاهما يسارًا، و- الاتجاه المعاكس (معاكسًا) إذا كان أحدهما يمينًا والآخر يسارًا.
ويتم نفس الشيء في حالة الفضاء الخامس2 (طائرة).
4. تحلل المتجه حسب الأساس.
لتبسيط التفكير، دعونا نفكر في هذا السؤال باستخدام مثال الفضاء المتجه ثلاثي الأبعاد ر3 .
دع https://pandia.ru/text/80/142/images/image021_36.gif" width="15" height="19"> يكون متجهًا عشوائيًا لهذه المساحة.
في المقالة الخاصة بالمتجهات ذات الأبعاد n، توصلنا إلى مفهوم الفضاء الخطي الناتج عن مجموعة من المتجهات ذات الأبعاد n. الآن علينا أن نأخذ في الاعتبار مفاهيم لا تقل أهمية، مثل البعد وأساس الفضاء المتجه. إنها مرتبطة بشكل مباشر بمفهوم نظام المتجهات المستقل خطيًا، لذلك يوصى أيضًا بتذكير نفسك بأساسيات هذا الموضوع.
دعونا نقدم بعض التعاريف.
التعريف 1
البعد من الفضاء المتجه- رقم يتوافق مع الحد الأقصى لعدد المتجهات المستقلة خطياً في هذا الفضاء.
التعريف 2
أساس الفضاء المتجه– مجموعة من المتجهات المستقلة خطياً، مرتبة ومتساوية في العدد مع البعد المكاني.
دعونا نفكر في مساحة معينة من المتجهات n. البعد الخاص بها يساوي n. لنأخذ نظامًا من ناقلات الوحدات n:
ه (1) = (1, 0, . . 0) ه (2) = (0, 1, . . , 0) ه (ن) = (0, 0, . . , 1)
نستخدم هذه المتجهات كمكونات للمصفوفة A: ستكون مصفوفة وحدة ذات البعد n في n. رتبة هذه المصفوفة هي n. ولذلك فإن نظام المتجهات e (1) , e (2) , . . . ، e(n) مستقلة خطيًا. في هذه الحالة، من المستحيل إضافة متجه واحد إلى النظام دون انتهاك استقلاله الخطي.
بما أن عدد المتجهات في النظام هو n، فإن بُعد فضاء المتجهات ذات الأبعاد n هو n، ومتجهات الوحدة هي e (1)، e (2)، . . . ، e (n) هي أساس المساحة المحددة.
من التعريف الناتج يمكننا أن نستنتج: أي نظام من المتجهات ذات الأبعاد n الذي يكون فيه عدد المتجهات أقل من n ليس أساسًا للمساحة.
إذا قمنا بتبديل المتجهين الأول والثاني، فسنحصل على نظام من المتجهات e (2) , e (1) , . . . ، ه (ن) . وسيكون أيضًا أساسًا لمساحة متجهة ذات أبعاد n. لنقم بإنشاء مصفوفة عن طريق أخذ متجهات النظام الناتج كصفوف لها. يمكن الحصول على المصفوفة من مصفوفة الهوية عن طريق تبديل الصفين الأولين، وستكون رتبتها n. النظام ه (2) , ه (1) , . . . ، e(n) مستقل خطيًا وهو أساس الفضاء المتجه ذو الأبعاد n.
ومن خلال إعادة ترتيب المتجهات الأخرى في النظام الأصلي، نحصل على أساس آخر.
يمكننا أن نأخذ نظامًا مستقلاً خطيًا من المتجهات غير الوحدة، وسيمثل أيضًا أساس الفضاء المتجهي ذو الأبعاد n.
التعريف 3
يحتوي الفضاء المتجه ذو البعد n على عدد من القواعد كما توجد أنظمة مستقلة خطيًا من ناقلات ذات أبعاد n للرقم n.
المستوى عبارة عن فضاء ثنائي الأبعاد - سيكون أساسه أي متجهين غير خطيين. سيكون أساس الفضاء ثلاثي الأبعاد هو أي ثلاثة نواقل غير متحدة المستوى.
دعونا نفكر في تطبيق هذه النظرية باستخدام أمثلة محددة.
مثال 1
البيانات الأولية:ثلاثة أبعاد
أ = (3 ، - 2 ، 1) ب = (2 ، 1 ، 2) ج = (3 ، - 1 ، - 2)
من الضروري تحديد ما إذا كانت المتجهات المحددة هي أساس مساحة متجهة ثلاثية الأبعاد.
حل
لحل المشكلة، قمنا بدراسة النظام المعطى لمتجهات الاعتماد الخطي. لنقم بإنشاء مصفوفة، حيث تكون الصفوف هي إحداثيات المتجهات. دعونا نحدد رتبة المصفوفة.
أ = 3 2 3 - 2 1 - 1 1 2 - 2 أ = 3 - 2 1 2 1 2 3 - 1 - 2 = 3 1 (- 2) + (- 2) 2 3 + 1 2 · (- 1) - 1 · 1 · 3 - (- 2) · 2 · (- 2) - 3 · 2 · (- 1) = = - 25 ≠ 0 ⇒ R a n k (A) = 3
وبالتالي، فإن المتجهات المحددة بشرط المشكلة تكون مستقلة خطيًا، وعددها يساوي بُعد فضاء المتجه - فهي أساس فضاء المتجه.
إجابة:المتجهات المشار إليها هي أساس مساحة المتجهات.
مثال 2
البيانات الأولية:ثلاثة أبعاد
أ = (3، - 2، 1) ب = (2، 1، 2) ج = (3، - 1، - 2) د = (0، 1، 2)
من الضروري تحديد ما إذا كان نظام المتجهات المحدد يمكن أن يكون أساسًا لمساحة ثلاثية الأبعاد.
حل
نظام المتجهات المحدد في بيان المشكلة يعتمد خطيا، لأن الحد الأقصى لعدد المتجهات المستقلة خطيًا هو 3. وبالتالي، لا يمكن لنظام المتجهات المحدد أن يكون بمثابة أساس لمساحة متجهة ثلاثية الأبعاد. ولكن تجدر الإشارة إلى أن النظام الفرعي للنظام الأصلي أ = (3، - 2، 1)، ب = (2، 1، 2)، ج = (3، - 1، - 2) هو الأساس.
إجابة:نظام المتجهات المشار إليه ليس أساسًا.
مثال 3
البيانات الأولية:ثلاثة أبعاد
أ = (1، 2، 3، 3) ب = (2، 5، 6، 8) ج = (1، 3، 2، 4) د = (2، 5، 4، 7)
هل يمكن أن تكون أساس الفضاء رباعي الأبعاد؟
حل
لنقم بإنشاء مصفوفة باستخدام إحداثيات المتجهات المعطاة كصفوف
أ = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
باستخدام الطريقة الغوسية، نحدد رتبة المصفوفة:
أ = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7 ~ 1 2 3 3 0 1 0 2 0 1 - 1 1 0 1 - 2 1 ~ ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 - 2 - 1 ~ 1 2 3 3 0 1 0 2 0 0 - 1 - 1 0 0 0 1 ⇒ ⇒ R a n k (A) = 4
وبالتالي، فإن نظام المتجهات المعطاة يكون مستقلاً خطيًا وعددها يساوي بُعد الفضاء المتجه - فهي أساس الفضاء المتجه رباعي الأبعاد.
إجابة:المتجهات المعطاة هي أساس الفضاء رباعي الأبعاد.
مثال 4
البيانات الأولية:ثلاثة أبعاد
أ (1) = (1 ، 2 ، - 1 ، - 2) أ (2) = (0 ، 2 ، 1 ، - 3) أ (3) = (1 ، 0 ، 0 ، 5)
هل تشكل أساس مساحة البعد 4؟
حل
النظام الأصلي للمتجهات مستقل خطيًا، لكن عدد المتجهات فيه ليس كافيًا ليصبح أساسًا لفضاء رباعي الأبعاد.
إجابة:لا، لا يفعلون ذلك.
تحلل المتجه إلى الأساس
لنفترض أن المتجهات التعسفية e (1) , e (2) , . . . ، e (n) هي أساس الفضاء المتجه ذو الأبعاد n. دعنا نضيف إليهم ناقلًا معينًا ذو أبعاد n x →: سيصبح نظام المتجهات الناتج معتمدًا خطيًا. تشير خصائص الاعتماد الخطي إلى أنه يمكن التعبير عن واحد على الأقل من نواقل مثل هذا النظام خطيًا من خلال النواقل الأخرى. بإعادة صياغة هذه العبارة، يمكننا القول إن واحدًا على الأقل من متجهات النظام التابع خطيًا يمكن توسيعه إلى المتجهات المتبقية.
وهكذا وصلنا إلى صياغة النظرية الأهم:
التعريف 4
يمكن تحليل أي متجه للفضاء المتجه ذي الأبعاد n بشكل فريد إلى أساس.
الدليل 1
دعونا نثبت هذه النظرية:
دعونا نضع أساس الفضاء المتجه ذو الأبعاد n - e (1) , e (2) , . . . ، ه (ن) . لنجعل النظام معتمدًا خطيًا عن طريق إضافة ناقل ذو أبعاد n x → إليه. يمكن التعبير عن هذا المتجه خطيًا بدلالة المتجهات الأصلية e:
س = س 1 · ه (1) + س 2 · ه (2) + . . . + x n · e (n) ، حيث x 1 , x 2 , . . . ، x n - بعض الأرقام.
الآن نثبت أن هذا التحلل فريد من نوعه. لنفترض أن الأمر ليس كذلك وأن هناك تحليلًا آخر مشابهًا:
س = س ~ 1 ه (1) + س 2 ~ ه (2) + . . . + x ~ n e (n) , حيث x ~ 1 , x ~ 2 , . . . , x ~ n - بعض الأرقام.
دعونا نطرح من الجانبين الأيسر والأيمن لهذه المساواة، على التوالي، الجانبين الأيسر والأيمن من المساواة x = x 1 · e (1) + x 2 · e (2) + . . . + س ن · ه (ن) . نحن نحصل:
0 = (س ~ 1 - س 1) · ه (1) + (س ~ 2 - س 2) · ه (2) + . . . (س ~ ن - س ن) ه (2)
نظام المتجهات الأساسية e (1) , e (2) , . . . ، e(n) مستقل خطيًا؛ من خلال تعريف الاستقلال الخطي لنظام المتجهات، فإن المساواة المذكورة أعلاه ممكنة فقط عندما تكون جميع المعاملات (x ~ 1 - x 1) , (x ~ 2 - x 2) , . . . ، (x ~ n - x n) ستكون مساوية للصفر. منها سيكون عادلا: x 1 = x ~ 1، x 2 = x ~ 2، . . . , س ن = س ~ ن . وهذا يثبت الخيار الوحيد لتحليل المتجه إلى الأساس.
في هذه الحالة، المعاملات x 1, x 2, . . . , x n تسمى إحداثيات المتجه x → في الأساس e (1) , e (2) , . . . ، ه (ن) .
توضح النظرية المثبتة التعبير "بالنظر إلى متجه ذو أبعاد n x = (x 1 , x 2 , . . . , x n)": يتم اعتبار المتجه x → n مساحة المتجه ذات الأبعاد، ويتم تحديد إحداثياته في أساس معين. ومن الواضح أيضًا أن نفس المتجه في أساس آخر للفضاء ذي الأبعاد n سيكون له إحداثيات مختلفة.
خذ بعين الاعتبار المثال التالي: لنفترض أنه في بعض أسس الفضاء المتجهي ذو الأبعاد n، يتم إعطاء نظام من المتجهات المستقلة خطيًا
وأيضا المتجه x = (x 1 , x 2 , . . . , x n) معطى.
المتجهات ه 1 (1) , ه 2 (2) , . . . ، e n (n) في هذه الحالة هي أيضًا أساس مساحة المتجه هذه.
لنفترض أنه من الضروري تحديد إحداثيات المتجه x → على الأساس e 1 (1) , e 2 (2) , . . . , e n (n) , يُشار إليه بـ x ~ 1 , x ~ 2 , . . . ، س ~ ن.
سيتم تمثيل Vector x → على النحو التالي:
س = س ~ 1 ه (1) + س ~ 2 ه (2) + . . . + س ~ ن ه (ن)
لنكتب هذا التعبير بالشكل الإحداثي:
(x 1 , x 2 , . . . , x n) = x ~ 1 (e (1) 1 , e (1) 2 , . . , e (1) n) + x ~ 2 (e (2 ) 1 , ه (2) 2 ، . . . ه (2) ن) + . . . + + x ~ n · (ه (ن) 1 ، ه (ن) 2 ، . . . ، ه (ن) ن) = = (x ~ 1 ه 1 (1) + x ~ 2 ه 1 (2) + . . . + x ~ n e 1 (n)، x ~ 1 e 2 (1) + x ~ 2 e 2 (2) + + . . + x ~ n e 2 (n)، . . . ، x ~ 1 e n (1) + س ~ 2 ه ن (2) + ... + س ~ ن ه ن (ن))
المساواة الناتجة تعادل نظام من التعبيرات الجبرية الخطية n مع n متغيرات خطية غير معروفة x ~ 1, x ~ 2, . . . ، س ~ ن:
x 1 = x ~ 1 ه 1 1 + x ~ 2 ه 1 2 + . . . + x ~ n e 1 n x 2 = x ~ 1 e 2 1 + x ~ 2 e 2 2 + . . . + x ~ n e 2 n ⋮ x n = x ~ 1 e n 1 + x ~ 2 e n 2 + . . . + س ~ ن ه ن ن
مصفوفة هذا النظام سيكون لها الشكل التالي:
ه 1 (1) ه 1 (2) ⋯ ه 1 (ن) ه 2 (1) ه 2 (2) ⋯ ه 2 (ن) ⋮ ⋮ ⋮ ⋮ ه ن (1) ه ن (2) ⋯ ه ن (ن)
دع هذه تكون مصفوفة A، وأعمدتها عبارة عن متجهات لنظام مستقل خطيًا من المتجهات e 1 (1)، e 2 (2)، . . . ، ه ن (ن) . رتبة المصفوفة هي n، ومحددها غير صفر. يشير هذا إلى أن نظام المعادلات له حل فريد، يتم تحديده بأي طريقة مناسبة: على سبيل المثال، طريقة كرامر أو طريقة المصفوفة. بهذه الطريقة يمكننا تحديد الإحداثيات x ~ 1، x ~ 2، . . . , x ~ n المتجه x → في الأساس e 1 (1) , e 2 (2) , . . . ، ه ن (ن) .
دعونا نطبق النظرية المدروسة على مثال محدد.
مثال 6
البيانات الأولية:يتم تحديد المتجهات على أساس الفضاء ثلاثي الأبعاد
ه (1) = (1 ، - 1 ، 1) ه (2) = (3 ، 2 ، - 5) ه (3) = (2 ، 1 ، - 3) س = (6 ، 2 ، - 7)
من الضروري تأكيد حقيقة أن نظام المتجهات e (1)، e (2)، e (3) يعمل أيضًا كأساس لمساحة معينة، وكذلك لتحديد إحداثيات المتجه x على أساس معين.
حل
سيكون نظام المتجهات e (1)، e (2)، e (3) هو أساس الفضاء ثلاثي الأبعاد إذا كان مستقلاً خطيًا. دعونا نكتشف هذا الاحتمال من خلال تحديد رتبة المصفوفة A، التي تمثل صفوفها المتجهات المعطاة e (1)، e (2)، e (3).
نستخدم الطريقة الغوسية:
أ = 1 - 1 1 3 2 - 5 2 - 3 ~ 1 - 1 1 0 5 - 8 0 3 - 5 ~ 1 - 1 1 0 5 - 8 0 0 - 1 5
ر أ ن ك (أ) = 3 . وبالتالي، فإن نظام المتجهات e (1)، e (2)، e (3) مستقل خطيًا وهو أساس.
دع المتجه x → له إحداثيات x ~ 1، x ~ 2، x ~ 3 في الأساس. يتم تحديد العلاقة بين هذه الإحداثيات بواسطة المعادلة:
س 1 = س ~ 1 ه 1 (1) + س ~ 2 ه 1 (2) + س ~ 3 ه 1 (3) × 2 = س ~ 1 ه 2 (1) + س ~ 2 ه 2 (2) + س ~ 3 ه 2 (3) × 3 = س ~ 1 ه 3 (1) + س ~ 2 ه 3 (2) + س ~ 3 ه 3 (3)
لنطبق القيم حسب ظروف المشكلة:
x ~ 1 + 3 x ~ 2 + 2 x ~ 3 = 6 - x ~ 1 + 2 x ~ 2 + x ~ 3 = 2 x ~ 1 - 5 x ~ 2 - 3 x 3 = - 7
دعونا نحل نظام المعادلات باستخدام طريقة كرامر:
∆ = 1 3 2 - 1 2 1 1 - 5 - 3 = - 1 ∆ x ~ 1 = 6 3 2 2 2 1 - 7 - 5 - 3 = - 1 , x ~ 1 = ∆ x ~ 1 ∆ = - 1 - 1 = 1 ∆ x ~ 2 = 1 6 2 - 1 2 1 1 - 7 - 3 = - 1 , x ~ 2 = ∆ x ~ 2 ∆ = - 1 - 1 = 1 ∆ x ~ 3 = 1 3 6 - 1 2 2 1 - 5 - 7 = - 1 , x ~ 3 = ∆ x ~ 3 ∆ = - 1 - 1 = 1
وبالتالي، فإن المتجه x → في الأساس e (1)، e (2)، e (3) له إحداثيات x ~ 1 = 1، x ~ 2 = 1، x ~ 3 = 1.
إجابة:س = (1، 1، 1)
العلاقة بين القواعد
لنفترض أنه في بعض أسس الفضاء المتجهي ذو الأبعاد n، يتم إعطاء نظامين مستقلين خطيًا للمتجهات:
ج (1) = (ج 1 (1) ، ج 2 (1) ، . . . ، ج ن (1)) ج (2) = (ج 1 (2) ، ج 2 (2) ، . . . ، ج ن (2)) ⋮ ج (ن) = (ج 1 (ن) , ه 2 (ن) , . . . , ج ن (ن))
ه (1) = (ه 1 (1) ، ه 2 (1) ، . . . ، ه ن (1)) ه (2) = (ه 1 (2) ، ه 2 (2) ، . . . ، ه ن (2)) ⋮ e (n) = (e 1 (n) , e 2 (n) , . . . , e n (n))
هذه الأنظمة هي أيضًا قواعد لمساحة معينة.
دع c ~ 1 (1) , c ~ 2 (1) , . . . , c ~ n (1) - إحداثيات المتجه c (1) في الأساس e (1) , e (2) , . . . ، e (3) ، فسيتم إعطاء العلاقة الإحداثية بواسطة نظام المعادلات الخطية:
ج 1 (1) = ج ~ 1 (1) ه 1 (1) + ج ~ 2 (1) ه 1 (2) + . . . + ج ~ ن (1) ه 1 (ن) ج 2 (1) = ج ~ 1 (1) ه 2 (1) + ج ~ 2 (1) ه 2 (2) + . . . + ج ~ ن (1) ه 2 (ن) ⋮ ج ن (1) = ج ~ 1 (1) ه ن (1) + ج ~ 2 (1) ه ن (2) + . . . + ج ~ ن (1) ه ن (ن)
ويمكن تمثيل النظام كمصفوفة على النحو التالي:
(ج 1 (1) , ج 2 (1) , . . . , ج ن (1)) = (ج ~ 1 (1) , ج ~ 2 (1) , . . . , ج ~ ن (1)) ه 1 (1) ه 2 (1) … ه ن (1) ه 1 (2) ه 2 (2) … ه ن (2) ⋮ ⋮ ⋮ ⋮ ه 1 (ن) ه 2 (ن) … ه ن (ن)
دعونا نقوم بنفس الإدخال للمتجه c (2) عن طريق القياس:
(ج 1 (2) , ج 2 (2) , . . . , ج ن (2)) = (ج ~ 1 (2) , ج ~ 2 (2) , . . . , ج ~ ن (2)) ه 1 (1) ه 2 (1) … ه ن (1) ه 1 (2) ه 2 (2) … ه ن (2) ⋮ ⋮ ⋮ ⋮ ه 1 (ن) ه 2 (ن) … ه ن (ن)
(ج 1 (ن) , ج 2 (ن) , . . . , ج ن (ن)) = (ج ~ 1 (ن) , ج ~ 2 (ن) , . . . , ج ~ ن (ن)) ه 1 (1) ه 2 (1) … ه ن (1) ه 1 (2) ه 2 (2) … ه ن (2) ⋮ ⋮ ⋮ ⋮ ه 1 (ن) ه 2 (ن) … ه ن (ن)
دعونا ندمج معادلات المصفوفة في تعبير واحد:
ج 1 (1) ج 2 (1) ⋯ ج ن (1) ج 1 (2) ج 2 (2) ⋯ ج ن (2) ⋮ ⋮ ⋮ ⋮ ج 1 (ن) ج 2 (ن) ⋯ ج ن (ن) = ج ~ 1 (1) ج ~ 2 (1) ⋯ ج ~ ن (1) ج ~ 1 (2) ج ~ 2 (2) ⋯ ج ~ ن (2) ⋮ ⋮ ⋮ ⋮ ج ~ 1 (ن) ج ~ 2 (ن) ⋯ ج ~ ن (ن) ه 1 (1) ه 2 (1) ⋯ ه ن (1) ه 1 (2) ه 2 (2) ⋯ ه ن (2) ⋮ ⋮ ⋮ ⋮ ه 1 (ن ) ه 2 (ن) ⋯ ه ن (ن)
سيحدد العلاقة بين متجهات قاعدتين مختلفتين.
باستخدام نفس المبدأ، من الممكن التعبير عن جميع المتجهات الأساسية e(1)، e(2)، . . . ، ه (3) من خلال الأساس ج (1)، ج (2)، . . . ، ج (ن):
ه 1 (1) ه 2 (1) ⋯ ه ن (1) ه 1 (2) ه 2 (2) ⋯ ه ن (2) ⋮ ⋮ ⋮ ⋮ ه 1 (ن) ه 2 (ن) ⋯ ه ن (ن) = ه ~ 1 (1) ه ~ 2 (1) ⋯ ه ~ ن (1) ه ~ 1 (2) ه ~ 2 (2) ⋯ ه ~ ن (2) ⋮ ⋮ ⋮ ⋮ ه ~ 1 (ن) ه ~ 2 (ن) ⋯ ه ~ ن (ن) ج 1 (1) ج 2 (1) ⋯ ج ن (1) ج 1 (2) ج 2 (2) ⋯ ج ن (2) ⋮ ⋮ ⋮ ⋮ ج 1 (ن ) ج 2 (ن) ⋯ ج ن (ن)
دعونا نعطي التعريفات التالية:
التعريف 5
مصفوفة ج ~ 1 (1) ج ~ 2 (1) ⋯ ج ~ ن (1) ج ~ 1 (2) ج ~ 2 (2) ⋯ ج ~ ن (2) ⋮ ⋮ ⋮ ⋮ ج ~ 1 (ن) ج ~ 2 (n) ⋯ c ~ n (n) هي مصفوفة الانتقال من الأساس e (1) , e (2) , . . . ، ه (3)
على الأساس ج (1) ، ج (2) ، . . . ، ج (ن) .
التعريف 6
مصفوفة e ~ 1 (1) e ~ 2 (1) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) هي مصفوفة الانتقال من الأساس c (1) , c (2) , . . . ، ج(ن)
على الأساس ه (1) , ه (2) , . . . ، ه (3) .
ومن هذه المساواة يتضح ذلك
ج ~ 1 (1) ج ~ 2 (1) ⋯ ج ~ ن (1) ج ~ 1 (2) ج ~ 2 (2) ⋯ ج ~ ن (2) ⋮ ⋮ ⋮ ⋮ ج ~ 1 (ن) ج ~ 2 (ن) ⋯ ج ~ ن (ن) ه ~ 1 (1) ه ~ 2 (1) ⋯ ه ~ ن (1) ه ~ 1 (2) ه ~ 2 (2) ⋯ ه ~ ن (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n) = 1 0 ⋯ 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1 e ~ 1 (1) e ~ 2 ( 1) ) ⋯ e ~ n (1) e ~ 1 (2) e ~ 2 (2) ⋯ e ~ n (2) ⋮ ⋮ ⋮ ⋮ e ~ 1 (n) e ~ 2 (n) ⋯ e ~ n (n ) · ج ~ 1 (1) ج ~ 2 (1) ⋯ ج ~ ن (1) ج ~ 1 (2) ج ~ 2 (2) ⋯ ج ~ ن (2) ⋮ ⋮ ⋮ ⋮ ج ~ 1 (ن) ج ~ 2 (ن) ⋯ ج ~ ن (ن) = 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1
أولئك. المصفوفات الانتقالية متبادلة.
دعونا نلقي نظرة على النظرية باستخدام مثال محدد.
مثال 7
البيانات الأولية:فمن الضروري العثور على مصفوفة الانتقال من الأساس
ج (1) = (1 ، 2 ، 1) ج (2) = (2 ، 3 ، 3) ج (3) = (3 ، 7 ، 1)
ه (1) = (3 ، 1 ، 4) ه (2) = (5 ، 2 ، 1) ه (3) = (1 ، 1 ، - 6)
تحتاج أيضًا إلى الإشارة إلى العلاقة بين إحداثيات المتجه التعسفي x → في القواعد المحددة.
حل
1. لتكن T هي المصفوفة الانتقالية، فإن المساواة ستكون صحيحة:
3 1 4 5 2 1 1 1 1 = ت 1 2 1 2 3 3 3 7 1
اضرب طرفي المساواة ب
1 2 1 2 3 3 3 7 1 - 1
ونحصل على:
ت = 3 1 4 5 2 1 1 1 - 6 1 2 1 2 3 3 3 7 1 - 1
2. تحديد مصفوفة الانتقال:
ت = 3 1 4 5 2 1 1 1 - 6 · 1 2 1 2 3 3 3 7 1 - 1 = = 3 1 4 5 2 1 1 1 - 6 · - 18 5 3 7 - 2 - 1 5 - 1 - 1 = - 27 9 4 - 71 20 12 - 41 9 8
3. دعونا نحدد العلاقة بين إحداثيات المتجه x → :
لنفترض أنه في الأساس ج (1) ، ج (2) ، . . . ، c (n) المتجه x → له إحداثيات x 1 ، x 2 ، x 3 ، إذن:
س = (س 1 ، س 2 ، س 3) 1 2 1 2 3 3 3 7 1 ,
وعلى الأساس ه (1) , ه (2) , . . . ، e (3) له إحداثيات x ~ 1، x ~ 2، x ~ 3، ثم:
س = (x ~ 1 , x ~ 2 , x ~ 3) 3 1 4 5 2 1 1 1 - 6
لأن إذا كان الطرفان الأيسران من هذه المتساويات متساويين، فيمكننا مساواة الطرفين الأيمن أيضًا:
(x 1 , x 2 , x 3) · 1 2 1 2 3 3 3 7 1 = (x ~ 1 , x ~ 2 , x ~ 3) · 3 1 4 5 2 1 1 1 - 6
اضرب كلا الطرفين على اليمين بـ
1 2 1 2 3 3 3 7 1 - 1
ونحصل على:
(x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) · 3 1 4 5 2 1 1 1 - 6 · 1 2 1 2 3 3 3 7 1 - 1 ⇔ ⇔ ( x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) T ⇔ ⇔ (x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3 ) · - 27 9 4 - 71 20 12 - 41 9 8
على الجانب الآخر
(x ~ 1، x ~ 2، x ~ 3) = (x 1، x 2، x 3) · - 27 9 4 - 71 20 12 - 41 9 8
تُظهر المساواة الأخيرة العلاقة بين إحداثيات المتجه x → في كلتا القاعدتين.
إجابة:مصفوفة الانتقال
27 9 4 - 71 20 12 - 41 9 8
ترتبط إحداثيات المتجه x → في القواعد المعطاة بالعلاقة:
(x 1 , x 2 , x 3) = (x ~ 1 , x ~ 2 , x ~ 3) · - 27 9 4 - 71 20 12 - 41 9 8
(x ~ 1، x ~ 2، x ~ 3) = (x 1، x 2، x 3) · - 27 9 4 - 71 20 12 - 41 9 8 - 1
إذا لاحظت وجود خطأ في النص، فيرجى تحديده والضغط على Ctrl+Enter