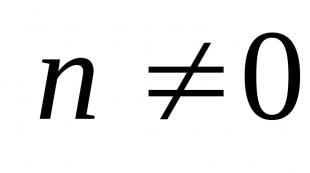hantverk

Typer av problem i elasticitetsteorin. Grundläggande ekvationer av elasticitetsteorin. Typer av problem i elasticitetsteorin Vad är ämnet för studier av den klassiska elasticitetsteorin

Ryska statsuniversitetet

olja och gas dem. I.M. Gubkina

Institutionen för teknisk mekanik

ABSTRAKT

"Teori om elasticitet"

Kompletterad av: Polyakov A.A.

Kontrolleras av: Evdokimov A.P.

Moskva 2011

elasticitetsteoretisk ekvation

1. Introduktion

Teori om stress-töjningstillstånd vid en punkt i en kropp

2.1 Stressteori

2 Deformationsteori

3 Förhållandet mellan stressat och deformerat tillstånd för elastiska kroppar

Grundläggande ekvationer av elasticitetsteorin. Typer av problem i elasticitetsteorin

1 Grundläggande ekvationer av elasticitetsteorin

2 Typer av problem i elasticitetsteorin

4 Ekvationer av teorin om elasticitet i förskjutningar (Lama ekvationer)

Variationsprinciper för elasticitetsteorin

1 Princip för möjliga förskjutningar (Lagrange-principen)

2 Principen för möjliga tillstånd (Castillano-principen)

3 Förhållandet mellan den exakta lösningen och lösningar som erhålls baserade på Lagrange- och Castigliano-principerna

Lista över begagnad litteratur

1. Introduktion

Teorier om spänningar och deformationer skapades av O. Cauchy. De anges i ett arbete som lämnades in till Paris Academy of Sciences 1822, vars sammanfattning publicerades 1823 och ett antal efterföljande artiklar. O. Koshi härledde tre jämviktsekvationer för en elementär tetraeder, bevisade lagen om parning av tangentiella spänningar, introducerade begreppen huvudaxlar och huvudspänningar och härledde differentialjämviktsekvationer (vanligtvis härleds de inte under styrkan av material). Han introducerade också ytan av normala spänningar (Cauchy-kvadricen), på vilken radievektorernas ändar är belägna, vars riktningar sammanfaller med normalernas riktning mot områdena, och värdet är omvänt proportionellt mot kvadratroten av det absoluta värdet av den normala spänningen i detta område, och det bevisades att denna yta är yta av andra ordningen centrerad vid ursprunget. Möjligheten att omvandla ytan av normalspänningar till huvudaxlar indikerar att det finns tre ömsesidigt huvudsakliga vinkelräta områden vid varje punkt.

En liknande skjuvspänningsyta introducerades av den ryska mekanikern G.V. Kolosov 1933

Den geometriska tolkningen av spänningstillståndet i rymden i form av en ellipsoid av spänningar gavs av G. Lame och B. Clapeyron i sina memoarer som lämnades in till Paris vetenskapsakademi 1828 och publicerades 1833.

Den geometriska representationen av spänningstillståndet på ett plan för en serie plattformar som går genom huvudaxeln, i form av en cirkel av spänningar, föreslogs av K. Kuhlman i sin bok 1866.

För det allmänna fallet med spänningstillståndet gavs en mycket tydlig geometrisk tolkning av det på planet av O. Mohr (det så kallade cirkulära Mohr-diagrammet) 1882. Av det kan ett antal viktiga slutsatser dras om huvudspänningarnas ytterlighet, positionen för de områden där tangentiella spänningar är maximala och om värdena för dessa maximala skjuvspänningar.

O. Cauchy gav en definition av töjningar, härledde deras beroende av förskjutningar i det speciella fallet med små töjningar (dessa beroenden härleds som regel inte under materialresistensförloppet), definierade begreppen huvudspänningar och principal töjningar och erhöll beroenden av spänningskomponenter på töjningskomponenter, som för isotrop och för en anisotrop elastisk kropp. I materialresistans fastställs vanligtvis töjningskomponenternas beroende av spänningskomponenterna för en isotrop kropp. De kallas den generaliserade Hookes lag, även om detta namn naturligtvis är godtyckligt, eftersom R. Hooke inte kände till begreppet stress.

I dessa beroenden introducerade Cauchy först två konstanter och skrev ner beroenden av spänningar på töjningar i formen

m, ,

Men senare O. Koshi antog konceptet L. Navier. Elastiska kroppar består enligt den av molekyler, mellan vilka det under deformation uppstår krafter som verkar i riktningarna för räta linjer som förbinder molekylerna och är proportionella mot förändringen i avstånden mellan molekylerna. Då är antalet elastiska konstanter för det allmänna fallet med en anisotrop kropp 15, och för en isotrop kropp får vi en elastisk konstant. S. Poisson höll fast vid denna hypotes, och i början - G. Lame och B. Clapeyron. Baserat på det fann Poisson att koefficienten för tvärtöjning är 1/4.

D. Green 1839 härledde förhållandet mellan spänningar och spänningar utan att använda hypotesen om den molekylära strukturen hos elastiska kroppar. Han erhöll dem baserat på principen om energibevarande, introducerade begreppet elastisk potential och visade att när man använder sex töjningskomponenters linjära beroende av sex spänningskomponenter, är 21 av 36 koefficienter oberoende, dvs. i det allmänna fallet med en anisotrop kropp är antalet elastiska konstanter 21 För en isotrop kropp reduceras antalet elastiska konstanter till två. En teori där antalet elastiska konstanter för en anisotrop kropp är 15, och för en isotrop kropp 1, kallades ibland "rarisk konstant" eller "unikonstant", och en teori där antalet elastiska konstanter för en anisotrop kropp är 21, och för en isotrop 2 - "multi-konstant".

Tvisten mellan anhängarna av dessa teorier fick fysiker till experimentell forskning.

G. Wertheim, baserat på mätningar av de inre volymerna av glas- och metallrör i axiell spänning, fastställde 1848 att den tvärgående deformationskoefficienten inte är lika med 1/4. Han ansåg det olika för olika material, men för många material var det nära 1/3.

OCH JAG. Kupffer, 1853, som testade metallstavar för spänning och vridning, fann också att förhållandet mellan moduler i skjuvning och spänning inte motsvarar en tvärgående töjning lika med 1/4.

År 1855 testade F. Neumann prover av rektangulärt tvärsnitt för böjning och mätte rotationsvinklarna för två ytor av balken (tvärsnittet antar en trapetsform). Som ett resultat visade han att koefficienten för tvärgående deformation inte är lika med 1/4. G. Kirchhoff, elev till F. Neumann, kom till samma slutsats på grundval av tester utförda 1859 för fogböjning och vridning av runda mässingsstänger, tätade i ena änden och belastade i den andra med en koncentrerad kraft, med mätningen av vridningsvinkeln för stången och sektionens rotationsvinkel.

En stor experimentell studie av koefficienterna för tvärdeformation för olika stålkvaliteter utfördes av en av eleverna till G. Kirchhoff, M.F. Okatov 1865 - 1866 Resultaten ges i hans doktorsavhandling.Vridnings- och böjtester av tunna prismor skurna ur enkristaller samt tester av kristallers kompressibilitet under enhetlig lika kompression utfördes av V. Voigt och beskrevs i hans talrika artiklar, senare. kombinerade i en bok publicerad 1910 De bekräftade riktigheten av multikonstanteorin.

En djupgående studie av den matematiska strukturen av Hookes lag för anisotropa kroppar genomfördes av mekanikern och ingenjören Jan Rychlevsky 1984 på grundval av begreppet ett elastiskt egentillstånd som han introducerade. I synnerhet visade han att 21 elastiska konstanter representerar sex sanna styvhetsmoduler, 12 styvhetsfördelare och tre vinklar.

2. Teori om stress-töjningstillstånd vid en punkt i en kropp

1 Stressteori

Interna kraftfaktorer som uppstår när en elastisk kropp belastas karakteriserar tillståndet för en viss sektion av kroppen, men svarar inte på frågan om vilken punkt i tvärsnittet som är mest belastad, eller, som de säger, den farliga punkten. Därför är det nödvändigt att ta hänsyn till ytterligare en kvantitet som kännetecknar kroppens tillstånd vid en given punkt.

Om en kropp på vilken yttre krafter appliceras är i jämvikt, uppstår interna motståndskrafter i någon av dess sektioner. Beteckna med den inre kraften som verkar på det elementära området och normalen till detta område genom då värdet

kallas full spänning.

I det allmänna fallet sammanfaller inte den totala spänningen i riktning med normalen till det elementära området, så det är bekvämare att arbeta med dess komponenter längs koordinataxlarna -

Om den yttre normalen sammanfaller med någon koordinataxel, till exempel med X-axeln, kommer spänningskomponenterna att ta formen, medan komponenten visar sig vara vinkelrät mot snittet och kallas normalspänning, och komponenterna kommer att ligga i sektionsplanet och kallas skjuvspänningar.

För att lätt kunna skilja mellan normal- och skjuvspänningar används vanligtvis andra beteckningar: - normalspänning, - skjuvning.

Låt oss från kroppen under inverkan av yttre krafter peka ut en oändligt liten parallellepiped, vars ytor är parallella med koordinatplanen och vars kanter har längd . På varje sida av en sådan elementär parallellepiped finns det tre spänningskomponenter som är parallella med koordinataxlarna. Totalt får vi 18 stresskomponenter på sex ansikten.

Normala spänningar betecknas som , där indexet anger normalen till motsvarande yta (det vill säga den kan ta värdena). Skjuvspänningar har formen ; här motsvarar det första indexet normalen till den plats på vilken den givna skjuvspänningen verkar, och den andra indikerar den axel som är parallell till vilken denna spänning är riktad (fig. 1).

Figur 1. Normal- och skjuvspänningar

För dessa spänningar används följande teckenregel. Den normala spänningen anses vara positiv i spänning, eller motsvarande, när den sammanfaller med riktningen för den yttre normalen till den plats på vilken den verkar. Den tangentiella spänningen anses vara positiv om den på platsen, normalen till vilken sammanfaller med koordinataxelns riktning parallellt med den, är riktad mot den positiva koordinataxeln som motsvarar denna spänning.

Stresskomponenter är funktioner av tre koordinater. Till exempel kan normalspänningen vid en punkt med koordinater betecknas

Vid en punkt som ligger på ett oändligt litet avstånd från den i fråga kan spänningen, upp till infinitesimals av första ordningen, utökas i en Taylor-serie:

För plattformar som är parallella med planet ändras endast x-koordinaten och stegen. Därför kommer den normala spänningen på parallellepipedens yta, som sammanfaller med planet, att vara Av 18 spänningskomponenter är därför endast nio okända.

I elasticitetsteorin är lagen om parning av skjuvspänningar bevisad, enligt vilken, längs två ömsesidigt vinkelräta områden, komponenterna av skjuvspänningar, vinkelräta mot skärningslinjerna för dessa områden, är lika med varandra:

Jämlikheter (2) leder till det faktum att av nio stresskomponenter som kännetecknar stresstillståndet vid en punkt i kroppen, återstår endast sex:

Det kan visas att påfrestningar (3) inte bara karaktäriserar kroppens stresstillstånd vid en given punkt, utan bestämmer det unikt. Kombinationen av dessa spänningar bildar en symmetrisk matris, som kallas spänningstensor:

(4)

När man multiplicerar en tensor med ett skalärt värde erhålls en ny tensor, vars alla komponenter är gånger större än komponenterna i den ursprungliga tensorn.

2 Deformationsteori

Under påverkan av yttre belastningar ändrar den elastiska kroppen sin form och deformeras. I det här fallet tar kroppens punkter en ny position. För att bestämma deformationen av en elastisk kropp jämför vi positionerna för kroppens punkter före och efter appliceringen av belastningen.

Betrakta en punkt av en olastad kropp och dess nya position efter appliceringen av lasten. Vektorn kallas punktförskjutningsvektorn (Fig. 2).

Fig.2. Punkt flytta vektor

Två typer av förskjutningar är möjliga: förskjutning av hela kroppen som helhet utan deformation - sådana förskjutningar studeras av teoretisk mekanik som förskjutningar av en absolut stel kropp, och förskjutning i samband med deformation av kroppen - sådana förskjutningar studeras av teorin av elasticitet.

Låt oss beteckna projektionerna av punktförskjutningsvektorn på respektive koordinataxlar. De är lika med skillnaden mellan motsvarande koordinater för punkterna och:

och är funktioner av koordinater:

Deformationen av kroppen orsakas av skillnaden i förskjutningarna av dess olika punkter. En oändligt liten parallellepiped med kanter utskurna ur en elastisk kropp nära en godtycklig punkt, på grund av olika förskjutningar av dess punkter, deformeras på ett sådant sätt att längden på dess kanter ändras och de initialt räta vinklarna mellan ytorna förvrängs.

Figur 3.3 visar två kanter av denna parallellepiped: och längden på kanten är lika med och kanten är

Efter deformation tar punkterna en position. I detta fall kommer punkten att få en förskjutning, vars komponenter i ritningens plan är lika, och punkten som separeras från punkten på ett oändligt litet avstånd kommer att få en förskjutning, vars komponenter kommer att skilja sig från komponenterna i punktens förskjutning med ett oändligt litet värde på grund av en förändring i koordinaten

Fig.3. Linjära och vinkeldeformationer

Komponenterna i punktförskjutningen kommer att skilja sig från komponenterna i punktförskjutningen med ett oändligt litet värde på grund av en förändring i koordinaten

Längden på ribbans projektion på axeln efter deformation:

Projektion av revbens absoluta förlängning på axeln

Relativ förlängning längs axeln

(6)

kallas linjär deformation i axelns riktning.

Likaså linjära deformationer längs axlarnas riktningar och

(7)

Tänk på förändringen i vinklarna mellan kanterna på parallellepipeden (Fig. 3). Tangensen för ribbans rotationsvinkel i planet

På grund av att deformationerna a är små, kan den linjära deformationen försummas på grund av dess litenhet jämfört med enhet, och då

På samma sätt kan du bestämma ribbans rotationsvinkel i samma plan:

Förvrängningen av en rät vinkel kallas vinkeldeformation och definieras som summan av ribbornas rotationsvinklar och:

(8)

På samma sätt bestäms vinkeldeformationer i två andra koordinatplan:

(9)

Formlerna (6)-(9) ger sex grundläggande beroenden för linjära och vinkeldeformationer på förskjutningskomponenterna. Dessa beroenden kallas Cauchy-ekvationerna:

(10)

I gränsen när längderna på parallellepipedens kanter tenderar mot noll, bestämmer Cauchy-relationerna de linjära och vinkelformade deformationerna i närheten av punkten

Positiva linjära deformationer motsvarar förlängningar och negativa till förkortningar. Skiftvinkeln anses vara positiv när vinkeln mellan de positiva riktningarna för motsvarande koordinataxlar minskar och negativ - annars.

På samma sätt som spänningstensorn beskrivs det deformerade tillståndet hos kroppen vid en given punkt av töjningstensorn

(11)

Liksom spänningstensorn är töjningstensorn en symmetrisk matris som innehåller nio komponenter, varav sex är olika.

2.3 Samband mellan stress och belastning för elastiska kroppar

Sambanden mellan påfrestningar och påfrestningar är av fysisk natur. Begränsat till små töjningar kan sambandet mellan spänningar och töjningar anses linjärt.

När man testar en stång i spänning (mekanisk provning av material kommer att diskuteras i detalj i nästa avsnitt), etableras ett proportionellt förhållande mellan normal spänning och linjär deformation i en riktning, vilket kallas Hookes lag:

där elasticitetskonstanten kallas longitudinell elasticitetsmodul.

På samma experimentella sätt etablerades ett samband mellan linjära deformationer i längsgående och tvärgående riktningar:

där - linjär deformation i tvärriktningen, - den andra elastiska konstanten, kallad Poissons förhållande.

I mekaniska tester för ren skjuvning fastställdes ett direkt proportionellt samband mellan skjuvspänning och vinkeldeformation i verkansplanet för denna spänning, vilket kallades Hookes lag i skjuvning:

där värdet är den tredje elasticitetskonstanten och kallas skjuvmodulen. Denna elastiska konstant är dock inte oberoende, eftersom förknippas med de två första

För att fastställa sambandet mellan spänningar och spänningar väljer vi en oändligt liten parallellepiped från kroppen (Fig. 1) och överväger verkan av endast normala spänningar. det leder till deformationer av högre storleksordning.

Låt oss bestämma förlängningen av revbenet parallellt med spänningen Under inverkan av denna spänning, enligt Hookes lag (3.12), kommer den relativa förlängningen av revbenet att inträffa

Spänning orsakar en liknande förlängning i riktningen vinkelrätt mot revbenet

och i riktning mot revbenet - förkortning, vilket enligt (13) är

eller, med hänsyn till deformationsuttrycket

På liknande sätt bestäms den relativa förkortningen av revbenet under inverkan av påkänning

Baserat på principen om oberoende av krafternas verkan, kan den totala relativa förlängningen av revbenet definieras som summan av förlängningarna från verkan av varje spänning:

På liknande sätt kan man definiera linjära deformationer längs riktningarna för de andra två axlarna:

I enlighet med Hookes lag i skjuvning (14) kan förhållandet mellan vinkeldeformationer och skjuvspänningar representeras oberoende för vart och ett av de tre planen parallella med koordinatplanen:

Således har sex formler erhållits som uttrycker ett linjärt samband mellan töjnings- och spänningskomponenterna i en isotrop elastisk kropp och kallas den generaliserade Hookes lag:

(16)

3. Grundläggande ekvationer av elasticitetsteorin. Typer av problem i elasticitetsteorin

Huvuduppgiften för elasticitetsteorin är bestämning av stress-töjningstillståndet enligt de givna förhållandena för belastning och fixering av kroppen.

Spännings-töjningstillståndet bestäms om komponenterna i spänningstensorn (s) och förskjutningsvektorn, nio funktioner finns.

3.1 Grundläggande ekvationer för elasticitetsteorin

För att hitta dessa nio funktioner måste man skriva ner de grundläggande ekvationerna i elasticitetsteorin, eller:

Differential Cauchies

(17)

var är komponenterna i tensorn i den linjära delen av Cauchy-deformationerna;

komponenter i tensorn av derivatan av förskjutning längs radien.

Differentiella jämviktsekvationer

var finns spänningstensorkomponenterna; är projektionen av kroppskraften på j-axeln.

Hookes lag för en linjärt elastisk isotrop kropp

var är de Lama konstanterna; för en isotrop kropp. Här är normal- och skjuvspänningar; töjnings- och skjuvningsvinklar, respektive.

Ovanstående ekvationer måste uppfylla Saint-Venant-beroendena

I elasticitetsteorin är problemet löst om alla grundläggande ekvationer är uppfyllda.

2 Typer av problem i elasticitetsteorin

Randvillkor på kroppens yta måste vara uppfyllda och beroende på typ av randvillkor finns det tre typer av problem inom elasticitetsteorin.

Första typen. Krafter ges på kroppens yta. Gränsförhållanden

Andra typen. Problem där förskjutning är specificerad på kroppsytan. Gränsförhållanden

Tredje typen. Blandade problem av elasticitetsteorin. Krafter ges på en del av kroppsytan, förskjutning ges på en del av kroppsytan. Gränsförhållanden

Problem där krafter eller förskjutningar är specificerade på kroppens yta, men det krävs för att hitta spännings-töjningstillståndet inuti kroppen och det som inte anges på ytan, kallas direkta problem. Om däremot spänningar, deformationer, förskjutningar etc. specificeras inuti kroppen, och det krävs att fastställa vad som inte är specificerat inuti kroppen, samt förskjutningar och spänningar på kroppens yta (det vill säga att hitta orsakerna som orsakade ett sådant stress-töjningstillstånd)), då kallas sådana problem inversa.

4 Ekvationer av teorin om elasticitet i förskjutningar (Lama ekvationer)

För att bestämma ekvationerna för teorin om elasticitet i förskjutningar, skriver vi: differentialjämviktsekvationer (18) Hookes lag för en linjärt elastisk isotrop kropp (19)

Om vi tar hänsyn till att deformationer uttrycks i termer av förskjutningar (17), skriver vi:

Det bör också erinras om att skjuvvinkeln är relaterad till förskjutningar av följande förhållande (17):

(23)

Genom att ersätta uttryck (22) i den första ekvationen av likheter (19), får vi att normalspänningarna

(24)

Observera att notationen u i detta fall inte innebär summering över i.

Genom att ersätta uttryck (23) i den andra ekvationen av likheter (19), får vi att skjuvspänningar

(25)

Låt oss skriva jämviktsekvationerna (18) i expanderad form för j = 1

(26)

Genom att ersätta uttryck i ekvation (26) för normala (24) och tangentiella (25) spänningar får vi

där λ är Lame-konstanten, som bestäms av uttrycket:

Vi ersätter uttryck (28) med ekvation (27) och skriver,

där bestäms av uttryck (22), eller i expanderad form

Vi delar uttryck (29) med G och lägger till liknande termer och får den första Lame-ekvationen:

(30)

var är Laplace-operatorn (övertonsoperator), som definieras som

(31)

På samma sätt kan du få:

(32)

Ekvationerna (30) och (32) kan skrivas på följande sätt:

(33)

Ekvationerna (33) eller (30) och (32) är Lame-ekvationerna. Om kroppskrafterna är noll eller konstanta, då

(34)

dessutom innebär notationen i detta fall inte summering över i. Här

Det kan visas att en sådan representation av förskjutningar i termer av en harmonisk funktion gör Lame-ekvationerna (33) till en identitet. Ofta kallas de för Popkovich-Grodsky-förhållandena. De fyra övertonsfunktionerna är inte nödvändiga, eftersom φ0 kan likställas med noll.

4. Variationsprinciper för elasticitetsteorin.

1 Princip för möjliga förskjutningar (Lagrange-principen)

Lagrange-principen. För en kropp i jämvikt är arbetet av yttre och inre krafter på alla möjliga infinitesimala förskjutningssteg noll.

Genom att använda Clapeyron-satsen, att för en elastiskt deformerad kropp genom att variera förskjutningen, får vi Lagrange-principen

Möjliga i mekaniken för deformerbara kroppar är sådana förskjutningar som tillfredsställer de yttre och inre begränsningar som åläggs kroppen.

Externa anslutningar är villkor för fixering, interna anslutningar är ett villkor för kontinuitet.

För att tillfredsställa de interna begränsningarna är det nödvändigt att förskjutningsinkrementen är kontinuerliga envärdesfunktioner för koordinaterna.

I denna form är Lagrange-principen giltig för alla deformerbara kroppar.

För elastiska kroppar erhölls det

(41)

Då kan (40), med hänsyn till (41), skrivas som

(42)

där W är den specifika stammen, och

Här är U en variation av hela kroppens potentiella energi.

Vi ersätter uttryck (43) med (42), och eftersom krafterna inte varierar, skriver vi det

(44)

Ekvation (44) är en variationslagrangekvation.

Om krafterna är konservativa representerar de två första integralerna förändringen i potentialen för yttre krafter under övergången från det odeformerade tillståndet till det deformerade.

Potential för yttre krafter

(45)

där - det möjliga arbetet av yttre krafter under övergången från det odeformerade till det deformerade tillståndet beräknas under antagandet att de yttre krafterna förblir oförändrade. Systemets totala energi

Sedan, med hänsyn till uttryck (44) - (46), kommer Lagrange-principen att skrivas:

det vill säga variationen av systemets totala energi i jämviktsläget på möjliga förskjutningar är lika med noll. Uttryck (47) är variationslagrangekvationen i fallet med verkan av endast konservativa krafter.

I positionen för stabil jämvikt är den totala energin P minimal,

Lagrangeprincipen är principen om minimal energi.

2 Principen för möjliga tillstånd (Castillano-principen)

Vi kommer att kalla möjliga tillstånd de som är i överensstämmelse med yttre och inre krafter, det vill säga uppfyller jämviktsekvationerna.

Ekvation (57) skriver Castigliano-principen. Med möjliga förändringar i kroppens spänningstillstånd är variationen lika med integralen över den del av kroppsytan på vilken förskjutningar ges av produkterna av möjliga ytkrafter och förskjutningar.

3 Förhållandet mellan den exakta lösningen och lösningar som erhålls baserade på Lagrange- och Castigliano-principerna

Baserat på Lagrange-principen, att välja några funktioner, eller en uppsättning av dem, och eftersom uppsättningen av funktioner är begränsad, får vi ett mindre antal frihetsgrader i systemet, vilket minskar strukturens frihetsgrader. Det vill säga, i energimässig mening visar sig lösningen vara stelare än den exakta.

Om vi tar integralegenskaperna, är den ungefärliga lösningen mer styvt integrerad.

Vid lösning av problemet med att belasta en gångjärnsbalk med en tvärkraft i mitten av spännvidden (fig. 1) kommer den ungefärliga lösningen att ge en mindre förskjutning under kraften än med den exakta lösningen.

exakt lösning

När man löser samma problem med hjälp av Castiglianos variationsprincip, eftersom kontinuitetsvillkoret inte är uppfyllt, får systemet mer frihet än i verkligheten.

Den exakta lösningen ligger mellan dessa två ungefärliga metoder (Lagrange och Castigliano). Ibland är skillnaden mellan de erhållna lösningarna liten.

5. Lista över använd litteratur

1. Aleksandrov A.V., Potapov V.D. Grunderna i teorin om elasticitet och plasticitet. 400 sidor. Högre skola. 1990.

2. Veretimus D.K. Grunderna i elasticitetsteorin Del I. Stressteori Metodguide för kursen "Grundläggande teorin om elasticitet och plasticitet." 2005.-37s.

Veretimus D.K. Grunderna i elasticitetsteorin Del II Teori om deformationer. Samband mellan det stressade och deformerade tillståndet Metodguide för kursen "Grundläggande av teorin om elasticitet och plasticitet", 2005.-53s.

Veretimus D.K. Elasticitetsteorins grunder Del III Elasticitetsteorins grundläggande ekvationer Typer av problem i elasticitetsteorin Metodguide för kursen "Grundläggande teorin om elasticitet och plasticitet", 2005.-45s.

I kroppar i vila eller i rörelse under påverkan av belastningar.

1. Problemet med elasticitetsteorin

Uppgiften för denna teori är att skriva matematiska ekvationer, vars lösning gör det möjligt att svara på följande frågor:

Vilka blir deformationerna av en viss kropp om belastningar av ett givet värde appliceras på den på kända platser?
vad blir spänningen i kroppen?

Frågan är, kroppen kommer att kollapsa, kommer att motstå dessa belastningar, nära relaterad till teorin om elasticitet, men strängt taget inte är inom hans kompetens.

Det finns många exempel - från bestämning av deformationer och spänningar i en laddad balk på stöd, till beräkningen av samma parametrar i kroppen på ett flygplan, raket, ubåt, i hjulet på en bil i pansaret på en tank när en projektil träffar, i en bergskedja när man lägger en adit, i ramen av ett höghus och så vidare.

För tekniska problem beräknas spänningar och töjningar i strukturer enligt förenklade teorier, logiskt baserade på teorin om elasticitet. Dessa teorier inkluderar: materialstyrkan, vars uppgift är beräkningen av stavar och balkar, såväl som bedömningen av spänningar som uppstår i zonerna för kontaktinteraktion mellan fasta ämnen; strukturell mekanik- design av stångsystem (t.ex. broar), och skalteori- en oberoende och välutvecklad gren av vetenskapen om deformation och stress, vars ämne är tunnväggiga skal - cylindriska, koniska, sfäriska och komplexa former.

2. Grundbegrepp i elasticitetsteorin

De grundläggande begreppen i elasticitetsteorin är spänningen som verkar på små plan, som mentalt kan dras i kroppen genom en given punkt P, deformationen av ett litet område av punkten P och förskjutningen av själva punkten P. Mer exakt, den mekaniska spänningstensorn, den lilla töjningstensorn och förskjutningsvektorn introduceras u i. Kort notation , Where-index I j ta värdena 1, 2, 3 (eller x, y, z) ska förstås som en matris i formen:

Den korta notationen för tensorn bör förstås på liknande sätt.

Om den fysiska punkten för kroppen M på grund av deformation har tagit en ny position i rymden P ", så är förskjutningsvektorn en vektor med komponenter (u x, u y, u z), eller kort sagt, u i. I teorin om små deformationer, komponenterna u i och anses vara små kvantiteter (strängt taget oändligt). Komponenter av en tensor, som också kallas spänningstensor Cauchy eller linjär töjningstensor och vektor u i relaterade beroenden:

Från den sista posten kan det ses att , Därför är deformationstensorn symmetrisk per definition.

Om en elastisk kropp under inverkan av yttre krafter är i jämvikt (d.v.s. hastigheterna för alla dess punkter är lika med noll), så är varje del av kroppen som kan separeras mentalt från den också i jämvikt. En oändligt liten rektangulär parallellepiped extraheras från kroppen, vars ytor är parallella med det kartesiska systemets koordinatplan. Från jämviktsförhållandet för en parallellepiped med kantstorlekar dx, dy, dz, Efter att ha övervägt förutsättningarna för kraftbalansen i projektioner kan vi få:

På liknande sätt erhålls jämviktsekvationer som uttrycker lika med noll av huvudmomentet för alla krafter som verkar på parallellepipeden, reducerade till formen:

Denna likhet innebär att spänningstensorn är en symmetrisk tensor och antalet okända komponenter i spänningstensorn minskar till 6. Det finns bara tre jämviktsekvationer, d.v.s. statikens ekvationer räcker inte för att lösa problemet. Utvägen är att uttrycka spänningar i termer av töjningar med hjälp av Hookes lag-ekvationer, och sedan uttrycka töjningar i termer av förskjutningar u i använda Cauchy-formlerna och ersätta resultatet i jämviktsekvationen. I detta fall erhålls tre differentialjämviktsekvationer med avseende på tre okända funktioner u x u y u z, de där. antalet okända kommer att motsvara antalet ekvationer. Dessa ekvationer kallas Navier-Cauchy-ekvationerna.

3. Randvillkor

Lösningen av problem i elasticitetsteorin reduceras till att integrera ett system av differentialekvationer i partiella derivator som bestämmer beteendet hos en elastisk kropp vid inre punkter. Dessa ekvationer kompletteras med förhållanden på ytan som begränsar kroppen. Dessa förhållanden bestämmer uppgifterna för antingen yttre ytkrafter eller förskjutningar av punkter på kroppens yta. Beroende på detta formuleras vanligtvis en av tre typer av gränsvärdesproblem.

Första gränsvärdesproblemet- kinematisk. I kroppens volym hittas komponenterna i förskjutningar, de förvärvar vissa värden på ytan. I tillståndet på kroppens yta är ytans ekvationer och värdena för komponenterna av förskjutningar på den sålunda inställda.

Det andra gränsvärdesproblemet- statisk. I det här fallet läggs inga restriktioner på rörelse på kroppens yta, och ytekvationerna är inställda, som riktar normalens cosinus till ytan och värdena för ytbelastningskomponenterna.

I det fall då kroppens yta sammanfaller med koordinatplanen kan randvillkoren formuleras direkt i termer av spänningar. Då räcker det att indikera ytans ekvation och ställa in värdena för spänningskomponenterna på den.

Det tredje gränsvärdesproblemet- blandat. I detta fall är kinematiska förhållanden inställda på en del av kroppsytan och statiska förhållanden på den andra.

Dessa tre problem uttömmer inte alla olika randvillkor. Till exempel, i något område av ytan kan inte alla tre förskjutningskomponenter eller ytlastkomponenter specificeras.

4. Se även

Källor

Timosjenko S.P., Goodyear J. Teori om elasticitet. M.: Nauka, 1979. 560 sid.

ELASTICITETSTEORI- en gren av kontinuummekanik som studerar förskjutningar, deformationer och spänningar hos vilande eller rörliga kroppar under påverkan av belastningar. Syftet med denna teori är härledningen av matematiska ekvationer, vars lösning gör det möjligt att besvara följande frågor: vad blir deformationen av denna speciella kropp om belastningar av ett givet värde appliceras på den på kända platser? Vad blir spänningen i kroppen? Frågan om huruvida kroppen kommer att kollapsa eller motstå dessa belastningar är nära relaterad till teorin om elasticitet, men ligger strängt taget inte inom denna teoris kompetens.

Antalet möjliga exempel är obegränsat - från att bestämma deformationer och spänningar i en balk som ligger på stöd och belastad med krafter, till att beräkna samma värden i strukturen av ett flygplan, ett fartyg, en ubåt, i hjulet på en vagn, i rustning när en projektil träffar, i en bergskedja när den passerar genom en adit, i ramen av ett höghus, etc. Här är det nödvändigt att göra en reservation: strukturer som består av tunnväggiga element beräknas enligt förenklade teorier, logiskt baserade på teorin om elasticitet; sådana teorier inkluderar: teorin om materialresistans mot belastningar (den berömda "sopromaten"), vars uppgift huvudsakligen är att beräkna stavar och balkar; strukturell mekanik - beräkning av stångsystem (till exempel broar); och slutligen är teorin om skal i själva verket ett oberoende och mycket högt utvecklat vetenskapsområde om deformationer och spänningar, vars ämne är de viktigaste strukturella elementen - tunnväggiga skal - cylindriska, koniska, sfäroidala och har mer komplexa former. Därför, i teorin om elasticitet, betraktas vanligtvis kroppar vars väsentliga dimensioner inte skiljer sig alltför mycket. Således betraktas en elastisk kropp av en given form, på vilken kända krafter verkar.

De grundläggande begreppen i elasticitetsteorin är de påfrestningar som verkar på små områden, som kan utföras mentalt i kroppen genom en given punkt M, deformationer av ett litet område av punkten M och flytta själva punkten M. Mer exakt, stresstensorer I j, liten töjningstensor e I j och förskjutningsvektor u i.

Kort beteckning s I j, där indexen i, j ta värden 1, 2, 3 ska förstås som en matris av formen:

Den korta notationen för tensorn e I j.

Om den fysiska punkten i kroppen M på grund av deformation, tog en ny position i rymden M´, då är förskjutningsvektorn en vektor med komponenter ( u x u y u z), eller kort sagt, u i. I teorin om små deformationer, komponenterna u i och e i anses vara små kvantiteter (strängt taget oändligt). Komponenter i e-tensorn I j och vektor u ijär relaterade av Cauchy-formlerna, som har formen:

Det kan ses att t.ex xy= e yx och generellt sett t.ex I j= e ji, så töjningstensorn är symmetrisk per definition.

Om en elastisk kropp under inverkan av yttre krafter är i jämvikt (d.v.s. hastigheterna för alla dess punkter är lika med noll), så är varje del av kroppen som kan separeras mentalt från den också i jämvikt. En liten (strängt taget, infinitesimal) rektangulär parallellepiped sticker ut från kroppen, vars ytor är parallella med det kartesiska systemets koordinatplan Oxyz(Figur 1).

Låt parallellepipedens kanter ha längder dx, dy, dz respektive (här, som vanligt dx det finns en skillnad x, etc.). Enligt spänningsteorin verkar komponenterna i spänningstensorn på parallellepipedens ytor, som betecknas:

på randen OADG:s xx, s xy, s xz

på randen OABC:s yx, s åå, s yz

på randen DABE:s zx, s zy, s zz

medan komponenterna med samma index (till exempel s xx) agerar vinkelrätt mot ansiktet, medan de med olika index agerar i ytplanet.

På motsatta ytor är värdena för spänningstensorkomponenterna med samma namn något annorlunda, detta beror på det faktum att de är funktioner av koordinater och ändras från punkt till punkt (alltid, förutom de kända enkla fallen), och förändringens litenhet är associerad med parallellepipedens små dimensioner, så vi kan anta att om på gränsen OABC spänning s åå, sedan på gränsen GDEF spänning s åå+ds åå, och det lilla värdet ds åå just på grund av dess litenhet kan den bestämmas med hjälp av expansionen i en Taylor-serie:

(här används partiella derivator, eftersom komponenterna i spänningstensorn beror på x, y, z).

På liknande sätt kan spänningarna på alla ansikten uttryckas i termer av s I j och ds I j. Vidare, för att gå från spänningar till krafter, måste du multiplicera storleken på spänningen med området på platsen där den verkar (till exempel s åå+ds åå multiplicera med dx dz). När alla krafter som verkar på parallellepipeden är bestämda är det möjligt, som man gör i statik, att skriva ner kroppens jämviktsekvation, medan det i alla ekvationer för huvudvektorn endast kommer att finnas kvar med derivator, eftersom själva spänningarna ta bort varandra, och faktorerna dx dy dz minskar och som ett resultat

På liknande sätt erhålls jämviktsekvationer som uttrycker likheten till noll av huvudmomentet för alla krafter som verkar på parallellepipeden, vilka reduceras till formen:

Dessa likheter innebär att spänningstensorn är en symmetrisk tensor. Således, för 6 okända komponenter I j det finns tre jämviktsekvationer, dvs. statikens ekvationer räcker inte för att lösa problemet. Utvägen är att uttrycka påfrestningarna I j genom deformationer e I j med hjälp av ekvationerna i Hookes lag, och sedan deformationen e I j uttrycka i termer av förskjutning u i använda Cauchy-formlerna och ersätta resultatet i jämviktsekvationerna. I detta fall erhålls tre differentialjämviktsekvationer med avseende på tre okända funktioner u x u y u z, dvs. antalet okända är lika med antalet ekvationer. Dessa ekvationer kallas Lame-ekvationerna

kroppskrafter (vikt etc.) tas inte med i beräkningen

D är Laplace-operatören, dvs.

Nu måste vi sätta gränsvillkor på kroppens yta;

Huvudtyperna av dessa tillstånd är följande:

1. Förskjutningar ges på en känd del av kroppens yta S 1, dvs. förskjutningsvektorn är lika med den kända vektorn med komponenter ( f x; f y; f z ):

u x = f(xyz)

u y= f(xyz)

u z= f(xyz)

(f x, f y, F Zär kända koordinatfunktioner)

2. På resten av ytan S 2 ges ytkrafter. Detta innebär att spänningsfördelningen inuti kroppen är sådan att spänningsvärdena i ytans omedelbara närhet, och i gränsen - på ytan på varje elementärt område skapar en spänningsvektor lika med den kända externa belastningsvektorn med komponenter ( Fx ;Fy ; F Z) ytkrafter. Matematiskt skrivs detta så här: om vid en punkt A yta, har enhetens normalvektor till denna yta komponenter n x, n y, nz då vid denna tidpunkt jämlikheterna med avseende på de (okända) komponenterna s I j:e I j, då för tre okända får vi sex ekvationer, det vill säga ett överbestämt system. Detta system kommer att ha en lösning endast om ytterligare villkor är uppfyllda för t.ex I j. Dessa villkor är kompatibilitetsekvationerna.

Dessa ekvationer kallas ofta kontinuitetsförhållanden, vilket innebär att de säkerställer kroppens kontinuitet efter deformation. Detta uttryck är figurativt, men felaktigt: dessa förhållanden säkerställer existensen av ett kontinuerligt förskjutningsfält, om komponenterna i deformationer (eller spänningar) tas som okända. Att inte uppfylla dessa villkor leder inte till en kränkning av kontinuiteten, utan till avsaknaden av en lösning på problemet.

Således ger elasticitetsteorin differentialekvationer och randvillkor som gör att vi kan formulera gränsvärdesproblem, vars lösning ger fullständig information om fördelningen av spänningar, töjningar och förskjutningar i de kroppar som är i fråga. Metoderna för att lösa sådana problem är mycket komplexa och de bästa resultaten får man genom att kombinera analytiska metoder med numeriska metoder med hjälp av kraftfulla datorer.

Vladimir Kuznetsov

GRUNDLAGEN FÖR ELASTICITETSTEORIN

AXISYMMETRISKA PROBLEM I ELASTICITETSTEORIN

GRUNDLAGEN FÖR ELASTICITETSTEORIN

Grundläggande bestämmelser, antaganden och notation Jämviktsekvationer för en elementär parallellepiped och en elementär tetraeder. Normal- och skjuvspänningar längs en lutande plattform

Bestämning av huvudspänningarna och de största skjuvspänningarna vid en punkt. Påfrestningar på oktaedriska platser Begreppet förskjutningar. Samband mellan deformationer och förskjutningar. Relativ

linjär deformation i en godtycklig riktning Deformationskompatibilitetsekvationer. Hookes lag för en isotrop kropp Planproblem i rektangulära koordinater Planproblem i polära koordinater

Möjliga lösningar på problem inom elasticitetsteorin. Lösningar på problem vid förskjutningar och spänningar Förekomst av ett temperaturfält. Korta slutsatser om avsnittet ENKLA AXISYMMETRISKA PROBLEM Ekvationer i cylindriska koordinater Ekvationer i cylindriska koordinater (forts.)

Deformation av ett tjockväggigt sfäriskt kärl Koncentrerad kraft som verkar på ett plan

Särskilda fall av belastning av ett elastiskt halvutrymme: jämn belastning över området för en cirkel, belastning på området av en cirkel längs en "halvklot", omvänt problem Att trycka en absolut stel boll i ett elastiskt halvutrymme . Problemet med elastisk kollaps av bollar tjockväggiga RÖR

Allmän information. Jämviktsekvation för ett rörelement Studie av spänningar under tryck på en av kretsarna. Hållfasthetsförhållanden för elastisk deformation Spänningar i kompositrör. Konceptet för beräkning av flerskiktsrör Beräkningsexempel

PLATOR, MEMBRANER Grundläggande definitioner och hypoteser

Differentialekvation för plattans krökta mittyta i rektangulära koordinater Cylindrisk och sfärisk böjning av plattan

Böjmoment för axelsymmetrisk böjning av en rund platta. Differentialekvation för den krökta mittytan på en rund platta Gränsförhållanden i runda plattor. De största påfrestningarna och deformationerna. styrka förhållanden. Termiska spänningar i plattor

Bestämning av krafter i membran. Kedjekrafter och spänningar. Ungefärlig bestämning av nedböjningar och spänningar i cirkulära membran Beräkningsexempel Beräkningsexempel (fortsättning)

1.1 Grundläggande bestämmelser, antaganden och symboler

Teorin om elasticitet är inriktad på den analytiska studien av stress-töjningstillståndet hos en elastisk kropp. Med hjälp av elasticitetsteorin kan lösningar erhållna med resistansantaganden verifieras

material, och gränserna för tillämpligheten av dessa lösningar är fastställda. Ibland sektioner av elasticitetsteorin, där, liksom i materialresistans, frågan om en dels lämplighet övervägs, men med hjälp av en ganska komplex matematisk apparat (beräkning av plattor, skal, arrayer), hänvisas de till. som tillämpad teori om elasticitet.

Detta kapitel beskriver de grundläggande begreppen i den matematiska linjära teorin om elasticitet. Tillämpningen av matematik på beskrivningen av fysiska fenomen kräver deras schematisering. I den matematiska elasticitetsteorin löses problem med så få antaganden som möjligt, vilket komplicerar de matematiska metoder som används för att lösa. Den linjära elasticitetsteorin antar att det finns ett linjärt samband mellan komponentspänningarna och töjningarna. För ett antal material (gummi, vissa kvaliteter av gjutjärn) kan ett sådant beroende, även med små deformationer, inte accepteras: diagrammet σ - ε inom elasticitetens gränser har samma form både under lastning och lossning, men i båda fallen är den kurvlinjär. När man studerar sådant material är det nödvändigt att använda beroenden av den olinjära teorin om elasticitet.

I matematisk linjär elasticitetsteori är baserad på följande antaganden:

1. Om mediets kontinuitet (kontinuitet). I detta fall, den atomistiska strukturen av ett ämne eller närvaron inga tomrum tas med i beräkningen.

2. På det naturliga tillståndet, på grundval av vilket det initiala spänningstillståndet (deformerat) av kroppen som uppstod före appliceringen av kraftåtgärder inte beaktas, det vill säga, det antas att deformationerna vid belastningsögonblicket av kroppen och spänningar vid någon av dess punkter är lika med noll. I närvaro av initiala spänningar kommer detta antagande att vara giltigt, om bara beroenden av den linjära elasticitetsteorin kan tillämpas på de resulterande spänningarna (summan av de initiala och som härrör från stötarna).

3. På homogenitet, på grundval av vilken det antas att kroppens sammansättning är densamma på alla punkter. Även om detta antagande för metaller inte ger stora fel, kan det för betong, när man överväger små volymer, leda till betydande fel.

4. På sfärisk isotropi, på grundval av vilken man tror att materialets mekaniska egenskaper är desamma i alla riktningar. Metallkristaller har inte denna egenskap, men för metallen som helhet, bestående av ett stort antal små kristaller, kan vi anta att denna hypotes är sann. För material med olika mekaniska egenskaper i olika riktningar, som till exempel för laminerade plaster, har en elasticitetsteori för ortotropa och anisotropa material utvecklats.

5. Om ideal elasticitet, på grundval av vilken den fullständiga försvinnandet av deformation efter avlägsnande av lasten antas. Som är känt, i verkliga kroppar under vilken belastning som helst, uppstår kvarvarande deformation. Därför antagandet

6. På det linjära förhållandet mellan komponentstammarna och stressar.

7. På deformationernas litenhet, på grundval av vilken det antas att de relativa linjära och vinkelformade deformationerna är små jämfört med enhet. För material som gummi, eller element som spiralfjädrar, har teorin om stora elastiska deformationer utvecklats.

När de löser problem med elasticitetsteorin använder de teoremet om lösningens unika: om de givna yttre yt- och volymkrafterna är i jämvikt, motsvarar de ett enda system av spänningar och förskjutningar. Positionen för lösningens unikhet är giltig om bara antagandet om kroppens naturliga tillstånd är giltigt (annars är ett oändligt antal lösningar möjliga) och antagandet om ett linjärt samband mellan deformationer och yttre krafter.

När man löser problem i elasticitetsteorin används ofta Saint-Venant-principen: om yttre krafter som appliceras på en liten sektion av en elastisk kropp ersätts av ett statiskt ekvivalent system av krafter som verkar på samma sektion (som har samma huvudvektor och samma huvudmoment), då kommer denna ersättning endast att orsaka en förändring i lokala deformationer .

På punkter som är tillräckligt långt borta från de platser där externa belastningar appliceras beror spänningarna lite på metoden för deras applicering. Belastningen, som under materialresistansens lopp schematiskt uttrycktes utifrån Saint-Venant-principen i form av en kraft eller ett koncentrerat moment, är i själva verket normal och skjuvspänningar fördelade på ett eller annat sätt på en viss del av kroppsytan. I detta fall kan olika spänningsfördelningar motsvara samma kraft eller kraftpar. Baserat på Saint-Venant-principen kan det anses att en förändring av krafter på en del av kroppsytan nästan inte har någon effekt på spänningar vid punkter belägna på tillräckligt stort avstånd från platsen för applicering av dessa krafter (jämfört med linjära dimensioner för det belastade området).

Placeringen av området som studeras, valt i kroppen (fig. 1), bestäms av riktningen cosinus för det normala N till området i det valda systemet av rektangulära koordinataxlar x, y och z.

Om P är resultanten av de inre krafter som verkar på den elementära arean som valts vid punkt A, så definieras den totala spänningen p N vid denna punkt längs arean med normalen N som gränsen för förhållandet i

följande formulär:

Vektorn pN kan sönderdelas i rymden i tre inbördes vinkelräta komponenter.

2. In i komponenterna σ N , τ N s och τ N t i riktningarna för normalen till platsen (normalspänning) och två inbördes vinkelräta axlar s och t (Fig. 1b) som ligger i platsens plan (tangentiellt påfrestningar). Enligt fig. 1, b

Om sektionen av kroppen eller området är parallell med ett av koordinatplanen, till exempel y0z (fig. 2), så kommer den tredje koordinataxeln x att vara vinkelrät mot detta område och spänningskomponenterna kommer att ha beteckningarna σ x , τ xy och τ xz .

Normal stress är positivt om det är drag och negativt om det är tryckande. Tecknet på skjuvspänning bestäms med hjälp av följande regel: om en positiv (drag) normal spänning längs platsen ger en positiv projektion, då tangentiell

spänningen över samma område anses vara positiv, förutsatt att den också ger en positiv projektion på motsvarande axel; om dragnormalspänningen ger en negativ projektion, så måste den positiva skjuvspänningen också ge en negativ projektion på motsvarande axel.

På fig. 3, till exempel, är alla spänningskomponenter som verkar på ytorna av den elementära parallellepipeden, som sammanfaller med koordinatplanen, positiva.

För att bestämma spänningstillståndet vid en punkt av en elastisk kropp är det nödvändigt att känna till de totala spänningarna p N för tre ömsesidigt vinkelräta områden som passerar genom denna punkt. Eftersom varje total spänning kan delas upp i tre komponenter, kommer spänningstillståndet att bestämmas om nio spänningskomponenter är kända. Dessa komponenter kan skrivas som en matris

kallas matrisen av spänningstensorkomponenter vid en punkt.

Varje horisontell linje i matrisen innehåller tre spänningskomponenter som verkar på samma område, eftersom de första ikonerna (namnet på normalen) är desamma för dem. Varje vertikal kolumn i tensorn innehåller tre spänningar parallella med samma axel, eftersom de andra tecknen (namnet på axeln parallell med vilken spänningen verkar) är desamma.

1.2 Jämviktsekvationer för en elementär parallellepiped

och elementär tetraeder

Låt oss peka ut en elementär parallellepiped med ribbstorlekarna dx, dy och dz vid punkten A som studeras (med koordinaterna x, y och z) av den spända elastiska kroppen med tre inbördes vinkelräta par av plan (fig. 2). På var och en av de tre ömsesidigt vinkelräta ytorna intill punkt A (närmast koordinatplanen) kommer tre spänningskomponenter att verka - normala och två tangentiella. Vi antar att de är positiva längs sidorna intill punkt A.

När man förflyttar sig från en yta som passerar genom punkt A till en parallell yta ändras spänningarna och tar emot steg. Till exempel, om spänningskomponenterna σ x \u003d f 1 (x, y, z), τ xy \u003d f 2 (x, y, z,), τ xz \u003d f 3 (x, y, z,) , sedan längs den parallella ytan, på grund av ökningen av endast en x-koordinat under övergången från en yta till en annan,

spänningskomponenter Det är möjligt att bestämma spänningar på alla ytor av en elementär parallellepiped, som visas i fig. 3.

Förutom påfrestningar som appliceras på ytorna på en elementär parallellepiped, verkar kroppskrafter på den: viktkrafter, tröghetskrafter. Låt oss beteckna projektionerna av dessa krafter, per volymenhet, på koordinataxlarna med X, Y och Z. Om vi är lika med noll summan av projektionerna på x-axeln för alla normala, tangentiella och volymetriska krafter,

agerar på en elementär parallellepiped, efter reduktion med produkten dxdydz får vi ekvationen

Efter att ha sammanställt liknande ekvationer för projektionerna av krafter på y- och z-axlarna, skriver vi tre differentialekvationer för jämvikten för en elementär parallellepiped erhållen av Cauchy,

När parallellepipedens dimensioner reduceras till noll förvandlas den till en punkt, och σ och τ är spänningskomponenterna längs tre ömsesidigt vinkelräta områden som passerar genom punkt A.

Om vi är lika med noll summan av momenten av alla krafter som verkar på en elementär parallellepiped, i förhållande till xc-axeln, parallell med x-axeln och passerar genom dess tyngdpunkt, får vi ekvationen

eller, med hänsyn till det faktum att de andra och fjärde termerna i ekvationen är av högre storleksordning jämfört med resten, efter reduktion med dxdydz

τ yz - τ zy = 0 eller τ yz = τ zy.

Genom att sammanställa liknande momentekvationer kring de centrala axlarna yc och zc, får vi tre ekvationer för lagen om parning av skjuvspänningar

τ xy = τ yx, τ yx = τ xy , τ zx = τ xz . (1.3)

Denna lag är formulerad enligt följande: tangentiella spänningar som verkar på ömsesidigt vinkelräta områden och riktade vinkelrätt mot skärningslinjen för områdena är lika stora och identiska i tecken.

Av de nio spänningskomponenterna i matrisen för tensorn T σ är alltså sex parvis lika med varandra, och för att bestämma spänningstillståndet vid en punkt är det tillräckligt att endast hitta följande sex spänningskomponenter:

Men de etablerade jämviktsförhållandena gav oss bara tre ekvationer (1.2), av vilka sex okända inte kan hittas. Sålunda är det direkta problemet med att bestämma spänningstillståndet vid en punkt, i det allmänna fallet, statiskt obestämt. För att avslöja denna statiska obestämbarhet behövs ytterligare geometriska och fysiska beroenden.

Låt oss skära den elementära parallellepipeden vid punkt A med ett plan som lutar mot dess ytor; låt det normala N till detta plan ha riktning cosinus l, m och n. Den resulterande geometriska figuren (fig. 4) är en pyramid med en triangulär bas - en elementär tetraeder. Vi kommer att anta att punkt A sammanfaller med koordinaternas ursprung, och tre ömsesidigt vinkelräta ytor av tetraedern sammanfaller med koordinatplanen.

Spänningskomponenterna som verkar på dessa ytor av tetraedern kommer att beaktas

positiv. De visas i fig. 4. Beteckna med , och projektionerna av den totala spänningen p N som verkar på den lutande ytan av BCD-tetraedern på x-, y- och z-axlarna. Arean av den lutande ytan BCD betecknas med dF. Då kommer området för ansikte ABC att vara dFp, ansikte ACD - dFl och ansikte ADB - dFt.

Låt oss komponera jämviktsekvationen för en tetraeder genom att projicera alla krafter som verkar på dess ytor på x-axeln; projektionen av kroppskraften ingår inte i projektionsekvationen, så

hur är värdet av den högre ordningen av litenhet i jämförelse med projektionerna av ytkrafter:

Genom att sammanställa projektionsekvationerna för krafterna som verkar på tetraedern på y- och z-axlarna får vi ytterligare två liknande ekvationer. Som ett resultat kommer vi att ha tre jämviktsekvationer för den elementära tetraedern

Låt oss dela en rumslig kropp med godtycklig form med ett system av inbördes vinkelräta plan хОу, yОz och хОz (fig. 5) i ett antal elementära parallellepipeder. På kroppens yta, elementär

tetraedrar, (krökta delar av ytan, på grund av sin litenhet, kan ersättas av plan). I detta fall kommer p N att representera belastningen på ytan, och ekvationerna (1.4) kommer att relatera denna belastning till spänningarna σ och τ i kroppen, dvs de kommer att representera randvillkoren för problemet med elasticitetsteorin. De villkor som definieras av dessa ekvationer kallas ytförhållanden.

Det bör noteras att i teorin om elasticitet representeras yttre belastningar av normala och tangentiella spänningar som appliceras enligt någon lag på områden som sammanfaller med kroppens yta.

1.3 Normal- och skjuvspänningar längs en sluttning

webbplats

Betrakta en elementär tetraeder ABCD, vars tre ytor är parallella med koordinatplanen, och den normala N till den fjärde sidan bildar vinklar med koordinataxlarna, vars cosinus är lika med l, m och n (fig. 6). . Låt oss anta att komponenterna för normal- och skjuvspänningar som verkar på områdena som ligger i koordinatplanen är givna, och vi kommer att bestämma spänningarna på BCD-området. Vi väljer ett nytt system med rektangulära koordinataxlar x 1, y 1 och z 1, så att x 1-axeln sammanfaller med den normala N,

Huvuduppgiften för elasticitetsteorin är bestämning av stress-töjningstillståndet enligt de givna förhållandena för belastning och fixering av kroppen.

Spännings-töjningstillståndet bestäms om komponenterna i spänningstensorn () och förskjutningsvektorn, nio funktioner, hittas.

Grundläggande ekvationer av elasticitetsteorin

För att hitta dessa nio funktioner måste man skriva ner de grundläggande ekvationerna i elasticitetsteorin, eller:

Differential Cauchies

var är komponenterna i tensorn i den linjära delen av Cauchy-deformationerna;

Komponenter av tensorn av derivatan av förskjutning längs radien.

Differentiella jämviktsekvationer

var finns spänningstensorkomponenterna; är projektionen av kroppskraften på j-axeln.

Hookes lag för en linjärt elastisk isotrop kropp

var är de Lama konstanterna; för en isotrop kropp. Här är normal- och skjuvspänningar; töjnings- och skjuvningsvinklar, respektive.

Ovanstående ekvationer måste uppfylla Saint-Venant-beroendena

I elasticitetsteorin är problemet löst om alla grundläggande ekvationer är uppfyllda.

Typer av problem i elasticitetsteorin

Randvillkor på kroppens yta måste vara uppfyllda och beroende på typ av randvillkor finns det tre typer av problem inom elasticitetsteorin.

Första typen. Krafter ges på kroppens yta. Gränsförhållanden

Andra typen. Problem där förskjutning är specificerad på kroppsytan. Gränsförhållanden

Tredje typen. Blandade problem av elasticitetsteorin. Krafter ges på en del av kroppsytan, förskjutning ges på en del av kroppsytan. Gränsförhållanden

Direkta och omvända problem i elasticitetsteorin

Elasticitetsteoriska ekvationer i förskjutningar (Lama ekvationer)

För att bestämma ekvationerna för teorin om elasticitet i förskjutningar skriver vi: differentialjämviktsekvationer (18) Hookes lag för en linjärt elastisk isotropisk kropp (19)

Om vi tar hänsyn till att deformationer uttrycks i termer av förskjutningar (17), skriver vi:

Det bör också erinras om att skjuvvinkeln är relaterad till förskjutningar av följande förhållande (17):

Genom att ersätta uttryck (22) i den första ekvationen av likheter (19), får vi att normalspänningarna

Observera att notationen u i detta fall inte innebär summering över i.

Genom att ersätta uttryck (23) i den andra ekvationen av likheter (19), får vi att skjuvspänningar

Låt oss skriva jämviktsekvationerna (18) i expanderad form för j = 1

Genom att ersätta uttryck i ekvation (26) för normala (24) och tangentiella (25) spänningar får vi

där l är Lame-konstanten, som bestäms av uttrycket:

Vi ersätter uttryck (28) med ekvation (27) och skriver,

där bestäms av uttryck (22), eller i expanderad form

Vi delar uttryck (29) med G och lägger till liknande termer och får den första Lame-ekvationen:

var är Laplace-operatorn (övertonsoperator), som definieras som

På samma sätt kan du få:

Ekvationerna (30) och (32) kan skrivas på följande sätt:

Ekvationerna (33) eller (30) och (32) är Lame-ekvationerna. Om kroppskrafterna är noll eller konstanta, då

dessutom innebär notationen i detta fall inte summering över i. Här

eller, med hänsyn till (31)

Att ersätta (22) i (34) och utföra transformationer får vi

och följaktligen

var finns en funktion som uppfyller denna jämlikhet. Om

därför är f en harmonisk funktion. Detta innebär att den volymetriska deformationen också är en harmonisk funktion.

Med tanke på att det tidigare antagandet är korrekt, tar vi den harmoniska operatorn från den i:te raden i Lame-ekvationen

Om kroppskrafterna är noll eller konstanta är förskjutningskomponenterna biharmoniska funktioner.

Det finns olika former av representation av biharmoniska funktioner i termer av harmoniska (som uppfyller Lames ekvationer).

där k = 1,2,3. Och