Serier med komplexa tal. Serier med komplexa termer. Power komplex serie
1. Komplexa tal. Komplexa tal formens anropade nummer x+iy, Var X Och y - riktiga nummer, i-imaginär enhet, definieras av jämlikhet i 2 = -1. Riktiga nummer X Och på kallas respektive giltig Och imaginära delar komplext tal z. För dem introduceras notationen: x=Rez; y=imz.
Geometriskt, varje komplext tal z=x+iy representeras av en prick M (x; y) koordinatplan xOy(Fig. 26). I det här fallet planet hej kallas det komplexa talplanet, eller planet för den komplexa variabeln z.
Polära koordinater r Och φ poäng M, som är bilden av ett komplext tal z, kallas modul Och argument komplext tal z; beteckningen introduceras för dem: r=|z|, φ=Argz.
Eftersom varje punkt i planet motsvarar ett oändligt antal värden för den polära vinkeln, som skiljer sig från varandra med 2kπ (k är ett positivt eller negativt heltal), är Arg en z-oändligt värderad funktion av z.
Det av värdena för den polära vinkeln φ , som uppfyller ojämlikheten –π< φ ≤ π kallas huvudvikt argument z och beteckna arg z.
I det följande benämningen φ spara endast för huvudvärdet av argumentet z , de där. låt oss sätta φ =argz, varvid för alla andra värden i argumentet z vi får jämställdheten
Arg z = arg z + 2kπ =φ + 2kπ.
Relationerna mellan modulen och argumentet för det komplexa talet z och dess reella och imaginära delar fastställs av formlerna
x = r cos φ; y = r sin φ.
Argument z kan också bestämmas med formeln
arg z = arctg (y/x) + C,
Var MED= 0 vid x > 0, MED= +π för x<0, på> 0; C \u003d - π at x < 0, på< 0.
Byter ut x Och på i komplex talnotation z = x+iy deras uttryck genom r Och φ , får vi den sk trigonometrisk form av ett komplext tal:
Komplexa tal z 1 \u003d x 1 + iy 1 Och z 2 \u003d x 2 + iy 2 anses vara likvärdig om och bara om deras verkliga och imaginära delar är lika separata:
zl = z2, Om x 1 = x 2, y 1 = y 2 .
För tal angivna i trigonometrisk form sker likhet om modulerna för dessa tal är lika, och argumenten skiljer sig åt med en heltalsmultipel av 2π:
z 1 = z 2, Om |z 1 | = |z 2 | Och Arg z 1 = Arg z 2 +2kπ.
Två komplexa tal z = x+iy och z = x -iy med lika reella och motsatta imaginära delar kallas konjugerad. För konjugerade komplexa tal, relationerna
|z 1 | = |z 2 |; arg z 1 = -arg z 2,
(den sista jämlikheten kan ges formen Arg z 1 + Arg z 2 = 2kπ).
Operationer på komplexa tal definieras av följande regler.

Tillägg. Om z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, Den där
Tillägget av komplexa tal följer de kommutativa och associativa lagarna:
![]()
Subtraktion. Om , Den där
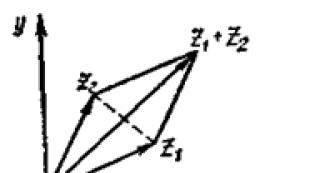
För en geometrisk förklaring av addition och subtraktion av komplexa tal är det användbart att representera dem inte som punkter på planet z, och vektorer: talet z = x + iy representeras av vektor har början vid punkten O ("noll"-punkten på planet - koordinaternas ursprung) och slutet vid punkten M(x; y). Därefter utförs addition och subtraktion av komplexa tal enligt regeln om addition och subtraktion av vektorer (fig. 27).
En sådan geometrisk tolkning av operationerna för addition och subtraktion av vektorer gör det enkelt att upprätta satser om modulen för summan och skillnaden av två och summan av flera komplexa tal, uttryckta av olikheterna:
| |z 1 |-|z 2 | | ≤ |z 1 ±z 2 | ≤ |z 1 | + |z 2 | ,
Dessutom är det bra att komma ihåg det modul för skillnaden mellan två komplexa tal z1 Och z2 är lika med avståndet mellan punkterna som är deras bilder på z-planet:| |zi-z2 |=d(zi,z2).
Multiplikation. Om z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2. Den där
z 1 z 2 \u003d (x 1 x 2 -y 1 y 2) + i (x 1 y 2 + x 2 y 1).
Således multipliceras komplexa tal som binomialer, med i 2 ersatt med -1.
Om då
Således, produktens modul är lika med produkten av modulerna i somnoektels, och produktens argument-summan av faktorernas argument. Multiplikationen av komplexa tal följer de kommutativa, associativa och distributiva (med avseende på addition) lagarna:
Division. För att hitta kvoten av två komplexa tal givna i algebraisk form, bör utdelningen och divisorn multipliceras med talet konjugerat till divisorn:

" Om ges i trigonometrisk form, alltså
Således, modulen för kvoten är lika med kvoten för modulen för utdelning och divisor, A argument privat är lika med skillnaden mellan argumenten för utdelningen och divisorn.
Exponentiering. Om z= , sedan genom Newtons binomialformel vi har
(Pär ett positivt heltal); i det resulterande uttrycket är det nödvändigt att ersätta graderna i deras betydelser:
i 2 \u003d -1; i3 = i; i4=1; jag 5 =1,...
och i allmänhet,
i 4k = 1; i 4k+1 =i; i 4k+2 = -1; i 4k+3 = -i .
Om då
(Här P kan vara antingen ett positivt heltal eller ett negativt heltal).
Särskilt,
(De Moivres formel).
Rotutvinning. Om Pär ett positivt heltal, sedan den n:te roten av det komplexa talet z har n olika värden, som hittas av formeln

där k=0, 1, 2, ..., n-1.
437.
Hitta (z 1 z 2)/z 3 if z1 = 3 + 5i, z2 = 2 + 3i, z3 = 1+2i.
∆
438.
siffra z= 2 + 5i.
∆ Hitta modulen för det komplexa talet: . Hitta huvudvärdet för argumentet: . Därför, ▲
439.
Representera komplexet i trigonometrisk form
siffra ![]()
∆ Hitta ![]() , ; , , dvs.
, ; , , dvs.
440.
Representera i trigonometrisk form komplex
nummer 1, i, -1, -i.
441.
Representera siffror ,
,
i trigonometrisk form och hitta sedan det komplexa talet
z 1/(z 2 z 3).
∆ Hitta
Därav,
442. Hitta alla värden.
∆ Vi skriver det komplexa talet i trigonometrisk form. Vi har , , . Därav,

Därav, , ,
443. Lös en binär ekvation ω 5 + 32i = 0.
∆ Låt oss skriva om ekvationen i formen ω 5 + 32i = 0. siffra -32i representerar i trigonometrisk form:
Om k = 0 då en).
k=1,(B).
k=2,(C).
k=3,(D).
k=4,(E).
Rötterna till tvåtermsekvationen motsvarar hörnen på en regelbunden femhörning inskriven i en cirkel med radie R=2 centrerad vid ursprunget (fig. 28).
I allmänhet rötterna till en tvåtermsekvation ω n \u003d a, Var A-komplext tal, motsvarar det regelbundna hörnet n-gon inskriven i en cirkel med centrum i origo och radie lika med ▲

444. Med hjälp av De Moivres formel, uttryck cos5φ Och sin5 φ genom cosφ Och sinφ.
∆ Vi transformerar den vänstra sidan av likheten enligt Newtons binomialformel:
Det återstår att likställa de verkliga och imaginära delarna av jämlikheten:
445. Givet ett komplext tal z=2-2i. Hitta Rez, Imz, |z|, argz.
446. z = -12 + 5i.
447 . Beräkna uttrycket med hjälp av Moivre-formeln (cos 2° + isin 2°) 45 .
448. Beräkna med hjälp av De Moivres formel.
449. Uttryck ett komplext tal i trigonometrisk form
z = 1 + cos 20° + är i 20°.
450. Utvärdera uttryck (2 + 3i) 3 .
451.
Utvärdera uttryck 
452. Utvärdera uttryck
453. Uttryck ett komplext tal i trigonometrisk form 5-3i.
454. Uttryck ett komplext tal i trigonometrisk form -1 + i.
455.
Utvärdera uttryck 
456.
Utvärdera uttryck  har tidigare presenterat faktorerna i täljaren och nämnaren i trigonometrisk form.
har tidigare presenterat faktorerna i täljaren och nämnaren i trigonometrisk form.
457. Hitta alla värden
458.
Lös en binär ekvation ![]()
459. uttrycka cos4φ Och sin4φ genom cosφ Och sinφ.
460. Visa att avståndet mellan punkter z1 Och z2 lika med | z2-z1|.
∆ Vi har z 1 \u003d x 1 + iy 1, z 2 \u003d x 2 + iy 2, z 2 -z 1 \u003d (x 2 -x 1) + i (y 2 -y 1), var
de där. | z2-z1| är lika med avståndet mellan de givna punkterna. ▲
461. Vilken linje beskrivs av punkten z, som uppfyller ekvationen där Med-konstant komplext tal, och R>0?
462.
Vad är den geometriska betydelsen av ojämlikheterna: 1) | z-c|
463. Vad är den geometriska betydelsen av ojämlikheterna: 1) Rez > 0; 2) im z< 0 ?
2. Serier med komplexa termer. Tänk på sekvensen av komplexa tal z 1, z 2 , z 3 , ..., var z p \u003d x p + iy p (n \u003d 1, 2, 3, ...). konstant antal c = a + bi kallad begränsa sekvenser z 1, z 2 , z 3 , ..., om för något godtyckligt litet antal δ>0 det finns ett nummer N, vad är meningen Z P med siffror n > N tillfredsställa ojämlikheten \z n-Med\< δ . Skriv i det här fallet .
Ett nödvändigt och tillräckligt villkor för att det ska finnas en gräns för en sekvens av komplexa tal är följande: talet c=a+biär gränsen för sekvensen av komplexa tal x 1 + iy 1, x 2 + iy 2, x 3 + iy 3, ... om och endast om , .
![]() (1)
(1)
vars medlemmar är komplexa tal kallas konvergerande, Om nth delsumma av serien S n för n → ∞ tenderar till en viss slutgräns. Annars kallas serie (1). avvikande.
Serie (1) konvergerar om och endast om serier med reella termer konvergerar
(2) Undersök konvergensen av serien. Denna serie, vars termer bildar en oändligt minskande geometrisk progression, konvergerar; därför konvergerar den givna serien med komplexa termer absolut. ^

474. Hitta konvergensområdet för en serie
19.4.1. Numeriska serier med komplexa termer. Alla grundläggande definitioner av konvergens, egenskaper hos konvergenta serier, konvergenskriterier för komplexa serier skiljer sig inte på något sätt från det verkliga fallet.
19.4.1.1. Grundläggande definitioner. Låt en oändlig följd av komplexa tal ges z 1 , z 2 , z 3 , …, z n , … .Den verkliga delen av numret z n vi kommer att beteckna a n , imaginär - b n
(de där. z n = a n + i b n , n = 1, 2, 3, …).
Nummerserie- skriv post.
Partiellbelopprad: S 1 = z 1 , S 2 = z 1 + z 2 , S 3 = z 1 + z 2 + z 3 , S 4 = z 1 + z 2 + z 3 + z 4 , …,
S n = z 1 + z 2 + z 3 + … + z n , …
Definition. Om det finns en gräns S
sekvenser av delsummor av serien för  , som är ett riktigt komplext tal, då sägs serien konvergera; siffra S
kallas summan av serien och skriv S
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... eller
, som är ett riktigt komplext tal, då sägs serien konvergera; siffra S
kallas summan av serien och skriv S
= z
1
+ z
2
+ z
3
+ … +
z
n
+ ... eller  .
.
Hitta de verkliga och imaginära delarna av delsummorna:
S n = z 1 + z 2 + z 3 + … + z n = (a 1 + i b 1) + (a 2 + i b 2) + (a 3 + i b 3) + … + (a n + i b n ) = (a 1 + a 2 + a 3 +…+ a n ) +
Där symboler  Och
Och  de reella och imaginära delarna av delsumman anges. En numerisk sekvens konvergerar om och endast om sekvenserna som består av dess reella och imaginära delar konvergerar. Således konvergerar en serie med komplexa termer om och endast om den serie som bildas av dess reella och imaginära delar konvergerar. En av metoderna för att studera konvergensen av serier med komplexa termer är baserad på detta påstående.
de reella och imaginära delarna av delsumman anges. En numerisk sekvens konvergerar om och endast om sekvenserna som består av dess reella och imaginära delar konvergerar. Således konvergerar en serie med komplexa termer om och endast om den serie som bildas av dess reella och imaginära delar konvergerar. En av metoderna för att studera konvergensen av serier med komplexa termer är baserad på detta påstående.
Exempel. Undersök efter konvergensserier  .
.
Låt oss skriva ut flera värden för uttrycket  : ytterligare värden upprepas med jämna mellanrum. Ett antal verkliga delar: ; serie imaginära delar ; båda serierna konvergerar (villkorligt), så den ursprungliga serien konvergerar.
: ytterligare värden upprepas med jämna mellanrum. Ett antal verkliga delar: ; serie imaginära delar ; båda serierna konvergerar (villkorligt), så den ursprungliga serien konvergerar.
19.4.1.2. Absolut konvergens.
Definition. Rad  kallad absolut konvergent om serien konvergerar
kallad absolut konvergent om serien konvergerar  , sammansatt av medlemmarnas absoluta värden.
, sammansatt av medlemmarnas absoluta värden.
Precis som för numeriska reella serier med godtyckliga termer är det lätt att bevisa att om serien konvergerar  , då konvergerar serien nödvändigtvis
, då konvergerar serien nödvändigtvis  (
( , så serien som bildas av de verkliga och imaginära delarna av serien
, så serien som bildas av de verkliga och imaginära delarna av serien  , konvergerar absolut). Om raden
, konvergerar absolut). Om raden  konvergerar, och serien
konvergerar, och serien  divergerar, då serien
divergerar, då serien  kallas villkorligt konvergent.
kallas villkorligt konvergent.
Rad  är en serie med icke-negativa termer, därför kan alla kända tecken (från jämförelsesatser till Cauchy-integralkriteriet) användas för att studera dess konvergens.
är en serie med icke-negativa termer, därför kan alla kända tecken (från jämförelsesatser till Cauchy-integralkriteriet) användas för att studera dess konvergens.
Exempel. Undersök efter konvergensserier  .
.
Låt oss göra en serie moduler ():  . Denna serie konvergerar (Cauchy-testet
. Denna serie konvergerar (Cauchy-testet  ), så den ursprungliga serien konvergerar absolut.
), så den ursprungliga serien konvergerar absolut.
19.4. 1 . 3 . Egenskaper för konvergerande serier. För konvergerande serier med komplexa termer är alla egenskaper för serier med reella termer sanna:
Ett nödvändigt kriterium för konvergens av en serie.
Den gemensamma termen för den konvergenta serien tenderar att vara noll som
 .
.
Om serien konvergerar  , då konvergerar någon av dess återstod. Omvänt, om någon återstod av serien konvergerar, då konvergerar serien själv.
, då konvergerar någon av dess återstod. Omvänt, om någon återstod av serien konvergerar, då konvergerar serien själv.
Om serien konvergerar, då summan av dess återstod eftern
-th term tenderar till noll vid
 .
.
Om alla termer i en konvergent serie multipliceras med samma talMed , då bevaras seriens konvergens, och summan multipliceras medMed .
Konvergenta rader (A
) Och (I
) kan läggas till och subtraheras term för term; den resulterande serien kommer också att konvergera, och dess summa är lika med
 .
.
Om termerna i den konvergerande serien grupperas godtyckligt och en ny serie består av summorna av termerna i varje par av parenteser, kommer denna nya serie också att konvergera, och dess summa kommer att vara lika med summan av den ursprungliga serien .
Om en serie konvergerar absolut, då för varje permutation av dess termer, bevaras konvergensen och summan ändras inte.
Om raderna (A
) Och (I
) konvergerar absolut till sina summor
 Och
Och
 , då konvergerar deras produkt för en godtycklig ordning av termer också absolut, och dess summa är lika med
, då konvergerar deras produkt för en godtycklig ordning av termer också absolut, och dess summa är lika med
 .
.
Visa symbol W 1 + W 2 +…+ W n +…= (1), Var W n = u n + i· v n (n = 1, 2, …) komplexa tal (sekvenser av komplexa tal) kallas nära komplexa tal.
Tal W n (n = 1, 2, …) kallad medlemmar av ett nummer, medlem W n kallad vanlig medlem i serien.
Skriv siffror S n = W 1 + W 2 +…+ W n (2) (n = 1, 2, …) , kallas delsummor av serien (1).
Ändlig eller oändlig gräns S sekvenser S n kallad summan av denna serie.
Om gräns Sär ändlig, då kallas serien konvergerande, om gränsen är oändlig, eller inte existerar alls, då serien avvikande.
Om S summan av serien (1), skriv sedan  .
.
Låta  , A
, A  . Självklart σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. Hur vet vi jämlikhet
. Självklart σ
n =
u 1
+
u 2
+…+
u n ,
τ
n =
v 1
+
v 2
+…+
v n. Hur vet vi jämlikhet
 (S naturligtvis) motsvarar två likheter
(S naturligtvis) motsvarar två likheter
 Och
Och
 . Därför är konvergensen av serie (1) ekvivalent med konvergensen av två reella serier:
. Därför är konvergensen av serie (1) ekvivalent med konvergensen av två reella serier:  Och
Och  . Därför sträcker sig de grundläggande egenskaperna hos konvergenta numeriska serier till konvergenta komplexa serier.
. Därför sträcker sig de grundläggande egenskaperna hos konvergenta numeriska serier till konvergenta komplexa serier.
Till exempel, för komplexa serier, är Cauchy-kriteriet giltigt: serie (1) konvergerar om och endast om för någon 
 , det för allan
>
Noch vilka som helstsid= 1, 2, … ojämlikheten.
, det för allan
>
Noch vilka som helstsid= 1, 2, … ojämlikheten.
Detta kriterium innebär direkt det nödvändiga kriteriet för seriens konvergens: för att serie (1) ska konvergera är det nödvändigt och tillräckligt att dess gemensamma termW n → 0 .
Följande egenskaper för konvergerande serier är giltiga: om raderna
 Och
Och
 konvergera till sina summorSOchd, sedan raderna
konvergera till sina summorSOchd, sedan raderna
 Och
Och
 konvergera till beloppenS
±
doch XS
.
konvergera till beloppenS
±
doch XS
.
Absolut konvergent serie av komplexa tal.
Serie av komplexa tal  (1) ringde absolut konvergent om serien konvergerar
(1) ringde absolut konvergent om serien konvergerar  (2).
(2).
Sats.
Varje absolut konvergent serie (1) av komplexa tal konvergerar.
Bevis.
Uppenbarligen är det tillräckligt för oss att fastställa att för serien (1) är villkoren för Cauchy-kriteriet för seriens konvergens uppfyllda. Ta någon  . På grund av den absoluta konvergensen av serie (1) konvergerar serie (2). Därför för de utvalda
. På grund av den absoluta konvergensen av serie (1) konvergerar serie (2). Därför för de utvalda 
 , det för någon n
>
N Och p=1,2,... ojämlikheten kommer att tillfredsställas
, det för någon n
>
N Och p=1,2,... ojämlikheten kommer att tillfredsställas  , Men
, Men 
 och ännu mer ojämlikheten
och ännu mer ojämlikheten  för alla n
>
N Och sid=1,2,…
Därför, för serien (1), är villkoren för Cauchy-kriteriet för konvergensen av den komplexa serien uppfyllda. Därför konvergerar serie (1). Teoremet är korrekt.
för alla n
>
N Och sid=1,2,…
Därför, för serien (1), är villkoren för Cauchy-kriteriet för konvergensen av den komplexa serien uppfyllda. Därför konvergerar serie (1). Teoremet är korrekt.
Sats.
För en serie av komplexa tal
 (1) är absolut konvergent, det är nödvändigt och tillräckligt att den verkliga serien konvergerar absolut
(1) är absolut konvergent, det är nödvändigt och tillräckligt att den verkliga serien konvergerar absolut
 (3) och
(3) och
 (4), varW n
=
u n +
i·
v n
(n
= 1, 2,…).
(4), varW n
=
u n +
i·
v n
(n
= 1, 2,…).
Bevis,
förlitar sig på följande uppenbara ojämlikheter
 (5)
(5)
Nödvändighet. Låt serien (1) konvergera absolut, låt oss visa att serien (3) och (4) absolut konvergerar, d.v.s. serien konvergerar  Och
Och  (6). Av den absoluta konvergensen av serie (1) följer att serie (2)
(6). Av den absoluta konvergensen av serie (1) följer att serie (2)  konvergerar, på grund av den vänstra sidan av olikhet (5), kommer serie (6) att konvergera, dvs serie (3) och (4) konvergerar absolut.
konvergerar, på grund av den vänstra sidan av olikhet (5), kommer serie (6) att konvergera, dvs serie (3) och (4) konvergerar absolut.
Lämplighet. Låt serierna (3) och (4) konvergera absolut, låt oss visa att serie (1) också konvergerar absolut, d.v.s. att serie (2) konvergerar. Det följer av den absoluta konvergensen av serie (3) och (4) att serie (6) konvergerar, så serien konvergerar också  . På grund av den högra sidan av olikhet (5) konvergerar därför serie (2), dvs. serie (1) konvergerar absolut.
. På grund av den högra sidan av olikhet (5) konvergerar därför serie (2), dvs. serie (1) konvergerar absolut.
Så den absoluta konvergensen för den komplexa serien (1) är ekvivalent med den absoluta konvergensen för den reella talserien (3) och (4). Därför är absolut konvergerande komplexa serier föremål för alla de grundläggande egenskaperna hos verkliga absolut konvergenta numeriska serier. I synnerhet för en absolut konvergent komplex serie är satsen om permutationen av dess termer giltig, d.v.s. att byta termer i en absolut konvergent serie påverkar inte summan av serien. För att fastställa den absoluta konvergensen för en komplex serie kan vilket kriterium som helst för konvergensen av en positiv serie användas.
Cauchy tecken.
Låt serie (1) ha en gräns
 , sedan omq
< 1 , то ряд (1) абсолютно сходится, если
q>1, sedan divergerar serie (1)..
, sedan omq
< 1 , то ряд (1) абсолютно сходится, если
q>1, sedan divergerar serie (1)..
Tecken på d'Alembert.
Om det finns en gräns för serien (1) av komplexa tal
 , sedan klq
< 1 этот ряд абсолютно сходится, а если
q> 1, då divergerar serien.
, sedan klq
< 1 этот ряд абсолютно сходится, а если
q> 1, då divergerar serien.
Exempel.
Undersök efter absoluta konvergensserier  , Här
, Här  .
.
Låt oss hitta
 . Självklart
. Självklart  =
=
 =
=
 . Därför är serien absolut konvergent.
. Därför är serien absolut konvergent.
Absolut konvergerande serier kan multipliceras. Produkten av en absolut konvergent och en konvergent serie konvergerar. Produkten av två konvergenter kan divergera.
Storlek: px
Starta intryck från sidan:
transkript
1 8 Komplexa talserier S av sekvensen (S) kallas summan av serien (46) Serien a k kallas -:e återstoden av serien (46) För en konvergent k-serie S S r och lm r, de ε > N, N: r< ε Для сходящегося ряда (46) необходимым и достаточным признаком его сходимости является критерий Коши: ряд (46) сходится тогда и только тогда, если ε >, N, N: a< ε p k k Необходимым условием сходимости ряда (46) является требование lm a Действительно, из сходимости ряда (46) следует, согласно критерию Коши, что ε >, N > att för p, följer att S S< ε Если сходится ряд ak k a (47) с действительными положительными членами, то очевидно, сходится и ряд (46), который в этом случае называется абсолютно сходящимся А для ряда (47) уже можно применить признаки Даламбера и Коши: ряд (47) сходится, если, начиная с a некоторого номера N соотношение l < a, N значит, сходится абсолютно ряд (46)), если a q <, N k ; и ряд (47) сходится (а,
2 9 Funktionsserier och deras egenskaper Uniform konvergens Weierstrass-sats Låt en oändlig följd av envärdiga funktioner ((Z)) definieras i en domän G i det komplexa planet Z ((Z)) Ett uttryck av formen U U (48) kommer att kallas en funktionell serie Serie (48) kallas konvergent i domänen G om Z G nummerserien som motsvarar den konvergerar Om serien (48) konvergerar i regionen G, så är det i denna region möjligt att definiera en enkel- värderad funktion, vars värde vid varje punkt i regionen G är lika med summan av motsvarande talserie (48) i regionen G Sedan G, > k () U k()< ε Заметим, что в общем случае N зависит и от ε и от Определение Если ε >, N(ε), N(ε): ε, N (ε,), N(ε,): domänen G k U k< ε G, то ряд (48) называется равномерно сходящимся в k k Если остаток ряда обозначить r U, то тогда условие равномерной сходимости ряда (48) можем записать в виде: r < ε, N(ε), G Достаточным признаком равномерной сходимости ряда (48) является признак Вейерштрасса: Если всюду в области G члены функционального ряда (48) могут быть мажорированы членами некоторого абсолютно сходящегося числового ряда a, те
3 a U, G, (49) då konvergerar serien (48) likformigt N Ja, eftersom serien a konvergerar, då >< ε, U U a < ε при N, что и доказывает равномерную k k k k k k сходимость ряда (48) в области G Приведем некоторые теоремы о равномерно сходящихся рядах Они доказываются совершенно также, как соответствующие теоремы вещественного анализа и поэтому приведем их без доказательства Теорема 5 Если функции U непрерывны в области G, а ряд U сходится в этой области равномерно к функции, то также непрерывна в G Теорема 6 Если ряд (48) непрерывных функций U сходится равномерно в области G к функции, то интеграл от этой функции по любой кусочногладкой кривой, целиком лежащей в области G, можно вычислить путем почленного интегрирования ряда (48), те Теорема 7 Если члены d U d U сходящегося в области G ряда U имеют непрерывные производные в этой области и ряд U равномерно сходится в G, то данный ряд U можно почленно дифференцировать в области G, причем U U, где U - сумма ряда
4 För funktionella serier i komplex analys finns Weierstrass-satsen, som gör att vi avsevärt kan stärka satsen om möjligheten till term-för-term-differentiering av en funktionell serie, känd från verklig analys. Innan vi konstaterar och bevisar det, noterar vi att serien U, som konvergerar likformigt längs linjen l, förblir likformigt efter att ha multiplicerat alla dess termer med funktionen ϕ begränsad till l. Låt faktiskt olikheten ϕ () vara uppfylld på linjen l< M Тогда для остатков ρ и r рядов U и U ϕ справедливо соотношение ϕ U U r < M r ρ ϕ ε и, тк N, >N:r< и одновременно с ним ρ < ε, то этим доказано M высказанное утверждение Если сумма данного ряда есть S, то сумма ряда, полученного после умножения на ϕ, очевидно будет ϕ S Теорема 8 (Вейерштрасса) Если члены ряда - аналитические в некоторой области G функции и этот ряд сходится в области G равномерно, то его сумма также является функцией аналитической в G, ряд можно почленно дифференцировать и полученный ряд F равномерно сходится к () F Выберем любую внутреннюю точку области G и построим круг столь малого радиуса с центром в этой точке, чтобы он целиком лежал внутри G (рис) В силу равномерной сходимости данного ряда в G, G ρ Рис он, в частности, равномерно сходится на окружности этого круга Пусть - любая точка на Умножим ряд () () () () () (5) на величину Полученный ряд
5 konvergerar också likformigt till sin summa () () () () (), eftersom funktion (5) är begränsad till, eftersom ρ för punkter i denna cirkel är cirkelns radie (kom ihåg: - här är en konstant) Då , enligt ovanstående, kan serie (5) integreras term för term: () d () d () d d π π π π På grund av funktionernas analyticitet kan Cauchy-formeln tillämpas på dem, på basis av av vilka vi erhåller () d π, (5) och summan av serien till höger i (5) är och därför erhåller vi likheten π () d vid punkten Tk - vilken punkt som helst i domänen G, då bevisas den första delen av satsen, vi får att serien konvergerar enhetligt och dess summa är lika med (k) (k)
6 serier av formen där potensserie Abels sats Ett mycket viktigt fall av allmänna funktionella serier är potensserier (), (53) - några komplexa tal, och - en fixpunkt i det komplexa planet serien, de allmänna satserna från föregående sektioner kan tillämpas. Som det fastställdes i dem är många egenskaper en konsekvens av enhetlig konvergens. För att bestämma konvergensområdet för potensserien (53) visar sig följande sats vara väsentlig. Sats 9 (Abel) Om potensserien (53) konvergerar någon gång, sedan konvergerar den absolut och vid vilken punkt som helst som uppfyller villkoret, dessutom i cirkeln< ρ, радиусом ρ, меньшим < сходится равномерно, ряд Δ Выберем произвольную точку, удовлетворяющую условию < Обозначим q сходимости ряда следовательно M >, att M, q< В силу необходимого признака его члены стремятся к нулю при, отсюда () M M q M, Тогда, где q < (54) Ряд справа в (54) бесконечно убывающая геометрическая прогрессия со знаменателем q < Тогда из (54) следует сходимость и рассматриваемого ряда
7 sid< достаточно в силу признака Вейерштрасса (53) В круге построить сходящийся числовой ряд, можорирующий данный ряд в рассматриваемой области Очевидно, таковым является ряд ρ M, также представляющий собой сумму бесконечной геометрической прогрессии со знаменателем, меньшим единицы Из теоремы Абеля можно вывести ряд следствий, в известной мере аналогичным следствиям из теоремы Абеля в теории степенных рядов вещественного анализа Если степенной ряд (53) расходится в некоторой точке, то он расходится и во всех точках, удовлетворяющих неравенству >Den exakta övre gränsen för avstånden från punkten till punkten där serien (53) konvergerar kallas konvergensradien för potensserien och regionen<, называется кругом сходимости степенного ряда В точках границы ряд может как сходиться так и расходиться Пример Найти область сходимости ряда Δ Находим радиус сходимости по признаку Даламбера lm () и наш ряд сходится в круге < При <, те, исследуется особо В этом случае и, значит, областью абсолютной сходимости является
8p< В круге любого радиуса ρ, меньшего чем радиус сходимости, степенной ряд (53) сходится равномерно 3 Внутри круга сходимости степенной ряд сходится к аналитической функции В самом деле, члены ряда u есть функции, аналитические на всей плоскости Z, ряд сходится в любой замкнутой подобласти круга сходимости Тогда по теореме Вейерштрасса сумма ряда есть аналитическая функция 4 Степенной ряд внутри круга сходимости можно почленно интегрировать и дифференцировать любое число раз, причем радиус сходимости полученных рядов равен радиусу сходимости исходного ряда 5 Коэффициенты степенного ряда (53) находятся по формулам! () () (55) Доказательство этого факта приводится методами, аналогичными методам вещественного анализа Ряд Тейлора Теорема Тейлора Нули аналитических функций Итак степенной ряд внутри круга сходимости определяет некоторую аналитическую функцию Возникает вопрос: можно ли функции, аналитической внутри некоторого круга, сопоставить степенной ряд, сходящийся в этом круге к данной функции? < Теорема 9 (Тейлора) Функция, аналитическая внутри круга, может быть представлена в этом круге сходящимся степенным рядом, причем этот ряд определен однозначно
9 Låt oss välja en godtycklig punkt inuti cirkeln ρ ρ< и построим окружность ρ точке радиусом < с центром в ρ (рис), содержащую точку внутри Такое построение возможно для любой точки внутри этого круга Так как < ρ, а внутри круга < Рис аналитична, то по формуле Коши имеем π ρ () d (56) Преобразуем подынтегральное выражение: (57) <, то < Так как Поэтому второй сомножитель справа в (57) можно представить как сумму степенного ряда (прогрессии), ту которая первый член есть, а знаменатель прогрессии есть Так как, те () () (58) ρ, то ряд (58) сходится равномерно по, так как он мажорируется сходящимся числовым рядом Подставляя (58) в (56) и интегрируя почленно, получаем ρ (< ρ)
10 Låt oss introducera notationen () d () ρ π () d () π ρ () och skriva om (59) som en potensserie som konvergerar vid den valda punkten: (59) (6) () (6) I formeln (6), grannskapet ρ kan ersättas, i kraft av Cauchy-satsen, av vilken sluten kontur som helst som ligger i regionen< и содержащим точку внутри Так как - произвольная точка данной области, то отсюда следует, что ряд (6) сходится к круге ρ < этот ряд сходится равномерно Итак, функция всюду внутри круга < аналитическая внутри круга <, причем в разлагается в этом круге в сходящийся степенной ряд Коэффициенты разложения (6) на основании формулы Коши для производных аналитической функции имеет вид () d () π ρ () ()! (6) Для доказательства единственности разложения (6) допустим, что имеет еще место формула разложения (), (6)
11 där det också skulle finnas en koefficient<, поэтому на основании формулы (55) Ряд (6) сходящимся в круге () () (6) Тем самым единственность определения коэффициентов доказана Разложение функции, аналитической в круге! <, что совпадает с, в сходящийся степенной ряд (6), часто называется разложением Тейлора, а сам ряд (6) Рядом Тейлора Доказанная теорема устанавливает взаимнооднозначное соответствие между функцией, аналитической в окрестности некоторой точки и степенным рядом с центром в этой точке, это означает эквивалентность конкретной аналитической функции, как функции бесконечное число раз дифференцируемой и функцией, представимой в виде суммы степенного ряда G и Заметим, наконец, что, если функция является аналитической в области G - внутренняя точка, то радиус сходимости ряда Тейлора () () () этой функции не меньше расстояния от точки до! границы области G (имеется в виду ближайшее расстояние) Пример Разложить в ряд Тейлора по степеням Δ Эта функция является аналитической на всей комплексной плоскости за исключением точек, Поэтому в круге < функция может быть ± разложена в ряд Тейлора При условии < выражение рассматриваться как сумма бесконечно убывающей прогрессии может q, q < Поэтому
12 , < Пример 3 Найти разложение в ряд Тейлора в круге < Определение по формуле (6) здесь довольно затруднительно Поэтому, представим π Так как < и <, то, используя геометрическую, получаем q q, Используя показательную форму чисел и находим окончательно 4 s π (63) Тк расстояние от центра разложения до ближайших особых точек (те до границы аналитичности) есть, то радиус сходимости ряда (63) есть Рис X Y
13 4 4 3 Exempel<, 4 3 < Ближайшей к центру разложения особой точкой является точка, до которой расстояние равно, поэтому В заключение приведем основные разложения: e (<)!! 3! cos! 4 3 4! ; (<)! ; s () m 3 3! 5 5! m m m!! (<) ()! ; m(m)(m)! ; l 3 3 () 4 (<) Если для аналитической функции (), то точка называется нулем аналитической функции В этом случае разложение функции в ряд Тейлора в окрестности точки имеет вид () () тк () Если в разложении функции окрестности точки и, следовательно, разложение имеет вид, в ряд Тейлора в,
14 då kallas punkten () (), (64) för funktionens nollpunkt Om, då kallas nollan ett primtal eller multiplicitet Från formlerna för koefficienterna för Taylor-serien ser vi att om punkten är en nolla i ordningen, då där () () kan skrivas om i formen, men () () () [ () ] () ϕ, ϕ () (), () ϕ och konvergenscirkeln för denna serie är uppenbarligen densamma som seriens (64) omvända påstående där vilken funktion som helst i formen är ett heltal, ϕ () och ordningen noll är nollor, och (±) Exempel 6 Hitta nollordningen för funktionen 8 s Utöka nämnaren i potenser: 3 3! 8 5 5! ! 5! 3! 5 5! ϕ
15 5 ϕ, där ϕ, och ϕ och en punkt för funktionen 3!, så att punkten 5! ϕ är analytisk i är nollan av den 5:e ordningen för den ursprungliga Laurent-serien och dess konvergensregion Nedbrytning av en analytisk funktion i en Laurent-serie Betrakta en serie av formen () där är en fixpunkt i det komplexa planet, (65) är några komplexa tal. Låt oss fastställa dess konvergensarea För att göra detta representerar vi (65) i formen centrerad vid en punkt med någon radie, och i synnerhet kan den vara lika med noll eller oändlighet Inuti cirkeln av konvergens, denna serie konvergerar till någon analytisk funktion av en komplex variabel, de (),< (67)
16 För att bestämma konvergensområdet för en serie variabler, inställning () () Sedan kommer denna serie att ta formen, låt oss göra en ersättning - en vanlig potensserie som konvergerar inuti sin konvergenscirkel till någon analytisk funktion ϕ () med en komplex variabel Låt konvergensradien för den resulterande potensserien vara r Då ϕ,< r Возвращаясь к старой переменной и полагая ϕ () () (68), >r Det följer att området för konvergens av serien, området utanför cirkeln r, vi får (69) () är<, то существует общая область сходимости этих рядов круговое кольцо r < <, в которой ряд (65) сходится к аналитической функции (), r < < (7) Так как ряды (67) и (68) являются обычными степенными рядами, то в указанной области функция обладает всеми свойствами суммы степенного ряда Это означает, что ряд Лорана сходится внутри своего кольца сходимости к некоторой функции, аналитической в данном кольце
17 Om r >, så har inte serierna (67) och (68) ett gemensamt konvergensområde, så i detta fall konvergerar serien (65) inte någonstans till någon funktion. Observera att serien är en vanlig del av serie (7), och exempel 7 Expandera - huvuddelen av raden (65) () a)< < ; б) >; V)< < называется правильной частью или в ряд Лорана в кольцах: Во всех кольцах функция регулярна (аналитична) и поэтому может быть представлена рядом Лорана (доказательство этого факта в следующем пункте) Перепишем функцию в виде а) Так как <, то второе слагаемое есть сумма убывающей геометрической прогрессии Поэтому () Здесь главная часть состоит из одного слагаемого < б) в этом случае, поэтому () 3
18 Denna expansion saknar en vanlig del< в) Для случая < функцию также надо привести к сходящейся геометрической прогрессии, но со знаменателем Это даст: 3 Заметим, что в главной части этого разложения присутствует одно слагаемое Возникает вопрос: можно ли функции аналитической в некотором круговом кольце, сопоставить ряд Лорана, сходящийся к этой функции в данном кольце? На этот вопрос отвечает Теорема Функция, аналитическая в круговом кольце < <, однозначно представляется в этом кольце сходящимся рядом Лорана дробь На Рис 3 Δ Зафиксируем произвольную точку внутри данного кольца и контурами окружности и с центром в, радиусы которых удовлетворяют условиям < < < < < (рис 3) Согласно формуле Коши для многосвязной области имеем π () d () выполняется неравенство q, можно представить в виде d (7) Поэтому
19 Vi utför term-för-term integration i (7), vilket är möjligt på grund av den enhetliga konvergensen av serien i, vi får d π, (7) där d π, (73) (7) vi kommer att ha π π d d, (för d), (74) där d π (75) Genom att ändra integrationsriktningen i (75) får vi
20 π () () d ()() d π, > (76) På grund av analysen av integranderna i (73) och (76) i den cirkulära ringen< < в соответствии с теоремой Коши значения интегралов не изменятся при произвольной деформации контуров интегрирования в области аналитичности Это позволяет объединить формулы (73) и (76): π () d (), ±, ±, (77) где - произвольный замкнутый контур, лежащий в указанном кольце и содержащий точку внутри Возвратимся теперь к формуле (7), получим где коэффициенты () (), (78) () для всех определяются однообразной формулой (77) Так как - люба точка кольца < <, то отсюда следует, что ряд (78) сходится к внутри данного кольца причем в замкнутом кольце < < ряд сходится к равномерно Доказательство единственности разложения (78) опускаем Из полученных результатов следует, что областью сходимости ряда (78) Лорана является круговое кольцо < <, на границах которого имеется хотя бы по одной особой точке аналитической функции ряд (78), к которой сходится Замечание Формула (77) для определения коэффициентов разложения в ряд Лорана (78) не всегда практически удобна Поэтому часто прибегают к разложению рациональной дроби на простейшие с использованием геометрической прогрессии, а также используют разложение в ряд Тейлора элементарные функции Приведем примеры
21 Exempel 8 Expandera Laurent-serien (de i potenser) Y i närheten av punkten ()() i Δ I det här fallet kommer vi att konstruera två cirkulära ringar centrerade i punkten (Fig. 4): a) en cirkel " utan centrum”< < ; Рис 4 X б) внешность круга >Den är analytisk i var och en av dessa ringar och har singulära punkter på gränserna. Låt oss utöka funktionen i potenser i var och en av dessa regioner)< < ; ; [ () () () ] () < Этот ряд сходится, так как Так что ()() () () () (), ; >) Här har vi 3, () () () () () är en konvergent serie, eftersom<
22 s Som ett resultat av ()() () () de, 3, 3 Exempel 9 Expandera funktionen Δ i en Laurent-serie i närheten av punkten Vi har:, s s s cos cos s s! cos 4 () () 3 4! 3! () 5! () (scos)!! 5
Ämne Komplex talserie Betrakta en talserie k ak med komplexa tal av formen En serie kallas konvergent om sekvensen S av dess delsummor S a k k konvergerar. Dessutom gränsen S för sekvensen
Ämne Funktionskomplex serie Definition. Om k, N, N U k G är uppfyllda på en gång, konvergenta i domänen G., så kallas serien likformigt Ett tillräckligt kriterium för seriens enhetliga konvergens är kriteriet
FÖRELÄSNING N37. Serie av analytiska funktioner. Nedbrytning av en analytisk funktion i en potensserie. Taylor-serien. Laurent-serien..Utökning av en analytisk funktion i en potensserie.....Taylor-serien.... 3.Utbyggnad av en analytisk
Modul Ämne Funktionssekvenser och serier Egenskaper för enhetlig konvergens av sekvenser och serier Effektserier Föreläsning Definitioner av funktionssekvenser och serier Enhetligt
Föreläsning 7 Taylor och Laurent serie 7. Taylor serie I denna del kommer vi att se att begreppen en potensserie och en analytisk funktion definierar samma objekt: vilken potensserie som helst med en positiv konvergensradie
Matematisk analys Avsnitt: Funktionsteori för en komplex variabel Ämne: Serier i det komplexa planet Föreläsare Yanushchik O.V. 217 9. Serier i det komplexa planet 1. Numeriska serier Låt sekvensen
5 Potensserier 5 Potensserier: definition, konvergensdomän Funktionsserier av formen (a + a) + a () + K + a () + K a) (, (5) tal kallas potensserier Tal
Federal Agency for Education Moscow State University of Geodesy and Cartography (MIIGAiK) METODOLOGISKA INSTRUKTIONER OCH UPPGIFTER FÖR SJÄLVSTÄNANDE ARBETE på kursen HÖGRE MATEMATIK
Funktionsserie Föreläsningar 7-8 1 Konvergensområde 1 En serie av formen u () u () u () u (), 1 2 u () där funktionerna definieras på ett visst intervall, kallas en funktionell serie. Uppsättningen av alla punkter
FÖRELÄSNING N38. En analytisk funktions beteende i oändligheten. speciella punkter. Funktionsrester.. grannskap av en punkt i oändligheten.....Laurent-expansion i en grannskap av en punkt i oändligheten... 3. Beteende
RYSKA FEDERATIONENS UTBILDNINGSMINISTERIE National Research Nizhny Novgorod State University uppkallad efter NI Lobachevsky NP Semerikova AA Dubkov AA Kharcheva SERIE ANALYTISKA FUNKTIONER
Utbildningsministeriet i Republiken Vitryssland Vitebsk State Technological University Ämne. "Rows" Institutionen för teoretisk och tillämpad matematik. utvecklad av Assoc. E.B. Dunina. Main
V.V. Zhuk, A.M. Kamachkin 1 Power-serien. Konvergensradie och konvergensintervall. Konvergensens natur. Integration och differentiering. 1.1 Konvergensradie och konvergensintervall. Funktionellt omfång
Ämne Laurent-serien och dess konvergensdomän. Betrakta en serie av formen n C n n C n n n n C n n där är en fixpunkt i det komplexa planet, är några komplexa tal. C n Denna serie kallas Laurent-serien.
FÖRELÄSNING N 7 .Kraft
Matematisk analys Avsnitt: Numeriska och funktionella serier Ämne: Potensserier. Utvidgning av en funktion i en kraftserie Lektor Rozhkova S.V. 3 g. 34. Power serie
4 serier av analytiska funktioner 4. Funktionella sekvenser Låt Ω C och f n: Ω C. En sekvens av funktioner (f n ) konvergerar punktvis till en funktion f: Ω C om för varje z Ω lim n f n(z) = f(z).
Funktionsserie Funktionsserie dess summa och area av funktionell o Låt en sekvens av funktioner k (k 1) ges i området Δ av reella eller komplexa tal
Föreläsningar förberedda av docent Musina MV Definition Uttryck av formen Numerisk och funktionell serie Numeriska serier: grundläggande begrepp (), där det kallas en talserie (eller bara en serie) Tal, medlemmar i en serie (beror på
Numerisk serie Numerisk sekvens Opr En numerisk sekvens är en numerisk funktion definierad på mängden naturliga tal x - en vanlig medlem av sekvensen x =, x =, x =, x =,
Ch Potensserie a a a En serie av formen a a a a a () kallas en potensserie, där, a, är konstanter, kallade koefficienter för serien. Ibland betraktas en potensserie av en mer allmän form: a a (a) a ( a) a (a) (), där
Föreläsning 8 Serie och singular poäng. Laurent-serien. Isolerade singulära punkter. 6. Serie- och singularpunkter 6.7. Laurent Series Theorem (P. Laurent): Om funktionen f() är analytisk i ringen r< a < R r R то она может быть разложена
Federal Agency for Education Federal State Educational Institution of Higher Professional Education SOUTHERN FEDERAL UNIVERSITY R. M. Gavrilova, G. S. Kostetskaya Methodical
Ämne 9 Potensserie En potensserie är en funktionell serie av formen, medan talen ... är seriens koefficienter, och seriens expansionspunkt., ..., ... R ... kallas centrum Power series Den allmänna termen för potensserien
4 Funktionsserie 4 Grundläggande definitioner Låt en oändlig sekvens av funktioner med en gemensam domän X u), u (), K, u (),K (DEFINITION Uttryck u) + u () + K + u () +
Föreläsning 3 Taylor- och Maclaurin-serier Tillämpning av effektserier Utvidgning av funktioner till effektserier Taylor- och Maclaurin-serier För applikationer är det viktigt att kunna expandera en given funktion till en potensserie, dessa funktioner
Föreläsning 6 Expansion av en funktion i en potensserie Unikhet med expansionen Taylor och Maclaurin-serien Expansion i en potensserie av några elementära funktioner Tillämpning av potensserier I tidigare föreläsningar
Metallurgiska fakulteten Institutionen för högre matematik
Laurent-serien En mer allmän typ av potensserier är serier som innehåller både positiva och negativa potenser av z z 0. Liksom Taylor-serier spelar de en viktig roll i teorin om analytiska funktioner.
Serier Numerisk serie Allmänna begrepp Def Om varje naturligt tal tilldelas ett visst nummer enligt en viss lag, så kallas uppsättningen av numrerade tal en numerisk sekvens,
S A Lavrenchenko wwwlwrecekoru Föreläsning Funktionsserier Begreppet funktionsserier Tidigare studerade vi talserier, det vill säga seriens medlemmar var tal. Nu övergår vi till studiet av funktionella serier, d.v.s.
Ämne Laurent-serien och dess konvergensdomän. En serie av formen där C (z z) n = C (z z) n + n n n= n= z i planet, är en fixpunkt i det komplexa C n kallas Laurent-serien. C n (z z) n= - något komplex
Föreläsning. funktionella rader. Funktionsseriedefinition En serie vars medlemmar är funktioner av x kallas en funktionell serie: u = u (x) + u + K+ u + K = Ge x ett visst värde på x, vi
SERIETEORI Serieteorin är den viktigaste komponenten i matematisk analys och finner både teoretiska och många praktiska tillämpningar. Skilja mellan numeriska och funktionella serier.
Konvergensradie Definition. En potensserie är en funktionell serie av formen c 0 + c (t a) + c 2 (t a) 2 + + c (t a) + = c (t a), () där c 0, c, c 2,.. ., c, ... C kallas kraftens koefficienter
MOSCOW STATE TECHNICAL UNIVERSITY OF CIVIL AVIATION V.M. Lyubimov, E.A. Zhukova, V.A. Ukhova, Yu.A. Shurinov
82 4. Avsnitt 4. Funktions- och effektserier 4.2. Lektion 3 4.2. Lektion 3 4.2.. Taylorexpansion av en funktion DEFINITION 4.2.. Låt funktionen y = f(x) vara oändligt differentierbar i något område
Föreläsning. Power-serien. Övertonsanalys; serie och Fouriertransform. Ortogonalitet egenskap.8. Allmän funktionsserie.8.. Undvikande av funktioner En serie U + U + U kallas en funktionell serie om dess
Starkov V.N. Material till den inledande föreläsningen Fråga 9. Nedbrytning av analytiska funktioner i potensserier Definition. En funktionell serie av formen ((... (..., där de komplexa konstanterna (koefficienter för serien
Sgups Institutionen för högre matematik Riktlinjer för implementering av en typisk beräkning "Rows" Novosibirsk 006 Lite teoretisk information Numerisk serie Let u ; u ; u ; ; u ; det finns ett oändligt antal
E yrke. Taylor rader. Summering av effektserier Mat. analys, app. Matematik, termin 3 Hitta expansionen av en funktion till en potensserie i potenser, beräkna potensseriens konvergensradie: A f()
Kapitelserie Den formella notationen av summan av medlemmarna i en viss numerisk sekvens Numeriska serier kallas en numeriska serier Summor S kallas partiella summor av en serie Om det finns en gräns lim S, S då serien
Övning 8 Rest 8 Definiera en rest 8 Beräkna rest 8 Logaritmisk rest 8 Definiera en rest Låt en isolerad singularpunkt för en funktion i en isolerad singular Restanalytisk
~ ~ FCF Derivat av en funktion av en komplex variabel FCF av Cauchy-Riemann-villkoret Begreppet regelbundenhet för FCF Avbildning och form av ett komplext tal Form av FCF: där den reella funktionen av två variabler är reell
METODOLOGISKA INSTRUKTIONER FÖR BERÄKNINGSUPPGIFTER PÅ KURS I HÖGRE MATEMATIK "ORDINÄRA DIFFERENTIALEKVATIONSSERIEN DUBBLA INTEGRALER" DEL III TEMASERIE Innehåll Serie Numerisk serie Konvergens och divergens
Federal Agency for Education Arkhangelsk State Technical University Faculty of Civil Engineering SERIEN Riktlinjer för att slutföra uppdrag för självständigt arbete Arkhangelsk
ELEMENT I FUNKTIONSTEORIN FÖR EN KOMPLEX VARIABEL OPERATIONELL Kalkylering
Matematisk analys Del 3. Numeriska och funktionella serier. Flera integraler. Fältteori. lärobok N.D.Vysk MATI-RGTU im. K.E. Tsiolkovsky Institutionen för högre matematik MATEMATISK ANALYS
Föreläsning 3. Avdrag. Huvudrestsatsen Restdelen av funktionen f () i en isolerad singularpunkt a är ett komplext tal lika med värdet av integralen f () 2 taget i positiv riktning i längs cirkeln
Lektion för numeriska och kraftserier. Nummerrader. Radsumma. Konvergenskriterier Beräkna summan av serien. 6 Beslut. Summan av termerna för en oändlig geometrisk progression q är, där q är nämnaren för progressionen.
S A Lavrenchenko wwwlawreceoru Föreläsning som representerar funktioner av Taylor-serien En användbar gräns Vid den senaste föreläsningen utvecklades följande strategi: av ett tillräckligt villkor för representabilitet av en funktion,
MV Deikalova KOMPLEX ANALYS Frågor till tentamen (grupp МХ-21, 215) Frågor från det första kollokviet 1 1. Differentieringsbarhet av en funktion av en komplex variabel vid en punkt. Villkor för Cauchy Riemann (D'Alembert Euler).
Alternativ Uppgift Beräkna värdet på funktionen och ge svaret i algebraisk form: a sh ; b l Lösning a Låt oss använda relationsformeln mellan trigonometrisk sinus och hyperbolisk sinus: ; sh -s Få
Föreläsning Numerisk serie Tecken på konvergens Talserie Tecken på konvergens Ett oändligt uttryck för en numerisk sekvens + + + +, sammansatt av medlemmar av en oändlig, kallas en numerisk serie
4. Funktionell serie, konvergensarea Konvergensområdet för en funktionell serie () är uppsättningen av värden för argumentet som denna serie konvergerar för. Funktion (2) kallas partialsumman av serien;
Föreläsning 3 Existens- och unikhetssats för lösning av en skalär ekvation Problemformulering Huvudresultat Betrakta Cauchy-problemet d f () d =, () =
UTBILDNINGSMINISTERIET OCH VETENSKAP I RYSSISKA FEDERATIONEN KAZAN STATE UNIVERSITY OF ARCHITECTURE AND CONSTRUCTION Institutionen för högre matematik NUMERISKA OCH FUNKTIONELLA SERIER Riktlinjer för
(funktionell serie potens serie konvergensregion ordning för att hitta konvergensintervallet - exempel konvergensintervall radie exempel) Låt en oändlig sekvens av funktioner ges, Funktionell
S A Lavrenchenko wwwlawrecekoru Föreläsning Representation av funktioner efter potensserie Inledning Representation av funktioner med potensserier är användbar för att lösa följande problem: - integration av funktioner
E yrke. Power-serien. Taylor Series Mat. analys, app. Matematik, termin 3 Hitta konvergensradien för en potensserie med hjälp av d'Alembert-kriteriet: (89 () n n (n!)) p (n +)! n= Taylor-serien f(x)
RYSKA FEDERATIONENS UTBILDNINGSMINISTERIET OCH VETENSKAP
RADER. Nummerrader. Grundläggande definitioner Låt en oändlig talföljd ges Uttrycket (oändlig summa) a, a 2,..., a n,... a i = a + a 2 + + a n +... () i= kallas a nummerserie. Tal
KAZAN STATE UNIVERSITY Institutionen för matematisk statistik
Ryska federationens utbildnings- och vetenskapsministerium VA Volkov SERIES OF THE FOURIER INTEGRAL Elektronisk textutgåva för utbildning För studenter av specialiteter 4865 Elektronik och automatisering av fysiska installationer;
џ. Begreppet en nummerserie. Låt en talföljd a, a 2,..., a,... ges. En talserie är ett uttryck a = a + a 2 +... + a +... (.) Tal a, a 2,... ., a,... kallas termer i serien, a
Metodisk utveckling Lösa problem på TFKP Komplexa tal Operationer på komplexa tal Komplexa plan Ett komplext tal kan representeras i algebraisk och trigonometrisk exponential
Siberian Mathematical Journal Juli augusti 2005. Volym 46, 4 UDC 517.53 KONVERGENSVILLKOR FÖR INTERPOLATIONSBREK VID KNUT SEPARERADE FRÅN FUNKTION SINGULAR POINTS AG Lipchinsky Sammanfattning: Anses
MOSKVA AUTOMOBILE AND ROAD STATE TECHNICAL UNIVERSITY (MADI)
Standardmetoder, men nådde en återvändsgränd med ett annat exempel.
Vad är svårigheten och var kan det finnas en hake? Låt oss lägga det tvåliga repet åt sidan, analysera lugnt orsakerna och bekanta oss med de praktiska lösningarna.
Först och viktigast: i de allra flesta fall, för att studera konvergensen av en serie, är det nödvändigt att tillämpa någon bekant metod, men den vanliga termen för serien är fylld med så knepigt fyllning att det inte alls är uppenbart vad man ska göra med det . Och du går runt i cirklar: det första tecknet fungerar inte, det andra fungerar inte, den tredje, fjärde, femte metoden fungerar inte, sedan kastas utkasten åt sidan och allt börjar om på nytt. Detta beror vanligtvis på bristande erfarenhet eller luckor i andra delar av kalkylen. I synnerhet om du springer sekvensgränser och ytligt demonterad funktionsbegränsningar, då blir det svårt.
Med andra ord, en person ser helt enkelt inte den nödvändiga lösningen på grund av brist på kunskap eller erfarenhet.
Ibland är "eclipse" också skyldig, när till exempel det nödvändiga kriteriet för seriens konvergens helt enkelt inte är uppfyllt, men på grund av okunskap, ouppmärksamhet eller försumlighet faller detta utom synhåll. Och det blir som i den där cykeln där professorn i matematik löste ett barnproblem med hjälp av vilda återkommande sekvenser och nummerserier =)
I de bästa traditionerna, omedelbart levande exempel: rader ![]() och deras släktingar - divergerar, eftersom det i teorin är bevisat sekvensgränser. Troligtvis kommer du under den första terminen att bli slagen ur själen för ett bevis på 1-2-3 sidor, men nu räcker det för att visa att det nödvändiga villkoret för seriens konvergens inte är uppfyllt, hänvisar till till kända fakta. Känd? Om studenten inte vet att roten till den n:e graden är en extremt kraftfull sak, säg serien
och deras släktingar - divergerar, eftersom det i teorin är bevisat sekvensgränser. Troligtvis kommer du under den första terminen att bli slagen ur själen för ett bevis på 1-2-3 sidor, men nu räcker det för att visa att det nödvändiga villkoret för seriens konvergens inte är uppfyllt, hänvisar till till kända fakta. Känd? Om studenten inte vet att roten till den n:e graden är en extremt kraftfull sak, säg serien ![]() sätta honom i hjulspår. Även om lösningen är som två och två: , d.v.s. av uppenbara skäl skiljer sig båda serierna åt. En blygsam kommentar "dessa gränser har bevisats i teorin" (eller till och med frånvaron överhuvudtaget) är tillräckligt för offset, trots allt är beräkningarna ganska tunga och de hör definitivt inte till avsnittet av numeriska serier.
sätta honom i hjulspår. Även om lösningen är som två och två: , d.v.s. av uppenbara skäl skiljer sig båda serierna åt. En blygsam kommentar "dessa gränser har bevisats i teorin" (eller till och med frånvaron överhuvudtaget) är tillräckligt för offset, trots allt är beräkningarna ganska tunga och de hör definitivt inte till avsnittet av numeriska serier.
Och efter att ha studerat nästa exempel kommer du bara att bli förvånad över kortheten och insynen i många lösningar:
Exempel 1
Undersök konvergensen av en serie
Lösning: först och främst, kontrollera utförandet nödvändigt kriterium för konvergens. Detta är ingen formalitet, utan en stor chans att ta itu med exemplet "liten blodsutgjutelse".
"Inspektion av scenen" antyder en divergerande serie (fallet med en generaliserad övertonsserie), men återigen uppstår frågan, hur man tar hänsyn till logaritmen i täljaren?
Ungefärliga exempel på uppgifter i slutet av lektionen.
Det är inte ovanligt när du måste föra ett tvåvägs (eller till och med trevägs) resonemang:
Exempel 6
Undersök konvergensen av en serie ![]()
Lösning: först, noggrant ta itu med täljarens floskel. Sekvensen är begränsad: . Sedan: ![]()
Låt oss jämföra vår serie med serien . På grund av den dubbla ojämlikheten som just erhållits kommer det för alla "sv" att vara sant: ![]()
Låt oss nu jämföra serien med den divergerande övertonsserien.
Bråknämnare mindre bråkets nämnare, alltså själva fraktionen – Mer bråk (skriv ner de första termerna, om de inte är tydliga). Således, för alla "en": ![]()
Så, som jämförelse, serien ![]() avviker tillsammans med den harmoniska serien.
avviker tillsammans med den harmoniska serien.
Om vi ändrar nämnaren lite: ![]() , då kommer den första delen av resonemanget att vara liknande:
, då kommer den första delen av resonemanget att vara liknande: ![]() . Men för att bevisa seriens divergens är endast gränstestet för jämförelse redan tillämpligt, eftersom ojämlikheten är falsk.
. Men för att bevisa seriens divergens är endast gränstestet för jämförelse redan tillämpligt, eftersom ojämlikheten är falsk.
Situationen med konvergerande serier är ”spegel”, det vill säga för en serie kan till exempel både jämförelsekriterier användas (olikheten är sann), och för en serie endast det begränsande kriteriet (olikheten är falsk).
Vi fortsätter vår safari genom det vilda, där en flock graciösa och saftiga antiloper skymtade vid horisonten:
Exempel 7
Undersök konvergensen av en serie
Lösning: det nödvändiga konvergenskriteriet är uppfyllt, och vi ställer återigen den klassiska frågan: vad ska man göra? Framför oss ligger något som liknar en konvergent serie, men det finns ingen tydlig regel här - sådana associationer är ofta vilseledande.
Ofta, men inte den här gången. Genom att använda Begränsa jämförelsekriteriet Låt oss jämföra vår serie med den konvergenta serien . Vid beräkning av gränsen använder vi underbar gräns ![]() , var som oändligt liten står:
, var som oändligt liten står: 
konvergerar tillsammans med bredvid .
Istället för att använda den vanliga artificiella tekniken multiplikation och division med en "tre", var det möjligt att initialt jämföra med en konvergent serie.
Men här är en varning önskvärd att konstantmultiplikatorn för den allmänna termen inte påverkar seriens konvergens. Och just i denna stil är lösningen i följande exempel utformad:
Exempel 8
Undersök konvergensen av en serie
Prov i slutet av lektionen.
Exempel 9
Undersök konvergensen av en serie
Lösning: i de tidigare exemplen använde vi sinusets boundedness, men nu är den här egenskapen ur spel. Nämnaren för en bråkdel av en högre tillväxtordningän täljaren, så när sinusargumentet och hela den gemensamma termen oändligt liten. Det nödvändiga villkoret för konvergens, som du förstår, är uppfyllt, vilket inte tillåter oss att smita från jobbet.
Vi kommer att genomföra spaning: i enlighet med anmärkningsvärd likvärdighet ![]() , kassera sinus mentalt och få en serie. Nåväl, något sånt....
, kassera sinus mentalt och få en serie. Nåväl, något sånt....
Ta ett beslut:
Låt oss jämföra serierna som studeras med de divergerande serierna. Vi använder gränsjämförelsekriteriet: 
Låt oss ersätta infinitesimalen med den ekvivalenta: för ![]() .
.

Ett annat ändligt tal än noll erhålls, vilket betyder att serien som studeras avviker tillsammans med den harmoniska serien.
Exempel 10
Undersök konvergensen av en serie
Detta är ett gör-det-själv-exempel.
För planering av ytterligare åtgärder i sådana exempel, hjälper den mentala avvisningen av sinus, arcsine, tangent, arctangens mycket. Men kom ihåg, denna möjlighet finns bara när oändligt liten argument, för inte så länge sedan stötte jag på en provocerande serie:
Exempel 11
Undersök konvergensen av en serie ![]() .
.
Lösning: det är värdelöst att använda bågtangensens begränsning här, och ekvivalensen fungerar inte heller. Utgången är förvånansvärt enkel: 
Studieserien avviker, eftersom det nödvändiga kriteriet för seriens konvergens inte är uppfyllt.
Det andra skälet"Gag on the job" består i en anständig sofistikering av den gemensamma medlemmen, vilket orsakar svårigheter av teknisk karaktär. Grovt sett, om serien som diskuteras ovan tillhör kategorin "figurer du gissar", så tillhör dessa kategorin "du bestämmer". Egentligen kallas detta komplexitet i "vanlig" mening. Alla kommer inte att korrekt lösa flera faktorer, grader, rötter och andra invånare på savannen. Naturligtvis orsakar factorial de flesta problemen:
Exempel 12
Undersök konvergensen av en serie
Hur höjer man en factorial till en makt? Lätt. Enligt regeln för operationer med befogenheter är det nödvändigt att höja varje faktor i produkten till en makt:
Och, naturligtvis, uppmärksamhet och återigen uppmärksamhet, d'Alembert-skylten fungerar traditionellt: 
Alltså serien som studeras konvergerar.
Jag påminner dig om en rationell teknik för att eliminera osäkerhet: när det är klart tillväxtordning täljare och nämnare - det är inte alls nödvändigt att lida och öppna parenteserna.
Exempel 13
Undersök konvergensen av en serie
Odjuret är mycket sällsynt, men det hittas, och det skulle vara orättvist att kringgå det med en kameralins.
Vad är dubbel utropsteckenfaktoriell? Faktorialen "lindar" produkten av positiva jämna tal: 
På samma sätt "vindar" faktorn upp produkten av positiva udda tal: 
Analysera vad som är skillnaden mellan
Exempel 14
Undersök konvergensen av en serie
Och i den här uppgiften, försök att inte bli förvirrad med graderna, underbara motsvarigheter Och underbara gränser.
Exempel på lösningar och svar i slutet av lektionen.
Men eleven får mata inte bara tigrar - listiga leoparder spårar också upp sitt byte:
Exempel 15
Undersök konvergensen av en serie ![]()
Lösning: det nödvändiga konvergenskriteriet, det begränsande kriteriet, d'Alembert- och Cauchykriterierna försvinner nästan omedelbart. Men det värsta av allt är att funktionen med ojämlikheter, som upprepade gånger har räddat oss, är maktlös. Ja, jämförelse med en divergerande serie är omöjlig, eftersom ojämlikheten ![]() felaktigt - multiplikatorlogaritmen ökar bara nämnaren, vilket minskar själva bråket
felaktigt - multiplikatorlogaritmen ökar bara nämnaren, vilket minskar själva bråket ![]() i förhållande till fraktionen. Och en annan global fråga: varför är vi initialt säkra på att vår serie
i förhållande till fraktionen. Och en annan global fråga: varför är vi initialt säkra på att vår serie ![]() är bunden att divergera och måste jämföras med vissa divergerande serier? Passar han överhuvudtaget?
är bunden att divergera och måste jämföras med vissa divergerande serier? Passar han överhuvudtaget?
Integrerad funktion? Felaktig integral ![]() framkallar en sorgsen stämning. Nu, om vi hade en rad
framkallar en sorgsen stämning. Nu, om vi hade en rad ![]() … I så fall, ja. Sluta! Det är så idéer föds. Vi fattar ett beslut i två steg:
… I så fall, ja. Sluta! Det är så idéer föds. Vi fattar ett beslut i två steg:
1) Först studerar vi seriens konvergens ![]() . Vi använder integrerad funktion:
. Vi använder integrerad funktion:![]()
Integrand kontinuerlig på

Alltså en siffra ![]() divergerar tillsammans med motsvarande felaktiga integral.
divergerar tillsammans med motsvarande felaktiga integral.
2) Jämför vår serie med den divergerande serien ![]() . Vi använder gränsjämförelsekriteriet:
. Vi använder gränsjämförelsekriteriet:
Ett annat ändligt tal än noll erhålls, vilket betyder att serien som studeras avviker tillsammans med sida vid sida ![]() .
.
Och det finns inget ovanligt eller kreativt i ett sådant beslut – det är så det ska avgöras!
Jag föreslår att självständigt utarbeta följande tvåsteg:
Exempel 16
Undersök konvergensen av en serie ![]()
En student med viss erfarenhet ser i de flesta fall omedelbart om serien konvergerar eller divergerar, men det händer att ett rovdjur skickligt döljer sig i buskarna:
Exempel 17
Undersök konvergensen av en serie ![]()
Lösning: vid första anblicken är det inte alls klart hur den här serien beter sig. Och om vi har dimma framför oss, är det logiskt att börja med en grov kontroll av det nödvändiga villkoret för seriens konvergens. För att eliminera osäkerhet använder vi en osänkbar multiplikations- och divisionsmetod genom adjoint uttryck:
Det nödvändiga tecknet på konvergens fungerade inte, men förde vår Tambov-kamrat fram i ljuset. Som ett resultat av de utförda transformationerna erhölls en ekvivalent serie ![]() , som i sin tur liknar en konvergent serie .
, som i sin tur liknar en konvergent serie .
Vi skriver en ren lösning:
Jämför denna serie med den konvergenta serien. Vi använder gränsjämförelsekriteriet:
Multiplicera och dividera med det adjointe uttrycket:

Ett annat ändligt tal än noll erhålls, vilket betyder att serien som studeras konvergerar tillsammans med bredvid .
Kanske har några en fråga, var kom vargarna ifrån på vår afrikanska safari? Vet inte. De kom förmodligen med den. Du kommer att få följande troféskinn:
Exempel 18
Undersök konvergensen av en serie ![]()
Ett exempel på lösning i slutet av lektionen
Och, slutligen, ytterligare en tanke som besöker många studenter i förtvivlan: istället för om man ska använda ett mer sällsynt kriterium för seriens konvergens? Tecken på Raabe, tecken på Abel, tecken på Gauss, tecken på Dirichlet och andra okända djur. Idén fungerar, men i verkliga exempel implementeras den mycket sällan. Personligen har jag under alla år av praktik bara tillgripit 2-3 gånger tecken på Raabe när ingenting verkligen hjälpte från standardarsenalen. Jag återger hela mitt extrema uppdrag:
Exempel 19
Undersök konvergensen av en serie
Lösning: Utan tvekan ett tecken på d'Alembert. Under beräkningarna använder jag aktivt egenskaperna för grader, liksom andra underbara gränsen:
Här är en för dig. D'Alemberts tecken gav inget svar, även om ingenting förebådade ett sådant utfall.
Efter att ha gått igenom manualen hittade jag en föga känd gräns som bevisats i teorin och tillämpade ett starkare radikalt Cauchy-kriterium:
Här är två till dig. Och, viktigast av allt, det är inte alls klart om serien konvergerar eller divergerar (en extremt sällsynt situation för mig). Nödvändigt tecken på jämförelse? Utan mycket hopp - även om jag på ett otänkbart sätt räknar ut täljarens och nämnarens tillväxtordning, garanterar detta fortfarande ingen belöning.
En komplett d'Alembert, men det värsta är att serien måste lösas. Behöver. Det kommer trots allt vara första gången jag ger upp. Och så kom jag ihåg att det verkade finnas några starkare tecken. Före mig var inte längre en varg, inte en leopard och inte en tiger. Det var en enorm elefant som viftade med en stor snabel. Jag var tvungen att plocka upp en granatkastare:
Tecken på Raabe
Tänk på en positiv talserie.
Om det finns en gräns  , Den där:
, Den där:
a) På rad avviker. Dessutom kan det resulterande värdet vara noll eller negativt.
b) På rad konvergerar. I synnerhet konvergerar serien för .
c) När Raabes skylt ger inget svar.
Vi sammanställer gränsen och förenklar noggrant fraktionen: 
Ja, bilden är milt sagt obehaglig, men jag blev inte längre förvånad. lopitala regler, och den första tanken, som det visade sig senare, visade sig vara korrekt. Men först, i ungefär en timme, vred jag och vände gränsen med "vanliga" metoder, men osäkerheten ville inte elimineras. Och att gå i cirklar är, som erfarenheten antyder, ett typiskt tecken på att fel sätt att lösa har valts.
Jag var tvungen att vända mig till rysk folkvisdom: "Om inget hjälper, läs instruktionerna." Och när jag öppnade 2:a volymen av Fichtenholtz, fann jag till min stora glädje en studie av en identisk serie. Och sedan gick lösningen enligt modellen.