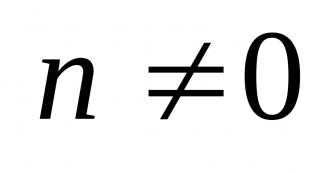Matanalysfunktion. Matematisk analys. Se vad "matematisk analys" är i andra ordböcker

Sammanställt av Yu.V.Obrubov

Kaluga - 2012

Introduktion till matematisk analys.

Riktiga nummer. Variabler och konstanter.

Ett av matematikens grundläggande begrepp är siffra. Positiva tal 1,2,3, ..., som erhålls genom att räkna, kallas naturlig. Siffrorna ... -3, -2, -1,0,1,2,3, ... kallas heltal. Tal som kan representeras som ett ändligt förhållande mellan två heltal (
) kallas rationell. Dessa inkluderar hela och bråktal, positiva och negativa tal. Tal som kan representeras som oändliga icke-repeterande bråk kallas irrationell. Exempel på irrationella tal är
,
. I uppsättningen irrationella tal skiljer de åt transcendentala tal. Dessa är tal som är resultatet av icke-algebraiska operationer. De mest kända av dessa är numret och icke-kamratnummer . Rationella och irrationella tal kallas giltig . Reella tal representeras av punkter på tallinjen. Varje punkt på talaxeln motsvarar ett enda reellt tal och, omvänt, till varje reellt tal motsvarar det en enda punkt på talaxeln. Således har en en-till-en-överensstämmelse etablerats mellan de reella talen och punkterna på tallinjen. Detta gör det möjligt att använda termerna "nummer a" och "punkt a" omväxlande.

I processen att studera olika fysiska, ekonomiska, sociala processer måste man ofta ta itu med kvantiteter som representerar de numeriska värdena för parametrarna för de fenomen som studeras. Samtidigt förändras vissa av dem, medan andra behåller sina värderingar.

variabel En storhet som antar olika numeriska värden kallas. En storhet vars numeriska värde inte ändras i ett givet problem eller experiment kallas konstant. Variabler betecknas vanligtvis med latinska bokstäver
och permanent
.

variabel anses given om uppsättningen värden som den kan ta är känd. Denna uppsättning kallas variabelns intervall.

Det finns olika typer av uppsättningar värden för en numerisk variabel.

intervall är uppsättningen av x-värden inneslutna mellan siffrorna a och b, medan siffrorna a och b inte hör till uppsättningen i fråga. Intervallet betecknas med: (a,b);a

segmentet kallas uppsättningen av x-värden inneslutna mellan siffrorna a och b, medan siffrorna a och b hör till uppsättningen i fråga. Segmentet betecknas med ,a≤x≤b.

Mängden av alla reella tal är ett öppet intervall. Betecknas: (- ∞,+ ∞), -∞<х <+∞, R.

Område till punkt x 0 ett godtyckligt intervall (а, b) som innehåller en punkt x 0 anropas, alla punkter i detta intervall uppfyller olikheten a

ε - grannskap av punkt a är ett intervall centrerat vid punkten a som uppfyller olikheten a–ε

Fungera. Grundläggande definitioner och begrepp.

Funktion är ett av de grundläggande begreppen inom matematisk analys. Låt X och Y vara godtyckliga mängder av reella tal.

Om varje nummer x X, enligt någon regel eller lag, tilldelas ett unikt väldefinierat reellt tal yY, då säger de att fungera med definitionsdomänen X och värdeuppsättningen Y. Ange y \u003d f (x). Variabeln x kallas argument funktioner.

Vid definitionen av en funktion är två punkter väsentliga: en angivelse av definitionsområdet och upprättandet av en korrespondenslag.

Definitionens omfattning eller existensområdet En funktion är en uppsättning argumentvärden för vilka funktionen finns, det vill säga den är vettig.

Byt område Funktionen kallas den uppsättning värden y som den tar för de tillåtna värdena på x.

Sätt att ställa in en funktion.

Analytiskt sätt att definiera en funktion.

Med denna metod för att ställa in funktionen skrivs korrespondenslagen som en formel (analytiskt uttryck) som anger med vilka matematiska transformationer, med hjälp av det kända värdet av argumentet x, du kan hitta motsvarande värde på y.

En funktion kan definieras av ett enda analytiskt uttryck över hela dess definitionsdomän eller representera en samling av flera analytiska uttryck.

Till exempel: y \u003d sin (x 2 + 1)

2. Tabellform för att ställa in en funktion

Som ett resultat av direkt observation eller experimentell studie av ett fenomen eller en process, skrivs värdena för argumentet x och motsvarande värden för y ut i en viss ordning.

Denna tabell definierar funktionen y för x.

Ett exempel på ett tabellformigt sätt att specificera en funktion kan vara tabeller över trigonometriska funktioner, tabeller över logaritmer, datum och växelkurser, temperatur och luftfuktighet, etc.

3. Grafiskt sätt att ställa in funktionen.

Det grafiska sättet att ställa in funktionen är att visa punkter (x, y) på koordinatplanet med hjälp av tekniska anordningar. Den grafiska metoden att specificera en funktion i matematisk analys används inte utan en grafisk illustration av analytiskt givna funktioner tillgrips alltid.

Sitter du i mörkret och läser mina artiklar? Spara din syn. Om du har ett favoritställe är det troligtvis en säng, så kan vägglampetter med leverans över hela Ukraina på sajten vara ett lämpligt alternativ. Läs i ljuset och ta hand om din syn.

Allt ska uttryckas så enkelt som möjligt, men inte enklare.
Albert Einstein

Vår resa börjar med en fiktiv karaktär som vi kommer att kalla John Doe. Han är en genomsnittlig arbetare som lätt kan hittas i vilken stad som helst i världen. Nästan varje dag vaknar John av höga larm och kör till jobbet i sin bil. Han tar hissen upp till sitt kontor, där han startar upp datorn och anger sitt användarnamn och lösenord. John gör alla dessa saker utan den minsta aning om hur de fungerar.

Han kanske skulle vara intresserad av att lära sig hur de apparater och apparater som han använder dagligen är ordnade och fungerar, men han har varken tid eller ork att göra detta. Han anser att bilar, hissar, datorer och väckarklockor är helt olika och komplexa mekanismer som inte har något gemensamt. Enligt John tar det år av studier att förstå hur var och en av dem fungerar.

Vissa människor ser saker lite annorlunda än vår John Doe. De vet att elmotorer i hissinstallationer är väldigt lika bilgeneratorer.

De vet att den programmerbara logiska styrenheten som styr elmotorn som är ansvarig för att flytta hissen är väldigt lik en John Doe arbetsdator. De vet att på en grundläggande nivå är PLC, väckarklocka och dator baserade på relativt enkel transistorteori. Vad John Doe och den genomsnittliga personen tycker är otroligt komplext är den vanligaste användningen av enkla mekaniska och elektriska principer av en hackare. Problemet är hur dessa principer tillämpas. Att abstrahera grundläggande principer från komplexa idéer gör att vi kan förstå och förenkla dem på ett sätt som gör rättvisa åt Albert Einsteins improviserade råd som citeras ovan.

Många av oss ser kalkyl som något komplext. (John Doe anser att principen för enheten och olika mekanismers funktion är densamma.) Du ser en hög av komplexa, intrikata saker. För att förstå dem behöver du mycket tid och ansträngning. Men vad händer om vi berättade att matematisk analys (kalkyl) inte är så komplicerad som det verkar vid första anblicken, liksom de flesta mekanismer? Att det finns några grundläggande principer som alla får förstå, och så fort du gör detta kommer du att få ett nytt perspektiv på världen och hur den fungerar?

En typisk calculus-lärobok innehåller cirka tusen sidor. En typisk John Doe kommer att se tusen svåra saker att förstå och studera, och en hacker kommer att se två grundläggande principer (derivata och integral) och 998 exempel på dessa principer. Tillsammans ska vi försöka ta reda på vilka dessa principer är. Baserat på arbetet utfört av Michael Starbird, professor vid University of Texas i Austin, kommer vi att använda vardagliga exempel som alla kan förstå. Matematisk analys avslöjar vår världs speciella skönhet - skönheten som uppstår när du kan observera den dynamiskt, inte statiskt. Vi hoppas att allt löser sig för dig.

Innan vi börjar vill jag kort gå igenom historien om kalkylens uppkomst, vars rötter ligger i en mycket noggrann analys av förändring och rörelse.

Zenons paradox

Zeno av Elea är en filosof som levde på 300-talet f.Kr. Han tog upp flera subtila men djupgående paradoxer, varav två så småningom ledde till födelsen av kalkyl. För att lösa Zenons paradoxer tog mänskligheten mer än två tusen år. Som du kan föreställa dig var det inte lätt. Svårigheterna var till stor del relaterade till idén om oändlighet. Vad är problemet med oändligheten ur en matematisk synvinkel? På 1600-talet lyckades Isaac Newton och Gottfried Leibniz lösa Zenons paradoxer och skapa matematisk analys. Låt oss ta en närmare titt på dessa paradoxer för att förstå varför det har varit så mycket hype runt dem.

Pil

Föreställ dig en pil som flyger genom luften. Vi kan med stor säkerhet säga att pilen är i rörelse. Tänk nu på pilen vid en viss tidpunkt. Hon rör sig inte längre utan är i vila. Men vi vet med säkerhet att pilen är i rörelse, hur kan den då vara i vila?! Detta är kärnan i denna paradox. Det kan tyckas dumt, men i verkligheten är det ett mycket komplext begrepp som bör övervägas ur en matematisk synvinkel.

Senare kommer vi att få reda på att vi har att göra med konceptet om en momentan förändringshastighet, som vi kommer att associera med idén om en av de två principerna för matematisk analys (kalkyl) - derivatan. Detta kommer att tillåta oss att beräkna pilens hastighet vid en viss tidpunkt - något som mänskligheten inte har kunnat göra på mer än två årtusenden.

Dikotomi

Låt oss titta på samma pil igen. Den här gången, föreställ dig att det flyger i vår riktning. Zeno hävdade att vi inte skulle röra oss, eftersom pilen aldrig kunde träffa oss. Föreställ dig att efter att pilen är i luften måste den täcka halva avståndet mellan bågen och målet. När hon når en viss punkt halvvägs, kommer hon återigen behöva täcka halva avståndet - den här gången mellan denna punkt och målet. Tänk om vi fortsätter med det. Pilen färdas alltså hela tiden halva avståndet mellan referenspunkten och målet. Med tanke på detta kan vi dra slutsatsen att pilen aldrig kommer att kunna träffa oss! I verkliga livet kommer pilen så småningom att träffa sitt mål, vilket gör att vi undrar vad paradoxen betyder.

Som i fallet med den första paradoxen kommer vi senare att överväga hur man löser detta problem med hjälp av en av principerna för matematisk analys - integralen. Integralen tillåter oss att se begreppet oändlighet som en matematisk funktion. Det är ett extremt kraftfullt verktyg, enligt forskare och ingenjörer.

Två grundläggande principer för kalkyl

Kärnan i de två grundläggande principerna för matematisk analys kan demonstreras genom att tillämpa dem för att lösa Zenos paradoxer.

Derivat. Derivaten är en metod som gör att vi kan beräkna hastigheten på pilen i Arrow Paradox. Vi gör detta genom att analysera pilens position med successivt minskande tidsintervall. Den exakta hastigheten på pilen kommer att bli känd när tiden mellan mätningarna visar sig vara oändligt liten.

Väsentlig. Integralen är en metod som gör att vi kan beräkna pilens position i dikotomiparadoxen. Vi kommer att göra detta genom att analysera pilens hastighet genom successivt minskande tidsintervall. Vi kommer att veta den exakta positionen för pilen när tiden mellan mätningarna visar sig vara oändligt liten.

Det är lätt att se vissa likheter mellan derivatan och integralen. Båda värdena beräknas under analysen av bommens position eller hastighet med gradvis minskande tidsintervall. Senare kommer vi att få reda på att integralen och derivatan i själva verket är två sidor av samma keramiska kondensator.

Varför ska vi studera grunderna i kalkyl?

Vi känner alla till Ohms lag, som kopplar samman ström, spänning och resistans till en enkel ekvation. Låt oss nu titta på Ohms lag med exemplet på en kondensator. Strömstyrkan hos en kondensator beror på spänning och tid. Tiden är i detta fall en kritisk variabel och måste beaktas vid alla dynamiska händelser. Matematisk analys låter oss förstå och uppskatta hur saker förändras över tid. När det gäller en kondensator är strömmen lika med kapacitansen gånger volt per sekund, eller i = C(dv/dt), där:

i - strömstyrka (momentan);
C - kapacitans, som mäts i farad;
dv - spänningsförändring;
dt är förändringen i tiden.

I denna krets finns det ingen elektrisk ström i kondensatorn. Voltmätaren visar batterispänning, men amperemätaren visar ingenting. Spänningen kommer inte att ändras så länge potentiometern förblir intakt. I detta fall är i = C(0/dt) = 0 amer. Men vad händer om vi börjar justera potentiometern? Att döma av ekvationen kommer den resulterande strömstyrkan att visas i kondensatorn. Denna ström kommer att bero på förändringen i spänningen, som är relaterad till hur snabbt potentiometern rör sig.

Dessa grafer visar förhållandet mellan spänningen i kondensatorn, strömmen och hastigheten med vilken vi vrider potentiometern. Vi gör det långsamt till en början. En ökning av hastigheten leder till en förändring i spänningen, vilket i sin tur framkallar en kraftig ökning av strömmen. På alla stadier är strömmen i kondensatorn proportionell mot spänningsförändringen i den.

Matematisk analys, eller mer exakt, derivatan, ger oss möjligheten att bestämma förändringshastigheten, så att vi vet exakt värdet av strömmen i kondensatorn vid en viss tidpunkt. På samma sätt kan vi beräkna den momentana hastigheten för Zenos pil. Detta är ett otroligt kraftfullt verktyg som borde finnas i din arsenal.

Materialet förbereddes specifikt för webbplatsen - enligt artikeln på webbplatsen hackaday.com

P.S. Jag heter Alexander. Det här är mitt personliga, oberoende projekt. Jag blir väldigt glad om du gillade artikeln. Vill du hjälpa sidan? Titta bara nedan för en annons för det du nyligen har letat efter.

Copyright-sajt © - Denna nyhet tillhör webbplatsen och är bloggens immateriella egendom, skyddad av upphovsrättslagen och kan inte användas någonstans utan en aktiv länk till källan. Läs mer - "Om författarskap"

Letar du efter detta? Kanske är det detta du inte hittat på så länge?

MATEMATISK ANALYS

del av matematiken, där funktioner och deras generaliseringar studeras med metoden gränser. Begreppet gräns är nära förknippat med begreppet en oändlig storhet; därför kan man också säga att M. a. studerar funktioner och deras generaliseringar med den infinitesimala metoden.

Namn "M. a." - en förkortad modifiering av det gamla namnet på denna del av matematiken - "Infinitesimal analys"; den senare avslöjar innehållet mer fullständigt, men det är också förkortat (titeln "Analys med hjälp av infinitesimals" skulle karakterisera ämnet mer exakt). I klassiska M. och. studieobjekten (analys) är i första hand funktioner. "Först och främst" eftersom utvecklingen av M. a. ledde till möjligheten att med sina metoder studera mer komplexa formationer än - funktionaler, operatörer etc.

I naturen och tekniken finns rörelser och processer överallt, to-rye beskrivs av funktioner; naturfenomens lagar brukar också beskrivas med funktioner. Därav den objektiva betydelsen av M. a. som ett sätt att lära sig funktioner.

M. a. i vid mening täcker en mycket stor del av matematiken. Det inkluderar differential, integralkalkyl, funktioner hos en komplex variabelteori, teori vanliga differentialekvationer, teori partiella differentialekvationer, teori integralekvationer, variationskalkyl, funktionell analys och lite annat matematiskt discipliner. Modern sifferteori Och sannolikhetsteori tillämpa och utveckla metoder M. och.

Icke desto mindre är termen M. a. används ofta för att bara nämna grunderna för matematisk analys som kombinerar teorin riktigt nummer, teori om gränser, teori rader, differential- och integralkalkyl och deras omedelbara tillämpningar, såsom teorin om maxima och minima, teorin implicita funktioner, Fourierserier, Fourierintegraler.

Fungera. I M. a. utgå från definitionen av en funktion enligt Lobachevsky och Dirichlet. Om för varje nummer xz i en viss uppsättning F-nummer, i kraft av k.-l. lag listas bland y, då definierar detta funktionen

från en variabel X. Funktionen definieras på liknande sätt

från variabler, var x=(x 1 , ..., x n) - punkt i n-dimensionellt utrymme; beakta även funktionerna

från poäng x=(x 1 , X 2 , ...) av något oändligt dimensionellt utrymme, som dock oftare kallas för funktionaler.

elementära funktioner. Grundläggande värde i M. och. spela elementära funktioner. I praktiken arbetar de huvudsakligen med elementära funktioner, de approximerar funktioner av mer komplex karaktär. Elementära funktioner kan betraktas inte bara för verkliga, utan också för komplexa x, då blir idéerna om dessa funktioner kompletta i en viss mening. I detta avseende har en viktig gren av M. a., kallad. teorin om funktioner för en komplex variabel, eller teorin analytiska funktioner.

Riktigt nummer. Begreppet en funktion bygger i huvudsak på begreppet ett reellt (rationellt och irrationellt) tal. Det tog slutligen form först i slutet av 1800-talet. I synnerhet har en logiskt felfri koppling etablerats mellan siffror och geometriska punkter. rät linje, vilket ledde till det formella underbyggandet av idéerna hos R. Descartes (R. Descartes, mitten av 1600-talet), som introducerade rektangulära koordinatsystem i matematiken och representationen av funktioner i dem med grafer.

Begränsa. I M. a. metoden för att studera funktioner är . Skilj mellan gränsen för en sekvens och gränsen för en funktion. Dessa begrepp bildades slutligen först på 1800-talet, även om andra greker hade en uppfattning om dem. forskare. Det räcker med att säga att Arkimedes (3:e århundradet f.Kr.) kunde beräkna segmentet av en parabel genom en process som vi skulle kalla passagen till gränsen (jfr. utmattningsmetod).

Kontinuerliga funktioner. En viktig funktion studerad i M. a., form kontinuerliga funktioner. En av de möjliga definitionerna av detta begrepp: funktion y=f(x).från en variabel X, ges på intervallet ( a, b), kallad kontinuerlig vid en punkt X, Om

Funktionen är kontinuerlig under intervallet ( a, b), om den är kontinuerlig på alla sina punkter; då är det en kurva, kontinuerlig i ordets vardagliga bemärkelse.

Derivat och . Bland kontinuerliga funktioner bör man peka ut funktioner som har derivat. Funktionsderivata

vid en punkt har hastigheten för sin förändring vid denna punkt, dvs gränsen

Om vi ​​har koordinaten för en punkt som rör sig längs y-axeln i tiden X, då är f "(x). den momentana hastigheten för en punkt åt gången X.

Med tecknet på derivatan f "(x) . bedöm arten av förändringen i f (x): om f "(z)> 0 ( f"(x) <0 ). på intervallet ( CD), så ökar (minskar) funktionen / på detta intervall. Om funktionen / vid punkten x når ett lokalt extremum (maximum eller minimum) och har en derivata vid denna punkt, är den senare lika med noll vid denna punkt f "(x 0) \u003d 0.

Jämlikhet (1) kan ersättas med motsvarande jämställdhet

där är en infinitesimal när, d.v.s. om funktionen f har en derivata i punkten X, sedan delas dess ökning vid denna punkt upp i två termer. Av dessa den första

är från (proportionell), den andra - tenderar att nollställas snabbare än

Värde (2) ref. differentiell funktioner som motsvarar inkrementet At small kan anses vara ungefär lika med dy:

Ovanstående resonemang om differentialen är karakteristiskt för M. a. De sträcker sig till funktioner av många variabler och till funktionaler.

Till exempel om funktionen

från variabler har kontinuerlig partiella derivat vid punkten x=(x 1 , ... , x n), sedan dess ökning motsvarande inkrement av oberoende variabler kan skrivas som

var på, dvs om alla

Här är den första termen på höger sida av (3) differentialen dz funktioner f. Det beror linjärt på och den andra termen tenderar att nollställas snabbare än

Låt det ges (se art. Variationskalkyl)

utvidgas till funktionsklasser x(t) , har en kontinuerlig derivata på intervallet och uppfyller randvillkoren x( t0)\u003d x 0, x( t1)=x l , Var x 0, x 1 - givna nummer; låt vidare vara klassen för funktionen h(t) , har en kontinuerlig derivata på och så att h( t0)=h(t1)=0. Uppenbarligen om

I variationskalkylen är det bevisat att under vissa förhållanden på L kan ökningen av den funktionella J(x) skrivas som

var

och därmed tenderar den andra termen på höger sida av (4) att nollställas snabbare än ||h||, och den första termen beror linjärt på. Den första termen i (4) kallas. variation av den funktionella och betecknas med dJ( x, h).

Väsentlig. Tillsammans med derivatan är den av grundläggande betydelse i M. a. Det finns obestämda och bestämda integraler.

Den obestämda integralen är nära relaterad till antiderivatfunktionen. Funktionen F(x). antiderivata av funktionen f på intervallet ( a, b) om på detta intervall F"(x) =f(x).

Den bestämda integralen (Riemann) för funktionen / på intervallet [ a, b] det finns en gräns

Om funktionen f är positiv och kontinuerlig på intervallet [ a, b], då är integralen av den på detta segment lika med arean av figuren som begränsas av kurvan y=f(x), axel Åh och direkt x=a, x=b.

Klassen av Riemann-integrerbara funktioner innehåller alla kontinuerliga på [ a, b]funktioner och vissa diskontinuerliga funktioner. Men de är alla nödvändigtvis begränsade. För obegränsade funktioner som inte växer särskilt snabbt, och även för vissa funktioner givna på oändliga intervall, introducerar man s.k. felaktiga integraler, kräver en dubbelpassage till gränsen för deras definition.

Konceptet med Riemann-integralen för en funktion av en variabel sträcker sig till funktioner av många variabler (se Multipel integral).

Däremot har M:s behov och. ledde till en generalisering av integralen i en helt annan riktning, betydelse Lebesgue integral eller mer allmänt Lebesgue-Stieltjes integral. Väsentligt i definitionen av dessa integraler är introduktionen för vissa mängder, kallade mätbara, av begreppet deras mått och, på grundval av detta, av begreppet en mätbar funktion. För mätbara funktioner och Lebesgue-Stieltjes-integralen introduceras. I detta fall övervägs ett brett utbud av olika mått och motsvarande klasser av mätbara uppsättningar och funktioner. Detta gör det möjligt att anpassa den eller den integralen till ett visst specifikt problem.

Newton-Leibniz formel. Det finns ett samband mellan derivatan och integralen, uttryckt med formeln (satsen) av Newton - Leibniz

Här är f(x) kontinuerlig på [ a, b] funktion, en F(x) - hennes prototyp.

Formula och Taylor. Tillsammans med derivatan och integralen, det viktigaste begreppet (forskningsverktyget) inom matematisk analys. är Taylor p Taylor-serien. Om funktionen f(x) , a har kontinuerliga derivator upp till ordningen p inklusive i en grannskap av punkten x 0, då kan den approximeras i denna grannskap med ett polynom

kallad dess Taylorpolynom (grader n). x-x 0:

(Taylor formel); medan approximationsfelet

tenderar till noll vid

snabbare än

Således kan funktionen f (x) i närheten av punkten x 0 approximeras med vilken grad av noggrannhet som helst med en mycket enkel funktion (polynom), som endast kräver aritmetik för dess beräkning. operationer - addition, subtraktion och multiplikation.

Av särskild vikt är de sk funktioner som är analytiska i ett visst område x 0 och har ett oändligt antal derivator, så att de för dem i denna grannskap vid kan representeras som en oändlig Taylor potensserie:

Taylor-expansions under vissa förhållanden är också möjliga för funktioner av många variabler, såväl som för funktionaler och operatorer.

Historisk referens. Fram till 1600-talet M. a. var en uppsättning lösningar på olika specifika problem; till exempel i integralkalkyl är dessa uppgifter för beräkning av figurers area, volymen av kroppar med krökta gränser, arbetet med en variabel kraft, etc. Varje uppgift eller särskilt problem löstes med sin egen metod, ibland komplex och besvärlig (för M. a.s förhistoria se artikel Infinitesimal kalkyl), M. a. som en enda och systematisk. det hela bildades i verk av I. Newton (I. Newton), G. Leibniz (G. Leibniz), L. Euler (L. Euler), J. Lagrange (J. Lagrange) och andra vetenskapsmän från den 17:e- 1700-talet, och hans - teorin om gränser - utvecklades av O. Komi (A. Cauchy) i början. 1800-talet Djup analys av de inledande begreppen i M. a. förknippades med utvecklingen under 1800- och 1900-talen. mängdlära, måttlära, funktionsteori för en reell variabel och ledde till olika generaliseringar.

Belyst.: La V a l l e - P u s s e n S.-J. e, En kurs i analys av infinitesimals, övers. från French, vol 1-2, Moskva, 1933; Ilyin V. A., Poznyak E. G., Fundamentals of Mathematical Analysis, 3:e upplagan, del 1, M., 1971; 2:a upplagan, del 2, M., 1980; Och l och N V. A., Sadovnichiy V. A., Seidov B. Kh., Mathematical Analysis, M., 1979; K u d r i v e i L. D., Matematisk analys, 2:a uppl., vol 1-2, M., 1973; Nikolsky S. M., Course of matematical analysis, 2:a upplagan, volym 1-2, M., 1975; Uitteker E. T., W a t s o n J. N., Kurs för modern analys, övers. från engelska, del 1-2, 2:a uppl., M., 1962-63; F och kht n o l ts G. M., Course of differential and integral calculus, 7th ed., vol. 1-2, M., 1970; 5:e upplagan, vol 3, M., 1970. S. M. Nikolsky.

Matematisk uppslagsverk. - M.: Sovjetiskt uppslagsverk. I. M. Vinogradov. 1977-1985.

Se vad "MATHEMATISK ANALYS" är i andra ordböcker:

MATEMATISK ANALYS, en uppsättning grenar av matematik som ägnas åt studier av funktioner med metoder för differentialkalkyl och integralkalkyl ... Modern Encyclopedia

En uppsättning grenar av matematik som ägnas åt studier av funktioner med metoder för differential- och integralkalkyl. Termen är mer pedagogisk än vetenskaplig: kurser i matematisk analys lärs ut på universitet och tekniska skolor ... Stor encyklopedisk ordbok

engelsk matematisk analys; tysk matematisk analys. En gren av matematik ägnas åt studier av funktioner med metoder för differential- och integralkalkyl. Antinazi. Encyclopedia of Sociology, 2009 ... Encyclopedia of Sociology

Exist., antal synonymer: 2 matan (2) matematisk analys (2) ASIS synonymordbok. V.N. Trishin. 2013 ... Synonym ordbok

MATEMATISK ANALYS- MATEMATISK ANALYS. En uppsättning grenar av matematik som ägnas åt studier av matematiska funktioner med metoder för differential- och integralkalkyl. Användning av metoder M. och. är ett effektivt sätt att lösa det viktigaste ... ... En ny ordbok över metodologiska termer och begrepp (teori och praktik för att lära ut språk)

matematisk analys- — SV matematisk analys Den gren av matematik som mest uttryckligen berör gränsprocessen eller begreppet konvergens; inkluderar teorierna om differentiering, … … Teknisk översättarhandbok

Matematisk analys- MATEMATISK ANALYS, en uppsättning avsnitt av matematik som ägnas åt studier av funktioner med metoder för differentialkalkyl och integralkalkyl. … Illustrerad encyklopedisk ordbok

"... om jag var tvungen att skapa en mekanism i det enda syftet att förstöra barnets naturliga nyfikenhet och hans kärlek till modellering, skulle jag knappast ha gjort det bättre än den redan har implementerats - jag skulle helt enkelt inte ha tillräckligt med fantasi för att konkurrera med sådana okänsliga, tråkiga idéer som förkroppsligas i moderna metoder för att studera matematik.

Tänk på att studera konst så här: Barn, ingen teckning på dagis. Låt oss istället studera färgprodukters kemi, ljusets fysik och ögats anatomi. Efter 12 års studier av dessa aspekter, om barn (mer exakt redan tonåringar) fortfarande inte hatar konst, kan de börja rita på egen hand. I slutändan har de nu en solid grund för att börja respektera konsten. Höger?

Även med poesi. Föreställ dig att studera detta citat (formel):

”Men huvudsaken: var sann mot dig själv; Då, precis som natt följer dag, kommer du inte att förråda andra.” -William Shakespeare, Hamlet

Det är ett elegant sätt att säga "var dig själv" (och om det betyder att skriva om matte respektlöst, så var det). Men om vi övervägde poesi i en matematikklass, istället för att leta efter mening, skulle vi räkna antalet stavelser, analysera jambisk pentameter, markera substantiv, verb och adjektiv.

Matematik och poesi är som olika sätt att förklara, att karakterisera samma sak. Formler är ett sätt att nå ett mål, ett sätt att uttrycka matematisk sanning.

Vi har glömt att matematiken fungerar med idéer, det är inte den mekaniska manipulationen av formlerna som uttrycker dessa idéer.

Tja, allt är klart, så vad är din bra idé?

Det här är vad jag inte kommer att göra: Jag kommer inte att återberätta läroböcker som jag redan har skrivit. Om du behöver svar här och nu, det finns massor av webbplatser, videohandledningar och 20 minuter att hjälpa.

Låt oss istället bemästra grunderna i kalkyl. Det räcker inte med ekvationer – jag vill ha ögonblick av insikt så att du verkligen ser deras innebörd och förstår matematikens språk.

Formella matematiska språket är helt enkelt ett sätt att kommunicera. Grafer, informativa animationer och klarspråk kan ge mer insikt än en sida med absurda bevis.

Men matematik är svårt!

Jag tror att vem som helst kan förstå de grundläggande principerna för kalkyl. Vi behöver inte vara poeter för att njuta av Shakespeares verk.

Det blir mycket lättare för dig om du kan algebra och är intresserad av matematik. För inte så länge sedan var läsning och skrivning ett verk av specialutbildade skriftlärare. Och idag kan vilket 10-årigt barn som helst göra det. Varför?

För vi förväntar oss det. Förväntningar spelar en stor roll för att utveckla möjligheter. Så förvänta dig att kalkyl bara är ett annat ämne. Vissa människor går ner till de minsta detaljerna (författare/matematiker). Men vi andra kan bara beundra vad som händer och försöka förstå det. Jag skulle vilja att alla behärskar de grundläggande begreppen matematisk analys och säger "Wow!".

Så vad handlar matematikanalys om?

Detta var ett enkelt exempel, men förstod du huvudidén? Vi tog skivan, delade den och satte ihop bitarna på ett lite annorlunda sätt. Matematisk analys visade att skivan och ringen är nära besläktade med varandra: skivan är egentligen en uppsättning ringar. Detta är ett mycket populärt ämne inom kalkyl: Stora saker består av mindre saker. Och ibland är det med dessa små föremål som det är lättare och tydligare att arbeta.

Några exempel

Många exempel i kalkyl är baserade på fysik. Detta är förstås underbart, men det kan vara svårt att uppfatta dem: ärligt talat är det långt ifrån alltid möjligt att ha i åtanke olika fysiska formler, som formeln för ett föremåls hastighet.

Jag gillar att börja med enkla visuella exempel eftersom det är så våra hjärnor fungerar. Ringen/cirkeln vi har undersökt - du kan modellera samma sak med flera stycken rör med olika diametrar: dela upp dem, rikta in dem och lägg dem i en grov triangel för att se till att matematiken verkligen fungerar. Med en enkel fysisk formel är detta osannolikt att göras.

Lite om matematisk rigor (för fanatiker av denna vetenskap)

Jag känner att pedantiska matematiker bränner sina tangentbord. Därför kommer jag bara att lägga in några ord om "striktighet". Vet du att vi inte lär ut kalkyl på det sätt som Newton eller Leibniz upptäckte det? De använde de intuitiva idéerna "flux" och "oändligt litet" som ersattes av gränser eftersom "Självklart fungerar det i praktiken. Men fungerar det i teorin?

Vi har skapat komplexa mekaniska modeller för att "exakt" bevisa kalkyler, men vi har tappat vår intuition i processen med sådana bevis.

Vi tittar på sockers sötma i termer av hjärnkemi, istället för att förklara det på vetenskapens språk ”Socker har mycket energi. Ät det."

Jag vill (och kan inte) lära ut kalkyl för studenter eller utbilda vetenskapsmän. Men skulle det vara dåligt om alla kunde förstå kalkyl på den "oprecisa" nivå som Newton förstod det på? För att det också ska förändra världen för dig, som det en gång gjorde för honom?

För tidigt fokus på precision skingra eleverna och gör matematik svår att lära sig. Här är ett bra exempel: talet e definieras tekniskt av en gräns, men det upptäcktes just med hjälp av en intuitiv gissning om tillväxt. Den naturliga logaritmen kan se ut som en integral, eller en tid att växa. Vilka förklaringar är bäst för nybörjare?

Låt oss rita lite för hand, och fördjupa oss i kemi längs vägen. Glad datoranvändning.

(P.S: En snäll läsare skapade ett animerat powerpoint-bildspel som hjälper till att presentera denna idé mer visuellt (det är bättre att titta på det i PowerPoint, animationer kommer att synas där). Tack!)

9 oktober 2015

Enligt ordboken för det ryska språket analys- detta är en metod för vetenskaplig forskning genom att beakta enskilda aspekter, egenskaper, komponenter i något. En av matematikens viktigaste grenar kallas matematisk analys och ofta till och med bara analys. Frågan uppstår genast: exakt vad som analyseras med matematisk analys? Svaret är klart - funktioner analyseras. Fungera(från latinets "funktion" - implementering) representerar förhållandet mellan variabla numeriska värden.

Eftersom analys är en forskningsmetod, uppstår en andra fråga: vad är denna metod? Svaret ger det andra namnet på matematisk analys - differential- och integralkalkyl. Calculus är en gren av matematiken som fastställer reglerna för beräkning. Ordet " differentiell" kommer från det latinska ordet "differentiering", dvs. skillnad. Ordet " väsentlig” har inte ett så tydligt ursprung ("integrator" - helhet; "integro" - återställ), men det har betydelsen av att kombinera delar till en helhet, återställa uppdelade skillnader. Denna återhämtning uppnås med summering.

Låt oss summera de första resultaten:

· huvudobjekt studerat i matematisk analys är funktionerna.

· Funktioner är beroenden av olika slag mellan variabla numeriska värden.

· Metoden för matematisk analys är differentiering– arbeta med skillnader i funktionsvärden, och integration- beräkning av summor.

För att behärska matematisk analys måste du alltså först och främst förstå begreppet funktion. Funktion är ett väsentligt matematiskt begrepp eftersom funktioner är ett matematiskt sätt att beskriva rörelse och förändring. Funktion är en process.

Den viktigaste typen av rörelse är mekanisk rörelse i en rak linje. När man rör sig mäts de avstånd som föremålet tillryggalägger, men detta är uppenbarligen inte tillräckligt för att helt beskriva rörelsen. Både Akilles och sköldpaddan kan röra sig lika långt från startpunkten, men deras rörelser skiljer sig åt i hastighet, och hastigheten kan inte mätas utan att mäta tiden.

Redan från övervägandet av detta exempel blir det tydligt att en variabel inte räcker för att beskriva rörelse och förändring. Det är intuitivt tydligt att tiden ändras jämnt, medan avståndet kan ändras antingen snabbare eller långsammare. Rörelsen beskrivs fullständigt om det vid varje tidpunkt är känt hur långt föremålet har rört sig bort från startpunkten. Så under mekanisk rörelse finns det en överensstämmelse mellan värdena för två variabler - tid, som förändras oberoende av någonting, och avstånd, som beror på tid. Detta faktum ligger till grund för definitionen av funktionen. De två variablerna kallas inte längre tid och avstånd.

Funktionsdefinition: fungera – är det en regel eller en lag, sätta varje värde på den oberoende variabeln X ett visst värde på den beroende variabeln på . Oberoende variabel X kallas ett argument, och det beroende på - funktion. Det sägs ibland att en funktion är ett samband mellan två variabler.

Hur visualiserar man vad en variabel är? En variabel är en tallinje (linjal eller skala) längs vilken en punkt (en termometer eller en nål med en pärla) rör sig. En funktion är en mekanism av kugghjul med två fönster x och y. Denna mekanism låter dig installera i fönstret X vilket värde som helst, men i lådan på värdet på funktionen kommer automatiskt att visas med hjälp av växlar.

Uppgift 1. Patientens temperatur mäts varje timme. Det finns en funktion - temperaturberoendet i tid. Hur presenterar man denna funktion? Svar: tabell och graf.

Funktionen är kontinuerlig, som rörelse är kontinuerlig, men i praktiken är det omöjligt att fixa denna kontinuitet. Du kan bara fånga enstaka argument och funktionsvärden. Det går dock fortfarande att beskriva kontinuitet teoretiskt.

Uppgift 2. Galileo Galilei upptäckte att en fritt fallande kropp färdas en avståndsenhet i den första sekunden, 3 enheter i den andra, 5 enheter i den tredje, etc. Bestäm tidens beroende av avståndet. indikation: Härled den allmänna formeln för sambandet mellan tillryggalagd sträcka och sträckantalet.

Sätt att ställa in funktioner.

Problem med matematisk analys.

Övergång från en representation av en funktion till en annan (beräkning av funktionsvärden, konstruktion av ungefärliga analytiska funktioner från experimentella numeriska och grafiska data, forskning av funktioner och plottning).

Matematisk studie av egenskaperna hos en funktion som process. Exempel 1: sök efter hastighet från en känd vägfunktion av tid (differentiering). Exempel 2: Hitta en väg med en känd funktion av hastighet kontra tid (integration).

	|	nästa föreläsning ==>
Kreativitet: Anteckningsböcker kontrolleras av x (vem?) lärare	|