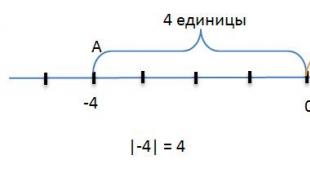
Korijeni jednadžbe 2. reda. Linearne homogene diferencijalne jednadžbe. Konstrukcija općeg rješenja linearne homogene

Homogene linearne diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima imaju oblik

gdje su p i q realni brojevi. Pogledajmo primjere kako se rješavaju homogene diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima.

Rješenje linearne homogene diferencijalne jednadžbe drugog reda ovisi o korijenima karakteristične jednadžbe. Karakteristična jednačina je jednačina k²+pk+q=0.

1) Ako su korijeni karakteristične jednadžbe različiti realni brojevi:

tada opće rješenje linearne homogene diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima ima oblik

2) Ako su korijeni karakteristične jednadžbe jednaki realni brojevi

(na primjer, s diskriminantom jednakim nuli), tada je opće rješenje homogene diferencijalne jednadžbe drugog reda

3) Ako su korijeni karakteristične jednadžbe kompleksni brojevi

(na primjer, s diskriminantom jednakom negativnom broju), tada se opće rješenje homogene diferencijalne jednadžbe drugog reda zapisuje u obliku

Primjeri rješavanja linearnih homogenih diferencijalnih jednadžbi drugog reda sa konstantnim koeficijentima

Naći opća rješenja homogenih diferencijalnih jednadžbi drugog reda:

Sastavljamo karakterističnu jednačinu: k²-7k+12=0. Njegov diskriminant je D=b²-4ac=1>0, tako da su korijeni različiti realni brojevi.

Dakle, opšte rješenje ovog homogenog DE 2. reda je

Sastavimo i riješimo karakterističnu jednačinu:

Korijeni su stvarni i različiti. Stoga imamo opće rješenje ove homogene diferencijalne jednadžbe:

U ovom slučaju, karakteristična jednačina

Korijeni su različiti i valjani. Stoga je ovdje opće rješenje homogene diferencijalne jednadžbe 2. reda

Karakteristična jednačina

Pošto su korijeni realni i jednaki, za ovu diferencijalnu jednačinu opće rješenje zapisujemo kao

Karakteristična jednačina je ovdje

Pošto je diskriminant negativan broj, korijeni karakteristične jednadžbe su kompleksni brojevi.

Opšte rješenje ove homogene diferencijalne jednadžbe drugog reda ima oblik

Karakteristična jednačina

Odavde nalazimo opće rješenje za ovaj diferencijal. jednadžbe:

Primjeri za samotestiranje.

§ 9. Linearne homogene diferencijalne jednačine drugog reda sa konstantnim koeficijentima

Definicija LODE drugog reda sa konstantnim koeficijentima

Karakteristična jednačina:

Slučaj 1. Diskriminant veći od nule

Slučaj 2. Diskriminant je nula

Slučaj 3. Diskriminant manji od nule

Algoritam pronalaženja opšte rešenje LOD drugog reda sa konstantnim koeficijentima

§ 10. Linearne nehomogene diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima

Određivanje LPDE drugog reda sa konstantnim koeficijentima

Metoda varijacije konstanti

Metoda za rješavanje LNDDE sa posebnom desnom stranom

Teorema o strukturi općeg rješenja LNDE

1. Funkcija r (x) – polinom stepena T

2. Funkcija r (x) – proizvod broja po eksponencijalna funkcija

3. Funkcija r (x) - suma trigonometrijske funkcije

Algoritam za pronalaženje općeg rješenja za LPDE sa posebnom desnom stranom

Aplikacija

§ 9. Linearne homogene diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima

Diferencijalna jednačina drugog reda naziva se linearna homogena diferencijalna jednadžba (LODE) sa konstantnim koeficijentima, ako izgleda ovako:

Gdje str I q

Da biste pronašli opće rješenje za LODE, dovoljno je pronaći njegova dva različita parcijalna rješenja i . Tada će opšte rješenje LODE-a imati oblik

Gdje WITH 1 i WITH

Leonard Euler je predložio da se traže posebna rješenja LDE u obliku

Gdje k– određeni broj.

Razlikovanje ove funkcije dvaput i zamjena izraza za at, y" I y" u jednačinu, dobijamo:

Rezultirajuća jednačina se zove karakteristična jednačina LODU. Da biste ga kompajlirali, dovoljno je zamijeniti u originalnoj jednadžbi y", y" I at shodno tome k 2 , k i 1:

Nakon rješavanja karakteristične jednačine, tj. pronašavši korene k 1 i k 2, naći ćemo i posebna rješenja za originalni LODE.

Karakteristična jednačina je kvadratna jednačina, njegovi korijeni se nalaze kroz diskriminant

U ovom slučaju moguća su sljedeća tri slučaja.

Slučaj 1. Diskriminant veći od nule , dakle, korijeni k 1 i k 2 važeći i različiti:

k 1¹ k 2

Gdje WITH 1 i WITH 2 – proizvoljne nezavisne konstante.

Slučaj 2. Diskriminant je nula , dakle, korijeni k 1 i k 2 realna i jednaka:

k 1 = k 2 = k

U ovom slučaju, opšte rješenje LODE-a ima oblik

Gdje WITH 1 i WITH 2 – proizvoljne nezavisne konstante.

Slučaj 3. Diskriminant manji od nule . U ovom slučaju, jednadžba nema pravi korijen:

Nema korijena.

U ovom slučaju, opšte rješenje LODE-a ima oblik

Gdje WITH 1 i WITH 2 – proizvoljne nezavisne konstante,

Dakle, pronalaženje općeg rješenja za LODE drugog reda sa konstantnim koeficijentima svodi se na pronalaženje korijena karakteristične jednadžbe i korištenje formula za općenito rješenje jednačine (bez pribjegavanja izračunavanju integrala).

Algoritam za pronalaženje općeg rješenja za LODE drugog reda sa konstantnim koeficijentima:

1. Svesti jednačinu na oblik gdje str I q– neki realni brojevi.

2. Kreirajte karakterističnu jednačinu.

3. Naći diskriminanta karakteristične jednačine.

4. Koristeći formule (vidi tabelu 1), u zavisnosti od predznaka diskriminanta, zapišite opšte rešenje.

Tabela 1

Tabela mogućih općih rješenja

U ovom članku ćemo ispitati principe rješavanja linearnih homogenih diferencijalnih jednadžbi drugog reda sa konstantnim koeficijentima, gdje su p i q proizvoljni realni brojevi. Prvo, fokusirajmo se na teoriju, a zatim primijenimo dobivene rezultate u rješavanju primjera i problema.

Ako naiđete na nepoznate termine, pogledajte odjeljak o definicijama i konceptima teorije diferencijalnih jednadžbi.

Hajde da formulišemo teoremu koja pokazuje u kom obliku pronaći opšte rešenje LOD-a.

Teorema.

Opće rješenje linearne homogene diferencijalne jednadžbe s kontinuiranim koeficijentima na integracijskom intervalu X određeno je linearnom kombinacijom , Gdje su linearno nezavisna parcijalna rješenja LDE na X, i proizvoljne su konstante.

Dakle, opšte rješenje linearne homogene diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima ima oblik y 0 =C 1 ⋅y 1 +C 2 ⋅y 2, gdje su y 1 i y 2 parcijalna linearno nezavisna rješenja, a C 1 i C 2 su proizvoljne konstante. Ostaje naučiti kako pronaći parcijalna rješenja y 1 i y 2.

Euler je predložio traženje posebnih rješenja u obliku .

Ako uzmemo parcijalno rješenje LODE drugog reda sa konstantnim koeficijentima, onda kada ovo rješenje zamenimo u jednačinu treba da dobijemo identičnost:

Tako smo dobili tzv karakteristična jednačina linearna homogena diferencijalna jednadžba drugog reda sa konstantnim koeficijentima. Rješenja k 1 i k 2 ove karakteristične jednačine određuju parcijalna rješenja našeg LODE drugog reda sa konstantnim koeficijentima.

Ovisno o koeficijentima p i q, korijeni karakteristične jednadžbe mogu biti:

U prvom slučaju linearno nezavisna parcijalna rješenja originalne diferencijalne jednadžbe su i , opće rješenje LODE drugog reda s konstantnim koeficijentima je .

Funkcije i su zaista linearno nezavisne, budući da je determinanta Wronskog različita od nule za bilo koji realni x za .

U drugom slučaju jedno posebno rješenje je funkcija . Kao drugo posebno rješenje uzimamo . Hajde da pokažemo šta je zaista određeno rešenje za LODE drugog reda sa konstantnim koeficijentima i dokažimo linearnu nezavisnost y 1 i y 2.

Kako su k 1 = k 0 i k 2 = k 0 isti korijeni karakteristične jednadžbe, ona ima oblik . Dakle, originalna je linearna homogena diferencijalna jednadžba. Zamijenimo ga u njega i uvjerimo se da jednačina postane identitet:

Dakle, to je djelomično rješenje originalne jednačine.

Pokažimo linearnu neovisnost funkcija i . Da bismo to učinili, izračunajmo determinantu Wronskog i uvjerimo se da je različita od nule.

Zaključak: linearno nezavisna parcijalna rješenja LODE drugog reda sa konstantnim koeficijentima su i , a opće rješenje postoji za .

U trećem slučaju imamo par složenih parcijalnih rješenja LDE i . Opšte rješenje će biti zapisano kao . Ova konkretna rješenja mogu se zamijeniti s dvije realne funkcije i , što odgovara realnom i imaginarnom dijelu. To se može jasno vidjeti ako transformiramo generalno rješenje , koristeći formule iz teorija funkcije kompleksne varijable tip:


gdje su C 3 i C 4 proizvoljne konstante.

Dakle, hajde da sumiramo teoriju.

Algoritam za pronalaženje općeg rješenja linearne homogene diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima.

Pogledajmo primjere za svaki slučaj.

Primjer.

Naći opće rješenje linearne homogene diferencijalne jednadžbe drugog reda sa konstantnim koeficijentima .

Linearna diferencijalna jednadžba 2. reda (LDE) ima sljedeći oblik:

gdje su , , i date funkcije koje su kontinuirane na intervalu na kojem se traži rješenje. Uz pretpostavku da je a 0 (x) ≠ 0, dijelimo (2.1) sa i, nakon uvođenja novih oznaka za koeficijente, zapisujemo jednačinu u obliku:

Prihvatimo bez dokaza da (2.2) ima jedinstveno rješenje na nekom intervalu koje zadovoljava sve početne uslove , , ako su na intervalu koji se razmatra funkcije , i kontinuirane. Ako je , tada se jednačina (2.2) naziva homogena, a jednačina (2.2) inače nehomogena.

Razmotrimo svojstva rješenja 2. reda.

Definicija. Linearna kombinacija funkcija je izraz , gdje su proizvoljni brojevi.

Teorema. Ako i – rješenje

tada će i njihova linearna kombinacija biti rješenje ove jednačine.

Dokaz.

Stavimo izraz u (2.3) i pokažemo da je rezultat identitet:

Preuredimo termine:

Kako su funkcije rješenja jednadžbe (2.3), onda je svaka zagrada u posljednjoj jednadžbi identično jednaka nuli, što je i trebalo dokazati.

Zaključak 1. Iz dokazane teoreme slijedi da ako je rješenje jednačine (2.3), onda postoji i rješenje ove jednačine.

Zaključak 2. Uz pretpostavku , vidimo da je zbir dva rješenja za Lod također rješenje ove jednačine.

Komentar. Svojstvo rješenja dokazanih u teoremi ostaje važeće za probleme bilo kojeg reda.

§3. Odrednica Vronskog.

Definicija. Za sistem funkcija se kaže da je linearno nezavisan na određenom intervalu ako se nijedna od ovih funkcija ne može predstaviti kao linearna kombinacija svih ostalih.

U slučaju dvije funkcije to znači da , tj. . Posljednji uslov se može prepisati kao ili . Odrednica u brojniku ovog izraza je se zove determinanta Wronskog za funkcije i . Dakle, determinanta Wronskog za dvije linearno nezavisne funkcije ne može biti identično jednaka nuli.

Neka je determinanta Wronskog za linearno nezavisna rješenja i jednadžbe (2.3). Uvjerimo se zamjenom da funkcija zadovoljava jednadžbu. (3.1)

Zaista, . Pošto funkcije i zadovoljavaju jednačinu (2.3), onda, tj. – rješenje jednačine (3.1). Pronađimo ovo rješenje: ; . gdje, . , , .

Na desnoj strani ove formule morate uzeti znak plus, jer se samo u ovom slučaju dobija identitet. dakle,

(3.2)

Ova formula se zove Liouville formula. Gore je pokazano da determinanta Wronskog za linearno nezavisne funkcije ne može biti identično jednaka nuli. Posljedično, postoji tačka u kojoj je determinanta za linearno nezavisna rješenja jednačine (2.3) različita od nule. Tada iz Liouvilleove formule slijedi da će funkcija biti različita od nule za sve vrijednosti u intervalu koji se razmatra, jer su za bilo koju vrijednost oba faktora na desnoj strani formule (3.2) različita od nule.

§4. Struktura općeg rješenja za lodu 2. reda.

Teorema. Ako su i linearno nezavisna rješenja jednadžbe (2.3), onda je njihova linearna kombinacija , gde su i proizvoljne konstante, biće opšte rešenje ove jednačine.

Dokaz.

Šta je rješenje jednadžbe (2.3), slijedi iz teoreme o svojstvima rješenja Lodo 2. reda. Samo treba da pokažemo da je rešenje će general, tj. potrebno je pokazati da se za bilo koje početne uslove mogu birati proizvoljne konstante na način da zadovolje ove uslove. Hajde da to zapišemo početni uslovi kao:

Konstante i iz ovog sistema linearnih algebarskih jednadžbi određuju se jedinstveno, jer je determinanta ovog sistema vrijednost determinante Wronskog za linearno nezavisna rješenja Lodua na:

,

a takva determinanta, kao što smo videli u prethodnom paragrafu, nije nula. Teorema je dokazana.

Primjer. Dokazati da je funkcija , gdje su i proizvoljne konstante, je opšte rješenje za Lod.

Rješenje.

Lako je provjeriti zamjenom da funkcije i zadovoljavaju ovu jednačinu. Ove funkcije su linearno nezavisne, jer . Dakle, prema teoremi o strukturi općeg rješenja, loda 2. reda je opšte rješenje ove jednačine.

Diferencijalne jednadžbe 2. reda

§1. Metode redukcije reda jednadžbe.

Diferencijalna jednačina drugog reda ima oblik:

https://pandia.ru/text/78/516/images/image002_107.gif" width="19" height="25 src=">.gif" width="119" height="25 src="> ( ili Differential" href="/text/category/differentcial/" rel="bookmark">Diferencijalna jednadžba 2. reda). Cauchyjev problem za diferencijalnu jednadžbu 2. reda (1..gif" width="85" height= "25 src =">.gif" width="85" height="25 src=">.gif" height="25 src=">.

Neka diferencijalna jednadžba 2. reda ima oblik: https://pandia.ru/text/78/516/images/image009_41.gif" height="25 src=">..gif" width="39" height=" 25 src=">.gif" width="265" height="28 src=">.

Dakle, jednačina 2. reda https://pandia.ru/text/78/516/images/image015_28.gif" width="34" height="25 src=">.gif" width="118" height =" 25 src=">.gif" width="117" height="25 src=">.gif" width="34" height="25 src=">. Rešavajući ga, dobijamo opšti integral originalne diferencijalne jednadžbe, u zavisnosti od dve proizvoljne konstante: DIV_ADBLOCK219">

Primjer 1. Riješite diferencijalnu jednadžbu https://pandia.ru/text/78/516/images/image021_18.gif" width="70" height="25 src=">.gif" height="25 src=">.gif " width="39" height="25 src=">.gif" width="157" height="25 src=">.gif" width="112" height="25 src=">.

Ovo je diferencijalna jednadžba sa odvojivim varijablama: https://pandia.ru/text/78/516/images/image026_19.gif" width="99" height="41 src=">, tj.gif" width= " 96" height="25 src=">.gif" width="53" height="25 src=">.gif" width="48" height="38 src=">..gif" width=" 99 " height="38 src=">..gif" width="95" height="25 src=">.

2..gif" width="117" height="25 src=">, tj.gif" width="102" height="25 src=">..gif" width="117" height= "25 src =">.gif" width="106" height="25 src=">.gif" width="34" height="25 src=">.gif" width="117" height="25 src=" >.gif" width="111" height="27 src=">

Rješenje.

IN zadata jednačina 2. red jasno ne uključuje traženu funkciju https://pandia.ru/text/78/516/images/image043_16.gif" width="98" height="25 src=">.gif" width="33 " height="25 src=">.gif" width="105" height="36 src=">, što je linearna jednadžba..gif" width="109" height="36 src=">.. gif" width ="144" height="36 src=">.gif" height="25 src="> od nekih funkcija..gif" width="25" height="25 src=">.gif" širina = "127" height="25 src=">.gif" width="60" height="25 src="> – redoslijed jednačine se snižava.

§2. Linearna diferencijalna jednadžba 2. reda.

Linearna diferencijalna jednadžba 2. reda (LDE) ima sljedeći oblik:

https://pandia.ru/text/78/516/images/image059_12.gif" width="42" height="25 src=">.gif" width="42" height="25 src=">. gif" width="42" height="25 src="> i nakon uvođenja novih oznaka za koeficijente, zapisujemo jednačinu u obliku:

https://pandia.ru/text/78/516/images/image064_12.gif" width="76" height="25 src=">.gif" width="35" height="25 src=">. gif" width="30" height="25 src="> kontinuirano..gif" width="165" height="25 src=">.gif" width="95" height="25 src="> – proizvoljnim brojevima.

Teorema. Ako https://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> - rješenje je

https://pandia.ru/text/78/516/images/image076_10.gif" width="182" height="25 src="> će također biti rješenje ove jednačine.

Dokaz.

Stavimo izraz https://pandia.ru/text/78/516/images/image077_11.gif" width="420" height="25 src=">.

Preuredimo termine:

https://pandia.ru/text/78/516/images/image073_10.gif" width="42" height="25 src=">.gif" width="54" height="25 src=">. gif" width="94" height="25 src="> je također rješenje ove jednačine.

Zaključak 2. Pod pretpostavkom da je https://pandia.ru/text/78/516/images/image083_11.gif" width="58" height="25 src="> također rješenje ove jednačine.

Komentar. Svojstvo rješenja dokazanih u teoremi ostaje važeće za probleme bilo kojeg reda.

§3. Odrednica Vronskog.

Definicija. Sistem funkcija https://pandia.ru/text/78/516/images/image084_10.gif" width="61" height="25 src=">.gif" width="110" height="47 src= " >..gif" width="106" height="42 src=">..gif" width="42" height="25 src=">.gif" width="181" height="47 src= " >.gif" width="42" height="25 src="> jednadžbe (2.3)..gif" width="182" height="25 src=">. (3.1)

Zaista, ..gif" width="18" height="25 src="> zadovoljava jednačinu (2..gif" width="42" height="25 src="> je rješenje jednadžbe (3.1). .gif" width="87" height="28 src=">..gif" width="182" height="34 src=">..gif" width="162" height="42 src="> .gif" width="51" height="25 src="> identitet je dobijen. Dakle,

https://pandia.ru/text/78/516/images/image107_7.gif" width="18" height="25 src=">, u kojoj je determinanta za linearno nezavisna rješenja jednadžbe (2..gif " width= "42" height="25 src=">.gif" height="25 src="> oba faktora na desnoj strani formule (3.2) nisu nula.

§4. Struktura općeg rješenja za lodu 2. reda.

Teorema. Ako su https://pandia.ru/text/78/516/images/image074_11.gif" width="42" height="25 src="> linearno nezavisna rješenja jednadžbe (2..gif" width=" 19" height="25 src=">.gif" width="129" height="25 src=">je rješenje jednadžbe (2.3), slijedi iz teoreme o svojstvima rješenja 2. reda. gif" width="85 " height="25 src=">.gif" width="19" height="25 src=">.gif" width="220" height="47">

Konstante https://pandia.ru/text/78/516/images/image003_79.gif" width="19" height="25 src="> iz ovog sistema linearnih algebarskih jednadžbi određene su jedinstveno, budući da je determinanta ovaj sistem je https: //pandia.ru/text/78/516/images/image006_56.gif" width="51" height="25 src=">:

https://pandia.ru/text/78/516/images/image116_7.gif" width="138" height="25 src=">.gif" width="19" height="25 src=">. gif" width="69" height="25 src=">.gif" width="235" height="48 src=">..gif" width="143" height="25 src="> (5 ..gif" width="77" height="25 src=">. Prema prethodnom pasusu, opšte rješenje Lod 2. reda se lako određuje ako su poznata dva linearno nezavisna parcijalna rješenja ove jednadžbe. Jednostavna metoda za pronalaženje parcijalnih rješenja jednadžbe sa konstantnim koeficijentima koje je predložio L. Euler..gif" width="25" height="26 src=">, dobijamo algebarska jednačina, što se zove karakteristika:

https://pandia.ru/text/78/516/images/image124_5.gif" width="59" height="26 src="> će biti rješenje jednadžbe (5.1) samo za one vrijednosti k koji su korijeni karakteristične jednadžbe (5.2)..gif" width="49" height="25 src=">..gif" width="76" height="28 src=">.gif" width= "205" height="47 src ="> i opće rješenje (5..gif" width="45" height="25 src=">..gif" width="74" height="26 src=" >..gif" width="83 " height="26 src=">. Provjerimo da li ova funkcija zadovoljava jednačinu (5.1)..gif" width="190" height="26 src=">. Zamjena ovih izraza u jednačinu (5.1), dobijamo

https://pandia.ru/text/78/516/images/image141_6.gif" width="328" height="26 src=">, jer..gif" width="137" height="26 src= ">.

Konkretna rješenja https://pandia.ru/text/78/516/images/image145_6.gif" width="86" height="28 src="> su linearno nezavisna, jer..gif" width="166" visina ="26 src=">.gif" width="45" height="25 src=">..gif" width="65" height="33 src=">.gif" width="134" visina = "25 src=">.gif" width="267" height="25 src=">.gif" width="474" height="25 src=">.

Obje zagrade na lijevoj strani ove jednakosti su identično jednake nuli..gif" width="174" height="25 src=">..gif" width="132" height="25 src="> je rješenje jednadžbe (5.1) ..gif" width="129" height="25 src="> će izgledati ovako:

https://pandia.ru/text/78/516/images/image162_6.gif" width="179" height="25 src="> f(x) (6.1)

je predstavljen kao zbir općeg rješenja https://pandia.ru/text/78/516/images/image164_6.gif" width="195" height="25 src="> (6.2)

i svako posebno rješenje https://pandia.ru/text/78/516/images/image166_6.gif" width="87" height="25 src="> će biti rješenje jednadžbe (6.1)..gif" width=" 272" height="25 src="> f(x). Ova jednakost je identitet, jer..gif" width="128" height="25 src="> f(x). Dakle.gif" width="85" height="25 src=">.gif" širina ="138" height="25 src=">.gif" width="18" height="25 src="> su linearno nezavisna rješenja ove jednadžbe. ovako:

https://pandia.ru/text/78/516/images/image173_5.gif" width="289" height="48 src=">

https://pandia.ru/text/78/516/images/image002_107.gif" width="19" height="25 src=">.gif" width="11" height="25 src=">. gif" width="51" height="25 src=">, a takva determinanta, kao što smo vidjeli gore, nije nula..gif" width="19" height="25 src="> iz sistema jednadžbi (6 ..gif" width="76" height="25 src=">.gif" width="76" height="25 src=">.gif" width="140" height="25 src" ="> će riješiti jednačinu

https://pandia.ru/text/78/516/images/image179_5.gif" width="91" height="25 src="> u jednadžbu (6.5), dobijamo

https://pandia.ru/text/78/516/images/image181_5.gif" width="140" height="25 src=">.gif" width="128" height="25 src="> f (x) (7.1)

gdje je https://pandia.ru/text/78/516/images/image185_5.gif" width="34" height="25 src="> jednadžba (7.1) u slučaju kada je desna strana f(x ) ima poseban oblik. Ova metoda se naziva metodom neodređenih koeficijenata i sastoji se u odabiru određenog rješenja ovisno o vrsti desne strane f(x). Razmotrimo desne strane sljedeće forme:

1..gif" width="282" height="25 src=">.gif" width="53" height="25 src=">, može biti nula. Naznačimo formu u kojoj se u ovom slučaju mora uzeti određeno rješenje.

a) Ako je broj https://pandia.ru/text/78/516/images/image191_5.gif" width="393" height="25 src=">.gif" width="157" height="25 src =>>.

Rješenje.

Za jednadžbu https://pandia.ru/text/78/516/images/image195_4.gif" width="86" height="25 src=">..gif" width="62" height="25 src = ">..gif" width="101" height="25 src=">.gif" width="153" height="25 src=">.gif" width="383" height="25 src= " >.

Oba dijela svodimo na https://pandia.ru/text/78/516/images/image009_41.gif" height="25 src="> na lijevoj i desnoj strani jednakosti

https://pandia.ru/text/78/516/images/image206_5.gif" width="111" height="40 src=">

Iz rezultirajućeg sistema jednadžbi nalazimo: https://pandia.ru/text/78/516/images/image208_5.gif" width="189" height="25 src=">, i opće rješenje zadata jednačina Tu je:

https://pandia.ru/text/78/516/images/image190_5.gif" width="11" height="25 src=">.gif" width="423" height="25 src=">,

gdje https://pandia.ru/text/78/516/images/image212_5.gif" width="158" height="25 src=">.

Rješenje.

Odgovarajuća karakteristična jednačina ima oblik:

https://pandia.ru/text/78/516/images/image214_6.gif" width="53" height="25 src=">.gif" width="85" height="25 src=">. gif" width="45" height="25 src=">.gif" width="219" height="25 src=">..gif" width="184" height="35 src=">. Final imamo sledeći izraz za opšte rešenje:

https://pandia.ru/text/78/516/images/image223_4.gif" width="170" height="25 src=">.gif" width="13" height="25 src="> odlično od nule. Naznačimo vrstu konkretnog rješenja u ovom slučaju.

a) Ako je broj https://pandia.ru/text/78/516/images/image227_5.gif" width="204" height="25 src=">,

gdje je https://pandia.ru/text/78/516/images/image226_5.gif" width="16" height="25 src="> korijen karakteristične jednadžbe za jednadžbu (5..gif" width="229 " height="25 src=">,

gdje https://pandia.ru/text/78/516/images/image229_5.gif" width="147" height="25 src=">.

Rješenje.

Korijeni karakteristične jednadžbe za jednadžbu https://pandia.ru/text/78/516/images/image231_4.gif" width="58" height="25 src=">.gif" width="203" visina ="25 src=">.

Desna strana jednačine date u primjeru 3 ima poseban oblik: f(x) https://pandia.ru/text/78/516/images/image235_3.gif" width="50" height="25 src= ">.gif " width="55" height="25 src=">.gif" width="229" height="25 src=">.

Za određivanje https://pandia.ru/text/78/516/images/image240_2.gif" width="11" height="25 src=">.gif" width="43" height="25 src=" > i zamijeni ga u datu jednačinu:

Citirajući slične pojmove, izjednačavajući koeficijente na https://pandia.ru/text/78/516/images/image245_2.gif" width="46" height="25 src=">.gif" width="100" height = "25 src=">.

Konačno opšte rješenje date jednačine je: https://pandia.ru/text/78/516/images/image249_2.gif" width="281" height="25 src=">.gif" width="47 " height ="25 src=">.gif" width="10" height="25 src="> respektivno, a jedan od ovih polinoma može biti jednak nuli. Naznačimo tip konkretnog rješenja u ovom općem slučaju .

a) Ako je broj https://pandia.ru/text/78/516/images/image255_2.gif" width="605" height="51">, (7.2)

gdje https://pandia.ru/text/78/516/images/image257_2.gif" width="121" height="25 src=">.

b) Ako je broj https://pandia.ru/text/78/516/images/image210_5.gif" width="80" height="25 src=">, tada će konkretno rješenje za lndu izgledati ovako:

https://pandia.ru/text/78/516/images/image259_2.gif" width="17" height="25 src=">. U izrazu (7..gif" width="121" height= " 25 src=">.

Primjer 4. Navedite vrstu određenog rješenja za jednadžbu

https://pandia.ru/text/78/516/images/image262_2.gif" width="129" height="25 src=">..gif" width="95" height="25 src="> . Opšte rješenje za Lodu ima oblik:

https://pandia.ru/text/78/516/images/image266_2.gif" width="183" height="25 src=">..gif" width="42" height="25 src="> ..gif" width="36" height="25 src=">.gif" width="351" height="25 src=">.

Dalji koeficijenti https://pandia.ru/text/78/516/images/image273_2.gif" width="34" height="25 src=">.gif" width="42" height="28 src=" > postoji posebno rješenje za jednadžbu sa desnom stranom f1(x), i Variation" href="/text/category/variatciya/" rel="bookmark">varijacije proizvoljnih konstanti (Lagrangeova metoda).

Direktno pronalaženje određenog rješenja jednačine, osim u slučaju jednačine sa konstantnim koeficijentima i posebnim slobodnim članovima, vrlo je teško. Stoga se za pronalaženje opšteg rješenja jednačine obično koristi metoda varijacije proizvoljnih konstanti, koja uvijek omogućava pronalaženje općeg rješenja jednačine u kvadraturama ako je poznat osnovni sistem rješenja odgovarajuće homogene jednačine . Ova metoda je sljedeća.

Prema gore navedenom, opšte rješenje linearne homogene jednadžbe je:

https://pandia.ru/text/78/516/images/image278_2.gif" width="46" height="25 src=">.gif" width="51" height="25 src="> – ne konstante, već neke, još nepoznate, funkcije f(x). . mora se uzeti iz intervala. Zapravo, u ovom slučaju, determinanta Wronskog je različita od nule u svim tačkama intervala, odnosno u cijelom prostoru - kompleksni korijen karakteristične jednadžbe..gif" width="20" height="25 src="> linearno nezavisna parcijalna rješenja oblika:

U općoj formuli rješenja, ovaj korijen odgovara izrazu oblika.