Vannastavna nastava - brojevni modul. Apsolutna vrijednost broja. Kompletne lekcije - Hipermarket znanja Modul nenegativnog broja je nenegativan broj

Ciljevi lekcije

Upoznavanje školaraca sa takvim matematičkim konceptom kao što je modul broja;
Učiti školarce vještinama pronalaženja modula brojeva;
Učvrstiti naučeno gradivo ispunjavanjem različitih zadataka;

Zadaci

Ojačati znanje djece o modulu brojeva;
Rješavanjem testnih zadataka provjeriti kako su učenici savladali naučeno gradivo;
Nastavite da usađujete interesovanje za časove matematike;
Negovati logičko mišljenje, radoznalost i upornost kod školaraca.

Plan lekcije

1. Opći pojmovi i definicija modula broja.
2. Geometrijsko značenje modula.
3. Modul broja i njegova svojstva.
4. Rješavanje jednačina i nejednačina koje sadrže modul broja.
5. Istorijski podaci o pojmu “modul broja”.
6. Zadatak za konsolidaciju znanja o obrađenoj temi.
7. Domaći.

Opći pojmovi o modulu broja

Modul broja obično se naziva sam broj ako nema negativnu vrijednost, ili je isti broj negativan, ali sa suprotnim predznakom.

To jest, modul nenegativnog realnog broja a je sam broj:

I, modul negativnog realnog broja x je suprotan broj:

Na snimku će to izgledati ovako:

Za pristupačnije razumijevanje, dajemo primjer. Tako, na primjer, modul broja 3 je 3, a također i modul broja -3 je 3.

Iz ovoga slijedi da modul broja označava apsolutnu vrijednost, odnosno njegovu apsolutnu vrijednost, ali ne uzimajući u obzir njegov predznak. Još jednostavnije rečeno, potrebno je ukloniti znak sa broja.

Modul broja može se označiti i izgledati ovako: |3|, |x|, |a| itd.

Tako je, na primjer, modul broja 3 označen kao |3|.

Takođe, treba imati na umu da modul broja nikada nije negativan: |a|≥ 0.

|5| = 5, |-6| = 6, |-12,45| = 12,45, itd.

Geometrijsko značenje modula

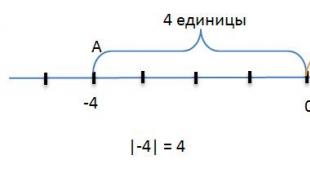
Modul broja je udaljenost koja se mjeri u jediničnim segmentima od početka do tačke. Ova definicija otkriva modul sa geometrijske tačke gledišta.

Uzmimo koordinatnu liniju i označimo dvije tačke na njoj. Neka ove tačke odgovaraju brojevima kao što su −4 i 2.

Sada obratimo pažnju na ovu cifru. Vidimo da tačka A, označena na koordinatnoj liniji, odgovara broju -4, a ako pažljivo pogledate, vidjet ćete da se ova tačka nalazi na udaljenosti od 4 jedinična segmenta od referentne točke 0. Iz toga slijedi da je dužina segmenta OA jednaka četiri jedinice. U ovom slučaju, dužina segmenta OA, odnosno broja 4, bit će modul broja -4.

U ovom slučaju, modul broja se označava i zapisuje na ovaj način: |−4| = 4.

Sada uzmimo i označimo tačku B na koordinatnoj liniji.

Ova tačka B će odgovarati broju +2 i, kao što vidimo, nalazi se na udaljenosti od dva jedinična segmenta od početka. Iz ovoga slijedi da je dužina segmenta OB jednaka dvije jedinice. U ovom slučaju, broj 2 će biti modul broja +2.

Na snimku će to izgledati ovako: |+2| = 2 ili |2| = 2.

Sada da sumiramo. Ako uzmemo neki nepoznati broj a i označimo ga na koordinatnoj pravoj kao tačku A, tada je u ovom slučaju udaljenost od tačke A do ishodišta, odnosno dužina segmenta OA, upravo modul broja „a ”.

U pisanom obliku će izgledati ovako: |a| = OA.

Modul broja i njegova svojstva

Pokušajmo sada istaknuti svojstva modula, razmotriti sve moguće slučajeve i zapisati ih koristeći literalne izraze:

Prvo, modul broja je nenegativan broj, što znači da je modul pozitivnog broja jednak samom broju: |a| = a, ako je a > 0;

Drugo, moduli koji se sastoje od suprotnih brojeva su jednaki: |a| = |–a|. Odnosno, ovo svojstvo nam govori da suprotni brojevi uvijek imaju jednake module, baš kao na koordinatnoj liniji, iako imaju suprotne brojeve, oni su na istoj udaljenosti od referentne točke. Iz ovoga slijedi da su moduli ovih suprotnih brojeva jednaki.

Treće, modul nule je jednak nuli ako je ovaj broj nula: |0| = 0 ako je a = 0. Ovdje možemo sa sigurnošću reći da je modul nule po definiciji nula, budući da odgovara početku koordinatne linije.

Četvrto svojstvo modula je da je modul proizvoda dva broja jednak proizvodu modula ovih brojeva. Pogledajmo sada pobliže šta to znači. Ako slijedimo definiciju, onda ti i ja znamo da će modul proizvoda brojeva a i b biti jednak a b, ili −(a b), ako je a b ≥ 0, ili – (a b), ako je a b veći od 0. B snimanje će izgledati ovako: |a b| = |a| |b|.

Peto svojstvo je da je modul kvocijenta brojeva jednak omjeru modula ovih brojeva: |a: b| = |a| : |b|.

I sljedeća svojstva modula brojeva:

Rješavanje jednadžbi i nejednačina koje uključuju modul broja

Kada počinjete rješavati probleme koji imaju brojčani modul, treba imati na umu da je za rješavanje takvog zadatka potrebno otkriti predznak modula koristeći poznavanje svojstava kojima ovaj problem odgovara.

Vježba 1

Tako, na primjer, ako se ispod znaka modula nalazi izraz koji ovisi o varijabli, onda modul treba proširiti u skladu s definicijom:

Naravno, prilikom rješavanja problema postoje slučajevi kada se modul otkriva jedinstveno. Ako, na primjer, uzmemo

, ovdje vidimo da je takav izraz pod predznakom modula nenegativan za bilo koje vrijednosti x i y.

Ili, na primjer, uzmimo

, vidimo da ovaj izraz modula nije pozitivan ni za jednu vrijednost z.

Zadatak 2

Ispred vas je prikazana koordinatna linija. Na ovoj liniji je potrebno označiti brojeve čiji će modul biti jednak 2.

Rješenje

Prije svega, moramo nacrtati koordinatnu liniju. Već znate da da biste to učinili, prvo na pravoj liniji trebate odabrati ishodište, smjer i jedinični segment. Zatim moramo postaviti tačke iz početka koje su jednake udaljenosti dva jedinična segmenta.

Kao što vidite, na koordinatnoj liniji postoje dvije takve tačke, od kojih jedna odgovara broju -2, a druga broju 2.

Istorijski podaci o modulu brojeva

Termin “modul” dolazi od latinskog naziva modulus, što znači “mjera”. Ovaj termin je skovao engleski matematičar Roger Cotes. Ali znak modula uveden je zahvaljujući njemačkom matematičaru Karlu Weierstrassu. Kada je napisan, modul se označava sledećim simbolom: | |.

Pitanja za konsolidaciju znanja o gradivu

U današnjoj lekciji upoznali smo se s takvim konceptom kao što je modul broja, a sada da provjerimo kako ste savladali ovu temu odgovarajući na postavljena pitanja:

1. Kako se zove broj koji je suprotan pozitivnom broju?
2. Kako se zove broj koji je suprotan negativnom broju?
3. Imenujte broj koji je suprotan nuli. Postoji li takav broj?
4. Imenujte broj koji ne može biti modul broja.
5. Definirajte modul broja.

Zadaća

1. Ispred vas su brojevi koje trebate složiti u opadajućem redoslijedu modula. Ako ispravno izvršite zadatak, saznat ćete ime osobe koja je prva uvela pojam “modul” u matematiku.

2. Nacrtajte koordinatnu liniju i pronađite udaljenost od M (-5) i K (8) do početka.

Predmeti > Matematika > Matematika 6. razred

Danas, prijatelji, neće biti šmrkanja i sentimentalnosti. Umesto toga, poslaću vas, bez pitanja, u borbu sa jednim od najstrašnijih protivnika u kursu algebre od 8. do 9. razreda.

Da, sve ste ispravno shvatili: govorimo o nejednakostima sa modulom. Pogledat ćemo četiri osnovne tehnike pomoću kojih ćete naučiti rješavati oko 90% takvih problema. Šta je sa preostalih 10%? Pa, o njima ćemo u posebnoj lekciji. :)

Međutim, prije nego što analiziram bilo koju od tehnika, želio bih vas podsjetiti na dvije činjenice koje već morate znati. U suprotnom, rizikujete da uopšte ne razumete materijal današnje lekcije.

Ono što već trebate znati

Kapetan Očevidnost kao da nagovještava da za rješavanje nejednakosti s modulom morate znati dvije stvari:

1. Kako se rješavaju nejednakosti;
2. Šta je modul?

Počnimo sa drugom tačkom.

Definicija modula

Ovdje je sve jednostavno. Postoje dvije definicije: algebarska i grafička. Za početak - algebarski:

Definicija. Modul broja $x$ je ili sam broj, ako nije negativan, ili broj nasuprot njemu, ako je originalni $x$ i dalje negativan.

Napisano je ovako:

\[\lijevo| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \right.\]

Jednostavno rečeno, modul je „broj bez minusa“. I upravo u toj dvojnosti (na nekim mjestima ne morate ništa raditi s originalnim brojem, ali na nekima ćete morati ukloniti neku vrstu minusa) je cijela poteškoća za početnike.

Postoji i geometrijska definicija. To je također korisno znati, ali ćemo se obratiti samo u složenim i nekim posebnim slučajevima, gdje je geometrijski pristup pogodniji od algebarskog (spojler: ne danas).

Definicija. Neka je tačka $a$ označena na brojevnoj pravoj. Zatim modul $\left| x-a \right|$ je rastojanje od tačke $x$ do tačke $a$ na ovoj pravoj.

Ako nacrtate sliku, dobićete nešto ovako:

Definicija grafičkog modula

Na ovaj ili onaj način, iz definicije modula odmah slijedi njegovo ključno svojstvo: modul broja je uvijek nenegativna veličina. Ova činjenica će biti crvena nit koja se provlači kroz cijeli naš današnji narativ.

Rješavanje nejednačina. Intervalna metoda

Pogledajmo sada nejednakosti. Ima ih jako puno, ali naš zadatak je sada da riješimo barem najjednostavniji od njih. One koje se svode na linearne nejednakosti, kao i na intervalnu metodu.

Imam dvije velike lekcije na ovu temu (usput, vrlo, VEOMA korisne - preporučujem da ih proučite):

1. Metoda intervala za nejednakosti (posebno pogledajte video);
2. Razlomke racionalne nejednakosti su vrlo opsežna lekcija, ali nakon nje nećete imati uopće pitanja.

Ako sve ovo znate, ako vas fraza „pređimo s nejednakosti na jednačinu“ ne tjera da imate nejasnu želju da se udarite o zid, onda ste spremni: dobrodošli u pakao na glavnu temu lekcije. :)

1. Nejednakosti oblika “Modulus je manji od funkcije”

Ovo je jedan od najčešćih problema s modulima. Potrebno je riješiti nejednakost oblika:

\[\lijevo| f\right| \ltg\]

Funkcije $f$ i $g$ mogu biti bilo koje, ali obično su polinomi. Primjeri takvih nejednakosti:

\[\početi(poravnati) & \lijevo| 2x+3 \desno| \lt x+7; \\ & \lijevo| ((x)^(2))+2x-3 \desno|+3\levo(x+1 \desno) \lt 0; \\ & \lijevo| ((x)^(2))-2\lijevo| x \right|-3 \right| \lt 2. \\\end(poravnati)\]

Svi se oni mogu riješiti doslovno u jednom redu prema sljedećoj shemi:

\[\lijevo| f\right| \lt g\Rightarrow -g \lt f \lt g\quad \left(\Rightarrow \left\( \begin(poravnati) & f \lt g, \\ & f \gt -g \\\end(poravnati) \desno.\desno)\]

Lako je vidjeti da smo se riješili modula, ali zauzvrat dobijamo dvostruku nejednakost (ili, što je ista stvar, sistem dvije nejednakosti). Ali ova tranzicija uzima u obzir apsolutno sve moguće probleme: ako je broj ispod modula pozitivan, metoda radi; ako je negativan, i dalje radi; pa čak i sa najneadekvatnijom funkcijom umjesto $f$ ili $g$, metoda će i dalje raditi.

Naravno, postavlja se pitanje: zar ne može biti jednostavnije? Nažalost, to nije moguće. Ovo je cijela poenta modula.

Međutim, dosta sa filozofiranjem. Rešimo par problema:

Zadatak. Riješite nejednačinu:

\[\lijevo| 2x+3 \desno| \lt x+7\]

Rješenje. Dakle, pred nama je klasična nejednakost oblika "modul je manji" - čak nema ništa za transformaciju. Radimo po algoritmu:

\[\početi(poravnati) & \lijevo| f\right| \lt g\Strelica desno -g \lt f \lt g; \\ & \lijevo| 2x+3 \desno| \lt x+7\Strelica desno -\lijevo(x+7 \desno) \lt 2x+3 \lt x+7 \\\kraj (poravnati)\]

Nemojte žuriti da otvarate zagrade ispred kojih stoji "minus": sasvim je moguće da ćete zbog svoje žurbe napraviti uvredljivu grešku.

\[-x-7 \lt 2x+3 \lt x+7\]

\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(align) \right.\]

\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \right.\]

\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \right.\]

Problem je sveden na dvije elementarne nejednakosti. Zabilježimo njihova rješenja na paralelnim brojevnim pravima:

Raskrsnica mnogih

Presjek ovih skupova će biti odgovor.

Odgovor: $x\in \levo(-\frac(10)(3);4 \desno)$

Zadatak. Riješite nejednačinu:

\[\lijevo| ((x)^(2))+2x-3 \desno|+3\levo(x+1 \desno) \lt 0\]

Rješenje. Ovaj zadatak je malo teži. Prvo, izolirajmo modul pomicanjem drugog člana udesno:

\[\lijevo| ((x)^(2))+2x-3 \desno| \lt -3\lijevo(x+1 \desno)\]

Očigledno, opet imamo nejednakost oblika „modul je manji“, pa se rješavamo modula koristeći već poznati algoritam:

\[-\left(-3\left(x+1 \desno) \right) \lt ((x)^(2))+2x-3 \lt -3\left(x+1 \right)\]

Pažnja: neko će reći da sam ja pomalo perverznjak sa svim ovim zagradama. Ali da vas još jednom podsjetim da je naš ključni cilj tačno riješiti nejednačinu i dobiti odgovor. Kasnije, kada savršeno savladate sve što je opisano u ovoj lekciji, možete to sami izopačiti kako želite: otvorite zagrade, dodajte minuse itd.

Za početak, jednostavno ćemo se riješiti dvostrukog minusa s lijeve strane:

\[-\left(-3\left(x+1 \desno) \right)=\left(-1 \right)\cdot \left(-3 \right)\cdot \left(x+1 \right) =3\lijevo(x+1 \desno)\]

Sada otvorimo sve zagrade u dvostrukoj nejednakosti:

Prijeđimo na dvostruku nejednakost. Ovoga puta kalkulacije će biti ozbiljnije:

\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(poravnati) \desno.\]

\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( poravnati)\desno.\]

Obje nejednakosti su kvadratne i mogu se riješiti intervalnom metodom (zato kažem: ako ne znate šta je ovo, bolje je da još ne preuzimate module). Pređimo na jednadžbu u prvoj nejednakosti:

\[\begin(align) & ((x)^(2))+5x=0; \\ & x\lijevo(x+5 \desno)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end(poravnati)\]

Kao što vidite, izlaz je nepotpuna kvadratna jednačina, koja se može riješiti na elementaran način. Pogledajmo sada drugu nejednakost sistema. Tamo ćete morati primijeniti Vietinu teoremu:

\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \right)\left(x+2 \right)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end(poravnati)\]

Dobivene brojeve označavamo na dvije paralelne prave (odvojeno za prvu nejednakost i odvojeno za drugu):

Opet, pošto rješavamo sistem nejednačina, zanima nas presjek osenčenih skupova: $x\in \left(-5;-2 \right)$. Ovo je odgovor.

Odgovor: $x\in \levo(-5;-2 \desno)$

Mislim da je nakon ovih primjera shema rješenja krajnje jasna:

1. Izolirajte modul pomicanjem svih ostalih pojmova na suprotnu stranu nejednakosti. Tako dobijamo nejednakost oblika $\left| f\right| \ltg$.
2. Riješite ovu nejednakost tako što ćete se riješiti modula prema gore opisanoj shemi. U nekom trenutku će biti potrebno preći sa dvostruke nejednakosti na sistem dva nezavisna izraza, od kojih se svaki već može posebno rešavati.
3. Konačno, preostaje samo da se ukrste rješenja ova dva nezavisna izraza - i to je to, dobićemo konačan odgovor.

Sličan algoritam postoji za nejednakosti sljedećeg tipa, kada je modul veći od funkcije. Međutim, postoji nekoliko ozbiljnih „ali“. Sada ćemo razgovarati o ovim "ali".

2. Nejednakosti oblika “Modul je veći od funkcije”

izgledaju ovako:

\[\lijevo| f\right| \gtg\]

Slično prethodnom? Izgleda. A ipak se takvi problemi rješavaju na potpuno drugačiji način. Formalno, shema je sljedeća:

\[\lijevo| f\right| \gt g\Strelica desno \levo[ \begin(poravnati) & f \gt g, \\ & f \lt -g \\\end(poravnati) \desno.\]

Drugim riječima, razmatramo dva slučaja:

1. Prvo, jednostavno zanemarimo modul i riješimo uobičajenu nejednakost;
2. Zatim, u suštini, širimo modul sa predznakom minus, a zatim množimo obe strane nejednakosti sa −1, dok ja imam predznak.

U ovom slučaju, opcije se kombiniraju uglastom zagradom, tj. Pred nama je kombinacija dva zahtjeva.

Napominjemo još jednom: ovo nije sistem, već totalitet, dakle u odgovoru skupovi se kombinuju, a ne seku. Ovo je fundamentalna razlika u odnosu na prethodnu tačku!

Općenito, mnogi studenti su potpuno zbunjeni sindikatima i raskrižjima, pa hajde da riješimo ovo pitanje jednom za svagda:

• "∪" je znak sindikata. U stvari, ovo je stilizovano slovo “U”, koje je do nas došlo iz engleskog jezika i skraćenica je za “Union”, tj. "Udruženja".
• "∩" je znak raskrsnice. Ovo sranje nije došlo niotkuda, već se jednostavno pojavilo kao kontrapunkt "∪".

Da biste još lakše zapamtili, samo privucite noge na ove znakove da napravite naočale (samo me nemojte sada optuživati ​​da promovišem ovisnost o drogama i alkoholizam: ako ozbiljno proučavate ovu lekciju, onda ste već narkoman):

Razlika između presjeka i unije skupova

Prevedeno na ruski, to znači sljedeće: unija (totalnost) uključuje elemente iz oba skupa, stoga ni na koji način nije manja od svakog od njih; ali raskrsnica (sistem) uključuje samo one elemente koji su istovremeno i u prvom i u drugom skupu. Stoga, presjek skupova nikada nije veći od izvornih skupova.

Pa je postalo jasnije? To je sjajno. Idemo dalje na praksu.

Zadatak. Riješite nejednačinu:

\[\lijevo| 3x+1 \desno| \gt 5-4x\]

Rješenje. Nastavljamo prema šemi:

\[\lijevo| 3x+1 \desno| \gt 5-4x\Strelica desno \levo[ \početak(poravnati) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\levo(5-4x \desno) \\\end(poravnati) \ tačno.\]

Svaku nejednakost u populaciji rješavamo:

\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(align) \right.\]

\[\left[ \begin(poravnati) & 7x \gt 4 \\ & -x \lt -6 \\ \end(poravnati) \desno.\]

\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(align) \right.\]

Svaki rezultirajući skup označavamo na brojevnoj liniji, a zatim ih kombiniramo:

Unija skupova

Sasvim je očigledno da će odgovor biti $x\in \left(\frac(4)(7);+\infty \right)$

Odgovor: $x\in \left(\frac(4)(7);+\infty \right)$

Zadatak. Riješite nejednačinu:

\[\lijevo| ((x)^(2))+2x-3 \desno| \gt x\]

Rješenje. Pa? Ništa - sve je isto. Od nejednakosti sa modulom prelazimo na skup od dvije nejednakosti:

\[\lijevo| ((x)^(2))+2x-3 \desno| \gt x\Strelica desno \left[ \begin(poravnati) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\kraj (poravnaj) \desno.\]

Rješavamo svaku nejednakost. Nažalost, korijeni tamo neće biti baš dobri:

\[\begin(poravnati) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end(poravnati)\]

Druga nejednakost je također pomalo divlja:

\[\begin(poravnati) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end(poravnati)\]

Sada trebate označiti ove brojeve na dvije ose - jednu os za svaku nejednakost. Međutim, morate označiti tačke ispravnim redoslijedom: što je broj veći, to se tačka dalje pomiče udesno.

I ovdje nas čeka postavka. Ako je sve jasno sa brojevima $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ (članovi u brojniku prvog razlomak su manji od članova u brojiocu drugog, pa je i zbir manji), sa brojevima $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt (21))(2)$ također neće biti poteškoća (pozitivan broj očito negativniji), onda sa zadnjim parom sve nije tako jasno. Što je veće: $\frac(-3+\sqrt(21))(2)$ ili $\frac(-1+\sqrt(13))(2)$? Postavljanje tačaka na brojevne prave i, zapravo, odgovor će zavisiti od odgovora na ovo pitanje.

Pa da uporedimo:

\[\begin(matrix) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matrica)\]

Izolirali smo korijen, dobili smo nenegativne brojeve na obje strane nejednakosti, tako da imamo pravo kvadrirati obje strane:

\[\begin(matrica) ((\left(2+\sqrt(13) \right))^(2))\vee ((\left(\sqrt(21) \right))^(2)) \ \ 4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matrica)\]

Mislim da nije pametno da $4\sqrt(13) \gt 3$, tako da $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$, konačne tačke na osi će biti postavljene ovako:

Slučaj ružnih korijena

Da vas podsjetim da rješavamo skup, tako da će odgovor biti unija, a ne sjecište osenčenih skupova.

Odgovor: $x\in \left(-\infty ;\frac(-3+\sqrt(21))(2) \desno)\bigcup \left(\frac(-1+\sqrt(13))(2 );+\infty \desno)$

Kao što vidite, naša shema odlično funkcionira i za jednostavne i za vrlo teške probleme. Jedina “slaba tačka” u ovom pristupu je ta što trebate ispravno uporediti iracionalne brojeve (i vjerujte mi: to nisu samo korijeni). Ali posebna (i vrlo ozbiljna) lekcija će biti posvećena pitanjima poređenja. I idemo dalje.

3. Nejednakosti sa nenegativnim "repovima"

Sada dolazimo do najzanimljivijeg dijela. Ovo su nejednakosti oblika:

\[\lijevo| f\right| \gt\lijevo| g\desno|\]

Uopšteno govoreći, algoritam o kojem ćemo sada govoriti je ispravan samo za modul. Radi u svim nejednačinama gdje su zagarantovani nenegativni izrazi s lijeve i desne strane:

Šta raditi s ovim zadacima? Samo se sjeti:

U nejednačinama sa nenegativnim „repom“, obje strane se mogu podići na bilo koju prirodnu potenciju. Neće biti dodatnih ograničenja.

Prije svega, zanimat će nas kvadratura - spaljuje module i korijene:

\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\lijevo(\sqrt(f) \desno))^(2))=f. \\\end(poravnati)\]

Samo nemojte ovo brkati sa uzimanjem korijena kvadrata:

\[\sqrt(((f)^(2)))=\left| f \right|\ne f\]

Napravljene su bezbrojne greške kada je student zaboravio da instalira modul! Ali ovo je sasvim druga priča (ovo su, takoreći, iracionalne jednadžbe), pa nećemo sada ulaziti u ovo. Hajde da bolje riješimo nekoliko problema:

Zadatak. Riješite nejednačinu:

\[\lijevo| x+2 \desno|\ge \levo| 1-2x \desno|\]

Rješenje. Odmah da primetimo dve stvari:

1. Ovo nije striktna nejednakost. Tačke na brojevnoj liniji će biti probušene.
2. Obje strane nejednakosti su očigledno nenegativne (ovo je svojstvo modula: $\left| f\left(x \right) \right|\ge 0$).

Stoga možemo kvadrirati obje strane nejednakosti da bismo se riješili modula i riješili problem koristeći uobičajenu metodu intervala:

\[\begin(align) & ((\left(\left| x+2 \right| \right))^(2))\ge ((\left(\left| 1-2x \right| \right) )^(2)); \\ & ((\lijevo(x+2 \desno))^(2))\ge ((\lijevo(2x-1 \desno))^(2)). \\\end(poravnati)\]

U poslednjem koraku sam se malo prevario: promenio sam redosled pojmova, koristeći prednost ravnosti modula (u stvari, pomnožio sam izraz $1-2x$ sa −1).

\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \right)-\left(x+2 \right) \right)\cdot \left(\left(2x-1 \right)+\left(x+2 \ desno)\desno)\le 0; \\ & \left(2x-1-x-2 \right)\cdot \left(2x-1+x+2 \right)\le 0; \\ & \left(x-3 \desno)\cdot \left(3x+1 \right)\le 0. \\\end(align)\]

Rješavamo metodom intervala. Pređimo sa nejednačine na jednačinu:

\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end(poravnati)\]

Pronađene korijene označavamo na brojevnoj pravoj. Još jednom: sve tačke su zasjenjene jer izvorna nejednakost nije stroga!

Uklanjanje znaka modula

Da vas podsjetim za one koji su posebno tvrdoglavi: uzimamo predznake iz posljednje nejednačine, koja je zapisana prije prelaska na jednadžbu. I farbamo preko potrebnih površina u istoj nejednakosti. U našem slučaju to je $\left(x-3 \right)\left(3x+1 \right)\le 0$.

OK, sve je gotovo. Problem je riješen.

Odgovor: $x\in \left[ -\frac(1)(3);3 \right]$.

Zadatak. Riješite nejednačinu:

\[\lijevo| ((x)^(2))+x+1 \desno|\le \levo| ((x)^(2))+3x+4 \desno|\]

Rješenje. Sve radimo isto. Neću komentarisati - samo pogledajte redosled radnji.

Na kvadrat:

\[\begin(poravnaj) & ((\left(\left| ((x)^(2))+x+1 \desno| \desno))^(2))\le ((\left(\left ((x)^(2))+3x+4 \desno| \desno))^(2)); \\ & ((\left(((x)^(2))+x+1 \desno))^(2))\le ((\left(((x)^(2))+3x+4 \desno))^(2)); \\ & ((\left(((x)^(2))+x+1 \desno))^(2))-((\left(((x)^(2))+3x+4 \ desno))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \desno)\puta \\ & \times \left(((x) ^(2))+x+1+((x)^(2))+3x+4 \desno)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)\le 0. \\\end(align)\]

Metoda intervala:

\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \right)=0 \\ & -2x-3=0\ Desna strelica x=-1,5; \\ & 2((x)^(2))+4x+5=0\Strelica desno D=16-40 \lt 0\Strelica desno \varnothing . \\\end(poravnati)\]

Na brojevnoj pravoj postoji samo jedan korijen:

Odgovor je čitav interval

Odgovor: $x\in \left[ -1.5;+\infty \right)$.

Mala napomena o zadnjem zadatku. Kao što je jedan od mojih učenika tačno primetio, oba submodularna izraza u ovoj nejednakosti su očigledno pozitivna, pa se znak modula može izostaviti bez štete po zdravlje.

Ali ovo je potpuno drugačiji nivo razmišljanja i drugačiji pristup - to se uslovno može nazvati metodom posljedica. O tome - u posebnoj lekciji. Pređimo sada na završni dio današnje lekcije i pogledajmo univerzalni algoritam koji uvijek radi. Čak i kada su svi dosadašnji pristupi bili nemoćni. :)

4. Metoda nabrajanja opcija

Šta ako sve ove tehnike ne pomognu? Ako se nejednakost ne može svesti na nenegativne repove, ako je nemoguće izolirati modul, ako općenito postoji bol, tuga, melankolija?

Tada na scenu stupa „teška artiljerija“ sve matematike – metoda grube sile. U odnosu na nejednakosti sa modulom to izgleda ovako:

1. Napišite sve submodularne izraze i postavite ih jednakima nuli;
2. Riješite rezultirajuće jednačine i označite korijene pronađene na jednoj brojevnoj pravoj;
3. Prava linija će biti podijeljena na nekoliko dijelova, unutar kojih svaki modul ima fiksni znak i stoga je jedinstveno otkriven;
4. Riješite nejednakost na svakom takvom odsječku (možete zasebno razmotriti korijenske granice dobivene u koraku 2 - radi pouzdanosti). Kombinujte rezultate - ovo će biti odgovor. :)

Pa kako? Slabo? Lako! Samo na duže vreme. Da vidimo u praksi:

Zadatak. Riješite nejednačinu:

\[\lijevo| x+2 \desno| \lt \lijevo| x-1 \right|+x-\frac(3)(2)\]

Rješenje. Ovo sranje se ne svodi na nejednakosti poput $\left| f\right| \lt g$, $\left| f\right| \gt g$ ili $\left| f\right| \lt \lijevo| g \right|$, tako da djelujemo unaprijed.

Zapisujemo submodularne izraze, izjednačavamo ih sa nulom i pronalazimo korijene:

\[\begin(align) & x+2=0\Strelica desno x=-2; \\ & x-1=0\Strelica desno x=1. \\\end(poravnati)\]

Ukupno imamo dva korijena koji dijele brojevnu pravu na tri dijela, unutar kojih se svaki modul otkriva na jedinstven način:

Particioniranje brojevne prave nulama submodularnih funkcija

Pogledajmo svaki odjeljak posebno.

1. Neka je $x \lt -2$. Tada su oba submodularna izraza negativna, a originalna nejednakost će biti prepisana na sljedeći način:

\[\begin(align) & -\left(x+2 \right) \lt -\left(x-1 \right)+x-1.5 \\ & -x-2 \lt -x+1+ x- 1.5 \\ & x \gt 1.5 \\\end(poravnati)\]

Imamo prilično jednostavno ograničenje. Presijecimo ga s početnom pretpostavkom da je $x \lt -2$:

\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1.5 \\\end(align) \right.\Rightarrow x\in \varnothing \]

Očigledno, varijabla $x$ ne može istovremeno biti manja od −2 i veća od 1,5. U ovoj oblasti nema rješenja.

1.1. Razmotrimo odvojeno granični slučaj: $x=-2$. Zamijenimo ovaj broj u originalnu nejednakost i provjerimo: da li je to istina?

\[\begin(poravnati) & ((\levo. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=-2) ) \ \ & 0 \lt \lijevo| -3\desno|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0.5\Strelica desno \varnothing . \\\end(poravnati)\]

Očigledno je da nas je lanac proračuna doveo do netačne nejednakosti. Dakle, originalna nejednakost je također netačna, a $x=-2$ nije uključeno u odgovor.

2. Neka sada $-2 \lt x \lt 1$. Lijevi modul će se već otvoriti sa „plus“, ali će se desni i dalje otvoriti sa „minus“. Imamo:

\[\begin(poravnati) & x+2 \lt -\left(x-1 \right)+x-1.5 \\ & x+2 \lt -x+1+x-1.5 \\& x \lt - 2.5 \\\end(poravnati)\]

Opet se ukrštamo s originalnim zahtjevom:

\[\left\( \begin(align) & x \lt -2.5 \\ & -2 \lt x \lt 1 \\\end(align) \right.\Rightarrow x\in \varnothing \]

I opet, skup rješenja je prazan, jer nema brojeva koji su i manji od −2,5 i veći od −2.

2.1. I opet poseban slučaj: $x=1$. Zamjenjujemo u originalnu nejednakost:

\[\begin(poravnati) & ((\levo. \left| x+2 \right| \lt \left| x-1 \right|+x-1.5 \right|)_(x=1)) \\ & \levo| 3\desno| \lt \lijevo| 0\desno|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0.5\Strelica desno \varnothing . \\\end(poravnati)\]

Slično kao u prethodnom “posebnom slučaju”, broj $x=1$ očigledno nije uključen u odgovor.

3. Posljednji dio reda: $x \gt 1$. Ovdje se otvaraju svi moduli sa znakom plus:

\[\početak(poravnati) & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\ \end(poravnati)\ ]

I opet siječemo pronađeni skup s originalnim ograničenjem:

\[\left\( \begin(align) & x \gt 4.5 \\ & x \gt 1 \\\end(align) \right.\Rightarrow x\in \left(4.5;+\infty \right)\ ]

Konačno! Pronašli smo interval koji će biti odgovor.

Odgovor: $x\in \levo(4,5;+\infty \desno)$

Na kraju, jedna napomena koja vas može spasiti od glupih grešaka pri rješavanju stvarnih problema:

Rješenja nejednačina sa modulima obično predstavljaju neprekidne skupove na brojevnoj pravoj - intervale i segmente. Izolovane tačke su mnogo rjeđe. A još rjeđe se dešava da se granica rješenja (kraj segmenta) poklapa s granicom raspona koji se razmatra.

Prema tome, ako granice (isti „posebni slučajevi“) nisu uključene u odgovor, onda područja lijevo i desno od ovih granica gotovo sigurno neće biti uključena u odgovor. I obrnuto: granica je ušla u odgovor, što znači da će i neka područja oko nje biti odgovori.

Imajte to na umu kada pregledavate svoja rješenja.

Ova lekcija će revidirati koncept modula realnog broja i predstaviti neke od njegovih osnovnih definicija, praćenih primjerima koji pokazuju upotrebu raznih od ovih definicija.

Predmet:Realni brojevi

lekcija:Modul realnog broja

1. Definicije modula

Razmotrimo takav koncept kao modul realnog broja; on ima nekoliko definicija.

Definicija 1. Udaljenost od tačke na koordinatnoj liniji do nule se naziva modulo broj, što je koordinata ove tačke (slika 1).

Primjer 1. . Imajte na umu da su moduli suprotnih brojeva jednaki i nenegativni, budući da je to udaljenost, ali ne može biti negativna, a udaljenost od brojeva simetričnih oko nule do ishodišta jednaka je.

Definicija 2. .

Primjer 2. Razmotrimo jedan od problema postavljenih u prethodnom primjeru kako bismo demonstrirali ekvivalentnost uvedenih definicija. , kao što vidimo, sa negativnim brojem ispod predznaka modula, dodavanjem još jednog minusa ispred njega dobija se nenegativan rezultat, kao što slijedi iz definicije modula.

Posljedica. Udaljenost između dvije tačke sa koordinatama na koordinatnoj liniji može se naći na sljedeći način bez obzira na relativni položaj tačaka (slika 2).

2. Osnovna svojstva modula

1. Modul bilo kojeg broja nije negativan

2. Modul proizvoda je proizvod modula

3. Kvocijentni modul je količnik modula

3. Rješavanje problema

Primjer 3. Riješite jednačinu.

Rješenje. Koristimo drugu definiciju modula: i napišemo našu jednačinu u obliku sistema jednačina za različite opcije otvaranja modula.

Primjer 4. Riješite jednačinu.

Rješenje. Slično rješenju prethodnog primjera, dobijamo da .

Primjer 5. Riješite jednačinu.

Rješenje. Rešimo kroz posljedicu iz prve definicije modula: . Prikažimo ovo na brojevnoj osi, uzimajući u obzir da će željeni korijen biti na udaljenosti od 2 od tačke 3 (slika 3).

Na osnovu slike dobijamo korijene jednadžbe: , budući da se tačke sa takvim koordinatama nalaze na udaljenosti od 2 od tačke 3, kako se zahteva u jednačini.

Odgovori. .

Primjer 6. Riješite jednačinu.

Rješenje. U usporedbi s prethodnim problemom, postoji samo jedna komplikacija - to je da nema potpune sličnosti s formulacijom posljedica o udaljenosti između brojeva na koordinatnoj osi, jer se ispod predznaka modula nalazi znak plus, a ne minus sign. Ali nije teško dovesti ga u traženu formu, što ćemo i učiniti:

Oslikajmo ovo na brojevnoj osi slično prethodnom rješenju (slika 4).

Korijeni jednadžbe .

Odgovori. .

Primjer 7. Riješite jednačinu.

Rješenje. Ova jednadžba je malo složenija od prethodne, jer je nepoznata na drugom mjestu i ima predznak minus, osim toga ima i brojčani množitelj. Da bismo riješili prvi problem, koristimo jedno od svojstava modula i dobijemo:

Da bismo riješili drugi problem, izvršimo promjenu varijabli: , što će nas dovesti do najjednostavnije jednačine . Po drugoj definiciji modula . Zamijenite ove korijene u jednadžbu zamjene i dobijete dvije linearne jednačine:

Odgovori. .

4. Kvadratni korijen i modul

Vrlo često, prilikom rješavanja problema s rootsom, nastaju moduli i treba obratiti pažnju na situacije u kojima se pojavljuju.

Na prvi pogled na ovaj identitet, mogu se pojaviti pitanja: "zašto postoji modul?" i "zašto je identitet lažan?" Ispostavilo se da možemo dati jednostavan protuprimjer na drugo pitanje: da li to mora biti istina, što je ekvivalentno, ali ovo je lažni identitet.

Nakon ovoga može se postaviti pitanje: „Zar takav identitet ne rješava problem?“, ali postoji i protuprimjer za ovaj prijedlog. Ako bi ovo trebalo biti istina, što je ekvivalentno, ali ovo je lažni identitet.

Prema tome, ako se sjetimo da je kvadratni korijen nenegativnog broja nenegativan broj, a vrijednost modula nije negativna, postaje jasno zašto je gornja tvrdnja istinita:

.

Primjer 8. Izračunajte vrijednost izraza.

Rješenje. U takvim zadacima važno je ne odmah se bezobzirno riješiti root-a, već koristiti gore spomenuti identitet, jer .

Sastoji se od pozitivnih (prirodnih) brojeva, negativnih brojeva i nule.

Svi negativni brojevi, i samo oni, manji su od nule. Na brojevnoj liniji negativni brojevi se nalaze lijevo od nule. Za njih, kao i za pozitivne brojeve, definiran je odnos reda, koji omogućava upoređivanje jednog cijelog broja s drugim.

Za svaki prirodan broj n postoji jedan i samo jedan negativan broj, označen -n, koji nadopunjuje n na nulu: n + (− n) = 0 . Oba broja se pozivaju suprotno jedno za drugo. Oduzimanje cijelog broja a je ekvivalentno dodavanju sa njegovom suprotnošću: -a.

Svojstva negativnih brojeva

Negativni brojevi slijede gotovo ista pravila kao prirodni brojevi, ali imaju neke posebne karakteristike.

Istorijska skica

Književnost

• Vygodsky M. Ya. Priručnik za osnovnu matematiku. - M.: AST, 2003. - ISBN 5-17-009554-6
• Glazer G.I. Istorija matematike u školi. - M.: Prosveta, 1964. - 376 str.

Linkovi

Wikimedia fondacija. 2010.

• Bezobzirno nanošenje štete
• Neotropics

Pogledajte šta je "nenegativan broj" u drugim rječnicima:

Realni broj- Realni ili realni broj je matematička apstrakcija koja je nastala iz potrebe mjerenja geometrijskih i fizičkih veličina okolnog svijeta, kao i izvođenja operacija kao što su vađenje korijena, izračunavanje logaritama, rješavanje... ... Wikipedia

obično mali nenegativni cijeli broj- Dio kodiranja koji predstavlja vrijednosti neograničenog nenegativnog cijelog broja, ali gdje je vjerovatnije da će se male vrijednosti češće pojavljivati ​​(ITU T X.691). Teme ... ... Vodič za tehnički prevodilac

REAL NUMBER- realni broj, pozitivan broj, negativan broj ili nula. Koncept brojnog broja nastao je proširenjem koncepta racionalnog broja. Potreba za ovim proširenjem je zbog praktične upotrebe matematike u izražavanju ... ... Mathematical Encyclopedia

prost broj- Prost broj je prirodan broj koji ima tačno dva različita prirodna djelitelja: jedan i sebe. Svi ostali prirodni brojevi, osim jednog, nazivaju se kompozitnim. Dakle, svi prirodni brojevi su veći od jednog... ... Wikipedia

prirodni broj- ▲ cijeli broj koji izražava, realan, broj prirodni broj nenegativan cijeli broj; izražava broj pojedinačnih celih objekata u čemu l. agregati; označavaju broj stvarnih celih objekata; izraz brojeva. četiri... Ideografski rečnik ruskog jezika

Decimala- Decimala je vrsta razlomka koja predstavlja način predstavljanja realnih brojeva u obliku u kojem je predznak razlomka: ili, ili, decimalni zarez koji služi kao separator između cijelog broja i razlomka broja. ... ... Wikipedia Wikipedia

Šef ShMO
nastavnici matematike _______Kalashnikova Zh.YuOpštinska budžetska obrazovna ustanova
"Srednja škola br. 89"
Tematski testovi iz matematike za 6. razred
prema udžbeniku I.I. Zubareva i A.G. Mordkovich
Sastavili: nastavnici matematike:
Kalašnjikova Zhanna Yurievna
Stolbova Ljudmila Antonovna
ZATO Seversk
2016
Sadržaj
Test br. 1…………………………………………………………………………………………….3-6
Test br. 2…………………………………………………………………………………………………….7-10
Test br. 3…………………………………………………………………………………………………………………………………….11-14
Odgovori………………………………………………………………………………………………………………………..15
Test br. 1 “Pozitivni i negativni brojevi”
Opcija 1
Unesite negativan razlomak:
-165
38
-7.92
67Opišite događaj “Na koordinatnoj zraci je označen broj -5,5”
Pouzdan
Nemoguće
Slučajno

Koji je od četiri broja najveći?
8,035
80,35
0,8035
803,5
Koja se tačka nalazi na koordinatnoj liniji desno od tačke O (0)?
M (-4)
E (-15)
K (15)
D(-1,2)
Noću je temperatura zraka iznosila -5°C. Tokom dana termometar je već bio +3 °C. Kako se promijenila temperatura zraka?
Povećano za 8o
Smanjeno za 2o
Povećano za 2o
Smanjeno za 8o
Tačka x(-2) je označena na koordinatnoj liniji – centar simetrije. Označite koordinate tačaka koje se nalaze na ovoj pravoj simetrično u odnosu na tačku x.

(-1) i (1)
(-1) i (1)
(3) i (-3)
(0) i (-4)
Koje tačke na koordinatnoj liniji nisu simetrične u odnosu na ishodište - tačka O (0).
B(-5) i C(5)
D(0,5) i E(-0,5)
M(-3) i K(13)
A(18) i X(-18)
Koliki je zbir brojeva 0,316+0,4?
0,356
0,716
4,316
0,32
Izračunaj 25% od broja 0,4.
0,1
0,001
10
100
Izračunajte razliku 9100 i 0,03
0,05
0,6
9,03
350Opcija 2
Unesite negativan razlomak.
8,63
-1045
913-0,2
Opišite događaj „Na koordinatnoj zraci označen je broj 7.“
Slučajno
Nemoguće
Pouzdan
Koji je broj najmanji?
15,49
154,9
1,549
1549
Koja od tačaka se nalazi na koordinatnoj liniji lijevo od tačke O(0).
A(-0,5)
U 6)
M(0,5)
K(38)
Tokom dana termometar je pokazivao +5°C, a uveče -2°C. Kako se promijenila temperatura zraka?
Povećano za 3o
Smanjeno za 7o
Smanjen za 3o
Povećano za 7o
Centar simetrije je označen na koordinatnoj liniji - tačka A(-3). Označite koordinate tačaka koje se nalaze na ovoj liniji simetrično u odnosu na tačku A.

(-2) i (2)
(0) i (-5)
(-6) i (1)
(-1) i (-5)
Koje tačke koordinatne prave nisu simetrične u odnosu na ishodište - tačka O(0).
A(6) i B(-6)
C(12) i D(-2)
M(-1) i K(1)
X (-9) i Y (9)
Koliki je zbir brojeva 0,237 i 0,3?
0,24
3,237
0,537
0,267
Izračunajte 20% od 0,5
10
0,1
0,2
0,01
Izračunajte razliku od 0,07 i 31001250,5
1
425 Test br. 2. Apsolutna vrijednost broja. Suprotni brojevi.
Opcija 1
Koji od datih brojeva ima najmanji modul
-11
1013-4,196
-4,2
Navedite netačnu jednačinu
85=-85
-1,9=1,9
35= 3558=-58 Modul nenegativnog broja je nenegativan broj. Da li je ova izjava istinita?
Da
br
Koji je od ovih brojeva suprotan broju -34?43-43-3434Kolika je vrijednost izraza -(-m) ako je m = -15
+15
-15
Izračunajte vrijednost izraza: -2,5∙4--919
-10
1
-1
Riješite jednačinu: x=40-40
40
40 ili -40
Koji se cijeli brojevi nalaze na koordinatnoj liniji između brojeva 2,75 i 3,9?
-2, -1, 1, 2
-1, 0, 1, 2, 3
-1, 0, 1, 2, 3, 4
-2, -1, 0, 1, 2, 3
Da li je tačna nejednakost -30>-50?
br
Navedite sve cijele brojeve x ako je x≤30, 1, 2
0, 1, 2, 3
0, 1, 2, 3, 4
1, 2, 3
Opcija 2
Koji broj ima najveći modul?
-0,6
-50,603
493550,530
Navedite netačnu jednačinu
-1,5=1,512=12-117=117-325=-325Može li modul negativnog broja biti negativan broj
Da
br

Koji je od ovih brojeva suprotan broju 124?
-24
24
-124124Kolika je vrijednost izraza –(-k), ako je k = -9
-9
+9
Izračunajte vrijednost izraza: 2,5:-0,5+1,250
15
-2,5
2,5
Riješite jednačinu x=100100
-100
100 ili -100
Koji se cijeli brojevi nalaze na koordinatnoj liniji između brojeva 1 i - 4.5
-4, -3, -2, -1, 0
-3, -2, -1
-5, -4, -3, -2, -1
-4, -3, -2, -1, 1
Da li je nejednakost -25 tačna?<-10?
Da
br
Navedite sve cijele brojeve x ako je x≤44, 3, 2
0, 1, 2, 3
1, 2, 3, 4
0, 1, 2, 3, 4
Test br. 3. Poređenje brojeva
Opcija 1
Koja od nejednakosti je netačna?
-20 > 2
0 < -1
-16 > -7
-5 < -3

-320 -920>
<
=
Je li istina da je broj 0 veći od bilo kojeg negativnog broja?
Da
br
Broj a nije negativan. Kako možemo zapisati ovu izjavu kao nejednakost?
a<0a≤0a≥0a>0 Označite najveći od datih brojeva.
0,16
-3018-0,4
0,01
Za koje prirodne vrijednosti x je istinita nejednakost x≤44, 3, 2?
1 , 2, 3, 4
4, 3, 2, 1
0, 1, 2, 3
Za koje je cjelobrojne vrijednosti y nejednakost y tačna?<-2?0
-1
0, -1, 1
Nema takvih vrijednosti
Brojevi -6; -3,8; -115; 0.8 nalazi se:
U opadajućem redosledu
U rastućem redosledu
U neredu
Na radiju je prenošena vremenska prognoza: očekuje se pad temperature do -20 °C. Opišite ovaj događaj:
Nemoguće
Pouzdan
Slučajno
Opcija 2
Koja od nejednakosti je tačna?
-5 > 0
6 < -17
-34 > -40
-9 < -63
Koji znak mora biti napisan između ovih razlomaka da bi nejednakost bila tačna?
-1315 -715<
>
=
Je li istina da je broj 0 manji od bilo kojeg negativnog broja?
Da
br
Broj x nije veći od nule. Kako možemo zapisati ovu izjavu kao nejednakost?
x≥0x>0x<0x≤0Укажите наименьшее из данных чисел.
-5,92
1,7
-1000
35Za koje prirodne vrijednosti a je tačna nejednakost a≤3?1, 2, 3
0, 1, 2, 3
1, 2
0, 1, 2
Za koje je cjelobrojne vrijednosti m tačna nejednakost m?<-4?-3, -2, -1
0, -1, -2, -3, 1, 2, 3
0
Nema takvih vrijednosti
Brojevi 1,2; -1,2; -427; -100 nalazi se:
U neredu
U rastućem redosledu
U opadajućem redosledu
Tačka A(5) je označena na koordinatnoj liniji. Na ovoj pravoj nasumično je označena još jedna tačka B. Ispostavilo se da je njena koordinata suprotan broj od 5. Opišite ovaj događaj.
Slučajno
Pouzdan
Nemoguće
Odgovori
Test br. 1 Test br. 2
Br. Opcija 1 Opcija 2
1 3 4
2 2 3
3 4 3
4 3 1
5 1 2
6 4 4
7 3 2
8 2 3
9 1 2
10 4 1
Br. Opcija 1 Opcija 2
1 3 2
2 1 4
3 1 2
4 4 3
5 2 1
6 3 4
7 3 3
8 4 1
9 1 2
10 2 4

Test br. 3
Br. Opcija 1 Opcija 2
1 4 3
2 1 2
3 1 2
4 3 4
5 1 3
6 2 1
7 4 4
8 2 3