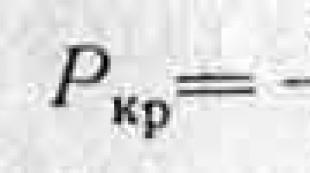Занаяти

Уравнение на равнина е разстоянието от точка до равнина. Разстояние от точка до равнина. начин. Векторен метод

Поддържането на вашата поверителност е важно за нас. Поради тази причина разработихме Политика за поверителност, която описва как използваме и съхраняваме вашата информация. Моля, прегледайте нашите практики за поверителност и ни уведомете, ако имате въпроси.

Събиране и използване на лична информация

Личната информация се отнася до данни, които могат да бъдат използвани за идентифициране или контакт с конкретно лице.

Може да бъдете помолени да предоставите вашата лична информация по всяко време, когато се свържете с нас.

По-долу са дадени някои примери за видовете лична информация, която можем да събираме и как можем да използваме тази информация.

Каква лична информация събираме:

Когато подадете заявление на сайта, ние може да съберем различна информация, включително вашето име, телефонен номер, имейл адрес и др.

Как използваме вашата лична информация:

Личната информация, която събираме, ни позволява да се свържем с вас с уникални оферти, промоции и други събития и предстоящи събития.
От време на време може да използваме вашата лична информация, за да изпращаме важни известия и съобщения.
Може също така да използваме лична информация за вътрешни цели, като например извършване на одити, анализ на данни и различни изследвания, за да подобрим услугите, които предоставяме, и да ви предоставим препоръки относно нашите услуги.
Ако участвате в теглене на награди, конкурс или подобна промоция, ние може да използваме предоставената от вас информация за администриране на такива програми.

Разкриване на информация на трети лица

Ние не разкриваме информацията, получена от вас, на трети страни.

Изключения:

При необходимост - в съответствие със закона, съдебна процедура, в съдебно производство и/или въз основа на публични искания или искания от държавни органи на територията на Руската федерация - да разкриете вашата лична информация. Може също така да разкрием информация за вас, ако преценим, че такова разкриване е необходимо или подходящо за целите на сигурността, правоприлагането или други обществено значими цели.
В случай на реорганизация, сливане или продажба, можем да прехвърлим личната информация, която събираме, на съответната трета страна приемник.

Защита на личната информация

Ние вземаме предпазни мерки – включително административни, технически и физически – за да защитим вашата лична информация от загуба, кражба и злоупотреба, както и неоторизиран достъп, разкриване, промяна и унищожаване.

Зачитане на вашата поверителност на фирмено ниво

За да гарантираме, че вашата лична информация е защитена, ние съобщаваме стандартите за поверителност и сигурност на нашите служители и стриктно прилагаме практиките за поверителност.

Определяне на разстоянието между: 1 - точка и равнина; 2 - прави и плоски; 3 - самолети; 4 - пресичащите се прави линии се разглеждат заедно, тъй като алгоритъмът за решаване на всички тези задачи е по същество един и същ и се състои от геометрични конструкции, които трябва да се извършат, за да се определи разстоянието между дадена точка A и равнина α. Ако има някаква разлика, тя се състои само в това, че в случаи 2 и 3, преди да започнете да решавате задачата, трябва да маркирате произволна точка A на правата m (случай 2) или равнината β (случай 3). разстояния между пресичащи се прави, първо ги затваряме в успоредни равнини α и β и след това определяме разстоянието между тези равнини.

Нека разгледаме всеки от отбелязаните случаи на решаване на проблеми.

1. Определяне на разстоянието между точка и равнина.

Разстоянието от точка до равнина се определя от дължината на перпендикулярен сегмент, прекаран от точка до равнината.

Следователно решението на този проблем се състои в последователно извършване на следните графични операции:

1) от точка А спускаме перпендикуляра към равнината α (фиг. 269);

2) намерете пресечната точка M на този перпендикуляр с равнината M = a ∩ α;

3) определете дължината на сегмента.

Ако равнината α е в общо положение, тогава за да се спусне перпендикуляр върху тази равнина, е необходимо първо да се определи посоката на хоризонталните и фронталните проекции на тази равнина. Намирането на пресечната точка на този перпендикуляр с равнината също изисква допълнителни геометрични конструкции.

Решението на задачата се опростява, ако равнината α заема определена позиция спрямо проекционните равнини. В този случай както проекцията на перпендикуляра, така и намирането на точката на срещата му с равнината се извършват без никакви допълнителни спомагателни конструкции.

ПРИМЕР 1. Определете разстоянието от точка А до фронтално проектираната равнина α (фиг. 270).

РЕШЕНИЕ. През A" начертаваме хоризонталната проекция на перпендикуляра l" ⊥ h 0α, а през A" - неговата челна проекция l" ⊥ f 0α. Отбелязваме точката M" = l" ∩ f 0α . От AM || π 2, тогава [A" M"] == |AM| = d.

От разглеждания пример става ясно колко просто се решава задачата, когато самолетът заема изпъкнала позиция. Следователно, ако в изходните данни е указана равнина на обща позиция, тогава преди да продължите с решението, равнината трябва да бъде преместена в позиция, перпендикулярна на която и да е равнина на проекция.

ПРИМЕР 2. Определете разстоянието от точка К до равнината, зададена от ΔАВС (фиг. 271).

1. Прехвърляме равнината ΔАВС в проектираща позиция *. За да направим това, преминаваме от системата xπ 2 /π 1 към x 1 π 3 /π 1: посоката на новата ос x 1 е избрана перпендикулярна на хоризонталната проекция на хоризонталната равнина на триъгълника.

2. Проектирайте ΔABC върху нова равнина π 3 (равнината ΔABC се проектира върху π 3, в [ C " 1 B " 1 ]).

3. Проектирайте точка K върху същата равнина (K" → K" 1).

4. През точката K" 1 прекарваме (K" 1 M" 1)⊥ отсечката [C" 1 B" 1]. Търсеното разстояние d = |K" 1 M" 1 |

Решението на проблема е опростено, ако равнината е дефинирана от следи, тъй като няма нужда да се чертаят проекции на линии на ниво.

ПРИМЕР 3. Определете разстоянието от точка K до равнината α, зададена от следите (фиг. 272).

* Най-рационалният начин за прехвърляне на равнината на триъгълника в позицията на проектиране е замяната на проекционните равнини, тъй като в този случай е достатъчно да се изгради само една спомагателна проекция.

РЕШЕНИЕ. Заменяме равнината π 1 с равнината π 3, за това начертаваме нова ос x 1 ⊥ f 0α. Върху h 0α отбелязваме произволна точка 1" и определяме нейната нова хоризонтална проекция върху равнината π 3 (1" 1). През точките X α 1 (X α 1 = h 0α 1 ∩ x 1) и 1" 1 прекарваме h 0α 1. Определяме новата хоризонтална проекция на точката K → K" 1. От точка K" 1 спускаме перпендикуляра до h 0α 1 и отбелязваме точката на пресичането му с h 0α 1 - M" 1. Дължината на сегмента K" 1 M" 1 ще покаже необходимото разстояние.

2. Определяне на разстоянието между права и равнина.

Разстоянието между права и равнина се определя от дължината на перпендикулярен сегмент, спуснат от произволна точка на правата до равнината (виж фиг. 248).

Следователно решението на проблема за определяне на разстоянието между права линия m и равнина α не се различава от примерите, обсъдени в параграф 1 за определяне на разстоянието между точка и равнина (виж Фиг. 270 ... 272). Като точка можете да вземете всяка точка, принадлежаща на права m.

3. Определяне на разстоянието между равнините.

Разстоянието между равнините се определя от размера на перпендикулярния сегмент, пуснат от точка, взета от една равнина до друга равнина.

От тази дефиниция следва, че алгоритъмът за решаване на проблема за намиране на разстоянието между равнините α и β се различава от подобен алгоритъм за решаване на проблема за определяне на разстоянието между правата m и равнината α само в това, че правата m трябва да принадлежи на равнината α , т.е., за да се определи разстоянието между равнините α и β, следва:

1) вземете права линия m в равнината α;

2) изберете произволна точка A на права m;

3) от точка А спуснете перпендикуляра l към равнината β;

4) определете точка M - точката на среща на перпендикуляра l с равнината β;

5) определете размера на сегмента.

На практика е препоръчително да се използва различен алгоритъм за решение, който ще се различава от дадения само по това, че преди да продължите с първата стъпка, равнините трябва да бъдат прехвърлени в положение на проекция.

Включването на тази допълнителна операция в алгоритъма опростява изпълнението на всички останали точки без изключение, което в крайна сметка води до по-просто решение.

ПРИМЕР 1. Определете разстоянието между равнините α и β (фиг. 273).

РЕШЕНИЕ. Преминаваме от системата xπ 2 /π 1 към x 1 π 1 /π 3. По отношение на новата равнина π 3 равнините α и β заемат изпъкнало положение, следователно разстоянието между новите челни следи f 0α 1 и f 0β 1 е желаното.

В инженерната практика често е необходимо да се реши задачата за изграждане на равнина, успоредна на дадена равнина и отдалечена от нея на дадено разстояние. Пример 2 по-долу илюстрира решението на такъв проблем.

ПРИМЕР 2. Необходимо е да се построят проекции на равнина β, успоредна на дадена равнина α (m || n), ако е известно, че разстоянието между тях е d (фиг. 274).

1. В равнината α начертайте произволни хоризонтални линии h (1, 3) и предни линии f (1, 2).

2. От точка 1 възстановяваме перпендикуляра l към равнината α(l" ⊥ h", l" ⊥ f").

3. На перпендикуляра l отбелязваме произволна точка A.

4. Определете дължината на отсечката - (позицията показва на диаграмата метрично неизкривената посока на правата l).

5. Поставете сегмента = d върху правата линия (1"A 0) от точка 1".

6. Маркирайте върху проекциите l" и l" точки B" и B", съответстващи на точка B 0.

7. През точка B прекарваме равнината β (h 1 ∩ f 1). Към β || α, е необходимо да се спазва условието h 1 || h и f 1 || f.

4. Определяне на разстоянието между пресичащите се прави.

Разстоянието между пресичащите се прави се определя от дължината на перпендикуляра, съдържащ се между успоредните равнини, на които принадлежат пресичащите се прави.

За да начертаете взаимно успоредни равнини α и β през пресичащи се прави m и f, е достатъчно да начертаете през точка A (A ∈ m) права линия p, успоредна на права линия f, и през точка B (B ∈ f) права k, успоредна на права m. Пресечните прави m и p, f и k определят взаимно успоредните равнини α и β (виж фиг. 248, e). Разстоянието между равнините α и β е равно на необходимото разстояние между пресечните прави m и f.

Може да се предложи друг начин за определяне на разстоянието между пресичащите се линии, който се състои в това, че с помощта на някакъв метод за трансформиране на ортогонални проекции една от пресичащите се линии се прехвърля в позицията на проектиране. В този случай една проекция на правата се изражда в точка. Разстоянието между новите проекции на пресичащи се линии (точка A" 2 и сегмент C" 2 D" 2) е необходимото.

На фиг. 275 е показано решение на задачата за определяне на разстоянието между пресичащите прави a и b, дадени отсечки [AB] и [CD]. Разтворът се извършва в следната последователност:

1. Преместете една от пресичащите се линии (a) в положение, успоредно на равнината π 3; За да направите това, преминете от системата от проекционни равнини xπ 2 /π 1 към новата x 1 π 1 /π 3, оста x 1 е успоредна на хоризонталната проекция на права линия a. Определете a" 1 [A" 1 B" 1 ] и b" 1.

2. Заменяйки равнината π 1 с равнината π 4, преместваме правата линия

и в позиция a" 2, перпендикулярна на равнината π 4 (новата ос x 2 е начертана перпендикулярно на a" 1).

3. Постройте нова хоризонтална проекция на права линия b" 2 - [ C" 2 D" 2 ].

4. Разстоянието от точка A" 2 до права C" 2 D" 2 (сегмент (A" 2 M" 2 ] (е необходимото.

Трябва да се има предвид, че прехвърлянето на една от пресичащите се линии в проектиращата позиция не е нищо повече от прехвърляне на равнините на успоредност, в които могат да бъдат затворени правите a и b, също в проектиращата позиция.

Всъщност, чрез преместване на права a до позиция, перпендикулярна на равнината π 4, ние гарантираме, че всяка равнина, съдържаща права a, е перпендикулярна на равнината π 4, включително равнината α, дефинирана от прави a и m (a ∩ m, m | | б). Ако сега начертаем права n, успоредна на a и пресичаща права b, тогава получаваме равнината β, която е втората равнина на успоредност, която съдържа пресичащите се прави a и b. Тъй като β || α, тогава β ⊥ π 4 .

Намирането на разстоянието от точка до равнина е често срещан проблем, който възниква при решаването на различни проблеми на аналитичната геометрия; например, този проблем може да се сведе до намиране на разстоянието между две пресичащи се прави линии или между права линия и равнина, успоредна на то.

Да разгледаме равнината $β$ и точка $M_0$ с координати $(x_0;y_0; z_0)$, която не принадлежи на равнината $β$.

Определение 1

Най-късото разстояние между точка и равнина ще бъде перпендикулярът, прекаран от точката $M_0$ към равнината $β$.

Фигура 1. Разстояние от точка до равнина. Author24 - онлайн обмен на студентски работи

По-долу обсъждаме как да намерим разстоянието от точка до равнина с помощта на метода на координатите.

Извеждане на формулата за координатния метод за намиране на разстоянието от точка до равнина в пространството

Перпендикуляр от точка $M_0$, пресичащ равнината $β$ в точка $M_1$ с координати $(x_1;y_1; z_1)$, лежи на права линия, чийто насочващ вектор е нормалният вектор на равнината $β$. В този случай дължината на единичния вектор $n$ е равна на единица. Съответно разстоянието от $β$ до точка $M_0$ ще бъде:

$ρ= |\vec(n) \cdot \vec(M_1M_0)|\left(1\right)$, където $\vec(M_1M_0)$ е нормалният вектор на равнината $β$ и $\vec( n)$ е единичният нормален вектор на разглежданата равнина.

В случай, че уравнението на равнината е дадено в общ вид $Ax+ By + Cz + D=0$, координатите на нормалния вектор на равнината са коефициентите на уравнението $\(A;B;C\ )$ и единичният нормален вектор в този случай има координатите , изчислени с помощта на следното уравнение:

$\vec(n)= \frac($A;B;C$)(\sqrt(A^2 + B^2 + C^2))\left(2\right)$.

Сега можем да намерим координатите на нормалния вектор $\vec(M_1M_0)$:

$\vec(M_0M_1)= $x_0 – x_1;y_0-y_1;z_0-z_1$\left(3\right)$.

Ние също така изразяваме коефициента $D$, като използваме координатите на точка, разположена в равнината $β$:

$D= Ax_1+By_1+Cz_1$

Координатите на единичния нормален вектор от равенството $(2)$ могат да бъдат заменени в уравнението на равнината $β$, тогава имаме:

$ρ= \frac(|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|)(\sqrt(A^2+B^2+C^2))= \frac( |Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|)(\sqrt(A^2+B^2+C^2)) = \frac(Ax_0+ By_0 + Cz_0 + D)(\sqrt(A^2 +B^2+C^2))\left(4\right)$

Равенството $(4)$ е формула за намиране на разстоянието от точка до равнина в пространството.

Общ алгоритъм за намиране на разстоянието от точка $M_0$ до равнина

Ако уравнението на равнината не е дадено в общ вид, първо трябва да го сведете до общ вид.
След това е необходимо да изразим от общото уравнение на равнината нормалния вектор на дадена равнина през точката $M_0$ и точка, принадлежаща на дадена равнина, за това трябва да използваме равенството $(3)$ .
Следващият етап е търсене на координатите на единичния нормален вектор на равнината по формулата $(2)$.
Накрая можете да започнете да намирате разстоянието от точката до равнината, това става чрез изчисляване на скаларното произведение на векторите $\vec(n)$ и $\vec(M_1M_0)$.

Условия на успоредност и перпендикулярност

1°. Условие за копланарност на две равнини

Нека са дадени две равнини:

А 1 х + б 1 г + ° С 1 z + д 1 = 0, н 1 = {А 1 ; б 1 ; ° С 1 } ≠ 0 ;(1)

А 2 х + б 2 г + ° С 2 z + д 2 = 0, н 2 = {А 2 ; б 2 ; ° С 2 } ≠ 0 .(2)

Кога са компланарни (т.е. успоредни или съвпадащи)? Очевидно това ще бъде така, ако и само ако техните нормални вектори са колинеарни. Прилагайки критерия за копланарност, получаваме

Изречение 1.Две равнини са компланарни тогава и само ако кръстосаното произведение на техните нормални вектори е равно на нулевия вектор:

[н 1 , н 2 ] = 0 .

2°. Условие за съвпадение на две равнини

Предложение 2.Равнините (1) и (2) съвпадат тогава и само ако всичките им четири коефициента са пропорционални, т.е. съществува число λ такова, че

А 2 = λ А 1 , б 2 = λ б 1 , ° С 2 = λ ° С 1 , д 2 = λ д 1 . (3)

Доказателство.Нека са изпълнени условия (3). Тогава уравнението на втората равнина може да се напише по следния начин:

λ А 1 х + λ б 1 г + λ ° С 1 z + λ д 1 = 0.

λ ≠ 0, иначе би било А 2 = б 2 = ° С 2 = д 2 = 0, което противоречи на условието н 2 ≠ 0 . Следователно последното уравнение е еквивалентно на уравнение (1), което означава, че двете равнини съвпадат.

Нека сега, напротив, знаем, че тези равнини съвпадат. Тогава техните нормални вектори са колинеарни, т.е. има число λ такова, че

А 2 = λ А 1 , б 2 = λ б 1 , ° С 2 = λ ° С 1 .

Уравнение (2) сега може да бъде пренаписано като:

λ А 1 х + λ б 1 г + λ ° С 1 z + д 2 = 0.

Умножавайки уравнение (1) по λ, получаваме еквивалентно уравнение на първата равнина (тъй като λ ≠ 0):

λ А 1 х + λ б 1 г + λ ° С 1 z + λ д 1 = 0.

Нека вземем малко точка ( х 0 , г 0 , z 0) от първата (и следователно втората) равнина и заместете нейните координати в последните две уравнения; получаваме правилните равенства:

λ А 1 х 0 + λ б 1 г 0 + λ ° С 1 z 0 + д 2 = 0 ;

λ А 1 х 0 + λ б 1 г 0 + λ ° С 1 z 0 + λ д 1 = 0.

Като извадим долната от горната, получаваме д 2 − λ д 1 = 0, т.е. д 2 = λ д 1, QED.

3°. Условие за перпендикулярност на две равнини

Очевидно за това е необходимо и достатъчно нормалните вектори да са перпендикулярни.

Предложение 3.Две равнини са перпендикулярни тогава и само ако скаларното произведение на нормалните вектори е нула:

(н 1 , н 2) = 0 .

Нека е дадено уравнението на равнината

брадва + от + Cz + д = 0, н = {А; б; ° С} ≠ 0 ,

и точка М 0 = (х 0 , г 0 , z 0). Нека изведем формулата за разстоянието от точка до равнина:

Нека вземем произволна точка Q = (х 1 , г 1 , z 1), лежащ в тази равнина. Координатите му отговарят на уравнението на равнината:

брадва 1 + от 1 + Cz 1 + д = 0.

Нека сега отбележим, че необходимото разстояние дравна на абсолютната стойност на векторната проекция спрямо посоката на вектора н (тук приемаме проекцията като числова величина, а не като вектор). След това прилагаме формулата за изчисляване на проекцията:

Подобна формула е валидна и за разстоянието дот точка М 0 = (х 0 , г 0) равнина към права линия, дадена от общото уравнение брадва + от + ° С = 0.

Нека има самолет . Нека начертаем нормално
през началото на координатите O. Нека дадено
– ъгли, образувани от нормалата с координатни оси.
. Позволявам – дължина на нормалния сегмент
докато се пресече с равнината. Ако приемем, че косинусите на посоката на нормалата са известни , извеждаме уравнението на равнината .

Позволявам
) е произволна точка от равнината. Единичният нормален вектор има координати. Нека намерим проекцията на вектора
към нормалното.

Тъй като точката Мпринадлежи на самолета, тогава

Това е уравнението на дадена равнина, т.нар нормално .

Разстояние от точка до равнина

Да се даде самолет ,М*
– точка в пространството, д – разстоянието му от самолета.

Определение. отклонение точки М*от самолета се нарича числото ( + д), Ако М* лежи от другата страна на равнината, където сочи положителната посока на нормалата , и номер (- д), ако точката се намира от другата страна на равнината:

Теорема. Нека самолетът с нормална единица се дава от нормалното уравнение:

Позволявам М*
– точка в пространството Отклонение t. М* от равнината се дава от израза

Доказателство.Проекция t.
* означаваме с нормално Q. Точково отклонение М*от равнината е равен

правило.Да намеря отклонение T. М* от равнината, трябва да замените координатите t в нормалното уравнение на равнината. М* . Разстоянието от точка до равнина е .

Намаляване на общото уравнение на равнината до нормална форма

Нека същата равнина се дефинира от две уравнения:

Общо уравнение

Нормално уравнение.

Тъй като и двете уравнения определят една и съща равнина, техните коефициенти са пропорционални:

Нека повдигнем на квадрат първите три равенства и ги съберем:

От тук ще намерим – нормализиращ фактор:

. (10)

Като умножим общото уравнение на равнината с нормализиращ коефициент, получаваме нормалното уравнение на равнината:

Примери за задачи по темата „Самолет“.

Пример 1.Създайте уравнение на равнината преминаващ през дадена точка
(2,1,-1) и успоредна на равнината.

Решение. Нормално за равнина :
. Тъй като равнините са успоредни, тогава нормалното също е нормален към желаната равнина . Използвайки уравнението на равнина, минаваща през дадена точка (3), получаваме за равнината уравнението:

Отговор:

Пример 2.Основата на перпендикуляр, падащ от началото към равнина , е смисълът
. Намерете уравнението на равнината .

Решение. вектор
е нормален към равнината . Точка М 0 принадлежи на самолета. Можете да използвате уравнението на равнина, минаваща през дадена точка (3):

Отговор:

Пример 3.Конструирайте равнина , преминавайки през точките

и перпендикулярна на равнината :.

Следователно, до известна степен М (х, г, z) е принадлежала на самолета , необходимо е три вектора
бяха компланарни:

=0.

Остава да разкрием детерминантата и да доведем получения израз до формата на общо уравнение (1).

Пример 4.Самолет се дава от общото уравнение:

Намерете точковото отклонение
от дадена равнина.

Решение. Нека приведем уравнението на равнината в нормална форма.

Нека заместим координатите на точката в полученото нормално уравнение М*.

Отговор:
.

Пример 5.Равнината пресича ли сегмента?

Решение. Да реже ABпресече равнината, отклонения И от самолета трябва да има различни знаци:

Пример 6.Пресечната точка на три равнини в една точка.

Системата има уникално решение, следователно трите равнини имат една обща точка.

Пример 7.Намиране на ъглополовящи на двустенен ъгъл, образуван от две дадени равнини.

Позволявам И - отклонение на някаква точка
от първа и втора равнина.

В едната ъглополовяща равнина (съответстваща на ъгъла, в който се намира началото на координатите) тези отклонения са равни по големина и знак, а в другата са равни по големина и противоположни по знак.

Това е уравнението на първата ъглополовяща равнина.

Това е уравнението на втората ъглополовяща равнина.

Пример 8.Определяне на местоположението на две дадени точки И спрямо двустенните ъгли, образувани от тези равнини.