Sinfdan tashqari dars - son moduli. Raqamning mutlaq qiymati. To'liq darslar - Bilim gipermarketi. Manfiy bo'lmagan sonning moduli manfiy bo'lmagan sondir.
Dars maqsadlari
Maktab o'quvchilarini sonning moduli kabi matematik tushuncha bilan tanishtirish;
Maktab o'quvchilariga raqamlar modullarini topish ko'nikmalarini o'rgatish;
Turli topshiriqlarni bajarish orqali o'rganilgan materialni mustahkamlash;
Vazifalar
Bolalarning raqamlar moduli haqidagi bilimlarini mustahkamlash;
Test topshiriqlarini yechish orqali talabalar o'rganilgan materialni qanday o'zlashtirganliklarini tekshirish;
Matematika darslariga qiziqishni oshirishda davom eting;
Maktab o'quvchilarida mantiqiy fikrlash, qiziquvchanlik va qat'iyatlilikni rivojlantirish.
Dars rejasi
1. Son modulining umumiy tushunchalari va ta’rifi.
2. Modulning geometrik ma’nosi.
3. Sonning moduli va uning xossalari.
4. Sonning moduli bo‘lgan tenglama va tengsizliklarni yechish.
5. “Son moduli” atamasi haqida tarixiy ma’lumotlar.
6. O`tilgan mavzu bo`yicha bilimlarni mustahkamlash uchun topshiriq.
7. Uyga vazifa.
Sonning moduli haqida umumiy tushunchalar
Raqamning moduli odatda manfiy qiymatga ega bo'lmasa yoki bir xil raqam manfiy bo'lsa, lekin qarama-qarshi belgisi bo'lsa, raqamning o'zi deb ataladi.
Ya'ni, manfiy bo'lmagan haqiqiy a sonning moduli sonning o'zi:
Va manfiy haqiqiy sonning moduli x ga qarama-qarshi sondir:
Yozishda u quyidagicha ko'rinadi:
Aniqroq tushunish uchun keling, misol keltiraylik. Masalan, 3 sonining moduli 3 ga, shuningdek -3 sonining moduli 3 ga teng.
Bundan kelib chiqadiki, sonning moduli mutlaq qiymatni, ya’ni mutlaq qiymatini bildiradi, lekin uning belgisini hisobga olmagan holda. Oddiyroq qilib aytganda, raqamdan belgini olib tashlash kerak.
Raqamning moduli quyidagicha belgilanishi mumkin: |3|, |x|, |a| va hokazo.
Demak, masalan, 3 sonining moduli |3| bilan belgilanadi.
Shuni ham yodda tutish kerakki, sonning moduli hech qachon manfiy bo'lmaydi: |a|≥ 0.
|5| = 5, |-6| = 6, |-12,45| = 12,45 va boshqalar.
Modulning geometrik ma'nosi
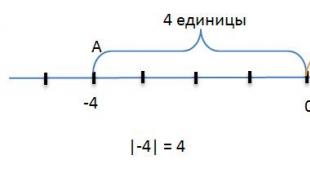
Raqamning moduli - bu boshdan nuqtagacha bo'lgan birlik segmentlarida o'lchanadigan masofa. Ushbu ta'rif modulni geometrik nuqtai nazardan ochib beradi.
Keling, koordinatali chiziqni olib, uning ustida ikkita nuqtani belgilaymiz. Bu nuqtalar -4 va 2 kabi raqamlarga mos kelsin.
Endi bu raqamga e'tibor qaratamiz. Koordinata chizig'ida ko'rsatilgan A nuqta -4 raqamiga mos kelishini ko'ramiz va agar diqqat bilan qarasangiz, bu nuqta 0 mos yozuvlar nuqtasidan 4 birlik segmentlari masofasida joylashganligini ko'rasiz. Bundan kelib chiqadiki, OA segmentining uzunligi to'rt birlikka teng. Bunda OA segmentining uzunligi, ya'ni 4 soni -4 sonining moduli bo'ladi.
Bunda sonning moduli shunday belgilanadi va yoziladi: |−4| = 4.
Endi koordinata chizig'idagi B nuqtasini olamiz va belgilaymiz.
Bu B nuqtasi +2 raqamiga to'g'ri keladi va biz ko'rib turganimizdek, u boshlang'ichdan ikkita birlik segmentlari masofasida joylashgan. Bundan kelib chiqadiki, OB segmentining uzunligi ikki birlikka teng. Bunday holda, 2 raqami +2 sonining moduli bo'ladi.
Yozuvda u quyidagicha ko'rinadi: |+2| = 2 yoki |2| = 2.
Endi xulosa qilaylik. Agar biz biron bir noma'lum a sonini olib, uni koordinata chizig'ida A nuqta deb belgilasak, bu holda A nuqtadan boshlang'ichgacha bo'lgan masofa, ya'ni OA segmentining uzunligi aniq "a" sonining moduli bo'ladi. ”.
Yozishda u quyidagicha ko'rinadi: |a| = OA.
Sonning moduli va uning xossalari
Keling, modulning xususiyatlarini ajratib ko'rsatishga harakat qilaylik, barcha mumkin bo'lgan holatlarni ko'rib chiqamiz va ularni harfiy iboralar yordamida yozamiz:
Birinchidan, sonning moduli manfiy bo'lmagan son bo'lib, musbat sonning moduli sonning o'ziga teng ekanligini bildiradi: |a| = a, agar a > 0 bo'lsa;
Ikkinchidan, qarama-qarshi sonlardan tashkil topgan modullar teng: |a| = |–a|. Ya'ni, bu xususiyat bizga qarama-qarshi sonlar har doim teng modullarga ega ekanligini aytadi, xuddi koordinata chizig'idagi kabi, ular qarama-qarshi raqamlarga ega bo'lsa-da, ular mos yozuvlar nuqtasidan bir xil masofada joylashgan. Bundan kelib chiqadiki, bu qarama-qarshi sonlarning modullari tengdir.
Uchinchidan, agar bu raqam nolga teng bo'lsa, nolning moduli nolga teng: |0| = 0, agar a = 0 bo'lsa. Bu erda biz ishonch bilan aytishimiz mumkinki, nol moduli ta'rifi bo'yicha nolga teng, chunki u koordinata chizig'ining boshiga mos keladi.
Modulning to‘rtinchi xossasi shundaki, ikkita son ko‘paytmasining moduli shu sonlar modullarining ko‘paytmasiga teng. Endi bu nimani anglatishini batafsil ko'rib chiqaylik. Agar biz ta'rifga amal qilsak, siz va men bilamizki, a va b raqamlari ko'paytmasining moduli a b ga teng bo'ladi yoki a b ≥ 0 bo'lsa - (a b), yoki a b dan katta bo'lsa - (a b) bo'ladi. 0. B yozuvi quyidagicha ko'rinadi: |a b| = |a| |b|.
Beshinchi xossa - sonlar bo'limining moduli shu sonlar modullarining nisbatiga teng: |a: b| = |a| : |b|.
Va raqam modulining quyidagi xususiyatlari:
Sonning moduli ishtirok etgan tenglamalar va tengsizliklarni yechish
Raqamli modulga ega bo'lgan masalalarni echishni boshlaganda, shuni yodda tutish kerakki, bunday vazifani hal qilish uchun ushbu masala mos keladigan xususiyatlarni bilishdan foydalangan holda modulning belgisini ochish kerak.
1-mashq
Masalan, agar modul belgisi ostida o'zgaruvchiga bog'liq ifoda mavjud bo'lsa, modul ta'rifga muvofiq kengaytirilishi kerak:
Albatta, muammolarni hal qilishda modul noyob tarzda ochilgan holatlar mavjud. Agar, masalan, olamiz
, bu erda modul belgisi ostidagi bunday ifoda x va y ning har qanday qiymatlari uchun manfiy emasligini ko'ramiz.
Yoki, masalan, olaylik
, biz ushbu modul ifodasi z ning hech qanday qiymatlari uchun ijobiy emasligini ko'ramiz.
Vazifa 2
Sizning oldingizda koordinatali chiziq ko'rsatilgan. Ushbu qatorda moduli 2 ga teng bo'lgan raqamlarni belgilash kerak.
Yechim
Avvalo, biz koordinata chizig'ini chizishimiz kerak. Buni amalga oshirish uchun avval to'g'ri chiziqda siz boshlang'ich, yo'nalish va birlik segmentini tanlashingiz kerakligini allaqachon bilasiz. Keyinchalik, biz ikkita birlik segmentining masofasiga teng bo'lgan nuqtalarni kelib chiqishidan joylashtirishimiz kerak.
Ko'rib turganingizdek, koordinata chizig'ida ikkita shunday nuqta mavjud bo'lib, ulardan biri -2 raqamiga, ikkinchisi esa 2 raqamiga to'g'ri keladi.
Sonlar moduli haqida tarixiy ma'lumotlar
"Modul" atamasi lotincha modulus nomidan kelib chiqqan bo'lib, "o'lchov" degan ma'noni anglatadi. Bu atama ingliz matematigi Rojer Kotes tomonidan kiritilgan. Ammo modul belgisi nemis matematigi Karl Veyershtrass tufayli kiritilgan. Yozilganda modul quyidagi belgi yordamida belgilanadi: | |.
Materiallar bo'yicha bilimlarni mustahkamlash uchun savollar
Bugungi darsimizda biz sonning moduli kabi tushuncha bilan tanishdik, endi esa berilgan savollarga javob berib, ushbu mavzuni qanday o‘zlashtirganingizni tekshirib ko‘ramiz:
1. Musbat songa qarama-qarshi bo‘lgan son qanday nomlanadi?
2. Manfiy songa qarama-qarshi bo‘lgan son qanday nomlanadi?
3. Nolga teskari sonni ayting. Bunday raqam bormi?
4. Sonning moduli bo‘la olmaydigan sonni ayting.
5. Sonning modulini aniqlang.
Uy vazifasi
1. Sizning oldingizda modullarning kamayish tartibida joylashtirishingiz kerak bo'lgan raqamlar mavjud. Agar siz topshiriqni to'g'ri bajarsangiz, "modul" atamasini matematikaga birinchi marta kiritgan shaxsning ismini bilib olasiz.
2. Koordinata chizig‘ini chizing va M (-5) va K (8) dan koordinatali nuqtagacha bo‘lgan masofani toping.
Bugun, do'stlar, snot yoki sentimentallik bo'lmaydi. Buning o'rniga, men sizni hech qanday savolsiz, 8-9-sinf algebra kursidagi eng dahshatli raqiblardan biri bilan jangga yuboraman.
Ha, siz hamma narsani to'g'ri tushundingiz: biz modulli tengsizliklar haqida gapiramiz. Biz to'rtta asosiy texnikani ko'rib chiqamiz, ular yordamida siz bunday muammolarning 90% ni hal qilishni o'rganasiz. Qolgan 10% haqida nima deyish mumkin? Xo'sh, biz ular haqida alohida darsda gaplashamiz. :)
Biroq, har qanday texnikani tahlil qilishdan oldin, siz allaqachon bilishingiz kerak bo'lgan ikkita faktni eslatib o'tmoqchiman. Aks holda, bugungi dars materialini umuman tushunmaslik xavfi bor.
Siz allaqachon bilishingiz kerak bo'lgan narsa
Kapitan Obviousness modulli tengsizliklarni hal qilish uchun siz ikkita narsani bilishingiz kerakligini ko'rsatmoqda:
- Tengsizliklar qanday hal qilinadi;
- Modul nima?
Ikkinchi nuqtadan boshlaylik.
Modul ta'rifi
Bu erda hamma narsa oddiy. Ikkita ta'rif mavjud: algebraik va grafik. Boshlash uchun - algebraik:
Ta'rif. $x$ sonining moduli, agar manfiy bo'lmasa, uning o'zi yoki asl $x$ hali ham manfiy bo'lsa, unga qarama-qarshi bo'lgan sondir.
Bu shunday yozilgan:
\[\chap| x \right|=\left\( \begin(align) & x,\ x\ge 0, \\ & -x,\ x \lt 0. \\\end(align) \o'ng.\]
Oddiy so'zlar bilan aytganda, modul "minussiz raqam" dir. Va aynan shu ikkilik (ba'zi joylarda siz asl raqam bilan hech narsa qilishingiz shart emas, boshqalarida esa qandaydir minusni olib tashlashingiz kerak bo'ladi), bu erda boshlang'ich talabalar uchun barcha qiyinchiliklar mavjud.
Geometrik ta'rif ham mavjud. Buni bilish ham foydalidir, lekin biz unga faqat murakkab va ba'zi maxsus holatlarda murojaat qilamiz, bu erda geometrik yondashuv algebraikdan ko'ra qulayroqdir (spoiler: bugungi kunda emas).
Ta'rif. Raqamlar qatorida $a$ nuqtasi belgilansin. Keyin modul $\left| x-a \right|$ - bu chiziqdagi $x$ nuqtadan $a$ nuqtagacha bo'lgan masofa.
Agar siz rasm chizsangiz, siz shunga o'xshash narsani olasiz:
Grafik modul ta'rifi Qanday bo'lmasin, modulning ta'rifidan uning asosiy xususiyati darhol quyidagicha bo'ladi: sonning moduli har doim manfiy bo'lmagan miqdordir. Bu haqiqat bizning bugungi hikoyamiz orqali qizil ip bo'ladi.
Tengsizliklarni yechish. Intervalli usul
Endi tengsizliklarni ko'rib chiqaylik. Ularning ko'pi bor, ammo bizning vazifamiz hech bo'lmaganda ulardan eng oddiyini hal qilishdir. Chiziqli tengsizliklarga, shuningdek, interval usuliga qisqartiruvchilar.
Menda ushbu mavzu bo'yicha ikkita katta saboq bor (Aytgancha, juda, juda foydali - men ularni o'rganishni tavsiya qilaman):
- Tengsizliklar uchun intervalli usul (ayniqsa, videoni tomosha qiling);
- Kasrli ratsional tengsizliklar - bu juda keng ko'lamli dars, ammo undan keyin sizda hech qanday savol bo'lmaydi.
Agar siz bularning barchasini bilsangiz, "tengsizlikdan tenglamaga o'tamiz" iborasi sizda o'zingizni devorga urish istagini uyg'otmasa, unda siz tayyorsiz: darsning asosiy mavzusiga do'zaxga xush kelibsiz. :)
1. “Modul funksiyadan kichik” shaklidagi tengsizliklar
Bu modullar bilan bog'liq eng keng tarqalgan muammolardan biridir. Shaklning tengsizligini yechish uchun talab qilinadi:
\[\chap| f\o'ng| \ltg\]
$f$ va $g$ funktsiyalari har qanday bo'lishi mumkin, lekin odatda ular polinomlardir. Bunday tengsizliklarga misollar:
\[\begin(align) & \left| 2x+3 \o'ng| \lt x+7; \\ & \chap| ((x)^(2))+2x-3 \o'ng|+3\chap(x+1 \o'ng) \lt 0; \\ & \chap| ((x)^(2))-2\chap| x \right|-3 \right| \lt 2. \\\end(tuzalash)\]
Ularning barchasini quyidagi sxema bo'yicha bir qatorda tom ma'noda hal qilish mumkin:
\[\chap| f\o'ng| \lt g\O'ng strelka -g \lt f \lt g\to'rt \chap (\O'ng strelka \chap\( \boshlang(hizalang) & f \lt g, \\ & f \gt -g \\\end(tekislang) \o'ng.\o'ng)\]
Biz moduldan xalos bo'lganimizni ko'rish oson, lekin buning evaziga biz qo'sh tengsizlikni olamiz (yoki bu bir xil narsa, ikkita tengsizlik tizimi). Ammo bu o'tish mutlaqo barcha mumkin bo'lgan muammolarni hisobga oladi: agar modul ostidagi raqam ijobiy bo'lsa, usul ishlaydi; salbiy bo'lsa, u hali ham ishlaydi; va $f$ yoki $g$ oʻrniga eng noadekvat funksiya bilan ham usul ishlaydi.
Tabiiyki, savol tug'iladi: oddiyroq bo'lishi mumkin emasmi? Afsuski, bu mumkin emas. Bu modulning butun nuqtasi.
Biroq, falsafalash bilan kifoya. Keling, bir nechta muammolarni hal qilaylik:
Vazifa. Tengsizlikni yeching:
\[\chap| 2x+3 \o'ng| \lt x+7\]
Yechim. Shunday qilib, bizning oldimizda "modul kamroq" shaklidagi klassik tengsizlik bor - hatto o'zgartirish uchun hech narsa yo'q. Biz algoritmga muvofiq ishlaymiz:
\[\begin(align) & \left| f\o'ng| \lt g\O'ng strelka -g \lt f \lt g; \\ & \chap| 2x+3 \o'ng| \lt x+7\O'ng strelka -\chap(x+7 \o'ng) \lt 2x+3 \lt x+7 \\\end(hizalang)\]
Oldindan "minus" qo'yilgan qavslarni ochishga shoshilmang: shoshqaloqligingiz tufayli siz haqoratli xatoga yo'l qo'yishingiz mumkin.
\[-x-7 \lt 2x+3 \lt x+7\]
\[\left\( \begin(align) & -x-7 \lt 2x+3 \\ & 2x+3 \lt x+7 \\ \end(hizalang) \o'ng.\]
\[\left\( \begin(align) & -3x \lt 10 \\ & x \lt 4 \\ \end(align) \o'ngga.\]
\[\left\( \begin(align) & x \gt -\frac(10)(3) \\ & x \lt 4 \\ \end(align) \o'ng.\]
Muammo ikkita elementar tengsizlikka qisqartirildi. Parallel sonlar toʻgʻrida ularning yechimlarini koʻrsatamiz:
Ko'pchilikning kesishishi
Bu to'plamlarning kesishishi javob bo'ladi.
Javob: $x\in \left(-\frac(10)(3);4 \right)$
Vazifa. Tengsizlikni yeching:
\[\chap| ((x)^(2))+2x-3 \o'ng|+3\chap(x+1 \o'ng) \lt 0\]
Yechim. Bu vazifa biroz qiyinroq. Birinchidan, ikkinchi atamani o'ngga siljitish orqali modulni ajratib olaylik:
\[\chap| ((x)^(2))+2x-3 \o'ng| \lt -3\chap(x+1 \o'ng)\]
Shubhasiz, bizda yana "modul kichikroq" ko'rinishidagi tengsizlik mavjud, shuning uchun biz allaqachon ma'lum bo'lgan algoritm yordamida moduldan xalos bo'lamiz:
\[-\left(-3\left(x+1 \o'ng) \o'ng) \lt ((x)^(2))+2x-3 \lt -3\chap(x+1 \o'ng)\]
Endi e'tibor bering: kimdir mana shu qavslar bilan men biroz buzuqman, deb aytadi. Lekin yana bir bor eslatib o'tamanki, bizning asosiy maqsadimiz tengsizlikni to‘g‘ri yeching va javobini oling. Keyinchalik, ushbu darsda tasvirlangan hamma narsani mukammal o'zlashtirganingizdan so'ng, uni o'zingiz xohlaganingizcha buzishingiz mumkin: qavslarni oching, minuslar qo'shing va hokazo.
Boshlash uchun biz chap tarafdagi ikkita minusdan xalos bo'lamiz:
\[-\left(-3\left(x+1 \o'ng) \o'ng)=\left(-1 \o'ng)\cdot \left(-3 \o'ng)\cdot \left(x+1 \o'ng) =3\chap(x+1 \o'ng)\]
Endi juft tengsizlikdagi barcha qavslarni ochamiz:
Keling, qo'sh tengsizlikka o'tamiz. Bu safar hisob-kitoblar jiddiyroq bo'ladi:
\[\left\( \begin(align) & ((x)^(2))+2x-3 \lt -3x-3 \\ & 3x+3 \lt ((x)^(2))+2x -3 \\ \end(tekislash) \o'ngga.\]
\[\left\( \begin(align) & ((x)^(2))+5x \lt 0 \\ & ((x)^(2))-x-6 \gt 0 \\ \end( tekislang)\o'ng.\]
Ikkala tengsizlik kvadratikdir va intervalli usul bilan yechilishi mumkin (shuning uchun men aytaman: agar bu nima ekanligini bilmasangiz, modullarni hali qabul qilmaslik yaxshiroqdir). Birinchi tengsizlikdagi tenglamaga o'tamiz:
\[\begin(align) & ((x)^(2))+5x=0; \\ & x\left(x+5 \o'ng)=0; \\ & ((x)_(1))=0;((x)_(2))=-5. \\\end (tekislash)\]
Ko'rib turganingizdek, chiqish elementar usulda echilishi mumkin bo'lgan to'liq bo'lmagan kvadrat tenglamadir. Endi sistemaning ikkinchi tengsizligini ko'rib chiqamiz. U erda siz Viet teoremasini qo'llashingiz kerak bo'ladi:
\[\begin(align) & ((x)^(2))-x-6=0; \\ & \left(x-3 \o'ng)\left(x+2 \o'ng)=0; \\& ((x)_(1))=3;((x)_(2))=-2. \\\end (tekislash)\]
Olingan raqamlarni ikkita parallel chiziqda belgilaymiz (birinchi tengsizlik uchun alohida, ikkinchisi uchun alohida):
Shunga qaramay, biz tengsizliklar tizimini yechayotganimiz sababli, bizni soyali to'plamlarning kesishishi qiziqtiradi: $x\in \left(-5;-2 \right)$. Bu javob.
Javob: $x\in \left(-5;-2 \right)$
Menimcha, ushbu misollardan keyin yechim sxemasi juda aniq:
- Boshqa barcha shartlarni tengsizlikning qarama-qarshi tomoniga o'tkazish orqali modulni ajratib oling. Shunday qilib, biz $\left| ko'rinishdagi tengsizlikka erishamiz f\o'ng| \ltg$.
- Ushbu tengsizlikni yuqorida tavsiflangan sxema bo'yicha moduldan qutulish orqali hal qiling. Bir nuqtada, qo'shaloq tengsizlikdan ikkita mustaqil ifoda tizimiga o'tish kerak bo'ladi, ularning har biri allaqachon alohida yechilishi mumkin.
- Va nihoyat, bu ikkita mustaqil iboraning yechimlarini kesishish qoladi - va biz yakuniy javobni olamiz.
Modul funktsiyadan katta bo'lsa, xuddi shunday algoritm quyidagi turdagi tengsizliklar uchun mavjud. Biroq, bir nechta jiddiy "lekin" bor. Biz hozir bu "lekin" haqida gaplashamiz.
2. “Modul funksiyadan katta” shaklidagi tengsizliklar
Ular shunday ko'rinadi:
\[\chap| f\o'ng| \gtg\]
Avvalgisiga o'xshashmi? Ga o'xshaydi. Va shunga qaramay, bunday muammolar butunlay boshqacha tarzda hal qilinadi. Rasmiy ravishda, sxema quyidagicha:
\[\chap| f\o'ng| \gt g\O'ng strelka \left[ \begin(align) & f \gt g, \\ & f \lt -g \\\end(hizalang) \o'ng.\]
Boshqacha qilib aytganda, biz ikkita holatni ko'rib chiqamiz:
- Birinchidan, biz oddiygina modulni e'tiborsiz qoldiramiz va odatdagi tengsizlikni hal qilamiz;
- Keyin, mohiyatiga ko'ra, biz modulni minus belgisi bilan kengaytiramiz va keyin tengsizlikning ikkala tomonini -1 ga ko'paytiramiz, menda esa ishora bor.
Bunday holda, variantlar kvadrat qavs bilan birlashtiriladi, ya'ni. Bizning oldimizda ikkita talabning kombinatsiyasi mavjud.
Yana bir bor e'tibor bering: bu tizim emas, balki butunlikdir javobda to'plamlar kesishgan emas, balki birlashtirilgan. Bu avvalgi nuqtadan tubdan farq qiladi!
Umuman olganda, ko'plab talabalar kasaba uyushmalari va chorrahalar bilan aralashib ketishadi, shuning uchun keling, bu masalani bir marta va umuman hal qilaylik:
- "∪" - ittifoq belgisi. Aslida, bu bizga ingliz tilidan kelgan va "Union" ning qisqartmasi bo'lgan stilize qilingan "U" harfi, ya'ni. "Assotsiatsiyalar".
- "∩" - kesishish belgisi. Bu axlat hech qayerdan kelmadi, balki shunchaki "∪" ga qarshi nuqta sifatida paydo bo'ldi.
Eslab qolish osonroq bo'lishi uchun, ko'zoynak yasash uchun oyoqlarini ushbu belgilarga torting (endi meni giyohvandlik va alkogolizmni targ'ib qilishda ayblamang: agar siz ushbu darsni jiddiy o'rganayotgan bo'lsangiz, demak siz allaqachon giyohvand bo'lgansiz):
To'plamlarning kesishishi va birlashuvi o'rtasidagi farq Rus tiliga tarjima qilinganda, bu quyidagilarni anglatadi: birlashma (jami) ikkala to'plamning elementlarini o'z ichiga oladi, shuning uchun u ularning har biridan kam emas; lekin kesishma (tizim) faqat birinchi to'plamda ham, ikkinchisida ham bir vaqtning o'zida bo'lgan elementlarni o'z ichiga oladi. Shuning uchun to'plamlarning kesishishi hech qachon manba to'plamlaridan katta bo'lmaydi.
Shunday qilib, aniqroq bo'ldimi? Bu ajoyib. Keling, amaliyotga o'tamiz.
Vazifa. Tengsizlikni yeching:
\[\chap| 3x+1 \o'ng| \gt 5-4x\]
Yechim. Biz sxema bo'yicha harakat qilamiz:
\[\chap| 3x+1 \o'ng| \gt 5-4x\O'ng strelka \chap[ \begin(hizala) & 3x+1 \gt 5-4x \\ & 3x+1 \lt -\left(5-4x \o'ng) \\\end(hizalang) \ to'g'ri.\]
Populyatsiyadagi har bir tengsizlikni hal qilamiz:
\[\left[ \begin(align) & 3x+4x \gt 5-1 \\ & 3x-4x \lt -5-1 \\ \end(hizalang) \o'ngga.\]
\[\left[ \begin(align) & 7x \gt 4 \\ & -x \lt -6 \\ \end(align) \o'ng.\]
\[\left[ \begin(align) & x \gt 4/7\ \\ & x \gt 6 \\ \end(hizala) \o'ng.\]
Biz har bir natija to'plamini raqamlar qatorida belgilaymiz va keyin ularni birlashtiramiz:
To'plamlar ittifoqi
Javob $x\in \left(\frac(4)(7);+\infty \right)$ bo'lishi aniq.
Javob: $x\in \left(\frac(4)(7);+\infty \right)$
Vazifa. Tengsizlikni yeching:
\[\chap| ((x)^(2))+2x-3 \o'ng| \gt x\]
Yechim. Nima bopti? Hech narsa - hammasi bir xil. Biz modulli tengsizlikdan ikkita tengsizliklar to'plamiga o'tamiz:
\[\chap| ((x)^(2))+2x-3 \o'ng| \gt x\O'ng strelka \left[ \begin(hizala) & ((x)^(2))+2x-3 \gt x \\ & ((x)^(2))+2x-3 \lt -x \\\oxirgi (tekislash) \o'ngga.\]
Biz har bir tengsizlikni hal qilamiz. Afsuski, u erda ildizlar juda yaxshi bo'lmaydi:
\[\begin(align) & ((x)^(2))+2x-3 \gt x; \\ & ((x)^(2))+x-3 \gt 0; \\&D=1+12=13; \\ & x=\frac(-1\pm \sqrt(13))(2). \\\end (tekislash)\]
Ikkinchi tengsizlik ham biroz yovvoyi:
\[\begin(align) & ((x)^(2))+2x-3 \lt -x; \\ & ((x)^(2))+3x-3 \lt 0; \\&D=9+12=21; \\ & x=\frac(-3\pm \sqrt(21))(2). \\\end (tekislash)\]
Endi siz bu raqamlarni ikkita o'qda belgilashingiz kerak - har bir tengsizlik uchun bitta o'q. Biroq, siz nuqtalarni to'g'ri tartibda belgilashingiz kerak: raqam qanchalik katta bo'lsa, nuqta o'ngga o'tadi.
Va bu erda bizni sozlash kutmoqda. Agar $\frac(-3-\sqrt(21))(2) \lt \frac(-1-\sqrt(13))(2)$ raqamlari bilan hamma narsa aniq bo'lsa (birinchi raqamdagi shartlar) kasr sekundning numeratoridagi hadlardan kichik, shuning uchun yig'indi ham kichik bo'ladi), raqamlar bilan $\frac(-3-\sqrt(13))(2) \lt \frac(-1+\sqrt) (21))(2)$ ham hech qanday qiyinchiliklar bo'lmaydi (ijobiy raqam aniqroq salbiy), keyin oxirgi juftlik bilan hamma narsa unchalik aniq emas. Qaysi biri kattaroq: $\frac(-3+\sqrt(21))(2)$ yoki $\frac(-1+\sqrt(13))(2)$? Raqamli chiziqlardagi nuqtalarning joylashishi va aslida javob bu savolga javobga bog'liq bo'ladi.
Shunday qilib, keling, taqqoslaylik:
\[\begin(matritsa) \frac(-1+\sqrt(13))(2)\vee \frac(-3+\sqrt(21))(2) \\ -1+\sqrt(13)\ vee -3+\sqrt(21) \\ 2+\sqrt(13)\vee \sqrt(21) \\\end(matritsa)\]
Biz ildizni ajratib oldik, tengsizlikning ikkala tomonida manfiy bo'lmagan raqamlarni oldik, shuning uchun biz ikkala tomonni kvadratga solish huquqiga egamiz:
\[\begin(matritsa) ((\left(2+\sqrt(13) \o'ng))^(2))\vee ((\left(\sqrt(21) \o'ng))^(2)) \ \ 4+4\sqrt(13)+13\vee 21 \\ 4\sqrt(13)\vee 3 \\\end(matritsa)\]
Menimcha, $4\sqrt(13) \gt 3$, shuning uchun $\frac(-1+\sqrt(13))(2) \gt \frac(-3+\sqrt(21)) ( 2)$ bo'lsa, o'qlardagi yakuniy nuqtalar quyidagicha joylashtiriladi:
Xunuk ildizlar ishi
Sizga shuni eslatib o'tamanki, biz to'plamni hal qilyapmiz, shuning uchun javob soyali to'plamlarning kesishmasi emas, balki birlashma bo'ladi.
Javob: $x\in \left(-\infty;\frac(-3+\sqrt(21))(2) \right)\bigcup \left(\frac(-1+\sqrt(13))(2) );+\infty \right)$
Ko'rib turganingizdek, bizning sxemamiz oddiy va juda qiyin muammolar uchun juda yaxshi ishlaydi. Ushbu yondashuvdagi yagona "zaif nuqta" shundaki, siz irratsional sonlarni to'g'ri taqqoslashingiz kerak (va menga ishoning: bu faqat ildizlar emas). Ammo taqqoslash masalalariga alohida (va juda jiddiy) dars ajratiladi. Va biz davom etamiz.
3. Salbiy bo'lmagan "dumlar" bilan tengsizliklar
Endi biz eng qiziqarli qismga o'tamiz. Bu shakldagi tengsizliklar:
\[\chap| f\o'ng| \gt\left| g\o'ng|\]
Umuman olganda, biz hozir gaplashadigan algoritm faqat modul uchun to'g'ri. U chap va o'ngda kafolatlangan salbiy bo'lmagan ifodalar mavjud bo'lgan barcha tengsizliklarda ishlaydi:
Bu vazifalar bilan nima qilish kerak? Faqat esda tuting:
Salbiy bo'lmagan "quyruq" bilan tengsizliklarda ikkala tomon ham har qanday tabiiy kuchga ko'tarilishi mumkin. Hech qanday qo'shimcha cheklovlar bo'lmaydi.
Avvalo, biz kvadratlashtirishga qiziqamiz - u modullar va ildizlarni yoqib yuboradi:
\[\begin(align) & ((\left(\left| f \right| \right))^(2))=((f)^(2)); \\ & ((\ chap (\ sqrt (f) \ o'ng)) ^ (2)) = f. \\\end (tekislash)\]
Buni kvadratning ildizini olish bilan adashtirmang:
\[\sqrt(((f)^(2)))=\chap| f \right|\ne f\]
Talaba modul o'rnatishni unutganida son-sanoqsiz xatolarga yo'l qo'yildi! Ammo bu butunlay boshqacha hikoya (bular, go'yo irratsional tenglamalar), shuning uchun biz hozir bunga kirmaymiz. Keling, bir nechta muammolarni yaxshiroq hal qilaylik:
Vazifa. Tengsizlikni yeching:
\[\chap| x+2 \right|\ge \left| 1-2x \o'ng|\]
Yechim. Keling, darhol ikkita narsaga e'tibor beraylik:
- Bu qat'iy tengsizlik emas. Raqam chizig'idagi nuqtalar teshiladi.
- Tengsizlikning ikkala tomoni ham manfiy emas (bu modulning xususiyati: $\left| f\left(x \right) \right|\ge 0$).
Shunday qilib, moduldan xalos bo'lish va muammoni odatiy interval usuli yordamida hal qilish uchun biz tengsizlikning ikkala tomonini kvadratga olamiz:
\[\begin(hizala) & ((\left(\left| x+2 \o'ng| \o'ng))^(2))\ge ((\left(\left| 1-2x \o'ng| \o'ng)) )^(2)); \\ & ((\left(x+2 \o'ng))^(2))\ge ((\left(2x-1 \o'ng))^(2)). \\\end (tekislash)\]
Oxirgi bosqichda men biroz aldadim: modulning tengligidan foydalanib, atamalar ketma-ketligini o'zgartirdim (aslida $1-2x$ ifodasini -1 ga ko'paytirdim).
\[\begin(align) & ((\left(2x-1 \right))^(2))-((\left(x+2 \right))^(2))\le 0; \\ & \left(\left(2x-1 \o'ng)-\left(x+2 \o'ng) \o'ng)\cdot \left(\left(2x-1 \o'ng)+\chap(x+2 \ o'ng)\o'ng)\le 0; \\ & \left(2x-1-x-2 \o'ng)\cdot \left(2x-1+x+2 \o'ng)\le 0; \\ & \left(x-3 \o'ng)\cdot \left(3x+1 \o'ng)\le 0. \\\end(align)\]
Interval usuli yordamida hal qilamiz. Tengsizlikdan tenglamaga o'tamiz:
\[\begin(align) & \left(x-3 \right)\left(3x+1 \right)=0; \\ & ((x)_(1))=3;((x)_(2))=-\frac(1)(3). \\\end (tekislash)\]
Topilgan ildizlarni raqamlar qatorida belgilaymiz. Yana bir bor: barcha nuqtalar soyali, chunki asl tengsizlik qat'iy emas!
Modul belgisidan qutulish
Ayniqsa, o'jar bo'lganlar uchun eslatib o'taman: biz tenglamaga o'tishdan oldin yozilgan oxirgi tengsizlikdan belgilarni olamiz. Va biz bir xil tengsizlikda talab qilinadigan maydonlarni bo'yab qo'yamiz. Bizning holatda bu $\left(x-3 \right)\left(3x+1 \right)\le 0$.
OK, endi hammasi tugadi. Muammo hal qilindi.
Javob: $x\in \left[ -\frac(1)(3);3 \right]$.
Vazifa. Tengsizlikni yeching:
\[\chap| ((x)^(2))+x+1 \right|\le \left| ((x)^(2))+3x+4 \o'ng|\]
Yechim. Biz hamma narsani xuddi shunday qilamiz. Men izoh bermayman - faqat harakatlar ketma-ketligiga qarang.
Kvadrati:
\[\begin(align) & ((\left(\left| ((x)^(2))+x+1 \o'ng| \o'ng))^(2))\le ((\left(\left) | ((x)^(2))+3x+4 \o'ng| \o'ng))^(2)); \\ & ((\left(((x)^(2))+x+1 \o'ng))^(2))\le ((\left(((x)^(2))+3x+4 \right)))^(2)); \\ & ((\left(((x)^(2))+x+1 \o'ng))^(2))-((\left(((x)^(2))+3x+4 \ o'ng))^(2))\le 0; \\ & \left(((x)^(2))+x+1-((x)^(2))-3x-4 \right)\times \\ & \times \left(((x)) ^(2))+x+1+((x)^(2))+3x+4 \o‘ng)\le 0; \\ & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \o'ng)\le 0. \\\end(align)\]
Interval usuli:
\[\begin(align) & \left(-2x-3 \right)\left(2((x)^(2))+4x+5 \o'ng)=0 \\ & -2x-3=0\ O'ng strelka x=-1,5; \\ & 2((x)^(2))+4x+5=0\Rightarrow D=16-40 \lt 0\Rightarrow \varnothing . \\\end (tekislash)\]
Raqamlar qatorida faqat bitta ildiz bor:
Javob butun intervaldir
Javob: $x\in \left[ -1.5;+\infty \right)$.
Oxirgi vazifa haqida kichik eslatma. Mening talabalarimdan biri aniq ta'kidlaganidek, ushbu tengsizlikdagi ikkala submodulli iboralar ham ijobiydir, shuning uchun modul belgisi sog'likka zarar bermasdan qoldirilishi mumkin.
Ammo bu butunlay boshqacha fikrlash darajasi va boshqa yondashuv - uni shartli ravishda oqibatlar usuli deb atash mumkin. Bu haqda - alohida darsda. Keling, bugungi darsning yakuniy qismiga o'tamiz va har doim ishlaydigan universal algoritmni ko'rib chiqamiz. Oldingi barcha yondashuvlar kuchsiz bo'lsa ham. :)
4. Variantlarni sanab o'tish usuli
Agar bu usullarning barchasi yordam bermasa-chi? Agar tengsizlikni salbiy bo'lmagan quyruqlarga qisqartirish mumkin bo'lmasa, modulni izolyatsiya qilishning iloji bo'lmasa, umuman olganda og'riq, qayg'u, melankolik bo'lsa?
Keyin hamma matematikaning "og'ir artilleriyasi" sahnaga chiqadi - shafqatsiz kuch usuli. Modulli tengsizliklarga nisbatan quyidagicha ko'rinadi:
- Barcha submodulli ifodalarni yozing va ularni nolga tenglang;
- Olingan tenglamalarni yeching va bitta son qatorida topilgan ildizlarni belgilang;
- To'g'ri chiziq bir nechta bo'limlarga bo'linadi, ularning ichida har bir modul o'zgarmas belgiga ega va shuning uchun noyob tarzda namoyon bo'ladi;
- Har bir bunday bo'lim bo'yicha tengsizlikni yeching (ishonchlilik uchun 2-bosqichda olingan ildiz-chegaralarni alohida ko'rib chiqishingiz mumkin). Natijalarni birlashtiring - bu javob bo'ladi. :)
Qanday? Zaifmi? Osonlik bilan! Faqat uzoq vaqt. Keling, amalda ko'rib chiqaylik:
Vazifa. Tengsizlikni yeching:
\[\chap| x+2 \o'ng| \lt \chap| x-1 \o'ng|+x-\frac(3)(2)\]
Yechim. Bu ahmoqlik $\left| kabi tengsizliklarga tushmaydi f\o'ng| \lt g$, $\chap| f\o'ng| \gt g$ yoki $\left| f\o'ng| \lt \chap| g \right|$, shuning uchun biz oldinga harakat qilamiz.
Biz submodulyar iboralarni yozamiz, ularni nolga tenglashtiramiz va ildizlarni topamiz:
\[\boshlang(align) & x+2=0\O'ng strelka x=-2; \\ & x-1=0\Oʻng strelka x=1. \\\end (tekislash)\]
Hammasi bo'lib, bizda raqamlar chizig'ini uchta bo'limga ajratadigan ikkita ildiz bor, ular ichida har bir modul o'ziga xos tarzda ochiladi:
Submodulyar funksiyalarning raqamlar qatorini nolga bo'lish
Keling, har bir bo'limni alohida ko'rib chiqaylik.
1. $x \lt -2$ bo'lsin. Keyin ikkala submodulli ibora ham manfiy bo'lib, asl tengsizlik quyidagicha qayta yoziladi:
\[\begin(hizala) & -\left(x+2 \o'ng) \lt -\left(x-1 \o'ng)+x-1,5 \\ & -x-2 \lt -x+1+ x- 1,5 \\ & x \gt 1,5 \\\end (tekislash)\]
Bizda juda oddiy cheklov bor. Keling, uni $x \lt -2$ degan dastlabki taxmin bilan kesishamiz:
\[\left\( \begin(align) & x \lt -2 \\ & x \gt 1,5 \\\end(align) \right.\O'ng strelka x\in \varnothing \]
Shubhasiz, $x$ o'zgaruvchisi bir vaqtning o'zida -2 dan kichik va 1,5 dan katta bo'lishi mumkin emas. Bu sohada hech qanday yechim yo'q.
1.1. Chegaraviy holatni alohida ko'rib chiqaylik: $x=-2$. Keling, bu raqamni asl tengsizlikka almashtiramiz va tekshiramiz: bu to'g'rimi?
\[\begin(hizala) & ((\chap. \chap| x+2 \o'ng| \lt \chap| x-1 \o'ng|+x-1,5 \o'ng|)_(x=-2) ) \ \ & 0 \lt \chap| -3\o'ng|-2-1,5; \\ & 0 \lt 3-3,5; \\ & 0 \lt -0,5\O'ng ko'rsatkich \varnothing . \\\end (tekislash)\]
Ko'rinib turibdiki, hisob-kitoblar zanjiri bizni noto'g'ri tengsizlikka olib keldi. Demak, asl tengsizlik ham noto'g'ri va $x=-2$ javobga kiritilmagan.
2. Endi $-2 \lt x \lt 1$ bo'lsin. Chap modul allaqachon "ortiqcha" bilan ochiladi, lekin o'ng modul hali ham "minus" bilan ochiladi. Bizda ... bor:
\[\boshlang(tuzala) & x+2 \lt -\chap(x-1 \o'ng)+x-1,5 \\ & x+2 \lt -x+1+x-1,5 \\& x \lt - 2.5 \\\end (tekislash)\]
Biz yana asl talab bilan kesishamiz:
\[\chap\( \begin(align) & x \lt -2,5 \\ & -2 \lt x \lt 1 \\\end(hizalang) \o'ng.\O'ng strelka x\in \varnothing \]
Va yana, yechimlar to'plami bo'sh, chunki ikkalasi ham -2,5 dan kichik va -2 dan katta bo'lgan raqamlar yo'q.
2.1. Va yana bir alohida holat: $x=1$. Biz asl tengsizlikni almashtiramiz:
\[\begin(hizala) & ((\chap. \chap| x+2 \o'ng| \lt \chap| x-1 \o'ng|+x-1,5 \o'ng|)_(x=1)) \\ & \left| 3\o'ng| \lt \chap| 0\o'ng|+1-1,5; \\ & 3 \lt -0,5; \\ & 3 \lt -0,5\O'ng strelka \varnothing . \\\end (tekislash)\]
Oldingi "maxsus holat"ga o'xshab, javobda $x=1$ raqami aniq kiritilmagan.
3. Qatorning oxirgi qismi: $x \gt 1$. Bu erda barcha modullar ortiqcha belgisi bilan ochiladi:
\[\boshlang(align) & x+2 \lt x-1+x-1,5 \\ & x+2 \lt x-1+x-1,5 \\ & x \gt 4,5 \\ \end(hizalang)\ ]
Va yana topilgan to'plamni asl cheklov bilan kesib o'tamiz:
\[\left\( \begin(align) & x \gt 4.5 \\ & x \gt 1 \\\ end(hizalang) \o'ng.\O'ng strelka x\ichida \chap(4,5;+\infty \o'ng)\ ]
Va nihoyat! Biz javob bo'ladigan intervalni topdik.
Javob: $x\in \left(4,5;+\infty \right)$
Va nihoyat, haqiqiy muammolarni hal qilishda sizni ahmoqona xatolardan qutqarishi mumkin bo'lgan bir eslatma:
Modulli tengsizliklarning yechimlari odatda raqamlar chizig‘idagi uzluksiz to‘plamlarni – intervallarni va segmentlarni ifodalaydi. Izolyatsiya qilingan nuqtalar kamroq tarqalgan. Va hatto kamroq hollarda, yechimning chegarasi (segmentning oxiri) ko'rib chiqilayotgan diapazonning chegarasiga to'g'ri keladi.
Binobarin, agar javobda chegaralar (xuddi shunday "maxsus holatlar") bo'lmasa, bu chegaralarning chap va o'ng tomonidagi joylar javobga deyarli kiritilmaydi. Va aksincha: chegara javobga kirdi, ya'ni uning atrofidagi ba'zi joylar ham javoblar bo'ladi.
Yechimlaringizni ko'rib chiqishda buni yodda saqlang.
Ushbu darsda haqiqiy sonning moduli tushunchasi ko'rib chiqiladi va uning ba'zi asosiy ta'riflari bilan tanishtiriladi, so'ngra ushbu ta'riflarning har xil ishlatilishini ko'rsatadigan misollar keltiriladi.
Mavzu:Haqiqiy raqamlar
Dars:Haqiqiy sonning moduli
1. Modul ta'riflari
Haqiqiy sonning moduli kabi tushunchani ko'rib chiqaylik, uning bir nechta ta'riflari mavjud.
Ta'rif 1. Koordinata chizig'idagi nuqtadan nolga qadar bo'lgan masofa deyiladi modul raqami, bu nuqtaning koordinatasi (1-rasm).
1-misol. 
. E'tibor bering, qarama-qarshi sonlarning mutlaq qiymatlari teng va manfiy emas, chunki bu masofa, lekin u manfiy bo'lishi mumkin emas va nolga yaqin simmetrik raqamlardan boshlang'ichgacha bo'lgan masofa tengdir.
Ta'rif 2. 
.
2-misol. Kiritilgan ta'riflarning ekvivalentligini ko'rsatish uchun oldingi misolda qo'yilgan masalalardan birini ko'rib chiqamiz. 
, biz ko'rib turganimizdek, modul belgisi ostida manfiy raqam bilan, uning oldiga yana bir minus qo'shilishi, modulning ta'rifidan kelib chiqqan holda, salbiy bo'lmagan natijani beradi.
Natija. Koordinata chizig'idagi koordinatali ikki nuqta orasidagi masofani quyidagicha topish mumkin 
nuqtalarning o'zaro joylashuvidan qat'i nazar (2-rasm).
2. Modulning asosiy xossalari
1. Har qanday sonning moduli manfiy emas
2. Mahsulotning moduli modullarning mahsulotidir
3. Bo'lim moduli modullarning ko'rsatkichidir
3. Muammoni hal qilish
3-misol. Tenglamani yeching.
Yechim. Keling, ikkinchi modul ta'rifidan foydalanamiz: 
va tenglamamizni modulni ochishning turli variantlari uchun tenglamalar tizimi shaklida yozing.
Misol 4. Tenglamani yeching.
Yechim. Oldingi misoldagi yechimga o'xshab, biz buni olamiz.
5-misol. Tenglamani yeching.
Yechim. Keling, modulning birinchi ta'rifidan kelib chiqadigan xulosa orqali hal qilaylik: . Kerakli ildiz 3-banddan 2 masofada bo'lishini hisobga olib, buni raqam o'qida tasvirlaymiz (3-rasm).
Rasmga asoslanib, biz tenglamaning ildizlarini olamiz: 
, chunki bunday koordinatali nuqtalar tenglamada talab qilinganidek, 3 nuqtadan 2 masofada joylashgan.
Javob. .
Misol 6. Tenglamani yeching.
Yechim. Oldingi muammo bilan solishtirganda, faqat bitta murakkablik bor - bu koordinata o'qidagi raqamlar orasidagi masofa haqidagi xulosani shakllantirish bilan to'liq o'xshashlik yo'q, chunki modul belgisi ostida minus emas, balki ortiqcha belgisi mavjud. belgisi. Ammo uni kerakli shaklga keltirish qiyin emas, biz buni qilamiz:
Buni oldingi yechimga o'xshash son o'qida tasvirlaymiz (4-rasm).
Tenglamaning ildizlari 
.
Javob. .
7-misol. Tenglamani yeching.
Yechim. Bu tenglama avvalgisiga qaraganda biroz murakkabroq, chunki noma'lum ikkinchi o'rinda turadi va minus belgisiga ega, qo'shimcha ravishda u raqamli ko'paytirgichga ham ega. Birinchi muammoni hal qilish uchun biz modul xususiyatlaridan birini ishlatamiz va quyidagilarni olamiz:
Ikkinchi masalani hal qilish uchun o'zgaruvchilarni o'zgartirishni amalga oshiramiz: , bu bizni eng oddiy tenglamaga olib boradi. Modulning ikkinchi ta'rifi bo'yicha 
. Ushbu ildizlarni almashtirish tenglamasiga qo'ying va ikkita chiziqli tenglamani oling:
Javob. 
.
4. Kvadrat ildiz va modul
Ko'pincha, ildizlar bilan bog'liq muammolarni hal qilishda modullar paydo bo'ladi va siz ular paydo bo'lgan vaziyatlarga e'tibor berishingiz kerak.
Ushbu o'ziga xoslikka birinchi qarashda savollar tug'ilishi mumkin: "nega u erda modul bor?" va "nima uchun shaxs noto'g'ri?" Ma'lum bo'lishicha, biz ikkinchi savolga oddiy qarama-qarshi misol keltira olamiz: agar bu to'g'ri bo'lsa, bu ekvivalent, ammo bu noto'g'ri identifikatsiya.
Shundan so'ng, savol tug'ilishi mumkin: "bunday identifikatsiya muammoni hal qilmaydimi?", lekin bu taklifga qarshi misol ham mavjud. Agar bu to'g'ri bo'lsa, bu ekvivalent, lekin bu noto'g'ri identifikatsiya.
Shunga ko‘ra, agar manfiy bo‘lmagan sonning kvadrat ildizi manfiy bo‘lmagan son, modul qiymati esa manfiy bo‘lmagan son ekanligini eslasak, yuqoridagi gap nima uchun to‘g‘ri ekanligi ayon bo‘ladi:
.
Misol 8. Ifodaning qiymatini hisoblang.
Yechim. Bunday vazifalarda, o'ylamasdan darhol ildizdan qutulish emas, balki yuqorida aytib o'tilgan o'ziga xoslikni qo'llash muhimdir, chunki .
Musbat (tabiiy) sonlar, manfiy sonlar va noldan iborat.
Barcha manfiy raqamlar va faqat ular noldan kichikdir. Raqamlar qatorida manfiy sonlar nolning chap tomonida joylashgan. Ular uchun, musbat sonlarga kelsak, bir butun sonni boshqasi bilan solishtirish imkonini beruvchi tartib munosabati aniqlanadi.
Har bir natural son uchun n bir va faqat bitta manfiy son bor, belgilangan -n, to‘ldiradi n nolga: n + (− n) = 0 . Ikkala raqam ham chaqiriladi qarama-qarshi bir-birlari uchun. Butun sonni ayirish a uni qarama-qarshisi bilan qo'shishga teng: -a.
Manfiy sonlarning xossalari
Salbiy raqamlar natural sonlar bilan deyarli bir xil qoidalarga amal qiladi, lekin ba'zi bir o'ziga xos xususiyatlarga ega.
Tarixiy eskiz
Adabiyot
- Vygodskiy M. Ya. Boshlang'ich matematika bo'yicha qo'llanma. - M.: AST, 2003. - ISBN 5-17-009554-6
- Glazer G.I. Maktabda matematika tarixi. - M.: Ta'lim, 1964. - 376 b.
Havolalar
Wikimedia fondi. 2010 yil.
- Ehtiyotsiz zarar etkazish
- Neotropiklar
Boshqa lug'atlarda "salbiy bo'lmagan raqam" nima ekanligini ko'ring:
Haqiqiy raqam- Haqiqiy yoki haqiqiy son - bu atrofdagi olamning geometrik va fizik miqdorlarini oʻlchash, shuningdek, ildizlarni ajratib olish, logarifmlarni hisoblash, yechish kabi amallarni bajarish zaruratidan kelib chiqqan matematik abstraksiya... ... Vikipediya.
odatda kichik manfiy bo'lmagan butun son- Cheklanmagan manfiy bo'lmagan butun sonning qiymatlarini ifodalovchi kodlashning bir qismi, lekin kichik qiymatlar ko'proq sodir bo'ladigan joylarda (ITU T X.691). Mavzular ...... Texnik tarjimon uchun qo'llanma
HAQIQIY RAQAM- haqiqiy son, musbat son, manfiy son yoki nol. Ratsional son tushunchasini kengaytirish natijasida son tushunchasi paydo bo'ldi. Ushbu kengayish zarurati matematikani ifodalashda amaliy foydalanish bilan ham bog'liq ... ... Matematik entsiklopediya
Bosh raqam- tub son - bu aniq ikkita tabiiy bo'luvchiga ega bo'lgan natural son: bitta va o'zi. Bittasidan tashqari barcha boshqa natural sonlar kompozit deb ataladi. Shunday qilib, barcha natural sonlar bittadan katta... ... Vikipediya
natural son- ▲ butun sonni ifodalovchi, haqiqiy, son natural son manfiy bo'lmagan butun son; alohida butun ob'ektlar sonini qanday l bilan ifodalaydi. agregatlar; haqiqiy butun ob'ektlar sonini belgilang; raqamlarning ifodasi. to'rtta ... Rus tilining ideografik lug'ati
O'nlik- O'nli kasr - bu kasrning bir turi bo'lib, haqiqiy sonlarni kasrning belgisi: yoki yoki, butun son va sonning kasr qismi o'rtasida ajratuvchi vazifasini bajaradigan o'nli nuqta bo'lgan shaklda ifodalash usulidir. .. ... Vikipediya Vikipediya
ShMO rahbari
matematika o'qituvchilari _______Kalashnikova Zh.YuMunitsipal byudjet ta'lim muassasasi
“89-sonli umumta’lim maktabi”
6-sinflar uchun matematika fanidan tematik testlar
I.I.ning darsligi bo'yicha. Zubareva va A.G. Mordkovich
Tuzuvchilar: matematika o'qituvchilari:
Kalashnikova Janna Yurievna
Stolbova Lyudmila Antonovna
ZATO Seversk
2016 yil
Tarkib
Test № 1………………………………………………………………………………….3-6
Test № 2………………………………………………………………………………………….7-10
Test № 3………………………………………………………………………………………………………….11-14
Javoblar……………………………………………………………………………………………………..15
Test №1 "Ijobiy va salbiy sonlar"
Variant 1
Salbiy kasr sonini kiriting:
-165
38
-7.92
67 “Koordinata nurida -5,5 raqami belgilangan” hodisasini tasvirlab bering.
Ishonchli
Mumkin emas
Tasodifiy
To'rtta raqamdan qaysi biri eng katta?
8,035
80,35
0,8035
803,5
Qaysi nuqta koordinata chizig‘ida O (0) nuqtadan o‘ng tomonda joylashgan?
M (-4)
E (-15)
K (15)
D(-1,2)
Kechasi havo harorati -5 ° S edi. Kun davomida termometr allaqachon +3 ° C edi. Havo harorati qanday o'zgargan?
8o ga oshdi
2o ga kamaydi
2o ga oshdi
8o ga kamaydi
X(-2) nuqtasi koordinata chizig'ida - simmetriya markazida belgilangan. Ushbu chiziqda joylashgan nuqtalarning koordinatalarini x nuqtaga simmetrik tarzda ko'rsating.
(-1) va (1)
(-1) va (1)
(3) va (-3)
(0) va (-4)
Koordinata chizig'idagi qaysi nuqtalar koordinata boshiga nisbatan simmetrik emas - O nuqta (0).
B(-5) va C(5)
D(0,5) va E(-0,5)
M(-3) va K(13)
A(18) va X(-18)
0,316+0,4 sonlarning yig’indisi nechaga teng?
0,356
0,716
4,316
0,32
0,4 sonining 25% ni hisoblang.
0,1
0,001
10
100
9100 va 0,03 ning farqini hisoblang
0,05
0,6
9,03
350 Variant 2
Salbiy kasr sonini kiriting.
8,63
-1045
913-0,2
“Koordinata nurida 7 raqami belgilangan” hodisasini tasvirlab bering.
Tasodifiy
Mumkin emas
Ishonchli
Qaysi raqam eng kichik?
15,49
154,9
1,549
1549
Nuqtalardan qaysi biri O(0) nuqtaning chap tomonidagi koordinata chizig`ida joylashgan.
A(-0,5)
AT 6)
M(0,5)
K(38)
Kunduzi termometr +5 ° C, kechqurun esa -2 ° C ni ko'rsatdi. Havoning harorati qanday o'zgargan?
3o ga oshdi
7o ga kamaydi
3o ga kamaydi
7o ga oshdi
Simmetriya markazi koordinatali chiziqda - A(-3) nuqtada belgilanadi. Ushbu chiziqda joylashgan nuqtalarning koordinatalarini A nuqtaga simmetrik tarzda ko'rsating.
(-2) va (2)
(0) va (-5)
(-6) va (1)
(-1) va (-5)
Koordinata chizig'ining qaysi nuqtalari koordinata boshiga nisbatan simmetrik emas - O(0) nuqtasi.
A(6) va B(-6)
C(12) va D(-2)
M(-1) va K(1)
X (-9) va Y (9)
0,237 va 0,3 sonlarining yig’indisi nechaga teng?
0,24
3,237
0,537
0,267
0,5 dan 20% ni hisoblang
10
0,1
0,2
0,01
0,07 va 31001250,5 ning farqini hisoblang
1
425Test № 2. Raqamning mutlaq qiymati. Qarama-qarshi raqamlar.
Variant 1
Berilgan raqamlardan qaysi biri eng kichik modulga ega
-11
1013-4,196
-4,2
Noto'g'ri tenglamani belgilang
85=-85
-1,9=1,9
35= 3558=-58 Manfiy bo'lmagan sonning moduli manfiy bo'lmagan sondir. Bu bayonot haqiqatmi?
Ha
Yo'q
Bu sonlardan qaysi biri -34 soniga qarama-qarshi?43-43-3434Agar m = -15 bo'lsa -(-m) ifodaning qiymati qanday bo'ladi?
+15
-15
Ifodaning qiymatini hisoblang: -2,5∙4--919
-10
1
-1
Tenglamani yeching: x=40-40
40
40 yoki -40
2.75 va 3.9 sonlari orasidagi koordinata chizigʻida qanday butun sonlar joylashgan?
-2, -1, 1, 2
-1, 0, 1, 2, 3
-1, 0, 1, 2, 3, 4
-2, -1, 0, 1, 2, 3
-30>-50 tengsizlik to'g'rimi?
Yo'q
Agar x≤30, 1, 2 bo‘lsa, barcha x sonlarni sanab o‘ting
0, 1, 2, 3
0, 1, 2, 3, 4
1, 2, 3
Variant 2
Qaysi raqam eng katta modulga ega?
-0,6
-50,603
493550,530
Noto'g'ri tenglamani belgilang
-1.5=1.512=12-117=117-325=-325Salbiy sonning moduli manfiy son boʻlishi mumkinmi?
Ha
Yo'q
Bu raqamlardan qaysi biri 124 ga qarama-qarshidir?
-24
24
-124124Agar k = -9 bo'lsa –(-k) ifodaning qiymati qanday bo'ladi
-9
+9
Ifodaning qiymatini hisoblang: 2,5:-0,5+1,250
15
-2,5
2,5
x=100100 tenglamani yeching
-100
100 yoki -100
1 va - 4.5 raqamlari orasidagi koordinata chizig'ida qanday butun sonlar joylashgan
-4, -3, -2, -1, 0
-3, -2, -1
-5, -4, -3, -2, -1
-4, -3, -2, -1, 1
-25 tengsizlik rostmi?<-10?
Ha
Yo'q
Agar x≤44, 3, 2 bo'lsa, barcha x sonlarni sanab o'ting
0, 1, 2, 3
1, 2, 3, 4
0, 1, 2, 3, 4
Test № 3. Raqamlarni taqqoslash
Variant 1
Tengsizliklardan qaysi biri noto'g'ri?
-20 > 2
0 < -1
-16 > -7
-5 < -3
-320 -920>
<
=
0 soni har qanday manfiy sondan katta ekanligi rostmi?
Ha
Yo'q
a soni manfiy emas. Ushbu bayonotni tengsizlik sifatida qanday yozishimiz mumkin?
a<0a≤0a≥0a>0 Berilgan sonlarning eng kattasini ko‘rsating.
0,16
-3018-0,4
0,01
X ning qaysi natural qiymatlari uchun x≤44, 3, 2 tengsizliklari to‘g‘ri bo‘ladi?
1 , 2, 3, 4
4, 3, 2, 1
0, 1, 2, 3
y ning qaysi butun qiymatlari uchun y tengsizlik to'g'ri bo'ladi?<-2?0
-1
0, -1, 1
Bunday qadriyatlar yo'q
Raqamlar -6; -3,8; -115; 0.8 joylashgan:
Kamaytirish tartibida
O'sish tartibida
Tartibsizlikda
Ob-havo ma'lumoti radio orqali uzatildi: havo harorati -20 ° C gacha tushishi kutilmoqda. Ushbu hodisani tasvirlab bering:
Mumkin emas
Ishonchli
Tasodifiy
Variant 2
Tengsizliklardan qaysi biri to'g'ri?
-5 > 0
6 < -17
-34 > -40
-9 < -63
Tengsizlik to'g'ri bo'lishi uchun bu kasrlar orasiga qanday belgi yozilishi kerak?
-1315 -715<
>
=
0 soni har qanday manfiy sondan kichik ekanligi rostmi?
Ha
Yo'q
X soni noldan katta emas. Ushbu bayonotni tengsizlik sifatida qanday yozishimiz mumkin?
x≥0x>0x<0x≤0Укажите наименьшее из данных чисел.
-5,92
1,7
-1000
35 a ning qaysi tabiiy qiymatlari uchun a≤3 tengsizlik rost?1, 2, 3
0, 1, 2, 3
1, 2
0, 1, 2
m ning qaysi butun qiymatlari uchun m tengsizlik to'g'ri bo'ladi?<-4?-3, -2, -1
0, -1, -2, -3, 1, 2, 3
0
Bunday qadriyatlar yo'q
1,2 raqamlari; -1,2; -427; -100 joylashgan:
Tartibsizlikda
O'sish tartibida
Kamaytirish tartibida
Koordinata chizig'ida A(5) nuqta belgilangan. Bu chiziqda yana bir B nuqtasi tasodifiy belgilangan edi.Uning koordinatasi 5 ga qarama-qarshi son bo'lib chiqdi. Ushbu hodisani tasvirlab bering.
Tasodifiy
Ishonchli
Mumkin emas
Javoblar
Test No 1 Test No 2
No 1-variant 2-variant
1 3 4
2 2 3
3 4 3
4 3 1
5 1 2
6 4 4
7 3 2
8 2 3
9 1 2
10 4 1
No 1-variant 2-variant
1 3 2
2 1 4
3 1 2
4 4 3
5 2 1
6 3 4
7 3 3
8 4 1
9 1 2
10 2 4
Test № 3
No 1-variant 2-variant
1 4 3
2 1 2
3 1 2
4 3 4
5 1 3
6 2 1
7 4 4
8 2 3
