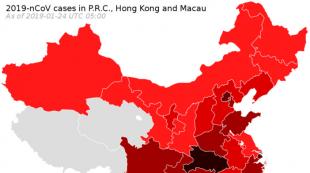
Dy janë të barabarta. Dy kundërshtarë të barabartë luajnë shah. Transformimet ekuivalente. Thjeshtimi i formulave
Përkufizimi. Dy ekuacione f 1 (x) = g 1 (x) dhe f 2 (x) = g 2 (x) quhen ekuivalente nëse bashkësitë e rrënjëve të tyre janë të njëjta.
Për shembull, ekuacionet x 2 - 9 = 0 dhe (2 X + 6)(X- 3) = 0 janë ekuivalente, pasi që të dy kanë si rrënjë numrat 3 dhe -3. Ekuacionet (3 X + 1)-2 = x 2- + 1 dhe x 2+ 1 = 0, pasi që të dyja nuk kanë rrënjë, d.m.th. grupet e rrënjëve të tyre janë të njëjta.
Përkufizimi. Zëvendësimi i një ekuacioni me një ekuacion ekuivalent quhet transformim ekuivalent.
Le të zbulojmë tani se cilat transformime bëjnë të mundur marrjen e ekuacioneve ekuivalente.
Teorema 1. Lëreni ekuacionin f(x) dhe g(x) dhënë në set dhe h(x) është një shprehje e përcaktuar në të njëjtin grup. Pastaj ekuacionet f(x) = g(x)(1) dhe f(x) + h(x) =g(x) + h(x) (2) janë ekuivalente.
Dëshmi. Shënoni me T 1 - grup zgjidhjesh të ekuacionit (1), dhe përmes T 2 - bashkësia e zgjidhjeve të ekuacionit (2). Atëherë ekuacionet (1) dhe (2) do të jenë ekuivalente nëse T 1 \u003d T 2. Për ta verifikuar këtë, është e nevojshme të tregohet se çdo rrënjë e T 1është një rrënjë e ekuacionit (2) dhe, anasjelltas, çdo rrënjë e T 2është rrënja e ekuacionit (1).
Lëreni numrin aështë rrënja e ekuacionit (1). Pastaj a? T 1 dhe kur zëvendësohet në ekuacionin (1) e kthen atë në një barazi të vërtetë numerike f(a) = g(a), dhe shprehja h(x) konvertohet në një shprehje numerike h(a) që ka kuptim në set x. Shtoni në të dyja anët e barazisë së vërtetë f(a) = g(a) shprehje numerike h(a). Ne marrim, sipas vetive të barazive të vërteta numerike, barazinë e vërtetë numerike f(a) + h(a) =g(a) + h(a), që tregon se aështë rrënja e ekuacionit (2).
Pra, është vërtetuar se çdo rrënjë e ekuacionit (1) është gjithashtu një rrënjë e ekuacionit (2), d.m.th. T 1 me T2.
Lëreni tani a - rrënja e ekuacionit (2). Pastaj a? T2 dhe kur zëvendësohet në ekuacionin (2) e kthen atë në një barazi të vërtetë numerike f(a) + h(a) =g(a) + h(a). Le t'i shtojmë të dy pjesëve të kësaj barazie një shprehje numerike - h(a), marrim barazinë e vërtetë numerike f(x) = g(x), gjë që tregon se numri a - rrënja e ekuacionit (1).
Pra, është vërtetuar se çdo rrënjë e ekuacionit (2) është gjithashtu një rrënjë e ekuacionit (1), d.m.th. T2 me T 1 .
Si T 1 me T 2 dhe T 2 me T 1 atëherë me përcaktimin e bashkësive të barabarta T 1= T 2, që do të thotë se ekuacionet (1) dhe (2) janë ekuivalente.
Kjo teoremë mund të formulohet ndryshe: nëse të dyja anët e ekuacionit me domenin e përkufizimit X shtoni të njëjtën shprehje me një variabël, të përcaktuar në të njëjtin grup, atëherë marrim një ekuacion të ri ekuivalent me atë të dhënë.
Nga kjo teoremë rrjedhin pasojat, të cilat përdoren në zgjidhjen e ekuacioneve:
1. Nëse shtojmë të njëjtin numër në të dy anët e ekuacionit, marrim një ekuacion që është ekuivalent me atë të dhënë.
2. Nëse ndonjë term (një shprehje numerike ose një shprehje me një ndryshore) transferohet nga një pjesë e ekuacionit në një tjetër, duke ndryshuar shenjën e termit në të kundërtën, atëherë marrim një ekuacion të barabartë me atë të dhënë.
Teorema 2. Lëreni ekuacionin f(x) = g(x) vendosur në set X dhe h (x) - një shprehje që përcaktohet në të njëjtin grup dhe nuk zhduket për asnjë vlerë X nga shumë x. Pastaj ekuacionet f(x) = g(x) dhe f(x) h(x) =g(x) h(x) janë ekuivalente.
Vërtetimi i kësaj teoreme është i ngjashëm me vërtetimin e Teoremës 1.
Teorema 2 mund të formulohet ndryshe: nëse të dyja anët e ekuacionit me domen X shumëzohemi me të njëjtën shprehje, e cila është përcaktuar në të njëjtin grup dhe nuk zhduket në të, atëherë marrim një ekuacion të ri të barabartë me atë të dhënë.
Përfundimi rrjedh nga kjo teoremë: nëse të dyja pjesët e ekuacionit shumëzohen (ose pjesëtohen) me të njëjtin numër të ndryshëm nga zero, atëherë marrim një ekuacion të barabartë me atë të dhënë.
Zgjidhja e ekuacioneve me një ndryshore
Zgjidh ekuacionin 1- x/3 = x/6, x ? R dhe të justifikojmë të gjitha transformimet që do të kryejmë në procesin e zgjidhjes.
| Transformimet | Arsyetimi për konvertim |
| 1. I sjellim shprehjet në anën e majtë dhe të djathtë të ekuacionit në një emërues të përbashkët: (6-2 X)/ 6 = X/6 | Kryen transformimin identik të shprehjes në anën e majtë të ekuacionit. |
| 2. Hiqni emëruesin e përbashkët: 6-2 X = X | I shumëzuam me 6 të dyja pjesët e ekuacionit (teorema 2), morëm një ekuacion të barabartë me atë të dhënë. |
| 3. Shprehjen -2x e transferojmë në anën e djathtë të ekuacionit me shenjën e kundërt: 6 = X+2X. | Ne përdorëm përfundimin nga teorema 1 dhe morëm një ekuacion të barabartë me atë të mëparshëm dhe, rrjedhimisht, me atë të dhënë. |
| 4. Ne paraqesim terma të ngjashëm në anën e djathtë të ekuacionit: 6 = 3 X. | Kryen transformimin identik të shprehjes. |
| 5. Ndani të dyja anët e ekuacionit me 3: X = 2. | Ne përdorëm konkluzionin nga teorema 2, morëm një ekuacion të barabartë me atë të mëparshëm, dhe kështu me këtë |
Meqenëse të gjitha transformimet që kemi kryer gjatë zgjidhjes së këtij ekuacioni ishin ekuivalente, mund të argumentohet se 2 është rrënja e këtij ekuacioni.
Nëse në procesin e zgjidhjes së ekuacionit, kushtet e teoremave 1 dhe 2 nuk plotësohen, atëherë mund të ndodhë humbja e rrënjëve ose mund të shfaqen rrënjë të jashtme. Prandaj, është e rëndësishme, kur kryhen transformime të ekuacionit për të marrë një më të thjeshtë, të sigurohet që ato të çojnë në një ekuacion të barabartë me atë të dhënë.
Merrni, për shembull, ekuacionin x(x - 1) = 2x, x? R. Le t'i ndajmë të dyja pjesët X, marrim ekuacionin X - 1 = 2, prej nga X= 3, d.m.th., ky ekuacion ka një rrënjë të vetme - numrin 3. Por a është e vërtetë kjo? Është e lehtë të shihet se nëse në këtë ekuacion në vend të ndryshores X duke zëvendësuar 0, do të kthehet në një barazi të vërtetë numerike 0 (0 - 1) = 2 0. Dhe kjo do të thotë se 0 është rrënja e këtij ekuacioni, të cilin e kemi humbur gjatë kryerjes së transformimeve. Le t'i analizojmë ato. Gjëja e parë që bëmë ishte të ndajmë të dyja anët e ekuacionit në X, ato. shumëzuar me shprehjen1/ x, por në X= Oh, nuk ka kuptim. Për rrjedhojë, ne nuk e përmbushëm kushtin e teoremës 2, e cila çoi në humbjen e rrënjës.
Për t'u siguruar që bashkësia e rrënjëve të këtij ekuacioni përbëhet nga dy numra 0 dhe 3, ne paraqesim një zgjidhje tjetër. Le të lëvizim shprehjen 2 X nga e djathta në të majtë: x(x- 1) - 2x \u003d 0. Ne nxjerrim kllapat në anën e majtë të ekuacionit X dhe jepni kushte të ngjashme: x(x - 3) = 0. Prodhimi i dy faktorëve është i barabartë me zero nëse dhe vetëm nëse të paktën njëri prej tyre është i barabartë me zero, prandaj x= 0 ose X- 3 = 0. Nga këtu marrim se rrënjët e këtij ekuacioni janë 0 dhe 3.
Në matematikën fillore bazë teorike zgjidhja e ekuacioneve është marrëdhënia ndërmjet komponentëve dhe rezultateve të veprimeve. Për shembull, zgjidhja e ekuacionit ( X 9):24 = 3 justifikohet si më poshtë. Meqenëse e panjohura është në divident, për të gjetur dividentin, duhet të shumëzoni pjesëtuesin me herësin: X 9 = 24 3, ose X 9 = 72.
Për të gjetur faktorin e panjohur, duhet ta ndani produktin me faktorin e njohur: x = 72:9 ose x = 8, pra, rrënja e këtij ekuacioni është numri 8.
Ushtrime
1 . Përcaktoni se cilat nga hyrjet e mëposhtme janë ekuacione me një ndryshore:
a) ( X-3) 5 = 12 X; d) 3 + (12-7) 5 = 16;
b) ( X-3) 5 = 12; e) ( X-3) y =12X;
në) ( X-3) 17 + 12; e) x 2 - 2x + 5 = 0.
2. Ekuacioni 2 X 4 + 4X 2 -6 = 0 jepet në grup numrat natyrorë. Shpjegoni pse numri 1 është rrënja e këtij ekuacioni, por 2 dhe -1 nuk janë rrënjët e tij.
3. Në ekuacionin ( X+ ...)(2X + 5) - (X - 3)(2X+ 1) = 20 një numër fshihet dhe zëvendësohet me pika. Gjeni numrin e fshirë nëse e dini se rrënja e këtij ekuacioni është numri 2.
4. Formuloni kushtet në të cilat:
a) numri 5 është rrënja e ekuacionit f(x) = g(x);
b) numri 7 nuk është rrënja e ekuacionit f(x) = g(x).
5. Përcaktoni se cilët nga çiftet e mëposhtëm të ekuacioneve janë ekuivalente në bashkësinë e numrave realë:
a) 3 + 7 X\u003d -4 dhe 2 (3 + 7l X) = -8;
6)3 + 7X= -4 dhe 6 + 7 X = -1;
c) 3 + 7 X= -4 dhe l X + 2 = 0.
6. Formuloni vetitë e relacionit të ekuivalencës së ekuacionit. Cilat prej tyre përdoren në procesin e zgjidhjes së ekuacionit?
7. Zgjidh ekuacionet (të gjitha janë dhënë në bashkësinë e numrave realë) dhe arsyeto të gjitha shndërrimet e kryera në procesin e thjeshtimit të tyre:
a) (7 x+4)/2 – x = (3x-5)/2;
b) x –(3x-2)/5 = 3 – (2x-5)/3;
në 2 - X)2-X (X + 1,5) = 4.
8. Nxënësi zgjidhi ekuacionin 5 X + 15 = 3 X+ 9 si më poshtë: vendosni numrin 5 jashtë kllapave në anën e majtë, dhe numrin 3 në anën e djathtë, mori ekuacionin 5 (x+ 3) = 3(X+ 3) dhe më pas ndani të dyja pjesët në një shprehje X+ 3. Mora barazinë 5 = 3 dhe arrita në përfundimin se ky ekuacion nuk ka rrënjë. A ka të drejtë studenti?
9. Zgjidh ekuacionin 2/(2- x) – ½ = 4/((2- x)x); X? R. A është numri 2 rrënja e këtij ekuacioni?
10. Zgjidhini ekuacionet duke përdorur marrëdhënien midis përbërësve dhe rezultateve të veprimeve:
a) ( X+ 70) 4 = 328; c) (85 X + 765): 170 = 98;
b) 560: ( X+ 9) - 56; G) ( X - 13581):709 = 306.
11. Zgjidh problemet në mënyra aritmetike dhe algjebrike:
a) Ka 16 libra më shumë në raftin e parë sesa në të dytin. Nëse hiqni 3 libra nga çdo raft, atëherë do të ketë një herë e gjysmë më shumë libra në raftin e parë sesa në të dytin. Sa libra ka në çdo raft?
b) Çiklisti e përshkoi gjithë rrugën nga kampi deri në stacion, e barabartë me 26 km, për 1 orë e 10 minuta. Për 40 minutat e para të kësaj kohe, ai voziti me të njëjtën shpejtësi, dhe pjesën tjetër të kohës - me një shpejtësi prej 3 km/h më pak. Gjeni shpejtësinë e çiklistit në pjesën e parë të udhëtimit.
Ore e hapur ne matematike "Skema Bernoulli. Zgjidhja e problemave duke perdorur skemen Bernoulli dhe Laplace"
didaktike: përvetësimi i aftësive dhe aftësive për të punuar me skemën Bernoulli për llogaritjen e probabiliteteve.
Zhvillimi: zhvillimi i aftësive për zbatimin e njohurive në praktikë, formimi dhe zhvillimi i të menduarit funksional të nxënësve, zhvillimi i aftësive të krahasimit, analizës dhe sintezës, aftësive të punës në dyshe, zgjerimi i fjalorit profesional.
Si të luani këtë lojë:
Edukative: nxitja e interesit për lëndën nëpërmjet përdorim praktik teoria, arritja e asimilimit të vetëdijshëm të materialit arsimor të studentëve, formimi i aftësisë për të punuar në ekip, përdorimi i saktë i termave kompjuterikë, interesimi për shkencën, respekti për profesionin e ardhshëm.
Njohuri shkencore: B
Lloji i mësimit: mësim i kombinuar:
- konsolidimi i materialit të mbuluar në klasat e mëparshme;
- tematike, teknologji informative-problematike;
- përgjithësimi dhe konsolidimi i materialit të studiuar në këtë orë mësimi.
Metoda e mësimdhënies: shpjeguese - ilustruese, problematike.
Kontrolli i njohurive: vrojtimi ballor, zgjidhja e problemit, prezantimi.
Pajisjet materiale dhe teknike të orës së mësimit. kompjuter, projektor multimedial.
Mbështetje metodologjike: materiale referimi, prezantim mbi temën e mësimit, fjalëkryq.
Gjatë orëve të mësimit
1. Momenti organizativ: 5 min.
(përshëndetje, gatishmëria e grupit për mësimin).
2. Kontrolli i njohurive:
Kontrolloni pyetjet përpara në sllajde: 10 min.
- përkufizimet e seksionit "Teoria e probabilitetit"
- koncepti kryesor i seksionit "Teoria e probabilitetit"
- cilat ngjarje studiohen nga "Teoria e Probabilitetit"
- karakteristikë e një ngjarjeje të rastësishme
- përkufizimi klasik i probabiliteteve
Duke përmbledhur. 5 minuta.
3. Zgjidhja e problemave në rreshta: 5 min.
Detyra 1. Hidhet një zare. Sa është probabiliteti për të marrë një numër çift më të vogël se 5?
Detyra 2. Ka nëntë tuba radio identikë në një kuti, tre prej të cilave ishin në përdorim. Gjatë ditës së punës, mjeshtrit iu desh të merrte dy tuba radio për të riparuar pajisjet. Sa është probabiliteti që të dy llambat të jenë përdorur?
Detyra 3. Janë tre filma të ndryshëm në tri salla kinemaje. Probabiliteti që të ketë bileta për një orë të caktuar në arkën e sallës së parë është 0,3, në arkën e sallës së dytë - 0,2 dhe në arkën e sallës së tretë - 0,4. Sa është probabiliteti që në një orë të caktuar të jetë e mundur të blihet një biletë për të paktën një film?
4. Kontrollimi në dërrasën e zezë si të zgjidhen problemet. Aplikimi 1. 5 min.
Përfundimi i 5-të për zgjidhjen e problemeve:
Probabiliteti i ndodhjes së një ngjarjeje është i njëjtë për secilën detyrë: m dhe n - konst
6. Vendosja e qëllimit përmes detyrës: 5 min.
Detyrë. Dy shahistë të barabartë luajnë shah. Sa është probabiliteti për të fituar dy ndeshje nga katër?
Sa është probabiliteti për të fituar tre ndeshje nga gjashtë (barazimet nuk merren parasysh)?
Pyetje. Mendoni dhe emërtoni ndryshimin midis pyetjeve të këtij problemi dhe pyetjeve të problemeve të mëparshme?
Duke arsyetuar, për krahasim, arrini një përgjigje: në pyetjet m dhe n janë të ndryshme.
7. Tema e mësimit:
Llogaritja e probabilitetit të ndodhjes së një ngjarjeje k herë nga n eksperimente me p-konst.
Nëse bëhen prova në të cilat probabiliteti i ndodhjes së ngjarjes A në çdo provë nuk varet nga rezultatet e sprovave të tjera, atëherë prova të tilla quhen të pavarura në lidhje me ngjarjen A. Provat, në secilën prej të cilave probabiliteti i shfaqjes së ngjarja është e njëjtë.
Formula e Bernulit. Probabiliteti që në n prova të pavarura, në secilën prej të cilave probabiliteti i ndodhjes së një ngjarjeje është i barabartë me p (0 ose Shtojca 2 formula Bernoulli, ku k,n-numra të vegjël ku q = 1-p Zgjidhje: Po luajnë shahistë të barabartë, kështu që probabiliteti për të fituar është p=1/2; pra probabiliteti për të humbur q është gjithashtu 1/2. Meqenëse probabiliteti për të fituar është konstant në të gjitha ndeshjet dhe nuk ka rëndësi se në çfarë radhe janë fituar lojërat, formula e Bernoulli është e zbatueshme. 5 minuta Gjeni probabilitetin që dy ndeshje nga katër do të fitohen: Gjeni probabilitetin që tre nga gjashtë ndeshje të fitohen: Meqenëse P4 (2) > P6 (3), ka më shumë gjasa për të fituar dy ndeshje nga katër sesa tre nga gjashtë. Gjeni probabilitetin që ngjarja A të ndodhë saktësisht 70 herë në 243 prova nëse probabiliteti që kjo ngjarje të ndodhë në çdo provë është 0,25. k=70, n=243 Kjo nënkupton që k dhe n janë numra të mëdhenj. Kjo do të thotë se është e vështirë të llogaritet sipas formulës së Bernulit. Për raste të tilla, aplikohet formula lokale Laplace: Shtojca 3 për vlerat pozitive të x është dhënë në Shtojcën 4; për vlerat negative të x-it përdorni të njëjtën tabelë dhe = . 1. Dy lojtarë të barabartë luajnë një lojë në të cilën barazimet përjashtohen. Sa është probabiliteti që lojtari i parë të fitojë: a) një lojë nga dy? b) dy nga katër? c) tre nga gjashtë? Përgjigje: a) ; b) ; në) 3. Prerë AB të ndara me një pikë Me në raport 2:1. Katër pikë hidhen në mënyrë të rastësishme në këtë segment. Gjeni probabilitetin që dy prej tyre të jenë në të majtë të pikës C dhe dy në të djathtë. Përgjigje: 4. Gjeni probabilitetin që ngjarja A të ndodhë saktësisht 70 herë në 243 prova nëse probabiliteti që kjo ngjarje të ndodhë në çdo provë është 0,25. Përgjigje: . 5. Probabiliteti për të pasur një djalë është 0,515. Gjeni probabilitetin që midis 100 të porsalindurve djemtë dhe vajzat të ndahen në mënyrë të barabartë. Përgjigje: 0,0782 6. Dyqani mori 500 shishe në enë qelqi. Probabiliteti që ndonjë nga shishet të thyhet gjatë transportit është 0.003. Gjeni probabilitetin që dyqani të marrë shishe të thyera: a) saktësisht dy; b) më pak se dy; c) të paktën dy; d) të paktën një. Përgjigje: a) 0,22; b) 0,20; c) 0,80; d) 0,95 7. Një fabrikë automobilash prodhon 80% të makinave pa defekte të rëndësishme. Sa është probabiliteti që mes 600 makinave të ardhura nga fabrika në bursë të automobilave, të jenë të paktën 500 makina pa defekte të theksuara? Përgjigje: 0,02. 8. Sa herë ju duhet të ktheni një monedhë në mënyrë që me një probabilitet prej 0,95 mund të prisni që frekuenca relative e stemës të devijojë nga probabiliteti R\u003d 0,5 pamja e stemës në një hedhje të një monedhe jo më shumë se 0,02? Përgjigje: n ≥ 2401. 9. Probabiliteti që një ngjarje të ndodhë në secilën prej 100 ngjarjeve të pavarura është konstante dhe e barabartë me fq=0.8. Gjeni probabilitetin që ngjarja të ndodhë: a) të paktën 75 herë dhe maksimumi 90 herë; b) të paktën 75 herë; c) jo më shumë se 74 herë. Përgjigje: a B C) . 10. Probabiliteti që një ngjarje të ndodhë në secilën prej provave të pavarura është 0,2. Gjeni se çfarë devijimi i frekuencës relative të ndodhjes së një ngjarjeje nga probabiliteti i saj mund të pritet me një probabilitet prej 0,9128 në 5000 prova. Përgjigje: 11. Sa herë duhet hedhur një monedhë në mënyrë që me një probabilitet 0,6 të pritet që devijimi i shpeshtësisë relative të paraqitjes së stemës nga probabiliteti. fq=0.5 do të jetë jo më shumë se 0.01 në vlerë absolute. Përgjigje: n = 1764. 12. Probabiliteti që një ngjarje të ndodhë në secilën prej 10,000 provave të pavarura është 0,75. Gjeni probabilitetin që frekuenca relative e ndodhjes së një ngjarjeje të devijojë nga probabiliteti i saj në vlerë absolute jo më shumë se 0.01. Përgjigje: . 13. Probabiliteti që një ngjarje të ndodhë në secilën prej provave të pavarura është 0,5. Gjeni numrin e provave n, në të cilën me një probabilitet prej 0,7698 mund të pritet që frekuenca relative e ndodhjes së një ngjarjeje të devijojë nga probabiliteti i saj në vlerë absolute jo më shumë se 0,02. Përkufizimi. Dy formula të algjebrës së logjikës A dhe B thirrur ekuivalente nëse marrin të njëjtat vlera logjike për çdo grup vlerash të propozimeve elementare të përfshira në formula. Ekuivalenca e formulave do të shënohet me shenjën dhe shënimin A AT do të thotë se formulat A dhe B janë ekuivalente. Për shembull, formulat e mëposhtme janë ekuivalente: Formula A quhet identike e vërtetë (ose tautologji), nëse merr vlerën 1 për të gjitha vlerat e variablave të përfshirë në të. Për shembull, formulat janë gjithashtu të vërteta ,
. Formula POR thirrur në mënyrë identike të rreme, nëse merr vlerën 0 për të gjitha vlerat e variablave të përfshirë në të. Për shembull, formula është identike e rreme. Është e qartë se lidhja e ekuivalencës është refleksive, simetrike dhe kalimtare. Midis koncepteve ekuivalencë dhe ekuivalencë ekziston lidhja e mëposhtme: nëse formulat POR dhe AT janë ekuivalente, pastaj formula POR AT- tautologjia, dhe anasjelltas, nëse formula POR AT- tautologjia, pastaj formulat POR dhe AT janë ekuivalente. Ekuivalencat më të rëndësishme të algjebrës së logjikës mund të ndahen në tre grupe. 1. Ekuivalencat bazë: Le të provojmë një nga ligjet e përthithjes. Merrni parasysh formulën .
Nëse kjo formulë a= 1 atëherë, padyshim, dhe ndërsa lidhja e dy propozimeve të vërteta. Lëreni tani në formulë A x = 0. Por atëherë, sipas përcaktimit të veprimit lidhor, lidhëza do të jetë e rreme dhe lidhëza .
Pra, në të gjitha rastet, vlerat e formulës POR përputhen me vlerat a, dhe për këtë arsye POR x. 2. Ekuivalencat që shprehin disa veprime logjike në terma të të tjerëve: Është e qartë se ekuivalencat 5 dhe 6 fitohen përkatësisht nga ekuivalencat 3 dhe 4, nëse marrim mohime nga të dyja pjesët e kësaj të fundit dhe përdorim ligjin e heqjes së mohimeve të dyfishta. Kështu, katër ekuivalencat e para kanë nevojë për provë. Le të vërtetojmë dy prej tyre: i pari dhe i treti. Meqenëse për të njëjtat vlera logjike X dhe në janë formula të vërteta , , , atëherë edhe lidhja do të jetë e vërtetë Lëreni tani X dhe në kanë vlera të ndryshme logjike. Atëherë ekuivalenca dhe një nga dy implikimet ose do të jenë të rreme. Në të njëjtën kohë do të jetë e rreme dhe lidhja Konsideroni ekuivalencën 3. Nëse X dhe në merrni vlera të vërteta në të njëjtën kohë, atëherë lidhja do të jetë e vërtetë x&y dhe mohim i rremë i lidhëzës. Në të njëjtën kohë, të dyja dhe dhe do të jenë të rreme, dhe për këtë arsye veçimi do të jetë gjithashtu i rremë .
Le të paktën një nga variablat X ose në merr vlerën false. Atëherë do të ketë një lidhje të rreme x&y dhe mohimi i tij i vërtetë. Në të njëjtën kohë, mohimi i të paktën njërit prej variablave do të jetë i vërtetë, dhe për këtë arsye disjunksioni do të jetë gjithashtu i vërtetë .
Prandaj, në të gjitha rastet, të dyja pjesët e ekuivalencës 3 marrin të njëjtat vlera logjike. Ekuivalencat 2 dhe 4 vërtetohen në mënyrë të ngjashme. Nga ekuivalencat e këtij grupi rezulton se çdo formulë e algjebrës së logjikës mund të zëvendësohet me një formulë ekuivalente me të, që përmban vetëm dy veprime logjike: lidhëz dhe mohim ose shkëputje dhe mohim. Përjashtimi i mëtejshëm i operacioneve logjike nuk është i mundur. Pra, nëse përdorim vetëm lidhje, atëherë tashmë një formulë e tillë si mohimi X nuk mund të shprehet duke përdorur operatorin lidhor. Sidoqoftë, ka operacione me të cilat mund të shprehet ndonjë nga pesë operacionet logjike që përdorim. Një operacion i tillë është, për shembull, operacioni "Schaeffer's stroke". Ky operacion simbolizohet x|y dhe përcaktohet nga tabela e mëposhtme e së vërtetës: Natyrisht, ka ekuivalenca: 2) x&y (x|y)|(x|y). Nga këto dy ekuivalenca rezulton se çdo formulë e algjebrës së logjikës mund të zëvendësohet nga një formulë ekuivalente që përmban vetëm veprimin "goditja e Schaeffer". Vini re se. Në mënyrë të ngjashme, operacioni mund të prezantohet 3. Ekuivalencat që shprehin ligjet bazë të algjebrës së logjikës: 1. x&y y&x - komutativiteti i lidhëzës. 2. x në y X- komutativiteti i disjunksionit. 3. x& (y& z) (x & y) & z- Asociativiteti i lidhëzës. 4. X(yz )
(X y) z është asociativiteti i disjunksionit. 5. x& (y z) (x&y) (x&z)- distributiviteti i lidhëzës në lidhje me disjunksionin. 6. X (y&z) (X y)& (x z )
- distributiviteti i disjunksionit në lidhje me lidhëzën. Le të provojmë të fundit nga ligjet e renditura. Nese nje X= 1, atëherë formulat do të jenë të vërteta X (y& z), X y, x z .
Por atëherë lidhja do të jetë gjithashtu e vërtetë (X y)& (x z ).
Kështu, në X= 1 të dyja pjesët e ekuivalencës 6 marrin të njëjtat vlera logjike (e vërtetë). Lëreni tani x = 0. Pastaj X (y&z) y&z, x në në dhe x z z ,
dhe për këtë arsye lidhëza X (y&z) y&z. Prandaj, këtu të dyja pjesët e ekuivalencës 6 janë ekuivalente me të njëjtën formulë y&z, dhe për këtë arsye merrni të njëjtat vlera boolean. § 5. Shndërrime ekuivalente të formulave Duke përdorur ekuivalencat e grupeve I, II dhe III, është e mundur të zëvendësohet një pjesë e formulës ose një formule me një formulë ekuivalente. Shndërrime të tilla formulash quhen ekuivalente. Shndërrimet ekuivalente përdoren për të vërtetuar ekuivalencat, për të sjellë formulat në një formë të caktuar, për të thjeshtuar formulat. Formula POR konsiderohet më e thjeshtë se formula ekuivalente AT, nëse përmban më pak shkronja, më pak operacione logjike. Në këtë rast, ekuivalenca dhe implikimi i operacioneve zakonisht zëvendësohen nga operacionet e ndarjes dhe lidhjes, dhe mohimi referohet si propozime elementare. Le të shqyrtojmë disa shembuj. 1. Vërtetoni ekuivalencën Përdorimi i ekuivalencave të grupeve I, II dhe III 2.
Thjeshtoni formulën Le të shkruajmë një zinxhir formulash ekuivalente: 3. Vërtetoni të vërtetën identike të formulës Le të shkruajmë një zinxhir formulash ekuivalente: Algjebra Boole Ekuivalencat e grupit III thonë se algjebra e logjikës ka ligje komutative dhe asociative në lidhje me veprimet e lidhjes dhe disjunksionit dhe një ligj shpërndarës të lidhjes në lidhje me disjunksionin; të njëjtat ligje ndodhin në algjebrën e numrave. Prandaj, mbi formulat e algjebrës së logjikës, mund të kryeni të njëjtat transformime që kryhen në algjebrën e numrave (hapja e kllapave, kllapa, kllapa e faktorit të përbashkët). Por në algjebrën e logjikës, transformime të tjera të bazuara në përdorimin e ekuivalencave janë gjithashtu të mundshme: Kjo veçori na lejon të arrijmë në përgjithësime të gjera. Konsideroni një grup jo bosh M elemente të çdo natyre ( x,y,z,...} ,
i cili përcakton marrëdhënien "=" (e barabartë me) dhe tre operacione: "+" (mbledhje), "" (shumëzimi) dhe "-" (mohim), duke iu nënshtruar aksiomave të mëposhtme: Ligjet komutative: 1a. x + y = y + x, 1b. X y = y X. Ligjet e shoqatës: 2a. x + (y + z)= (x + y) + z, 2b. X (në z) = (x y) z. Ligjet e shpërndarjes: 3a. (x + y) z = (x z ) + (y G) 3b. (x y) + z = (x+z) (y + z). Ligjet e idempotencës: 4a. x + x = x, 4b. X x = x. Ligji i mohimit të dyfishtë: Ligjet e De Morganit: 6a. ,
6b .
. Ligjet e përthithjes: 7a. x + (y X)= X, 7b. X (y + x) = x. Një turmë e tillë M thirrur algjebër boolean. Nëse nën elementet kryesore x, y, z, ... nënkuptojnë pohime, sipas veprimeve "+", "", "-" disjuksion, lidhëz, mohim, përkatësisht, dhe konsideroni shenjën e barabartë si shenjë ekuivalence, pastaj, siç vijon nga ekuivalencat e grupeve I, II dhe III. , plotësohen të gjitha aksiomat e algjebrës së Bulit. Në ato raste kur, për një sistem të caktuar aksiomash, është e mundur të zgjidhen objekte specifike dhe marrëdhënie specifike ndërmjet tyre, në mënyrë që të plotësohen të gjitha aksiomat, themi se interpretimi(ose model) ky sistem aksiomash. Pra, algjebra e logjikës është një interpretim i algjebrës së Bulit. Algjebra e Boole ka edhe interpretime të tjera. Për shembull, nëse nën elementët kryesorë x, y, z, ... grupe M grupe mesatare, nën veprimet "+", "", "-" bashkim, kryqëzim, plotësues, përkatësisht, dhe nën shenjën e barabartë - shenjën e barazisë së bashkësive, atëherë vijmë te algjebra e bashkësive. Është e lehtë të verifikohet se në algjebrën e bashkësive plotësohen të gjitha aksiomat e algjebrës së Bulit. Ndër interpretimet e ndryshme të algjebrës së Bulit, ka interpretime të një natyre teknike. Një prej tyre do të diskutohet më poshtë. Siç do të tregohet, ai luan një rol të rëndësishëm në automatizimin modern. Funksionet e algjebrës së logjikës Siç u përmend tashmë, kuptimi i formulës së algjebrës së logjikës varet plotësisht nga kuptimet e pohimeve të përfshira në këtë formulë. Prandaj, formula e algjebrës së logjikës është funksion i propozimeve elementare të përfshira në të. Për shembull, formula është një funksion tre variabla f(x,y,z). Një tipar i këtij funksioni është fakti që argumentet e tij marrin njërën nga dy vlerat: zero ose një, ndërsa funksioni gjithashtu merr një nga dy vlerat: zero ose një. Përkufizimi. Funksioni logjik i algjebrës variablat ha (ose Funksioni Boolean) Quhet një funksion prej n variablash, ku secila variabël merr dy vlera: 0 dhe 1, dhe në të njëjtën kohë, funksioni mund të marrë vetëm një nga dy vlerat: 0 ose 1. Është e qartë se formulat identike të vërteta dhe identike të gabuara të algjebrës së logjikës janë funksione konstante dhe dy formula ekuivalente shprehin të njëjtin funksion. Le të zbulojmë se cili është numri i funksioneve të n variablave. Natyrisht, çdo funksion i algjebrës së logjikës (si dhe formula e algjebrës së logjikës) mund të përcaktohet duke përdorur një tabelë të së vërtetës, e cila do të përmbajë 2 n rreshta. Prandaj, çdo funksion i n variablave merr 2n vlera, të përbërë nga zero dhe njëshe. Kështu, një funksion prej n variablash përcaktohet plotësisht nga një grup vlerash zero dhe njësh me gjatësi 2 n. (Numri i përgjithshëm i grupeve zero dhe njësh me gjatësi 2 n është i barabartë me . Prandaj, numri i të ndryshme funksionet e algjebrës logjike P variablat është e barabartë me . Në veçanti, ekzistojnë katër funksione të ndryshme të një ndryshoreje, dhe gjashtëmbëdhjetë funksione të ndryshme të dy ndryshoreve. Le të shkruajmë të gjitha funksionet e algjebrës së logjikës dhe dy variabla. Konsideroni një tabelë të së vërtetës për funksione të ndryshme të një ndryshoreje. Duket qartë si: Nga kjo tabelë rezulton se dy funksione të një ndryshoreje do të jenë konstante: f 1 (x)= 1, f 4 (x) = 0, dhe f 2 (x) X, dhe f 3 (x) .
Tabela e së vërtetës për të gjitha funksionet e mundshme të dy variablave është: f i = f i (x, y) Është e qartë se shprehjet analitike për këto funksione mund të shkruhen si më poshtë. Seksioni 2. Ekuivalenca logjike e formulave. Format normale për formulat e algjebrës propozicionale Marrëdhënia e ekuivalencës Me ndihmën e tabelave të së vërtetës, mund të përcaktohet se në cilat grupe të vlerave të së vërtetës të ndryshoreve hyrëse formula do të marrë një vlerë të vërtetë ose të gabuar (si dhe një deklaratë që ka strukturën logjike përkatëse), cilat formula do të jenë tautologji ose kontradikta, dhe gjithashtu të përcaktojë nëse dy formula të dhëna ekuivalente. Në logjikë, dy fjali thuhet se janë ekuivalente nëse janë të dyja të vërteta ose të dyja të gabuara. Fjala "njëkohësisht" në këtë frazë është e paqartë. Pra, për fjalitë "Nesër do të jetë e martë" dhe "Dje ishte e diel" kjo fjalë ka një kuptim të mirëfilltë: të hënën janë të dyja të vërteta, dhe në pjesën tjetër të javës janë të dyja të rreme. Për ekuacionet " x = 2"dhe" 2x = 4» "njëkohësisht" do të thotë "me të njëjtat vlera të ndryshores". Parashikimet "Nesër do të bjerë shi" dhe "Nuk është e vërtetë që nesër nuk do të bjerë shi" do të konfirmohen njëkohësisht (rezultojnë të jenë të vërteta) ose nuk do të konfirmohen (rezultojnë të rreme). Në thelb, ky është i njëjti parashikim, i shprehur në dy forma të ndryshme, të cilat mund të përfaqësohen nga formulat X dhe . Këto formula marrin njëkohësisht vlerën "e vërtetë" ose vlerën "false". Për të kontrolluar, mjafton të bëni një tabelë të së vërtetës: Ne shohim që vlerat e së vërtetës në kolonën e parë dhe të fundit janë të njëjta. Formula të tilla, si dhe fjalitë që u përgjigjen, konsiderohen natyrshëm ekuivalente. Formulat F 1 dhe F 2 quhen ekuivalente nëse ekuivalenti i tyre është një tautologji. Ekuivalenca e dy formulave shkruhet si më poshtë: (lexo: formula F1është e barabartë me formulën F2). Ekzistojnë tre mënyra për të kontrolluar nëse formulat janë ekuivalente: 1) bëni ekuivalentin e tyre dhe përdorni tabelën e së vërtetës për të kontrolluar nëse është një tautologji; 2) për secilën formulë, bëni një tabelë të vërtetësisë dhe krahasoni rezultatet përfundimtare; nëse në kolonat totale për të njëjtat grupe vlerash të ndryshueshme
vlerat e së vërtetës së të dy formulave do të jenë të barabarta, atëherë formulat janë ekuivalente; 3) me ndihmën e shndërrimeve ekuivalente. Shembulli 2.1: Gjeni nëse formulat janë ekuivalente: 1) , ; 2), . 1) Le të përdorim metodën e parë për të përcaktuar ekuivalencën, domethënë të zbulojmë nëse ekuivalenca e formulave është një tautologji. Le të bëjmë një ekuivalencë të formulave: . Formula që rezulton përmban dy ndryshore të ndryshme ( POR dhe AT) dhe 6 operacione: 1) ; 2) ; 3) ; 4) ; 5) ; 6). Kjo do të thotë që tabela përkatëse e së vërtetës do të ketë 5 rreshta dhe 8 kolona: Nga kolona e fundit e tabelës së së vërtetës, mund të shihet se ekuivalenca e përpiluar është një tautologji dhe, për rrjedhojë, . 2) Për të zbuluar nëse formulat dhe formulat janë ekuivalente, ne përdorim metodën e dytë, d.m.th., përpilojmë një tabelë të vërtetësisë për secilën nga formulat dhe krahasojmë kolonat përfundimtare. ( Koment. Për të përdorur në mënyrë efektive metodën e dytë, është e nevojshme që të gjitha tabelat e përpiluara të së vërtetës të fillojnë në të njëjtën mënyrë, d.m.th. grupet e vlerave të ndryshueshme ishin të njëjta në rreshtat përkatës
.) Formula ka dy ndryshore të ndryshme dhe 2 operacione, që do të thotë se tabela përkatëse e së vërtetës ka 5 rreshta dhe 4 kolona: Formula ka dy ndryshore të ndryshme dhe 3 operacione, që do të thotë se tabela përkatëse e së vërtetës ka 5 rreshta dhe 5 kolona: Duke krahasuar kolonat përfundimtare të tabelave të përpiluara të së vërtetës (meqenëse tabelat fillojnë në të njëjtën mënyrë, ne mund të shpërfillim grupet e vlerave të variablave), shohim se ato nuk përputhen dhe, për rrjedhojë, formulat nuk janë ekuivalente (). Shprehja nuk është një formulë (sepse simboli " " nuk i referohet ndonjë operacioni logjik). Ajo shpreh qëndrim ndërmjet formulave (si dhe barazia ndërmjet numrave, paralelizmi ndërmjet drejtëzave etj.). Teorema mbi vetitë e relacionit të ekuivalencës është e vlefshme: Teorema 2.1. Marrëdhënia e ekuivalencës ndërmjet formulave propozicionale të algjebrës: 1) në mënyrë refleksive: ; 2) në mënyrë simetrike: nëse , atëherë ; 3) në mënyrë kalimtare: nëse dhe , atëherë . Ligjet e logjikës Ekuivalencat e formulave logjike propozicionale shpesh quhen ligjet e logjikës. Ne rendisim më të rëndësishmet prej tyre: 1. - ligji i identitetit. 2. - ligji i mesit të përjashtuar 3. - ligji i kontradiktës 4. - disjuksioni me zero 5. - lidhja me zero 6. - shkëputje me njësi 7. - lidhje me njësinë 8. - ligji i mohimit të dyfishtë 9. - komutativiteti i lidhëzës 10. – komutativiteti i disjunksionit 11. - asociativiteti i lidhëzës 12. - asociativiteti i disjuksionit 13. – shpërndarja e lidhëzës 14. – disjunksion distributive 15. - ligjet e idempotencës 16. 17. 18. 19. 20. - ligjet që shprehin ekuivalencën nëpërmjet veprimeve të tjera logjike Ligjet e logjikës përdoren për të thjeshtuar formulat komplekse dhe për të vërtetuar se formulat janë identike të vërteta ose të rreme. Transformimet ekuivalente. Thjeshtimi i formulave Nëse në formulat ekuivalente kudo zëvendësojmë të njëjtën formulë në vend të ndonjë ndryshoreje, atëherë edhe formulat e marra rishtazi do të rezultojnë të jenë ekuivalente në përputhje me rregullin e zëvendësimit. Në këtë mënyrë, nga çdo ekuivalencë mund të merret çdo numër ekuivalencash të reja. Shembulli 1: Nëse në ligjin e De Morgan-it në vend të X zëvendësoj , në vend të Y zëvendësojmë , atëherë marrim një ekuivalencë të re . Vlefshmëria e ekuivalencës së fituar është e lehtë për t'u kontrolluar duke përdorur tabelën e së vërtetës. Nëse ndonjë formulë që është pjesë e formulës F, të zëvendësohet me një formulë ekuivalente me formulën, atëherë formula që rezulton do të jetë e barabartë me formulën F. Pastaj, për formulën nga Shembulli 2, mund të bëjmë zëvendësimet e mëposhtme: - ligji i mohimit të dyfishtë; - ligji i De Morganit; - ligji i mohimit të dyfishtë; – ligji i asociacionit; Me vetinë e kalueshmërisë së relacionit të ekuivalencës, mund të pohojmë se Zëvendësimi i një formule me një tjetër, ekuivalente me të, quhet transformim ekuivalent
formulat. Nën thjeshtimi
formulat që nuk përmbajnë shenja nënkuptimi dhe ekuivalence kuptojnë një transformim ekuivalent që çon në një formulë që nuk përmban mohime të formulave jo elementare (në veçanti, mohime të dyfishta) ose përmban në total një numër më të vogël shenjash lidhëse dhe shkëputëse se origjinali. një. Shembulli 2.2: Le të thjeshtojmë formulën Në hapin e parë, ne zbatuam ligjin që e shndërron nënkuptimin në një ndarje. Në hapin e dytë u zbatua ligji komutativ. Në hapin e tretë u zbatua ligji i idempotencës. Në të katërtin - ligji i De Morgan. Dhe në të pestën - ligji i mohimit të dyfishtë. Vërejtje 1. Nëse një formulë e caktuar është një tautologji, atëherë çdo formulë ekuivalente me të është gjithashtu një tautologji. Kështu, transformimet ekuivalente mund të përdoren gjithashtu për të vërtetuar të vërtetën identike të formulave të caktuara. Për ta bërë këtë, kjo formulë duhet të reduktohet me transformime ekuivalente në një nga formulat që janë tautologji. Vërejtje 2. Disa tautologji dhe ekuivalenca kombinohen në çifte (ligji i kontradiktës dhe ligji i ligjeve alternative, komutative, asociative, etj.). Në këto korrespondenca, të ashtuquajturat parimi i dualitetit
. Quhen dy formula që nuk përmbajnë shenja të nënkuptimit dhe ekuivalencës e dyfishtë
, nëse secili prej tyre mund të merret nga tjetri duke i zëvendësuar shenjat përkatësisht me . Parimi i dualitetit thotë si më poshtë: Teorema 2.2: Nëse dy formula që nuk përmbajnë shenja nënkuptimi dhe ekuivalence janë ekuivalente, atëherë formulat e tyre të dyfishta janë gjithashtu ekuivalente. forma normale formë normaleështë një mënyrë sintaksore e paqartë për të shkruar një formulë që zbaton një funksion të caktuar. Duke përdorur ligjet e njohura të logjikës, çdo formulë mund të shndërrohet në një formulë ekuivalente të formës Shembulli 2.3: Në formula të mëdha ose me shndërrime të shumëfishta, është zakon të hiqet shenja lidhore (për analogji me shenjën e shumëzimit): . Shohim që pas transformimeve të kryera, formula është një disjuksion i tre lidhëzave. Kjo formë quhet trajtë normale disjunctive
(DNF). Një element i vetëm i një DNF quhet lidhëza elementare
ose njësi përbërëse. Në mënyrë të ngjashme, çdo formulë mund të reduktohet në një formulë ekuivalente, e cila do të jetë një lidhje elementesh, secila prej të cilave do të jetë një ndarje e ndryshoreve logjike me ose pa një shenjë mohimi. Kjo do të thotë, secila formulë mund të reduktohet në një formulë ekuivalente të formës Shembulli 2.4: Një element i vetëm i CNF quhet ndarje elementare
ose përbërësi i zeros. Natyrisht, çdo formulë ka pafundësisht shumë DNF dhe CNF. Shembulli 2.5: Le të gjejmë disa DNF për formulën Forma normale perfekte SDNF (DNF perfekt) është një DNF i tillë në të cilin çdo lidhje elementare përmban të gjitha pohimet elementare, ose mohimet e tyre një herë, lidhëzat elementare nuk përsëriten. SKNF (CNF perfekt) është një CNF e tillë në të cilën çdo ndarje elementare përmban të gjitha propozimet elementare ose mohimet e tyre një herë, ndarjet elementare nuk përsëriten. Shembulli 2.6: 1) - SDNF 2) 1 - SKNF Le të formulojmë tiparet karakteristike të SDNF (SKNF). 1) Të gjithë anëtarët e disjunksionit (lidhëzës) janë të ndryshëm; 2) Të gjithë anëtarët e secilës lidhëz (disjunksion) janë të ndryshëm; 3) Asnjë lidhëz (disjunksion) nuk përmban edhe një ndryshore edhe mohimin e saj; 4) Çdo lidhje (disjunksion) përmban të gjitha variablat e përfshira në formulën origjinale. Siç mund ta shohim, karakteristikat (por jo format!) kënaqin përkufizimin e dualitetit, kështu që mjafton të kuptojmë një formë për të mësuar se si t'i marrim të dyja. Është e lehtë të merret SDNF (SKNF) nga DNF (CNF) me ndihmën e transformimeve ekuivalente. Meqenëse rregullat për marrjen e formave normale të përsosura janë gjithashtu të dyfishta, ne do të analizojmë në detaje rregullin për marrjen e SMNF dhe do të formulojmë rregullin për marrjen e SKNF në mënyrë të pavarur duke përdorur përkufizimin e dualitetit. Rregulli i përgjithshëm për reduktimin e një formule në SDNF duke përdorur transformime ekuivalente është:
Për të dhënë formulën F, e cila nuk është identike e rreme, me SDNF, mjafton: 1) sillni atë në disa DNF; 2) hiqni anëtarët e disjuksionit që përmban ndryshoren së bashku me mohimin e saj (nëse ka); 3) nga të njëjtët anëtarë të ndarjes (nëse ka), hiqni të gjithë përveç njërit; 4) hiqni të gjithë anëtarët identikë të secilës lidhëz, përveç njërit (nëse ka); 5) nëse ndonjë lidhëz nuk përmban një variabël nga variablat e përfshirë në formulën origjinale, shtoni një term në këtë lidhje dhe zbatoni ligjin përkatës shpërndarës; 6) nëse ndarja që rezulton përmban të njëjtat terma, përdorni recetën 3. Formula që rezulton është SDNF e kësaj formule. Shembulli 2.7: Le të gjejmë SDNF dhe SKNF për formulën Meqenëse DNF për këtë formulë është gjetur tashmë (shih Shembullin 2.5), ne do të fillojmë duke marrë SDNF: 2) në disjuksionin që rezulton nuk ka ndryshore së bashku me mohimet e tyre; 3) nuk ka anëtarë të njëjtë në disjuksion; 4) nuk ka ndryshore identike në asnjë lidhje; 5) lidhëza e parë elementare përmban të gjitha ndryshoret e përfshira në formulën origjinale dhe lidhëzës së dytë elementare i mungon një ndryshore z, pra t'i shtojmë një term dhe të zbatojmë ligjin shpërndarës: ; 6) është e lehtë të shihet se të njëjtat terma u shfaqën në ndarje, kështu që ne heqim një (parashkrimi 3); 3) hiqni një nga ndarjet identike: 4) nuk ka terma identikë në ndarjet e mbetura; 5) asnjë nga ndarjet elementare nuk i përmban të gjitha ndryshoret e përfshira në formulën origjinale, kështu që secilin prej tyre e plotësojmë me lidhëzën : ; 6) nuk ka ndarje identike në lidhëzën që rezulton, kështu që forma lidhore e gjetur është e përsosur. Meqenëse në agregatin e SKNF dhe SDNF formulat F 8 anëtarë, atëherë me shumë mundësi ata janë gjetur saktë. Çdo formulë e kënaqshme (e kundërshtueshme) ka një SDNF të vetme dhe një SKNF të vetme. Një tautologji nuk ka SKNF dhe një kontradiktë nuk ka SDNF.8. Detyrë.
9. Hartoni një algoritëm për zgjidhjen e problemës: 5 min.
10. Zgjidhja e problemës me analizë në dërrasën e zezë. Aneksi 5. 10 min.
11. Përmbledhja e informacionit të mësimit përmes prezantimeve
.
Prandaj, në këtë rast, të dyja pjesët e ekuivalencës kanë të njëjtat vlera të vërteta.. Kështu, në këtë rast, të dyja pjesët e ekuivalencës kanë të njëjtat vlera logjike.x y x|y
.
.
.
x f 1 (x)
f 2 (x)
f 3 (x)
f 3 (x)
1
x
y
f1
f2
f 3
f4
f5
f6
f7
f 8
f9
f 10
f 11
f 12
f 13
f 14
f 15
f 16
X
1
0
1
0
1
0
POR
AT
1
1
0
0
0
1
0
1
1
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
0
0
1
1
1
0
1
1
POR
AT
1
1
1
0
1
0
0
1
0
1
1
0
0
0
1
0
POR
AT
1
1
0
0
1
1
0
0
1
1
0
1
1
0
0
0
0
1
1
1
; 
- ligjet e përthithjes
; 
- Ligjet e De Morganit
është ligji që shpreh nënkuptimin nëpërmjet disjuksionit
- ligji i kundërpozicionit
është ligji i idempotencës.
.
.
, ku dhe secila është ose një ndryshore, ose mohimi i një ndryshoreje, ose një lidhje variablash ose mohimet e tyre. Me fjalë të tjera, çdo formulë mund të reduktohet në një formulë ekuivalente të një forme të thjeshtë standarde, e cila do të jetë një ndarje elementesh, secila prej të cilave është një lidhje e variablave të ndryshëm logjikë të veçantë, qoftë me ose pa një shenjë mohimi.
, ku dhe secila është ose një ndryshore, ose mohimi i një ndryshoreje, ose një ndarje e ndryshoreve ose mohimet e tyre. Kjo formë quhet formë normale lidhore
(KNF).
.
.
;
