რიცხვის განსაზღვრა მისი ლოგარითმით. ლოგარითმების თვისებები და მათი ამონახსნების მაგალითები. ყოვლისმომცველი სახელმძღვანელო (2020). ფსიქოლოგია და ბიოლოგია

მოცემულია ლოგარითმის ძირითადი თვისებები, ლოგარითმის გრაფიკი, განსაზღვრების დომენი, მნიშვნელობების სიმრავლე, ძირითადი ფორმულები, მატება და კლება. განიხილება ლოგარითმის წარმოებულის პოვნა. და ასევე ინტეგრალური, გაფართოება დენის სერიადა წარმოდგენა რთული რიცხვების გამოყენებით.

შინაარსი

დომენი, მნიშვნელობების ნაკრები, მზარდი, კლებადი

ლოგარითმი მონოტონური ფუნქციაა, ამიტომ მას არ აქვს ექსტრემები. ლოგარითმის ძირითადი თვისებები წარმოდგენილია ცხრილში.

დომენი	0 < x < + ∞	0 < x < + ∞
ღირებულებების დიაპაზონი	- ∞ < y < + ∞	- ∞ < y < + ∞
მონოტონური	მონოტონურად იზრდება	მონოტონურად მცირდება
ნულები, y = 0	x = 1	x = 1
კვეთის წერტილები ორდინატთა ღერძით, x = 0	არა	არა
	+ ∞	- ∞
	- ∞	+ ∞

პირადი ღირებულებები

მე-10 ბაზის ლოგარითმი ეწოდება ათობითი ლოგარითმიდა აღინიშნება შემდეგნაირად:

ლოგარითმი ბაზამდე ედაურეკა ბუნებრივი ლოგარითმი:

ლოგარითმების ძირითადი ფორმულები

შებრუნებული ფუნქციის განსაზღვრებიდან გამომდინარე ლოგარითმის თვისებები:

ლოგარითმების ძირითადი თვისება და მისი შედეგები

ბაზის შეცვლის ფორმულა

ლოგარითმი არის ლოგარითმის აღების მათემატიკური ოპერაცია. ლოგარითმების აღებისას ფაქტორების ნამრავლი გარდაიქმნება ტერმინთა ჯამებად.
პოტენციაცია არის მათემატიკური ოპერაცია ლოგარითმის საპირისპიროდ. პოტენციაციის დროს მოცემული ბაზა ამაღლებულია გამოხატვის ხარისხამდე, რომელზედაც ხდება პოტენციაცია. ამ შემთხვევაში ტერმინების ჯამები გარდაიქმნება ფაქტორების პროდუქტებად.

ლოგარითმების ძირითადი ფორმულების დადასტურება

ლოგარითმებთან დაკავშირებული ფორმულები გამომდინარეობს ექსპონენციური ფუნქციების ფორმულებიდან და შებრუნებული ფუნქციის განსაზღვრებიდან.

განვიხილოთ ექსპონენციალური ფუნქციის თვისება
.
მერე
.
გამოვიყენოთ ექსპონენციალური ფუნქციის თვისება
:
.

მოდით დავამტკიცოთ ბაზის ჩანაცვლების ფორმულა.
;
.
თუ დავუშვებთ c = b, გვაქვს:

ინვერსიული ფუნქცია

ლოგარითმის შებრუნება a-ს ბაზაზე არის ექსპონენციალური ფუნქციამაჩვენებლით ა.

თუ, მაშინ

თუ, მაშინ

ლოგარითმის წარმოებული

x მოდულის ლოგარითმის წარმოებული:
.
n-ე რიგის წარმოებული:
.
ფორმულების გამოყვანა >>>

ლოგარითმის წარმოებული რომ ვიპოვოთ, ის უნდა დაიყვანოთ ფუძემდე ე.
;
.

ინტეგრალური

ლოგარითმის ინტეგრალი გამოითვლება ნაწილებით ინტეგრირებით: .
Ისე,

გამოთქმები რთული რიცხვების გამოყენებით

განვიხილოთ კომპლექსური რიცხვების ფუნქცია ზ:
.
გამოვხატოთ რთული რიცხვი ზმოდულის საშუალებით რდა არგუმენტი φ :
.
შემდეგ, ლოგარითმის თვისებების გამოყენებით, გვაქვს:
.
ან

თუმცა, არგუმენტი φ არ არის ცალსახად განსაზღვრული. თუ დააყენებთ
, სადაც n არის მთელი რიცხვი,
მაშინ ეს იქნება იგივე რიცხვი სხვადასხვასთვის ნ.

ამრიგად, ლოგარითმი, როგორც რთული ცვლადის ფუნქცია, არ არის ერთმნიშვნელოვანი ფუნქცია.

დენის სერიის გაფართოება

როდესაც გაფართოება ხდება:

ცნობები:
ი.ნ. ბრონშტეინი, კ.ა. სემენდიაევი, მათემატიკის სახელმძღვანელო ინჟინრებისა და კოლეჯის სტუდენტებისთვის, „ლან“, 2009 წ.

Იხილეთ ასევე:

ჩვენ ვაგრძელებთ ლოგარითმების შესწავლას. ამ სტატიაში ვისაუბრებთ ლოგარითმების გამოთვლა, ამ პროცესს ე.წ ლოგარითმი. ჯერ გავიგებთ ლოგარითმების გამოთვლას განმარტებით. შემდეგი, მოდით შევხედოთ, თუ როგორ არის ნაპოვნი ლოგარითმების მნიშვნელობები მათი თვისებების გამოყენებით. ამის შემდეგ, ჩვენ ყურადღებას გავამახვილებთ ლოგარითმების გამოთვლაზე სხვა ლოგარითმების თავდაპირველად მითითებული მნიშვნელობებით. და ბოლოს, მოდით ვისწავლოთ ლოგარითმის ცხრილების გამოყენება. მთელი თეორია მოცემულია მაგალითებით დეტალური გადაწყვეტილებებით.

გვერდის ნავიგაცია.

ლოგარითმების გამოთვლა განმარტებით

უმარტივეს შემთხვევებში შესაძლებელია საკმაოდ სწრაფად და მარტივად შესრულება ლოგარითმის პოვნა განსაზღვრებით. მოდით, უფრო დეტალურად განვიხილოთ, თუ როგორ ხდება ეს პროცესი.

მისი არსი არის b რიცხვის წარმოდგენა a c სახით, საიდანაც, ლოგარითმის განმარტებით, რიცხვი c არის ლოგარითმის მნიშვნელობა. ანუ, განმარტებით, ტოლობების შემდეგი ჯაჭვი შეესაბამება ლოგარითმის პოვნას: log a b=log a a c =c.

ამრიგად, ლოგარითმის განსაზღვრებით გამოთვლა მთავრდება c რიცხვის პოვნამდე, რომ c = b და თავად რიცხვი c არის ლოგარითმის სასურველი მნიშვნელობა.

წინა აბზაცებში მოცემული ინფორმაციის გათვალისწინებით, როდესაც ლოგარითმის ნიშნის ქვეშ რიცხვი მოცემულია ლოგარითმის ბაზის გარკვეული სიმძლავრით, შეგიძლიათ დაუყოვნებლივ მიუთითოთ რის ტოლია ლოგარითმი - ის უდრის მაჩვენებელს. მოდით ვაჩვენოთ მაგალითების გადაწყვეტილებები.

მაგალითი.

იპოვეთ log 2 2 −3 და ასევე გამოთვალეთ რიცხვის e 5,3 ბუნებრივი ლოგარითმი.

გამოსავალი.

ლოგარითმის განმარტება საშუალებას გვაძლევს დაუყოვნებლივ ვთქვათ, რომ log 2 2 −3 =−3. მართლაც, რიცხვი ლოგარითმის ნიშნის ქვეშ უდრის 2-ს −3 ხარისხს.

ანალოგიურად, ჩვენ ვპოულობთ მეორე ლოგარითმს: lne 5.3 =5.3.

პასუხი:

log 2 2 −3 =−3 და lne 5,3 =5,3.

თუ რიცხვი b ლოგარითმის ნიშნის ქვეშ არ არის მითითებული, როგორც ლოგარითმის ფუძის სიმძლავრე, მაშინ საჭიროა ყურადღებით დაათვალიეროთ, რომ ნახოთ შესაძლებელია თუ არა რიცხვის b გამოსახვა a c სახით. ხშირად ეს წარმოდგენა საკმაოდ აშკარაა, განსაკუთრებით მაშინ, როდესაც რიცხვი ლოგარითმის ნიშნის ქვეშ უდრის ბაზის ხარისხს 1, ან 2, ან 3, ...

მაგალითი.

გამოთვალეთ ლოგარითმები log 5 25 და .

გამოსავალი.

ადვილი მისახვედრია, რომ 25=5 2, ეს საშუალებას გაძლევთ გამოთვალოთ პირველი ლოგარითმი: log 5 25=log 5 5 2 =2.

გადავიდეთ მეორე ლოგარითმის გამოთვლაზე. რიცხვი შეიძლება წარმოდგენილი იყოს 7-ის ხარისხად: (იხილეთ საჭიროების შემთხვევაში). აქედან გამომდინარე, .

გადავიწეროთ მესამე ლოგარითმი შემდეგი ფორმით. ახლა თქვენ ხედავთ ამას , საიდანაც ვასკვნით, რომ . მაშასადამე, ლოგარითმის განმარტებით .

მოკლედ, გამოსავალი შეიძლება დაიწეროს შემდეგნაირად: .

პასუხი:

ჟურნალი 5 25=2, და .

როდესაც ლოგარითმის ნიშნის ქვეშ არის საკმარისად დიდი ბუნებრივი რიცხვი, მაშინ არ იქნება ზიანის მომტანი მისი ძირითადი ფაქტორებად გადაქცევა. ხშირად გვეხმარება ისეთი რიცხვის წარმოდგენაში, როგორიც არის ლოგარითმის ფუძის გარკვეული სიმძლავრე და, შესაბამისად, ამ ლოგარითმის განსაზღვრებით გამოთვლა.

მაგალითი.

იპოვეთ ლოგარითმის მნიშვნელობა.

გამოსავალი.

ლოგარითმების ზოგიერთი თვისება საშუალებას გაძლევთ დაუყოვნებლივ მიუთითოთ ლოგარითმების მნიშვნელობა. ეს თვისებები მოიცავს ერთის ლოგარითმის თვისებას და ფუძის ტოლი რიცხვის ლოგარითმის თვისებას: log 1 1=log a a 0 =0 და log a=log a 1 =1. ანუ, როდესაც ლოგარითმის ნიშნის ქვეშ არის რიცხვი 1 ან რიცხვი ტოლი ლოგარითმის ფუძისა, მაშინ ამ შემთხვევებში ლოგარითმები უდრის 0-ს და 1-ს.

მაგალითი.

რის ტოლია ლოგარითმები და log10?

გამოსავალი.

ვინაიდან , მაშინ ლოგარითმის განმარტებიდან გამომდინარეობს .

მეორე მაგალითში რიცხვი 10 ლოგარითმის ნიშნის ქვეშ ემთხვევა მის ფუძეს, ამიტომ ათეულის ათწილადი ლოგარითმი უდრის ერთს, ანუ lg10=lg10 1 =1.

პასუხი:

და lg10=1.

გაითვალისწინეთ, რომ ლოგარითმების გამოთვლა განმარტებით (რაზეც წინა აბზაცში ვისაუბრეთ) გულისხმობს ტოლობის log a a p =p გამოყენებას, რაც ლოგარითმების ერთ-ერთი თვისებაა.

პრაქტიკაში, როდესაც რიცხვი ლოგარითმის ნიშნის ქვეშ და ლოგარითმის ფუძის ქვეშ არის ადვილად წარმოდგენილი, როგორც გარკვეული რიცხვის სიმძლავრე, ძალიან მოსახერხებელია ფორმულის გამოყენება. , რომელიც შეესაბამება ლოგარითმების ერთ-ერთ თვისებას. მოდით შევხედოთ ლოგარითმის პოვნის მაგალითს, რომელიც ასახავს ამ ფორმულის გამოყენებას.

მაგალითი.

გამოთვალეთ ლოგარითმი.

გამოსავალი.

პასუხი:

.

ლოგარითმების თვისებები, რომლებიც ზემოთ არ არის ნახსენები, ასევე გამოიყენება გამოთვლებში, მაგრამ ამაზე ვისაუბრებთ შემდეგ აბზაცებში.

ლოგარითმების პოვნა სხვა ცნობილი ლოგარითმების მეშვეობით

ამ პარაგრაფში მოცემული ინფორმაცია აგრძელებს ლოგარითმების თვისებების გამოყენების თემას მათი გამოთვლისას. მაგრამ აქ მთავარი განსხვავება ისაა, რომ ლოგარითმების თვისებები გამოიყენება ორიგინალური ლოგარითმის სხვა ლოგარითმით გამოხატვისთვის, რომლის მნიშვნელობა ცნობილია. გარკვევისთვის მოვიყვანოთ მაგალითი. ვთქვათ, ვიცით, რომ log 2 3≈1.584963, შემდეგ შეგვიძლია ვიპოვოთ, მაგალითად, log 2 6 მცირე ტრანსფორმაციის განხორციელებით ლოგარითმის თვისებების გამოყენებით: log 2 6=log 2 (2 3)=log 2 2+log 2 3≈ 1+1,584963=2,584963 .

ზემოთ მოყვანილ მაგალითში საკმარისი იყო პროდუქტის ლოგარითმის თვისების გამოყენება. თუმცა, ბევრად უფრო ხშირად საჭიროა ლოგარითმების თვისებების უფრო ფართო არსენალის გამოყენება, რათა გამოვთვალოთ ორიგინალური ლოგარითმი მოცემულების მეშვეობით.

მაგალითი.

გამოთვალეთ 27-ის ლოგარითმი 60-მდე, თუ იცით, რომ log 60 2=a და log 60 5=b.

გამოსავალი.

ასე რომ, ჩვენ უნდა ვიპოვოთ ჟურნალი 60 27. ადვილი მისახვედრია, რომ 27 = 3 3 და ორიგინალური ლოგარითმი, სიმძლავრის ლოგარითმის თვისების გამო, შეიძლება გადაიწეროს როგორც 3·log 60 3.

ახლა ვნახოთ, როგორ გამოვხატოთ log 60 3 ცნობილი ლოგარითმების მიხედვით. ფუძის ტოლი რიცხვის ლოგარითმის თვისება საშუალებას გვაძლევს დავწეროთ ტოლობის ჟურნალი 60 60=1. მეორეს მხრივ, log 60 60=log60(2 2 3 5)= log 60 2 2 +log 60 3+log 60 5= 2·log 60 2+log 60 3+log 60 5 . ამრიგად, 2 ლოგი 60 2+ლოგი 60 3+ლოგი 60 5=1. აქედან გამომდინარე, log 60 3=1−2·log 60 2−log 60 5=1−2·a−b.

დაბოლოს, ჩვენ ვიანგარიშებთ თავდაპირველ ლოგარითმს: log 60 27=3 log 60 3= 3·(1−2·a−b)=3−6·a−3·b.

პასუხი:

log 60 27=3·(1−2·a−b)=3−6·a−3·b.

ცალკე, აღსანიშნავია ფორმის ლოგარითმის ახალ ბაზაზე გადასვლის ფორმულის მნიშვნელობა. . ის საშუალებას გაძლევთ გადახვიდეთ ლოგარითმებიდან ნებისმიერი ფუძით ლოგარითმებზე კონკრეტული ფუძის მქონე ლოგარითმებზე, რომელთა მნიშვნელობები ცნობილია ან შესაძლებელია მათი პოვნა. ჩვეულებრივ, ორიგინალური ლოგარითმიდან, გარდამავალი ფორმულის გამოყენებით, ისინი გადადიან ლოგარითმებზე ერთ-ერთ 2, e ან 10 ფუძეზე, რადგან ამ ბაზებისთვის არის ლოგარითმების ცხრილები, რომლებიც საშუალებას აძლევს მათი მნიშვნელობების გამოთვლას გარკვეული ხარისხით. სიზუსტე. შემდეგ აბზაცში ჩვენ გაჩვენებთ, თუ როგორ კეთდება ეს.

ლოგარითმის ცხრილები და მათი გამოყენება

ლოგარითმის მნიშვნელობების სავარაუდო გაანგარიშებისთვის შეიძლება გამოყენებულ იქნას ლოგარითმის ცხრილები. ყველაზე ხშირად გამოყენებული ბაზის 2 ლოგარითმის ცხრილი, ბუნებრივი ლოგარითმის ცხრილი და ათობითი ლოგარითმის ცხრილი. ათობითი რიცხვების სისტემაში მუშაობისას მოსახერხებელია ლოგარითმების ცხრილის გამოყენება, რომელიც დაფუძნებულია ათეულზე. მისი დახმარებით ჩვენ ვისწავლით ლოგარითმების მნიშვნელობების პოვნას.

წარმოდგენილი ცხრილი საშუალებას გაძლევთ იპოვოთ რიცხვების ათობითი ლოგარითმების მნიშვნელობები 1000-დან 9999-მდე (სამი ათობითი ადგილით) ათიათასიანი სიზუსტით. ჩვენ გავაანალიზებთ ლოგარითმის მნიშვნელობის პოვნის პრინციპს ათობითი ლოგარითმების ცხრილის გამოყენებით კონკრეტული მაგალითის გამოყენებით - ეს უფრო ნათელია. მოდი ვიპოვოთ log1.256.

ათობითი ლოგარითმების ცხრილის მარცხენა სვეტში ვხვდებით 1.256 რიცხვის პირველ ორ ციფრს, ანუ ვპოულობთ 1.2-ს (სიცხადისთვის ეს რიცხვი შემოხაზულია ლურჯად). 1.256 რიცხვის მესამე ციფრი (ციფრი 5) გვხვდება ორმაგი ხაზის მარცხნივ პირველ ან ბოლო სტრიქონში (ეს რიცხვი შემოხაზულია წითლად). ორიგინალური რიცხვის 1.256 მეოთხე ციფრი (ციფრი 6) გვხვდება ორმაგი ხაზის მარჯვნივ პირველ ან ბოლო სტრიქონში (ეს რიცხვი შემოხაზულია მწვანე ხაზით). ახლა ჩვენ ვპოულობთ რიცხვებს ლოგარითმის ცხრილის უჯრედებში მონიშნული მწკრივისა და მონიშნული სვეტების კვეთაზე (ეს რიცხვები მონიშნულია ნარინჯისფრად). მონიშნული რიცხვების ჯამი იძლევა ათწილადის ლოგარითმის სასურველ მნიშვნელობას მეოთხე ათწილადამდე, ანუ log1.236≈0.0969+0.0021=0.0990.

შესაძლებელია თუ არა, ზემოთ მოყვანილი ცხრილის გამოყენებით, ვიპოვოთ რიცხვების ათობითი ლოგარითმების მნიშვნელობები, რომლებსაც აქვთ სამზე მეტი ციფრი ათწილადის წერტილის შემდეგ, ისევე როგორც ის, ვინც სცილდება 1-დან 9.999-მდე დიაპაზონს? Დიახ, შეგიძლია. მოდით აჩვენოთ, თუ როგორ კეთდება ეს მაგალითით.

გამოვთვალოთ lg102.76332. ჯერ უნდა დაწერო ნომერი სტანდარტული ფორმით: 102.76332=1.0276332·10 2. ამის შემდეგ მანტისა უნდა დამრგვალდეს მესამე ათწილადამდე, გვაქვს 1.0276332 10 2 ≈1.028 10 2, მაშინ როცა თავდაპირველი ათობითი ლოგარითმი დაახლოებით უდრის მიღებული რიცხვის ლოგარითმს, ანუ ვიღებთ log102.76332≈lg1.028·10 2. ახლა ჩვენ ვიყენებთ ლოგარითმის თვისებებს: lg1.028·10 2 =lg1.028+lg10 2 =lg1.028+2. საბოლოოდ, ათწილადი ლოგარითმების ცხრილიდან ვპოულობთ lg1.028 ლოგარითმის მნიშვნელობას lg1.028≈0.0086+0.0034=0.012. შედეგად, ლოგარითმის გამოთვლის მთელი პროცესი ასე გამოიყურება: log102.76332=log1.0276332 10 2 ≈lg1.028 10 2 = log1.028+lg10 2 =log1.028+2≈0.012+2=2.012.

დასასრულს, აღსანიშნავია, რომ ათობითი ლოგარითმების ცხრილის გამოყენებით შეგიძლიათ გამოთვალოთ ნებისმიერი ლოგარითმის სავარაუდო მნიშვნელობა. ამისათვის საკმარისია გამოიყენოთ გარდამავალი ფორმულა, რომ გადავიდეთ ათობითი ლოგარითმებზე, იპოვოთ მათი მნიშვნელობები ცხრილში და შეასრულოთ დარჩენილი გამოთვლები.

მაგალითად, გამოვთვალოთ ჟურნალი 2 3 . ლოგარითმის ახალ ბაზაზე გადასვლის ფორმულის მიხედვით გვაქვს . ათობითი ლოგარითმების ცხრილიდან ვხვდებით log3≈0.4771 და log2≈0.3010. ამრიგად, .

ბიბლიოგრაფია.

• კოლმოგოროვი A.N., Abramov A.M., Dudnitsyn Yu.P. და სხვა ალგებრა და ანალიზის საწყისები: სახელმძღვანელო ზოგადსაგანმანათლებლო დაწესებულებების 10-11 კლასებისთვის.
• გუსევი V.A., Mordkovich A.G. მათემატიკა (სახელმძღვანელო ტექნიკურ სასწავლებლებში შესვლისთვის).

რა არის ლოგარითმი?

ყურადღება!
არის დამატებითი
მასალები 555-ე სპეციალურ ნაწილში.
მათთვის, ვინც ძალიან "არ არის ძალიან ..."
და მათთვის, ვინც "ძალიან...")

რა არის ლოგარითმი? როგორ ამოხსნათ ლოგარითმები? ეს კითხვები ბევრ კურსდამთავრებულს აბნევს. ტრადიციულად, ლოგარითმების თემა განიხილება რთული, გაუგებარი და საშინელი. განსაკუთრებით განტოლებები ლოგარითმებით.

ეს აბსოლუტურად არ შეესაბამება სიმართლეს. აბსოლუტურად! არ გჯერა? ჯარიმა. ახლა, სულ რაღაც 10-20 წუთში თქვენ:

1. გაიგებთ რა არის ლოგარითმი.

2. ისწავლეთ ექსპონენციალური განტოლებების მთელი კლასის ამოხსნა. მაშინაც კი, თუ მათ შესახებ არაფერი გსმენიათ.

3. ისწავლეთ მარტივი ლოგარითმების გამოთვლა.

უფრო მეტიც, ამისათვის თქვენ მხოლოდ უნდა იცოდეთ გამრავლების ცხრილი და როგორ ავიყვანოთ რიცხვი ხარისხამდე...

ვგრძნობ, რომ ეჭვი გეპარება... კარგი, კარგი, მონიშნე დრო! წადი!

პირველ რიგში, ამოხსენით ეს განტოლება თქვენს თავში:

თუ მოგწონთ ეს საიტი...

სხვათა შორის, მე მაქვს კიდევ რამდენიმე საინტერესო საიტი თქვენთვის.)

შეგიძლიათ ივარჯიშოთ მაგალითების ამოხსნაში და გაიგოთ თქვენი დონე. ტესტირება მყისიერი გადამოწმებით. ვისწავლოთ - ინტერესით!)

შეგიძლიათ გაეცნოთ ფუნქციებს და წარმოებულებს.

როგორც საზოგადოება განვითარდა და წარმოება უფრო რთული გახდა, მათემატიკაც განვითარდა. მოძრაობა მარტივიდან რთულამდე. ჩვეულებრივი აღრიცხვიდან შეკრებისა და გამოკლების მეთოდის გამოყენებით, მათი განმეორებითი გამეორებით, მივედით გამრავლებისა და გაყოფის ცნებამდე. გამრავლების განმეორებითი მოქმედების შემცირება გახდა ექსპონენტაციის კონცეფცია. რიცხვების დამოკიდებულების პირველი ცხრილები ფუძეზე და გაძლიერების რაოდენობაზე შეადგინა ჯერ კიდევ VIII საუკუნეში ინდოელმა მათემატიკოსმა ვარასენამ. მათგან შეგიძლიათ დაითვალოთ ლოგარითმების გაჩენის დრო.

ისტორიული ჩანახატი

მე-16 საუკუნეში ევროპის აღორძინებამ ასევე ხელი შეუწყო მექანიკის განვითარებას. თ საჭირო იყო დიდი გამოთვლებიგამრავლებასთან და გაყოფასთან დაკავშირებული მრავალნიშნა რიცხვები. უძველესი მაგიდები დიდ მომსახურებას აძლევდა. მათ შესაძლებელი გახადეს რთული ოპერაციების ჩანაცვლება უფრო მარტივი - შეკრება და გამოკლება. დიდი წინგადადგმული ნაბიჯი იყო მათემატიკოს მაიკლ შტიფელის ნაშრომი, რომელიც გამოქვეყნდა 1544 წელს, რომელშიც მან გააცნობიერა მრავალი მათემატიკოსის იდეა. ამან შესაძლებელი გახადა ცხრილების გამოყენება არა მხოლოდ ხარისხებისთვის ფორმაში მარტივი რიცხვები, არამედ თვითნებური რაციონალებისთვისაც.

1614 წელს შოტლანდიელმა ჯონ ნაპიერმა, რომელმაც ეს იდეები განავითარა, პირველად შემოიტანა ახალი ტერმინი „რიცხვის ლოგარითმი“. შედგენილია ახალი რთული ცხრილები სინუსების და კოსინუსების ლოგარითმების, ასევე ტანგენტების გამოსათვლელად. ამან მნიშვნელოვნად შეამცირა ასტრონომების მუშაობა.

დაიწყო ახალი ცხრილების გამოჩენა, რომლებსაც წარმატებით იყენებდნენ მეცნიერები სამი საუკუნის განმავლობაში. ბევრი დრო გავიდა, სანამ ალგებრაში ახალმა ოპერაციამ დასრულებული ფორმა შეიძინა. მოცემულია ლოგარითმის განმარტება და შესწავლილი იქნა მისი თვისებები.

მხოლოდ მე-20 საუკუნეში, კალკულატორისა და კომპიუტერის მოსვლასთან ერთად, კაცობრიობამ მიატოვა უძველესი ცხრილები, რომლებიც წარმატებით მუშაობდნენ მე-13 საუკუნეში.

დღეს b-ის ლოგარითმს ვუწოდებთ a-ს დასაფუძნებლად x რიცხვს, რომელიც არის a-ის ძალა b-ის გასაკეთებლად. ეს იწერება ფორმულის სახით: x = log a(b).

მაგალითად, log 3(9) იქნება 2-ის ტოლი. ეს აშკარაა, თუ დაიცავთ განმარტებას. თუ 3-ს ავწევთ 2-ის ხარისხზე, მივიღებთ 9-ს.

ამრიგად, ჩამოყალიბებული განმარტება ადგენს მხოლოდ ერთ შეზღუდვას: რიცხვები a და b უნდა იყოს რეალური.

ლოგარითმების სახეები

კლასიკურ განმარტებას რეალური ლოგარითმი ეწოდება და რეალურად არის a x = b განტოლების ამონახსნი. ვარიანტი a = 1 არის მოსაზღვრე და არ არის საინტერესო. ყურადღება: 1 ნებისმიერი სიმძლავრის მიმართ უდრის 1-ს.

ლოგარითმის რეალური მნიშვნელობაგანისაზღვრება მხოლოდ მაშინ, როდესაც ბაზა და არგუმენტი მეტია 0-ზე და ბაზა არ უნდა იყოს 1-ის ტოლი.

განსაკუთრებული ადგილი მათემატიკის სფეროშიითამაშეთ ლოგარითმები, რომლებიც დასახელდება მათი ბაზის ზომის მიხედვით:

წესები და შეზღუდვები

ლოგარითმების ფუნდამენტური თვისებაა წესი: ნამრავლის ლოგარითმი ტოლია ლოგარითმული ჯამის. log abp = log a(b) + log a(p).

ამ განცხადების ვარიანტად იქნება: log c(b/p) = log c(b) - log c(p), კოეფიციენტის ფუნქცია უდრის ფუნქციების სხვაობას.

წინა ორი წესიდან ადვილად ჩანს, რომ: log a(b p) = p * log a(b).

სხვა თვისებები მოიცავს:

კომენტარი. არ არის საჭირო ჩვეულებრივი შეცდომის დაშვება - ჯამის ლოგარითმი არ არის ლოგარითმების ჯამის ტოლი.

მრავალი საუკუნის განმავლობაში, ლოგარითმის პოვნა საკმაოდ შრომატევადი ამოცანა იყო. მათემატიკოსებმა გამოიყენეს პოლინომიური გაფართოების ლოგარითმული თეორიის ცნობილი ფორმულა:

ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*(( x^n)/n), სადაც n არის 1-ზე მეტი ნატურალური რიცხვი, რომელიც განსაზღვრავს გამოთვლის სიზუსტეს.

სხვა საფუძვლებით ლოგარითმები გამოითვალეს ერთი ფუძიდან მეორეზე გადასვლის თეორემისა და პროდუქტის ლოგარითმის თვისების გამოყენებით.

ვინაიდან ეს მეთოდი ძალიან შრომატევადი და პრაქტიკული პრობლემების გადაჭრისასრთული განსახორციელებელი, გამოვიყენეთ ლოგარითმების წინასწარ შედგენილი ცხრილები, რამაც საგრძნობლად დააჩქარა მთელი სამუშაო.

ზოგიერთ შემთხვევაში გამოიყენებოდა ლოგარითმების სპეციალურად შედგენილი გრაფიკები, რომლებიც ნაკლებ სიზუსტეს იძლეოდნენ, მაგრამ საგრძნობლად აჩქარებდნენ სასურველი მნიშვნელობის ძიებას. y = log a(x) ფუნქციის მრუდი, რომელიც აგებულია რამდენიმე წერტილზე, საშუალებას გაძლევთ გამოიყენოთ ჩვეულებრივი სახაზავი ფუნქციის მნიშვნელობის საპოვნელად ნებისმიერ სხვა წერტილში. ინჟინრები დიდი დროამ მიზნით გამოიყენებოდა ე.წ.

მე-17 საუკუნეში გაჩნდა პირველი დამხმარე ანალოგური გამოთვლითი პირობები, რომელიც მე-19 საუკუნედასრულებული სახე შეიძინა. ყველაზე წარმატებულ მოწყობილობას ეწოდა სლაიდის წესი. მოწყობილობის სიმარტივის მიუხედავად, მისმა გარეგნობამ მნიშვნელოვნად დააჩქარა ყველა საინჟინრო გამოთვლების პროცესი და ამის გადაჭარბება ძნელია. ამჟამად, ცოტა ადამიანი იცნობს ამ მოწყობილობას.

კალკულატორებისა და კომპიუტერების გამოჩენამ ნებისმიერი სხვა მოწყობილობის გამოყენება უაზრო გახადა.

განტოლებები და უტოლობა

ლოგარითმების გამოყენებით სხვადასხვა განტოლებისა და უტოლობების ამოსახსნელად გამოიყენება შემდეგი ფორმულები:

• გადასვლა ერთი ბაზიდან მეორეზე: log a(b) = log c(b) / log c(a);
• წინა ვარიანტის შედეგად: log a(b) = 1 / log b(a).

უტოლობების გადასაჭრელად სასარგებლოა ვიცოდეთ:

• ლოგარითმის მნიშვნელობა დადებითი იქნება მხოლოდ იმ შემთხვევაში, თუ ბაზა და არგუმენტი ერთზე დიდი ან ნაკლებია; თუ ერთი პირობა მაინც დაირღვა, ლოგარითმის მნიშვნელობა უარყოფითი იქნება.
• თუ ლოგარითმის ფუნქცია გამოიყენება უტოლობის მარჯვენა და მარცხენა მხარეს, ხოლო ლოგარითმის ფუძე ერთზე მეტია, მაშინ უტოლობის ნიშანი შენარჩუნებულია; წინააღმდეგ შემთხვევაში იცვლება.

პრობლემების ნიმუში

განვიხილოთ ლოგარითმების გამოყენების რამდენიმე ვარიანტი და მათი თვისებები. მაგალითები განტოლებების ამოხსნით:

განვიხილოთ ლოგარითმის სიმძლავრეში მოთავსების ვარიანტი:

• ამოცანა 3. გამოთვალეთ 25^log 5(3). ამოხსნა: პრობლემის პირობებში ჩანაწერი მსგავსია (5^2)^log5(3) ან 5^(2 * log 5(3)). მოდით სხვანაირად ჩავწეროთ: 5^log 5(3*2), ან რიცხვის კვადრატი, როგორც ფუნქციის არგუმენტი, შეიძლება დაიწეროს როგორც თავად ფუნქციის კვადრატი (5^log 5(3))^2. ლოგარითმების თვისებების გამოყენებით, ეს გამოხატულება უდრის 3^2. პასუხი: გაანგარიშების შედეგად ვიღებთ 9-ს.

პრაქტიკული გამოყენება

როგორც წმინდა მათემატიკური ინსტრუმენტი, ის შორს არის ნამდვილი ცხოვრებარომ ლოგარითმა მოულოდნელად შეიძინა დიდი მნიშვნელობარეალური სამყაროს ობიექტების აღწერისთვის. ძნელია იპოვოთ მეცნიერება, სადაც ის არ გამოიყენება. ეს სრულად ეხება არა მხოლოდ ბუნებრივ, არამედ ჰუმანიტარული სფეროებიცოდნა.

ლოგარითმული დამოკიდებულებები

აქ მოცემულია რიცხვითი დამოკიდებულების რამდენიმე მაგალითი:

მექანიკა და ფიზიკა

ისტორიულად, მექანიკა და ფიზიკა ყოველთვის ვითარდებოდა გამოყენებით მათემატიკური მეთოდებიკვლევას და იმავდროულად ემსახურებოდა მათემატიკის, მათ შორის ლოგარითმების განვითარების სტიმულს. ფიზიკის კანონების უმეტესობის თეორია დაწერილია მათემატიკის ენაზე. მოვიყვანოთ აღწერის მხოლოდ ორი მაგალითი ფიზიკური კანონებილოგარითმის გამოყენებით.

ისეთი რთული სიდიდის გამოთვლის პრობლემა, როგორიც არის რაკეტის სიჩქარე, შეიძლება გადაწყდეს ციოლკოვსკის ფორმულის გამოყენებით, რომელმაც საფუძველი ჩაუყარა კოსმოსის კვლევის თეორიას:

V = I * ln (M1/M2), სადაც

• V არის თვითმფრინავის საბოლოო სიჩქარე.
• I - ძრავის სპეციფიკური იმპულსი.
• M 1 - რაკეტის საწყისი მასა.
• M 2 – საბოლოო მასა.

კიდევ ერთი მნიშვნელოვანი მაგალითი- ეს გამოიყენება კიდევ ერთი დიდი მეცნიერის მაქს პლანკის ფორმულაში, რომელიც ემსახურება თერმოდინამიკაში წონასწორობის მდგომარეობის შეფასებას.

S = k * ln (Ω), სადაც

• S – თერმოდინამიკური თვისება.
• k – ბოლცმანის მუდმივი.
• Ω არის სხვადასხვა მდგომარეობის სტატისტიკური წონა.

Ქიმია

ნაკლებად აშკარაა ფორმულების გამოყენება ქიმიაში, რომლებიც შეიცავს ლოგარითმების თანაფარდობას. მხოლოდ ორი მაგალითი მოვიყვანოთ:

• ნერნსტის განტოლება, გარემოს რედოქსული პოტენციალის მდგომარეობა ნივთიერებების აქტივობასთან და წონასწორობის მუდმივთან მიმართებაში.
• ისეთი მუდმივების გამოთვლა, როგორიცაა ავტოლიზის ინდექსი და ხსნარის მჟავიანობა, ასევე შეუძლებელია ჩვენი ფუნქციის გარეშე.

ფსიქოლოგია და ბიოლოგია

და საერთოდ არ არის გასაგები, რა კავშირი აქვს მას ფსიქოლოგიას. გამოდის, რომ შეგრძნების სიძლიერე კარგად არის აღწერილი ამ ფუნქციით, როგორც სტიმულის ინტენსივობის მნიშვნელობის შებრუნებული თანაფარდობა ქვედა ინტენსივობის მნიშვნელობასთან.

ზემოაღნიშნული მაგალითების შემდეგ, გასაკვირი აღარ არის, რომ ლოგარითმების თემა ფართოდ გამოიყენება ბიოლოგიაში. მთელი ტომები შეიძლება დაიწეროს ლოგარითმული სპირალების შესაბამისი ბიოლოგიური ფორმების შესახებ.

სხვა სფეროები

როგორც ჩანს, სამყაროს არსებობა შეუძლებელია ამ ფუნქციასთან კავშირის გარეშე და ის მართავს ყველა კანონს. განსაკუთრებით მაშინ, როდესაც ბუნების კანონები დაკავშირებულია გეომეტრიული პროგრესია. ღირს MatProfi ვებსაიტზე მიბრუნება და ასეთი მაგალითები ბევრია საქმიანობის შემდეგ სფეროებში:

სია შეიძლება იყოს უსასრულო. ამ ფუნქციის ძირითადი პრინციპების დაუფლების შემდეგ, შეგიძლიათ ჩაძიროთ უსაზღვრო სიბრძნის სამყაროში.

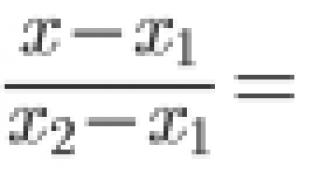
ლოგარითმი დადებითი რიცხვი N ბაზამდე(ბ> 0, ბ 1 ) ე.წ x , რომელზეც თქვენ უნდა ააშენოთბ მისაღებად N .

ლოგარითმის აღნიშვნა:

ეს ჩანაწერი უდრის შემდეგს:b x = N .

მაგალითები: ჟურნალი 3 81 = 4, ვინაიდან 3 4 = 81;

ჟურნალი 1/3 27 = – 3, ვინაიდან (1/3) - 3 = 3 3 = 27.

ლოგარითმის ზემოაღნიშნული განმარტება შეიძლება დაიწეროს როგორც იდენტურობა:

ლოგარითმების ძირითადი თვისებები.

1) ჟურნალი ბ= 1 , რადგან ბ 1 = ბ.

ბ

2) ჟურნალი 1 = 0 , რადგან ბ 0 = 1 .

ბ

3) პროდუქტის ლოგარითმი უდრის ფაქტორების ლოგარითმების ჯამს:

ჟურნალი ( აბ) = ჟურნალი ა+ ჟურნალი ბ.

4) კოეფიციენტის ლოგარითმი უდრის დივიდენდისა და გამყოფის ლოგარითმებს შორის სხვაობას:

ჟურნალი ( ა/ბ) = ჟურნალი ა- ჟურნალი ბ.

5) სიმძლავრის ლოგარითმი ტოლია მაჩვენებლისა და მისი ფუძის ლოგარითმის ნამრავლის:

ჟურნალი (ბ კ ) = კჟურნალი ბ.

ამ ქონების შედეგი შემდეგია:ფესვის ლოგარითმი უდრის რადიკალური რიცხვის ლოგარითმს გაყოფილი ფესვის ძალაზე:

6) თუ ლოგარითმის საფუძველი არის ხარისხი, მაშინ მნიშვნელობა მაჩვენებლის ინვერსია, შეიძლება ამოღებულ იქნას ჟურნალის ნიშნიდანრითმა:

ბოლო ორი თვისება შეიძლება გაერთიანდეს ერთში:

7) გარდამავალი მოდულის ფორმულა (ე.ი.ე . გადასვლა ერთი ბაზიდანლოგარითმი სხვა ბაზაზე):

განსაკუთრებულ შემთხვევაში, როცა N=aჩვენ გვაქვს:

ათწილადი ლოგარითმი დაურეკა ბაზის ლოგარითმი 10. დანიშნულიალგ, ე.ი. ჟურნალი 10 ნ = ლგ ნ. რიცხვების ლოგარითმები 10, 100, 1000, ...გვ რიცხვები არის 1, 2, 3, ..., შესაბამისადიმათ. ბევრი დადებითი აქვს

ერთეული, რამდენი ნული არის ლოგარითმულ რიცხვში ერთის შემდეგ. რიცხვების ლოგარითმები 0.1, 0.01, 0.001, ...გვ ავნა შესაბამისად – 1, –2, –3,…, ე.ი. გქონდეთ იმდენი უარყოფითი, რამდენიც არის ნულები ერთამდე ლოგარითმულ რიცხვში ( დათვლა და ნულოვანი რიცხვები). ლოგარითმები სხვა რიცხვებს აქვთ წილადი ნაწილი, რომელსაც ეწოდება მანტისა. მთელილოგარითმის ნაწილი ეწოდება დამახასიათებელი. პრაქტიკული გამოყენებისთვისათწილადი ლოგარითმები ყველაზე მოსახერხებელია.

ბუნებრივი ლოგარითმი დაურეკა ბაზის ლოგარითმი ე. იგი დანიშნულია ln, ე.ი. ჟურნალი ენ = ლნ ნ. ნომერი ეირაციონალურია, ესსავარაუდო ღირებულება 2.718281828.ის არის ზღვარი, რომლისკენაც რიცხვი მიისწრაფვის(1 + 1 / ნ) ნ შეუზღუდავი ზრდითნ(სმ. პირველი მშვენიერი ლიმიტი ).
რაც არ უნდა უცნაური იყოს, ბუნებრივი ლოგარითმები ძალიან მოსახერხებელი აღმოჩნდა განხორციელებისას სხვადასხვა სახისფუნქციების ანალიზთან დაკავშირებული ოპერაციები.ლოგარითმების გამოთვლა ფუძემდეეგანხორციელდა ბევრად უფრო სწრაფად, ვიდრე ნებისმიერი სხვა მიზეზის გამო.