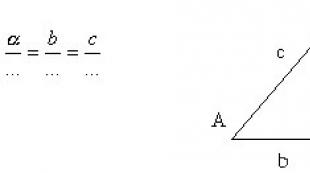Բնական թվերի համակարգի կառուցման աքսիոմատիկ մոտեցում: Աքսիոմատիկ մեթոդներ մաթեմատիկայի մեջ. Հիմնական հասկացություններ և սահմանումներ

Բազմիմաստություն

Բազմիմաստությունը կամ բառերի բազմիմաստությունը առաջանում է այն պատճառով, որ լեզուն ներկայացնում է մի համակարգ, որը սահմանափակ է իրական իրականության անսահման բազմազանության համեմատ, այնպես որ, ակադեմիկոս Վինոգրադովի խոսքերով, «Լեզուն ստիպված է անթիվ իմաստներ բաշխել մեկի կամ տակ. հիմնական հասկացությունների մեկ այլ ռուբիկ»: (Վինոգրադով «Ռուսաց լեզու» 1947): Անհրաժեշտ է տարբերակել բառի տարբեր գործածությունները մեկ բառային-իմաստային տարբերակում և բառի իրական տարբերությունը: Այսպիսով, օրինակ, (das)Ol բառը կարող է նշանակել մի շարք տարբեր յուղեր, բացառությամբ կովի (որի համար կա Կարագ բառը): Սակայն սրանից չի բխում, որ տարբեր յուղեր նշելով, Օլ բառն ամեն անգամ տարբեր նշանակություն կունենա՝ բոլոր դեպքերում դրա իմաստը նույնն է լինելու, այն է՝ յուղ (ամեն ինչ, բացի կովիից)։ Ճիշտ այնպես, ինչպես, օրինակ, Tisch table բառի իմաստը, անկախ նրանից, թե կոնկրետ դեպքում բառը ինչ տեսակի աղյուսակ է նշանակում: Այլ է իրավիճակը, երբ Օլ բառը նշանակում է նավթ։ Այստեղ առաջին պլան է մղվում ոչ թե նավթի յուղայնության առումով տարբեր տեսակի յուղերի նմանությունը, այլ յուղի առանձնահատուկ որակը՝ դյուրավառությունը։ Եվ միևնույն ժամանակ վառելիքի տարբեր տեսակներ նշանակող բառերը կապվելու են Ol բառի հետ՝ Kohl, Holz և այլն։ Սա հնարավորություն է տալիս Օլ (կամ, այլ կերպ ասած, երկու բառաբանական-իմաստային տարբերակ) բառից տարբերելու երկու իմաստ՝ 1) յուղ (ոչ կենդանի) 2) յուղ։
Որպես կանոն, նոր իմաստներ են առաջանում՝ գոյություն ունեցող բառերից մեկը նոր առարկայի կամ երևույթի փոխանցելով: Այսպես են ձևավորվում փոխաբերական իմաստները։ Դրանք հիմնված են կամ առարկաների նմանության կամ մի առարկայի մյուսի հետ կապի վրա: Հայտնի են անվան փոխանցման մի քանի տեսակներ. Դրանցից ամենակարեւորը փոխաբերությունն է կամ մետոնիմիկան։
Փոխաբերության մեջ փոխանցումը հիմնված է իրերի գույնի, ձևի, շարժման բնույթի և այլնի նմանության վրա: Բոլոր փոխաբերական փոփոխություններով, սկզբնական հայեցակարգի որոշ նշաններ մնում են

Համանունություն

Բառի բազմիմաստությունը այնքան մեծ և բազմակողմանի խնդիր է, որ բառարանագիտության մեջ բազմաթիվ խնդիրներ ինչ-որ կերպ առնչվում են դրան: Մասնավորապես, համանունության խնդիրը որոշ առումներով շփվում է այս խնդրի հետ։
Հոմանիշներն այն բառերն են, որոնք հնչում են նույնը, բայց ունեն տարբեր իմաստներ: Որոշ դեպքերում համանունները առաջանում են բազմիմաստությունից, որը ենթարկվել է ոչնչացման գործընթացի։ Բայց համանունները կարող են առաջանալ նաև ձայնային պատահական համընկնումների արդյունքում։ Բանալին, որը դուռը բացում է, իսկ բանալին՝ զսպանակ կամ թրթուր՝ սանրվածք և թրթուր՝ գյուղատնտեսական գործիք.
Հոմանիշներն առանձնանում են բառաբանական (վերաբերվում են խոսքի մի մասի, օրինակ՝ բանալին՝ կողպեք բացել, իսկ բանալին՝ զսպանակ. աղբյուր) ձևաբանական (վերաբերվում են խոսքի տարբեր մասերին, օրինակ՝ երեքը թվանշան է։ , երեքը մեջ բայ է հրամայական տրամադրություն), բառա-քերականական, որոնք ստեղծվում են դարձի արդյունքում, երբ տվյալ բառն անցնում է խոսքի մեկ այլ մաս։ օրինակ անգլերենով նայիր-նայիր և նայիր-նայիր. Հատկապես շատ են բառա-քերականական համանունները Անգլերեն Լեզու.
Հոմոֆոնները և հոմոգրաֆները պետք է տարբերվեն համանուններից: Հոմոֆոնները տարբեր բառեր են, որոնք թեև տարբեր են իրենց ուղղագրությամբ, բայց արտասանությամբ նույնն են, օրինակ՝ սոխ - մարգագետին, Սեյտե - էջ և Սաիտ - թել։
Հոմոգրաֆներն այնքան տարբեր բառեր են, որոնք ունեն նույն ուղղագրությունը, թեև դրանք տարբեր կերպ են արտասանվում (ինչպես հնչյունային կազմության, այնպես էլ բառի մեջ շեշտադրման տեղի տեսանկյունից), օրինակ՝ Ամրոց՝ ամրոց։

Հոմանիշ

Հոմանիշներն այն բառերն են, որոնք իմաստով մոտ են, բայց հնչում են տարբեր կերպ՝ արտահայտելով մեկ հասկացության երանգներ:
Կան երեք տեսակի հոմանիշներ.
1. Հայեցակարգային կամ գաղափարագրական. Նրանք միմյանցից տարբերվում են բառապաշարային իմաստով։ Այս տարբերությունն ակնհայտ է տարբեր աստիճաններովնշանակված հատկանիշը (ցրտահարություն - սառը, ուժեղ, հզոր, հզոր), իր նշանակման բնույթով (վերմակ բաճկոն - ծածկված բաճկոն - լիցքավորված բաճկոն), արտահայտված հայեցակարգի շրջանակներում (դրոշակ - դրոշ, համարձակ - համարձակ), բառապաշարային իմաստի կապակցվածության աստիճանը (շագանակագույն - շագանակագույն, սև - սև):
2. Հոմանիշները ոճական կամ գործառական են: Նրանք միմյանցից տարբերվում են օգտագործման ոլորտում, օրինակ՝ աչքեր՝ աչքեր, դեմք՝ դեմք, ճակատ՝ ճակատ։ Հոմանիշներ էմոցիոնալ - գնահատող: Այս հոմանիշները բացահայտ արտահայտում են խոսողի վերաբերմունքը նշանակված անձի, առարկայի կամ երևույթի նկատմամբ: Օրինակ՝ երեխային կարելի է հանդիսավոր կերպով անվանել երեխա, սիրալիրորեն փոքրիկ տղա և փոքրիկ տղա, արհամարհանքով տղա և ծծող, ինչպես նաև ուժեղացնել ու արհամարհանքով՝ լակոտ, ծծող, բութ։
3. Հականիշներ - բառերի համակցություններ, որոնք իրենց բառապաշարային իմաստով հակադիր են, օրինակ՝ վերև - ներքև, սպիտակ - սև, խոսեք - լուռ, բարձր - հանգիստ:

Անտոնիմիա

Հականիշների երեք տեսակ կա.
1. Աստիճանական և համակարգված հակադրությունների հականիշներ, օրինակ՝ սպիտակ - սև, հանգիստ - բարձրաձայն, մոտ - հեռավոր, բարի - չար և այլն։ Այս հականիշներն իրենց իմաստով ընդհանրություններ ունեն, ինչը թույլ է տալիս նրանց հակադրել։ Այսպիսով, սև և սպիտակ հասկացությունները նշանակում են հակադիր գունային հասկացություններ:
2. Կոմպլեմենտար և դարձի հակադիրների հականիշներ՝ պատերազմ - խաղաղություն, ամուսին - կին, ամուսնացած - ամուրի, հնարավոր - անհնար, փակ - բաց:
3. Հասկացությունների երկփեղկ բաժանման հականիշներ. Դրանք հաճախ նույն արմատական ​​բառերն են՝ ժողովրդական՝ ապազգային, օրինական՝ անօրինական, մարդասիրական՝ անմարդկային։
Հետաքրքրություն է ներկայացնում այսպես կոչված ներբառային հականիշություն, երբ հակադրվում են նույն նյութական պատյան ունեցող բառերի իմաստները։ Օրինակ, ռուսերենում փող տալ մեկին փող տալ նշանակում է «պարտ տալ», իսկ ինչ-որ մեկից պարտք վերցնել արդեն նշանակում է ինչ-որ մեկից պարտք վերցնել: Իմաստների ներբառային հակադրությունը կոչվում է էնանտոսեմիա։

6. Համակարգի աքսիոմատիկ կառուցում բնական թվեր. Մաթեմատիկական տեսության կառուցման աքսիոմատիկ մեթոդ. Աքսիոմային համակարգի պահանջները՝ հետևողականություն, անկախություն, ամբողջականություն: Պեանոյի աքսիոմատիկա. Բնական թվի հայեցակարգը աքսիոմատիկ դիրքից: Peano աքսիոմային համակարգի մոդելներ. Բնական թվերի գումարում և բազմապատկում աքսիոմատիկ դիրքերից: Բնական թվերի բազմության հերթականությունը. Բնական թվերի բազմության հատկությունները. Բնական թվերի բազմության հանում և բաժանում աքսիոմատիկ դիրքերից: Մաթեմատիկական ինդուկցիայի մեթոդ. Զրոյի ներդրում և ոչ բացասական ամբողջ թվերի բազմության կառուցում։ Թեորեմ մնացորդով բաժանման մասին.

Հիմնական հասկացություններ և սահմանումներ

Թիվ -դա որոշակի քանակի արտահայտություն է։

Բնական թիվանորոշ շարունակական հաջորդականության տարր:

Բնական թվեր (բնական թվեր) -թվեր, որոնք բնականաբար առաջանում են հաշվելու ժամանակ (և՛ թվարկման, և՛ հաշվարկի իմաստով):

Բնական թվերը սահմանելու երկու մոտեցում կա. թվերն օգտագործվում են.

ապրանքների ցուցակագրում (համարակալում) (առաջին, երկրորդ, երրորդ, ...);

ապրանքների քանակի նշանակում (առանց առարկաների, մեկ ապրանքի, երկու ապրանքի, ...):

Աքսիոմա -սրանք են որոշակի տեսության հիմնական ելակետերը (ինքնին հասկանալի սկզբունքներ), որոնցից այս տեսության մնացած բովանդակությունը քաղվում է դեդուկցիայի միջոցով, այսինքն՝ զուտ տրամաբանական միջոցներով։

Այն թիվը, որն ունի ընդամենը երկու բաժանարար (թիվն ինքնին և մեկը), կոչվում է. պարզ թիվ.

Բաղադրյալ թիվայն թիվն է, որն ունի երկուից ավելի բաժանարար:

§2. Բնական թվերի աքսիոմատիկա

Բնական թվերը ստացվում են առարկաները հաշվելով և մեծությունները չափելով։ Բայց եթե չափման ժամանակ ի հայտ են գալիս բնական թվերից բացի այլ թվեր, ապա հաշվումը հանգեցնում է միայն բնական թվերի։ Հաշվելու համար ձեզ անհրաժեշտ է թվերի հաջորդականություն, որը սկսվում է մեկով և որը թույլ է տալիս անցնել մի թվից մյուսին այնքան անգամ, որքան անհրաժեշտ է: Այսինքն՝ մեզ բնական շարքի հատված է պետք։ Ուստի բնական թվերի համակարգի հիմնավորման խնդիրը լուծելիս առաջին հերթին անհրաժեշտ էր պատասխանել այն հարցին, թե ինչ է թիվը որպես բնական շարքի տարր։ Սրա պատասխանը տրվել է երկու մաթեմատիկոսների աշխատություններում. գերմանացի Գրասմանը և իտալացի Պեանոն:Նրանք առաջարկեցին աքսիոմատիկա, որում բնական թիվը հիմնավորված էր որպես անորոշ շարունակական հաջորդականության տարր։

Բնական թվերի համակարգի աքսիոմատիկ կառուցումն իրականացվում է ըստ ձևակերպված կանոնների.

Հինգ աքսիոմները կարելի է համարել որպես հիմնական հասկացությունների աքսիոմատիկ սահմանում.

1-ը բնական թիվ է;

Հաջորդ բնական թիվը բնական թիվ է.

1-ը չի հետևում որևէ բնական թվի.

Եթե ​​բնական թիվ Ահետևում է բնական թվին բև բնական թվից դուրս Հետ, Դա բԵվ Հետնույնական են;

Եթե ​​որևէ դրույթ ապացուցված է 1-ի համար և եթե այն ենթադրությունից, որ այն ճիշտ է բնական թվի համար n, հետևում է, որ դա ճիշտ է հետևյալի համար nբնական թիվ, ապա այս նախադասությունը ճիշտ է բոլոր բնական թվերի համար:

Միավոր– սա բնական շարքի առաջին համարն է , ինչպես նաև տասնորդական թվային համակարգի թվանշաններից մեկը։

Ենթադրվում է, որ նույն նշանով ցանկացած կատեգորիայի միավորի նշանակումը (բավականին մոտ է ժամանակակիցին) առաջին անգամ հայտնվել է Հին Բաբելոնում մոտավորապես մ.թ.ա. 2 հազար տարի: ե.

Հին հույները, որոնք թվեր էին համարում միայն բնական թվերը, դրանցից յուրաքանչյուրը համարում էին միավորների հավաքածու։ Ինքնին միավորին հատուկ տեղ է հատկացված՝ այն թիվ չի համարվել։

Ի. Նյուտոնը գրել է. «... թվով մենք հասկանում ենք ոչ այնքան միավորների հավաքածու, որքան մի մեծության վերացական կապը մեկ այլ մեծության հետ, որը պայմանականորեն ընդունված է մեր կողմից որպես միավոր»: Այսպիսով, մեկն արդեն զբաղեցրել է իր արժանի տեղը այլ թվերի շարքում։

Թվերի վրա թվաբանական գործողություններն ունեն տարբեր հատկություններ: Դրանք կարելի է բնութագրել բառերով, օրինակ. «Ժամկետների տեղերը փոխելով գումարը չի փոխվում»։ Կարող եք գրել տառերով՝ a+b = b+a: Կարելի է արտահայտվել հատուկ տերմիններով.

Մենք հաճախ սովորությունից դրդված կիրառում ենք թվաբանության հիմնական օրենքները՝ առանց գիտակցելու.

1) կոմուտատիվ օրենք (փոխադարձություն), - թվերի գումարման և բազմապատկման հատկություն՝ արտահայտված ինքնություններով.

a+b = b+a a*b = b*a;

2) կոմբինացիոն օրենք (ասոցիատիվություն), - թվերի գումարման և բազմապատկման հատկություն՝ արտահայտված ինքնություններով.

(a+b)+c = a+(b+c) (a*b)*c = a*(b*c);

3) բաշխման իրավունք (բաշխում), - հատկություն, որը կապում է թվերի գումարումն ու բազմապատկումը և արտահայտվում է նույնականությամբ.

a*(b+c) = a*b+a*c (b+c) *a = b*a+c*a.

Բազմապատկման գործողության փոխադարձ, համակցական և բաշխիչ (ավելացման հետ կապված) օրենքներն ապացուցելուց հետո բնական թվերի վրա թվաբանական գործողությունների տեսության հետագա կառուցումը որևէ հիմնարար դժվարություն չի ներկայացնում։

Ներկայումս մեր մտքում կամ թղթի վրա մենք անում ենք միայն առավելագույնը պարզ հաշվարկներ, ավելի ու ավելի բարդ հաշվողական աշխատանք վստահելով հաշվիչներին և համակարգիչներին: Այնուամենայնիվ, բոլոր համակարգիչների աշխատանքը՝ պարզ և բարդ, հիմնված է ամենապարզ գործողության՝ բնական թվերի գումարման վրա։ Ստացվում է, որ ամենաբարդ հաշվարկները կարող են կրճատվել մինչև գումարման, բայց այս գործողությունը պետք է կատարվի միլիոնավոր անգամներ:

Աքսիոմատիկ մեթոդներ մաթեմատիկայի մեջ

Մաթեմատիկական տրամաբանության զարգացման հիմնական պատճառներից է համատարած աքսիոմատիկ մեթոդտարբեր մաթեմատիկական տեսությունների կառուցման մեջ, առաջին հերթին՝ երկրաչափություն, իսկ հետո՝ թվաբանություն, խմբերի տեսություն և այլն։ Աքսիոմատիկ մեթոդկարող է սահմանվել որպես տեսություն, որը կառուցված է չսահմանված հասկացությունների և նրանց միջև փոխհարաբերությունների նախապես ընտրված համակարգի վրա:

Մաթեմատիկական տեսության աքսիոմատիկ կառուցման մեջ նախապես ընտրված է չսահմանված հասկացությունների և նրանց միջև հարաբերությունների որոշակի համակարգ։ Այս հասկացությունները և հարաբերությունները կոչվում են հիմնական: Հաջորդը, մուտքագրեք աքսիոմներդրանք. առանց ապացույցների ընդունված տեսության հիմնական դրույթները։ Տեսության հետագա ամբողջ բովանդակությունը տրամաբանորեն բխում է աքսիոմներից: Առաջին անգամ մաթեմատիկական տեսության աքսիոմատիկ կառուցումը ձեռնարկեց Էվկլիդեսը երկրաչափության կառուցման մեջ։

Աքսիոմատիկ մեթոդ մաթեմատիկայի մեջ.

Բնական շարքերի աքսիոմատիկ տեսության հիմնական հասկացություններն ու հարաբերությունները. Բնական թվի սահմանում.

Բնական թվերի գումարում.

Բնական թվերի բազմապատկում.

Բնական թվերի բազմության հատկությունները

Բնական թվերի հանում և բաժանում.

Աքսիոմատիկ մեթոդ մաթեմատիկայի մեջ

Ցանկացած մաթեմատիկական տեսության աքսիոմատիկ կառուցման ժամանակ պահպանվում են հետևյալ կանոնները. որոշակի կանոններ:

1. Տեսության որոշ հասկացություններ ընտրված են որպես հիմնականև ընդունվում են առանց սահմանման։

2. Ձևակերպված են աքսիոմներ, որոնք այս տեսության մեջ ընդունվում են առանց ապացույցների, դրանք բացահայտում են հիմնական հասկացությունների հատկությունները։

3. Տրված է տեսության յուրաքանչյուր հայեցակարգ, որը չի պարունակվում հիմնականների ցանկում սահմանում, դրա իմաստը բացատրում է հիմնական և նախորդ հասկացությունների օգնությամբ։

4. Տեսության յուրաքանչյուր դրույթ, որը չի պարունակվում աքսիոմների ցանկում, պետք է ապացուցվի: Նման առաջարկները կոչվում են թեորեմներև ապացուցել դրանք դիտարկվողին նախորդող աքսիոմների և թեորեմների հիման վրա։

Աքսիոմային համակարգը պետք է լինի.

ա) հետևողական.մենք պետք է վստահ լինենք, որ աքսիոմների տվյալ համակարգից բոլոր հնարավոր եզրակացությունները անելով՝ երբեք չենք գա հակասության.

բ) անկախՈչ մի աքսիոմ չպետք է լինի այս համակարգի այլ աքսիոմների հետևանք:

V) լի, եթե դրա շրջանակներում միշտ հնարավոր է ապացուցել կամ տվյալ պնդումը, կամ դրա ժխտումը։

Աքսիոմատիկ տեսության կառուցման առաջին փորձը կարելի է համարել Էվկլիդեսի երկրաչափության ներկայացումը իր «Էլեմենտներում» (Ք.ա. III դ.): Երկրաչափության և հանրահաշվի կառուցման աքսիոմատիկ մեթոդի զարգացման գործում նշանակալի ներդրում է ունեցել Ն.Ի. Լոբաչևսկին և Է.Գալուան։ 19-րդ դարի վերջին։ Իտալացի մաթեմատիկոս Պեանոն թվաբանության աքսիոմների համակարգ է մշակել։

Բնական թվերի աքսիոմատիկ տեսության հիմնական հասկացություններն ու հարաբերությունները։ Բնական թվի սահմանում.

Որպես հիմնական (չսահմանված) հասկացություն որոշակի բազմության մեջ Ն ընտրված է վերաբերմունքը , ինչպես նաև օգտագործում է բազմությունների տեսական հասկացություններ, ինչպես նաև տրամաբանության կանոններ։

Տարրը անմիջապես հաջորդող տարրը Ա,նշանակել Ա».

«Ուղիղ հետևել» հարաբերությունը բավարարում է հետևյալ աքսիոմներին.

Պեանոյի աքսիոմները:

Աքսիոմա 1. Առատությամբ Ն ուղղակիորեն կա տարր ոչ հաջորդըոչ այս հավաքածուի որևէ տարրի համար: Եկեք զանգենք նրան միավորև նշվում է խորհրդանիշով 1 .

Աքսիոմա 2. Յուրաքանչյուր տարրի համար Ա -ից Ն կա միայն մեկ տարր Ա" , անմիջապես հաջորդում է Ա .

Աքսիոմա 3. Յուրաքանչյուր տարրի համար Ա -ից Նկա առավելագույնը մեկ տարր, որին անմիջապես հաջորդում է Ա .

Աքսիոմա 4.Ցանկացած ենթաբազմություն Մ հավաքածուներ Ն համընկնում է Ն , եթե այն ունի հետևյալ հատկությունները՝ 1) 1 մեջ պարունակվող Մ ; 2) այն փաստից, որ Ա մեջ պարունակվող Մ , դրանից բխում է, որ Ա" մեջ պարունակվող Մ.

Սահմանում 1. Մի փունջ Ն , որի տարրերի համար հաստատվում է կապը «ուղղակի հետևեք 1-4 աքսիոմները բավարարող, կոչվում է բնական թվերի հավաքածու, և դրա տարրերն են բնական թվեր.

IN այս սահմանումըԿոմպլեկտի տարրերի բնույթի մասին ոչինչ չի ասվում Ն . Այսպիսով, դա կարող է լինել ցանկացած բան: Ընտրելով որպես հավաքածու Ն ինչ-որ կոնկրետ բազմություն, որի վրա տրված է «ուղղակիորեն հետևում» հատուկ կապը, որը բավարարում է 1-4 աքսիոմները, մենք ստանում ենք. այս համակարգի մոդելը աքսիոմա.

Ստանդարտ մոդելՊեանոյի աքսիոմային համակարգը հասարակության պատմական զարգացման գործընթացում առաջացած թվերի շարք է՝ 1,2,3,4,... Բնական շարքը սկսվում է 1 թվով (աքսիոմա 1); յուրաքանչյուր բնական թվի անմիջապես հաջորդում է մեկ բնական թիվ (աքսիոմա 2); յուրաքանչյուր բնական թիվ անմիջապես հաջորդում է առավելագույնը մեկ բնական թվի (աքսիոմա 3). սկսած 1 թվից և շարժվելով իրար հաջորդող բնական թվերին՝ ստանում ենք այդ թվերի ամբողջությունը (աքսիոմա 4):

Այսպիսով, մենք սկսեցինք բնական թվերի համակարգի աքսիոմատիկ կառուցումը` ընտրելով հիմնականը «ուղղակիորեն հետևել» հարաբերություններինև աքսիոմներ, որոնք նկարագրում են դրա հատկությունները: Տեսության հետագա կառուցումը ներառում է բնական թվերի հայտնի հատկությունների և դրանց վրա կատարվող գործողությունների դիտարկումը: Նրանք պետք է բացահայտվեն սահմանումների և թեորեմների մեջ, այսինքն. զուտ տրամաբանորեն բխում են «ուղղակիորեն հետևում» հարաբերությունից և 1-4 աքսիոմներից:

Առաջին հայեցակարգը, որը մենք կներկայացնենք բնական թիվ սահմանելուց հետո վերաբերմունքը «անմիջապես նախորդում է» , որը հաճախ օգտագործվում է բնական շարքի հատկությունները դիտարկելիս։

Սահմանում 2.Եթե ​​բնական թիվ բ ուղղակիորեն հետևում էբնական թիվ Ա, այդ թիվը Ա կանչեց անմիջապես նախորդող(կամ նախորդ) համարը բ .

«Նախորդում» հարաբերությունն ունի մի շարք հատկություններ.

Թեորեմ 1. Միավորը չունի նախորդ բնական թիվ:

Թեորեմ 2. Յուրաքանչյուր բնական թիվ Ա, բացի 1-ից, ունի մեկ նախորդ թիվ բ,այնպիսին է, որ բ»= Ա.

Բնական թվերի տեսության աքսիոմատիկ կառուցումը չի դիտարկվում ոչ սկզբնականում, ոչ էլ մեջ ավագ դպրոց. Այնուամենայնիվ, «ուղղակիորեն հետևում են» հարաբերության այն հատկությունները, որոնք արտացոլված են Պեանոյի աքսիոմներում, ուսումնասիրության առարկա են մաթեմատիկայի սկզբնական դասընթացում: Արդեն առաջին դասարանում առաջին տասնյակի թվերը դիտարկելիս պարզ է դառնում, թե ինչպես կարելի է ստանալ յուրաքանչյուր թիվ։ Օգտագործվում են «հետևում» և «նախորդում» հասկացությունները: Յուրաքանչյուր նոր թիվ գործում է որպես թվերի բնական շարքի ուսումնասիրված հատվածի շարունակություն։ Աշակերտները համոզված են, որ յուրաքանչյուր թվի հաջորդում է հաջորդը, և, առավել ևս, միայն մի բան, որ թվերի բնական շարքն անվերջ է։

Բնական թվերի գումարում

Ըստ աքսիոմատիկ տեսության կառուցման կանոնների՝ բնական թվերի գումարման սահմանումը պետք է ներմուծվի՝ օգտագործելով միայն կապը. «ուղղակի հետևել», և հասկացություններ «բնական համար»Եվ «նախորդ համարը».

Ավելացման սահմանումը նախաբանենք հետևյալ նկատառումներով. Եթե ​​որևէ բնական թվի Աավելացնել 1, ստանում ենք թիվը Ա»,անմիջապես հաջորդում է Ա, այսինքն. Ա+ 1= ա"և, հետևաբար, ստանում ենք ցանկացած բնական թվին 1 գումարելու կանոնը: Բայց ինչպես գումարել թվին Աբնական թիվ բ,տարբերվում է 1-ից Եկեք օգտագործենք հետևյալ փաստը. եթե գիտենք, որ 2 + 3 = 5, ապա գումարը 2 + 4 = 6 է, որը անմիջապես հաջորդում է 5 թվին։ Դա տեղի է ունենում, քանի որ 2 + 4 գումարում երկրորդ անդամը անմիջապես հաջորդող թիվն է։ թիվը 3. Այսպիսով, 2 + 4 =2+3 " =(2+3)". Վերջիվերջո մենք ունենք, .

Այս փաստերը հիմք են հանդիսանում աքսիոմատիկ տեսության մեջ բնական թվերի գումարման սահմանման համար։

Սահմանում 3. Բնական թվերի գումարումհանրահաշվական գործողություն է, որն ունի հետևյալ հատկությունները.

Թիվ ա + բ կանչեց թվերի գումարը ԱԵվ բ , և թվերն իրենք ԱԵվ բ - պայմանները.

Որպես հիմնական հասկացություն, երբ
թվաբանության աքսիոմատիկ կառուցում
բնական թվերն ընդունում են հարաբերակցությունը
«ուղղակիորեն հետևել» տրված է
ոչ դատարկ հավաքածու Ն.
Անմիջապես հաջորդող տարրը
տարր a, նշանակում է a»:

Աքսիոմա 1. N բազմության մեջ կա
տարրը նույնպես անմիջապես չի հաջորդում
այս հավաքածուի որ տարրի հետևում: Մենք կանենք
անվանեք այն միավոր:
Աքսիոմ 2. Ն-ի a տարրի համար
կա միայն մեկ տարր ա»,
անմիջապես հաջորդող ա.

Աքսիոմ 3. Ն-ի a տարրի համար
կա առավելագույնը մեկ տարր
որին անմիջապես հաջորդում է ա.
Աքսիոմա 4. Մ-ի յուրաքանչյուր ենթաբազմություն
N հավաքածուն ունի հետևյալ հատկությունները.
1) միավորը պատկանում է M բազմությանը.
2) Մ-ում a-ի պարունակությունից հետեւում է, որ
որ a»-ն պարունակվում է M-ում, ապա M-ը համընկնում է
սահմանել Ն.

Բնական թվի սահմանում

N բազմություն, որի տարրերի համար հաստատված է կապը
«ուղղակիորեն հետևել», բավարարելով 1-4 աքսիոմները,
կոչվում է բնական թվերի բազմություն, իսկ դրա տարրերը բնական թվեր են։

Հավելում

Սահմանում. Բնական թվերի գումարումը կոչվում է
հանրահաշվական գործողություն հետևյալ հատկություններով.
1) (Ɐa ∈ N) a + 1 = a",
2) (Ɐa, b ∈ N) a + b"=(a+b)".
a+b թիվը կոչվում է a և b թվերի, իսկ a և b թվերի գումարը
պայմանները.
Եկեք համաձայնենք հետևյալ նշումի շուրջ.
1" = 2; 2" = 3; 3" = 4; 4" = 5 և այլն:

Ավելացման հատկությունները

Թեորեմ 3. Բնական թվերի գումարում գոյություն ունի և այն
միայն
Թեորեմ 4. (Ɐ a, b, c ∈ N)(a + b) + c = a + (b + c)
Թեորեմ 5. (Ɐ a, b ∈ N) a+b = b+a

Բազմապատկում

Բնական թվերի բազմապատկումը կոչվում է հանրահաշվական
գործողություն հետևյալ հատկություններով.
1)(Ɐ a ∈ N) a·1 =a;
2)(Ɐ a, b ∈ N) a·b" = a·b + a.
a b թիվը կոչվում է a և b թվերի արտադրյալ, իսկ թվերն իրենք՝ a և
բ - բազմապատկիչներ

Բազմապատկման հատկությունները

Թեորեմ 7. Բնական թվերի բազմապատկում գոյություն ունի, և այն
միայն.
Թեորեմ 8. (Ɐ a, b, c ∈ N)(a + b) c = ac + b c - բաշխվածություն
դեպի աջ՝ հավելման համեմատ։
Թեորեմ 9. (Ɐ a, b, c ∈ N) a·(b + c) = + a·c - ձախ բաշխում.
ավելացման վերաբերյալ.
Թեորեմ 10. (Ɐ a, b, c ∈ N) (a b) c = a (b c) - ասոցիատիվություն.
բազմապատկում.
Թեորեմ 11. (Ɐ a, b ∈ N) a·b = a·b - բազմապատկման փոխադարձություն.

Ինքնաթեստի հարցեր

1. Կարո՞ղ է աքսիոմ 3-ը ձևակերպել հետևյալ կերպ. «Յուրաքանչյուր տարրի համար
իսկ N-ում կա մեկ տարր, որին անմիջապես հաջորդում է
պետք ա"?
2. Շարունակե՛ք բնական թվի սահմանումը` «Բնական թիվ
կոչվում է բազմության տարր...»:
3. Ճի՞շտ է, որ յուրաքանչյուր բնական թիվ ստացվում է նախորդից։
ավելացնելով մեկը?
4. Բազմապատկման ի՞նչ հատկություններ կարելի է կիրառել գտնելիս
արտահայտությունների իմաստները.
ա) 5 · (10 + 4); բ) 125·15·6; գ) (8·379)·125?

գրականություն

Ստոյլովա Լ.Պ.
Մաթեմատիկա. Դասագիրք ուսանողների համար. ավելի բարձր պեդ. դասագիրք հաստատություններ.
Մ.: «Ակադեմիա» հրատարակչական կենտրոն. 2002. - 424 էջ.

GOUVPO

Տուլա նահանգ Մանկավարժական համալսարան

Լ.Ն.Տոլստոյի անունով

ԹՎԱՅԻՆ ՀԱՄԱԿԱՐԳԵՐ

Տուլա 2008 թ

Թվային համակարգեր

Ձեռնարկը նախատեսված է մանկավարժական համալսարանի մաթեմատիկական մասնագիտությունների ուսանողների համար և մշակվել է «Թվային համակարգեր» դասընթացի պետական ​​ստանդարտին համապատասխան: Ներկայացված է տեսական նյութ։ Վերլուծվում են բնորոշ առաջադրանքների լուծումները: Տրվում են գործնական պարապմունքներում լուծելու վարժություններ։

Կազմել է -

ՏՊՄՀ անվ. ֆիզիկամաթեմատիկական գիտությունների թեկնածու, հանրահաշվի և երկրաչափության ամբիոնի դոցենտ։ Լ.Ն.Տոլստոյ Յու.Ա.Իգնատով

Գրախոս -

ֆիզիկամաթեմատիկական գիտությունների թեկնածու, ամբիոնի պրոֆեսոր մաթեմատիկական վերլուծությունՏՊՄՀ անվ. Լ.Ն.Տոլստոյ Ի.Վ.Դենիսով

Ուսումնական հրատարակություն

Թվային համակարգեր

Կազմեց

ԻԳՆԱՏՈՎ Յուրի Ալեքսանդրովիչ

© Յու.Իգնատով, 2008 թ

ԹՎԱՅԻՆ ՀԱՄԱԿԱՐԳԵՐ

Այս դասընթացը ներառում է մաթեմատիկայի հիմունքները: Այն ապահովում է հիմնական թվային համակարգերի խիստ աքսիոմատիկ կառուցում` բնական, ամբողջ թիվ, ռացիոնալ, իրական, բարդ, ինչպես նաև քառյակներ: Այն հիմնված է ֆորմալ աքսիոմատիկ համակարգերի տեսության վրա, որը քննարկվել է մաթեմատիկական տրամաբանության ընթացքում։

Յուրաքանչյուր պարբերությունում թեորեմները համարակալված են առաջինը: Եթե ​​անհրաժեշտ է հղում կատարել մեկ այլ պարբերության թեորեմին, ապա կիրառվում է աստիճանական համարակալում. պարբերության համարը դրվում է թեորեմի համարից առաջ: Օրինակ, թեորեմ 1.2.3-ը թեորեմ 3-ն է 1.2 պարբերությունից:

Ամբողջ թվեր

Բնական թվերի աքսիոմատիկ տեսություն

Աքսիոմատիկ տեսությունը սահմանվում է հետևյալ տարրերով.

հաստատունների մի շարք;

Գործողությունները ցույց տալու համար ֆունկցիոնալ նշանների մի շարք;

Նախադրյալ խորհրդանիշների մի շարք հարաբերություններ ներկայացնելու համար.

Վերոնշյալ տարրերը կապող աքսիոմների ցանկ:

Ֆորմալ աքսիոմատիկ տեսության համար նշվում են նաև եզրակացության կանոններ, որոնց օգնությամբ ապացուցվում են թեորեմները։ Այս դեպքում բոլոր պնդումները գրվում են բանաձևերի տեսքով, որոնց իմաստը նշանակություն չունի, և այդ բանաձևերի վրա կատարվում են փոխակերպումներ՝ համաձայն տրված կանոնների։ Սուբստանտիվ աքսիոմատիկ տեսության մեջ եզրակացության կանոնները հստակեցված չեն։ Ապացույցներն իրականացվում են սովորական տրամաբանական կառուցվածքների հիման վրա, որոնք հաշվի են առնում ապացուցվող հայտարարությունների իմաստը:

Այս դասընթացը կառուցում է հիմնական թվային համակարգերի իմաստալից տեսություններ:

Աքսիոմատիկ տեսության ամենակարևոր պահանջը դրա հետևողականությունն է: Հետևողականության ապացույցն իրականացվում է մեկ այլ տեսության մեջ տեսության մոդել կառուցելով։ Այնուհետև դիտարկվող տեսության հետևողականությունը կրճատվում է մինչև այն տեսության հետևողականությունը, որով կառուցված է մոդելը:

Ամբողջ թվերի համակարգի համար մոդելը կառուցվում է բնական թվերի համակարգի շրջանակներում, ռացիոնալ թվերի համար՝ ամբողջ թվերի համակարգում և այլն։ Արդյունքը աքսիոմատիկ տեսությունների շղթա է, որտեղ յուրաքանչյուր տեսություն հիմնված է նախորդի վրա։ Բայց այս շղթայի առաջին տեսության համար, այն է՝ բնական թվերի տեսությունը, մոդել կառուցելու տեղ չկա: Հետևաբար, բնական թվերի համակարգի համար անհրաժեշտ է կառուցել մի տեսություն, որի համար մոդելի առկայությունը կասկածից վեր է, թեև դա անհնար է խստորեն ապացուցել։

Տեսությունը պետք է լինի շատ պարզ. Այդ նպատակով բնական թվերի համակարգը դիտարկում ենք միայն որպես առարկաներ հաշվելու գործիք։ Գումարման, բազմապատկման և կարգի հարաբերությունները պետք է որոշվեն նշված ձևով տեսության կառուցումից հետո:

Հաշվելու կարիքների համար բնական թվերի համակարգը պետք է լինի հաջորդականություն, որով սահմանվում է առաջին տարրը (միավորը), իսկ յուրաքանչյուր տարրի համար՝ հաջորդը։ Դրան համապատասխան մենք ստանում ենք հետևյալ տեսությունը.

Մշտական 1 (միավոր):

Գործառույթի խորհրդանիշ«¢». Նշանակում է միանվագ «հետևել» գործողությունը, այսինքն Ա¢ - հետևյալ թիվը Ա. Այս դեպքում համարը Ականչեց նախորդՀամար Ա¢.

Չկան հատուկ նախադրյալ նիշեր: Օգտագործվում են սովորական հավասարության կապը և բազմություն-տեսական հարաբերությունները։ Նրանց համար աքսիոմներ չեն նշվի:

Նշվում է այն բազմությունը, որի վրա հիմնված է տեսությունը Ն.

Աքսիոմներ:

(N1) (" ա) ա¢ ¹ 1 (մեկը չի հետևում որևէ թվի):

(N2) (" ա)("բ) (ա¢ = բ¢ ® ա = բ) (յուրաքանչյուր թիվ ունի առավելագույնը մեկ նախորդ):

(N3) Մ Í Ն, 1Օ Մ, ("ա)(աÎ Մ ® ա¢Î Մ) Þ Մ = Ն(մաթեմատիկական ինդուկցիայի աքսիոմա).

Վերոնշյալ աքսիոմատիկան առաջարկվել է (փոքր փոփոխություններով) իտալացի մաթեմատիկոս Պեանոյի կողմից վերջ XIXդարում։

Դժվար չէ աքսիոմներից որոշ թեորեմներ դուրս բերել։

Թեորեմ 1. (Մաթեմատիկական ինդուկցիայի մեթոդ). Թող Ռ(n) – բազմության վրա սահմանված նախադրյալ Ն. Թող դա ճիշտ լինի Ռ(1) և (" n)(Պ(n)® Պ(n¢)). Հետո Ռ(n) նույնատիպ ճշմարիտ պրեդիկատ է Ն.

Ապացույց. Թող Մ- բնական թվերի հավաքածու n, ինչի համար Ռ(n) ճիշտ է. Այնուհետև 1Օ Մըստ թեորեմի պայմանների. Հաջորդը, եթե nÎ Մ, Դա Պ(n) ճշմարիտ ըստ սահմանման Մ, Պ(n¢) ճշմարիտ է թեորեմի պայմանների համաձայն, և n¢Î Մ a-priory Մ. Ինդուկցիոն աքսիոմի բոլոր նախադրյալները բավարարված են, հետևաբար, Մ = Ն. Ըստ սահմանման Մ, Դա նշանակում է որ Ռ(n) ճիշտ է բոլոր թվերի համար Ն. Թեորեմն ապացուցված է.

Թեորեմ 2.Ցանկացած թիվ ԱԹիվ 1-ն ունի նախադրյալ, և միայն մեկը.

Ապացույց. Թող Մ– բնական թվերի բազմություն, որը պարունակում է 1 և բոլոր այն թվերը, որոնք ունեն նախորդներ: Այնուհետև 1Օ Մ. Եթե աÎ Մ, Դա ա¢Î Մ, որովհետեւ ա¢ ունի նախադրյալ (այս պայմանը նույնիսկ չի օգտագործվում աÎ Մ) Այսպիսով, ինդուկցիայի աքսիոմով Մ = Ն. Թեորեմն ապացուցված է.

Թեորեմ 3.Ցանկացած թիվ տարբերվում է հաջորդից։

Զորավարժություններ. Որոշելով բնական թվերը 1¢ = 2, 2¢ = 3, 3¢ = 4, 4¢ = 5, 5¢ = 6, ապացուցեք, որ 2 ¹ 6:

Բնական թվերի գումարում

Բնական թվերի գումարման համար տրված է հետևյալ ռեկուրսիվ սահմանումը.

Սահմանում.Բնական թվերի գումարումը երկուական գործողություն է, որը վերաբերում է բնական թվերին ԱԵվ բհամապատասխանում է թվին ա+բ, ունենալով հետևյալ հատկությունները.

(S1) Ա + 1 = Ա¢ ցանկացածի համար Ա;

(S2) ա+բ¢ = ( ա+բ)¢ ցանկացածի համար ԱԵվ բ.

Պահանջվում է ապացուցել, որ այս սահմանումը ճիշտ է, այսինքն՝ գոյություն ունի տվյալ հատկություններին բավարարող գործողություն։ Այս առաջադրանքը շատ պարզ է թվում. բավական է ինդուկցիա իրականացնել բ, հաշվելով Աամրագրված. Այս դեպքում անհրաժեշտ է ընտրել հավաքածու Մարժեքներ բ, որի համար վիրահատությունը ա+բսահմանված է և բավարարում է պայմանները (S1) և (S2): Ինդուկտիվ անցում կատարելիս պետք է ենթադրել, որ համար բվիրահատությունը կատարվում է, և ապացուցեք, որ դա արվում է բ¢. Բայց սեփականության մեջ (S2), որը պետք է բավարարվի բ, արդեն կա հղում դեպի ա+բ¢. Սա նշանակում է, որ այս հատկությունը ինքնաբերաբար ենթադրում է գործողության առկայությունը ա+բ¢, և, հետևաբար, հաջորդ թվերի համար՝ ի վերջո, համար ա+բ¢ գույքը (S2) նույնպես պետք է բավարարվի: Կարելի է կարծել, որ դա միայն հեշտացնում է խնդիրը՝ ինդուկտիվ քայլը չնչին դարձնելով. ապացուցված պնդումը պարզապես կրկնում է ինդուկտիվ վարկածը: Բայց այստեղ դժվարությունը ինդուկցիայի հիմքի ապացույցի մեջ է: Արժեքի համար բ= 1, հատկությունները (S1) և (S2) նույնպես պետք է բավարարվեն: Բայց հատկությունը (S2), ինչպես ցույց է տրված, ենթադրում է գործողության առկայություն 1-ին հաջորդող բոլոր արժեքների համար: Սա նշանակում է, որ ինդուկցիայի հիմքը ստուգելը ենթադրում է ապացույց ոչ թե մեկի, այլ բոլոր թվերի համար, և ինդուկցիան կորցնում է իր իմաստը. ինդուկցիայի հիմքը համընկնում է ապացուցվող հայտարարության հետ:

Վերոնշյալ պատճառաբանությունը չի նշանակում, որ ռեկուրսիվ սահմանումները սխալ են կամ ամեն անգամ մանրակրկիտ հիմնավորում են պահանջում: Դրանք արդարացնելու համար հարկավոր է օգտագործել բնական թվերի հատկությունները, որոնք միայն այս փուլում են հաստատվում։ Երբ դրանք հաստատվեն, ռեկուրսիվ սահմանումների վավերականությունը կարող է ապացուցվել: Առայժմ ապացուցենք գումարման գոյությունը ինդուկցիայի միջոցով Ա(S1) և (S2) բանաձևերում կապ չկա ավելացման միջև ԱԵվ Ա¢.

Թեորեմ 1.Բնական թվերի գումարումը միշտ էլ իրագործելի է, և դա եզակի է:

Ապացույց. ա) Նախ մենք ապացուցում ենք եզակիությունը: Եկեք շտկենք այն Ա. Հետո վիրահատության արդյունքը ա+բկա մի ֆունկցիա ից բ. Ենթադրենք, կան երկու նման գործառույթներ զ(բ) Եվ է(բ), ունենալով հատկություններ (S1) և (S2): Ապացուցենք, որ նրանք հավասար են։

Թող Մ- իմաստների մի շարք բ, ինչի համար զ(բ) = է(բ) Ըստ սեփականության (S1)
զ(1) = Ա + 1 = Ա¢ և է(1) = Ա + 1 = Ա¢ նշանակում է զ(1) = է(1), և 1Օ Մ.

Թող հիմա բÎ Մ, այն է զ(բ) = է(բ) Ըստ սեփականության (S2)

զ(բ¢) = ա+բ¢ = ( ա+բ)¢= զ(բ)¢, է(բ¢) = ա+բ¢ = ( ա+բ)¢= է(բ)¢ = զ(բ¢),

Նշանակում է, բ¢Î Մ. Ինդուկցիայի աքսիոմով Մ = Ն. Եզակիությունն ապացուցված է։

բ) Այժմ ինդուկցիայի միջոցով Ափաստենք գործողության առկայությունը ա+բ. Թող Մ- այդ արժեքների հավաքածու Ա, որի համար վիրահատությունը ա+բհատկություններով (S1) և (S2) սահմանված է բոլորի համար բ.

Թող Ա= 1. Բերենք նման գործողության օրինակ: Ըստ սահմանման մենք ենթադրում ենք 1 + բ == բ¢. Եկեք ցույց տանք, որ այս գործողությունը բավարարում է հատկությունները (S1) և (S2): (S1) ունի 1 + 1 = 1¢ ձև, որը համապատասխանում է սահմանմանը: Ստուգում (S2): 1 + բ¢ =( բ¢)¢ =
= (1+ բ)¢, և (S2) բավարարված է: Այսպիսով, 1Օ Մ.

Թող հիմա ԱÎ Մ. Ապացուցենք դա Ա¢Î Մ. Մենք հավատում ենք ըստ սահմանման
ա¢ + բ = (ա+ բ)¢. Հետո

ա¢ + 1 = (ա+ 1) ¢ = ( Ա¢)¢,

ա¢ + բ¢ = ( ա+ բ¢)¢ = (( ա+ բ)¢)¢ = ( ա¢ + բ)¢,

և հատկությունները (S1) և (S2) բավարարված են:

Այսպիսով, Մ = Ն, իսկ գումարումը սահմանվում է բոլոր բնական թվերի համար։ Թեորեմն ապացուցված է.

Թեորեմ 2.Բնական թվերի գումարումն ասոցիատիվ է, այսինքն

(ա+բ) + գ = ա + (բ+գ).

Ապացույց. Եկեք շտկենք այն ԱԵվ բև իրականացնել ինդուկցիա Հետ. Թող Մ- այդ թվերի մի շարք Հետ, որի համար ճիշտ է հավասարությունը։ Հատկությունների հիման վրա (S1) և (S2) մենք ունենք.

(ա+բ) + 1 = (ա+բ)¢ = ( ա+բ¢) = ա+(բ+ 1) Þ 1Օ Մ.

Թող հիմա ՀետÎ Մ. Հետո

(ա+բ) + գ¢ = (( ա+բ) + գ)¢ = ( ա+(բ + գ))¢ = ա+(բ + գ)¢ = ա+(բ + գ¢),

Եվ գ¢Î Մ. Ըստ աքսիոմայի (N3) Մ = Ն. Թեորեմն ապացուցված է.

Թեորեմ 3.Բնական թվերի գումարումը կոմուտատիվ է, այսինքն

a + b = b + a. (1)

Ապացույց. Եկեք շտկենք այն Աև իրականացնել ինդուկցիա բ.

Թող բ= 1, այսինքն՝ անհրաժեշտ է ապացուցել հավասարությունը

Ա + 1 = 1 + Ա. (2)

Մենք ապացուցում ենք այս հավասարությունը ինդուկցիայի միջոցով Ա.

ժամը Ա= 1 հավասարությունը չնչին է: Թող դա արվի դրա համար Ա, եկեք ապացուցենք դրա համար Ա¢. Մենք ունենք

Ա¢ + 1 = ( Ա + 1) + 1 = (1 + Ա) + 1 = (1 + Ա)¢ = 1 + Ա¢.

Ինդուկտիվ անցումը ավարտված է: Մաթեմատիկական ինդուկցիայի սկզբունքով հավասարությունը (2) ճիշտ է բոլորի համար Ա. Սա ապացուցում է ինդուկցիոն հիմքի հայտարարությունը բ.

Այժմ (1) բանաձևը բավարարվի բ. Եկեք ապացուցենք դրա համար բ¢. Մենք ունենք

ա +բ¢ = ( ա +բ)¢ = ( բ + ա)¢ = բ + ա¢ = բ + (ա + 1) = բ + (1 + ա) = (բ + 1) + ա = բ¢ + ա.

Օգտագործելով մաթեմատիկական ինդուկցիայի սկզբունքը, թեորեմն ապացուցված է.

Թեորեմ 4.ա + բ ¹ բ.

Ապացույցը վարժություն է։

Թեորեմ 5.Ցանկացած թվերի համար ԱԵվ բտեղի է ունենում հետևյալ դեպքերից մեկը և միայն մեկը.

1) ա = բ.

2) Կա մի թիվ կայնպիսին է, որ a = b + k.

3) Կա մի թիվ լայնպիսին է, որ b = a + l.

Ապացույց. Թեորեմ 4-ից հետևում է, որ այդ դեպքերից առավելագույնը տեղի է ունենում, քանի որ, ակնհայտորեն, 1) և 2-րդ դեպքերը, ինչպես նաև 1) և 3-րդ դեպքերը չեն կարող տեղի ունենալ միաժամանակ: Եթե ​​2) և 3) դեպքերը տեղի են ունեցել միաժամանակ, ապա a = b + k=
= (Ա + լ) + կ = Ա+ (լ + կ), ինչը կրկին հակասում է 4-րդ թեորեմին։ Եկեք ապացուցենք, որ այդ դեպքերից գոնե մեկը միշտ լինում է։

Թող ընտրվի մի թիվ ԱԵվ Մ –դրանցից շատերը բ,որոնցից յուրաքանչյուրի համար տրված ատեղի է ունենում 1), 2) կամ 3) դեպք:

Թող բ= 1. Եթե ա= 1, ապա մենք ունենք դեպք 1): Եթե Ա¹ 1, ապա թեորեմ 1.1.2-ով մենք ունենք

a = k" = k + 1 = 1 + k,

այսինքն՝ ունենք գործ 2) համար բ= 1. Այսպիսով, 1-ը պատկանում է Մ.

Թող բպատկանում է Մ.Այնուհետև հնարավոր են հետևյալ դեպքերը.

- Ա = բ,Նշանակում է, բ» = բ + 1 = Ա+ 1, այսինքն, մենք ունենք դեպք 3) համար բ»;

- Ա = b+k,եւ եթե կ= 1, ապա Ա = բ+ 1 = բ», այսինքն, դեպք 1) տեղի է ունենում համար բ»;

եթե կԹիվ 1, ուրեմն k = t"Եվ

a = b + t" = b + (t + 1)= բ + (1+ մ) = (բ+ 1)+ m = բ¢ + մ,

այսինքն դեպք 2) տեղի է ունենում համար բ»;

- բ = ա+լ, և բ» =(ա + լ)¢ = Ա + լ¢, այսինքն, մենք ունենք դեպք 3) համար բ».

Բոլոր դեպքերում բ»պատկանում է Մ.Թեորեմն ապացուցված է.

Զորավարժություններ. Գումարի սահմանման հիման վրա ապացուցեք, որ 1 + 1 = 2, 1 + 2 = 3, 2 + 2 = 4, 2 + 3 = 5, 2 + 4 = 3 + 3 = 6:

Բնական թվերի բազմապատկում

Սահմանում.Բնական թվերի բազմապատկումը երկուական գործողություն է, որը վերաբերում է բնական թվերին ԱԵվ բհամապատասխանում է թվին աբ(կամ a×b), ունենալով հետևյալ հատկությունները.

(P1) Ա× 1 = Աորեւէ մեկի համար Ա;

(P2) աբ» = աբ + ացանկացածի համար ԱԵվ բ.

Ինչ վերաբերում է բազմապատկման սահմանմանը, ապա գումարման սահմանման վերաբերյալ նախորդ պարբերությունում արված բոլոր մեկնաբանությունները մնում են ուժի մեջ։ Մասնավորապես, դրանից դեռ պարզ չէ, որ կա համապատասխանություն սահմանման մեջ տրված հատկությունների հետ։ Ուստի հետևյալ թեորեմը, որը նման է թեորեմ 1.2.1-ին, ունի հիմնարար կարևոր նշանակություն.

Թեորեմ 1.Բնական թվերի միայն մեկ բազմապատկում կա։ Այլ կերպ ասած, բազմապատկումը միշտ հնարավոր է իրականացնել և միանշանակ:

Ապացույցը բավականին նման է թեորեմ 1.2.1-ի ապացույցին և առաջարկվում է որպես վարժություն:

Հետևյալ թեորեմներում ձևակերպված բազմապատկման հատկությունները հեշտությամբ ապացուցվում են. Յուրաքանչյուր թեորեմի ապացույցը հիմնված է նախորդների վրա։

Թեորեմ 2.(Իրավունքի բաշխման օրենք): ա+բ)c = ac + bc.

Թեորեմ 3.Բազմապատկումը փոխադարձ է. ab = ba.

Թեորեմ 4.(Ձախ բաշխման օրենք): գ(ա+բ)= сa + сb.

Թեորեմ 5.Բազմապատկումը ասոցիատիվ է. ա(մ.թ.ա) = (աբ)գ.

Սահմանում. Semiring-ը համակարգ է, որտեղ + և × գումարման և բազմապատկման երկուական գործողություններ են, որոնք բավարարում են աքսիոմները.

(1) կոմուտատիվ կիսախումբ է, այսինքն՝ գումարումը կոմուտատիվ է և ասոցիատիվ.

(2) – կիսախումբ, այսինքն՝ բազմապատկումը ասոցիատիվ է.

(3) աջ և ձախ բաշխումը պահպանվում է:

Հանրահաշվական տեսակետից բնական թվերի համակարգը գումարման և բազմապատկման նկատմամբ կազմում է կիսամյակ:

Զորավարժություններ. Ապրանքի սահմանման հիման վրա ապացուցել, որ
2×2 = 4, 2×3 = 6:

Զորավարժություններ

Ապացուցեք ինքնությունը.

1. 1 2 + 2 2 + ... + n 2 = .

2. 1 3 + 2 3 + ... + n 3 = .

Գտեք գումարը.

3. .

4. .

5. .

6. 1x1! + 2x2! + ... + n×n!.

Ապացուցե՛ք անհավասարությունները.

7. n 2 < 2n для n > 4.

8. 2n < n! Համար n³ 4.

9. (1 + x)n³ 1 + nx, Որտեղ x > –1.

10. ժամը n > 1.

11. ժամը n > 1.

12. .

13. Գտեք ինդուկցիայի ապացույցի սխալը, որ բոլոր թվերը հավասար են: Մենք ապացուցում ենք համարժեք պնդում. ցանկացած շարքում nթվեր, բոլոր թվերը հավասար են միմյանց: ժամը n= 1 պնդումը ճիշտ է: Թող դա ճշմարիտ լինի n = կ, եկեք ապացուցենք դրա համար n = կ+ 1. Վերցրեք մի շարք կամայական
(կ+ 1) թվեր. Նրանից հանենք մեկ թիվ Ա. Ձախ կթվերը, ինդուկտիվ վարկածով դրանք հավասար են միմյանց։ Մասնավորապես, երկու թվեր հավասար են բԵվ Հետ. Հիմա եկեք հանենք համարը հավաքածուից Հետև միացրեք այն Ա. Ստացված հավաքածուում դեռ կա կթվեր, ինչը նշանակում է, որ դրանք նույնպես հավասար են միմյանց: Մասնավորապես, ա = բ. Նշանակում է, a = b = c, և վերջ ( կ+ 1) թվերը հավասար են միմյանց. Ինդուկտիվ անցումը ավարտված է, և հայտարարությունը ապացուցված է:

14. Ապացուցեք մաթեմատիկական ինդուկցիայի ուժեղացված սկզբունքը.

Թող Ա(n) պրեդիկատ է բնական թվերի բազմության վրա։ Թող Ա(1) ճշմարիտ և ճշմարտությունից Ա(կ) բոլոր թվերի համար կ < մպետք է ճշմարիտ լինի Ա(մ) Հետո Ա(n) ճիշտ է բոլորի համար n.

Պատվիրված հավաքածուներ

Եկեք հիշենք կարգի հարաբերության հետ կապված հիմնական սահմանումները:

Սահմանում. f («վերևում») հարաբերությունը բազմության վրա Մկանչեց պատվերի հարաբերություն, կամ պարզապես որպեսզի, եթե այս կապը անցողիկ է և հակասիմետրիկ։ Համակարգ բ Մ, fñ կոչվում է պատվիրված հավաքածու.

Սահմանում. խիստ կարգ, եթե հակառեֆլեքսային է, և ազատ կարգը, եթե ռեֆլեքսային:

Սահմանում. F կարգի հարաբերությունը կոչվում է հարաբերություն գծային կարգը, եթե միացված է, այսինքն ա ¹ բÞ ազ բÚ բզ ա. Այն կարգը, որը գծային չէ, կոչվում է մասնակի.

Սահմանում.Թող á Մ Ա- ենթաբազմություն Մ. Տարր Տհավաքածուներ Ականչեց ամենափոքրը, եթե այն փոքր է հավաքածուի մյուս բոլոր տարրերից Ա, այն է

("XÎ Ա)(X ¹ Տ® Xզ Տ).

Սահմանում.Թող á Մ, fñ – պատվիրված հավաքածու, Ա- ենթաբազմություն Մ. Տարր Տհավաքածուներ Ականչեց նվազագույն, եթե կոմպլեկտում Աչկա ավելի փոքր տարր, այսինքն (" XÎ Ա)(X ¹ Տ® Ø Տզ X).

Նմանապես որոշվում են ամենամեծ և առավելագույն տարրերը:

Զորավարժություններ

1. Ապացուցեք, որ անցումային և հակառեֆլեքսային հարաբերությունը կարգի հարաբերություն է:

2. Ապացուցեք, որ բազմության վրա բաժանելիության M կապը Նկա մասնակի պատվերի հարաբերություն.

3. Ապացուցեք, որ բազմությունը կարող է ունենալ առավելագույնը մեկ ամենամեծ և առավելագույնը մեկ ամենափոքր տարր:

4. Գտեք բազմության բոլոր նվազագույն, առավելագույն, մեծ և փոքր տարրերը (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) բաժանելիության կապի համար:

5. Ապացուցեք, որ եթե հավաքածուն ունի ամենափոքր տարրը, ապա դա միակ նվազագույն տարրն է:

6. Քանի՞ ձևով կարող ենք սահմանել գծային կարգը երեք տարրերից բաղկացած բազմության վրա: գծային ու խիստ? գծային և անփույթ?

7. Թող á Մ, fñ-ը գծային կարգավորված բազմություն է։ Ապացուցեք, որ պայմանով սահմանված հարաբերությունը

ա > բ Û ազ բ & ա¹ բ

խիստ գծային կարգի հարաբերություն է։

8. Թող á Մ, fñ-ը գծային կարգավորված բազմություն է։ Ապացուցեք, որ պայմանով սահմանված ³ հարաբերությունը

ա ³ բ Û ազ բ Ú ա= բ,

ոչ խիստ գծային կարգի հարաբերություն է։

Սահմանում.Գծային կարգավորված հավաքածու բ Մ, fñ, որտեղ յուրաքանչյուր ոչ դատարկ ենթաբազմություն ունի ամենափոքր տարրը կոչվում է բավական կանոնակարգված. f հարաբերությունն այս դեպքում կոչվում է հարաբերություն ամբողջական պատվեր.

Համաձայն 1.4.6 թեորեմի՝ բնական թվերի համակարգը լրիվ դասավորված բազմություն է։

Սահմանում.Թող á Մ A տարրով առանձնացված ընդմիջում, կոչվում է հավաքածու Ռ աբոլոր տարրերը ստորև Աև տարբերվում է Ա, այն է

Ռ ա = {x Î Մï ազ x, x¹ ա}.

Մասնավորապես, եթե Անվազագույն տարրն է, ուրեմն Ռ ա = Æ.

Թեորեմ 1.(Տրանսֆինիտային ինդուկցիայի սկզբունքը). Թող á Մ, fñ ամբողջությամբ պատվիրված հավաքածու է և Ա Í Մ. Թողեք յուրաքանչյուր տարրի համար Ա-ից Մպատկանելությունից Ամիջակայքի բոլոր տարրերը Ռ ահետևում է դրան ԱÎ Ա. Հետո Ա = Մ.

Ապացույց.

Թող Ա" = Մ\Աբազմությունների բազմությունների տեսական տարբերությունն է ՄԵվ Ա.Եթե Ա"= Æ, ապա Ա = Մ,իսկ թեորեմը ճշմարիտ է: Եթե Ա"¹ Æ , հետո, քանի որ Մլրիվ պատվիրված կոմպլեկտ է, հետո լրակազմ Ա"պարունակում է ամենափոքր տարրը Տ.Այս դեպքում նախորդող բոլոր տարրերը Տև տարբերվում է Տ,չեն պատկանում Ա"և հետևաբար պատկանում են Ա.Այսպիսով, Р մ Í Ա.Ուստի թեորեմի պայմաններով Տ Î Ա,եւ, հետեւաբար Տ Ï Ա»,հակառակ ենթադրության.

Թող á Ա; fñ-ը պատվիրված հավաքածու է: Մենք դա կենթադրենք Ա- վերջավոր հավաքածու: Յուրաքանչյուր տարրով Ահավաքածուներ Աեկեք համեմատենք մի կետ Տ (Ա) տրված հարթության այնպես, որ եթե տարր Աանմիջապես հետևում է տարրին բ,ապա մատնանշեք Տ (ա) մենք կտեղադրենք կետից վեր T(b)և դրանք միացնել հատվածով: Արդյունքում մենք ստանում ենք այս դասավորված բազմությանը համապատասխան գրաֆիկ։

Զորավարժություններ

9. Թող á Մ, fñ-ը ամբողջովին պատվիրված հավաքածու է, բ Î Մ, սÎ Մ.Ապացուցեք, որ կամ Pb = Ռ ս,կամ Pb Ì Ռ ս,կամ Ռ ս Ì Pb.

10. Թող á Մ, f 1 с and b Լ, f 2 ñ ամբողջությամբ դասավորված բազմություններ են այնպես, որ
Մ Ç L=Æ . Առատությամբ Մ È ԼԵկեք սահմանենք երկուական f հարաբերություն հետևյալ պայմաններով.

1) եթե ա, բÎ Մ,Դա, ազ բ Û ազ 1 բ;

2) եթե ա, բÎ Լ,Դա, ազ բ Û ազ 2 բ;

3) եթե ԱÎ Մ, բÎ Լ,Դա, ազ բ.

Ապացուցեք, որ համակարգը բ ՄÈ Լ, fñ-ը ամբողջությամբ պատվիրված հավաքածու է։

Պատվիրված կիսախմբեր

Սահմանում.Կիսախումբկոչվում է հանրահաշիվ á Ա, *ñ, որտեղ *-ը ասոցիատիվ երկուական գործողություն է:

Սահմանում.Կիսախումբ á Ա, *ñ կոչվում է կրճատում ունեցող կիսախմբ, եթե այն բավարարում է հատկությունները

ա*գ = բ*գ Þ ա = բ;գ*a = c*բ Þ ա = բ.

Սահմանում.Պատվիրված կիսախմբկոչվում է համակարգ բ Ա, +, fñ, որտեղ:

1) համակարգ բ Ա, +ñ – կիսախումբ;

2) համակարգ բ Ա, fñ – պատվիրված հավաքածու;

3) f հարաբերությունը կիսախմբային գործողության նկատմամբ միատոն է, այսինքն
ազ բ Þ ա+գզ բ + գ, գ + ազ գ+բ.

Պատվիրված կիսախմբ á Ա, +, fñ կոչվում են պատվիրված խումբ, եթե համակարգը բ Ա, +ñ – խումբ.

Պատվերի տեսակներին համապատասխան որոշվում են հարաբերությունները գծային կարգով կիսախումբ, գծային կարգով խումբ, մասամբ պատվիրված կիսախումբ, խիստ կարգավորված կիսախումբև այլն:

Թեորեմ 1.Պատվիրված կիսախմբում á Ա, +, fñ անհավասարությունները կարելի է ավելացնել, այսինքն ազ բ, գզ դ Þ ա+գզ բ+դ.

Ապացույց. Մենք ունենք

ազ բ Þ ա+գզ բ + գ, գզ դ Þ բ+գզ բ + դ,

որտեղից անցողիկությամբ ա+գզ բ+դ. Թեորեմն ապացուցված է.

Վարժություն 1. Ապացուցեք, որ բնական թվերի համակարգը բազմապատկման և բաժանման մասով կիսախմբ է:

Հեշտ է տեսնել, որ համակարգը բ Ն, +, >ñ – խիստ կարգավորված կիսախումբ, բ Ն, +, ³ñ-ը ոչ խիստ կարգավորված կիսախումբ է: Մենք կարող ենք բերել á կիսախմբի նման դասավորության օրինակ Ն, +ñ, որի կարգը ոչ խիստ է, ոչ էլ ոչ խիստ։

Վարժություն 2. Բնական թվերի համակարգում f կարգը սահմանենք հետևյալ կերպ. ազ բ Û ա ³ բ & ա¹ 1. Ապացուցեք, որ բ Ն, +, fñ-ը դասավորված կիսախումբ է, որտեղ կարգը ոչ խիստ է, ոչ էլ ոչ խիստ:

Օրինակ 1.Թող Ա– բնական թվերի բազմություն, որը հավասար չէ մեկին: Եկեք սահմանենք հարաբերակցությունը f in Ահետևյալ կերպ.

ազ բ Û ($ կÎ Ն)(ա = բ+կ) & բԹիվ 3.

Ապացուցեք, որ համակարգը բ Ա, +, fñ-ը մասամբ և խիստ կարգավորված կիսախումբ է։

Ապացույց. Եկեք ստուգենք անցողիկությունը.

ազ բ, բզ գ Þ a = b + k, bԹիվ 3, b = c + l, c¹ 3 Þ a = c +(k+l), ք¹ 3 Þ ազ գ.

Որովհետեւ ազ բ Þ ա > բ, ապա հակառեֆլեքսիվությունը բավարարված է։ 2.1.1 վարժությունից հետևում է, որ f-ը խիստ կարգի հարաբերություն է։ Պատվերը մասնակի է, քանի որ 3-րդ և 4-րդ տարրերը որևէ առնչություն չունեն:

f հարաբերությունը միապաղաղ է գումարման նկատմամբ։ Իրոք, պայմանը ազ բ Þ ա+գզ բ+գկարող էր խախտվել միայն այն ժամանակ, երբ
բ+գ= 3. Բայց գումարը կարող է հավասար լինել 3-ի, քանի որ դա հնարավոր է Աոչ մի միավոր:

Երկու տարրերից բաղկացած խումբը չի կարող գծային և խստորեն դասավորվել: Փաստորեն, թող 0-ը և 1-ը լինեն նրա տարրերը (0-ը խմբի զրոն է): Ենթադրենք, որ 1 > 0: Այնուհետև մենք ստանում ենք 0 = 1 + 1 > 0 + 1 = 1:

Թեորեմ 2.Յուրաքանչյուր գծային կարգով չեղարկվող կիսախմբում կարելի է գծային և խստորեն պատվիրել:

Ապացույց. Թող á Ա, +, fñ-ը դասավորված կիսախումբ է: Խիստ կարգի հարաբերությունը սահմանվում է այնպես, ինչպես վարժության 2.1.5-ում. ա > բ Û ազ բ & ա¹ բ. Ցույց տանք, որ 3) պայմանը պատվիրված կիսախմբի սահմանումից բավարարված է։

ա > բ Þ ազ բ, ա¹ բÞ ա+գզ բ+գ.

Եթե ա+գ = բ+գապա, նվազեցնելով, ստանում ենք ա = բ, որը հակասում է պայմանին
Ա > բ. Նշանակում է, ա+գ ¹ բ+գ, Եվ ա+գ > բ+գ. Նմանապես ստուգվում է 3) պայմանի երկրորդ մասը, որն ապացուցում է թեորեմը։

Թեորեմ 3.Եթե ​​բ Ա, +, fñ-ը գծային և խիստ դասավորված կիսախումբ է, ապա.

1) Ա + Հետ = բ + գ Û ա = բ Û գ + ա = Հետ + բ;

2) Ա + Հետզ բ + գ Û Ազ բ Û Հետ + ազ Հետ + բ.

Ապացույց. Թող Ա + Հետ = բ + գ. Եթե ա ¹ բ, ապա կապի շնորհիվ Ազ բկամ
բզ ա. Բայց հետո համապատասխանաբար Ա + Հետզ բ+ գկամ բ + Հետզ ա+ գ, որը հակասում է պայմանին Ա + Հետ = բ + գ. Նույն կերպ են վարվում նաև այլ դեպքեր:

Այսպիսով, յուրաքանչյուր գծային և խստորեն պատվիրված կիսախումբը չեղյալ համարվող կիսախումբ է:

Սահմանում.Թող á Ա, +, fñ-ը դասավորված կիսախումբ է: Տարր Ահավաքածուներ Ակոչվում է դրական (բացասական), եթե ա + ա¹ ԱԵվ ա+ազ Ա(համապատասխանաբար Ազ ա + ա).

Օրինակ 2.Ապացուցեք, որ կարգավորված փոխադարձ կիսախմբի տարրը դրական տարրից ավելի մեծ չեղարկումով պարտադիր չէ, որ դրական լինի:

Լուծում. Եկեք օգտագործենք օրինակ 1. Մենք ունենք 2 + 2 f 2, ինչը նշանակում է, որ 2-ը դրական տարր է: 3 = 2 + 1, ինչը նշանակում է 3 f 2: Միևնույն ժամանակ, 3 + 3 f 3 հարաբերությունը չի գործում, ինչը նշանակում է, որ 3-ը դրական տարր չէ:

Թեորեմ 4.Չեղյալ համարվող կոմուտատիվ կիսախմբի դրական տարրերի գումարը դրական է:

Ապացույց. Եթե ա + ազ ԱԵվ բ+բզ բ, ապա թեորեմ 1-ով

ա + ա+ բ+բզ ա + բ Þ ( ա + բ)+ (ա+բ) զ ա + բ.

Մնում է ստուգել, ​​որ ( ա + բ)+ (ա+բ)¹ ա + բ.Մենք ունենք:

բ+բզ բ Þ ա+բ+բզ ա+բ(1)

Եկեք ձևացնենք, որ ( ա + բ)+ (ա+բ)=ա + բ.Փոխարինելով (1)՝ մենք ստանում ենք

ա+բ+բզ ա+բ+ա+բ Þ ազ ա+ա.

Հակասիմետրիայի պատճառով a = a + a. Սա հակասում է այն փաստին, որ տարրը Ադրական.

Թեորեմ 5.Եթե Ագծային և խիստ կարգավորված կիսախմբի դրական տարր է, այնուհետև ցանկացածի համար բմենք ունենք ա+բզ բ, բ + ազ բ.

Ապացույց. Մենք ունենք ա+ ազ Ա Þ ա+ ա+ բզ ա+ բ. Եթե ​​դա ճիշտ չէ ա+ բզ բ,ապա գծայինության շնորհիվ պահպանվում է ա+բ=բկամ բզ ա+ բ. Ձախից ավելացում Ա, ստանում ենք համապատասխանաբար ա+ ա+ բ= ա+ բկամ ա+ բզ ա+ ա+ բ. Այս պայմանները հակասում են կարգի հարաբերության հակասիմետրիկությանը և խստությանը։

Թեորեմ 6.Թող á Ա, +, fñ – գծային և խիստ կարգավորված կիսախումբ, ԱÎ ԱԵվ Ա+ Ա¹ ա. Այնուհետև տարրերը.

Ա, 2*Ա, 3*Ա, ...

բոլորը տարբեր են: Եթե ​​այս դեպքում համակարգը բ Ա, +, fñ-ը խումբ է, ապա բոլոր տարրերը տարբեր են.

0, Ա,–Ա, 2*Ա, - 2*ա, 3*ա, –3*Ա, ...

(տակ կ*ա, կÎ Ն , աÎ Ա, նշանակում է գումար ա+ …+ ա, Պարունակող կպայմանները)

Ապացույց. Եթե ա + Ազ Ա, Դա ա + Ա + Ազ ա + աև այլն։ Արդյունքում մենք ստանում ենք շղթա ... զ կազ… զ 4 Ա f3 Ա f2 Ազ Ա. Անցումայինության և հակասիմետրիկության շնորհիվ դրա բոլոր տարրերը տարբեր են։ Խմբում շղթան կարող է շարունակվել մյուս ուղղությամբ՝ ավելացնելով տարր՝ Ա.

Հետևանք.Անջատում ունեցող վերջավոր կիսախմբը, եթե նրա տարրերի թիվը առնվազն 2 է, չի կարող գծային կարգվել:

Թեորեմ 7.Թող á Ա, +, fñ-ը գծային կարգավորված խումբ է։ Հետո

ազ ա Û բզ բ.

Ապացույցը վարժություն է։

Այսպիսով, յուրաքանչյուր գծային կարգավորված խումբ կամ խիստ կամ ոչ խիստ կարգավորված է: Այս կարգերը նշելու համար մենք կօգտագործենք համապատասխանաբար > և ³ նշանները:

Զորավարժություններ

3. Ապացուցեք, որ գծային և խիստ դասավորված կիսախմբի դրական տարրերի գումարը դրական է:

4. Ապացուցեք, որ դրական տարրից մեծ կիսախմբի յուրաքանչյուր գծային և խիստ դասավորված տարր ինքնին դրական է:

5. Ապացուցեք, որ դասավորված կիսախմբը գծային կարգավորված է, եթե և միայն այն դեպքում, երբ նրա տարրերի ցանկացած վերջավոր բազմություն ունի միայն մեկ ամենամեծ տարր:

6. Ապացուցեք, որ գծային կարգավորված խմբի դրական տարրերի բազմությունը դատարկ չէ:

7. Թող á Ա, +, fñ-ը գծային և խիստ կարգավորված խումբ է։ Ապացուցեք, որ տարրը Ահամակարգեր Աեթե և միայն եթե դրական է, եթե Ա > 0.

8. Ապացուցեք, որ բնական թվերի հավելումային կիսախմբում կա միայն մեկ գծային և խիստ կարգ, որում դրական տարրերի բազմությունը դատարկ չէ:

9. Ապացուցեք, որ ամբողջ թվերի բազմապատկվող կիսախմբը չի կարող գծային դասավորվել:

Պատվիրված մատանիներ

Սահմանում.Համակարգ բ Ա, +, ×, fñ կոչվում է հրամայել է կիսաֆաբրիկատ, Եթե

1) համակարգ բ Ա, +, ×ñ – կիսաեզրափակիչ;

2) համակարգ բ Ա, +, fñ – պատվիրված կիսախմբով ոչ դատարկ հավաքածուով Ա+ դրական տարրեր;

3) միապաղաղությունը պահպանվում է դրական տարրերով բազմապատկման նկատմամբ, այսինքն՝ եթե ՀետÎ Ա+ և Ազ բ, Դա ակզ մ.թ.ա, մոտզ կբ.

Դրական տարրհրամայել է կիսաֆաբրիկատ Աá կարգավորված կիսախմբի ցանկացած դրական տարր է Ա, +, fñ.

Հրամայեց կիսամյակային բ Ա, +, ×, fñ կոչվում է պատվիրված մատանին (դաշտ), եթե կիսամյակային բ Ա, +, ×ñ – օղակ (համապատասխանաբար դաշտ):

Սահմանում.Թող á Ա, +, ×, fñ – պատվիրված կիսագնդում: Համակարգի f կարգը Ականչեց Արքիմեդ,և համակարգը Ա - Արքիմեդը հրամայեց.եթե, ինչ էլ որ լինի դրական տարրերը ԱԵվ բհամակարգեր Ա, կարող եք նշել նման բնական թիվ Պ,Ինչ ԱԺզ բ.

Օրինակ 1.Բնական թվերի կիսամյակը > (մեծ քան) հարաբերությամբ գծային, խիստ և արքիմեդյան կարգի կիսամյակում է:

Գծային կարգավորված օղակի համար բ Ա, +, ×, 0, fñ համակարգ բ Ա, +, 0, fñ-ը գծային կարգավորված խումբ է: Սա ենթադրում է, համաձայն թեորեմ 2.2.7-ի, որ f-ի կարգը կա՛մ խիստ է, կա՛մ ոչ խիստ: Առատությամբ Ակարող եք մուտքագրել (2.1.5. և 2.1.6 վարժություններ) նոր գծային կարգը, որը խիստ կլինի, եթե f-ի կարգը ոչ խիստ է, և ոչ խիստ, եթե f-ի կարգը խիստ է։ Այս դիտողության հետ կապված՝ գծային կարգավորված ռինգում ԱՍովորաբար դիտարկվում են երկու երկուական կարգի հարաբերություններ, որոնցից մեկը՝ խիստ, նշվում է նշանով >, իսկ երկրորդը՝ ոչ խիստ, նշվում է ³-ով։

Հետևյալի համար օգտակար է հիշել, որ գծային կարգավորված օղակում տարրը Ադրական է, եթե և միայն, եթե Ա> 0 (վարժություն 2.2.7):

Թեորեմ 1.Թող համակարգը բ Ա,+,×,0,>ñ – գծային կարգավորված օղակ: Հետո ցանկացած տարրի համար Ա-ից Ակամ Ա = 0, կամ Ա> 0, կամ - Ա > 0.

Ապացույց. Տարրերի միջև գծայինության և խստության շնորհիվ
ա+ աԵվ Ահարաբերություններից միայն մեկն է ա+ ա>ա, ա+ ա = ա, ա+ ա < ա. Առաջին դեպքում Ա- դրական տարր. Երկրորդում մենք ավելացնում ենք երկու մասերը. Աև մենք ստանում ենք Ա= 0. Երրորդ դեպքում երկու կողմերին էլ ավելացնում ենք. ա – ա – աև մենք ստանում ենք - ա < -ա-ա, որտեղ - ա- դրական տարր.

Թեորեմ 2.Գծային կարգավորված օղակի դրական տարրերի գումարը և արտադրյալը դրական են:

Ապացույցը վարժություն է։

Թեորեմ 3.Գծային կարգավորված օղակում ցանկացած ոչ զրոյական տարրի քառակուսին դրական է:

Ապացույցը վարժություն է։

Թեորեմ 4.Գծային կարգավորված դաշտում, եթե ա> 0, ապա ա –1 > 0.

Ապացույցը վարժություն է։

Թեորեմ 5. ( Պատվերի չափանիշ) . Մատանի á Ա, +, ×, 0ñ եթե և միայն այն ժամանակ կարող է լինել գծային և խիստ կարգավորված (այսինքն՝ ներմուծել գծային և խիստ կարգ), եթե բազմությունը Աունի ենթաբազմություն Ա+ , բավարարելով պայմանները.

1) ԱÎ Ա + Þ Ա¹ 0 & – ԱÏ Ա + ;

Ա¹ 0 Þ ԱÎ Ա + Ú – ԱÎ Ա + ;

2)ա, բÎ Ա + Þ ա+ բÎ Ա + & աբÎ Ա + .

Ապացույց. Թող նախ á Ա,+,×,0,>ñ – գծային կարգավորված օղակ: Որպես ցանկալի ենթաբազմություն Ա+ այս դեպքում, 1-ին և 2-րդ թեորեմների ուժով, համակարգի բազմաթիվ դրական տարրեր կարող են հայտնվել Ա.

Թող հիմա Ա+-ը b օղակի ենթաբազմություն է Ա,+,×,0ñ՝ բավարարելով թեորեմի պայմանները։ Փորձենք ներմուծել գծային կարգ > á օղակում Ա,+,×,0ñ. Եկեք սահմանենք այս հարաբերությունը հետևյալ կերպ.

Ա > բ Û ա – բ Î Ա + .

Հեշտ է ստուգել, ​​որ մեր ներկայացրած հարաբերությունը կապված է, հակառեֆլեքսիվ, հակասիմետրիկ, անցումային և միատոն՝ կապված որևէ տարրով գումարման և բազմապատկման հետ։ Ա + .

Մի փունջ Ա+ 4-րդ թեորեմի պայմաններում նշված հատկություններով կոչվում են ռինգի դրական մասը á Ա,+,×,0ñ. Հետագայում ցանկացած ռինգում կարգուկանոն մտցնելիս դրանում կփնտրենք «դրական մասը»։ Եթե ​​ռինգում այդպիսի մաս կա, ապա մատանին կարելի է պատվիրել, եթե ոչ, ապա չի կարելի, եթե կան մի քանի նման չհամընկնող դրական մասեր, ապա այն կարելի է պատվիրել մի քանի ձևով։

Վերոնշյալից հետևում է, որ գծային կարգավորված օղակ սահմանելիս, երկուական հարաբերության փոխարեն >, որպես հիմնական հարաբերություն կարելի է վերցնել միանման «դրական մաս»:

Թեորեմ 6. ( Գծային կարգի եզակիության չափանիշ) . Թող Ա+ և Ա++ – օղակի դրական մասեր բ Ա,+,×,0ñ. Հետո

Ա + = Ա ++ Û Ա + Í Ա ++ .

Պահանջներ աքսիոմային համակարգի, Peano աքսիոմներ. Ցանկացած մաթեմատիկական տեսություն աքսիոմատիկորեն կառուցելիս պահպանվում են որոշակի կանոններ. 1) տեսության որոշ հասկացություններ ընտրվում են որպես հիմնական և ընդունվում առանց սահմանման. 2) տեսության յուրաքանչյուր հասկացություն, որը չի պարունակվում հիմնականների ցանկում, տրվում է սահմանում. Դրա իմաստը բացատրում է հիմնականի և նախորդի օգնությամբ տրված հասկացություններ. 3) ձևակերպվում են աքսիոմներ, այսինքն՝ դրույթներ, որոնք տվյալ տեսության մեջ ընդունվում են առանց ապացույցի։ Աքսիոմները բացահայտում են հիմնական հասկացությունների հատկությունները: 4) տեսության յուրաքանչյուր դրույթ, որը չի պարունակվում աքսիոմների ցանկում, պետք է ապացուցված լինի: Նման դրույթները կոչվում են թեորեմներ։ Դրանք ապացուցված են այս մեկին նախորդող աքսիոմների և թեորեմների հիման վրա։

ԱՅԴ. Մաթեմատիկական տեսության կառուցման աքսիոմատիկ մեթոդն անցնում է մի քանի փուլով. 2) հիմնական հարաբերությունների ներդրում (օրինակ՝ անդամակցության հարաբերություն բազմությունների տեսության մեջ). 3) նշելով հիմնական հասկացությունները և հիմնական հարաբերությունները՝ ներմուծվում է այլ հասկացությունների և հարաբերությունների սահմանումը (օրինակ՝ բազմությունների տեսության մեջ՝ միություն, խաչմերուկ, տարբերություն, լրացում հասկացությունները)։

Տեսության աքսիոմատիկ կառուցման մեջ բոլոր պնդումները ստացվում են աքսիոմներից ապացույցներով: Նման տեսության հիմքը աքսիոմների համակարգն է, և աքսիոմային համակարգի վրա դրվում են հատուկ պահանջներ՝ 1) աքսիոմային համակարգը պետք է լինի հետևողական։ Աքսիոմների համակարգը կոչվում է հետևողական, եթե դրանից տրամաբանորեն հնարավոր չէ դուրս բերել երկու միմյանց բացառող դրույթներ: Այլ կերպ ասած, անհնար է բխեցնել մի պնդում և տվյալ հայտարարության ժխտումը, որպեսզի դրանք միաժամանակ ճշմարիտ լինեն: Աքսիոմային համակարգի հետևողականությունը ստուգելու համար բավական է կառուցել այս համակարգի մոդելը: 2) աքսիոմների համակարգը պետք է անկախ լինի. Աքսիոմների համակարգը կոչվում է անկախ, եթե այս համակարգի աքսիոմներից ոչ մեկը այլ աքսիոմների հետևանք չէ: Այլ կերպ ասած, այս համակարգի յուրաքանչյուր աքսիոմա չի կարելի եզրակացնել մյուս աքսիոմներից։ Աքսիոմների համակարգի անկախությունն ապացուցելու համար բավական է կառուցել այս համակարգի մոդելը։ 3) աքսիոմների համակարգը պետք է լինի ամբողջական, այսինքն. Տվյալ տեսության մեջ ընտրված աքսիոմների թիվը պետք է բավարար լինի նոր հասկացություններ, հարաբերություններ ներմուծելու, թեորեմներ ապացուցելու և ամբողջ տեսությունը կառուցելու համար:

Միևնույն տեսությունն աքսիոմատիկորեն կառուցելիս կարող են օգտագործվել աքսիոմների տարբեր համակարգեր, բայց դրանք պետք է լինեն համարժեք։ «Անմիջապես հետևել» կապը վերցված է որպես հիմնական հասկացություն բնական թվերի համակարգի աքսիոմատիկ կառուցման մեջ: Հայտնի են նաև «կոմպլեկտ», «բազմության տարր», տրամաբանության կանոն հասկացությունները։ Տարրը, որը անմիջապես հաջորդում է a տարրին, նշանակվում է a - հիմնական:

«Ուղիղ հետևել» հարաբերությունների էությունը բացահայտվում է հետևյալ աքսիոմներում. 2) բնական թվերի բազմությունից (N) a տարրի համար կա եզակի a տարր: , անմիջապես հաջորդող ա. 3) N-ի a տարրի համար կա առավելագույնը մեկ տարր, որին անմիջապես հաջորդում է a-ն: 4) N ​​բազմության ցանկացած M ենթաբազմություն, որն ունի 1 M հատկություններ, և քանի որ a-ն պարունակվում է M-ում, ի՞նչ է նշանակում a-ն: Մ–ում պարունակվող, համընկնում է N բազմության հետ։

Աքսիոմների թվարկված համակարգերը կոչվում են Պյանո աքսիոմներ։ ԱՅԴ. այն թվերի բազմությունը, որի համար հաստատված է անմիջապես հաջորդ առնչությունը, որը բավարարում է Պյանոյի աքսիոմներին, կոչվում է բնական թվերի բազմություն, իսկ դրա տարրը՝ բնական թիվ։ Չորրորդ աքսիոմը նկարագրում է թվերի բնական շարքի անվերջությունը և կոչվում է ինդուկցիայի աքսիոմ։ Դրա հիման վրա մաթեմատիկական ինդուկցիայի մեթոդով իրականացվում է տարբեր պնդումների ապացույց, որը հետևյալն է՝ ապացուցելու համար, որ տվյալ պնդումը ճիշտ է ցանկացած բնական թվի համար, անհրաժեշտ է՝ 1) ապացուցել, որ այս պնդումը ճշմարիտ է մեկի համար, 2) այն դրույթից, որ պնդումը ճշմարիտ է կամայական k թվի համար, ապացուցեք, որ այն ճիշտ է հաջորդ k թվի համար։

N բազմության սահմանումը ոչինչ չի ասում այս բազմության բնույթի մասին, ինչը նշանակում է, որ այն կարող է լինել ցանկացած բան: Որպես N բազմություն ընտրելով ցանկացած բազմություն, որի վրա տրված է Պեանոյի աքսիոմներին անմիջապես հետևելու և բավարարելու առնչությունը, մենք ստանում ենք այս աքսիոմային համակարգի մոդելը: Նմանատիպ բոլոր մոդելների միջև կարելի է մեկ առ մեկ համապատասխանություն հաստատել: Այս մոդելները կտարբերվեն միայն տարրերի բնույթով, անվանումով և նշանակմամբ: Թիվ՝ 1, 2, 3, 4, 5… 0,00,000,0000,00000,… Ѕ, 1/3, ј, 1/5,