Karte

Zdravo studente. Kako pronaći određeno rješenje DE približno koristeći niz? Redovi. Osnovni koncepti. Neophodan znak konvergencije

power series.

Koristeći redove stepena moguće je integrisati diferencijalne jednadžbe.

Razmotrimo linearnu diferencijalnu jednačinu oblika:

Ako se svi koeficijenti i desna strana ove jednačine prošire u redove stepena koji konvergiraju u određenom intervalu, tada postoji rješenje ove jednačine u nekom malom susjedstvu nulte tačke koje zadovoljava početne uvjete.

Ovo rješenje se može predstaviti nizom stepena:

Da bismo pronašli rješenje, ostaje odrediti nepoznate konstante c i.

Ovaj problem se može riješiti metoda poređenja neizvjesnih koeficijenata. Zamjenjujemo pisani izraz za željenu funkciju u originalnu diferencijalnu jednačinu, izvodeći sve potrebne operacije sa stepenom redova (diferencijacija, sabiranje, oduzimanje, množenje itd.)

Zatim izjednačavamo koeficijente na istim stepenima X na lijevoj i desnoj strani jednačine. Kao rezultat toga, uzimajući u obzir početne uslove, dobijamo sistem jednačina iz kojeg sukcesivno određujemo koeficijente c i.

Imajte na umu da je ova metoda primjenjiva i na nelinearne diferencijalne jednadžbe.

Primjer. Naći rješenje jednačine sa početnim uslovima y(0)=1, y’(0)=0.

Rješenje jednačine tražit ćemo u obliku

Dobivene izraze zamjenjujemo u originalnu jednačinu:

Odavde dobijamo:

………………

Dobijamo zamjenom početnih uslova u izraze za željenu funkciju i njen prvi izvod:

Konačno dobijamo:

Postoji još jedna metoda za rješavanje diferencijalnih jednadžbi pomoću serija. To se zove metoda sekvencijalne diferencijacije.

Pogledajmo isti primjer. Tražit ćemo rješenje diferencijalne jednadžbe u obliku proširenja nepoznate funkcije u Maclaurinov red.

Ako su dati početni uslovi y(0)=1, y’(0)=0 zamijenimo u originalnu diferencijalnu jednadžbu, to ćemo dobiti

Nakon zamjene dobijenih vrijednosti dobijamo:

Fourierova serija.

(Jean Baptiste Joseph Fourier (1768 – 1830) – francuski matematičar)

Trigonometrijski niz.

Definicija. Trigonometrijski niz nazvan nizom oblika:

ili, ukratko,

Realni brojevi a i, b i nazivaju se koeficijenti trigonometrijskog niza.

Ako niz gore prikazanog tipa konvergira, tada je njegov zbir periodična funkcija s periodom 2p, jer funkcije sin nx i cos nx također periodične funkcije sa periodom 2p.

Neka trigonometrijski redovi konvergiraju jednoliko na segmentu [-p; p], pa prema tome na bilo kojem segmentu zbog periodičnosti, a njegov zbir je jednak f(x).

Odredimo koeficijente ove serije.

Za rješavanje ovog problema koristimo sljedeće jednakosti:

Valjanost ovih jednakosti proizilazi iz primjene trigonometrijskih formula na integrand. Pogledajte Integracija trigonometrijskih funkcija za više informacija.

Jer funkcija f(x) je kontinuiran na intervalu [-p; p], onda postoji integral

Ovaj rezultat se dobija kao rezultat činjenice da.

Odavde dobijamo:

Slično, množimo izraz za proširenje funkcije u niz sa sin nx i integrirati u rasponu od -p do p.

Dobijamo:

Izraz za koeficijent a 0 je poseban slučaj za izražavanje koeficijenata a n.

Dakle, ako je funkcija f(x)– bilo koja periodična funkcija perioda 2p, kontinuirana na intervalu [-p; p] ili imaju konačan broj tačaka diskontinuiteta prve vrste na ovom segmentu, tada koeficijenti

postoje i zovu se Fourierovi koeficijenti za funkciju f(x).

Definicija. Blizu Fouriera za funkciju f(x) naziva se trigonometrijski niz čiji su koeficijenti Fourierovi koeficijenti. Ako je Fourierov red funkcije f(x) konvergira mu u svim svojim tačkama kontinuiteta, onda kažemo da je funkcija f(x) proširuje u Fourierov niz.

Dovoljni znaci razgradljivosti u Fourierovom nizu.

Teorema. (Dirichletova teorema) Ako funkcija f(x) ima period od 2p i na segmentu

[-p;p] je kontinuiran ili ima konačan broj tačaka diskontinuiteta prve vrste, a segment

[-p;p] se može podijeliti na konačan broj segmenata tako da unutar svakog od njih funkcija f(x) bude monotona, tada Fourierov red za funkciju f(x) konvergira za sve vrijednosti x, a u tačkama kontinuiteta funkcije f(x) njen zbir je jednak f(x), a u tačkama diskontinuiteta njen zbir je jednak , tj. aritmetička sredina graničnih vrijednosti lijevo i desno. U ovom slučaju, Fourierov red funkcije f(x) ravnomjerno konvergira na bilo kojem segmentu koji pripada intervalu kontinuiteta funkcije f(x).

Poziva se funkcija f(x) za koju su ispunjeni uvjeti Dirichletove teoreme po komadima monotono na segmentu [-p;p].

Teorema. Ako funkcija f(x) ima period od 2p, osim toga, f(x) i njen izvod f'(x) su kontinuirane funkcije na intervalu [-p;p] ili imaju konačan broj diskontinuiteta točaka prva vrsta na ovom intervalu, zatim serija Fourierova funkcija f(x) konvergira za sve vrijednosti x, a u tačkama kontinuiteta njen zbir je jednak f(x), a u tačkama diskontinuiteta jednak je . U ovom slučaju, Fourierov red funkcije f(x) ravnomjerno konvergira na bilo kojem segmentu koji pripada intervalu kontinuiteta funkcije f(x).

Funkcija koja zadovoljava uslove ove teoreme naziva se komadno – glatko na segmentu [-p;p].

Proširenje neperiodične funkcije u Fourierov red.

Problem proširenja neperiodične funkcije u Fourierov red se, u principu, ne razlikuje od proširenja periodične funkcije u Fourierov red.

Recimo funkciju f(x) je zadan na intervalu i na tom intervalu je monoton po komadima. Razmotrimo proizvoljnu periodičnu monotonu funkciju po komadima f 1 (x) sa tačkom 2T ³ ïb-aï, koji se poklapa sa funkcijom f(x) na segmentu .

a - 2T a a b a+2T a + 4T x

Dakle, funkcija f(x) je dodano. Sada funkcija f 1 (x) proširuje u Fourierov niz. Zbir ovog niza u svim tačkama segmenta poklapa se sa funkcijom f(x), one. možemo pretpostaviti da je funkcija f(x) proširen u Fourierov niz na segmentu .

Dakle, ako je funkcija f(x) data na intervalu jednakom 2p, ona se ne razlikuje od proširenja u niz periodične funkcije. Ako je segment na kojem je data funkcija manji od 2p, onda se funkcija proširuje na interval (b, a + 2p) tako da su sačuvani uvjeti za proširenje u Fourierov red.

Uopšteno govoreći, u ovom slučaju, nastavak date funkcije na segment (interval) dužine 2p može se izvesti na beskonačan broj načina, pa će sumi rezultirajućeg niza biti različiti, ali će se poklapati sa datim funkcija f(x) na segmentu.

Fourierov red za parne i neparne funkcije.

Zapazimo sljedeća svojstva parnih i neparnih funkcija:

2) Proizvod dvije parne i neparne funkcije je parna funkcija.

3) Proizvod parnih i neparnih funkcija je neparna funkcija.

Valjanost ovih svojstava može se lako dokazati na osnovu definicije parnih i neparnih funkcija.

Ako je f(x) parna periodična funkcija sa periodom 2p, koja zadovoljava uslove ekspanzije u Fourierov red, onda možemo napisati:

Dakle, za parnu funkciju Fourierov red je napisan:

Slično, dobijamo proširenje Fourierovog reda za neparnu funkciju:

Primjer. Proširite u Fourierov red periodičnu funkciju s periodom T = 2p na intervalu [-p;p].

Zadata funkcija je neparna, stoga tražimo Fourierove koeficijente u obliku:

Definicija. Fourierovi redovi na ortogonalnom sistemu funkcija j 1 (x), j 2 (x), …,jn(x) naziva se niz oblika:

čiji su koeficijenti određeni formulom:

Gdje f(x)= je zbir niza koji uniformno konvergira na segmentu duž ortogonalnog sistema funkcija. f(x) – bilo koja funkcija koja je kontinuirana ili ima konačan broj točaka diskontinuiteta prve vrste na segmentu.

U slučaju ortonormalnog sistema funkcija određuju se koeficijenti:

Kada koristite kompjutersku verziju “ Viši kurs matematike” moguće je pokrenuti program koji proširuje proizvoljnu funkciju u Fourierov niz.

Taylor serija. Maclaurin serija

Neka je funkcija koja se može diferencirati beskonačan broj puta u okolini tačke, tj. ima derivate bilo kojeg reda. Taylorov red funkcije u tački je potencijski red

U posebnom slučaju niza (1.8) naziva se Maclaurinov red:

Postavlja se pitanje: U kojim slučajevima se Taylorov red za funkciju diferenciranu beskonačan broj puta u susjedstvu tačke poklapa sa funkcijom?

Mogu postojati slučajevi kada Taylorov red funkcije konvergira, ali njegov zbir nije jednak

Predstavimo dovoljan uslov za konvergenciju Taylorovog reda funkcije ovoj funkciji.

Teorema 1.4: ako u intervalu funkcija ima derivate bilo kojeg reda i svi su ograničeni u apsolutnoj vrijednosti istim brojem, tj. tada Taylorov red ove funkcije konvergira na za bilo koji od ovih intervala, tj. postoji jednakost

Potrebne su posebne studije da bi se utvrdilo da li ova jednakost vrijedi na krajevima intervala konvergencije.

Treba napomenuti da ako se funkcija proširi u niz stepena, onda je ovaj niz Taylorov (Maclaurin) niz ove funkcije, a ovo proširenje je jedinstveno.

Diferencijalne jednadžbe

Obična diferencijalna jednadžba n-tog reda za funkciju argumenta je relacija oblika

gdje je data funkcija njegovih argumenata.

U nazivu ove klase matematičkih jednadžbi, izraz „diferencijalne“ naglašava da one uključuju derivate (funkcije nastale kao rezultat diferencijacije); izraz “običan” označava da željena funkcija zavisi samo od jednog realnog argumenta.

Obična diferencijalna jednadžba ne mora eksplicitno sadržavati argument željene funkcije i bilo kojeg od njenih izvoda, ali najviši izvod mora biti uključen u jednačinu n-og reda.

Na primjer,

A) - jednačina prvog reda;

B) - jednačina trećeg reda.

Prilikom pisanja običnih diferencijalnih jednadžbi često se koristi notacija za derivacije u terminima diferencijala:

B) - jednačina drugog reda;

D) - jednačina prvog reda koja nakon dijeljenja ekvivalentnim oblikom formira sljedeću jednačinu:

Funkcija se naziva rješenjem obične diferencijalne jednadžbe ako se, kada se u nju zamijeni, pretvori u identitet.

Pronalaženje jednom ili drugom metodom, na primjer, selekcijom, jedne funkcije koja zadovoljava jednačinu ne znači njeno rješavanje. Rješavanje obične diferencijalne jednadžbe znači pronalaženje svih funkcija koje formiraju identitet kada se zamijene u jednadžbu. Za jednadžbu (1.10), porodica takvih funkcija se formira pomoću proizvoljnih konstanti i naziva se općim rješenjem obične diferencijalne jednadžbe n-tog reda, a broj konstanti se poklapa sa redoslijedom jednadžbe: Opće rješenje možda neće biti eksplicitno razriješen u odnosu na U ovom slučaju, rješenje se obično naziva općim integralom jednačine (1.10).

Dodeljivanjem nekih dozvoljenih vrednosti svim proizvoljnim konstantama u opštem rešenju ili u opštem integralu, dobijamo određenu funkciju koja više ne sadrži proizvoljne konstante. Ova funkcija se naziva parcijalno rješenje ili parcijalni integral jednadžbe (1.10). Za pronalaženje vrijednosti proizvoljnih konstanti, a samim tim i određenog rješenja, koriste se različiti dodatni uvjeti za jednadžbu (1.10). Na primjer, takozvani početni uslovi mogu se specificirati na:

Na desnoj strani početnih uslova (1.11) navedene su numeričke vrijednosti funkcije i izvoda, a ukupan broj početnih uslova jednak je broju definisanih proizvoljnih konstanti.

Problem pronalaženja određenog rješenja jednačine (1.10) na osnovu početnih uslova naziva se Cauchyjev problem.

Integriranje diferencijalnih jednadžbi pomoću niza

U opštem slučaju, nemoguće je pronaći tačno rešenje obične diferencijalne jednačine prvog reda (ODE) njenom integracijom. Štaviše, ovo nije izvodljivo za ODE sistem. Ova okolnost je dovela do stvaranja velikog broja približnih metoda za rješavanje ODE-a i njihovih sistema. Među aproksimativnim metodama mogu se izdvojiti tri grupe: analitičke, grafičke i numeričke. Naravno, takva klasifikacija je u određenoj mjeri proizvoljna. Na primjer, grafička metoda Eulerovih izlomljenih linija leži u osnovi jedne od metoda za numeričko rješavanje diferencijalne jednadžbe.

Integracija ODE-a korištenjem nizova stepena je približna analitička metoda, koja se obično primjenjuje na linearne jednačine najmanje drugog reda. Radi jednostavnosti, ograničavamo se na razmatranje linearne homogene ODE drugog reda s promjenjivim koeficijentima

Napomena: prilično široka klasa funkcija može biti predstavljena u obliku

gdje su neke konstante. Ovaj izraz se naziva potencijskim redom.

Pretpostavimo da se funkcije mogu proširiti u nizove koji konvergiraju u intervalu:

Vrijedi sljedeća teorema (izostavljajući dokaz, iznosimo samo njegovu formulaciju).

Teorema 1.5: ako funkcije imaju oblik (1.13), tada se svako rješenje ODE (1.12) može predstaviti kao niz stepena koji konvergira na:

Ova teorema ne samo da omogućava da se rješenje predstavi u obliku stepena reda, već, što je najvažnije, opravdava konvergenciju reda (1.14). Radi jednostavnosti stavljamo (1.13) i (1.14) i tražimo rješenje za ODE (1.12) u obliku

Zamjenom (1.15) u (1.12) dobijamo jednakost

Za ispunjenje (1.16) potrebno je da koeficijent za svaki stepen bude jednak nuli.

Iz ovog uslova dobijamo beskonačan sistem linearnih algebarskih jednačina

iz kojih se sukcesivno mogu pronaći ako se zadaju vrijednosti i (u slučaju Cauchyjevog problema za ODE (1.12), one su uključene u početne uslove).

Ako su funkcije racionalne, tj.

gdje su polinomi, onda u blizini tačaka u kojima rješenje u obliku stepena niza možda ne postoji, a ako postoji, može divergirati svuda osim u tački.Ova okolnost je bila poznata L. Euleru, koji je razmatrao jednačinu prvog reda

Ova jednačina je zadovoljena redovima stepena

Međutim, nije teško uočiti da se ova serija za bilo koga razlikuje

Rješenje ODE u obliku divergentnog niza stepena naziva se formalno.

MINISTARSTVO OBRAZOVANJA I NAUKE REPUBLIKE KAZAHSTAN

Državni univerzitet Sjevernog Kazahstana

njima. M. Kozybaeva

Fakultet informacionih tehnologija

Odsjek za matematiku

Radovi zaštićeni

sa ocjenom "___________"

"___"___________ godina 2013

glava odjel____________

A. Tadzhigitov

PREDMETNI rad iz matematike

„INTEGRACIJA DIFERENCIJALNIH JEDNAČINA

KORIŠĆENJE SERIJE SNAGE"

ŠEF: Valeeva M.B. ___________

Petropavlovsk 2013

ADAPTA

Berilgen kurstyk zhumysta qatarlarmen zhane diferencijali tendemelermen baylanysty theorylyk suraktar karastyrylgan. Diferencijali integralnog dauynyn mysaldary zhəne manganaz qatarlardyn komegimen karastyrylgan.

ANOTATION

Ovaj rad ispituje teorijska pitanja vezana za redove i diferencijalne jednadžbe. Razmatraju se primjeri integracije diferencijalnih jednadžbi korištenjem nizova stepena.

dati rad se smatraju teorijskim pitanjima koja se odnose na redove i diferencijalne jednadžbe. Razmatraju se primjeri integracionih parcijalnih diferencijalnih jednadžbi pomoću nizova stepena.

UVOD

OSNOVNI POJMOVI U VEZI SREDOVA I DIFERENCIJALNIH JEDNAČINA

1 reda. Osnovni koncepti. Neophodan znak konvergencije

2 Power series. Svojstva potencijskog reda

3 Taylor Row. Maclaurin serija

4 Diferencijalne jednadžbe

5 Integracija diferencijalnih jednadžbi pomoću serija

PRIMJERI UPOTREBE POstepenih redova U INTEGRIRANJU DIFERENCIJALNIH JEDNAČINA

1 Airy jednadžba

2 Beselova jednačina

3 Primjeri integracije

4 Primjeri integracije u Maple-u

ZAKLJUČAK

UVOD

Termin "diferencijalna jednačina" dolazi od Leibniza (1676, objavljen 1684). Početak istraživanja diferencijalnih jednačina datira još iz vremena Leibniza i Newtona, u čijim su radovima proučavani prvi problemi koji su doveli do takvih jednačina. Leibniz, Newton, braća J. i I. Bernoulli razvili su metode za integraciju običnih diferencijalnih jednačina. Kao univerzalna metoda korištena su proširenja integrala diferencijalnih jednadžbi u redove stepena.

U današnje vrijeme, široko rasprostranjeno uvođenje računskih metoda u nauku, povezano s pojavom računarskih alata velike snage, zahtijeva ponovnu procjenu značaja različitih grana matematike, a posebno dijelova teorije običnih diferencijalnih jednačina. Trenutno je sve veći značaj metoda za kvalitativno istraživanje rješenja diferencijalnih jednačina, kao i metoda za približno pronalaženje rješenja.

Rješenja mnogih diferencijalnih jednadžbi nisu izražena u elementarnim funkcijama ili kvadraturama. U tim slučajevima se koriste aproksimativne metode za integraciju diferencijalnih jednadžbi. Jedna takva metoda je predstavljanje rješenja jednadžbe kao niz stepena; zbir konačnog broja članova ovog niza će biti približno jednak željenom rješenju. Ovo određuje relevantnost odabrane teme istraživanja.

Svrha ovog rada: pokazati upotrebu metode stepena redova u integraciji diferencijalnih jednadžbi.

Predmet istraživanja je proces integracije diferencijalnih jednadžbi metodom stepena redova.

Predmet istraživanja su oblici, metode i sredstva integracije diferencijalnih jednadžbi po stepenu niza.

U skladu sa ciljem, glavni ciljevi ovog rada mogu se formulisati:

Pregledajte osnovne koncepte vezane za redove i diferencijalne jednadžbe.

Analizirati metodu integracije diferencijalnih jednadžbi koristeći redove stepena.

Primijenite metodu potencijskog niza za rješavanje raznih problema.

Struktura rada: naslovna strana, obrazac za rad, sažetak, sadržaj, uvod, glavni dio, zaključak, lista literature.

Glavni dio rada sastoji se od dva poglavlja. Prvo poglavlje otkriva koncepte redova, nizova stepena, Taylorovog reda i diferencijalnih jednadžbi. U drugom poglavlju razmatraju se primjeri integracije diferencijalnih jednadžbi po stepenu niza.

Za proučavanje teorijskog dijela rada korišteni su materijali iz nastavne literature i periodike koji su navedeni u popisu korištene literature.

Obim rada: 26 strana.

1. OSNOVNI POJMOVI KOJI SE ODNOSE NA REDOVNE I DIFERENCIJALNE JEDNAČINE

1.1 Redovi. Osnovni koncepti. Neophodan znak konvergencije

U matematičkim aplikacijama, kao iu rješavanju nekih problema u ekonomiji, statistici i drugim oblastima, uzimaju se u obzir zbirovi sa beskonačnim brojem pojmova. Ovdje ćemo dati definiciju šta se podrazumijeva pod takvim iznosima.

Neka je dat beskonačan niz brojeva. Brojevni niz ili jednostavno niz je izraz (zbir) oblika

,(1.1)

brojevi se nazivaju članovi niza, zajednički ili n-ti član serije.

Za definiranje niza (1.1) dovoljno je navesti funkciju prirodnog argumenta izračunavanja n-tog člana niza njegovim brojem

Primjer 1.1. Neka . Red

(1.2)

naziva se harmonijski niz.

Od članova serije (1.1) formiramo numerički niz parcijalnih suma Gdje - zbir prvih članova niza, koji se naziva n-ti parcijalni zbir, tj.

(1.3)

Redoslijed brojeva uz neograničeno povećanje broja može:

) imaju konačan limit;

) nemaju konačnu granicu (granica ne postoji ili je jednaka beskonačnosti).

Niz (1.1) naziva se konvergentan ako niz njegovih parcijalnih suma (1.3) ima konačan limit, tj.

U ovom slučaju, broj se naziva zbir serije (1.1) i zapisuje se

Niz (1.1) se naziva divergentnim ako niz njegovih parcijalnih suma nema konačan limit. Divergentnom nizu nije dodijeljen zbir.

Dakle, problem nalaženja zbira konvergentnog niza (1.1) je ekvivalentan izračunavanju granice niza njegovih parcijalnih suma.

Dokaz teoreme slijedi iz činjenice da , i ako

S je onda zbir serije (1.1).

Uslov (1.4) je neophodan, ali ne i dovoljan uslov za konvergenciju reda. To jest, ako zajednički član niza teži nuli na , to ne znači da niz konvergira. Na primjer, za harmonijski niz (1.2)

međutim, to se razlikuje.

Posljedica (dovoljan znak divergencije niza): ako zajednički član niza ne teži nuli, onda se ovaj niz divergira.

Primjer 1.2. Ispitajte konvergenciju serije

Za ovu seriju Stoga se ova serija razlikuje.

1.1 1.2 Serija snage. Svojstva potencijskog reda

Snažni redovi su poseban slučaj funkcionalnih serija.

Potencijski niz je funkcionalni niz oblika

ovdje su konstantni realni brojevi koji se nazivaju koeficijenti niza stepena;

Neki konstantni broj;

Varijabla koja uzima vrijednosti iz skupa realnih brojeva.

Kada stepen stepena (1.5) poprimi oblik

(1.6)

Niz stepena (1.5) naziva se niz stepena razlike, a red (1.6) je niz stepena. Ako se promenljivoj dodeli bilo koja vrednost, onda se niz stepena (1.5) (ili (1.6)) pretvara u broj nizovi koji se mogu konvergirati ili divergirati.

Područje konvergencije niza stepena je skup vrijednosti na kojima konvergira niz stepena.

Teorema 1.2 (Abelov teorem): ako se red stepena (1.6) konvergira u tada on apsolutno konvergira za sve vrijednosti koje zadovoljavaju nejednakost, ali ako se red (1.6) divergira u tada divergira za sve vrijednosti koje zadovoljavaju nejednakost

Abelov teorem daje jasnu predstavu o strukturi područja konvergencije potencijskog reda.

Teorema 1.3: područje konvergencije niza stepena (1.6) poklapa se sa jednim od sljedećih intervala:

) ; 2) ; 3) ; 4) ,

gdje je neki nenegativni realni broj ili

Broj se naziva radijus konvergencije, interval se naziva interval konvergencije stepena reda (1.6).

Ako tada interval konvergencije predstavlja cijelu brojevnu pravu

Ako tada interval konvergencije degeneriše do tačke

Napomena: ako je interval konvergencije za niz stepena (1.2), onda - interval konvergencije za niz stepena (1.5).

Iz teoreme 1.3 proizilazi da je za praktično pronalaženje područja konvergencije niza stepena (1.6) dovoljno pronaći njegov polumjer konvergencije i razjasniti pitanje konvergencije ovog niza na krajevima intervala konvergencije, tj. at and

Radijus konvergencije niza stepena može se pronaći pomoću jedne od sljedećih formula:

d'Alembertova formula:

Cauchy formula:

Primjer 1.3. Pronađite radijus konvergencije, interval konvergencije i područje konvergencije stepena niza

Nađimo radijus konvergencije ovog niza koristeći formulu

U našem slučaju

Posljedično, interval konvergencije ovog niza ima oblik

Proučimo konvergenciju niza na krajevima intervala konvergencije.

koji se razilazi kao harmonijski niz.

Kada se niz stepena pretvori u niz brojeva

Ovo je naizmjenični niz, čiji članovi smanjuju apsolutnu vrijednost i

Prema tome, prema Leibnizovom kriteriju, ovaj brojni niz konvergira.

Dakle, interval je područje konvergencije datog niza stepena.

Red stepena (1.6) je funkcija definisana u intervalu konvergencije, tj.

Evo nekih svojstava funkcije:

Svojstvo 1. Funkcija je kontinuirana na bilo kojem segmentu koji pripada intervalu konvergencije

Svojstvo 2. Funkcija je diferencibilna na intervalu i njen izvod se može naći diferenciranjem niza (1.6) po članu, tj.

za sve

Svojstvo 3. Neodređeni integral funkcije za sve može se dobiti počlanom integracijom niza (1.6), tj.

za sve

Treba napomenuti da se diferencijacijom po članu i integracijom stepena niza njegov polumjer konvergencije ne mijenja, ali se njegova konvergencija na krajevima intervala može promijeniti.

Navedena svojstva vrijede i za redove stepena (1.5).

Primjer 1.4. Razmotrimo redove snage

Područje konvergencije ovog niza, kao što je prikazano u primjeru 1.3, je interval

Hajde da razlikujemo ovu seriju pojam po pojam:

(1.7)

Proučimo ponašanje ove serije na krajevima intervala konvergencije.

Ovaj brojčani niz divergira jer nije ispunjen nužni kriterij konvergencije

koji ne postoji.

Kada se niz stepena (1.7) pretvori u niz brojeva

koji takođe divergira jer nije zadovoljen nužni kriterijum konvergencije.

Posljedično, područje konvergencije redova stepena dobijenih diferencijacijom po članu originalnog niza stepena se promijenilo i poklapa se s intervalom .

1.3 Taylor serija. Maclaurin serija

Neka je funkcija koja se može diferencirati beskonačan broj puta u okolini tačke, tj. ima derivate bilo kog reda. Taylorov red funkcije u tački je potencijski red

(1.8)

U posebnom slučaju niza (1.8) naziva se Maclaurinov red:

Postavlja se pitanje: U kojim slučajevima se Taylorov red za funkciju diferenciranu beskonačan broj puta u okolini tačke poklapa sa funkcijom?

Mogu postojati slučajevi kada Taylorov red funkcije konvergira, ali njegov zbir nije jednak

Predstavimo dovoljan uslov za konvergenciju Taylorovog reda funkcije ovoj funkciji.

Teorema 1.4: ako je u intervalu funkcija ima derivate bilo kojeg reda i svi su ograničeni u apsolutnoj vrijednosti na isti broj, tj. tada Taylorov red ove funkcije konvergira na za bilo koji od ovih intervala one. postoji jednakost

Potrebne su posebne studije da bi se utvrdilo da li ova jednakost vrijedi na krajevima intervala konvergencije.

Treba napomenuti da ako se funkcija proširi u niz stepena, onda je ovaj niz Taylorov (Maclaurin) niz ove funkcije, a ovo proširenje je jedinstveno.

1.4 Diferencijalne jednadžbe

Obična diferencijalna jednadžba n-tog reda za funkciju argumenta je relacija oblika

gdje je data funkcija njegovih argumenata.

Obična diferencijalna jednadžba ne mora eksplicitno sadržavati argument željene funkcije i bilo kojeg od njenih izvoda, ali najviši izvod mora biti uključen u jednačinu n-og reda.

Na primjer,

A) - jednačina prvog reda;

B) - jednačina trećeg reda.

Prilikom pisanja običnih diferencijalnih jednadžbi često se koristi notacija za derivacije u terminima diferencijala:

IN) - jednačina drugog reda;

G) - jednačina prvog reda koja, nakon dijeljenja ekvivalentnim oblikom, formira sljedeću jednačinu:

Funkcija se naziva rješenjem obične diferencijalne jednadžbe ako se, kada se u nju zamijeni, pretvori u identitet.

Na desnoj strani početnih uslova (1.11) navedene su numeričke vrijednosti funkcije i izvoda, a ukupan broj početnih uslova jednak je broju definisanih proizvoljnih konstanti.

Problem pronalaženja određenog rješenja jednačine (1.10) na osnovu početnih uslova naziva se Cauchyjev problem.

1.5 Integracija diferencijalnih jednadžbi pomoću serija

(1.12)

Napomena: prilično široka klasa funkcija može biti predstavljena u obliku

gdje su neke konstante. Ovaj izraz se naziva potencijskim redom.

Pretpostavimo da se funkcije mogu proširiti u nizove koji konvergiraju u intervalu:

Vrijedi sljedeća teorema (izostavljajući dokaz, iznosimo samo njegovu formulaciju).

Teorema 1.5: ako funkcije imaju oblik (1.13), tada se svako rješenje ODE (1.12) može predstaviti kao niz stepena koji konvergira na:

(1.14)

(1.15)

Zamjenom (1.15) u (1.12) dobijamo jednakost

Za ispunjenje (1.16) potrebno je da koeficijent za svaki stepen bude jednak nuli.

Iz ovog uslova dobijamo beskonačan sistem linearnih algebarskih jednačina

iz kojih se sukcesivno mogu pronaći ako se zadaju vrijednosti i (u slučaju Cauchyjevog problema za ODE (1.12) one su uključene u početne uslove ).

Ako su funkcije racionalne, tj.

Ova jednačina je zadovoljena redovima stepena

Međutim, nije teško uočiti da se ova serija za bilo koga razlikuje

Rješenje ODE u obliku divergentnog niza stepena naziva se formalno.

2. PRIMJERI KORIŠĆENJA STEPENOG REDOVA PRI INTEGRIRANJU DIFERENCIJALNIH JEDNAČINA

Airy equation

Rješenje Airyjeve jednačine

Tražićemo u obliku stepena niza (1.15). Tada će jednakost (1.16) poprimiti oblik

Koeficijent za je jednak Prema tome, Pošto je koeficijent jednak nuli, nalazimo da je koeficijent za jednak Odavde

Iz ove formule dobijamo

Slično nalazimo

Šanse ostaju neizvjesne. Da bismo pronašli osnovni sistem rješenja, prvo postavljamo a zatim obrnuto. U prvom slučaju imamo

iu drugom

Na osnovu teoreme 1.5, ovi redovi su konvergentni svuda na brojevnoj pravoj

Funkcije se zovu Airy funkcije. Za velike vrijednosti, asimptotičko ponašanje ovih funkcija opisuje se formulama

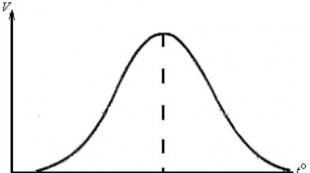
Grafikoni ovih funkcija prikazani su na slici 1.

Slika 1

Sa neograničenim povećanjem, nule bilo kojeg rješenja Airyeve jednadžbe se neograničeno približavaju jedna drugoj, što je vidljivo iz asimptotičkog prikaza ovih rješenja, ali uopće nije očito iz reprezentacije Airyjevih funkcija u obliku konvergentne snage serije. Iz toga slijedi da je metoda traženja rješenja ODE pomoću niza, općenito govoreći, od male koristi pri rješavanju primijenjenih problema, a sam prikaz rješenja u obliku serije otežava analizu kvalitativnih svojstava. dobijenog rastvora.

2.1 Beselova jednačina

Linearna diferencijalna jednadžba sa promjenjivim koeficijentima, koja ima oblik

nazvana Besselova jednačina.

Rješenje jednačine (2.1) tražit ćemo u obliku generaliziranog niza stepena, tj. proizvodi nekog stepena na stepskoj seriji:

(2.2)

Zamjenom generaliziranog niza stepena u jednačinu (2.1) i izjednačavanjem koeficijenata za svaki stepen na lijevoj strani jednačine na nulu, dobijamo sistem

Pod pretpostavkom da iz ovog sistema nalazimo Neka onda iz druge jednačine sistema nalazimo i iz jednačine koja daje vrijednosti 3,5,7,..., zaključujemo da za koeficijente s parnim brojevima dobijamo izraze

Zamjenom pronađenih koeficijenata u niz (2.2) dobijamo rješenje

pri čemu koeficijent ostaje proizvoljan.

Jer svi se koeficijenti određuju na sličan način samo u slučaju kada nije jednak cijelom broju. Tada se rješenje može dobiti zamjenom vrijednosti u prethodnom rješenju sa:

Rezultirajući redovi snaga konvergiraju za sve vrijednosti , što se lako utvrđuje na osnovu D'Alembertovog testa. Rješenja i su linearno nezavisna, jer njihov omjer nije konstantan.

Rješenje pomnoženo konstantom naziva se Besselova funkcija (ili cilindrična funkcija) reda prve vrste i označava se simbolom Rješenje se označava

Općenito prihvaćen izbor konstante uključuje gama funkciju, koja je određena nepravilnim integralom:

Prema tome, opšte rješenje jednačine (2.1) za necijeli broj ima oblik gdje i su proizvoljne konstante.

2.2 Primjeri integracije

U slučajevima kada jednačina zahtijeva rješavanje Cauchyjevog problema pod početnim uvjetom, rješenje se može tražiti korištenjem Taylorovog reda:

gdje se daljnji derivati nalaze uzastopnim diferenciranjem izvorne jednadžbe i zamjenom u rezultat diferencijacije umjesto vrijednosti i svih ostalih pronađenih naknadnih izvoda. Slično, jednačine višeg reda mogu se integrirati korištenjem Taylorovog reda.

Primjer 2.1. Približno integrirajte jednačinu koristeći Taylorov red tako što ćete uzeti prvih šest članova ekspanzije koji nisu nula.

Iz jednačine početnih uslova nalazimo Diferencirajući ovu jednačinu, dobijamo sukcesivno

Vjerovanje i korištenje značenja dosljedno nalazimo da traženo rješenje ima oblik

Primjer 2.2. Pronađite prva četiri (ne-nula) člana ekspanzije. I

Zamjenom pronađenih vrijednosti u niz (2.3) dobijamo željeno rješenje sa navedenom tačnošću:

2.3 Primjeri integracije u Maple-u

Da biste pronašli analitička rješenja diferencijalnih jednačina u Mapleu, koristite naredbu dsolve(eq,var,options), gdje je eq diferencijalna jednadžba, var su nepoznate funkcije, opcije su parametri. Parametri mogu ukazivati na metodu za rješavanje problema, na primjer, po defaultu se traži analitičko rješenje: type=exact. Prilikom sastavljanja diferencijalnih jednadžbi, naredba diff se koristi za označavanje izvoda, na primjer, diferencijalna jednačina se piše u obliku: diff(y(x),x$2)+y(x)=x.

Da biste pronašli približno rješenje diferencijalne jednadžbe u obliku stepena niza, u naredbi dsolve trebate navesti parametar type=series (ili jednostavno serija) nakon varijabli. Da bi se označio redosled dekompozicije, tj. Redosledu stepena do kojeg se vrši dekompozicija treba da prethodi definicija redosleda sa naredbom Order:=n.

Ako se opće rješenje diferencijalne jednadžbe traži u obliku proširenja niza stepena, tada će koeficijenti na potencijama pronađene ekspanzije sadržavati nepoznate vrijednosti funkcije na nuli i njenih derivata, itd. Izraz dobiven u izlaznoj liniji imat će oblik sličan proširenju željenog rješenja u Maclaurinov red, ali s različitim koeficijentima za potencije. Da bi se izolovalo određeno rešenje, moraju se specificirati početni uslovi, itd., a broj ovih početnih uslova mora da se poklapa sa redosledom odgovarajuće diferencijalne jednačine.

Proširenje u niz stepena je serijskog tipa, tako da ga za dalji rad sa ovim nizom treba konvertovati u polinom pomoću naredbe convert(%,polynom), a zatim odabrati desnu stranu rezultirajućeg izraza pomoću rhs( %) komanda.

> cond:=y(0)=1, D(y)(0)=1, (D@@2)(y)(0)=1;

> dsolve((de,cond),y(x));

> y1:=rhs(%):

> dsolve((de,kond),y(x),serija);

Napomena: tip rješenja diferencijalne jednadžbe u obliku niza je serija, pa se za daljnju upotrebu takvog rješenja (proračuni ili crtanje) mora konvertovati u polinom pomoću naredbe convert.

stepen serije diferencijalnih jednačina

> pretvoriti(%, polinom): y2:=rhs(%):

> p1:=ploča(y1, x=-3..3, debljina=2, boja=crna):

> p2:=plot(y2, x=-3..3, stil linije=3, debljina=2, boja=crna):

> with(plots): display(p1,p2);

Slika 2 pokazuje da se najbolja aproksimacija tačnog rješenja nizom stepena postiže približno u intervalu

Slika 2

ZAKLJUČAK

Ciljevi postavljeni u nastavnom radu su u potpunosti ostvareni, riješeni su sljedeći zadaci:

Definirani su osnovni koncepti vezani za redove i diferencijalne jednadžbe.

Razmatra se metoda integracije diferencijalnih jednadžbi korištenjem niza stepena.

Problemi na ovu temu su riješeni.

U ovom predmetnom radu gradi se i sistematizovano za korišćenje studentima tokom samostalnog izučavanja metode integracije diferencijalnih jednačina korišćenjem niza stepena. Razmatraju se koncepti serija i diferencijalnih jednačina. Približni proračuni su izvršeni pomoću serija.

Rad se može koristiti kao nastavno sredstvo studentima tehničkih i matematičkih specijalnosti.

Rezultati rada mogu poslužiti kao osnova za dalja istraživanja.

LISTA KORIŠTENE REFERENCE

1 Tricomi F. Diferencijalne jednadžbe. Prevod sa engleskog. - M.: Bukinist, 2003. - 352 str.

Vlasova B. A., Zarubin B. S., Kuvyrkin G. N. Približne metode matematičke fizike: Udžbenik za univerzitete. - M.: Izdavačka kuća MSTU im. N. E. Bauman, 2001. - 700 str.

Budak B. M. Fomin S. V. Višestruki integrali i serije. - M.: Fizmatlit, 2002. - 512 str.

Demidovich B.P. Zbirka zadataka i vježbi iz matematičke analize. - M.: Izdavačka kuća Mosk. Univerzitet CheRo, 2000. - 624 s.

Krasnov M. L., Kiselev A. I., Makarenko G. I., itd. Sva viša matematika: Udžbenik. T. 3. - M.: Izdavačka kuća Editorial URSS, 2005. - 240 str.

Yablonsky A. I., Kuznetsov A. V., Shilkina E. I. i dr. Viša matematika: Opšti kurs: Udžbenik. - M.: Više. škola, 2000.- 351 str.

Malakhov A. N., Maksyukov N. I., Nikishkin V. A. Viša matematika. - M.: EAOI, 2008. - 315 str.

Markov L. N., Razmyslovich G. P. Viša matematika. Dio 2. Osnove matematičke analize i elementi diferencijalnih jednačina. - M.: Amalfeya, 2003. - 352 str.

Agafonov S. A., German A. D., Muratova T. V. Diferencijalne jednadžbe. - M.: Izdavačka kuća MSTU im. N.E. Bauman, 2004. - 352 str.

Coddington E. A., Levinson N. Teorija običnih diferencijalnih jednadžbi. - M.: Amalfeya, 2001. - 475 str.

Fikhtengolts G. M. Kurs diferencijalnog i integralnog računa. T. 2. - M.: Fizmatlit, 2001. - 810 str.

Kako pronaći određeno rješenje DE približno koristeći niz?

Nastavljajući proučavanje praktične primjene teorije serija, razmotrimo još jedan uobičajeni problem, čiji naziv vidite u naslovu. I, da se ne bismo osjećali kao kosilica tokom čitave lekcije, hajde da odmah shvatimo suštinu zadatka. Tri pitanja i tri odgovora:

Šta treba da nađete? Posebno rješenje diferencijalne jednadžbe. Nagovještaj između redova šapuće da je do ovog trenutka preporučljivo barem razumjeti o čemu se radi diferencijalna jednadžba i šta je njegovo rešenje.

KAKO je potrebno ovo rješenje? Otprilike - koristeći seriju.

I treće logično pitanje: zašto otprilike? Već sam obradio ovo pitanje na času. Euler i Runge-Kutta metode, ali ponavljanje neće škoditi. Budući da sam pristalica specifičnosti, vratit ću se na najjednostavnije diferencijalna jednadžba. Na prvom predavanju o difuzerima pronađeno je njegovo opšte rešenje (skup eksponencijala) i posebno rešenje koje odgovara početnom uslovu. Grafikon funkcije je najčešća linija koju je lako prikazati na crtežu.

Ali ovo je elementaran slučaj. U praksi postoji veliki broj diferencijalnih jednadžbi koje se ne mogu točno riješiti analitički (barem trenutno poznatim metodama). Drugim riječima, kako god izvrtali takvu jednačinu, neće je biti moguće integrirati. A kvaka je u tome opće rješenje (familija linija na ravni) može postojati. I tada u pomoć priskaču metode računske matematike.

Upoznajmo našu radost!

Tipičan problem je formuliran na sljedeći način:

… , koji zadovoljava početni uslov, u obliku tri (rjeđe – četiri ili pet) različiti od nule pojmovi Taylor serija.

Traženo određeno rješenje se proširuje u ovu seriju prema dobro poznatoj formuli:

Jedino što se umjesto slova “ef” ovdje koristi “igrek” (tako se događa).

Ideja i značenje su takođe poznati: za neke difuzore i pod određenim uslovima (nećemo ulaziti u teoriju) ugrađen niz stepena će konvergirati do željenog konkretnog rješenja. To jest, što više članova serije razmatramo, to će graf odgovarajućeg polinoma tačnije aproksimirati graf funkcije.

Treba napomenuti da se gore navedeno odnosi na najjednostavnije slučajeve. Provedimo jednostavnu dječju studiju na istoj kahlici:

Primjer 1

Naći približno parcijalno rješenje diferencijalne jednadžbe koje zadovoljava početni uvjet u obliku prva četiri člana Taylorovog reda različita od nule.

Rješenje: u uslovima ovog problema, stoga se opšta Tejlorova formula transformiše u poseban slučaj Proširenje Maclaurin serije:

Gledajući malo unaprijed, reći ću da je u praktičnim zadacima ova kompaktnija serija mnogo češća.

Unesite obje radne formule u svoju referentnu knjigu.

Hajde da razumemo značenja. Pogodno je numerisati faze rješenja:

0) U nultom koraku zapisujemo vrijednost koja je uvijek poznata iz uslova. U bilježnici je preporučljivo zaokružiti konačne rezultate bodova tako da su jasno vidljivi i da se ne izgube u rješenju. Iz tehničkih razloga, zgodnije mi je da ih istaknem podebljanim slovima. osim toga, imajte na umu da ova vrijednost nije nula! Na kraju krajeva, uslov zahtijeva pronalaženje četiri ne-nulačlanovi serije.

1) Hajde da izračunamo. Da biste to učinili, zamijenite poznatu vrijednost u desnu stranu originalne jednadžbe umjesto "y":

2) Hajde da izračunamo. Prvo nađemo drugi derivat:

Vrijednost pronađenu u prethodnom pasusu zamjenjujemo na desnu stranu:

Već imamo tri različita od nule člana ekspanzije, potreban nam je još jedan:

Primjer 2

Pronađite približno parcijalno rješenje diferencijalne jednadžbe , zadovoljavajući početni uslov u obliku prva tri različita od nule člana Tejlorovog reda.

Rješenje počinje standardnom frazom:

U ovom problemu, dakle:

Sada uzastopno pronalazimo vrijednosti - dok se ne dobiju tri ne-nula rezultat. Ako budete imali sreće, oni će biti drugačiji od nule – ovo je idealan slučaj sa minimalnom količinom posla.

Skratimo tačke rješenja:

0) Po uslovu. Evo prvog uspjeha.

1) Hajde da izračunamo. Prvo, riješimo originalnu jednačinu u odnosu na prvi izvod, odnosno izrazimo . Zamijenimo poznate vrijednosti u desnu stranu:

Dobili smo volan i to nije dobro, jer nas zanima ne-nula značenja. Međutim, nula - isti rezultat, koje ne zaboravljamo zaokružiti ili istaknuti na neki drugi način.

2) Pronađite drugi izvod i zamijenite poznate vrijednosti u desnu stranu:

Drugi je „nije nula“.

3) Pronađite izvod drugog izvoda:

Generalno, zadatak pomalo podsjeća na priču o repi, kada djed, baka i unuka u pomoć zovu bubu, mačku itd. A zapravo, svaki sljedeći derivat se izražava kroz svoje „prethodnike“.

Zamijenimo poznate vrijednosti u desnu stranu:

Treća vrijednost različita od nule. Izvukli su repu.

Pažljivo i pažljivo zamijenite "podebljane" brojeve u našu formulu:

Odgovori: željena približna ekspanzija određenog rješenja:

U razmatranom primjeru na drugom mjestu je bila samo jedna nula, i to nije tako loše. Općenito, nule se mogu pojaviti koliko god želite i bilo gdje. Ponavljam, vrlo je važno istaknuti ih uz rezultate koji nisu nula, kako se ne bi zbunili u zamjenama u završnoj fazi.

Izvolite - bagel je na prvom mjestu:

Primjer 3

Naći približno parcijalno rješenje diferencijalne jednadžbe koje odgovara početnom uvjetu u obliku prva tri člana Taylorovog reda različita od nule.

Približan primjer zadatka na kraju lekcije. Tačke algoritma možda neće biti numerisane (ostavljajući, na primjer, prazne linije između koraka), ali preporučujem početnicima da se pridržavaju strogog predloška.

Zadatak koji se razmatra zahtijeva povećanu pažnju - ako pogriješite u bilo kojem koraku, onda će i sve ostalo biti pogrešno! Stoga bi vaša bistra glava trebala raditi kao sat. Avaj, ovo nije integrali ili difuzori, koji se mogu pouzdano riješiti čak iu zamornom stanju, jer omogućavaju efikasnu provjeru.

U praksi je mnogo češći Proširenje Maclaurin serije:

Primjer 4

Rješenje: u principu, možete odmah zapisati Maclaurin ekspanzija, ali je akademskije početi formalizirati problem s općim slučajem:

Proširivanje određenog rješenja diferencijalne jednadžbe pod početnim uvjetom ima oblik:

U ovom slučaju, dakle:

0) Po uslovu.

Pa šta možeš... Nadajmo se da će biti manje nula.

1) Hajde da izračunamo. Prvi derivat je već spreman za upotrebu. Zamijenimo vrijednosti:

2) Nađimo drugi izvod:

I zamenimo to:

Stvari su išle dobro!

3) Pronađite . Zapisat ću to vrlo detaljno:

Imajte na umu da se uobičajena algebarska pravila primjenjuju na derivate: dovođenje sličnih pojmova u posljednjem koraku i zapisivanje proizvoda kao stepena: (ibid.).

Zamenimo sve što je stečeno mukotrpnim radom:

Rađaju se tri vrijednosti različite od nule.

Zamjenjujemo "podebljane" brojeve u Maclaurinovu formulu, čime dobijamo približnu ekspanziju određenog rješenja:

Odgovori:

Da to riješite sami:

Primjer 5

Približno predstaviti određeno rješenje diferencijalne jednadžbe koje odgovara datom početnom uvjetu kao zbir prva tri različita od nule člana potencijskog reda.

Uzorak dizajna na kraju lekcije.

Kao što vidite, problem sa određenim proširenjem u Maclaurin serija ispostavilo se da je to još teže od opšteg slučaja. Složenost zadatka koji se razmatra, kao što smo upravo vidjeli, ne leži toliko u samoj dekompoziciji, koliko u poteškoćama diferencijacije. Štaviše, ponekad morate pronaći 5-6 derivata (ili čak više), što povećava rizik od greške. I na kraju lekcije, nudim nekoliko zadataka povećane složenosti:

Primjer 6

Riješite diferencijalnu jednadžbu približno koristeći proširenje određenog rješenja u Maclaurinov red, ograničavajući se na prva tri člana niza različita od nule

Rješenje: imamo difuziju drugog reda, ali to praktično ne mijenja stvar. Prema uslovu, odmah se traži da koristimo Maclaurin seriju, koju nećemo propustiti iskoristiti. Zapišimo poznato proširenje, uzimajući više pojmova za svaki slučaj:

Algoritam radi potpuno isto:

0) – po uslovu.

1) – prema stanju.

2) Razriješimo originalnu jednačinu s obzirom na drugi izvod: .

I zamenimo:

Prva vrijednost različita od nule

Kliknite na derivate i izvršite zamjene:

Zamenimo i:

Zamenimo:

Druga vrijednost različita od nule.

5) – usput predstavljamo slične derivate.

Zamenimo:

Konačno. Međutim, može biti i gore.

Dakle, približna ekspanzija željenog određenog rješenja je:

Ministarstvo obrazovanja Republike Bjelorusije

Obrazovne ustanove

„Mogiljevski državni univerzitet po imenu A.A. Kuleshova"

Odjel MAiVT-a

Konstruiranje rješenja diferencijalnih jednadžbi pomoću serija

Rad na kursu

Završio: student 3. godine B grupe

Fizičko-matematički fakultet

Yuskaeva Alexandra Maratovna

naučni savjetnik:

Morozov Nikolaj Porfirijevič

MOGILJEV, 2010

Uvod

1. Diferencijalne jednadžbe višeg reda

1.1. Koncept linearne diferencijalne jednadžbe n-tog reda

2. Integracija diferencijalnih jednadžbi pomoću serija

2.1. Integracija diferencijalnih jednadžbi pomoću nizova stepena.

2.2. Integracija diferencijalnih jednadžbi korištenjem generaliziranih redova stepena.

3. Posebni slučajevi upotrebe generalizovanih redova stepena pri integraciji diferencijalnih jednačina.

3.1. Beselova jednačina.

3.2. Hipergeometrijska jednačina ili Gausova jednačina.

4. Primena metode integracije običnih diferencijalnih jednadžbi korišćenjem redova u praksi.

Zaključak

Književnost

Uvod

U opštem slučaju, nemoguće je pronaći tačno rešenje obične diferencijalne jednadžbe prvog reda integracijom. Štaviše, ovo nije izvodljivo za sistem običnih diferencijalnih jednačina. Ova okolnost dovela je do stvaranja velikog broja aproksimativnih metoda za rješavanje običnih diferencijalnih jednadžbi i njihovih sistema. Među aproksimativnim metodama mogu se izdvojiti tri grupe: analitičke, grafičke i numeričke. Naravno, takva klasifikacija je u određenoj mjeri proizvoljna. Na primjer, grafička metoda Eulerovih izlomljenih linija leži u osnovi jedne od metoda za numeričko rješavanje diferencijalne jednadžbe.

Integracija običnih diferencijalnih jednadžbi koristeći redove stepena je približna analitička metoda, koja se obično primjenjuje na linearne jednadžbe najmanje drugog reda.

Analitičke metode se nalaze u kursu o diferencijalnim jednadžbama. Za jednačine prvog reda (sa odvojivim varijablama, homogene, linearne itd.), kao i za neke vrste jednačina višeg reda (npr. linearne sa konstantnim koeficijentima), moguće je dobiti rješenja u obliku formula kroz analitičke transformacije.

Svrha rada je analiza jedne od približnih analitičkih metoda, kao što je integracija običnih diferencijalnih jednadžbi pomoću nizova, te njihova primjena u rješavanju diferencijalnih jednadžbi.

Diferencijalne jednadžbe višeg reda

Obična diferencijalna jednadžba n-tog reda je relacija oblika

gdje je F poznata funkcija svojih argumenata, definirana u određenom domenu;

x - nezavisna varijabla;

y je funkcija varijable x koju treba odrediti;

y’, y”, …, y (n) - derivati funkcije y.

U ovom slučaju, pretpostavlja se da je y (n) stvarno uključen u diferencijalnu jednačinu. Bilo koji drugi argument funkcije F možda neće eksplicitno sudjelovati u ovom odnosu.

Svaka funkcija koja zadovoljava datu diferencijalnu jednačinu naziva se njeno rješenje ili integral. Rješavanje diferencijalne jednadžbe znači pronalaženje svih njenih rješenja. Ako je za traženu funkciju y moguće dobiti formulu koja daje sva rješenja date diferencijalne jednadžbe i samo njih, onda kažemo da smo pronašli njeno opće rješenje, odnosno opći integral.

Opšte rješenje diferencijalne jednadžbe n-tog reda sadrži n proizvoljnih konstanti c 1, c 2,..., c n i ima oblik.

1.1. Koncept linearne diferencijalne jednadžben-th red

Diferencijalna jednadžba n-tog reda naziva se linearnom ako je prvog stepena u odnosu na skup veličina y, y’, ..., y (n). Dakle, linearna diferencijalna jednadžba n-tog reda ima oblik:

gdje su poznate kontinuirane funkcije od x.

Ova jednačina se naziva nehomogena linearna jednačina ili jednačina s desnom stranom. Ako je desna strana jednadžbe identično jednaka nuli, tada se linearna jednačina naziva homogena diferencijalna linearna jednadžba i ima oblik

Ako je n jednako 2, onda dobijamo linearnu jednačinu drugog reda, koja će biti napisana kao: Baš kao i linearna jednačina n-tog reda, jednačina drugog reda može biti homogena () i nehomogena.

Integracija diferencijalnih jednadžbi pomoću serija.

Rješenja obične diferencijalne jednadžbe iznad prvog reda sa promjenjivim koeficijentima nisu uvijek izražena u terminima elementarnih funkcija, a integracija takve jednačine se rijetko svodi na kvadrature.

2.1. Integracija diferencijalnih jednadžbi pomoću nizova stepena.

Najčešći metod integracije ovih jednačina je predstavljanje željenog rješenja u obliku niza stepena. Razmotrimo jednačine drugog reda sa promjenjivim koeficijentima

Napomena1. Prilično široka klasa funkcija može se predstaviti u obliku

gdje su neke konstante. Ovaj izraz se naziva potencijskim redom. Ako su njegove vrijednosti jednake odgovarajućim vrijednostima funkcije za bilo koji x iz intervala (x 0 - T; x 0 + T), tada se takav niz naziva konvergentan u ovom intervalu.

Pretpostavimo da su funkcije a(x), b(x) analitičke funkcije jednačine (2.1) na intervalu (x 0 - T; x 0 + T), T > 0, tj. prošireni su u nizove snage:

Vrijedi sljedeća teorema (izostavljajući dokaz, iznosimo samo njegovu formulaciju).

Teorema_1. Ako funkcije a(x), b(x) imaju oblik (2.2), tada se svako rješenje y(x) obične diferencijalne jednadžbe (2.1) može predstaviti kao konvergentno kao |x - x 0 |< Т степенного ряда:

Ova teorema ne samo da omogućava da se rješenje predstavi u obliku stepena reda, već i, što je najvažnije, opravdava konvergenciju reda (2.3).

Algoritam za takvu reprezentaciju je sljedeći. Radi praktičnosti, stavimo x 0 = 0 u (2.2) i (2.3) i potražimo rješenje obične diferencijalne jednadžbe (2.1) u obliku

Zamjenom (2.4) u (2.1) dobijamo jednakost

Da bi se ispunila (2.5), potrebno je da koeficijent za svaki stepen x bude jednak nuli. Iz ovog uslova dobijamo beskonačan sistem linearnih algebarskih jednačina

………………………………………….

…………………………………………………………………. .

Iz rezultirajućeg beskonačnog sistema linearnih algebarskih jednadžbi može se sukcesivno pronaći, ..., ako se postave vrijednosti i (u slučaju Cauchyjevog problema za običnu diferencijalnu jednadžbu (2.1), mogu se uvesti početni uvjeti = , =).

Ako su funkcije a(x), b(x) racionalne, tj. , b , gdje su polinomi, onda u blizini tačaka u kojima ili, rješenje u obliku niza stepena možda ne postoji, a ako postoji, može divergirati svuda osim u tački x = 0. Ova okolnost bio poznat L. Euleru, koji je razmatrao jednačinu prvog reda

Ova jednačina je zadovoljena redovima stepena

Međutim, nije teško uočiti da se ova serija za bilo koga razlikuje. Rješenje obične diferencijalne jednadžbe u obliku divergentnog stupnja naziva se formalno.

Jedan od najupečatljivijih i najrazumljivijih primjera upotrebe ove metode integracije je Airyjeva jednačina ili

Sva rješenja ove jednadžbe su cijele funkcije x. Tada ćemo tražiti rješenje Airyjeve jednačine u obliku niza stepena (2.4). Tada jednakost (2.5) poprima oblik

Postavimo koeficijent za svaku potenciju x jednak nuli. Imamo

……………………………

Koeficijent za nulti stepen x je jednak 2y 2. Prema tome, y 2 = 0. Tada iz jednakosti koeficijenta na nulu nalazimo = . Koeficijent je jednak. Odavde.

Iz ove formule dobijamo

Šanse ostaju neizvjesne. Da bismo pronašli osnovni sistem rješenja, prvo postavljamo = 1, = 0, a zatim obrnuto. U prvom slučaju imamo

iu drugom

Na osnovu teoreme 1, ovi redovi su konvergentni svuda na brojevnoj pravoj.

Funkcije i nazivaju se Airy funkcije. Za velike vrijednosti x, asimptotičko ponašanje ovih funkcija opisano je sljedećim formulama i.

Grafikoni ovih funkcija prikazani su na Sl. 2.1. Otkrivamo da se s neograničenim povećanjem x, nule bilo kojeg rješenja Airyeve jednadžbe približavaju na neodređeno vrijeme, što je također vidljivo iz asimptotičkog prikaza ovih rješenja, ali uopće nije očito iz reprezentacije Airyjevih funkcija u obliku konvergentnih redova stepena. Iz toga slijedi da je metoda traženja rješenja obične diferencijalne jednadžbe pomoću niza, općenito govoreći, od male koristi u rješavanju primijenjenih problema, a sam prikaz rješenja u obliku niza otežava analizu kvalitativne osobine dobijenog rastvora.

2.2. Integracija diferencijalnih jednadžbi korištenjem generaliziranih redova stepena.

Dakle, ako su u jednadžbi (2.1) funkcije a(x), b(x) racionalne, tada se tačke u kojima ili nazivaju singularne tačke jednačine (2.1).

Za jednačinu drugog reda

u kojoj su a(x), b(x) analitičke funkcije u intervalu |x - x 0 |< а, точка х = 0 является особой точкой, лишь только один из коэффициентов а 0 или b 0 в разложении функций а(х) и b(х) в степенной ряд отличен от нуля. Это пример простейшей особой точки, так называемой регулярной особой точки (или особой точки первого рода).

U blizini singularne tačke x = x 0, rješenja u obliku niza stepena možda ne postoje; u ovom slučaju rješenja se moraju tražiti u obliku generaliziranog niza stepena:

gdje λ i, …, () treba odrediti.

Teorema_2. Da bi jednadžba (2.6) imala barem jedno posebno rješenje u obliku generalizovanog niza stepena (2.7) u okolini singularne tačke x = x 0, dovoljno je da ova jednačina ima oblik

Ovo su konvergentni redovi stepena, a koeficijenti istovremeno nisu jednaki nuli, jer inače tačka x = x 0 nije posebna tačka i postoje dva linearno nezavisna rešenja, holomorfna u tački x = x 0 . Štaviše, ako se nizovi (2.7”) uključeni u koeficijente jednačine (2.7’) konvergiraju u području | x - x 0 |< R, то и ряд, входящий в решение (2.7), заведомо сходится в той же области.

Razmotrimo jednačinu (2.6) za x > 0. Zamjenom izraza (2.7) za x 0 = 0 u ovu jednačinu imamo

Izjednačavajući koeficijente na stepenu x na nulu, dobijamo rekurentni sistem jednačina:

……..........................……………………………………………. (2.8)

gdje je naznačeno

Budući da onda λ mora zadovoljiti jednačinu

koja se zove definitivna jednačina. Neka su korijeni ove jednadžbe. Ako razlika nije cijeli broj, tada je za bilo koji cijeli broj k > 0, što znači da je korištenjem navedene metode moguće konstruirati dva linearno nezavisna rješenja jednadžbe (2.6):

Ako je razlika cijeli broj, tada pomoću gornje metode možete konstruirati jedno rješenje u obliku generaliziranog niza. Poznavajući ovo rješenje, koristeći formulu Liouville-Ostrogradsky, možete pronaći drugo linearno nezavisno rješenje:

Iz iste formule proizilazi da se rješenje može tražiti u obliku

(broj A može biti jednak nuli).

Posebni slučajevi upotrebe generalizovanih redova stepena pri integraciji diferencijalnih jednačina.

3.1. Beselova jednačina.

Beselova jednačina je jedna od najvažnijih diferencijalnih jednačina u matematici i njenim primenama. Rješenja Beselove jednačine, koja čine njen osnovni sistem funkcija, nisu elementarne funkcije. Ali oni su prošireni u nizove stepena, čiji se koeficijenti izračunavaju prilično jednostavno.

Razmotrimo Beselovu jednačinu u opštem obliku:

Mnogi problemi matematičke fizike svode se na ovu jednačinu.

Budući da se jednadžba ne mijenja kada se x zamijeni sa -x, dovoljno je uzeti u obzir nenegativne vrijednosti x. Jedina singularna tačka je x=0. Jednačina koja definira x=0 je, . Ako je 0, tada jednadžba koja definira ima dva korijena: i. Nađimo rješenje ove jednačine u obliku generaliziranog niza stepena

onda, zamenivši y, y" i y" u originalnu jednačinu, dobijamo

Dakle, smanjivanjem za, imamo

Da bi ova jednakost vrijedila identično, koeficijenti moraju zadovoljiti jednačine

Nađimo rješenje koje odgovara korijenu definirajuće jednačine λ = n. Zamjenom λ = n u posljednje jednakosti vidimo da možemo uzeti bilo koji broj osim nule, broj = 0, a za k = 2, 3, ... imamo

Dakle, za sve m = 0, 1, 2, … .

Dakle, svi koeficijenti su pronađeni, što znači da će rješenje jednačine (3.1) biti zapisano u obliku

Hajde da predstavimo funkciju

nazvana Ojlerova gama funkcija. Uzimajući u obzir šta i šta za cele brojeve, kao i odabir proizvoljne konstante, biće zapisano u obliku

naziva se Beselova funkcija prve vrste n-tog reda.

Drugo posebno rješenje Besselove jednadžbe, linearno nezavisno, traži se u obliku

Jednačine za određivanje at imaju oblik

Pod pretpostavkom da nađemo

Po konvenciji, n nije cijeli broj, tako da su svi koeficijenti s parnim brojevima jedinstveno izraženi kroz:

dakle,

Pod pretpostavkom da predstavljamo y 2 (x) u obliku

naziva se Besselova funkcija prve vrste s negativnim indeksom.

Dakle, ako n nije cijeli broj, tada su sva rješenja originalne Besselove jednadžbe linearne kombinacije Besselove funkcije i: .

3.2. Hipergeometrijska jednačina ili Gausova jednačina.

Hipergeometrijska jednadžba (ili Gausova jednadžba) je jednadžba oblika

gdje su α, β, γ realni brojevi.

Tačke su singularne tačke jednačine. Oba su regularna, jer su u okolini ovih tačaka koeficijenti Gaussove jednadžbe zapisani u normalnom obliku

može se predstaviti kao generalizovani niz stepena.

Hajde da se uverimo u ovo. Zaista, primjećujući to

jednačina (3.2) se može napisati kao

Ova jednadžba je poseban slučaj jednačine

i ovdje je tačka x=0 regularna singularna tačka Gaussove jednačine.

Konstruirajmo fundamentalni sistem rješenja Gaussove jednačine u blizini singularne tačke x=0.

Definirajuća jednačina koja odgovara tački x=0 ima oblik

Njegovi korijeni i njihova razlika nije cijeli broj.

Dakle, u blizini singularne tačke x=0, moguće je konstruisati fundamentalni sistem rešenja u obliku generalizovanih redova stepena

od kojih prvi odgovara nultom korijenu definirajuće jednadžbe i običan je niz stepena, tako da je rješenje holomorfno u okolini singularne tačke x=0. Drugo rješenje je očigledno neholomorfno u tački x=0. Konstruirajmo prvo određeno rješenje koje odgovara nultom korijenu definirajuće jednačine.

Dakle, tražit ćemo posebno rješenje jednačine (3.2) u obliku

Zamjenom (3.3) u (3.2) dobijamo

Izjednačavajući slobodni termin sa nulom, dobijamo.

Neka bude, onda ćemo dobiti.

Izjednačavajući koeficijent na nuli, nalazimo:

Stoga, traženo određeno rješenje ima oblik:

Niz na desnoj strani naziva se hipergeometrijski niz, jer kada je α=1, β=γ prelazi u geometrijsku progresiju

Prema Teoremu_2, niz (3.4) konvergira kao |x|<1, так же как и ряд (3.5), и, следовательно, представляет в этом интервале решение уравнения (3.2).

Drugo posebno rješenje ima oblik:

Umjesto pronalaženja metode neodređenih koeficijenata, zamijenit ćemo željenu funkciju u Gaussovoj jednadžbi koristeći formulu

Dobijamo Gaussovu jednačinu

u kojoj ulogu parametara α, β i γ imaju i.

Stoga, konstruiranjem parcijalnog rješenja ove jednačine koje odgovara nultom korijenu definirajuće jednačine i zamjenom u (3.6), dobijamo drugo parcijalno rješenje ove Gaussove jednadžbe u obliku:

Opšte rješenje Gaussove jednačine (3.2) će biti:

Koristeći izgrađeni fundamentalni sistem rješenja Gaussove jednadžbe u okolini singularne tačke x=0, lako se može konstruisati fundamentalni sistem rješenja ove jednačine u okolini singularne tačke x=1, koji je ujedno i regularan singularna tačka.

U tu svrhu ćemo singularnu tačku x = 1 koja nas zanima prenijeti u tačku t = 0 i zajedno s njom singularnu tačku x = 0 u tačku t = 1 linearnom zamjenom nezavisne varijable x = 1 - t.

Provodeći ovu supstituciju u ovoj Gaussovoj jednačini, dobijamo

Ovo je Gausova jednadžba sa parametrima. Ima u susjedstvu |t|<1 особой точки t = 0 фундаментальную систему решений

Vraćajući se na varijablu x, tj. postavljanjem t = 1 - x, dobijamo fundamentalni sistem rješenja originalne Gaussove jednadžbe u blizini tačke | x - 1|< 1 особой точки х = 1

Opće rješenje Gaussove jednačine (3.2) u regiji će biti

Primena metode integracije običnih diferencijalnih jednadžbi korišćenjem redova u praksi.

Primjer_1. (br. 691) Izračunajte prvih nekoliko koeficijenata serije (do koeficijenta na x 4 uključujući) sa početnim uslovima

Iz početnih uslova slijedi da sada pronađemo preostale koeficijente:

Primjer_2. (br. 696) Izračunajte prvih nekoliko koeficijenata serije (do koeficijenta na x 4 uključujući) sa početnim uslovima

Rješenje: Rješenje jednačine ćemo tražiti u obliku

Dobivene izraze zamjenjujemo u originalnu jednačinu:

Predstavljajući desnu stranu u obliku niza stepena i izjednačavajući koeficijente za iste stepene x u obe strane jednačine, dobijamo:

Pošto je prema uslovu potrebno izračunati koeficijente serije do koeficijenta na x 4 uključujući, dovoljno je izračunati koeficijente.

Iz početnih uslova slijedi da je i 2. Sada ćemo pronaći preostale koeficijente:

Shodno tome, rješenje jednačine će biti zapisano u obliku

Primjer_3. (br. 700) Naći linearno nezavisna rješenja u obliku niza stepena jednačine. Ako je moguće, izrazite zbir rezultirajućeg niza koristeći elementarne funkcije.

Rješenje. Rješenje jednačine tražit ćemo u obliku niza

Diferenciramo ovaj niz dvaput i zamenimo ga u ovu jednačinu, imamo

Zapišimo prvih nekoliko članova niza u rezultirajuću jednadžbu:

Izjednačavajući koeficijente pri jednakim snagama x na nulu, dobijamo sistem jednačina za određivanje:

………………………………….

Iz ovih jednačina nalazimo

Pretpostavimo da će tada samo koeficijenti biti različiti od nule. Shvatili smo to

Jedno rješenje jednačine je konstruirano

Drugo rješenje, linearno nezavisno od pronađenog, dobijamo pretpostavkom. Tada će se samo koeficijenti razlikovati od nule:

Redovi koji predstavljaju i konvergiraju za bilo koju vrijednost x i su analitičke funkcije. Dakle, sva rješenja izvorne jednadžbe su analitičke funkcije za sve vrijednosti x. Sva rješenja su izražena formulom, gdje su C 1, C 2 proizvoljne konstante:

Budući da se zbir rezultirajućeg niza može lako izraziti pomoću elementarnih funkcija, on će se napisati kao:

Primjer_4. (br. 711) Riješite jednačinu 2x 2 y" + (3x - 2x 2)y" - (x + 1)y = 0.

Rješenje. Tačka x = 0 je regularna singularna tačka ove jednačine. Sastavljamo definirajuću jednačinu: njeni korijeni su λ 1 = 1/2 i λ 2 = - 1. Tražimo rješenje izvorne jednačine koje odgovara korijenu λ = λ 1 u obliku

Zamjenom i u originalnu jednačinu, imamo

Odavde, smanjivanjem za, dobijamo

Izjednačavajući koeficijente na istim stepenima x, imamo jednačine za određivanje:

Postavljanje y 0 = 1, nalazimo

dakle,

Tražimo rješenje originalne jednadžbe koje odgovara korijenu λ = λ 2 u obliku

Zamjenom ovog izraza u originalnu jednačinu i izjednačavanjem koeficijenata na istim potencijama x, dobijamo ili Stavljajući y 0 = 1, nalazimo

Opće rješenje originalne jednadžbe zapisujemo u obliku gdje su i proizvoljne konstante.

Zaključak

Rješavanje jednadžbi koje sadrže nepoznate funkcije i njihove derivate na stepene veće od prve ili na neki složeniji način često je vrlo teško.

Posljednjih godina takve diferencijalne jednadžbe privlače sve veću pažnju. Kako su rješenja jednadžbi često vrlo složena i teško ih je predstaviti jednostavnim formulama, značajan dio moderne teorije posvećen je kvalitativnoj analizi njihovog ponašanja, tj. razvoj metoda koje omogućavaju da se, bez rješavanja jednadžbe, kaže nešto značajno o prirodi rješenja u cjelini: na primjer, da su sva ograničena, ili da imaju periodičnu prirodu, ili da na određeni način zavise od koeficijenti.

U toku kursa izvršena je analiza metode integracije diferencijalnih jednadžbi korišćenjem stepena i generalizovanih redova stepena.

književnost:

Matveev N.V. Metode za integraciju običnih diferencijalnih jednadžbi. Ed. 4. rev. i dodatne Minsk, „Najviši. škola”, 1974. - 768 str. sa bolesnim.
Agafonov S.A., German A.D., Muratova T.V. Diferencijalne jednadžbe: Udžbenik. za univerzitete / Ed. B.C. Zarubina, A.P. Krischenko. - 3. izd., stereotip. -M.: Izdavačka kuća MSTU im. N.E. Bauman, 2004. - 352 str.
Bugrov Ya. S., Nikolsky S. M. Viša matematika. T.3: Diferencijalne jednadžbe. Višestruki integrali. Redovi. Funkcije kompleksne varijable: Udžbenik. za univerzitete: U 3 toma / Ya. S. Bugrov, S. M. Nikolsky; Ed. V. A. Sadovnichy. — 6. izd., stereotip. — M.: Drfa, 2004. —— 512 str.: ilustr.
Samoleinko A. M., Krivosheya S. A., Perestyuk N. A. Diferencijalne jednadžbe: primjeri i problemi. Udžbenik dodatak. - 2. izd., revidirano. - M.: Više. škola, 1989. - 383 str.: ilustr.
Filippov A.F. Zbirka zadataka o diferencijalnim jednadžbama. Udžbenik priručnik za univerzitete. - M.: Fizmatizd, 1961. - 100 str.: ilustr.

Skinuti: Nemate pristup preuzimanju datoteka sa našeg servera.