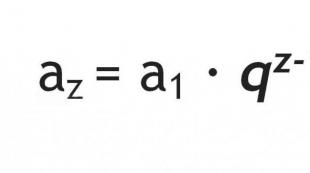Gumene narukvice

Šta je sila, zbrajanje sila, rezultanta. Newtonovi zakoni. Pravilo sabiranja sila Šta je sabiranje sila

Razmotrimo kretanje materijalne tačke (slika 46) u inercijskom referentnom sistemu pod dejstvom sila izazvanih interakcijom tačaka sa drugim tačkama i tijelima (tj. koje nastaju kao rezultat interakcije materijalnih objekata).

Imajte na umu da kada se krećete u neinercijskom referentnom sistemu, relativna kretanja su delimično određena kretanjem samog referentnog sistema.

Jednačine kretanja su sastavljene na osnovu Newtonovih zakona.

Traktat “Matematički principi prirodne filozofije”:

1687 – godina nastanka teorijska mehanika.

Newtonovi zakoni su idealizirani zakoni prirode, ali za praksu je to prihvatljivo u vrlo širokim granicama.

Hajde da se predstavimo mjere kretanja.

Količina pokreta– jednako umnošku mase m vektorom brzine tačke:

gdje je m = const > 0 mjera inercije materije.

Moment impulsa u odnosu na ishodište (slika 47):

Kinetička energija materijalne tačke:

Kasnije ćemo pokazati da je u nizu slučajeva kretanje tačke jasnije opisano kroz ili T.

Kada formulišemo Newtonove zakone, označavamo:

Sila interakcije između tačaka i;

Ukupna sila primijenjena na tačku M koja djeluje s mnogo tačaka.

Njutnov prvi zakon: materijalna tačka ostaje u stanju mirovanja ili ravnomernog pravolinijskog kretanja u odnosu na inercijski referentni sistem sve dok sile koje deluju na nju ne promene ovo stanje.

To jest, izolovana tačka ili miruje ili se kreće pravolinijsko i jednoliko. Razlog za promjenu kretanja je izvan same tačke.

Njutnov drugi zakon: vremenski izvod količine gibanja materijalne tačke je geometrijski jednak sili primijenjenoj na tačku. Ili, sa konstantnom masom, proizvod mase tačke i njenog apsolutnog ubrzanja geometrijski je jednak sili primijenjenoj na materijalnu tačku, tj.

ili ako je m = konst.

Veza između kinematičke veličine – ubrzanja i dinamičke veličine – sile kroz koeficijent proporcionalnosti – masa.

Njutnov treći zakon: bilo koje dvije materijalne tačke međusobno djeluju silama usmjerenim duž prave linije koja povezuje ove tačke, jednake po veličini i suprotno usmjerene (slika 48).

Razmotrimo uticaj tačke M1 na druge tačke (slika 49).

Jer imamo ubrzanje:

Princip nezavisnog delovanja sila: ubrzanje uzrokovano silom određeno je samo tom silom i ne ovisi o drugim silama.

Posljedica:

; označavanje

Geometrijski zbir ubrzanja uzrokovanih silama interakcije tačke M1 sa drugim tačkama proporcionalan je geometrijskom zbiru sila interakcije – pravilo paralelograma za sabiranje sila.

Od čega zavisi snaga? ?

1) iz koordinata tačke u datom trenutku;

2) iz praistorije kretanja (starenje);

3) iz okoline (temperatura);

4) otpor vazduha.

Idealizacija: sile ovise samo o koordinatama tačke, o prvim derivacijama i eksplicitno o vremenu:

U praksi je to prihvatljivo.

Razvoj fizike doveo je do promjene nekih zastarjelih koncepata i pojašnjenja granica područja unutar kojih vrijedi Newtonova mehanika: njegov koncept apsolutnog prostora sada je zamijenjen konceptom inercijalnog referentnog okvira; ustanovljeno je da Njutnova mehanika – klasična mehanika – nije primenljiva ako su relativne brzine tačaka uporedive sa brzinom svetlosti [ovo je oblast relativističke ili Ajnštajnove mehanike]; Klasična mehanika je također neprimjenjiva za proučavanje fenomena mikrosvijeta (ovo je polje kvantne mehanike). Ali oni su zasnovani na klasičnoj mehanici. U drugim oblastima => klasična mehanika daje prilično tačne rezultate.

Kontrolna pitanja:

1. Šta se zove dinamika?

2. Navedite mjere kretanja materijalne tačke

3. Formulirajte Newtonove zakone.

4. Koje su granice dometa Njutnove klasične mehanike?

Predavanje 16. Diferencijalne jednadžbe kretanja tačke

Razmotrimo kretanje slobodne materijalne tačke u inercijskom referentnom sistemu u Dekartovim koordinatama. Iz Njutnovog 2. zakona:

, ,

Štaviše, Fx, Fy, Fz – mogu zavisiti od koordinata, prvih izvoda, vremena: .

Ako je poznat zakon kretanja (na primjer iz kinematike):

tada => Fx(t), Fy(t), Fz(t). Ovo prvi (direktni) problem dinamike tačke.

Ako je sila poznata, onda je za proučavanje kretanja potrebno integrirati diferencijalne jednadžbe - to je problem dinamike druge (inverzne) tačke.

Oblici diferencijalnih jednadžbi kretanja

1) Njutnov 2. zakon – za impuls.

2) Pomnožite sa (vektorski):

ili -jednadžba ugaonog momenta.

[Zašto? - na svoju ruku. Uzmi račun ].

Vremenski izvod momenta količine kretanja geometrijski je jednak momentu sile.

Detaljan unos (koordinate):

3) Pomnožite skalarno sa elementarnim pomacima:

- jednadžba kinetičke energije.

Diferencijal kinetičke energije tačke jednak je elementarnom radu zbira sila primijenjenih na tačku na stvarnom pomaku.

O prvim integralima(zakoni očuvanja).

Iz diferencijalnih jednadžbi: funkcija koordinata, njihovih vremenskih izvoda, koja je konstantna na osnovu jednačina (odnosno, njen vremenski izvod je nula) => naziva se prvim integralom.

Dobijamo sledeće uslove.

Ako - zatim prvo integralno

1) Ako je Fx = 0, onda , - integral impulsa ( zakon održanja impulsa).

2) Ako (tj. projekcija momenta sile na os z),

Integral ugaonog momenta ( zakon održanja ugaonog momenta).

3) Dobijmo energetski integral.

Neka je desna strana ukupni diferencijal neke skalarne funkcije – potencijal polja sila .

Da bude totalni diferencijal:

1) - odnosno polje stacionarno(ne zavisi od t).

2) sa uslovima iz više matematike:

; ;

Inače: ako i, onda a jednadžba za kinetičku energiju će biti u totalnim diferencijalima:

Integracija:

Hajde da predstavimo potencijalnu energiju:

onda: - energetski integral ( zakon održanja mehaničke energije).

Ako je polje sile potencijalno i stacionarno, tada je zbroj kinetičke i potencijalne energije slobodne materijalne tačke jednak konstanti.

E0 – mehanička energija; nalazi se iz početnih uslova.

Energija je očuvana, odnosno očuvana => polje se zove konzervativan.

Pokažimo da rad sila konzervativnog polja ne ovisi o vrsti putanje, već je jednak razlici vrijednosti funkcije P na kraju i početku kretanja (Sl. 51).

Q.E.D.

Rad konzervativnih sila polja na zatvorenom pomaku je nula (slika 52).

Kontrolna pitanja:

1. Formulirajte direktne i inverzne probleme dinamike.

2. Napišite jednačinu za ugaoni moment tačke.

3. Šta se naziva pero integral diferencijalne jednačine?

4. Koje polje sila se naziva konzervativnim?

Predavanje 17. Posebne vrste polja sile

1) Zavisi samo snaga od vremena– polje je homogeno, ali nije stacionarno.

;

Isto tako za y i z.

2) Projekcije sila zavise samo od odgovarajućih koordinata.

Množenje sa dx i integracija:

Ponovo diferencirajte da provjerite:

; .

(znak je uzet iz početnih uslova).

Razdvajanje varijabli:

3) Zavisi samo projekcija sile iz projekcije brzine na istoj osi.

označavajući:

Razdvajanje varijabli:

Dakle, u svakom od tri specijalna slučaja polja sila, s obzirom na silu, masu i početne uslove, određuju se izrazi za brzinu i ubrzanje tačke.

Kontrolna pitanja:

1. Koja je suština metode razdvajanja varijabli pri rješavanju diferencijalnih jednačina?

2. Šta je posebno u integraciji jednačine kretanja tačke ako sila zavisi samo od koordinate?

3. U kojim problemima iz stvarnog života sila zavisi od brzine tačke?

Predavanje 18. Osnove dinamike sistema tačaka

Razmotrimo kretanje n slobodnih materijalnih tačaka u odnosu na inercijski referentni sistem (slika 53).

Masa tačke.

Težina cijelog sistema:

Nazovimo centar mase sistema tačkom C, čiji je poluprečnik vektor

Osnovne mjere kretanja sistema materijalnih tačaka:

1. Ukupni impuls sistema (geometrijski zbir impulsa materijalnih tačaka).

Gdje je brzina tačke.

Razmotrimo sistem tačaka sa konstantnim masama => diferencirajući:

;

gdje je brzina centra mase.

dakle,

Količina kretanja sistema materijalnih tačaka jednaka je količini kretanja mase čitavog sistema koncentrisanog u centru mase.

2. Zbir ugaonog momenta ili ugaonog momenta sistema:

je predstavljen kao monom samo u slučaju jednakih brzina svih tačaka sistema.

3. Kinetička energija sistema:

Takođe nije uvijek predstavljen u obliku jednog termina.

Snage dijelimo na vanjske i unutrašnje.

Vanjske sile djeluju na dio masa izvan sistema.

Unutrašnje sile– sile interakcije između tačaka sistema.

Označimo:

Ukupna spoljna sila do tačke

Ukupna sila interakcije između tačke i drugih tačaka u sistemu.

Podjela na unutrašnje i vanjske sile je uslovna.

Dobijmo neka svojstva unutrašnjih sila.

Razmotrimo tačke i (slika 54).

Iz Njutnovog trećeg zakona:

Unutrašnja sila po tački:

Očigledno:

dakle, zbir unutrašnjih sila i zbir momenata unutrašnjih sila jednak je nuli u odnosu na bilo koju tačku i bilo koju osu.

Razmotrimo iznos osnovni rad unutrašnje sile.

Neka , Gdje,

Udaljenost između tačaka.

Radite na elementarnim stvarnim pomacima interakcijskih sila između dvije tačke:

[ - projekcija na, uključujući znak].

Označimo zbir elementarnih radova unutrašnjih sila:

(d – znači “na elementarnim pokretima”)

Kontrolna pitanja:

1. Šta se zove centar mase sistema materijalnih tačaka?

2. Navedite glavne mjere kretanja sistema materijalnih tačaka.

Force. Sabiranje snaga

Sve promjene u prirodi nastaju kao rezultat interakcije između tijela. Lopta leži na tlu i neće se početi kretati osim ako je ne gurnete nogom; opruga se neće istegnuti ako joj pričvrstite teret itd. Kada tijelo stupi u interakciju s drugim tijelima, brzina njegovog kretanja se mijenja. U fizici često ne ukazuju koje tijelo i kako djeluje na dato tijelo, već kažu da „na tijelo djeluje sila“.

Sila je fizička veličina koja kvantitativno karakterizira djelovanje jednog tijela na drugo, uslijed čega tijelo mijenja svoju brzinu. Sila je vektorska veličina. To jest, pored numeričke vrijednosti, sila ima smjer. Sila je označena slovom F i u međunarodnom sistemu se mjeri u njutnima. 1 njutn je sila koju tijelo teško 1 kg, u mirovanju, pruža u 1 sekundi brzinom od 1 metar u sekundi bez trenja. Snagu možete mjeriti pomoću posebnog uređaja - dinamometra.

U zavisnosti od prirode interakcije u mehanici, razlikuju se tri vrste sila:

gravitacija,
elastična sila,
sila trenja.

U pravilu na tijelo djeluje ne jedna, već nekoliko sila. U ovom slučaju se uzima u obzir rezultanta sila. Rezultantna sila je sila koja djeluje na isti način kao nekoliko sila koje istovremeno djeluju na tijelo. Koristeći rezultate eksperimenata, možemo zaključiti: rezultanta sila usmjerenih duž jedne prave u jednom smjeru usmjerena je u istom smjeru, a njena vrijednost je jednaka zbroju vrijednosti tih sila. Rezultanta dvije sile usmjerene duž jedne prave u suprotnim smjerovima usmjerena je prema većoj sili i jednaka je razlici vrijednosti tih sila.

Djelovanja tijela jedno na drugo opisuju se pomoću sila. Sile koje karakteriziraju interakcije koje dovode do promjene ili brzine tijela, ili njegovog oblika i veličine. Osim toga, rezultat djelovanja jednog tijela na drugo također ovisi o smjeru ovog djelovanja.

U SI sistemu, sila se mjeri u njutnima (1 N).

1 N je sila koja tijelu mase 1 kg daje ubrzanje od 1 m/s2.

Svaku silu karakterizira numerička vrijednost (modul), smjer i tačka primjene.

Na crtežima su sile, kao i druge vektorske veličine, označene strelicama. Početak strelice se poklapa sa tačkom primene sile, smer strelice označava smer sile, a dužina strelice je proporcionalna veličini sile.
Sabiranje snaga. Rezultat

Vrlo rijetko na tijelo djeluje samo jedna sila, najčešće - dvije ili tri. Ako na tijelo djeluje više sila, onda će rezultat njihovog djelovanja biti isti kao što bi bio da je na njega djelovala sila, koja se naziva rezultanta.

Pitanje za učenike prilikom izlaganja novog materijala

1. Koja je mjera interakcije između tijela?

2. Navedite primjere djelovanja sila u mehanici.

3. Šta određuje djelovanje sile na tijelo?

4. Kako izračunati rezultantu više sila?

Učvršćivanje naučenog materijala

1. Treniramo se za rješavanje problema

1. Na tijelo djeluju dvije sile u međusobno okomitim smjerovima. Kolika je veličina rezultantne sile ako su moduli sile 5 i 12 N?
2. Modul rezultantnih sila koje djeluju u međusobno okomitim smjerovima jednak je 50 N. Modul jedne od sila je jednak 25 N. Koliki je modul druge sile?

3. Izračunajte modul rezultante dvije sile koje tvore ugao od 60° između sebe, ako je svaka sila jednaka 600 N.

2. Test pitanja

1. Kako se karakteriše svaka sila?

2. Šta trebate znati za izračunavanje sile?

3. Kako izračunati rezultantu više od dvije sile?

4. Možda je rezultanta dvije sile 4 H i 5 N, koje djeluju na tijelo duž jedne prave, jednaka 2 N? S N? 8 N? 10 N?

Šta smo naučili na času?

Djelovanje tijela ili čestica jedno na drugo naziva se interakcija.

Sila je vektorska veličina, koja je mjera utjecaja drugih tijela na tijelo, uslijed čega tijelo dobiva ubrzanje ili mijenja oblik i veličinu.

1 N je sila koja daje ubrzanje od 1 m/s2 tijelu težine 1 kg.

Rezultantna sila je sila čije djelovanje zamjenjuje djelovanje više sila koje istovremeno djeluju na tijelo.

Kada na jedno tijelo istovremeno djeluje više sila, tijelo se kreće ubrzanjem, što je vektorski zbir ubrzanja koja bi nastala pod djelovanjem svake sile posebno. Sile koje djeluju na tijelo i primijenjene na jednu tačku sabiraju se prema pravilu vektorskog sabiranja.

Vektorski zbir svih sila koje istovremeno djeluju na tijelo naziva se rezultantna sila i određena je pravilom vektorskog zbrajanja sila: $\overrightarrow(R)=(\overrightarrow(F))_1+(\overrightarrow(F)) _2+(\overrightarrow(F)) _3+\dots +(\overrightarrow(F))_n=\sum^n_(i=1)((\overrightarrow(F))_i)$.

Rezultirajuća sila ima isti učinak na tijelo kao zbir svih sila koje se na njega primjenjuju.

Za dodavanje dvije sile koristi se pravilo paralelograma (slika 1):

Slika 1. Sabiranje dvije sile prema pravilu paralelograma

U ovom slučaju, nalazimo modul zbira dvije sile koristeći kosinus teorem:

Ako trebate dodati više od dvije sile primijenjene u jednoj tački, onda koristite pravilo poligona: ~ sa kraja prve sile nacrtajte vektor jednak i paralelan drugoj sili; od kraja druge sile - vektor jednak i paralelan trećoj sili, i tako dalje.

Slika 2. Sabiranje sila prema pravilu poligona

Vektor zatvaranja povučen od tačke primjene sila do kraja posljednje sile jednak je po veličini i smjeru rezultanti. Na slici 2 ovo pravilo je ilustrovano primjerom pronalaženja rezultante četiri sile $(\overrightarrow(F))_1,\ (\overrightarrow(F))_2,(\overrightarrow(F))_3,(\overrightarrow (F) )_4$. Imajte na umu da vektori koji se dodaju ne pripadaju nužno istoj ravni.

Rezultat sile koja djeluje na materijalnu tačku ovisi samo o njenom modulu i smjeru. Čvrsto tijelo ima određene dimenzije. Dakle, sile jednake veličine i smjera uzrokuju različita kretanja krutog tijela ovisno o mjestu primjene. Prava linija koja prolazi kroz vektor sile naziva se linija djelovanja sile.

Slika 3. Sabiranje sila primijenjenih na različite točke tijela

Ako se sile primjenjuju na različite točke tijela i ne djeluju paralelno jedna s drugom, tada se rezultanta primjenjuje na tačku sjecišta linija djelovanja sila (slika 3).

Tačka je u ravnoteži ako je vektorski zbir svih sila koje djeluju na nju jednak nuli: $\sum^n_(i=1)((\overrightarrow(F))_i)=\overrightarrow(0)$. U ovom slučaju, zbir projekcija ovih sila na bilo koju koordinatnu osu je također nula.

Zamjena jedne sile sa dvije, primijenjene na istoj tački i koje proizvode isti učinak na tijelo kao ova jedna sila, naziva se razlaganjem sila. Dekompozicija sila se vrši, kao i njihovo sabiranje, po pravilu paralelograma.

Problem razlaganja jedne sile (čiji je modul i smjer poznati) na dvije, primijenjene u jednoj tački i koje djeluju pod uglom jedna prema drugoj, ima jedinstveno rješenje u sljedećim slučajevima, ako je poznato:

pravci obe komponente sila;
modul i pravac jedne od komponentnih sila;
moduli obe komponente sila.

Neka, na primjer, želimo da razložimo silu $F$ na dvije komponente koje leže u istoj ravni sa F i usmjerene duž pravih a i b (slika 4). Da biste to učinili, dovoljno je povući dvije linije paralelne sa a i b od kraja vektora koji predstavlja F. Segmenti $F_A$ i $F_B$ će prikazati potrebne sile.

Slika 4. Dekompozicija vektora sile po pravcima

Druga verzija ovog problema je pronaći jednu od projekcija vektora sile date vektore sile i drugu projekciju. (Sl. 5 a).

Slika 5. Pronalaženje projekcije vektora sile pomoću datih vektora

Problem se svodi na konstruisanje paralelograma duž dijagonale i jedne od stranica, poznatog iz planimetrije. Na slici 5b takav paralelogram je konstruisan i naznačena je potrebna komponenta $(\overrightarrow(F))_2$ sile $(\overrightarrow(F))$.

Drugo rješenje je da se sili doda silu jednaku - $(\overrightarrow(F))_1$ (slika 5c).Kao rezultat dobijamo željenu silu $(\overrightarrow(F))_2$.

Tri sile~$(\overrightarrow(F))_1=1\ N;;\ (\overrightarrow(F))_2=2\ N;;\ (\overrightarrow(F))_3=3\ N$ primijenjene na jednu tačku, leže u istoj ravni (slika 6 a) i prave uglove~ sa horizontalom $\alpha =0()^\circ ;;\beta =60()^\circ ;;\gamma =30()^ \ circ $odnosno. Pronađite rezultantu ovih sila.

Nacrtajmo dvije međusobno okomite ose OX i OY tako da se os OX poklapa sa horizontalom duž koje je usmjerena sila $(\overrightarrow(F))_1$. Projektujmo ove sile na koordinatne ose (slika 6b). Projekcije $F_(2y)$ i $F_(2x)$ su negativne. Zbir projekcija sila na osu OX jednak je projekciji na ovu osu rezultante: $F_1+F_2(cos \beta \ )-F_3(cos \gamma \ )=F_x=\frac(4-3 \sqrt(3))(2)\ približno -0,6\ H$. Slično, za projekcije na osu OY: $-F_2(sin \beta \ )+F_3(sin \gamma =F_y=\ )\frac(3-2\sqrt(3))(2)\približno -0,2\ H $ . Modul rezultante je određen Pitagorinom teoremom: $F=\sqrt(F^2_x+F^2_y)=\sqrt(0,36+0,04)\približno 0,64\ N$. Smjer rezultante se određuje pomoću ugla između rezultante i ose (slika 6 c): $tg\varphi =\frac(F_y)(F_x)=\ \frac(3-2\sqrt(3)) (4-3\sqrt (3))\približno 0,4$

Sila $F = 1kH$ primjenjuje se u tački B konzole i usmjerena je okomito prema dolje (slika 7a). Pronađite komponente ove sile u smjerovima štapova nosača. Potrebni podaci prikazani su na slici.

F = 1 kN = 1000N

$(\mathbf \beta )$ = $30^(\circ)$

$(\overrightarrow(F))_1,\ (\overrightarrow(F))_2$ - ?

Neka su šipke pričvršćene za zid u tačkama A i C. Dekompozicija sile $(\overrightarrow(F))$ na komponente duž pravca AB i BC prikazana je na slici 7b. Ovo pokazuje da je $\left|(\overrightarrow(F))_1\right|=Ftg\beta \približno 577\ H;\ \ $

\[\left|(\overrightarrow(F))_2\right|=F(cos \beta \ )\približno 1155\ H. \]

Odgovor: $\left|(\overrightarrow(F))_1\right|$=577 N; $\left|(\overrightarrow(F))_2\right|=1155\ N$

Rezultirajuća sila ima isti učinak na tijelo kao zbir svih sila koje se na njega primjenjuju.

Za dodavanje dvije sile koristi se pravilo paralelograma (slika 1):

Slika 1. Sabiranje dvije sile prema pravilu paralelograma

U ovom slučaju, nalazimo modul zbira dvije sile koristeći kosinus teorem:

Slika 2. Sabiranje sila prema pravilu poligona

Slika 3. Sabiranje sila primijenjenih na različite točke tijela

Ako se sile primjenjuju na različite točke tijela i ne djeluju paralelno jedna s drugom, tada se rezultanta primjenjuje na tačku sjecišta linija djelovanja sila (slika 3).

pravci obe komponente sila;
modul i pravac jedne od komponentnih sila;
moduli obe komponente sila.

Slika 4. Dekompozicija vektora sile po pravcima

Druga verzija ovog problema je pronaći jednu od projekcija vektora sile date vektore sile i drugu projekciju. (Sl. 5 a).

Slika 5. Pronalaženje projekcije vektora sile pomoću datih vektora

Drugo rješenje je da se sili doda silu jednaku - $(\overrightarrow(F))_1$ (slika 5c).Kao rezultat dobijamo željenu silu $(\overrightarrow(F))_2$.

Sila $F = 1kH$ primjenjuje se u tački B konzole i usmjerena je okomito prema dolje (slika 7a). Pronađite komponente ove sile u smjerovima štapova nosača. Potrebni podaci prikazani su na slici.