Bajke

Koncept konusa. Konus kao geometrijska figura Kolika je dužina generatrise konusa

Koje izlaze iz jedne tačke (vrh konusa) i koje prolaze kroz ravnu površinu.

Dešava se da je konus dio tijela koji ima ograničenu zapreminu i dobija se kombinovanjem svakog segmenta koji povezuje vrh i tačke ravne površine. Ovo poslednje, u ovom slučaju, jeste osnovu konusa, a za konus se kaže da počiva na ovoj osnovi.

Kada je osnova konusa poligon, to već jeste piramida .

Kružni konus- ovo je tijelo koje se sastoji od kružnice (osnova konusa), tačke koja ne leži u ravni ove kružnice (vrh konusa i svi segmenti koji spajaju vrh konusa sa tačkama baza).

Segmenti koji spajaju vrh konusa i tačke osnovne kružnice nazivaju se formiranje konusa. Površina konusa se sastoji od baze i bočne površine.

Bočna površina je ispravna n-ugljična piramida upisana u konus:

S n =½P n l n,

Gdje Pn- obim osnove piramide, i l n- apotema.

Po istom principu: za bočnu površinu krnjeg stošca s osnovnim polumjerima R 1, R 2 i formiranje l dobijamo sledeću formulu:

S=(R 1 +R 2)l.

Pravi i kosi kružni konusi jednake osnove i visine. Ova tijela imaju isti volumen:

Svojstva konusa.

Kada površina osnove ima granicu, to znači da i volumen konusa ima granicu i jednak je trećem dijelu proizvoda visine i površine baze.

Gdje S- bazna površina, H- visina.

Dakle, svaki konus koji leži na ovoj osnovi i ima vrh koji se nalazi na ravni paralelnoj bazi ima jednak volumen, jer su im visine iste.

Težište svakog konusa sa zapreminom koja ima granicu nalazi se na četvrtini visine od baze.
Čvrsti ugao na vrhu pravog kružnog konusa može se izraziti sljedećom formulom:

Gdje α - ugao otvaranja konusa.

Bočna površina takvog konusa, formula:

i ukupna površina (tj. zbir površina bočne površine i baze), formula:

S=πR(l+R),

Gdje R- poluprečnik osnove, l— dužina generatrise.

Zapremina kružnog konusa, formula:

Za skraćeni konus (ne samo ravan ili kružni), zapreminu, formulu:

Gdje S 1 I S 2- površina gornje i donje baze,

h I H- udaljenosti od ravni gornje i donje baze do vrha.

Presjek ravni s pravim kružnim konusom jedan je od konusnih presjeka.

U ovoj lekciji ćemo se upoznati s takvom figurom kao što je konus. Proučimo elemente konusa i vrste njegovih presjeka. I saznat ćemo s kojom figurom konus ima mnogo zajedničkih svojstava.

Fig.1. Objekti u obliku konusa

U svijetu je ogroman broj stvari u obliku konusa. Često ih i ne primjećujemo. Korneti na putu koji upozoravaju na radove na putu, krovovi dvoraca i kuća, korneti za sladoled - svi ovi objekti imaju oblik korneta (vidi sliku 1).

Rice. 2. Pravokutni trokut

Razmotrimo proizvoljan pravougaoni trougao sa kracima i (vidi sliku 2).

Rice. 3. Ravni kružni konus

Rotacijom datog trokuta oko jedne od kateta (bez gubitka općenitosti, neka je to kateta), hipotenuza će opisati površinu, a katet će opisati krug. Tako će se dobiti tijelo koje se naziva pravi kružni konus (vidi sliku 3).

Rice. 4. Vrste čunjeva

Pošto govorimo o ravnom kružnom konusu, očigledno postoji i indirektni i ne-kružni? Ako je osnova konusa kružnica, ali vrh nije projektovan u središte ovog kruga, onda se takav konus naziva nagnutim. Ako osnova nije krug, već proizvoljna figura, onda se takvo tijelo ponekad naziva i konus, ali, naravno, ne kružno (vidi sliku 4).

Tako ponovo dolazimo do analogije koja nam je već poznata iz rada sa cilindrima. U stvari, konus je nešto poput piramide, samo što piramida ima poligon u osnovi, a konus (koji ćemo razmotriti) ima krug (vidi sliku 5).

Segment ose rotacije (u našem slučaju to je krak) zatvoren unutar konusa naziva se osa konusa (vidi sliku 6).

Rice. 5. Konus i piramida

Rice. 6. - os konusa

Rice. 7. Baza konusa

Krug formiran rotacijom druge noge () naziva se baza konusa (vidi sliku 7).

A dužina ovog kraka je poluprečnik osnove stošca (ili, jednostavnije, poluprečnik stošca) (vidi sliku 8).

Rice. 8. - radijus konusa

Rice. 9. - vrh konusa

Vrh oštrog ugla rotacionog trougla koji leži na osi rotacije naziva se vrh konusa (vidi sliku 9).

Rice. 10. - visina konusa

Visina konusa je segment povučen od vrha konusa okomito na njegovu osnovu (vidi sliku 10).

Ovdje možete imati pitanje: kako se onda segment osi rotacije razlikuje od visine konusa? Zapravo, oni se poklapaju samo u slučaju pravog konusa; ako pogledate nagnuti konus, primijetit ćete da su to dva potpuno različita segmenta (vidi sliku 11).

Rice. 11. Visina u kosom konusu

Vratimo se na pravi konus.

Rice. 12. Generatori konusa

Segmenti koji povezuju vrh konusa sa tačkama kružnice njegove baze nazivaju se generatori konusa. Usput, sve generatrice desnog konusa su jednake jedna drugoj (vidi sliku 12).

Rice. 13. Prirodni konusni objekti

U prijevodu s grčkog, konos znači "šišarka". U prirodi ima dovoljno objekata koji imaju oblik konusa: smreka, planina, mravinjak itd. (vidi sliku 13).

Ali navikli smo na činjenicu da je konus ravan. Ima jednake generatrise, a visina mu se poklapa sa osom. Takav konus smo nazvali pravi konus. U školskom kursu geometrije obično se uzimaju u obzir ravni konusi, a prema zadanim postavkama svaki konus se smatra desnim kružnim. Ali već smo rekli da ne postoje samo ravni čunjevi, već i nagnuti.

Rice. 14. Okomit presjek

Vratimo se pravim čunjevima. „Isecite“ konus ravninom koja je okomita na osu (vidi sliku 14).

Koja će figura biti na rezu? Naravno da je krug! Podsjetimo da se ravan kreće okomito na osu, a samim tim i paralelno s bazom, koja je kružnica.

Rice. 15. Kosi dio

Sada postupno naginjemo ravninu presjeka. Tada će se naš krug početi postepeno pretvarati u sve izduženiji oval. Ali samo dok se ravnina preseka ne sudari sa osnovnim krugom (vidi sliku 15).

Rice. 16. Vrste sekcija na primjeru šargarepe

Oni koji vole eksperimentalno istraživati svijet mogu to provjeriti uz pomoć šargarepe i noža (pokušajte rezati kriške od šargarepe pod različitim uglovima) (vidi sliku 16).

Rice. 17. Aksijalni presjek konusa

Presjek konusa ravninom koja prolazi kroz njegovu osu naziva se aksijalni presjek konusa (vidi sliku 17).

Rice. 18. Jednakokraki trougao - presjek

Ovdje dobijamo potpuno drugačiji presjek: trokut. Ovaj trougao je jednakokraki (vidi sliku 18).

U ovoj lekciji učili smo o cilindričnoj površini, vrstama cilindra, elementima cilindra i sličnosti cilindra sa prizmom.

Generator konusa je 12 cm i nagnut je prema ravni osnove pod uglom od 30 stepeni. Pronađite aksijalni poprečni presjek konusa.

Rješenje

Razmotrimo traženi aksijalni presjek. Ovo je jednakokraki trougao u kojem su stranice 12 stepeni, a osnovni ugao 30 stepeni. Zatim možete nastaviti na različite načine. Ili možete nacrtati visinu, pronaći je (polovina hipotenuze, 6), zatim bazu (pomoću Pitagorine teoreme), a zatim površinu.

Rice. 19. Ilustracija za problem

Ili odmah pronađite ugao na vrhu - 120 stepeni - i izračunajte površinu kao poluproizvod stranica i sinusa ugla između njih (odgovor će biti isti).

Geometrija. Udžbenik za 10-11 razred. Atanasyan L.S. i drugi 18. izd. - M.: Obrazovanje, 2009. - 255 str.
Geometrija 11. razred, A.V. Pogorelov, M.: Obrazovanje, 2002
Radna sveska iz geometrije 11. razred, V.F. Butuzov, Yu.A. Glazkov

Yaklass.ru ().
Uztest.ru ().
Bitclass.ru ().

Zadaća

) - tijelo u euklidskom prostoru dobijeno kombinovanjem svih zraka koje izlaze iz jedne tačke ( vrhovi konus) i prolazi kroz ravnu površinu. Ponekad je konus dio takvog tijela koji ima ograničenu zapreminu i dobija se kombinovanjem svih segmenata koji povezuju vrh i tačke ravne površine (potonje se u ovom slučaju naziva osnovu konus, a konus se zove oslanjajući se po ovoj osnovi). Ako je osnova konusa poligon, takav konus je piramida.

Enciklopedijski YouTube

1 / 4

✪ Kako napraviti konus od papira.

Titlovi

Povezane definicije

Segment koji povezuje vrh i granicu baze naziva se generatrisa konusa.
Unija generatora konusa se zove generatrix(ili strana) konusna površina. Formirajuća površina konusa je konična površina.
Segment koji je spušten okomito iz vrha na ravan baze (kao i dužina takvog segmenta) naziva se visina konusa.
Konusni ugao- ugao između dve suprotne generatrise (ugao na vrhu konusa, unutar konusa).
Ako osnova stošca ima centar simetrije (na primjer, to je krug ili elipsa) i ortogonalna projekcija vrha stošca na ravan baze poklapa se s tim centrom, tada se konus naziva direktno. U ovom slučaju naziva se ravna linija koja povezuje vrh i centar baze konusna osovina.
Kosi (skloni) konus - konus čija se ortogonalna projekcija temena na bazu ne poklapa sa njegovim centrom simetrije.
Kružni konus- konus čija je osnova kružnica.
Pravi kružni konus(često se jednostavno naziva konus) može se dobiti rotiranjem pravokutnog trokuta oko linije koja sadrži krak (ova linija predstavlja os konusa).
Konus koji počiva na elipsi, paraboli ili hiperboli naziva se respektivno eliptični, parabolic I hiperbolički konus(poslednja dva imaju beskonačan volumen).
Dio stošca koji leži između osnove i ravni paralelne bazi i koji se nalazi između vrha i baze naziva se skraćeni konus, ili konusni sloj.

Svojstva

Ako je površina baze konačna, tada je i volumen konusa konačan i jednak jednoj trećini proizvoda visine i površine baze.

V = 1 3 S H , (\displaystyle V=(1 \over 3)SH,)

Gdje S- bazna površina, H- visina. Dakle, svi čunjevi koji počivaju na datoj osnovici (konačne površine) i imaju vrh koji se nalazi na datoj ravni paralelnoj bazi imaju jednak volumen, jer su im visine jednake.

Težište bilo kojeg stošca s konačnim volumenom nalazi se na četvrtini visine od baze.
Čvrsti ugao na vrhu pravog kružnog konusa jednak je

2 π (1 − cos ⁡ α 2) , (\displaystyle 2\pi \left(1-\cos (\alpha \preko 2)\desno),) gdje je α ugao otvaranja konusa.

Bočna površina takvog konusa jednaka je

S = π R l , (\displaystyle S=\pi Rl,)

i ukupna površina (tj. zbir površina bočne površine i baze)

S = π R (l + R), (\displaystyle S=\pi R(l+R),) Gdje R- poluprečnik osnove, l = R 2 + H 2 (\displaystyle l=(\sqrt (R^(2)+H^(2))))- dužina generatrise.

Zapremina kružnog (ne nužno pravog) konusa je jednaka

V = 1 3 π R 2 H . (\displaystyle V=(1 \preko 3)\pi R^(2)H.)

Za skraćeni konus (ne nužno ravan i kružni), volumen je jednak:

V = 1 3 (H S 2 − h S 1) , (\displaystyle V=(1 \over 3)(HS_(2)-hS_(1)),)

gdje su S 1 i S 2 površine gornje (najbliže vrhu) i donje baze, respektivno, h I H- udaljenosti od ravni gornje i donje baze do vrha.

Presjek ravni s pravim kružnim konusom je jedan od konusnih presjeka (u nedegeneriranim slučajevima - elipsa, parabola ili hiperbola, ovisno o položaju rezne ravnine).

Jednačina konusa

Jednadžbe koje definiraju bočnu površinu pravog kružnog konusa s kutom otvaranja od 2Θ, vrhom u početku i osom koja se poklapa s osom Oz :

U sfernom koordinatnom sistemu sa koordinatama ( r, φ, θ) :

θ = Θ. (\displaystyle \theta =\Theta.)

U cilindričnom koordinatnom sistemu sa koordinatama ( r, φ, z) :

z = r ⋅ ctg ⁡ Θ (\displaystyle z=r\cdot \operatorname (ctg) \Theta) ili r = z ⋅ tan ⁡ Θ . (\displaystyle r=z\cdot \operatorname (tg) \Theta .)

U kartezijanskom koordinatnom sistemu sa koordinatama (x, y, z) :

z = ± x 2 + y 2 ⋅ krevetac ⁡ Θ . (\displaystyle z=\pm (\sqrt (x^(2)+y^(2)))\cdot \operatorname (ctg) \Theta .) Ova jednadžba u kanonskom obliku je zapisana kao

gdje su konstante a, With određena proporcijom c / a = cos ⁡ Θ / sin ⁡ Θ . (\displaystyle c/a=\cos \Theta /\sin \Theta .) Ovo pokazuje da je bočna površina pravog kružnog konusa površina drugog reda (tzv konusna površina). Općenito, konusna površina drugog reda počiva na elipsi; u odgovarajućem kartezijanskom koordinatnom sistemu (os Oh I OU paralelno sa osovinama elipse, vrh stošca se poklapa sa ishodištem, centar elipse leži na osi Oz) njegova jednadžba ima oblik

x 2 a 2 + y 2 b 2 − z 2 c 2 = 0 , (\displaystyle (\frac (x^(2))(a^(2)))+(\frac (y^(2))( b^(2)))-(\frac (z^(2))(c^(2)))=0,)

i a/c I b/c jednaka poluosama elipse. U najopštijem slučaju, kada konus leži na proizvoljnoj ravnoj površini, može se pokazati da je jednadžba bočne površine stošca (sa vrhom u početku) data jednadžbom f (x, y, z) = 0, (\displaystyle f(x,y,z)=0,) gdje je funkcija f (x, y, z) (\displaystyle f(x,y,z)) je homogena, odnosno zadovoljava uslov f (α x , α y , α z) = α n f (x, y, z) (\displaystyle f(\alpha x,\alpha y,\alpha z)=\alpha ^(n)f(x,y ,z)) za bilo koji realan broj α.

Skeniraj

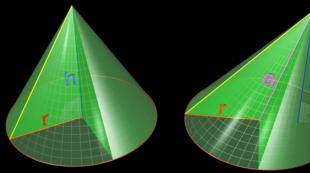
Pravi kružni konus kao tijelo rotacije formira se od pravokutnog trokuta koji rotira oko jedne od kateta, gdje h- visina stošca od centra baze do vrha - je krak pravokutnog trougla oko kojeg se vrši rotacija. Drugi krak pravouglog trougla r- radijus u osnovi konusa. Hipotenuza pravouglog trougla je l- formiranje konusa.

Za kreiranje konusnog skeniranja mogu se koristiti samo dvije količine r I l. Osnovni radijus r definira krug osnove stošca u razvoju, a sektor bočne površine stošca je određen generatriksom bočne površine l, što je radijus sektora bočne površine. Sektorski ugao φ (\displaystyle \varphi ) u razvoju bočne površine stošca određuje se formula:

φ = 360° ( r/l) .

Konus (tačnije, kružni konus) je tijelo koje se sastoji od kruga - osnove stošca, tačke koja ne leži u ravni ove kružnice - vrha stošca i svih segmenata koji povezuju vrh stošca sa tačkama osnove (slika 1) Segmenti koji povezuju vrh konusa sa tačkama osnovne kružnice nazivaju se generatori konusa. Svi generatori konusa su međusobno jednaki. Površina konusa se sastoji od baze i bočne površine.
Rice. 1
Konus se naziva pravim ako je prava linija koja povezuje vrh konusa sa središtem baze okomita na ravan osnove. Vizuelno, pravi kružni konus se može zamisliti kao tijelo koje se dobije rotacijom pravokutnog trokuta oko svoje noge kao ose (slika 2).
Rice. 2
Visina konusa je okomica koja se spušta od njegovog vrha do ravni baze. Za pravi konus, osnova visine poklapa se sa središtem baze. Osa pravog kružnog konusa je prava linija koja sadrži njegovu visinu.
Presjek konusa ravninom koja prolazi kroz njegov vrh je jednakokraki trokut čije stranice čine konus (slika 3). Konkretno, jednakokraki trokut je aksijalni presjek konusa. Ovo je presek koji prolazi kroz osu stošca (slika 4).
Rice. 3 Fig. 4

Površina konusa
Bočna površina stošca, kao i bočna površina cilindra, može se okrenuti na ravan tako što se preseče duž jedne od generatrisa (sl. 2, a, b). Razvoj bočne površine stošca je kružni sektor (slika 2.6), čiji je polumjer jednak generatrisi stošca, a dužina luka ovog sektora je obim osnove stošca.
Područje bočne površine stošca uzima se kao područje njegovog razvoja. Izrazimo površinu S bočne površine stošca kroz njegovu generatricu l i polumjer osnove r.
Površina kružnog sektora - razvoj bočne površine stošca (slika 2) - jednaka je (Pl2a)/360, gdje je a stepen mjera luka ABA", dakle
Strana = (Pl2a)/360. (*)
Izrazimo a u terminima l i r. Pošto je dužina luka ABA" jednaka 2Pr (obim osnove stošca), onda je 2Pr = Pla/180, odakle je a=360r/l. Zamjenom ovog izraza u formulu (*) dobijamo:
Sside = Prl. (**)
Dakle, površina bočne površine stošca jednaka je proizvodu polovine obima baze i generatrikse.
Ukupna površina konusa je zbir površina bočne površine i baze. Za izračunavanje površine Scon ukupne površine konusa dobija se formula: Scon = Pr (l + r). (***)

Frustum
Uzmimo proizvoljan konus i nacrtamo reznu ravan okomitu na njegovu osu. Ova ravan se siječe sa konusom u krugu i dijeli konus na dva dijela. Jedan od dijelova je konus, a drugi se naziva krnji konus. Osnova prvobitnog konusa i kružnica dobijena rezanjem ovog konusa ravninom nazivaju se osnovicama krnjeg stošca, a segment koji povezuje njihova središta naziva se visina krnjeg stošca.

Dio konične površine koji omeđuje krnji konus naziva se njegova bočna površina, a segmenti generatrisa konusne površine zatvoreni između baza nazivaju se generatori krnjeg konusa. Svi generatori skraćenog konusa su međusobno jednaki (dokažite sami).
Površina bočne površine skraćenog konusa jednaka je umnošku polovine zbira dužina krugova baza i generatora: Sside = P (r + r1) l.

Dodatne informacije o konusu
1. U geologiji postoji pojam „veneza“. Ovo je oblik reljefa nastao akumulacijom klastičnih stijena (šljunak, šljunak, pijesak) koje planinske rijeke nose u podbrdsku ravnicu ili u ravniju, širu dolinu.
2. U biologiji postoji koncept „konusa rasta“. Ovo je vrh izdanka i korijen biljke, koji se sastoji od ćelija obrazovnog tkiva.
3. „Šešarke“ je porodica morskih mekušaca podklase prosobranch. Ljuska je kupasta (2–16 cm), jarke boje. Postoji preko 500 vrsta čunjeva. Žive u tropima i suptropima, grabežljivci su i imaju otrovnu žlijezdu. Ugriz čunjeva je veoma bolan. Smrtni slučajevi su poznati. Školjke se koriste kao ukrasi i suveniri.
4. Prema statistikama, svake godine 6 ljudi na milion stanovnika umre od udara groma na Zemlju (češće u južnim zemljama). To se ne bi dogodilo da su gromobrana posvuda, jer se formira sigurnosni konus. Što je gromobran veći, to je veći volumen takvog konusa. Neki ljudi pokušavaju da se sakriju od pražnjenja ispod drveta, ali drvo nije provodnik, na njemu se nakupljaju naboji i drvo može biti izvor napona.
5. U fizici se susreće koncept „čvrstog ugla“. Ovo je ugao u obliku konusa izrezan u kuglu. Jedinica solidnog ugla je 1 steradijan. 1 steradijan je čvrsti ugao čiji je poluprečnik na kvadrat jednak površini dela sfere koju seče. Ako u ovaj kut postavimo izvor svjetlosti od 1 kandela (1 svijeća), dobićemo svjetlosni tok od 1 lumena. Svjetlost filmske kamere ili reflektora širi se u obliku stošca.