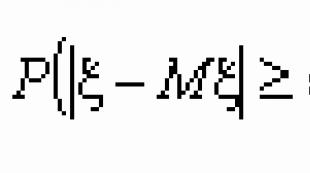Təsadüfi hadisələrin tədqiqi təcrübəsi göstərir ki, fərdi müşahidələrin, hətta eyni şəraitdə aparılanların nəticələri çox fərqli ola bilsə də, eyni zamanda, kifayət qədər çox sayda müşahidə üçün orta nəticələr sabitdir və zəif asılıdır. fərdi müşahidələrin nəticələri.

Təsadüfi hadisələrin bu əlamətdar xassəsinin nəzəri əsası budur böyük ədədlər qanunu. "Böyük ədədlər qanunu" adı çoxlu sayda təsadüfi hadisələrin orta nəticələrinin sabitliyini təyin edən və bu sabitliyin səbəbini izah edən bir qrup teoremləri birləşdirir.

Böyük ədədlər qanununun ən sadə forması və tarixən bu bölmənin ilk teoremidir Bernoulli teoremi, hansı ki, əgər bütün sınaqlarda hadisənin baş vermə ehtimalı eynidirsə, sınaqların sayı artdıqca, hadisənin tezliyi hadisənin baş vermə ehtimalına meyl edir və təsadüfi olmağı dayandırır.

Puasson teoremi göstərir ki, bir sıra müstəqil sınaqlarda hadisənin tezliyi onun ehtimallarının arifmetik ortasına meyl edir və təsadüfi olmağı dayandırır.

Ehtimal nəzəriyyəsinin limit teoremləri, teoremlər Moivre-Laplas hadisənin baş vermə tezliyinin sabitliyinin xarakterini izah edin. Bu təbiət ondan ibarətdir ki, sınaqların sayının qeyri-məhdud artması ilə (hadisə ehtimalı bütün sınaqlarda eyni olarsa) hadisənin baş vermə sayının məhdudlaşdırıcı paylanmasıdır. normal paylanma.

Mərkəzi Limit Teoremi geniş yayılmasını izah edir normal qanun paylamalar. Teoremdə deyilir ki, hər dəfə sonlu dispersiyaya malik çoxlu sayda müstəqil təsadüfi dəyişənlərin əlavə edilməsi nəticəsində təsadüfi kəmiyyət əmələ gələrsə, bu təsadüfi dəyişənin paylanma qanunu praktiki olaraq belə çıxır. normal qanunla.

Aşağıda verilmiş teorem " başlığı ilə Böyük ədədlər qanunu" müəyyən, kifayət qədər ümumi şəraitdə təsadüfi dəyişənlərin sayının artması ilə onların arifmetik ortasının riyazi gözləntilərin arifmetik ortasına meyl etdiyini və təsadüfi olmağı dayandırdığını bildirir.

Lyapunov teoremi geniş yayılmasını izah edir normal qanun paylanması və onun formalaşma mexanizmini izah edir. Teorem bildirməyə imkan verir ki, çoxlu sayda müstəqil təsadüfi kəmiyyətin əlavə edilməsi nəticəsində yaranan, cəminin dispersiyasına nisbətən dispersiyaları kiçik olan təsadüfi kəmiyyətin paylanma qanunu çevrilir. praktiki olaraq həyata keçirilir normal qanunla. Və təsadüfi dəyişənlər həmişə sonsuz sayda səbəblər tərəfindən yaradıldığından və çox vaxt onların heç biri təsadüfi dəyişənin özünün dispersiyası ilə müqayisə edilə bilən dispersiyaya malik olmadığından, praktikada rast gəlinən təsadüfi dəyişənlərin əksəriyyəti normal paylanma qanununa tabedir.

Böyük ədədlər qanununun keyfiyyət və kəmiyyət ifadələri əsaslanır Çebışev bərabərsizliyi. Təsadüfi dəyişənin dəyərinin onun riyazi gözləntisindən sapmasının müəyyən müəyyən edilmiş ədəddən çox olması ehtimalının yuxarı həddini müəyyən edir. Maraqlıdır ki, Çebışev bərabərsizliyi hadisənin baş vermə ehtimalını təxmin edir paylanması məlum olmayan təsadüfi dəyişən üçün yalnız onun riyazi gözləntiləri və dispersiyaları məlumdur.

Çebışev bərabərsizliyi. Təsadüfi dəyişən x dispersiyaya malikdirsə, hər hansı e > 0 üçün aşağıdakı bərabərsizlik yerinə yetirilir: , Harada M x və D x - x təsadüfi kəmiyyətinin riyazi gözləntiləri və dispersiyaları.

Bernoulli teoremi. m n n Bernoulli sınaqlarında uğur sayı və p fərdi sınaqda uğur ehtimalı olsun. O zaman istənilən e > 0 üçün bu doğrudur .

Mərkəzi limit teoremi.Əgər təsadüfi dəyişənlər x 1 , x 2 , …, x n , … qoşa-müstəqildirsə, eyni şəkildə paylanırsa və sonlu dispersiyaya malikdirsə, onda n ® üçün x (- ,) şəklində bərabərdir.

Uğurlu satış işçilərinin sirri nədir? Hər hansı bir şirkətdə ən yaxşı satış işçilərini müşahidə etsəniz, onların bir ümumi cəhətinin olduğunu görəcəksiniz. Onların hər biri daha çox insanla görüşür və daha az uğur qazanan satıcılardan daha çox təqdimatlar edir. Bu insanlar başa düşürlər ki, satış rəqəmlər oyunudur və nə qədər çox insan öz məhsul və ya xidmətləri haqqında danışsa, bir o qədər çox sövdələşmə bağlayacaqlar – hamısı budur. Başa düşürlər ki, nəinki onlara mütləq “hə” deyəcək azsaylılarla, həm də onların təklifinə marağı o qədər də böyük olmayanlarla ünsiyyət qursalar, ortalar qanunu onların xeyrinə işləyəcək.

Gəliriniz satışların sayından asılı olacaq, eyni zamanda, etdiyiniz təqdimatların sayı ilə düz mütənasib olacaq. Ortalar qanununu başa düşdükdən və tətbiq etdikdən sonra yeni işə başlamaq və ya yeni sahədə işləmək ilə bağlı narahatlıq azalmağa başlayacaq. Nəticə etibarilə, pul qazanmaq qabiliyyətinə nəzarət hissi və inam artmağa başlayacaq. Əgər siz sadəcə təqdimatlar etsəniz və bu prosesdə bacarıqlarınızı artırsanız, sövdələşmələr gələcək.

Sövdələşmələrin sayı haqqında düşünmək əvəzinə, təqdimatların sayı haqqında daha yaxşı düşünün. Səhər oyanıb, axşam evə gəlib məhsulunuzu kim alacaq deyə düşünməyin mənası yoxdur. Bunun əvəzinə hər gün neçə zəng etməli olduğunuzu planlaşdırmaq daha yaxşıdır. Və sonra, nə olursa olsun - bütün bu zəngləri edin! Bu yanaşma işinizi asanlaşdıracaq - çünki bu, sadə və konkret məqsəddir. Konkret və əldə edilə bilən hədəfinizin olduğunu bilsəniz, planlaşdırılmış sayda zəng etmək sizin üçün daha asan olacaq. Bu proses zamanı bir neçə dəfə “bəli” eşitsəniz, bir o qədər yaxşıdır!

Və əgər "yox" desəniz, axşam siz bacardığınız hər şeyi vicdanla etdiyinizi hiss edəcəksiniz və gündə nə qədər pul qazandığınız və ya nə qədər yoldaş qazandığınız barədə düşüncələrdən əziyyət çəkməyəcəksiniz.

Tutaq ki, sizin şirkətinizdə və ya biznesinizdə orta satış işçisi hər dörd təqdimata bir sövdələşmə bağlayır. İndi təsəvvür edin ki, göyərtədən kartlar çəkirsiniz. Üç kostyumun hər bir kartı - kürək, brilyant və dəyənək - məhsul, xidmət və ya fürsəti peşəkar şəkildə təqdim etdiyiniz bir təqdimatdır. Bunu bacardığınız qədər yaxşı edirsiniz, amma hələ də müqaviləni bağlamırsınız. Və hər bir ürək kartı pul əldə etməyə və ya yeni bir yoldaş əldə etməyə imkan verən bir müqavilədir.

Belə bir vəziyyətdə, göyərtədən mümkün qədər çox kart çəkmək istəməzdinizmi? Tutaq ki, sizə pul ödəyərkən və ya hər dəfə ürək kartı çəkdiyiniz zaman sizə yeni bir yoldaş təklif edərkən, istədiyiniz qədər kart çəkmək təklif olunur. Siz həvəslə kartları çəkməyə başlayacaqsınız, indicə çıxardığınız kartın nə uyğun olduğunu fərqinə varmayacaqsınız.

Bilirsiniz ki, əlli iki kartdan ibarət göyərtədə on üç ürək var. Və iki göyərtədə iyirmi altı ürək kartı var və s. Kürək, brilyant və ya gürz çəkərkən məyus olacaqsınız? Əlbəttə yox! Siz yalnız düşünəcəksiniz ki, hər bir belə “darıx” sizi nəyə yaxınlaşdırır? Ürək kartına!

Amma bilirsən nə? Artıq sizə belə bir təklif verilib. İstədiyiniz qədər qazanmaq və həyatınızda çəkmək istədiyiniz qədər ürək çəkmək üçün unikal bir vəziyyətdəsiniz. Və sadəcə vicdanla "kart çəksəniz", bacarıqlarınızı təkmilləşdirsəniz və bir az kürək, almaz və dəyənəklərə dözsəniz, əla satıcı olacaqsınız və uğur qazanacaqsınız.

Satışı bu qədər əyləncəli edən şeylərdən biri də odur ki, siz hər dəfə göyərtəni qarışdırdığınız zaman kartların fərqli şəkildə qarışdırılmasıdır. Bəzən bütün ürəklər göyərtənin əvvəlində sona çatır və uğurlu bir seriyadan sonra (bizə elə görünəndə ki, biz heç vaxt itirməyəcəyik!) fərqli kostyumun uzun bir sıra kartları bizi gözləyir. Və digər vaxtlarda, ilk ürək əldə etmək üçün sonsuz sayda kürək, gürz və almazdan keçməlisən. Və bəzən müxtəlif kostyumların kartları ciddi şəkildə görünür. Ancaq hər halda, əlli iki kartın hər göyərtəsində, bir qayda olaraq, həmişə on üç ürək var. Sadəcə kartları tapana qədər çıxarın.

Kimdən: Leylya,  

Böyük ədədlər haqqında sözlər testlərin sayına aiddir - təsadüfi dəyişənin çox sayda dəyəri və ya çox sayda təsadüfi dəyişənlərin məcmu təsiri nəzərə alınır. Bu qanunun mahiyyəti belədir: fərdi təsadüfi dəyişənin tək bir təcrübədə hansı dəyəri alacağını proqnozlaşdırmaq mümkün olmasa da, çoxlu sayda müstəqil təsadüfi dəyişənlərin hərəkətinin ümumi nəticəsi öz təsadüfi mahiyyətini itirir və ola bilər. demək olar ki, etibarlı şəkildə proqnozlaşdırıla bilər (yəni yüksək ehtimalla). Məsələn, bir sikkənin hansı tərəfə düşəcəyini təxmin etmək mümkün deyil. Ancaq 2 ton sikkə atsanız, o zaman böyük əminliklə deyə bilərik ki, gerb yuxarıya düşən sikkələrin çəkisi 1 tona bərabərdir.

Böyük ədədlər qanunu, ilk növbədə, bir sınaqda təsadüfi dəyişənin orta dəyərdən verilən dəyərdən çox olmayan bir dəyəri qəbul etmə ehtimalını qiymətləndirən Çebışev bərabərsizliyinə aiddir.

Çebışev bərabərsizliyi. Qoy X- ixtiyari təsadüfi dəyişən, a=M(X) , A D(X) - onun variasiyası. Sonra

Misal. Maşını işə salan qolun diametrinin nominal (yəni tələb olunan) dəyəri bərabərdir 5 mm, və dispersiya artıq yoxdur 0.01 (bu, maşının dəqiqlik tolerantlığıdır). Bir kolun istehsalı zamanı diametrinin nominaldan sapmasının daha az olacağı ehtimalını hesablayın. 0,5 mm .

Həll. Qoy r.v. X– istehsal olunan kolun diametri. Şərtə görə, onun riyazi gözləntisi nominal diametrə bərabərdir (maşın parametrlərində sistematik nasazlıq olmadıqda): a=M(X)=5 , və dispersiya D(X)≤0,01. Çebışev bərabərsizliyinin tətbiqi ε = 0,5, alırıq:

Beləliklə, belə bir sapma ehtimalı olduqca yüksəkdir və buna görə də belə bir nəticəyə gələ bilərik ki, bir hissənin bir istehsalında diametrin nominaldan kənara çıxması demək olar ki, müəyyəndir. 0,5 mm .

Mənasında standart sapma σ xarakterizə edir orta təsadüfi dəyişənin mərkəzindən sapması (yəni onun riyazi gözləntisindən). Çünki bu orta sapma, sonra sınaq zamanı böyük (o-ya vurğu) sapmalar mümkündür. Nə qədər böyük sapmalar praktiki olaraq mümkündür? Normal paylanmış təsadüfi dəyişənləri öyrənərkən biz “üç siqma” qaydasını əldə etdik: normal paylanmış təsadüfi dəyişən X tək testdə-dən praktiki olaraq orta səviyyəsindən kənara çıxmır 3σ, Harada σ= σ(X)– r.v-nin standart sapması. X. Bu qaydanı bərabərsizliyi əldə etdiyimizdən götürdük

.

İndi ehtimalını qiymətləndirək ixtiyari təsadüfi dəyişən X standart kənarlaşmanın üç qatından çox olmayan orta göstəricidən fərqlənən dəyəri qəbul edin. Çebışev bərabərsizliyinin tətbiqi ε = 3σ və bunu nəzərə alaraq D(Х)= σ 2 , alırıq:

.

Beləliklə, ümumiyyətlə Təsadüfi dəyişənin ortadan üç standart kənarlaşmadan çox olma ehtimalını təxmin edə bilərik. 0.89 , normal paylanma üçün isə bu ehtimalla təmin edilə bilər 0.997 .

Çebışev bərabərsizliyi müstəqil eyni paylanmış təsadüfi dəyişənlər sisteminə ümumiləşdirilə bilər.

Ümumiləşdirilmiş Çebışev bərabərsizliyi. Əgər müstəqil təsadüfi dəyişənlər X 1 , X 2 , … , X n M(X i )= a və fərqlər D(X i )= D, Bu

At n=1 bu bərabərsizlik yuxarıda formalaşdırılan Çebışev bərabərsizliyinə çevrilir.

Müvafiq məsələlərin həlli üçün müstəqil əhəmiyyət kəsb edən Çebışev bərabərsizliyindən Çebışev teoreminin isbatı üçün istifadə olunur. Əvvəlcə bu teoremin mahiyyətindən danışacağıq, sonra isə onun formal ifadəsini verəcəyik.

Qoy X 1 , X 2 , … , X n– riyazi gözləntiləri olan çoxlu sayda müstəqil təsadüfi dəyişənlər M(X 1 )=a 1 , … , M(X n )=a n. Baxmayaraq ki, onların hər biri eksperiment nəticəsində orta hesabla (yəni riyazi gözləntidən) uzaq bir dəyər ala bilsə də, təsadüfi dəyişən
, onların arifmetik ortasına bərabərdir, çox güman ki, sabit ədədə yaxın qiymət alacaq
(bu, bütün riyazi gözləntilərin ortasıdır). Bu aşağıdakı deməkdir. Test nəticəsində müstəqil təsadüfi dəyişənlər olsun X 1 , X 2 , … , X n(onların çoxu var!) uyğun olaraq dəyərlər aldı X 1 , X 2 , … , X n müvafiq olaraq. Sonra bu dəyərlərin özləri müvafiq təsadüfi dəyişənlərin orta dəyərlərindən uzaq ola bilərsə, onların orta dəyəri
çox güman ki, rəqəmə yaxın olacaq
. Beləliklə, çoxlu sayda təsadüfi dəyişənlərin arifmetik ortası artıq öz təsadüfi xarakterini itirir və böyük dəqiqliklə proqnozlaşdırıla bilir. Bu, dəyərlərin təsadüfi kənara çıxması ilə izah edilə bilər X i-dan a i müxtəlif əlamətlərə malik ola bilər və buna görə də ümumilikdə bu sapmalar çox güman ki, kompensasiya olunur.

Terema Çebışev (böyük ədədlər qanunuÇebışev şəklində). Qoy X 1 , X 2 , … , X n … – dispersiyaları eyni sayda məhdud olan ikili müstəqil təsadüfi dəyişənlər ardıcıllığı. Onda ε ədədini nə qədər kiçik götürsək də, bərabərsizlik ehtimalı

sayı istəsə birə yaxın olacaq n kifayət qədər böyük təsadüfi dəyişənlər götürün. Formal olaraq bu o deməkdir ki, teorem şərtləri altında

Bu cür yaxınlaşma ehtimalla yaxınlaşma adlanır və işarələnir:

Beləliklə, Çebışev teoremi deyir ki, əgər kifayət qədər çox sayda müstəqil təsadüfi dəyişən varsa, bir testdə onların arifmetik ortası demək olar ki, etibarlı şəkildə riyazi gözləntilərinin ortasına yaxın bir dəyər alacaqdır.

Çox vaxt Çebışev teoremi təsadüfi dəyişənlərin olduğu vəziyyətlərdə tətbiq olunur X 1 , X 2 , … , X n … eyni paylanmaya malikdir (yəni eyni paylanma qanunu və ya eyni ehtimal sıxlığı). Əslində, bu, sadəcə olaraq eyni təsadüfi dəyişənin çoxlu sayda nümunəsidir.

Nəticə(ümumiləşdirilmiş Çebışev bərabərsizliyi). Əgər müstəqil təsadüfi dəyişənlər X 1 , X 2 , … , X n … riyazi gözləntilərlə eyni paylanmaya malikdir M(X i )= a və fərqlər D(X i )= D, Bu

, yəni.
.

Sübut ümumiləşdirilmiş Çebışev bərabərsizliyindən limitə keçməklə gəlir n→∞ .

Bir daha qeyd edək ki, yuxarıda yazılan bərabərliklər kəmiyyətin dəyərinə zəmanət vermir
üçün səy göstərir A saat n→∞. Bu kəmiyyət hələ də təsadüfi bir dəyişən olaraq qalır və onun fərdi dəyərləri olduqca uzaq ola bilər A. Ancaq belə bir ehtimal (uzaq A) dəyərlərin artması ilə n 0-a meyl edir.

Şərh. Nəticənin nəticəsi müstəqil təsadüfi dəyişənlər olduqda daha ümumi vəziyyətdə də etibarlıdır. X 1 , X 2 , … , X n … fərqli paylanmalara malikdir, lakin eyni riyazi gözləntilərə malikdir (bərabər A) və birgə məhdud fərqlər. Bu, müəyyən bir kəmiyyətin ölçülməsinin düzgünlüyünü proqnozlaşdırmağa imkan verir, hətta bu ölçmələr müxtəlif alətlərlə aparılsa belə.

Kəmiyyətləri ölçərkən bu nəticənin tətbiqini daha ətraflı nəzərdən keçirək. Bəzi cihazdan istifadə edək n həqiqi dəyəri bərabər olan eyni kəmiyyətin ölçüləri A və biz bilmirik. Belə ölçmələrin nəticələri X 1 , X 2 , … , X n bir-birindən (və həqiqi dəyərdən) əhəmiyyətli dərəcədə fərqlənə bilər A) müxtəlif təsadüfi amillərə görə (təzyiq dəyişiklikləri, temperatur, təsadüfi vibrasiya və s.). Nəzərə alın ki, r.v. X– kəmiyyətin birdəfəlik ölçülməsi üçün alətin oxunması, həmçinin r.v. X 1 , X 2 , … , X n– birinci, ikinci, ..., son ölçmədə alətin oxunması. Beləliklə, kəmiyyətlərin hər biri X 1 , X 2 , … , X n s.v.-in nümunələrindən yalnız biri var. X, və buna görə də onların hamısı r.v. ilə eyni paylanmaya malikdir. X. Ölçmə nəticələri bir-birindən asılı olmadığı üçün r.v. X 1 , X 2 , … , X n müstəqil hesab edilə bilər. Cihaz sistematik xəta yaratmırsa (məsələn, miqyasda sıfır "sönmür", yay uzanmır və s.), onda riyazi gözləntilərin olduğunu güman edə bilərik. M(X) = a, və buna görə də M(X 1 ) = ... = M(X n ) = a. Beləliklə, yuxarıdakı nəticənin şərtləri təmin edilir və buna görə də kəmiyyətin təxmini dəyəri kimi A təsadüfi dəyişənin “reallaşdırılmasını” götürə bilərik
təcrübəmizdə (bir sıra aparılmasından ibarətdir nölçmələr), yəni.

.

Çox sayda ölçmə ilə, bu düsturdan istifadə edərək yaxşı hesablama dəqiqliyi praktiki olaraq müəyyəndir. Bu, çox sayda ölçmə ilə onların arifmetik ortasının ölçülən dəyərin həqiqi dəyərindən praktiki olaraq çox da fərqlənməməsi praktiki prinsipin əsaslandırılmasıdır.

Riyazi statistikada geniş istifadə olunan “nümunə götürmə” üsulu təsadüfi dəyişənin nisbətən kiçik dəyərlərindən məqbul dəqiqliklə obyektiv xüsusiyyətlərini əldə etməyə imkan verən böyük ədədlər qanununa əsaslanır. Ancaq bu, növbəti hissədə müzakirə olunacaq.

Misal. Müəyyən bir kəmiyyət sistematik təhriflərə yol verməyən bir ölçü cihazında ölçülür A bir dəfə (alınan dəyər X 1 ), sonra başqa 99 dəfə (əldə edilmiş dəyərlər X 2 , … , X 100 ). Həqiqi ölçmə dəyəri üçün A ilk ölçmənin nəticəsi ilk olaraq alınır
, sonra isə bütün ölçmələrin arifmetik ortası
. Cihazın ölçmə dəqiqliyi elədir ki, ölçmənin standart sapması σ 1-dən çox deyil (buna görə də fərq D=σ 2 həmçinin 1-dən çox deyil). Hər bir ölçmə metodu üçün ölçmə xətasının 2-dən çox olmama ehtimalını təxmin edin.

Həll. Qoy r.v. X– bir ölçmə üçün alət oxunması. Sonra şərtlə M(X)=a. Verilən suallara cavab vermək üçün ümumiləşdirilmiş Çebışev bərabərsizliyini tətbiq edirik

ε-da =2 üçün ilk n=1 və sonra üçün n=100 . Birinci halda alırıq
, və ikincidə. Beləliklə, ikinci hal praktiki olaraq göstərilən ölçmə dəqiqliyinə zəmanət verir, birincisi isə bu mənada böyük şübhələr yaradır.

Yuxarıdakı ifadələri Bernoulli sxemində yaranan təsadüfi dəyişənlərə tətbiq edək. Bu sxemin mahiyyətini xatırlayaq. Qoy istehsal olunsun n hər biri bəzi hadisələri ehtiva edən müstəqil sınaqlar A eyni ehtimalla görünə bilər R, A q=1–r(mənada bu, əks hadisənin baş vermə ehtimalıdır - hadisənin baş verməməsi A) . Gəlin bir az xərcləyək n belə testlər. Təsadüfi dəyişənləri nəzərdən keçirək: X 1 - hadisənin baş vermə sayı A V 1 --ci sınaq, ..., X n- hadisənin baş vermə sayı A V n- ci sınaq. Hamısı s.v. dəyərlər qəbul edə bilər 0 və ya 1 (hadisə A testdə görünə bilər və ya olmaya bilər) və dəyəri 1 şərtə görə hər sınaqda ehtimalla qəbul edilir səh(hadisənin baş vermə ehtimalı A hər sınaqda) və dəyər 0 ehtimalla q= 1 – səh. Beləliklə, bu kəmiyyətlər eyni paylama qanunlarına malikdir:

X 1

X n

Buna görə də, bu kəmiyyətlərin orta dəyərləri və onların fərqləri də eynidir: M(X 1 )=0 ∙ q+1 ∙ p= p, …, M(X n )= səh ; D(X 1 )=(0 2 ∙ q+1 2 ∙ səh)− səh 2 = səh∙(1− səh)= səh ∙ q, … , D(X n )= səh ∙ q. Bu dəyərləri ümumiləşdirilmiş Çebışev bərabərsizliyinə əvəz edərək əldə edirik

.

Aydındır ki, r.v. X=X 1 +…+X n hadisənin baş vermə sayıdır A bütünlüklə n testlər (necə deyərlər - "uğurların sayı" n testlər). Aparılanlara icazə verin n sınaq hadisəsi A-də meydana çıxdı k onlardan. Onda əvvəlki bərabərsizlik belə yazıla bilər

.

Amma miqyası
, hadisənin baş vermə sayının nisbətinə bərabərdir A V n müstəqil sınaqlar, sınaqların ümumi sayına, əvvəllər nisbi hadisə tezliyi adlanırdı A V n testlər. Buna görə bərabərsizlik var

.

İndi limitə dönün n→∞, alırıq
, yəni.
(ehtimalla). Bu, Bernulli formasında böyük ədədlər qanununun məzmununu təşkil edir. Bundan belə nəticə çıxır ki, kifayət qədər çox sayda testlə n nisbi tezliyin özbaşına kiçik sapmaları
hadisələrin onun ehtimalından R- demək olar ki, etibarlı hadisələr və böyük sapmalar - demək olar ki, mümkün deyil. Nisbi tezliklərin belə sabitliyi ilə bağlı nəticə (əvvəllər haqqında danışdığımız eksperimental fakt) hadisənin nisbi tezliyinin dəyişdiyi bir ədəd kimi hadisənin ehtimalının əvvəllər təqdim edilmiş statistik tərifini əsaslandırır.

Nəzərə alsaq ki, ifadə səh∙ q= səh∙(1− səh)= səh− səh 2 dəyişmə intervalını keçmir
(bu seqmentdə bu funksiyanın minimumunu tapmaqla bunu yoxlamaq asandır), yuxarıdakı bərabərsizlikdən
bunu əldə etmək asandır

,

müvafiq problemlərin həllində istifadə olunur (onlardan biri aşağıda veriləcəkdir).

Misal. Sikkə 1000 dəfə atıldı. Gerbin görünüşünün nisbi tezliyinin onun ehtimalından kənarlaşmasının 0,1-dən az olması ehtimalını qiymətləndirin.

Həll. Bərabərsizliyin tətbiqi
saat səh= q=1/2 , n=1000 , ε=0,1, alacağıq.

Misal. Əvvəlki nümunənin şərtlərinə uyğun olaraq nömrənin olması ehtimalını təxmin edin k atılan emblemlər aralığında olacaq 400 əvvəl 600 .

Həll. Vəziyyət 400< k<600 bunun mənası 400/1000< k/ n<600/1000 , yəni. 0.4< W n (A)<0.6 və ya
. Əvvəlki misaldan da gördüyümüz kimi, belə bir hadisənin baş vermə ehtimalı heç də az deyil 0.975 .

Misal. Hər hansı bir hadisənin baş vermə ehtimalını hesablamaq üçün A Hadisədə 1000 təcrübə aparıldı A 300 dəfə ortaya çıxdı. Nisbi tezliyin (300/1000 = 0,3-ə bərabər) həqiqi ehtimaldan uzaq olması ehtimalını təxmin edin R 0,1-dən çox olmamalıdır.

Həll. Yuxarıdakı bərabərsizliyin tətbiqi
n=1000, ε=0.1 üçün alırıq.

Böyük və müxtəlif material üzərində aşkar edilmiş təsadüfi hadisələrin baş vermə tezliklərinin sabitləşməsi fenomeni əvvəlcə heç bir əsaslandırmaya malik deyildi və sırf empirik bir fakt kimi qəbul edildi. Bu sahədə ilk nəzəri nəticə 1713-cü ildə nəşr olunan və böyük ədədlər qanunlarının əsasını qoyan məşhur Bernulli teoremi oldu.

Bernoulli teoremi öz məzmununda həddi teoremdir, yəni çox sayda müşahidə ilə ehtimal parametrlərinin nə olacağını söyləyən asimptotik məna ifadəsidir. Bu tip bütün müasir çoxsaylı ifadələrin əcdadı məhz Bernulli teoremidir.

Bu gün belə görünür ki, böyük ədədlərin riyazi qanunu bir çox real proseslərin hansısa ümumi xassəsinin əksidir.

Böyük ədədlər qanununa bu qanunun tətbiqinin tükənmiş potensial imkanlarına uyğun gələn ən geniş əhatə dairəsini vermək istəyi ilə əsrimizin ən böyük riyaziyyatçılarından biri A. N. Kolmoqorov onun mahiyyətini belə ifadə etdi: böyük ədədlər qanunu "çox sayda təsadüfi amillərin ümumi hərəkətinin təsadüfdən demək olar ki, müstəqil nəticəyə gətirdiyi ümumi prinsip."

Beləliklə, böyük ədədlər qanununun iki şərhi var. Biri riyazidir, spesifik riyazi modellər, formulalar, nəzəriyyələrlə əlaqələndirilir, ikincisi isə bu çərçivədən kənara çıxan daha ümumidir. İkinci şərh, zahiri olaraq belə davamlılığa malik olmayan çoxlu sayda gizli və ya görünən əməliyyat amilləri fonunda praktikada tez-tez müşahidə olunan az və ya çox yönlü hərəkətin formalaşması fenomeni ilə əlaqələndirilir. İkinci şərhlə əlaqəli nümunələr azad bazarda qiymətlərin müəyyən edilməsi və müəyyən bir məsələ ilə bağlı ictimai rəyin formalaşmasıdır.

Böyük ədədlər qanununun bu ümumi şərhini qeyd edərək, bu qanunun xüsusi riyazi formulalarına müraciət edək.

Yuxarıda dediyimiz kimi, ehtimal nəzəriyyəsi üçün birinci və əsaslı ən vacibi Bernulli teoremidir. Ətraf aləmin ən mühüm qanunlarından birini əks etdirən bu riyazi faktın məzmunu aşağıdakılara gəlir.

Şərtləri ardıcıl olaraq testdən testə təkrarlanan əlaqəsiz (yəni müstəqil) testlər ardıcıllığını nəzərdən keçirin. Hər bir testin nəticəsi bizi maraqlandıran hadisənin görünüşü və ya baş verməməsidir A.

Bu prosedur (Bernoulli sxemi) bir çox praktik sahələr üçün xarakterik hesab edilə bilər: yeni doğulmuş uşaqların ardıcıllığında "oğlan - qız", gündəlik meteoroloji müşahidələr ("yağış yağdı - olmadı"), istehsal olunan məhsulların axınına nəzarət ( "normal - qüsurlu") və s.

Hadisənin baş vermə tezliyi A saat P testlər ( t A -

hadisə tezliyi A V P testlər) böyümə ilə malikdir P onun dəyərini sabitləşdirmək meyli empirik faktdır.

Bernoulli teoremi.İstənilən ixtiyari kiçik müsbət ədədi seçək e Sonra

Biz vurğulayırıq ki, Bernullinin müəyyən riyazi modeldə (Bernulli sxemində) müəyyən etdiyi riyazi faktı tezlik sabitliyinin empirik şəkildə müəyyən edilmiş qanunauyğunluğu ilə qarışdırmaq olmaz. Bernoulli sadəcə (9.1) düsturunu qeyd etməklə kifayətlənməyib, təcrübənin ehtiyaclarını nəzərə alaraq, bu düsturda mövcud olan bərabərsizliyə qiymət verib. Aşağıda bu şərhə müraciət edəcəyik.

Bernoulli'nin böyük ədədlər qanunu, onu təkmilləşdirməyə çalışan çoxlu sayda riyaziyyatçının tədqiqat obyekti olmuşdur. Bu təkmilləşdirmələrdən biri ingilis riyaziyyatçısı Moivre tərəfindən əldə edilmişdir və hazırda Moivre-Laplas teoremi adlanır. Bernoulli sxemində normallaşdırılmış kəmiyyətlərin ardıcıllığını nəzərdən keçirin:

Moivrin inteqral teoremi - Laplas.İstənilən iki rəqəmi seçək X ( Və x 2. Bu halda x, x 7, sonra at P -» °°

Əgər (9.3) düsturunun sağ tərəfində dəyişən x x sonsuzluğa meyl edir, onda yalnız x 2-dən asılı olaraq yaranan hədd (indeks 2 bu halda çıxarıla bilər) paylama funksiyası olacaq, buna deyilir. standart normal paylama, və ya Gauss qanunu.

(9.3) düsturunun sağ tərəfi y =-ə bərabərdir F(x 2) - F(x x). F(x 2)-> 1 saat x 2-> °° və F(x,) -> 0 at x, -> Kifayət qədər böyük seçiminə görə

X] > 0 və X]n mütləq qiymətdə kifayət qədər böyükdür, aşağıdakı bərabərsizliyi əldə edirik:

Formula (9.2) nəzərə alınmaqla, praktiki olaraq etibarlı hesablamalar çıxara bilərik:

Əgər y = 0,95 etibar səviyyəsi (yəni, 0,05 səhv ehtimalı) kiməsə qeyri-kafi görünə bilərsə, yuxarıda qeyd olunan üç siqma qaydasından istifadə edərək “təhlükəsiz oynaya” və bir az daha geniş etimad intervalı qura bilərsiniz:

Bu interval çox yüksək etimad səviyyəsinə uyğundur y = 0,997 (normal paylama cədvəllərinə baxın).

Sikkə atmağın nümunəsini nəzərdən keçirək. Gəlin bir sikkə ataq n = 100 dəfə. Tezlik ola bilərmi R ehtimaldan çox fərqli olacaq R= 0,5 (sikkənin simmetrik olduğunu nəzərə alsaq), məsələn, sıfıra bərabər olacaqmı? Bunun üçün gerbin bir dəfə də olsun yerə düşməməsi lazımdır. Belə bir hadisə nəzəri cəhətdən mümkündür, lakin biz artıq oxşar ehtimalları hesablamışıq; bu hadisə üçün o, bərabər olacaq Bu dəyər

son dərəcə kiçik, onun sırası onluq nöqtədən sonra 30 sıfır olan bir ədəddir. Belə bir ehtimalı olan bir hadisəni praktiki olaraq qeyri-mümkün hesab etmək olar. Çox sayda təcrübə ilə ehtimaldan tezliyin hansı sapmaları praktiki olaraq mümkündür? Moivre-Laplas teoremindən istifadə edərək bu suala belə cavab veririk: ehtimalla saat= 0,95 gerb tezliyi R etimad intervalına uyğundur:

0.05 səhv kiçik görünmürsə, təcrübələrin sayını artırmalısınız (sikkə atma). Artan zaman P etimad intervalının eni azalır (təəssüf ki, istədiyimiz qədər tez deyil, əksinə -Jn). Məsələn, nə vaxt P= 10,000 biz bunu alırıq R etibarlılıq ehtimalı ilə etimad intervalında yatır saat= 0,95: 0,5 ±0,01.

Beləliklə, biz tezliyi ehtimala yaxınlaşdırmaq məsələsini kəmiyyətcə başa düşdük.

İndi onun tezliyinə əsasən hadisənin baş vermə ehtimalını tapaq və bu yaxınlaşmanın xətasını qiymətləndirək.

Gəlin çoxlu sayda təcrübə aparaq P(bir sikkə atmaq), hadisənin tezliyini tapın A və biz onun ehtimalını qiymətləndirmək istəyirik R.

Böyük ədədlər qanunundan P belə olur:

İndi təqribi bərabərliyin (9.7) praktiki olaraq mümkün səhvini qiymətləndirək. Bunun üçün (9.5) bərabərsizliyindən aşağıdakı formada istifadə edirik:

Tapmaq R By R(9.8) bərabərsizliyini həll etməliyik, bunun üçün onun kvadratını tutmalı və müvafiq kvadrat tənliyi həll etməliyik. Nəticədə əldə edirik:

Harada

Təxmini hesablama üçün R By R(9.8) düsturunda ola bilər R sağda ilə əvəz edin R və ya (9.10), (9.11) düsturlarında qəbul edin

Sonra alırıq:

İcazə verin P= 400 təcrübə tezlik dəyəri əldə edilmişdir R= 0,25, onda y = 0,95 inam səviyyəsi ilə tapırıq:

Əgər ehtimalı daha dəqiq bilməliyiksə, məsələn, 0,01-dən çox olmayan xəta ilə? Bunun üçün təcrübələrin sayını artırmaq lazımdır.

(9.12) düsturunda ehtimalı qəbul etsək R= 0.25, biz xəta dəyərini verilmiş qiymət 0.01-ə bərabərləşdiririk və bunun üçün tənlik alırıq. P:

Bu tənliyi həll edərək əldə edirik n~ 7500.

İndi başqa bir sualı nəzərdən keçirək: təcrübələrdə əldə edilən tezlikin ehtimaldan kənara çıxmasını təsadüfi səbəblərlə izah etmək olarmı, yoxsa bu kənarlaşma ehtimalın bizim gözlədiyimiz kimi olmadığını göstərir? Başqa sözlə, təcrübə qəbul edilmiş statistik fərziyyəni təsdiq edirmi və ya əksinə, onun rədd edilməsini tələb edirmi?

Məsələn, bir sikkə atın P= 800 dəfə, gerbin görünmə tezliyini alırıq R= 0,52. Biz sikkənin asimmetrik olduğundan şübhələnirdik. Bu şübhə haqlıdırmı? Bu suala cavab vermək üçün sikkənin simmetrik olması fərziyyəsindən çıxış edəcəyik (p = 0,5). Etibar intervalını tapaq (etibar ehtimalı ilə saat= 0,95) gerbin görünmə tezliyi üçün. Təcrübədə əldə edilən dəyər isə R= 0,52 bu intervala uyğun gəlir - hər şey normaldır, sikkənin simmetriyası ilə bağlı qəbul edilmiş fərziyyə eksperimental məlumatlarla ziddiyyət təşkil etmir. Formula (9.12) at R= 0,5 0,5 ± 0,035 interval verir; alınan dəyər p = 0.52 bu intervala uyğun gəlir, bu o deməkdir ki, sikkə asimmetriya şübhələrindən "təmizlənməlidir".

Təsadüfi hadisələrdə müşahidə olunan riyazi gözləntidən müxtəlif sapmaların təsadüfi və ya “əhəmiyyətli” olub olmadığını mühakimə etmək üçün oxşar üsullardan istifadə olunur. Məsələn, qablaşdırılmış malların bir neçə nümunəsində az çəki təsadüfən aşkarlanıb, yoxsa bu, müştərilərin sistemli şəkildə aldadılmasından xəbər verir? Yeni dərmandan istifadə edən xəstələrdə sağalma sürəti təsadüfən artıb, yoxsa bu, dərmanın təsiri ilə bağlıdır?

Normal qanun, ehtimal nəzəriyyəsində və onun praktiki tətbiqlərində xüsusilə mühüm rol oynayır. Yuxarıda gördük ki, təsadüfi dəyişən - Bernulli sxemində hansısa hadisənin baş vermə sayı - ilə P-» °° normal qanuna endirilir. Ancaq daha ümumi bir nəticə var.

Mərkəzi limit teoremi.Çoxlu sayda müstəqil (və ya zəif asılı) təsadüfi dəyişənlərin dispersiya sırasına görə müqayisə oluna bilən cəmi, terminlərin paylanma qanunlarının nə olmasından asılı olmayaraq normal qanuna uyğun olaraq paylanır. Yuxarıdakı ifadə mərkəzi limit nəzəriyyəsinin kobud keyfiyyət ifadəsidir. Bu teorem çoxlu formalara malikdir, bir-birindən təsadüfi dəyişənlərin şərt sayının artması ilə cəminin “normallaşdırılması” üçün təmin etməli olduğu şərtlərlə fərqlənir.

Normal paylanma sıxlığı Dx) düsturla ifadə edilir:

Harada A - təsadüfi dəyişənin riyazi gözləntisi X s= V7) onun standart kənarlaşmasıdır.

(x 1? x 2) intervalına düşmə ehtimalını hesablamaq üçün inteqraldan istifadə olunur:

Sıxlıqda (9.14) inteqral elementar funksiyalarla ifadə edilmədiyindən (“qəbul edilmir”), o zaman (9.14) hesablamaq üçün standart normal paylanmanın inteqral paylanma funksiyasının cədvəllərindən istifadə edirlər. a = 0, a = 1 (belə cədvəllər ehtimal nəzəriyyəsi üzrə istənilən dərslikdə mövcuddur):

(10.15) tənliyindən istifadə etməklə (9.14) ehtimalı düsturla ifadə edilir:

Misal. Təsadüfi dəyişənin olma ehtimalını tapın X, parametrlərlə normal paylanmaya malik olması A, a, riyazi gözlənti modulundan 3-dən çox olmayan kənara çıxacaq.

(9.16) düsturu və normal qanunun paylanma funksiyası cədvəlindən istifadə edərək əldə edirik:

Misal. 700 müstəqil eksperimentin hər birində hadisə A daimi ehtimalla baş verir R= 0,35. Hadisənin baş vermə ehtimalını tapın A Baş verəcək:

• 1) tam olaraq 270 dəfə;
• 2) 270-dən az və 230 dəfədən çox;
• 3) 270 dəfədən çox.

Riyazi gözləntinin tapılması A = və s və standart sapma:

təsadüfi dəyişən - hadisənin baş vermə sayı A:

Mərkəzləşdirilmiş və normallaşdırılmış dəyərin tapılması X:

Normal paylanma sıxlığı cədvəllərindən tapırıq f(x):

İndi tapaq R w (x,> 270) = P 700 (270 F(1.98) = = 1 - 0.97615 = 0.02385.

Böyük sayda problemlərin tədqiqində ciddi addım 1867-ci ildə P. L. Çebışev tərəfindən atıldı. O, müstəqil təsadüfi dəyişənlərdən riyazi gözləntilərin və dispersiyaların mövcudluğundan başqa heç nə tələb olunmadığı çox ümumi bir hal hesab edirdi.

Çebışev bərabərsizliyi.İxtiyari olaraq kiçik müsbət e ədədi üçün aşağıdakı bərabərsizlik yerinə yetirilir:

Çebışev teoremi.Əgər x x, x 2, ..., x p - ikili müstəqil təsadüfi dəyişənlər, hər birinin riyazi gözləntiləri var E(Xj) = ci və variasiya D(x,) =) və dispersiyalar vahid məhduddur, yəni. 1,2 ..., onda hər hansı ixtiyari kiçik müsbət ədəd üçün e aşağıdakı əlaqə mövcuddur:

Nəticə. Əgər a,= aio, -o 2 , i= 1.2 ..., onda

Tapşırıq. Sikkə neçə dəfə atılmalıdır ki, ehtimal ondan az olmasın y - 0,997, gerbin düşmə tezliyinin (0,499; 0,501) intervalında olacağını iddia etmək olar?

Fərz edək ki, sikkə simmetrikdir, p - q - 0.5. (9.19) düsturunda Çebışev teoremini təsadüfi dəyişənə tətbiq edək X- gerbin görünmə tezliyi P sikkə atışları. Biz bunu artıq yuxarıda göstərmişik X = X x + X 2+ ... +X„, Harada X t - sikkə başdırsa 1 dəyərini, quyruqdursa 0 dəyərini alan təsadüfi dəyişən. Belə ki:

Ehtimal işarəsi altında göstərilən hadisəyə əks olan hadisə üçün bərabərsizliyi (9.19) yazaq:

Bizim vəziyyətimizdə [e = 0.001, cj 2 = /?-p)]t gerbdə baş verənlərin sayıdır. P atma. Bu kəmiyyətləri sonuncu bərabərsizliklə əvəz edərək və məsələnin şərtlərinə uyğun olaraq bərabərsizliyin ödənilməli olduğunu nəzərə alaraq, əldə edirik:

Verilmiş nümunə təsadüfi dəyişənlərin müəyyən sapmalarının ehtimallarını qiymətləndirmək üçün Çebışev bərabərsizliyindən istifadə etmək imkanını göstərir (həmçinin bu ehtimalların hesablanması ilə bağlı bu misal kimi problemlər). Çebışev bərabərsizliyinin üstünlüyü ondadır ki, təsadüfi dəyişənlərin paylanması qanunları haqqında bilik tələb etmir. Əlbəttə ki, belə bir qanun məlumdursa, Çebışev qeyri-bərabərliyi çox təxmini hesablamalar verir.

Gəlin eyni misala baxaq, lakin sikkə atmağın Bernulli sxeminin xüsusi halı olması faktından istifadə edək. Uğurların sayı (nümunədə - gerblərin sayı) binomial qanuna tabedir və böyük P bu qanun Moivre-Laplas inteqral teoreminə görə riyazi gözlənti ilə normal qanunla təmsil oluna bilər. a = pr = n? 0,5 və standart sapma ilə a = yfnpq - 25=0,5l/l. Təsadüfi dəyişən - gerbin düşmə tezliyi - riyazi gözləntiyə = 0,5 və standart sapmaya malikdir

Sonra bizdə:

Son bərabərsizlikdən alırıq:

Normal paylama cədvəllərindən tapırıq:

Görürük ki, normal yaxınlaşma gerbin ehtimalının qiymətləndirilməsində verilmiş xətanı təmin edən sikkə atışlarının sayını verir ki, bu da Çebışev bərabərsizliyindən istifadə etməklə əldə edilən qiymətləndirmə ilə müqayisədə 37 dəfə kiçikdir (lakin Çebışev bərabərsizliyi bunu etməyə imkan verir. tədqiq olunan təsadüfi kəmiyyətin paylanma qanunu haqqında məlumatımız olmadığı halda oxşar hesablamalar).

İndi (9.16) düsturu ilə həll edilmiş tətbiqi məsələni nəzərdən keçirək.

Rəqabət problemi. İki rəqabət aparan dəmir yolu şirkətinin hər birində Moskva və Sankt-Peterburq arasında bir qatar var. Bu qatarlar təxminən eyni təchiz olunmuşdur və təxminən eyni vaxtda yola düşür və çatır. Belə iddia edək P= 1000 sərnişin müstəqil və təsadüfi olaraq öz qatarını seçir, buna görə də sərnişinlər tərəfindən qatar seçimi üçün riyazi model olaraq Bernoulli sxemindən istifadə edirik. Pçətinliklər və uğur ehtimalı R= 0,5. Şirkət bir-birinə zidd olan iki şərti nəzərə alaraq qatarda neçə oturacaq təqdim edəcəyinə qərar verməlidir: bir tərəfdən boş yerlərin olmasını istəmirsiniz, digər tərəfdən isə insanların qatardan narazı olmasını istəmirsiniz. yerlərin olmaması (növbəti dəfə rəqib şirkətlərə üstünlük verəcəklər). Əlbəttə ki, qatarda təmin edilə bilər P= 1000 yer, amma sonra boş yerlər olacaq. Moivre-nin inteqral nəzəriyyəsindən istifadə edərək qəbul edilmiş riyazi model çərçivəsində təsadüfi dəyişən - qatardakı sərnişinlərin sayı - Laplas riyazi gözlənti ilə normal qanuna tabe olur. a = pr = p/2 və dispersiya a 2 = npq = p/4 ardıcıl olaraq. Ehtimal ki, daha çox s sərnişinlər nisbəti ilə müəyyən edilir:

Risk səviyyəsini təyin edin A, yəni daha çoxunun gəlməsi ehtimalı s sərnişinlər:

Buradan:

Əgər A normal qanunun paylanma funksiyasının cədvəllərindən tapılan sonuncu tənliyin riskinin köküdür, onda əldə edirik:

Əgər, məsələn, P = 1000, A= 0,01 (bu risk səviyyəsi yerlərin sayı deməkdir s 100-dən 99-da kifayət edəcək), onda x a ~ 2.33 və s = 537 yer. Üstəlik, hər iki şirkət eyni risk səviyyələrini qəbul edərsə A= 0,01, onda iki qatarda cəmi 1074 oturacaq olacaq, onlardan 74-ü boş olacaq. Eynilə, hesablamaq olar ki, 514 yer bütün hallarda 80%, 549 oturacaq isə 1000 işdən 999-da kifayət edər.

Oxşar mülahizələr digər rəqabət aparan xidmət problemlərinə də aiddir. Məsələn, əgər T kinoteatrlar da buna görə yarışır P Tamaşaçılar, o zaman qəbul edilməlidir R= -. alırıq,

oturacaqların sayı nə qədərdir s kinoteatrda nisbəti ilə müəyyən edilməlidir:

Boş yerlərin ümumi sayı bərabərdir:

üçün A = 0,01, P= 1000 və T= 2, 3, 4, bu ədədin dəyərləri müvafiq olaraq təxminən 74, 126, 147-yə bərabərdir.

Başqa bir misala baxaq. Qatardan ibarət olsun P - 100 vaqon. Hər bir avtomobilin çəkisi riyazi gözlənti ilə təsadüfi dəyişəndir A - 65 ton və orta kvadrat gözlənti o = 9 ton Lokomotiv çəkisi 6600 tondan çox olmadıqda bir qatarı daşıya bilər; əks halda, ikinci bir lokomotiv bağlamalı olacaqsınız. Bunu etməməyiniz ehtimalını tapmaq lazımdır.

fərdi avtomobillərin çəkisi: , eyni riyazi gözləntinin olması A - 65 və eyni fərq d- o 2 = 81. Riyazi gözləntilər qaydasına görə: E(x) - 100 * 65 = 6500. Dispersiyaların toplanması qaydasına görə: D(x) = 100 x 81 = 8100. Kökü çıxararaq standart kənarlaşmanı tapırıq. Bir lokomotivin qatarı çəkməsi üçün qatarın çəkisi olmalıdır X məhdudlaşdırıcı olduğu ortaya çıxdı, yəni (0; 6600) intervalına düşdü. Təsadüfi dəyişən x - 100 şərtin cəmi - normal paylanmış hesab edilə bilər. (9.16) düsturundan istifadə edərək əldə edirik:

Buradan belə çıxır ki, lokomotiv təxminən 0,864 ehtimalla qatarın öhdəsindən gələcək. İndi qatardakı vaqonların sayını iki azaldaq, yəni götürək P= 98. İndi lokomotivin qatarla "öhdəsindən gəlmək" ehtimalını hesablayaraq, 0,99 sıra dəyərini alırıq, yəni demək olar ki, müəyyən bir hadisə, baxmayaraq ki, bunun üçün yalnız iki vaqon çıxarılmalı idi.

Beləliklə, çox sayda təsadüfi dəyişənlərin cəmi ilə məşğul oluruqsa, normal qanundan istifadə edə bilərik. Təbii ki, burada sual yaranır: cəminin paylanma qanununun artıq “normallaşdırılması” üçün neçə təsadüfi dəyişən əlavə etmək lazımdır? Bu, terminlərin paylanması qanunlarının nə olmasından asılıdır. Elə mürəkkəb qanunlar var ki, normallaşma yalnız çox sayda terminlə baş verir. Ancaq bu qanunları riyaziyyatçılar icad edirlər, təbiət, bir qayda olaraq, qəsdən belə çətinliklər yaratmır. Adətən praktikada normal qanundan istifadə edə bilmək üçün beş-altı termin kifayətdir.

Eyni şəkildə paylanmış təsadüfi dəyişənlərin cəminin paylanma qanununun “normallaşması” sürəti (0, 1) intervalında vahid paylanmaya malik təsadüfi dəyişənlər nümunəsi ilə təsvir edilə bilər. Belə bir paylanmanın əyrisi artıq normal qanuna bənzəməyən düzbucaqlı formasına malikdir. İki belə müstəqil dəyişən əlavə edək - biz Simpson qanunu adlanan qanuna görə paylanmış təsadüfi dəyişən alırıq, qrafik təsviri ikitərəfli üçbucaq şəklindədir. Bu da normal qanun kimi görünmür, amma daha yaxşıdır. Və üç belə bərabər paylanmış təsadüfi dəyişəni toplasanız, normal əyriyə çox oxşar olan üç parabola seqmentindən ibarət əyri alırsınız. Altı belə təsadüfi dəyişəni toplasanız, normaldan fərqlənməyən əyri alırsınız. Bu, normal paylanmış təsadüfi kəmiyyətin alınması üçün geniş istifadə olunan metodun əsasını təşkil edir və bütün müasir kompüterlər vahid paylanmış (0, 1) təsadüfi ədədlər üçün sensorlarla təchiz edilmişdir.

Bunu yoxlamaq üçün praktik üsullardan biri kimi aşağıdakı üsul tövsiyə olunur. Səviyyə ilə bir hadisənin tezliyi üçün etimad intervalı qururuq saatÜç siqma qaydasına görə = 0,997:

və onun hər iki ucu (0, 1) seqmentindən kənara çıxmazsa, normal qanundan istifadə etmək olar. Etibar intervalının hüdudlarından hər hansı biri seqmentdən kənardadırsa (0, 1), onda normal qanundan istifadə etmək olmaz. Bununla belə, bəzi şərtlərdə, bəzi təsadüfi hadisənin tezliyi üçün binomial qanun, normal olana meyl etmirsə, başqa bir qanuna meyl edə bilər.

Bir çox tətbiqlərdə Bernoulli sxemi təsadüfi bir təcrübənin riyazi modeli kimi istifadə olunur, burada sınaqların sayı P böyükdür, təsadüfi hadisə olduqca nadirdir, yəni. R = və s kiçik deyil, həm də böyük deyil (O -5-20 diapazonunda dəyişir). Bu halda, məhdudlaşdırıcı əlaqə var:

Formula (9.20) binom qanunu üçün Puasson yaxınlaşması adlanır, çünki onun sağ tərəfindəki ehtimal paylanması Puasson qanunu adlanır. Puasson paylanmasının nadir hadisələr üçün ehtimal paylanması olduğu deyilir, çünki limitlər təmin edildikdə baş verir: P -»°°, R-»0, lakin X = pr oo.

Misal. Ad günləri. Ehtimal nədir R t (k) 500 nəfərlik cəmiyyətdə Kimə insanlar Yeni il günü doğulublar? Əgər bu 500 nəfər təsadüfi seçilərsə, o zaman müvəffəqiyyət ehtimalı ilə Bernoulli sxemini tətbiq etmək olar. P = 1/365. Sonra

Müxtəlif ehtimallar üçün hesablamalar Kimə aşağıdakı dəyərləri verin: RU = 0,3484...; R 2 = 0,2388...; R 3 = 0,1089...; P 4 = 0,0372...; R 5 = 0,0101...; R 6= 0,0023... üçün Puasson düsturundan istifadə edərək müvafiq təxminlər X = 500 1/365 = 1,37

aşağıdakı dəyərləri verin: Ru = 0,3481...; R 2 = 0,2385...; P ъ = 0,1089; R 4 = 0,0373...; P 5 = 0,0102...; P 6 = 0,0023... Bütün səhvlər yalnız dördüncü onluq yerindədir.

Nadir hadisələrin Puasson qanunundan istifadə edə biləcəyiniz vəziyyətlərin nümunələri.

Telefon stansiyasında, aşağı ehtimalla səhv bir əlaqə baş verir R, adətən R~0,005. Onda Puasson düsturu bizə verilən ümumi əlaqə sayı üçün səhv birləşmələrin olma ehtimalını tapmağa imkan verir. n~ 1000 nə vaxt X = pr =1000 0,005 = 5.

Çörəkləri bişirərkən xəmirə kişmiş əlavə edin. Qarışdırmağa görə, kişmiş çörəklərinin tezliyinin təxminən Poisson paylanmasına uyğun olacağı gözlənilməlidir R p (k, X), Harada X- xəmirdə kişmişin sıxlığı.

Radioaktiv maddə i-hissəcikləri buraxır. D-hissəciklərin sayının zamanla çatdığı hadisə t verilən məkan sahəsi sabit bir dəyər alır üçün, Puasson qanununa tabedir.

X-şüalarına məruz qaldıqda dəyişdirilmiş xromosomlu canlı hüceyrələrin sayı Poisson paylanmasına uyğundur.

Beləliklə, böyük ədədlər qanunları təsadüfi bir təcrübənin elementar nəticələrinin naməlum ehtimallarının qiymətləndirilməsi ilə əlaqəli riyazi statistika problemini həll etməyə imkan verir. Bu biliklər sayəsində biz ehtimal nəzəriyyəsinin üsullarını praktiki olaraq mənalı və faydalı edirik. Böyük ədədlərin qanunları naməlum elementar ehtimallar haqqında məlumatın başqa formada - statistik fərziyyələrin yoxlanılması formasında əldə edilməsi məsələsini də həll etməyə imkan verir.

Statistik fərziyyələrin yoxlanılması problemlərinin həlli üçün tərtib və ehtimal mexanizmini daha ətraflı nəzərdən keçirək.

Böyük ədədlər qanunu ehtimal nəzəriyyəsində sabit paylanmadan kifayət qədər böyük sonlu seçmənin empirik ortasının (arifmetik ortası) bu paylanmanın nəzəri ortasına (riyazi gözləntiyə) yaxın olduğunu bildirir. Konvergensiyanın növündən asılı olaraq, ehtimalla yaxınlaşma baş verdiyi zaman böyük ədədlərin zəif qanunu ilə yaxınlaşma demək olar ki, hər yerdə baş verən böyük ədədlərin güclü qanunu arasında fərq qoyulur.

Həmişə hər hansı bir əvvəlcədən ehtimalla daha az olan məhdud sayda sınaqlar var 1 bəzi hadisənin baş vermə tezliyi onun ehtimalından mümkün qədər az fərqlənəcəkdir.

Böyük ədədlər qanununun ümumi mənası: çoxlu sayda eyni və müstəqil təsadüfi amillərin birgə hərəkəti həddə təsadüfdən asılı olmayan nəticəyə gətirib çıxarır.

Sonlu nümunə təhlili əsasında ehtimalın qiymətləndirilməsi üsulları bu xüsusiyyətə əsaslanır. Bunun bariz nümunəsi seçicilər arasında sorğu əsasında seçki nəticələrinin proqnozlaşdırılmasıdır.

Ensiklopedik YouTube

1 / 5

✪ Böyük ədədlər qanunu

✪ 07 - Ehtimal nəzəriyyəsi. Böyük ədədlər qanunu

✪ 42 Böyük Ədədlər Qanunu

✪ 1 - Çebışevin böyük ədədlər qanunu

✪ 11-ci sinif, 25-ci dərs, Qauss əyrisi. Böyük ədədlər qanunu

Altyazılar

Riyaziyyatda və ehtimal nəzəriyyəsində bəlkə də ən intuitiv qanun olan böyük ədədlər qanununa baxaq. Və çox şeyə aid olduğu üçün bəzən istifadə olunur və səhv başa düşülür. İcazə verin, əvvəlcə onu dəqiqlik üçün müəyyən edim, sonra intuisiya haqqında danışaq. Təsadüfi dəyişəni götürək, məsələn, X. Tutaq ki, biz onun riyazi gözləntisini və ya əhali üçün orta qiymətini bilirik. Böyük Ədədlər Qanunu sadəcə olaraq deyir ki, əgər biz təsadüfi kəmiyyətin müşahidələrinin n-ci sayından nümunə götürsək və bütün bu müşahidələrin ortasını götürsək... Bir dəyişəni götürək. Gəlin onu X adlandıraq ki, n alt simvolu və yuxarı hissəsində çubuq var. Bu, təsadüfi dəyişənimizin müşahidələrinin n-ci sayının arifmetik ortasıdır. Budur mənim ilk müşahidəm. Təcrübəni bir dəfə edirəm və bu müşahidə edirəm, sonra təkrar edirəm və bu müşahidə edirəm və yenidən edirəm və bunu alıram. Mən bu təcrübəni n-ci dəfə keçirirəm və sonra müşahidələrimin sayına bölürəm. Budur mənim nümunəm. Burada etdiyim bütün müşahidələrin orta göstəricisidir. Böyük Ədədlər Qanunu bizə deyir ki, mənim seçmə ortalamam təsadüfi dəyişənin gözlənilən dəyərinə yaxınlaşacaq. Yaxud mən də yaza bilərəm ki, mənim nümunəvi ortalamam sonsuzluğa meyilli n-ci kəmiyyət üçün əhali ortasına yaxınlaşacaq. Mən “yaxınlaşma” və “konvergensiya” arasında aydın fərq qoymayacağam, lakin ümid edirəm ki, intuitiv olaraq başa düşəcəksiniz ki, burada kifayət qədər böyük bir nümunə götürsəm, bütövlükdə əhali üçün gözlənilən dəyəri əldə edəcəm. Düşünürəm ki, çoxunuz intuitiv şəkildə başa düşürsünüz ki, əgər mən böyük nümunələrlə kifayət qədər testlər etsəm, nəticədə testlər gözlənilən dəyər və ehtimalı və bütün cazı nəzərə alaraq gözlədiyim dəyərləri verəcək. Ancaq düşünürəm ki, bunun niyə baş verdiyi çox vaxt aydın deyil. Bunun niyə belə olduğunu izah etməyə başlamazdan əvvəl konkret bir nümunə verim. Böyük Ədədlər Qanunu bizə deyir ki... Tutaq ki, bizdə təsadüfi dəyişən X var. Bu, ədalətli sikkənin 100 atışındakı başların sayına bərabərdir. Hər şeydən əvvəl bu təsadüfi dəyişənin riyazi gözləntisini bilirik. Bu, sikkə atışlarının və ya sınaqların sayının hər hansı bir sınağın uğur şansına vurulmasıdır. Beləliklə, bu 50-yə bərabərdir. Yəni, böyük ədədlər qanunu deyir ki, nümunə götürsək və ya bu sınaqları orta hesabla götürsəm, alacam. .. İlk dəfə test edəndə 100 dəfə sikkə atacağam, ya da yüz qəpik olan qutunu götürüb silkələyəcəm, sonra neçə baş aldığımı sayıb, deyək ki, 55 rəqəmini alacağam. X1 olardı. Sonra qutunu yenidən silkələyirəm və 65 rəqəmini alıram. Sonra yenə və 45 alıram. Və bunu n sayda edirəm və sonra onu sınaqların sayına bölürəm. Böyük ədədlər qanunu bizə deyir ki, n sonsuzluğa yaxınlaşdıqca bu orta (bütün müşahidələrimin ortası) 50-yə yaxınlaşacaq. İndi bunun niyə baş verdiyi barədə bir az danışmaq istərdim. Bir çox insanlar hesab edir ki, əgər 100 sınaqdan sonra mənim nəticəsim orta göstəricidən yuxarıdırsa, ehtimal qanunlarına görə, fərqi kompensasiya etmək üçün daha çox və ya daha az baş almalıyam. Bu, tam olaraq baş verəcək şey deyil. Buna çox vaxt “qumarbazın səhvi” deyirlər. İcazə verin sizə fərqi göstərim. Aşağıdakı nümunədən istifadə edəcəyəm. İcazə verin qrafik çəkim. Rəngi ​​dəyişək. Bu n, mənim x oxu n-dir. Bu, edəcəyim testlərin sayıdır. Və mənim Y oxum nümunə orta olacaq. Biz bilirik ki, bu ixtiyari dəyişənin riyazi gözləntisi 50-dir. İcazə verin onu çəkim. Bu 50-dir. Gəlin öz nümunəmizə qayıdaq. Əgər n olarsa... İlk imtahanımda 55 aldım, bu mənim orta göstəricimdir. Mənim yalnız bir məlumat giriş nöqtəm var. Sonra iki testdən sonra 65 alıram. Beləliklə, mənim orta balım 2-yə bölünən 65+55 olacaq. Bu, 60-dır. Ortalamam bir az yüksəldi. Sonra 45 aldım, bu da arifmetik ortalamamı yenidən aşağı saldı. 45-ci süjeti çəkməyə hazırlaşmıram. İndi bütün bunları orta hesabla götürməliyəm. 45+65 nəyə bərabərdir? Nöqtəni təmsil etmək üçün bu dəyəri hesablayaq. Bu, 165-i 3-ə bölür. Bu 53-dür. Xeyr, 55. Beləliklə, ortalama 55-ə enir. Bu testləri davam etdirə bilərik. Üç sınaq etdikdən və bu ortalamanı əldə etdikdən sonra, bir çox insanlar ehtimal tanrılarının gələcəkdə daha az baş əldə etməyimizə əmin olacağını və növbəti bir neçə sınaqda orta göstəricini aşağı salmaq üçün daha aşağı balların olacağını düşünür. Amma həmişə belə olmur. Gələcəkdə ehtimal həmişə eyni qalır. Həmişə 50% şansım olacaq ki, mənim başım olacaq. Bu, əvvəlcə gözlədiyimdən daha çox müəyyən sayda baş aldığım üçün deyil, sonra birdən quyruq almalıyam. Bu qumarbazın səhvidir. Qeyri-mütənasib çox sayda baş almağınız o demək deyil ki, nə vaxtsa qeyri-mütənasib çox sayda quyruq almağa başlayacaqsınız. Bu tamamilə doğru deyil. Böyük ədədlər qanunu bizə bunun vacib olmadığını deyir. Deyək ki, müəyyən məhdud sayda testlərdən sonra orta balınız... Bunun ehtimalı kifayət qədər kiçikdir, amma, buna baxmayaraq... Tutaq ki, orta göstəriciniz bu işarəyə çatıb - 70. "Vay, gözlənilən dəyərdən uzaqlaşdıq" deyə düşünürsən. Amma böyük ədədlər qanunu deyir ki, bizim neçə test etdiyimizə əhəmiyyət vermir. Qarşıda hələ sonsuz sayda çağırışlarımız var. Xüsusilə belə bir vəziyyətdə bu sonsuz sayda sınaqdan riyazi gözlənti aşağıdakı kimi olardı. Hansısa böyük dəyəri ifadə edən sonlu ədədə gəldikdə, onunla birləşən sonsuz ədəd yenə gözlənilən dəyərə gətirib çıxaracaq. Bu, əlbəttə ki, çox boş bir şərhdir, lakin böyük ədədlər qanunu bizə bunu deyir. Vacibdir. Bu bizə demir ki, əgər biz çoxlu baş alsaq, o zaman kompensasiya etmək üçün birtəhər quyruq almaq ehtimalı artacaq. Bu qanun bizə deyir ki, hələ də sonsuz sayda sınaqlarınız qalıbsa, məhdud sayda sınaqda nəticənin nə olmasının əhəmiyyəti yoxdur. Əgər onlardan kifayət qədər etsəniz, yenidən gözlənilən dəyərə qayıdacaqsınız. Bu mühüm məqamdır. Bu barədə düşünün. Amma lotereya və kazinolarda praktikada bundan hər gün istifadə edilmir, baxmayaraq ki, məlumdur ki, kifayət qədər testlər etsəniz... Hətta hesablaya bilərik... normadan ciddi şəkildə kənara çıxma ehtimalımız nə qədərdir? Amma kazinolar və lotereyalar hər gün bu prinsiplə işləyir ki, əgər kifayət qədər insanı, təbii ki, qısa müddətdə, kiçik bir nümunə ilə götürsəniz, bir neçə nəfər cekpotu vuracaq. Amma uzun müddət ərzində sizi oynamağa dəvət etdikləri oyunların parametrlərinə görə kazino həmişə qalib gələcək. Bu, intuitiv olan mühüm ehtimal prinsipidir. Baxmayaraq ki, bəzən sizə formal olaraq təsadüfi dəyişənlərlə izah edildikdə, hər şey bir az qarışıq görünür. Bütün bu qanun deyir ki, nümunələr nə qədər çox olarsa, bu nümunələrin arifmetik ortası həqiqi ortaya meyl edəcəkdir. Və daha dəqiq desək, seçdiyiniz nümunənin arifmetik ortası təsadüfi dəyişənin riyazi gözləntisi ilə birləşəcəkdir. Hamısı budur. Növbəti videoda görüşənədək!

Böyük ədədlərin zəif qanunu

Böyük ədədlərin zəif qanunu 1713-cü ildə bunu sübut edən Yakob-Bernoullinin şərəfinə Bernulli teoremi də adlanır.

Eyni şəkildə paylanmış və korrelyasiya olunmayan təsadüfi dəyişənlərin sonsuz ardıcıllığı (ardıcıl sadalanması) olsun. Yəni onların kovariantlığı c o v (X i , X j) = 0 , ∀ i ≠ j (\displaystyle \mathrm (cov) (X_(i),X_(j))=0,\;\forall i\not =j). Qoy . Birincinin nümunə ortalaması ilə işarə edək n (\displaystyle n)üzvlər:

.

Sonra X ¯ n → P μ (\displaystyle (\bar (X))_(n)\to ^(\!\!\!\!\!\!\mathbb (P) )\mu ).

Yəni istənilən müsbət üçün ε (\displaystyle \varepsilon)

lim n → ∞ Pr (| X ¯ n − μ |< ε) = 1. {\displaystyle \lim _{n\to \infty }\Pr \!\left(\,|{\bar {X}}_{n}-\mu |<\varepsilon \,\right)=1.}

Gücləndirilmiş Böyük Ədədlər Qanunu

Müstəqil eyni paylanmış təsadüfi dəyişənlərin sonsuz ardıcıllığı olsun ( X i ) i = 1 ∞ (\displaystyle \(X_(i)\)_(i=1)^(\infty )), bir ehtimal fəzasında müəyyən edilmişdir (Ω , F , P) (\displaystyle (\Omega,(\mathcal (F)),\mathbb (P))). Qoy E X i = μ , ∀ i ∈ N (\displaystyle \mathbb (E) X_(i)=\mu ,\;\forall i\in \mathbb (N) ). ilə işarə edək X ¯ n (\displaystyle (\bar (X))_(n)) birincinin nümunə ortalaması n (\displaystyle n)üzvlər:

X ¯ n = 1 n ∑ i = 1 n X i , n ∈ N (\displaystyle (\bar (X))_(n)=(\frac (1)(n))\sum \limitlər _(i=) 1)^(n)X_(i),\;n\in \mathbb (N) ).

Sonra X ¯ n → μ (\displaystyle (\bar (X))_(n)\to \mu ) demək olar ki, həmişə.

Pr (lim n → ∞ X ¯ n = μ) = 1. (\displaystyle \Pr \!\left(\lim _(n\to \infty )(\bar (X))_(n)=\mu \ sağ)=1.) .

Hər hansı bir riyazi qanun kimi, böyük ədədlər qanunu da yalnız müəyyən dərəcədə dəqiqliklə qarşılana bilən müəyyən fərziyyələr altında real dünyaya tətbiq edilə bilər. Məsələn, ardıcıl sınaq şərtləri çox vaxt qeyri-müəyyən müddətə və mütləq dəqiqliklə təmin edilə bilməz. Bundan əlavə, böyük ədədlər qanunu yalnız danışır ehtimalsızlıq orta dəyərin riyazi gözləntidən əhəmiyyətli dərəcədə sapması.