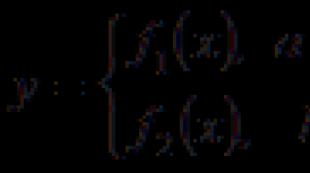Riyazi analiz.

Emalatxana.

İxtisas üzrə universitet tələbələri üçün:

"Dövlət və Bələdiyyə İdarəsi"

T.Z. Pavlova

Kolpaşevo 2008

Fəsil 1. Təhlilə giriş

1.1 Funksiyalar. Ümumi xüsusiyyətlər

1.2 Limitlər nəzəriyyəsi

1.3 Funksiyanın davamlılığı

2.1 Törəmənin tərifi

2.4 Funksiyaların araşdırılması

2.4.1 Tam Funksiya Tədqiqat Planı

2.4.2 Funksiyaların öyrənilməsi nümunələri

2.4.3. Seqmentdəki funksiyanın ən böyük və ən kiçik qiyməti

2.5 L'Hopital qaydası

3.1 Qeyri-müəyyən inteqral

3.1.1 Anlayışlar və xassələr

3.1.2 İnteqrallar cədvəli

3.1.3 İnteqrasiyanın əsas üsulları

3.2 Müəyyən inteqral

3.2.2 Müəyyən inteqralın hesablanması üsulları

Fəsil 4. Bir neçə dəyişənlərin funksiyaları

4.1 Əsas anlayışlar

4.2 Bir neçə dəyişənli funksiyaların hədləri və davamlılığı

4.3.3 Ümumi diferensial və onun təxmini hesablamalara tətbiqi

Fəsil 5. Klassik optimallaşdırma üsulları

6.1 Utility funksiyası.

6.2 Laqeydlik xətləri

6.3 Büdcə dəsti

Ev tapşırıqları

1.1 Funksiyalar. Ümumi xüsusiyyətlər

Ədədi funksiya həqiqi ədədlərin D çoxluğunda müəyyən edilir, əgər dəyişənin hər bir dəyəri y dəyişəninin hansısa yaxşı müəyyən edilmiş real dəyəri ilə əlaqələndirilir, burada D funksiyanın oblastıdır.

Funksiyanın analitik təsviri:

açıq şəkildə:;

dolayısı ilə:;

parametrik formada:

tərif sahəsində müxtəlif düsturlar:

Xüsusiyyətlər.

Hətta funksiyası:. Məsələn, funksiya cütdür, çünki ...

Qəribə funksiya: ... Məsələn, funksiya təkdir, çünki ...

Dövri funksiya: , burada T funksiyanın dövrüdür,. Məsələn, triqonometrik funksiyalar.

Monoton funksiya. Əgər tərif sahəsinin hər hansı biri üçün - funksiya artır, - azalır. Məsələn, - artan və - azalan.

Məhdud funksiya. Belə bir M rəqəmi varsa. Məsələn, funksiyalar və bəri .

Nümunə 1. Funksiyaların tərif sahəsini tapın.

+ 2 – 3 +

1.2 Limitlər nəzəriyyəsi

Tərif 1... Funksiyanın həddi b ədədidir, əgər hər hansı biri üçün (ixtiyari kiçik müsbət ədəddir) bərabərsizliyin təmin olunduğu arqumentin belə qiymətini tapmaq olar.

Təyinat:.

Tərif 2... Əgər hər hansı biri üçün (ixtiyari kiçik müsbət ədəddir) müsbət ədəd varsa, at funksiyasının həddi b ədədidir ki, bərabərsizliyi ödəyən x-in bütün qiymətləri üçün bərabərsizlik baş verir.

Təyinat:.

Tərif 3. Funksiya və ya, əgər və ya üçün sonsuz kiçik adlanır.

Xüsusiyyətlər.

1. Sonlu sayda sonsuz kiçik kəmiyyətlərin cəbri cəmi sonsuz kiçik kəmiyyətdir.

2. Sonsuz kiçik kəmiyyətin məhdud funksiya ilə hasili (sabit, başqa bir sonsuz kiçik kəmiyyət) sonsuz kiçik kəmiyyətdir.

3. Sonsuz kiçik kəmiyyətin həddi sıfırdan fərqli olan funksiyaya bölünmə hissəsi sonsuz kiçik kəmiyyətdir.

Tərif 4. Funksiya, if at sonsuz böyük adlanır.

Xüsusiyyətlər.

1. Sonsuz böyük kəmiyyətin həddi sıfırdan fərqli funksiya ilə hasili sonsuz böyük kəmiyyətdir.

2. Sonsuz böyük qiymətlə məhdud funksiyanın cəmi sonsuz böyük qiymətdir.

3. Sonsuz böyük kəmiyyətin həddi olan funksiyaya bölünməsinin əmsalı sonsuz böyük kəmiyyətdir.

teorem.(Sonsuz kiçik kəmiyyətlə sonsuz böyük kəmiyyət arasındakı əlaqə.) Əgər funksiya () nöqtəsində sonsuz kiçikdirsə, funksiya () nöqtəsində sonsuz böyük kəmiyyətdir. Və əksinə, funksiya () nöqtəsində sonsuz böyükdürsə, funksiya () nöqtəsində sonsuz kiçikdir.

Limit teoremləri.

1. Funksiya birdən çox limitə malik ola bilməz.

2. Bir neçə funksiyanın cəbri cəminin həddi bu funksiyaların hədlərinin cəbri cəminə bərabərdir:

3. Bir neçə funksiyanın hasilinin həddi bu funksiyaların hədlərinin hasilinə bərabərdir:

4. Dərəcə həddi həddin dərəcəsinə bərabərdir:

5. Bölən həddi varsa, bölgü həddi limitlərin bölünməsinə bərabərdir:

.

6. İlk diqqətəlayiq hədd.

Nəticələr:

7. İkinci əlamətdar hədd:

Nəticələr:

Ekvivalent sonsuz kiçik dəyərlər:

Limitlərin hesablanması.

Limitlər hesablanarkən hədlər haqqında əsas teoremlərdən, fasiləsiz funksiyaların xassələrindən və bu teoremlərdən və xassələrdən irəli gələn qaydalardan istifadə olunur.

Qayda 1. Funksiyanın bu nöqtədə kəsilməz olan nöqtəsində həddi tapmaq üçün funksiyada x arqumentinin yerinə onun limit qiymətini limit işarəsi altında əvəz etmək lazımdır.

Nümunə 2. Tapın

Qayda 2.Əgər kəsrin həddi tapılarkən məxrəcin həddi sıfır, payın həddi isə sıfırdan fərqli olarsa, belə funksiyanın həddi belədir.

Nümunə 3. Tapın

Qayda 3.Əgər kəsrin həddi tapılarkən məxrəcin həddi bərabərdirsə və payın həddi sıfırdan fərqlidirsə, belə funksiyanın həddi sıfırdır.

Nümunə 4. Tapın

Çox vaxt arqument üçün limit dəyərinin dəyişdirilməsi kimi qeyri-müəyyən ifadələrlə nəticələnir

.

Bu hallarda funksiyanın limitinin tapılması qeyri-müəyyənliyin açıqlanması adlanır. Qeyri-müəyyənliyi açıqlamaq üçün limitə keçməzdən əvvəl bu ifadəni çevirmək lazımdır. Qeyri-müəyyənlikləri açıqlamaq üçün müxtəlif üsullardan istifadə olunur.

Qayda 4... Növün qeyri-müəyyənliyi sublimit funksiyasının çevrilməsi yolu ilə aşkar edilir, beləliklə, pay və məxrəcdə həddi sıfır olan amili seçmək və onun ilə kəsri azaltaraq, hissənin həddini tapmaq üçün. Bunun üçün pay və məxrəc ya vurulur, ya da pay və məxrəcə birləşdirilən ifadələrlə vurulur.

Qayda 5. Sublimit ifadəsi triqonometrik funksiyaları ehtiva edirsə, o zaman növlərin qeyri-müəyyənliyini ifşa etmək üçün ilk diqqətəlayiq hədd istifadə olunur.

.

Qayda 6... Formanın qeyri-müəyyənliyini açıqlamaq üçün alt həddi kəsrin payı və məxrəci arqumentin ən yüksək dərəcəsinə bölünməli və sonra bölmənin həddi tapılmalıdır.

Mümkün nəticələr:

1) istənilən hədd, əgər bu səlahiyyətlər eynidirsə, payın və məxrəcin arqumentinin ən yüksək güclərindəki əmsalların nisbətinə bərabərdir;

2) payın arqumentinin dərəcəsi məxrəcin arqumentinin dərəcəsindən yüksək olarsa, hədd sonsuzluğa bərabərdir;

3) payın arqumentinin dərəcəsi məxrəcin arqumentinin dərəcəsindən aşağı olarsa, hədd sıfırdır.

a)

ildən

Dərəcələr bərabərdir, yəni limit daha yüksək dərəcələrdə əmsalların nisbətinə bərabərdir, yəni. ...

b)

Hissənin, məxrəcin dərəcəsi 1-dir, yəni həddi var

v)

Hissənin dərəcəsi 1-dir, məxrəcin dərəcəsi isə 0-dır.

Qayda 7... Formanın qeyri-müəyyənliyini aşkar etmək üçün subliminal fraksiyanın payı və məxrəci birləşdirici ifadə ilə vurulmalıdır.

Misal 10.

Qayda 8... İkinci əlamətdar hədd və onun nəticələri növlərin qeyri-müəyyənliyini aşkar etmək üçün istifadə olunur.

Bunu sübut etmək olar

Misal 11.

Misal 12.

Misal 13.

Qayda 9... Subliminal funksiyası sonsuz kiçik olan qeyri-müəyyənlikləri açıqlayarkən, bu sonsuzluqların sərhədlərini dəyişdirmək lazımdır. onlara ekvivalent olan sonsuz kiçik elementlərin hüdudları üzrə.

Misal 14.

Misal 15.

Qayda 10. L'Hôpital Qaydası (bax 2.6).

1.3 Funksiyanın davamlılığı

Arqument kimi funksiyanın həddi a-ya meyl edərsə, mövcud olarsa və bu nöqtədə funksiyanın dəyərinə bərabər olarsa, funksiya bir nöqtədə davamlıdır.

Ekvivalent şərtlər:

1. ;

3.

Qırılma nöqtəsinin təsnifatı:

birinci növ fasilə

Birdəfəlik - birtərəfli məhdudiyyətlər mövcuddur və bərabərdir;

Ölümcül (atlama) - birtərəfli məhdudiyyətlər bərabər deyil;

ikinci növ fasiləsizlik: bir nöqtədə funksiyanın limiti mövcud deyil.

Nümunə 16. Bir nöqtədə funksiyanın kəsilməzliyinin xarakterini təyin edin və ya bu nöqtədə funksiyanın davamlılığını sübut edin.

çünki funksiya müəyyən edilməmişdir, ona görə də bu nöqtədə davamlı deyil. Çünki və müvafiq olaraq, , onda birinci növ çıxarıla bilən kəsilmə nöqtəsidir.

b)

(a) tapşırığı ilə müqayisədə funksiya elə bir nöqtədə uzadılır ki , buna görə də bu funksiya bu nöqtədə davamlıdır.

Funksiya müəyyən edilmədikdə;

.

Çünki birtərəfli sərhədlərdən biri sonsuzdur, onda ikinci növ qırılma nöqtəsidir.

Fəsil 2. Diferensial hesablama

2.1 Törəmənin tərifi

Törəmə tərifi

Verilmiş funksiyanın və ya törəməsi, arqument artımı sıfıra meyl etdikdə, funksiya artımının müvafiq arqument artımına nisbətinin həddidir:

Və ya .

Törəmənin mexaniki mənası funksiyanın dəyişmə sürətidir. Törəmənin həndəsi mənası, funksiyanın qrafikinə toxunan meyl bucağının tangensidir:

2.2 Diferensiasiya üçün əsas qaydalar

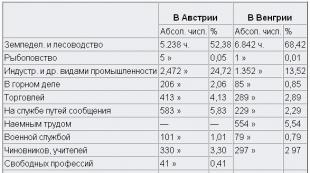
ad	Funksiya	törəmə
Sabit əmsala vurma
İki funksiyanın cəbri cəmi
İki funksiyanın məhsulu
Şəxsi iki funksiya
Kompleks funksiya

Əsas elementar funksiyaların törəmələri

P / p No.	Funksiya adı	Funksiya və onun törəməsi
1	Sabit
2	güc funksiyası xüsusi hallar
3	eksponensial funksiya xüsusi hal
4	loqarifmik funksiya xüsusi hal
5	triqonometrik funksiyalar
6	tərs triqonometrik

b)

2.3 Daha yüksək dərəcəli törəmələr

Funksiyanın ikinci dərəcəli törəməsi

Funksiyanın ikinci dərəcəli törəməsi:

Misal 18.

a) Funksiyanın ikinci dərəcəli törəməsini tapın.

Həll. Əvvəlcə birinci dərəcəli törəməni tapaq .

Birinci dərəcəli törəmənin törəməsini götürək.

Nümunə 19. Funksiyanın üçüncü dərəcəli törəməsini tapın.

2.4 Funksiyaların araşdırılması

2.4.1 Tam funksiya tədqiqi üçün plan:

Tam Funksiya Tədqiqat Planı:

1. Elementar tədqiqat:

Domen və dəyərlər diapazonunu tapın;

Ümumi xassələri tapın: paritet (qəriblik), dövrilik;

Koordinat oxları ilə kəsişmə nöqtələrini tapın;

Davamlılıq sahələrini müəyyənləşdirin.

2. Asimptotlar:

Şaquli asimptotları tapın, əgər;

Əyri asimptotları tapın:.

Hər hansı bir rəqəm varsa, onda - üfüqi asimptotlar.

3. Tədqiqatdan istifadə edərək:

Kritik nöqtələri tapın, o. mövcud və ya mövcud olmayan nöqtələr;

Artan intervalları müəyyən edin, olanlar. intervallar, hansı və azalan funksiyalar -;

Ekstremu müəyyən edin: keçərkən işarəni "+"-dan "-"-yə dəyişdiyi nöqtələr maksimum nöqtələr, "-"-dən "+"-a qədər - minimumdur.

4. Tədqiqatdan istifadə edərək:

Mövcud olan və ya olmayan nöqtələri tapın;

Qabarıqlıq sahələrini tapın, yəni. konkavlərin olduğu intervallar;

Bükülmə nöqtələrini tapın, yəni. keçərkən işarəni dəyişən nöqtələr.

1. Tədqiqatın ayrı-ayrı elementləri tapıldıqca tədricən qrafikə salınır.

2. Əgər funksiyanın qrafikinin qurulmasında çətinliklər yaranarsa, onda funksiyanın qiymətləri bəzi əlavə nöqtələrdə tapılır.

3. Tədqiqatın məqsədi funksiyanın davranışının xarakterini təsvir etməkdir. Buna görə də, dəqiq bir qrafik deyil, tapılmış elementlərin (ekstrema, əyilmə nöqtələri, asimptotlar və s.) aydın şəkildə göstərildiyi onun yaxınlaşması qurulur.

4. Yuxarıdakı plana ciddi riayət etmək lazım deyil; funksiyanın davranışının xarakterik elementlərini nəzərdən qaçırmamaq vacibdir.

2.4.2 Funksiya tədqiqatının nümunələri:

1)

2) funksiya təkdir:

.

3) Asimptotlar.

- şaquli asimptotlar, çünki

Oblik asimptot.

5)

- əyilmə nöqtəsi.

2) funksiya təkdir:

3) Asimptotlar: Şaquli asimptotlar yoxdur.

Meyilli:

- əyri asimptotlar

4) - funksiya artır.

- əyilmə nöqtəsi.

Bu funksiyanın sxematik diaqramı:

2) Ümumi funksiya

3) Asimptotlar

- əyri asimptotlar yoxdur

- üfüqi asimptot at

- əyilmə nöqtəsi

Bu funksiyanın sxematik diaqramı:

2) Asimptotlar.

- şaquli asimptot, çünki

- əyri asimptotlar yoxdur

, - üfüqi asimptot

Bu funksiyanın sxematik diaqramı:

2) Asimptotlar

- şaquli asimptot at, bəri

- əyri asimptotlar yoxdur

, - üfüqi asimptot

3) - intervalların hər birində funksiya azalır.

Bu funksiyanın sxematik diaqramı:

Seqmentdə funksiyanın ən böyük və ən kiçik qiymətini tapmaq üçün diaqramdan istifadə edə bilərsiniz:

1. Funksiyanın törəməsini tapın.

2. Funksiyanın mövcud və ya olmayan kritik nöqtələrini tapın.

3. Verilmiş seqmentə və onun uclarına aid kritik nöqtələrdə funksiyanın qiymətini tapın və onlardan ən böyüyünü və ən kiçiyini seçin.

Misal. Verilmiş seqmentdə funksiyanın ən kiçik və ən böyük qiymətini tapın.

25. arasında

2) - kritik nöqtələr

26. arasında.

Törəmə mövcud deyil, lakin 1 bu intervala aid deyil. Funksiya intervalda azalır, yəni ən böyük dəyər yoxdur, ən kiçik qiymət var.

2.5 L'Hopital qaydası

teorem. İki sonsuz kiçik və ya sonsuz böyük funksiyanın nisbət həddi, əgər sonuncu göstərilən mənada mövcuddursa, onların törəmələrinin (sonlu və ya sonsuz) nisbətinin həddi ilə bərabərdir.

Bunlar. növün qeyri-müəyyənliklərini açıqlayarkən və ya aşağıdakı düsturdan istifadə edə bilərsiniz:

.

27.

Fəsil 3. İnteqral hesablama

3.1 Qeyri-müəyyən inteqral

3.1.1 Anlayışlar və xassələr

Tərif 1. Funksiya if üçün antitörəmə adlanır.

Tərif 2. f (x) funksiyasının qeyri-müəyyən inteqralı bu funksiya üçün bütün əks törəmələrin məcmusudur.

Təyinat: , burada c ixtiyari sabitdir.

Qeyri-müəyyən inteqral xassələr

1. Qeyri-müəyyən inteqralın törəməsi:

2. Qeyri-müəyyən inteqralın diferensialı:

3. Diferensialın qeyri-müəyyən inteqralı:

4. İki funksiyanın cəminin (fərqinin) qeyri-müəyyən inteqralı:

5. Sabit əmsalın qeyri-müəyyən inteqral işarəsindən kənara çıxarılması:

3.1.2 İnteqrallar cədvəli

.1.3 İnteqrasiyanın əsas üsulları

1. Qeyri-müəyyən inteqralın xassələrindən istifadə.

Misal 29.

2. Diferensial işarənin altına gətirmək.

Misal 30.

3. Dəyişən dəyişdirmə üsulu:

a) inteqralda əvəzlənmə

harada - orijinaldan daha asan inteqrasiya olunan funksiya; - funksiyaya tərs funksiya; funksiyasının əks törəməsidir.

Misal 31.

b) formanın inteqralında əvəz:

Misal 32.

Misal 33.

4. Parçalar üzrə inteqrasiya üsulu:

Misal 34.

Misal 35.

İnteqralı ayrıca götürək

Gəlin inteqralımıza qayıdaq:

3.2 Müəyyən inteqral

3.2.1 Müəyyən inteqral anlayışı və onun xassələri

Tərif. Fasiləsiz funksiya hansısa intervalda verilsin. Gəlin onun qrafikini quraq.

Yuxarıdan əyri ilə, soldan və sağdan düz xətlərlə və aşağıdan a və b nöqtələri arasında absis oxunun seqmenti ilə məhdudlaşan fiqur əyri trapesiya adlanır.

S - sahə - əyri trapezoid.

Aralığı nöqtələrlə bölün və əldə edin:

İnteqral cəmi:

Tərif. Müəyyən inteqral inteqral cəminin həddidir.

Müəyyən inteqral xassələri:

1. Sabit amili inteqral işarəsindən çıxarmaq olar:

2. İki funksiyanın cəbri cəminin inteqralı bu funksiyaların inteqrallarının cəbri cəminə bərabərdir:

3. Əgər inteqrasiya seqmenti hissələrə bölünürsə, onda bütün seqment üzərindəki inteqral yaranan hissələrin hər biri üçün inteqralların cəminə bərabərdir, yəni. hər hansı a, b, c üçün:

4. Əgər seqment üzrədirsə, onda

5. İnteqralın işarəsi dəyişərkən, inteqrasiyanın hədləri dəyişdirilə bilər:

6.

7. Nöqtədəki inteqral 0-a bərabərdir:

8.

9. (“orta haqqında”) y = f (x) üzərində inteqrasiya olunan funksiya olsun. Sonra , burada, f (c) f (x)-in orta qiymətidir:

10. Nyuton-Leybnits düsturu

,

burada F (x) f (x) üçün antitörəmədir.

3.2.2 Müəyyən inteqralın hesablanması üsulları.

1. Birbaşa inteqrasiya

Misal 35.

a)

b)

v)

e)

2. Müəyyən inteqral işarəsi altında dəyişənlərin dəyişməsi .

Misal 36.

2. Müəyyən inteqralda hissələr üzrə inteqrasiya .

Misal 37.

a)

b)

e)

3.2.3 Müəyyən inteqralın tətbiqləri

Xarakterik	Funksiya növü	Düstur
	Kartezyen koordinatlarında
əyri sektor sahəsi	qütb koordinatlarında
əyri trapesiya sahəsi	parametrik formada
qövs uzunluğu	Kartezyen koordinatlarında
qövs uzunluğu	qütb koordinatlarında
qövs uzunluğu	parametrik formada
bədən həcmi fırlanma	Kartezyen koordinatlarında
verilmiş eninə ilə bədən həcmi en kəsiyi

Misal 38. Xətlərlə məhdudlaşan formanın sahəsini hesablayın: və .

Həll: Bu funksiyaların qrafiklərinin kəsişmə nöqtələrini tapaq. Bunun üçün funksiyaları bərabərləşdiririk və tənliyi həll edirik

Beləliklə, kəsişmə nöqtələri və.

Düsturdan istifadə edərək fiqurun sahəsini tapırıq

.

Bizim vəziyyətimizdə

Cavab: sahə (kvadrat vahidlərə) bərabərdir.

4.1 Əsas anlayışlar

Tərif. Əgər hansısa qaydaya görə, müəyyən dəstdən hər bir müstəqil nömrə cütünə z dəyişəninin bir və ya bir neçə qiyməti təyin edilirsə, onda z dəyişəni iki dəyişənin funksiyası adlanır.

Tərif. z funksiyasının oblastı z funksiyasının mövcud olduğu cütlər çoxluğudur.

İki dəyişənli funksiyanın oblastı Oxy koordinat müstəvisindəki nöqtələr toplusudur. Z-koordinatı tətbiq adlanır və sonra funksiyanın özü E 3 fəzasında hansısa səth kimi təsvir olunur. Məsələn:

Misal 39. Funksiyanın oblastını tapın.

a)

Sağ tərəfdəki ifadə yalnız üçün məna daşıyır. Bu o deməkdir ki, bu funksiyanın oblastı başlanğıcda mərkəzləşdirilmiş R radiuslu dairənin daxilində və sərhədində yerləşən bütün nöqtələrin toplusudur.

Bu funksiyanın sahəsi düz xətlərin nöqtələri istisna olmaqla, müstəvinin bütün nöqtələridir, yəni. koordinat oxları.

Tərif. Funksiya səviyyəli xətlər formanın tənlikləri ilə təsvir edilən koordinat müstəvisində əyrilər ailəsidir.

Misal 40. Funksiya səviyyəli xətləri tapın .

Həll. Verilmiş funksiyanın səviyyə xətləri tənliklə təsvir olunan müstəvidə əyrilər ailəsidir

Sonuncu tənlik radiusun O 1 (1, 1) nöqtəsində mərkəzləşdirilmiş dairələr ailəsini təsvir edir. Bu funksiya ilə təsvir edilən inqilab səthi (paraboloid) x = 1, y = 1 tənlikləri ilə verilən oxdan uzaqlaşdıqca “daha ​​dik” olur. (şək. 4).

4.2 Bir neçə dəyişənli funksiyaların hədləri və davamlılığı.

1. Limitlər.

Tərif. Hər bir ixtiyari kiçik ədəd üçün şərtin hər hansı bir nöqtə üçün doğru olduğu bir ədəd varsa, bir nöqtə nöqtəyə meyl etdiyi üçün A rəqəmi funksiyanın həddi adlanır və şərt ... Yazırlar: .

Misal 41. Limitləri tapın:

olanlar. həddi asılıdır və buna görə də mövcud deyil.

2. Davamlılıq.

Tərif. Nöqtə funksiyanın təyini oblastına aid olsun. Onda funksiya əgər nöqtədə davamlı adlanır

(1)

üstəlik, məqam ixtiyari şəkildə mətləbə meyl edir.

Əgər hər hansı bir nöqtədə (1) şərti ödənilmirsə, bu nöqtə funksiyanın kəsilmə nöqtəsi adlanır. Bu, aşağıdakı hallarda ola bilər:

1) Funksiya nöqtədə müəyyən edilməyib.

2) Heç bir məhdudiyyət yoxdur.

3) Bu hədd mövcuddur, lakin bərabər deyil.

Misal 42. Verilmiş funksiyanın nöqtədə kəsilməz olub-olmadığını müəyyən edin, əgər.

Başa düşdüm deməli, bu funksiya nöqtədə davamlıdır.

limit k-dən asılıdır, yəni. o, verilmiş nöqtədə mövcud deyildir, yəni funksiyanın bu nöqtədə kəsikliyi var.

4.3 Bir neçə dəyişənli funksiyaların törəmələri və diferensialları

4.3.1 Birinci dərəcəli qismən törəmələr

X arqumentinə münasibətdə funksiyanın qismən törəməsi y dəyişəninin sabit qiymətində bir x dəyişənin funksiyasının adi törəməsidir və işarə olunur:

y arqumentinə münasibətdə funksiyanın qismən törəməsi x dəyişəninin sabit qiymətində bir y dəyişəninin funksiyasının adi törəməsidir və işarə olunur:

Misal 43. Funksiyaların qismən törəmələrini tapın.

4.3.2 İkinci dərəcəli qismən törəmələr

İkinci dərəcəli qismən törəmələr birinci dərəcəli qismən törəmələrin qismən törəmələridir. Formanın iki dəyişəninin funksiyası üçün dörd növ ikinci dərəcəli qismən törəmələr mümkündür:

Müxtəlif dəyişənlərə münasibətdə diferensiasiyanın aparıldığı ikinci dərəcəli qismən törəmələrə qarışıq törəmələr deyilir. İki dəfə diferensiallanan funksiyanın ikinci dərəcəli qarışıq törəmələri bərabərdir.

Misal 44. İkinci dərəcəli qismən törəmələri tapın.

4.3.3 Ümumi diferensial və onun təxmini hesablamalara tətbiqi.

Tərif. İki dəyişənli funksiyanın birinci dərəcəli diferensialı düsturla tapılır

.

Misal 45. Funksiya üçün tam diferensialı tapın.

Həll. Gəlin qismən törəmələri tapaq:

.

X və y arqumentlərinin kiçik artımları üçün funksiya təxminən dz-ə bərabər artım əldə edir, yəni. ...

Bir nöqtədə funksiyanın təxmini dəyərini tapmaq üçün düstur, əgər onun nöqtədəki dəqiq dəyəri məlumdursa:

Misal 46. Tapın .

Həll. qoy,

Sonra formuladan istifadə edirik

Cavab verin. .

Misal 47. Təxminən hesablayın.

Həll. Bir funksiyanı nəzərdən keçirək. bizdə var

Misal 48. Təxmini hesablayın.

Həll. Funksiyanı nəzərdən keçirin ... Biz əldə edirik:

Cavab verin. .

4.3.4 Gizli funksiyaların differensasiyası

Tərif. Funksiya z-ə münasibətdə həll olunmayan tənlik ilə verilirsə, ona gizli deyilir.

Belə bir funksiyanın qismən törəmələri düsturlarla tapılır:

Misal 49. Tənliklə verilmiş z funksiyasının qismən törəmələrini tapın .

Həll.

Tərif. Funksiya y-ə münasibətdə həll olunmayan tənlik ilə verilirsə, ona gizli deyilir.

Belə bir funksiyanın törəməsi düsturla tapılır:

.

Misal 50. Bu funksiyaların törəmələrini tapın.

5.1 Bir neçə dəyişənli funksiyanın yerli ekstremumu

Tərif 1. Funksiya əgər nöqtədə maksimuma malikdir

Tərif 2. Funksiya əgər nöqtədə minimuma malikdir nöqtəyə kifayət qədər yaxın və ondan fərqli olan bütün nöqtələr üçün.

Ekstremum üçün zəruri şərt. Funksiya müəyyən bir nöqtədə ekstremuma çatarsa, funksiyanın qismən törəmələri yox olur və ya bu nöqtədə mövcud olmur.

Qismən törəmələrin yox olduğu və ya mövcud olmadığı nöqtələrə kritik deyilir.

Ekstremumun kifayət qədər əlaməti. Funksiya kritik nöqtənin bəzi qonşuluğunda müəyyən edilsin və bu nöqtədə davamlı ikinci dərəcəli qismən törəmələr olsun.

1) nöqtədə lokal maksimuma malikdir, əgər və əgər;

2) nöqtədə yerli minimuma malikdir, əgər və;

3) nöqtədə yerli ekstremum yoxdursa;

İki dəyişənli funksiyanın ekstremumunun tədqiqi sxemi.

1. Funksiyanın qismən törəmələrini tapın: və.

2. Tənliklər sistemini həll edin və funksiyanın kritik nöqtələrini tapın.

3. İkinci dərəcəli qismən törəmələri tapın, kritik nöqtələrdə onların dəyərlərini hesablayın və kifayət qədər şərtdən istifadə edərək, ekstremalların mövcudluğu haqqında nəticə çıxarın.

4. Funksiyanın ekstremumunu tapın.

Misal 51. Funksiyanın ekstremallarını tapın .

1) qismən törəmələri tapın.

2) Tənliklər sistemini həll edin

4) İkinci dərəcəli qismən törəmələri və onların kritik nöqtələrdə qiymətlərini tapın:. Bu nöqtədə alırıq:

deməli, nöqtədə ekstremum yoxdur. Bu nöqtədə alırıq:

deməli, nöqtədə minimum var.

5.2 Qlobal ekstremum (funksiyanın ən yüksək və ən aşağı dəyəri)

Bəzi qapalı çoxluqda davamlı olan bir neçə dəyişənli funksiyanın ən böyük və ən kiçik qiymətləri ya ekstremal nöqtələrdə, ya da çoxluğun sərhəddində əldə edilir.

Ən yüksək və ən aşağı dəyərləri tapmaq sxemi.

1) Bölgənin daxilində yerləşən kritik nöqtələri tapın, bu nöqtələrdə funksiyanın qiymətini hesablayın.

2) Sahənin sərhədində funksiyanı araşdırın; haşiyə bir neçə fərqli xəttdən ibarətdirsə, onda tədqiqat hər bir sahə üçün ayrıca aparılmalıdır.

3) Alınan funksiyanın qiymətlərini müqayisə edin və ən böyüyü və ən kiçikini seçin.

Misal 52. Düzbucaqlıda ən böyük və ən kiçik funksiya qiymətlərini tapın.

Həll. 1) Funksiyanın kritik nöqtələrini tapın, bunun üçün qismən törəmələri tapırıq: və tənliklər sistemini həll edirik:

A kritik nöqtəsi alındı. Nəticə nöqtəsi göstərilən ərazinin daxilində yerləşir,

Sahənin sərhədi dörd seqmentdən ibarətdir: və. hər seqmentdə funksiyanın ən böyük və ən kiçik qiymətini tapın.

4) Alınan nəticələri müqayisə edin və nöqtələrdə tapın .

Fəsil 6. İstehlakçı Seçimi Modeli

Biz fərz edəcəyik ki, n fərqli mal var. Sonra müəyyən bir əmtəə dəsti n-ölçülü vektor ilə işarələnəcəkdir , i-ci məhsulun miqdarı haradadır. X malların bütün dəstlərinin çoxluğuna fəza deyilir.

Fərdi istehlakçının seçimi üstünlük münasibəti ilə səciyyələnir: hesab edilir ki, istehlakçı hər hansı iki dəst haqqında daha çox arzu olunanı deyə bilər və ya onlar arasında fərq görmür. Üstünlük əlaqəsi keçidlidir: əgər çoxluq çoxluğa, çoxluğa üstünlük verilirsə, çoxluq çoxluğa üstünlük verilir. Güman edəcəyik ki, istehlakçı davranışı fərdi istehlakçının aksiomu ilə tam təsvir olunur: hər bir fərdi istehlakçı öz üstünlükləri sisteminə əsaslanaraq istehlak, alış və s. haqqında qərar qəbul edir.

6.1 Utility funksiyası

X istehlak dəstlərinin çoxluğunda funksiya müəyyən edilir , istehlak dəstindəki dəyəri istehlakçının bu dəst üçün fərdi təxmininə bərabərdir. Funksiya istehlakçının faydalı funksiyası və ya istehlakçının üstünlük funksiyası adlanır. Bunlar. hər bir istehlakçının öz kommunal funksiyası var. Lakin istehlakçıların bütün dəstini müəyyən istehlakçılar sinfinə (yaşa, əmlak vəziyyətinə və s. görə) bölmək olar və hər bir sinfə bəzi, bəlkə də, orta hesablanmış faydalı funksiyalar təyin edilə bilər.

Beləliklə, funksiya istehlakçı təxmini və ya müəyyən bir dəsti alarkən fərdin ehtiyaclarının ödənilməsi səviyyəsidir. Əgər müəyyən bir fərd üçün dəst dəstdən üstündürsə, o zaman.

Utility funksiyasının xüsusiyyətləri.

1.

Faydalılıq funksiyasının ilk qismən törəmələri məhsulların marjinal faydalılıqları adlanır. Bu xassədən belə çıxır ki, bir məhsulun istehlakının artması, digər məhsulların istehlakının dəyişməz qalması istehlakçıların qiymətləndirilməsinin artmasına səbəb olur. Vektor funksiyanın qradiyentidir, funksiyanın ən böyük artım istiqamətini göstərir. Funksiya üçün onun qradiyenti məhsulların marjinal faydalarının vektorudur.

2.

Bunlar. hər hansı bir əmtəənin marjinal faydalılığı istehlakın artması ilə azalır.

3.

Bunlar. hər bir məhsulun marjinal faydalılığı digər məhsulun miqdarı ilə artır.

Bəzi növ kommunal funksiyalar.

1) Neoklassik:.

2) Kvadrat: matrisin mənfi müəyyən olduğu və üçün.

3) Loqarifmik funksiya:.

6.2 Laqeydlik xətləri

Tətbiq olunan problemlərdə və istehlakçı seçimi modellərində tez-tez iki mal dəstinin xüsusi bir halından istifadə olunur, yəni. faydalı funksiya iki dəyişəndən asılı olduqda. Laqeydlik xətti fərdin ehtiyaclarının eyni səviyyədə ödənilməsinə malik olan istehlak dəstlərini birləşdirən xəttdir. Mahiyyət etibarı ilə laqeydlik xətləri funksiya səviyyəsinin xətləridir. Laqeydlik xətti tənlikləri: .

Laqeydlik xətlərinin əsas xassələri.

1. Ehtiyacların ödənilməsinin müxtəlif səviyyələrinə uyğun gələn laqeydlik xətləri toxunmur və kəsişmir.

2. Laqeydlik xətləri azalır.

3. Laqeydlik xətləri aşağıya doğru qabarıqdır.

Əmlak 2 mühüm təxmini bərabərliyi nəzərdə tutur.

Bu nisbət fərdin öz ehtiyaclarının ödənilmə səviyyəsini dəyişmədən birinci məhsulun istehlakını bir vahid azaltmaqla (artırmaqla) ikinci məhsulun istehlakını nə qədər artırmalı (azalmalı) olduğunu göstərir. Nisbət birinci məhsulun ikinci ilə əvəzlənmə sürəti, dəyər isə birinci məhsulun ikinci ilə əvəzlənmə sürəti adlanır.

Misal 53. Əgər birinci əmtəənin marjinal faydalılığı 6, ikincisi isə 2-dirsə, birinci əmtəənin istehlakının bir vahid azalması ilə ikinci əmtəənin istehlakını 3 vahid artırmaq lazımdır. ehtiyacların eyni səviyyədə ödənilməsi.

6.3 Büdcə dəsti

Qoy - n məhsul toplusunun qiymət vektoru; I - fərdin bir sıra məhsulların alınmasına sərf etməyə hazır olduğu gəliri. Verilmiş qiymətlərlə dəyəri I-dən çox olmayan mallar dəstləri çoxluğu B büdcə çoxluğu adlanır. Bundan başqa, maya dəyəri I olan mallar çoxluğu B büdcə çoxluğunun G sərhəddi adlanır. B çoxluğu G sərhəddi və təbii məhdudiyyətlərlə məhdudlaşır.

Büdcə dəsti bərabərsizliklər sistemi ilə təsvir olunur:

İki əmtəə dəsti üçün büdcə dəsti B (şək. 1) koordinat oxları və düz xətt ilə məhdudlaşan koordinat sistemində üçbucaqdır.

6.4 İstehlakçı tələbi nəzəriyyəsi

İstehlak nəzəriyyəsində belə güman edilir ki, istehlakçı həmişə öz faydalılığını maksimuma çatdırmağa çalışır və onun üçün yeganə məhdudiyyət onun əmtəə dəstinin alınmasına sərf edə biləcəyi məhdud gəlir Idir. Ümumiyyətlə, istehlakçı seçimi problemi (bazarda rasional istehlakçı davranışı problemi) aşağıdakı kimi formalaşdırılır: istehlak dəstini tapın. , bu da verilmiş büdcə məhdudiyyəti üçün faydalı funksiyasını maksimuma çatdırır. Bu problemin riyazi modeli:

İki məhsul dəsti halında:

Həndəsi cəhətdən bu problemin həlli G büdcə çoxluğunun sərhədi ilə laqeydlik xətti arasındakı əlaqə nöqtəsidir.

Bu problemin həlli tənliklər sisteminin həllinə endirilir:

(1)

Bu sistemin həlli istehlakçı seçimi probleminin həllidir.

İstehlakçı seçimi probleminin həlli tələb nöqtəsi adlanır. Bu tələb nöqtəsi qiymətlərdən və gəlirdən asılıdır I. Yəni. tələb nöqtəsi tələbin funksiyasıdır. Öz növbəsində, tələb funksiyası hər biri arqumentdən asılı olan n funksiyalar toplusudur:

Bu funksiyalar müvafiq malların tələb funksiyaları adlanır.

Nümunə 54. Bazarda iki əmtəənin məlum qiymətləri və I gəlirləri üçün faydalılıq funksiyası formaya malikdirsə, tələb funksiyalarını tapın. .

Həll. Faydalı funksiyanı fərqləndirək:

.

(1)-də alınan ifadələri əvəz edin və tənliklər sistemini əldə edin:

Bu zaman hər bir məhsul üçün xərc istehlakçının gəlirinin yarısını təşkil edəcək və alınan məhsulun məbləği ona sərf olunan məbləğə bərabər məhsulun qiymətinə bölünəcək.

Nümunə 55. Faydalılıq birinci yaxşı, ikincisi,

birinci məhsulun qiyməti, ikincinin qiyməti. Gəlir. Faydalılığı artırmaq üçün istehlakçı nə qədər almalıdır?

Həll. Faydalı funksiyaların törəmələrini tapaq, onları (1) sistemində əvəz edək və həll edək:

Bu əmtəə dəsti faydalılığı maksimuma çatdırmaq baxımından istehlakçı üçün optimaldır.

Sınaq ayrıca dəftərdə qeydlər kitabının nömrəsinin sonuncu rəqəmi ilə seçilən varianta uyğun aparılmalıdır. Hər bir problemdə şərt, ətraflı həll və nəticə olmalıdır.

1. Hesablamaya giriş

Tapşırıq 1. Funksiya sahəsini tapın.

5.

Məsələ 2. Funksiyaların hədlərini tapın.

.

Tapşırıq 3. Funksiyanın kəsilmə nöqtələrini tapın və onların tipini təyin edin.

1. 2. 3.

Fəsil 2. Bir dəyişənli funksiyanın diferensial hesabı

Tapşırıq 4. Bu funksiyaların törəmələrini tapın.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - arcsin x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e 5 x - 1) 6; c) y =; d) y =; e) y = x 8 ++ + 5; f) y = 3 x - arcsin x.

5.a) y = 2x 3 - + e x; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sintq;

d) y = 3x 4 - - 9+ 9; e) y =;

f) y = x 2 + arcsin x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4x 4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x 2 - x; f) y = e sin 3 x + 2.

Tapşırıq 5. Funksiyanı tədqiq edin və onun qrafikini qurun.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9.a) b) c).

10. a) b) v) .

Tapşırıq 6. Verilmiş seqmentdə funksiyanın ən böyük və ən kiçik qiymətini tapın.

1. .

3. .

6. .

8. .

9. .

10. .

Fəsil 3. İnteqral hesablama

Məsələ 7. Qeyri-müəyyən inteqralları tapın.

1.a) b);

2.a) ; b) c) d).

4. G)

5.a) ; b); v) ; G).

6.a) ; b); v); G)

7.a) ; b) ; v) ; G)

8.a) ; b); v) ; G) .

9.a) ; b) c); G).

10.a) b) v) ; G) .

Məsələ 8. Müəyyən inteqralları hesablayın.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Məsələ 9. Uyğun olmayan inteqralları tapın və ya onların ayrıldığını sübut edin.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Məsələ 10. Əyrilərlə məhdudlaşan sahənin sahəsini tapın

1. .2. .

5. 6.

7. , .8..

10. , .

Fəsil 4. Bir neçə dəyişənli funksiyanın diferensial hesabı.

Tapşırıq 11. Funksiya sahəsini tapın (rəsmdə göstərin).

Məsələ 12. üçün funksiyanın davamlılığını tədqiq edin

Məsələ 13. Dolayı müəyyən edilmiş funksiyanın törəməsini tapın.

Məsələ 14. Təxmini hesablayın

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

Məsələ 15. Ekstrema üçün funksiyanı araşdırın.

7. .

8. .

9. .

10. .

Məsələ 16. Verilmiş qapalı sahədə funksiyanın ən böyük və ən kiçik qiymətini tapın.

1.düzbucaqlıda

2.

3. düzbucaqlıda

4.parabola ilə məhdudlaşan bölgədə

Və absis.

5.kvadrat

6.koordinat oxları və düz xətt ilə məhdudlaşan üçbucaqda

7.koordinat oxları və düz xətt ilə məhdudlaşan üçbucaqda

8. koordinat oxları və düz xətt ilə məhdudlaşan üçbucaqda

9.parabola ilə sərhədlənmiş bölgədə

Və absis.

10.parabola ilə sərhədlənmiş bölgədə

Və absis.

Əsas

1. M.S. Crassus, B.P. Çuprynov. Riyaziyyatın əsasları və onun iqtisadi təhsildə tətbiqi: Dərslik. - 4-cü nəşr, Isp. - M .: Delo, 2003.

2. M.S. Crassus, B.P. Çuprynov. İqtisadi ixtisaslar üçün riyaziyyat: Dərslik. - 4-cü nəşr, Isp. - M .: Delo, 2003.

3. M.S. Crassus, B.P. Çuprynov. İqtisadiyyat üzrə bakalavr dərəcəsi üçün riyaziyyat. Dərs kitabı. - 4-cü nəşr, Isp. - M .: Delo, 2005.

4. İqtisadçılar üçün ali riyaziyyat. Universitetlər üçün dərslik / N.Ş. Kremer, B.A. Putko, İ.M. Trishin, M.N. Fridman; Ed. prof. N.Ş. Kremer, - 2-ci nəşr, Yenidən işlənmiş. və əlavə edin. - M: BİRLİK, 2003.

5. Kremer N.Ş, Putko BA, Trişin İ.M., Fridman MN İqtisadi ixtisaslar üçün ali riyaziyyat. Dərslik və seminar (I və II hissələr) / Ed. prof. N.Ş. Kremer, - 2-ci nəşr, Yenidən işlənmiş. və əlavə edin. - M: Ali təhsil, 2007. - 893s. - (Elmlərin əsasları)

6. Danko P.E., Popov A.G., Kozhevnikova T.Ya. Təlimlərdə və məsələlərdə ali riyaziyyat. M. orta məktəbi. 1999.

Əlavə

1. İ.İ. Bavrin, V.L. Dənizçilər. Ali riyaziyyat. "Vlados Humanitar Nəşriyyat Mərkəzi", 2002.

2. İ.A. Zaitsev. Ali riyaziyyat. "Ali məktəb", 1998.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, İ.G. Şandra. İqtisadiyyatda riyaziyyat / iki hissədə /. M. Maliyyə və statistika. 1999.

tələbələr üçün tibbi, pediatrik, stomatoloji

və profilaktik tibb fakültələri

laboratoriya işlərinə

“Riyazi analizin əsas anlayışları”

1. Mövzunun elmi-metodiki əsaslandırılması:

Törəmə və diferensial anlayışlar riyazi analizin əsas anlayışlarından biridir. Törəmələrin hesablanması fizika və riyaziyyatda bir çox məsələlərin həlli zamanı (sürət, sürətlənmə, təzyiq və s. tapmaq) zəruridir. Törəmə anlayışının əhəmiyyəti, xüsusən də funksiyanın törəməsi onun arqumenti dəyişdikdə bu funksiyanın dəyişmə sürətini xarakterizə etməsi ilə müəyyən edilir.

Diferensialın istifadəsi təxmini hesablamalar aparmağa, həmçinin səhvləri qiymətləndirməyə imkan verir.

Funksiyaların törəmələrinin və diferensiallarının tapılması üsulları və onların tətbiqi diferensial hesablamanın əsas problemini təşkil edir. Törəmə anlayışına ehtiyac hərəkət sürətinin hesablanması və əyriyə toxunan bucağın tapılması məsələsinin tərtibi ilə əlaqədar yaranır. Tərs məsələ də mümkündür: sürətlə qət edilən məsafəni təyin edin və toxunan yamacın tangensi ilə uyğun funksiyanı tapın. Bu tərs məsələ qeyri-müəyyən inteqral anlayışına gətirib çıxarır.

Müəyyən inteqral anlayışı bir sıra praktiki məsələlərdə, xüsusən müstəvi fiqurların sahələrinin hesablanması, dəyişən qüvvənin gördüyü işin hesablanması və funksiyanın orta qiymətinin tapılması məsələlərində istifadə olunur.

Müxtəlif fiziki, kimyəvi, bioloji proseslərin və hadisələrin riyazi təsvirində çox vaxt təkcə tədqiq olunan kəmiyyətləri deyil, həm də bu kəmiyyətlərin müxtəlif sıralarının törəmələrini ehtiva edən tənliklərdən istifadə olunur. Məsələn, bakteriyaların çoxalma qanununun ən sadə versiyasına görə, çoxalma sürəti müəyyən bir zamanda bakteriyaların sayına mütənasibdir. Əgər bu kəmiyyət N (t) ilə işarələnirsə, onda törəmənin fiziki mənasına uyğun olaraq, bakteriyaların çoxalma sürəti N (t) törəməsidir və yuxarıdakı qanun əsasında yaza bilərik. nisbət N "(t) = k ∙ N, burada k> 0 - mütənasiblik əmsalı Nəticə tənlik cəbri deyil, çünki o, təkcə naməlum N (t) funksiyasını deyil, həm də onun birinci dərəcəli törəməsini ehtiva edir.

2. Qısa nəzəriyyə:

1. Törəmə anlayışına aparan problemlər

1. Maddi nöqtənin v sürətinin tapılması məsələsi... Bəzi maddi nöqtə düzxətli hərəkət etsin. Bir anda t 1 nöqtə mövqedədir M 1. Bir anda t 2 hamilə M 2 . Aralığı işarə edək M 1 , M 2 boyunca ΔS; t 2 - t 1 = Δt... Dəyər orta hərəkət sürəti adlanır. Bir mövqedə nöqtənin ani sürətini tapmaq üçün M 1 zəruri Δt sıfıra meyl edir. Riyazi olaraq bu o deməkdir

, (1)

Beləliklə, maddi nöqtənin ani sürətini tapmaq üçün funksiyanın artımının nisbətinin həddini hesablamaq lazımdır. ΔSΔt arqumentinin artımına bir şərtlə Δt → 0.

2. Funksiya qrafikinə toxunanın meyl bucağının tapılması məsələsi.

Şəkil 1

Bəzi funksiyaların qrafikini nəzərdən keçirək y = f (x). Meyil bucağı nədir
nöqtədə tangens M 1 ? nöqtədə M 1 funksiyanın qrafikinə tangens çəkin. Qrafikdə ixtiyari bir nöqtə seçin M 2 və sekant çəkin. Oxa doğru əyilmişdir OH bucaq altında α 1 ... düşünün ΔM 1 M 2 A:

, (2)

Əgər nöqtə M 1 düzəldin və işarələyin M 2 yaxınlaşın M 1 , sonra sekant M 1 M 2 nöqtədə funksiyanın qrafikinə toxunan nöqtəyə gedəcək M 1 və yaza bilərsiniz:

, (3)

Beləliklə, arqument artımı sıfıra meyl edərsə, funksiya artımının arqument artımına nisbətinin limitini hesablamaq lazımdır.

y = f (x) funksiyasının Δy artımının verilmiş x nöqtəsində Δx arqumentinin artımına nisbətinin həddi. 0 Δx sıfıra meylli olduğundan, verilmiş nöqtədə funksiyanın törəməsi adlanır.

Törəmə qeydi: y ", f" (x), ... Tərifinə görə

, (4)

burada Δx = x 2 -x 1 arqumentin artımıdır (arqumentin iki sonrakı kifayət qədər yaxın dəyəri arasındakı fərq), Δy = y 2 -y 1 funksiyanın artımıdır (qiymətlər arasındakı fərq ​arqumentin bu qiymətlərinə uyğun gələn funksiya).

Verilmiş funksiyanın törəməsinin tapılması onun adlanır fərqləndirmə... Əsas elementar funksiyaların diferensiallaşdırılması hazır düsturlara (cədvələ bax) uyğun olaraq həyata keçirilir, həmçinin Qaydalar:

Cəbri cəminin törəməsi funksiyaları bu funksiyaların törəmələrinin cəminə bərabərdir:

(u+ υ )"= u" + υ "

2. İki funksiyanın hasilinin törəməsi birincinin törəməsi ilə ikinci funksiyanın, ikincinin törəməsi ilə birinci funksiyanın hasillərinin cəminə bərabərdir:

(u ∙υ ) "= u"υ + uυ "

3. Bölmənin törəməsi iki funksiyanın kəsrinə bərabərdir ki, onun payı məxrəcin törəməsi ilə məxrəcin hasilləri ilə məxrəcin törəməsi ilə paylayıcı arasında fərq, məxrəc isə məxrəcin kvadratıdır:

Törəmənin fiziki mənası. (4) və (1) bəndlərinin müqayisəsi maddi nöqtənin düzxətli hərəkətinin ani sürətinin onun koordinatının zamandan asılılığının törəməsinə bərabər olduğunu nəzərdə tutur.

Funksiya törəməsinin ümumi mənası onun xarakterizə etməsidir funksiyanın dəyişmə sürəti (sürəti). müəyyən bir arqument dəyişikliyi üçün. Fiziki, kimyəvi və digər proseslərin sürəti, məsələn, bədənin soyuma sürəti, kimyəvi reaksiya sürəti, bakteriyaların çoxalma sürəti və s., həmçinin törəmə vasitəsilə ifadə edilir.

Törəmənin həndəsi mənası. Funksiya qrafikinə çəkilmiş tangensin maillik bucağının tangensinin böyüklüyünə riyaziyyatda deyilir. tangensin yamacı.

Diferensiallanan funksiyanın qrafikinə hər hansı bir nöqtədə toxunan meylinin mailliyi ədədi olaraq bu nöqtədəki funksiyanın törəməsinə bərabərdir.

Bu bəyanat deyilir törəmənin həndəsi mənası.

Məqalənin məzmunu

RİYAİ ANALİZ, müxtəlif dəyişmə proseslərinin kəmiyyətcə öyrənilməsi üsullarını təmin edən riyaziyyat sahəsi; dəyişmə sürətinin öyrənilməsi (diferensial hesab) və əyrilərin uzunluqlarının, əyri konturlar və səthlərlə məhdudlaşan fiqurların sahələri və həcmlərinin müəyyən edilməsi (inteqral hesab) ilə məşğul olur. Riyazi analiz problemləri üçün onların həllinin limit anlayışı ilə əlaqələndirilməsi xarakterikdir.

Riyazi analizə 1665-ci ildə İ.Nyuton və (təxminən 1675-ci ildə) müstəqil olaraq Q.Leybnits təşəbbüs göstərmiş, baxmayaraq ki, mühüm hazırlıq işləri İ.Kepler (1571–1630), F.Kavalyeri (1598–1647), P.Ferma tərəfindən aparılmışdır. (1601– 1665), J. Uollis (1616-1703) və İ. Barrou (1630-1677).

Təqdimatı daha canlı etmək üçün biz qrafiklərin dilinə müraciət edəcəyik. Odur ki, oxucu bu məqaləni oxumazdan əvvəl ANALİTİK HƏNDƏSİ məqaləsinə nəzər salmağı faydalı hesab edə bilər.

DIFFERENSİAL HESABLAMA

Tangentlər.

şək. Şəkil 1 əyrinin bir hissəsini göstərir y = 2x – x 2, arasında bağlandı x= –1 və x= 3. Bu əyrinin kifayət qədər kiçik seqmentləri düz görünür. Başqa sözlə, əgər R Bu əyrinin ixtiyari nöqtəsidir, onda bu nöqtədən keçən və nöqtənin kiçik qonşuluğunda əyrinin yaxınlaşması olan bir neçə düz xətt var. R, və qonşuluq nə qədər kiçik olsa, yaxınlaşma bir o qədər yaxşı olar. Belə düz xətt nöqtədəki əyriyə toxunan adlanır R... Diferensial hesablamanın əsas vəzifəsi tangensin mövcud olduğu əyrinin istənilən nöqtəsində tangensin istiqamətini tapmağa imkan verən ümumi metod qurmaqdır. Kəskin qırılma ilə əyri təsəvvür etmək çətin deyil (şək. 2). Əgər R- belə bir fasilənin üstü, sonra təxminən bir düz xətt qura bilərsiniz PT 1 - nöqtənin sağında R və başqa bir yaxınlaşma xətti RT 2 - nöqtənin solunda R... Ancaq bir nöqtədən keçən tək düz xətt yoxdur R, bu da nöqtənin yaxınlığındakı əyriyə eyni dərəcədə yaxşı yaxınlaşdı P həm sağa, həm də sola, deməli, nöqtədəki tangens P mövcud deyil.

şək. 1 tangens FROM mənşəyi vasitəsilə çəkilir O= (0,0). Bu xəttin yamacı 2-dir, yəni. absis 1 dəyişdikdə ordinat 2 artırsa x və y- ixtiyari nöqtənin koordinatları FROM, sonra, uzaqlaşır O məsafədə X vahidlərdən sağa, uzaqlaşırıq O 2-də y vahidlər yuxarı. Beləliklə, y/x= 2 və ya y = 2x... Bu tangens tənliyidir FROM döngəyə y = 2x – x 2 nöqtədə O.

İndi nöqtədən keçən xətlər çoxluğundan niyə izah etmək lazımdır O, seçilmiş düz xətt idi FROM... Yamacı 2 olan düz xəttin digər düz xətlərdən fərqi nədir? Bir sadə cavab var və biz çevrəyə toxunan analogiyadan istifadə etmək istəyinə qarşı durmaqda çətinlik çəkirik: tangens FROMəyri ilə yalnız bir ümumi nöqtəyə malikdir, halbuki nöqtədən keçən hər hansı digər qeyri-şaquli düz xətt O, əyrini iki dəfə kəsir. Bunu aşağıdakı kimi yoxlamaq olar.

İfadədən bəri y = 2x – x 2-ni çıxmaqla əldə etmək olar X 2 of y = 2x(düz xəttin tənlikləri FROM), sonra dəyərlər y qrafik üçün daha az bilik var y nöqtə istisna olmaqla, bütün nöqtələrdə düz xətt üçün x= 0. Deməli, qrafik nöqtədən başqa hər yerdədir O aşağıda yerləşir FROM, və bu xətt və qrafikin yalnız bir ümumi nöqtəsi var. Üstəlik, əgər y = mx- nöqtədən keçən başqa düz xəttin tənliyi O, onda iki kəsişmə nöqtəsi olacağına əmin olun. Həqiqətən, mx = 2x – x 2 təkcə üçün deyil x= 0, həm də üçün x = 2 – m... Və yalnız nə vaxt m= 2 hər iki kəsişmə nöqtəsi üst-üstə düşür. şək. 3-də halı göstərir m 2-dən azdır, yəni sağda O ikinci kəsişmə nöqtəsi var.

Nə FROM- nöqtədən keçən yeganə qeyri-şaquli düz xətt O və qrafiklə yalnız bir ümumi nöqtəyə malikdir, onun ən vacib xüsusiyyəti deyil. Həqiqətən də, başqa qrafiklərə müraciət etsək, ümumi halda qeyd etdiyimiz tangensin xassəsinin yerinə yetirilmədiyi tezliklə aydın olar. Məsələn, əncirdən. 4 əyrinin qrafikinin (1,1) nöqtəsinə yaxın olduğunu görmək olar y = x 3 düz xətt ilə yaxşı təxmin edilir RT, bununla belə, onunla birdən çox ortaq nöqtə var. Bununla belə, nəzərə almaq istərdik RT nöqtədə bu qrafikə tangens R... Buna görə də, birinci nümunədə bizə çox yaxşı xidmət edəndən fərqli olaraq, tangensi vurğulamaq üçün başqa bir yol tapmaq lazımdır.

Tutaq ki, nöqtə vasitəsilə O və ixtiyari bir nöqtə Q = (h,k) əyrinin qrafikində y = 2x – x 2 (şəkil 5) düz xətt (sekant adlanır) çəkilir. Əyri tənliyinə dəyərlərin əvəz edilməsi x = h və y = k, biz bunu alırıq k = 2h – h 2, buna görə də sekantın yamacıdır

Çox kiçik ilə h məna m 2-yə yaxın. Üstəlik, seçmək h 0-a kifayət qədər yaxın edə bilərik m ixtiyari olaraq 2-yə yaxın. Bunu deyə bilərik m"Həddinə çatır" 2-yə bərabər olduqda h sıfıra meyl edir və ya hədd nə olursa olsun müçün 2-ə bərabərdir h sıfıra meyl edir. Bu simvolik olaraq aşağıdakı kimi yazılır:

Sonra nöqtədə qrafikə toxunan O nöqtədən keçən düz xətt kimi müəyyən edilir O, bu həddə bərabər yamac ilə. Tangensin bu tərifi ümumiyyətlə tətbiq olunur.

Bu yanaşmanın üstünlüklərini başqa bir misalla göstərək: əyrinin qrafikinə toxunanın yamacını tapın. y = 2x – x 2 ixtiyari bir nöqtədə P = (x,y), özümüzü ən sadə halla məhdudlaşdırmırıq P = (0,0).

Qoy Q = (x + h, y + k) - diaqramda məsafədə yerləşən ikinci nöqtə h sağında R(şək. 6). Yamacı tapmaq tələb olunur k/h sekant PQ... Nöqtə Q məsafədədir

oxun üstündə X.

Mötərizələri genişləndirərək tapırıq:

Bu tənlikdən çıxmaq y = 2x – x 2, nöqtədən şaquli məsafəni tapırıq R nöqtəsinə Q:

Buna görə də yamac m sekant PQ bərabərdir

İndi ki h sıfıra meyllidir, m 2-2-yə meyllidir x; biz son qiyməti tangensin yamacı kimi qəbul edəcəyik PT... (Eyni nəticə alınarsa h nöqtənin seçiminə uyğun gələn mənfi qiymətlər alır Q solunda P.) Bunun üçün qeyd edin x= 0 nəticə əvvəlki ilə eynidir.

İfadə 2 - 2 x 2-nin törəməsi adlanır x – x 2. Köhnə günlərdə törəmə "diferensial nisbət" və "diferensial əmsal" da adlanırdı. Əgər ifadə 2 x – x 2 təyin f(x), yəni.

onda törəmə işarə edilə bilər

Funksiyanın qrafikinə toxunan maili tapmaq üçün y = f(x) bir nöqtədə əvəz edilməlidir fў ( x) bu nöqtəyə uyğun gələn dəyər X... Beləliklə, yamac fў (0) = 2 üçün X = 0, fў (0) = 0 üçün X= 1 və fў (2) = –2 üçün X = 2.

Törəmə də işarələnmişdir saatў , dy/dx, D x y və Du.

Fakt budur ki, əyri y = 2x – x Verilmiş nöqtənin yaxınlığındakı 2 bu nöqtədə onun tangensindən praktiki olaraq fərqlənmir, toxunma nöqtəsində "əyrinin yamacı" kimi tangensin yamacından danışmağa imkan verir. Beləliklə, iddia edə bilərik ki, nəzərdən keçirilən əyrinin mailliyi (0,0) nöqtəsində 2 mailliyə malikdir. x= 0 dəyişmə dərəcəsi y nisbətən x 2-dir. (2,0) nöqtəsində tangensin (və əyrinin) mailliyi –2-dir. (Mənfi işarə o deməkdir ki x dəyişən y azalır.) (1,1) nöqtəsində tangens üfüqidir. Döngə deyirik y = 2x – x 2 bu nöqtədə stasionar qiymətə malikdir.

Yüksəklər və aşağılar.

Biz yalnız əyri olduğunu göstərdik f(x) = 2x – x 2 (1,1) nöqtəsində sabitdir. Çünki fў ( x) = 2 – 2x = 2(1 – x), üçün aydındır x 1-dən az, fў ( x) müsbətdir və buna görə də y artır; saat x, böyük 1, fў ( x) mənfidir və buna görə də y azalır. Beləliklə, Şəkildə göstərilən nöqtənin (1,1) yaxınlığında. 6 hərf M, məna saat bir nöqtəyə qədər böyüyür M, nöqtədə stasionar M və nöqtədən sonra azalır M... Bu nöqtə "maksimum" adlanır, çünki dəyər saat bu nöqtədə onun kifayət qədər kiçik bir məhəlləsində hər hansı bir dəyərini aşır. Eynilə, "minimum" bütün dəyərlərin yaxınlığında olan bir nöqtə kimi müəyyən edilir y saydan çox saat elə bu məqamda. Törəmə olmasına baxmayaraq bu da baş verə bilər f(x) bir nöqtədə yox olur, bu nöqtənin yaxınlığında onun işarəsi dəyişmir. Nə maksimum, nə də minimum olmayan belə bir nöqtəyə əyilmə nöqtəsi deyilir.

Nümunə olaraq əyrinin stasionar nöqtəsini tapaq

Bu funksiyanın törəməsidir

və da yox olur x = 0, X= 1 və X= –1; olanlar. (0,0), (1, –2/15) və (–1, 2/15) nöqtələrində. Əgər X sonra -1-dən bir qədər azdır fў ( x) mənfi; əgər X sonra -1-dən bir qədər çox fў ( x) müsbətdir. Beləliklə, nöqtə (–1, 2/15) maksimumdur. Eynilə, (1, –2/15) nöqtəsinin minimum olduğunu göstərmək olar. Amma törəmə fў ( x) (0,0) nöqtəsindən əvvəl və sonra mənfidir. Buna görə də (0,0) əyilmə nöqtəsidir.

Əyrinin formasının, eləcə də əyrinin oxun kəsişməsi faktının öyrənilməsi X saat f(x) = 0 (yəni, üçün X= 0 və ya) onun qrafikini təxminən şəkildə göstərildiyi kimi təqdim etməyə imkan verir. 7.

Ümumiyyətlə, qeyri-adi halları (düz xətt seqmentlərini və ya sonsuz sayda əyilmələri ehtiva edən əyriləri) istisna etsək, əyrinin nisbi mövqeyi və toxunan nöqtənin yaxınlığındakı tangens üçün dörd variant var. R. (Sm... düyü. 8, burada tangensin müsbət yamacı var.)

1) Nöqtənin hər iki tərəfində Rəyri tangensdən yuxarıda yerləşir (şək. 8, a). Bu vəziyyətdə nöqtədə əyri olduğunu söyləyirlər R aşağıya doğru qabarıq və ya konkav.

2) Nöqtənin hər iki tərəfində Rəyri tangensdən aşağıda yerləşir (şək. 8, b). Bu halda əyrinin yuxarıya doğru qabarıq və ya sadəcə qabarıq olduğu deyilir.

3) və 4) Əyri nöqtənin bir tərəfində tangensdən yuxarıda yerləşir R və aşağıda - digər tərəfdən. Bu halda R- əyilmə nöqtəsi.

Dəyərlərin müqayisəsi fў ( x) hər iki tərəfində R nöqtədəki dəyəri ilə R, müəyyən bir problemdə bu dörd işdən hansının həll edilməli olduğunu müəyyən etmək mümkündür.

Proqramlar.

Yuxarıda göstərilənlərin hamısı müxtəlif sahələrdə mühüm tətbiqlər tapır. Məsələn, cəsəd saniyədə 200 fut ilkin sürətlə şaquli olaraq yuxarı atılırsa, o zaman hündürlük s vasitəsilə yerləşəcəklər t başlanğıc nöqtəsi ilə müqayisədə saniyə olacaq

Baxdığımız nümunələrdə olduğu kimi hərəkət edərək, tapırıq

bu dəyər c-də yox olur. törəmə fў ( x) c qiymətinə qədər müsbət, bu vaxtdan sonra isə mənfi olur. Beləliklə, s qədər artır, sonra stasionar olur, sonra isə azalır. Bu, yuxarıya atılan bir cismin hərəkətinin ümumi təsviridir. Bədənin ən yüksək nöqtəyə nə vaxt çatdığını ondan bilirik. Bundan əlavə, əvəzedici t= 25/4 düym f(t), biz 625 fut, maksimum qaldırma alırıq. Bu vəzifədə fў ( t) fiziki məna daşıyır. Bu törəmə bədənin zaman anında hərəkət etdiyi sürəti göstərir t.

İndi başqa bir tətbiq növünə nəzər salaq (şək. 9). 75 sm 2 sahəsi olan bir karton vərəqdən kvadrat dibi olan bir qutu etmək tələb olunur. Maksimum həcmə malik olması üçün bu qutu nə qədər böyük olmalıdır? Əgər X- qutunun əsasının tərəfi və h- onun hündürlüyü, onda qutunun həcmidir V = x 2 h, və səth sahəsi 75 =-dir x 2 + 4xh... Tənliyi çevirərək alırıq:

Əldə edilən V bərabər olduğu ortaya çıxır

və da yox olur X= 5. Sonra

və V= 125/2. Funksiya qrafiki V = (75x – x 3) / 4 Şəkildə göstərilmişdir. 10 (mənfi dəyərlər X bu problemdə heç bir fiziki məna olmadığı üçün buraxılmışdır).

Törəmələri.

Diferensial hesablamanın mühüm vəzifəsi törəmələri tez və rahat tapmağa imkan verən metodların yaradılmasıdır. Məsələn, bunu hesablamaq asandır

(Sabitin törəməsi təbii ki, sıfırdır.) Ümumi qaydanı çıxarmaq çətin deyil:

harada n- istənilən tam və ya kəsr. Məsələn,

(Bu nümunə kəsr eksponentlərinin nə qədər faydalı olduğunu göstərir.)

Budur ən vacib düsturlardan bəziləri:

Aşağıdakı qaydalar da var: 1) əgər iki funksiyanın hər biri g(x) və f(x) törəmələri var, onda onların cəminin törəməsi bu funksiyaların törəmələrinin cəminə, fərqin törəməsi isə törəmələrin fərqinə bərabərdir, yəni.

2) iki funksiyanın hasilinin törəməsi düsturla hesablanır:

3) iki funksiyanın nisbətinin törəməsi formaya malikdir

4) sabitə vurulan funksiyanın törəməsi bu funksiyanın törəməsi ilə vurulan sabitə bərabərdir, yəni.

Tez-tez olur ki, bir funksiyanın dəyərlərini mərhələlərlə hesablamaq lazımdır. Məsələn, günahı hesablamaq üçün x 2, əvvəlcə tapmaq lazımdır u = x 2 və sonra ədədin sinusunu hesablayın u... Biz sözdə "zəncir qaydası"ndan istifadə edərək belə mürəkkəb funksiyaların törəməsini tapırıq:

Bizim nümunəmizdə f(u) = günah u, fў ( u) = cos u, deməli,

Bu və digər oxşar qaydalar bir çox funksiyaların törəmələrini dərhal yazmağa imkan verir.

Xətti yaxınlaşmalar.

Törəməni bilməklə bir çox hallarda funksiyanın qrafikini bu nöqtədə onun tangensinin hansısa nöqtəsinə yaxın yerdə əvəz edə bilməyimiz böyük əhəmiyyət kəsb edir, çünki düz xətlərlə işləmək daha asandır.

Bu fikir funksiyaların təxmini qiymətlərinin hesablanmasında birbaşa tətbiq tapır. Məsələn, dəyəri hesablamaq olduqca çətindir x= 1.033. Amma 1.033 rəqəminin 1-ə yaxın olmasından və ondan istifadə edə bilərsiniz. Yaxın x= 1 heç bir ciddi səhvə yol vermədən tangens əyrisinin qrafikini əvəz edə bilərik. Belə bir tangensin mailliyi törəmənin dəyərinə bərabərdir ( x 1/3) ў = (1/3) x x = 1-də –2/3, yəni 1/3. (1,1) nöqtəsi əyri üzərində yerləşdiyindən və bu nöqtədə əyriyə toxunanın mailliyi 1/3 olduğundan, tangensin tənliyi formaya malikdir.

Bu xəttdə X = 1,033

Nəticə dəyər y həqiqi dəyərə çox yaxın olmalıdır y; və həqiqətən də, həqiqi olandan yalnız 0,00012 çoxdur. Riyazi analizdə bu növ xətti yaxınlaşmanın dəqiqliyini artırmaq üçün üsullar işlənib hazırlanmışdır. Bu üsullar təxmini hesablamalarımızın etibarlılığını təmin edir.

Yuxarıda təsvir olunan prosedur faydalı bir qeyd təklif edir. Qoy P- funksiyanın qrafikinə uyğun gələn nöqtə f dəyişən X və funksiyaya icazə verin f(x) fərqləndirilir. Nöqtə yaxınlığında əyrinin qrafikini dəyişdirin R ona tangens, bu nöqtədə çəkilir. Əgər X məbləğinə görə dəyişdirin h, onda tangensin ordinatı dəyərlə dəyişəcək h H f ў ( x). Əgər hçox kiçikdir, onda sonuncu qiymət ordinatdakı həqiqi dəyişikliyə yaxşı yaxınlaşmadır y qrafika. Əgər əvəzinə h simvolunu yazacağıq dx(bu məhsul deyil!), lakin ordinatda dəyişiklik y işarələmək dy, onda alırıq dy = f ў ( x)dx, və ya dy/dx = f ў ( x) (sm... düyü. on bir). Buna görə də əvəzinə Dy və ya f ў ( x) simvolu çox vaxt törəməni bildirmək üçün istifadə olunur dy/dx... Bu qeydin rahatlığı əsasən zəncirvari qaydanın açıq-aydın görünüşündən asılıdır (mürəkkəb funksiyanın diferensiallaşdırılması); yeni notasiyada bu düstur belə görünür:

bunun nəzərdə tutulduğu yerdə saat asılıdır u, a uöz növbəsində asılıdır X.

Böyüklük dy diferensial adlanır saat; əslində ondan asılıdır iki dəyişənlər, yəni: from X və artımlar dx... Artan zaman dxçox kiçik, böyüklük dy dəyərdə müvafiq dəyişikliyə yaxındır y... Ancaq artım olduğunu düşünmək dx az, ehtiyac yoxdur.

Törəmə funksiyası y = f(x) işarə etdik f ў ( x) və ya dy/dx... Çox vaxt törəmənin törəməsini götürmək mümkündür. Nəticə ikinci törəmə adlanır f (x) və işarələnir f ўў ( x) və ya d 2 y/dx 2. Məsələn, əgər f(x) = x 3 – 3x 2, onda f ў ( x) = 3x 2 – 6x və f ўў ( x) = 6x- 6. Oxşar təyinatlar daha yüksək dərəcəli törəmələr üçün istifadə olunur. Bununla belə, çox sayda tiredən qaçınmaq üçün (törəmə sırasına bərabər) dördüncü törəmə (məsələn) belə yazıla bilər. f (4) (x) və törəmə n-ci sifariş kimi f (n) (x).

Göstərilə bilər ki, bir nöqtədə əyri ikinci törəmə müsbət olarsa aşağıya doğru qabarıq, ikinci törəmə mənfi olarsa yuxarı qabarıq olur.

Əgər funksiyanın ikinci törəməsi varsa, onda kəmiyyətin dəyişməsi y artıma uyğundur dx dəyişən X, təxminən düsturla hesablana bilər

Bu yaxınlaşma, ümumiyyətlə, diferensial tərəfindən veriləndən daha yaxşıdır fў ( x)dx... Bu əyrinin bir hissəsini düz xəttlə deyil, parabola ilə əvəz etməyə uyğundur.

Əgər funksiyası f(x) daha yüksək dərəcəli törəmələr var, onda

Qalanı isə

harada x- arasında bir sıra x və x + dx... Yuxarıdakı nəticə qalan Taylor düsturu adlanır. Əgər f(x) bütün sifarişlərin törəmələri var, onda adətən R n® 0 üçün n ® Ґ .

İNTEQRAL HESABLAMA

Kvadratlar.

Əyrixətti müstəvi fiqurların sahələri öyrənilərkən riyazi analizin yeni aspektləri aşkarlanır. Hətta qədim yunanlar belə problemləri həll etməyə çalışdılar, məsələn, bir dairənin sahəsini təyin etmək ən çətin vəzifələrdən biri idi. Arximed bu problemin həllində böyük uğur əldə etdi, o da parabolik seqmentin sahəsini tapmağı bacardı (şək. 12). Çox mürəkkəb mülahizələrin köməyi ilə Arximed sübut etdi ki, parabolik seqmentin sahəsi təsvir olunan düzbucaqlının sahəsinin 2/3 hissəsidir və buna görə də bu halda (2/3) (16) bərabərdir. = 32/3. Daha sonra görəcəyimiz kimi, bu nəticəni riyazi analiz üsulları ilə asanlıqla əldə etmək olar.

Nyuton və Leybnisin sələfləri, əsasən Kepler və Kavalieri əyri xətti fiqurların sahələrinin hesablanması problemini çətin ki, məntiqi adlandırmaq mümkün olmayan, lakin son dərəcə məhsuldar olduğu ortaya çıxan bir üsulla həll etdilər. Uollis 1655-ci ildə Kepler və Kavalyerinin üsullarını Dekartın (analitik həndəsə) üsulları ilə birləşdirib yeni yaranan cəbrdən istifadə etdikdə Nyutonun meydana çıxması üçün səhnə tamamilə hazırlanmışdı.

Uollis sahəsinin hesablanması tələb olunan rəqəmi hər biri təxminən düzbucaqlı hesab edilən çox dar zolaqlara böldü. Sonra o, yaxınlaşan düzbucaqlıların sahələrini topladı və ən sadə hallarda, zolaqların sayı sonsuzluğa meyilli olduqda düzbucaqlıların sahələrinin cəminin meyl göstərdiyi qiyməti aldı. şək. 13 əyri altındakı sahənin zolaqlarına bəzi bölmələrə uyğun gələn düzbucaqlıları göstərir y = x 2 .

Əsas teorem.

Nyuton və Leybnisin böyük kəşfi sahələr cəminin həddinə keçmək üçün zəhmətli prosesi istisna etməyə imkan verdi. Bu, kvadrat anlayışına yeni baxış sayəsində edildi. Məsələ ondadır ki, ordinatın soldan sağa hərəkəti nəticəsində yaranan əyrinin altındakı sahəni təsəvvür etməliyik və ordinatların süpürülən sahəsinin nə qədər sürətlə dəyişdiyini soruşmalıyıq. Ərazinin əvvəlcədən məlum olduğu iki xüsusi halı nəzərdən keçirsək, bu sualın cavabının açarını alacağıq.

Xətti funksiyanın qrafikinin altındakı sahədən başlayaq y = 1 + xçünki bu halda sahəni elementar həndəsədən istifadə etməklə hesablamaq olar.

Qoy A(x) Təyyarənin düz xətt arasında qapalı hissəsidir y = 1 + x və bir seqment OQ(şək. 14). Avtomobil sürərkən QP sağ sahə A(x) artır. Necə sürətli? Bu suala cavab vermək çətin deyil, çünki bilirik ki, trapezoidin sahəsi onun hündürlüyünün əsaslarının yarısının cəminə bərabərdir. Beləliklə,

Ərazi dəyişmə dərəcəsi A(x) törəməsi ilə müəyyən edilir

Biz bunu görürük Aў ( x) ordinatı ilə üst-üstə düşür saat xal R... Bu təsadüfdürmü? Şəkildə göstərilən parabolanı yoxlamağa çalışaq. 15. Kvadrat A (x) parabolanın altında saat = X 0 ilə 2 aralığında X bərabərdir A(x) = (1 / 3)(x)(x 2) = x 3/3. Bu sahənin dəyişmə sürəti ifadə ilə müəyyən edilir

ordinatla tam üst-üstə düşür saat hərəkət nöqtəsi R.

Əgər fərz etsək ki, bu qayda ümumiyyətlə elə yerinə yetirilir ki

funksiyanın qrafiki altında olan sahənin dəyişmə sürətidir y = f(x), onda bu hesablamalar və digər sahələr üçün istifadə edilə bilər. Əslində nisbət Aў ( x) = f(x) əsas teoremi ifadə edir, onu aşağıdakı kimi tərtib etmək olar: törəmə və ya sahənin funksiyası kimi dəyişmə sürəti X, funksiyanın qiymətinə bərabərdir f (x) nöqtəsində X.

Məsələn, funksiyanın qrafikinin altındakı sahəni tapmaq üçün y = x 0-dan 3-ə qədər X(Şəkil 16), biz qoyduq

Mümkün cavab budur:

törəməsi olduğundan X 4/4 həqiqətən bərabərdir X 3. Üstəlik, A(x) üçün sıfıra bərabərdir X= 0, olduğu kimi A(x) həqiqətən bir sahədir.

Riyazi analiz sübut edir ki, yuxarıdakı ifadədən başqa başqa bir cavab A(x), mövcud deyil. Gəlin aşağıdakı evristik (qeyri-ciddi) mülahizədən istifadə edərək bu ifadənin inandırıcı olduğunu göstərək. Tutaq ki, ikinci həll yolu var V(x). Əgər A(x) və V(x) sıfır dəyərdən eyni vaxtda "Başla" X= 0 və hər zaman eyni sürətlə dəyişir, sonra onların dəyərləri №-də olur X fərqli ola bilməz. Onlar hər yerdə eyni olmalıdır; buna görə də yalnız bir həll yolu var.

Nisbəti necə əsaslandırmaq olar? Aў ( x) = f(x) ümumiyyətlə? Bu suala yalnız bir funksiya olaraq ərazinin dəyişmə sürətini öyrənməklə cavab vermək olar Xümumiyyətlə. Qoy m- funksiyanın ən kiçik qiyməti f (x) aralığında Xəvvəl ( x + h), a M- eyni intervalda bu funksiyanın ən böyük qiyməti. Daha sonra gedərək sahənin artımı Xüçün ( x + h) iki düzbucağın sahələri arasında qapalı olmalıdır (şək. 17). Hər iki düzbucağın əsasları bərabərdir h... Kiçik düzbucaqlının hündürlüyü var m və sahə mh, daha böyük, müvafiq olaraq, M və Mh... Əraziyə qarşı X(şək. 18) görünə bilər ki, absis ilə dəyişdikdə h, ordinatın dəyəri (yəni, sahə) arasına əlavə edilmiş məbləğlə artır. mh və Mh... Bu qrafikdəki sekant yamac arasındadır m və M... nə vaxt olur h sıfıra meyllidir? Əgər funksiyanın qrafiki y = f(x) davamlıdır (yəni, kəsiklər ehtiva etmir), onda M, və m meyl edir f(x). Buna görə də yamac Aў ( x) funksiyası kimi ərazinin sahəsi X bərabərdir f(x). Məhz belə bir nəticəyə gəlmək lazım idi.

Leybniz əyri altındakı sahə üçün təklif etdi y = f(x) 0-dan a təyinat

Ciddi bir yanaşma ilə, bu sözdə müəyyən inteqral Wallis üsulu ilə müəyyən məbləğlərin həddi kimi müəyyən edilməlidir. Yuxarıdakı nəticəni nəzərə alsaq, belə bir funksiyanı tapmaq şərtilə bu inteqralın hesablandığı aydın olur A(x), da yox olur X= 0 və törəməsi var Aў ( x) bərabərdir f (x). Belə bir funksiyanın tapılması adətən inteqrasiya adlanır, baxmayaraq ki, bu əməliyyatı antidiferensasiya adlandırmaq daha məqsədəuyğun olardı, yəni, müəyyən mənada diferensiallaşmaya tərsdir. Polinom vəziyyətində inteqrasiya sadədir. Məsələn, əgər

fərqləndirmə yolu ilə yoxlamaq asandır A(x).

Sahəni hesablamaq üçün A 1 əyri altında y = 1 + x + x 0 və 1 ordinatları arasında olan 2/2, sadəcə yazırıq

və əvəz edir X= 1, alırıq A 1 = 1 + 1/2 + 1/6 = 5/3. Kvadrat A(x) 0-dan 2-yə bərabərdir A 2 = 2 + 4/2 + 8/6 = 16/3. Şəkildən göründüyü kimi. 19, 1 və 2 ordinatları arasındakı sahədir A 2 – A 1 = 11/3. Adətən müəyyən inteqral kimi yazılır

Cildlər.

Oxşar əsaslandırma inqilab cisimlərinin həcmlərini hesablamağı təəccüblü dərəcədə sadələşdirir. Bunu qədim yunanların onlara məlum olan üsullardan istifadə edərək çox çətinliklə həll edə bildikləri başqa bir klassik problem olan topun həcminin hesablanması nümunəsi ilə nümayiş etdirək.

Təyyarənin radius dairəsinin dörddə biri daxilində qapalı hissəsini fırladın r, ox ətrafında 360 ° bucaq altında X... Nəticədə, həcmini qeyd etdiyimiz bir yarımkürə (şəkil 20) alırıq V(x). Hansı nisbətdə olduğunu müəyyən etmək tələb olunur V(x) artması ilə x... -dən irəliləyir X Kimə X + h, səs artımının həcmdən az olduğunu yoxlamaq asandır səh(r 2 – x 2)h dairəvi silindr radiusu və hündürlüyü h, və həcmdən daha çox səh[r 2 – (x + h) 2 ]h silindr radiusu və hündürlüyü h... Buna görə də funksiyanın qrafikində V(x) sekantın mailliyi arasındadır səh(r 2 – x 2) və səh[r 2 – (x + h) 2]. Nə vaxt h sıfıra meyl edir, yamac meyl edir

At x = r alırıq

yarımkürənin həcmi üçün və buna görə də 4 p r Bütün topun həcmi üçün 3/3.

Bənzər bir üsul əyrilərin uzunluqlarını və əyri səthlərin sahələrini tapmağa imkan verir. Məsələn, əgər a(x) - qövs uzunluğu PRşək. 21, o zaman vəzifəmiz hesablamaqdır aў( x). Evristik səviyyədə biz nəticənin ciddi sübutu üçün zəruri olan həddi adi keçidə müraciət etməməyə imkan verən hiylədən istifadə edirik. Tutaq ki, funksiyanın dəyişmə sürəti a(x) nöqtəsində Rəyri onun tangensi ilə əvəz edilsəydi, eynidir PT nöqtədə P... Ancaq əncirdən. 21 addım atarkən birbaşa görünə bilər h nöqtənin sağına və ya soluna X boyunca RT məna a(x) dəyişir

Buna görə də funksiyanın dəyişmə sürəti a(x) edir

Funksiyanın özünü tapmaq üçün a(x), yalnız bərabərliyin sağ tərəfindəki ifadəni inteqrasiya etmək lazımdır. Belə çıxır ki, əksər funksiyaları inteqrasiya etmək çətindir. Buna görə də inteqral hesablama metodlarının inkişafı riyazi analizin böyük hissəsini təşkil edir.

Antiderivativlər.

Törəməsi verilmiş funksiyaya bərabər olan hər bir funksiya f(x), üçün antiderivativ (və ya primitiv) adlanır f(x). Məsələn, X 3/3 funksiyanın əks törəməsidir X 2, çünki ( x 3/3) ў = x 2. Əlbəttə X 3/3 funksiyanın yeganə əks törəməsi deyil X 2 ildən x 3 /3 + Cüçün də törəmədir X hər hansı bir sabit üçün 2 İLƏ... Bununla belə, bundan sonra biz bu cür əlavə sabitləri buraxmağa razı olacağıq. Ümumiyyətlə

harada n Müsbət tam ədəddir, çünki ( x n + 1/(n+ 1)) ў = x n... Münasibət (1) daha ümumi mənada, əgər varsa n istənilən rasional ədədlə əvəz edin k-1 istisna olmaqla.

Verilmiş funksiya üçün ixtiyari antitörəmə funksiyası f(x) adətən qeyri-müəyyən inteqralı adlanır f(x) və kimi işarələyin

Məsələn, bəri (günah x) ў = cos x, formula etibarlıdır

Bir çox hallarda, verilmiş funksiyanın qeyri-müəyyən inteqralı üçün düstur olduqda, onu qeyri-müəyyən inteqralların çoxlu geniş çap olunmuş cədvəllərində tapmaq olar. Elementar funksiyaların inteqralları cədvəllidir (bunlara dərəcələr, loqarifmlər, eksponensial funksiyalar, triqonometrik funksiyalar, tərs triqonometrik funksiyalar, həmçinin toplama, çıxma, vurma və bölmə əməliyyatlarından istifadə etməklə onların sonlu birləşmələri daxildir). Cədvəl inteqrallarından istifadə edərək daha mürəkkəb funksiyaların inteqrallarını hesablaya bilərsiniz. Qeyri-müəyyən inteqralları hesablamağın bir çox yolu var; bunlardan ən geniş yayılmışı dəyişən əvəzetmə və ya əvəzetmə üsuludur. Bu ondan ibarətdir ki, əgər qeyri-müəyyən inteqralda əvəz etmək istəsək (2) x bəzi diferensiallaşan funksiya üzərində x = g(u), inteqralın dəyişməməsi üçün lazımdır x ilə əvəz edilmişdir gў ( u)du... Başqa sözlə, bərabərlik

(əvəzetmə 2 x = u, haradan 2 dx = du).

Budur, başqa bir inteqrasiya üsulu - hissələr üzrə inteqrasiya üsulu. Artıq məlum olan düstura əsaslanır

Sol və sağ tərəfləri birləşdirərək və bunu nəzərə alaraq

Bu düstur hissələr üzrə inteqrasiya düsturu adlanır.

Misal 2. Tapmaq tələb olunur. Çünki cos x= (günah x) є, bunu yaza bilərik

(5) dən, təyinat u = x və v= günah x, alırıq

Və o vaxtdan (-cos x) ў = günah x tapırıq və

Vurğulamaq lazımdır ki, biz özümüzü çoxsaylı hazırcavab üsulların toplandığı çox geniş bir mövzuya yalnız çox qısa bir girişlə məhdudlaşdırdıq.

İki dəyişənin funksiyaları.

Döngəyə görə y = f(x) biz iki tapşırığı nəzərdən keçirdik.

1) Verilmiş nöqtədə əyriyə toxunan meylin mailliyini tapın. Bu problem törəmənin dəyərini hesablamaqla həll edilir fў ( x) müəyyən edilmiş nöqtədə.

2) Ox seqmentinin üstündəki əyrinin altındakı sahəni tapın Xşaquli xətlərlə məhdudlaşır X = a və X = b... Bu məsələ müəyyən inteqralın hesablanması ilə həll edilir.

Bu problemlərin hər birinin səthi vəziyyətində bir analoqu var z = f(x,y).

1) Verilmiş nöqtədə səthə toxunan müstəvini tapın.

2) Səthin altındakı müstəvi hissəsinin üstündəki həcmi tapın huəyri ilə məhdudlaşır İLƏ, və yan tərəfdən - təyyarəyə perpendikulyarlar xy sərhəd əyrisinin nöqtələrindən keçən İLƏ (sm... düyü. 22).

Aşağıdakı nümunələr bu vəzifələrin necə yerinə yetirildiyini göstərir.

Misal 4. Səthə toxunan müstəvini tapın

nöqtəsində (0,0,2).

Müstəvidə yerləşən iki kəsişən xətt verilirsə, müstəvi müəyyən edilir. Bu sətirlərdən biri ( l 1) biz təyyarəyə minəcəyik xz (saat= 0), ikinci ( l 2) - təyyarədə yz (x = 0) (sm... düyü. 23).

Hər şeydən əvvəl, əgər saat= 0, onda z = f(x,0) = 2 – 2x – 3x 2. ilə bağlı törəmə X ilə işarələnir fў x(x,0) = –2 – 6x, at X= 0 -2 dəyərinə malikdir. Düz l 1 tənliklərlə verilmişdir z = 2 – 2x, saat= 0 - toxunan İLƏ 1, səthin təyyarə ilə kəsişmə xətləri saat= 0. Eynilə, əgər X= 0, onda f(0,y) = 2 – y – y 2 və törəmə ilə əlaqədar saat formasına malikdir

Çünki fў y(0,0) = –1, əyri İLƏ 2 - səthin təyyarə ilə kəsişmə xətti yz- tangensi var l 2 tənliklərlə verilmişdir z = 2 – y, X= 0. İstədiyiniz tangens müstəvisi hər iki düz xətti ehtiva edir l 1 və l 2 və tənliklə yazılır

Bu təyyarənin tənliyidir. Bundan əlavə, düz xətlər alırıq l 1 və l 2, müvafiq olaraq, saat= 0 və X = 0.

Tənliyin (7) həqiqətən də tangens müstəvisini təyin etməsi faktı, əgər bu tənliyin (6) tənliyinə daxil edilmiş birinci dərəcəli hədləri ehtiva etdiyini və ikinci dərəcəli hədlərin tənlikdə təmsil oluna biləcəyini görsək, evristik səviyyədə yoxlanıla bilər. forma -. Çünki bu ifadə bütün dəyərlər üçün mənfidir X və saat, Bundan başqa X = saat= 0, səth (6) nöqtədən başqa, müstəvidən (7) aşağıda hər yerdə yerləşir R= (0,0,0). Səthin (6) yuxarıya doğru qabarıq olduğunu deyə bilərik R.

Misal 5. Səthə toxunan müstəvini tapın z = f(x,y) = x 2 – y 2 mənşəli 0.

Səthdə saat= 0 bizdə: z = f(x,0) = x 2 və fў x(x,0) = 2x... Üstündə İLƏ 1, kəsişmə xətləri, z = x 2. nöqtədə O yamacdır fў x(0,0) = 0. Təyyarədə X= 0 bizdə: z = f(0,y) = –y 2 və fў y(0,y) = –2y... Üstündə İLƏ 2, kəsişmə xətləri, z = –y 2. nöqtədə Oəyrinin yamacı İLƏ 2 bərabərdir fў y(0,0) = 0. Təğviləri olduğundan İLƏ 1 və İLƏ 2 baltadır X və saat, onları ehtiva edən tangens müstəvisi müstəvidir z = 0.

Bununla belə, mənşəyin yaxınlığında səthimiz tangens müstəvisinin bir tərəfində deyil. Həqiqətən, əyri İLƏ 1 hər yerdə, 0 nöqtəsindən başqa, tangens müstəvisinin və əyrinin üstündə yerləşir İLƏ 2 - müvafiq olaraq aşağıda. Səth tangens müstəvisini kəsir z düz xətlərdə = 0 saat = X və saat = –X... Belə bir səthin başlanğıcda yəhər nöqtəsi olduğu deyilir (şək. 24).

Qismən törəmələr.

Əvvəlki nümunələrdə biz törəmələrdən istifadə etdik f (x,y) açıqdır X və tərəfindən saat... İndi bu cür törəmələri daha ümumi nəzərdən keçirək. Əgər iki dəyişənin funksiyası varsa, məsələn, F(x,y) = x 2 – xy, onda biz hər bir nöqtədə onun "qismən törəmələrindən" ikisini təyin edə bilərik, birini funksiya ilə əlaqədar olaraq fərqləndirərək X və fiksasiya saat, digərinə görə fərqləndirərək saat və fiksasiya X... Bu törəmələrdən birincisi kimi işarələnir fў x(x,y) və ya ¶ f/¶ x; ikinci - necə f f ў y... Əgər hər iki qarışıq törəmə (tərəfindən X və saat, açıq saat və X) davamlıdır, onda ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x; nümunəmizdə ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x = –1.

Qismən törəmə fў x(x,y) funksiyanın dəyişmə sürətini göstərir f nöqtədə ( x,y) artım istiqamətində X, a fў y(x,y) funksiyanın dəyişmə sürətidir f yüksələn istiqamət saat... Funksiya dəyişmə dərəcəsi f nöqtədə ( X,saat) bucaq yaradan düz xəttin istiqamətində q oxun müsbət istiqaməti ilə X, funksiyasının törəməsi adlanır f doğru; onun qiyməti funksiyanın iki qismən törəməsinin birləşməsidir tangens müstəvisində f demək olar ki, bərabərdir (kiçik dx və dy) əsl dəyişiklik z səthdə, lakin diferensialın hesablanması adətən daha asandır.

Mürəkkəb funksiyanın və ya zəncir qaydasının törəməsi kimi tanınan dəyişən dəyişmə metodundan artıq nəzərdən keçirdiyimiz düstur, birölçülü halda saat asılıdır X, a X asılıdır t, formasına malikdir:

İki dəyişənin funksiyaları üçün oxşar düstur belədir:

Qismən fərqləndirmə anlayışlarını və təyinatlarını daha yüksək ölçülərə ümumiləşdirmək asandır. Xüsusilə, əgər səth tənlik ilə dolaylı olaraq verilirsə f(x,y,z) = 0 olarsa, səthə toxunan müstəvinin tənliyi daha simmetrik formada verilə bilər: nöqtədə toxunan müstəvi tənliyi ( x (x 2/4)], sonra üzərində inteqrasiya olunur X 0-dan 1-ə. Yekun nəticə 3/4-dür.

Formula (10) ikiqat inteqral deyilən kimi də şərh edilə bilər, yəni. elementar "hüceyrələrin" həcmlərinin cəminin həddi kimi. Hər bir belə hüceyrənin D bazası var x D y və düzbucaqlı əsasın hansısa nöqtəsindən yuxarı səthin hündürlüyünə bərabər hündürlük ( sm... düyü. 26). Göstərilə bilər ki, düstur (10) üzrə hər iki baxış nöqtəsi ekvivalentdir. Mexanikada olan ağırlıq mərkəzlərini və çoxsaylı momentləri tapmaq üçün ikiqat inteqrallardan istifadə olunur.

Riyazi aparatın daha ciddi əsaslandırılması.

İndiyə qədər biz intuitiv səviyyədə hesablama anlayışlarını və üsullarını təqdim etdik və həndəsi fiqurlara müraciət etməkdən çəkinmədik. 19-20-ci əsrlərdə ortaya çıxan daha sərt üsulları qısaca nəzərdən keçirmək bizim üçün qalır.

19-cu əsrin əvvəllərində “riyazi analizin yaradılması”nda hücum və basqın dövrü başa çatdıqda onun əsaslandırılması məsələləri ön plana çıxdı. Abel, Koşi və bir sıra başqa görkəmli riyaziyyatçıların əsərlərində “həddin”, “fasiləsiz funksiya”, “birləşən sıralar” anlayışları dəqiq müəyyən edilmişdir. Bu, riyazi analizin etibarlı tədqiqat alətinə çevrilməsi üçün onun əsasına məntiqi nizam gətirmək üçün lazım idi. Hərtərəfli əsaslandırma ehtiyacı 1872-ci ildə Weierstrass tərəfindən hər yerdə davamlı, lakin heç bir yerdə diferensiallana bilməyən funksiyaların kəşfindən sonra daha aydın oldu (belə funksiyaların qrafikində hər nöqtədə fasilə var). Bu nəticə riyaziyyatçılarda böyük təəssürat yaratdı, çünki bu, onların həndəsi intuisiyasına açıq şəkildə zidd idi. Həndəsi intuisiyanın etibarsızlığının daha parlaq nümunəsi D. Peano tərəfindən qurulmuş, müəyyən bir kvadratı tamamilə dolduran davamlı əyri idi, yəni. bütün nöqtələrindən keçir. Bu və digər kəşflər riyaziyyatın “arifmetizasiyası” proqramının yaranmasına səbəb oldu, yəni. ədəd anlayışından istifadə edərək bütün riyazi anlayışları əsaslandıraraq onu daha etibarlı etmək. Riyaziyyatın əsaslarına dair əsərlərdə aydınlıqdan demək olar ki, puritan şəkildə imtinanın öz tarixi əsası var idi.

Müasir məntiqi sərtlik qanunlarına görə, əyrinin altındakı sahə haqqında danışmaq yolverilməzdir. y = f(x) və ox seqmentinin üstündə X, hətta f- əvvəlcə "sahə" termininin dəqiq mənasını təyin etmədən və bu şəkildə müəyyən edilmiş ərazinin həqiqətən mövcud olduğunu müəyyən etmədən davamlı funksiya. Bu problem 1854-cü ildə müəyyən inteqral anlayışının dəqiq tərifini verən B. Riemann tərəfindən uğurla həll edildi. O vaxtdan bəri müəyyən inteqral anlayışının arxasında cəmləmə ideyası bir çox dərin araşdırmaların və ümumiləşdirmələrin mövzusu olmuşdur. Nəticə etibarı ilə bu gün inteqral hər yerdə kəsikli olsa belə, müəyyən inteqrala məna vermək mümkündür. Yaradılmasında A.Lebesq (1875–1941) və digər riyaziyyatçıların böyük töhfə verdiyi yeni inteqrasiya konsepsiyaları müasir riyazi analizin gücünü və gözəlliyini artırdı.

Bütün bu və digər anlayışların təfərrüatlarına varmaq çətin ki. Biz özümüzü yalnız həddi və müəyyən inteqralın ciddi təriflərini verməklə məhdudlaşdıracağıq.

Sonda deyək ki, riyazi analiz alim və mühəndisin əlində son dərəcə qiymətli alət olmaqla bu gün də səmərəli fikir mənbəyi kimi riyaziyyatçıların diqqətini cəlb edir. Eyni zamanda, müasir inkişaf 20-ci əsrdə riyazi analizin bu cür dominant tərəfindən getdikcə daha çox mənimsənildiyini göstərir. mücərrəd cəbr və topologiya kimi riyaziyyatın sahələri.

Törəmə və onun hesablanması üsullarını bilmədən riyaziyyatda fiziki məsələləri və ya nümunələri həll etmək qətiyyən mümkün deyil. Törəmə riyazi analizdə ən vacib anlayışlardan biridir. Bugünkü məqaləmizi bu fundamental mövzuya həsr etmək qərarına gəldik. Törəmə nədir, onun fiziki və həndəsi mənası nədir, funksiyanın törəməsi necə hesablanır? Bütün bu suallar bir yerdə birləşdirilə bilər: törəməni necə başa düşmək olar?

Törəmənin həndəsi və fiziki mənası

Qoy bir funksiya olsun f (x) müəyyən intervalla verilir (a, b) ... x və x0 nöqtələri bu intervala aiddir. X dəyişdikdə, funksiyanın özü də dəyişir. Arqumentin dəyişdirilməsi - onun dəyərləri arasındakı fərq x-x0 ... Bu fərq kimi yazılır delta x və arqument artımı adlanır. Bir funksiyanın dəyişməsi və ya artması bir funksiyanın dəyərlərinin iki nöqtədə fərqidir. Törəmə tərifi:

Bir nöqtədə funksiyanın törəməsi, sonuncu sıfıra meyl etdikdə, verilmiş nöqtədə funksiyanın artımının arqumentin artımına nisbətinin həddidir.

Əks halda, belə yazıla bilər:

Belə bir hədd tapmağın nə mənası var? Və budur:

nöqtədə funksiyanın törəməsi OX oxu arasındakı bucağın tangensi ilə bu nöqtədə funksiyanın qrafikinə toxunan tangensə bərabərdir.

Törəmənin fiziki mənası: yolun zamana görə törəməsi düzxətli hərəkətin sürətinə bərabərdir.

Həqiqətən, məktəb vaxtlarından hər kəs sürətin şəxsi yol olduğunu bilir. x = f (t) və vaxt t ... Müəyyən bir müddət ərzində orta sürət:

Bir anda hərəkət sürətini tapmaq üçün t0 limiti hesablamaq lazımdır:

Birinci qayda: sabiti çıxarın

Sabit törəmənin işarəsindən kənara köçürülə bilər. Üstəlik, bunu etmək lazımdır. Riyaziyyatda nümunələri həll edərkən, bir qayda olaraq götürün - ifadəni sadələşdirə bilirsinizsə, sadələşdirməyə əmin olun .

Misal. Törəməni hesablayaq:

İkinci qayda: funksiyaların cəminin törəməsi

İki funksiyanın cəminin törəməsi bu funksiyaların törəmələrinin cəminə bərabərdir. Eyni şey funksiyalar fərqinin törəməsi üçün də keçərlidir.

Biz bu teoremin isbatını verməyəcəyik, əksinə praktiki bir nümunəyə baxacağıq.

Funksiyanın törəməsini tapın:

Üçüncü qayda: funksiyaların hasilinin törəməsi

İki diferensiallanan funksiyanın hasilinin törəməsi düsturla hesablanır:

Nümunə: funksiyanın törəməsini tapın:

Həll:

Burada mürəkkəb funksiyaların törəmələrinin hesablanması haqqında danışmaq vacibdir. Mürəkkəb funksiyanın törəməsi bu funksiyanın törəməsinin müstəqil dəyişənə münasibətdə aralıq arqumentin törəməsi ilə hasilinə bərabərdir.

Yuxarıdakı nümunədə biz aşağıdakı ifadə ilə qarşılaşırıq:

Bu halda, ara arqument beşinci gücə 8x-dir. Belə bir ifadənin törəməsini hesablamaq üçün əvvəlcə aralıq arqumentə görə xarici funksiyanın törəməsini hesablayırıq, sonra isə müstəqil dəyişənə görə bilavasitə ara arqumentin törəməsinə vururuq.

Dördüncü qayda: iki funksiyanın bölünmə törəməsi

İki funksiyanın bölünməsinin törəməsini təyin etmək üçün düstur:

Sizə sıfırdan dummies üçün törəmələr haqqında danışmağa çalışdıq. Bu mövzu göründüyü qədər sadə deyil, ona görə də xəbərdar olun: misallarda tez-tez tələlər olur, ona görə də törəmələri hesablayarkən diqqətli olun.

Bu və digər mövzularla bağlı istənilən sualınız üçün tələbə xidmətinə müraciət edə bilərsiniz. Qısa müddətdə biz sizə ən çətin testi həll etməyə və əvvəllər törəmələrin hesablanması ilə məşğul olmamısınızsa belə, tapşırıqların öhdəsindən gəlməyə kömək edəcəyik.

Bunun üzərində biz ən sadə törəmələri təhlil etdik, həmçinin diferensiallaşdırma qaydaları və törəmələri tapmaq üçün bəzi üsullarla tanış olduq. Beləliklə, əgər siz funksiyaların törəmələri ilə çox maraqlanmırsınızsa və ya bu məqalənin bəzi məqamları tam aydın deyilsə, əvvəlcə yuxarıdakı dərsi oxuyun. Zəhmət olmasa, ciddi əhval-ruhiyyəyə kökləyin - material asan deyil, amma yenə də onu sadə və əlçatan bir şəkildə təqdim etməyə çalışacağam.

Təcrübədə mürəkkəb funksiyanın törəməsi ilə çox tez-tez məşğul olmaq lazımdır, hətta deyərdim ki, demək olar ki, həmişə, sizə törəmələri tapmaq üçün tapşırıqlar veriləndə.

Mürəkkəb funksiyanı diferensiallaşdırmaq üçün qaydada (№ 5) cədvələ baxırıq:

Anlamaq. İlk öncə səs yazısına diqqət edək. Burada iki funksiyamız var - və üstəlik, funksiya, obrazlı desək, funksiyaya daxil edilmişdir. Bu cür funksiyaya (bir funksiya digərinin içində yerləşdikdə) mürəkkəb funksiya adlanır.

Funksiyanı çağıracağam xarici funksiya və funksiyası - daxili (və ya iç-içə) funksiya.

! Bu təriflər nəzəri deyil və tapşırıqların yekun dizaynında əks olunmamalıdır. Mən qeyri-rəsmi ifadələrdən "xarici funksiya", "daxili" funksiyanı yalnız materialı başa düşməyinizi asanlaşdırmaq üçün istifadə edirəm.

Vəziyyəti aydınlaşdırmaq üçün düşünün:

Misal 1

Funksiyanın törəməsini tapın

Sinusun altında bizdə təkcə "X" hərfi deyil, tam ədəd ifadəsi var, ona görə də dərhal cədvəldən törəməni tapmaq mümkün olmayacaq. Həmçinin qeyd edirik ki, burada ilk dörd qaydanı tətbiq etmək qeyri-mümkündür, görünür, bir fərq var, amma fakt budur ki, bir sinusu "parçalaya" bilməzsiniz:

Bu misalda, artıq mənim izahatlarımdan intuitiv olaraq aydın olur ki, funksiya mürəkkəb funksiyadır, çoxhədli isə daxili funksiya (yuvalama) və xarici funksiyadır.

İlk addım, mürəkkəb funksiyanın törəməsi tapılarkən yerinə yetirilməli olan, yəni Hansı funksiyanın daxili, hansının xarici olduğunu müəyyənləşdirin.

Sadə misallarda polinomun sinusun altında yerləşdiyi aydın görünür. Bəs hər şey aydın deyilsə? Hansı funksiyanın xarici, hansının daxili olduğunu dəqiq necə müəyyən etmək olar? Bunu etmək üçün zehni olaraq və ya qaralama üzərində edilə bilən aşağıdakı texnikadan istifadə etməyi təklif edirəm.

Təsəvvür edin ki, bir ifadənin dəyərini kalkulyatorda hesablamalıyıq (bir əvəzinə hər hansı bir rəqəm ola bilər).

Əvvəlcə nə hesablayacağıq? Hər şeydən əvvəl aşağıdakı hərəkəti yerinə yetirməli olacaqsınız:, beləliklə, polinom daxili funksiya olacaq:

İkincisi tapmaq lazımdır, ona görə də sinus xarici funksiya olacaq:

Bizdən sonra Həll etmək, çözmək daxili və xarici funksiyalarla mürəkkəb funksiyanın diferensiasiya qaydasını tətbiq etməyin vaxtıdır .

Qərar verməyə başlayırıq. Dərsdən Törəməni necə tapa bilərəm? hər hansı bir törəmənin həllinin dizaynının həmişə belə başladığını xatırlayırıq - ifadəni mötərizələrə əlavə edirik və yuxarı sağda bir vuruş qoyuruq:

Birinci xarici funksiyanın törəməsini (sinusunu) tapın, elementar funksiyaların törəmələri cədvəlinə baxın və buna diqqət yetirin. Bütün cədvəl düsturları hətta "x" mürəkkəb ifadə ilə əvəz edilsə belə tətbiq olunur, bu halda:

Qeyd edək ki, daxili funksiya dəyişməyib, toxunmuruq.

Yaxşı, bu, tamamilə aydındır

Düsturun tətbiqinin nəticəsi son dizaynda belə görünür:

Sabit amil adətən ifadənin əvvəlində yerləşdirilir:

Hər hansı bir qarışıqlıq varsa, həllini yazın və izahatları yenidən oxuyun.

Misal 2

Funksiyanın törəməsini tapın

Misal 3

Funksiyanın törəməsini tapın

Həmişə olduğu kimi yazırıq:

Gəlin anlayaq ki, harda xarici funksiyamız var, harada isə daxili funksiyamız var. Bunu etmək üçün ifadənin dəyərini hesablamağa çalışın (zehni və ya qaralamada). Əvvəlcə nə edilməlidir? Hər şeydən əvvəl, bazanın nəyə bərabər olduğunu hesablamalısınız: bu, polinomun daxili funksiya olduğunu bildirir:

Və yalnız bundan sonra eksponentasiya yerinə yetirilir, buna görə də güc funksiyası xarici funksiyadır:

Formula görə , əvvəlcə xarici funksiyanın törəməsini, bu halda dərəcəsini tapmaq lazımdır. Cədvəldə tələb olunan düsturu axtarırıq:. Bir daha təkrar edirik: istənilən cədvəl formul təkcə “x” üçün deyil, həm də mürəkkəb ifadə üçün etibarlıdır... Beləliklə, mürəkkəb funksiyanın diferensiasiya qaydasının tətbiqinin nəticəsi sonrakı:

Bir daha vurğulayıram ki, xarici funksiyanın törəməsini götürəndə daxili funksiya bizim üçün dəyişmir:

İndi daxili funksiyanın çox sadə törəməsini tapmaq və nəticəni bir az "daraqlamaq" qalır:

Misal 4

Funksiyanın törəməsini tapın

Bu, müstəqil həll üçün bir nümunədir (cavab təlimatın sonunda).

Mürəkkəb bir funksiyanın törəməsi haqqında anlayışı möhkəmləndirmək üçün şərhsiz bir nümunə verəcəyəm, bunu özünüz anlamağa çalışacağam, xarici və daxili funksiyanın harada olduğunu fərz edin, niyə vəzifələr bu şəkildə həll edildi?

Misal 5

a) funksiyanın törəməsini tapın

b) funksiyanın törəməsini tapın

Misal 6

Funksiyanın törəməsini tapın

Burada kökümüz var və kökü fərqləndirmək üçün o, dərəcə kimi göstərilməlidir. Beləliklə, əvvəlcə funksiyanı diferensiasiya üçün uyğun formaya gətiririk:

Funksiyanı təhlil edərək belə nəticəyə gəlirik ki, üç həddin cəmi daxili funksiya, eksponentasiya isə xarici funksiyadır. Mürəkkəb funksiyanın diferensiasiya qaydasını tətbiq edirik :

Dərəcə yenidən radikal (kök) kimi təmsil olunur və daxili funksiyanın törəməsi üçün cəmini fərqləndirmək üçün sadə bir qayda tətbiq edirik:

Hazır. Siz həmçinin ifadəni mötərizədə ortaq məxrəcə gətirə və hər şeyi bir kəsrdə yaza bilərsiniz. Əlbəttə ki, xoşdur, amma çətin uzun törəmələr əldə edildikdə, bunu etməmək daha yaxşıdır (çaşmaq, lazımsız səhv etmək asandır və müəllimin yoxlaması əlverişsiz olacaq).

Misal 7

Funksiyanın törəməsini tapın

Bu, müstəqil həll üçün bir nümunədir (cavab təlimatın sonunda).

Maraqlıdır ki, bəzən mürəkkəb funksiyanın diferensiallaşdırılması qaydası əvəzinə, bölmənin diferensiallaşdırılması qaydasından istifadə etmək olar. , lakin belə bir həll təhrif kimi qeyri-adi görünəcək. Budur tipik bir nümunə:

Misal 8

Funksiyanın törəməsini tapın

Burada bölməni fərqləndirmək üçün qaydadan istifadə edə bilərsiniz , lakin mürəkkəb funksiyanın diferensiallaşdırılması qaydası vasitəsilə törəmə tapmaq daha sərfəlidir:

Funksiyanı diferensiasiya üçün hazırlayırıq - mənfini törəmə işarəsindən kənara çıxarırıq və kosinusu paylayıcıya qaldırırıq:

Kosinus daxili funksiyadır, eksponentasiya xarici funksiyadır.
Biz öz qaydamızdan istifadə edirik :

Daxili funksiyanın törəməsini tapın, kosinusu yenidən aşağı salın:

Hazır. Baxılan nümunədə işarələrdə çaşqınlıq yaratmamaq vacibdir. Yeri gəlmişkən, bunu qayda ilə həll etməyə çalışın , cavablar uyğun olmalıdır.

Misal 9

Funksiyanın törəməsini tapın

Bu, müstəqil həll üçün bir nümunədir (cavab təlimatın sonunda).

İndiyə qədər biz mürəkkəb funksiyada yalnız bir əlavənin olduğu hallara baxdıq. Praktik tapşırıqlarda siz tez-tez törəmələrə rast gələ bilərsiniz, burada yuva quran kuklalar kimi biri digərinin içərisində, 3 və ya hətta 4-5 funksiya eyni anda yuvalanır.

Misal 10

Funksiyanın törəməsini tapın

Bu funksiyanın əlavələrini anlayaq. Test dəyərindən istifadə edərək ifadəni qiymətləndirməyə çalışırıq. Bir kalkulyatora necə güvənə bilərik?

Əvvəlcə tapmaq lazımdır, yəni arcsine ən dərin yuvadır:

Onda birinin qövsünün kvadratı alınmalıdır:

Və nəhayət, 7-ni gücə qaldırın:

Yəni, bu nümunədə üç fərqli funksiya və iki əlavəmiz var, ən daxili funksiya arksinus, ən xarici funksiya isə eksponensial funksiyadır.

həll etməyə başlayırıq

Qaydaya görə əvvəlcə xarici funksiyanın törəməsini götürməlisiniz. Törəmələr cədvəlinə baxırıq və eksponensial funksiyanın törəməsini tapırıq: Yeganə fərq ondadır ki, “x” əvəzinə kompleks ifadəmiz var ki, bu düsturun etibarlılığını inkar etmir. Deməli, mürəkkəb funksiyanın diferensiasiya qaydasının tətbiqinin nəticəsi növbəti.