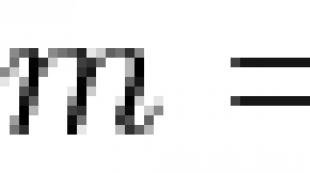Teorema e pikës kufitare. Teorema Bolzano-Weierstrass. Zgjerim në rastin e një hapësire me dimension arbitrar

Përkufizimi v.7. Një pikë x € R në vijën numerike quhet pikë kufitare e një sekuence (xn) nëse për çdo lagje U (x) dhe çdo numër natyror N është e mundur të gjendet një element xn që i përket kësaj lagje me numër më të madh se LG, d.m.th. x 6 R - pika kufi nëse. Me fjalë të tjera, një pikë x do të jetë një pikë kufi për (xn) nëse ndonjë nga lagjet e saj përmban elementë të kësaj sekuence me numra arbitrarisht të mëdhenj, megjithëse ndoshta jo të gjithë elementët me numra n > N. Prandaj, pohimi i mëposhtëm është mjaft i qartë . Deklarata b.b. Nëse lim(xn) = 6 6 R, atëherë b është pika e vetme kufitare e sekuencës (xn). Në të vërtetë, në bazë të përkufizimit 6.3 të kufirit të një sekuence, të gjithë elementët e saj, duke filluar nga një numër i caktuar, bien në çdo fqinjësi të vogël arbitrarisht të pikës 6, dhe për këtë arsye elementët me numër arbitrarisht të madh nuk mund të bien në afërsi të ndonjë pike tjetër. . Rrjedhimisht, kushti i përkufizimit 6.7 plotësohet vetëm për një pikë të vetme 6. Megjithatë, jo çdo pikë kufi (nganjëherë quhet pikë e hollë e kondensuar) e një sekuence është kufiri i saj. Kështu, sekuenca (b.b) nuk ka kufi (shih shembullin 6.5), por ka dy pika kufi x = 1 dhe x = - 1. Sekuenca ((-1) pp) ka dy pika të pafundme +oo dhe si pika kufi - me vijën numerike të zgjeruar, bashkimi i së cilës shënohet me një simbol oo. Kjo është arsyeja pse ne mund të supozojmë se pikat kufitare të pafundme përkojnë, dhe pika e pafundme oo, sipas (6.29), është kufiri i kësaj sekuence. Pikat kufizuese të vijës numerike të renditjes Vërtetim i testit Weierstrass dhe kriterit Cauchy. Le të jepet sekuenca (jn) dhe numrat k të formojnë një sekuencë në rritje të numrave të plotë pozitivë. Atëherë sekuenca (Vnb ku yn = xkn> quhet nënrenditje e sekuencës origjinale. Natyrisht, nëse (i„) ka numrin 6 si kufi, atëherë çdo nënsekuencë e saj ka të njëjtin kufi, pasi duke u nisur nga një numër i caktuar të gjithë elementët si të sekuencës origjinale ashtu edhe të ndonjë prej nënsekuencave të saj bien në çdo fqinjësi të zgjedhur të pikës 6. Në të njëjtën kohë, çdo pikë kufi e një nënsekuencë është gjithashtu një pikë kufi për sekuencën. Teorema 9. Nga çdo sekuencë që ka një Pika kufitare, mund të zgjidhet një nënsekuencë që ka si kufi këtë pikë kufi. Le të jetë b pika kufitare e sekuencës (xn), atëherë, sipas përkufizimit 6. 7 pikë kufitare, për çdo n ka një element që i përket lagjes U (6, 1/n) të pikës b me rreze 1/n. Nënrenditja e përbërë nga pikat ijtj, ...1 ..., ku zjfcn€U(6, 1/n) Vn 6 N, ka një kufi në pikën 6. Në të vërtetë, për një e > 0 arbitrare, mund të zgjidhet N. sikurse. Atëherë të gjithë elementët e nënsekuencës, duke filluar me numrin km, do të bien në ^-lagjen U(6, e) të pikës 6, e cila korrespondon me kushtin 6.3 të përcaktimit të kufirit të sekuencës. Teorema e kundërt është gjithashtu e vërtetë. Pikat kufizuese të vijës numerike të renditjes Vërtetim i testit Weierstrass dhe kriterit Cauchy. Teorema 8.10. Nëse një sekuencë ka një nënsekuencë me kufirin 6, atëherë b është pika kufitare e kësaj sekuence. Nga përkufizimi 6.3 i kufirit të një sekuence rrjedh se, duke u nisur nga një numër i caktuar, të gjithë elementët e nënsekuencës me kufirin b bien në një lagje U(b, ​​e) me rreze arbitrare e. Meqenëse elementët e nënsekuencës janë njëkohësisht elementë të sekuencës (xn)> elementët xn bien brenda kësaj fqinjësie me po aq numra të mëdhenj arbitrarisht, dhe kjo, në bazë të përkufizimit 6.7, do të thotë se b është pika kufitare e sekuencës (n). Vërejtje 0.2. Teoremat 6.9 dhe 6.10 vlejnë edhe në rastin kur pika kufitare është e pafundme, nëse gjatë vërtetimit të fqinjësisë merto të U(6, 1 /n) marrim në konsideratë lagjen (ose lagjet).Kushti në të cilin një nënrend konvergjen mund të izolohet nga një sekuencë vendoset nga teorema e mëposhtme: Teorema 6.11 (Bolzano - Weierstrass) Çdo varg i kufizuar përmban një nënsekuencë që konvergon në një kufi të fundëm. Le të jenë të gjithë elementët e sekuencës (an) midis numrave a dhe 6 , pra xn € [a, b] Vn € N. Ndani segmentin [a, b] në gjysmë. Atëherë të paktën një nga gjysmat e tij do të përmbajë një numër të pafund elementësh të sekuencës, pasi përndryshe i gjithë segmenti [a, b] do të përmbante një numër të fundëm të tyre, gjë që është e pamundur. Le të jetë ] ai i gjysmave të segmentit [a , 6], i cili përmban një grup të pafund elementësh të sekuencës (zn) (ose nëse të dyja gjysmat janë të tilla , pastaj ndonjë prej tyre).Ngjashëm, nga segmenti që përmban një grup të pafund elementësh të sekuencës, etj. Duke vazhduar këtë proces, do të ndërtojmë një sistem segmentesh të mbivendosur me bn - an = (6- a)/2P. Sipas parimit të segmenteve të mbivendosur, ekziston një pikë x që u përket të gjitha këtyre segmenteve. Kjo pikë do të jetë pika kufitare për sekuencën (xn) - Në fakt, për çdo e-lagje U(x, e) = (xx + e) ​​pikë x ekziston një segment C U(x, e) (ai mjafton vetëm të zgjedhësh n nga pabarazia (, që përmban një numër të pafund elementësh të sekuencës (sn). Sipas përkufizimit 6.7, x është pika kufitare e kësaj sekuence. Pastaj, nga teorema 6.9, ka një nënsekuencë që konvergon në pikën x. Metoda e arsyetimit e përdorur në vërtetimin e kësaj teoreme (nganjëherë quhet lema Bolzano-Weyer-Strass) dhe e lidhur me përgjysmimin vijues të segmenteve në shqyrtim njihet si metoda Bolzano. Kjo teoremë thjeshton shumë vërtetimin e shumë teoremave komplekse. Kjo ju lejon të provoni një numër teoremash kryesore në një mënyrë të ndryshme (ndonjëherë më të thjeshtë). Shtojca 6.2. Vërtetimi i testit Weierstrass dhe kriteri Cauchy Së pari, vërtetojmë Pohimin 6.1 (Testi i Weierstrass për konvergjencën e një sekuence monotonike të kufizuar). Le të supozojmë se sekuenca (jn) nuk është në rënie. Atëherë grupi i vlerave të tij kufizohet më sipër dhe, me Teoremën 2.1, ka një suprem të cilin e shënojmë me sup(xn) të jetë R. Për shkak të vetive të supremit (shih 2.7) Pikat kufitare të sekuencës janë numri Vërtetimi i testit Weierstrass dhe kriteri Cauchy. Sipas përkufizimit 6.1 për një sekuencë jozvogëluese kemi ose Pastaj > Ny dhe duke marrë parasysh (6.34) marrim që i përgjigjet përkufizimit 6.3 të kufirit të sekuencës, d.m.th. 31im(sn) dhe lim(xn) = 66R. Nëse sekuenca (xn) nuk është në rritje, atëherë rrjedha e vërtetimit është e ngjashme. Tani le të kalojmë në vërtetimin e mjaftueshmërisë së kriterit Kochia për konvergjencën e një sekuence (shih deklaratën 6.3), pasi domosdoshmëria e kushtit të kriterit rrjedh nga teorema 6.7. Le të jetë themelore sekuenca (jn). Sipas përkufizimit 6.4, duke pasur parasysh një € > 0 arbitrare, mund të gjejmë një numër N(s) të tillë që m^N dhe n^N nënkuptojnë. Pastaj, duke marrë m - N, për Vn > N marrim € £ Meqenëse sekuenca në shqyrtim ka një numër të fundëm elementësh me numra që nuk e kalojnë N, rrjedh nga (6.35) se sekuenca themelore është e kufizuar (për krahasim, shih vërtetimi i teoremës 6.2 mbi kufirin e një sekuence konvergjente). Për një grup vlerash të një sekuence të kufizuar, ekzistojnë kufijtë infimum dhe supremum (shih Teoremën 2.1). Për grupin e vlerave të elementit për n > N, ne shënojmë këto fytyra përkatësisht an = inf xn dhe bjy = sup xn. Me rritjen e N, nuk zvogëlohet infimumi ekzakt, dhe supremi i saktë nuk rritet, d.m.th. . A marr një sistem klimatizimi? segmentet Sipas parimit të segmenteve të mbivendosur, ekziston një pikë e përbashkët që u përket të gjitha segmenteve. Le ta shënojmë me b. Kështu, me Nga krahasimi (6. 36) dhe (6.37) si rezultat marrim që korrespondon me Përkufizimin 6.3 të kufirit të sekuencës, d.m.th. 31im(x„) dhe lim(sn) = 6 6 R. Bolzano filloi të studionte sekuencat themelore. Por ai nuk kishte një teori rigoroze të numrave realë, dhe për këtë arsye ai nuk ishte në gjendje të provonte konvergjencën e sekuencës themelore. Cauchy e bëri këtë, duke marrë si të mirëqenë parimin e segmenteve të mbivendosur, të cilin Cantor e vërtetoi më vonë. Jo vetëm që kriteri për konvergjencën e një sekuence i jepet emri Cauchy, por sekuenca themelore shpesh quhet sekuenca Cauchy, dhe parimi i segmenteve të mbivendosur është emëruar sipas Cantor. Pyetje dhe detyra 8.1. Vërtetoni se: 6.2. Jepni shembuj të sekuencave jokonvergjente me elementë që u përkasin bashkësive Q dhe R\Q. 0.3. Në cilat kushte termat e progresioneve aritmetike dhe gjeometrike formojnë sekuenca zvogëluese dhe rritëse? 6.4. Vërtetoni marrëdhëniet që pasojnë nga tabela. 6.1. 6.5. Ndërtoni shembuj të sekuencave që priren në pikat e pafundme +oo, -oo, oo dhe një shembull të një sekuence që konvergohet në pikën 6 € R. c.v. A mund të mos jetë një sekuencë e pakufizuar b.b.? Nëse po, atëherë jepni një shembull. në 7. Ndërtoni një shembull të një sekuence divergjente të përbërë nga elementë pozitivë që nuk kanë as një kufi të fundëm dhe as të pafund. 6.8. Vërtetoni konvergjencën e vargut (jn) të dhënë me formula rekurente sn+i = sin(xn/2) me kushtin “1 = 1. 6.9. Vërtetoni se lim(xn)=09 nëse sn+i/xn-»g€ .

Ndani segmentin [ a 0 ,b 0 ] në gjysmë në dy segmente të barabarta. Të paktën një nga segmentet rezultuese përmban një numër të pafund termash të sekuencës. Le ta shënojmë atë [ a 1 ,b 1 ] .

Në hapin tjetër do të përsërisim procedurën me segmentin [ a 1 ,b 1 ]: ndajeni atë në dy segmente të barabarta dhe zgjidhni prej tyre atë në të cilin shtrihet një numër i pafund termash të sekuencës. Le ta shënojmë atë [ a 2 ,b 2 ] .

Duke vazhduar procesin, marrim një sekuencë segmentesh të mbivendosur

në të cilën çdo pasues është gjysma e të mëparshmes dhe përmban një numër të pafund termash të sekuencës ( x k } .

Gjatësitë e segmenteve priren në zero:

Në bazë të parimit Cauchy-Cantor të segmenteve të mbivendosur, ekziston një pikë e vetme ξ që u përket të gjitha segmenteve:

Nga ndërtimi në çdo segment [a m ,b m ] ka një numër të pafund termash të sekuencës. Le të zgjedhim me radhë

duke vëzhguar kushtin e rritjes së numrave:

Pastaj pasardhësi konvergon në pikën ξ. Kjo rrjedh nga fakti se distanca nga ξ nuk e kalon gjatësinë e segmentit që i përmban ato [a m ,b m ] , ku

Zgjerim në rastin e një hapësire me dimension arbitrar

Teorema Bolzano-Weierstrass përgjithësohet lehtësisht në rastin e një hapësire me dimension arbitrar.

Le të jepet një sekuencë pikash në hapësirë:

(indeksi i poshtëm është numri i anëtarit të sekuencës, indeksi i sipërm është numri i koordinatave). Nëse sekuenca e pikave në hapësirë ​​është e kufizuar, atëherë secila prej sekuencave numerike të koordinatave:

gjithashtu i kufizuar ( - numri koordinativ).

Në sajë të versionit njëdimensional të teoremës Bolzano-Weirstrass nga sekuenca ( x k) mund të zgjedhim një nënsekuencë pikash, koordinatat e para të të cilave formojnë një sekuencë konvergjente. Nga pasardhja që rezulton, ne zgjedhim edhe një herë një nënsekuencë që konvergon përgjatë koordinatës së dytë. Në këtë rast, konvergjenca përgjatë koordinatës së parë do të ruhet për faktin se çdo nënsekuencë e një sekuence konvergjente gjithashtu konvergon. Dhe kështu me radhë.

Pas n marrim një sekuencë të caktuar hapash

e cila është një vijimësi e , dhe konvergon përgjatë secilës prej koordinatave. Nga kjo rrjedh se kjo pasardhëse konvergon.

Histori

Teorema Bolzano-Weierstrass (për rastin n= 1) u vërtetua për herë të parë nga matematikani çek Bolzano në 1817. Në veprën e Bolzanos, ajo veproi si një lemë në vërtetimin e teoremës mbi vlerat e ndërmjetme të një funksioni të vazhdueshëm, i njohur tani si teorema Bolzano-Cauchy. Megjithatë, këto dhe rezultate të tjera, të vërtetuara nga Bolzano shumë kohë përpara Cauchy dhe Weierstrass, kaluan pa u vënë re.

Vetëm gjysmë shekulli më vonë, Weierstrass, pavarësisht nga Bolzano, e rizbuloi dhe vërtetoi këtë teoremë. Fillimisht e quajtur teorema e Weierstrass-it, përpara se puna e Bolzanos të bëhej e njohur dhe e pranuar.

Sot kjo teoremë mban emrat e Bolzanos dhe Weierstrass. Kjo teoremë shpesh quhet Lema Bolzano-Weierstrass, dhe ndonjehere Lema e pikës kufitare.

Teorema Bolzano-Weierstrass dhe koncepti i kompaktësisë

Teorema Bolzano-Weierstrass përcakton vetinë e mëposhtme interesante të një grupi të kufizuar: çdo sekuencë pikash M përmban një nënsekuencë konvergjente.

Kur provojnë propozime të ndryshme në analizë, ata shpesh përdorin teknikën e mëposhtme: ata përcaktojnë një sekuencë pikash që ka disa veti të dëshiruara, dhe më pas zgjedhin një nënsekuencë prej saj që gjithashtu e ka atë, por tashmë është konvergjente. Për shembull, kështu vërtetohet teorema e Weierstrass se një funksion i vazhdueshëm në një interval është i kufizuar dhe merr vlerat e tij më të mëdha dhe më të vogla.

Efektiviteti i një teknike të tillë në përgjithësi, si dhe dëshira për të shtrirë teoremën e Weierstrass në hapësira arbitrare metrike, e shtynë matematikanin francez Maurice Fréchet të prezantojë konceptin në 1906. kompaktësia. Vetia e grupeve të kufizuara në , e vendosur nga teorema Bolzano-Weierstrass, është, në mënyrë figurative, që pikat e grupit janë të vendosura mjaft "afër" ose "kompakt": pasi kemi bërë një numër të pafund hapash përgjatë këtij grupi, ne do sigurisht që afrohemi sa të duam me ndonjë pikë në hapësirë.

Frechet prezanton përkufizimin e mëposhtëm: grup M thirrur kompakte, ose kompakte, nëse çdo sekuencë e pikave të saj përmban një nënsekuencë që konvergon në një pikë të kësaj bashkësie. Supozohet se në set M metrika është e përcaktuar, domethënë është

Përkufizimi 1. Një pikë x e një drejtëze të pafundme quhet pikë kufitare e sekuencës (x n) nëse në çdo fqinjësi elektronike të kësaj pike ka pafundësisht shumë elementë të sekuencës (x n).

Lema 1. Nëse x është një pikë kufitare e sekuencës (x k ), atëherë nga kjo sekuencë mund të zgjedhim një nënrend (x n k ), duke konverguar në numrin x.

Koment. Deklarata e kundërt është gjithashtu e vërtetë. Nëse nga sekuenca (x k) është e mundur të zgjidhet një nënsekuencë që konvergon me numrin x, atëherë numri x është pika kufitare e sekuencës (x k). Në të vërtetë, në çdo fqinjësi elektronike të pikës x ka pafundësisht shumë elementë të nënrenditjes, dhe rrjedhimisht të vetë sekuencës (x k ).

Nga Lema 1 rrjedh se mund të japim një përkufizim tjetër të pikës kufitare të një sekuence, ekuivalente me Përkufizimin 1.

Përkufizimi 2. Një pikë x e një drejtëze të pafundme quhet pikë kufitare e një sekuence (x k ), nëse nga kjo sekuencë është e mundur të zgjidhet një nënsekuencë që konvergon në x.

Lema 2.Çdo sekuencë konvergjente ka vetëm një pikë kufi, e cila përkon me kufirin e asaj sekuence.

Koment. Nëse sekuenca konvergon, atëherë nga Lema 2 ajo ka vetëm një pikë kufi. Megjithatë, nëse (xn) nuk është konvergjente, atëherë mund të ketë disa pika kufitare (dhe, në përgjithësi, pafundësisht shumë pika kufitare). Le të tregojmë, për shembull, se (1+(-1) n ) ka dy pika kufitare.

Në të vërtetë, (1+(-1) n )=0,2,0,2,0,2,... ka dy pika kufi 0 dhe 2, sepse nënrenditjet (0)=0,0,0,... dhe (2)=2,2,2,... të këtij vargu kanë si kufi numrat përkatësisht 0 dhe 2. Ky sekuencë nuk ka pika të tjera kufitare. Në të vërtetë, le të jetë x çdo pikë në boshtin e numrave përveç pikave 0 dhe 2. Le të marrim e >0 kështu

i vogël në mënyrë që e - lagjet e pikave 0, x dhe 2 të mos kryqëzohen. Fqinjsia elektronike e pikave 0 dhe 2 përmban të gjithë elementët e sekuencës dhe për këtë arsye fqinjësia elektronike e pikës x nuk mund të përmbajë pafundësisht shumë elementë (1+(-1) n ) dhe për këtë arsye nuk është pikë kufitare e kësaj sekuence.

Teorema.Çdo sekuencë e kufizuar ka të paktën një pikë kufi.

Koment. Asnjë numër x që tejkalon , është një pikë kufizuese e sekuencës (x n), d.m.th. - pika kufitare më e madhe e sekuencës (x n).

Le të jetë x çdo numër më i madh se . Le të zgjedhim e>0 aq të vogël sa

dhe x 1 О(x), në të djathtë të x 1 ka një numër të kufizuar elementësh të vargut (x n) ose nuk ka fare, d.m.th. x nuk është një pikë kufitare e sekuencës (x n ).

Përkufizimi. Pika më e madhe kufitare e sekuencës (x n) quhet kufiri i sipërm i sekuencës dhe shënohet me simbolin. Nga vërejtja rezulton se çdo sekuencë e kufizuar ka një kufi të sipërm.

Në mënyrë të ngjashme, prezantohet koncepti i një kufiri më të ulët (si pika më e vogël kufitare e sekuencës (x n )).

Pra, ne kemi vërtetuar deklaratën e mëposhtme. Çdo sekuencë e kufizuar ka kufijtë e sipërm dhe të poshtëm.

Le të formulojmë teoremën e mëposhtme pa prova.

Teorema. Në mënyrë që sekuenca (x n) të jetë konvergjente, është e nevojshme dhe e mjaftueshme që ai të jetë i kufizuar dhe kufiri i sipërm dhe i poshtëm i tij të përkojë.

Rezultatet e këtij seksioni çojnë në teoremën kryesore të mëposhtme të Bolzano-Weierstrass.

Teorema Bolzano-Weierstrass. Nga çdo sekuencë e kufizuar mund të zgjidhni një nënsekuencë konvergjente.

Dëshmi. Meqenëse sekuenca (x n ) është e kufizuar, ajo ka të paktën një pikë kufi x. Pastaj nga kjo sekuencë mund të zgjedhim një nënsekuencë që konvergon në pikën x (pason nga Përkufizimi 2 i pikës kufitare).

Koment. Nga çdo sekuencë e kufizuar mund të izolohet një sekuencë konvergjente monotonike.