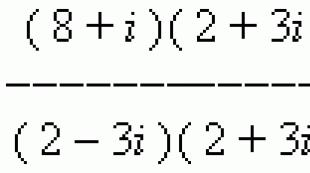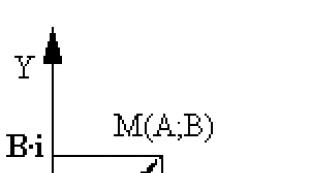Numrat kompleks

Imagjinare Dhe numra komplekse. Abshisa dhe ordinata

numër kompleks. Lidh numrat kompleks.

Veprimet me numra kompleks. Gjeometrike

paraqitjen e numrave kompleks. plan kompleks.

Moduli dhe argumenti i një numri kompleks. trigonometrike

forma komplekse e numrave. Operacione me komplekse

numrat në formë trigonometrike. Formula Moivre.

Informacion bazë për imagjinare Dhe numra komplekse janë dhënë në rubrikën “Numrat imagjinarë dhe kompleksë”. Nevoja për këta numra të një lloji të ri u shfaq gjatë zgjidhjes së ekuacioneve kuadratike për rastinD< 0 (здесь Dështë diskriminues i ekuacionit kuadratik). Për një kohë të gjatë, këta numra nuk gjetën përdorim fizik, prandaj u quajtën numra "imagjinarë". Sidoqoftë, tani ato përdoren shumë gjerësisht në fusha të ndryshme të fizikës.

dhe teknologjia: inxhinieria elektrike, hidro- dhe aerodinamika, teoria e elasticitetit, etj.

Numrat kompleks shkruhen si:a+bi. Këtu a Dhe b – numra realë , A i – njësi imagjinare. e. i 2 = –1. Numri a thirrur abshissa, a b - ordinatenumër kompleksa + b .Dy numra kompleksa+bi Dhe a-bi thirrur konjuguar numra komplekse.

Marrëveshjet kryesore:

1. Numri realAmund të shkruhet edhe në formënumri kompleks:një + 0 i ose a - 0 i. Për shembull, hyrjet 5 + 0i dhe 5-0 ido të thotë të njëjtin numër 5 .

2. Numri kompleks 0 + bithirrur thjesht imagjinare numri. Regjistrimibido të thotë njësoj si 0 + bi.

3. Dy numra kompleksa+bi Dhec + dikonsiderohen të barabartë nësea = c Dhe b = d. Përndryshe numrat kompleks nuk janë të barabartë.

Shtim. Shuma e numrave kompleksa+bi Dhe c + diquhet numër kompleks (a+c ) + (b+d ) i .Kështu, kur shtohet numrat kompleksë, abshisat dhe ordinatat e tyre shtohen veçmas.

Ky përkufizim ndjek rregullat për trajtimin e polinomeve të zakonshëm.

Zbritja. Dallimi midis dy numrave kompleksa+bi(e reduktuar) dhe c + di(i zbritur) quhet një numër kompleks (a-c ) + (b-d ) i .

Kështu, kur zbriten dy numra kompleksë, abshisat dhe ordinatat e tyre zbriten veçmas.

Shumëzimi. Prodhimi i numrave kompleksa+bi Dhe c + di quhet numër kompleks.

(ac-bd ) + (ad+bc ) i .Ky përkufizim buron nga dy kërkesa:

1) numrat a+bi Dhe c + diduhet të shumohen si algjebrike binomet,

2) numri ika pronën kryesore:i 2 = – 1.

SHEMBULL ( a + bi )(a-bi) = a 2 +b 2 . Prandaj, puna

dy numra komplekse të konjuguar janë të barabartë me realin

numër pozitiv.

Divizioni. Ndani një numër kompleksa+bi (i ndashëm) me një tjetërc + di(ndarëse) - do të thotë të gjesh numrin e tretëe + fi(chat), e cila, kur shumëzohet me një pjesëtuesc + di, e cila rezulton në dividenta + b .

Nëse pjesëtuesi nuk është zero, pjesëtimi është gjithmonë i mundur.

SHEMBULL Gjeni (8+i ) : (2 – 3 i) .

Zgjidhje Le ta rishkruajmë këtë raport si thyesë:

Duke shumëzuar numëruesin dhe emëruesin e tij me 2 + 3i

DHE Pas kryerjes së të gjitha transformimeve, marrim:

Paraqitja gjeometrike e numrave kompleks. Numrat realë përfaqësohen me pika në vijën numerike:

Këtu është pika Ado të thotë numër -3, pikëBështë numri 2, dhe O- zero. Në të kundërt, numrat kompleks përfaqësohen me pika në planin koordinativ. Për këtë, ne zgjedhim koordinatat drejtkëndore (karteziane) me të njëjtat shkallë në të dy boshtet. Pastaj numri kompleksa+bi do të përfaqësohet me një pikë P me abshisë a dhe ordinata b (shih fig.). Ky sistem koordinativ quhet plan kompleks .

modul numër kompleks quhet gjatësia e vektoritOP, duke paraqitur një numër kompleks në koordinatë ( të integruara) aeroplan. Moduli i numrave kompleksa+bi shënohet me | a+bi| ose letre r

Konsideroni një ekuacion kuadratik.

Le të përcaktojmë rrënjët e saj.

Nuk ka numër real, katrori i të cilit është -1. Por nëse formula përcakton operatorin i si njësi imagjinare, atëherë zgjidhja e këtij ekuacioni mund të shkruhet në formë . ku Dhe - numrat kompleks, në të cilët -1 është pjesa reale, 2 ose në rastin e dytë -2 është pjesa imagjinare. Pjesa imagjinare është gjithashtu një numër real (real). Pjesa imagjinare e shumëzuar me njësinë imagjinare do të thotë tashmë numër imagjinar.

Në përgjithësi, një numër kompleks ka formën

z = x + iy ,

Ku x, y janë numra realë, është një njësi imagjinare. Në një numër shkencash të aplikuara, për shembull, në inxhinierinë elektrike, elektronikë, teorinë e sinjalit, njësia imagjinare shënohet me j. Numrat realë x = Re(z) Dhe y=Une jam(z) thirrur pjesë reale dhe imagjinare numrat z. Shprehja quhet formë algjebrike shënimi i një numri kompleks.

Çdo numër real është një rast i veçantë i një numri kompleks në formë . Një numër imagjinar është gjithashtu një rast i veçantë i një numri kompleks. .

Përkufizimi i grupit të numrave kompleks C

Kjo shprehje lexohet si më poshtë: vendos ME, i përbërë nga elementë të tillë që x Dhe y i përkasin grupit të numrave realë R dhe është njësia imagjinare. Vini re se etj.

Dy numra kompleks Dhe janë të barabarta nëse dhe vetëm nëse pjesët e tyre reale dhe imagjinare janë të barabarta, d.m.th. Dhe .

Numrat dhe funksionet komplekse përdoren gjerësisht në shkencë dhe teknologji, në veçanti, në mekanikë, analiza dhe llogaritje të qarqeve AC, elektronikën analoge, teorinë dhe përpunimin e sinjalit, teorinë e kontrollit automatik dhe shkenca të tjera të aplikuara.

1. Aritmetika e numrave kompleks

Mbledhja e dy numrave kompleks konsiston në mbledhjen e pjesëve reale dhe imagjinare të tyre, d.m.th.

Prandaj, ndryshimi i dy numrave kompleks

Numri kompleks thirrur komplekse konjuguar numri z=x +i.y.

Numrat kompleks të konjuguar z dhe z * ndryshojnë në shenjat e pjesës imagjinare. Është e qartë se

.

Çdo barazi midis shprehjeve komplekse mbetet e vlefshme nëse në këtë barazi kudo i zëvendësohet nga - i, d.m.th. shkoni te barazia e numrave të konjuguar. Numrat i Dhe – i janë të padallueshme algjebrikisht sepse .

Prodhimi (shumëzimi) i dy numrave kompleks mund të llogaritet si më poshtë:

Ndarja e dy numrave kompleks:

Shembull:

1. Aeroplan kompleks

Një numër kompleks mund të paraqitet grafikisht në një sistem koordinativ drejtkëndor. Le të vendosim një sistem koordinativ drejtkëndor në plan (x, y).

në bosht kau ne do të rregullojmë pjesët reale x, quhet bosht real (real)., në bosht Oy– pjesë imagjinare y numra komplekse. Ajo mban emrin bosht imagjinar. Për më tepër, çdo numër kompleks korrespondon me një pikë të caktuar të rrafshit, dhe një plan i tillë quhet plan kompleks. pikë A rrafshi kompleks do t'i përgjigjet vektorit OA.

Numri x thirrur abshissa numër kompleks, numër y – ordinator.

Një palë numrash komplekse të konjuguar shfaqen si pika të vendosura në mënyrë simetrike rreth boshtit real.

Nëse në set aeroplan sistemi i koordinatave polar, pastaj çdo numër kompleks z përcaktuar nga koordinatat polare. ku modul numrat është rrezja polare e pikës dhe këndi - argumenti i këndit të tij polar ose numrit kompleks z.

Moduli i numrave kompleks gjithmonë jo negative. Argumenti i një numri kompleks nuk është i përcaktuar në mënyrë unike. Vlera kryesore e argumentit duhet të plotësojë kushtin . Çdo pikë e rrafshit kompleks gjithashtu korrespondon me vlerën totale të argumentit. Argumentet që ndryshojnë me një shumëfish të 2π konsiderohen të barabarta. Argumenti i numrit zero nuk është i përcaktuar.

Vlera kryesore e argumentit përcaktohet nga shprehjet:

Është e qartë se

ku
, .

Paraqitja e numrave komplekse z si

thirrur formë trigonometrike numër kompleks.

Shembull.

1. Forma eksponenciale e numrave kompleks

Zbërthimi në Seria Maclaurin për funksionet e argumentit real duket si:

Për funksionin eksponencial të një argumenti kompleks z dekompozimi është i ngjashëm

.

Zgjerimi i serisë Maclaurin për funksionin eksponencial të argumentit imagjinar mund të përfaqësohet si

Identiteti që rezulton quhet Formula e Euler-it.

Për një argument negativ, duket si

Duke i kombinuar këto shprehje, ne mund të përcaktojmë shprehjet e mëposhtme për sinusin dhe kosinusin

.

Duke përdorur formulën e Euler-it, nga forma trigonometrike e paraqitjes së numrave kompleks

në dispozicion demonstrative formë (eksponenciale, polare) e një numri kompleks, d.m.th. përfaqësimi i saj në formë

,

Ku - koordinatat polare të një pike me koordinata drejtkëndore ( x,y).

Konjugati i një numri kompleks shkruhet në formë eksponenciale si më poshtë.

Për formën eksponenciale, është e lehtë të përcaktohen formulat e mëposhtme për shumëzimin dhe pjesëtimin e numrave kompleks

Kjo do të thotë, në formë eksponenciale, prodhimi dhe ndarja e numrave kompleksë është më e lehtë sesa në formën algjebrike. Gjatë shumëzimit, modulet e faktorëve shumëzohen dhe argumentet shtohen. Ky rregull zbatohet për çdo numër faktorësh. Në veçanti, kur shumëzoni një numër kompleks z në i vektoriale z rrotullohet në drejtim të kundërt të akrepave të orës me 90

Në pjesëtim, moduli i numëruesit ndahet me modulin e emëruesit dhe argumenti i emëruesit zbritet nga argumenti i numëruesit.

Duke përdorur formën eksponenciale të numrave kompleksë, mund të merren shprehje për identitete të njohura trigonometrike. Për shembull, nga identiteti

duke përdorur formulën Euler, ne mund të shkruajmë

Duke barazuar pjesët reale dhe imagjinare në këtë shprehje, marrim shprehje për kosinusin dhe sinusin e shumës së këndeve

1. Fuqitë, rrënjët dhe logaritmet e numrave kompleksë

Ngritja e një numri kompleks në një fuqi natyrore n prodhuar sipas formulës

Shembull. Llogaritni .

Imagjinoni një numër në formë trigonometrike

’

Duke aplikuar formulën e fuqizimit, marrim

Vendosja e vlerës në shprehje r= 1, marrim të ashtuquajturin Formula e De Moivre, me të cilin mund të përcaktoni shprehjet për sinuset dhe kosinuset e këndeve të shumta.

Rrënja n fuqia e një numri kompleks z Ajo ka n vlera të ndryshme të përcaktuara nga shprehja

Shembull. Le të gjejmë.

Për ta bërë këtë, ne shprehim numrin kompleks () në formën trigonometrike

.

Sipas formulës për llogaritjen e rrënjës së një numri kompleks, marrim

Logaritmi i një numri kompleks zështë një numër w, per cilin . Logaritmi natyror i një numri kompleks ka një numër të pafund vlerash dhe llogaritet me formulën

Përbëhet nga pjesë reale (kosinus) dhe imagjinare (sinus). Një stres i tillë mund të përfaqësohet si një vektor i gjatësisë U m, faza fillestare (këndi), rrotulluese me shpejtësi këndore ω .

Për më tepër, nëse shtohen funksione komplekse, atëherë shtohen pjesët e tyre reale dhe imagjinare. Nëse një funksion kompleks shumëzohet me një funksion konstant ose real, atëherë pjesët reale dhe imagjinare të tij shumëzohen me të njëjtin faktor. Diferencimi/integrimi i një funksioni të tillë kompleks reduktohet në diferencim/integrim të pjesëve reale dhe imagjinare.

Për shembull, diferencimi i shprehjes komplekse të stresit

është ta shumëzosh atë me iω është pjesa reale e funksionit f(z), dhe është pjesa imagjinare e funksionit. Shembuj: .

Kuptimi z përfaqësohet nga një pikë në rrafshin kompleks z dhe vlera përkatëse w- një pikë në planin kompleks w. Kur shfaqet w = f(z) linjat e avionit z kalojnë në vijat e aeroplanit w, figurat e një rrafshi në figura të një tjetri, por format e vijave ose figurave mund të ndryshojnë ndjeshëm.

		Forma algjebrike e shkrimit të një numri kompleks .......................................... ......................
		Rrafshi i numrave kompleks ..................................................... ................................................................ ......................
		Numrat komplekse të konjuguar ..................................................... ..................................................... ..............
	Veprimet me numra komplekse në formë algjebrike ...................................... .....................
		Mbledhja e numrave kompleks ..................................................... ................................................................ ......................
		Zbritja e numrave kompleks ..................................................... .......................................................... ..........
		Shumëzimi i numrave kompleks ..................................................... .......................................................... .........
		Pjestimi i numrave kompleks ..................................................... ..................................................... .....................
	Forma trigonometrike e një numri kompleks .............................................. ......................................
	Veprimet me numra kompleks në formë trigonometrike ................................................ .............
		Shumëzimi i numrave kompleks në formë trigonometrike................................................ ................................
		Ndarja e numrave kompleks në formë trigonometrike ................................................ ......................
		Ngritja e një numri kompleks në një fuqi të plotë pozitiv
		Nxjerrja e rrënjës së një fuqie të plotë pozitive nga një numër kompleks
		Ngritja e një numri kompleks në një fuqi racionale .......................................... ......................
		Seritë komplekse ................................................ ................................................................ .................................................
		Seritë e numrave kompleks ..................................................... ..................................................... ..............
		Seritë e fuqisë në planin kompleks ................................................ .................................................
		Seritë e dyanshme të fuqisë në planin kompleks ...................................... ......................
		Funksionet e një ndryshoreje komplekse ..................................................... ................................................................ ......................
		Funksionet themelore elementare ..................................................... ................................................ ..........
		Formulat e Euler ...................................................... .................................................. ..........................
		Forma eksponenciale e paraqitjes së një numri kompleks .......................................... ...... .
		Marrëdhënia ndërmjet funksioneve trigonometrike dhe hiperbolike ..........................................
		Funksioni logaritmik ..................................................... ................................................................ .....................
		Funksionet e përgjithshme eksponenciale dhe të përgjithshme të fuqisë ................................................ ................................................
	Diferencimi i funksioneve të një ndryshoreje komplekse.......................................... .....................
		Kushtet Cauchy-Riemann ................................................ .......................................................... ......... ............
		Formulat për llogaritjen e derivatit ................................................... ................................................
		Vetitë e veprimit të diferencimit .............................................. ................................................
		Vetitë e pjesëve reale dhe imagjinare të një funksioni analitik ...................................... .......

	Rikuperimi i një funksioni të një ndryshoreje komplekse nga realja ose imagjinare e saj
		Metoda numër 1. Përdorimi i integralit lakor ................................................ ......... .......
		Metoda numër 2. Zbatimi i drejtpërdrejtë i kushteve Cauchy-Riemann..........................................
		Metoda numër 3. Nëpërmjet derivatit të funksionit të dëshiruar .......................................... ......................................
	Integrimi i funksioneve të një ndryshoreje komplekse.......................................... .................................
	Formula integrale e Cauchy ..................................................... ................................................ . ..
	Zgjerimi i funksioneve në seritë Taylor dhe Laurent .......................................... ....................................
	Zerot dhe pikat njëjës të një funksioni të një ndryshoreje komplekse ................................... ....... ......
		Zerot e një funksioni të një ndryshoreje komplekse .......................................... ................................................
		Pika të izoluara njëjës të një funksioni të një ndryshoreje komplekse .......................................... ......

14.3 Pika në pafundësi si një pikë njëjës e një funksioni të një ndryshoreje komplekse

	Tërheqjet ................................................ ................................................ . ................................................
		Zbritja në pikën përfundimtare ..................................................... .......................................................... .............
		Mbetja e një funksioni në një pikë në pafundësi ................................... ................................................
	Llogaritja e integraleve duke përdorur mbetjet ................................................ .................................................
	Pyetje për vetë-ekzaminim ..................................................... ................................................................ ......................
	literatura...................................................... ................................................ . ................................
	Indeksi i lëndës................................................ ................................................ . .............

Parathënie

Është mjaft e vështirë të ndash saktë kohën dhe përpjekjen në përgatitjen për pjesët teorike dhe praktike të një provimi ose certifikimi të modulit, veçanërisht pasi gjithmonë nuk ka kohë të mjaftueshme gjatë seancës. Dhe siç tregon praktika, jo të gjithë mund ta përballojnë këtë. Si rezultat, gjatë provimit, disa studentë zgjidhin saktë problemat, por e kanë të vështirë t'u përgjigjen pyetjeve më të thjeshta teorike, ndërsa të tjerët mund të formulojnë një teoremë, por nuk mund ta zbatojnë atë.

Rekomandimet e tanishme metodologjike për përgatitjen për provimin në lëndën Teoria e Funksioneve të Variablave Komplekse (TFV) janë një përpjekje për të zgjidhur këtë kontradiktë dhe për të siguruar përsëritjen e njëkohshme të materialit teorik dhe praktik të lëndës. Të udhëhequr nga parimi "Teoria pa praktikë është e vdekur, praktika pa teori është e verbër", ato përmbajnë si pozicionet teorike të lëndës në nivelin e përkufizimeve dhe formulimeve, ashtu edhe shembuj që ilustrojnë zbatimin e secilit pozicion teorik të dhënë, dhe kështu e bëjnë atë. më lehtë për t'u mbajtur mend dhe kuptuar.

Qëllimi i rekomandimeve të propozuara metodologjike është të ndihmojë studentin të përgatitet për provimin në nivelin bazë. Me fjalë të tjera, është përpiluar një udhëzues i zgjeruar pune që përmban pikat kryesore të përdorura në orët e kursit TFKT dhe të nevojshme gjatë kryerjes së detyrave të shtëpisë dhe përgatitjes për aktivitetet e kontrollit. Përveç punës së pavarur të studentëve, ky publikim elektronik arsimor mund të përdoret gjatë zhvillimit të orëve në formë interaktive duke përdorur një tabelë elektronike ose për vendosjen në një sistem të mësimit në distancë.

Ju lutemi vini re se kjo punë nuk zëvendëson tekstet shkollore apo shënimet e leksioneve. Për një studim të thelluar të materialit, rekomandohet t'i referoheni seksioneve përkatëse të botimit të botuar në Universitetin Teknik Shtetëror të Moskës. N.E. Libër mësimi bazë Bauman.

Në fund të manualit ka një listë të literaturës së rekomanduar dhe një indeks lëndor, i cili përfshin të gjitha ato të theksuara në tekst. kursive të theksuara kushtet. Indeksi përbëhet nga hiperlidhje për seksionet ku këto terma janë të përcaktuara ose të përshkruara në mënyrë strikte dhe ku jepen shembuj për të ilustruar përdorimin e tyre.

Manuali është i destinuar për studentët e vitit të dytë të të gjitha fakulteteve të MSTU. N.E. Bauman.

1. Forma algjebrike e shkrimit të një numri kompleks

Regjistrimi i formës z \u003d x + iy, ku x, y janë numra realë, i është një njësi imagjinare (d.m.th. i 2 = - 1)

quhet forma algjebrike e numrit kompleks z. Në këtë rast, x quhet pjesa reale e numrit kompleks dhe shënohet Re z (x \u003d Re z), y quhet pjesa imagjinare e numrit kompleks dhe shënohet Im z (y \u003d Im z).

Shembull. Pjesa reale e numrit kompleks z = 4 − 3i është Re z = 4, dhe pjesa imagjinare është Im z = − 3.

2. Rrafshi i numrave kompleks

NË konsiderojnë teoritë e funksioneve të një ndryshoreje komplekseplani i numrave kompleks, që shënohet ose, ose përdoren shkronjat që tregojnë numrat kompleks z, w etj.

Boshti horizontal i rrafshit kompleks quhet bosht real, mbi të ndodhen numrat realë z = x + 0 i = x.

Boshti vertikal i planit kompleks quhet bosht imagjinar, ai ka

3. Numrat komplekse të konjuguar

Quhen numrat z = x + iy dhe z = x − iy konjuguar kompleks. Në planin kompleks, ato korrespondojnë me pika që janë simetrike rreth boshtit real.

4. Veprimet me numra kompleks në formë algjebrike

4.1 Mbledhja e numrave kompleks

Shuma e dy numrave kompleks

z 1 = x 1 + iy 1

dhe z 2 = x 2 + iy 2 quhet numër kompleks

z1 + z2

= (x 1 + iy 1 ) + (x 2 + iy 2 ) = ( x 1 + x 2 ) + i (y 1 + y 2 ) .

operacion

shtesat

numrat kompleksë është i ngjashëm me veprimin e mbledhjes së binomeve algjebrike.

Shembull. Shuma e dy numrave kompleks z 1 = 3 + 7i dhe z 2

= −1 +2 i

do të jetë një numër kompleks

z 1 + z 2 = (3 +7 i ) +(−1 +2 i ) = (3 −1 ) +(7 +2 ) i = 2 +9 i .

Natyrisht,

shuma në një kompleks

të konjuguara

është

e vlefshme

z + z = (x + iy) + (x − iy) = 2 x = 2 Rez .

4.2 Zbritja e numrave kompleks

Ndryshimi i dy numrave kompleks z 1 = x 1 + iy 1

X 2 +iy 2

thirrur

gjithëpërfshirëse

numri z 1 − z 2 = (x 1 + iy 1 ) − (x 2 + iy 2 ) = (x 1 − x 2 ) + i (y 1 − y 2 ) .

Shembull. Dallimi midis dy numrave kompleks

z 1 = 3 −4 i

dhe z2

= −1 +2 i

do të ketë një gjithëpërfshirës

numri z 1 − z 2 = (3 − 4i ) − (− 1+ 2i ) = (3 − (− 1) ) + (− 4 − 2) i = 4 − 6i .

ndryshim

konjuguar kompleks

është

z − z = (x + iy) − (x − iy) = 2 iy = 2 i Im z .

4.3 Shumëzimi i numrave kompleks

Prodhimi i dy numrave kompleks

z 1 = x 1 + iy 1

dhe z 2 = x 2 + iy 2

quhet kompleks

z 1z 2 = (x 1 + iy 1 )(x 2 + iy 2 ) = x 1x 2 + iy 1x 2 + iy 2 x 1 + i 2 y 1 y 2

= (x 1x 2 − y 1 y 2 ) + i (y 1x 2 + y 2 x ) .

Kështu, veprimi i shumëzimit të numrave kompleks është i ngjashëm me veprimin e shumëzimit të binomeve algjebrike, duke marrë parasysh faktin se i 2 = − 1.

PËRKUFIZIM

Forma algjebrike e një numri kompleks është të shkruhet numri kompleks \(\ z \) si \(\ z=x+i y \) ku \(\ x \) dhe \(\ y \) janë numra realë, \ (\ i \ ) është një njësi imagjinare që plotëson relacionin \(\ i^(2)=-1 \)

Numri \(\ x \) quhet pjesa reale e numrit kompleks \(\ z \) dhe shënohet \(\ x=\emri i operatorit(Re) z \)

Numri \(\ y \) quhet pjesa imagjinare e numrit kompleks \(\ z \) dhe shënohet \(\ y=\emri i operatorit(Im) z \)

Për shembull:

Numri kompleks \(\ z=3-2 i \) dhe numri i lidhur me të \(\ \mbi vijën (z)=3+2 i \) shkruhen në formë algjebrike.

Vlera imagjinare \(\ z=5 i \) shkruhet në formë algjebrike.

Përveç kësaj, në varësi të problemit që zgjidhet, ju mund të shndërroni një numër kompleks në një numër trigonometrik ose eksponencial.

Detyrë

Shkruani numrin \(\ z=\frac(7-i)(4)+13 \) në formë algjebrike, gjeni pjesët reale dhe imagjinare të tij, si dhe numrin e konjuguar.

Zgjidhje.

Duke zbatuar termin e ndarjes së thyesave dhe rregullin e mbledhjes së thyesave, marrim:

\(\ z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac( 1)(4) i \)

Prandaj, pjesa reale e numrit kompleks \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) është numri \(\ x=\emri i operatorit(Re) z= \frac(59) (4) \) , pjesa imagjinare është një numër \(\ y=\emri i operatorit(Im) z=-\frac(1)(4) \)

Numri i konjuguar: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)

Përgjigju

\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \emri i operatorit(Re) z=\frac(59)(4) \), \(\ \operatorname(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)

Veprimet e numrave kompleksë në krahasimin e formës algjebrike

Dy numra kompleks \(\ z_(1)=x_(1)+i y_(1) \) janë të barabartë nëse \(\ x_(1)=x_(2) \), \(\ y_(1)= y_ (2) \) d.m.th. Pjesët e tyre reale dhe imagjinare janë të barabarta.

Detyrë

Përcaktoni për cilin x dhe y dy numra kompleks \(\ z_(1)=13+y i \) dhe \(\ z_(2)=x+5 i \) janë të barabartë.

Zgjidhje

Sipas përkufizimit, dy numra kompleksë janë të barabartë nëse pjesët e tyre reale dhe imagjinare janë të barabarta, d.m.th. \(\ x=13 \), \(\ y=5 \).

Përgjigje \(\ x=13 \), \(\ y=5 \)

shtesë

Mbledhja e numrave kompleks \(\ z_(1)=x_(1)+i y_(1) \) bëhet me mbledhjen e drejtpërdrejtë të pjesëve reale dhe imagjinare:

\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\majtas(x_(1)+x_(2)\djathtas) +i\majtas(y_(1)+y_(2)\djathtas) \)

Detyrë

Gjeni shumën e numrave kompleks \(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \)

Zgjidhje.

Pjesa reale e numrit kompleks \(\ z_(1)=-7+5 i \) është numri \(\ x_(1)=\emri i operatorit(Re) z_(1)=-7 \) , imagjinar pjesë është numri \( \ y_(1)=\mathrm(Im) \), \(\ z_(1)=5 \) . Pjesët reale dhe imagjinare të numrit kompleks \(\ z_(2)=13-4 i \) janë \(\ x_(2)=\emri i operatorit(Re) z_(2)=13 \) dhe \(\ y_ (2 )=\emri i operatorit(Im) z_(2)=-4 \) .

Prandaj, shuma e numrave kompleks është:

\(\ z_(1)+z_(2)=\majtas(x_(1)+x_(2)\djathtas)+i\left(y_(1)+y_(2)\djathtas)=(-7+ 13)+i(5-4)=6+i\)

Përgjigju

\(\z_(1)+z_(2)=6+i \)

Lexoni më shumë rreth shtimit të numrave kompleks në një artikull të veçantë: Shtimi i numrave kompleks.

Zbritja

Zbritja e numrave kompleks \(\ z_(1)=x_(1)+i y_(1) \) dhe \(\ z_(2)=x_(2)+i y_(2) \) bëhet me anë të drejtpërdrejtë zbritja e pjesëve reale dhe imagjinare:

\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\majtas(x_(2)+i y_(2)\djathtas)=x_(1)-x_(2) +\majtë(i y_(1)-i y_(2)\djathtas)=\majtas(x_(1)-x_(2)\djathtas)+i\left(y_(1)-y_(2)\djathtas )\)

Detyrë

gjeni ndryshimin e numrave kompleks \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)

Zgjidhje.

Gjeni pjesët reale dhe imagjinare të numrave kompleksë \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) :

\(\ x_(1)=\emri i operatorit(Re) z_(1)=17, x_(2)=\emri i operatorit(Re) z_(2)=15 \)

\(\ y_(1)=\emri i operatorit(Im) z_(1)=-35, y_(2)=\emri i operatorit(Im) z_(2)=5 \)

Pra ndryshimi i numrave kompleks është:

\(\ z_(1)-z_(2)=\majtas(x_(1)-x_(2)\djathtas)+i\left(y_(1)-y_(2)\djathtas)=(17-15 )+i(-35-5)=2-40 i \)

Përgjigju

\(\ z_(1)-z_(2)=2-40 i \) shumëzimi

Shumëzimi i numrave kompleks \(\ z_(1)=x_(1)+i y_(1) \) dhe \(\ z_(2)=x_(2)+i y_(2) \) kryhet drejtpërdrejt nga duke gjeneruar numra në formë algjebrike, duke marrë parasysh vetinë e njësisë imagjinare \(\ i^(2)=-1 \) :

\(\ z_(1) \cdot z_(2)=\majtas(x_(1)+i y_(1)\djathtas) \cdot\left(x_(2)+i y_(2)\djathtas)=x_ (1) \cdot x_(2)+i^(2) \cdot y_(1) \cdot y_(2)+\left(x_(1) \cdot i y_(2)+x_(2) \cdot i y_(1)\djathtas)= \)

\(\ =\majtas(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\djathtas)+i\left(x_(1) \cdot y_(2)+x_(2 ) \cdot y_(1)\djathtas) \)

Detyrë

Gjeni prodhimin e numrave kompleks \(\ z_(1)=1-5 i \)

Zgjidhje.

Kompleksi i numrave kompleks:

\(\ z_(1) \cdot z_(2)=\majtas(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\djathtas)+i\majtas(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\djathtas)=(1 \cdot 5-(-5) \cdot 2)+i(1 \cdot 2+(-5) \cdot 5 )=15-23 i \)

Përgjigju

\(\ z_(1) \cdot z_(2)=15-23 i \) ndarje

Faktori i numrit kompleks \(\ z_(1)=x_(1)+i y_(1) \) dhe \(\ z_(2)=x_(2)+i y_(2) \) përcaktohet duke shumëzuar numëruesi dhe emëruesi i numrit të konjuguar me një emërues:

\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\majtas (x_(1)+i y_(1)\djathtas)\majtas(x_(2)-i y_(2)\djathtas))(\majtas(x_(2)+i y_(2)\djathtas)\majtas (x_(2)-i y_(2)\djathtas))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2) +y_(2)^(2)+i \frac(x_(2) \cdot y_(1)-x_(1) \cdot y_(2))(x_(2)^(2)+y_(2 )^(2) \)

Detyrë

Të pjesëtohet numri 1 me numrin kompleks \(\ z=1+2 i \).

Zgjidhje.

Meqenëse pjesa imagjinare e numrit real 1 është zero, faktori është:

\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^( 2)+2^(2))=\frac(1)(5)-i \frac(2)(5) \)

Përgjigju

\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)

Plani i mësimit.

1. Momenti organizativ.

2. Prezantimi i materialit.

3. Detyrë shtëpie.

4. Përmbledhja e mësimit.

Gjatë orëve të mësimit

I. Momenti organizativ.

II. Prezantimi i materialit.

Motivimi.

Zgjerimi i bashkësisë së numrave realë konsiston në faktin se numrave realë u shtohen numra të rinj (imagjinarë). Futja e këtyre numrave lidhet me pamundësinë e nxjerrjes së rrënjës nga një numër negativ në grupin e numrave realë.

Prezantimi i konceptit të një numri kompleks.

Numrat imagjinarë me të cilët plotësojmë numrat realë shkruhen si bi, Ku iështë njësia imagjinare, dhe i 2 = - 1.

Bazuar në këtë, marrim përkufizimin e mëposhtëm të një numri kompleks.

Përkufizimi. Një numër kompleks është një shprehje e formës a+bi, Ku a Dhe b janë numra realë. Në këtë rast, plotësohen kushtet e mëposhtme:

a) Dy numra kompleks a 1 + b 1 i Dhe a 2 + b 2 i e barabartë nëse dhe vetëm nëse a 1 = a 2, b1=b2.

b) Mbledhja e numrave kompleks përcaktohet nga rregulli:

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

c) Shumëzimi i numrave kompleks përcaktohet nga rregulli:

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

Forma algjebrike e një numri kompleks.

Shkrimi i një numri kompleks në formë a+bi quhet trajta algjebrike e një numri kompleks, ku A- pjesa reale biështë pjesa imagjinare, dhe bështë një numër real.

Numri kompleks a+bi konsiderohet e barabartë me zero nëse pjesët reale dhe imagjinare të tij janë të barabarta me zero: a=b=0

Numri kompleks a+bi në b = 0 konsiderohet të jetë një numër real a: a + 0i = a.

Numri kompleks a+bi në a = 0 quhet thjesht imagjinar dhe shënohet bi: 0 + bi = bi.

Dy numra kompleks z = a + bi Dhe = a – bi, të cilat ndryshojnë vetëm në shenjën e pjesës imagjinare, quhen të konjuguara.

Veprimet mbi numrat kompleks në formë algjebrike.

Veprimet e mëposhtme mund të kryhen në numra kompleks në formë algjebrike.

1) Shtesa.

Përkufizimi. Shuma e numrave kompleks z 1 = a 1 + b 1 i Dhe z 2 = a 2 + b 2 i quhet një numër kompleks z, pjesa reale e së cilës është e barabartë me shumën e pjesëve reale z1 Dhe z2, dhe pjesa imagjinare është shuma e pjesëve imagjinare të numrave z1 Dhe z2, kjo eshte z = (a 1 + a 2) + (b 1 + b 2)i.

Numrat z1 Dhe z2 quhen terma.

Shtimi i numrave kompleks ka këto veti:

1º. Komutativiteti: z1 + z2 = z2 + z1.

2º. Asociacioni: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. Numri kompleks -a -bi quhet e kundërta e një numri kompleks z = a + bi. Numri kompleks i kundërt i numrit kompleks z, shënohet -z. Shuma e numrave kompleks z Dhe -z barazohet me zero: z + (-z) = 0

Shembulli 1: Shtoni (3 - i) + (-1 + 2i).

(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Zbritja.

Përkufizimi. Zbrit nga numri kompleks z1 numër kompleks z2 z,Çfarë z + z 2 = z 1.

Teorema. Dallimi i numrave kompleks ekziston dhe, për më tepër, është unik.

Shembulli 2: Zbrit (4 - 2i) - (-3 + 2i).

(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.

3) Shumëzimi.

Përkufizimi. Prodhimi i numrave kompleks z 1 =a 1 +b 1 i Dhe z 2 \u003d a 2 + b 2 i quhet një numër kompleks z, e përcaktuar nga barazia: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.

Numrat z1 Dhe z2 quhen faktorë.

Shumëzimi i numrave kompleks ka këto veti:

1º. Komutativiteti: z 1 z 2 = z 2 z 1.

2º. Asociacioni: (z 1 z 2)z 3 = z 1 (z 2 z 3)

3º. Shpërndarja e shumëzimit në lidhje me mbledhjen:

(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.

4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2është një numër real.

Në praktikë, shumëzimi i numrave kompleks kryhet sipas rregullit të shumëzimit të shumës me shumën dhe ndarjes së pjesëve reale dhe imagjinare.

Në shembullin vijues, merrni parasysh shumëzimin e numrave kompleks në dy mënyra: me rregull dhe duke shumëzuar shumën me shumën.

Shembulli 3: Shumëzoni (2 + 3i) (5 – 7i).

1 mënyrë. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + i.

2 mënyra. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.

4) Divizioni.

Përkufizimi. Ndani një numër kompleks z1 në një numër kompleks z2, do të thotë të gjesh një numër kaq kompleks z, Çfarë z z 2 = z 1.

Teorema. Herësi i numrave kompleks ekziston dhe është unik nëse z2 ≠ 0 + 0i.

Në praktikë, herësi i numrave kompleks gjendet duke shumëzuar numëruesin dhe emëruesin me konjugatin e emëruesit.

Le z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Pastaj

.

Në shembullin e mëposhtëm, ne kryejmë pjesëtimin me formulën dhe rregullin e shumëzimit me konjugatin e emëruesit.

Shembulli 4. Gjeni një herës .

5) Ngritja në një fuqi të plotë pozitiv.

a) Fuqitë e unitetit imagjinar.

Duke përfituar nga barazia i 2 \u003d -1, është e lehtë të përcaktohet çdo fuqi numër i plotë pozitiv i njësisë imagjinare. Ne kemi:

i 3 \u003d i 2 i \u003d -i,

i 4 \u003d i 2 i 2 \u003d 1,

i 5 \u003d i 4 i \u003d i,

i 6 \u003d i 4 i 2 \u003d -1,

i 7 \u003d i 5 i 2 \u003d -i,

i 8 = i 6 i 2 = 1 etj.

Kjo tregon se vlerat e gradës në, Ku n- një numër i plotë pozitiv, i përsëritur periodikisht kur treguesi rritet me 4 .

Prandaj, për të rritur numrin i në një fuqi të plotë pozitiv, ndajeni eksponentin me 4 dhe i ngritur i te fuqia, eksponenti i së cilës është pjesa e mbetur e ndarjes.

Shembulli 5 Llogaritni: (i 36 + i 17) i 23.

i 36 = (i 4) 9 = 1 9 = 1,

i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 i = i.

i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.

(i 36 + i 17) i 23 \u003d (1 + i) (- i) \u003d - i + 1 \u003d 1 - i.

b) Ngritja e një numri kompleks në një fuqi të plotë pozitiv kryhet sipas rregullit të ngritjes së një binomi në fuqinë përkatëse, pasi është një rast i veçantë i shumëzimit të faktorëve kompleksë identikë.

Shembulli 6 Llogaritni: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.