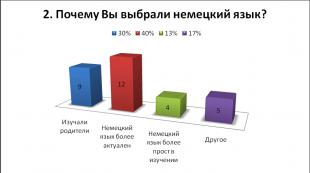
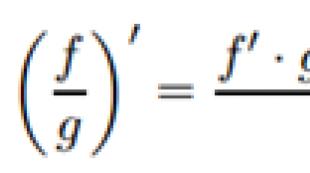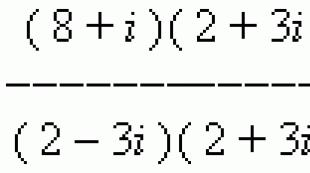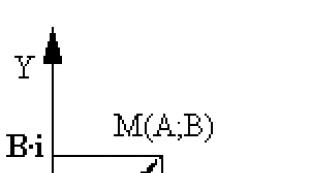Për çfarë është një numër kompleks? §1. Numrat kompleksë: përkufizimet bazë. Zbritja dhe pjesëtimi i numrave kompleks
REFERENCA HISTORIKE
Numrat kompleksë u futën në matematikë për të bërë të mundur marrjen e rrënjës katrore të çdo numri real. Megjithatë, kjo nuk është arsye e mjaftueshme për të futur numra të rinj në matematikë. Doli që nëse kryeni llogaritjet sipas rregullave të zakonshme për shprehjet në të cilat ndodh rrënja katrore e një numri negativ, atëherë mund të arrini në një rezultat që nuk përmban më rrënjën katrore të një numri negativ. Në shekullin XVI. Cardano gjeti një formulë për zgjidhjen e një ekuacioni kub. Doli se kur një ekuacion kub ka tre rrënjë reale, rrënja katrore e një numri negativ ndodh në formulën Cardano. Prandaj, rrënjët katrore të numrave negativë filluan të përdoren në matematikë dhe i quajtën numra imagjinarë - kështu, si të thuash, ata fituan të drejtën e një ekzistence të paligjshme. Gausi u dha të drejta të plota civile numrave imagjinarë, i cili i quajti numra kompleks, dha një interpretim gjeometrik dhe vërtetoi teoremën themelore të algjebrës, e cila thotë se çdo polinom ka të paktën një rrënjë reale.
1. KONCEPTI I NJË NUMRI KOMPLEKS
Zgjidhja e shumë problemeve në matematikë dhe fizikë reduktohet në zgjidhjen e ekuacioneve algjebrike. Prandaj, studimi i ekuacioneve algjebrike është një nga pyetjet më të rëndësishme në matematikë. Dëshira për t'i bërë ekuacionet të zgjidhshme është një nga arsyet kryesore për zgjerimin e konceptit të numrit.
Pra, për zgjidhshmërinë e ekuacioneve të formës X+A=B nuk mjaftojnë numrat pozitivë. Për shembull, ekuacioni X+5=2 nuk ka rrënjë pozitive. Prandaj, duhet të futni numra negativë dhe zero.
Në bashkësinë e numrave racionalë, ekuacionet algjebrike të shkallës së parë janë të zgjidhshme, d.m.th. ekuacionet e formës A · X+B=0 (A0). Megjithatë, ekuacionet algjebrike të shkallës më të lartë se një mund të mos kenë rrënjë racionale. Për shembull, të tilla janë ekuacionet X 2 =2, X 3 =5. Nevoja për të zgjidhur ekuacione të tilla ishte një nga arsyet për futjen e numrave irracionalë. Numrat racional dhe irracional formojnë bashkësinë e numrave realë.
Megjithatë, numrat realë nuk janë të mjaftueshëm për të zgjidhur ndonjë ekuacion algjebrik. Për shembull, një ekuacion kuadratik me koeficientë realë dhe një diskriminues negativ nuk ka rrënjë reale. Më i thjeshti prej tyre është ekuacioni X 2 +1=0. Prandaj, është e nevojshme të zgjerohet grupi i numrave realë duke shtuar numra të rinj në të. Këta numra të rinj, së bashku me numrat realë, formojnë një bashkësi, e cila quhet bashkësi numra komplekse.
Le të zbulojmë fillimisht se çfarë forme duhet të kenë numrat kompleksë. Supozojmë se në bashkësinë e numrave komplekse ekuacioni X 2 +1=0 ka një rrënjë. Këtë rrënjë e shënojmë me shkronjë i Kështu, i është një numër kompleks i tillë që i 2 = –1.
Sa i përket numrave realë, duhet të prezantohen veprimet e mbledhjes dhe shumëzimit të numrave kompleksë në mënyrë që shuma dhe prodhimi i tyre të jenë numra kompleks. Pastaj, në veçanti, për çdo numër real A dhe B shprehja A + B i mund të mendohet si një paraqitje e përgjithshme e një numri kompleks. Emri "kompleks" vjen nga fjala "i përbërë": nga forma e shprehjes A + B i .
Numrat kompleks quhen shprehje të formës A+B i , ku A dhe B janë numra realë, dhe i është një personazh i tillë që i 2 = –1, dhe shënohet me shkronjën Z.
Numri A quhet pjesa reale e numrit kompleks A+B i, dhe numri B është pjesa imagjinare e tij. Numri i quhet njësi imagjinare.
Për shembull, pjesa reale e numrit kompleks 2+3 i është 2 dhe imagjinarja është 3.
Për një përkufizim rigoroz të një numri kompleks, është e nevojshme të prezantohet koncepti i barazisë për këta numra.
Dy numra kompleks A+B i dhe C+D i thirrur të barabartë nëse dhe vetëm nëse A=C dhe B=D, d.m.th. kur pjesët e tyre reale dhe imagjinare janë të barabarta.
2. INTERPRETIMI GJEOMETRIK I NJË NUMRI KOMPLEKS

Numrat realë përfaqësohen gjeometrikisht me pika në vijën numerike. Numri kompleks A+B i mund të shihet si një çift numrash realë (A;B). Prandaj, është e natyrshme të paraqesim një numër kompleks si pika në rrafsh. Në një sistem koordinativ drejtkëndor, numri kompleks Z=A+B· i përfaqësohet nga një pikë e rrafshët me koordinata (A;B), dhe kjo pikë shënohet me të njëjtën shkronjë Z (Figura 1). Natyrisht, korrespondenca e marrë në këtë rast është një me një. Ai bën të mundur interpretimin e numrave kompleksë si pika në rrafshin në të cilin zgjidhet sistemi i koordinatave. Ky plan koordinativ quhet plan kompleks . Abshisa quhet bosht real , sepse mbi të ka pika që i korrespondojnë numrave realë. Boshti y quhet bosht imagjinar – përmban pika që u korrespondojnë numrave kompleksë imagjinarë.

Jo më pak i rëndësishëm dhe i përshtatshëm është interpretimi i numrit kompleks A+B i si vektor, d.m.th. vektorë me origjinë në një pikë
O(0;0) dhe përfundon në pikën M(A;B) (Figura 2).
Korrespondenca e krijuar midis grupit të numrave kompleksë, nga njëra anë, dhe grupeve të pikave ose vektorëve të rrafshit, nga ana tjetër, lejon që numrat kompleks të jenë pika ose vektorë.
3.MODULI I NJË NUMRI KOMPLEKS
Le të jetë një numër kompleks Z=A+B· i . E konjuguar Me Z quhet një numër kompleks A – B i , e cila shënohet me , d.m.th.
A-B i .
Vini re se = A + B i , pra për çdo numër kompleks Z kemi barazinë =Z.
modul numri kompleks Z=A+B i thirrur numri dhe shënohet me , d.m.th.
Nga formula (1) rrjedh se për çdo numër kompleks Z, dhe =0 nëse dhe vetëm nëse Z=0, d.m.th. kur A=0 dhe B=0. Le të vërtetojmë se për çdo numër kompleks Z formulat janë të vlefshme:
4. MBLEDHJA DHE SHUMËZIMI I NUMRAVE KOMPLEKS
shuma dy numra kompleks A+B i dhe C+D i quhet numër kompleks (A+C ) + ( B+D)· i , d.m.th. ( A+B i) + ( C+D i)=( A+C) + (B+D) ipuna dy numra kompleks A+B i dhe C+D i quhet numër kompleks (A C – B D)+(A D+B C) i , d.m.th.
(A + B i ) (C + D i )=(A C – B D) + (A D + B C) i
Nga formula rezulton se mbledhja dhe shumëzimi mund të kryhen sipas rregullave të veprimeve me polinome, duke supozuar i 2 = -1. Veprimet e mbledhjes dhe shumëzimit të numrave kompleks kanë vetitë e numrave realë. Karakteristikat themelore:
Transferimi i pronës:
Z 1 + Z 2 \u003d Z 2 + Z 1, Z 1 Z 2 \u003d Z 2 Z 1
Vetia shoqëruese:
(Z 1 + Z 2) + Z 3 \u003d Z 1 + (Z 2 + Z 3), (Z 1 Z 2) Z 3 \u003d Z 1 (Z 2 Z 3)
Prona e shpërndarjes:
Z 1 (Z 2 + Z 3) \u003d Z 1 Z 2 + Z 1 Z 3
Paraqitja gjeometrike e shumës së numrave kompleksë

Sipas përkufizimit të mbledhjes së dy numrave kompleksë, pjesa reale e shumës është e barabartë me shumën e pjesëve reale të termave, pjesa imagjinare e shumës është e barabartë me shumën e pjesëve imagjinare të termave. Koordinatat e shumës së vektorëve përcaktohen në të njëjtën mënyrë:
Shuma e dy vektorëve me koordinata (A 1 ;B 1) dhe (A 2 ;B 2) është një vektor me koordinata (A 1 +A 2 ;B 1 +B 2). Prandaj, për të gjetur vektorin që korrespondon me shumën e numrave kompleksë Z 1 dhe Z 2, duhet të shtoni vektorët që korrespondojnë me numrat kompleks Z 1 dhe Z 2 .
Shembulli 1: Gjeni shumën dhe prodhimin e numrave kompleks Z 1 =2 - 3× i Dhe
Z 2 \u003d -7 + 8 × i .
Z 1 + Z 2 \u003d 2 - 7 + (-3 + 8) × i = - 5 + 5× i
Z 1× Z 2 = (2 – 3× i )× (–7 + 8× i ) = –14 + 16× i + 21× i + 24 = 10 + 37× i

5. ZBRITJA DHE PJESIMI I NUMRAVE KOMPLEKS
Zbritja e numrave kompleks është veprim i kundërt i mbledhjes: për çdo numër kompleks Z 1 dhe Z 2 ekziston, dhe për më tepër, vetëm një, numri Z, i tillë që:
Nëse u shtojmë të dyja pjesëve të barazisë (–Z 2) të kundërtën e numrit Z 2:
Z + Z 2 + (-Z 2) \u003d Z 1 + (-Z 2), prej nga
Numri Z \u003d Z 1 + Z 2 quhet dallimi i numrave Z 1 dhe Z 2 .
Pjesëtimi paraqitet si inversi i shumëzimit:
Z × Z 2 \u003d Z 1
Duke i ndarë të dy pjesët me Z 2, marrim:
Ky ekuacion tregon se Z 2 0

Paraqitja gjeometrike e ndryshimit të numrave kompleks
Diferenca Z 2 - Z 1 e numrave kompleks Z 1 dhe Z 2 korrespondon me diferencën e vektorëve që u korrespondojnë numrave Z 1 dhe Z 2 . Moduli i ndryshimit të dy numrave kompleks Z 2 dhe Z 1 sipas përcaktimit të modulit është gjatësia e vektorit Z 2 - Z 1 . Ne e ndërtojmë këtë vektor si shumën e vektorëve Z 2 dhe (–Z 1) (Figura 4). Kështu, moduli i ndryshimit të dy numrave kompleks është distanca midis pikave të planit kompleks që u korrespondojnë këtyre numrave.
Ky interpretim i rëndësishëm gjeometrik i modulit të ndryshimit të dy numrave kompleks bën të mundur përdorimin me sukses të fakteve të thjeshta gjeometrike.
Shembulli 2: Janë dhënë numrat kompleks Z 1 = 4 + 5 i dhe Z 2 = 3 + 4 i . Gjeni ndryshimin Z 2 - Z 1 dhe herësin
Z 2 - Z 1 \u003d (3 + 4 ) i) – (4 + 5 i) = –1 – i
=![]() =
=
6. FORMA TRIGONOMETRIKE E NJË NUMRI KOMPLEKS

Shkrimi i një numri kompleks Z si A+B i thirrur forma algjebrike numër kompleks. Përveç formës algjebrike, përdoren edhe forma të tjera të shkrimit të numrave kompleksë.
Merrni parasysh formë trigonometrike shënimi i një numri kompleks. Pjesë reale dhe imagjinare të një numri kompleks Z=A+B i shprehen në termat e modulit të tij = r dhe argumentit j si më poshtë:
A= r cosj; B= r sinj .
Numri Z mund të shkruhet kështu:
Z= r cosj + i sinj = r (cosj + i sinj)
Z = r (cosj + i sinj ) (2)
Kjo hyrje quhet forma trigonometrike e një numri kompleks .
r = është moduli i numrit kompleks.
Numri j quhet argumenti i numrit kompleks.
Argumenti i numrit kompleks Z0 është vlera e këndit ndërmjet drejtimit pozitiv të boshtit real dhe vektorit Z, dhe vlera e këndit konsiderohet pozitive nëse numërimi është në të kundërt të akrepave të orës dhe negative nëse është në drejtim të akrepave të orës.
Për numrin Z=0, argumenti nuk është i përcaktuar dhe vetëm në këtë rast numri jepet vetëm nga moduli i tij.
Siç u përmend më lart = r =, barazia (2) mund të shkruhet si
A+B i =· cosj + i · sinj, prej nga, duke barazuar pjesët reale dhe imagjinare, marrim:
cosj =, sinj = (3)
Nëse sinj ndaje me cosj marrim:
tgj= (4)
Kjo formulë është më e përshtatshme për t'u përdorur për të gjetur argumentin j sesa formula (3). Megjithatë, jo të gjitha vlerat e j që plotësojnë barazinë (4) janë argumente të numrit A + B i . Prandaj, kur gjeni argumentin, duhet të keni parasysh se në cilin tremujor ndodhet pika A + B i .
7. VETITË E MODULIT DHE ARGUMENTI I NJË NUMRI KOPLEKS
Duke përdorur formën trigonometrike, është e përshtatshme të gjesh produktin dhe herësin e numrave kompleksë.
Le të Z 1 = r 1 ( cosj 1 +i sinj 1), Z 2 = r 2 ( cosj 2 +i sinj 2). Pastaj:
Z 1 Z 2 = r 1 r 2 =
= r 1 r 2 .
Kështu, produkti i numrave kompleksë të shkruar në formë trigonometrike mund të gjendet me formulën:
Z 1 Z 2 = r 1 r 2 (5)
Nga formula (5) rezulton se kur numrat kompleks shumëzohen, moduli i tyre shumëzohet dhe argumentet shtohen.
Nëse Z 1 \u003d Z 2 atëherë marrim:
Z2=2= r 2 (cos2j +i sin2j)
Z 3 \u003d Z 2 Z \u003d r 2 ( cos2j +i sin2j ) r (cosj + i sinj )=
= r 3 ( cos3j +i sin3j)
Në përgjithësi, për çdo numër kompleks Z=r (cosj + i sinj )0 dhe çdo numër natyror n, formula është e vlefshme:
Zn=[ r (cosj + i sinj )] n = r n (cosnj + i sinnj),(6)
e cila quhet formula e De Moivre.
Herësi i dy numrave kompleksë të shkruar në formë trigonometrike mund të gjendet me formulën:
 [cos(j 1 – j 2) + i mëkat(j 1 - j 2)].(7)
[cos(j 1 – j 2) + i mëkat(j 1 - j 2)].(7)
 =
=  = cos(–j 2) + i mëkat (–j 2)
= cos(–j 2) + i mëkat (–j 2)
Duke përdorur formulën 5
 (cosj 1 + i sinj 1)× (cos(–j 2) + i sin(–j 2)) =
(cosj 1 + i sinj 1)× (cos(–j 2) + i sin(–j 2)) =
cos(j 1 – j 2) + i mëkat(j 1 - j 2).
Shembulli 3:
Numrin -8 e shkruajmë në formë trigonometrike
8 = 8 (cos(p + 2p k ) + i sin(p + 2p k )), k О Z
Le të jetë Z = r× (cosj + i×
r 3× (cos3j + i× sin3j ) = 8 (cos(p + 2p k ) + i sin(p + 2p k )), k О Z
Atëherë 3j =p + 2p k , k О Z
j= , k О Z
Prandaj:
Z = 2 (cos() + i sin()), k О Z
k = 0,1,2...
k = 0
Z 1 = 2 (cos + i mëkat) = 2 ( i) = 1+× i
k = 1
Z 2 = 2 (cos( + ) + i sin( + )) = 2 (cosp + i sinp) = –2
k = 2
Z 3 = 2 (cos( + ) + i sin( + )) = 2 (cos + i sin) = 1–× i
Përgjigje: Z 13 =; Z 2 \u003d -2
Shembulli 4:
Numrin 1 e shkruajmë në formë trigonometrike
1 = 1 (cos(2p k ) + i sin(2p k )), k О Z
Le të jetë Z = r× (cosj + i× sinj ), atëherë ky ekuacion do të shkruhet si:
r 4× (cos4j + i× sin4j ) = cos(2p k ) + i sin(2p k )), k О Z
4j = 2p k , k О Z
j = , k О Z
Z = cos + i× mëkat
k = 0,1,2,3...
k = 0
Z1 = cos0+ i× sin0 = 1 + 0 = 1
k = 1
Z2 = cos + i× mëkat=0+ i = i
k = 2
Z 3 \u003d cosp + i sinp = -1 + 0 = -1
k = 3
Z4 = cos+ i× mëkat
Përgjigje: Z 13 = 1
Z 24 = i
8. Përhapja dhe nxjerrja e rrënjës
Formula 6 tregon se ngritja e numrit kompleks r (cosj + i sinj ) te një fuqi numër i plotë pozitiv me një eksponent natyror, moduli i tij rritet në një fuqi me të njëjtin eksponent dhe argumenti shumëzohet me eksponentin.
[ r (cosj + i sinj )] n = r n (cos nj + i sin nj )
Numri Z thirrur rrënjë shkallë n nga numri w (i shënuar me ) nëse Z n =w .
Nga ky përkufizim del se çdo zgjidhje e ekuacionit Z n = wështë rrënja e shkallës n nga numri w. Me fjalë të tjera, për të nxjerrë rrënjën e shkallës n nga numri w mjafton të zgjidhet ekuacioni Z n =w. Nëse w =0, atëherë për çdo n ekuacioni Z n = w ka vetëm një zgjidhje Z= 0. Nëse w 0, atëherë Z0 , dhe, rrjedhimisht, Z dhe w mund të paraqiten në formë trigonometrike
Z = r (cosj + i sinj ), w = p (komod + i mëkatar)
Ekuacioni Z n = w do të marrë formën:
r n (cos nj + i sin nj ) = p (komod + i mëkatar)
Dy numra kompleksë janë të barabartë nëse dhe vetëm nëse moduli i tyre është i barabartë dhe argumentet e tyre ndryshojnë në terma që janë shumëfish të 2p. Prandaj, r n = p dhe nj = y + 2p k , ku kн Z ose r = dhe j= , ku kн Z.
Pra, të gjitha zgjidhjet mund të shkruhen si më poshtë:
Z K =, kн Z (8)
Formula 8 quhet Formula e dytë e De Moivre.
Kështu, nëse w 0, atëherë ka saktësisht n rrënjë të shkallës n nga numri w: të gjitha ato janë të përfshira në formulën 8. Të gjitha rrënjët e shkallës n nga numri w kanë të njëjtin modul, por argumente të ndryshëm që ndryshojnë në shumëfishin e numrit. Nga kjo rrjedh se numrat kompleks që janë rrënjë të shkallës n nga numri kompleks w korrespondojnë me pikat e rrafshit kompleks të vendosur në kulmet e një n-këndor të rregullt të brendashkruar në një rreth me rreze të përqendruar në pikën. Z = 0.
Simboli nuk ka një kuptim të qartë. Prandaj, kur e përdorni, duhet të kuptoni qartë se çfarë nënkuptohet me këtë simbol. Për shembull, duke përdorur shënimin , duhet të mendoni për ta bërë të qartë se ky simbol nënkupton një çift numrash kompleksë i Dhe -i , ose një, pastaj cili.
Ekuacionet e fuqive më të larta
Formula 8 përcakton të gjitha rrënjët e një ekuacioni me dy terma të shkallës n. Situata është pa masë më e ndërlikuar në rastin e një ekuacioni të përgjithshëm algjebrik të shkallës n:
a n × Z n+ a n–1× Z n–1 +...+ a 1× Z 1 + a 0 = 0(9)
Ku a n ,..., a 0 jepen numra kompleks.
Në kursin e matematikës së lartë, vërtetohet teorema e Gausit: çdo ekuacion algjebrik ka të paktën një rrënjë në bashkësinë e numrave kompleksë. Kjo teoremë u vërtetua nga matematikani gjerman Carl Gauss në 1779.
Bazuar në teoremën e Gausit, ne mund të vërtetojmë se ana e majtë e ekuacionit 9 mund të përfaqësohet gjithmonë si produkt:
,
Ku Z 1 , Z 2 ,..., Z K janë disa numra të ndryshëm kompleks,
dhe a 1 ,a 2 ,...,a k janë numra natyrorë dhe:
a 1 + a 2 + ... + a k = n
Kjo nënkupton që numrat Z 1 , Z 2 ,..., Z K janë rrënjët e ekuacionit 9. Në këtë rast, ata thonë se Z 1 është një rrënjë e shumëfishimit a 1 , Z 2 është një rrënjë e shumëfishimit a 2 dhe kështu me radhë.
Teorema e Gausit dhe teorema e sapoformuluar japin zgjidhje për ekzistencën e rrënjëve, por nuk thonë asgjë se si të gjenden këto rrënjë. Nëse rrënjët e shkallës së parë dhe të dytë mund të gjenden lehtësisht, atëherë për ekuacionet e fuqisë së tretë dhe të katërt formulat janë të rënda, dhe për ekuacionet e një shkalle më të lartë se e katërta formula të tilla nuk ekzistojnë fare. Mungesa e një metode të përgjithshme nuk pengon gjetjen e të gjitha rrënjëve të ekuacionit. Për të zgjidhur një ekuacion me koeficientë të plotë, teorema e mëposhtme është shpesh e dobishme: rrënjët me numra të plotë të çdo ekuacioni algjebrik me koeficientë të plotë janë pjesëtues të termit konstant.
Le të vërtetojmë këtë teoremë:
Le të jetë Z = k një rrënjë e plotë e ekuacionit
a n× Z n + a n–1× Z n–1 +...+ a 1× Z 1 + a 0 = 0
me koeficientë të plotë. Pastaj
a n× k n + a n–1× k n–1 +...+ a 1× k 1 + a 0 = 0
a 0 = – k(a n× k n–1 + a n–1× k n–2 +...+ a 1)
Numri në kllapa, sipas supozimeve të bëra, është padyshim një numër i plotë, që do të thotë se k është një pjesëtues i numrit a 0 .
9.EKUACION KUADRATIK ME NJË KOMPLEKS TË PANJOHUR
Konsideroni ekuacionin Z 2 = a, ku a është një numër real i dhënë, Z është një i panjohur.
Ky është ekuacioni:
Numrin a e shkruajmë në formën a = (– 1)× (– a) = i 2× = i 2× () 2 . Atëherë ekuacioni Z 2 = a do të shkruhet në formën: Z 2 - i 2×() 2 = 0
ato. (Z- i× )(Z + i× ) = 0
Prandaj, ekuacioni ka dy rrënjë: Z 1.2 = i×
Koncepti i paraqitur i një rrënjë nga një numër negativ na lejon të shkruajmë rrënjët e çdo ekuacioni kuadratik me koeficientë realë
a× Z 2 + b× Z + c = 0
Sipas formulës së përgjithshme të njohur
Z 1,2 = ![]() (10)
(10)
Pra, për çdo real a(a0), b, c, rrënjët e ekuacionit mund të gjenden me formulën 10. Për më tepër, nëse diskriminuesi, d.m.th. shprehje radikale në formulën 10
D \u003d b 2 - 4 × a × c
është pozitiv, atëherë ekuacioni a× Z 2 + b× Z + c = 0 ka dy rrënjë reale të dallueshme. Nëse D = 0, atëherë ekuacioni a × Z 2 + b × Z + c = 0 ka një rrënjë. Nëse D< 0, то уравнение a× Z 2 + b× Z + c = 0 имеет два различных комплексных корня.
Rrënjët komplekse të një ekuacioni kuadratik kanë të njëjtat veti si vetitë e njohura të rrënjëve reale.
Le të formulojmë ato kryesore:
Le të jenë Z 1 ,Z 2 rrënjët e ekuacionit kuadratik a× Z 2 + b× Z + c = 0, a0. Atëherë vetitë janë të vërteta:
Z 1× Z 2 =
- Për të gjithë kompleksin Z, formula
a × Z 2 + b × Z + c \u003d a × (Z - Z 1) × (Z - Z 2)
Shembulli 5:
Z 2 - 6 Z + 10 \u003d 0
D \u003d b 2 - 4 a c
D \u003d 6 2 - 4 10 \u003d - 4
– 4 = i 2 ·4
Z 1,2 = ![]()
Përgjigje: Z 1 \u003d Z 2 \u003d 3 + i
Shembulli 6:
3 Z 2 +2 Z + 1 = 0
D \u003d b 2 - 4 a c
D \u003d 4 - 12 \u003d - 8
D \u003d -1 8 \u003d 8 i 2
Z 1,2 = = 
Përgjigje: Z 1 \u003d Z 2 \u003d -
Shembulli 7:
Z 4 - 8 Z 2 - 9 = 0
t 2 - 8 t - 9 = 0
D \u003d b 2 - 4 a c \u003d 64 + 36 \u003d 100
t 1 \u003d 9 t 2 \u003d - 1
Z 2 \u003d 9 Z 2 \u003d - 1
Z 3,4 = i
Përgjigje: Z 1.2 \u003d 3, Z 3.4 \u003d i
Shembulli 8:
Z 4 + 2 Z 2 - 15 \u003d 0
t 2 + 2 t - 15 \u003d 0
D \u003d b 2 - 4 a c \u003d 4 + 60 \u003d 64
t 1,2 = = = –14
t 1 \u003d - 5 t 2 \u003d 3
Z 2 \u003d - 5 Z 2 \u003d 3
Z 2 \u003d - 1 5 Z 3.4 \u003d
Z2 = i 2 ·5
Z 1,2 = i
Përgjigje: Z 1,2 = i , Z 3,4 =
Shembulli 9:
Z 2 = 24 10 i
Le të jetë Z = X + Y i
(X + Y i ) 2 = X 2 + 2 X Y i Y2
X 2 + 2 X Y Y i Y 2 = 24 10 i
(X 2 Y 2) + 2 X Y i = 24 10 i
 shumëzo me X 2 0
shumëzo me X 2 0
X 4 - 24 X 2 - 25 = 0
t 2 - 24 t - 25 = 0
t 1 t 2 \u003d - 25
t 1 \u003d 25 t 2 \u003d - 1
X 2 \u003d 25 X 2 \u003d - 1 - nuk ka zgjidhje
X 1 \u003d 5 X 2 \u003d - 5
Y 1 = - Y 2 =
Y 1 = - 1 Y 2 = 1
Z 1,2 \u003d (5 - i )
Përgjigje: Z 1,2 \u003d (5 - i )
DETYRAT:
(2 - Y) 2 + 3 (2 - Y) Y + Y 2 = 6
4 - 4 Y + Y 2 + 6 Y - 3 Y 2 + Y 2 = 6
-Y 2 + 2Y - 2 \u003d 0 / -1
Y 2 - 2Y + 2 = 0
D \u003d b 2 - 4 a c \u003d 4 - 8 \u003d - 4
– 4 = – 1 4 = 4 i 2
Y 1,2 = = = 1 i
Y 1 = 1- i Y 2 \u003d 1 + i
X 1 = 1 + i X 2 \u003d 1– i
Përgjigje: (1 + i ; 1–i }
{1–i ; 1 + i }
Le ta sheshojmë
Nëse keni nevojë të emërtoni distancën midis dy qyteteve, atëherë mund të jepni një numër të vetëm në milje, kilometra ose njësi të tjera të distancës lineare. Sidoqoftë, nëse duhet të përshkruani se si të shkoni nga një qytet në tjetrin, atëherë duhet të jepni më shumë informacion sesa vetëm distancën midis dy pikave në hartë. Në këtë rast, ia vlen të thuhet për drejtimin në të cilin duhet të lëvizni dhe rreth.
Lloji i informacionit që shpreh një dimension njëdimensional quhet një sasi skalare në shkencë. Skalarët janë numra që përdoren në shumicën e llogaritjeve matematikore. Për shembull, masa dhe shpejtësia që zotëron një objekt janë sasi skalare.
Për të analizuar me sukses dukuritë natyrore, duhet të punojmë me objekte abstrakte dhe metoda të afta për të përfaqësuar madhësi shumëdimensionale. Këtu është e nevojshme të braktisni numrat skalorë në favor të atyre komplekse. Ato bëjnë të mundur shprehjen e dy dimensioneve njëkohësisht.
Numrat kompleksë kuptohen më lehtë kur paraqiten grafikisht. Nëse një rresht ka një gjatësi dhe drejtim të caktuar, atëherë kjo do të jetë një paraqitje grafike. Zakonisht njihet edhe si vektor.
Dallimet midis sasive komplekse dhe skalare
Llojet e tilla të numrave si numra të plotë, racionalë dhe realë janë të njohur për fëmijët nga shkolla. Të gjithë kanë një dimensionalitet. Drejtësia e vijës numerike e ilustron këtë grafikisht. Mund të lëvizni lart ose poshtë mbi të, por të gjitha "lëvizjet" përgjatë kësaj linje do të kufizohen në boshtin horizontal. Numrat njëdimensional, skalar janë të mjaftueshëm për të numëruar numrin e artikujve, për të shprehur peshën ose për të matur tensionin DC të një baterie. Por ato nuk mund të nënkuptojnë diçka më komplekse. Skalarët nuk mund të shprehin njëkohësisht distancën dhe drejtimin midis dy qyteteve, ose amplituda me fazën. Është e nevojshme që këto lloje numrash të përfaqësohen tashmë në formën e një diapazoni shumëdimensional vlerash. Me fjalë të tjera, ne kemi nevojë për sasi vektoriale që mund të kenë jo vetëm një madhësi, por edhe një drejtim të përhapjes.
konkluzioni
Një numër skalar është një lloj objekti matematikor që njerëzit janë mësuar ta përdorin në jetën e përditshme - është temperatura, gjatësia, pesha, etj. Një numër kompleks është një vlerë që përfshin dy lloje të dhënash.
Një vektor është një paraqitje grafike e një numri kompleks. Duket si një shigjetë me një pikënisje dhe një gjatësi dhe drejtim të përcaktuar. Ndonjëherë fjala "vektor" përdoret në inxhinierinë radio, ku shpreh zhvendosjen e fazës midis sinjaleve.
Gjatë studimit të vetive të një ekuacioni kuadratik, u vendos një kufizim - për një diskriminues më të vogël se zero, nuk ka zgjidhje. Menjëherë u përcaktua se bëhet fjalë për një grup numrash realë. Mendja kureshtare e një matematikani do të interesohet - cili është sekreti që përmban rezerva për vlerat reale?
Me kalimin e kohës, matematikanët prezantuan konceptin e numrave kompleksë, ku vlera e kushtëzuar e rrënjës së dytë të minus një merret si njësi.
Referencë historike
Teoria matematikore zhvillohet në mënyrë sekuenciale, nga e thjeshta në komplekse. Le të kuptojmë se si lindi koncepti i quajtur "numër kompleks" dhe pse është i nevojshëm.
Që nga kohra të lashta, baza e matematikës ka qenë llogaria e zakonshme. Studiuesit dinin vetëm grupin natyror të vlerave. Mbledhja dhe zbritja ishin të thjeshta. Ndërsa marrëdhëniet ekonomike u bënë më komplekse, shumëzimi filloi të përdoret në vend të shtimit të të njëjtave vlera. Kishte një operacion të anasjelltë të shumëzimit - pjesëtimit.
Koncepti i një numri natyror kufizoi përdorimin e veprimeve aritmetike. Është e pamundur të zgjidhen të gjitha problemet e ndarjes në grupin e vlerave të plota. çoi fillimisht në konceptin e kuptimeve racionale, dhe më pas në kuptimet irracionale. Nëse për racionalen është e mundur të tregohet vendndodhja e saktë e pikës në vijë, atëherë për irracionalen është e pamundur të tregohet një pikë e tillë. Ju mund të përafroni vetëm intervalin. Bashkimi i numrave racionalë dhe irracionalë formoi një grup real, i cili mund të përfaqësohet si një vijë e caktuar me një shkallë të caktuar. Çdo hap përgjatë vijës është një numër natyror, dhe midis tyre ka vlera racionale dhe irracionale.
Filloi epoka e matematikës teorike. Zhvillimi i astronomisë, mekanikës, fizikës kërkonte zgjidhjen e ekuacioneve gjithnjë e më komplekse. Në përgjithësi, rrënjët e ekuacionit kuadratik u gjetën. Kur zgjidhën një polinom kub më kompleks, shkencëtarët hasën në një kontradiktë. Koncepti i një rrënjë kubike nga një negativ ka kuptim, por për një rrënjë katrore, merret pasiguria. Për më tepër, ekuacioni kuadratik është vetëm një rast i veçantë i atij kubik.
Në vitin 1545, italiani J. Cardano propozoi prezantimin e konceptit të një numri imagjinar.
Ky numër ishte rrënja e dytë e minus një. Termi numër kompleks u formua përfundimisht vetëm treqind vjet më vonë, në veprat e matematikanit të famshëm Gauss. Ai propozoi zgjerimin zyrtar të të gjitha ligjeve të algjebrës në numrin imagjinar. Linja e vërtetë është zgjeruar në një aeroplan. Bota është bërë më e madhe.
Konceptet bazë
Kujtoni një numër funksionesh që kanë kufizime në grupin real:
- y = arcsin(x), e përcaktuar në rangun e vlerave midis asaj negative dhe pozitive.
- y = ln(x), ka kuptim për argumente pozitive.
- rrënja katrore y = √x, e llogaritur vetëm për x ≥ 0.
Duke treguar i = √(-1), ne prezantojmë një koncept të tillë si një numër imagjinar, kjo do të heqë të gjitha kufizimet nga fusha e përkufizimit të funksioneve të mësipërme. Shprehjet si y = arcsin(2), y = ln(-4), y = √(-5) kanë kuptim në një hapësirë të numrave kompleksë.
Forma algjebrike mund të shkruhet si shprehje z = x + i×y në bashkësinë e vlerave reale x dhe y, dhe i 2 = -1.
Koncepti i ri heq të gjitha kufizimet në përdorimin e çdo funksioni algjebrik dhe në pamjen e tij i ngjan një grafiku të një vije të drejtë në koordinatat e vlerave reale dhe imagjinare.
Aeroplan kompleks
Forma gjeometrike e numrave kompleks na lejon vizualisht të përfaqësojmë shumë nga vetitë e tyre. Në boshtin Re(z) shënojmë vlerat reale të x, në Im(z) - vlerat imagjinare të y, atëherë pika z në aeroplan do të shfaqë vlerën komplekse të kërkuar.

Përkufizimet:
- Re(z) - bosht real.
- Im(z) - nënkupton boshtin imagjinar.
- z është një pikë e kushtëzuar e një numri kompleks.
- Vlera numerike e gjatësisë së vektorit nga pika zero në z quhet modul.
- Boshti real dhe imagjinar e ndajnë rrafshin në katërshe. Me një vlerë pozitive të koordinatave - tremujori I. Kur argumenti i boshtit real është më i vogël se 0, dhe boshti imagjinar është më i madh se tremujori 0 - II. Kur koordinatat janë negative - tremujori III. Tremujori i fundit, i katërt përmban shumë vlera reale pozitive dhe vlera imagjinare negative.
Kështu, në një plan me vlera të koordinatave x dhe y, gjithmonë mund të vizualizohet një pikë e një numri kompleks. Simboli i futet për të ndarë pjesën reale nga ajo imagjinare.
Vetitë
- Kur vlera e argumentit imagjinar është zero, marrim vetëm një numër (z = x), i cili ndodhet në boshtin real dhe i përket grupit real.
- Në një rast të veçantë, kur vlera e argumentit real bëhet zero, shprehja z = i×y korrespondon me vendndodhjen e pikës në boshtin imagjinar.
- Forma e përgjithshme z = x + i×y do të jetë për vlera jo zero të argumenteve. Do të thotë vendndodhjen e pikës që karakterizon numrin kompleks në një nga lagjet.
shënim trigonometrik
Kujtoni sistemin e koordinatave polar dhe përkufizimin e sin dhe cos. Është e qartë se me ndihmën e këtyre funksioneve është e mundur të përshkruhet vendndodhja e çdo pike në aeroplan. Për ta bërë këtë, mjafton të dihet gjatësia e rrezes polare dhe këndi i prirjes ndaj boshtit real.
Përkufizimi. Një hyrje e formës ∣z ∣ e shumëzuar me shumën e funksioneve trigonometrike cos(ϴ) dhe pjesës imagjinare i ×sin(ϴ) quhet numër kompleks trigonometrik. Këtu përcaktimi është këndi i prirjes ndaj boshtit real
ϴ = arg(z), dhe r = ∣z∣, gjatësia e traut.
Nga përkufizimi dhe vetitë e funksioneve trigonometrike, vijon formula shumë e rëndësishme De Moivre:
z n = r n × (cos(n × ϴ) + i × sin(n × ϴ)).
Duke përdorur këtë formulë, është e përshtatshme për të zgjidhur shumë sisteme ekuacionesh që përmbajnë funksione trigonometrike. Sidomos kur lind detyra e fuqizimit.
Moduli dhe faza
Për të përfunduar përshkrimin e një grupi kompleks, ne propozojmë dy përkufizime të rëndësishme.
Duke ditur teoremën e Pitagorës, është e lehtë të llogaritet gjatësia e rrezes në sistemin e koordinatave polar.
r = ∣z∣ = √(x 2 + y 2), një shënim i tillë në hapësirën komplekse quhet "modul" dhe karakterizon distancën nga 0 në një pikë në plan.
Këndi i prirjes së rrezes komplekse ndaj vijës reale ϴ zakonisht quhet faza.
Nga përkufizimi mund të shihet se pjesët reale dhe imagjinare përshkruhen duke përdorur funksione ciklike. Gjegjësisht:
- x = r × cos(ϴ);
- y = r × sin(ϴ);
Në të kundërt, faza lidhet me vlerat algjebrike përmes formulës:
ϴ = arctan(x / y) + μ, korrigjimi μ futet për të marrë parasysh periodicitetin e funksioneve gjeometrike.
Formula e Euler-it
Matematikanët shpesh përdorin formën eksponenciale. Numrat e planit kompleks shkruhen si shprehje
z = r × e i × ϴ , që rrjedh nga formula e Euler-it.

Një regjistrim i tillë është bërë i përhapur për llogaritjen praktike të sasive fizike. Forma e paraqitjes në formën e numrave komplekse eksponenciale është veçanërisht e përshtatshme për llogaritjet inxhinierike, ku bëhet e nevojshme llogaritja e qarqeve me rryma sinusoidale dhe është e nevojshme të dihet vlera e integraleve të funksioneve me një periudhë të caktuar. Llogaritjet në vetvete shërbejnë si një mjet në projektimin e makinave dhe mekanizmave të ndryshëm.
Përcaktimi i Operacioneve
Siç u përmend tashmë, të gjitha ligjet algjebrike të punës me funksionet themelore matematikore zbatohen për numrat kompleks.
operacion shuma
Gjatë shtimit të vlerave komplekse shtohen edhe pjesët reale dhe imagjinare të tyre.
z = z 1 + z 2 , ku z 1 dhe z 2 janë numra kompleks të përgjithshëm. Duke transformuar shprehjen, pas hapjes së kllapave dhe thjeshtimit të shënimit, marrim argumentin real x \u003d (x 1 + x 2), argumentin imagjinar y \u003d (y 1 + y 2).
Në grafik, kjo duket si shtimi i dy vektorëve, sipas rregullit të mirënjohur të paralelogramit.

operacioni i zbritjes
Konsiderohet si një rast i veçantë i mbledhjes, kur një numër është pozitiv, tjetri është negativ, pra ndodhet në tremujorin e pasqyrës. Shënimi algjebrik duket si ndryshimi midis pjesëve reale dhe imagjinare.
z \u003d z 1 - z 2, ose, duke marrë parasysh vlerat e argumenteve, në mënyrë të ngjashme me operacionin e mbledhjes, marrim për vlerat reale x \u003d (x 1 - x 2) dhe imagjinare y \u003d (y 1 - y 2).
Shumëzimi në rrafshin kompleks
Duke përdorur rregullat për punën me polinome, nxjerrim një formulë për zgjidhjen e numrave kompleksë.
Duke ndjekur rregullat e përgjithshme algjebrike z=z 1 ×z 2 , ne përshkruajmë çdo argument dhe japim të ngjashëm. Pjesët reale dhe imagjinare mund të shkruhen si më poshtë:
- x \u003d x 1 × x 2 - y 1 × y 2,
- y = x 1 × y 2 + x 2 × y 1.
Duket më bukur nëse përdorim numra kompleksë eksponencialë.
Shprehja duket kështu: z = z 1 × z 2 = r 1 × e i ϴ 1 × r 2 × e i ϴ 2 = r 1 × r 2 × e i(ϴ 1+ ϴ 2) .
Divizioni
Kur e konsiderojmë veprimin e pjesëtimit si të kundërt të veprimit të shumëzimit, marrim një shprehje të thjeshtë në formë eksponenciale. Pjestimi i vlerës së z 1 me z 2 është rezultat i ndarjes së moduleve të tyre dhe diferencës së fazës. Formalisht, kur përdorni formën eksponenciale të numrave kompleksë, duket kështu:
z \u003d z 1 / z 2 \u003d r 1 × e i ϴ 1 / r 2 × e i ϴ 2 \u003d r 1 / r 2 × e i (ϴ 1- ϴ 2) .
Në formën e shënimit algjebrik, operacioni i pjesëtimit të numrave të planit kompleks është shkruar pak më i ndërlikuar:
Duke shkruar argumentet dhe duke kryer transformime polinomiale, është e lehtë të merren vlerat x \u003d x 1 × x 2 + y 1 × y 2, përkatësisht, y \u003d x 2 × y 1 - x 1 × y 2, megjithatë, brenda hapësirës së përshkruar, kjo shprehje ka kuptim, nëse z 2 ≠ 0.
Ne nxjerrim rrënjën
Të gjitha sa më sipër mund të zbatohen në përkufizimin e funksioneve më komplekse algjebrike - ngritja në çdo fuqi dhe anasjelltas me të - nxjerrja e rrënjës.
Duke përdorur konceptin e përgjithshëm të ngritjes në fuqinë n, marrim përkufizimin:
z n = (r × e i ϴ) n .
Duke përdorur vetitë e zakonshme, ne mund ta rishkruajmë atë në formën:
z n = r n × e i ϴ n .
Ne morëm një formulë të thjeshtë për ngritjen e një numri kompleks në një fuqi.
Nga përkufizimi i gradës marrim një pasojë shumë të rëndësishme. Një fuqi çift i njësisë imagjinare është gjithmonë 1. Çdo fuqi teke e njësisë imagjinare është gjithmonë -1.
Tani le të studiojmë funksionin e anasjelltë - nxjerrjen e rrënjës.
Për thjeshtësi të shënimit, marrim n = 2. Rrënja katrore w e vlerës komplekse z në planin kompleks C zakonisht konsiderohet të jetë shprehja z = ±, e cila është e vlefshme për çdo argument real më të madh ose të barabartë me zero. Për w ≤ 0, nuk ka zgjidhje.
Le të shohim ekuacionin kuadratik më të thjeshtë z 2 = 1. Duke përdorur formulat e numrave kompleksë, rishkruajmë r 2 × e i 2ϴ = r 2 × e i 2ϴ = e i 0 . Mund të shihet nga regjistrimi se r 2 = 1 dhe ϴ = 0, pra, kemi një zgjidhje unike të barabartë me 1. Por kjo bie ndesh me konceptin që z = -1, gjithashtu korrespondon me përkufizimin e një rrënjë katrore.
Le të kuptojmë se çfarë nuk marrim parasysh. Nëse kujtojmë shënimin trigonometrik, atëherë rivendosim deklaratën - me një ndryshim periodik në fazën ϴ, numri kompleks nuk ndryshon. Le të tregojmë p vlerën e periudhës, atëherë kemi r 2 × e i 2ϴ = e i (0+ p) , prej nga 2ϴ = 0 + p, ose ϴ = p / 2. Prandaj, kemi e i 0 = 1 dhe e i p / 2 = -1. Ne morëm zgjidhjen e dytë, e cila korrespondon me kuptimin e përgjithshëm të rrënjës katrore.
Pra, për të gjetur një rrënjë arbitrare të një numri kompleks, ne do të ndjekim procedurën.
- Shkruajmë formën eksponenciale w= ∣w∣ × e i (arg (w) + pk) , k është një numër i plotë arbitrar.
- Numri i dëshiruar mund të paraqitet edhe në formën e Euler-it z = r × e i ϴ .
- Le të përdorim përkufizimin e përgjithshëm të funksionit të nxjerrjes së rrënjës r n *e i n ϴ = ∣w∣ × e i (arg (w) + pk) .
- Nga vetitë e përgjithshme të barazisë së moduleve dhe argumenteve, shkruajmë r n = ∣w∣ dhe nϴ = arg (w) + p×k.
- Regjistrimi përfundimtar i rrënjës së një numri kompleks përshkruhet me formulën z = √∣w∣ × e i (arg (w) + pk) / n .
- Komentoni. Vlera ∣w∣ është, sipas përkufizimit, një numër real pozitiv, kështu që çdo rrënjë e fuqisë ka kuptim.
Fusha dhe konjugimi
Si përfundim, japim dy përkufizime të rëndësishme, të cilat kanë pak rëndësi për zgjidhjen e problemeve të aplikuara me numra komplekse, por janë thelbësore në zhvillimin e mëtejshëm të teorisë matematikore.
Shprehjet për mbledhje dhe shumëzim thuhet se formojnë një fushë nëse plotësojnë aksiomat për çdo element të planit kompleks z:
- Nga një ndryshim në vendet e termave komplekse, shuma komplekse nuk ndryshon.
- Deklarata është e vërtetë - në një shprehje komplekse, çdo shumë e dy numrave mund të zëvendësohet nga vlera e tyre.
- Ekziston një vlerë neutrale 0 për të cilën z + 0 = 0 + z = z është e vërtetë.
- Për çdo z ka një të kundërt - z, mbledhja e së cilës jep zero.
- Kur ndryshohen vendet e faktorëve kompleks, produkti kompleks nuk ndryshon.
- Shumëzimi i çdo dy numrash mund të zëvendësohet me vlerën e tyre.
- Ekziston një vlerë neutrale 1, shumëzimi me të cilin nuk ndryshon numrin kompleks.
- Për çdo z ≠ 0, ka një reciproke prej z -1 që, kur shumëzohet, rezulton në 1.
- Shumëzimi i shumës së dy numrave me një të tretën është i barabartë me shumëzimin e secilit prej tyre me atë numër dhe mbledhjen e rezultateve.
- 0 ≠ 1.
Numrat z 1 = x + i×y dhe z 2 = x - i×y quhen të konjuguar.
Teorema. Për konjugimin, deklarata është e vërtetë:
- Lidhja e shumës është e barabartë me shumën e elementeve të konjuguar.
- Lidhja e një produkti është e barabartë me produktin e konjugimeve.
- e barabartë me vetë numrin.
Në algjebrën e përgjithshme, veti të tilla quhen automorfizma fushore.

Shembuj
Duke ndjekur rregullat dhe formulat e mësipërme për numrat kompleks, mund t'i përdorni lehtësisht ato.
Le të shqyrtojmë shembujt më të thjeshtë.
Detyra 1. Duke përdorur ekuacionin 3y +5 x i= 15 - 7i, përcaktoni x dhe y.
Zgjidhje. Kujtoni përkufizimin e barazive komplekse, pastaj 3y = 15, 5x = -7. Prandaj, x = -7 / 5, y = 5.
Detyra 2. Llogaritni vlerat 2 + i 28 dhe 1 + i 135.
Zgjidhje. Natyrisht, 28 është një numër çift, nga pasoja e përcaktimit të një numri kompleks në fuqi, kemi i 28 = 1, që do të thotë se shprehja është 2 + i 28 = 3. Vlera e dytë, i 135 = - 1, pastaj 1 + i 135 = 0.
Detyra 3. Llogaritni prodhimin e vlerave 2 + 5i dhe 4 + 3i.
Zgjidhje. Nga vetitë e përgjithshme të shumëzimit të numrave kompleks fitojmë (2 + 5i)X(4 + 3i) = 8 - 15 + i(6 + 20). Vlera e re do të jetë -7 + 26i.
Detyra 4. Njehsoni rrënjët e ekuacionit z 3 = -i.
Zgjidhje. Ka disa mënyra për të gjetur një numër kompleks. Le të shqyrtojmë një nga të mundshmet. Sipas përkufizimit, ∣ - i∣ = 1, faza për -i është -p / 4. Ekuacioni origjinal mund të rishkruhet si r 3 *e i 3ϴ = e - p/4+ pk , prej nga z = e - p / 12 + pk /3 , për çdo numër të plotë k.
Bashkësia e tretësirave ka formën (e - ip/12 , e ip /4 , e i 2 p/3).
Pse duhen numra kompleksë
Historia njeh shumë shembuj kur shkencëtarët, duke punuar në një teori, as që mendojnë për zbatimin praktik të rezultateve të tyre. Matematika është, para së gjithash, një lojë e mendjes, një respektim i rreptë i marrëdhënieve shkak-pasojë. Pothuajse të gjitha ndërtimet matematikore reduktohen në zgjidhjen e ekuacioneve integrale dhe diferenciale, dhe ato, nga ana tjetër, me njëfarë përafrimi, zgjidhen duke gjetur rrënjët e polinomeve. Këtu së pari ndeshemi me paradoksin e numrave imagjinarë.

Shkencëtarët e natyrës, duke zgjidhur probleme plotësisht praktike, duke iu drejtuar zgjidhjeve të ekuacioneve të ndryshme, zbulojnë paradokse matematikore. Interpretimi i këtyre paradokseve çon në zbulime absolutisht të mahnitshme. Natyra e dyfishtë e valëve elektromagnetike është një shembull i tillë. Numrat kompleks luajnë një rol vendimtar në kuptimin e vetive të tyre.
Kjo, nga ana tjetër, ka gjetur zbatim praktik në optikë, radio elektronike, energji dhe shumë fusha të tjera teknologjike. Një shembull tjetër, shumë më i vështirë për t'u kuptuar fenomenet fizike. Antimateria ishte parashikuar në majë të një stilolapsi. Dhe vetëm pas shumë vitesh fillojnë përpjekjet për ta sintetizuar atë fizikisht.

Nuk duhet menduar se situata të tilla ekzistojnë vetëm në fizikë. Jo më pak zbulime interesante bëhen në jetën e egër, në sintezën e makromolekulave, gjatë studimit të inteligjencës artificiale. Dhe e gjithë kjo është për shkak të zgjerimit të vetëdijes sonë, duke shmangur mbledhjen dhe zbritjen e thjeshtë të vlerave natyrore.
SubjektiNumrat kompleksë dhe polinomet
Ligjërata 22
§1. Numrat kompleksë: përkufizimet bazë
Simboli  futni raportin
futni raportin  dhe quhet njësi imagjinare. Me fjale te tjera,
dhe quhet njësi imagjinare. Me fjale te tjera,  .
.
Përkufizimi.
Shprehja e formës  , Ku
, Ku  , quhet numër kompleks dhe numri
, quhet numër kompleks dhe numri  quhet pjesa reale e një numri kompleks
quhet pjesa reale e një numri kompleks  dhe shënojnë
dhe shënojnë  , numri
, numri  - pjesa imagjinare
- pjesa imagjinare  dhe shënojnë
dhe shënojnë  .
.
Nga ky përkufizim del se numra realë janë ata numra kompleksë pjesa imagjinare e të cilëve është e barabartë me zero.
Është i përshtatshëm për të paraqitur numrat kompleksë si pika të një rrafshi në të cilin është dhënë një sistem koordinativ drejtkëndor kartezian, domethënë: një numër kompleks  pikë ndeshjeje
pikë ndeshjeje  dhe anasjelltas. në bosht
dhe anasjelltas. në bosht  shfaqen numra realë dhe quhet bosht real. Numrat kompleks të formularit
shfaqen numra realë dhe quhet bosht real. Numrat kompleks të formularit 
 quhen thjesht imagjinare. Ato tregohen si pika në bosht.
quhen thjesht imagjinare. Ato tregohen si pika në bosht.  , i cili quhet bosht imagjinar. Ky rrafsh, i cili shërben për paraqitjen e numrave kompleksë, quhet plan kompleks. Një numër kompleks që nuk është real, d.m.th. sikurse
, i cili quhet bosht imagjinar. Ky rrafsh, i cili shërben për paraqitjen e numrave kompleksë, quhet plan kompleks. Një numër kompleks që nuk është real, d.m.th. sikurse  , nganjëherë quhet imagjinare.
, nganjëherë quhet imagjinare.
Dy numra kompleksë thuhet se janë të barabartë nëse dhe vetëm nëse kanë të njëjtat pjesë reale dhe imagjinare.
Mbledhja, zbritja dhe shumëzimi i numrave kompleksë kryhen sipas rregullave të zakonshme të algjebrës polinomiale, duke marrë parasysh faktin se 
 . Operacioni i ndarjes mund të përkufizohet si inversi i operacionit të shumëzimit dhe mund të vërtetohet unike e rezultatit (nëse pjesëtuesi është i ndryshëm nga zero). Sidoqoftë, në praktikë, përdoret një qasje e ndryshme.
. Operacioni i ndarjes mund të përkufizohet si inversi i operacionit të shumëzimit dhe mund të vërtetohet unike e rezultatit (nëse pjesëtuesi është i ndryshëm nga zero). Sidoqoftë, në praktikë, përdoret një qasje e ndryshme.
Numrat kompleks  Dhe
Dhe  quhen të konjuguara, në rrafshin kompleks ato përfaqësohen me pika simetrike rreth boshtit real. Është e qartë se:
quhen të konjuguara, në rrafshin kompleks ato përfaqësohen me pika simetrike rreth boshtit real. Është e qartë se:
1)

 ;
;
2)
 ;
;
3)
 .
.
Tani ndahu  në
në  mund të bëhet si më poshtë:
mund të bëhet si më poshtë:
 .
.
Nuk është e vështirë ta tregosh këtë
 ,
,
ku simbol  do të thotë çdo veprim aritmetik.
do të thotë çdo veprim aritmetik.
Le  ndonjë numër imagjinar dhe
ndonjë numër imagjinar dhe  është një variabël real. Prodhimi i dy binomeve
është një variabël real. Prodhimi i dy binomeve
është një trinom katror me koeficientë realë.
Tani, duke pasur numra kompleksë në dispozicion, ne mund të zgjidhim çdo ekuacion kuadratik  .Nese atehere
.Nese atehere
dhe ekuacioni ka dy rrënjë komplekse të konjuguara
 .
.
Nëse  , atëherë ekuacioni ka dy rrënjë reale të ndryshme. Nëse
, atëherë ekuacioni ka dy rrënjë reale të ndryshme. Nëse  , atëherë ekuacioni ka dy rrënjë identike.
, atëherë ekuacioni ka dy rrënjë identike.
§2. Forma trigonometrike e një numri kompleks
Siç u përmend më lart, numri kompleks  i përshtatshëm për t'u paraqitur me një pikë
i përshtatshëm për t'u paraqitur me një pikë  . Një numër i tillë mund të identifikohet edhe me vektorin e rrezes së kësaj pike
. Një numër i tillë mund të identifikohet edhe me vektorin e rrezes së kësaj pike  . Me këtë interpretim, mbledhja dhe zbritja e numrave kompleks kryhet sipas rregullave të mbledhjes dhe zbritjes së vektorëve. Për shumëzimin dhe ndarjen e numrave kompleks, një formë tjetër është më e përshtatshme.
. Me këtë interpretim, mbledhja dhe zbritja e numrave kompleks kryhet sipas rregullave të mbledhjes dhe zbritjes së vektorëve. Për shumëzimin dhe ndarjen e numrave kompleks, një formë tjetër është më e përshtatshme.
Ne prezantojmë në planin kompleks  sistemi i koordinatave polar. Pastaj ku
sistemi i koordinatave polar. Pastaj ku  ,
, dhe numri kompleks
dhe numri kompleks  mund të shkruhet si:
mund të shkruhet si:
Kjo formë shënimi quhet trigonometrike (në ndryshim nga forma algjebrike  ). Në këtë formë, numri
). Në këtë formë, numri  quhet modul dhe
quhet modul dhe  - argumenti i numrit kompleks
- argumenti i numrit kompleks  . Ato janë shënuar:
. Ato janë shënuar:  ,
,
 . Për modulin, ne kemi formulën
. Për modulin, ne kemi formulën 

Argumenti i numrit përcaktohet në mënyrë të paqartë, por deri në një term  ,
, . Vlera e argumentit që plotëson pabarazitë
. Vlera e argumentit që plotëson pabarazitë  , quhet kryesor dhe shënohet
, quhet kryesor dhe shënohet  . Pastaj,
. Pastaj,  . Për vlerën kryesore të argumentit, mund të merrni shprehjet e mëposhtme:
. Për vlerën kryesore të argumentit, mund të merrni shprehjet e mëposhtme:
 ,
,
argumenti i numrit  konsiderohet të jetë e papërcaktuar.
konsiderohet të jetë e papërcaktuar.
Kushti për barazinë e dy numrave kompleks në formë trigonometrike ka formën: modulet e numrave janë të barabartë dhe argumentet ndryshojnë me një shumëfish.  .
.
Gjeni prodhimin e dy numrave kompleks në formë trigonometrike:
Pra, kur shumëzohen numrat, modulet e tyre shumëzohen dhe argumentet shtohen.
Në mënyrë të ngjashme, mund të konstatohet se gjatë pjesëtimit, modulet e numrave ndahen dhe argumentet zbriten.
Duke e kuptuar fuqinë si shumëzim të shumëfishtë, mund të marrim formulën për ngritjen e një numri kompleks në një fuqi:
Ne nxjerrim një formulë për  - rrënjë
- rrënjë  fuqia e një numri kompleks
fuqia e një numri kompleks  (të mos ngatërrohet me rrënjën aritmetike të një numri real!). Operacioni i nxjerrjes së rrënjës është i anasjellta e operacionit të fuqizimit. Kjo është arsyeja pse
(të mos ngatërrohet me rrënjën aritmetike të një numri real!). Operacioni i nxjerrjes së rrënjës është i anasjellta e operacionit të fuqizimit. Kjo është arsyeja pse  është një numër kompleks
është një numër kompleks  sikurse
sikurse  .
.
Le  i njohur, dhe
i njohur, dhe  kërkohet të gjendet. Pastaj
kërkohet të gjendet. Pastaj
Nga barazia e dy numrave kompleksë në formë trigonometrike, rezulton se
 ,
,
 ,
, .
.
Nga këtu  (është një rrënjë aritmetike!),
(është një rrënjë aritmetike!),
 ,
,
 .
.
Është e lehtë ta verifikosh këtë  vetëm mund të pranojë
vetëm mund të pranojë  vlera thelbësisht të ndryshme, për shembull, kur
vlera thelbësisht të ndryshme, për shembull, kur  . Në fund kemi formulën:
. Në fund kemi formulën:
,
 .
.
Pra, rrënja  shkalla e th nga një numër kompleks ka
shkalla e th nga një numër kompleks ka  vlera të ndryshme. Në planin kompleks, këto vlera janë të vendosura saktë në kulmet
vlera të ndryshme. Në planin kompleks, këto vlera janë të vendosura saktë në kulmet  -gon i gdhendur në një rreth me rreze
-gon i gdhendur në një rreth me rreze  me qendër në origjinë. Rrënja "e parë" ka një argument
me qendër në origjinë. Rrënja "e parë" ka një argument  , argumentet e dy rrënjëve “fqinj” ndryshojnë nga
, argumentet e dy rrënjëve “fqinj” ndryshojnë nga  .
.
Shembull.
Le të marrim rrënjën kubike të njësisë imagjinare:  ,
, ,
, . Pastaj:
. Pastaj:

 ,
,
§1. Numrat kompleks
1°. Përkufizimi. Shënim algjebrik.
Përkufizimi 1.
Numrat kompleks quhen çifte të renditura numrash realë  Dhe
Dhe  , nëse për to përcaktohet koncepti i barazisë, veprimet e mbledhjes dhe shumëzimit që plotësojnë aksiomat e mëposhtme:
, nëse për to përcaktohet koncepti i barazisë, veprimet e mbledhjes dhe shumëzimit që plotësojnë aksiomat e mëposhtme:
1) Dy numra  Dhe
Dhe  e barabartë nëse dhe vetëm nëse
e barabartë nëse dhe vetëm nëse  ,
,
 , d.m.th.
, d.m.th.
|
|
2) Shuma e numrave kompleks  Dhe
Dhe 
 dhe të barabartë
dhe të barabartë  , d.m.th.
, d.m.th.
|
|
3) Prodhimi i numrave kompleks  Dhe
Dhe  thirret numri
thirret numri  dhe e barabartë me , d.m.th.
dhe e barabartë me , d.m.th.
|
|
Shënohet bashkësia e numrave kompleksë C.

Formulat (2), (3) për numrat e formës  marrin formën
marrin formën
prej nga rezulton se veprimet e mbledhjes dhe shumëzimit për numrat e formës  përkojnë me mbledhjen dhe shumëzimin për numrat realë një numër kompleks të formës
përkojnë me mbledhjen dhe shumëzimin për numrat realë një numër kompleks të formës  identifikohet me një numër real
identifikohet me një numër real  .
.
Numri kompleks  thirrur njësi imagjinare dhe shënohet
thirrur njësi imagjinare dhe shënohet  , d.m.th.
, d.m.th.  Pastaj nga (3)
Pastaj nga (3)
Nga (2),(3) që do të thotë
|
|
Shprehja (4) quhet shënim algjebrik numër kompleks.
Në formën algjebrike, veprimet e mbledhjes dhe shumëzimit marrin formën:
Shënohet numri kompleks  ,
,

 - pjesa reale,
- pjesa reale,  është pjesa imagjinare,
është pjesa imagjinare,  është një numër thjesht imagjinar. Përcaktimi:
është një numër thjesht imagjinar. Përcaktimi:  ,
,
 .
.
Përkufizimi 2. Numri kompleks  thirrur konjuguar me një numër kompleks
thirrur konjuguar me një numër kompleks  .
.
Vetitë e konjugimit kompleks.
1)
2)
 .
.
3) Nëse  , Kjo
, Kjo  .
.
4)
 .
.
5)
 është një numër real.
është një numër real.
Vërtetimi kryhet me llogaritje të drejtpërdrejtë.
Përkufizimi 3. Numri  thirrur modul numër kompleks
thirrur modul numër kompleks  dhe shënohet
dhe shënohet  .
.
Është e qartë se  , dhe
, dhe 

 . Formulat janë gjithashtu të dukshme:
. Formulat janë gjithashtu të dukshme:  Dhe
Dhe  .
.
2°. Vetitë e veprimeve të mbledhjes dhe shumëzimit.
1) Komutativiteti:  ,
,
 .
.
2) Asociacioni:,  .
.
3) Shpërndarja: .
Vërtetimi 1) - 3) kryhet me llogaritje të drejtpërdrejta bazuar në vetitë e ngjashme për numrat realë.
4)
 ,
,
 .
.
5)

 ,
,

 C
C
 !
!
 , duke përmbushur ekuacionin
, duke përmbushur ekuacionin  . Të tillë
. Të tillë
6)

 ,
,
 C,
C,

 0,
0,
 !
!
 :
:
 . Të tillë
. Të tillë  gjendet duke shumëzuar ekuacionin me
gjendet duke shumëzuar ekuacionin me 



 .
.
Shembull.
Imagjinoni një numër kompleks  në formë algjebrike. Për ta bërë këtë, shumëzoni numëruesin dhe emëruesin e thyesës me konjugatin e emëruesit. Ne kemi:
në formë algjebrike. Për ta bërë këtë, shumëzoni numëruesin dhe emëruesin e thyesës me konjugatin e emëruesit. Ne kemi:
3 °. Interpretimi gjeometrik i numrave kompleks. Forma trigonometrike dhe eksponenciale e shkrimit të një numri kompleks.
°. Interpretimi gjeometrik i numrave kompleks. Forma trigonometrike dhe eksponenciale e shkrimit të një numri kompleks.
Le të jepet një sistem koordinativ drejtkëndor në rrafsh. Pastaj 

 C mund të lidhet një pikë në rrafsh me koordinata
C mund të lidhet një pikë në rrafsh me koordinata  .(shih Fig. 1). Është e qartë se një korrespondencë e tillë është një me një. Në këtë rast, numrat realë qëndrojnë në boshtin e abshisave, dhe numrat thjesht imagjinarë shtrihen në boshtin e ordinatave. Prandaj, boshti i abshisave quhet bosht real, dhe boshti y − bosht imagjinar. Rrafshi në të cilin shtrihen numrat kompleks quhet plan kompleks.
.(shih Fig. 1). Është e qartë se një korrespondencë e tillë është një me një. Në këtë rast, numrat realë qëndrojnë në boshtin e abshisave, dhe numrat thjesht imagjinarë shtrihen në boshtin e ordinatave. Prandaj, boshti i abshisave quhet bosht real, dhe boshti y − bosht imagjinar. Rrafshi në të cilin shtrihen numrat kompleks quhet plan kompleks.
Vini re se  Dhe
Dhe  janë simetrike për origjinën, dhe
janë simetrike për origjinën, dhe  Dhe
Dhe  janë simetrike në lidhje me Ox.
janë simetrike në lidhje me Ox.
Çdo numër kompleks (d.m.th., çdo pikë në rrafsh) mund të shoqërohet me një vektor me fillimin në pikën O dhe fundin në pikën  . Korrespondenca midis vektorëve dhe numrave kompleks është një me një. Prandaj, vektori që korrespondon me numrin kompleks
. Korrespondenca midis vektorëve dhe numrave kompleks është një me një. Prandaj, vektori që korrespondon me numrin kompleks  , e shënuar me të njëjtën shkronjë
, e shënuar me të njëjtën shkronjë 
D  linjë vektoriale
linjë vektoriale  që korrespondon me numrin kompleks
që korrespondon me numrin kompleks  , është e barabartë me
, është e barabartë me  , dhe
, dhe  ,
,
 .
.
Duke përdorur interpretimin e vektorit, mund të shihet se vektori  − shuma e vektorëve
− shuma e vektorëve  Dhe
Dhe  , A
, A  − shuma e vektorëve
− shuma e vektorëve  Dhe
Dhe  .(shih Fig. 2). Prandaj, pabarazitë e mëposhtme janë të vërteta:
.(shih Fig. 2). Prandaj, pabarazitë e mëposhtme janë të vërteta:
Së bashku me gjatësinë  vektoriale
vektoriale  prezantojmë këndin
prezantojmë këndin  ndërmjet vektorit
ndërmjet vektorit  dhe boshti Ox, i numëruar nga drejtimi pozitiv i boshtit Ox: nëse numërimi është kundër akrepave të orës, atëherë shenja e këndit konsiderohet pozitive, nëse në drejtim të akrepave të orës, atëherë negative. Ky kënd quhet argumenti i numrit kompleks dhe shënohet
dhe boshti Ox, i numëruar nga drejtimi pozitiv i boshtit Ox: nëse numërimi është kundër akrepave të orës, atëherë shenja e këndit konsiderohet pozitive, nëse në drejtim të akrepave të orës, atëherë negative. Ky kënd quhet argumenti i numrit kompleks dhe shënohet  . Këndi
. Këndi  nuk është përcaktuar në mënyrë unike, por me saktësi
nuk është përcaktuar në mënyrë unike, por me saktësi  …. Për
…. Për  argumenti nuk është i përcaktuar.
argumenti nuk është i përcaktuar.
Formulat (6) përcaktojnë të ashtuquajturat shënim trigonometrik numër kompleks.
Nga (5) del se nëse  Dhe
Dhe  Se
Se
|
|
Nga (5)  me çfarë
me çfarë  Dhe
Dhe  Një numër kompleks është i përcaktuar në mënyrë unike. E kundërta nuk është e vërtetë: domethënë, nga numri kompleks
Një numër kompleks është i përcaktuar në mënyrë unike. E kundërta nuk është e vërtetë: domethënë, nga numri kompleks  modulin e tij
modulin e tij  është unike, dhe argumenti
është unike, dhe argumenti  , për shkak të (7), − me saktësi
, për shkak të (7), − me saktësi  . Nga (7) rezulton gjithashtu se argumenti
. Nga (7) rezulton gjithashtu se argumenti  mund të gjendet si zgjidhje e ekuacionit
mund të gjendet si zgjidhje e ekuacionit

Megjithatë, jo të gjitha zgjidhjet e këtij ekuacioni janë zgjidhje të (7).
Ndër të gjitha vlerat e argumentit të një numri kompleks, zgjidhet një, i cili quhet vlera kryesore e argumentit dhe shënohet  . Zakonisht vlera kryesore e argumentit zgjidhet ose në interval
. Zakonisht vlera kryesore e argumentit zgjidhet ose në interval  , ose në interval
, ose në interval 
Në formë trigonometrike, është i përshtatshëm për të kryer operacione të shumëzimit dhe ndarjes.
Teorema 1. Moduli i prodhimit të numrave kompleks  Dhe
Dhe  është i barabartë me produktin e moduleve, dhe argumenti është i barabartë me shumën e argumenteve, d.m.th.
është i barabartë me produktin e moduleve, dhe argumenti është i barabartë me shumën e argumenteve, d.m.th.
 , A .
, A .
Në mënyrë të ngjashme
 ,
,

Dëshmi. Le , . Pastaj me shumëzim të drejtpërdrejtë marrim:
Në mënyrë të ngjashme
 .■
.■
Pasoja(Formula e De Moivre). Për  Formula e Moivre është e vlefshme
Formula e Moivre është e vlefshme
P  shembull.
Le të gjejë vendndodhjen gjeometrike të pikës
shembull.
Le të gjejë vendndodhjen gjeometrike të pikës  . Nga teorema 1 rezulton se .
. Nga teorema 1 rezulton se .
Prandaj, për ta ndërtuar atë, së pari duhet të ndërtoni një pikë  , e cila është e anasjellta
, e cila është e anasjellta  rreth njësisë rrethore dhe më pas gjeni një pikë simetrike me të rreth boshtit x.
rreth njësisë rrethore dhe më pas gjeni një pikë simetrike me të rreth boshtit x.
Le  , d.m.th.
, d.m.th.  Numri kompleks
Numri kompleks  shënohet
shënohet  , d.m.th.
, d.m.th. 

 R formula Euler është e vlefshme
R formula Euler është e vlefshme
|
|
Sepse  , Kjo
, Kjo  ,
,
 . Nga teorema 1
. Nga teorema 1  po në lidhje me funksionin
po në lidhje me funksionin  është e mundur të punohet si me një funksion të zakonshëm eksponencial, d.m.th. barazitë janë të vërteta
është e mundur të punohet si me një funksion të zakonshëm eksponencial, d.m.th. barazitë janë të vërteta
 ,
,
 ,
,
 .
.
Nga (8)  shënimi eksponencial numër kompleks
shënimi eksponencial numër kompleks
 , Ku
, Ku  ,
,

Shembull. .
4°. Rrënjët  fuqia e një numri kompleks.
fuqia e një numri kompleks.
Merrni parasysh ekuacionin
|
|
Le  , dhe zgjidhja e barazimit (9) kërkohet në formën
, dhe zgjidhja e barazimit (9) kërkohet në formën  . Pastaj (9) merr formën
. Pastaj (9) merr formën  , prej nga e gjejmë atë
, prej nga e gjejmë atë  ,
,
 , d.m.th.
, d.m.th.
 ,
,
 ,
,
 .
.
Kështu, ekuacioni (9) ka rrënjë
|
|
Le të tregojmë se midis (10) ka saktësisht  rrënjë të ndryshme. Vërtet,
rrënjë të ndryshme. Vërtet, 
 janë të ndryshme, sepse argumentet e tyre janë të ndryshme dhe ndryshojnë më pak se
janë të ndryshme, sepse argumentet e tyre janë të ndryshme dhe ndryshojnë më pak se  . Me tutje,
. Me tutje,  , sepse
, sepse  . Në mënyrë të ngjashme
. Në mënyrë të ngjashme  .
.
Kështu, ekuacioni (9) për  ka pikërisht
ka pikërisht  rrënjët
rrënjët  të vendosura në kulmet e një të rregullti
të vendosura në kulmet e një të rregullti  -gon i gdhendur në një rreth me rreze
-gon i gdhendur në një rreth me rreze  me qendër T.O.
me qendër T.O.
Kështu, është vërtetuar

Teorema 2. nxjerrja e rrënjës  fuqia e një numri kompleks
fuqia e një numri kompleks  gjithmonë e mundur. Të gjitha vlerat rrënjësore
gjithmonë e mundur. Të gjitha vlerat rrënjësore  shkalla e
shkalla e  ndodhet në krye të saktë
ndodhet në krye të saktë  -gon i gdhendur në një rreth me qendër në zero dhe rreze
-gon i gdhendur në një rreth me qendër në zero dhe rreze  . Ku,
. Ku,
Pasoja. Rrënjët  -shkalla e 1 shprehet me formulën
-shkalla e 1 shprehet me formulën
 .
.
Prodhimi i dy rrënjëve të 1 është një rrënjë, 1 është një rrënjë  -shkalla e unitetit,
-shkalla e unitetit,  rrënjë
rrënjë 

 :
:
 .
.

 ,
,
 .
.
 +
+ =
= .
. ∙=.
∙=.
 ,
,
 .
.
 ,
,
 ME
,
ME
,
 N
.
N
.
 ,
,
 .
.