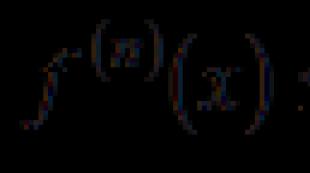Artizanatit

Ekuacioni i një rrafshi është distanca nga një pikë në një plan. Distanca nga një pikë në një aeroplan. mënyrë. Metoda vektoriale

Ruajtja e privatësisë suaj është e rëndësishme për ne. Për këtë arsye, ne kemi zhvilluar një politikë të privatësisë që përshkruan se si ne përdorim dhe ruajmë informacionin tuaj. Ju lutemi rishikoni praktikat tona të privatësisë dhe na tregoni nëse keni ndonjë pyetje.

Mbledhja dhe përdorimi i informacionit personal

Informacioni personal i referohet të dhënave që mund të përdoren për të identifikuar ose kontaktuar një person specifik.

Mund t'ju kërkohet të jepni informacionin tuaj personal në çdo kohë kur na kontaktoni.

Më poshtë janë disa shembuj të llojeve të informacionit personal që mund të mbledhim dhe se si mund ta përdorim këtë informacion.

Çfarë informacioni personal mbledhim:

Kur dorëzoni një aplikim në sajt, ne mund të mbledhim informacione të ndryshme, duke përfshirë emrin tuaj, numrin e telefonit, adresën e emailit, etj.

Si i përdorim të dhënat tuaja personale:

Informacioni personal që mbledhim na lejon t'ju kontaktojmë me oferta unike, promovime dhe ngjarje të tjera dhe ngjarje të ardhshme.
Herë pas here, ne mund të përdorim të dhënat tuaja personale për të dërguar njoftime dhe komunikime të rëndësishme.
Ne gjithashtu mund të përdorim të dhënat personale për qëllime të brendshme, si kryerja e auditimeve, analizave të të dhënave dhe kërkimeve të ndryshme, me qëllim që të përmirësojmë shërbimet që ofrojmë dhe t'ju ofrojmë rekomandime në lidhje me shërbimet tona.
Nëse merrni pjesë në një tërheqje çmimesh, konkurs ose promovim të ngjashëm, ne mund të përdorim informacionin që ju jepni për të administruar programe të tilla.

Zbulimi i informacionit palëve të treta

Ne nuk ua zbulojmë informacionin e marrë nga ju palëve të treta.

Përjashtimet:

Nëse është e nevojshme - në përputhje me ligjin, procedurën gjyqësore, në procedurat ligjore dhe/ose në bazë të kërkesave publike ose kërkesave nga organet qeveritare në Federatën Ruse - për të zbuluar informacionin tuaj personal. Ne gjithashtu mund të zbulojmë informacione për ju nëse përcaktojmë se një zbulim i tillë është i nevojshëm ose i përshtatshëm për qëllime sigurie, zbatimi të ligjit ose qëllime të tjera me rëndësi publike.
Në rast të një riorganizimi, bashkimi ose shitjeje, ne mund t'i transferojmë informacionet personale që mbledhim te pala e tretë pasardhëse e aplikueshme.

Mbrojtja e informacionit personal

Ne marrim masa paraprake - duke përfshirë administrative, teknike dhe fizike - për të mbrojtur informacionin tuaj personal nga humbja, vjedhja dhe keqpërdorimi, si dhe qasja, zbulimi, ndryshimi dhe shkatërrimi i paautorizuar.

Respektimi i privatësisë suaj në nivel kompanie

Për t'u siguruar që informacioni juaj personal është i sigurt, ne i komunikojmë punonjësve tanë standardet e privatësisë dhe sigurisë dhe zbatojmë në mënyrë rigoroze praktikat e privatësisë.

Përcaktimi i distancës ndërmjet: 1 - pikës dhe planit; 2 - i drejtë dhe i sheshtë; 3 - aeroplanë; 4 - kalimi i drejtëzave konsiderohen së bashku, pasi algoritmi i zgjidhjes për të gjitha këto probleme është në thelb i njëjtë dhe përbëhet nga konstruksione gjeometrike që duhet të kryhen për të përcaktuar distancën midis një pike të caktuar A dhe planit α. Nëse ka ndonjë ndryshim, ai konsiston vetëm në faktin se në rastet 2 dhe 3, përpara se të filloni të zgjidhni problemin, duhet të shënoni një pikë arbitrare A në vijën e drejtë m (rasti 2) ose rrafshin β (rasti 3). distancat ndërmjet vijave të kryqëzimit, fillimisht i mbyllim në plane paralele α dhe β dhe më pas përcaktojmë distancën ndërmjet këtyre rrafsheve.

Le të shqyrtojmë secilin nga rastet e përmendura të zgjidhjes së problemit.

1. Përcaktimi i distancës ndërmjet një pike dhe një rrafshi.

Distanca nga një pikë në një plan përcaktohet nga gjatësia e një segmenti pingul të tërhequr nga një pikë në plan.

Prandaj, zgjidhja e këtij problemi konsiston në kryerjen e njëpasnjëshme të operacioneve grafike të mëposhtme:

1) nga pika A e ulim pingulen me rrafshin α (Fig. 269);

2) gjeni pikën M të prerjes së kësaj pingule me rrafshin M = a ∩ α;

3) përcaktoni gjatësinë e segmentit.

Nëse rrafshi α është në pozicionin e përgjithshëm, atëherë për të ulur një pingul në këtë rrafsh, është e nevojshme që së pari të përcaktohet drejtimi i projeksioneve horizontale dhe ballore të këtij rrafshi. Gjetja e pikës së takimit të kësaj pingule me rrafshin kërkon edhe ndërtime gjeometrike shtesë.

Zgjidhja e problemit thjeshtohet nëse rrafshi α zë një pozicion të veçantë në raport me rrafshet e projeksionit. Në këtë rast si projeksioni i pingules ashtu edhe gjetja e pikës së takimit të saj me rrafshin kryhen pa asnjë ndërtim ndihmës shtesë.

SHEMBULL 1. Përcaktoni distancën nga pika A në rrafshin e projektimit ballor α (Fig. 270).

ZGJIDHJE. Nëpërmjet A" vizatojmë projeksionin horizontal të l" ⊥ h 0α, dhe përmes A" - projeksionin e tij ballor l" ⊥ f 0α. Shënojmë pikën M" = l" ∩ f 0α . Që nga AM || π 2, pastaj [A" M"] == |AM| = d.

Nga shembulli i konsideruar, është e qartë se sa thjesht zgjidhet problemi kur avioni zë një pozicion projektues. Prandaj, nëse një plan i përgjithshëm i pozicionit është specifikuar në të dhënat e burimit, atëherë përpara se të vazhdohet me zgjidhjen, rrafshi duhet të zhvendoset në një pozicion pingul me çdo plan projeksioni.

SHEMBULL 2. Përcaktoni distancën nga pika K deri në rrafshin e specifikuar nga ΔАВС (Fig. 271).

1. Transferojmë rrafshin ΔАВС në pozicionin e projektimit *. Për ta bërë këtë, ne kalojmë nga sistemi xπ 2 /π 1 në x 1 π 3 /π 1: drejtimi i boshtit të ri x 1 zgjidhet pingul me projeksionin horizontal të planit horizontal të trekëndëshit.

2. Projektoni ΔABC në një plan të ri π 3 (aeroplani ΔABC është projektuar në π 3, në [ C " 1 B " 1 ]).

3. Projektoni pikën K në të njëjtin rrafsh (K" → K" 1).

4. Nëpër pikën K" 1 vizatojmë (K" 1 M" 1)⊥ segmentin [C" 1 B" 1]. Distanca e kërkuar d = |K" 1 M" 1 |

Zgjidhja e problemit thjeshtohet nëse rrafshi përcaktohet me gjurmë, pasi nuk ka nevojë të vizatohen projeksione të linjave të nivelit.

SHEMBULL 3. Përcaktoni distancën nga pika K në rrafshin α, të specifikuar nga gjurmët (Fig. 272).

* Mënyra më racionale për të transferuar rrafshin e trekëndëshit në pozicionin e projektimit është zëvendësimi i rrafsheve të projeksionit, pasi në këtë rast mjafton të ndërtohet vetëm një projeksion ndihmës.

ZGJIDHJE. Zëvendësojmë rrafshin π 1 me rrafshin π 3, për këtë vizatojmë një bosht të ri x 1 ⊥ f 0α. Në h 0α shënojmë një pikë arbitrare 1" dhe përcaktojmë projeksionin e saj të ri horizontal në rrafshin π 3 (1" 1). Nëpër pikat X α 1 (X α 1 = h 0α 1 ∩ x 1) dhe 1" 1 vizatojmë h 0α 1. Përcaktojmë projeksionin e ri horizontal të pikës K → K" 1. Nga pika K" 1 e ulim pingulen me h 0α 1 dhe shënojmë pikën e kryqëzimit të saj me h 0α 1 - M" 1. Gjatësia e segmentit K" 1 M" 1 do të tregojë distancën e kërkuar.

2. Përcaktimi i distancës ndërmjet vijës së drejtë dhe rrafshit.

Distanca ndërmjet një vije dhe një rrafshi përcaktohet nga gjatësia e një segmenti pingul të rënë nga një pikë arbitrare në vijë në rrafsh (shih Fig. 248).

Prandaj, zgjidhja e problemit të përcaktimit të distancës ndërmjet drejtëzës m dhe planit α nuk ndryshon nga shembujt e diskutuar në paragrafin 1 për përcaktimin e distancës midis një pike dhe një rrafshi (shih Fig. 270 ... 272). Si pikë, mund të merrni çdo pikë që i përket rreshtit m.

3. Përcaktimi i distancës ndërmjet planeve.

Distanca midis planeve përcaktohet nga madhësia e segmentit pingul të rënë nga një pikë e marrë në një rrafsh në një plan tjetër.

Nga ky përkufizim del se algoritmi për zgjidhjen e problemit të gjetjes së distancës ndërmjet rrafsheve α dhe β ndryshon nga një algoritëm i ngjashëm për zgjidhjen e problemit të përcaktimit të distancës ndërmjet drejtëzës m dhe planit α vetëm në atë drejtëzë m duhet t'i përkasë rrafshit α. , d.m.th., për të përcaktuar distancën midis planeve α dhe β, vijon:

1) merr një vijë të drejtë m në rrafshin α;

2) zgjidhni një pikë arbitrare A në rreshtin m;

3) nga pika A, ulni pingulën l në rrafshin β;

4) caktoni pikën M - pikën e takimit të pingules l me rrafshin β;

5) përcaktoni madhësinë e segmentit.

Në praktikë, këshillohet përdorimi i një algoritmi të ndryshëm zgjidhjeje, i cili do të ndryshojë nga ai i dhënë vetëm në atë që, përpara se të vazhdohet me hapin e parë, aeroplanët duhet të transferohen në pozicionin e projeksionit.

Përfshirja e këtij operacioni shtesë në algoritëm thjeshton ekzekutimin e të gjitha pikave të tjera pa përjashtim, gjë që përfundimisht çon në një zgjidhje më të thjeshtë.

SHEMBULL 1. Përcaktoni distancën midis planeve α dhe β (Fig. 273).

ZGJIDHJE. Ne lëvizim nga sistemi xπ 2 /π 1 në x 1 π 1 / π 3. Në lidhje me rrafshin e ri π 3, rrafshet α dhe β zënë një pozicion të projektuar, prandaj distanca ndërmjet gjurmëve të reja ballore f 0α 1 dhe f 0β 1 është ajo e dëshiruara.

Në praktikën inxhinierike, shpesh është e nevojshme të zgjidhet problemi i ndërtimit të një rrafshi paralel me një plan të caktuar dhe largimit prej tij në një distancë të caktuar. Shembulli 2 më poshtë ilustron zgjidhjen e një problemi të tillë.

SHEMBULL 2. Kërkohet ndërtimi i projeksioneve të një rrafshi β paralel me një rrafsh të caktuar α (m || n), nëse dihet se distanca ndërmjet tyre është d (Fig. 274).

1. Në rrafshin α, vizatoni vija arbitrare horizontale h (1, 3) dhe vijat e përparme f (1,2).

2. Nga pika 1 rivendosim pingulën l në rrafshin α(l" ⊥ h", l" ⊥ f").

3. Në pingulën l shënojmë një pikë arbitrare A.

4. Përcaktoni gjatësinë e segmentit - (pozicioni tregon në diagram drejtimin metrikisht të pashtrembëruar të drejtëzës l).

5. Vendosni segmentin = d në vijën e drejtë (1"A 0) nga pika 1".

6. Shënoni në projeksionet l" dhe l" pikat B" dhe B", që korrespondojnë me pikën B 0.

7. Nëpër pikën B vizatojmë rrafshin β (h 1 ∩ f 1). Te β || α, është e nevojshme të respektohet kushti h 1 || h dhe f 1 || f.

4. Përcaktimi i distancës ndërmjet drejtëzave të kryqëzuara.

Distanca ndërmjet drejtëzave të kryqëzuara përcaktohet nga gjatësia e pingules që gjendet ndërmjet rrafsheve paralele të cilave u përkasin vijat e kryqëzuara.

Për të tërhequr rrafshet paralele të ndërsjellë α dhe β përmes drejtëzave të kryqëzuara m dhe f, mjafton të vizatoni përmes pikës A (A ∈ m) një drejtëz p paralele me drejtëzën f dhe përmes pikës B (B ∈ f) një drejtëz k paralele me të drejtën m . Drejtëzat ndërprerëse m dhe p, f dhe k përcaktojnë rrafshet paralele reciproke α dhe β (shih Fig. 248, e). Distanca ndërmjet rrafsheve α dhe β është e barabartë me distancën e kërkuar ndërmjet vijave të kryqëzimit m dhe f.

Një mënyrë tjetër mund të propozohet për përcaktimin e distancës midis vijave kryqëzuese, e cila konsiston në faktin se, duke përdorur një metodë të transformimit të projeksioneve ortogonale, njëra nga linjat kryqëzuese transferohet në pozicionin e projektimit. Në këtë rast, një projeksion i vijës degjeneron në një pikë. Distanca midis projeksioneve të reja të vijave të kryqëzimit (pika A" 2 dhe segmenti C" 2 D" 2) është ajo e kërkuar.

Në Fig. 275 tregon një zgjidhje për problemin e përcaktimit të distancës midis vijave të kryqëzimit a dhe b, duke dhënë segmentet [AB] dhe [CD]. Zgjidhja kryhet në sekuencën e mëposhtme:

1. Transferoni një nga vijat e kryqëzimit (a) në një pozicion paralel me rrafshin π 3; Për ta bërë këtë, lëvizni nga sistemi i planeve të projeksionit xπ 2 / π 1 në x 1 π 1 / π 3 të ri, boshti x 1 është paralel me projeksionin horizontal të vijës së drejtë a. Përcaktoni a" 1 [A" 1 B" 1 ] dhe b" 1.

2. Duke zëvendësuar rrafshin π 1 me rrafshin π 4, përkthejmë vijën e drejtë.

dhe në pozicionin a" 2, pingul me rrafshin π 4 (boshti i ri x 2 është tërhequr pingul me a" 1).

3. Ndërtoni një projeksion të ri horizontal të drejtëzës b" 2 - [ C" 2 D" 2 ].

4. Distanca nga pika A" 2 në vijën e drejtë C" 2 D" 2 (segmenti (A" 2 M" 2 ] (është ajo e kërkuara.

Duhet pasur parasysh se kalimi i njërës prej vijave të kryqëzimit në pozicionin e projektimit nuk është gjë tjetër veçse kalimi i rrafsheve të paralelizmit, në të cilin mund të mbyllen drejtëzat a dhe b, edhe në pozicionin e projektimit.

Në fakt, duke lëvizur drejtëzën a në një pozicion pingul me rrafshin π 4, ne sigurojmë që çdo plan që përmban drejtëzën a është pingul me rrafshin π 4, duke përfshirë rrafshin α të përcaktuar nga drejtëzat a dhe m (a ∩ m, m | | b). Nëse tani vizatojmë një drejtëzë n, paralele me a dhe drejtëzën e prerë b, atëherë fitojmë rrafshin β, i cili është rrafshi i dytë i paralelizmit, i cili përmban drejtëzat e prera a dhe b. Që β || α, pastaj β ⊥ π 4 .

Gjetja e distancës nga një pikë në një rrafsh është një problem i zakonshëm që lind kur zgjidhen probleme të ndryshme të gjeometrisë analitike; për shembull, ky problem mund të reduktohet në gjetjen e distancës midis dy drejtëzave të kryqëzuara ose midis një drejteje dhe një rrafshi paralel me atë.

Konsideroni rrafshin $β$ dhe një pikë $M_0$ me koordinata $(x_0;y_0; z_0)$ që nuk i përket rrafshit $β$.

Përkufizimi 1

Distanca më e shkurtër midis një pike dhe një rrafshi do të jetë pingulja e tërhequr nga pika $M_0$ në rrafshin $β$.

Figura 1. Distanca nga një pikë në një plan. Autor24 - shkëmbim online i punimeve të studentëve

Më poshtë do të diskutojmë se si të gjejmë distancën nga një pikë në një plan duke përdorur metodën e koordinatave.

Nxjerrja e formulës për metodën e koordinatave për gjetjen e distancës nga një pikë në një plan në hapësirë

Një pingul nga pika $M_0$ që pret rrafshin $β$ në pikën $M_1$ me koordinatat $(x_1;y_1; z_1)$ shtrihet në një vijë të drejtë, vektori i drejtimit të së cilës është vektori normal i rrafshit $β$. Në këtë rast, gjatësia e vektorit njësi $n$ është e barabartë me një. Prandaj, distanca nga $β$ në pikën $M_0$ do të jetë:

$ρ= |\vec(n) \cdot \vec(M_1M_0)|\left(1\djathtas)$, ku $\vec(M_1M_0)$ është vektori normal i planit $β$ dhe $\vec( n)$ është vektori normal njësi i rrafshit në shqyrtim.

Në rastin kur ekuacioni i rrafshit jepet në formën e përgjithshme $Ax+ By + Cz + D=0$, koordinatat e vektorit normal të planit janë koeficientët e ekuacionit $\(A;B;C\ )$, dhe vektori normal i njësisë në këtë rast ka koordinatat , të llogaritura duke përdorur ekuacionin e mëposhtëm:

$\vec(n)= \frac($A;B;C$)(\sqrt(A^2 + B^2 + C^2))\majtas(2\djathtas)$.

Tani mund të gjejmë koordinatat e vektorit normal $\vec(M_1M_0)$:

$\vec(M_0M_1)= $x_0 – x_1;y_0-y_1;z_0-z_1$\majtas(3\djathtas)$.

Ne shprehim gjithashtu koeficientin $D$ duke përdorur koordinatat e një pike që shtrihet në rrafshin $β$:

$D= Ax_1+By_1+Cz_1$

Koordinatat e vektorit normal të njësisë nga barazia $(2)$ mund të zëvendësohen në ekuacionin e planit $β$, atëherë kemi:

$ρ= \frac(|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|)(\sqrt(A^2+B^2+C^2))= \frac( |Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|)(\sqrt(A^2+B^2+C^2)) = \frac(Ax_0+ By_0 + Cz_0 + D)(\sqrt(A^2 +B^2+C^2))\majtas(4\djathtas)$

Barazia $(4)$ është një formulë për gjetjen e distancës nga një pikë në një plan në hapësirë.

Algoritmi i përgjithshëm për gjetjen e distancës nga pika $M_0$ në një plan

Nëse ekuacioni i aeroplanit nuk është dhënë në formë të përgjithshme, së pari duhet ta reduktoni në formën e përgjithshme.
Pas kësaj, është e nevojshme të shprehim nga ekuacioni i përgjithshëm i planit vektorin normal të një rrafshi të caktuar përmes pikës $M_0$ dhe një pike që i përket një rrafshi të caktuar, për këtë duhet të përdorim barazinë $(3)$ .
Faza tjetër është kërkimi i koordinatave të vektorit normal të njësisë së avionit duke përdorur formulën $(2)$.
Më në fund, mund të filloni të gjeni distancën nga pika në rrafsh, kjo bëhet duke llogaritur produktin skalar të vektorëve $\vec(n)$ dhe $\vec(M_1M_0)$.

Kushtet e paralelizmit dhe pingulitetit

1°. Kushti për bashkëplanaritetin e dy rrafsheve

Le të jepen dy plane:

A 1 x + B 1 y + C 1 z + D 1 = 0, n 1 = {A 1 ; B 1 ; C 1 } ≠ 0 ;(1)

A 2 x + B 2 y + C 2 z + D 2 = 0, n 2 = {A 2 ; B 2 ; C 2 } ≠ 0 .(2)

Kur janë ato koplanare (d.m.th. paralele apo të rastësishme)? Natyrisht, ky do të jetë rasti nëse dhe vetëm nëse vektorët e tyre normalë janë kolinearë. Duke zbatuar kriterin e koplanaritetit, marrim

Fjalia 1. Dy rrafshe janë koplanare nëse dhe vetëm nëse prodhimi kryq i vektorëve të tyre normal është i barabartë me vektorin zero:

[n 1 , n 2 ] = 0 .

2°. Kushti për koincidencën e dy planeve

Propozimi 2. Planet (1) dhe (2) përkojnë nëse dhe vetëm nëse të katër koeficientët e tyre janë proporcionalë, d.m.th., ekziston një numër λ i tillë që

A 2 = λ A 1 , B 2 = λ B 1 , C 2 = λ C 1 , D 2 = λ D 1 . (3)

Dëshmi. Le të plotësohen kushtet (3). Atëherë ekuacioni i planit të dytë mund të shkruhet si më poshtë:

λ A 1 x + λ B 1 y + λ C 1 z + λ D 1 = 0.

λ ≠ 0, përndryshe do të ishte A 2 = B 2 = C 2 = D 2 = 0, që bie ndesh me kushtin n 2 ≠ 0 . Prandaj, ekuacioni i fundit është ekuivalent me ekuacionin (1), që do të thotë se dy rrafshet përkojnë.

Le të dimë tani, përkundrazi, se këta avionë përkojnë. Atëherë vektorët e tyre normalë janë kolinearë, pra ekziston një numër λ i tillë që

A 2 = λ A 1 , B 2 = λ B 1 , C 2 = λ C 1 .

Ekuacioni (2) tani mund të rishkruhet si:

λ A 1 x + λ B 1 y + λ C 1 z + D 2 = 0.

Duke shumëzuar ekuacionin (1) me λ, marrim një ekuacion ekuivalent të planit të parë (pasi λ ≠ 0):

λ A 1 x + λ B 1 y + λ C 1 z + λ D 1 = 0.

Le të marrim një pikë ( x 0 , y 0 , z 0) nga rrafshi i parë (dhe rrjedhimisht i dyti) dhe zëvendësoni koordinatat e tij në dy ekuacionet e fundit; marrim barazitë e sakta:

λ A 1 x 0 + λ B 1 y 0 + λ C 1 z 0 + D 2 = 0 ;

λ A 1 x 0 + λ B 1 y 0 + λ C 1 z 0 + λ D 1 = 0.

Duke zbritur pjesën e poshtme nga e sipërmja, marrim D 2 − λ D 1 = 0, d.m.th. D 2 = λ D 1, QED.

3°. Kushti për pingulësinë e dy rrafsheve

Natyrisht, për këtë është e nevojshme dhe e mjaftueshme që vektorët normalë të jenë pingul.

Propozimi 3. Dy plane janë pingul nëse dhe vetëm nëse produkti skalar i vektorëve normalë është zero:

(n 1 , n 2) = 0 .

Le të jepet ekuacioni i rrafshët

Sëpatë + Nga + Cz + D = 0, n = {A; B; C} ≠ 0 ,

dhe periudha M 0 = (x 0 , y 0 , z 0). Le të nxjerrim formulën për distancën nga një pikë në një plan:

Le të marrim një pikë arbitrare P = (x 1 , y 1 , z 1), i shtrirë në këtë aeroplan. Koordinatat e tij plotësojnë ekuacionin e rrafshët:

Sëpatë 1 + Nga 1 + Cz 1 + D = 0.

Le të vërejmë tani se distanca e kërkuar d e barabartë me vlerën absolute të projeksionit vektorial në drejtim të vektorit n (këtu projeksionin e marrim si madhësi numerike dhe jo si vektor). Më pas, ne aplikojmë formulën për të llogaritur projeksionin:

Një formulë e ngjashme është e vlefshme për distancën d nga pika M 0 = (x 0 , y 0) plani në një drejtëz të dhënë nga ekuacioni i përgjithshëm Sëpatë + Nga + C = 0.

Le të ketë një aeroplan . Le të vizatojmë një normale
përmes origjinës së koordinatave O. Le të jepet
– këndet e formuara nga normalja me boshte koordinative.
. Le – gjatësia e segmentit normal
derisa të kryqëzohet me rrafshin. Duke supozuar se dihen kosinuset e drejtimit të normales , nxjerrim ekuacionin e rrafshit .

Le
) është një pikë arbitrare në rrafsh. Vektori normal i njësisë ka koordinata. Le të gjejmë projeksionin e vektorit
në normale.

Që nga pika M i takon aeroplanit, pra

Ky është ekuacioni i një rrafshi të caktuar, i quajtur normale .

Largësia nga pika në aeroplan

Le të jepet një aeroplan ,M*
- pikë në hapësirë, d – largësia e tij nga avioni.

Përkufizimi. Devijimi pikë M* nga avioni quhet numri ( + d), Nëse M* shtrihet në anën tjetër të rrafshit ku tregon drejtimi pozitiv i normales , dhe numri (- d), nëse pika ndodhet në anën tjetër të aeroplanit:

Teorema. Lëreni aeroplanin me njësi normale jepet nga ekuacioni normal:

Le M*
– pika në hapësirë Devijimi t. M* nga rrafshi jepet me shprehjen

Dëshmi. Projeksioni t.
* shënojmë me normale P. Devijimi i pikës M* nga avioni është i barabartë

Rregulli. Per te gjetur devijimi T. M* nga rrafshi, ju duhet të zëvendësoni koordinatat t në ekuacionin normal të planit. M* . Distanca nga një pikë në një aeroplan është .

Reduktimi i ekuacionit të planit të përgjithshëm në formë normale

Le të përkufizohet i njëjti rrafsh nga dy ekuacione:

Ekuacioni i përgjithshëm

Ekuacioni normal.

Meqenëse të dy ekuacionet përcaktojnë të njëjtin plan, koeficientët e tyre janë proporcional:

Le të vendosim në katror tre barazitë e para dhe t'i mbledhim ato:

Nga këtu do të gjejmë – faktori normalizues:

. (10)

Duke shumëzuar ekuacionin e përgjithshëm të rrafshit me një faktor normalizues, marrim ekuacionin normal të rrafshit:

Shembuj të problemeve në temën "Aeroplan".

Shembulli 1. Krijo një ekuacion të aeroplanit duke kaluar nëpër një pikë të caktuar
(2,1,-1) dhe paralel me rrafshin.

Zgjidhje. Normal për aeroplan :
. Meqenëse aeroplanët janë paralelë, atëherë ato normale është gjithashtu normale me planin e dëshiruar . Duke përdorur ekuacionin e një rrafshi që kalon nëpër një pikë të caktuar (3), marrim për rrafshin ekuacioni:

Përgjigje:

Shembulli 2. Baza e një pingule ka rënë nga origjina në një plan , është pika
. Gjeni ekuacionin e rrafshit .

Zgjidhje. Vektor
është normale për aeroplanin . Pika M 0 i përket aeroplanit. Ju mund të përdorni ekuacionin e një rrafshi që kalon nëpër një pikë të caktuar (3):

Përgjigje:

Shembulli 3. Ndërtoni aeroplan , duke kaluar nëpër pika

dhe pingul me rrafshin :.

Prandaj, për një moment M (x, y, z) i përkiste aeroplanit , është e nevojshme që tre vektorë
ishin të përbashkëta:

=0.

Mbetet për të zbuluar përcaktorin dhe për ta sjellë shprehjen që rezulton në formën e ekuacionit të përgjithshëm (1).

Shembulli 4. Aeroplan jepet nga ekuacioni i përgjithshëm:

Gjeni devijimin e pikës
nga një aeroplan i caktuar.

Zgjidhje. Le ta sjellim ekuacionin e rrafshit në formën normale.

Le të zëvendësojmë koordinatat e pikës në ekuacionin normal që rezulton M*.

Përgjigje:
.

Shembulli 5. A e pret rrafshi segmentin?

Zgjidhje. Te presesh AB kaloi aeroplanin, devijimet Dhe nga avioni duhet të ketë shenja të ndryshme:

Shembulli 6. Kryqëzimi i tre planeve në një pikë.

Sistemi ka një zgjidhje unike, prandaj, të tre planet kanë një pikë të përbashkët.

Shembulli 7. Gjetja e përgjysmuesve të një këndi dykëndor të formuar nga dy rrafshe të dhëna.

Le Dhe - devijimi i një pike
nga rrafshi i parë dhe i dytë.

Në njërin nga rrafshet përgjysmuese (që korrespondon me këndin në të cilin shtrihet origjina e koordinatave) këto devijime janë të barabarta në madhësi dhe shenjë, dhe në anën tjetër ato janë të barabarta në madhësi dhe të kundërta në shenjë.

Ky është ekuacioni i rrafshit të parë përgjysmues.

Ky është ekuacioni i rrafshit të dytë përgjysmues.

Shembulli 8. Përcaktimi i vendndodhjes së dy pikave të dhëna Dhe në raport me këndet dihedrale të formuara nga këto rrafshe.