Математик анализ.

Семинар.

Их дээд сургуулийн оюутнуудад зориулсан мэргэжлээр:

"Төрийн болон хотын захиргаа"

Т.З. Павлова

Колпашево 2008 он

1-р бүлэг Шинжилгээний танилцуулга

1.1 Функцүүд. Ерөнхий шинж чанарууд

1.2 Хязгаарын онол

1.3 Функцийн тасралтгүй байдал

2.1 Деривативын тодорхойлолт

2.4 Функцуудыг судлах

2.4.1 Бүрэн үйл ажиллагааны судалгааны төлөвлөгөө

2.4.2 Функц судлалын жишээ

2.4.3. Сегмент дээрх функцийн хамгийн том ба хамгийн бага утга

2.5 L'Hospital-ийн дүрэм

3.1 Тодорхой бус интеграл

3.1.1 Тодорхойлолт ба шинж чанарууд

3.1.2 Интегралын хүснэгт

3.1.3 Интеграцийн үндсэн аргууд

3.2 Тодорхой интеграл

3.2.2 Тодорхой интегралыг тооцоолох арга

4-р бүлэг

4.1 Үндсэн ойлголтууд

4.2 Хэд хэдэн хувьсагчийн функцүүдийн хязгаар ба тасралтгүй байдал

4.3.3 Нийт дифференциал ба түүнийг ойролцоо тооцоололд хэрэглэх

5-р бүлэг

6.1 Хэрэглээний функц.

6.2 хайхрамжгүй байдлын шугам

6.3 Төсвийн багц

Гэрийн даалгавар

1.1 Функцүүд. Ерөнхий шинж чанарууд

Хэрэв хувьсагчийн утга бүр нь y хувьсагчийн тодорхой тодорхойлогдсон бодит утгатай холбоотой байвал тоон функцийг бодит тоонуудын D олонлог дээр тодорхойлно, энд D нь функцийн муж болно.

Функцийн аналитик дүрслэл:

тодорхой: ;

далд: ;

параметрийн хэлбэрээр:

Тодорхойлолт дахь өөр өөр томъёонууд:

Үл хөдлөх хөрөнгө.

Тэгш функц: . Жишээлбэл, функц нь тэгш, учир нь .

Хачирхалтай функц: . Жишээлбэл, функц нь сондгой, учир нь .

Тогтмол функц: , энд T нь функцийн үе, . Жишээлбэл, тригонометрийн функцууд.

монотон функц. Тодорхойлолтын аль нэг домэйны хувьд функц нь нэмэгдэж байгаа бол - буурч байна. Жишээлбэл, - нэмэгдэж, - буурч байна.

Хязгаарлагдмал онцлог. Хэрэв ийм M тоо байвал . Жишээлбэл, функцууд ба , учир нь .

Жишээ 1. Функцийн хамрах хүрээг ол.

+ 2 – 3 +

1.2 Хязгаарын онол

Тодорхойлолт 1. Функцийн хязгаар нь b тоо бөгөөд хэрэв байгаа бол ( дурын жижиг эерэг тоо ) тэгш бус байдал биелсэнээс эхлэн аргументийн ийм утгыг олох боломжтой.

Тэмдэглэл: .

Тодорхойлолт 2. Функцийн хязгаар нь b тоо бөгөөд хэрэв байгаа бол (- дур зоргоороо жижиг эерэг тоо) тэгш бус байдлыг хангаж буй бүх x утгуудын хувьд тэгш бус байдал үнэн байх тийм эерэг тоо байна.

Тэмдэглэл: .

Тодорхойлолт 3.Функцийг эсвэл -ийн хувьд хязгааргүй жижиг гэж нэрлэдэг, хэрэв эсвэл.

Үл хөдлөх хөрөнгө.

1. Хязгааргүй тооны хязгааргүй жижиг хэмжигдэхүүний алгебрийн нийлбэр нь хязгааргүй бага хэмжигдэхүүн юм.

2. Төгсгөлгүй бага хэмжигдэхүүн ба хязгаарлагдмал функцийн үржвэр (тогтмол, өөр хязгааргүй хэмжигдэхүүн) нь хязгааргүй жижиг хэмжигдэхүүн юм.

3. Хязгаар нь тэгээс ялгаатай функцэд хязгааргүй жижиг хэмжигдэхүүнийг хуваах коэффициент нь хязгааргүй бага хэмжигдэхүүн юм.

Тодорхойлолт 4. if -ийн хувьд функцийг хязгааргүй том гэж нэрлэдэг.

Үл хөдлөх хөрөнгө.

1. Хязгаар нь тэгээс ялгаатай функцийн хязгааргүй их хэмжигдэхүүнийг үржвэрлэх нь хязгааргүй их хэмжигдэхүүн юм.

2. Төгсгөлгүй их хэмжигдэхүүн ба хязгаарлагдмал функцийн нийлбэр нь хязгааргүй их хэмжигдэхүүн юм.

3. Хязгааргүй их хэмжигдэхүүнийг хязгаартай функцэд хуваах коэффициент нь хязгааргүй их хэмжигдэхүүн юм.

Теорем.(Хязгааргүй жижиг утга ба хязгааргүй их утгын хоорондын хамаарал.) Хэрэв функц () дээр хязгааргүй жижиг бол функц () дээр хязгааргүй том утгатай байна. Мөн эсрэгээр, функц нь () дээр хязгааргүй том бол функц нь () дээр хязгааргүй бага утгатай болно.

Хязгаарын теоремууд.

1. Функц нэгээс илүү хязгаартай байж болохгүй.

2. Хэд хэдэн функцийн алгебрийн нийлбэрийн хязгаар нь эдгээр функцүүдийн хязгаарын алгебрийн нийлбэртэй тэнцүү байна.

3. Хэд хэдэн функцийн үржвэрийн хязгаар нь эдгээр функцүүдийн хязгаарын үржвэртэй тэнцүү байна.

4. Зэрэглэлийн хязгаар нь хязгаарын зэрэгтэй тэнцүү байна:

5. Хуваагч хязгаар байгаа бол хуваагчийн хязгаар нь хязгаарын хуваагчтай тэнцүү байна.

.

6. Анхны гайхалтай хязгаар.

Үр дагавар:

7. Хоёр дахь гайхалтай хязгаар:

Үр дагавар:

Тэнцвэртэй хязгааргүй бага хэмжигдэхүүн:

Хязгаарлалтын тооцоо.

Хязгаарыг тооцохдоо хязгаарын үндсэн теоремууд, тасралтгүй функцүүдийн шинж чанар, эдгээр теорем, шинж чанаруудаас үүсэх дүрмийг ашиглана.

Дүрэм 1Энэ цэгт тасралтгүй байгаа функцийн цэг дээрх хязгаарыг олохын тулд хязгаарын тэмдгийн доорх функцэд х аргументын оронд түүний хязгаарын утгыг орлуулах шаардлагатай.

Жишээ 2. Хай

Дүрэм 2Бутархайн хязгаарыг олохдоо хуваагчийн хязгаар нь тэгтэй тэнцүү, хуваагчийн хязгаар нь тэг биш байвал ийм функцийн хязгаар нь -тэй тэнцүү байна.

Жишээ 3. Хай

Дүрэм 3Хэрэв бутархайн хязгаарыг олоход хуваагчийн хязгаар тэнцүү, хуваагчийн хязгаар нь тэг биш байвал ийм функцийн хязгаар тэгтэй тэнцүү байна.

Жишээ 4 Хай

Ихэнхдээ аргументийн хязгаарын утгыг орлуулах нь тодорхойгүй хэлбэрийн илэрхийлэлд хүргэдэг

.

Эдгээр тохиолдолд функцийн хязгаарыг олохыг тодорхойгүй байдлын тодруулга гэж нэрлэдэг. Тодорхой бус байдлыг илчлэхийн тулд хязгаарт хүрэхээсээ өмнө энэ илэрхийлэлд өөрчлөлт оруулах шаардлагатай. Тодорхой бус байдлыг илрүүлэхийн тулд янз бүрийн арга техникийг ашигладаг.

Дүрэм 4. Хэлбэрийн тодорхойгүй байдал нь дэд хязгаарын функцийг хувиргах замаар илэрдэг бөгөөд ингэснээр тоологч ба хуваарьт хязгаар нь тэг байх хүчин зүйлийг сонгож, түүгээр бутархайг багасгаж, хэсгийн хязгаарыг олно. Үүнийг хийхийн тулд хүртэгч ба хуваагчийг хүчин зүйлээр ялгах юм уу тоо болон хуваагчтай хавсарсан илэрхийллээр үржүүлнэ.

Дүрэм 5Хэрэв дэд хязгаарын илэрхийлэл нь тригонометрийн функцуудыг агуулж байвал эхний гайхалтай хязгаарыг маягтын тодорхойгүй байдлыг илрүүлэхэд ашиглана.

.

Дүрэм 6. Маягтын тодорхойгүй байдлыг илрүүлэхийн тулд доод бутархайн хуваагч ба хуваагчийг аргументийн хамгийн дээд зэрэгт хувааж, дараа нь хэсгийн хязгаарыг олох хэрэгтэй.

Боломжит үр дүн:

1) хүссэн хязгаар нь тоологч ба хуваагчийн аргументуудын хамгийн дээд түвшний коэффициентүүдийн харьцаатай тэнцүү, хэрэв эдгээр хүч нь ижил байвал;

2) тоологчийн аргументийн зэрэг нь хуваагч аргументийн зэргээс өндөр байвал хязгаар нь хязгааргүйтэй тэнцүү;

3) тоологчийн аргументын зэрэг нь хуваагч аргументийн зэргээс доогуур байвал хязгаар нь тэг болно.

а)

учир нь

Зэрэг нь тэнцүү бөгөөд энэ нь хязгаар нь өндөр зэрэглэлийн коэффициентүүдийн харьцаатай тэнцүү байна гэсэн үг, i.e. .

б)

Тоолуурын зэрэг, хуваагч нь 1 бөгөөд энэ нь хязгаар нь тэнцүү гэсэн үг юм

v)

Тоолуурын зэрэг нь 1, хуваагч нь , тэгэхээр хязгаар нь 0 байна.

Дүрэм 7. Маягтын тодорхойгүй байдлыг илрүүлэхийн тулд доод бутархайн хүртэгч ба хуваагчийг коньюгат илэрхийллээр үржүүлэх шаардлагатай.

Жишээ 10

Дүрэм 8. Зүйлийн тодорхой бус байдлыг илрүүлэхийн тулд хоёр дахь гайхалтай хязгаар, түүний үр дагаврыг ашигладаг.

Үүнийг баталж болно

Жишээ 11.

Жишээ 12.

Жишээ 13

Дүрэм 9. Доод хязгаарын функц нь b.m.v. агуулсан тодорхой бус байдлыг тодруулахдаа эдгээр b.m.v.-ийн хязгаарыг солих шаардлагатай. b.m-ийн хязгаарт, тэдгээртэй тэнцэхүйц.

Жишээ 14

Жишээ 15

Дүрэм 10 L'Hospital-ийн дүрэм (2.6-г үзнэ үү).

1.3 Функцийн тасралтгүй байдал

Хэрэв аргумент нь а руу чиглэж байгаа функцийн хязгаар байгаа бөгөөд энэ цэг дэх функцийн утгатай тэнцүү бол тухайн цэг дээр функц тасралтгүй байна.

Ижил нөхцөл:

1. ;

3.

Хагарлын цэгүүдийн ангилал:

Эхний төрлийн хагарал

Зөөврийн - нэг талын хязгаарлалтууд байдаг бөгөөд тэдгээр нь тэнцүү байна;

Үхлийн (үсрэх) - нэг талын хязгаар нь тэнцүү биш;

Хоёрдахь төрлийн тасалдал: цэг дээрх функцийн хязгаар байхгүй.

Жишээ 16. Тухайн цэг дээрх функцийн тасалдлын мөн чанарыг тогтоох эсвэл энэ цэг дэх функцийн тасралтгүй байдлыг нотлох.

-ийн хувьд функц тодорхойлогдоогүй тул энэ үед тасралтгүй биш байна. Учир нь мөн үүний дагуу, , дараа нь эхний төрлийн тасархай цэг юм.

б)

(a) даалгавартай харьцуулахад функц нь цэг дээр өргөтгөсөн тул , тэгэхээр өгөгдсөн функц өгөгдсөн цэг дээр тасралтгүй байна.

Функц нь тодорхойлогдоогүй үед;

.

Учир нь нэг талт хязгааруудын нэг нь хязгааргүй, дараа нь хоёр дахь төрлийн тасалдлын цэг юм.

2-р бүлэг

2.1 Деривативын тодорхойлолт

Дериватив тодорхойлолт

Өгөгдсөн функцийн дериватив буюу өгөгдсөн функц нь аргументийн өсөлт тэг болох хандлагатай үед функцын өсөлтийг аргументийн харгалзах өсөлттэй харьцуулах хязгаар юм.

Эсвэл .

Деривативын механик утга нь функцийн өөрчлөлтийн хурд юм. Деривативын геометрийн утга нь функцын графиктай шүргэгчийн налуугийн тангенс юм.

2.2 Ялгах үндсэн дүрэм

Нэр	Чиг үүрэг	Дериватив
Тогтмол хүчин зүйлээр үржүүлэх
Хоёр функцийн алгебрийн нийлбэр
Хоёр функцийн бүтээгдэхүүн
Хоёр функцийн коэффициент
Нарийн төвөгтэй функц

Үндсэн энгийн функцүүдийн деривативууд

Үгүй p / p	Функцийн нэр	Функц ба түүний дериватив
1	тогтмол
2	эрчим хүчний функц онцгой тохиолдлууд
3	экспоненциал функц онцгой тохиолдол
4	логарифм функц онцгой тохиолдол
5	тригонометрийн функцууд
6	урвуу тригонометр

б)

2.3 Дээд зэрэглэлийн дериватив

Функцийн хоёрдугаар эрэмбийн дериватив

Функцийн хоёрдугаар эрэмбийн дериватив:

Жишээ 18.

a) Функцийн хоёрдугаар эрэмбийн деривативыг ол.

Шийдэл. Эхлээд нэгдүгээр эрэмбийн деривативыг олъё .

Эхний эрэмбийн деривативаас бид деривативыг дахин авна.

Жишээ 19. Функцийн гуравдугаар эрэмбийн деривативыг ол.

2.4 Функцуудыг судлах

2.4.1 Бүрэн үйл ажиллагааны судалгааны төлөвлөгөө:

Бүрэн үйл ажиллагааны судалгааны төлөвлөгөө:

1. Анхан шатны судалгаа:

Тодорхойлолт, утгын хүрээг олох;

Ерөнхий шинж чанарыг олж мэдээрэй: тэгш (сондгой), үе үе;

Координатын тэнхлэгүүдтэй огтлолцох цэгүүдийг олох;

Тогтмол байдлын талбайг тодорхойлох.

2. Асимптотууд:

Хэрэв босоо асимптотуудыг ол;

Ташуу асимптотуудыг ол: .

Хэрэв ямар нэгэн тоо байвал хэвтээ асимптотууд байна.

3. Судалгааг ашиглан:

Чухал цэгүүдийг олоорой. байгаа эсвэл байхгүй цэгүүд;

Өсөх интервалыг тодорхойлох, тэдгээр. функцийн бууралт ба завсар - ;

Хэт цэгүүдийг тодорхойлно уу: "+" -ээс "-" хүртэл тэмдэг нь шилжих үед хамгийн их цэгүүд, "-" -ээс "+" хүртэл хамгийн бага цэгүүд байна.

4. Судалгааг ашиглан:

Байгаа эсвэл байхгүй цэгүүдийг олох;

Гүдгэр хэсгүүдийг олох, i.e. цоорхой, дээр нь болон хонхорхой -;

Гулзайлтын цэгүүдийг олох, өөрөөр хэлбэл. тэмдэг өөрчлөгдөх шилжилтийн цэгүүд.

1. Судалгааны бие даасан элементүүдийг олсныхоо дагуу график дээр аажмаар зурна.

2. Хэрэв функцийн графикийг бүтээхэд хүндрэл гарвал функцийн утгыг зарим нэмэлт цэгүүдээс олно.

3. Судалгааны зорилго нь функцийн зан үйлийн мөн чанарыг тодорхойлох явдал юм. Тиймээс яг тодорхой график биш, харин олсон элементүүдийг (экстрем, гулзайлтын цэг, асимптот гэх мэт) тодорхой тэмдэглэсэн ойролцоолсон графикийг бүтээсэн болно.

4. Дээрх төлөвлөгөөг хатуу мөрдөх шаардлагагүй; функцийн зан үйлийн онцлог шинж чанаруудыг алдахгүй байх нь чухал юм.

2.4.2 Функц судлалын жишээ:

1)

2) сондгой функц:

.

3) Асимптотууд.

оноос хойш босоо асимптотууд байна

Ташуу асимптот.

5)

- гулзайлтын цэг.

2) сондгой функц:

3) Асимптотууд: Босоо асимптотууд байдаггүй.

Налуу:

ташуу асимптотууд юм

4) - функц нэмэгдэж байна.

- гулзайлтын цэг.

Энэ функцийн бүдүүвч график:

2) Ерөнхий функц

3) Асимптотууд

- ташуу асимптот байхгүй

үед хэвтээ асимптот байна

- гулзайлтын цэг

Энэ функцийн бүдүүвч график:

2) Асимптотууд.

оноос хойш босоо асимптот байна

- ташуу асимптот байхгүй

, хэвтээ асимптот

Энэ функцийн бүдүүвч график:

2) Асимптотууд

үед босоо асимптот байна, учир нь

- ташуу асимптот байхгүй

, хэвтээ асимптот

3) – интервал бүр дээр функц буурдаг.

Энэ функцийн бүдүүвч график:

Сегмент дээрх функцийн хамгийн том ба хамгийн бага утгыг олохын тулд та схемийг ашиглаж болно.

1. Функцийн деривативыг ол.

2. Функцийн орших эсвэл байхгүй чухал цэгүүдийг ол.

3. Өгөгдсөн сегмент болон түүний төгсгөлд хамаарах эгзэгтэй цэгүүд дэх функцийн утгыг олж, тэдгээрийн хамгийн том, хамгийн багыг сонго.

Жишээ. Хамгийн багыг ол хамгийн өндөр үнэ цэнэЭнэ сегмент дээрх функцууд.

25. хооронд

2) - чухал цэгүүд

26. хооронд.

Дериватив нь -д байхгүй, гэхдээ 1 нь энэ интервалд хамаарахгүй. Функц нь интервал дээр буурдаг бөгөөд энэ нь хамгийн их утга байхгүй, харин хамгийн бага утгатай гэсэн үг юм.

2.5 L'Hospital-ийн дүрэм

Теорем. Хязгааргүй бага буюу хязгааргүй хоёрын харьцааны хязгаар том функцуудХэрэв сүүлийнх нь заасан утгаараа байгаа бол тэдгээрийн деривативуудын харьцааны хязгаартай тэнцүү (хязгааргүй эсвэл хязгааргүй).

Тэдгээр. төрлийн тодорхой бус байдлыг тодруулахдаа та дараах томъёог ашиглаж болно.

.

27.

Бүлэг 3. Интеграл тооцоо

3.1 Тодорхой бус интеграл

3.1.1 Тодорхойлолт ба шинж чанарууд

Тодорхойлолт 1. Хэрэв функцийг эсрэг дериватив гэж нэрлэдэг.

Тодорхойлолт 2. f(x) функцийн тодорхойгүй интеграл нь энэ функцийн бүх эсрэг деривативуудын олонлог юм.

Зориулалт: , энд c нь дурын тогтмол юм.

Тодорхойгүй интегралын шинж чанарууд

1. Тодорхой бус интегралын дериватив:

2. Тодорхойгүй интегралын дифференциал:

3. Дифференциалын тодорхойгүй интеграл:

4. Хоёр функцийн нийлбэрийн (ялгаа) тодорхойгүй интеграл:

5. Тодорхой бус интегралын тэмдгээс тогтмол хүчин зүйлийг авч үзвэл:

3.1.2 Интегралын хүснэгт

.1.3 Интеграцийн үндсэн аргууд

1. Тодорхойгүй интегралын шинж чанарыг ашиглах.

Жишээ 29.

2. Дифференциалын тэмдгийн доор авчрах.

Жишээ 30.

3. Хувьсах солих арга:

a) интегралд орлуулах

хаана - анхныхаас илүү нэгтгэхэд хялбар функц; - функц, урвуу функц; - функцийн эсрэг дериватив.

Жишээ 31.

б) маягтын интегралд орлуулах:

Жишээ 32.

Жишээ 33.

4. Хэсгийн аргаар нэгтгэх:

Жишээ 34.

Жишээ 35.

Интегралыг тусад нь авна

Интеграл руугаа буцъя:

3.2 Тодорхой интеграл

3.2.1 Тодорхой интегралын тухай ойлголт, түүний шинж чанарууд

Тодорхойлолт.Тасралтгүй функцийг зарим интервал дээр өгье. Зохицуулъя.

Дээрхээс муруйгаар, зүүн ба баруун талаас шулуун шугамаар, доороос нь а ба b цэгүүдийн хоорондох абсцисса тэнхлэгийн хэрчмээр хүрээлэгдсэн дүрсийг муруйн трапец гэнэ.

S - талбай - муруй шугаман трапец.

Интервалыг цэгээр хувааж, дараахыг авна уу:

Интеграл нийлбэр:

Тодорхойлолт. Тодорхой интеграл нь интеграл нийлбэрийн хязгаар юм.

Тодорхой интегралын шинж чанарууд:

1. Интеграл тэмдгээс тогтмол хүчин зүйлийг гаргаж болно.

2. Хоёр функцийн алгебрийн нийлбэрийн интеграл нь эдгээр функцүүдийн интегралуудын алгебрийн нийлбэртэй тэнцүү байна.

3. Хэрэв интегралын сегментийг хэсэг болгон хуваасан бол бүхэл сегмент дээрх интеграл нь үүссэн хэсэг тус бүрийн интегралын нийлбэртэй тэнцүү байна, өөрөөр хэлбэл. ямар ч a, b, c:

4. Хэрэв сегмент дээр байвал ба

5. Интегралын хязгаарыг сольж болох ба интегралын тэмдэг өөрчлөгдөнө.

6.

7. Цэг дэх интеграл нь 0-тэй тэнцүү:

8.

9. (“дундажын тухай”) y = f(x) дээр интегралдах функц байг. Дараа нь , энд , f(c) нь f(x)-ийн дундаж утга юм:

10. Ньютон-Лейбницийн томъёо

,

Энд F(x) нь f(x)-ийн эсрэг дериватив юм.

3.2.2 Тодорхой интегралыг тооцоолох арга.

1. Шууд нэгтгэх

Жишээ 35.

а)

б)

v)

д)

2. Тодорхой интегралын тэмдгийн дор хувьсагчийн өөрчлөлт .

Жишээ 36.

2. Тодорхой интеграл дахь хэсгүүдийн интеграл .

Жишээ 37.

а)

б)

д)

3.2.3 Тодорхой интегралын хэрэглээ

Онцлог шинж чанартай	Функцийн төрөл	Томъёо
	Декарт координатаар
муруй шугаман салбарын талбай	туйлын координатаар
муруй трапецын талбай	параметрийн хэлбэрээр
нумын урт	Декарт координатаар
нумын урт	туйлын координатаар
нумын урт	параметрийн хэлбэрээр
биеийн эзэлхүүн эргэлт	Декарт координатаар
өгөгдсөн хөндлөн огтлолтой биеийн эзэлхүүн Хэсэг

Жишээ 38. Зургийн талбайг тооцоол, шугамаар хязгаарлагдсан: болон .

Шийдэл:Эдгээр функцүүдийн графикуудын огтлолцох цэгүүдийг ол. Үүнийг хийхийн тулд бид функцуудыг тэгшитгэж, тэгшитгэлийг шийднэ

Тэгэхээр, огтлолцох цэгүүд ба .

Томъёог ашиглан зургийн талбайг ол

.

Манай тохиолдолд

Хариулт: талбай нь (квадрат нэгж).

4.1 Үндсэн ойлголтууд

Тодорхойлолт. Хэрэв тодорхой олонлогийн бие даасан тоо бүрт z хувьсагчийн нэг буюу хэд хэдэн утгыг ямар нэг дүрмийн дагуу өгсөн бол z хувьсагчийг хоёр хувьсагчийн функц гэж нэрлэдэг.

Тодорхойлолт. z функцийн домэйн нь z функц байгаа хосуудын багц юм.

Хоёр хувьсагчийн функцийн муж нь Oxy координатын хавтгай дээрх тодорхой цэгүүдийн багц юм. z-координатыг хэрэглүүр гэж нэрлэдэг бөгөөд дараа нь функц нь өөрөө E 3 орон зайд ямар нэг гадаргуу хэлбэрээр дүрслэгддэг. Жишээ нь:

Жишээ 39. Функцийн хамрах хүрээг ол.

а)

Баруун талд байгаа илэрхийлэл нь зөвхөн . Энэ нь уг функцийн домэйн нь эх цэгт төвтэй R радиустай тойргийн дотор ба хил дээр байрлах бүх цэгүүдийн олонлог юм гэсэн үг юм.

Энэ функцын домэйн нь шугамын цэгүүдээс бусад хавтгайн бүх цэгүүд, i.e. координатын тэнхлэгүүд.

Тодорхойлолт. Функцийн түвшний шугамууд нь хэлбэрийн тэгшитгэлээр дүрслэгдсэн координатын хавтгай дээрх муруйн бүлгүүд юм.

Жишээ 40 Онцлог түвшний шугамыг ол .

Шийдэл. Өгөгдсөн функцийн түвшний шугамууд нь тэгшитгэлээр дүрслэгдсэн хавтгай дахь муруйн гэр бүл юм

Сүүлийн тэгшитгэл нь радиусын О 1 (1, 1) цэг дээр төвлөрсөн тойргийн бүлгийг дүрсэлдэг. Энэ функцээр дүрслэгдсэн эргэлтийн гадаргуу (параболоид) тэнхлэгээс холдох тусам "эгц" болдог ба үүнийг x = 1, y = 1 тэгшитгэлээр өгөгдсөн. (Зураг 4)

4.2 Хэд хэдэн хувьсагчийн функцүүдийн хязгаар ба тасралтгүй байдал.

1. Хязгаарлалт.

Тодорхойлолт. Цэг нь цэг рүү чиглэж байгаа тул А тоог функцийн хязгаар гэж нэрлэдэг, хэрэв дурын жижиг тоо бүрийн хувьд нөхцөл нь аль ч цэгт үнэн байх тийм тоо байвал нөхцөл нь мөн үнэн болно. . Бичнэ үү: .

Жишээ 41. Хязгаарыг ол:

тэдгээр. хязгаар нь -аас хамаардаг бөгөөд энэ нь байхгүй гэсэн үг юм.

2. Тасралтгүй байдал.

Тодорхойлолт. Уг цэгийг функцийн тодорхойлолтын мужид хамааруулъя. Дараа нь функцийг хэрэв цэг дээр тасралтгүй гэж нэрлэдэг

(1)

мөн цэг нь дур зоргоороо цэг рүү чиглэдэг.

Хэрэв (1) нөхцөл аль ч цэгт хангагдахгүй бол энэ цэгийг функцийн таслах цэг гэнэ. Энэ нь дараах тохиолдолд тохиолдож болно.

1) Функц нь цэг дээр тодорхойлогдоогүй байна.

2) Ямар ч хязгаарлалт байхгүй.

3) Энэ хязгаар байгаа боловч -тэй тэнцүү биш байна.

Жишээ 42. Өгөгдсөн функц нь бол цэг дээр тасралтгүй эсэхийг тодорхойл.

Ойлголоо тэгэхээр энэ функц цэг дээр тасралтгүй .

хязгаар нь k-ээс хамаарна, өөрөөр хэлбэл. Энэ нь энэ үед байхгүй бөгөөд энэ нь функц нь энэ үед тасалдалтай байна гэсэн үг юм.

4.3 Хэд хэдэн хувьсагчийн функцүүдийн дериватив ба дифференциал

4.3.1 Нэгдүгээр эрэмбийн хэсэгчилсэн дериватив

Х аргументтай холбоотой функцийн хэсэгчилсэн дериватив нь у хувьсагчийн тогтмол утгын нэг х хувьсагчийн функцын ердийн дериватив бөгөөд дараах байдлаар тэмдэглэнэ.

y аргументтай холбоотой функцийн хэсэгчилсэн дериватив нь x хувьсагчийн тогтмол утгын хувьд нэг у хувьсагчийн функцийн ердийн дериватив бөгөөд үүнийг дараах байдлаар тэмдэглэнэ.

Жишээ 43. Функцийн хэсэгчилсэн деривативуудыг ол.

4.3.2 Хоёрдугаар эрэмбийн хэсэгчилсэн дериватив

Хоёрдугаар эрэмбийн хэсэгчилсэн деривативууд нь нэгдүгээр эрэмбийн хэсэгчилсэн деривативуудын хэсэгчилсэн деривативууд юм. Маягтын хоёр хувьсагчийн функцийн хувьд дөрвөн төрлийн хоёрдугаар эрэмбийн хэсэгчилсэн дериватив боломжтой.

Янз бүрийн хувьсагчдаас ялгах 2-р эрэмбийн хэсэгчилсэн деривативуудыг холимог дериватив гэж нэрлэдэг. Хоёр дахин дифференциалагдах функцийн холимог хоёрдугаар эрэмбийн деривативууд тэнцүү байна.

Жишээ 44. Хоёрдугаар эрэмбийн хэсэгчилсэн деривативуудыг ол.

4.3.3 Нийт дифференциал ба түүнийг ойролцоо тооцоололд хэрэглэх.

Тодорхойлолт. Хоёр хувьсагчийн функцийн эхний эрэмбийн дифференциалыг томъёогоор олно

.

Жишээ 45. Функцийн нийт дифференциалыг ол.

Шийдэл. Хэсэгчилсэн деривативуудыг олцгооё:

.

X ба y аргументуудыг бага зэрэг нэмэгдүүлснээр функц нь ойролцоогоор dz-тэй тэнцүү өсөлтийг хүлээн авдаг, өөрөөр хэлбэл. .

Тухайн цэг дээрх функцийн яг тодорхой утгыг мэддэг бол тухайн цэг дээрх функцийн ойролцоо утгыг олох томъёо:

Жишээ 46 Ол .

Шийдэл. зөвшөөрөх,

Дараа нь бид томъёог ашиглана

Хариулах. .

Жишээ 47. Ойролцоогоор тооцоол.

Шийдэл. Функцийг авч үзье. Бидэнд байгаа

Жишээ 48. Ойролцоогоор тооцоол.

Шийдэл. Функцийг авч үзье . Бид авах:

Хариулах. .

4.3.4. Далд функцийн ялгаа

Тодорхойлолт. Функцийг z-ийн хувьд шийдвэрлэх боломжгүй тэгшитгэлээр өгөгдсөн бол далд гэж нэрлэдэг.

Ийм функцийн хэсэгчилсэн деривативуудыг дараах томъёогоор олно.

Жишээ 49. z функцийн хэсэгчилсэн деривативуудыг ол. тэгшитгэлээр өгөгдсөн .

Шийдэл.

Тодорхойлолт. Функцийг у-ийн хувьд шийдвэрлэх боломжгүй тэгшитгэлээр өгөгдсөн бол далд гэж нэрлэдэг.

Ийм функцийн деривативыг дараах томъёогоор олно.

.

Жишээ 50. Эдгээр функцийн деривативуудыг ол.

5.1 Хэд хэдэн хувьсагчийн функцийн орон нутгийн экстремум

Тодорхойлолт 1. Функц нь if цэгт максимумтай байна

Тодорхойлолт 2. Функц нь if цэгт минимумтай байна цэгт хангалттай ойр, түүнээс ялгаатай бүх цэгүүдийн хувьд.

Экстремум үүсэх зайлшгүй нөхцөл. Хэрэв функц цэг дээр экстремумд хүрвэл функцийн хэсэгчилсэн дериватив алга болно эсвэл тухайн цэгт байхгүй болно.

Хэсэгчилсэн дериватив алга болох эсвэл байхгүй цэгүүдийг чухал гэж нэрлэдэг.

Экстремумын хангалттай шинж тэмдэг. Функцийг эгзэгтэй цэгийн зарим хэсэгт тодорхойлж, энэ цэг дээр тасралтгүй хоёр дахь эрэмбийн хэсэгчилсэн деривативтай байг.

1) хэрэв ба цэг дээр орон нутгийн максимумтай байна;

2) хэрэв ба цэг дээр орон нутгийн доод хэмжээтэй байна;

3) цэг дээр орон нутгийн экстремум байхгүй бол ;

Хоёр хувьсагчийн функцийн экстремумыг судлах схем.

1. : ба функцийн хэсэгчилсэн деривативуудыг ол.

2. Тэгшитгэлийн системийг шийдэж, функцийн критик цэгүүдийг ол.

3. Хоёрдахь эрэмбийн хэсэгчилсэн деривативуудыг олж, чухал цэгүүдэд утгыг нь тооцоолж, хангалттай нөхцөлийг ашиглан экстремум байгаа эсэх талаар дүгнэлт гарга.

4. Функцийн экстремумыг ол.

Жишээ 51. Функцийн экстремумыг ол .

1) Хэсэгчилсэн деривативуудыг олцгооё.

2) Тэгшитгэлийн системийг шийд

4) Хоёрдахь эрэмбийн хэсэгчилсэн деривативууд ба тэдгээрийн чухал цэгүүдийн утгыг ол: . Энэ үед бид дараахь зүйлийг авна.

Энэ нь цэг дээр экстремум байхгүй гэсэн үг юм. Энэ үед бид дараахь зүйлийг авна.

хамгийн бага цэг дээр гэсэн үг.

5.2 Глобал экстремум (функцийн хамгийн том ба хамгийн бага утга)

Зарим хаалттай олонлог дээр тасралтгүй үргэлжлэх хэд хэдэн хувьсагчийн функцийн хамгийн том ба хамгийн бага утгууд нь экстремум цэгүүд эсвэл олонлогийн хил дээр хүрдэг.

Хамгийн том ба хамгийн бага утгыг олох схем.

1) Тухайн муж дотор байрлах чухал цэгүүдийг олж, эдгээр цэгүүд дэх функцийн утгыг тооцоол.

2) Бүс нутгийн хил дээрх функцийг судлах; хэрэв хил нь хэд хэдэн өөр шугамаас бүрдэх бол судалгааг хэсэг тус бүрээр тусад нь хийх ёстой.

3) Функцийн олж авсан утгуудыг харьцуулж, хамгийн том, хамгийн жижигийг сонгоно уу.

Жишээ 52. Тэгш өнцөгт дэх функцын хамгийн том ба хамгийн бага утгыг ол.

Шийдэл. 1) Функцийн эгзэгтэй цэгүүдийг ол, үүний тулд хэсэгчилсэн деривативуудыг олно: , тэгшитгэлийн системийг шийд.

Бид А эгзэгтэй цэгийг авсан. Үүссэн цэг нь өгөгдсөн талбайн дотор байна.

Бүс нутгийн хил нь дөрвөн сегментээс бүрдэнэ: i. сегмент тус бүрийн функцийн хамгийн том ба хамгийн бага утгыг ол.

4) Хүлээн авсан үр дүнг харьцуулж, цэг дээр нь авцгаая .

Бүлэг 6. Хэрэглэгчийн сонголтын загвар

Бид n өөр бараа байна гэж таамаглах болно. Дараа нь зарим багц барааг n хэмжээст вектороор тэмдэглэнэ , i-р бүтээгдэхүүний тоо хэмжээ хаана байна. X барааны бүх багцыг орон зай гэж нэрлэдэг.

Хувь хүний ​​​​сонголт нь давуу байдлын хамаарлаар тодорхойлогддог: хэрэглэгч аль ч хоёр багцын талаар илүү их хүсч буй зүйлийг хэлж чадна гэж үздэг, эсвэл тэдгээрийн хоорондын ялгааг олж хараагүй гэж үздэг. Давуу эрхийн хамаарал нь шилжилттэй байна: хэрэв олонлогийг олонлогоос илүүд үзэж, олонлогийг олонлогоос илүүд үздэг бол олонлогийг олонлогоос илүүд үздэг. Хэрэглэгчийн зан төлөвийг бие даасан хэрэглэгчийн аксиомоор бүрэн дүрсэлсэн гэж бид таамаглах болно: хувь хүн бүр өөрийн сонголтын системд үндэслэн хэрэглээ, худалдан авалт гэх мэт шийдвэрийг гаргадаг.

6.1 Хэрэглээний функц

Хэрэглэгчийн багц X багц дээр функц , хэрэглэгчийн багц дээрх үнэ цэнэ нь тухайн хүний ​​хэрэглэгчийн үнэлгээтэй тэнцүү байна. Уг функцийг хэрэглэгчийн хэрэглээний функц эсвэл хэрэглэгчийн давуу функц гэж нэрлэдэг. Тэдгээр. хэрэглэгч бүр өөрийн гэсэн ашигтай функцтэй байдаг. Гэхдээ бүхэл бүтэн хэрэглэгчдийн багцыг хэрэглэгчдийн тодорхой ангилалд (нас, өмчийн байдал гэх мэт) хувааж болох бөгөөд ангилал тус бүрд зарим, магадгүй дундаж хэрэглээний функцийг хуваарилж болно.

Тиймээс функц нь хэрэглэгчийн үнэлгээ эсвэл энэ багцыг олж авахдаа тухайн хүний ​​​​хэрэгцээний сэтгэл ханамжийн түвшин юм. Тухайн хувь хүний ​​багцаас багцыг илүүд үзэх юм бол .

Хэрэглээний функцын шинж чанарууд.

1.

Хэрэглээний функцийн эхний хэсэгчилсэн деривативуудыг бүтээгдэхүүний ахиу ашиг гэж нэрлэдэг. Энэ шинж чанараас харахад нэг бүтээгдэхүүний хэрэглээ бусад бүтээгдэхүүний ижил хэрэглээтэй нэмэгдэж байгаа нь хэрэглэгчийн үнэлгээг нэмэгдүүлэхэд хүргэдэг. Вектор нь функцийн градиент бөгөөд энэ нь функцийн хамгийн их өсөлтийн чиглэлийг харуулдаг. Функцийн хувьд түүний градиент нь бүтээгдэхүүний ахиу хэрэглээний вектор юм.

2.

Тэдгээр. Аливаа барааны ахиу ашиг нь хэрэглээ нэмэгдэх тусам буурдаг.

3.

Тэдгээр. Бүтээгдэхүүн бүрийн ахиу ашиг нь нөгөө бүтээгдэхүүний тоо хэмжээгээр нэмэгддэг.

Зарим төрлийн хэрэглээний функцууд.

1) Неоклассик: .

2) дөрвөлжин: , матриц нь сөрөг тодорхой ба төлөө.

3) Логарифм функц: .

6.2 хайхрамжгүй байдлын шугам

Хэрэглээний асуудал, хэрэглэгчийн сонголтын загварт хоёр барааны багцын онцгой тохиолдлыг ихэвчлэн ашигладаг, жишээлбэл. Хэрэглээний функц нь хоёр хувьсагчаас хамаарах үед. хайхрамжгүй байдлын шугам нь тухайн хүний ​​хэрэгцээг хангах ижил түвшний хэрэглэгчийн багцыг холбосон шугам юм. Үндсэндээ хайхрамжгүй байдлын шугамууд нь функциональ түвшний шугамууд юм. Үл тоомсорлох шугамын тэгшитгэлүүд: .

Үл хайхрах шугамын үндсэн шинж чанарууд.

1. Хэрэгцээний сэтгэл ханамжийн янз бүрийн түвшинд тохирсон хайхрамжгүй байдлын шугамууд хүрч, огтлолцохгүй.

2. хайхрамжгүй байдлын шугамууд багасна.

3. хайхрамжгүй байдлын шугамууд нь доошоо гүдгэр байна.

2-р өмч нь ойролцоогоор чухал тэгш байдлыг илэрхийлдэг.

Энэ харьцаа нь тухайн хүн өөрийн хэрэгцээг хангах түвшинг өөрчлөхгүйгээр эхний бүтээгдэхүүний хэрэглээг нэг нэгжээр бууруулах (өсгөх) үед хоёр дахь бүтээгдэхүүний хэрэглээг хэр их хэмжээгээр нэмэгдүүлэх (бууруулах) ёстойг харуулдаг. Энэ харьцааг эхний бүтээгдэхүүнийг хоёр дахь бүтээгдэхүүнээр солих хурд, утгыг эхний бүтээгдэхүүнийг хоёр дахь бүтээгдэхүүнээр солих ахиуц хувь гэж нэрлэдэг.

Жишээ 53. Хэрэв эхний барааны ахиу ашиг нь 6, хоёр дахь нь 2 бол эхний барааны хэрэглээ нэг нэгжээр буурахад хоёр дахь барааны хэрэглээг нэгэн зэрэг 3 нэгжээр нэмэгдүүлэх шаардлагатай. хэрэгцээг хангах түвшин.

6.3 Төсвийн багц

Болъё n бүтээгдэхүүний багцын үнийн вектор; Би бол тухайн хүний ​​орлого бөгөөд түүнийг багц бүтээгдэхүүн худалдан авахад зарцуулахад бэлэн байна. Өгөгдсөн үнээр хамгийн ихдээ I үнэтэй багц барааны багцыг төсвийн багц B гэнэ.Энэ тохиолдолд I өртөгтэй багц барааны багцыг B төсвийн багцын G зааг гэнэ.Иймд. B олонлог нь G хил ба байгалийн хязгаарлалтаар хязгаарлагдана.

Төсвийн багцыг тэгш бус байдлын системээр тодорхойлно.

Хоёр барааны багцын хувьд төсвийн багц В (Зураг 1) нь координатын систем дэх гурвалжин бөгөөд координатын тэнхлэгүүд болон шулуун шугамаар хязгаарлагддаг.

6.4 Хэрэглэгчийн эрэлтийн онол

Хэрэглээний онолын хувьд хэрэглэгч өөрийн ашиг тусаа нэмэгдүүлэхийг үргэлж эрэлхийлдэг гэж үздэг бөгөөд түүний цорын ганц хязгаарлалт бол түүний багц бараа худалдаж авахад зарцуулж болох хязгаарлагдмал орлого юм. Ерөнхийдөө хэрэглэгчийн сонголтын асуудал (зах зээл дэх хэрэглэгчийн оновчтой зан үйлийн асуудал) дараах байдлаар томьёолжээ: хэрэглэгчийн багцыг ол. , энэ нь төсвийн хязгаарлалтыг харгалзан ашигтай функцийг дээд зэргээр нэмэгдүүлдэг. Энэ даалгаврын математик загвар:

Хоёр зүйлийн багц тохиолдолд:

Геометрийн хувьд энэ асуудлын шийдэл нь төсвийн багц G-ийн хил ба ялгаагүй шугамын хоорондох холбоо цэг юм.

Энэ асуудлын шийдлийг тэгшитгэлийн системийг шийдвэрлэхэд багасгасан.

(1)

Энэхүү системийн шийдэл нь хэрэглэгчдийн сонголтын асуудлыг шийдэх шийдэл юм.

Хэрэглэгчийн сонголтын асуудлыг шийдэх гарцыг эрэлтийн цэг гэж нэрлэдэг. Энэ эрэлтийн цэг нь үнэ, орлогоос хамаарна I. I.e. эрэлтийн цэг нь эрэлтийн функц юм. Эрэлтийн функц нь n функцын багц бөгөөд тус бүр нь аргументаас хамаарна.

Эдгээр функцийг тухайн барааны эрэлтийн функц гэж нэрлэдэг.

Жишээ 54. Зах зээл дээрх хоёр барааны багц, тэдгээрийн мэдэгдэж буй үнэ, орлого I-д ашигтай функц нь хэлбэртэй байвал эрэлтийн функцийг ол. .

Шийдэл. Бид хэрэглээний функцийг ялгадаг:

.

Бид олж авсан илэрхийлэлийг (1) -д орлуулж, тэгшитгэлийн системийг олж авна.

Энэ тохиолдолд бүтээгдэхүүн тус бүрийн зардал нь хэрэглэгчийн орлогын тал хувь байх бөгөөд худалдан авсан бүтээгдэхүүний дүн нь түүнд зарцуулсан дүнтэй тэнцүү бөгөөд бүтээгдэхүүний үнэд хуваагдана.

Жишээ 55. Нэгдүгээр бүтээгдэхүүнд хэрэглүүрийн функцийг , хоёрдугаарт ,

эхний барааны үнэ, хоёр дахь барааны үнэ. Орлого. Хэрэглээг дээд зэргээр нэмэгдүүлэхийн тулд хэрэглэгч хэр их бараа худалдаж авах ёстой вэ?

Шийдэл. Хэрэглээний функцын деривативуудыг олоод (1) системд орлуулж, шийднэ үү.

Энэхүү багц бараа нь ашиг тусыг нэмэгдүүлэхийн тулд хэрэглэгчдэд оновчтой байдаг.

Тусдаа дэвтэрт бүртгэлийн дэвтрийн дугаарын сүүлийн цифрээр сонгосон сонголтын дагуу хяналтын ажлыг гүйцэтгэнэ. Асуудал бүр нь нөхцөл, нарийвчилсан шийдэл, дүгнэлтийг агуулсан байх ёстой.

1. Тооцооллын талаархи танилцуулга

Даалгавар 1. Функцийн домайныг ол.

5.

Даалгавар 2. Функцийн хязгаарыг ол.

.

Даалгавар 3. Функцийн таслах цэгүүдийг олж, төрлийг нь тодорхойлно.

1. 2. 3.

2-р бүлэг

Даалгавар 4. Эдгээр функцийн деривативыг ол.

1. а); b) c) y = ;

d) y = x 6 + + + 5; д) y \u003d x tg x + ln sin x + e 3x;

е) y \u003d 2 x - arcsin x.

2. а) ; б) y =; в) y = ; г) y \u003d x 2 - + 3; e) y = e cos ; е) y =.

3. a) y = lnx; б) y =; в) y = ln;

4. a) y = ; б) y \u003d (e 5 x - 1) 6; в) y = ; d) y =; e) y = x 8 ++ + 5; е) y \u003d 3 x - arcsin x.

5. a) y \u003d 2x 3 - + e x; б) y =; в) y = ;

d) y =; e) y = 2 cos ; е) y =.

6. a) y = lnx; б) y =; в) y = ln;

d) y =; д) y \u003d x 7 + + 1; f) y = 2.

7. а) ; б) y =; в) y = ; г) y \u003d x 2 + xsinx +; e) y = e cos ; е) y =.

8. a) y = ; б) y \u003d (3 x - 4) 6; в) y = sintg;

d) y = 3x 4 - - 9+ 9; e) y = ;

д) y \u003d x 2 + arcsin x - x.

9. а); б) ; в) y = ; г) y \u003d 5 нүгэл 3 х; д) y \u003d x 3 - - 6+ 3; е) y = 4x 4 + ln.

10. а) б) y =; в) y = (3 x - 4) 6 ; d) y =; д) y \u003d x 2 - x; е) y \u003d e sin 3 x + 2.

Даалгавар 5. Функцийг судалж, графикийг нь байгуул.

1. a) b) c).

2. а) б) v) .

3. а) б) v) .

4. б) v)

5. а) б) v) .

6. а) б) v) .

7. a) b) c).

8. a) b) c).

9. a) b) c).

10. а) б) v) .

Даалгавар 6. Өгөгдсөн интервал дээрх функцийн хамгийн том ба хамгийн бага утгыг ол.

1. .

3. .

6. .

8. .

9. .

10. .

Бүлэг 3. Интеграл тооцоо

Даалгавар 7. Тодорхой бус интегралыг ол.

1. а) б);

2. а) ;б) в) г).

4. G)

5. а) ; б); v); G).

6. а) ; б); v); G)

7. а) ; б) ; v); G)

8. а) ; б); v) ; G) .

9. а) ; б) в); G).

10. а) б) v); G) .

Даалгавар 8. Тодорхой интегралыг тооцоол.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Бодлого 9. Буруу интегралыг олох буюу тэдгээрийн салж буйг батал.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Бодлого 10. Муруйгаар хүрээлэгдсэн талбайн талбайг ол

1. .2. .

5. 6.

7. , .8..

10. , .

Бүлэг 4. Хэд хэдэн хувьсагчийн функцийн дифференциал тооцоо.

Даалгавар 11. Функцийн домайныг ол (зураг дээр харуулав).

Бодлого 12. төлөө функцийн тасралтгүй байдлыг судал

Даалгавар 13. Далд өгөгдсөн функцийн деривативыг ол.

Бодлого 14. Ойролцоогоор тооцоол

1. а); б) ; v)

2. а) ; б) ; v) .

3. а) ; б) ; v) .

4. а) ; б) ; v) .

5. а); б) ; v) .

6. а); б) ; v) .

7. а); б) ; v) .

8. а) ;б) ; v)

9. а) ; б) ; v) .

10. a) ;b) ; v)

Бодлого 15. Экстремумын функцийг судал.

7. .

8. .

9. .

10. .

Бодлого 16. Өгөгдсөн битүү талбайд функцийн хамгийн том ба хамгийн бага утгыг ол.

1. тэгш өнцөгт

2.

3. тэгш өнцөгт

4. параболоор хязгаарлагдсан талбайд

Мөн абсцисса.

5. квадрат

6. координатын тэнхлэгүүд ба шулуун шугамаар хязгаарлагдсан гурвалжинд

7. координатын тэнхлэгүүд болон шулуун шугамаар хязгаарлагдсан гурвалжинд

8. координатын тэнхлэг ба шулуун шугамаар хязгаарлагдсан гурвалжинд

9. параболоор хүрээлэгдсэн хэсэгт

Мөн абсцисса.

10. параболоор хүрээлэгдсэн талбайд

Мөн абсцисса.

Үндсэн

1. М.С. Красс, B.P. Чупрынов. Математикийн үндэс ба түүнийг эдийн засгийн боловсролд ашиглах нь: Сурах бичиг. - 4-р хэвлэл, Испани. - М.: Дело, 2003 он.

2. М.С. Красс, B.P. Чупрынов. Эдийн засгийн мэргэжлээр математик: Сурах бичиг. - 4-р хэвлэл, Испани. - М.: Дело, 2003 он.

3. М.С. Красс, B.P. Чупрынов. Эдийн засгийн бакалаврын математик. Сурах бичиг. - 4-р хэвлэл, Испани. - М.: Дело, 2005 он.

4. Эдийн засагчдад зориулсан дээд математик. Их дээд сургуулиудад зориулсан сурах бичиг / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Эд. проф. Н.Ш. Кремер, - 2-р хэвлэл, шинэчилсэн. болон нэмэлт - М: ЮНИТИ, 2003.

5. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н.Эдийн засгийн мэргэжлээр дээд математик. Сурах бичиг ба практикум (I ба II хэсэг) / Ed. проф. Н.Ш. Кремер, - 2-р хэвлэл, шинэчилсэн. болон нэмэлт – М: Өндөр боловсрол, 2007. - 893 он. - (Шинжлэх ухааны үндэс)

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Дасгал, даалгаварт дээд математик. М. ахлах сургууль. 1999 он.

Нэмэлт

1. I.I. Баврин, В.Л. Далайчид. Дээд математик. "Владосын хүмүүнлэгийн хэвлэлийн төв", 2002 он.

2. I.A. Зайцев. Дээд математик. "Ахлах сургууль", 1998 он.

3. А.С. Солодовников, В.А. Бабаицев, А.В. Брайлов, И.Г. Шандра. Эдийн засаг дахь математик /хоёр хэсэг/. М.Санхүү, статистик. 1999 он.

оюутнуудад зориулсан эмнэлгийн, хүүхдийн, шүдний

эмчилгээний болон урьдчилан сэргийлэх факультетууд

лабораторийн ажилд

"Математик анализын үндсэн ойлголтууд"

1. Сэдвийн шинжлэх ухаан, арга зүйн үндэслэл:

Дериватив ба дифференциал гэсэн ойлголтууд нь математик шинжилгээний үндсэн ойлголтуудын нэг юм. Физик, математикийн олон асуудлыг (хурд, хурдатгал, даралтыг олох гэх мэт) шийдвэрлэхэд деривативын тооцоо шаардлагатай байдаг. Деривативын тухай ойлголтын ач холбогдол нь ялангуяа функцийн дериватив нь аргумент өөрчлөгдөх үед энэ функцийн өөрчлөлтийн хурдыг тодорхойлдог гэдгээр тодорхойлогддог.

Дифференциал ашиглах нь ойролцоогоор тооцоолол хийх, түүнчлэн алдааг үнэлэх боломжийг олгодог.

Функцийн дериватив ба дифференциалыг олох арга, тэдгээрийн хэрэглээ нь дифференциал тооцооллын үндсэн ажил юм. Хөдөлгөөний хурдыг тооцоолох, муруйн шүргэгчийн өнцгийг олох асуудлыг томъёолохтой холбогдуулан деривативын тухай ойлголтын хэрэгцээ үүсдэг. Урвуу асуудал бас боломжтой: хурдаар туулсан зайг тодорхойлж, шүргэгчийн налуугийн шүргэгчээр харгалзах функцийг ол. Ийм урвуу бодлого нь тодорхойгүй интеграл гэсэн ойлголтод хүргэдэг.

Тодорхой интеграл гэдэг ойлголтыг хэд хэдэн практик бодлогод, ялангуяа хавтгай дүрсүүдийн талбайг тооцоолох, хувьсах хүчний гүйцэтгэсэн ажлыг тооцоолох, функцийн дундаж утгыг олоход ашигладаг.

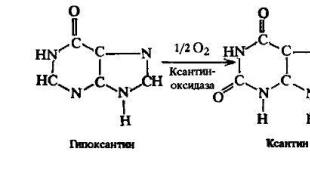
Төрөл бүрийн физик, хими, биологийн үйл явц, үзэгдлийн математикийн тодорхойлолтод зөвхөн судалж буй хэмжигдэхүүнүүдийг төдийгүй эдгээр хэмжигдэхүүний янз бүрийн дарааллын деривативуудыг агуулсан тэгшитгэлийг ихэвчлэн ашигладаг. Жишээлбэл, бактерийн нөхөн үржихүйн хуулийн хамгийн энгийн хувилбарын дагуу нөхөн үржихүйн хурд нь тухайн үеийн нянгийн тоотой пропорциональ байна. Хэрэв энэ тоог N(t) гэж тэмдэглэвэл деривативын физик утгын дагуу нянгийн үржих хурд нь N(t)-ийн дериватив бөгөөд дурдсан хуулийн үндсэн дээр бид бичиж болно. харьцаа N "(t) \u003d k∙N, энд k\u003e 0 - пропорциональ байдлын коэффициент Үүссэн тэгшитгэл нь зөвхөн үл мэдэгдэх N(t) функцийг төдийгүй түүний нэгдүгээр эрэмбийн деривативыг агуулдаг тул алгебрийн бус байна.

2. Товч онол:

1. Деривативын тухай ойлголтод хүргэж буй асуудлууд

1. Материаллаг цэгийн v хурдыг олох бодлого. Материаллаг цэгийг шулуун хөдөлгөөн хийцгээе. Цаг хугацааны хувьд т 1 цэг байрлалд байна М 1. Цаг хугацааны хувьд т 2 жирэмсэн М 2 . Интервалыг тэмдэглэ М 1 , М 2 хөндлөн ∆S; т 2 – т 1 =Δt. Энэ утгыг хөдөлгөөний дундаж хурд гэж нэрлэдэг. Нэг байрлал дахь цэгийн агшин зуурын хурдыг олох М 1 шаардлагатай Δtтэг рүү чиглүүл. Математикийн хувьд энэ нь тийм гэсэн үг юм

, (1)

Тиймээс материаллаг цэгийн агшин зуурын хурдыг олохын тулд функцийн өсөлтийн харьцааны хязгаарыг тооцоолох шаардлагатай. ∆SΔt аргументийн өсөлтөд гэж заасан ∆t→0.

2. Функцийн графикт шүргэгчийн налуу өнцгийг олох асуудал.

Зураг 1

Зарим функцийн графикийг авч үзье y=f(x).Налуу өнцөг гэж юу вэ
цэг дээр зурсан шүргэгч М 1 ? Яг цэг дээр М 1 функцийн графикт шүргэгч зур. Графикаас дурын цэгийг сонго М 2 мөн секант зур. Энэ нь тэнхлэг рүү хазайсан байна Өөөнцгөөр α 1 . Санаж үз ΔМ 1 М 2 Х:

, (2)

Хэрэв цэг бол М 1 засах, цэг тавих М 2 хандлага М 1 , дараа нь секант М 1 М 2 цэг дээрх функцийн графикт шүргэгч болно М 1 мөн та бичиж болно:

, (3)

Тиймээс хэрэв аргументийн өсөлт нь тэг байх хандлагатай бол функцийн өсөлтийг аргументийн өсөлттэй харьцуулах харьцааны хязгаарыг тооцоолох шаардлагатай.

y=f(x) функцийн Δy өсөлтийг өгөгдсөн x цэг дэх Δx аргументийн өсөлттэй харьцуулах хязгаар. 0 Δx тэг рүү чиглэдэг тул тухайн цэг дэх функцийн дериватив гэж нэрлэдэг.

Дериватив тэмдэглэгээ: y", f "(x), . Тодорхойлолтоор

, (4)

Энд Δx=х 2 -х 1 нь аргументийн өсөлт (аргументын хангалттай ойрхон хоёр утгын зөрүү), Δy=y 2 -y 1 нь функцийн өсөлт (утгуудын зөрүү ​аргументийн эдгээр утгуудад тохирох функцийн).

Өгөгдсөн функцийн деривативыг олохыг түүний гэнэ ялгах. Үндсэн үндсэн функцүүдийн ялгааг бэлэн томъёоны дагуу (хүснэгтийг үз), түүнчлэн ашиглан хийдэг. дүрэм:

Алгебрийн нийлбэрийн дериватив функц нь эдгээр функцүүдийн деривативуудын нийлбэртэй тэнцүү байна.

(у+ υ )"= у" + υ "

2. Хоёр функцийн үржвэрийн дериватив нь хоёр дахь функцийн деривативын үржвэрийн нийлбэр ба эхний функцийн деривативын нийлбэртэй тэнцүү байна.

(у∙υ )"=у"υ +уυ "

3. Хэсгийн дериватив Хоёр функцийн хуваарь нь бутархайтай тэнцүү бөгөөд хуваагч нь хуваарийн үржвэр ба хувагчийн дериватив ба хуваагч ба деривативын зөрүү бөгөөд хуваагч нь хувагчийн квадрат байна:

Деривативын физик утга. (4) ба (1)-ийн харьцуулалтаас харахад материаллаг цэгийн шулуун шугаман хөдөлгөөний агшин зуурын хурд нь түүний координатын хугацаанаас хамаарах деривативтай тэнцүү байна.

Функцийн деривативын ерөнхий утга нь түүнийг тодорхойлох явдал юм үйл ажиллагааны өөрчлөлтийн хурд (хурд).аргументийн өөрчлөлтийг харгалзан үзвэл. Биеийн хөргөлтийн хурд, химийн урвалын хурд, бактерийн нөхөн үржих хурд гэх мэт физик, химийн болон бусад үйл явцын хурдыг дериватив ашиглан илэрхийлдэг.

Деривативын геометрийн утга.Функцийн графикт татсан шүргэгчийн налуугийн тангенсийн утгыг математикт гэнэ. шүргэгчийн налуу.

Дифференциалагдах функцийн графикт ямар нэгэн цэгт татсан шүргэгчийн налуу нь тухайн цэг дэх функцийн деривативтай тоон хувьд тэнцүү байна.

Энэ мэдэгдлийг гэж нэрлэдэг деривативын геометрийн утга.

Өгүүллийн агуулга

МАТЕМАТИК ШИНЖИЛГЭЭ,Өөрчлөлтийн янз бүрийн үйл явцыг тоон байдлаар судлах аргуудыг хангадаг математикийн салбар; өөрчлөлтийн хурдыг (дифференциал тооцоолол) судлах, муруй контур ба гадаргуугаар хязгаарлагдсан дүрсүүдийн муруй, талбай, эзэлхүүний уртыг тодорхойлох (интеграл тооцоо) асуудлыг авч үздэг. Математик шинжилгээний асуудлын хувьд тэдгээрийн шийдэл нь хязгаарын тухай ойлголттой холбоотой байдаг нь ердийн зүйл юм.

Математик анализын эхлэлийг 1665 онд И.Ньютон, (ойролцоогоор 1675 онд) Г.Лейбниц нар тус тус тавьсан боловч чухал бэлтгэл ажлыг И.Кеплер (1571–1630), Ф.Кавальери (1598–1647), П.Фермат (1601–1665), Ж.Уоллис (1616–1703), И.Барроу (1630–1677).

Илтгэлийг илүү амьд болгохын тулд бид график хэл рүү хандах болно. Тиймээс уншигч танд энэ нийтлэлийг уншихаасаа өмнө АНАЛИТИК ГЕОМЕТР гэсэн өгүүллийг судлах нь ашигтай байх болов уу.

ДИФФЕРЕНЦИАЛ ТООЦОО

Шүргэх.

Зураг дээр. 1-т муруйн фрагментийг харуулав y = 2х – х 2 хооронд хаалттай х= –1 ба х= 3. Энэ муруйн хангалттай жижиг сегментүүд шулуун харагдаж байна. Өөрөөр хэлбэл, хэрэв Рнь энэ муруйн дурын цэг юм, тэгвэл энэ цэгийг дайран өнгөрч, тухайн цэгийн жижиг хэсэгт муруйн ойролцоолсон шулуун шугам байна. Р, мөн ойр орчмын хэмжээ бага байх тусам илүү сайн болно. Ийм шугамыг цэг дээрх муруйтай шүргэгч гэж нэрлэдэг Р. Дифференциал тооцооллын гол үүрэг бол шүргэгч байгаа муруйн аль ч цэгт шүргэгчийн чиглэлийг олох боломжийг олгодог ерөнхий аргыг бүтээх явдал юм. Хурц завсарлагатай муруйг төсөөлөхөд хялбар байдаг (Зураг 2). Хэрэв Рнь ийм завсарлагааны орой бол ойролцоогоор шулуун шугамыг байгуулах боломжтой PT 1 - цэгийн баруун талд Рболон өөр ойролцоо шугам RT 2 - цэгийн зүүн талд Р. Гэхдээ энэ цэгийг дайран өнгөрдөг ганц шугам байдаггүй Р, энэ нь цэгийн ойролцоо муруйд адилхан сайн ойртсон Пбаруун ба зүүн талд хоёуланд нь тул цэг дээрх шүргэгч Пбайдаггүй.

Зураг дээр. 1 шүргэгч FROMгарал үүслээр нь зурсан О= (0,0). Энэ шулуун шугамын налуу нь 2, i.e. абсцисса 1-ээр өөрчлөгдөхөд ординат 2-оор нэмэгдэнэ.Хэрэв хболон yдээрх дурын цэгийн координатууд юм FROM, дараа нь холдох Озайд Xнэгж баруун тийш, бид холдох О 2 дээр yнэгж хүртэл. Тиймээс, y/х= 2, эсвэл y = 2х. Энэ бол шүргэгч тэгшитгэл юм FROMмуруй руу y = 2х – х 2 цэг дээр О.

Одоо яагаад гэдгийг цэгийг дайран өнгөрч буй шугамын багцаас тайлбарлах шаардлагатай байна О, шулуун шугамыг сонгосон FROM. 2 налуутай шулуун шугам бусад шулуун шугамаас ямар ялгаатай вэ? Нэг энгийн хариулт байдаг бөгөөд тойрогтой шүргэгчийн зүйрлэлийг ашиглан үүнийг өгөх уруу таталтыг эсэргүүцэх нь бидэнд хэцүү байдаг: шүргэгч. FROMнь муруйтай зөвхөн нэг нийтлэг цэгтэй байдаг бол уг цэгийг дайран өнгөрдөг бусад босоо бус шугамууд О, муруйг хоёр удаа гатлана. Үүнийг дараах байдлаар баталгаажуулж болно.

Илэрхийлснээс хойш y = 2х – х 2-ыг хасаж авч болно X 2-ын y = 2х(шууд шугамын тэгшитгэл FROM), дараа нь утгууд yграфикийн хувьд мэдлэг багатай yцэгээс бусад бүх цэгт шулуун шугамын хувьд х= 0. Иймд график нь цэгээс бусад газарт байна О, доор байрладаг FROM, мөн энэ шугам болон график нь зөвхөн нэг нийтлэг цэгтэй байна. Үүнээс гадна хэрэв y = mx- цэгийг дайран өнгөрөх бусад шулуун шугамын тэгшитгэл О, дараа нь огтлолцох хоёр цэг байх ёстой. Үнэхээр, mx = 2х – х 2 нь зөвхөн биш х= 0, гэхдээ бас х = 2 – м. Тэгээд зөвхөн хэзээ м= 2 уулзварын хоёр цэг давхцаж байна. Зураг дээр. 3 нь хэзээ тохиолдлыг харуулж байна м 2-оос бага тул баруун талд Охоёр дахь уулзвар бий.

Юу FROMцэгийг дайран өнгөрөх цорын ганц босоо бус шугам юм ОГрафиктай зөвхөн нэг нийтлэг цэгтэй байх нь түүний хамгийн чухал шинж чанар биш юм. Үнэн хэрэгтээ, хэрэв бид бусад график руу шилжих юм бол бидний тэмдэглэсэн шүргэгчийн шинж чанар ерөнхийдөө хангагдаагүй нь удахгүй тодорхой болно. Жишээлбэл, зурагнаас. 4 (1,1) цэгийн ойролцоо муруйн график байгааг харж болно y = х 3-ыг шулуун шугамаар сайн ойролцоолсон RT, гэхдээ энэ нь нэгээс олон нийтлэг зүйлтэй. Гэсэн хэдий ч бид анхаарч үзэхийг хүсч байна RTцэг дээрх энэ графиктай шүргэнэ Р. Тиймээс, эхний жишээн дээр бидэнд маш сайн үйлчилсэнээс өөр шүргэгчийг тодруулах арга замыг олох шаардлагатай байна.

Үүнийг цэгээр нь авч үзье Омөн дурын цэг Q = (h,к) муруйн график дээр y = 2х – х 2 (Зураг 5) шулуун шугамыг (секант гэж нэрлэдэг) зурсан. Муруйн тэгшитгэлд утгуудыг орлуулах х = hболон y = к, бид үүнийг ойлгодог к = 2h – h 2, тиймээс секантын налуу нь тэнцүү байна

Маш бага хэмжээгээр hутга учир мойрхон 2. Түүнээс гадна сонгох h 0-д хангалттай ойрхон, бид хийж чадна мдур мэдэн 2-т ойртоно.Бид үүнийг хэлж чадна м"хязгаарт очдог" нь 2-той тэнцүү үед hтэг рүү чиглэдэг, эсвэл хязгаар нь юу вэ мүед 2-той тэнцүү hтэг рүү чиглэж байна. Бэлгэдлийн хувьд дараах байдлаар бичигдсэн байна.

Дараа нь цэг дээрх графикт шүргэгч Оцэгээр дамжин өнгөрөх шугам гэж тодорхойлогддог О, энэ хязгаартай тэнцэх налуутай. Шүргэгчийн энэхүү тодорхойлолтыг ерөнхий тохиолдолд хэрэглэнэ.

Бид энэ аргын давуу талыг өөр нэг жишээгээр харуулах болно: муруйн графиктай шүргэгчийн налууг олох болно. y = 2х – х 2 дурын цэг дээр П = (х,y), хамгийн энгийн тохиолдлоор хязгаарлагдахгүй, хэзээ П = (0,0).

Болъё Q = (х + h, y + к) нь зайд байрлах график дээрх хоёр дахь цэг юм hбаруун талд Р(Зураг 6). Налуугийн коэффициентийг олох шаардлагатай к/hсекант PQ. Цэг Qзайд байдаг

тэнхлэг дээгүүр X.

Хаалтуудыг өргөжүүлбэл бид дараахь зүйлийг олно.

Энэ тэгшитгэлээс хасах y = 2х – х 2 , цэгээс босоо зайг ол Рцэг хүртэл Q:

Тиймээс налуу мсекант PQтэнцүү байна

Одоо тэр hтэг рүү чиглэдэг м 2 - 2 хүртэл байдаг х; Бид шүргэгчийн налуугийн сүүлчийн утгыг авна PT. (Хэрэв ижил үр дүн гарна hсөрөг утгыг авдаг бөгөөд энэ нь цэгийн сонголттой тохирч байна Qзүүн талд П.) Үүнийг анхаарна уу х= 0 үр дүн нь өмнөхтэй ижил байна.

Илэрхийлэл 2 - 2 х 2-ын дериватив гэж нэрлэдэг х – х 2. Хуучин өдрүүдэд деривативыг "дифференциал харьцаа", "дифференциал коэффициент" гэж бас нэрлэдэг байв. Хэрэв илэрхийлэл 2 х – х 2 томилно е(х), i.e.

дараа нь деривативыг тэмдэглэж болно

Функцийн графикт шүргэгчийн налууг олохын тулд y = е(х) хэзээ нэгэн цагт орлуулах шаардлагатай еў ( х) энэ цэгт тохирох утга X. Тиймээс налуу еў (0) = 2 хувьд X = 0, еμ (0) = 0 хувьд X= 1 ба е¢ (2) = -2 цаг X = 2.

Дериватив нь мөн тэмдэглэгдсэн байна цагтў , dy/dx, D x yболон Хий.

Баримт нь муруй y = 2х – хӨгөгдсөн цэгийн ойролцоох 2 нь энэ цэг дэх шүргэгчээс бараг ялгагдахгүй тул шүргэгчийн налууг контактын цэг дээрх "муруйны налуу" гэж хэлэх боломжийг бидэнд олгодог. Тиймээс бидний авч үзэж буй муруйн налуу нь (0,0) цэг дээр 2 налуутай байна гэж бид баталж болно. х= 0 өөрчлөлтийн хувь yхарьцангуй хтэнцүү 2. (2,0) цэг дээр шүргэгчийн налуу (болон муруй) -2 байна. (Хасах тэмдэг нь гэсэн утгатай ххувьсагч yбуурна.) (1,1) цэгт шүргэгч хэвтээ байна. Бид муруйг хэлдэг y = 2х – хЭнэ үед 2 нь хөдөлгөөнгүй утгатай байна.

Дээд ба доод.

Бид зүгээр л муруй гэдгийг харуулсан е(х) = 2х – х 2 (1,1) цэг дээр хөдөлгөөнгүй байна. Учир нь еў ( х) = 2 – 2х = 2(1 – х), хэзээ гэдэг нь тодорхой байна х, 1-ээс бага, еў ( х) эерэг, тиймээс yнэмэгддэг; цагт х, том 1, еў ( х) сөрөг, тиймээс yбуурдаг. Тиймээс, зурагт заасан (1,1) цэгийн ойролцоо. 6 үсэг М, гэсэн утгатай цагтцэг хүртэл өсдөг М, цэг дээр хөдөлгөөнгүй Мба цэгийн дараа буурна М. Ийм цэгийг "хамгийн их" гэж нэрлэдэг, учир нь үнэ цэнэ цагтэнэ үед түүний хангалттай жижиг хөршийн аль ч утгаасаа давсан. Үүний нэгэн адил "хамгийн бага" нь эргэн тойронд бүх утгыг илэрхийлэх цэг гэж тодорхойлогддог yүнэ цэнээс давсан цагтяг энэ мөчид. Энэ нь мөн тохиолдож болно гэсэн хэдий ч дериватив е(х) хэзээ нэгэн цагт алга болж, энэ цэгийн ойролцоо тэмдэг нь өөрчлөгддөггүй. Хамгийн их ч биш, хамгийн бага ч биш ийм цэгийг гулзайлтын цэг гэж нэрлэдэг.

Жишээ болгон муруйн хөдөлгөөнгүй цэгийг олъё

Энэ функцийн дериватив нь

мөн цагт алга болно х = 0, X= 1 ба X= –1; тэдгээр. (0,0), (1, –2/15) ба (–1, 2/15) цэгүүдэд. Хэрэв X-1-ээс бага зэрэг бага еў ( х) сөрөг; хэрэв X-1-ээс арай илүү, тэгвэл еў ( х) эерэг байна. Тиймээс (–1, 2/15) цэг нь хамгийн дээд цэг юм. Үүний нэгэн адил цэг (1, -2/15) нь хамгийн бага гэдгийг харуулж болно. Гэхдээ дериватив еў ( х) нь (0,0) цэгийн өмнө болон дараа нь сөрөг байна. Тиймээс (0,0) нь гулзайлтын цэг юм.

Судалгааг муруйн хэлбэр, мөн муруй нь тэнхлэгтэй огтлолцох талаар хийсэн. Xцагт е(х) = 0 (жишээ нь X= 0 эсвэл ) нь зурагт үзүүлсэн шиг түүний графикийг ойролцоогоор дүрслэх боломжийг бидэнд олгоно. 7.

Ерөнхийдөө, хэрэв та ер бусын тохиолдлыг (шулуун шугамын сегмент эсвэл хязгааргүй тооны гулзайлт агуулсан муруй) хасвал дөрвөн сонголт байна. харьцангуй байрлалшүргэгч цэгийн ойролцоох муруй ба шүргэгч Р. (см. будаа. 8, шүргэгч нь эерэг налуутай байна.)

1) Цэгийн хоёр тал дээр Рмуруй нь шүргэгчээс дээгүүр байрладаг (Зураг 8, а). Энэ тохиолдолд бид цэг дээрх муруй гэж хэлдэг Рдоошоо гүдгэр эсвэл хотгор.

2) Цэгийн хоёр тал дээр Рмуруй нь шүргэгчийн доор байрладаг (Зураг 8, б). Энэ тохиолдолд муруйг дээшээ гүдгэр эсвэл зүгээр л гүдгэр гэж нэрлэдэг.

3) ба 4) Муруй нь цэгийн нэг талд шүргэгчээс дээш байрлана Рба доор - нөгөө талд. Энэ тохиолдолд Р- гулзайлтын цэг.

Үнэ цэнийг харьцуулах еў ( х) хоёр талд Рцэг дээрх үнэ цэнээр нь Р, та эдгээр дөрвөн тохиолдлын аль нь тодорхой асуудалд шийдвэрлэх ёстойг тодорхойлж болно.

Хэрэглээ.

Дээр дурдсан бүхэн нь янз бүрийн салбарт чухал хэрэглээг олж авдаг. Жишээлбэл, хэрэв биеийг секундэд 200 фут хурдтайгаар босоогоор дээш шидвэл өндөр с, түүгээр дамжуулан тэдгээр нь байрлах болно тэхлэх цэгтэй харьцуулахад секунд байх болно

Бидний авч үзсэн жишээнүүдийн адилаар бид олж мэднэ

энэ утга нь s үед алга болно. Дериватив еў ( х) c хүртэл эерэг, энэ хугацааны дараа сөрөг байна. Тиймээс, схүртэл нэмэгдэж, дараа нь хөдөлгөөнгүй болж, улмаар буурдаг. Энэ бол дээш шидэгдсэн биеийн хөдөлгөөний ерөнхий тодорхойлолт юм. Үүнээс бид бие нь хамгийн дээд цэгтээ хүрэх үед суралцдаг. Дараа нь орлуулах т= 25/4 инч е(т), бид 625 фут, хамгийн их өргөх өндөр авдаг. Энэ даалгаварт еў ( т) физикийн утгатай. Энэ дериватив нь тухайн үед биеийн хөдөлж буй хурдыг харуулдаг т.

Одоо өөр төрлийн хэрэглээний талаар авч үзье (Зураг 9). 75 см 2 талбай бүхий картон хуудаснаас дөрвөлжин ёроолтой хайрцаг хийх шаардлагатай. Энэ хайрцгийг хамгийн их эзлэхүүнтэй байлгахын тулд ямар хэмжээтэй байх ёстой вэ? Хэрэв X- хайрцагны суурийн тал ба hнь түүний өндөр, дараа нь хайрцагны эзэлхүүн тэнцүү байна В = х 2 h, мөн гадаргуугийн талбай нь 75 = байна х 2 + 4хх. Тэгшитгэлийг хувиргаснаар бид дараахь зүйлийг авна.

-ийн дериватив Втэнцүү болж байна

мөн цагт алга болно X= 5. Дараа нь

болон В= 125/2. Функцийн график В = (75х – х 3)/4-ийг зурагт үзүүлэв. 10 (сөрөг утгууд XЭнэ асуудалд ямар ч физик утга агуулаагүй тул орхигдуулсан).

Дериватив.

Дифференциал тооцооллын чухал ажил бол деривативыг хурдан бөгөөд хялбар олох боломжийг олгодог аргуудыг бий болгох явдал юм. Жишээлбэл, үүнийг тооцоолоход хялбар байдаг

(Тогтмолын дериватив нь мэдээж тэг юм.) Ерөнхий дүрмийг гаргахад хэцүү биш:

хаана n- дурын бүхэл тоо эсвэл бутархай. Тухайлбал,

(Энэ жишээ нь бутархай илтгэгчид хэр ашигтай болохыг харуулж байна.)

Энд хамгийн чухал зарим томъёо байна:

Мөн дараах дүрмүүд байдаг: 1) хэрэв хоёр функц тус бүр g(х) ба е(х) нь деривативтай бол тэдгээрийн нийлбэрийн дериватив нь эдгээр функцүүдийн деривативуудын нийлбэртэй тэнцүү, ялгааны дериватив нь деривативуудын зөрүүтэй тэнцүү байна, i.e.

2) хоёр функцийн үржвэрийн деривативыг дараахь томъёогоор тооцоолно.

3) хоёр функцийн харьцааны дериватив нь хэлбэртэй байна

4) тогтмол тоогоор үржүүлсэн функцийн дериватив нь энэ функцийн деривативаар үржүүлсэн тогтмолтай тэнцүү, өөрөөр хэлбэл.

Функцийн утгыг үе шаттайгаар тооцоолох шаардлагатай болдог. Жишээлбэл, нүглийг тооцоолох х 2, бид эхлээд олох хэрэгтэй у = х 2 , дараа нь аль хэдийн тооны синусыг тооцоол у. Бид "гинжин дүрэм" гэж нэрлэгддэг ийм нарийн төвөгтэй функцүүдийн деривативыг олдог.

Бидний жишээнд е(у) = нүгэл у, еў ( у) = cos у, тиймээс,

Эдгээр болон бусад ижил төстэй дүрмүүд нь олон функцийн деривативуудыг нэн даруй бичих боломжтой болгодог.

Шугаман ойролцоо тооцоолол.

Деривативыг мэдсэнээр бид олон тохиолдолд аль нэг цэгийн ойролцоох функцын графикийг тухайн цэг дэх шүргэгчээр нь сольж чаддаг нь шулуун шугамтай ажиллахад хялбар байдаг тул маш чухал юм.

Энэ санаа нь функцүүдийн ойролцоо утгыг тооцоолоход шууд хэрэглэгдэхүүнийг олдог. Жишээлбэл, утгыг тооцоолоход хэцүү байдаг х= 1.033. Гэхдээ та 1.033 тоо 1-тэй ойролцоо байгааг ашиглаж болно. хаах х= 1 бид шүргэгч муруй графикийг ямар ч ноцтой алдаа гаргахгүйгээр сольж болно. Ийм шүргэгчийн налуу нь деривативын утгатай тэнцүү байна ( х 1/3)ў = (1/3) х x = 1-ийн хувьд –2/3, өөрөөр хэлбэл. 1/3. (1,1) цэг нь муруй дээр байрлах ба энэ цэг дэх муруй руу шүргэгчийн налуу нь 1/3 байх тул шүргэгч тэгшитгэл нь дараах хэлбэртэй байна.

Энэ шулуун шугам дээр X = 1,033

Хүлээн авсан үнэ цэнэ yбодит үнэ цэнэд маш ойрхон байх ёстой y; бөгөөд үнэндээ энэ нь үнэнээс ердөө 0.00012-оор илүү байна. Математикийн шинжилгээнд ийм шугаман ойролцоо тооцооллын нарийвчлалыг сайжруулах боломжтой аргуудыг боловсруулсан. Эдгээр аргууд нь бидний ойролцоогоор тооцооллын найдвартай байдлыг баталгаажуулдаг.

Сая тайлбарласан процедур нь нэг хэрэгтэй тэмдэглэгээг санал болгож байна. Болъё П- функцийн графикт харгалзах цэг ехувьсагч X, мөн функцийг зөвшөөр е(х) ялгах боломжтой. Цэгийн ойролцоох муруйн графикийг өөрчилье Ртэр үед түүнтэй шүргэнэ. Хэрэв Xүнэ цэнэ болгон өөрчлөх h, тэгвэл шүргэгч ординат нь утгаараа өөрчлөгдөнө hХ е ў ( х). Хэрэв hмаш бага бол сүүлчийн утга нь ординатын жинхэнэ өөрчлөлттэй ойролцоо утгатай байна yграфик. Хэрэв оронд нь hБид тэмдэг бичих болно dx(энэ бол бүтээгдэхүүн биш!), Харин ординатын өөрчлөлт yтэмдэглэнэ dy, тэгвэл бид авна dy = е ў ( х)dx, эсвэл dy/dx = е ў ( х) (см. будаа. арван нэгэн). Тиймээс оронд нь Dyэсвэл е ў ( х) деривативыг илэрхийлэхийн тулд тэмдгийг ихэвчлэн ашигладаг dy/dx. Энэ тэмдэглэгээний тав тухтай байдал нь голчлон гинжин дүрмийн тодорхой харагдах байдлаас хамаардаг (нийлмэл функцийг ялгах); шинэ тэмдэглэгээнд энэ томъёо дараах байдалтай байна.

Энэ нь хаана байна гэсэн үг юм цагт-аас хамаарна у, a уэргээд хамаарна X.

Үнэ цэнэ dyдифференциал гэж нэрлэдэг цагт; үнэндээ үүнээс хамаарна хоёрхувьсагч, тухайлбал: from Xболон нэмэгдэл dx. Өсөх үед dxмаш жижиг, хэмжээ dyутгын харгалзах өөрчлөлттэй ойролцоо байна y. Гэхдээ нэмэгдлээ гэж бодъё dxбага, шаардлагагүй.

Функцийн дериватив y = е(х) бид тэмдэглэв е ў ( х) эсвэл dy/dx. Ихэнхдээ деривативын деривативыг авах боломжтой байдаг. Үр дүнг хоёр дахь дериватив гэж нэрлэдэг е (х) ба тэмдэглэсэн е ўў ( х) эсвэл г 2 y/dx 2. Жишээлбэл, хэрэв е(х) = х 3 – 3х 2, тэгвэл е ў ( х) = 3х 2 – 6хболон е ўў ( х) = 6х– 6. Үүнтэй төстэй тэмдэглэгээг илүү-ийн деривативт ашигладаг өндөр захиалга. Гэсэн хэдий ч олон тооны анхны тооноос зайлсхийхийн тулд (үүсмэлийн дараалалтай тэнцүү) дөрөв дэх деривативыг (жишээлбэл) дараах байдлаар бичиж болно. е (4) (х), ба дериватив n-р дараалал е (n) (х).

Хоёрдахь дериватив эерэг байвал нэг цэгийн муруй доош гүдгэр, хоёр дахь дериватив сөрөг байвал дээшээ гүдгэр болохыг харуулж болно.

Хэрэв функц нь хоёр дахь деривативтай бол утгын өөрчлөлт yөсөлттэй тохирч байна dxхувьсагч X, ойролцоогоор томъёогоор тооцоолж болно

Энэ ойролцоолсон үзүүлэлт нь дифференциалаар өгөгдсөнөөс ерөнхийдөө илүү сайн байдаг еў ( х)dx. Энэ нь муруйн хэсгийг солих нь шулуун шугам байхаа больсон, харин парабол юм.

Хэрэв функц байгаа бол е(х) өндөр эрэмбийн деривативууд байдаг, тэгвэл

Үлдсэн нэр томъёо нь хэлбэртэй байна

хаана х- хооронд хэдэн тоо хболон х + dx. Дээрх үр дүнг үлдэгдэлтэй Тейлорын томъёо гэж нэрлэдэг. Хэрэв е(х) бүх дарааллын деривативтай, дараа нь ихэвчлэн R n® 0 нь n ® Ґ .

ИНТЕГРАЛ ТООЦОО

Квадратууд.

Муруй шугаман хавтгай дүрсүүдийн талбайг судлах нь математик шинжилгээний шинэ талыг нээж өгдөг. Эртний Грекчүүд ч ийм асуудлыг шийдэхийг оролдсон бөгөөд жишээлбэл, тойргийн талбайг тодорхойлох нь хамгийн хэцүү ажлуудын нэг байв. Архимед энэ асуудлыг шийдвэрлэхэд маш их амжилтанд хүрсэн бөгөөд тэрээр параболик сегментийн талбайг олж чадсан (Зураг 12). Архимед маш нарийн үндэслэлийг ашиглан параболик сегментийн талбай нь хүрээлэгдсэн тэгш өнцөгтийн талбайн 2/3 нь бөгөөд энэ тохиолдолд (2/3)(16) = 32/ тэнцүү болохыг нотолсон. 3. Бид дараа нь харах болно, энэ үр дүнг математикийн шинжилгээний аргаар хялбархан олж авах боломжтой.

Ньютон, Лейбниц нарын өмнөх хүмүүс, голчлон Кеплер, Кавальери нар муруй шугаман дүрсүүдийн талбайг тооцоолох асуудлыг логикийн хувьд зөв гэж нэрлэх аргагүй боловч маш үр дүнтэй арга замаар шийдсэн. Уоллис 1655 онд Кеплер, Кавальери нарын аргыг Декартын (аналитик геометр) аргуудтай хослуулж, шинээр төрсөн алгебрийн давуу талыг ашиглах үед Ньютон гарч ирэх үе шат бүрэн бэлтгэгдсэн байв.

Уоллис талбайг тооцоолох шаардлагатай байсан зургийг маш нарийн тууз болгон хуваасан бөгөөд тус бүр нь ойролцоогоор тэгш өнцөгт гэж тооцогддог. Дараа нь тэр ойролцоох тэгш өнцөгтүүдийн талбайг нэмж, хамгийн энгийн тохиолдолд туузны тоо хязгааргүй болох үед тэгш өнцөгтүүдийн талбайн нийлбэр хандлагатай байсан утгыг олж авсан. Зураг дээр. 13-т муруй доорх талбайн зарим судалтай тохирох тэгш өнцөгтүүдийг харуулав y = х 2 .

Үндсэн теорем.

Ньютон, Лейбниц нарын агуу нээлт нь талбайн нийлбэрийн хязгаарт шилжих хүнд хэцүү үйл явцыг арилгах боломжтой болсон. Энэ нь газар нутгийн үзэл баримтлалыг шинээр харсны ачаар хийгдсэн. Хамгийн гол нь ординатыг зүүнээс баруун тийш хөдөлгөснөөр үүссэн муруйн доорх талбайг төлөөлж, ординатаар шүүрдсэн хэсэг хэр хурдан өөрчлөгдөж байгааг асуух хэрэгтэй. Хэрэв бид тухайн газар нутгийг урьдчилан мэддэг хоёр онцгой тохиолдлыг авч үзвэл энэ асуултад хариулах түлхүүрийг олж авна.

Шугаман функцийн график доорх талбайгаас эхэлье y = 1 + х, учир нь энэ тохиолдолд талбайг энгийн геометр ашиглан тооцоолж болно.

Болъё А(х) нь шулуун шугамын хооронд бэхлэгдсэн хавтгайн хэсэг юм y = 1 + хба сегмент OQ(Зураг 14). Жолоо барьж байхдаа QPбаруун дөрвөлжин А(х) нэмэгддэг. Ямар хурдаар? Трапецын талбай нь түүний өндрийн үржвэр ба суурийн нийлбэрийн хагастай тэнцүү гэдгийг бид мэдэж байгаа тул энэ асуултад хариулахад хэцүү биш юм. Тиймээс,

Талбайн өөрчлөлтийн хурд А(х) түүний деривативаар тодорхойлогдоно

Бид үүнийг харж байна Аў ( х) ординаттай давхцаж байна цагтоноо Р. Энэ нь санамсаргүй хэрэг үү? Зураг дээр үзүүлсэн параболыг шалгахыг хичээцгээе. 15. Дөрвөлжин А (х) параболын доор цагт = X 0-ээс 2-ын хооронд байна Xтэнцүү байна А(х) = (1 / 3)(х)(х 2) = х 3/3. Энэ талбайн өөрчлөлтийн хурдыг илэрхийллээр тодорхойлно

энэ нь ординаттай яг таарч байна цагтхөдлөх цэг Р.

Энэ дүрэм ерөнхий тохиолдолд үйлчилнэ гэж үзвэл тийм

функцийн график доорх талбайн өөрчлөлтийн хурд юм y = е(х), дараа нь үүнийг бусад талбайн тооцоонд ашиглаж болно. Үнэндээ харьцаа Аў ( х) = е(х) нь дараах байдлаар томьёолж болох үндсэн теоремыг илэрхийлнэ: дериватив буюу талбайн өөрчлөлтийн хурдыг функцээр илэрхийлнэ. X, функцийн утгатай тэнцүү байна е (х) цэг дээр X.

Жишээлбэл, функцийн график доорх талбайг олох y = х 0-ээс 3 хүртэл X(Зураг 16), бид тавьсан

Боломжит хариултыг уншина:

-ийн уламжлалаас хойш X 4/4 нь үнэхээр тэнцүү X 3 . Түүнээс гадна, А(х) нь тэг байна X= 0, хэрэв байх ёстой А(х) нь үнэхээр газар нутаг юм.

Математикийн шинжилгээнд дээрх илэрхийллээс өөр хариулт байхгүй нь батлагдсан А(х), байдаггүй. Дараах эвристик (хатуу бус) үндэслэлийг ашиглан энэхүү мэдэгдэл нь үнэмшилтэй гэдгийг харуулъя. Хоёрдахь шийдэл байна гэж бодъё В(х). Хэрэв А(х) ба В(х) тэг утгаас нэгэн зэрэг "эхлэх" X= 0 ба үргэлж ижил хурдаар өөрчлөгддөг бол тэдгээрийн утга хэзээ ч өөрчлөгдөхгүй Xөөр болж чадахгүй. Тэд хаа сайгүй таарч байх ёстой; Тиймээс өвөрмөц шийдэл байдаг.

Та харьцааг хэрхэн зөвтгөх вэ Аў ( х) = е(х) ерөнхийдөө? Энэ асуултын хариуг зөвхөн талбайн өөрчлөлтийн хурдыг функц болгон судалж байж болно Xерөнхийдөө. Болъё м- функцийн хамгийн бага утга е (х) -аас эхлэн интервалд Xөмнө ( х + h), a Мнь ижил интервал дахь энэ функцийн хамгийн том утга юм. Дараа нь өнгөрөх үед талбай нэмэгдэнэ X( х + h) хоёр тэгш өнцөгтийн талбайн хооронд хаалттай байх ёстой (Зураг 17). Хоёр тэгш өнцөгтийн суурь нь тэнцүү байна h. Жижиг тэгш өнцөгт нь өндөртэй мболон талбай mh, тус тус илүү том, Мболон Мh. Талбай дээр vs. X(Зураг 18) нь абсцисса руу шилжихэд байгааг харж болно h, ординатын утга (өөрөөр хэлбэл талбай) хоорондын хэмжээгээр нэмэгддэг mhболон Мh. Энэ график дахь секантын налуу нь хооронд байна мболон М. хэзээ юу болох вэ hтэг рүү явах уу? Хэрэв функцийн график y = е(х) тасралтгүй (өөрөөр хэлбэл тасалдал агуулаагүй), дараа нь М, ба мхандлагатай е(х). Тиймээс налуу Аў ( х) функц болох талбайн график Xтэнцүү байна е(х). Ийм л дүгнэлтэд хүрэх ёстой байсан.

Лейбниц муруйн доорх талбайг санал болгосон y = е(х) 0-ээс атэмдэглэгээ

Нарийн арга барилаар тодорхой интеграл гэж нэрлэгддэг энэхүү интегралыг Уоллисын аргаар тодорхой нийлбэрийн хязгаар гэж тодорхойлох ёстой. Дээр олж авсан үр дүнгээс харахад энэ интеграл нь ийм функцийг олох боломжтой нөхцөлд тооцогдох нь тодорхой байна. А(х), хэзээ алга болдог X= 0 ба дериватив байна Аў ( х) тэнцүү е (х). Ийм функцийг олохыг ихэвчлэн интеграл гэж нэрлэдэг боловч энэ үйлдлийг дифференциалын эсрэг гэж нэрлэх нь илүү тохиромжтой бөгөөд энэ нь тодорхой утгаараа ялгаатай байдлын урвуу утгатай юм. Олон гишүүнтийн хувьд интеграл нь хялбар байдаг. Жишээлбэл, хэрэв

ялгах замаар шалгахад хялбар байдаг А(х).

Талбайг тооцоолохын тулд А 1 муруй дор y = 1 + х + х 0 ба 1-ийн ординатуудын хооронд 2 / 2-ыг бид зүгээр л бичнэ

болон орлуулах замаар X= 1, бид олж авна А 1 = 1 + 1/2 + 1/6 = 5/3. Дөрвөлжин А(х) 0-ээс 2 хүртэл байна А 2 = 2 + 4/2 + 8/6 = 16/3. Зураг дээрээс харж болно. 19, 1 ба 2-р ординатуудын хооронд хүрээлэгдсэн талбай нь А 2 – А 1 = 11/3. Үүнийг ихэвчлэн тодорхой интеграл хэлбэрээр бичдэг

Эзлэхүүн.

Үүнтэй төстэй үндэслэл нь хувьсгалын биетүүдийн хэмжээг тооцоолоход гайхалтай хялбар болгодог. Эртний Грекчүүд өөрсдийн мэддэг аргуудыг ашиглан маш их бэрхшээлтэй шийдэж чадсан өөр нэг сонгодог асуудал болох бөмбөгний эзэлхүүнийг тооцоолох жишээн дээр үүнийг харуулъя.

Радиустай тойргийн дөрөвний нэг дотор хүрээлэгдсэн онгоцны нэг хэсгийг эргүүлье r, тэнхлэгийн эргэн тойронд 360 ° өнцгөөр X. Үүний үр дүнд бид хагас бөмбөрцөг (Зураг 20) авдаг бөгөөд түүний эзлэхүүнийг бид тэмдэглэдэг В(х). Энэ нь ямар хурдтай байгааг тодорхойлох шаардлагатай В(х) нэмэгдэж байна х. -аас явж байна Xруу X + h, эзлэхүүний өсөлт нь эзлэхүүнээс бага байгаа эсэхийг шалгахад хялбар байдаг х(r 2 – х 2)hрадиус ба өндөртэй дугуй цилиндр h, мөн эзлэхүүнээс илүү х[r 2 – (х + h) 2 ]hцилиндрийн радиус ба өндөр h. Тиймээс функцийн график дээр В(х) секантын налууг хооронд нь битүүмжилнэ х(r 2 – х 2) ба х[r 2 – (х + h) 2 ]. Хэзээ hтэг рүү чиглэдэг, налуу нь тэг рүү чиглэдэг

At х = rбид авдаг

бөмбөрцгийн эзэлхүүний хувьд, тиймээс 4 p rБөмбөгний нийт эзэлхүүний хувьд 3/3.

Үүнтэй төстэй арга нь муруйн урт ба муруй гадаргуугийн талбайг олох боломжийг олгодог. Жишээлбэл, хэрэв а(х) - нумын урт PRЗураг дээр. 21, дараа нь бидний даалгавар бол тооцоолох явдал юм аў( х). Эвристик түвшинд бид үр дүнг хатуу нотлоход зайлшгүй шаардлагатай хязгаарт хүрэх ердийн гарцыг ашиглахгүй байх арга техникийг ашиглах болно. Функцийн өөрчлөлтийн хурд гэж үзье а(х) цэг дээр Рмуруйг шүргэгчээр нь сольсонтой адил PTцэг дээр П. Гэхдээ зурагнаас. 21 нь гишгэх үед шууд харагдана hцэгийн баруун эсвэл зүүн талд Xдагуу RTутга учир а(х) өөрчлөгдөнө

Тиймээс функцийн өөрчлөлтийн хурд а(х) байна

Функцийг өөрөө олохын тулд а(х), тэгш байдлын баруун талд байгаа илэрхийллийг нэгтгэх шаардлагатай. Ихэнх функцүүдэд нэгтгэх нь нэлээд хэцүү байдаг. Тиймээс интеграл тооцооллын аргуудыг хөгжүүлэх нь математик шинжилгээний томоохон хэсэг юм.

Примитивүүд.

Өгөгдсөн функцтэй дериватив нь тэнцүү функц бүр е(х), эсрэг дериватив (эсвэл анхдагч) гэж нэрлэдэг е(х). Тухайлбал, X 3/3 - функцийн эсрэг дериватив X 2 учир нь ( х 3 /3)ў = х 2. Мэдээжийн хэрэг X 3/3 нь функцийн цорын ганц эсрэг дериватив биш юм X 2 учир нь х 3 /3 + Cнь мөн дериватив юм X 2 тогтмол хувьд ХАМТ. Гэсэн хэдий ч дараах зүйлд бид ийм нэмэлт тогтмолуудыг орхихыг зөвшөөрч байна. Ерөнхийдөө

хаана nэерэг бүхэл тоо, учир нь ( x n + 1/(n+ 1))ў = x n. (1) харилцаа нь бүр илүү ерөнхий утгаараа хангагдсан бол nдурын рационал тоогоор солино к, -1-ээс бусад.

Өгөгдсөн функцийн дурын эсрэг дериватив функц е(х)-ийг ихэвчлэн -ийн тодорхойгүй интеграл гэж нэрлэдэг е(х) гэж тэмдэглэнэ

Жишээлбэл, хойш (нүгэл х)ў = cos х, томъёо

Өгөгдсөн функцийн тодорхойгүй интегралын томъёо байдаг олон тохиолдолд үүнийг тодорхойгүй интегралын олон тооны өргөн хэвлэгдсэн хүснэгтээс олж болно. Энгийн функцүүдийн интегралууд нь хүснэгт хэлбэртэй байдаг (тэдгээрт хүч, логарифм, экспоненциал функц, тригонометрийн функц, урвуу тригонометрийн функц, түүнчлэн нэмэх, хасах, үржүүлэх, хуваах замаар олж авсан төгсгөлийн хослолууд орно). Хүснэгтийн интегралын тусламжтайгаар интегралыг илүү төвөгтэй функцүүдээс ч бас тооцоолж болно. Тодорхой бус интегралыг тооцоолох олон арга байдаг; Эдгээрээс хамгийн түгээмэл нь хувьсах буюу орлуулах арга юм. Энэ нь тодорхойгүй интегралд орлуулахыг хүсвэл (2) хзарим дифференциалагдах функц руу х = g(у), интеграл өөрчлөгдөхгүй байхын тулд зайлшгүй шаардлагатай х-ээр сольсон gў ( у)ду. Өөрөөр хэлбэл тэгш байдал

(орлуулалт 2 х = у, хаанаас 2 dx = ду).

Интеграцийн өөр нэг аргыг танилцуулъя - хэсэгчлэн нэгтгэх аргыг. Энэ нь сайн мэддэг томьёо дээр суурилдаг

Зүүн ба баруун талыг нэгтгэж, үүнийг харгалзан үзсэний дараа

Энэ томъёог интеграцийн томъёо гэж нэрлэдэг.

Жишээ 2. олох хэрэгтэй. Учир нь cos х= (нүгэл х)ў, бид үүнийг бичиж болно

(5) -аас у = хболон v= нүгэл х, бид авдаг

Түүнээс хойш (-cos х)ў = нүгэл хбид үүнийг олж ба

Бид маш өргөн хүрээтэй сэдвийн талаар маш товч танилцуулгаар хязгаарлагдаж, олон тооны заль мэх хуримтлагдсан гэдгийг онцлон тэмдэглэх нь зүйтэй.

Хоёр хувьсагчийн функцууд.

Муруйн улмаас y = е(х), бид хоёр асуудлыг авч үзсэн.

1) Өгөгдсөн цэг дээрх муруйн шүргэгчийн налууг ол. Энэ асуудлыг деривативын утгыг тооцоолох замаар шийддэг еў ( х) өгөгдсөн цэг дээр.

2) Тэнхлэгийн сегмент дээрх муруй доорх талбайг ол Xбосоо шугамаар хязгаарлагдсан X = аболон X = б. Энэ асуудлыг тодорхой интегралыг тооцоолох замаар шийддэг.

Эдгээр асуудал бүр нь гадаргуугийн хувьд аналогтой байдаг z = е(х,y).

1) Өгөгдсөн цэг дээр гадаргуутай шүргэгч хавтгайг ол.

2) Хавтгайн хэсгийн дээрх гадаргуугийн доорх эзэлхүүнийг ол ху, хязгаарлагдмал муруй ХАМТ, ба хажуу талд - хавтгайд перпендикуляр xyхилийн муруйн цэгүүдийг дайран өнгөрөх ХАМТ (см. будаа. 22).

Дараах жишээнүүд эдгээр асуудлыг хэрхэн шийдэж байгааг харуулж байна.

Жишээ 4. Гадаргуутай шүргэгч хавтгайг ол

цэг дээр (0,0,2).

Хавтгайн дотор байрлах огтлолцох хоёр шугам өгөгдсөн бол хавтгайг тодорхойлно. Эдгээр мөрүүдийн нэг л 1) бид онгоцонд суух болно xz (цагт= 0), хоёр дахь ( л 2) - онгоцонд yz (х = 0) (см. будаа. 23).

Юуны өмнө, хэрэв цагт= 0, тэгвэл z = е(х,0) = 2 – 2х – 3х 2. -тай холбоотой дериватив X, тэмдэглэсэн еў х(х,0) = –2 – 6х, цагт X= 0 нь -2 гэсэн утгатай. Чигээрээ л 1 тэгшитгэлээр өгөгдсөн z = 2 – 2х, цагт= 0 - шүргэгч ХАМТ 1 , гадаргуугийн хавтгайтай огтлолцох шугамууд цагт= 0. Үүний нэгэн адил хэрэв X= 0, тэгвэл е(0,y) = 2 – y – y 2 , мөн хамаарах дериватив цагтхэлбэртэй байна

Учир нь еў y(0.0) = -1, муруй ХАМТ 2 - гадаргуугийн хавтгайтай огтлолцох шугам yz- шүргэгчтэй л 2 тэгшитгэлээр өгөгдсөн z = 2 – y, X= 0. Хүссэн шүргэгч хавтгай нь хоёр шулууныг агуулна л 1 ба л 2 ба тэгшитгэлээр бичигдэнэ

Энэ бол онгоцны тэгшитгэл юм. Үүнээс гадна бид шууд авдаг л 1 ба л 2 гэж үзвэл, тус тус цагт= 0 ба X = 0.

Тэгшитгэл (7) нь шүргэгч хавтгайг үнэхээр тодорхойлж байгаа нь энэ тэгшитгэлд (6) тэгшитгэлийн нэгдүгээр эрэмбийн гишүүн, хоёр дахь эрэмбийн гишүүдийг дараах хэлбэрээр илэрхийлж болохыг анзаарвал эвристик түвшинд шалгаж болно. . Учир нь энэ илэрхийлэл бүх утгын хувьд сөрөг байна Xболон цагт, Түүнээс гадна X = цагт= 0, гадаргуу (6) нь цэгээс бусад бүх газарт хавтгай (7) доор байрладаг Р= (0,0,0). Гадаргууг (6) цэг дээр дээшээ гүдгэр гэж хэлж болно Р.

Жишээ 5. Гадаргуутай шүргэгч хавтгайг ол z = е(х,y) = х 2 – y 0 гарал үүсэлтэй 2.

Гадаргуу дээр цагт= 0 бидэнд байна: z = е(х,0) = х 2 ба еў х(х,0) = 2х. Дээр ХАМТ 1, огтлолцлын шугам, z = х 2. Яг цэг дээр Оналуу байна еў х(0,0) = 0. Хавтгай дээр X= 0 бидэнд байна: z = е(0,y) = –y 2 ба еў y(0,y) = –2y. Дээр ХАМТ 2, огтлолцлын шугам, z = –y 2. Яг цэг дээр Омуруй налуу ХАМТ 2 тэнцүү еў y(0,0) = 0. Шүргэдэг тул ХАМТ 1 ба ХАМТ 2 нь тэнхлэг Xболон цагт, тэдгээрийг агуулсан шүргэгч хавтгай нь хавтгай юм z = 0.

Гэсэн хэдий ч гарал үүслийн ойролцоо бидний гадаргуу шүргэгч хавтгайтай нэг тал дээр байдаггүй. Үнэхээр муруй ХАМТ 1 нь 0 цэг ба муруйгаас бусад газарт шүргэгч хавтгайн дээр байрладаг ХАМТ 2 - тус тусын доор. Гадаргуу нь шүргэгч хавтгайтай огтлолцдог z= 0 шулуун шугамаар цагт = Xболон цагт = –X. Ийм гадаргуугийн эхэнд эмээлийн цэг байдаг (Зураг 24).

Хувийн деривативууд.

Өмнөх жишээнүүдэд бид деривативуудыг ашигласан е (х,y) дээр Xболон өөр цагт. Одоо ийм деривативуудыг илүү ерөнхий байдлаар авч үзье. Хэрэв бид хоёр хувьсагчийн функцтэй бол, жишээлбэл, Ф(х,y) = х 2 – xy, дараа нь бид цэг бүрт түүний "хэсэгчилсэн дериватив"-ийн хоёрыг, нэгийг нь функцийг ялгах замаар тодорхойлж болно. Xболон засах цагт, болон бусадтай холбоотойгоор ялгах цагтболон засах X. Эдгээр деривативуудын эхнийхийг дараах байдлаар тэмдэглэв еў х(х,y) эсвэл ¶ е/¶ х; хоёр дахь нь яаж ее y. Холимог дериватив хоёулаа бол (хэрэв Xболон цагт, дээр цагтболон X) тасралтгүй, дараа нь ¶ 2 е/¶ х¶ y= ¶ 2 е/¶ y¶ х; бидний жишээнд ¶ 2 е/¶ х¶ y= ¶ 2 е/¶ y¶ х = –1.

Хэсэгчилсэн дериватив еў х(х,y) функцийн өөрчлөлтийн хурдыг заана ецэг дээр ( х,y) нэмэгдүүлэх чиглэлд X, a еў y(х,y) нь функцийн өөрчлөлтийн хурд юм еөгсөх чиглэлд цагт. Функцийн өөрчлөлтийн хурд ецэг дээр ( X,цагт) өнцгийг бүрдүүлж буй шулуун шугамын чиглэлд qэерэг тэнхлэгийн чиглэлтэй X, функцийн дериватив гэж нэрлэдэг ечиглэсэн; түүний утга нь функцийн хоёр хэсэгчилсэн деривативын хослол юм Шүргэдэг хавтгай дахь f нь бараг тэнцүү байна (жижиг dxболон dy) жинхэнэ өөрчлөлт zгадаргуу дээр, гэхдээ дифференциалыг тооцоолох нь ихэвчлэн хялбар байдаг.

Нэг хэмжээст тохиолдолд нийлмэл функцийн дериватив буюу гинжин дүрэм гэж нэрлэгддэг хувьсах аргын өөрчлөлтөөс бидний аль хэдийн авч үзсэн томьёо. цагт-аас хамаарна X, a X-аас хамаарна т, харагдаж байна:

Хоёр хувьсагчийн функцүүдийн хувьд ижил төстэй томъёо нь дараах хэлбэртэй байна.

Хэсэгчилсэн ялгавартай байдлын тухай ойлголт, тэмдэглэгээг илүү өндөр хэмжигдэхүүнүүдэд хялбархан ерөнхийлж болно. Ялангуяа тэгшитгэлээр гадаргууг далд хэлбэрээр өгсөн бол е(х,y,z) = 0, гадаргууд шүргэгч хавтгайн тэгшитгэлийг илүү тэгш хэмтэй хэлбэрээр өгч болно: цэг дээрх шүргэгч хавтгайн тэгшитгэл ( x(x 2 /4)], дараа нь дээр нэгтгэнэ X 0-ээс 1 хүртэл. Эцсийн үр дүн 3/4 байна.

Формула (10) нь давхар интеграл гэж нэрлэгддэг, i.e. энгийн "эс"-ийн эзлэхүүний нийлбэрийн хязгаар гэж. Ийм эс бүр нь D суурьтай байдаг хД yтэгш өнцөгт суурийн зарим цэг дээрх гадаргуугийн өндөртэй тэнцүү өндөр ( см. будаа. 26). Томъёо (10) дээрх хоёр үзэл бодол нь тэнцүү байгааг харуулж болно. Давхар интегралыг механикт тулгардаг хүндийн төв болон олон тооны моментуудыг олоход ашигладаг.

Математикийн аппаратын илүү нарийн үндэслэл.

Одоогийн байдлаар бид математикийн шинжилгээний үзэл баримтлал, аргуудыг зөн совингийн түвшинд танилцуулж, геометрийн дүрсийг ашиглахаас буцахгүй байна. 19-20-р зуунд бий болсон илүү хатуу аргуудыг товч авч үзэх нь бидэнд үлдлээ.

19-р зууны эхэн үед "математикийн анализыг бий болгох" -ын дайралт, довтолгооны эрин үе дуусах үед түүнийг зөвтгөх тухай асуултууд урган гарч ирэв. Абел, Коши болон бусад хэд хэдэн шилдэг математикчдын бүтээлүүдэд "хязгаарлалт", "тасралтгүй функц", "конвергент цуваа" гэсэн ойлголтуудыг нарийн тодорхойлсон байдаг. Энэ нь математикийн шинжилгээний үндэс суурийг логик дарааллаар нэвтрүүлэх, найдвартай судалгааны хэрэгсэл болгоход зайлшгүй шаардлагатай байв. 1872 онд Вейерштрасс хаа сайгүй үргэлжилдэг боловч хаана ч ялгагдахгүй функцүүдийг нээсний дараа (ийм функцүүдийн график цэг бүр дээр завсарлагатай) бүрэн үндэслэлтэй байх хэрэгцээ улам бүр тодорхой болсон. Энэ үр дүн нь математикчдад гайхалтай сэтгэгдэл төрүүлэв, учир нь энэ нь тэдний геометрийн зөн совинтой илт зөрчилдөж байв. Геометрийн зөн совингийн найдваргүй байдлын илүү тод жишээ бол тодорхой квадратыг бүрэн дүүргэсэн Д.Пианогийн бүтээсэн тасралтгүй муруй байв. түүний бүх цэгийг дайран өнгөрдөг. Эдгээр болон бусад нээлтүүд нь математикийн "арифметизаци" хөтөлбөрийг амьдралд авчирсан, i.e. тооны ухагдахууны тусламжтайгаар математикийн бүх ойлголтыг нотлох замаар илүү найдвартай болгох. Математикийн үндэс суурьтай холбоотой бүтээлүүдийг дүрслэхээс бараг цэвэршсэн байдлаар татгалзсан нь түүхэн үндэслэлтэй байв.

Логик хатуу байдлын орчин үеийн хууль тогтоомжийн дагуу муруйн доорх талбайн талаар ярих нь хүлээн зөвшөөрөгдөхгүй y = е(х) ба тэнхлэгийн сегментээс дээш X, тэр ч байтугай еЭнэ нь "талбай" гэсэн нэр томъёоны яг утгыг урьдаас тодорхойлоогүй, мөн ийм байдлаар тодорхойлсон газар нутаг үнэхээр байдаг гэдгийг тогтоогоогүй байж үргэлжилсэн функц юм. Энэ асуудлыг 1854 онд Б.Риман амжилттай шийдэж, тодорхой интеграл гэдэг ойлголтын нарийн тодорхойлолтыг өгчээ. Түүнээс хойш тодорхой интеграл гэсэн ойлголтын нийлбэрийн санаа нь олон гүнзгий судалгаа, ерөнхий дүгнэлтийн сэдэв байсаар ирсэн. Үүний үр дүнд өнөөдөр интеграл хаа сайгүй тасархай байсан ч тодорхой интегралд утга учир өгөх боломжтой болсон. А.Лебесг (1875–1941) болон бусад математикчид асар их хувь нэмэр оруулсан интеграцийн шинэ үзэл баримтлал нь орчин үеийн математик шинжилгээний хүч, гоо үзэсгэлэнг нэмэгдүүлсэн.

Эдгээр болон бусад ойлголтуудын талаар дэлгэрэнгүй ярих нь зохимжгүй байх болно. Бид хязгаар ба тодорхой интегралын нарийн тодорхойлолтыг өгөхөөр хязгаарлагдаж байна.

Эцэст нь хэлэхэд математикийн шинжилгээ нь эрдэмтэн, инженер хүний ​​гарт байдаг туйлын үнэ цэнэтэй хэрэглүүр байсаар өнөөг хүртэл үр өгөөжтэй санаа бодлын эх сурвалж болж математикчдын анхаарлыг татсаар байгааг хэлье. Үүний зэрэгцээ орчин үеийн хөгжил нь 20-р зуунд математикийн шинжилгээг ийм давамгайлсан шинж чанар улам бүр шингээж байгааг харуулж байх шиг байна. хийсвэр алгебр, топологи зэрэг математикийн салбарууд.

Дериватив, түүнийг тооцоолох аргын талаар мэдлэггүйгээр математикийн физикийн бодлого, жишээг шийдвэрлэх нь туйлын боломжгүй юм. Дериватив нь математик шинжилгээний хамгийн чухал ойлголтуудын нэг юм. Бид өнөөдрийн нийтлэлийг энэ үндсэн сэдэвт зориулахаар шийдсэн. Дериватив гэж юу вэ, түүний физик, геометрийн утга нь юу вэ, функцийн деривативыг хэрхэн тооцоолох вэ? Эдгээр бүх асуултыг нэг дор нэгтгэж болно: деривативыг хэрхэн ойлгох вэ?

Деривативын геометрийн болон физикийн утга

Функц байх болтугай f(x) , тодорхой интервалаар өгөгдсөн (а, б) . Энэ интервалд x ба x0 цэгүүд хамаарна. X өөрчлөгдөхөд функц нь өөрөө өөрчлөгддөг. Аргументийн өөрчлөлт - түүний утгуудын ялгаа x-x0 . Энэ ялгааг дараах байдлаар бичнэ дельта х ба аргументын өсөлт гэж нэрлэдэг. Функцийн өөрчлөлт эсвэл өсөлт нь хоёр цэг дэх функцийн утгуудын зөрүү юм. Дериватив тодорхойлолт:

Тухайн цэг дэх функцийн дериватив нь өгөгдсөн цэг дэх функцын өсөлтийг аргументийн өсөлттэй харьцуулсан харьцааны хязгаар нь тэг байх хандлагатай байдаг.

Үгүй бол дараах байдлаар бичиж болно.

Ийм хязгаар олох нь ямар учиртай юм бэ? Гэхдээ аль нь:

цэг дээрх функцийн дериватив нь OX тэнхлэг хоорондын өнцгийн тангенс ба тухайн цэг дэх функцийн графиктай шүргэгчтэй тэнцүү байна.

физик утгадериватив: замын цаг хугацааны дериватив нь шулуун шугамын хөдөлгөөний хурдтай тэнцүү байна.

Сургуулийн наснаас эхлэн хурд бол хувийн зам гэдгийг бүгд мэддэг. x=f(t) ба цаг хугацаа т . Тодорхой хугацааны дундаж хурд:

Нэг удаад хөдөлгөөний хурдыг олж мэдэх t0 Та хязгаарыг тооцоолох хэрэгтэй:

Нэгдүгээр дүрэм: тогтмолыг гарга

Тогтмолыг деривативын тэмдгээс гаргаж авч болно. Түүнээс гадна үүнийг хийх ёстой. Математикийн жишээг шийдвэрлэхдээ дүрмээр бол - Хэрэв та илэрхийллийг хялбарчилж чадвал хялбарчлахаа мартуузай .

Жишээ. Деривативыг тооцоолъё:

Хоёрдугаар дүрэм: функцүүдийн нийлбэрийн дериватив

Хоёр функцийн нийлбэрийн дериватив нь эдгээр функцүүдийн деривативуудын нийлбэртэй тэнцүү байна. Функцийн ялгааны деривативын хувьд ч мөн адил.

Бид энэ теоремыг нотлохгүй, харин практик жишээг авч үзэх болно.

Функцийн деривативыг ол:

Гуравдугаар дүрэм: функцүүдийн үржвэрийн дериватив

Хоёр дифференциалагдах функцийн үржвэрийн деривативыг дараахь томъёогоор тооцоолно.

Жишээ нь: функцийн деривативыг ол:

Шийдэл:

Энд нарийн төвөгтэй функцүүдийн деривативын тооцооны талаар хэлэх нь чухал юм. Комплекс функцийн дериватив нь бие даасан хувьсагчийн хувьд завсрын аргументийн деривативын завсрын аргументтай харьцуулахад энэ функцийн деривативын үржвэртэй тэнцүү байна.

Дээрх жишээнд бид дараах илэрхийлэлтэй тулгарлаа.

Энэ тохиолдолд завсрын аргумент нь тав дахь зэрэглэлд 8x байна. Ийм илэрхийллийн деривативыг тооцоолохын тулд эхлээд завсрын аргументтай холбоотой гадаад функцийн деривативыг авч үзээд дараа нь бие даасан хувьсагчийн хувьд завсрын аргументийн деривативаар үржүүлнэ.

Дөрөвдүгээр дүрэм: Хоёр функцийн хуваалтын дериватив

Хоёр функцийн категорийн деривативыг тодорхойлох томъёо:

Бид даммигийн деривативын талаар эхнээс нь ярихыг хичээсэн. Энэ сэдэв нь санагдсан шиг тийм ч энгийн зүйл биш тул анхааруулах хэрэгтэй: жишээнүүдэд алдаанууд ихэвчлэн байдаг тул деривативыг тооцоолохдоо болгоомжтой байгаарай.

Энэ болон бусад сэдвээр асуух зүйл байвал оюутны үйлчилгээтэй холбогдож болно. Богино хугацаанд бид танд хамгийн хэцүү хяналтыг шийдэж, өмнө нь деривативын тооцоолол хийж байгаагүй байсан ч даалгавруудыг шийдвэрлэхэд тань туслах болно.

Үүн дээр бид хамгийн энгийн деривативуудад дүн шинжилгээ хийж, мөн ялгах дүрэм, дериватив олох зарим техниктэй танилцсан. Тиймээс, хэрэв та функцийн деривативын талаар тийм ч сайн биш эсвэл энэ өгүүллийн зарим зүйл бүрэн ойлгомжгүй байвал эхлээд дээрх хичээлийг уншина уу. Ноцтой сэтгэл санааг тохируулна уу - материал нь тийм ч хялбар биш, гэхдээ би үүнийг энгийн бөгөөд ойлгомжтой байдлаар харуулахыг хичээх болно.

Практикт та нийлмэл функцийн деривативтай маш олон удаа харьцах хэрэгтэй болдог, тэр ч байтугай дериватив олох даалгавар өгөх үед би бараг үргэлж хэлэх болно.

Нарийн төвөгтэй функцийг ялгах дүрмийн (№ 5) хүснэгтээс бид харж байна.

Бид ойлгож байна. Юуны өмнө тэмдэглэгээг авч үзье. Энд бид хоёр функцтэй - ба , функц нь дүрсээр хэлбэл функцэд үүрлэсэн байна. Ийм төрлийн функцийг (нэг функц нөгөөд нь үүрлэсэн үед) нийлмэл функц гэж нэрлэдэг.

Би функцийг дуудах болно гадаад функц, болон функц – дотоод (эсвэл үүрлэсэн) функц.

! Эдгээр тодорхойлолтууд нь онолын хувьд биш бөгөөд даалгаврын эцсийн загварт тусгагдаагүй байх ёстой. Би зөвхөн материалыг ойлгоход хялбар болгох үүднээс "гадаад функц", "дотоод" функцийг албан бус хэллэгээр ашигладаг.

Нөхцөл байдлыг тодруулахын тулд дараахь зүйлийг анхаарч үзээрэй.

Жишээ 1

Функцийн деривативыг ол

Синусын доор бид зөвхөн "x" үсэг биш, харин бүхэл бүтэн илэрхийлэлтэй тул хүснэгтээс деривативыг шууд олох нь ажиллахгүй болно. Энд эхний дөрвөн дүрмийг хэрэглэх боломжгүй гэдгийг бид анзаарч байгаа, ялгаа байгаа юм шиг байгаа юм, гэхдээ синусыг "урагдах" боломжгүй юм.

Энэ жишээн дээр миний тайлбараас харахад функц нь нарийн төвөгтэй функц, олон гишүүнт нь дотоод функц (суулгах), гадаад функц болох нь ойлгомжтой байна.

Эхний алхам, нийлмэл функцийн деривативыг олоход заавал гүйцэтгэх ёстой аль функц нь дотоод, аль нь гадаад болохыг ойлгох.

Энгийн жишээнүүдийн хувьд олон гишүүнт синусын дор үүрлэсэн нь тодорхой юм шиг санагддаг. Гэхдээ энэ нь тодорхойгүй байвал яах вэ? Аль функц нь гадаад, аль нь дотоод гэдгийг яг яаж тодорхойлох вэ? Үүнийг хийхийн тулд би оюун ухаанаар эсвэл ноорог дээр хийж болох дараах техникийг ашиглахыг санал болгож байна.

Илэрхийллийн утгыг тооцоолуураар (нэг биш, ямар ч тоо байж болно) тооцоолох хэрэгтэй гэж төсөөлөөд үз дээ.

Бид эхлээд юуг тооцох вэ? Юуны өмнөта дараах үйлдлийг гүйцэтгэх хэрэгтэй болно: , тиймээс олон гишүүнт дотоод функц болно:

ХоёрдугаартТа олох хэрэгтэй, тиймээс синус нь гадаад функц байх болно:

Бидний дараа ОЙЛГОХдотоод болон гадаад функцтэй бол нийлмэл функцийг ялгах дүрмийг хэрэглэх цаг болжээ .

Бид шийдэж эхэлнэ. Хичээлээс Деривативыг хэрхэн олох вэ?Аливаа деривативын шийдлийн загвар үргэлж ингэж эхэлдэг гэдгийг бид санаж байна - бид илэрхийлэлийг хаалтанд хийж, баруун дээд буланд зураас тавьдаг.

Эхлээдбид гадаад функцийн деривативыг (синус) олоод, энгийн функцүүдийн деривативын хүснэгтийг хараад . Бүх хүснэгтийн томьёо нь "x"-г нийлмэл илэрхийллээр сольсон ч хэрэгжинэ, энэ тохиолдолд:

Дотоод функцийг анхаарна уу өөрчлөгдөөгүй, бид үүнд хүрэхгүй.

За энэ нь ойлгомжтой

Томьёог хэрэглэсний үр дүн цэвэрхэн дараах байдлаар харагдаж байна.

Тогтмол хүчин зүйлийг ихэвчлэн илэрхийллийн эхэнд байрлуулдаг.

Хэрэв үл ойлголцол байвал шийдвэрээ цаасан дээр бичиж, тайлбарыг дахин уншина уу.

Жишээ 2

Функцийн деривативыг ол

Жишээ 3

Функцийн деривативыг ол

Бид үргэлж бичдэг:

Бидэнд гадаад функц хаана байна, дотоод функц хаана байна вэ гэдгийг олж мэдэв. Үүнийг хийхийн тулд бид (сэтгэцийн хувьд эсвэл ноорог дээр) илэрхийллийн утгыг тооцоолохыг оролддог. Эхлээд юу хийх хэрэгтэй вэ? Юуны өмнө та суурь нь юутай тэнцүү болохыг тооцоолох хэрэгтэй бөгөөд энэ нь олон гишүүнт дотоод функц гэсэн үг юм.

Зөвхөн дараа нь экспонентаци хийгддэг тул чадлын функц нь гадаад функц юм.

Томъёоны дагуу , эхлээд та гадаад функцийн деривативыг олох хэрэгтэй, энэ тохиолдолд зэрэг. Хүснэгтээс бид хүссэн томъёог хайж байна. Бид дахин давтана: Хүснэгтийн аливаа томьёо нь зөвхөн "x"-д төдийгүй нийлмэл илэрхийлэлд хүчинтэй байна. Тиймээс нарийн төвөгтэй функцийг ялгах дүрмийг хэрэглэсний үр дүн дараачийн:

Гадаад функцийн деривативыг авахад дотоод функц өөрчлөгдөхгүй гэдгийг би дахин онцолж байна.

Одоо дотоод функцийн маш энгийн деривативыг олж, үр дүнг бага зэрэг "самнах" л үлдлээ.

Жишээ 4

Функцийн деривативыг ол

Энэ бол жишээ юм бие даасан шийдэл(хичээлийн төгсгөлд хариулах).

Нарийн төвөгтэй функцийн деривативын талаархи ойлголтыг нэгтгэхийн тулд би тайлбаргүйгээр жишээ өгөх болно, үүнийг өөрөө олж мэдэхийг хичээ, учир нь, гадаад, дотоод функц нь хаана байна, яагаад даалгавруудыг ингэж шийдсэн бэ?

Жишээ 5

a) Функцийн деривативыг ол

б) Функцийн деривативыг ол

Жишээ 6

Функцийн деривативыг ол

Энд бид язгууртай бөгөөд уг үндсийг ялгахын тулд үүнийг зэрэг хэлбэрээр илэрхийлэх ёстой. Тиймээс бид эхлээд функцийг ялгахын тулд зохих хэлбэрт оруулдаг.

Функцэд дүн шинжилгээ хийснээр бид гурван гишүүний нийлбэр нь дотоод функц, экспоненциал нь гадаад функц гэсэн дүгнэлтэд хүрсэн. Бид нарийн төвөгтэй функцийг ялгах дүрмийг ашигладаг :

Зэрэг нь дахин радикал (үндэс) хэлбэрээр илэрхийлэгддэг бөгөөд дотоод функцийн деривативын хувьд бид нийлбэрийг ялгах энгийн дүрмийг хэрэгжүүлдэг.

Бэлэн. Мөн та илэрхийллийг хаалтанд нийтлэг хуваагч руу авчирч, бүгдийг нэг бутархай болгон бичиж болно. Энэ нь мэдээжийн хэрэг үзэсгэлэнтэй, гэхдээ төвөгтэй урт деривативуудыг олж авбал үүнийг хийхгүй байх нь дээр (төөрөлдөх, шаардлагагүй алдаа гаргах, багш шалгахад тохиромжгүй байх болно).

Жишээ 7

Функцийн деривативыг ол

Энэ бол өөрийгөө шийдэх жишээ юм (хичээлийн төгсгөлд хариулах).

Заримдаа нарийн төвөгтэй функцийг ялгах дүрмийн оронд хуваалтыг ялгах дүрмийг ашиглаж болно гэдгийг тэмдэглэх нь сонирхолтой юм. , гэхдээ ийм шийдэл нь ер бусын гажуудал мэт харагдах болно. Энд ердийн жишээ байна:

Жишээ 8

Функцийн деривативыг ол

Энд та хуваалтыг ялгах дүрмийг ашиглаж болно , гэхдээ нийлмэл функцийг ялгах дүрмээр дамжуулан деривативыг олох нь илүү ашигтай байдаг.

Бид функцийг ялгахад бэлтгэдэг - бид деривативын хасах тэмдгийг гаргаж, косинусыг тоологч руу нэмнэ.

Косинус нь дотоод функц, экспоненциал нь гадаад функц юм.
Өөрийн дүрмээ ашиглацгаая :

Бид дотоод функцийн деривативыг олоод косинусыг дахин тохируулна:

Бэлэн. Үзэж буй жишээн дээр шинж тэмдгүүдэд андуурахгүй байх нь чухал юм. Дашрамд хэлэхэд, үүнийг дүрмээр шийдэхийг хичээ , хариултууд таарч байх ёстой.

Жишээ 9

Функцийн деривативыг ол

Энэ бол өөрийгөө шийдэх жишээ юм (хичээлийн төгсгөлд хариулах).

Одоогийн байдлаар бид нарийн төвөгтэй функцэд зөвхөн нэг үүрлэсэн тохиолдлуудыг авч үзсэн. Практик даалгаврын хувьд та үүрлэх хүүхэлдэй гэх мэт 3 эсвэл бүр 4-5 функцийг нэг дор байрлуулдаг деривативуудыг олох боломжтой.

Жишээ 10

Функцийн деривативыг ол

Бид энэ функцийн хавсралтыг ойлгож байна. Бид туршилтын утгыг ашиглан илэрхийлэлийг үнэлэхийг оролддог. Бид тооцоолуур дээр яаж тооцох вэ?

Эхлээд та олох хэрэгтэй бөгөөд энэ нь арксинус нь хамгийн гүн үүрлэдэг гэсэн үг юм.

Эв нэгдлийн энэ нумыг квадрат болгох ёстой:

Эцэст нь бид долоог хүчирхэг болгон өсгөв:

Өөрөөр хэлбэл, энэ жишээнд бид гурван өөр функц, хоёр үүртэй байх ба хамгийн дотоод функц нь арксинус, хамгийн гадна талын функц нь экспоненциал функц юм.

Бид шийдэж эхэлнэ

Дүрмийн дагуу эхлээд та гадаад функцийн деривативыг авах хэрэгтэй. Бид деривативын хүснэгтийг харж, экспоненциал функцийн деривативыг олно: Цорын ганц ялгаа нь "x"-ийн оронд бид нийлмэл илэрхийлэлтэй байгаа нь энэ томъёоны хүчинтэй байдлыг үгүйсгэхгүй. Тиймээс нарийн төвөгтэй функцийг ялгах дүрмийг хэрэглэсний үр дүн дараачийн.