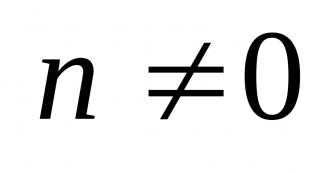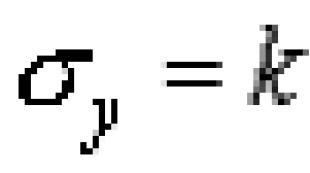शिल्प

लोच के सिद्धांत में समस्याओं के प्रकार. लोच के सिद्धांत के बुनियादी समीकरण. लोच के सिद्धांत में समस्याओं के प्रकार लोच के शास्त्रीय सिद्धांत के अध्ययन का विषय क्या है?

रूसी राज्य विश्वविद्यालय

उन्हें तेल और गैस दें। आई.एम. गुबकिना

तकनीकी यांत्रिकी विभाग

अमूर्त

"लोच का सिद्धांत"

द्वारा पूरा किया गया: पॉलाकोव ए.ए.

जाँच की गई: एवडोकिमोव ए.पी.

मॉस्को 2011

लोच सिद्धांत समीकरण

1 परिचय

शरीर के एक बिंदु पर तनाव-तनाव की स्थिति का सिद्धांत

2.1 तनाव सिद्धांत

2 विरूपण सिद्धांत

3 लोचदार निकायों के लिए तनावग्रस्त और विकृत अवस्था के बीच संबंध

लोच के सिद्धांत के बुनियादी समीकरण. लोच के सिद्धांत में समस्याओं के प्रकार

1 लोच सिद्धांत के मूल समीकरण

लोच के सिद्धांत में 2 प्रकार की समस्याएं

4 विस्थापन में लोच के सिद्धांत के समीकरण (लंगड़ा समीकरण)

लोच सिद्धांत के विभिन्न सिद्धांत

1 संभावित विस्थापन का सिद्धांत (लैग्रेंज सिद्धांत)

2 संभावित अवस्थाओं का सिद्धांत (कैस्टिलानो सिद्धांत)

3 लैग्रेंज और कैस्टिग्लिआनो सिद्धांतों के आधार पर प्राप्त सटीक समाधान और समाधान के बीच संबंध

प्रयुक्त साहित्य की सूची

1 परिचय

तनाव और विकृति के सिद्धांत ओ. कॉची द्वारा बनाए गए थे। वे 1822 में पेरिस एकेडमी ऑफ साइंसेज को सौंपे गए एक काम में दिए गए हैं, जिसका सारांश 1823 में प्रकाशित हुआ था और बाद के कई लेख भी प्रकाशित हुए थे। ओ. कोशी ने प्राथमिक चतुष्फलक के संतुलन के तीन समीकरण निकाले, स्पर्शरेखीय तनावों के युग्मन के नियम को सिद्ध किया, प्रमुख अक्षों और प्रमुख तनावों की अवधारणाओं को पेश किया, और विभेदक संतुलन समीकरण निकाले (आमतौर पर वे ताकत के दौरान प्राप्त नहीं होते हैं) सामग्री)। उन्होंने सामान्य तनाव (कौची क्वाड्रिक) की सतह भी पेश की, जिस पर त्रिज्या वैक्टर के सिरे स्थित हैं, जिनकी दिशाएं क्षेत्रों के सामान्य की दिशा से मेल खाती हैं, और मान वर्गमूल के व्युत्क्रमानुपाती होता है इस क्षेत्र में सामान्य तनाव के निरपेक्ष मान का, और यह सिद्ध हो गया कि यह सतह मूल बिंदु पर केन्द्रित दूसरे क्रम की सतह है। सामान्य तनाव की सतह को प्रमुख अक्षों में बदलने की संभावना प्रत्येक बिंदु पर तीन परस्पर प्रमुख लंबवत क्षेत्रों के अस्तित्व को इंगित करती है।

एक समान कतरनी तनाव सतह रूसी मैकेनिक जी.वी. द्वारा पेश की गई थी। 1933 में कोलोसोव

तनाव के दीर्घवृत्ताभ के रूप में अंतरिक्ष में तनाव की स्थिति की ज्यामितीय व्याख्या जी. लेम और बी. क्लैपेरॉन ने अपने संस्मरणों में दी थी, जो 1828 में पेरिस एकेडमी ऑफ साइंसेज को प्रस्तुत किया गया था और 1833 में प्रकाशित हुआ था।

मुख्य अक्ष से गुजरने वाले प्लेटफार्मों की एक श्रृंखला के लिए एक विमान पर तनाव की स्थिति का ज्यामितीय प्रतिनिधित्व, तनाव के एक चक्र के रूप में, के. कुहलमैन ने 1866 में अपनी पुस्तक में प्रस्तावित किया था।

तनाव की स्थिति के सामान्य मामले के लिए, विमान पर इसकी एक बहुत ही स्पष्ट ज्यामितीय व्याख्या 1882 में ओ. मोहर (तथाकथित परिपत्र मोहर आरेख) द्वारा दी गई थी। इससे, इसके बारे में कई महत्वपूर्ण निष्कर्ष निकाले जा सकते हैं प्रमुख तनावों की चरम सीमा, उन क्षेत्रों की स्थिति जिनमें स्पर्शरेखीय तनाव अधिकतम हैं, और इन अधिकतम कतरनी तनावों के मूल्यों के बारे में।

ओ. कॉची ने उपभेदों की एक परिभाषा दी, छोटे उपभेदों के विशेष मामले में विस्थापन पर उनकी निर्भरता प्राप्त की (ये निर्भरताएं, एक नियम के रूप में, सामग्री की ताकत के दौरान प्राप्त नहीं होती हैं), प्रमुख तनाव और प्रमुख की अवधारणाओं को परिभाषित किया तनाव, और तनाव घटकों पर तनाव घटकों की निर्भरता प्राप्त की, जैसे कि आइसोट्रोपिक के लिए, और एक अनिसोट्रोपिक लोचदार शरीर के लिए। सामग्रियों के प्रतिरोध में, एक आइसोट्रोपिक शरीर के लिए तनाव घटकों पर तनाव घटकों की निर्भरता आमतौर पर स्थापित की जाती है। उन्हें सामान्यीकृत हुक का नियम कहा जाता है, हालाँकि, निश्चित रूप से, यह नाम सशर्त है, क्योंकि आर. हुक तनाव की अवधारणा को नहीं जानते थे।

इन निर्भरताओं में, कॉची ने सबसे पहले दो स्थिरांक पेश किए और तनाव पर तनाव की निर्भरता को फॉर्म में लिखा

एम, ,

हालाँकि, बाद में ओ. कोशी ने एल. नेवियर की अवधारणा को अपनाया। इसके अनुसार, लोचदार पिंड अणुओं से बने होते हैं, जिनके बीच विरूपण के दौरान, बल उत्पन्न होते हैं जो अणुओं को जोड़ने वाली सीधी रेखाओं की दिशा में कार्य करते हैं और अणुओं के बीच की दूरी में परिवर्तन के समानुपाती होते हैं। फिर अनिसोट्रोपिक शरीर के सामान्य मामले के लिए लोचदार स्थिरांक की संख्या 15 है, और एक आइसोट्रोपिक शरीर के लिए हमें एक लोचदार स्थिरांक प्राप्त होता है। एस. पॉइसन ने इस परिकल्पना का पालन किया, और शुरुआत में - जी. लेम और बी. क्लैपेरॉन ने। इसके आधार पर पॉइसन ने पाया कि अनुप्रस्थ विकृति का गुणांक 1/4 है।

डी. ग्रीन ने 1839 में लोचदार निकायों की आणविक संरचना की परिकल्पना का उपयोग किए बिना तनाव और तनाव के बीच संबंध निकाला। उन्होंने उन्हें ऊर्जा के संरक्षण के सिद्धांत के आधार पर प्राप्त किया, लोचदार क्षमता की अवधारणा को पेश किया, और दिखाया कि छह तनाव घटकों पर छह तनाव घटकों की रैखिक निर्भरता का उपयोग करते समय, 36 में से 21 गुणांक स्वतंत्र होते हैं, यानी सामान्य मामले में। एक अनिसोट्रोपिक शरीर में, लोचदार स्थिरांक की संख्या 21 है। एक आइसोट्रोपिक शरीर के लिए, लोचदार स्थिरांक की संख्या कम होकर दो हो जाती है। एक सिद्धांत जिसमें अनिसोट्रोपिक शरीर के लिए लोचदार स्थिरांक की संख्या 15 है, और एक आइसोट्रोपिक शरीर के लिए 1 है, को कभी-कभी "रैरिक स्थिरांक" या "यूनीकॉन्स्टेंट" कहा जाता है, और एक सिद्धांत जिसमें अनिसोट्रोपिक शरीर के लिए लोचदार स्थिरांक की संख्या होती है 21, और एक आइसोट्रोपिक 2 के लिए - "बहु-स्थिरांक"।

इन सिद्धांतों के समर्थकों के बीच विवाद ने भौतिकविदों को प्रायोगिक अनुसंधान के लिए प्रेरित किया।

जी. वर्थाइम ने अक्षीय तनाव में कांच और धातु पाइपों की आंतरिक मात्रा के माप के आधार पर 1848 में स्थापित किया कि अनुप्रस्थ विरूपण का गुणांक 1/4 के बराबर नहीं है। उन्होंने इसे विभिन्न सामग्रियों के लिए अलग-अलग माना, लेकिन कई सामग्रियों के लिए यह 1/3 के करीब था।

और मैं। कुफ़्फ़र ने 1853 में तनाव और मरोड़ के लिए धातु की छड़ों का परीक्षण करते हुए यह भी पाया कि कतरनी और तनाव में मॉड्यूली का अनुपात 1/4 के बराबर अनुप्रस्थ तनाव के अनुरूप नहीं है।

1855 में, एफ. न्यूमैन ने झुकने के लिए आयताकार क्रॉस-सेक्शन के नमूनों का परीक्षण किया और बीम के दो चेहरों के घूर्णन के कोणों को मापा (क्रॉस सेक्शन एक ट्रेपोजॉइडल आकार लेता है)। परिणामस्वरूप, उन्होंने दिखाया कि अनुप्रस्थ विरूपण का गुणांक 1/4 के बराबर नहीं है। एफ. न्यूमैन के छात्र जी. किरचॉफ, 1859 में गोल पीतल की छड़ों के जोड़ मोड़ने और मरोड़ने के लिए किए गए परीक्षणों के आधार पर इसी निष्कर्ष पर पहुंचे, जिन्हें एक छोर पर सील किया गया था और दूसरे छोर पर एक केंद्रित बल के साथ लोड किया गया था। छड़ के मोड़ के कोण और अनुभाग के घूर्णन के कोण का माप।

स्टील के विभिन्न ग्रेडों के लिए अनुप्रस्थ विरूपण के गुणांक का एक बड़ा प्रायोगिक अध्ययन जी. किरचॉफ, एम.एफ. के छात्रों में से एक द्वारा किया गया था। 1865 - 1866 में ओकाटोव परिणाम उनके डॉक्टरेट शोध प्रबंध में दिए गए हैं। एकल क्रिस्टल से काटे गए पतले प्रिज्मों के मरोड़ और झुकने के परीक्षण, साथ ही समान समान संपीड़न के तहत क्रिस्टल की संपीड़न क्षमता के परीक्षण, वी. वोइग्ट द्वारा किए गए थे और बाद में उनके कई लेखों में वर्णित किए गए थे। 1910 में प्रकाशित एक पुस्तक में संयुक्त रूप से उन्होंने बहु-स्थिर सिद्धांत की शुद्धता की पुष्टि की।

अनिसोट्रोपिक निकायों के लिए हुक के नियम की गणितीय संरचना का गहन अध्ययन मैकेनिक और इंजीनियर जान रिचलेव्स्की द्वारा 1984 में उनके द्वारा प्रस्तुत लोचदार ईजेनस्टेट की अवधारणा के आधार पर किया गया था। विशेष रूप से, उन्होंने दिखाया कि 21 लोचदार स्थिरांक छह वास्तविक कठोरता मॉड्यूल, 12 कठोरता वितरक और तीन कोणों का प्रतिनिधित्व करते हैं।

2. शरीर के एक बिंदु पर तनाव-तनाव की स्थिति का सिद्धांत

1 तनाव सिद्धांत

आंतरिक बल कारक जो तब उत्पन्न होते हैं जब एक लोचदार शरीर को लोड किया जाता है जो शरीर के एक विशेष खंड की स्थिति को दर्शाता है, लेकिन इस सवाल का जवाब नहीं देता है कि क्रॉस सेक्शन का कौन सा बिंदु सबसे अधिक लोड है, या, जैसा कि वे कहते हैं, खतरनाक बिंदु है। इसलिए, किसी दिए गए बिंदु पर शरीर की स्थिति को दर्शाने वाली कुछ अतिरिक्त मात्रा पर विचार करना आवश्यक है।

यदि कोई पिंड जिस पर बाहरी बल लागू होते हैं, संतुलन में है, तो उसके किसी भी खंड में आंतरिक प्रतिरोध बल उत्पन्न होते हैं। प्रारंभिक क्षेत्र पर कार्य करने वाले आंतरिक बल और फिर इस क्षेत्र के सामान्य से मूल्य को निरूपित करें

पूर्ण वोल्टेज कहा जाता है।

सामान्य स्थिति में, कुल तनाव प्राथमिक क्षेत्र के सामान्य के साथ दिशा में मेल नहीं खाता है, इसलिए समन्वय अक्षों के साथ इसके घटकों के साथ काम करना अधिक सुविधाजनक है -

यदि बाहरी सामान्य किसी समन्वय अक्ष के साथ मेल खाता है, उदाहरण के लिए, एक्स अक्ष के साथ, तो तनाव घटक रूप ले लेंगे, जबकि घटक अनुभाग के लंबवत हो जाता है और इसे सामान्य तनाव कहा जाता है, और घटक झूठ बोलेंगे अनुभाग तल और कतरनी तनाव कहलाते हैं।

सामान्य और कतरनी तनावों के बीच आसानी से अंतर करने के लिए, आमतौर पर अन्य पदनामों का उपयोग किया जाता है: - सामान्य तनाव, - कतरनी।

आइए हम बाहरी बलों की कार्रवाई के तहत शरीर से एक असीम रूप से छोटे समानांतर चतुर्भुज को बाहर निकालें, जिसके चेहरे समन्वय विमानों के समानांतर हैं, और जिनके किनारों की लंबाई है। ऐसे प्राथमिक समांतर चतुर्भुज के प्रत्येक चेहरे पर, तीन तनाव घटक होते हैं जो समन्वय अक्षों के समानांतर होते हैं। कुल मिलाकर, हमें छह चेहरों पर 18 तनाव घटक मिलते हैं।

सामान्य तनावों को इस प्रकार दर्शाया जाता है, जहां सूचकांक संबंधित चेहरे पर सामान्य को दर्शाता है (अर्थात, यह मान ले सकता है)। कतरनी तनाव का रूप होता है; यहां पहला सूचकांक उस साइट के सामान्य से मेल खाता है जिस पर दिया गया कतरनी तनाव कार्य करता है, और दूसरा उस अक्ष को इंगित करता है जिसके समानांतर यह तनाव निर्देशित होता है (चित्र 1)।

चित्र .1। सामान्य और कतरनी तनाव

इन वोल्टेज के लिए, निम्नलिखित संकेत नियम अपनाया जाता है। सामान्य तनाव को तनाव में या समकक्ष रूप से सकारात्मक माना जाता है, जब यह उस साइट पर बाहरी सामान्य की दिशा से मेल खाता है जिस पर यह कार्य करता है। स्पर्शरेखीय तनाव को सकारात्मक माना जाता है यदि साइट पर, सामान्य जो इसके समानांतर समन्वय अक्ष की दिशा के साथ मेल खाता है, यह इस वोल्टेज के अनुरूप सकारात्मक समन्वय अक्ष की ओर निर्देशित होता है।

तनाव घटक तीन निर्देशांकों के कार्य हैं। उदाहरण के लिए, निर्देशांक वाले किसी बिंदु पर सामान्य तनाव को दर्शाया जा सकता है

एक ऐसे बिंदु पर जो विचाराधीन बिंदु से अतिसूक्ष्म दूरी पर है, वोल्टेज, पहले क्रम के अतिसूक्ष्म तक, टेलर श्रृंखला में विस्तारित किया जा सकता है:

उन प्लेटफार्मों के लिए जो विमान के समानांतर हैं, केवल x निर्देशांक बदलता है, और वृद्धि होती है इसलिए, समानांतर चतुर्भुज के चेहरे पर, जो विमान के साथ मेल खाता है, सामान्य तनाव होगा इसलिए, 18 वोल्टेज घटकों में से केवल नौ अज्ञात हैं।

लोच के सिद्धांत में, कतरनी तनावों के युग्मन का नियम सिद्ध होता है, जिसके अनुसार, दो परस्पर लंबवत क्षेत्रों के साथ, इन क्षेत्रों की प्रतिच्छेदन रेखाओं के लंबवत कतरनी तनाव के घटक एक दूसरे के बराबर होते हैं:

समानताएं (2) इस तथ्य को जन्म देती हैं कि शरीर के एक बिंदु पर तनाव की स्थिति को दर्शाने वाले नौ तनाव घटकों में से केवल छह ही बचे हैं:

यह दिखाया जा सकता है कि तनाव (3) न केवल किसी दिए गए बिंदु पर शरीर की तनाव स्थिति की विशेषता बताते हैं, बल्कि इसे विशिष्ट रूप से निर्धारित करते हैं। इन तनावों का संयोजन एक सममित मैट्रिक्स बनाता है, जिसे तनाव टेंसर कहा जाता है:

(4)

किसी टेन्सर को स्केलर मान से गुणा करने पर, एक नया टेन्सर प्राप्त होता है, जिसके सभी घटक मूल टेन्सर के घटकों से कई गुना बड़े होते हैं।

2 विरूपण सिद्धांत

बाहरी भार के प्रभाव में, लोचदार शरीर अपना आकार बदलता है और विकृत हो जाता है। ऐसे में शरीर के बिंदु कुछ नई स्थिति ले लेते हैं। एक लोचदार शरीर की विकृति का निर्धारण करने के लिए, हम भार के आवेदन से पहले और बाद में शरीर के बिंदुओं की स्थिति की तुलना करते हैं।

किसी उतारे गए पिंड के एक बिंदु और भार लगाने के बाद उसकी नई स्थिति पर विचार करें। वेक्टर को बिंदु विस्थापन वेक्टर कहा जाता है (चित्र 2)।

अंक 2। बिंदु गतिमान सदिश

दो प्रकार के विस्थापन संभव हैं: विरूपण के बिना पूरे शरीर का विस्थापन - ऐसे विस्थापनों का अध्ययन सैद्धांतिक यांत्रिकी द्वारा बिल्कुल कठोर शरीर के विस्थापन के रूप में किया जाता है, और शरीर के विरूपण से जुड़े विस्थापन - ऐसे विस्थापनों का अध्ययन सिद्धांत द्वारा किया जाता है लोच का.

आइए हम निर्देशांक अक्षों पर बिंदु विस्थापन वेक्टर के प्रक्षेपणों को क्रमशः निर्दिष्ट करें। वे बिंदुओं के संगत निर्देशांक के बीच अंतर के बराबर हैं और :

और निर्देशांक के कार्य हैं:

शरीर की विकृति उसके विभिन्न बिंदुओं के विस्थापन में अंतर के कारण होती है। एक मनमाना बिंदु के पास एक लोचदार शरीर से काटे गए किनारों वाला एक असीम छोटा समानांतर चतुर्भुज, अपने बिंदुओं के विभिन्न विस्थापनों के कारण, इस तरह से विकृत हो जाता है कि इसके किनारों की लंबाई बदल जाती है और चेहरों के बीच प्रारंभिक समकोण विकृत हो जाते हैं।

चित्र 3.3 इस समांतर चतुर्भुज के दो किनारों को दर्शाता है: और किनारे की लंबाई बराबर है और किनारा है

विरूपण के बाद, बिंदु एक स्थिति लेते हैं। इस मामले में, बिंदु को एक विस्थापन प्राप्त होगा, जिसके घटक ड्राइंग के विमान में बराबर हैं, और अनंत छोटी दूरी पर बिंदु से अलग किए गए बिंदु को एक विस्थापन प्राप्त होगा, जिसके घटक निर्देशांक में परिवर्तन के कारण बिंदु विस्थापन के घटकों से एक अनंत मान से भिन्न होंगे

चित्र 3. रैखिक और कोणीय विकृतियाँ

निर्देशांक में परिवर्तन के कारण बिंदु विस्थापन के घटक बिंदु विस्थापन के घटकों से अनंत मान से भिन्न होंगे

विरूपण के बाद धुरी पर पसली के प्रक्षेपण की लंबाई:

धुरी पर पसली के पूर्ण बढ़ाव का प्रक्षेपण

अक्ष के अनुदिश सापेक्ष बढ़ाव

(6)

अक्ष की दिशा में रैखिक विरूपण कहलाता है।

इसी प्रकार, अक्षों की दिशाओं के अनुदिश रैखिक विकृतियाँ और

(7)

समांतर चतुर्भुज के किनारों के बीच के कोणों में परिवर्तन पर विचार करें (चित्र 3)। समतल में पसली के घूर्णन कोण का स्पर्शरेखा

विकृतियों की लघुता के कारण, रैखिक विकृति को एकता की तुलना में इसकी लघुता के कारण उपेक्षित किया जा सकता है, और फिर

इसी प्रकार, आप उसी तल में पसली के घूमने का कोण निर्धारित कर सकते हैं:

समकोण की विकृति को कोणीय विकृति कहा जाता है और इसे पसलियों के घूर्णन के कोणों के योग के रूप में परिभाषित किया जाता है और:

(8)

उसी तरह, दो अन्य समन्वय विमानों में कोणीय विकृतियाँ निर्धारित की जाती हैं:

(9)

सूत्र (6)-(9) विस्थापन घटकों पर रैखिक और कोणीय विकृतियों के लिए छह बुनियादी निर्भरताएँ देते हैं। इन निर्भरताओं को कॉची समीकरण कहा जाता है:

(10)

उस सीमा में जब समांतर चतुर्भुज के किनारों की लंबाई शून्य हो जाती है, कॉची संबंध बिंदु के आसपास के क्षेत्र में रैखिक और कोणीय विकृतियों को निर्धारित करते हैं

सकारात्मक रैखिक विकृतियाँ बढ़ाव के अनुरूप होती हैं, और नकारात्मक विकृतियाँ लघुकरण के अनुरूप होती हैं। शिफ्ट कोण को सकारात्मक माना जाता है जब संबंधित समन्वय अक्षों की सकारात्मक दिशाओं के बीच का कोण कम हो जाता है और नकारात्मक - अन्यथा।

स्ट्रेस टेंसर के समान, किसी दिए गए बिंदु पर शरीर की विकृत स्थिति का वर्णन स्ट्रेन टेंसर द्वारा किया जाता है

(11)

स्ट्रेस टेंसर की तरह, स्ट्रेन टेंसर एक सममित मैट्रिक्स है जिसमें नौ घटक होते हैं, जिनमें से छह अलग-अलग होते हैं।

2.3 लोचदार निकायों के लिए तनाव और तनाव के बीच संबंध

तनाव और तनाव के बीच संबंध भौतिक प्रकृति के होते हैं। छोटे तनावों तक सीमित, तनाव और तनाव के बीच संबंध को रैखिक माना जा सकता है।

तनाव में एक छड़ का परीक्षण करते समय (सामग्री के यांत्रिक परीक्षण पर अगले भाग में विस्तार से चर्चा की जाएगी), सामान्य तनाव और एक दिशा में रैखिक विरूपण के बीच एक आनुपातिक संबंध स्थापित होता है, जिसे हुक का नियम कहा जाता है:

जहां लोचदार स्थिरांक को अनुदैर्ध्य लोच का मापांक कहा जाता है।

उसी प्रयोगात्मक तरीके से, अनुदैर्ध्य और अनुप्रस्थ दिशाओं में रैखिक विकृतियों के बीच एक संबंध स्थापित किया गया था:

जहां - अनुप्रस्थ दिशा में रैखिक विरूपण, - दूसरा लोचदार स्थिरांक, जिसे पॉइसन अनुपात कहा जाता है।

शुद्ध कतरनी के लिए यांत्रिक परीक्षणों में, इस तनाव की कार्रवाई के तल में कतरनी तनाव और कोणीय विरूपण के बीच एक सीधे आनुपातिक संबंध स्थापित किया गया था, जिसे कतरनी में हुक का नियम कहा जाता था:

जहां मान तीसरा लोचदार स्थिरांक है और इसे कतरनी मापांक कहा जाता है। हालाँकि, यह लोचदार स्थिरांक स्वतंत्र नहीं है, क्योंकि पहले दो से संबद्ध

तनाव और तनाव के बीच संबंध स्थापित करने के लिए, हम शरीर से एक असीम रूप से छोटे समानांतर चतुर्भुज का चयन करते हैं (चित्र 1) और केवल सामान्य तनाव की क्रिया पर विचार करते हैं। यह छोटेपन के उच्च क्रम की विकृतियों की ओर ले जाता है।

आइए तनाव के समानांतर पसली के बढ़ाव का निर्धारण करें, इस तनाव की कार्रवाई के तहत, हुक के नियम (3.12) के अनुसार, पसली का सापेक्ष बढ़ाव होगा

तनाव पसली की लंबवत दिशा में समान लम्बाई का कारण बनता है

और पसली की दिशा में - छोटा करना, जो (13) के अनुसार है

या, विरूपण अभिव्यक्ति को ध्यान में रखते हुए

इसी तरह, तनाव के प्रभाव में पसली का सापेक्ष छोटा होना निर्धारित होता है

बलों की कार्रवाई की स्वतंत्रता के सिद्धांत के आधार पर, पसली के कुल सापेक्ष बढ़ाव को प्रत्येक तनाव की कार्रवाई से बढ़ाव के योग के रूप में परिभाषित किया जा सकता है:

इसी प्रकार, कोई अन्य दो अक्षों की दिशाओं के साथ रैखिक विकृतियों को परिभाषित कर सकता है:

कतरनी (14) में हुक के नियम के अनुसार, कोणीय विकृतियों और कतरनी तनावों के बीच संबंध को समन्वयित विमानों के समानांतर तीन विमानों में से प्रत्येक के लिए स्वतंत्र रूप से दर्शाया जा सकता है:

इस प्रकार, छह सूत्र प्राप्त किए गए हैं जो एक आइसोट्रोपिक लोचदार शरीर में तनाव और तनाव घटकों के बीच एक रैखिक संबंध व्यक्त करते हैं और सामान्यीकृत हुक का नियम कहलाते हैं:

(16)

3. लोच के सिद्धांत के मूल समीकरण। लोच के सिद्धांत में समस्याओं के प्रकार

लोच के सिद्धांत का मुख्य कार्य शरीर को लोड करने और ठीक करने की दी गई शर्तों के अनुसार तनाव-तनाव की स्थिति का निर्धारण करना है।

तनाव-तनाव की स्थिति निर्धारित की जाती है यदि तनाव टेंसर और विस्थापन वेक्टर के घटक, नौ कार्य पाए जाते हैं।

3.1 लोच सिद्धांत के मूल समीकरण

इन नौ कार्यों को खोजने के लिए, किसी को लोच के सिद्धांत के मूल समीकरण लिखना होगा, या:

विभेदक कैचियाँ

(17)

कॉची विकृतियों के रैखिक भाग के टेंसर के घटक कहाँ हैं;

त्रिज्या के साथ विस्थापन के व्युत्पन्न के टेंसर के घटक।

विभेदक संतुलन समीकरण

तनाव टेंसर घटक कहाँ हैं; जे अक्ष पर शरीर के बल का प्रक्षेपण है।

रैखिक रूप से लोचदार आइसोट्रोपिक शरीर के लिए हुक का नियम

लंगड़ा स्थिरांक कहाँ हैं; एक आइसोट्रोपिक शरीर के लिए. यहां सामान्य और अपरूपण तनाव हैं; क्रमशः तनाव और कतरनी कोण।

उपरोक्त समीकरणों को सेंट-वेनेंट निर्भरता को संतुष्ट करना चाहिए

लोच के सिद्धांत में, यदि सभी बुनियादी समीकरण संतुष्ट हों तो समस्या हल हो जाती है।

लोच के सिद्धांत में 2 प्रकार की समस्याएं

शरीर की सतह पर सीमा स्थितियों को पूरा किया जाना चाहिए और, सीमा स्थितियों के प्रकार के आधार पर, लोच के सिद्धांत में तीन प्रकार की समस्याएं होती हैं।

प्रथम प्रकार. शरीर की सतह पर बल दिये जाते हैं। सीमा की स्थितियाँ

दूसरा प्रकार. समस्याएँ जिनमें शरीर की सतह पर विस्थापन निर्दिष्ट होता है। सीमा की स्थितियाँ

तीसरा प्रकार. लोच के सिद्धांत की मिश्रित समस्याएं। बल शरीर की सतह के एक भाग पर दिया जाता है, विस्थापन शरीर की सतह के एक भाग पर दिया जाता है। सीमा की स्थितियाँ

ऐसी समस्याएँ जिनमें शरीर की सतह पर बल या विस्थापन निर्दिष्ट होते हैं, लेकिन शरीर के अंदर तनाव-तनाव की स्थिति का पता लगाना आवश्यक होता है और जो सतह पर निर्दिष्ट नहीं होता है, उसे प्रत्यक्ष समस्याएँ कहा जाता है। यदि, हालांकि, शरीर के अंदर तनाव, विकृति, विस्थापन आदि निर्दिष्ट हैं, और यह निर्धारित करना आवश्यक है कि शरीर के अंदर क्या निर्दिष्ट नहीं है, साथ ही शरीर की सतह पर विस्थापन और तनाव (अर्थात, खोजने के लिए) वे कारण जिनके कारण ऐसी तनाव-तनाव की स्थिति उत्पन्न हुई)), तो ऐसी समस्याओं को व्युत्क्रम कहा जाता है।

4 विस्थापन में लोच के सिद्धांत के समीकरण (लंगड़े समीकरण)

विस्थापन में लोच के सिद्धांत के समीकरण निर्धारित करने के लिए, हम लिखते हैं: अंतर संतुलन समीकरण (18) रैखिक रूप से लोचदार आइसोट्रोपिक शरीर के लिए हुक का नियम (19)

यदि हम इस बात को ध्यान में रखें कि विकृतियाँ विस्थापन (17) के रूप में व्यक्त की जाती हैं, तो हम लिखते हैं:

यह भी याद रखना चाहिए कि कतरनी कोण निम्नलिखित संबंध (17) द्वारा विस्थापन से संबंधित है:

(23)

समानता के पहले समीकरण (19) में अभिव्यक्ति (22) को प्रतिस्थापित करने पर, हम पाते हैं कि सामान्य तनाव

(24)

ध्यान दें कि इस मामले में u अंकन i का योग नहीं दर्शाता है।

अभिव्यक्ति (23) को समानता के दूसरे समीकरण (19) में प्रतिस्थापित करने पर, हम पाते हैं कि अपरूपण तनाव

(25)

आइए हम j = 1 के लिए संतुलन समीकरण (18) को विस्तारित रूप में लिखें

(26)

सामान्य (24) और स्पर्शरेखा (25) तनावों के लिए समीकरण (26) अभिव्यक्तियों में प्रतिस्थापित करने पर, हम प्राप्त करते हैं

जहां λ लंगड़ा स्थिरांक है, जो अभिव्यक्ति द्वारा निर्धारित होता है:

हम अभिव्यक्ति (28) को समीकरण (27) में प्रतिस्थापित करते हैं और लिखते हैं,

जहां अभिव्यक्ति (22) द्वारा या विस्तारित रूप में निर्धारित किया जाता है

हम अभिव्यक्ति (29) को जी से विभाजित करते हैं और समान पद जोड़ते हैं और पहला लंगड़ा समीकरण प्राप्त करते हैं:

(30)

लाप्लास ऑपरेटर (हार्मोनिक ऑपरेटर) कहां है, जिसे इस प्रकार परिभाषित किया गया है

(31)

इसी प्रकार, आप प्राप्त कर सकते हैं:

(32)

समीकरण (30) और (32) इस प्रकार लिखे जा सकते हैं:

(33)

समीकरण (33) या (30) और (32) लचर समीकरण हैं। यदि शरीर का बल शून्य या स्थिर है, तो

(34)

इसके अलावा, इस मामले में अंकन i का योग नहीं दर्शाता है। यहाँ

यह दिखाया जा सकता है कि हार्मोनिक फ़ंक्शन के संदर्भ में विस्थापन का ऐसा प्रतिनिधित्व लंगड़ा समीकरण (33) को एक पहचान में बदल देता है। अक्सर उन्हें पॉपकोविच-ग्रोडस्की स्थितियाँ कहा जाता है। चार हार्मोनिक फ़ंक्शन आवश्यक नहीं हैं, क्योंकि φ0 को शून्य के बराबर किया जा सकता है।

4. लोच के सिद्धांत के विभिन्न सिद्धांत।

1 संभावित विस्थापन का सिद्धांत (लैग्रेंज सिद्धांत)

लैग्रेंज सिद्धांत. संतुलन में एक शरीर के लिए, किसी भी संभावित असीम विस्थापन वृद्धि पर बाहरी और आंतरिक बलों का कार्य शून्य है।

क्लैपेरॉन प्रमेय का उपयोग करते हुए, कि विस्थापन को अलग करके एक लोचदार रूप से विकृत शरीर के लिए, हम लैग्रेंज सिद्धांत प्राप्त करते हैं

विकृत पिंडों की यांत्रिकी में ऐसे विस्थापन संभव हैं जो शरीर पर लगाए गए बाहरी और आंतरिक अवरोधों को संतुष्ट करते हैं।

बाहरी कनेक्शन फिक्सिंग की शर्तें हैं, आंतरिक कनेक्शन निरंतरता की स्थिति हैं।

आंतरिक बाधाओं को संतुष्ट करने के लिए, यह आवश्यक है कि विस्थापन वृद्धि निर्देशांक के निरंतर एकल-मूल्य वाले कार्य हों।

इस रूप में लैग्रेंज सिद्धांत किसी भी विकृत पिंड के लिए मान्य है।

लोचदार निकायों के लिए, यह प्राप्त किया गया था

(41)

तब (40), (41) को ध्यान में रखते हुए, इस प्रकार लिखा जा सकता है

(42)

जहां W विशिष्ट स्ट्रेन है, और

यहाँ U शरीर की संपूर्ण स्थितिज ऊर्जा का एक रूप है।

हम अभिव्यक्ति (43) को (42) में प्रतिस्थापित करते हैं, और, चूँकि बल भिन्न नहीं होते हैं, इसलिए हम उसे लिखते हैं

(44)

समीकरण (44) एक परिवर्तनशील लैग्रेंज समीकरण है।

यदि बल रूढ़िवादी हैं, तो पहले दो अभिन्न अंग विकृत अवस्था से विकृत अवस्था में संक्रमण के दौरान बाहरी बलों की क्षमता में परिवर्तन का प्रतिनिधित्व करते हैं।

बाहरी ताकतों की संभावना

(45)

जहां - विकृत से विकृत अवस्था में संक्रमण के दौरान बाहरी ताकतों के संभावित कार्य की गणना इस धारणा के तहत की जाती है कि बाहरी ताकतें अपरिवर्तित रहती हैं। सिस्टम की कुल ऊर्जा

फिर, अभिव्यक्ति (44) - (46) को ध्यान में रखते हुए, लैग्रेंज सिद्धांत लिखा जाएगा:

अर्थात्, संभावित विस्थापन पर संतुलन स्थिति में सिस्टम की कुल ऊर्जा का परिवर्तन शून्य के बराबर है। अभिव्यक्ति (47) केवल रूढ़िवादी बलों की कार्रवाई के मामले में परिवर्तनशील लैग्रेंज समीकरण है।

स्थिर संतुलन की स्थिति में कुल ऊर्जा P न्यूनतम होती है,

लैग्रेंज सिद्धांत न्यूनतम ऊर्जा का सिद्धांत है।

2 संभावित अवस्थाओं का सिद्धांत (कैस्टिलानो सिद्धांत)

हम संभावित अवस्थाएँ उन्हें कहेंगे जो बाहरी और आंतरिक शक्तियों के अनुरूप हों, यानी संतुलन समीकरणों को संतुष्ट करती हों।

समीकरण (57) कैस्टिग्लिआनो सिद्धांत लिखता है। शरीर की तनाव स्थिति में संभावित परिवर्तनों के साथ, भिन्नता शरीर की सतह के उस हिस्से पर अभिन्न के बराबर होती है जिस पर संभावित सतह बलों और विस्थापन के उत्पादों से विस्थापन दिया जाता है।

लैग्रेंज सिद्धांत के आधार पर, कुछ कार्यों, या उनमें से एक सेट को चुनना, और चूंकि कार्यों का सेट सीमित है, हमें सिस्टम की स्वतंत्रता की डिग्री की एक छोटी संख्या मिलती है, इस प्रकार संरचना की स्वतंत्रता की डिग्री कम हो जाती है। अर्थात्, ऊर्जा के अर्थ में, समाधान सटीक समाधान से अधिक कठोर हो जाता है।

यदि हम अभिन्न विशेषताओं को लेते हैं, तो अनुमानित समाधान अधिक कठोरता से अभिन्न होता है।

स्पैन के बीच में एक अनुप्रस्थ बल के साथ एक हिंगेड बीम को लोड करने की समस्या को हल करते समय (छवि 1), अनुमानित समाधान सटीक समाधान की तुलना में बल के तहत एक छोटा विस्थापन देगा।

सटीक समाधान

कैस्टिग्लिआनो वैरिएबल सिद्धांत का उपयोग करके उसी समस्या को हल करते समय, चूंकि निरंतरता की स्थिति संतुष्ट नहीं होती है, सिस्टम को वास्तविकता की तुलना में अधिक स्वतंत्रता मिलती है।

सटीक समाधान इन दो अनुमानित तरीकों (लैग्रेंज और कैस्टिग्लिआनो) के बीच है। कभी-कभी प्राप्त समाधानों के बीच अंतर छोटा होता है।

5. प्रयुक्त साहित्य की सूची

1. अलेक्जेंड्रोव ए.वी., पोटापोव वी.डी. लोच और प्लास्टिसिटी के सिद्धांत के मूल सिद्धांत। 400 पेज। हायर स्कूल। 1990।

2. वेरेटिमस डी.के. लोच के सिद्धांत के मूल सिद्धांत। भाग I. तनाव सिद्धांत। पाठ्यक्रम के लिए पद्धति संबंधी मार्गदर्शिका "लोच और प्लास्टिसिटी के सिद्धांत के मूल सिद्धांत।" 2005.-37s.

वेरेटिमस डी.के. लोच के सिद्धांत के मूल सिद्धांत। भाग II। विकृतियों का सिद्धांत। तनावग्रस्त और विकृत अवस्था के बीच संबंध। पाठ्यक्रम के लिए पद्धति संबंधी मार्गदर्शिका "लोच और प्लास्टिसिटी के सिद्धांत के मूल सिद्धांत", 2005।-53पी।

वेरेटिमस डी.के. लोच के सिद्धांत के मूल सिद्धांत। भाग III। लोच के सिद्धांत के मूल समीकरण। लोच के सिद्धांत में समस्याओं के प्रकार। पाठ्यक्रम के लिए पद्धति संबंधी मार्गदर्शिका "लोच और प्लास्टिसिटी के सिद्धांत के मूल सिद्धांत", 2005.-45पी।

आराम की अवस्था में या भार के प्रभाव में गतिमान पिंडों में।

1. लोच सिद्धांत की समस्या

इस सिद्धांत का कार्य गणितीय समीकरण लिखना है, जिसके समाधान से निम्नलिखित प्रश्नों के उत्तर देना संभव हो जाता है:

यदि किसी विशेष पिंड पर ज्ञात स्थानों पर किसी दिए गए मान का भार लगाया जाए तो उसकी विकृतियाँ क्या होंगी?
शरीर में कितना तनाव होगा?

सवाल यह है कि शरीर ढह जाएगा, इन भारों का सामना करेगा, लोच के सिद्धांत से निकटता से संबंधित है, लेकिन, सख्ती से कहें तो, यह उसकी क्षमता के भीतर नहीं है।

ऐसे कई उदाहरण हैं - समर्थन पर भरी हुई बीम में विकृति और तनाव के निर्धारण से लेकर, एक विमान, रॉकेट, पनडुब्बी के शरीर में समान मापदंडों की गणना, एक टैंक के कवच में एक कार के पहिये में जब एक प्रक्षेप्य किसी पर्वत श्रृंखला में, किसी ऊंची इमारत के फ्रेम में, किसी ऊंची इमारत के फ्रेम में, आदि से टकराता है।

इंजीनियरिंग समस्याओं के मामले में, संरचनाओं में तनाव और तनाव की गणना सरलीकृत सिद्धांतों के अनुसार की जाती है, जो तार्किक रूप से लोच के सिद्धांत पर आधारित होती है। इन सिद्धांतों में शामिल हैं: सामग्री की ताकत, जिसका कार्य छड़ों और बीमों की गणना करना है, साथ ही ठोस पदार्थों के संपर्क संपर्क के क्षेत्रों में उत्पन्न होने वाले तनाव का आकलन करना है; संरचनात्मक यांत्रिकी- बार सिस्टम (जैसे पुल) का डिज़ाइन, और शैल सिद्धांत- विरूपण और तनाव के विज्ञान की एक स्वतंत्र और अच्छी तरह से विकसित शाखा, जिसका विषय पतली दीवार वाले गोले हैं - बेलनाकार, शंक्वाकार, गोलाकार और जटिल आकार।

2. लोच के सिद्धांत की मूल अवधारणाएँ

लोच के सिद्धांत की मूल अवधारणाएं छोटे विमानों पर कार्य करने वाला तनाव है, जिसे मानसिक रूप से किसी दिए गए बिंदु पी के माध्यम से शरीर में खींचा जा सकता है, बिंदु पी के एक छोटे से पड़ोस की विकृति और बिंदु पी का विस्थापन। सटीक रूप से, यांत्रिक तनाव टेंसर, छोटे स्ट्रेन टेंसर और विस्थापन वेक्टर पेश किए गए हैं तुम मैंलघु अंकन, जहां सूचकांक मैं, जेमान 1, 2, 3 (या) लें एक्स, वाई, जेड)इसे इस रूप में एक मैट्रिक्स के रूप में समझा जाना चाहिए:

टेंसर के लिए संक्षिप्त नोटेशन को इसी तरह समझा जाना चाहिए।

यदि विरूपण के कारण शरीर के भौतिक बिंदु एम ने अंतरिक्ष पी में एक नई स्थिति ले ली है, तो विस्थापन वेक्टर घटकों के साथ एक वेक्टर है (यू एक्स, यू वाई, यू जेड),या, संक्षेप में, तुम मैंछोटे विकृतियों के सिद्धांत में, घटक तुम मैंऔर छोटी मात्राएँ (सख्ती से कहें तो, अतिसूक्ष्म) मानी जाती हैं। टेंसर के घटक, जिसे भी कहा जाता है तनाव टेंसर कॉचीया रैखिक तनाव टेंसरऔर वेक्टर तुम मैंसंबंधित निर्भरताएँ:

अंतिम प्रविष्टि से, यह देखा जा सकता है कि, इसलिए, विरूपण टेंसर परिभाषा के अनुसार सममित है।

यदि बाहरी बलों की कार्रवाई के तहत एक लोचदार शरीर संतुलन में है (यानी, इसके सभी बिंदुओं की गति शून्य के बराबर है), तो शरीर का कोई भी हिस्सा जिसे मानसिक रूप से इससे अलग किया जा सकता है वह भी संतुलन में है। शरीर से एक असीम रूप से छोटा आयताकार समांतर चतुर्भुज निकाला जाता है, जिसके चेहरे कार्टेशियन प्रणाली के समन्वय विमानों के समानांतर होते हैं। किनारे के आकार वाले समांतर चतुर्भुज के लिए संतुलन की स्थिति से डीएक्स, डाई, डीजेड,अनुमानों में बलों के संतुलन की शर्तों पर विचार करने के बाद, हम प्राप्त कर सकते हैं:

इसी प्रकार, समांतर चतुर्भुज पर कार्य करने वाले सभी बलों के मुख्य क्षण के शून्य की समानता को व्यक्त करते हुए, संतुलन समीकरण प्राप्त किए जाते हैं:

इस समानता का अर्थ है कि तनाव टेंसर एक सममित टेंसर है और तनाव टेंसर के अज्ञात घटकों की संख्या घटकर 6 हो जाती है। केवल तीन संतुलन समीकरण हैं, यानी। समस्या को हल करने के लिए सांख्यिकी के समीकरण पर्याप्त नहीं हैं। इसका तरीका यह है कि हुक के नियम समीकरणों का उपयोग करके तनाव को तनाव के रूप में व्यक्त किया जाए, और फिर तनाव को विस्थापन के रूप में व्यक्त किया जाए। तुम मैंकॉची सूत्रों का उपयोग करके, और परिणाम को संतुलन समीकरण में प्रतिस्थापित करें। इस मामले में, तीन अज्ञात कार्यों के संबंध में तीन अंतर संतुलन समीकरण प्राप्त होते हैं यू एक्स यू वाई यू जेड,वे। अज्ञातों की संख्या समीकरणों की संख्या के अनुरूप होगी। इन समीकरणों को नेवियर-कॉची समीकरण कहा जाता है।

3. सीमा की स्थितियाँ

लोच के सिद्धांत में समस्याओं का समाधान आंशिक डेरिवेटिव में अंतर समीकरणों की एक प्रणाली को एकीकृत करने के लिए कम किया जाता है जो आंतरिक बिंदुओं पर एक लोचदार शरीर के व्यवहार को निर्धारित करता है। ये समीकरण शरीर को बांधने वाली सतह की स्थितियों से पूरक होते हैं। ये स्थितियाँ बाहरी सतह बलों या शरीर की सतह पर बिंदुओं के विस्थापन के कार्यों को निर्धारित करती हैं। इसके आधार पर, आमतौर पर तीन प्रकार की सीमा मूल्य समस्याओं में से एक तैयार की जाती है।

पहली सीमा मान समस्या- गतिज। पिंड के आयतन में विस्थापन के घटक पाए जाते हैं, वे सतह पर कुछ निश्चित मान प्राप्त कर लेते हैं। पिंड की सतह पर स्थिति में सतह के समीकरण तथा उस पर विस्थापन के घटकों के मान इस प्रकार निर्धारित किये जाते हैं।

दूसरी सीमा मान समस्या- स्थैतिक. इस मामले में, शरीर की सतह पर गति पर कोई प्रतिबंध नहीं लगाया जाता है, और सतह समीकरण सेट किए जाते हैं, जो सतह पर सामान्य के कोसाइन और सतह भार घटकों के मूल्यों को निर्देशित करते हैं।

ऐसे मामले में जब शरीर की सतह समन्वय विमानों के साथ मेल खाती है, सीमा की स्थिति सीधे तनाव के संदर्भ में तैयार की जा सकती है। फिर यह सतह के समीकरण को इंगित करने और उस पर तनाव घटकों के मूल्यों को निर्धारित करने के लिए पर्याप्त है।

तीसरी सीमा मान समस्या- मिश्रित। इस मामले में, शरीर की सतह के एक हिस्से पर गतिज स्थितियाँ निर्धारित होती हैं, और दूसरे पर स्थैतिक स्थितियाँ।

ये तीन समस्याएं सभी प्रकार की सीमा स्थितियों को समाप्त नहीं करती हैं। उदाहरण के लिए, सतह के कुछ क्षेत्र में, सभी तीन विस्थापन घटकों या सतह भार घटकों को निर्दिष्ट नहीं किया जा सकता है।

4. यह भी देखें

सूत्रों का कहना है

टिमोशेंको एस.पी., गुडइयर जे.लोच का सिद्धांत. एम.: नौका, 1979. 560 पी.

लोच का सिद्धांत- सातत्य यांत्रिकी की एक शाखा जो भार के प्रभाव में आराम कर रहे या गतिमान पिंडों के विस्थापन, विकृति और तनाव का अध्ययन करती है। इस सिद्धांत का उद्देश्य गणितीय समीकरणों की व्युत्पत्ति है, जिसका समाधान निम्नलिखित प्रश्नों के उत्तर देने की अनुमति देता है: यदि किसी दिए गए मान का भार ज्ञात स्थानों पर लागू किया जाता है तो इस विशेष शरीर का विरूपण क्या होगा? शरीर में कितना तनाव होगा? यह सवाल कि क्या शरीर ढह जाएगा या इन भारों का सामना करेगा, लोच के सिद्धांत से निकटता से संबंधित है, लेकिन, सख्ती से कहें तो, इस सिद्धांत की क्षमता के भीतर नहीं है।

संभावित उदाहरणों की संख्या असीमित है - एक विमान, जहाज, पनडुब्बी की संरचना में समान मूल्यों की गणना करने के लिए, एक वैगन के पहिये में, समर्थन पर पड़ी और बलों से भरी हुई बीम में विकृति और तनाव का निर्धारण करने से, कवच में जब कोई प्रक्षेप्य टकराता है, पर्वत श्रृंखला में जब किसी एडिट से होकर गुजरता है, किसी ऊंची इमारत के फ्रेम में, आदि। यहां आरक्षण करना आवश्यक है: पतली दीवार वाले तत्वों से युक्त संरचनाओं की गणना सरलीकृत सिद्धांतों के अनुसार की जाती है, तार्किक रूप से लोच के सिद्धांत पर आधारित होती है; ऐसे सिद्धांतों में शामिल हैं: भार की कार्रवाई के लिए सामग्रियों के प्रतिरोध का सिद्धांत (प्रसिद्ध "सोप्रोमैट"), जिसका कार्य मुख्य रूप से छड़ और बीम की गणना करना है; संरचनात्मक यांत्रिकी - बार सिस्टम की गणना (उदाहरण के लिए, पुल); और, अंत में, गोले का सिद्धांत, वास्तव में, विकृतियों और तनावों के बारे में विज्ञान का एक स्वतंत्र और बहुत उच्च विकसित क्षेत्र है, जिसका विषय सबसे महत्वपूर्ण संरचनात्मक तत्व हैं - पतली दीवार वाले गोले - बेलनाकार, शंक्वाकार, गोलाकार , और अधिक जटिल आकार वाले। इसलिए, लोच के सिद्धांत में, आमतौर पर उन निकायों पर विचार किया जाता है जिनके आवश्यक आयाम बहुत अधिक भिन्न नहीं होते हैं। इस प्रकार, किसी दिए गए आकार का एक लोचदार शरीर माना जाता है, जिस पर ज्ञात बल कार्य करते हैं।

लोच के सिद्धांत की मूल अवधारणाएँ छोटे क्षेत्रों पर कार्य करने वाले तनाव हैं, जिन्हें मानसिक रूप से किसी दिए गए बिंदु के माध्यम से शरीर में ले जाया जा सकता है। एम, बिंदु के एक छोटे से पड़ोस की विकृति एमऔर बिंदु को ही आगे बढ़ा रहा है एम. अधिक सटीक रूप से, तनाव टेंसर एस आईजे, छोटा स्ट्रेन टेंसर ई आईजेऔर विस्थापन वेक्टर तुम मैं.

संक्षिप्त पदनाम एस आईजे, जहां सूचकांक मैं, जेमान 1, 2, 3 को फॉर्म के मैट्रिक्स के रूप में समझा जाना चाहिए:

टेंसर ई के लिए संक्षिप्त संकेतन आईजे.

यदि शरीर का भौतिक बिंदु एमविरूपण के कारण अंतरिक्ष में एक नया स्थान ले लिया एम, तो विस्थापन वेक्टर घटकों वाला एक वेक्टर है ( यू एक्स यू वाई यू जेड), या, संक्षेप में, तुम मैं. छोटे विकृतियों के सिद्धांत में, घटक तुम मैंऔर ई मैंछोटी मात्राएँ (सख्ती से कहें तो, अतिसूक्ष्म) मानी जाती हैं। ई टेंसर के घटक आईजेऔर वेक्टर यू आईजेकॉची सूत्रों से संबंधित हैं, जिनका रूप इस प्रकार है:

यह देखा जा सकता है कि ई xy=इ हाँ, और, सामान्यतया, ई आईजे=इ जी, इसलिए स्ट्रेन टेंसर परिभाषा के अनुसार सममित है।

यदि बाहरी बलों की कार्रवाई के तहत एक लोचदार शरीर संतुलन में है (यानी, इसके सभी बिंदुओं की गति शून्य के बराबर है), तो शरीर का कोई भी हिस्सा जिसे मानसिक रूप से इससे अलग किया जा सकता है वह भी संतुलन में है। एक छोटा (सख्ती से कहें तो, बहुत छोटा) आयताकार समान्तर चतुर्भुज शरीर से बाहर निकलता है, जिसके चेहरे कार्टेशियन प्रणाली के समन्वय विमानों के समानांतर होते हैं ऑक्सीज़(चित्र .1)।

मान लीजिए कि समांतर चतुर्भुज के किनारों की लंबाई है डीएक्स, डीवाई, dzक्रमशः (यहाँ, हमेशा की तरह डीएक्सएक अंतर है एक्स, वगैरह।)। तनाव सिद्धांत के अनुसार, तनाव टेंसर के घटक समांतर चतुर्भुज के चेहरों पर कार्य करते हैं, जिन्हें दर्शाया गया है:

कगार पर ओएडीजी:एस xx, एस xy, एस xz

कगार पर OABC:एस हाँ, एस Y y, एस yz

कगार पर डीएबीई:एस zx, एस ज़ी, एस zz

जबकि समान सूचकांक वाले घटक (उदाहरण के लिए, एस xx) चेहरे के लंबवत कार्य करते हैं, जबकि विभिन्न सूचकांक वाले क्षेत्र तल में कार्य करते हैं।

विपरीत चेहरों पर, एक ही नाम के तनाव टेंसर घटकों के मान थोड़े भिन्न होते हैं, यह इस तथ्य के कारण है कि वे निर्देशांक के कार्य हैं और एक बिंदु से दूसरे बिंदु पर बदलते हैं (हमेशा, ज्ञात सरलतम मामलों को छोड़कर), और परिवर्तन की लघुता समांतर चतुर्भुज के छोटे आयामों से जुड़ी है, इसलिए हम मान सकते हैं कि यदि कगार पर है OABCवोल्टेज एस Y y, फिर कगार पर जीडीईएफवोल्टेज एस Y y+डीएस Y y, और छोटा मान डी.एस Y yठीक इसके छोटेपन के कारण, इसे टेलर श्रृंखला में विस्तार का उपयोग करके निर्धारित किया जा सकता है:

(यहां, आंशिक व्युत्पन्न का उपयोग किया जाता है, क्योंकि तनाव टेंसर के घटक निर्भर करते हैं एक्स, य, जेड).

इसी प्रकार, सभी चेहरों पर तनाव को एस के संदर्भ में व्यक्त किया जा सकता है आईजेऔर डी.एस आईजे. इसके अलावा, तनाव से बल की ओर बढ़ने के लिए, आपको तनाव के परिमाण को उस साइट के क्षेत्र से गुणा करना होगा जिस पर यह कार्य करता है (उदाहरण के लिए, एस Y y+डीएस Y yगुणा करके डीएक्स डीजेड). जब समांतर चतुर्भुज पर कार्य करने वाली सभी शक्तियां निर्धारित हो जाती हैं, तो यह संभव है, जैसा कि स्थैतिक में किया जाता है, शरीर के संतुलन समीकरण को लिखना, जबकि मुख्य वेक्टर के लिए सभी समीकरणों में केवल डेरिवेटिव वाले शब्द ही रहेंगे, क्योंकि तनाव स्वयं एक दूसरे को रद्द करें, और कारक डीएक्स डाई डीजेडकम हो गए हैं और परिणामस्वरूप

इसी प्रकार, संतुलन समीकरण प्राप्त होते हैं जो समांतर चतुर्भुज पर कार्य करने वाले सभी बलों के मुख्य क्षण के शून्य की समानता को व्यक्त करते हैं, जिन्हें इस रूप में घटाया जाता है:

इन समानताओं का मतलब है कि तनाव टेंसर एक सममित टेंसर है। इस प्रकार, 6 अज्ञात घटकों के लिए आईजेतीन संतुलन समीकरण हैं, अर्थात् समस्या को हल करने के लिए सांख्यिकी के समीकरण पर्याप्त नहीं हैं। इससे बाहर निकलने का तरीका तनावों को व्यक्त करना है आईजेविकृतियों के माध्यम से ई आईजेहुक के नियम के समीकरणों का उपयोग करके, और फिर विरूपण ई आईजेविस्थापन के रूप में व्यक्त करें तुम मैंकॉची सूत्रों का उपयोग करके, और परिणाम को संतुलन समीकरणों में प्रतिस्थापित करें। इस मामले में, तीन अज्ञात कार्यों के संबंध में तीन अंतर संतुलन समीकरण प्राप्त होते हैं यू एक्स यू वाई यू जेड, अर्थात। अज्ञातों की संख्या समीकरणों की संख्या के बराबर है। इन समीकरणों को लंगड़ा समीकरण कहा जाता है

शरीर के बल (वजन, आदि) को ध्यान में नहीं रखा जाता है

D लाप्लास ऑपरेटर है, अर्थात

अब हमें शरीर की सतह पर सीमा की स्थिति निर्धारित करने की आवश्यकता है;

इन स्थितियों के मुख्य प्रकार इस प्रकार हैं:

1. विस्थापन शरीर की सतह के ज्ञात भाग S 1 पर दिया जाता है, अर्थात। विस्थापन वेक्टर घटकों के साथ ज्ञात वेक्टर के बराबर है ( एफएक्स; एफय; एफ z ):

यू एक्स = एफ(xyz)

तुम हो= एफ(xyz)

यू z= एफ(xyz)

(एफएक्स, एफ वाई, fzज्ञात समन्वय कार्य हैं)

2. शेष सतह पर एस 2 को सतही बल दिए गए हैं। इसका मतलब यह है कि शरीर के अंदर तनाव वितरण ऐसा है कि सतह के तत्काल आसपास और सीमा में तनाव मान - प्रत्येक प्रारंभिक क्षेत्र की सतह पर घटकों के साथ ज्ञात बाहरी लोड वेक्टर के बराबर एक तनाव वेक्टर बनाते हैं ( एफ एक्स ;वित्तीय वर्ष ; Fz) सतही बल। गणितीय रूप से, इसे इस प्रकार लिखा जाता है: यदि एक बिंदु पर एसतह, इस सतह पर इकाई सामान्य वेक्टर में घटक होते हैं एन एक्स, n y, न्यूजीलैंडफिर इस बिंदु पर (अज्ञात) घटकों के संबंध में समानताएं हैं आईजे: इ आईजे, तो तीन अज्ञात के लिए हमें छह समीकरण मिलते हैं, यानी एक अतिनिर्धारित प्रणाली। इस प्रणाली का समाधान तभी होगा जब ई के लिए अतिरिक्त शर्तें पूरी होंगी आईजे. ये स्थितियाँ अनुकूलता समीकरण हैं।

इन समीकरणों को अक्सर निरंतरता की स्थिति कहा जाता है, जिसका अर्थ है कि वे विरूपण के बाद शरीर की निरंतरता सुनिश्चित करते हैं। यह अभिव्यक्ति आलंकारिक है, लेकिन गलत है: ये स्थितियाँ निरंतर विस्थापन क्षेत्र के अस्तित्व को सुनिश्चित करती हैं, यदि विकृतियों (या तनाव) के घटकों को अज्ञात के रूप में लिया जाता है। इन शर्तों को पूरा करने में विफलता से निरंतरता का उल्लंघन नहीं होता है, बल्कि समस्या के समाधान का अभाव होता है।

इस प्रकार, लोच का सिद्धांत अंतर समीकरण और सीमा स्थितियां प्रदान करता है जो हमें सीमा मूल्य समस्याओं को तैयार करने की अनुमति देता है, जिसका समाधान विचाराधीन निकायों में तनाव, तनाव और विस्थापन के वितरण के बारे में पूरी जानकारी प्रदान करता है। ऐसी समस्याओं को हल करने के तरीके बहुत जटिल हैं, और शक्तिशाली कंप्यूटर का उपयोग करके विश्लेषणात्मक तरीकों को संख्यात्मक तरीकों के साथ जोड़कर सर्वोत्तम परिणाम प्राप्त किए जाते हैं।

व्लादिमीर कुज़नेत्सोव

लोच के सिद्धांत की नींव

लोच सिद्धांत की अक्ष सममितीय समस्याएं

लोच के सिद्धांत की नींव

बुनियादी प्रावधान, धारणाएँ और संकेतन एक प्राथमिक समान्तर चतुर्भुज और एक प्राथमिक चतुष्फलक के लिए संतुलन समीकरण। एक झुके हुए मंच के साथ सामान्य और कतरनी तनाव

एक बिंदु पर मुख्य तनाव और सबसे बड़े कतरनी तनाव का निर्धारण। अष्टफलकीय स्थलों पर तनाव विस्थापन की अवधारणा। विकृतियों और विस्थापनों के बीच संबंध. रिश्तेदार

एक मनमानी दिशा में रैखिक विरूपण विरूपण संगतता समीकरण। आइसोट्रोपिक पिंड के लिए हुक का नियम आयताकार निर्देशांक में समतल समस्या, ध्रुवीय निर्देशांक में समतल समस्या

लोच के सिद्धांत में समस्याओं के संभावित समाधान। विस्थापन और तनाव में समस्याओं का समाधान तापमान क्षेत्र की उपस्थिति। अनुभाग सरल अक्ष सममितीय समस्याएँ, बेलनाकार निर्देशांक में समीकरण, बेलनाकार निर्देशांक में समीकरण पर संक्षिप्त निष्कर्ष (जारी)

एक मोटी दीवार वाले गोलाकार बर्तन का विरूपण, एक समतल पर कार्य करने वाला संकेंद्रित बल

एक लोचदार अर्ध-स्थान को लोड करने के विशेष मामले: एक सर्कल के क्षेत्र पर समान लोडिंग, एक "गोलार्द्ध" के साथ एक सर्कल के क्षेत्र पर लोड करना, उलटा समस्या एक लोचदार आधे में एक बिल्कुल कठोर गेंद का इंडेंटेशन- अंतरिक्ष। मोटी दीवार वाले पाइपों की गेंदों के लोचदार पतन की समस्या

सामान्य जानकारी। पाइप तत्व का संतुलन समीकरण किसी एक सर्किट पर दबाव के तहत तनाव का अध्ययन। समग्र पाइपों में लोचदार विरूपण तनाव के लिए ताकत की स्थिति। बहुपरत पाइपों की गणना की अवधारणा गणना उदाहरण

प्लेटें, झिल्ली बुनियादी परिभाषाएँ और परिकल्पनाएँ

आयताकार निर्देशांक में प्लेट की घुमावदार मध्य सतह का विभेदक समीकरण प्लेट का बेलनाकार और गोलाकार झुकना

एक गोल प्लेट के अक्षसममितीय मोड़ के लिए झुकने के क्षण। एक गोल प्लेट की घुमावदार मध्य सतह का विभेदक समीकरण गोल प्लेटों में सीमा की स्थिति। सबसे बड़ा तनाव और विक्षेप। ताकत की स्थिति. प्लेटों में थर्मल तनाव

झिल्लियों में बलों का निर्धारण. श्रृंखला बल और तनाव. वृत्ताकार डायाफ्राम में विक्षेपण और तनाव का अनुमानित निर्धारण गणना उदाहरण गणना उदाहरण (जारी)

1.1 बुनियादी प्रावधान, धारणाएँ और प्रतीक

लोच के सिद्धांत का उद्देश्य एक लोचदार शरीर की तनाव-तनाव स्थिति का विश्लेषणात्मक अध्ययन करना है। लोच के सिद्धांत की सहायता से, प्रतिरोध मान्यताओं का उपयोग करके प्राप्त समाधानों को सत्यापित किया जा सकता है

सामग्री, और इन समाधानों की प्रयोज्यता की सीमाएँ स्थापित की जाती हैं। कभी-कभी लोच के सिद्धांत के अनुभाग, जिसमें, सामग्री के प्रतिरोध के रूप में, एक भाग की उपयुक्तता के प्रश्न पर विचार किया जाता है, लेकिन एक जटिल गणितीय उपकरण (प्लेटों, गोले, सरणियों की गणना) का उपयोग करके, उन्हें संदर्भित किया जाता है लोच के व्यावहारिक सिद्धांत के रूप में।

यह अध्याय लोच के गणितीय रैखिक सिद्धांत की बुनियादी अवधारणाओं को रेखांकित करता है। भौतिक घटनाओं के वर्णन के लिए गणित के अनुप्रयोग के लिए उनके योजनाबद्धीकरण की आवश्यकता होती है। लोच के गणितीय सिद्धांत में, समस्याओं को न्यूनतम संभव संख्या में मान्यताओं के साथ हल किया जाता है, जो समाधान के लिए उपयोग की जाने वाली गणितीय विधियों को जटिल बनाता है। लोच का रैखिक सिद्धांत घटक तनाव और तनाव के बीच एक रैखिक संबंध के अस्तित्व को मानता है। कई सामग्रियों (रबर, कच्चा लोहा के कुछ ग्रेड) के लिए, ऐसी निर्भरता, यहां तक कि छोटी विकृतियों के साथ भी स्वीकार नहीं की जा सकती है: लोच की सीमा के भीतर आरेख σ - ε का लोडिंग और अनलोडिंग दोनों के तहत समान आकार होता है, लेकिन दोनों ही स्थितियों में यह वक्ररेखीय है। ऐसी सामग्रियों का अध्ययन करते समय, लोच के गैर-रेखीय सिद्धांत की निर्भरता का उपयोग करना आवश्यक है।

में लोच का गणितीय रैखिक सिद्धांत निम्नलिखित मान्यताओं पर आधारित है:

1. माध्यम की सातत्यता (निरंतरता) पर. इस मामले में, किसी पदार्थ की परमाणु संरचना या उपस्थितिकिसी भी रिक्तता पर ध्यान नहीं दिया जाता है।

2. प्राकृतिक अवस्था पर, जिसके आधार पर बल क्रियाओं के प्रयोग से पहले उत्पन्न शरीर की प्रारंभिक तनाव (विकृत) स्थिति को ध्यान में नहीं रखा जाता है, अर्थात, यह माना जाता है कि शरीर को लोड करने के समय, विकृतियाँ और इसके किसी भी बिंदु पर तनाव शून्य के बराबर है। प्रारंभिक तनावों की उपस्थिति में, यह धारणा मान्य होगी, यदि केवल लोच के रैखिक सिद्धांत की निर्भरता को परिणामी तनावों (प्रारंभिक और प्रभावों से उत्पन्न होने वाले योग) पर लागू किया जा सकता है।

3. समरूपता पर, जिसके आधार पर यह माना जाता है कि शरीर की संरचना सभी बिंदुओं पर समान है। जबकि धातुओं के लिए यह धारणा बड़ी त्रुटियाँ नहीं देती है, कंक्रीट के लिए, छोटी मात्रा पर विचार करते समय, यह महत्वपूर्ण त्रुटियाँ पैदा कर सकता है।

4. गोलाकार आइसोट्रॉपी पर जिसके आधार पर ऐसा माना जाता हैसामग्री के यांत्रिक गुण सभी दिशाओं में समान हैं। धातु क्रिस्टल में यह गुण नहीं होता है, लेकिन समग्र रूप से धातु के लिए, जिसमें बड़ी संख्या में छोटे क्रिस्टल होते हैं, हम मान सकते हैं कि यह परिकल्पना सत्य है। विभिन्न दिशाओं में विभिन्न यांत्रिक गुणों वाली सामग्रियों के लिए, जैसे, उदाहरण के लिए, लेमिनेटेड प्लास्टिक के लिए, ऑर्थोट्रोपिक और अनिसोट्रोपिक सामग्रियों की लोच का एक सिद्धांत विकसित किया गया है।

5. आदर्श लोच के बारे में, जिसके आधार पर भार हटाने के बाद विकृति का पूर्ण रूप से गायब होना मान लिया जाता है। जैसा कि ज्ञात है, किसी भी लोडिंग के तहत वास्तविक निकायों में, अवशिष्ट विरूपण होता है। इसलिए, धारणा

6. घटक उपभेदों के बीच रैखिक संबंध पर औरतनाव.

7. विकृतियों की लघुता पर, जिसके आधार पर यह माना जाता है कि सापेक्ष रैखिक एवं कोणीय विकृतियाँ एकता की तुलना में छोटी होती हैं। रबर जैसी सामग्रियों या कॉइल स्प्रिंग्स जैसे तत्वों के लिए, बड़े लोचदार विरूपण का सिद्धांत विकसित किया गया है।

लोच के सिद्धांत की समस्याओं को हल करते समय, वे समाधान की विशिष्टता पर प्रमेय का उपयोग करते हैं: यदि दी गई बाहरी सतह और शरीर की ताकतें संतुलन में हैं, तो वे तनाव और विस्थापन की एक एकल प्रणाली के अनुरूप हैं।समाधान की विशिष्टता की स्थिति तभी मान्य है जब केवल शरीर की प्राकृतिक स्थिति की धारणा मान्य है (अन्यथा, अनंत संख्या में समाधान संभव हैं) और विकृतियों और बाहरी ताकतों के बीच एक रैखिक संबंध की धारणा मान्य है।

लोच के सिद्धांत में समस्याओं को हल करते समय, सेंट-वेनेंट सिद्धांत का अक्सर उपयोग किया जाता है: यदि किसी लोचदार पिंड के एक छोटे खंड पर लगाए गए बाहरी बलों को उसी खंड (समान मुख्य वेक्टर और समान मुख्य क्षण वाले) पर कार्य करने वाले बलों की एक स्थिर समकक्ष प्रणाली द्वारा प्रतिस्थापित किया जाता है, तो यह प्रतिस्थापन केवल स्थानीय विकृतियों में बदलाव का कारण बनेगा। .

उन स्थानों से पर्याप्त दूरी पर जहां बाहरी भार लगाया जाता है, तनाव उनके आवेदन की विधि पर बहुत कम निर्भर करता है। भार, जो सामग्रियों के प्रतिरोध के दौरान एक बल या एक केंद्रित क्षण के रूप में सेंट-वेनेंट सिद्धांत के आधार पर योजनाबद्ध रूप से व्यक्त किया गया था, वास्तव में सामान्य है और कतरनी तनाव एक तरह से या किसी अन्य तरीके से वितरित किया जाता है शरीर की सतह का एक निश्चित क्षेत्र। इस मामले में, विभिन्न तनाव वितरण एक ही बल या बलों की जोड़ी के अनुरूप हो सकते हैं। सेंट-वेनेंट सिद्धांत के आधार पर, यह माना जा सकता है कि शरीर की सतह के एक हिस्से पर बलों में बदलाव से इन बलों के आवेदन के स्थान से पर्याप्त बड़ी दूरी पर स्थित बिंदुओं पर तनाव पर लगभग कोई प्रभाव नहीं पड़ता है (तुलना में) भारित क्षेत्र के रैखिक आयाम)।

अध्ययन के तहत क्षेत्र की स्थिति, शरीर में चयनित (छवि 1), आयताकार समन्वय अक्ष x, y और z की चयनित प्रणाली में क्षेत्र के लिए सामान्य एन के दिशा कोसाइन द्वारा निर्धारित की जाती है।

यदि P बिंदु A पर चयनित प्रारंभिक क्षेत्र पर कार्य करने वाले आंतरिक बलों का परिणाम है, तो सामान्य N के साथ क्षेत्र के साथ इस बिंदु पर कुल तनाव p N को अनुपात की सीमा के रूप में परिभाषित किया गया है

निम्नलिखित प्रपत्र:

वेक्टर पी एन को अंतरिक्ष में तीन परस्पर लंबवत घटकों में विघटित किया जा सकता है।

2. घटकों में σ एन, τ एन एस और τ एन टी साइट के सामान्य (सामान्य तनाव) की दिशाओं में और दो परस्पर लंबवत अक्ष एस और टी (छवि 1 बी) साइट के विमान में झूठ बोलते हैं (स्पर्शरेखा) तनाव)। चित्र 1 के अनुसार, बी

यदि शरीर या क्षेत्र का खंड समन्वय विमानों में से एक के समानांतर है, उदाहरण के लिए y0z (छवि 2), तो तीसरा समन्वय अक्ष x इस क्षेत्र के लिए सामान्य होगा और तनाव घटकों में पदनाम σ x होंगे, τ xy और τ xz .

सामान्य तनाव यदि तन्य है तो सकारात्मक है और यदि संपीड़ित है तो नकारात्मक है। कतरनी तनाव का संकेत निम्नलिखित नियम का उपयोग करके निर्धारित किया जाता है: यदि साइट के साथ एक सकारात्मक (तन्य) सामान्य तनाव एक सकारात्मक प्रक्षेपण देता है, तो स्पर्शरेखा

उसी क्षेत्र पर तनाव को सकारात्मक माना जाता है, बशर्ते कि यह संबंधित अक्ष पर भी सकारात्मक प्रक्षेपण देता हो; यदि तन्य सामान्य तनाव नकारात्मक प्रक्षेपण देता है, तो सकारात्मक कतरनी तनाव को भी संबंधित अक्ष पर नकारात्मक प्रक्षेपण देना चाहिए।

अंजीर पर. 3, उदाहरण के लिए, प्राथमिक समांतर चतुर्भुज के चेहरों पर कार्य करने वाले सभी तनाव घटक, समन्वय विमानों के साथ मेल खाते हैं, सकारात्मक हैं।

किसी लोचदार पिंड के एक बिंदु पर तनाव की स्थिति निर्धारित करने के लिए, इस बिंदु से गुजरने वाले तीन परस्पर लंबवत क्षेत्रों के लिए कुल तनाव पी एन जानना आवश्यक है। चूँकि प्रत्येक कुल तनाव को तीन घटकों में विघटित किया जा सकता है, यदि नौ तनाव घटक ज्ञात हों तो तनाव की स्थिति निर्धारित की जाएगी। इन घटकों को मैट्रिक्स के रूप में लिखा जा सकता है

एक बिंदु पर तनाव टेंसर घटकों का मैट्रिक्स कहा जाता है।

मैट्रिक्स की प्रत्येक क्षैतिज रेखा में एक ही क्षेत्र पर कार्य करने वाले तीन तनाव घटक होते हैं, क्योंकि पहले चिह्न (सामान्य का नाम) उनके लिए समान होते हैं। टेंसर के प्रत्येक ऊर्ध्वाधर स्तंभ में एक ही अक्ष के समानांतर तीन तनाव होते हैं, क्योंकि दूसरे चिह्न (उस अक्ष का नाम जिसके समानांतर तनाव कार्य करता है) समान होते हैं।

1.2 प्रारंभिक समांतर चतुर्भुज के लिए संतुलन समीकरण

और प्राथमिक चतुष्फलक

आइए हम विमानों के तीन परस्पर लंबवत जोड़े (छवि 2) द्वारा तनावग्रस्त लोचदार शरीर के अध्ययन के तहत बिंदु ए (निर्देशांक x, y और z के साथ) पर किनारे के आकार dx, dy और dz के साथ एक प्राथमिक समानांतर चतुर्भुज आवंटित करें। बिंदु A (समन्वय तलों के निकटतम) से सटे तीन परस्पर लंबवत चेहरों में से प्रत्येक पर, तीन तनाव घटक कार्य करेंगे - सामान्य और दो स्पर्शरेखा। हम मानते हैं कि वे बिंदु A के निकटवर्ती फलकों पर धनात्मक हैं।

बिंदु A से गुजरने वाले चेहरे से समानांतर चेहरे की ओर जाने पर, तनाव बदल जाता है और वृद्धि प्राप्त होती है। उदाहरण के लिए, यदि तनाव घटक σ x = f 1 (x, y, z), τ xy = f 2 (x, y, z,), τ xz = f 3 (x, y,z,) , फिर समानांतर फलक के साथ, एक फलक से दूसरे फलक पर संक्रमण के दौरान केवल एक x निर्देशांक की वृद्धि के कारण,

तनाव घटक प्राथमिक समांतर चतुर्भुज के सभी चेहरों पर तनाव निर्धारित करना संभव है, जैसा कि अंजीर में दिखाया गया है। 3.

प्राथमिक समान्तर चतुर्भुज के चेहरों पर लागू तनावों के अलावा, शरीर बल इस पर कार्य करते हैं: भार बल, जड़त्व बल। आइए हम निर्देशांक अक्षों पर, प्रति इकाई आयतन, इन बलों के प्रक्षेपणों को X, Y और Z द्वारा निरूपित करें। यदि हम सभी सामान्य, स्पर्शरेखा और आयतन बलों के x-अक्ष पर प्रक्षेपणों के योग को शून्य के बराबर करते हैं,

प्राथमिक समांतर चतुर्भुज पर कार्य करते हुए, उत्पाद dxdydz द्वारा कमी के बाद हम समीकरण प्राप्त करते हैं

Y और z अक्षों पर बलों के प्रक्षेपण के लिए समान समीकरण संकलित करने के बाद, हम कॉची द्वारा प्राप्त प्राथमिक समांतर चतुर्भुज के संतुलन के लिए तीन अंतर समीकरण लिखते हैं,

जब समांतर चतुर्भुज के आयाम शून्य हो जाते हैं, तो यह एक बिंदु में बदल जाता है, और σ और τ बिंदु ए से गुजरने वाले तीन परस्पर लंबवत क्षेत्रों के साथ तनाव घटक होते हैं।

यदि हम x c अक्ष के सापेक्ष, x अक्ष के समानांतर और इसके गुरुत्वाकर्षण के केंद्र से गुजरने वाले प्राथमिक समानांतर चतुर्भुज पर कार्य करने वाले सभी बलों के क्षणों के योग को शून्य के बराबर करते हैं, तो हमें समीकरण प्राप्त होता है

या, इस तथ्य को ध्यान में रखते हुए कि समीकरण के दूसरे और चौथे पद dxdydz द्वारा घटाने के बाद बाकी की तुलना में छोटेपन के उच्च क्रम के हैं

τ yz - τ zy = 0 या τ yz = τ zy.

केंद्रीय अक्षों y c और z c के बारे में आघूर्णों के समान समीकरणों को संकलित करते हुए, हमें अपरूपण प्रतिबलों के युग्मन के नियम के तीन समीकरण प्राप्त होते हैं

τ xy = τ yx, τ yx = τ xy, τ zx = τ xz। (1.3)

यह कानून इस प्रकार तैयार किया गया है:परस्पर लंबवत क्षेत्रों पर कार्य करने वाले और क्षेत्रों की प्रतिच्छेदन रेखा के लंबवत निर्देशित स्पर्शरेखीय तनाव परिमाण में समान और संकेत में समान होते हैं।

इस प्रकार, टेंसर टी σ के मैट्रिक्स के नौ तनाव घटकों में से छह जोड़ीदार एक दूसरे के बराबर हैं, और एक बिंदु पर तनाव की स्थिति निर्धारित करने के लिए, केवल निम्नलिखित छह तनाव घटकों को ढूंढना पर्याप्त है:

लेकिन स्थापित संतुलन स्थितियों ने हमें केवल तीन समीकरण (1.2) दिए, जिनमें से छह अज्ञात नहीं पाए जा सकते। इस प्रकार, एक बिंदु पर तनाव की स्थिति निर्धारित करने की सीधी समस्या, सामान्य स्थिति में, सांख्यिकीय रूप से अनिश्चित है। इस स्थिर अनिश्चितता को प्रकट करने के लिए अतिरिक्त ज्यामितीय और भौतिक निर्भरता की आवश्यकता होती है।

आइए हम प्रारंभिक समांतर चतुर्भुज को उसके फलकों की ओर झुके हुए समतल द्वारा बिंदु A पर काटें; मान लीजिए कि इस तल के सामान्य N की दिशा कोसाइन l, m और n हैं। परिणामी ज्यामितीय आकृति (चित्र 4) एक त्रिकोणीय आधार वाला एक पिरामिड है - एक प्राथमिक टेट्राहेड्रोन। हम मान लेंगे कि बिंदु A निर्देशांक की उत्पत्ति के साथ मेल खाता है, और टेट्राहेड्रोन के तीन परस्पर लंबवत चेहरे समन्वय विमानों के साथ मेल खाते हैं।

टेट्राहेड्रोन के इन चेहरों पर कार्य करने वाले तनाव घटकों पर विचार किया जाएगा

सकारात्मक। उन्हें आकृति में दिखाया जाता है। 4. x, y और z अक्षों पर BCD टेट्राहेड्रोन के झुके हुए चेहरे पर अभिनय करने वाले कुल तनाव p N के अनुमान और अनुमान को निरूपित करें। झुके हुए फलक BCD का क्षेत्रफल dF द्वारा दर्शाया जाता है। तब फलक ABC का क्षेत्रफल dFp, फलक ACD - dFl और फलक ADB - dFt होगा।

आइए हम एक चतुष्फलक के फलकों पर कार्यरत सभी बलों को x-अक्ष पर प्रक्षेपित करके उसका संतुलन समीकरण बनाएं; शरीर के बल का प्रक्षेपण प्रक्षेपण समीकरण में शामिल नहीं है, इसलिए

सतही बलों के प्रक्षेपण की तुलना में लघुता के उच्च क्रम का मूल्य कैसा है:

y और z अक्षों पर टेट्राहेड्रोन पर कार्य करने वाले बलों के लिए प्रक्षेपण समीकरणों को संकलित करने पर, हमें दो और समान समीकरण प्राप्त होते हैं। परिणामस्वरूप, हमारे पास प्राथमिक चतुष्फलक के लिए तीन संतुलन समीकरण होंगे

आइए हम मनमाने आकार के एक स्थानिक पिंड को परस्पर लंबवत विमानों хОу, yОz और хОz (चित्र 5) की एक प्रणाली द्वारा कई प्राथमिक समानांतर चतुर्भुजों में विभाजित करें। शरीर की सतह पर, प्राथमिक

टेट्राहेड्रा, (सतह के घुमावदार खंड, उनकी छोटीता के कारण, विमानों द्वारा प्रतिस्थापित किए जा सकते हैं)। इस मामले में, पी एन सतह पर भार का प्रतिनिधित्व करेगा, और समीकरण (1.4) इस भार को शरीर में तनाव σ और τ से संबंधित करेंगे, यानी, वे लोच सिद्धांत की समस्या की सीमा स्थितियों का प्रतिनिधित्व करेंगे। इन समीकरणों द्वारा परिभाषित शर्तों को कहा जाता है सतह की स्थितियाँ.

यह ध्यान दिया जाना चाहिए कि लोच के सिद्धांत में, बाहरी भार को शरीर की सतह के साथ मेल खाने वाले क्षेत्रों पर कुछ कानून के अनुसार लागू सामान्य और स्पर्शरेखा तनाव द्वारा दर्शाया जाता है।

1.3 ढलान के साथ सामान्य और अपरूपण तनाव

साइट

एक प्रारंभिक चतुष्फलक ABCD पर विचार करें, जिसके तीन फलक निर्देशांक तलों के समानांतर हैं, और चौथे फलक का सामान्य N निर्देशांक अक्षों के साथ कोण बनाता है, जिनकी कोज्या l, m और n के बराबर हैं (चित्र 6) . हम मान लेंगे कि समन्वय विमानों में स्थित क्षेत्रों पर कार्य करने वाले सामान्य और कतरनी तनाव के घटक दिए गए हैं, और हम बीसीडी क्षेत्र पर तनाव का निर्धारण करेंगे। हम आयताकार निर्देशांक अक्षों x 1, y 1 और z 1 की एक नई प्रणाली चुनते हैं, ताकि x 1 अक्ष सामान्य N के साथ संपाती हो,

तनाव-तनाव की स्थिति निर्धारित की जाती है यदि तनाव टेंसर () और विस्थापन वेक्टर, नौ कार्यों के घटक पाए जाते हैं।

लोच सिद्धांत के मूल समीकरण

विभेदक कैचियाँ

कॉची विकृतियों के रैखिक भाग के टेंसर के घटक कहाँ हैं;

त्रिज्या के साथ विस्थापन के व्युत्पन्न के टेंसर के घटक।

विभेदक संतुलन समीकरण

तनाव टेंसर घटक कहाँ हैं; जे अक्ष पर शरीर के बल का प्रक्षेपण है।

रैखिक रूप से लोचदार आइसोट्रोपिक शरीर के लिए हुक का नियम

उपरोक्त समीकरणों को सेंट-वेनेंट निर्भरता को संतुष्ट करना चाहिए

लोच के सिद्धांत में समस्याओं के प्रकार

प्रथम प्रकार. शरीर की सतह पर बल दिये जाते हैं। सीमा की स्थितियाँ

लोच के सिद्धांत की प्रत्यक्ष और व्युत्क्रम समस्याएं

विस्थापन में लोच सिद्धांत समीकरण (लंगड़ा समीकरण)

विस्थापन में लोच के सिद्धांत के समीकरणों को निर्धारित करने के लिए, हम लिखते हैं: अंतर संतुलन समीकरण (18) एक रैखिक लोचदार आइसोट्रोपिक शरीर के लिए हुक का नियम (19)