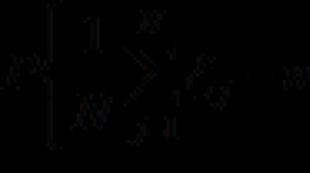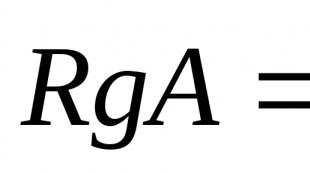एक विषमांगी प्रणाली का सामान्य समाधान. रैखिक समीकरणों की सजातीय प्रणालियाँ सजातीय प्रणालियों का समाधान 0

रेखीय समीकरण कहलाता है सजातीय, यदि इसका मुक्त पद शून्य के बराबर है, और अन्यथा अमानवीय है। सजातीय समीकरणों से युक्त प्रणाली को सजातीय कहा जाता है और इसका सामान्य रूप होता है:

यह स्पष्ट है कि प्रत्येक सजातीय प्रणाली सुसंगत है और इसका एक शून्य (तुच्छ) समाधान है। इसलिए, जब रैखिक समीकरणों की सजातीय प्रणालियों पर लागू किया जाता है, तो अक्सर गैर-शून्य समाधानों के अस्तित्व के प्रश्न का उत्तर ढूंढना पड़ता है। इस प्रश्न का उत्तर निम्नलिखित प्रमेय के रूप में तैयार किया जा सकता है।

प्रमेय . रैखिक समीकरणों की एक सजातीय प्रणाली का एक गैर-शून्य समाधान होता है यदि और केवल तभी जब इसकी रैंक अज्ञात की संख्या से कम हो .

सबूत: आइए मान लें कि जिस प्रणाली की रैंक बराबर है उसका समाधान गैर-शून्य है। जाहिर है यह इससे अधिक नहीं है. यदि सिस्टम के पास एक अनूठा समाधान है। चूँकि सजातीय रैखिक समीकरणों की प्रणाली में हमेशा शून्य समाधान होता है, तो शून्य समाधान यह अद्वितीय समाधान होगा। इस प्रकार, गैर-शून्य समाधान केवल के लिए संभव हैं।

परिणाम 1 : समीकरणों की एक सजातीय प्रणाली, जिसमें समीकरणों की संख्या अज्ञात की संख्या से कम होती है, का हमेशा एक गैर-शून्य समाधान होता है।

सबूत: यदि समीकरणों की एक प्रणाली है, तो प्रणाली की रैंक समीकरणों की संख्या से अधिक नहीं है, अर्थात। . इस प्रकार, शर्त पूरी हो जाती है और इसलिए, सिस्टम के पास एक गैर-शून्य समाधान होता है।

परिणाम 2 : अज्ञात के साथ समीकरणों की एक सजातीय प्रणाली का एक गैर-शून्य समाधान होता है यदि और केवल तभी जब इसका निर्धारक शून्य हो।

सबूत: आइए मान लें कि रैखिक सजातीय समीकरणों की एक प्रणाली, जिसके मैट्रिक्स में निर्धारक के साथ एक गैर-शून्य समाधान होता है। फिर, सिद्ध प्रमेय के अनुसार, और इसका अर्थ है कि मैट्रिक्स एकवचन है, अर्थात। .

क्रोनेकर-कैपेली प्रमेय: एक SLU सुसंगत है यदि और केवल तभी जब सिस्टम मैट्रिक्स की रैंक इस सिस्टम के विस्तारित मैट्रिक्स की रैंक के बराबर हो। एक सिस्टम यूआर को सुसंगत कहा जाता है यदि इसमें कम से कम एक समाधान हो।

रैखिक बीजगणितीय समीकरणों की सजातीय प्रणाली.

n चर वाले m रैखिक समीकरणों की एक प्रणाली को रैखिक सजातीय समीकरणों की एक प्रणाली कहा जाता है यदि सभी मुक्त पद 0 के बराबर हों। रैखिक सजातीय समीकरणों की एक प्रणाली हमेशा सुसंगत होती है, क्योंकि इसका हमेशा कम से कम शून्य समाधान होता है। रैखिक सजातीय समीकरणों की एक प्रणाली का एक गैर-शून्य समाधान होता है यदि और केवल तभी जब चर के लिए इसके गुणांक के मैट्रिक्स की रैंक चर की संख्या से कम हो, यानी। रैंक ए के लिए (एन। कोई रैखिक संयोजन

लिन सिस्टम समाधान. सजातीय. ur-ii भी इस प्रणाली का एक समाधान है।

रैखिक स्वतंत्र समाधान e1, e2,...,ek की एक प्रणाली को मौलिक कहा जाता है यदि प्रणाली का प्रत्येक समाधान समाधानों का एक रैखिक संयोजन है। प्रमेय: यदि रैखिक सजातीय समीकरणों की प्रणाली के चर के लिए गुणांक के मैट्रिक्स का रैंक आर चर एन की संख्या से कम है, तो सिस्टम के समाधान की प्रत्येक मौलिक प्रणाली में एनआर समाधान होते हैं। इसलिए, रैखिक प्रणाली का सामान्य समाधान. एक दिन ur-th का रूप है: c1e1+c2e2+...+skek, जहां e1, e2,..., ek समाधान की कोई मौलिक प्रणाली है, c1, c2,...,ck मनमानी संख्याएं हैं और k=n-r। n चर वाले m रैखिक समीकरणों की प्रणाली का सामान्य समाधान योग के बराबर है

इसके अनुरूप प्रणाली का सामान्य समाधान सजातीय है। रैखिक समीकरण और इस प्रणाली का एक मनमाना विशेष समाधान।

7. रैखिक स्थान. उपस्थान। आधार, आयाम. रैखिक खोल. रैखिक स्थान कहलाता है n आयामी, यदि इसमें रैखिक रूप से स्वतंत्र वैक्टरों की एक प्रणाली शामिल है, और बड़ी संख्या में वैक्टरों की कोई भी प्रणाली रैखिक रूप से निर्भर है। नंबर पर कॉल किया जाता है आयाम (आयामों की संख्या)रैखिक स्थान और द्वारा निरूपित किया जाता है। दूसरे शब्दों में, किसी स्थान का आयाम इस स्थान के रैखिक रूप से स्वतंत्र वैक्टरों की अधिकतम संख्या है। यदि ऐसी कोई संख्या मौजूद है, तो स्थान को परिमित-आयामी कहा जाता है। यदि, किसी प्राकृतिक संख्या n के लिए, अंतरिक्ष में रैखिक रूप से स्वतंत्र वैक्टर से युक्त एक प्रणाली है, तो ऐसे स्थान को अनंत-आयामी (लिखित:) कहा जाता है। निम्नलिखित में, जब तक कि अन्यथा न कहा गया हो, परिमित-आयामी स्थानों पर विचार किया जाएगा।

एन-आयामी रैखिक स्थान का आधार रैखिक रूप से स्वतंत्र वैक्टर का एक क्रमबद्ध संग्रह है ( आधार वैक्टर).

आधार के संदर्भ में एक वेक्टर के विस्तार पर प्रमेय 8.1। यदि एन-आयामी रैखिक स्थान का आधार है, तो किसी भी वेक्टर को आधार वैक्टर के रैखिक संयोजन के रूप में दर्शाया जा सकता है:

V=v1*e1+v2*e2+…+vn+en
और, इसके अलावा, एकमात्र तरीके से, अर्थात्। गुणांक विशिष्ट रूप से निर्धारित होते हैं।दूसरे शब्दों में, अंतरिक्ष के किसी भी वेक्टर को एक आधार में और इसके अलावा, एक अनोखे तरीके से विस्तारित किया जा सकता है।

दरअसल, अंतरिक्ष का आयाम है। सदिशों की प्रणाली रैखिक रूप से स्वतंत्र है (यह एक आधार है)। किसी भी वेक्टर को आधार में जोड़ने के बाद, हमें एक रैखिक रूप से निर्भर प्रणाली प्राप्त होती है (क्योंकि इस प्रणाली में एन-आयामी अंतरिक्ष के वैक्टर होते हैं)। 7 रैखिक रूप से आश्रित और रैखिक रूप से स्वतंत्र वैक्टर की संपत्ति का उपयोग करके, हम प्रमेय का निष्कर्ष प्राप्त करते हैं।

उच्च व्यावसायिक शिक्षा के संघीय राज्य बजटीय शैक्षणिक संस्थान की कलुगा शाखा

"मॉस्को स्टेट टेक्निकल यूनिवर्सिटी का नाम एन.ई. के नाम पर रखा गया" बाउमन"

(मॉस्को स्टेट टेक्निकल यूनिवर्सिटी की खार्कोव शाखा का नाम एन.ई. बाउमन के नाम पर रखा गया है)

व्लायकोव एन.डी.

सजातीय SLAEs का समाधान

अभ्यास आयोजित करने के लिए दिशानिर्देश

विश्लेषणात्मक ज्यामिति के पाठ्यक्रम पर

कलुगा 2011

पाठ उद्देश्य पृष्ठ 4

पाठ योजना पृष्ठ 4

आवश्यक सैद्धान्तिक जानकारी पृ.5

व्यावहारिक भाग पृ.10

कवर की गई सामग्री की निपुणता की निगरानी करना पृष्ठ 13

होमवर्क पृष्ठ 14

घंटों की संख्या: 2

पाठ मकसद:

SLAE के प्रकार और उन्हें हल करने के तरीकों के बारे में अर्जित सैद्धांतिक ज्ञान को व्यवस्थित करें।

सजातीय SLAE को हल करने में कौशल हासिल करें।

शिक्षण योजना:

सैद्धांतिक सामग्री की संक्षेप में रूपरेखा प्रस्तुत करें।

एक सजातीय SLAE को हल करें.

एक सजातीय SLAE के समाधान की मूलभूत प्रणाली खोजें।

एक सजातीय SLAE का एक विशेष समाधान खोजें।

एक सजातीय SLAE को हल करने के लिए एक एल्गोरिदम तैयार करें।

अपना वर्तमान होमवर्क जांचें.

सत्यापन कार्य करें.

अगले सेमिनार का विषय प्रस्तुत करें.

वर्तमान होमवर्क सबमिट करें.

आवश्यक सैद्धांतिक जानकारी.

मैट्रिक्स रैंक.

हार।मैट्रिक्स की रैंक वह संख्या है जो इसके गैर-शून्य नाबालिगों के बीच अधिकतम क्रम के बराबर है। मैट्रिक्स की रैंक को द्वारा दर्शाया जाता है।

यदि कोई वर्ग मैट्रिक्स गैर-एकवचन है, तो उसकी रैंक उसके क्रम के बराबर होती है। यदि कोई वर्ग मैट्रिक्स एकवचन है, तो उसकी रैंक उसके क्रम से कम होती है।

एक विकर्ण मैट्रिक्स की रैंक उसके गैर-शून्य विकर्ण तत्वों की संख्या के बराबर होती है।

या।जब किसी मैट्रिक्स को ट्रांसपोज़ किया जाता है, तो उसकी रैंक नहीं बदलती, यानी।
.

या।किसी मैट्रिक्स की रैंक उसकी पंक्तियों और स्तंभों के प्रारंभिक परिवर्तनों से नहीं बदलती है।

आधार पर प्रमेय गौण.

हार।नाबालिग
मैट्रिक्स यदि दो शर्तें पूरी होती हैं तो इसे बुनियादी कहा जाता है:

क) यह शून्य के बराबर नहीं है;

बी) इसका क्रम मैट्रिक्स की रैंक के बराबर है .

आव्यूह कई आधार अवयस्क हो सकते हैं।

मैट्रिक्स पंक्तियाँ और स्तंभ , जिसमें चयनित मूल अवयस्क स्थित है, मूल कहलाते हैं।

या।आधार पर प्रमेय गौण. मैट्रिक्स की मूल पंक्तियाँ (स्तंभ)। , इसके किसी भी आधार अवयस्क के अनुरूप
, रैखिक रूप से स्वतंत्र हैं। मैट्रिक्स की कोई भी पंक्तियाँ (स्तंभ)। , में शामिल नहीं है
, आधार पंक्तियों (स्तंभों) के रैखिक संयोजन हैं।

या।किसी भी मैट्रिक्स के लिए, उसकी रैंक उसकी रैखिक रूप से स्वतंत्र पंक्तियों (स्तंभों) की अधिकतम संख्या के बराबर होती है।

मैट्रिक्स की रैंक की गणना. प्राथमिक परिवर्तन की विधि.

प्राथमिक पंक्ति परिवर्तनों का उपयोग करके, किसी भी मैट्रिक्स को सोपानक रूप में कम किया जा सकता है। चरण मैट्रिक्स की रैंक गैर-शून्य पंक्तियों की संख्या के बराबर है। इसमें आधार लघु है, जो प्रत्येक पंक्ति में बाईं ओर से पहले गैर-शून्य तत्वों के अनुरूप स्तंभों के साथ गैर-शून्य पंक्तियों के चौराहे पर स्थित है।

SLAU. बुनियादी परिभाषाएँ.

हार।प्रणाली

(15.1)

नंबर SLAE गुणांक कहलाते हैं। नंबर
समीकरणों के मुक्त पद कहलाते हैं।

प्रपत्र (15.1) में SLAE प्रविष्टि को निर्देशांक कहा जाता है।

हार।एक SLAE को सजातीय कहा जाता है यदि
. अन्यथा इसे विषमांगी कहा जाता है।

हार। SLAE का समाधान अज्ञात मानों का एक सेट है, जिसे प्रतिस्थापित करने पर, सिस्टम का प्रत्येक समीकरण एक पहचान में बदल जाता है। किसी SLAE के किसी विशिष्ट समाधान को उसका विशेष समाधान भी कहा जाता है।

SLAE को हल करने का अर्थ है दो समस्याओं को हल करना:

पता लगाएं कि क्या SLAE के पास समाधान हैं;

यदि वे मौजूद हैं तो सभी समाधान खोजें।

हार।एक SLAE को संयुक्त कहा जाता है यदि उसके पास कम से कम एक समाधान हो। अन्यथा, इसे असंगत कहा जाता है।

हार।यदि SLAE (15.1) का कोई समाधान है, और अद्वितीय है, तो इसे निश्चित कहा जाता है, और यदि समाधान अद्वितीय नहीं है, तो इसे अनिश्चित कहा जाता है।

हार।यदि समीकरण (15.1) में
,SLAE को वर्ग कहा जाता है।

एसएलएयू रिकॉर्डिंग फॉर्म।

समन्वय प्रपत्र (15.1) के अलावा, SLAE रिकॉर्ड अक्सर इसके अन्य अभ्यावेदन में उपयोग किए जाते हैं।

(15.2)

संबंध को SLAE नोटेशन का वेक्टर रूप कहा जाता है।

यदि हम मैट्रिक्स के उत्पाद को आधार के रूप में लेते हैं, तो SLAE (15.1) को इस प्रकार लिखा जा सकता है:

(15.3)

या
.

फॉर्म (15.3) में SLAE (15.1) के अंकन को मैट्रिक्स कहा जाता है।

सजातीय SLAEs.

सजातीय प्रणाली
रैखिक बीजगणितीय समीकरण के साथ अज्ञात रूप की एक प्रणाली है

सजातीय SLAE हमेशा सुसंगत होते हैं, क्योंकि हमेशा एक शून्य समाधान होता है।

गैर-शून्य समाधान के अस्तित्व के लिए मानदंड.एक सजातीय वर्ग SLAE के लिए एक गैर-शून्य समाधान मौजूद होने के लिए, यह आवश्यक और पर्याप्त है कि इसका मैट्रिक्स एकवचन हो।

या।यदि कॉलम
,
, …,
एक सजातीय SLAE के समाधान हैं, तो उनमें से कोई भी रैखिक संयोजन भी इस प्रणाली का एक समाधान है।

परिणाम. यदि एक सजातीय SLAE का एक गैर-शून्य समाधान है, तो इसमें अनंत संख्या में समाधान हैं।

ऐसे समाधान खोजने का प्रयास करना स्वाभाविक है
,
, …,
सिस्टम ताकि किसी भी अन्य समाधान को उनके रैखिक संयोजन के रूप में और इसके अलावा, एक अनूठे तरीके से प्रस्तुत किया जा सके।

हार।का कोई भी सेट
रैखिक रूप से स्वतंत्र स्तंभ
,
, …,
, जो एक सजातीय SLAE के समाधान हैं
, कहाँ - अज्ञात की संख्या, और - इसके मैट्रिक्स की रैंक , इस सजातीय SLAE के समाधान की मूलभूत प्रणाली कहलाती है।

रैखिक समीकरणों की सजातीय प्रणालियों का अध्ययन और समाधान करते समय, हम सिस्टम के मैट्रिक्स में आधार माइनर को ठीक करेंगे। आधार लघु आधार स्तंभों के अनुरूप होगा और इसलिए, आधार अज्ञात होगा। शेष अज्ञात को हम निःशुल्क कहेंगे।

या।एक सजातीय SLAE के सामान्य समाधान की संरचना पर। अगर
,
, …,
- एक सजातीय SLAE के समाधान की मनमानी मौलिक प्रणाली
, तो इसके किसी भी समाधान को फॉर्म में दर्शाया जा सकता है

कहाँ , …,- कुछ स्थायी हैं.

वह। एक सजातीय SLAE के सामान्य समाधान का रूप होता है

व्यावहारिक भाग.

निम्नलिखित प्रकार के SLAE के समाधानों के संभावित सेट और उनकी चित्रमय व्याख्या पर विचार करें।

;
;
.

क्रैमर के सूत्रों और मैट्रिक्स विधि का उपयोग करके इन प्रणालियों को हल करने की संभावना पर विचार करें।

गॉस विधि का सार समझाइये।

निम्नलिखित समस्याओं का समाधान करें.

उदाहरण 1. एक सजातीय SLAE को हल करें। एफएसआर खोजें।

.

आइए सिस्टम के मैट्रिक्स को लिखें और इसे चरणबद्ध रूप में कम करें।

.

सिस्टम में अनंत रूप से कई समाधान होंगे। एफएसआर में शामिल होंगे
कॉलम.

आइए शून्य रेखाओं को हटा दें और सिस्टम को फिर से लिखें:

.

हम मूल माइनर को ऊपरी बाएँ कोने में मानेंगे। वह।
- बुनियादी अज्ञात, और
- मुक्त। आइए व्यक्त करें
निःशुल्क के माध्यम से
:

;

चलो रखो
.

अंततः हमारे पास है:

- उत्तर का समन्वय रूप, या

- उत्तर का मैट्रिक्स रूप, या

- उत्तर का वेक्टर रूप (वेक्टर - कॉलम एफएसआर कॉलम हैं)।

एक सजातीय SLAE को हल करने के लिए एल्गोरिदम।

एफएसआर और निम्नलिखित प्रणालियों का सामान्य समाधान खोजें:

№2.225(4.39)

. उत्तर:

№2.223(2.37)

. उत्तर:

№2.227(2.41)

. उत्तर:

एक सजातीय SLAE को हल करें:

. उत्तर:

एक सजातीय SLAE को हल करें:

. उत्तर:

अगले सेमिनार के विषय की प्रस्तुति.

रैखिक अमानवीय समीकरणों को हल करने की प्रणालियाँ।

कवर की गई सामग्री की महारत की निगरानी करना।

परीक्षण कार्य 3-5 मिनट। 10वें नंबर से शुरू करते हुए, जर्नल में 4 छात्र विषम संख्याओं के साथ भाग लेते हैं

इन चरणों का पालन करें: ; ;	इन चरणों का पालन करें:
	निर्धारक की गणना करें:

इन चरणों का पालन करें: अपरिभाषित	इन चरणों का पालन करें:
इसका व्युत्क्रम मैट्रिक्स ज्ञात कीजिए:	निर्धारक की गणना करें:

गृहकार्य:

1. समस्याओं का समाधान करें:

№ 2.224, 2.226, 2.228, 2.230, 2.231, 2.232.

2. निम्नलिखित विषयों पर व्याख्यान के माध्यम से कार्य करें:

रैखिक बीजगणितीय समीकरणों की प्रणाली (एसएलएई)। रिकॉर्डिंग के समन्वय, मैट्रिक्स और वेक्टर रूप। SLAEs की अनुकूलता के लिए क्रोनेकर-कैपेली मानदंड। विषम SLAEs. एक सजातीय SLAE के गैर-शून्य समाधान के अस्तित्व के लिए एक मानदंड। एक सजातीय SLAE के समाधान के गुण। एक सजातीय SLAE के समाधान की मौलिक प्रणाली, इसके अस्तित्व पर प्रमेय। समाधान की सामान्य मौलिक प्रणाली. एक सजातीय SLAE के सामान्य समाधान की संरचना पर प्रमेय। एक अमानवीय SLAE के सामान्य समाधान की संरचना पर प्रमेय।

रैखिक समीकरणों की वह प्रणाली जिसमें सभी मुक्त पद शून्य के बराबर हों, कहलाती है सजातीय :

कोई भी सजातीय प्रणाली हमेशा सुसंगत होती है, क्योंकि वह हमेशा सुसंगत होती है शून्य (मामूली ) समाधान। सवाल उठता है कि किन परिस्थितियों में एक सजातीय प्रणाली का गैर-तुच्छ समाधान होगा।

प्रमेय 5.2.एक सजातीय प्रणाली का एक गैर-तुच्छ समाधान होता है यदि और केवल तभी जब अंतर्निहित मैट्रिक्स की रैंक उसके अज्ञात की संख्या से कम हो।

परिणाम. एक वर्ग सजातीय प्रणाली का एक गैर-तुच्छ समाधान होता है यदि और केवल तभी जब सिस्टम के मुख्य मैट्रिक्स का निर्धारक शून्य के बराबर न हो।

उदाहरण 5.6.पैरामीटर एल के मान निर्धारित करें जिस पर सिस्टम में गैर-तुच्छ समाधान हैं, और ये समाधान खोजें:

समाधान. जब मुख्य मैट्रिक्स का निर्धारक शून्य के बराबर हो तो इस प्रणाली का एक गैर-तुच्छ समाधान होगा:

इस प्रकार, सिस्टम गैर-तुच्छ है जब l=3 या l=2। l=3 के लिए, सिस्टम के मुख्य मैट्रिक्स की रैंक 1 है। फिर, केवल एक समीकरण छोड़कर यह मान लें य=एऔर जेड=बी, हम पाते हैं एक्स=बी-ए, अर्थात।

l=2 के लिए, सिस्टम के मुख्य मैट्रिक्स की रैंक 2 है। फिर, माइनर को आधार के रूप में चुनें:

हमें एक सरलीकृत प्रणाली मिलती है

यहीं से हमें वह मिलता है एक्स=जेड/4, y=z/2. विश्वास जेड=4ए, हम पाते हैं

एक सजातीय प्रणाली के सभी समाधानों का सेट बहुत महत्वपूर्ण है रैखिक संपत्ति : यदि कॉलम X 1 और एक्स 2 - एक सजातीय प्रणाली AX = 0 का समाधान, फिर उनका कोई रैखिक संयोजनए एक्स 1 + बी एक्स 2 इस प्रणाली का समाधान भी होगा. दरअसल, तब से कुल्हाड़ी 1 = 0 और कुल्हाड़ी 2 = 0 , वह ए(ए एक्स 1 + बी एक्स 2) = ए कुल्हाड़ी 1 + बी कुल्हाड़ी 2 = a · 0 + b · 0 = 0. यह इस गुण के कारण है कि यदि एक रैखिक प्रणाली में एक से अधिक समाधान हैं, तो इन समाधानों की संख्या अनंत होगी।

रैखिक रूप से स्वतंत्र स्तंभ इ 1 , इ 2 , ई के, जो एक सजातीय प्रणाली के समाधान हैं, कहलाते हैं समाधान की मौलिक प्रणाली रैखिक समीकरणों की सजातीय प्रणाली यदि इस प्रणाली का सामान्य समाधान इन स्तंभों के रैखिक संयोजन के रूप में लिखा जा सकता है:

यदि एक सजातीय प्रणाली है एनचर, और सिस्टम के मुख्य मैट्रिक्स की रैंक बराबर है आर, वह क = एन आर.

उदाहरण 5.7.रैखिक समीकरणों की निम्नलिखित प्रणाली के समाधान की मूलभूत प्रणाली खोजें:

समाधान. आइए सिस्टम के मुख्य मैट्रिक्स की रैंक खोजें:

इस प्रकार, समीकरणों की इस प्रणाली के समाधानों का सेट आयाम का एक रैखिक उपस्थान बनाता है एन आर= 5 - 2 = 3। आइए आधार के रूप में लघु को चुनें

फिर, केवल मूल समीकरणों (बाकी इन समीकरणों का एक रैखिक संयोजन होगा) और मूल चर (हम बाकी, तथाकथित मुक्त चर को दाईं ओर ले जाते हैं) को छोड़कर, हम समीकरणों की एक सरलीकृत प्रणाली प्राप्त करते हैं:

विश्वास एक्स 3 = ए, एक्स 4 = बी, एक्स 5 = सी, हम देखतें है

विश्वास ए= 1, बी = सी= 0, हमें पहला मूल समाधान प्राप्त होता है; विश्वास बी= 1, ए = सी= 0, हमें दूसरा मूल समाधान प्राप्त होता है; विश्वास सी= 1, ए = बी= 0, हमें तीसरा मूल समाधान प्राप्त होता है। परिणामस्वरूप, समाधान की सामान्य मौलिक प्रणाली का रूप ले लेगी

मौलिक प्रणाली का उपयोग करते हुए, एक सजातीय प्रणाली का सामान्य समाधान इस प्रकार लिखा जा सकता है

एक्स = ऐ 1 + होना 2 + सीई 3. ए

आइए रैखिक समीकरणों की एक अमानवीय प्रणाली के समाधान के कुछ गुणों पर ध्यान दें एएक्स=बीऔर समीकरणों की संगत सजातीय प्रणाली के साथ उनका संबंध कुल्हाड़ी = 0.

एक अमानवीय प्रणाली का सामान्य समाधानसंगत सजातीय प्रणाली AX = 0 के सामान्य समाधान और अमानवीय प्रणाली के एक मनमाना विशेष समाधान के योग के बराबर है. वास्तव में, चलो वाई 0 एक अमानवीय प्रणाली का एक मनमाना विशेष समाधान है, अर्थात। एय 0 = बी, और वाई- एक विषम प्रणाली का सामान्य समाधान, अर्थात्। अय=बी. एक समानता को दूसरे से घटाने पर, हमें प्राप्त होता है
ए(Y Y 0) = 0, अर्थात Y Y 0 संगत सजातीय प्रणाली का सामान्य समाधान है कुल्हाड़ी=0. इस तरह, Y Y 0 = एक्स, या वाई=वाई 0 + एक्स. क्यू.ई.डी.

मान लीजिए कि अमानवीय प्रणाली का रूप AX = B है 1 + बी 2 . तब ऐसी प्रणाली का सामान्य समाधान X = X के रूप में लिखा जा सकता है 1 + एक्स 2 , जहां कुल्हाड़ी 1 = बी 1 और कुल्हाड़ी 2 = बी 2. यह गुण सामान्य रूप से किसी भी रैखिक प्रणाली (बीजगणितीय, अंतर, कार्यात्मक, आदि) की सार्वभौमिक संपत्ति को व्यक्त करता है। भौतिकी में इस गुण को कहा जाता है सुपरपोजिशन सिद्धांत, इलेक्ट्रिकल और रेडियो इंजीनियरिंग में - सुपरपोजिशन का सिद्धांत. उदाहरण के लिए, रैखिक विद्युत सर्किट के सिद्धांत में, किसी भी सर्किट में धारा को प्रत्येक ऊर्जा स्रोत के कारण अलग-अलग धाराओं के बीजगणितीय योग के रूप में प्राप्त किया जा सकता है।

रैखिक समीकरणों की सजातीय प्रणाली कुल्हाड़ी = 0हमेशा एक साथ। इसमें गैर-तुच्छ (गैर-शून्य) समाधान हैं यदि आर= रैंक ए< n .

सजातीय प्रणालियों के लिए, मूल चर (जिनके गुणांक मूल लघु बनाते हैं) को प्रपत्र के संबंधों द्वारा मुक्त चर के माध्यम से व्यक्त किया जाता है:

तब एन आररैखिक रूप से स्वतंत्र वेक्टर समाधान होंगे:

और कोई भी अन्य समाधान उनका एक रैखिक संयोजन है। वेक्टर समाधान एक सामान्यीकृत मौलिक प्रणाली बनाएं।

एक रैखिक स्थान में, रैखिक समीकरणों की एक सजातीय प्रणाली के समाधान का सेट आयाम का एक उपस्थान बनाता है एन आर; - इस उपस्थान का आधार.

प्रणाली एमके साथ रैखिक समीकरण एनअज्ञात(या, रैखिक प्रणाली

यहाँ एक्स 1 , एक्स 2 , …, एक्स एन ए 11 , ए 12 , …, एक एम.एन- सिस्टम गुणांक - और बी 1 , बी 2 , … बी एम एक आई.जेमैं) और अज्ञात ( जे

सिस्टम (1) कहा जाता है सजातीयबी 1 = बी 2 = … = बी एम= 0), अन्यथा - विजातीय.

सिस्टम (1) कहा जाता है वर्ग, यदि संख्या एमसंख्या के बराबर समीकरण एनअज्ञात।

समाधानसिस्टम (1) - सेट एननंबर सी 1 , सी 2 , …, सी एन, जैसे कि प्रत्येक का प्रतिस्थापन सी मैंके बजाय एक्स मैंसिस्टम में (1) इसके सभी समीकरणों को सर्वसमिकाओं में बदल देता है।

सिस्टम (1) कहा जाता है संयुक्त गैर संयुक्त

समाधान सी 1 (1) , सी 2 (1) , …, सी एन(1) और सी 1 (2) , सी 2 (2) , …, सी एन विभिन्न

सी 1 (1) = सी 1 (2) , सी 2 (1) = सी 2 (2) , …, सी एन (1) = सी एन (2) .

निश्चित ढुलमुल. यदि अज्ञात से अधिक समीकरण हैं, तो इसे कहा जाता है नए सिरे से परिभाषित.

रैखिक समीकरणों को हल करने की प्रणालियाँ

मैट्रिक्स समीकरणों को हल करना ~ गॉस विधि

रैखिक समीकरणों की प्रणालियों को हल करने की विधियों को दो समूहों में विभाजित किया गया है:

1. सटीक तरीके, जो एक सिस्टम की जड़ों की गणना के लिए परिमित एल्गोरिदम हैं (व्युत्क्रम मैट्रिक्स का उपयोग करके सिस्टम को हल करना, क्रैमर का नियम, गॉस की विधि, आदि),

2. पुनरावृत्तीय तरीके, जो अभिसरण पुनरावृत्ति प्रक्रियाओं (पुनरावृत्ति विधि, सीडेल विधि, आदि) के माध्यम से दी गई सटीकता के साथ सिस्टम का समाधान प्राप्त करना संभव बनाता है।

अपरिहार्य पूर्णांकन के कारण, सटीक विधियों के परिणाम भी अनुमानित होते हैं। पुनरावृत्तीय विधियों का उपयोग करते समय, इसके अतिरिक्त, विधि की त्रुटि भी जोड़ी जाती है।

पुनरावृत्त विधियों का प्रभावी उपयोग प्रारंभिक सन्निकटन के सफल चयन और प्रक्रिया के अभिसरण की गति पर काफी हद तक निर्भर करता है।

मैट्रिक्स समीकरणों को हल करना

सिस्टम पर विचार करें एनरैखिक बीजगणितीय समीकरण के संबंध में एनअज्ञात एक्स 1 , एक्स 2 , …, एक्स एन:

.

(15)

आव्यूह ए, जिसके स्तंभ संबंधित अज्ञात के लिए गुणांक हैं, और पंक्तियाँ संबंधित समीकरण में अज्ञात के लिए गुणांक हैं, कहलाती हैं सिस्टम का मैट्रिक्स; मैट्रिक्स-कॉलम बी, जिसके तत्व सिस्टम के समीकरणों के दाहिने हाथ हैं, कहलाते हैं दाईं ओर का मैट्रिक्सया केवल सिस्टम का दाहिना भाग. कॉलम मैट्रिक्स एक्स, जिसके तत्व अज्ञात अज्ञात हैं, कहलाते हैं सिस्टम समाधान.

यदि मैट्रिक्स ए- गैर-विशेष, यानी, डेट एक e 0 के बराबर है, तो सिस्टम (13), या इसके समतुल्य मैट्रिक्स समीकरण (14) का एक अद्वितीय समाधान है।

वास्तव में, विवरण प्रदान किया गया ए बराबर नहीं है 0 एक व्युत्क्रम मैट्रिक्स है ए-1 . समीकरण (14) के दोनों पक्षों को मैट्रिक्स से गुणा करना ए-1 हमें मिलता है:

(16)

सूत्र (16) समीकरण (14) का समाधान देता है और यह अद्वितीय है।

फ़ंक्शन का उपयोग करके रैखिक समीकरणों की प्रणालियों को हल करना सुविधाजनक है हल करो.

हल( ए, बी)

समाधान वेक्टर लौटा दिया गया है एक्सऐसा है कि ओह= बी।

तर्क:

ए- वर्गाकार, गैर-एकवचन मैट्रिक्स।

बी- एक वेक्टर जिसमें पंक्तियों की संख्या उतनी ही है जितनी मैट्रिक्स में पंक्तियाँ हैं ए .

चित्र 8 तीन अज्ञात में तीन रैखिक समीकरणों की एक प्रणाली का समाधान दिखाता है।

गॉस विधि

गाऊसी विधि, जिसे गाऊसी उन्मूलन विधि भी कहा जाता है, में यह तथ्य शामिल है कि सिस्टम (13) को अज्ञात के क्रमिक उन्मूलन द्वारा त्रिकोणीय मैट्रिक्स के साथ एक समतुल्य प्रणाली में घटा दिया जाता है:

मैट्रिक्स नोटेशन में, इसका मतलब है कि पहले (गॉसियन विधि का प्रत्यक्ष दृष्टिकोण), पंक्तियों पर प्राथमिक संचालन द्वारा, सिस्टम के विस्तारित मैट्रिक्स को चरणबद्ध रूप में कम किया जाता है:

और फिर (गॉसियन विधि के विपरीत) इस चरण मैट्रिक्स को पहले में बदल दिया जाता है एनकॉलम में हमें एक यूनिट मैट्रिक्स मिलता है:

.

अंतिम, ( एन+1) इस मैट्रिक्स के कॉलम में सिस्टम (13) का समाधान है।

मैथकैड में, गॉसियन विधि की आगे और पीछे की चालें फ़ंक्शन द्वारा निष्पादित की जाती हैं rref(ए).

चित्र 9 गॉसियन विधि का उपयोग करके रैखिक समीकरणों की एक प्रणाली का समाधान दिखाता है, जो निम्नलिखित कार्यों का उपयोग करता है:

rref( ए)

मैट्रिक्स का स्टेप फॉर्म वापस कर दिया गया है ए.

संवर्द्धन( ए, में)

स्थान द्वारा बनाई गई एक सरणी लौटाता है ए और में अगल बगल। सरणियों ए और में पंक्तियों की संख्या समान होनी चाहिए.

सबमैट्रिक्स( ए, आईआर, जूनियर, आईसी, जेसी)

सभी तत्वों से युक्त एक सबमैट्रिक्स लौटाता है आईआरद्वारा जे आरऔर कॉलम के साथ मैं सीद्वारा जे.सी.सुनिश्चित करें कि आईआर जे आरऔर

मैं सी जेसी,अन्यथा पंक्तियों और/या स्तंभों का क्रम उलट दिया जाएगा।

चित्र 9.

विधि का वर्णन

n अज्ञात के साथ n रैखिक समीकरणों की एक प्रणाली के लिए (एक मनमाना क्षेत्र पर)

सिस्टम मैट्रिक्स के निर्धारक के साथ Δ शून्य से भिन्न, समाधान फॉर्म में लिखा गया है

(सिस्टम मैट्रिक्स के i-वें कॉलम को फ्री टर्म्स के कॉलम से बदल दिया गया है)।
दूसरे रूप में, क्रैमर का नियम इस प्रकार तैयार किया गया है: किसी भी गुणांक c1, c2, ..., cn के लिए निम्नलिखित समानता है:

इस रूप में, क्रैमर का सूत्र इस धारणा के बिना मान्य है कि Δ शून्य से भिन्न है; यह भी आवश्यक नहीं है कि सिस्टम के गुणांक एक अभिन्न रिंग के तत्व हों (सिस्टम का निर्धारक शून्य का विभाजक भी हो सकता है) गुणांक वलय). हम यह भी मान सकते हैं कि या तो सेट b1,b2,...,bn और x1,x2,...,xn, या सेट c1,c2,...,cn, में गुणांक रिंग के तत्व शामिल नहीं हैं सिस्टम का, लेकिन इस रिंग के ऊपर कुछ मॉड्यूल। इस रूप में, क्रैमर के सूत्र का उपयोग किया जाता है, उदाहरण के लिए, ग्राम निर्धारक और नाकायमा के लेम्मा के सूत्र के प्रमाण में।

35) क्रोनेकर-कैपेली प्रमेय

n अज्ञात में m अमानवीय रैखिक समीकरणों की एक प्रणाली के सुसंगत होने के लिए, यह आवश्यक और पर्याप्त है कि आवश्यकता का प्रमाण। मान लीजिए कि प्रणाली (1.13) सुसंगत है, अर्थात ऐसी संख्याएँ मौजूद हैं एक्स 1 =α 1 , एक्स 2 =α 2 , …, एक्स एन = α एन ,क्या (1.15) आइए विस्तारित मैट्रिक्स के अंतिम कॉलम से इसके पहले कॉलम को घटाएं, जिसे α 1 से गुणा किया गया है, दूसरे को - α 2 से गुणा किया गया है, ..., nth - α n से गुणा किया गया है, यानी मैट्रिक्स के अंतिम कॉलम से (1.14) हमें समानताओं के बाएँ पक्षों को घटाना चाहिए (1.15)। तब हमें मैट्रिक्स मिलता है जिनकी रैंक प्रारंभिक परिवर्तनों के परिणामस्वरूप नहीं बदलेगी और। लेकिन यह स्पष्ट है, और इसलिए पर्याप्तता का प्रमाण है। मान लीजिए और निश्चितता के लिए क्रम r का एक गैर-शून्य लघु मैट्रिक्स के ऊपरी बाएँ कोने में स्थित है: इसका मतलब यह है कि मैट्रिक्स की शेष पंक्तियों को पहली r पंक्तियों के रैखिक संयोजन के रूप में प्राप्त किया जा सकता है, अर्थात, मैट्रिक्स की m-r पंक्तियों को कुछ संख्याओं द्वारा गुणा की गई पहली r पंक्तियों के योग के रूप में दर्शाया जा सकता है। लेकिन फिर सिस्टम (1.13) के पहले आर समीकरण स्वतंत्र हैं, और बाकी उनके परिणाम हैं, यानी, पहले आर समीकरणों की प्रणाली का समाधान स्वचालित रूप से शेष समीकरणों का समाधान है। दो संभावित मामले हैं. 1. आर=एन. फिर पहले आर समीकरणों से युक्त प्रणाली में समीकरणों और अज्ञातों की संख्या समान है और सुसंगत है, और इसका समाधान अद्वितीय है। 2.आर (1.16) "मुक्त" अज्ञात एक्सआर +1, एक्सआर +2 , …, एक्स n को कोई भी मान दिया जा सकता है। फिर अज्ञात को संबंधित मान मिलते हैं एक्स 1 , एक्स 2 , …, एक्सआर। इस मामले में सिस्टम (1.13) सुसंगत है, लेकिन अनिश्चित है। टिप्पणी। क्रम r का शून्येतर लघु, जहाँ r एक्स 1 , एक्स 2 , …, एक्सआर को बेसिक भी कहा जाता है, बाकी सभी फ्री हैं। सिस्टम (1.16) को छोटा कहा जाता है। यदि मुक्त अज्ञात को निरूपित किया जाता है एक्स आर +1 =सी 1 , एक्स आर +2 =सी 2 , …, एक्स एन = सी एन - आर, तो मूल अज्ञात उन पर निर्भर करेगा, अर्थात, n अज्ञात के साथ m समीकरणों की एक प्रणाली का समाधान X = ( एक्स 1 (सी 1 , …, सी एन - आर), एक्स 2 (सी 1 , …, सी एन - आर), …, एक्स आर(सी 1 , …, सी एन - आर), सी 1 , सी 2 , …, सी एन - आर) टी, जहां टी प्रतीक का अर्थ स्थानांतरण है। सिस्टम के इस समाधान को सामान्य कहा जाता है।

36) निश्चितता, अनिश्चितता
प्रणाली एमके साथ रैखिक समीकरण एनअज्ञात(या, रैखिक प्रणाली) रैखिक बीजगणित में फॉर्म के समीकरणों की एक प्रणाली है

यहाँ एक्स 1 , एक्स 2 , …, एक्स एन- अज्ञात जिन्हें निर्धारित करने की आवश्यकता है। ए 11 , ए 12 , …, एक एम.एन- सिस्टम गुणांक - और बी 1 , बी 2 , … बी एम- मुक्त सदस्य - ज्ञात माने जाते हैं। गुणांक सूचकांक ( एक आई.जे) सिस्टम समीकरण संख्याओं को दर्शाते हैं ( मैं) और अज्ञात ( जे), जिस पर यह गुणांक क्रमशः खड़ा होता है।

सिस्टम (1) कहा जाता है सजातीय, यदि इसके सभी मुक्त पद शून्य के बराबर हैं ( बी 1 = बी 2 = … = बी एम= 0), अन्यथा - विजातीय.

सिस्टम (1) कहा जाता है संयुक्त, यदि इसका कम से कम एक समाधान है, और गैर संयुक्त, यदि उसके पास एक भी समाधान नहीं है।

प्रकार (1) की एक संयुक्त प्रणाली में एक या अधिक समाधान हो सकते हैं।

समाधान सी 1 (1) , सी 2 (1) , …, सी एन(1) और सी 1 (2) , सी 2 (2) , …, सी एन(2) रूप की संयुक्त प्रणालियाँ (1) कहलाती हैं विभिन्न, यदि कम से कम एक समानता का उल्लंघन होता है:

सी 1 (1) = सी 1 (2) , सी 2 (1) = सी 2 (2) , …, सी एन (1) = सी एन (2) .

प्रपत्र (1) की संयुक्त प्रणाली कहलाती है निश्चित, यदि इसका कोई अनूठा समाधान है; यदि इसके कम से कम दो अलग-अलग समाधान हैं, तो इसे कहा जाता है ढुलमुल

37) गॉस विधि का उपयोग करके रैखिक समीकरणों की प्रणालियों को हल करना

मूल प्रणाली को इस तरह दिखने दें

आव्यूह एसिस्टम का मुख्य मैट्रिक्स कहा जाता है, बी- निःशुल्क सदस्यों का कॉलम।

फिर, पंक्तियों में प्राथमिक परिवर्तनों की संपत्ति के अनुसार, इस प्रणाली के मुख्य मैट्रिक्स को चरणबद्ध रूप में कम किया जा सकता है (समान परिवर्तनों को मुक्त शब्दों के कॉलम पर लागू किया जाना चाहिए):

फिर वेरिएबल्स को कॉल किया जाता है मुख्य चर. बाकी सभी को बुलाया जाता है मुक्त.

अनुकूलता की स्थितिसंपादित करें

सभी के लिए उपरोक्त शर्त को अनुकूलता के लिए एक आवश्यक और पर्याप्त शर्त के रूप में तैयार किया जा सकता है:

याद रखें कि एक संयुक्त प्रणाली की रैंक उसके मुख्य मैट्रिक्स (या विस्तारित मैट्रिक्स, क्योंकि वे समान हैं) की रैंक है।

कलन विधि

विवरण

गॉसियन विधि का उपयोग करके SLAE को हल करने के लिए एल्गोरिदम को दो चरणों में विभाजित किया गया है।

§ पहले चरण में, तथाकथित प्रत्यक्ष चाल को अंजाम दिया जाता है, जब, पंक्तियों पर प्राथमिक परिवर्तनों के माध्यम से, सिस्टम को एक चरणबद्ध या त्रिकोणीय रूप में लाया जाता है, या यह स्थापित किया जाता है कि सिस्टम असंगत है। अर्थात्, मैट्रिक्स के पहले कॉलम के तत्वों में से, एक गैर-शून्य तत्व का चयन करें, इसे पंक्तियों को पुनर्व्यवस्थित करके सबसे ऊपर की स्थिति में ले जाएं, और पुनर्व्यवस्था के बाद शेष पंक्तियों से परिणामी पहली पंक्ति को घटाएं, इसे एक मान से गुणा करें इनमें से प्रत्येक पंक्ति के पहले तत्व और पहली पंक्ति के पहले तत्व के अनुपात के बराबर, इस प्रकार उसके नीचे के कॉलम को शून्य कर दिया जाता है। इन परिवर्तनों के पूरा होने के बाद, पहली पंक्ति और पहले कॉलम को मानसिक रूप से काट दिया जाता है और तब तक जारी रखा जाता है जब तक कि शून्य आकार का मैट्रिक्स न रह जाए। यदि किसी भी पुनरावृत्ति पर पहले कॉलम के तत्वों के बीच कोई गैर-शून्य तत्व नहीं है, तो अगले कॉलम पर जाएं और एक समान ऑपरेशन करें।

§ दूसरे चरण में, तथाकथित रिवर्स चाल को अंजाम दिया जाता है, जिसका सार सभी परिणामी बुनियादी चर को गैर-बुनियादी चर के रूप में व्यक्त करना और समाधान की एक मौलिक प्रणाली का निर्माण करना है, या, यदि सभी चर हैं बुनियादी, फिर संख्यात्मक रूप से रैखिक समीकरणों की प्रणाली का एकमात्र समाधान व्यक्त करें। यह प्रक्रिया अंतिम समीकरण से शुरू होती है, जिसमें से संबंधित मूल चर को व्यक्त किया जाता है (और केवल एक ही होता है) और पिछले समीकरणों में प्रतिस्थापित किया जाता है, और इसी तरह, "चरणों" तक बढ़ते हुए। प्रत्येक पंक्ति बिल्कुल एक आधार चर से मेल खाती है, इसलिए अंतिम (शीर्षतम) को छोड़कर हर चरण पर, स्थिति बिल्कुल अंतिम पंक्ति के मामले को दोहराती है।

गाऊसी विधि के लिए क्रम की आवश्यकता होती है हे(एन 3) क्रियाएँ।

यह विधि इस पर निर्भर करती है:

38)क्रोनेकर-कैपेली प्रमेय।
एक प्रणाली सुसंगत है यदि और केवल तभी जब उसके मुख्य मैट्रिक्स की रैंक उसके विस्तारित मैट्रिक्स की रैंक के बराबर हो।

रैखिक सजातीय समीकरणों की प्रणाली- का रूप ∑a k i x i = 0 है। जहां m > n या m रैखिक समीकरणों की एक सजातीय प्रणाली हमेशा सुसंगत होती है, क्योंकि rangA = rangB। इसका स्पष्ट रूप से शून्य से युक्त एक समाधान है, जिसे कहा जाता है मामूली.

सेवा का उद्देश्य. ऑनलाइन कैलकुलेटर को SLAE के लिए एक गैर-तुच्छ और मौलिक समाधान खोजने के लिए डिज़ाइन किया गया है। परिणामी समाधान एक Word फ़ाइल में सहेजा जाता है (उदाहरण समाधान देखें)।

निर्देश। मैट्रिक्स आयाम चुनें:

रैखिक सजातीय समीकरणों की प्रणालियों के गुण

सिस्टम के लिए गैर-तुच्छ समाधान, यह आवश्यक और पर्याप्त है कि इसके मैट्रिक्स की रैंक अज्ञात की संख्या से कम हो।

प्रमेय. मामले में एक प्रणाली एम=एन एक गैर-तुच्छ समाधान है यदि और केवल यदि इस प्रणाली का निर्धारक शून्य के बराबर है।

प्रमेय. किसी प्रणाली के समाधानों का कोई भी रैखिक संयोजन भी उस प्रणाली का एक समाधान है।
परिभाषा. रैखिक सजातीय समीकरणों की प्रणाली के समाधानों के समुच्चय को कहा जाता है समाधान की मौलिक प्रणाली, यदि इस सेट में रैखिक रूप से स्वतंत्र समाधान शामिल हैं और सिस्टम का कोई भी समाधान इन समाधानों का एक रैखिक संयोजन है।

प्रमेय. यदि सिस्टम मैट्रिक्स की रैंक r अज्ञात की संख्या n से कम है, तो (n-r) समाधानों से युक्त समाधानों की एक मौलिक प्रणाली मौजूद है।

रैखिक सजातीय समीकरणों की प्रणालियों को हल करने के लिए एल्गोरिदम

1. मैट्रिक्स की रैंक ज्ञात करना.
2. हम मूल लघु का चयन करते हैं। हम आश्रित (मूल) और मुक्त अज्ञात में अंतर करते हैं।
3. हम सिस्टम के उन समीकरणों को काट देते हैं जिनके गुणांकों को आधार माइनर में शामिल नहीं किया जाता है, क्योंकि वे दूसरों के परिणाम हैं (बेस माइनर पर प्रमेय के अनुसार)।
4. हम मुक्त अज्ञात वाले समीकरणों के पदों को दाईं ओर ले जाते हैं। परिणामस्वरूप, हमें r अज्ञात के साथ r समीकरणों की एक प्रणाली प्राप्त होती है, जो दिए गए समीकरण के बराबर है, जिसका निर्धारक गैर-शून्य है।
5. हम अज्ञात को हटाकर परिणामी प्रणाली का समाधान करते हैं। हम ऐसे संबंध पाते हैं जो आश्रित चरों को स्वतंत्र चरों के माध्यम से व्यक्त करते हैं।
6. यदि मैट्रिक्स की रैंक चर की संख्या के बराबर नहीं है, तो हम सिस्टम का मौलिक समाधान ढूंढते हैं।
7. रंग = n के मामले में हमारे पास एक तुच्छ समाधान है।

उदाहरण। सदिशों की प्रणाली (a 1, a 2,...,a m) का आधार खोजें, आधार के आधार पर सदिशों को रैंक करें और व्यक्त करें। यदि 1 =(0,0,1,-1), और 2 =(1,1,2,0), और 3 =(1,1,1,1), और 4 =(3,2,1) ,4), और 5 =(2,1,0,3).
आइए सिस्टम का मुख्य मैट्रिक्स लिखें:

तीसरी पंक्ति को (-3) से गुणा करें। आइए चौथी पंक्ति को तीसरी पंक्ति में जोड़ें:

0	0	1	-1
0	0	-1	1
0	-1	-2	1
3	2	1	4
2	1	0	3

चौथी पंक्ति को (-2) से गुणा करें। आइए 5वीं पंक्ति को (3) से गुणा करें। आइए 5वीं पंक्ति को 4थी में जोड़ें:
आइए दूसरी पंक्ति को पहली पंक्ति में जोड़ें:
आइए मैट्रिक्स की रैंक ज्ञात करें।
इस मैट्रिक्स के गुणांक वाली प्रणाली मूल प्रणाली के बराबर है और इसका रूप है:
- एक्स 3 = - एक्स 4
- x 2 - 2x 3 = - x 4
2x 1 + x 2 = - 3x 4
अज्ञात को ख़त्म करने की विधि का उपयोग करते हुए, हम एक गैर-तुच्छ समाधान पाते हैं:
हमने आश्रित चर x 1 , x 2 , x 3 को मुक्त x 4 के माध्यम से व्यक्त करने वाले संबंध प्राप्त किए, अर्थात, हमें एक सामान्य समाधान मिला:
एक्स 3 = एक्स 4
एक्स 2 = - एक्स 4
एक्स 1 = - एक्स 4