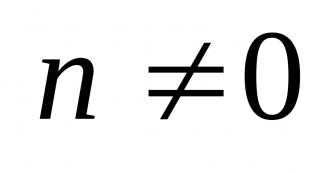Mati analüüsi funktsioon. Matemaatiline analüüs. Vaadake, mis on "matemaatiline analüüs" teistes sõnaraamatutes
Koostanud Yu.V.Obrubov
Kaluga - 2012
Sissejuhatus matemaatilisesse analüüsi.
Reaalarvud. Muutujad ja konstandid.
Üks matemaatika põhimõisteid on number.
Kutsutakse positiivseid numbreid 1,2,3, ..., mis saadakse loendamisel loomulik.
Arve ... -3, -2, -1,0,1,2,3, ... nimetatakse täisarvudeks. Arvud, mida saab esitada kahe täisarvu lõpliku suhtena ( 
) kutsutakse ratsionaalne.
Nende hulka kuuluvad täis- ja murdarvud, positiivsed ja negatiivsed arvud. Nimetatakse arve, mida saab esitada lõpmatute mittekorduvate murdudena irratsionaalne.
Irratsionaalarvude näited on 
,
. Irratsionaalarvude hulgas eristavad nad transtsendentaalne
numbrid. Need on arvud, mis on mittealgebraliste tehete tulemus. Tuntuimad neist on number 
ja mitte-eakaaslaste number 
. Nimetatakse ratsionaal- ja irratsionaalarvud kehtiv
. Reaalarvud on tähistatud punktidega arvureal. Iga punkt arvteljel vastab ühele reaalarvule ja vastupidi, igale reaalarvule vastab üks punkt arvuteljel. Seega on reaalarvude ja arvujoone punktide vahel loodud üks-ühele vastavus. See võimaldab kasutada mõisteid "number a" ja "punkt a" vaheldumisi.
Erinevate füüsikaliste, majanduslike, sotsiaalsete protsesside uurimisel tuleb sageli tegeleda suurustega, mis esindavad uuritavate nähtuste parameetrite arvväärtusi. Samal ajal mõned neist muutuvad, teised aga säilitavad oma väärtused.
muutuv
Nimetatakse suurust, mis võtab erinevaid arvväärtusi. Nimetatakse suurust, mille arvväärtus antud ülesandes või katses ei muutu konstantne.
Muutujaid tähistatakse tavaliselt ladina tähtedega 
ja püsiv 
.
muutuv 
loetakse antud, kui on teada väärtuste kogum, mida see võtta võib. Seda komplekti nimetatakse muutuja vahemikuks.
Numbrilise muutuja väärtuste komplekte on mitmesuguseid.
intervall
on arvude a ja b vahele jääv x väärtuste hulk, samas kui numbrid a ja b ei kuulu vaadeldavasse hulka. Intervalli tähistatakse: (a,b);a segment
nimetatakse arvude a ja b vahele jäävate x väärtuste kogumiks, samas kui arvud a ja b kuuluvad vaadeldavasse hulka. Segmenti tähistatakse ,a≤x≤b-ga. Kõigi reaalarvude hulk on avatud intervall. Tähistatakse: (- ∞,+ ∞), -∞<х <+∞, R. Punkti x naabruskond
0
kutsutakse suvaline intervall (а, b), mis sisaldab punkti x 0, kõik selle intervalli punktid rahuldavad ebavõrdsust a ε
- punkti a naabruskond
on intervall, mille keskpunkt on punkt a, mis rahuldab ebavõrdsust a–ε Funktsioon on üks matemaatilise analüüsi põhimõisteid. Olgu X ja Y reaalarvude suvalised hulgad. Kui igale arvule x X määratakse mõne reegli või seaduse kohaselt kordumatu täpselt määratletud reaalarv yY, siis öeldakse, et funktsiooni
definitsiooni domeeniga X ja väärtuste komplektiga Y. Määrake y \u003d f (x). Muutujat x nimetatakse argument
funktsioonid. Funktsiooni definitsioonis on olulised kaks punkti: määratlusvaldkonna märge ja vastavusseaduse kehtestamine. Määratluse ulatus
või eksistentsi piirkonda
Funktsioon on argumentide väärtuste kogum, mille jaoks funktsioon on olemas, see tähendab, et sellel on mõte. Vaheta ala
Funktsiooni nimetatakse väärtuste kogumiks y, mis kulub x lubatud väärtuste jaoks. Funktsiooni seadistamise viisid.
Funktsiooni defineerimise analüütiline viis. Selle funktsiooni seadistusmeetodiga kirjutatakse vastavusseadus valemina (analüütilise avaldisena), mis näitab, milliste matemaatiliste teisendustega, kasutades argumendi x teadaolevat väärtust, leiate y vastava väärtuse. Funktsiooni saab defineerida ühe analüütilise avaldise abil kogu selle definitsioonipiirkonna ulatuses või esindada mitme analüütilise avaldise kogumit. Näiteks: y \u003d sin (x 2 + 1) 2. Tabelikujuline funktsiooni seadmise viis Nähtuse või protsessi otsese vaatluse või eksperimentaalse uurimise tulemusena kirjutatakse argumendi x väärtused ja y vastavad väärtused välja teatud järjekorras. See tabel määratleb x funktsiooni y. Funktsiooni määramise tabelilise viisi näideteks võivad olla trigonomeetriliste funktsioonide tabelid, logaritmide, kuupäevade ja vahetuskursside, temperatuuri ja niiskuse tabelid jne. 3. Funktsiooni seadistamise graafiline viis. Funktsiooni graafiline seadistamise viis on punktide (x, y) kuvamine koordinaattasandil tehniliste seadmete abil. Matemaatilises analüüsis funktsiooni määramise graafilist meetodit ei kasutata, vaid alati kasutatakse analüütiliselt antud funktsioonide graafilist illustreerimist. Kõik tuleks sõnastada võimalikult lihtsalt, kuid mitte lihtsamalt. Meie teekond algab väljamõeldud tegelasega, keda kutsume John Doeks. Ta on keskmine töötaja, keda võib hõlpsasti leida igas maailma linnas. Peaaegu iga päev ärkab John valjude häirete peale ja sõidab oma autoga tööle. Ta sõidab liftiga oma kontorisse, kus ta käivitab arvuti ja sisestab oma kasutajanime ja parooli. John teeb kõiki neid asju, ilma et neil oleks vähimatki aimu, kuidas need toimivad. Võib-olla oleks tal huvi saada teada, kuidas on paigutatud ja toimivad tema igapäevaselt kasutatavad seadmed ja seadmed, kuid tal pole selleks aega ega jõudu. Ta peab autosid, lifte, arvuteid ja äratuskellasid täiesti erinevateks ja keerukateks mehhanismideks, millel pole midagi ühist. Johni sõnul kulub aastaid õppimist, et mõista, kuidas igaüks neist töötab. Mõned inimesed näevad asju veidi teisiti kui meie John Doe. Nad teavad, et liftipaigaldiste elektrimootorid on väga sarnased autogeneraatoritega. Nad teavad, et programmeeritav loogikakontroller, mis juhib lifti liigutamise eest vastutavat elektrimootorit, on väga sarnane John Doe tööarvutiga. Nad teavad, et põhitasandil põhinevad PLC, äratuskell ja arvuti suhteliselt lihtsal transistoriteoorial. See, mida John Doe ja tavainimene peavad uskumatult keeruliseks, on häkkerite kõige levinum lihtsate mehaaniliste ja elektriliste põhimõtete kasutamine. Probleem on selles, kuidas neid põhimõtteid rakendatakse. Põhiprintsiipide lahutamine keerulistest ideedest võimaldab meil neid mõista ja lihtsustada viisil, mis vastab Albert Einsteini ülaltoodud ekspromptidele. Paljud meist peavad arvutust millekski keeruliseks. (John Doe peab seadme põhimõtet ja erinevate mehhanismide toimimist samaks.) Näete kuhjaga keerulisi ja keerukaid asju. Nende mõistmiseks on vaja palju aega ja vaeva. Aga mis siis, kui me ütleksime teile, et matemaatiline analüüs (arvutus) pole nii keeruline, kui esmapilgul tundub, nagu ka enamik mehhanisme? Kas on mõned põhiprintsiibid, millest igaüks peab aru saama, ja niipea kui te seda teete, avaneb teil maailmale ja selle toimimisele uus vaade? Tüüpiline arvutamise õpik sisaldab umbes tuhat lehekülge. Tüüpiline John Doe näeb selles tuhat raskesti mõistetavat ja uuritavat asja ning häkker näeb kahte põhiprintsiipi (tuletis ja integraal) ja 998 näidet nendest põhimõtetest. Püüame koos välja mõelda, mis need põhimõtted on. Tuginedes Austini Texase ülikooli professori Michael Starbirdi tehtud tööle, kasutame igapäevaseid näiteid, millest igaüks aru saab. Matemaatiline analüüs paljastab meie maailma erilise ilu – ilu, mis tekib siis, kui suudad seda jälgida dünaamiliselt, mitte staatiliselt. Loodame, et kõik läheb teie jaoks korda. Enne kui alustame, tahaksin põgusalt läbi käia kalkulatsiooni tekkeloo, mille juured on väga hoolikas muutuste ja liikumise analüüsis. Zenoni paradoks Zenon Eleast on filosoof, kes elas 4. sajandil eKr. Ta tõstatas mitu peent, kuid sügavat paradoksi, millest kaks viisid lõpuks arvutuse sünnini. Zenoni paradokside lahendamiseks kulus inimkonnal rohkem kui kaks tuhat aastat. Nagu võite arvata, polnud see lihtne. Raskused olid suuresti seotud lõpmatuse ideega. Mis on lõpmatuse probleem matemaatilisest vaatenurgast? 17. sajandil suutsid Isaac Newton ja Gottfried Leibniz lahendada Zenoni paradoksid ja luua matemaatilise analüüsi. Vaatleme neid paradokse lähemalt, et mõista, miks nende ümber on nii palju kära olnud. Nool Kujutage ette noolt, mis lendab läbi õhu. Võime väga kindlalt väita, et nool liigub. Nüüd kaaluge noolt teatud ajahetkel. Ta ei liigu enam, vaid puhkab. Aga me teame kindlalt, et nool on liikumises, siis kuidas saab ta olla puhkeasendis?! See on selle paradoksi olemus. See võib tunduda rumal, kuid tegelikult on see väga keeruline mõiste, mida tuleks käsitleda matemaatilisest vaatenurgast. Hiljem saame teada, et tegemist on hetkelise muutumiskiiruse kontseptsiooniga, mida seostame matemaatilise analüüsi (arvutuse) kahest põhimõttest ühe - tuletise - ideega. See võimaldab meil arvutada noole kiirust teatud ajahetkel – see on midagi, mida inimkond pole suutnud enam kui kaks aastatuhandet. Dihhotoomia Vaatame uuesti seda sama noolt. Seekord kujutage ette, et see lendab meie suunas. Zeno väitis, et me ei tohiks liikuda, sest nool ei saa meid kunagi tabada. Kujutage ette, et pärast seda, kui nool on õhus, peab see läbima poole vibu ja sihtmärgi vahelisest vahemaast. Kui ta jõuab poolel teel teatud punkti, peab ta jälle läbima poole vahemaast – seekord selle punkti ja sihtmärgi vahel. Kujutage ette, kui me seda jätkame. Nool läbib seega pidevalt poole võrdluspunkti ja sihtmärgi vahelist vahemaad. Seda arvestades võime järeldada, et nool ei suuda meid kunagi tabada! Päriselus tabab nool lõpuks oma sihtmärki, jättes meid mõtlema, mida paradoks tähendab. Nagu esimese paradoksi puhul, kaalume hiljem, kuidas seda ülesannet lahendada, kasutades üht matemaatilise analüüsi põhimõtet - integraali. Integraal võimaldab meil vaadelda lõpmatuse mõistet kui matemaatilist funktsiooni. Teadlaste ja inseneride sõnul on see äärmiselt võimas tööriist. Arvutuse kaks põhiprintsiipi Matemaatilise analüüsi kahe põhiprintsiibi olemust saab näidata, rakendades neid Zenoni paradokside lahendamisel. Tuletis. Tuletis on meetod, mis võimaldab meil arvutada noole kiirust noole paradoksis. Teeme seda, analüüsides noole asukohta järjest vähenevate ajavahemike järel. Noole täpne kiirus selgub siis, kui mõõtmistevaheline aeg lõpmatult väikeseks osutub. Integraalne. Integraal on meetod, mis võimaldab meil arvutada noole asukoha dihhotoomia paradoksis. Teeme seda, analüüsides noole kiirust järjest vähenevate ajavahemike kaudu. Noole täpse asukoha saame teada siis, kui mõõtmistevaheline aeg osutub lõpmatult väikeseks. Tuletise ja integraali vahel on lihtne näha mõningaid sarnasusi. Mõlemad väärtused arvutatakse noole asendi või kiiruse analüüsimisel järk-järgult vähenevate ajavahemike järel. Hiljem saame teada, et integraal ja tuletis on tegelikult ühe ja sama keraamilise kondensaatori kaks külge. Miks peaksime õppima arvutamise põhitõdesid? Me kõik teame Ohmi seadust, mis seob voolu, pinge ja takistuse üheks lihtsaks võrrandiks. Vaatame nüüd Ohmi seadust kondensaatori näitel. Kondensaatori voolutugevus sõltub pingest ja ajast. Aeg on sel juhul kriitiline muutuja ja seda tuleb iga dünaamilise sündmuse puhul arvesse võtta. Matemaatiline analüüs võimaldab meil mõista ja hinnata, kuidas asjad aja jooksul muutuvad. Kondensaatori puhul võrdub vool mahtuvuse korda voltidega sekundis või i = C(dv/dt), kus: i - voolutugevus (hetk); Selles vooluringis ei ole kondensaatoris elektrivoolu. Voltmeeter näitab aku pinget, kuid ampermeeter ei näita midagi. Pinge ei muutu seni, kuni potentsiomeeter jääb puutumata. Sel juhul i = C(0/dt) = 0 amer. Aga mis juhtub, kui hakkame potentsiomeetrit reguleerima? Võrrandi järgi otsustades ilmub kondensaatorisse saadud voolutugevus. See vool sõltub pinge muutusest, mis on seotud potentsiomeetri liigutamise kiirusega. Need graafikud näitavad seost kondensaatoris oleva pinge, voolu ja potentsiomeetri pööramise kiiruse vahel. Algul teeme seda aeglaselt. Kiiruse suurenemine toob kaasa pinge muutuse, mis omakorda kutsub esile voolu järsu suurenemise. Kõigil etappidel on kondensaatori vool võrdeline selles oleva pinge muutumise kiirusega. Matemaatiline analüüs või täpsemalt tuletis annab meile võimaluse määrata muutuse kiirust, nii et me teame täpselt kondensaatori voolu väärtust teatud ajahetkel. Samamoodi saame arvutada Zenoni noole hetkkiiruse. See on uskumatult võimas tööriist, mis peaks olema teie arsenalis. Materjal koostati spetsiaalselt saidi jaoks - vastavalt saidi hackaday.com artiklile P.S. Minu nimi on Aleksander. See on minu isiklik, sõltumatu projekt. Mul on väga hea meel, kui teile artikkel meeldis. Kas soovite saiti aidata? Lihtsalt vaadake allpool reklaami selle kohta, mida olete hiljuti otsinud. Autoriõiguste sait © – see uudis kuulub saidile ja on ajaveebi intellektuaalomand, kaitstud autoriõiguse seadusega ja seda ei saa kasutada ilma aktiivse allika lingita. Loe lähemalt - "Autorsuse kohta" Kas otsite seda? Võib-olla on see see, mida te pole nii kaua leidnud? MATEMAATILINE ANALÜÜS matemaatika osa, milles funktsioonid ja nende üldistusi uuritakse meetodiga piirid. Piirmäära mõiste on tihedalt seotud lõpmata väikese suuruse mõistega, seetõttu võib ka öelda, et M. a. uurib funktsioone ja nende üldistusi lõpmata väikesel meetodil. Nimi "M. a." - selle matemaatika osa vana nime lühendatud modifikatsioon - "Lõpmatu analüüs"; viimane paljastab sisu täielikumalt, kuid on ka lühendatud (pealkiri "Analüüs infinitesimaalide abil" iseloomustaks teemat täpsemalt). Klassikalises M. ja. uurimisobjektid (analüüs) on eelkõige funktsioonid. "Esiteks", sest areng M. a. andis võimaluse uurida selle meetoditega keerukamaid moodustisi kui - funktsionaale, operaatoreid jne. Looduses ja tehnikas leidub liikumisi ja protsesse kõikjal, to-rukki kirjeldatakse funktsioonide kaupa; ka loodusnähtuste seaduspärasid kirjeldatakse tavaliselt funktsioonidega. Sellest ka objektiivne tähtsus M. a. funktsioonide õppimise vahendina. M. a. selle mõiste laiemas tähenduses hõlmab väga suurt osa matemaatikast. See sisaldab diferentsiaal-, integraalarvutus, kompleksmuutujate teooria funktsioonid, teooria tavalised diferentsiaalvõrrandid, teooria osadiferentsiaalvõrrandid, teooria integraalvõrrandid, variatsioonide arvutamine, funktsionaalne analüüs ja muud matemaatikat distsipliinid. Kaasaegne arvuteooria Ja tõenäosusteooria rakendada ja arendada meetodeid M. ja. Sellest hoolimata on mõiste M. a. kasutatakse sageli ainult matemaatilise analüüsi aluseid, mis ühendavad teooriat tegelik arv, piiriteooria, teooria read, diferentsiaal- ja integraalarvutused ning nende vahetud rakendused, nagu maksimumide ja miinimumide teooria, teooria kaudsed funktsioonid, Fourier' jada, Fourier' integraalid. Funktsioon. Aastal M. a. lähtuma funktsiooni definitsioonist Lobatševski ja Dirichlet' järgi. Kui teatud F-arvude hulga iga arvu xz korral k.-l. seadus on loetletud y, siis see määrab funktsiooni ühest muutujast X. Funktsioon on määratletud sarnaselt muutujatest, kus x=(x 1 , ..., x n) -
n-mõõtmelise ruumi punkt; kaaluge ka funktsioone punktidest x=(x 1 , X 2 ,
...) mõnest lõpmatumõõtmelisest ruumist, mida aga sagedamini nimetatakse funktsionaalideks. elementaarsed funktsioonid. Põhiväärtus M. ja. mängida elementaarsed funktsioonid. Praktikas opereerivad need põhiliselt elementaarfunktsioonidega, ligikaudselt keerulisema iseloomuga funktsioone. Elementaarfunktsioone saab käsitleda mitte ainult reaalsete, vaid ka komplekssete x-ide puhul; siis saavad ideed nende funktsioonide kohta teatud mõttes täielikuks. Sellega seoses on oluline M. a. haru, nn. kompleksmuutuja funktsioonide teooria ehk teooria analüütilised funktsioonid. Päris number. Funktsiooni mõiste põhineb sisuliselt reaal- (ratsionaal- ja irratsionaalarvu) mõistel. Lõplikult võttis see kuju alles 19. sajandi lõpus. Eelkõige on loodud loogiliselt veatu seos arvude ja geomeetriliste punktide vahel. sirgjoon, mis tõi kaasa R. Descartes'i ideede formaalse põhjendamise (R. Descartes, 17. saj keskpaik), kes tõi matemaatikasse ristkülikukujulised koordinaatsüsteemid ja nendes funktsioonide kujutamise graafidega. Piirang. Aastal M. a. funktsioonide uurimise meetod on . Tehke vahet jada piiril ja funktsiooni piiril. Need mõisted kujunesid lõplikult välja alles 19. sajandil, kuigi teistel kreeklastel oli neist ettekujutus. teadlased. Piisab, kui öelda, et Archimedes (3. sajand eKr) suutis arvutada parabooli lõigu protsessi abil, mida me nimetaksime läbipääsuks piirini (vt. ammendumise meetod). Pidevad funktsioonid. M. a.-s uuritud oluline funktsioon, vorm pidevad funktsioonid.Üks selle mõiste võimalikest definitsioonidest: funktsioon y=f(x).ühest muutujast X, antud intervallile ( a, b),
helistas pidev mingis punktis X, Kui Funktsioon on pidev intervallil ( a, b),
kui see on pidev kõigis oma punktides; siis on see kõver, pidev selle sõna igapäevases tähenduses. Tuletis ja . Pidevate funktsioonide hulgast tuleks välja tuua funktsioonid, millel on tuletis. Funktsiooni tuletis punktis on selle muutumise kiirus selles punktis, st piir Kui meil on ajas piki y-telge liikuva punkti koordinaat X, siis f "(x). on punkti hetkekiirus korraga X. Tuletise f märgiga "(x) .
otsustage f (x) muutuse olemuse üle: kui f "(z)> 0 ( f"(x) <0
).
intervallil ( c, d), siis funktsioon / suureneb (väheneb) sellel intervallil. Kui funktsioon / punktis x jõuab kohaliku ekstreemumini (maksimumi või miinimumini) ja sellel on selles punktis tuletis, siis on viimane selles punktis võrdne nulliga f "(x 0) \u003d 0. Võrdsuse (1) saab asendada samaväärse võrdsusega kus on lõpmatult väike mil, st kui funktsioonil f on punktis tuletis X, siis selle juurdekasv selles punktis jagatakse kaheks liikmeks. Neist esimene on alates (proportsionaalne), teine - kipub nulli kiiremini kui Väärtus (2) ref. diferentsiaal juurdekasvule vastavad funktsioonid At väike võib pidada ligikaudu võrdseks dy: Ülaltoodud arutluskäik diferentsiaali kohta on iseloomulik M. a. Need laienevad paljude muutujate funktsioonidele ja funktsioonidele. Näiteks kui funktsioon muutujatest on pidev osatuletised punktis x=(x 1 , ... , x n), siis selle juurdekasv
Sõltumatute muutujate juurdekasvule vastavad saab kirjutada kui kus st kui üldse Siin on esimene liige (3) paremal küljel diferentsiaal dz funktsioonid f. See sõltub lineaarselt ja teine liige kipub nulli kiiremini kui Las see antakse (vt art. Variatsioonide arvutus) laiendatud funktsiooniklassidele x(t) ,
millel on intervallil pidev tuletis ja mis vastab piirtingimustele x( t0)\u003d x 0, x( t1)=x l , Kus x 0, x 1 - antud numbrid; Olgu lisaks funktsiooni h(t) klass ,
millel on pidev tuletis ja selline, et h( t0)=h(t1)=0. Ilmselgelt kui Variatsioonide arvutamisel on tõestatud, et teatud tingimustel L-l saab funktsionaalse J(x) juurdekasvu kirjutada kui kus ja seega kipub (4) paremal küljel olev teine liige nullini kiiremini kui ||h|| ja esimene liige sõltub lineaarselt. Esimest liiget punktis (4) kutsutakse. funktsiooni variatsioon ja seda tähistatakse dJ( x, h). Integraalne. Koos tuletisega on see fundamentaalse tähtsusega M. a. On määramata ja kindlad integraalid. Määramatu integraal on tihedalt seotud antiderivatiivse funktsiooniga. Funktsioon F(x). funktsiooni f antiderivaat intervallil ( a, b), kui sellel intervallil F"(x) =f(x). Funktsiooni / kindel integraal (Riemanni) intervallil [ a, b] on piir Kui funktsioon f on positiivne ja pidev lõigul [ a, b],
siis on selle integraal sellel lõigul võrdne kõveraga piiratud joonise pindalaga y=f(x), telg Oh ja otsene x=a, x=b. Riemanni integreeritavate funktsioonide klass sisaldab kõiki pidevaid [ a, b]funktsioonid ja mõned katkendlikud funktsioonid. Kuid need kõik on tingimata piiratud. Piiramata funktsioonide jaoks, mis ei kasva väga kiiresti, ja ka teatud funktsioonide jaoks, mis on antud lõpmatutel intervallidel, võetakse kasutusele nn. valed integraalid, mis nõuavad kahekordset läbimist nende määratlemise piirini. Riemanni integraali mõiste ühe muutuja funktsiooni jaoks laieneb paljude muutujate funktsioonidele (vt. Mitu integraali). Seevastu M. vajadused ja. tõi kaasa integraali üldistamise hoopis teises suunas, tähenduses Lebesgue'i integraal või üldisemalt Lebesgue-Stieltjesi integraal. Nende integraalide defineerimisel on oluline tutvustada teatud hulkade jaoks, mida nimetatakse mõõdetavateks, nende mõõtme mõiste ja selle põhjal mõõdetava funktsiooni mõiste. Mõõdetavate funktsioonide jaoks võetakse kasutusele Lebesgue-Stieltjesi integraal. Sel juhul võetakse arvesse laia valikut erinevaid mõõte ning vastavaid mõõdetavate hulkade ja funktsioonide klasse. See võimaldab kohandada seda või seda integraali teatud konkreetse probleemiga. Newtoni-Leibnizi valem. Tuletise ja integraali vahel on seos, mida väljendab valem (teoreem) Newton - Leibniz Siin on f(x) pidev [ a, b] funktsioon F(x) -
tema prototüüp. Vormel ja Taylor. Koos tuletise ja integraaliga matemaatilise analüüsi kõige olulisem mõiste (uurimisvahend). on Taylor p Taylori seeria. Kui funktsioon f(x) , a helistas selle Taylori polünoom (n-kraadi). x-x 0: (Taylori valem); samas kui lähendusviga kipub nulli kell kiiremini kui Seega saab punkti x 0 läheduses olevat funktsiooni f (x). mis tahes täpsusega lähendada väga lihtsa funktsiooniga (polünoomiga), mille arvutamiseks on vaja ainult aritmeetikat. tehted – liitmine, lahutamine ja korrutamine. Eriti olulised on nn funktsioonid, mis on analüütilised teatud naabruses x 0 ja millel on lõpmatu arv tuletisi, nii et nende jaoks selles naabruses saab neid esitada lõpmatu Taylori astmereana: Taylori laiendused on teatud tingimustel võimalikud ka paljude muutujate funktsioonide, aga ka funktsioonide ja operaatorite jaoks. Ajalooline viide. Kuni 17. sajandini M. a. oli lahenduste kogum erinevatele konkreetsetele probleemidele; näiteks integraalarvutuses on need ülesanded kujundite pindalade, kõverate piiridega kehade ruumalade, muutuva jõu töö jne arvutamiseks. Iga ülesanne või konkreetne probleem lahendati oma meetodiga, mõnikord keeruline ja tülikas (M. a. eelajaloo kohta vaata artiklit Lõpmatu väikearvutus),
M. a. ühtse ja süstemaatilisena. tervik kujunes välja I. Newtoni (I. Newton), G. Leibnizi (G. Leibniz), L. Euleri (L. Euler), J. Lagrange'i (J. Lagrange) ja teiste XVII a. 18. sajandil ja tema – piiride teooria – töötas alguses välja O. Komi (A. Cauchy). 19. sajand M. a. algkontseptsioonide süvaanalüüs. seostati arenguga 19. ja 20. sajandil. hulgateooria, mõõtmisteooria, reaalmuutuja funktsioonide teooria ja tõi kaasa mitmesuguseid üldistusi. Valgus: La V a l l e - P u s s e n S.-J. e, Infinitesimaalide analüüsi kursus, tlk. prantsuse keelest, kd 1-2, Moskva, 1933; Ilyin V. A., Poznyak E. G., Matemaatilise analüüsi alused, 3. väljaanne, 1. osa, M., 1971; 2. väljaanne, 2. osa, M., 1980; Ja l ja N V. A., Sadovnichiy V. A., Seidov B. Kh., Matemaatiline analüüs, M., 1979; K u d r i v e in L. D., Matemaatiline analüüs, 2. väljaanne, kd 1-2, M., 1973; Nikolsky S. M., Matemaatilise analüüsi kursus, 2. väljaanne, kd 1-2, M., 1975; Uitteker E. T., W a t s o n J. N., Kaasaegse analüüsi kursus, tlk. inglise keelest, osa 1-2, 2. väljaanne, M., 1962-63; F ja kht n gol'ts G. M., Diferentsiaal- ja integraalarvutuse kursus, 7. väljaanne, kd 1-2, M., 1970; 5. väljaanne, 3. köide, M., 1970. S. M. Nikolsky. Matemaatiline entsüklopeedia. - M.: Nõukogude entsüklopeedia. I. M. Vinogradov. 1977-1985. MATEMAATILINE ANALÜÜS, matemaatika harude kogum, mis on pühendatud funktsioonide uurimisele diferentsiaalarvutuse ja integraalarvutuse meetodite abil ... Kaasaegne entsüklopeedia Matemaatika harude kogum, mis on pühendatud funktsioonide uurimisele diferentsiaal- ja integraalarvutuse meetodite abil. Mõiste on pigem pedagoogiline kui teaduslik: matemaatilise analüüsi kursusi õpetatakse ülikoolides ja tehnikakoolides ... Suur entsüklopeediline sõnaraamat Inglise matemaatiline analüüs; saksa keel matemaatiline analüüs. Matemaatika haru, mis on pühendatud funktsioonide uurimisele diferentsiaal- ja integraalarvutuse meetodite abil. Antinazi. Sotsioloogia entsüklopeedia, 2009 ... Sotsioloogia entsüklopeedia Olemas., sünonüümide arv: 2 matan (2) matemaatiline analüüs (2) ASIS sünonüümide sõnastik. V.N. Trishin. 2013... Sünonüümide sõnastik MATEMAATILINE ANALÜÜS- MATEMAATILINE ANALÜÜS. Matemaatika harude kogum, mis on pühendatud matemaatiliste funktsioonide uurimisele diferentsiaal- ja integraalarvutuse meetodite abil. Meetodite kasutamine M. ja. on tõhus vahend kõige olulisemate ...... Uus metoodiliste terminite ja mõistete sõnastik (keelte õpetamise teooria ja praktika) matemaatiline analüüs- — ET matemaatiline analüüs Matemaatika haru, mis on kõige selgemalt seotud piirprotsessi või konvergentsi mõistega; sisaldab diferentseerumisteooriaid,…… Tehnilise tõlkija käsiraamat Matemaatiline analüüs- MATEMAATILINE ANALÜÜS, matemaatika osade kogum, mis on pühendatud funktsioonide uurimisele diferentsiaalarvutuse ja integraalarvutuse meetodite abil. … Illustreeritud entsüklopeediline sõnaraamat “... kui ma peaksin looma mehhanismi, mille ainus eesmärk on hävitada lapse loomulik uudishimu ja tema modellindusarmastus, siis vaevalt oleks mul läinud paremini, kui see on juba rakendatud – mul poleks lihtsalt piisavalt kujutlusvõimet, et konkureerida selliste tundetute, tuimade ideedega, mis sisalduvad tänapäevastes matemaatikaõppemeetodites. Mõelge kauni kunsti õppimisele järgmiselt: lapsed, lasteaias ei joonista. Selle asemel uurigem värvitoodete keemiat, valguse füüsikat ja silma anatoomiat. Kui lapsed (täpsemalt juba teismelised) pärast 12 aastat nende aspektide uurimist ikka veel kunsti ei vihka, võivad nad ise joonistama hakata. Lõpuks on neil nüüd tugev alus, et hakata kunsti austama. eks? Ka luulega. Kujutage ette, et uurite seda tsitaati (valemit): “Aga peaasi: ole endale truu; Siis, nagu öö järgneb päevale, ei reeda sa teisi. -William Shakespeare, Hamlet See on elegantne viis öelda "ole sina ise" (ja kui see tähendab matemaatikast lugupidamatult kirjutamist, siis olgu see nii). Aga kui me matemaatikatunnis mõtleksime luulele, siis tähenduse otsimise asemel loeksime silpide arvu, analüüsiksime jaambilist pentameetrit, märgiksime nimisõnu, tegusõnu ja omadussõnu. Matemaatika ja luule on justkui erinevad viisid ühe ja sama asja seletamiseks, iseloomustamiseks. Valemid on vahend eesmärgi saavutamiseks, viis matemaatilise tõe väljendamiseks. Oleme unustanud, et matemaatika opereerib ideedega, mitte mehaaniline manipuleerimine valemitega, mis neid ideid väljendavad. Siin on see, mida ma ei tee: ma ei hakka ümber jutustama õpikuid, mille olen juba kirjutanud. Kui vajate vastuseid siin ja praegu, on palju veebisaite, videoõpetusi ja 20 minutit aitama. Selle asemel omandame arvutamise põhitõed. Võrranditest ei piisa – ma tahan sissevaatehetki, et te tõesti näeksite nende tähendust ja mõistaksite matemaatika keelt. Ametlik matemaatiline keel on lihtsalt suhtlusviis. Graafikud, informatiivsed animatsioonid ja lihtne keel võivad anda parema ülevaate kui lehekülg ebaselgeid tõendeid. Arvan, et igaüks saab aru arvutamise põhiprintsiipidest. Me ei pea olema luuletajad, et nautida Shakespeare'i teoseid. Teil on palju lihtsam, kui tunnete algebrat ja tunnete huvi matemaatika vastu. Mitte nii kaua aega tagasi oli lugemine ja kirjutamine spetsiaalse väljaõppe saanud kirjatundjate töö. Ja täna saab sellega hakkama iga 10-aastane laps. Miks? Sest me ootame seda. Ootused mängivad võimaluste arendamisel tohutut rolli. Nii et oodake, et arvutus oleks lihtsalt üks teema. Mõned inimesed taanduvad pisimate detailideni (kirjanikud/matemaatikud). Kuid me ülejäänud saame lihtsalt toimuvat imetleda ja proovida seda mõista. Soovin, et kõik saaksid selgeks matemaatilise analüüsi põhimõisted ja ütleksid “Vau!”. See oli lihtne näide, aga kas saite põhiideest aru? Võtsime ketta, jagasime ära ja panime veidi teistmoodi tükid kokku. Matemaatiline analüüs näitas, et ketas ja rõngas on üksteisega tihedalt seotud: ketas on tegelikult rõngaste komplekt. See on arvutustes väga populaarne teema: suured asjad koosnevad väiksematest asjadest. Ja mõnikord on nende väikeste objektidega lihtsam ja selgem töötada. Paljud arvutuse näited põhinevad füüsikal. See on muidugi imeline, kuid nende tajumine võib olla keeruline: ausalt öeldes pole kaugeltki alati võimalik silmas pidada erinevaid füüsikalisi valemeid, näiteks objekti kiiruse valemit. Mulle meeldib alustada lihtsate visuaalsete näidetega, sest nii meie aju töötab. Rõngas/ring, mida oleme uurinud – võite sama asja modelleerida mitme erineva läbimõõduga torutükiga: jagada need osadeks, joondada ja asetada jämedaks kolmnurgaks, et veenduda, kas matemaatika tõesti töötab. Lihtsa füüsikalise valemiga seda tõenäoliselt ei tehta. Ma tunnen, et pedantsed matemaatikud põletavad oma klaviatuure. Seetõttu lisan vaid paar sõna "ranguse" kohta. Kas teate, et me ei õpeta arvutamist nii, nagu Newton või Leibniz selle avastas? Nad kasutasid intuitiivseid ideid "voog" ja "lõpmatult väike", mis asendati piiridega, sest "Muidugi see praktikas töötab. Aga kas see teoorias töötab? Oleme arvutuse "täpseks" tõestamiseks loonud keerukaid mehaanilisi mudeleid, kuid oleme selliste tõestuste käigus kaotanud intuitsiooni. Suhkru magusust vaatleme ajukeemia seisukohalt, selle asemel, et seda teaduskeeles seletada „Suhkrus on palju energiat. Söö seda." Ma ei taha (ja ei saa) õpilastele arvutamist õpetada ega teadlasi koolitada. Kuid kas oleks halb, kui kõik saaksid arvutusest aru "ebatäpsel" tasemel, mil Newton sellest aru sai? Et see muudaks ka teie jaoks maailma, nagu see kunagi tema jaoks? Enneaegne täpsusele keskendumine hajutab õpilasi ja muudab matemaatika õppimise keeruliseks. Siin on hea näide: arv e on tehniliselt defineeritud piiriga, kuid see avastati täpselt kasvu kohta intuitiivse oletuse abil. Naturaalne logaritm võib tunduda integraalina või kasvuajana. Millised seletused on algajatele parimad? Joonistame veidi käsitsi ja sukeldume teel keemiasse. Head arvuti kasutamist. (P.S: Üks lahke lugeja koostas animeeritud powerpointi slaidiseansi, mis aitab seda ideed visuaalsemalt esitleda (parem on vaadata PowerPointis, seal on näha animatsioonid). Aitäh!) Vene keele sõnaraamatu järgi analüüs- see on teadusliku uurimise meetod, mis võtab arvesse millegi üksikuid aspekte, omadusi, komponente. Üks tähtsamaid matemaatika harusid on nn matemaatiline analüüs ja sageli isegi lihtsalt analüüs. Kohe tekib küsimus: mida täpselt analüüsitakse matemaatilise analüüsiga? Vastus on selge - funktsioone analüüsitakse. Funktsioon(ladina keelest "funktsioon" - rakendamine) tähistab muutujate arvväärtuste vahelist seost. Kuna analüüs on uurimismeetod, tekib teine küsimus: mis see meetod on? Vastus annab matemaatilise analüüsi teise nime - diferentsiaal- ja integraalarvutus. Arvutamine on matemaatika haru, mis kehtestab arvutamise reeglid. sõna" diferentsiaal" tuleneb ladinakeelsest sõnast "diferentseerimine", st. erinevus. sõna" lahutamatu” pole nii selget päritolu (“integraator” – tervik; “integro” – taastamine), kuid selle tähendus on osade tervikuks ühendamine, erinevusteks purustatud taastamine. See taastumine saavutatakse koos summeerimine. Võtame esimesed tulemused kokku: · peamised objektid uurinud matemaatilises analüüsis on funktsioonid. · Funktsioonid on erinevat tüüpi sõltuvused muutuvate arvväärtuste vahel. · Matemaatilise analüüsi meetod on diferentseerimine– töötada funktsiooni väärtuste erinevustega ja integratsiooni- summade arvutamine. Seega peate matemaatilise analüüsi valdamiseks kõigepealt mõistma funktsiooni mõistet. Funktsioon on kõige olulisem matemaatiline mõiste, kuna funktsioonid on matemaatiline viis liikumise ja muutuste kirjeldamiseks. Funktsioon on protsess. Kõige olulisem liikumisviis on mehaaniline liikumine sirgjooneliselt. Liikumisel mõõdetakse objekti läbitud vahemaid, kuid liikumise täielikuks kirjeldamiseks sellest selgelt ei piisa. Nii Achilleus kui kilpkonn võivad liikuda lähtepunktist sama kaugele, kuid nende liikumine erineb kiiruselt ning kiirust ei saa mõõta ilma aega mõõtmata. Juba selle näite käsitlemisest selgub, et liikumise ja muutumise kirjeldamiseks ühest muutujast ei piisa. Intuitiivselt on selge, et aeg muutub ühtlaselt, samas kui vahemaa võib muutuda kas kiiremini või aeglasemalt. Liikumine on täielikult kirjeldatud, kui igal ajahetkel on teada, kui kaugele objekt on lähtepunktist eemaldunud. Niisiis on mehaanilise liikumise ajal vastavus kahe muutuja väärtuse vahel - aeg, mis muutub millestki sõltumatult, ja kaugus, mis sõltub ajast. See asjaolu on funktsiooni määratluse aluseks. Neid kahte muutujat ei nimetata enam ajaks ja vahemaaks. Funktsiooni määratlus: funktsiooni – kas see on reegel või seadus, pannes iga sõltumatu muutuja väärtuse X
sõltuva muutuja teatud väärtus juures
. Sõltumatu muutuja X
nimetatakse argumendiks ja sõltuvaks juures
- funktsioon. Mõnikord öeldakse, et funktsioon on seos kahe muutuja vahel. Kuidas visualiseerida, mis on muutuja? Muutuja on arvujoon (joonlaud või skaala), mida mööda liigub punkt (termomeeter või teraga nõel). Funktsioon on kahe aknaga x ja y hammasrataste mehhanism. See mehhanism võimaldab teil aknasse installida X
mis tahes väärtuses, kuid karbis juures
funktsiooni väärtus kuvatakse automaatselt hammasrataste abil. Ülesanne 1. Patsiendi temperatuuri mõõdetakse iga tund. On funktsioon - temperatuuri sõltuvus ajast. Kuidas seda funktsiooni esitada? Vastus: tabel ja graafik. Funktsioon on pidev, nagu liikumine on pidev, kuid praktikas on seda järjepidevust võimatu fikseerida. Saate püüda ainult üksikuid argumendi ja funktsiooni väärtusi. Teoreetiliselt on järjepidevust siiski võimalik kirjeldada. 2. ülesanne. Galileo Galilei avastas, et vabalt langev keha läbib kaugusühiku esimesel sekundil, 3 ühikut teisel, 5 ühikut kolmandal jne. Määrake aja sõltuvus vahemaast. näidustus: tuletage läbitud vahemaa ja vahemaa arvu vahelise seose üldvalem. Funktsioonide seadistamise viisid. Matemaatilise analüüsi ülesanded. Üleminek funktsiooni ühelt esitusviisilt teisele (funktsiooni väärtuste arvutamine, ligikaudsete analüütiliste funktsioonide konstrueerimine eksperimentaalsetest arv- ja graafilistest andmetest, funktsioonide uurimine ja joonistamine). Funktsiooni kui protsessi omaduste matemaatiline uurimine. Näide 1: kiiruse otsimine teadaoleva aja teefunktsiooni järgi (diferentseerimine). Näide 2: tee leidmine teadaoleva kiiruse ja aja funktsiooni abil (integreerimine).Funktsioon. Põhimõisted ja mõisted.
Albert Einstein
C - mahtuvus, mida mõõdetakse faradides;
dv - pinge muutus;
dt on aja muutus. 
Vaadake, mis on "MATEMAATILINE ANALÜÜS" teistes sõnaraamatutes:
Noh, see kõik on selge, nii et mis on teie suurepärane idee?
Aga matemaatika on raske!
Milles seisneb matemaatikaanalüüs?
Paar näidet
Natuke matemaatilisest rangusest (selle teaduse fanaatikutele)
|
järgmine loeng ==>
Loovus: vihikuid kontrollib x (kes?) õpetaja |
