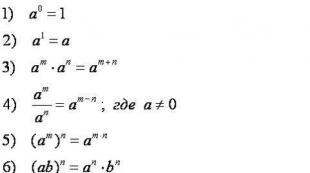A B in Cuba. Construction of the cube. Where do the formulas of abbreviated multiplication come from
The exercise is an operation, closely related to multiplication, this operation is the result of a multiple multiplication of any number on itself. I will depict the formula: a1 * a2 * ... * an \u003d an.
For example, a \u003d 2, n \u003d 3: 2 * 2 * 2 \u003d 2 ^ 3 \u003d 8.
In general, the exhibition is often used in various formulas in mathematics and physics. This feature has a more scientific destination than four main: addition, subtraction, multiplication, division.
Erection
The erection of the number is not complicated. It is associated with multiplication similar to multiplication and addition. Recording an is a summary of N-th, the number of numbers "A" multiplied by each other.
Consider the exercise into the extent to the easiest examples, moving to complex.
For example, 42. 42 \u003d 4 * 4 \u003d 16. Four squared (second degree) is sixteen. If you do not understand the multiplication of 4 * 4, then read our to become about multiplication.
Consider another example: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 . Five in Cuba (in the third degree) is equal to one hundred and twenty five.
Another example: 9 ^ 3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729 . Nine in Cuba equals seven hundreds of twenty nine.
Formulas
To competently erect to the extent, you need to remember and know the formulas listed below. There is nothing over natural, the main thing is to understand the essence and then they will not only be remembered, but they will seem light.

Erecting
What represents yourself alone? This is a product of numbers and variables in any quantity. For example, two - unrochene. And this is the erection of such universions this article.
Taking advantage of the formulas for the exercise to calculate the construction of universal to the degree will not be difficult.
For example, (3x ^ 2y ^ 3) ^ 2 \u003d 3 ^ 2 * x ^ 2 * 2 * y ^ (3 * 2) \u003d 9x ^ 4Y ^ 6; If it is unoccupied to the degree, then each composite is unobed into the degree.
Easy to the degree variable already having a degree, the degree is multiplied. For example, (x ^ 2) ^ 3 \u003d x ^ (2 * 3) \u003d x ^ 6;
Negative
Negative degree - the opposite number. What is the opposite number? Any number x reverse will be 1 / x. That is, x-1 \u003d 1 / x. This is the essence of a negative degree.
Consider an example (3Y) ^ - 3:
(3Y) ^ - 3 \u003d 1 / (27Y ^ 3).
Why is that? Since there is a minus to degree, then this expression is simply transferred to the denominator, and then erected into its third degree. Just right?
Cross-degree
Let's start considering the issue on a specific example. 43/2. What does the degree 3/2? 3 - Numerator, means the erection of the number (in this case 4) in the cube. The number 2 is the denominator, it is the extraction of the root of the second degree from among (in this case 4).
Then we get a square root of 43 \u003d 2 ^ 3 \u003d 8. Answer: 8.
So, the denominator of the fractional degree can be, both 3 and 4 and to infinity by any number and this number determines the degree of square root extracted from the specified number. Of course, the denominator cannot be zero.
Rapid root
If the root is erected into a degree equal to the degree of the root itself, then the answer will be a feeding expression. For example, (√h) 2 \u003d x. And so in any case equality of the degree of root and the degree of construction of the root.
If (√x) ^ 4. That (√x) ^ 4 \u003d x ^ 2. To check the decision transfer the expression to the expression with a fractional degree. Since the root is square, the denominator is 2. And if the root is erected into the fourth degree, then the numerator 4. We get 4/2 \u003d 2. Answer: x \u003d 2.
In any case, the best option is simply transferred to the expression with a fractional degree. If the fraction does not shrink, then this answer will and will be, provided that the root of the specified number is not allocated.
Consturbation in the degree of integrated number
What is a comprehensive number? A complex number is an expression having the formula A + B * I; A, B - valid numbers. I - the number that the number -1 gives in the square.
Consider an example. (2 + 3i) ^ 2.
(2 + 3i) ^ 2 \u003d 22 +2 * 2 * 3i + (3i) ^ 2 \u003d 4 + 12i ^ -9 \u003d -5 + 12i.
Sign up for the course "Accelerate the oral account, not mental arithmetic" to learn how to quickly and correctly fold, deduct, multiply, divide, erect numbers into a square and even extract the roots. For 30 days, you will learn how to use easy techniques to simplify arithmetic operations. In each lesson, new techniques, understandable examples and useful tasks.
Online
With the help of our calculator, you can calculate the erection of the number to the degree:
Grade 7
The exercise is beginning to pass schoolchildren only in the seventh grade.
The exercise is an operation, closely related to multiplication, this operation is the result of a multiple multiplication of any number on itself. I will depict the formula: a1 * a2 * ... * an \u003d an.
For example, a \u003d 2, n \u003d 3: 2 * 2 * 2 \u003d 2 ^ 3 \u003d 8.
Examples for solving:

Presentation
Presentation on the exercise to the extent calculated on the seventh graders. The presentation can clarify some incomprehensible moments, but probably there will be no such moments thanks to our article.
Outcome
We reviewed only the top of the iceberg to understand the mathematics better - sign up for our course: accelerate the oral account is not a mental arithmetic.
From the course you will not just recognize dozens of techniques for simplified and fast multiplication, addition, multiplication, divisions, calculating interest, but also work them in special tasks and educational games! The oral account also requires a lot of attention and concentrations that are actively trained in solving interesting tasks.
Mathematical expressions (formulas) abbreviated multiplication (Square amounts and differences, Cube amounts and differences, the difference of squares, the amount and difference of cubes) are extremely replaced in many areas of accurate sciences. These 7 character recordings are not replaced by simplifying expressions, solving equations, with multiplication of polynomials, reducing fractions, solving integrals and many other things. So it will be very useful to figure out how they are obtained, for which they are needed, and most importantly, how to remember them and then apply. Then apply formulas of abbreviated multiplication In practice, the most difficult will see what is H.and what is u. Obviously, no restrictions for a. and b.no, which means it can be any numeric or letter expressions.
And so here they:
First x 2 - U 2. \u003d (x - y) (x + y) . To calculate square difference Two expressions need to multiply the difference between these expressions on their sums.
Second (x + y) 2 \u003d X 2. + 2h + in 2 . To find square amount Two expressions need to be added to the square of the first expression to add a double product of the first expression on the second plus the square of the second expression.
Third (x - y) 2 \u003d X 2. - 2h + in 2. To calculate square differencetwo expressions are needed from the square of the first expression to take away a double product of the first expression on the second plus the square of the second expression.
Fourth (x + y) 3 \u003d x 3. + 3x 2 y + 3h 2 + 3. To calculate cube amounttwo expressions need to be added to the Cuba of the first expression to add a tripled work of the square of the first expression on the second plus the tripled product of the first expression on the square plus cube of the second expression.
Fifth (x - y) 3 \u003d x 3. - 3x 2 y + 3h 2 - 3.. To calculate cube differencetwo expressions are necessary from the first expression cube to take the tripled work of the square of the first expression on the second plus the tripled product of the first expression on the second minus cube of the second expression.
Six x 3 + 3. \u003d (x + y) (x 2 - Hu + U 2) To calculate the amount of cubestwo expressions need to multiply the sums of the first and second expression on an incomplete square of the difference of these expressions.
Seventh x 3 - 3. \u003d (x - y) (x 2 + Hu + U 2) To make calculation cubic differencestwo expressions need to multiply the difference between the first and second expression on the incomplete square of the sum of these expressions.
It is not difficult to remember that all formulas are applied to the work of calculations and in the opposite direction (right to left).
About 4 thousand years ago on the existence of these patterns. They were widely used by residents of ancient Babylon and Egypt. But in those epochs, they expressed verbally or geometrically and during the calculations did not use the letters.
We will understand proof of Square Summa(a + b) 2 \u003d a 2 + 2ab + b 2.
First this mathematical pattern Proved an ancient Greek scientist Euclide, who worked in Alexandria in the III century BC, he used a geometric way to evof the formula, since scientists of ancient Ellala did not use the letters to designate numbers. They were universally used not "A 2", but "square on the segment A", not "AB", but "rectangle, concluded between segments A and B".
In the previous lesson, we dealt with the decomposition of multipliers. Two ways were mastered: making a common factor for brackets and grouping. In this lesson - the next powerful way: formulas of abbreviated multiplication. In a brief record - FSU.
The formulas of the abbreviated multiplication (the square of the sum and difference, the cube of the amount and difference, the difference of squares, the sum and the difference of cubes) are extremely necessary in all sections of mathematics. They are used in simplifying expressions, solving equations, multiplication of polynomials, reduction of fractions, solving integrals, etc. etc. In short, there is every reason to deal with them. To understand how they are taken, why are they needed, how to remember them and how to apply.
We understand?)
Where do abbreviated multiplication formulas come from?
Equality 6 and 7 are not written very familiar. As if on the contrary. This is specially.) Any equality works both from left to right and right to left. In such a record, it is clear where the FSU comes from.
They are taken from multiplication.) For example:
(A + B) 2 \u003d (A + B) (A + B) \u003d A 2 + AB + BA + B 2 \u003d A 2 + 2AB + B 2
That's all, no scientific tricks. Just change the brackets and give these. So it turns out all formulas of abbreviated multiplication. Abbreviated Multiplication is because in the formulas themselves there is no multiplication of brackets and bringing similar. Reduced.) Immediately given the result.
FSU need to know by heart. Without the first three, you can not dream about the troika, without the rest - about the fourth with a five.)
Why do the formulas of abbreviated multiplication need?
There are two reasons, learn, even to get these formulas. The first - the finished answer on the machine sharply reduces the number of errors. But this is not the main reason. But the second ...
If you like this site ...
By the way, I have another couple of interesting sites for you.)
It can be accessed in solving examples and find out your level. Testing with instant check. Learn - with interest!)
You can get acquainted with features and derivatives.
Formulas or abbreviated multiplication rules are used in arithmetic, or rather - in algebra, for a faster process of calculating large algebraic expressions. The formulas themselves are obtained from the rules existing in the algebra to multiply several polynomials.
The use of these formulas provides a fairly operational solution of various mathematical tasks, and also helps to simplify expressions. The rules of algebraic transformations allow you to perform some manipulations with expressions, following which it is possible to obtain an expression on the right side in the left part of the equality, or to convert the right-hand part of the equality (to obtain an expression that stands in the left side after the equality sign).
It is convenient to know the formulas used for abbreviated multiplication, as well as they are often used in solving problems and equations. Below are the basic formulas included in this list, and their name.
Square amount
In order to calculate the square of the amount, it is necessary to find the amount consisting of the square of the first term, doubled the product of the first term on the second and square of the second. In the form of expression, this rule is written as follows: (A + C) ² \u003d a² + 2as + C².
Square difference
To calculate the square of the difference, it is necessary to calculate the amount consisting of the square of the first number twice the first number to the second (taken with the opposite sign) and the square of the second number. In the form of expression, this rule is as follows: (a - c) ² \u003d a² - 2as + C².
Square difference
The formula for the difference of the two numbers erected into the square is equal to the amount of the sum of these numbers on their difference. In the form of expression, this rule is as follows: A² - C² \u003d (A + C) · (A - C).
Cube amount
In order to calculate the cube of the sums of the two components, it is necessary to calculate the amount consisting of the cube of the first term, tripled work of the square of the first term and the second, tripled product of the first term and the second in the square, as well as the cube of the second term. In the form of expression, this rule is as follows: (a + c) ³ \u003d a³ + 3a² + 3As² + C³.

The amount of cubes
According to the formula, it is equal to the amount of the amount of the terms of the components on their incomplete square of the difference. In the form of expression, this rule is as follows: A³ + C³ \u003d (A + C) · (A² - AC + C²).
Example. It is necessary to calculate the volume of the shape, which is formed by the addition of two cubes. Also known only the values \u200b\u200bof their parties.
If the values \u200b\u200bof the parties are small, then perform calculations simply.
If the length of the parties are expressed in bulky numbers, then in this case it is easier to apply the "amount of cubes" formula, which will significantly simplify calculations.

Cube difference
The expression for cubic difference sounds like this: as the sum of the third degree of the first term, the tripled negative work of the square of the first member on the second, tripled work of the first member to the square of the second and negative cube of the second term. In the form of a mathematical expression a cube difference looks like this: (A - C) ³ \u003d a³ - 3A² + 3As² - C³.

Cubic differences
Cube difference formula differs from the amount of cubes only one sign. Thus, the difference of cubes is a formula equal to the product of data difference between their incomplete square sum. The difference of cubes is as follows: a 3 - from 3 \u003d (a - c) (and 2 + AC + C 2).
Example. It is necessary to calculate the volume of the figure that will remain after subtracting from the volume of the blue cube of a yellow outline figure of yellow, which is also a cube. Only the magnitude of the side of a small and large cube is known.
If the values \u200b\u200bof the parties are small, then the calculations are quite simple. And if the lengths of the parties are expressed in significant numbers, it is necessary to apply the formula entitled "Differences of cubes" (or "Cube of the difference"), which will significantly simplify calculations.
Three faults, each of which is equal x. (\\ displaystyle x.) This arithmetic operation is called "erection in the cube", its result is indicated x 3 (\\ displaystyle x ^ (3)):
x 3 \u003d x ⋅ x ⋅ x (\\ displaystyle x ^ (3) \u003d x \\ cdot x \\ cdot x)For the construction of the cube reverse operation is the extraction of cubic root. The geometric name of the third degree " cubic"Is due to the fact that antique mathematicians considered the cubes as cubic numbers, special kind of figured numbers (see below), since the list of numbers X (\\ DisplayStyle X) equal to the volume of the cube with the rib length equal X (\\ DisplayStyle X).
Cube sequence
, , , , , 125, 216, 343, 512, 729, , 1331, , 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648, 12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000, 68921, 74088, 79507, 85184, 91125, 97736, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616, 185193, 195112, 205379, 216000, 226981, 238328…The amount of cubes first N (\\ DisplayStyle N) Positive Natural Numbers is calculated by the formula:
Σ i \u003d 1 ni 3 \u003d 1 3 + 2 3 + 3 3 + ... + n 3 \u003d (n (n + 1) 2) 2 (\\ displaystyle \\ Sum _ (i \u003d 1) ^ (n) i ^ (3 ) \u003d 1 ^ (3) + 2 ^ (3) + 3 ^ (3) + \\ ldots + n ^ (3) \u003d \\ left (((\\ FRAC (n (n + 1)) (2)) \\ RIGHT) ^ (2))Withdrawal of formula
The amount of cubes can be displayed using the multiplication table and the sum of the sum of arithmetic progression. Considering as an illustration of the method, two multiplication tables 5 × 5, carry out reasoning for the tables of N × n.
|
|
The amount of numbers in K-oh (k \u003d 1,2, ...) selected area of \u200b\u200bthe first table:
k 2 + 2 k Σ l \u003d 1 k - 1 l \u003d k 2 + 2 kk (k - 1) 2 \u003d k 3 (\\ displaystyle k ^ (2) + 2k \\ sum _ (l \u003d 1) ^ (k- 1) L \u003d k ^ (2) + 2K (\\ FRAC (k (k - 1)) (2)) \u003d k ^ (3))And the sum of numbers in K-oh (k \u003d 1,2, ...) selected area of \u200b\u200bthe second table, which is an arithmetic progression:
k Σ l \u003d 1 n l \u003d k n (n + 1) 2 (\\ displaystyle k \\ sum _ (l \u003d 1) ^ (n) l \u003d k (\\ FRAC (n (n + 1)) (2)))Summing through all the selected areas of the first table, we get the same number as summing over all selected areas of the second table:
Σ k \u003d 1 nk 3 \u003d Σ k \u003d 1 nkn (n + 1) 2 \u003d n (n + 1) 2 σ k \u003d 1 nk \u003d (n (n + 1) 2) 2 (\\ displaystyle \\ Sum _ (k \u003d 1) ^ (n) k ^ (3) \u003d \\ sum _ (k \u003d 1) ^ (n) k (\\ FRAC (n (n + 1)) (2)) \u003d (\\ FRAC (n (n + 1)) (2)) \\ Sum _ (k \u003d 1) ^ (n) k \u003d \\ left (((\\ FRAC (n (n + 1)) (2)) \\ right) ^ (2))Some properties
- In the decimal record, the cube may end on any digit (unlike the square)
- In the decimal record, the two last Cubes can be 00, 01, 03, 04, 07, 08, 09, 11, 19, 21, 23, 29, 29, 21, 23, 29, 31 32, 33, 36, 37, 39, 41, 43, 44, 47, 52, 53, 51, 52, 59, 61, 51, 52, 53, 61 , 73, 75, 76, 77, 79, 81, 83, 84, 87, 88, 89, 91, 92, 93, 96, 97, 99. The dependence of the penultimate digit of the cube from the latter can be represented as the following table:
Cuba as curly numbers
"Cubic number" Q n \u003d n 3 (\\ displaystyle q_ (n) \u003d n ^ (3)) Historically, it was considered a variety of spatial figure numbers. It can be represented as a difference of squares of successive triangular numbers. T N (\\ DisplayStyle T_ (N)):
Q n \u003d (t n) 2 - (t n - 1) 2, n ⩾ 2 (\\ displaystyle q_ (n) \u003d (t_ (n)) ^ (2) - (t_ (n - 1)) ^ (2 ), n \\ geqslant 2) Q 1 + q 2 + q 3 + ⋯ + q n \u003d (t n) 2 (\\ displaystyle q_ (1) + q_ (2) + q_ (3) + \\ dots + q_ (n) \u003d (t_ (n) ) ^ (2))The difference between two adjacent cubic numbers is a centered hexagonal number.
The expression of a cubic number through tetrahedral Π N (3) (\\ displaystyle \\ pi _ (n) ^ ((3))).