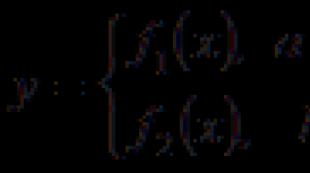Matematička analiza.

Radionica.

Za studente univerziteta u specijalnosti:

"Državna i opštinska uprava"

T.Z. Pavlova

Kolpaševo 2008

Poglavlje 1. Uvod u analizu

1.1 Funkcije. Opća svojstva

1.2 Teorija granica

1.3 Kontinuitet funkcije

2.1 Definicija izvedenice

2.4 Istraživanje funkcija

2.4.1 Studijski plan pune funkcije

2.4.2 Primjeri proučavanja funkcija

2.4.3. Najveća i najmanja vrijednost funkcije na segmentu

2.5 L'Hôpitalovo pravilo

3.1 Neodređeni integral

3.1.1 Definicije i svojstva

3.1.2 Tabela integrala

3.1.3 Osnovne metode integracije

3.2 Definitivni integral

3.2.2 Metode za izračunavanje definitivnog integrala

Poglavlje 4. Funkcije nekoliko varijabli

4.1 Osnovni koncepti

4.2 Granice i kontinuitet funkcija nekoliko varijabli

4.3.3 Ukupni diferencijal i njegova primjena na aproksimativne proračune

Poglavlje 5. Klasične metode optimizacije

6.1 Korisna funkcija.

6.2 Linije ravnodušnosti

6.3 Budžet je postavljen

Domaći zadaci

1.1 Funkcije. Opća svojstva

Numerička funkcija je definirana na skupu D realnih brojeva ako je svakoj vrijednosti varijable pridružena neka dobro definirana realna vrijednost varijable y, gdje je D domen funkcije.

Analitički prikaz funkcije:

eksplicitno:;

implicitno:;

u parametarskom obliku:

različite formule u oblasti definicije:

Svojstva.

Ravnomjerna funkcija:. Na primjer, funkcija je parna, pošto ...

Neparna funkcija: ... Na primjer, funkcija je neparna, jer ...

Periodična funkcija: , gdje je T period funkcije,. Na primjer, trigonometrijske funkcije.

Monotonska funkcija. Ako je za bilo koju domenu definicije - funkcija raste, - opada. Na primjer, - povećanje i - smanjenje.

Ograničena funkcija. Ako postoji broj M takav da. Na primjer, funkcije i, pošto .

Primjer 1. Pronađite domen definicije funkcija.

+ 2 – 3 +

1.2 Teorija granica

Definicija 1... Granica funkcije u je broj b ako se za bilo koji (- proizvoljno mali pozitivan broj) može pronaći takva vrijednost argumenta, počevši od koje je nejednakost zadovoljena.

Oznaka:.

Definicija 2... Granica funkcije u je broj b ako za bilo koji (je proizvoljno mali pozitivan broj) postoji pozitivan broj takav da za sve vrijednosti x koje zadovoljavaju nejednakost vrijedi nejednakost.

Oznaka:.

Definicija 3. Funkcija se zove beskonačno mala za ili, ako je ili.

Svojstva.

1. Algebarski zbir konačnog broja infinitezimalnih veličina je infinitezimalna veličina.

2. Proizvod beskonačno male količine ograničenom funkcijom (konstanta, druga beskonačno mala količina) je beskonačno mala veličina.

3. Kvocijent dijeljenja beskonačno male količine funkcijom čija je granica različita od nule je beskonačno mala veličina.

Definicija 4. Funkcija se naziva beskonačno velikom at, if.

Svojstva.

1. Proizvod beskonačno velike količine na funkciju, čija je granica različita od nule, je beskonačno velika količina.

2. Zbir beskonačno velike vrijednosti i ograničene funkcije je beskonačno velika vrijednost.

3. Količnik dijeljenja beskonačno velike količine funkcijom koja ima ograničenje je beskonačno velika količina.

Teorema.(Odnos između beskonačno male količine i beskonačno velike količine.) Ako je funkcija beskonačno mala u (), tada je funkcija beskonačno velika količina u (). I obrnuto, ako je funkcija beskonačno velika u (), tada je funkcija beskonačno mala u ().

Granične teoreme.

1. Funkcija ne može imati više od jednog ograničenja.

2. Granica algebarskog zbira nekoliko funkcija jednaka je algebarskom zbiru granica ovih funkcija:

3. Granica proizvoda nekoliko funkcija jednaka je proizvodu granica ovih funkcija:

4. Granica stepena je jednaka stepenu granice:

5. Granica količnika je jednaka količniku granica ako postoji granica djelitelja:

.

6. Prva izuzetna granica.

Posljedice:

7. Druga izuzetna granica:

Posljedice:

Ekvivalentne beskonačno male vrijednosti za:

Obračun limita.

Prilikom izračunavanja granica koriste se osnovne teoreme o granicama, svojstva kontinuiranih funkcija i pravila koja proizlaze iz ovih teorema i svojstava.

Pravilo 1. Da bismo pronašli granicu u tački funkcije koja je u ovoj tački kontinuirana, potrebno je njenu graničnu vrijednost zamijeniti u funkciji pod znakom granice umjesto argumenta x.

Primjer 2. Pronađite

Pravilo 2. Ako je pri pronalaženju granice razlomka granica nazivnika nula, a granica brojnika različita od nule, tada je granica takve funkcije.

Primjer 3. Pronađite

Pravilo 3. Ako je pri pronalaženju granice razlomka granica nazivnika jednaka, a granica brojnika različita od nule, tada je granica takve funkcije nula.

Primjer 4. Pronađite

Često, zamjena granične vrijednosti za argument rezultira nedefiniranim izrazima poput

.

Pronalaženje granice funkcije u ovim slučajevima naziva se otkrivanje nesigurnosti. Da bi se otkrila nesigurnost, potrebno je transformirati ovaj izraz prije nego što se ode do granice. Za otkrivanje nesigurnosti koriste se različite tehnike.

Pravilo 4... Nesigurnost tipa otkriva se transformacijom podgranične funkcije, kako bi se u brojiocu i nazivniku odabrao faktor čija je granica nula, i, smanjivši razlomak za njega, pronašao granicu količnika. Da bi se to uradilo, brojilac i imenilac se ili množe ili množe izrazima konjugiranim sa brojnikom i imeniocem.

Pravilo 5. Ako izraz sublimit sadrži trigonometrijske funkcije, tada se prva izvanredna granica koristi za razotkrivanje nesigurnosti vrste.

.

Pravilo 6... Da bi se otkrila nesigurnost oblika at, brojilac i nazivnik podgraničnog razlomka moraju se podijeliti s najvišim stupnjem argumenta, a zatim se mora pronaći granica količnika.

Mogući rezultati:

1) željena granica je jednaka odnosu koeficijenata na najvećim stepenima argumenta brojnika i imenioca, ako su ti stepeni isti;

2) granica je jednaka beskonačnosti ako je stepen argumenta brojioca veći od stepena argumenta imenioca;

3) granica je nula ako je stepen argumenta brojioca manji od stepena argumenta nazivnika.

a)

pošto

Stepeni su jednaki, što znači da je granica jednaka odnosu koeficijenata na višim stepenima, tj. ...

b)

Stepen brojioca, nazivnik je 1, što znači da je granica

v)

Stepen brojioca je 1, stepen nazivnika je, pa je granica 0.

Pravilo 7... Da bi se otkrila nesigurnost oblika, brojnik i imenilac podgraničnog razlomka moraju se pomnožiti konjugiranim izrazom.

Primjer 10.

Pravilo 8... Druga izuzetna granica i njene posljedice koriste se za otkrivanje nesigurnosti vrste.

To se može dokazati

Primjer 11.

Primjer 12.

Primjer 13.

Pravilo 9... Prilikom otkrivanja neizvjesnosti čija subliminalna funkcija sadrži infinitezimalnu, potrebno je zamijeniti granice tih beskonačnosti. na granicama infinitezimalnih elemenata koji su njima ekvivalentni.

Primjer 14.

Primjer 15.

Pravilo 10. L'Hôpitalovo pravilo (vidi 2.6).

1.3 Kontinuitet funkcije

Funkcija je kontinuirana u nekoj tački ako granica funkcije dok argument teži ka a, postoji i jednaka je vrijednosti funkcije u ovoj tački.

Ekvivalentni uslovi:

1. ;

3.

Klasifikacija prelomne tačke:

lom prve vrste

Jednokratna - jednostrane granice postoje i jednake su;

Fatalni (skok) - jednostrane granice nisu jednake;

diskontinuitet druge vrste: granica funkcije u tački ne postoji.

Primjer 16. Utvrditi prirodu diskontinuiteta funkcije u nekoj tački ili dokazati kontinuitet funkcije u ovoj tački.

jer funkcija nije definirana, stoga nije kontinuirana u ovoj tački. Jer i shodno tome, , tada je tačka uklonjivog diskontinuiteta prve vrste.

b)

u poređenju sa zadatkom (a), funkcija je proširena u tački tako da , dakle, ova funkcija je kontinuirana u ovoj tački.

Kada funkcija nije definirana;

.

Jer jedna od jednostranih granica je beskonačna, onda je to tačka prekida druge vrste.

Poglavlje 2. Diferencijalni račun

2.1 Definicija izvedenice

Definicija izvoda

Izvod ili derivacija date funkcije je granica omjera prirasta funkcije i odgovarajućeg prirasta argumenta kada prirast argumenta teži nuli:

Or .

Mehaničko značenje derivacije je brzina promjene funkcije. Geometrijsko značenje derivacije je tangenta ugla nagiba tangente na graf funkcije:

2.2 Osnovna pravila za diferencijaciju

Ime	Funkcija	Derivat
Množenje konstantnim faktorom
Algebarski zbir dviju funkcija
Proizvod dvije funkcije
Privatne dvije funkcije
Kompleksna funkcija

Derivati ​​osnovnih elementarnih funkcija

P / p br.	Naziv funkcije	Funkcija i njen derivat
1	konstantan
2	funkcija snage posebnim slučajevima
3	eksponencijalna funkcija poseban slučaj
4	logaritamska funkcija poseban slučaj
5	trigonometrijske funkcije
6	obrnuto trigonometrijski

b)

2.3 Derivati ​​višeg reda

Izvod funkcije drugog reda

Izvod funkcije drugog reda:

Primjer 18.

a) Pronađite izvod funkcije drugog reda.

Rješenje. Nađimo prvo derivaciju prvog reda .

Uzmimo izvod izvoda prvog reda.

Primjer 19. Pronađite izvod funkcije trećeg reda.

2.4 Istraživanje funkcija

2.4.1 Plan za kompletnu studiju funkcije:

Studijski plan pune funkcije:

1. Osnovno istraživanje:

Pronađite domen i raspon vrijednosti;

Saznati opšta svojstva: parnost (neparnost), periodičnost;

Naći tačke preseka sa koordinatnim osama;

Odredite područja konstantnosti.

2. Asimptote:

Pronađite vertikalne asimptote ako;

Pronađite kose asimptote:.

Ako bilo koji broj, onda - horizontalne asimptote.

3. Istražite koristeći:

Pronađite kritične tačke, one. tačke u kojima postoji ili ne postoji;

Odrediti intervale povećanja, tj. intervali, na kojima i opadajuće funkcije -;

Odrediti ekstreme: tačke, pri prolasku kroz koje menja predznak sa "+" na "-", su maksimalne tačke, od "-" do "+" - minimum.

4. Istražite koristeći:

Pronađite tačke u kojima postoji ili ne postoji;

Pronađite područja konveksnosti, tj. intervali u kojima se nalaze udubljenja;

Pronađite tačke pregiba, tj. tačke pri prolasku kroz koje se mijenja predznak.

1. Pojedini elementi studije iscrtavaju se na grafikonu postepeno, kako se nalaze.

2. Ako postoje poteškoće s konstrukcijom grafa funkcije, tada se vrijednosti funkcije nalaze u nekim dodatnim točkama.

3. Svrha studije je da opiše prirodu ponašanja funkcije. Dakle, ne gradi se tačan graf, već njegova aproksimacija na kojoj su jasno naznačeni pronađeni elementi (ekstremumi, prevojne tačke, asimptote itd.).

4. Nije potrebno striktno pridržavati se gore navedenog plana; važno je ne previdjeti karakteristične elemente ponašanja funkcije.

2.4.2 Primjeri studije funkcije:

1)

2) Funkcija je neparna:

.

3) Asimptote.

- vertikalne asimptote, jer

Kosa asimptota.

5)

- tačka pregiba.

2) Funkcija je neparna:

3) Asimptote: Ne postoje vertikalne asimptote.

nagnut:

- kose asimptote

4) - funkcija se povećava.

- tačka pregiba.

Šematski dijagram ove funkcije:

2) Opća funkcija

3) Asimptote

- nema kosih asimptota

- horizontalna asimptota na

- tačka pregiba

Šematski dijagram ove funkcije:

2) Asimptote.

- vertikalna asimptota, jer

- nema kosih asimptota

, - horizontalna asimptota

Šematski dijagram ove funkcije:

2) Asimptote

- vertikalna asimptota na, pošto

- nema kosih asimptota

, - horizontalna asimptota

3) - funkcija se smanjuje u svakom od intervala.

Šematski dijagram ove funkcije:

Da biste pronašli najveću i najmanju vrijednost funkcije na segmentu, možete koristiti dijagram:

1. Pronađite izvod funkcije.

2. Naći kritične tačke funkcije u kojima postoji ili ne postoji.

3. Odrediti vrijednost funkcije u kritičnim tačkama koje pripadaju datom segmentu i na njegovim krajevima i izabrati najveću i najmanju od njih.

Primjer. Pronađite najmanju i najveću vrijednost funkcije na datom segmentu.

25. između

2) - kritične tačke

26. između.

Izvod ne postoji u, ali 1 ne pripada ovom intervalu. Funkcija se smanjuje u intervalu, što znači da ne postoji najveća vrijednost, već najmanja vrijednost.

2.5 L'Hôpitalovo pravilo

Teorema. Granica omjera dvije beskonačno male ili beskonačno velike funkcije jednaka je granici omjera njihovih derivacija (konačnih ili beskonačnih), ako ova druga postoji u navedenom smislu.

One. kada otkrivate nesigurnosti tipa ili, možete koristiti formulu:

.

27.

Poglavlje 3. Integralni račun

3.1 Neodređeni integral

3.1.1 Definicije i svojstva

Definicija 1. Funkcija se zove antiderivativna za if.

Definicija 2. Neodređeni integral funkcije f (x) je skup svih antiderivata za ovu funkciju.

Oznaka: , gdje je c proizvoljna konstanta.

Neodređena integralna svojstva

1. Derivat neodređenog integrala:

2. Diferencijal neodređenog integrala:

3. Neodređeni integral diferencijala:

4. Neodređeni integral zbira (razlike) dvije funkcije:

5. Premještanje konstantnog faktora izvan predznaka neodređenog integrala:

3.1.2 Tabela integrala

.1.3 Osnovne metode integracije

1. Koristeći svojstva neodređenog integrala.

Primjer 29.

2. Dovođenje pod znak diferencijala.

Primjer 30.

3. Varijabilna metoda zamjene:

a) zamjena u integralu

gdje - funkcija koju je lakše integrirati od originalne; - funkcija inverzna funkciji; je antiderivat funkcije.

Primjer 31.

b) zamjena u integralu oblika:

Primjer 32.

Primjer 33.

4. Metoda integracije po dijelovima:

Primjer 34.

Primjer 35.

Uzmimo zasebno integral

Vratimo se našem integralu:

3.2 Definitivni integral

3.2.1 Pojam određenog integrala i njegova svojstva

Definicija. Neka je dana kontinuirana funkcija na nekom intervalu. Hajde da napravimo njen graf.

Lik omeđen odozgo krivom, lijevo i desno pravim linijama, a odozdo segmentom ose apscise između tačaka a i b naziva se zakrivljeni trapez.

S - površina - zakrivljeni trapez.

Podijelite interval sa tačkama i dobijete:

Integralni zbir:

Definicija. Definitivni integral je granica integralnog zbira.

Definitivna integralna svojstva:

1. Konstantni faktor se može izvaditi iz predznaka integrala:

2. Integral algebarskog zbira dvije funkcije jednak je algebarskom zbiru integrala ovih funkcija:

3. Ako se segment integracije podijeli na dijelove, tada je integral po cijelom segmentu jednak zbiru integrala za svaki od nastalih dijelova, tj. za bilo koje a, b, c:

4. Ako na segmentu, onda

5. Granice integracije se mogu mijenjati, dok se predznak integrala mijenja:

6.

7. Integral u tački je jednak 0:

8.

9. (“o srednjoj”) Neka je y = f (x) funkcija integrabilna na. Onda , gdje je f (c) prosječna vrijednost f (x) na:

10. Newton-Leibnizova formula

,

gdje je F (x) antiderivat za f (x).

3.2.2 Metode za izračunavanje definitivnog integrala.

1. Direktna integracija

Primjer 35.

a)

b)

v)

e)

2. Promjena varijabli pod predznakom određenog integrala .

Primjer 36.

2. Integracija po dijelovima u određenom integralu .

Primjer 37.

a)

b)

e)

3.2.3 Primjena određenog integrala

Karakteristično	Vrsta funkcije	Formula
	u kartezijanskim koordinatama
oblast zakrivljenog sektora	u polarnim koordinatama
zakrivljeno područje trapeza	u parametarskom obliku
dužina luka	u kartezijanskim koordinatama
dužina luka	u polarnim koordinatama
dužina luka	u parametarskom obliku
zapremine tela rotacija	u kartezijanskim koordinatama
zapremine tela sa datim poprečnim presjek

Primjer 38. Izračunajte površinu oblika ograničenog linijama: i .

Rješenje: Nađimo tačke presjeka grafova ovih funkcija. Da bismo to učinili, izjednačavamo funkcije i rješavamo jednačinu

Dakle, tačke preseka i.

Površinu figure pronalazimo pomoću formule

.

U našem slučaju

Odgovor: površina je jednaka (kvadratne jedinice).

4.1 Osnovni koncepti

Definicija. Ako se, prema nekom pravilu, svakom paru nezavisnih brojeva iz određenog skupa dodijeli jedna ili više vrijednosti varijable z, tada se varijabla z naziva funkcijom dvije varijable.

Definicija. Domen funkcije z je skup parova za koje postoji funkcija z.

Domen funkcije dvije varijable je skup tačaka na koordinatnoj ravni Oxy. Z-koordinata se naziva aplikat, a tada se sama funkcija prikazuje kao neka površina u prostoru E 3. Na primjer:

Primjer 39. Pronađite domenu funkcije.

a)

Izraz na desnoj strani ima značenje samo za. To znači da je domen ove funkcije skup svih tačaka koje leže unutar i na granici kružnice polumjera R sa središtem u početku.

Domen ove funkcije su sve tačke ravni, osim tačaka pravih, tj. koordinatne ose.

Definicija. Linije na nivou funkcije su porodica krivulja na koordinatnoj ravni opisanih jednadžbama oblika.

Primjer 40. Pronađite linije nivoa funkcije .

Rješenje. Linije nivoa date funkcije su porodica krivulja u ravni koju opisuje jednačina

Posljednja jednadžba opisuje porodicu krugova sa centrom u tački poluprečnika O 1 (1, 1). Površina okretanja (paraboloid) opisana ovom funkcijom postaje "strmija" kako se udaljava od ose, što je dato jednadžbama x = 1, y = 1. (Slika 4)

4.2 Granice i kontinuitet funkcija nekoliko varijabli.

1. Ograničenja.

Definicija. Broj A naziva se granica funkcije jer tačka teži točki, ako za svaki proizvoljno mali broj postoji broj takav da je uvjet istinit za bilo koju tačku, a uvjet ... Zapisuju: .

Primjer 41. Pronađite granice:

one. granica zavisi od, pa stoga i ne postoji.

2. Kontinuitet.

Definicija. Neka tačka pripada domenu definicije funkcije. Tada se funkcija naziva kontinuiranom u tački if

(1)

štaviše, tačka teži tački na proizvoljan način.

Ako u bilo kojoj tački uvjet (1) nije zadovoljen, tada se ova tačka naziva tačka diskontinuiteta funkcije. To može biti u sljedećim slučajevima:

1) Funkcija nije definirana u tački.

2) Nema ograničenja.

3) Ova granica postoji, ali nije jednaka.

Primjer 42. Odrediti da li je data funkcija kontinuirana u tački, ako.

Shvatio sam dakle, ova funkcija je kontinuirana u tački.

granica zavisi od k, tj. ne postoji u datoj tački, što znači da funkcija ima diskontinuitet u ovoj tački.

4.3 Derivati ​​i diferencijali funkcija nekoliko varijabli

4.3.1 Parcijalni derivati ​​prvog reda

Parcijalni izvod funkcije u odnosu na argument x je običan izvod funkcije jedne varijable x za fiksnu vrijednost varijable y i označava se:

Parcijalni izvod funkcije u odnosu na argument y je običan izvod funkcije jedne varijable y na fiksnoj vrijednosti varijable x i označava se:

Primjer 43. Naći parcijalne izvode funkcija.

4.3.2 Parcijalni derivati ​​drugog reda

Parcijalni derivati ​​drugog reda su parcijalni derivati ​​parcijalnih izvoda prvog reda. Za funkciju dvije varijable oblika moguća su četiri tipa parcijalnih izvoda drugog reda:

Parcijalni derivati ​​drugog reda, u kojima se diferencijacija vrši u odnosu na različite varijable, nazivaju se mješoviti derivati. Mješoviti derivati ​​drugog reda dvostruko diferencibilne funkcije su jednaki.

Primjer 44. Naći parcijalne izvode drugog reda.

4.3.3 Ukupni diferencijal i njegova primjena na aproksimativne proračune.

Definicija. Diferencijal prvog reda funkcije dvije varijable nalazi se po formuli

.

Primjer 45. Pronađite ukupni diferencijal za funkciju.

Rješenje. Nađimo parcijalne izvode:

.

Za male inkremente argumenata x i y, funkcija dobija prirast približno jednak dz, tj. ...

Formula za pronalaženje približne vrijednosti funkcije u tački, ako je poznata njena tačna vrijednost u tački:

Primjer 46. Nađi .

Rješenje. neka ,

Zatim koristimo formulu

Odgovori. .

Primjer 47. Približno izračunajte.

Rješenje. Razmotrimo funkciju. Imamo

Primjer 48. Približno izračunajte.

Rješenje. Razmotrite funkciju ... Dobijamo:

Odgovori. .

4.3.4 Implicitna diferencijacija funkcija

Definicija. Funkcija se naziva implicitna ako je data jednadžbom koja nije rješiva ​​s obzirom na z.

Parcijalni derivati ​​takve funkcije nalaze se po formulama:

Primjer 49. Naći parcijalne izvode funkcije z date jednadžbom .

Rješenje.

Definicija. Funkcija se naziva implicitnom ako je data jednadžbom koja nije rješiva ​​s obzirom na y.

Derivat takve funkcije se nalazi po formuli:

.

Primjer 50. Naći izvode ovih funkcija.

5.1 Lokalni ekstremum funkcije nekoliko varijabli

Definicija 1. Funkcija ima maksimum u tački if

Definicija 2. Funkcija ima minimum u tački if za sve tačke koje su dovoljno bliske tački i različite od nje.

Neophodan uslov za ekstrem. Ako funkcija dostigne ekstrem u nekoj tački, tada parcijalni derivati ​​funkcije nestaju ili ne postoje u ovoj tački.

Tačke u kojima parcijalni derivati ​​nestaju ili ne postoje nazivaju se kritičnim.

Dovoljan znak ekstrema. Neka je funkcija definirana u nekom susjedstvu kritične točke i ima kontinuirane parcijalne izvode drugog reda u ovoj tački

1) ima lokalni maksimum u tački, ako i;

2) ima lokalni minimum u tački, ako i;

3) nema lokalni ekstrem u tački ako;

Shema studije za ekstremum funkcije dvije varijable.

1. Naći parcijalne izvode funkcije: i.

2. Riješite sistem jednačina i pronađite kritične tačke funkcije.

3. Pronađite parcijalne izvode drugog reda, izračunajte njihove vrijednosti u kritičnim tačkama i, koristeći dovoljan uslov, izvedite zaključak o prisutnosti ekstrema.

4. Pronađite ekstreme funkcije.

Primjer 51. Naći ekstreme funkcije .

1) Pronađite parcijalne izvode.

2) Riješiti sistem jednačina

4) Pronađite parcijalne izvode drugog reda i njihove vrijednosti u kritičnim tačkama:. U tački dobijamo:

dakle, ne postoji ekstremum u tački. U tački dobijamo:

dakle, u tački postoji minimum.

5.2 Globalni ekstrem (najviša i najniža vrijednost funkcije)

Najveća i najmanja vrijednost funkcije više varijabli, kontinuirane na nekom zatvorenom skupu, postižu se ili u tačkama ekstrema ili na granici skupa.

Šema za pronalaženje najveće i najniže vrijednosti.

1) Pronađite kritične tačke koje leže unutar regije, izračunajte vrijednost funkcije u tim tačkama.

2) Istražite funkciju na granici područja; ako se granica sastoji od nekoliko različitih linija, onda se studija mora provesti za svaku lokaciju posebno.

3) Uporedite dobijene vrednosti funkcije i izaberite najveću i najmanju.

Primjer 52. Pronađite najveću i najmanju vrijednost funkcije u pravokutniku.

Rješenje. 1) Pronađite kritične tačke funkcije, za to nađemo parcijalne izvode:, i riješite sistem jednačina:

Primljena je kritična tačka A. Rezultirajuća tačka leži unutar navedene oblasti,

Granicu područja čine četiri segmenta: i. pronaći najveću i najmanju vrijednost funkcije na svakom segmentu.

4) Uporedite dobijene rezultate i pronađite to u tačkama .

Poglavlje 6. Model izbora potrošača

Pretpostavićemo da postoji n različitih roba. Tada će određeni skup dobara biti označen n-dimenzionalnim vektorom , gdje je količina i-tog proizvoda. Skup svih skupova dobara X naziva se prostor.

Izbor pojedinačnog potrošača karakterizira odnos preferencija: vjeruje se da potrošač može reći za bilo koja dva skupa, što je poželjnije, ili ne vidi razliku između njih. Relacija preferencije je tranzitivna: ako je skup poželjniji od skupa, a skup je poželjniji od skupa, tada je skup poželjniji od skupa. Pretpostavićemo da je ponašanje potrošača u potpunosti opisano aksiomom pojedinačnog potrošača: svaki pojedinačni potrošač donosi odluku o potrošnji, kupovini itd., na osnovu svog sistema preferencija.

6.1 Korisna funkcija

Na skupu potrošačkih skupova X definirana je funkcija , čija je vrijednost na potrošačkom skupu jednaka potrošačkoj procjeni pojedinca za ovaj skup. Funkcija se naziva funkcija korisnosti potrošača ili funkcija preferencije potrošača. One. svaki potrošač ima svoju vlastitu funkciju korisnosti. Ali cijeli skup potrošača može se podijeliti u određene klase potrošača (po godinama, imovinskom statusu, itd.) i svakoj klasi se može dodijeliti neka, možda, prosječna funkcija korisnosti.

Dakle, funkcija je procjena potrošača ili nivo zadovoljenja potreba pojedinca prilikom kupovine datog kompleta. Ako je skup poželjniji od skupa za datu osobu, onda.

Svojstva korisnih funkcija.

1.

Prvi parcijalni derivati ​​funkcije korisnosti nazivaju se granične korisnosti proizvoda. Iz ovog svojstva proizlazi da povećanje potrošnje jednog proizvoda dok potrošnja ostalih proizvoda ostaje nepromijenjena dovodi do povećanja ocjene potrošača. Vector je gradijent funkcije, pokazuje smjer najvećeg rasta funkcije. Za funkciju, njen gradijent je vektor graničnih korisnosti proizvoda.

2.

One. granična korisnost bilo koje robe opada sa povećanjem potrošnje.

3.

One. granična korisnost svakog proizvoda raste sa količinom drugog proizvoda.

Neke vrste uslužnih funkcija.

1) Neoklasični:.

2) Kvadrat: gdje je matrica negativno određena i za .

3) Logaritamska funkcija:.

6.2 Linije ravnodušnosti

U primijenjenim problemima i modelima izbora potrošača često se koristi poseban slučaj skupa od dva dobra, tj. kada funkcija korisnosti zavisi od dvije varijable. Linija ravnodušnosti je linija koja povezuje potrošačke skupove koji imaju isti nivo zadovoljenja potreba pojedinca. U suštini, linije indiferentnosti su linije nivoa funkcije. Jednačine indiferentne linije: .

Osnovna svojstva linija indiferentnosti.

1. Linije ravnodušnosti, koje odgovaraju različitim nivoima zadovoljenja potreba, ne dodiruju se i ne ukrštaju.

2. Linije indiferentnosti se smanjuju.

3. Linije ravnodušnosti su konveksne prema dolje.

Svojstvo 2 implicira važnu približnu jednakost.

Ovaj odnos pokazuje koliko pojedinac treba da poveća (smanji) potrošnju drugog proizvoda, a da smanji (poveća) potrošnju prvog proizvoda za jednu jedinicu bez promene stepena zadovoljenja svojih potreba. Omjer se naziva stopa zamjene prvog proizvoda drugim, a vrijednost se naziva granična stopa zamjene prvog proizvoda drugim.

Primjer 53. Ako je granična korisnost prvog dobra 6, a drugog - 2, tada sa smanjenjem potrošnje prvog dobra za jednu jedinicu, potrebno je povećati potrošnju drugog dobra za 3 jedinice sa isti nivo zadovoljenja potreba.

6.3 Budžet je postavljen

Neka - vektor cijena za skup od n proizvoda; I - prihod pojedinca koji je spreman potrošiti na kupovinu seta proizvoda. Skup skupova dobara koji ne koštaju više od I po datim cijenama naziva se budžetski skup B. Štaviše, skup skupova dobara koji koštaju I naziva se granica G budžetskog skupa B. skup B je omeđen granicom G i prirodnim ograničenjima.

Budžetski skup je opisan sistemom nejednakosti:

Za slučaj skupa od dva dobra, budžetski skup B (slika 1) je trougao u koordinatnom sistemu, omeđen koordinatnim osa i pravom linijom.

6.4 Teorija potrošačke potražnje

U teoriji potrošnje pretpostavlja se da potrošač uvijek nastoji maksimizirati svoju korisnost i jedino ograničenje za njega je ograničeni prihod I koji može potrošiti na kupovinu skupa dobara. Općenito, problem izbora potrošača (problem racionalnog ponašanja potrošača na tržištu) je formuliran na sljedeći način: pronaći skup potrošača , koji maksimizira svoju funkciju korisnosti za dato ograničenje budžeta. Matematički model ovog problema:

U slučaju seta od dva proizvoda:

Geometrijski, rješenje ovog problema je dodirna tačka između granice budžetskog skupa G i linije indiferencije.

Rješenje ovog problema svodi se na rješavanje sistema jednačina:

(1)

Rješenje ovog sistema je rješenje problema izbora potrošača.

Rješenje problema potrošačkog izbora naziva se tačka potražnje. Ova tačka potražnje zavisi od cena i prihoda I. tj. tačka potražnje je funkcija potražnje. Zauzvrat, funkcija potražnje je skup od n funkcija, od kojih svaka ovisi o argumentu:

Ove funkcije se nazivaju funkcije potražnje za odgovarajućom robom.

Primjer 54. Za skup od dva dobra na tržištu, poznate cijene za njih i prihod I, pronaći funkcije potražnje ako funkcija korisnosti ima oblik .

Rješenje. Hajde da razlikujemo funkciju korisnosti:

.

Zamenite dobijene izraze u (1) i dobijete sistem jednačina:

U tom slučaju trošak za svaki proizvod iznosit će polovicu prihoda potrošača, a iznos kupljenog proizvoda jednak je iznosu potrošenom na njega, podijeljenom s cijenom proizvoda.

Primjer 55. Neka funkcija korisnosti za prvo dobro, drugo,

cijena prvog proizvoda, cijena drugog. Prihodi . Koliko potrošač treba da kupi da bi maksimizirao korisnost?

Rješenje. Nađimo derivate funkcija korisnosti, zamijenimo ih u sistem (1) i riješimo ga:

Ovaj skup roba je optimalan za potrošača u smislu maksimiziranja korisnosti.

Test treba izvršiti u skladu sa opcijom odabranom posljednjom cifrom broja matične knjige u posebnoj bilježnici. Svaki problem treba da sadrži uslov, detaljno rješenje i zaključak.

1. Uvod u račun

Zadatak 1. Pronađite domen funkcije.

5.

Problem 2. Pronađite granice funkcija.

.

Zadatak 3. Pronađite prijelomne točke funkcije i odredite njihov tip.

1. 2. 3.

Poglavlje 2. Diferencijalni račun funkcije jedne varijable

Zadatak 4. Pronađite izvode ovih funkcija.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - arcsin x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e 5 x - 1) 6; c) y =; d) y =; e) y = x 8 ++ + 5; f) y = 3 x - arcsin x.

5.a) y = 2x 3 - + e x; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sintg;

d) y = 3x 4 - - 9+ 9; e) y =;

f) y = x 2 + arcsin x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4x 4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x 2 - x; f) y = e sin 3 x + 2.

Zadatak 5. Istražite funkciju i izgradite njen graf.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9.a) b) c).

10. a) b) v) .

Zadatak 6. Odrediti najveću i najmanju vrijednost funkcije na datom segmentu.

1. .

3. .

6. .

8. .

9. .

10. .

Poglavlje 3. Integralni račun

Zadatak 7. Naći neodređene integrale.

1.a) b);

2.a) b) c) d).

4. G)

5.a) ; b); v) ; G).

6.a) ; b); v); G)

7.a) ; b) ; v) ; G)

8.a) ; b); v) ; G) .

9.a) ; b) c); G).

10.a) b) v) ; G) .

Zadatak 8. Izračunati određene integrale.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Zadatak 9. Naći nepravilne integrale ili dokazati da divergiraju.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Zadatak 10. Nađite površinu površine ograničene krivuljama

1. .2. .

5. 6.

7. , .8..

10. , .

Poglavlje 4. Diferencijalni račun funkcije više varijabli.

Zadatak 11. Pronađite domen funkcije (prikažite na crtežu).

Zadatak 12. Istražiti kontinuitet funkcije za

Zadatak 13. Naći derivaciju implicitno definirane funkcije.

Zadatak 14. Približno izračunajte

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

Zadatak 15. Istražiti funkciju za ekstreme.

7. .

8. .

9. .

10. .

Zadatak 16. Odrediti najveću i najmanju vrijednost funkcije u datom zatvorenom području.

1.u pravougaoniku

2.

3.u pravougaoniku

4.u području ograničenom parabolom

I apscisa.

5.kvadrat

6.u trokutu omeđenom koordinatnim osa i pravom linijom

7.u trokutu omeđenom koordinatnim osa i pravom linijom

8. u trokutu omeđenom koordinatnim osa i pravom linijom

9.u području ograničenom parabolom

I apscisa.

10.u području ograničenom parabolom

I apscisa.

Glavni

1. M.S. Crassus, B.P. Chuprynov. Osnove matematike i njena primena u ekonomskom obrazovanju: Udžbenik. - 4. izd., Isp. - M.: Delo, 2003.

2. M.S. Crassus, B.P. Chuprynov. Matematika za ekonomske specijalnosti: Udžbenik. - 4. izd., Isp. - M.: Delo, 2003.

3. M.S. Crassus, B.P. Chuprynov. Matematika za dodiplomski studij ekonomije. Udžbenik. - 4. izd., Isp. - M.: Delo, 2005.

4. Viša matematika za ekonomiste. Udžbenik za univerzitete / N.Sh. Kremer, B.A. Putko, I.M. Trišin, M.N. Friedman; Ed. prof. N.Sh. Kremer, - 2. izd., revidirano. i dodati. - M: JEDINSTVO, 2003.

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman MN Viša matematika za ekonomske specijalnosti. Udžbenik i radionica (I i II dio) / Ed. prof. N.Sh. Kremer, - 2. izd., revidirano. i dodati. - M: Visoko obrazovanje, 2007. - 893 str. - (Osnove nauka)

6. Danko P.E., Popov A.G., Kozhevnikova T.Ya. Viša matematika u vježbama i problemima. M. gimnazija. 1999.

Dodatno

1. I.I. Bavrin, V.L. Mornari. Viša matematika. "Humanitarno-izdavački centar Vlados", 2002.

2. I.A. Zaitsev. Viša matematika. "Srednja škola", 1998.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, I.G. Shandra. Matematika u ekonomiji /u dva dijela/. M. Finansije i statistika. 1999.

za studente medicinski, pedijatrijski, stomatološki

i fakultete preventivne medicine

na laboratorijske radove

"Osnovni koncepti matematičke analize"

1. Naučno-metodološko utemeljenje teme:

Derivatni i diferencijalni koncepti su jedan od osnovnih pojmova matematičke analize. Izračunavanje izvoda je neophodno pri rješavanju mnogih zadataka iz fizike i matematike (nalaženje brzine, ubrzanja, pritiska itd.). Važnost koncepta derivacije, posebno, određena je činjenicom da derivacija funkcije karakterizira brzinu promjene ove funkcije kada se promijeni njen argument.

Upotreba diferencijala omogućava izvođenje približnih proračuna, kao i procjenu grešaka.

Metode pronalaženja izvoda i diferencijala funkcija i njihova primjena predstavljaju glavni problem diferencijalnog računa. Potreba za konceptom derivacije javlja se u vezi sa formulisanjem problema izračunavanja brzine kretanja i nalaženja ugla tangente na krivulju. Moguć je i inverzni problem: odredite pređenu udaljenost prema brzini i pronađite odgovarajuću funkciju tangentom nagiba tangente. Ovaj inverzni problem vodi do koncepta neodređenog integrala.

Koncept određenog integrala koristi se u brojnim praktičnim problemima, posebno u problemima izračunavanja površina ravnih figura, izračunavanja rada promjenjive sile i pronalaženja prosječne vrijednosti funkcije.

U matematičkom opisu različitih fizičkih, hemijskih, bioloških procesa i pojava često se koriste jednačine koje sadrže ne samo proučavane veličine, već i njihove derivate različitih redova ovih veličina. Na primjer, prema najjednostavnijoj verziji zakona umnožavanja bakterija, stopa reprodukcije je proporcionalna broju bakterija u datom trenutku. Ako je ova veličina označena sa N (t), onda je u skladu sa fizičkim značenjem derivata brzina razmnožavanja bakterija derivat N (t), a na osnovu navedenog zakona možemo napisati omjer N "(t) = k ∙ N, gdje je k> 0 - koeficijent proporcionalnosti Rezultirajuća jednačina nije algebarska, jer sadrži ne samo nepoznatu funkciju N (t), već i njen izvod prvog reda.

2. Kratka teorija:

1. Problemi koji vode do koncepta derivata

1. Problem nalaženja brzine v materijalne tačke... Neka materijalna tačka izvrši pravolinijsko kretanje. U trenutku t 1 tačka je na poziciji M 1. U trenutku t 2 trudna M 2 . Označimo interval M 1 , M 2 preko ΔS; t 2 - t 1 = Δt... Vrijednost se naziva prosječna brzina kretanja. Da biste pronašli trenutnu brzinu tačke na poziciji M 1 neophodno Δt teže nuli. Matematički, to znači da

, (1)

Dakle, da bi se pronašla trenutna brzina materijalne tačke, potrebno je izračunati granicu omjera prirasta funkcije ΔS na prirast argumenta Δt pod uslovom da Δt → 0.

2. Problem nalaženja ugla nagiba tangente na graf funkcije.

Slika 1

Razmotrimo graf neke funkcije y = f (x). Koliki je ugao nagiba
tangenta u tački M 1 ? U tački M 1 nacrtati tangentu na graf funkcije. Odaberite proizvoljnu tačku na grafikonu M 2 i nacrtajte sekantu. Ona je nagnuta prema osi OH pod uglom α 1 ... Razmislite ΔM 1 M 2 O:

, (2)

Ako tačka M 1 popravi i pokaži M 2 približiti se M 1 , zatim sekansa M 1 M 2 će ići na tangentu na graf funkcije u tački M 1 a možete napisati:

, (3)

Stoga je potrebno izračunati granicu omjera prirasta funkcije i prirasta argumenta ako prirast argumenta teži nuli.

Granica omjera prirasta Δy funkcije y = f (x) i prirasta argumenta Δx u datoj tački x 0 kako Δx teži nuli, naziva se derivacija funkcije u datoj tački.

Derivativna notacija: y ", f" (x), ... Po definiciji

, (4)

gdje je Δx = x 2 -x 1 prirast argumenta (razlika između dvije sljedeće dovoljno bliske vrijednosti argumenta), Δy = y 2 -y 1 je prirast funkcije (razlika između vrijednosti ​​funkcije koja odgovara ovim vrijednostima argumenta).

Pronalaženje derivacije date funkcije naziva se njenom diferencijaciju... Diferencijacija glavnih elementarnih funkcija vrši se prema gotovim formulama (vidi tabelu), kao i korištenjem pravila:

Derivat algebarskog zbira funkcije jednaka zbroju derivacija ovih funkcija:

(u+ υ )"= u" + υ "

2. Derivat proizvoda dvije funkcije jednak je zbiru proizvoda druge funkcije izvodom prve i prve funkcije izvodom druge:

(u ∙υ ) "= u"υ + uυ "

3. Derivat količnika od dvije funkcije jednak je razlomku, čiji je brojnik razlika između proizvoda nazivnika derivacijom brojnika i brojnika derivacijom nazivnika, a nazivnik je kvadrat nazivnika:

Fizičko značenje izvedenice. Poređenje (4) i (1) implicira da je trenutna brzina pravolinijskog kretanja materijalne tačke jednaka derivaciji zavisnosti njene koordinate od vremena.

Opšte značenje derivacije funkcije je da karakteriše brzina (brzina) promjene funkcije za datu promjenu argumenta. Brzina fizičkih, hemijskih i drugih procesa, na primer, brzina hlađenja tela, brzina hemijske reakcije, brzina razmnožavanja bakterija itd., takođe se izražava pomoću derivata.

Geometrijsko značenje izvedenice. Veličina tangente ugla nagiba tangente povučene na graf funkcije naziva se u matematici nagib tangente.

Nagib tangente na graf diferencijabilne funkcije u nekoj tački je numerički jednak derivaciji funkcije u ovoj tački.

Ova izjava se zove geometrijsko značenje izvedenice.

Sadržaj članka

MATEMATIČKA ANALIZA, grana matematike koja pruža metode za kvantitativno proučavanje različitih procesa promjena; bavi se proučavanjem brzine promjene (diferencijalni račun) i određivanjem dužina krivih, površina i volumena figura ograničenih zakrivljenim konturama i površinama (integralni račun). Za probleme matematičke analize karakteristično je da je njihovo rješavanje povezano s pojmom granice.

Matematičku analizu pokrenuo je 1665. I. Newton i (oko 1675.) nezavisno G. Leibniz, iako su važne pripremne radove izvršili I. Kepler (1571–1630), F. Cavalieri (1598–1647), P. Ferma (1601–1665), J. Wallis (1616-1703) i I. Barrow (1630-1677).

Da bi prezentacija bila življa, pribjegavat ćemo jeziku grafikona. Stoga bi čitatelju moglo biti od pomoći da prije čitanja ovog članka pogleda članak ANALITIČKA GEOMETRIJA.

DIFERENCIJALNI RAČUN

Tangente.

Na sl. 1 prikazuje fragment krive y = 2x – x 2, zaključen između x= –1 i x= 3. Dovoljno mali segmenti ove krive izgledaju pravo. Drugim riječima, ako R Ako je proizvoljna tačka ove krive, onda postoji neka prava linija koja prolazi kroz ovu tačku i predstavlja aproksimaciju krive u malom susjedstvu tačke R, i što je susjedstvo manje, to je bolja aproksimacija. Takva prava linija naziva se tangenta na krivu u tački R... Glavni zadatak diferencijalnog računa je da se izgradi opći metod koji vam omogućava da pronađete smjer tangente u bilo kojoj tački na krivulji gdje tangenta postoji. Nije teško zamisliti krivinu sa oštrim prekidom (slika 2). Ako R- vrh takvog prekida, onda možete izgraditi približnu ravnu liniju PT 1 - desno od tačke R i još jedna aproksimirajuća linija RT 2 - lijevo od tačke R... Ali ne postoji jedna prava linija koja prolazi kroz tačku R, koji se jednako dobro približio krivulji u blizini tačke P i desno i lijevo, dakle tangenta u tački P ne postoji.

Na sl. 1 tangenta OD provučen kroz ishodište O= (0,0). Nagib ove linije je 2, tj. kada se apscisa promijeni za 1, ordinata se povećava za 2. Ako x i y- koordinate proizvoljne tačke na OD, zatim, udaljavajući se od O na daljinu X jedinice na desno, mi se udaljavamo O na 2 y jedinice gore. dakle, y/x= 2, ili y = 2x... Ovo je tangentna jednadžba OD do krivine y = 2x – x 2 u tački O.

Sada je potrebno objasniti zašto iz skupa pravih koje prolaze kroz tačku O, izabrana je prava linija OD... Koja je razlika između prave linije sa nagibom od 2 i drugih pravih linija? Postoji jedan jednostavan odgovor i teško nam je odoljeti iskušenju da se poslužimo analogijom tangente na kružnicu: tangenta OD ima samo jednu zajedničku tačku sa krivom, dok svaka druga ne-vertikalna prava linija koja prolazi kroz tačku O, dva puta siječe krivu. Ovo se može provjeriti na sljedeći način.

Od izraza y = 2x – x 2 se može dobiti oduzimanjem X 2 of y = 2x(jednadžbe prave linije OD), zatim vrijednosti y manje je znanja za graf y za pravu liniju u svim tačkama, osim u tački x= 0. Dakle, graf je svuda, osim tačke O nalazi ispod OD, a ova linija i graf imaju samo jednu zajedničku tačku. Štaviše, ako y = mx- jednadžba neke druge prave linije koja prolazi kroz tačku O, tada sigurno postoje dvije točke sjecišta. stvarno, mx = 2x – x 2 ne samo za x= 0, ali i za x = 2 – m... I to samo kada m= 2 obje presečne tačke se poklapaju. Na sl. 3 pokazuje slučaj kada m manje od 2, dakle desno od O postoji druga raskrsnica.

Šta OD- jedina nevertikalna prava linija koja prolazi kroz tačku O i imaju samo jednu zajedničku tačku sa grafom, a ne njegovo najvažnije svojstvo. Zaista, ako se okrenemo drugim grafovima, uskoro će postati jasno da svojstvo tangente koje smo zabilježili u općem slučaju nije ispunjeno. Na primjer, sa sl. 4 može se vidjeti da je u blizini tačke (1,1) grafik krive y = x 3 je dobro aproksimirana ravnom linijom RT, koji, međutim, ima više od jedne zajedničke tačke s njim. Međutim, željeli bismo razmotriti RT tangenta na ovaj graf u tački R... Stoga je potrebno pronaći neki drugi način da istaknemo tangentu od onog koji nam je tako dobro poslužio u prvom primjeru.

Pretpostavimo da kroz tačku O i proizvoljna tačka Q = (h,k) na grafu krive y = 2x – x 2 (Sl. 5) nacrtana je prava linija (koja se zove sekansa). Zamjena vrijednosti u jednadžbu krive x = h i y = k, shvatili smo k = 2h – h 2, dakle, nagib sekante je

Sa vrlo malim h značenje m blizu 2. Štaviše, biranje h dovoljno blizu 0 što možemo m proizvoljno blizu 2. Možemo to reći m"Teži do granice" jednako 2 kada h teži nuli, ili bilo kojoj granici m jednako 2 for h teži nuli. Ovo je simbolično zapisano na sljedeći način:

Zatim tangenta na graf u tački O definisan kao prava linija koja prolazi kroz tačku O, sa nagibom jednakim ovoj granici. Ova definicija tangente je općenito primjenjiva.

Pokažimo prednosti ovog pristupa još jednim primjerom: pronađite nagib tangente na graf krivulje y = 2x – x 2 u proizvoljnoj tački P = (x,y), ne ograničavajući se na najjednostavniji slučaj kada P = (0,0).

Neka Q = (x + h, y + k) - druga tačka na grafikonu, koja se nalazi na udaljenosti h desno od R(sl. 6). Potrebno je pronaći nagib k/h secant PQ... Dot Q je na udaljenosti

iznad ose X.

Proširujući zagrade, nalazimo:

Oduzimanje od ove jednačine y = 2x – x 2, nalazimo vertikalnu udaljenost od tačke R do tačke Q:

Dakle, nagib m secant PQ je jednako sa

Sad to h teži nuli, m teži 2 - 2 x; zadnju vrijednost ćemo uzeti kao nagib tangente PT... (Isti rezultat će se dobiti ako h uzima negativne vrijednosti, što odgovara izboru tačke Q na lijevoj strani P.) Imajte na umu da za x= 0 rezultat je isti kao i prethodni.

Izraz 2 - 2 x naziva se derivat od 2 x – x 2. U starim danima, derivat se nazivao i "diferencijalni odnos" i "diferencijalni koeficijent". Ako izraz 2 x – x 2 odrediti f(x), tj.

onda se derivacija može označiti

Da biste saznali nagib tangente na graf funkcije y = f(x) u nekom trenutku, mora biti zamijenjen fў ( x) vrijednost koja odgovara ovoj tački X... Dakle, nagib f u (0) = 2 for X = 0, f u (0) = 0 for X= 1 i f u (2) = –2 for X = 2.

Izvod je također označen atў , dy/dx, D x y i Du.

Činjenica da je kriva y = 2x – x 2 blizu date tačke se praktično ne razlikuje od svoje tangente u ovoj tački, što nam omogućava da govorimo o nagibu tangente kao o "nagibu krive" u tački tangente. Dakle, možemo tvrditi da nagib krive koja se razmatra ima u tački (0,0) nagib 2. Takođe se može reći da na x= 0 stopa promjene y relativno x je 2. U tački (2,0), nagib tangente (i krive) je –2. (Znak minus znači da kao x varijabla y opada.) U tački (1,1) tangenta je horizontalna. Kažemo krivulja y = 2x – x 2 ima stacionarnu vrijednost u ovoj tački.

Highs and Lows.

Upravo smo pokazali da je kriva f(x) = 2x – x 2 miruje u tački (1,1). Jer fў ( x) = 2 – 2x = 2(1 – x), jasno je da za x manje od 1, fў ( x) je pozitivan, i stoga y povećava; at x, veliki 1, fў ( x) je negativan, i stoga y smanjuje se. Dakle, u blizini tačke (1,1) prikazane na Sl. 6 pismo M, značenje at raste do tačke M, nepomičan u tački M i opada nakon tačke M... Ova tačka se naziva "maksimum" jer je vrijednost at u ovom trenutku premašuje bilo koju od njegovih vrijednosti u dovoljno malom susjedstvu. Slično, "minimum" je definisan kao tačka u čijoj blizini se vrednuju sve vrednosti y nadmašiti broj at u ovom trenutku. Takođe se može desiti da iako derivat od f(x) u nekom trenutku i nestaje, njegov predznak se ne mijenja u blizini ove tačke. Takva tačka, koja nije ni maksimum ni minimum, naziva se tačka pregiba.

Kao primjer, pronađimo stacionarnu tačku krive

Izvod ove funkcije je

i nestaje na x = 0, X= 1 i X= –1; one. u tačkama (0,0), (1, –2/15) i (–1, 2/15). Ako X onda nešto manje od -1 fў ( x) je negativan; ako X onda nešto više od -1 fў ( x) je pozitivan. Dakle, tačka (–1, 2/15) je maksimum. Slično, može se pokazati da je tačka (1, –2/15) minimum. Ali derivat fў ( x) je negativan i prije i poslije točke (0,0). Prema tome, (0,0) je tačka pregiba.

Provedeno istraživanje oblika krivulje, kao i činjenice da kriva siječe os X at f(x) = 0 (tj. za X= 0 ili) omogućava vam da predstavite njegov graf približno kao što je prikazano na Sl. 7.

Općenito, ako izuzmemo neobične slučajeve (krive koje sadrže segmente pravih linija ili beskonačan broj krivina), postoje četiri opcije za relativni položaj krivulje i tangente u blizini tangentne točke R. (Cm... pirinač. 8 gdje tangenta ima pozitivan nagib.)

1) Sa obe strane tačke R kriva leži iznad tangente (slika 8, a). U ovom slučaju kažu da je kriva u tački R konveksno prema dolje ili konkavno.

2) Sa obe strane tačke R kriva se nalazi ispod tangente (slika 8, b). U ovom slučaju se kaže da je kriva konveksna prema gore ili jednostavno konveksna.

3) i 4) Kriva se nalazi iznad tangente na jednoj strani tačke R a ispod - na drugoj. U ovom slučaju R- tačka pregiba.

Poređenje vrijednosti fў ( x) sa obe strane R sa svojom vrijednošću u tački R, moguće je odrediti koji od ova četiri slučaja treba obraditi u određenom problemu.

Prijave.

Sve navedeno nalazi značajnu primjenu u raznim oblastima. Na primjer, ako se tijelo baci okomito prema gore početnom brzinom od 200 stopa u sekundi, tada će visina s na kojoj će se nalaziti t sekundi u odnosu na početnu tačku će biti

Postupajući na isti način kao u primjerima koje smo razmatrali, nalazimo

ova vrijednost nestaje na c. Derivat fў ( x) je pozitivna do vrijednosti c i negativna nakon ovog vremena. dakle, s raste na, zatim postaje stacionarno, a zatim opada. Ovo je opći opis kretanja tijela bačenog prema gore. Iz njega znamo kada tijelo dostigne svoju najvišu tačku. Dalje, zamena t= 25/4 in f(t), dobijamo 625 stopa, maksimalno podizanje. U ovom zadatku fў ( t) ima fizičko značenje. Ovaj izvod pokazuje brzinu kojom se tijelo kreće u datom trenutku t.

Razmotrimo sada drugu vrstu aplikacije (slika 9). Potrebno je napraviti kutiju s kvadratnim dnom od kartonskog lista površine 75 cm 2. Koliko ova kutija mora biti velika da bi imala maksimalan volumen? Ako X- strana osnove kutije i h- njegova visina, tada je zapremina kutije V = x 2 h, a površina je 75 = x 2 + 4xh... Transformacijom jednačine dobijamo:

Izvedeno iz V ispada da je jednaka

i nestaje na X= 5. Onda

i V= 125/2. Funkcijski graf V = (75x – x 3) / 4 je prikazano na sl. 10 (negativne vrijednosti X izostavljen jer nema fizičkog značenja u ovom problemu).

Derivati.

Važan zadatak diferencijalnog računa je stvaranje metoda koje vam omogućavaju da brzo i jednostavno pronađete derivate. Na primjer, to je lako izračunati

(Izvod konstante je, naravno, nula.) Nije teško izvesti opšte pravilo:

gdje n- bilo koji cijeli broj ili razlomak. Na primjer,

(Ovaj primjer pokazuje koliko su korisni razlomci eksponenta.)

Evo nekih od najvažnijih formula:

Postoje i sljedeća pravila: 1) ako svaka od dvije funkcije g(x) i f(x) ima izvode, onda je izvod njihovog zbira jednak zbiru izvoda ovih funkcija, a izvod razlike je jednak razlici izvoda, tj.

2) derivacija proizvoda dvije funkcije izračunava se po formuli:

3) derivacija odnosa dviju funkcija ima oblik

4) izvod funkcije pomnozen konstantom jednak je konstanti pomnozenoj sa izvodom ove funkcije, tj.

Često se dešava da se vrijednosti funkcije moraju izračunati u fazama. Na primjer, za izračunavanje grijeha x 2, prvo moramo pronaći u = x 2, a zatim izračunajte sinus broja u... Izvod takvih složenih funkcija nalazimo koristeći takozvano "pravilo lanca":

U našem primjeru f(u) = grijeh u, fў ( u) = cos u, dakle,

Ova i druga slična pravila omogućavaju da se odmah zapišu derivati ​​mnogih funkcija.

Linearne aproksimacije.

Činjenica da, poznavajući derivaciju, u mnogim slučajevima možemo zamijeniti graf funkcije blizu neke tačke njene tangente u ovoj tački je od velike važnosti, jer je s pravim linijama lakše raditi.

Ova ideja nalazi direktnu primjenu u izračunavanju približnih vrijednosti funkcija. Na primjer, prilično je teško izračunati vrijednost kada x= 1.033. Ali možete iskoristiti činjenicu da je broj 1,033 blizu 1 i to. Zatvori x= 1 možemo zamijeniti graf tangentne krive bez ozbiljne greške. Nagib takve tangente jednak je vrijednosti derivacije ( x 1/3) u = (1/3) x–2/3 pri x = 1, tj 1/3. Budući da tačka (1,1) leži na krivulji i da je nagib tangente na krivu u ovoj tački 1/3, jednačina tangente ima oblik

Na ovoj liniji u X = 1,033

Rezultirajuća vrijednost y treba da bude veoma blizu pravoj vrednosti y; i, zaista, samo je 0,00012 više od pravog. U matematičkoj analizi razvijene su metode za poboljšanje tačnosti ove vrste linearne aproksimacije. Ove metode osiguravaju pouzdanost naših približnih proračuna.

Upravo opisana procedura sugerira korisnu notaciju. Neka P- tačka koja odgovara na grafu funkcije f varijabla X i neka funkcija f(x) je diferencibilan. Zamijenite grafik krive blizu tačke R tangenta na nju, nacrtana u ovoj tački. Ako X promijeniti po iznosu h, tada će se ordinata tangente promijeniti za vrijednost h H f ў ( x). Ako h je vrlo mala, onda je potonja vrijednost dobra aproksimacija pravoj promjeni ordinate y grafika. Ako umjesto h napisaćemo simbol dx(ovo nije proizvod!), već promjena ordinate y označiti dy, onda dobijamo dy = f ў ( x)dx, ili dy/dx = f ў ( x) (cm... pirinač. jedanaest). Stoga, umjesto Dy ili f ў ( x) simbol se često koristi za označavanje izvedenice dy/dx... Pogodnost ove notacije zavisi uglavnom od eksplicitnog izgleda pravila lanca (diferencijacija složene funkcije); u novoj notaciji ova formula izgleda ovako:

gde se podrazumeva da at zavisi od u, a u zauzvrat zavisi od X.

Veličina dy zove diferencijal at; u stvari zavisi od dva varijable, i to: from X i inkrementi dx... Kada se inkrement dx veoma mala, magnitude dy je blizu odgovarajuće promjene vrijednosti y... Ali pretpostaviti da je prirast dx malo, nema potrebe.

Derivativna funkcija y = f(x) označili smo f ў ( x) ili dy/dx... Često je moguće uzeti derivat izvedenice. Rezultat se naziva drugi derivat od f (x) i označeno f ўў ( x) ili d 2 y/dx 2. Na primjer, ako f(x) = x 3 – 3x 2, onda f ў ( x) = 3x 2 – 6x i f ўў ( x) = 6x- 6. Slične oznake se koriste za derivate višeg reda. Međutim, da bi se izbjegao veliki broj crtica (jednak redoslijedu izvedenice), četvrti izvod (na primjer) može se napisati kao f (4) (x), i derivat n-ti red kao f (n) (x).

Može se pokazati da je kriva u nekoj tački konveksna prema dolje ako je drugi izvod pozitivan, a konveksna prema gore ako je drugi izvod negativan.

Ako funkcija ima drugi izvod, onda je promjena u količini y odgovara inkrementu dx varijabla X, može se približno izračunati po formuli

Ova aproksimacija je općenito bolja od one koju daje diferencijal fў ( x)dx... To odgovara zamjeni dijela krive parabolom, a ne pravom linijom.

Ako je funkcija f(x) onda postoje derivati ​​višeg reda

Ostatak je

gdje x- neki broj između x i x + dx... Gornji rezultat naziva se Taylor formula ostatka. Ako f(x) ima derivate svih redova, tada obično R n® 0 for n ® Ґ .

INTEGRALNI RAČUN

Kvadrati.

Prilikom proučavanja područja krivolinijskih ravnih figura, otkrivaju se novi aspekti matematičke analize. Čak su i stari Grci pokušavali riješiti takve probleme, za koje je određivanje, na primjer, površine kruga bio jedan od najtežih zadataka. Veliki uspjeh u rješavanju ovog problema postigao je Arhimed, koji je uspio pronaći i površinu paraboličnog segmenta (slika 12). Uz pomoć vrlo kompliciranog zaključivanja, Arhimed je dokazao da je površina paraboličnog segmenta 2/3 površine opisanog pravougaonika i stoga je u ovom slučaju jednaka (2/3) (16) = 32/3. Kao što ćemo kasnije vidjeti, ovaj rezultat se lako može dobiti metodama matematičke analize.

Prethodnici Newtona i Leibniza, uglavnom Kepler i Cavalieri, riješili su problem izračunavanja površina krivolinijskih figura metodom koja se teško može nazvati logičnom, ali koja se pokazala izuzetno plodnom. Kada je Wallis 1655. spojio metode Keplera i Cavalierija sa Descartesovim metodama (analitička geometrija) i koristio novorođenu algebru, pozornica za pojavu Newtona bila je potpuno pripremljena.

Wallis je podijelio lik, čiju je površinu trebalo izračunati, na vrlo uske trake, od kojih se svaka približno smatrala pravokutnikom. Zatim je sabrao površine aproksimirajućih pravougaonika i, u najjednostavnijim slučajevima, dobio vrijednost kojoj teži zbir površina pravokutnika kada broj pruga teži beskonačnosti. Na sl. 13 prikazuje pravokutnike koji odgovaraju nekoj podjeli na trake površine ispod krive y = x 2 .

Glavna teorema.

Veliko otkriće Newtona i Leibniza omogućilo je da se isključi naporan proces prelaska na granicu zbira površina. To je učinjeno zahvaljujući novom pogledu na koncept kvadrata. Poenta je u tome da moramo zamisliti površinu ispod krivulje koju generira ordinata koja se kreće s lijeva na desno i pitati koliko se brzo mijenja područje koje su ordinate izbrisale. Ključ za odgovor na ovo pitanje dobit ćemo ako razmotrimo dva posebna slučaja u kojima je područje unaprijed poznato.

Počnimo s površinom ispod grafa linearne funkcije y = 1 + x jer se u ovom slučaju površina može izračunati pomoću elementarne geometrije.

Neka A(x) Da li je dio ravni zatvoren između prave y = 1 + x i segment OQ(sl. 14). Tokom vožnje QP desno područje A(x) povećava. Koliko brzo? Nije teško odgovoriti na ovo pitanje, jer znamo da je površina trapeza jednaka umnošku njegove visine poluzbirom njegovih baza. dakle,

Stopa promjene područja A(x) određena je njegovom derivacijom

Vidimo to Aў ( x) poklapa se sa ordinatom at bodova R... Je li ovo slučajnost? Pokušajmo provjeriti parabolu prikazanu na sl. 15. Kvadrat A (x) ispod parabole at = X 2 u rasponu od 0 do X je jednako sa A(x) = (1 / 3)(x)(x 2) = x 3/3. Brzina promjene ove površine određena je izrazom

koja se tačno poklapa sa ordinatom at pokretna tačka R.

Ako pretpostavimo da je ovo pravilo općenito ispunjeno na način da

je stopa promjene površine ispod grafika funkcije y = f(x), onda se ovo može koristiti za proračune i druga područja. Zapravo, omjer Aў ( x) = f(x) izražava temeljnu teoremu, koja bi se mogla formulirati na sljedeći način: derivacija ili brzina promjene površine kao funkcija X, jednako je vrijednosti funkcije f (x) u tački X.

Na primjer, da biste pronašli područje ispod grafa funkcije y = x 3 od 0 do X(Sl. 16), stavljamo

Mogući odgovor je:

budući da je derivat od X 4/4 je zaista jednako X 3. Štaviše, A(x) je jednako nuli za X= 0, kako bi trebalo biti ako A(x) je zaista područje.

Matematička analiza dokazuje da je još jedan odgovor osim gornjeg izraza za A(x), ne postoji. Pokažimo da je ova izjava uvjerljiva koristeći sljedeće heurističko (nerigorozno) rezonovanje. Pretpostavimo da postoji neko drugo rješenje V(x). Ako A(x) i V(x) "Pokreni" istovremeno od nulte vrijednosti na X= 0 i cijelo vrijeme se mijenjaju istom brzinom, a zatim njihove vrijednosti na br X ne može postati drugačiji. Moraju biti svuda isti; dakle, postoji samo jedno rešenje.

Kako se taj odnos može opravdati? Aў ( x) = f(x) Uglavnom? Na ovo pitanje se može odgovoriti samo proučavanjem stope promjene površine u funkciji od X Uglavnom. Neka m- najmanja vrijednost funkcije f (x) u rasponu od X prije ( x + h), a M- najveća vrijednost ove funkcije u istom intervalu. Zatim povećanje površine od koje se ide X Za ( x + h) mora biti zatvoren između površina dva pravougaonika (slika 17). Osnove oba pravougaonika su jednake h... Manji pravougaonik ima visinu m i područje mh, veći, respektivno, M i Mh... Na parceli površine naspram X(Sl. 18) može se vidjeti da kada se apscisa promijeni za h, vrijednost ordinate (tj. površine) uvećava se za iznos koji se nalazi između mh i Mh... Sekantni nagib u ovom grafu je između m i M... šta se dešava kada h teži nuli? Ako je graf funkcije y = f(x) je kontinuiran (tj. ne sadrži diskontinuitete), onda M, i m Nastojati f(x). Dakle, nagib Aў ( x) parcela površine u funkciji X je jednako sa f(x). Do takvog zaključka je trebalo doći.

Leibniz je predložio područje ispod krivulje y = f(x) od 0 do a oznaka

S rigoroznim pristupom, ovaj takozvani definitivni integral mora se definirati kao granica određenih suma na Wallisov način. S obzirom na gornji rezultat, jasno je da je ovaj integral izračunat pod uvjetom da možemo pronaći takvu funkciju A(x), koji nestaje na X= 0 i ima izvod Aў ( x) jednak f (x). Pronalaženje takve funkcije obično se naziva integracijom, iako bi bilo prikladnije ovu operaciju nazvati antidiferencijacijom, što znači da je ona, na neki način, inverzna diferencijaciji. U slučaju polinoma, integracija je jednostavna. Na primjer, ako

što je lako provjeriti diferenciranjem A(x).

Za izračunavanje površine A 1 ispod krive y = 1 + x + x 2/2, zatvoren između ordinata 0 i 1, jednostavno pišemo

i zamena X= 1, dobijamo A 1 = 1 + 1/2 + 1/6 = 5/3. Square A(x) od 0 do 2 je jednako A 2 = 2 + 4/2 + 8/6 = 16/3. Kao što se vidi sa sl. 19, površina između ordinata 1 i 2 je A 2 – A 1 = 11/3. Obično se piše kao određeni integral

Volume.

Slično razmišljanje čini iznenađujuće jednostavnim izračunavanje volumena tijela okretanja. Pokažimo to na primjeru izračunavanja zapremine lopte, još jednog klasičnog problema koji su stari Grci, koristeći im poznate metode, s velikom mukom uspjeli riješiti.

Zarotirajte dio ravnine unutar četvrtine kruga radijusa r, pod uglom od 360° oko ose X... Kao rezultat, dobijamo hemisferu (slika 20), čiji volumen označavamo V(x). Potrebno je odrediti stopu po kojoj se V(x) sa povećanjem x... Idemo dalje od X To X + h, lako je provjeriti da je prirast volumena manji od volumena str(r 2 – x 2)h polumjer i visina kružnog cilindra h, i više od volumena str[r 2 – (x + h) 2 ]h radijus i visina cilindra h... Dakle, na grafu funkcije V(x) nagib sekansa je između str(r 2 – x 2) i str[r 2 – (x + h) 2]. Kada h teži nuli, nagib teži ka

At x = r dobijamo

za zapreminu hemisfere, pa prema tome 4 p r 3/3 za volumen cijele lopte.

Slična metoda vam omogućava da pronađete dužine krivulja i površine zakrivljenih površina. Na primjer, ako a(x) - dužina luka PR na sl. 21, onda je naš zadatak da izračunamo aў( x). Na heurističkoj razini koristimo trik koji nam omogućava da ne pribjegnemo uobičajenom prijelasku do granice, što je neophodno za rigorozni dokaz rezultata. Pretpostavimo da je stopa promjene funkcije a(x) u tački R je isto kao što bi bilo da je krivulja zamijenjena njenom tangentom PT u tački P... Ali sa sl. 21 se može direktno vidjeti kada se korača h desno ili lijevo od tačke X zajedno RT značenje a(x) mijenja u

Dakle, brzina promjene funkcije a(x) je

Da biste pronašli samu funkciju a(x), potrebno je samo integrirati izraz na desnoj strani jednakosti. Ispostavilo se da je većinu funkcija teško integrirati. Stoga razvoj metoda integralnog računanja čini veliki dio matematičke analize.

Antiderivati.

Svaka funkcija čiji je izvod jednak datoj funkciji f(x), naziva se antiderivativ (ili primitivan) za f(x). Na primjer, X 3/3 je antiderivat za funkciju X 2, pošto ( x 3/3) u = x 2. Naravno X 3/3 nije jedini antiderivat funkcije X 2 od x 3 /3 + C je također derivat za X 2 za bilo koju konstantu WITH... Međutim, u nastavku ćemo se složiti da izostavimo takve aditivne konstante. Uglavnom

gdje n je pozitivan cijeli broj, budući da ( x n + 1/(n+ 1)) u = x n... Relacija (1) vrijedi u još generalnijem smislu ako n zamijeniti bilo kojim racionalnim brojem k osim -1.

Proizvoljna antiderivativna funkcija za datu funkciju f(x) se obično naziva neodređenim integralom f(x) i označimo ga kao

Na primjer, budući da (grijeh x) u = cos x, formula je važeća

U mnogim slučajevima, kada postoji formula za neodređeni integral date funkcije, ona se može naći u brojnim široko objavljenim tabelama neodređenih integrala. Integrali elementarnih funkcija su tabelarni (to uključuje stepene, logaritme, eksponencijalnu funkciju, trigonometrijske funkcije, inverzne trigonometrijske funkcije, kao i njihove konačne kombinacije dobijene operacijama sabiranja, oduzimanja, množenja i dijeljenja). Koristeći tabelarne integrale, možete izračunati integrale složenijih funkcija. Postoji mnogo načina za izračunavanje neodređenih integrala; najčešći od njih je varijabilna supstitucija ili metoda zamjene. Sastoji se u tome da ako želimo zamijeniti u neodređenom integralu (2) x na nekoj diferencijabilnoj funkciji x = g(u), da se integral ne bi promijenio, neophodno je x zamijenjen sa gў ( u)du... Drugim riječima, jednakost

(zamjena 2 x = u, odakle 2 dx = du).

Evo još jedne metode integracije - metoda integracije po dijelovima. Zasnovan je na već poznatoj formuli

Integrisavši levu i desnu stranu, i vodeći računa o tome

Ova formula se zove formula za integraciju po dijelovima.

Primjer 2. Potrebno je pronaći. Pošto cos x= (grijeh x) u, možemo to napisati

Od (5), postavka u = x i v= grijeh x, dobijamo

I pošto (–cos x) u = sin x nalazimo da i

Treba naglasiti da smo se ograničili samo na vrlo kratak uvod u vrlo opsežnu temu, u kojoj su se nakupile brojne duhovite tehnike.

Funkcije dvije varijable.

Zbog krivine y = f(x) razmotrili smo dva zadatka.

1) Pronađite nagib tangente na krivu u datoj tački. Ovaj problem se rješava izračunavanjem vrijednosti derivata fў ( x) na navedenoj tački.

2) Pronađite površinu ispod krive iznad segmenta ose X omeđen vertikalnim linijama X = a i X = b... Ovaj problem se rješava izračunavanjem određenog integrala.

Svaki od ovih problema ima analogiju u slučaju površine z = f(x,y).

1) Pronađite ravan tangente na površinu u datoj tački.

2) Pronađite volumen ispod površine iznad dijela ravni hu omeđen krivom WITH, a sa strane - okomite na ravan xy prolazeći kroz tačke granične krivulje WITH (cm... pirinač. 22).

Sljedeći primjeri pokazuju kako se ovi zadaci ostvaruju.

Primjer 4. Pronađite tangentnu ravan na površinu

u tački (0,0,2).

Ravan je definisana ako su date dve prave koje se u njoj seku. Jedan od ovih redova ( l 1) ulazimo u avion xz (at= 0), drugi ( l 2) - u avionu yz (x = 0) (cm... pirinač. 23).

Prije svega, ako at= 0, onda z = f(x,0) = 2 – 2x – 3x 2. Derivat u odnosu na X označeno sa fў x(x,0) = –2 – 6x, at X= 0 ima vrijednost –2. Pravo l 1 dat jednačinama z = 2 – 2x, at= 0 - tangenta na WITH 1, linije presjeka površine s ravninom at= 0. Slično, ako X= 0, onda f(0,y) = 2 – y – y 2, i derivat u odnosu na at ima oblik

Jer fў y(0,0) = –1, kriva WITH 2 - linija presjeka površine sa ravninom yz- ima tangentu l 2 dat jednadžbama z = 2 – y, X= 0. Željena tangentna ravan sadrži obe prave l 1 i l 2 i zapisuje se jednadžbom

Ovo je jednadžba ravnine. Osim toga, dobijamo ravne linije l 1 i l 2, postavljanje, odnosno at= 0 i X = 0.

Činjenica da jednačina (7) zaista definira tangentnu ravan može se provjeriti na heurističkom nivou ako primijetimo da ova jednačina sadrži članove prvog reda uključene u jednačinu (6), a da se članovi drugog reda mogu predstaviti u oblik -. Pošto je ovaj izraz negativan za sve vrijednosti X i at, Osim toga X = at= 0, površina (6) leži svuda ispod ravni (7), osim tačke R= (0,0,0). Možemo reći da je površina (6) u tački konveksna prema gore R.

Primjer 5. Pronađite tangentnu ravan na površinu z = f(x,y) = x 2 – y 2 na početku 0.

Na površini at= 0 imamo: z = f(x,0) = x 2 i fў x(x,0) = 2x... Na WITH 1, linije raskrsnice, z = x 2. U tački O nagib je fў x(0,0) = 0. Na ravni X= 0 imamo: z = f(0,y) = –y 2 i fў y(0,y) = –2y... Na WITH 2, linije raskrsnice, z = –y 2. U tački O nagib krivine WITH 2 je jednako fў y(0,0) = 0. Pošto su tangente na WITH 1 i WITH 2 su sjekire X i at, tangentna ravan koja ih sadrži je ravan z = 0.

Međutim, u blizini ishodišta, naša površina nije na jednoj strani tangentne ravni. Zaista, kriva WITH 1 svuda, osim tačke 0, leži iznad tangentne ravni i krive WITH 2 - odnosno ispod njega. Površina siječe tangentnu ravan z= 0 u ravnim linijama at = X i at = –X... Kaže se da takva površina ima tačku sedla u početku (slika 24).

Parcijalni derivati.

U prethodnim primjerima koristili smo derivate iz f (x,y) na X i po at... Razmotrimo sada takve derivate općenito. Ako imamo funkciju od dvije varijable, npr. F(x,y) = x 2 – xy, tada možemo definirati u svakoj tački dva njegova "parcijalna izvoda", jedan diferenciranjem funkcije u odnosu na X i popravljanje at, drugi diferenciranjem u odnosu na at i popravljanje X... Prvi od ovih derivata se označava kao fў x(x,y) ili ¶ f/¶ x; drugo - kako f f ý y... Ako su oba mješovita derivata (od X i at, na at i X) su kontinuirani, onda ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x; u našem primjeru ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x = –1.

Parcijalni derivat fў x(x,y) označava brzinu promjene funkcije f u tački ( x,y) u pravcu povećanja X, a fў y(x,y) Brzina promjene funkcije f uzlazni pravac at... Stopa promjene funkcije f u tački ( X,at) u pravcu prave linije koja čini ugao q sa pozitivnim smjerom ose X, naziva se derivacija funkcije f prema; njegova vrijednost je kombinacija dva parcijalna izvoda funkcije f u tangentnoj ravni je skoro jednak (za male dx i dy) istinska promjena z na površini, ali izračunavanje diferencijala je obično lakše.

Formula koju smo već razmatrali iz metode promjene varijable, poznate kao izvod složene funkcije ili lančano pravilo, u jednodimenzionalnom slučaju kada at zavisi od X, a X zavisi od t, ima oblik:

Za funkcije dvije varijable, slična formula je:

Lako je generalizirati koncepte i oznake parcijalne diferencijacije na više dimenzije. Posebno, ako je površina implicitno data jednadžbom f(x,y,z) = 0, jednadžbi tangentne ravnine na površinu može se dati simetričniji oblik: jednačina tangentne ravnine u tački ( x (x 2/4)], onda se integriše preko X 0 prema 1. Konačan rezultat je 3/4.

Formula (10) se može tumačiti i kao tzv. dvostruki integral, tj. kao granica zbira volumena elementarnih "ćelija". Svaka takva ćelija ima bazu D x D y i visina jednaka visini površine iznad neke tačke pravougaone osnove ( cm... pirinač. 26). Može se pokazati da su obje tačke gledišta na formulu (10) ekvivalentne. Dvostruki integrali se koriste za pronalaženje centara gravitacije i brojnih momenata koji se nalaze u mehanici.

Rigoroznije obrazloženje matematičkog aparata.

Do sada smo predstavili koncepte i metode računa na intuitivnom nivou i bez oklijevanja pribjegavamo geometrijskim oblicima. Ostaje nam da ukratko razmotrimo rigoroznije metode koje su se pojavile u 19. i 20. veku.

Početkom 19. vijeka, kada je završila era juriša i nasrtaja u "stvaranju matematičke analize", u prvi plan izbijaju pitanja njene opravdanosti. U djelima Abela, Cauchyja i niza drugih istaknutih matematičara, pojmovi "granične", "kontinuirane funkcije", "konvergentnog niza" su precizno definirani. To je bilo neophodno kako bi se doveo logički poredak u osnovu matematičke analize kako bi ona postala pouzdan alat za istraživanje. Potreba za temeljnim opravdanjem postala je još očiglednija nakon što je Weierstrass 1872. otkrio svuda kontinuirane, ali nigdje diferencibilne funkcije (graf takvih funkcija ima prekid u svakoj tački). Ovaj rezultat je ostavio ogroman utisak na matematičare, jer je bio u suprotnosti sa njihovom geometrijskom intuicijom. Još upečatljiviji primjer nepouzdanosti geometrijske intuicije bila je kontinuirana kriva koju je konstruirao D. Peano, a koja u potpunosti ispunjava određeni kvadrat, tj. prolazeći kroz sve njegove tačke. Ova i druga otkrića dala su povoda za program "aritmetizacije" matematike, tj. čineći ga pouzdanijim potkrepljujući sve matematičke koncepte pomoću koncepta broja. Gotovo puritanska apstinencija od jasnoće u radovima o osnovama matematike imala je svoje istorijsko opravdanje.

Prema modernim kanonima logičke strogosti, nedopustivo je govoriti o površini ispod krivulje. y = f(x) i iznad segmenta ose X, čak f- kontinuirana funkcija, bez prethodnog definiranja tačnog značenja pojma "područje" i bez utvrđivanja da ovako određeno područje zaista postoji. Ovaj problem je 1854. godine uspješno riješio B. Riemann, koji je dao preciznu definiciju pojma određenog integrala. Od tada, ideja sumiranja iza pojma određenog integrala bila je predmet mnogih dubokih studija i generalizacija. Kao rezultat toga, danas je moguće dati značenje određenom integralu, čak i ako je integrand svuda diskontinuiran. Novi koncepti integracije, čijem stvaranju su A. Lebesgue (1875–1941) i drugi matematičari dali veliki doprinos, povećali su snagu i ljepotu moderne matematičke analize.

Teško da bi bilo prikladno ulaziti u detalje svih ovih i drugih koncepata. Ograničićemo se samo na davanje rigoroznih definicija granice i određenog integrala.

Na kraju, recimo da matematička analiza, kao izuzetno vrijedan alat u rukama naučnika i inženjera, i danas privlači pažnju matematičara kao izvor plodonosnih ideja. Istovremeno, čini se da savremeni razvoj ukazuje na to da je matematička analiza sve više apsorbovana od strane takvih dominantnih u 20. veku. grane matematike poput apstraktne algebre i topologije.

Apsolutno je nemoguće riješiti fizičke probleme ili primjere iz matematike bez poznavanja derivacije i metoda njenog izračunavanja. Derivat je jedan od najvažnijih koncepata u matematičkoj analizi. Odlučili smo posvetiti današnji članak ovoj temeljnoj temi. Šta je derivacija, koje je njeno fizičko i geometrijsko značenje, kako izračunati izvod funkcije? Sva ova pitanja mogu se spojiti u jedno: kako razumjeti derivat?

Geometrijsko i fizičko značenje izvedenice

Neka postoji funkcija f (x) dati u nekom intervalu (a, b) ... Tačke h i h0 pripadaju ovom intervalu. Kada se x promijeni, mijenja se i sama funkcija. Promjena argumenta - razlika između njegovih vrijednosti x-x0 ... Ova razlika je zapisana kao delta x i naziva se povećanje argumenta. Promjena ili povećanje funkcije je razlika u vrijednostima funkcije u dvije točke. Definicija izvedenice:

Derivat funkcije u tački je granica omjera prirasta funkcije u datoj tački i priraštaja argumenta kada potonji teži nuli.

Inače, može se napisati ovako:

Koja je poenta u pronalaženju takve granice? A evo šta:

derivacija funkcije u tački jednaka je tangenti ugla između ose OX i tangente na graf funkcije u ovoj tački.

Fizičko značenje izvedenice: derivacija putanje u odnosu na vrijeme jednaka je brzini pravolinijskog kretanja.

Zaista, još od školskih dana svi znaju da je brzina privatan put. x = f (t) i vrijeme t ... Prosječna brzina u određenom vremenskom periodu:

Da biste saznali brzinu kretanja u datom trenutku t0 morate izračunati granicu:

Prvo pravilo: izvadite konstantu

Konstanta se može pomjeriti izvan predznaka derivacije. Štaviše, to se mora uraditi. Prilikom rješavanja primjera iz matematike uzmite kao pravilo - ako možete pojednostaviti izraz, budite sigurni da ste ga pojednostavili .

Primjer. Izračunajmo derivaciju:

Drugo pravilo: derivacija zbira funkcija

Derivat zbira dviju funkcija jednak je zbroju izvoda ovih funkcija. Isto vrijedi i za derivaciju razlike funkcija.

Nećemo dati dokaz ove teoreme, već ćemo razmotriti praktični primjer.

Pronađite derivaciju funkcije:

Treće pravilo: derivacija proizvoda funkcija

Derivat proizvoda dvije diferencijabilne funkcije izračunava se po formuli:

Primjer: pronađite derivaciju funkcije:

Rješenje:

Ovdje je važno reći o izračunavanju izvoda složenih funkcija. Derivat kompleksne funkcije jednak je umnošku derivacije ove funkcije u odnosu na međuargument na derivaciju srednjeg argumenta u odnosu na nezavisnu varijablu.

U gornjem primjeru susrećemo izraz:

U ovom slučaju, srednji argument je 8x na peti stepen. Da bismo izračunali derivaciju takvog izraza, prvo izračunamo derivaciju eksterne funkcije u odnosu na međuargument, a zatim pomnožimo sa derivacijom neposrednog međuargumena u odnosu na nezavisnu varijablu.

Četvrto pravilo: kvocijentni izvod dvije funkcije

Formula za određivanje derivacije kvocijenta dvije funkcije:

Pokušali smo vam reći o derivatima za lutke od nule. Ova tema nije tako jednostavna kao što zvuči, pa budite upozoreni: u primjerima često postoje zamke, stoga budite oprezni pri izračunavanju izvedenica.

Za sva pitanja o ovoj i drugim temama možete se obratiti studentskoj službi. Za kratko vrijeme pomoći ćemo vam da riješite najteži test i riješite se zadataka, čak i ako nikada prije niste radili računanje izvedenica.

Na kojoj smo analizirali najjednostavnije izvode, a takođe se upoznali sa pravilima diferencijacije i nekim tehnikama za pronalaženje izvoda. Stoga, ako niste baš previše s izvedenicama funkcija, ili neke tačke ovog članka nisu sasvim jasne, onda prvo pročitajte gornju lekciju. Molim vas, uključite se u ozbiljno raspoloženje - materijal nije lak, ali ću se ipak potruditi da ga predstavim na jednostavan i pristupačan način.

U praksi se sa izvodom složene funkcije morate suočiti vrlo često, čak bih rekao, skoro uvijek, kada vam se daju zadaci da nađete izvode.

U tabeli gledamo pravilo (br. 5) za razlikovanje složene funkcije:

Razumijevanje. Prije svega, obratimo pažnju na snimak. Ovdje imamo dvije funkcije - i, osim toga, funkcija je, figurativno rečeno, ugrađena u funkciju. Funkcija ove vrste (kada je jedna funkcija ugniježđena u drugu) naziva se složena funkcija.

Ja ću pozvati funkciju eksterna funkcija i funkciju - unutrašnja (ili ugniježđena) funkcija.

! Ove definicije nisu teorijske i ne bi se trebale pojaviti u konačnom dizajnu zadataka. Koristim neformalne izraze "spoljna funkcija", "unutrašnja" funkcija samo da bih vam olakšao razumevanje materijala.

Da biste razjasnili situaciju, razmotrite:

Primjer 1

Pronađite izvod funkcije

Pod sinusom nemamo samo slovo "X", već i celobrojni izraz, tako da neće biti moguće odmah pronaći izvod iz tabele. Također primjećujemo da je ovdje nemoguće primijeniti prva četiri pravila, čini se da postoji razlika, ali činjenica je da ne možete "rastrgnuti" sinus:

U ovom primjeru, već iz mojih objašnjenja, intuitivno je jasno da je funkcija složena funkcija, a polinom je interna funkcija (gniježđenje), i eksterna funkcija.

Prvi korak, koji se mora izvesti prilikom pronalaženja derivacije kompleksne funkcije, je to utvrditi koja je funkcija unutrašnja, a koja eksterna.

U slučaju jednostavnih primjera, čini se jasnim da je polinom ugniježđen ispod sinusa. Ali šta ako sve nije očigledno? Kako tačno odrediti koja funkcija je eksterna, a koja interna? Da biste to učinili, predlažem korištenje sljedeće tehnike, koja se može raditi mentalno ili na nacrtu.

Zamislite da trebamo izračunati vrijednost izraza u na kalkulatoru (umjesto jedan, može postojati bilo koji broj).

Šta ćemo prvo izračunati? Kao prvo morat ćete izvesti sljedeću radnju:, tako da će polinom biti interna funkcija:

Drugo morat će se pronaći, tako da će sinus biti vanjska funkcija:

Nakon nas Shvatio sa unutrašnjim i eksternim funkcijama, vreme je da se primeni pravilo diferencijacije složene funkcije .

Počinjemo da odlučujemo. Sa lekcije Kako da pronađem derivat? sjećamo se da dizajn rješenja bilo koje derivacije uvijek počinje ovako - stavljamo izraz u zagrade i stavljamo crtu gore desno:

Prvo pronađite izvod eksterne funkcije (sinus), pogledajte tabelu izvoda elementarnih funkcija i uočite to. Sve tabelarne formule su primjenjive čak i ako se "x" zamijeni složenim izrazom, u ovom slučaju:

Imajte na umu da je unutrašnja funkcija nije se promijenilo, mi to ne diramo.

Pa, to je sasvim očigledno

Rezultat primjene formule u konačnom dizajnu to izgleda ovako:

Konstantni faktor se obično stavlja na početak izraza:

Ako dođe do zabune, zapišite rješenje i ponovo pročitajte objašnjenja.

Primjer 2

Pronađite izvod funkcije

Primjer 3

Pronađite izvod funkcije

Kao i uvek, zapisujemo:

Hajde da shvatimo gde imamo spoljnu funkciju, a gde unutrašnju. Da biste to učinili, pokušajte (mentalno ili na nacrtu) izračunati vrijednost izraza u. Šta prvo treba uraditi? Prije svega, morate izračunati čemu je jednaka baza: što znači da je polinom interna funkcija:

I tek tada se izvodi eksponencijacija, dakle, funkcija snage je vanjska funkcija:

Prema formuli , prvo morate pronaći derivaciju eksterne funkcije, u ovom slučaju stepen. Traženu formulu tražimo u tabeli:. Ponavljamo ponovo: bilo koja tablična formula vrijedi ne samo za "x", već i za složeni izraz... Dakle, rezultat primjene pravila diferencijacije složene funkcije sljedeći:

Ponovo naglašavam da kada uzmemo derivaciju vanjske funkcije, unutrašnja funkcija se za nas ne mijenja:

Sada ostaje pronaći vrlo jednostavan izvod unutrašnje funkcije i malo "pročešljati" rezultat:

Primjer 4

Pronađite izvod funkcije

Ovo je primjer za nezavisno rješenje (odgovor na kraju tutorijala).

Da bih učvrstio razumijevanje derivacije složene funkcije, dat ću primjer bez komentara, pokušajte sami to shvatiti, spekulirati gdje je vanjska, a gdje unutrašnja funkcija, zašto su zadaci riješeni na ovaj način?

Primjer 5

a) Naći derivaciju funkcije

b) Naći derivaciju funkcije

Primjer 6

Pronađite izvod funkcije

Ovdje imamo korijen, a da bismo ga razlikovali, on mora biti predstavljen kao stepen. Dakle, prvo dovedemo funkciju u oblik prikladan za diferencijaciju:

Analizirajući funkciju dolazimo do zaključka da je zbir tri člana interna funkcija, a eksponencijacija eksponencijalna funkcija. Primjenjujemo pravilo diferencijacije kompleksne funkcije :

Stepen je opet predstavljen kao radikal (korijen), a za derivaciju interne funkcije primjenjujemo jednostavno pravilo za diferenciranje sume:

Spreman. Također možete dovesti izraz do zajedničkog nazivnika u zagradama i sve zapisati u jednom razlomku. Lijepo, naravno, ali kada se dobiju glomazni dugi derivati, bolje je to ne raditi (lako se zbuniti, napraviti nepotrebnu grešku, a nastavniku će biti nezgodno provjeriti).

Primjer 7

Pronađite izvod funkcije

Ovo je primjer za nezavisno rješenje (odgovor na kraju tutorijala).

Zanimljivo je primijetiti da se ponekad, umjesto pravila za diferenciranje kompleksne funkcije, može koristiti pravilo za diferenciranje kvocijenta , ali takvo rješenje će izgledati neobično kao perverzija. Evo tipičnog primjera:

Primjer 8

Pronađite izvod funkcije

Ovdje možete koristiti pravilo za razlikovanje količnika , ali je mnogo isplativije pronaći izvod kroz pravilo diferencijacije složene funkcije:

Pripremamo funkciju za diferencijaciju - pomičemo minus izvan predznaka derivacije i podižemo kosinus na brojnik:

Kosinus je interna funkcija, eksponencijacija je vanjska funkcija.
Koristimo naše pravilo :

Pronađite izvod interne funkcije, resetirajte kosinus natrag:

Spreman. U razmatranom primjeru važno je da se ne zbunite u znakovima. Usput, pokušaj to riješiti pravilom , odgovori se moraju podudarati.

Primjer 9

Pronađite izvod funkcije

Ovo je primjer za nezavisno rješenje (odgovor na kraju tutorijala).

Do sada smo gledali slučajeve u kojima smo imali samo jedan prilog u složenoj funkciji. U praktičnim zadacima često možete pronaći derivate, gdje se, poput lutkica za gniježđenje, jedna u drugoj, ugniježđuju 3 ili čak 4-5 funkcija odjednom.

Primjer 10

Pronađite izvod funkcije

Hajde da razumemo priloge ove funkcije. Pokušavam procijeniti izraz koristeći vrijednost testa. Kako bismo računali na kalkulator?

Prvo morate pronaći, što znači da je arcsin najdublje gniježđenje:

Tada ovaj arcsin od jedan treba kvadrirati:

I na kraju, podignite 7 na potenciju:

To jest, u ovom primjeru imamo tri različite funkcije i dva priloga, dok je najnutarnja funkcija arcsinus, a najudaljenija funkcija eksponencijalna funkcija.

Počinjemo da rešavamo

Po pravilu prvo morate uzeti derivaciju eksterne funkcije. Gledamo tablicu izvoda i nalazimo izvod eksponencijalne funkcije: Jedina razlika je u tome što umjesto "x" imamo složen izraz, koji ne negira valjanost ove formule. Dakle, rezultat primjene pravila diferencijacije složene funkcije sljedeći.