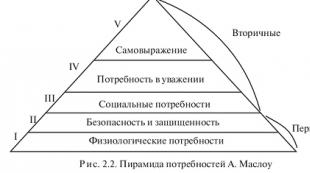
Кой въведе производното? Какво е производна? Определение и значение на производна функция. Геометричен смисъл на производната на функция в точка
Задача B9 дава графика на функция или производна, от която трябва да определите една от следните величини:
- Стойността на производната в дадена точка x 0,
- Максимални или минимални точки (екстремни точки),
- Интервали на нарастващи и намаляващи функции (интервали на монотонност).
Функциите и производните, представени в този проблем, са винаги непрекъснати, което прави решението много по-лесно. Въпреки факта, че задачата принадлежи към раздела на математическия анализ, дори и най-слабите ученици могат да я направят, тъй като тук не се изискват дълбоки теоретични познания.
За намиране на стойността на производната, точките на екстремум и интервалите на монотонност има прости и универсални алгоритми - всички те ще бъдат разгледани по-долу.
Прочетете внимателно условията на задача B9, за да избегнете глупави грешки: понякога попадате на доста дълги текстове, но има няколко важни условия, които влияят на хода на решението.
Изчисляване на производната стойност. Метод с две точки
Ако за задачата е дадена графика на функция f(x), допирателна към тази графика в точка x 0, и се изисква да се намери стойността на производната в тази точка, се прилага следният алгоритъм:
- Намерете две „адекватни“ точки на допирателната графика: техните координати трябва да са цели числа. Нека означим тези точки като A (x 1 ; y 1) и B (x 2 ; y 2). Запишете правилно координатите - това е ключов момент в решението и всяка грешка тук ще доведе до неправилен отговор.
- Познавайки координатите, е лесно да се изчисли увеличението на аргумента Δx = x 2 − x 1 и увеличението на функцията Δy = y 2 − y 1 .
- Накрая намираме стойността на производната D = Δy/Δx. С други думи, трябва да разделите увеличението на функцията на увеличението на аргумента - и това ще бъде отговорът.
Още веднъж да отбележим: точките A и B трябва да се търсят именно по допирателната, а не по графиката на функцията f(x), както често се случва. Допирателната задължително ще съдържа поне две такива точки - в противен случай проблемът няма да бъде формулиран правилно.
Разгледайте точки A (−3; 2) и B (−1; 6) и намерете увеличенията:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Нека намерим стойността на производната: D = Δy/Δx = 4/2 = 2.
Задача. Фигурата показва графика на функцията y = f(x) и допирателна към нея в точката с абсцисата x 0. Намерете стойността на производната на функцията f(x) в точката x 0 .
Помислете за точки A (0; 3) и B (3; 0), намерете увеличенията:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Сега намираме стойността на производната: D = Δy/Δx = −3/3 = −1.
Задача. Фигурата показва графика на функцията y = f(x) и допирателна към нея в точката с абсцисата x 0. Намерете стойността на производната на функцията f(x) в точката x 0 .
Разгледайте точки A (0; 2) и B (5; 2) и намерете увеличенията:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Остава да намерим стойността на производната: D = Δy/Δx = 0/5 = 0.
От последния пример можем да формулираме правило: ако допирателната е успоредна на оста OX, производната на функцията в точката на допирателна е нула. В този случай дори не е нужно да броите нищо - просто погледнете графиката.
Изчисляване на максимални и минимални точки
Понякога, вместо графика на функция, задача B9 дава графика на производната и изисква намиране на максималната или минималната точка на функцията. В тази ситуация двуточковият метод е безполезен, но има друг, още по-прост алгоритъм. Първо, нека дефинираме терминологията:
- Точката x 0 се нарича максимална точка на функцията f(x), ако в някаква околност на тази точка е изпълнено неравенството f(x 0) ≥ f(x).
- Точката x 0 се нарича точка на минимум на функцията f(x), ако в някаква околност на тази точка е изпълнено неравенството f(x 0) ≤ f(x).
За да намерите максималните и минималните точки от производната графика, просто изпълнете следните стъпки:
- Преначертайте производната графика, като премахнете цялата ненужна информация. Както показва практиката, ненужните данни само пречат на решението. Затова маркираме нулите на производната на координатната ос - и това е всичко.
- Намерете знаците на производната на интервалите между нулите. Ако за дадена точка x 0 е известно, че f'(x 0) ≠ 0, тогава са възможни само две опции: f'(x 0) ≥ 0 или f'(x 0) ≤ 0. Знакът на производната е лесно се определя от оригиналния чертеж: ако графиката на производната лежи над оста OX, тогава f'(x) ≥ 0. И обратното, ако графиката на производната лежи под оста OX, тогава f'(x) ≤ 0.
- Отново проверяваме нулите и знаците на производната. Там, където знакът се променя от минус на плюс, е минималната точка. Обратно, ако знакът на производната се промени от плюс на минус, това е максималната точка. Броенето винаги се извършва отляво надясно.
Тази схема работи само за непрекъснати функции - в задача B9 няма други.
Задача. Фигурата показва графика на производната на функцията f(x), дефинирана на интервала [−5; 5]. Намерете минималната точка на функцията f(x) върху тази отсечка.
Нека се отървем от ненужната информация и оставим само границите [−5; 5] и нули на производната x = −3 и x = 2.5. Отбелязваме и знаците:
Очевидно в точката x = −3 знакът на производната се променя от минус на плюс. Това е минималната точка.
Задача. Фигурата показва графика на производната на функцията f(x), дефинирана на интервала [−3; 7]. Намерете максималната точка на функцията f(x) на този сегмент.
Нека преначертаем графиката, оставяйки само границите [−3; 7] и нули на производната x = −1.7 и x = 5. Нека отбележим знаците на производната върху получената графика. Ние имаме:
![]()
Очевидно в точката x = 5 знакът на производната се променя от плюс на минус - това е максималната точка.
Задача. На фигурата е показана графика на производната на функцията f(x), дефинирана на интервала [−6; 4]. Намерете броя на максималните точки на функцията f(x), принадлежащи на отсечката [−4; 3].
От условията на задачата следва, че е достатъчно да се разгледа само частта от графиката, ограничена от сегмента [−4; 3]. Затова изграждаме нова графика, на която отбелязваме само границите [−4; 3] и нули на производната вътре в него. А именно точки x = −3,5 и x = 2. Получаваме:
![]()
На тази графика има само една максимална точка x = 2. Именно в тази точка знакът на производната се променя от плюс на минус.
Малка бележка за точки с нецелочислени координати. Например в последната задача беше разгледана точката x = −3,5, но със същия успех можем да вземем x = −3,4. Ако проблемът е компилиран правилно, подобни промени не трябва да влияят на отговора, тъй като точките „без определено място на пребиваване“ не участват пряко в решаването на проблема. Разбира се, този трик няма да работи с цели точки.
Намиране на интервали на нарастващи и намаляващи функции
В такъв проблем, подобно на максималните и минималните точки, се предлага да се използва графиката на производната, за да се намерят области, в които самата функция нараства или намалява. Първо, нека дефинираме какво е увеличаване и намаляване:
- Казва се, че функция f(x) нараства на отсечка, ако за всеки две точки x 1 и x 2 от тази отсечка е вярно следното твърдение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . С други думи, колкото по-голяма е стойността на аргумента, толкова по-голяма е стойността на функцията.
- Функция f(x) се нарича намаляваща на отсечка, ако за всеки две точки x 1 и x 2 от тази отсечка е вярно следното твърдение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Тези. По-голямата стойност на аргумента съответства на по-малка стойност на функцията.
Нека формулираме достатъчни условия за увеличаване и намаляване:
- За да расте непрекъсната функция f(x) върху отсечката , достатъчно е нейната производна вътре в отсечката да е положителна, т.е. f’(x) ≥ 0.
- За да намалява една непрекъсната функция f(x) върху отсечката , е достатъчно нейната производна вътре в отсечката да е отрицателна, т.е. f’(x) ≤ 0.
Нека приемем тези твърдения без доказателства. По този начин получаваме схема за намиране на интервали на нарастване и намаляване, която в много отношения е подобна на алгоритъма за изчисляване на точки на екстремум:
- Премахнете цялата ненужна информация. В оригиналната графика на производната се интересуваме предимно от нулите на функцията, така че ще оставим само тях.
- Отбележете знаците на производната на интервалите между нулите. Когато f’(x) ≥ 0, функцията нараства, а когато f’(x) ≤ 0, тя намалява. Ако проблемът поставя ограничения върху променливата x, ние допълнително ги маркираме на нова графика.
- Сега, след като знаем поведението на функцията и ограниченията, остава да изчислим необходимото количество в проблема.
Задача. Фигурата показва графика на производната на функцията f(x), дефинирана на интервала [−3; 7.5]. Намерете интервалите на спадане на функцията f(x). В отговора си посочете сумата от целите числа, включени в тези интервали.
Както обикновено, нека преначертаем графиката и да маркираме границите [−3; 7.5], както и нули на производната x = −1.5 и x = 5.3. След това отбелязваме знаците на производната. Ние имаме:
![]()
Тъй като производната е отрицателна на интервала (− 1,5), това е интервалът на намаляваща функция. Остава да се сумират всички цели числа, които са вътре в този интервал:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Задача. На фигурата е показана графика на производната на функцията f(x), дефинирана на интервала [−10; 4]. Намерете интервалите на нарастване на функцията f(x). В отговора си посочете дължината на най-голямата от тях.
Да се отървем от ненужната информация. Нека оставим само границите [−10; 4] и нули на производната, които този път бяха четири: x = −8, x = −6, x = −3 и x = 2. Нека маркираме знаците на производната и получаваме следната картина:
Ние се интересуваме от интервалите на нарастваща функция, т.е. където f’(x) ≥ 0. Има два такива интервала на графиката: (−8; −6) и (−3; 2). Нека изчислим техните дължини:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Тъй като трябва да намерим дължината на най-големия от интервалите, записваме стойността l 2 = 5 като отговор.
Нека функцията е дефинирана в точка и част от нейната околност. Нека дадем на аргумента увеличение, така че точката да попада в домейна на дефиниция на функцията. След това функцията ще бъде увеличена.
ОПРЕДЕЛЕНИЕ. Производна на функция в точка се нарича граница на съотношението на приращението на функцията в тази точка към приращението на аргумента, при (ако тази граница съществува и е крайна), т.е.
Означаваме: ,,,.
Производна на функция в точка отдясно (вляво) Наречен
(ако тази граница съществува и е крайна).
Обозначава се от: , – производна в точката отдясно,
, е производната в точката отляво.
Очевидно е вярна следната теорема.
ТЕОРЕМА. Една функция има производна в точка тогава и само ако в тази точка производните на функцията отдясно и отляво съществуват и са равни една на друга. освен това
Следващата теорема установява връзка между съществуването на производна на функция в точка и непрекъснатостта на функцията в тази точка.
ТЕОРЕМА (необходимо условие за съществуване на производна на функция в точка). Ако една функция има производна в точка, тогава функцията в тази точка е непрекъсната.
ДОКАЗАТЕЛСТВО
Нека съществува. Тогава
![]() ,
,
където е безкрайно малко at.
Коментирайте
производна на функция и обозначават
диференциация на функцията .
ГЕОМЕТРИЧНО И ФИЗИЧЕСКО ЗНАЧЕНИЕ
1) Физическо значение на производната. Ако функцията и нейният аргумент са физически величини, тогава производната е скоростта на промяна на променлива спрямо променливата в дадена точка. Например, ако е разстоянието, изминато от точка във времето, тогава нейната производна е скоростта в момента. Ако е количеството електричество, протичащо през напречното сечение на проводника в даден момент от време, тогава е скоростта на промяна в количеството електричество в един момент от време, т.е. сила на тока в даден момент.
2) Геометрично значение на производната.
Нека е някаква крива, да е точка от кривата. 
Всяка права линия, пресичаща поне две точки, се нарича секуща .
Допирателна към крива в точка наречена гранична позиция на секанс, ако точката се стреми към, движейки се по крива.
От дефиницията е очевидно, че ако в дадена точка съществува допирателна към крива, то тя е единствената
Помислете за крива (т.е. графика на функция). Нека има невертикална допирателна в точка. Неговото уравнение: (уравнение на права линия, минаваща през точка и имаща ъглов коефициент). 
По дефиниция на наклона
където е ъгълът на наклона на правата спрямо оста.
Нека е ъгълът на наклона на секанса спрямо оста, където. Тъй като е допирателна, тогава кога
следователно
Така получихме това – ъглов коефициент на допирателната към графиката на функцията в точката(геометричен смисъл на производната на функция в точка). Следователно уравнението на допирателната към кривата в точка може да бъде написано във формата
Коментирайте . Права линия, минаваща през точка, перпендикулярна на допирателната, начертана към кривата в точката, се нарича нормално към кривата в точката . Тъй като ъгловите коефициенти на перпендикулярни прави линии са свързани със съотношението, уравнението на нормалата към кривата в точка ще има формата
![]() , Ако .
, Ако .
Ако , тогава допирателната към кривата в точката ще има формата
и нормално.
ДОПИРАТЕЛНИ И НОРМАЛНИ УРАВНЕНИЯ
Уравнение на тангенс
Нека функцията е дадена от уравнението г=f(х), трябва да напишете уравнението допирателнав точката х 0. От определението за производна:
г/(х)=limΔ х→0Δ гΔ х
Δ г=f(х+Δ х)−f(х).
Уравнението допирателнакъм графиката на функцията: г=kx+b (к,b=конст). От геометричния смисъл на производната: f/(х 0)=tgα= кзащото х 0 и f(х 0)∈ права линия, тогава уравнението допирателнасе записва като: г−f(х 0)=f/(х 0)(х−х 0), или
г=f/(х 0)· х+f(х 0)−f/(х 0)· х 0.

Нормално уравнение
нормално- е перпендикулярна на допирателна(виж снимката). Въз основа на това:
tgβ= tg(2π−α)= ctgα=1 tgα=1 f/(х 0)
защото ъгълът на наклон на нормалата е ъгъл β1, тогава имаме:
tgβ1= tg(π−β)=− tgβ=−1 f/(х).
точка ( х 0,f(х 0))∈ нормално, уравнението приема формата:
г−f(х 0)=−1f/(х 0)(х−х 0).
ДОКАЗАТЕЛСТВО
Нека съществува. Тогава
![]() ,
,
където е безкрайно малко at.
Но това означава, че е непрекъснат в точка (вижте геометричната дефиниция на непрекъснатостта). ∎
Коментирайте . Непрекъснатостта на функция в точка не е достатъчно условие за съществуването на производна на тази функция в точка. Например функция е непрекъсната, но няма производна в точка. Наистина ли,
и следователно не съществува.
Очевидно съответствието е функция, дефинирана на някакво множество. Викат я производна на функция и обозначават
Операцията за намиране на функция за нейната производна функция се нарича диференциация на функцията .
Производна на сбор и разлика
Нека са дадени функции f(x) и g(x), чиито производни са ни известни. Например можете да вземете елементарните функции, обсъдени по-горе. След това можете да намерите производната на сбора и разликата на тези функции:
(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’
И така, производната на сумата (разликата) на две функции е равна на сумата (разликата) на производните. Възможно е да има повече термини. Например (f + g + h)’ = f’ + g’ + h’.
Строго погледнато, в алгебрата няма концепция за „изваждане“. Съществува понятието „отрицателен елемент“. Следователно разликата f − g може да се пренапише като сумата f + (−1) g и тогава остава само една формула - производната на сумата.
Съдържанието на статията
ПРОИЗВОДНО– производна на функцията г = f(х), дадени на определен интервал ( а, b) в точка хот този интервал се нарича границата, към която клони съотношението на нарастването на функцията fв този момент към съответното увеличение на аргумента, когато увеличението на аргумента клони към нула.
Производната обикновено се обозначава по следния начин:
Други обозначения също са широко използвани:
Незабавна скорост.
Нека точката Мсе движи по права линия. Разстояние сподвижна точка, считано от някаква начална позиция М 0 , зависи от времето T, т.е. сима функция на времето T: с= f(T). Нека в някакъв момент от времето Tподвижна точка Мбеше на разстояние сот изходна позиция М 0 и в някой следващ момент T+D Tсе оказа в положение М 1 - на разстояние с+D сот начална позиция ( виж снимка.).
Така за определен период от време Д Tразстояние ссе променя със сумата D с. В този случай те казват, че през интервала от време D Tвеличина сполучено увеличение D с.
Средната скорост не може във всички случаи точно да характеризира скоростта на движение на дадена точка Мв даден момент T. Ако, например, тялото в началото на интервала D Tсе движи много бързо и накрая много бавно, тогава средната скорост няма да може да отрази посочените характеристики на движението на точката и да даде представа за истинската скорост на движението й в момента T. За да изразите по-точно истинската скорост, като използвате средната скорост, трябва да вземете по-кратък период от време D T. Най-пълно характеризира скоростта на движение на дадена точка в момента Tграницата, към която клони средната скорост при D T® 0. Тази граница се нарича текуща скорост:
По този начин скоростта на движение в даден момент се нарича граница на коефициента на нарастване на пътя D скъм нарастване на времето D T, когато нарастването на времето клони към нула. защото
Геометричен смисъл на производната. Тангента към графиката на функция.
Конструирането на допирателни линии е един от онези проблеми, довели до раждането на диференциалното смятане. Първата публикувана работа, свързана с диференциалното смятане, написана от Лайбниц, беше озаглавена Нов метод за максимуми и минимуми, както и допирателни, за които нито дробните, нито ирационалните величини са пречка, и специален вид смятане за това.
Нека кривата е графиката на функцията г =f(х) в правоъгълна координатна система ( см. ориз.).
На някаква стойност хфункцията има значение г =f(х). Тези ценности хИ гточката на кривата съответства М 0(х, г). Ако аргументът хдайте увеличение D х, след това новата стойност на аргумента х+D хсъответства на новата стойност на функцията y+д г = f(х + д х). Съответстващата точка на кривата ще бъде точката М 1(х+D х,г+D г). Ако начертаете секуща М 0М 1 и означен с j ъгълът, образуван от напречна с положителната посока на оста вол, от фигурата веднага става ясно, че .
Ако сега Д хклони към нула, тогава точката М 1 се движи по кривата, приближавайки се до точката М 0 и ъгъл й промени с D х. При Dx® 0 ъгълът j клони към определена граница a и правата, минаваща през точката М 0 и компонентът с положителна посока на оста x, ъгъл a, ще бъде желаната тангенс. Наклонът му е:
следователно f´( х) = tga
тези. производна стойност f´( х) за дадена стойност на аргумент хе равен на тангенса на ъгъла, образуван от допирателната към графиката на функцията f(х) в съответната точка М 0(х,г) с положителна посока на оста вол.
Диференцируемост на функциите.
Определение. Ако функцията г = f(х) има производна в точката х = х 0, тогава функцията е диференцируема в тази точка.
Непрекъснатост на функция с производна. Теорема.
Ако функцията г = f(х) е диференцируем в даден момент х = х 0, тогава той е непрекъснат в тази точка.
Следователно функцията не може да има производна в точките на прекъсване. Неправилен е обратният извод, т.е. от факта, че в един момент х = х 0 функция г = f(х) е непрекъснат, не означава, че е диференцируем в тази точка. Например функцията г = |х| непрекъснато за всички х(–Ґ x x = 0 няма производна. В тази точка няма допирателна към графиката. Има дясна допирателна и лява допирателна, но те не съвпадат.
Някои теореми за диференцируеми функции. Теорема за корените на производната (теорема на Рол).Ако функцията f(х) е непрекъснат на сегмента [а,b], е диференцируем във всички вътрешни точки на този сегмент и в краищата х = аИ х = bотива на нула ( f(а) = f(b) = 0), след това вътре в сегмента [ а,b] има поне една точка х= с, а c b, в която производната fў( х) отива на нула, т.е. fў( ° С) = 0.
Теорема за крайно нарастване (теорема на Лагранж).Ако функцията f(х) е непрекъснат на интервала [ а, b] и е диференцируем във всички вътрешни точки на този сегмент, след това вътре в сегмента [ а, b] има поне една точка с, а c b това
f(b) – f(а) = fў( ° С)(b– а).
Теорема за съотношението на нарастванията на две функции (теорема на Коши).Ако f(х) И ж(х) – две непрекъснати на отсечката функции [а, b] и диференцируеми във всички вътрешни точки на този сегмент, и жў( х) не изчезва никъде в този сегмент, след това в сегмента [ а, b] има такава точка х = с, а c b това
Производни от различни поръчки.
Нека функцията г =f(х) е диференцируем на някакъв интервал [ а, b]. Производни стойности f ў( х), най-общо казано, зависят от х, т.е. производна f ў( х) също е функция на х. При диференцирането на тази функция получаваме така наречената втора производна на функцията f(х), което е означено f ўў ( х).
Производна н-ти ред на функция f(х) се нарича производна (от първи ред) на производната н- 1- и се обозначава със символа г(н) = (г(н– 1))ў.
Диференциали от различни поръчки.
Функционален диференциал г = f(х), Където х– независима променлива, да dy = f ў( х)dx, някаква функция от х, но от хсамо първият фактор може да зависи f ў( х), вторият фактор ( dx) е нарастването на независимата променлива хи не зависи от стойността на тази променлива. защото dyима функция от х, тогава можем да определим диференциала на тази функция. Диференциалът на диференциала на функция се нарича втори диференциал или диференциал от втори ред на тази функция и се обозначава д 2г:
д(dx) = д 2г = f ўў( х)(dx) 2 .
Диференциал н-от първи ред се нарича първи диференциал на диференциала н- 1- ти ред:
d n y = д(d n–1г) = f(н)(х)dx(н).
Частична производна.
Ако една функция зависи не от един, а от няколко аргумента x i(азварира от 1 до н,аз= 1, 2,… н),f(х 1,х 2,… x n), тогава в диференциалното смятане се въвежда концепцията за частична производна, която характеризира скоростта на промяна на функция на няколко променливи, когато се променя само един аргумент, например, x i. Частична производна от 1-ви ред по отношение на x iсе определя като обикновена производна и се приема, че всички аргументи освен x i, поддържайте постоянни стойности. За частни производни се въвежда обозначението
Дефинираните по този начин частни производни от първи ред (като функции на едни и същи аргументи) могат от своя страна също да имат частни производни, това са частни производни от втори ред и т.н. Такива производни, взети от различни аргументи, се наричат смесени. Непрекъснатите смесени производни от един и същи ред не зависят от реда на диференциране и са равни една на друга.
Анна Чугайнова
(\large\bf Производна на функция)
Помислете за функцията y=f(x), посочен на интервала (а, б). Позволявам х- всяка фиксирана точка от интервала (а, б), А Δx- произволно число, така че стойността x+Δxсъщо принадлежи към интервала (а, б). Този номер Δxнаречено увеличение на аргумента.
Определение. Увеличаване на функцията y=f(x)в точката х, съответстващ на увеличението на аргумента Δx, да се обадим на номера
Δy = f(x+Δx) - f(x).
Ние вярваме в това Δx ≠ 0. Разгледайте в дадена фиксирана точка хсъотношението на нарастването на функцията в тази точка към съответното увеличение на аргумента Δx
Ще наричаме това отношение отношение на разликата. Тъй като стойността хсчитаме за фиксирано, съотношението на разликата е функция на аргумента Δx. Тази функция е дефинирана за всички стойности на аргументи Δx, принадлежащи на някаква достатъчно малка околност на точката Δx=0, с изключение на самата точка Δx=0. По този начин имаме право да разгледаме въпроса за съществуването на граница на посочената функция при Δx → 0.
Определение. Производна на функция y=f(x)в дадена фиксирана точка хнаречен лимит при Δx → 0коефициент на разлика, т.е
При условие, че това ограничение съществува.
Обозначаване. y′(x)или f′(x).
Геометрично значение на производната: Производна на функция f(x)в този момент хравен на тангенса на ъгъла между оста воли допирателна към графиката на тази функция в съответната точка:
f′(x 0) = \tgα.
Механично значение на производната: Производната на пътя спрямо времето е равна на скоростта на праволинейно движение на точката:
Уравнение на допирателна към права y=f(x)в точката M 0 (x 0, y 0)приема формата
y-y 0 = f′(x 0) (x-x 0).
Нормалната към крива в дадена точка е перпендикулярът на допирателната в същата точка. Ако f′(x 0)≠ 0, тогава уравнението на нормалата към правата y=f(x)в точката M 0 (x 0, y 0)е написано така:

Концепцията за диференцируемост на функция
Нека функцията y=f(x)определени през определен интервал (а, б), х- някаква фиксирана стойност на аргумент от този интервал, Δx- всяко увеличение на аргумента, така че стойността на аргумента x+Δx ∈ (a, b).
Определение. функция y=f(x)наречена диференцируема в дадена точка х, ако увеличение Δyтази функция в точката х, съответстващ на увеличението на аргумента Δx, могат да бъдат представени във формата
Δy = A Δx +αΔx,
Където А- някакво число, независимо от Δx, А α - функция аргумент Δx, което е безкрайно малко при Δx→ 0.
Тъй като произведението на две безкрайно малки функции αΔxе безкрайно малко от по-висок порядък от Δx(свойство на 3 безкрайно малки функции), тогава можем да напишем:
Δy = A Δx +o(Δx).
Теорема. За да може функцията y=f(x)беше диференцируем в дадена точка х, е необходимо и достатъчно той да има крайна производна в тази точка. При което A=f′(x), това е
Δy = f′(x) Δx +o(Δx).
Операцията за намиране на производната обикновено се нарича диференциране.
Теорема. Ако функцията y=f(x) х, тогава той е непрекъснат в тази точка.
Коментирайте. От непрекъснатостта на функцията y=f(x)в този момент х, най-общо казано, диференцируемостта на функцията не следва f(x)в този момент. Например функцията y=|x|- непрекъснато в точка х=0, но няма производна.
Понятие за диференциална функция
Определение. Функционален диференциал y=f(x)произведението на производната на тази функция и нарастването на независимата променлива се нарича х:
dy = y′ Δx, df(x) = f′(x) Δx.
За функция y=xполучаваме dy=dx=x′Δx = 1· Δx= Δx, това е dx=Δx- диференциалът на независима променлива е равен на нарастването на тази променлива.
Така можем да пишем
dy = y′ dx, df(x) = f′(x) dx
![]()
Диференциал dyи нарастване Δyфункции y=f(x)в този момент х, като и двете съответстват на едно и също увеличение на аргумента Δx, най-общо казано, не са равни помежду си.
Геометрично значение на диференциала: Диференциалът на функция е равен на нарастването на ординатата на допирателната към графиката на тази функция, когато аргументът се увеличава Δx.
Правила за диференциране
Теорема. Ако всяка от функциите u(x)И v(x)диференцируеми в дадена точка х, след това сумата, разликата, произведението и частното на тези функции (частното при условие, че v(x)≠ 0) също са диференцируеми в тази точка и формулите важат:

Разгледайте сложната функция y=f(φ(x))≡ F(x), Където y=f(u), u=φ(x). В такъв случай uНаречен междинен аргумент, х - независима променлива.
Теорема. Ако y=f(u)И u=φ(x)са диференцируеми функции на техните аргументи, тогава производната на сложна функция y=f(φ(x))съществува и е равно на произведението на тази функция по отношение на междинния аргумент и производната на междинния аргумент по отношение на независимата променлива, т.е.
![]()
Коментирайте. За сложна функция, която е суперпозиция на три функции y=F(f(φ(x))), правилото за диференциране има формата
y′ x = y′ u u′ v v′ x,
къде са функциите v=φ(x), u=f(v)И y=F(u)- диференцируеми функции на техните аргументи.
Теорема. Нека функцията y=f(x)нараства (или намалява) и е непрекъснат в някаква околност на точката х 0. Нека освен това тази функция е диференцируема в посочената точка х 0и неговата производна в този момент f′(x 0) ≠ 0. Тогава в някаква околност на съответната точка y 0 =f(x 0)обратното е дефинирано за y=f(x)функция x=f -1 (y), а посочената обратна функция е диференцируема в съответната точка y 0 =f(x 0)и за неговата производна в този момент гформулата е валидна

Таблица с производни

Инвариантност на формата на първия диференциал
Нека разгледаме диференциала на сложна функция. Ако y=f(x), x=φ(t)- функциите на техните аргументи са диференцируеми, тогава производната на функцията y=f(φ(t))изразено с формулата
y′ t = y′ x x′ t.
А-приорат dy=y′ t dt, тогава получаваме
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,
dy = y′ x dx.
И така, ние сме доказали
Свойство за инвариантност на формата на първия диференциал на функция: както в случая, когато аргументът хе независима променлива и в случай, че аргументът хсама по себе си е диференцируема функция на новата променлива, диференциала dyфункции y=f(x)е равно на производната на тази функция, умножена по диференциала на аргумента dx.
Приложение на диференциала в приближените изчисления
Показахме, че диференциалът dyфункции y=f(x), най-общо казано, не е равно на нарастването Δyтази функция. Въпреки това, до безкрайно малка функция от по-висок порядък на малкост от Δx, приблизителното равенство е валидно
Δy ≈ dy.
Съотношението се нарича относителна грешка на равенството на това равенство. защото Δy-dy=o(Δx), тогава относителната грешка на това равенство става толкова малка, колкото желаете, с намаляване |Δх|.
Като се има предвид това Δy=f(x+δ x)-f(x), dy=f′(x)Δx, получаваме f(x+δ x)-f(x) ≈ f′(x)Δxили
f(x+δ x) ≈ f(x) + f′(x)Δx.
Това приблизително равенство позволява с грешка o(Δx)функция за замяна f(x)в малък квартал на точката х(т.е. за малки стойности Δx) линейна функция на аргумента Δx, стоящ от дясната страна.
Производни от по-висок порядък
Определение. Втора производна (или производна от втори ред) на функция y=f(x)се нарича производна на нейната първа производна.
Нотация за втората производна на функция y=f(x):
Механично значение на втората производна. Ако функцията y=f(x)описва закона за движение на материална точка по права линия, след това втората производна f″(x)равно на ускорението на движеща се точка в момента х.
Третата и четвъртата производни се определят по подобен начин.
Определение. нта производна (или производна н-ти ред) функции y=f(x)се нарича нейна производна n-1та производна:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.
Обозначения: y″′, y IV, y Vи т.н.
Геометрично значение на производната
|
ОПРЕДЕЛЕНИЕ НА ДОПАТАТЕЛНА КЪМ КРИВА Допирателна към крива y=ƒ(x)в точката Мсе нарича гранично положение на секуща, прекарана през точка Ми точката, съседна на него М 1крива, при условие че точката М 1се приближава неограничено по кривата до точката М. ГЕОМЕТРИЧНО ЗНАЧЕНИЕ НА ПРОИЗВОДНАТА Производна на функция y=ƒ(x)в точката х 0 е числено равно на тангенса на ъгъла на наклон спрямо оста одопирателна към кривата y=ƒ(x)в точката M (x 0; ƒ (x 0)). |
ВАРИАЦИЯ ДОТИКА КЪМ КРИВА Точкова до кривата y=ƒ(x)точно Мсе нарича гранично положение на правата, прекарана през точката Ми следващата точка с нея М 1криво, извън ума, каква точка М 1кривата неизбежно се приближава до точката М. ГЕОМЕТРИЧЕН ЗМИСТ ПОХИДНОЙ Подобни функции y=ƒ(x)точно х 0числено равна на тангенса на наклона към оста одотичен, изнесен до кривата y=ƒ(x)точно M (x 0; ƒ (x 0)). |
Практическо значение на производната
Нека да разгледаме какво на практика означава количеството, което намерихме като производна на определена функция.
Преди всичко, производна- това е основната концепция на диференциалното смятане, характеризираща скоростта на изменение на функция в дадена точка.
Какво е "скорост на промяна"? Нека си представим функцията f(x) = 5. Независимо от стойността на аргумента (x), стойността му не се променя по никакъв начин. Тоест скоростта на изменението му е нула.
Сега разгледайте функцията f(x) = x. Производната на x е равна на едно. Наистина, лесно е да се забележи, че за всяка промяна на аргумента (x) с единица, стойността на функцията също се увеличава с единица.
От гледна точка на получената информация, сега нека да разгледаме таблицата с производни на прости функции. Въз основа на това физическият смисъл на намирането на производната на функция веднага става ясен. Това разбиране трябва да улесни решаването на практически проблеми.
Съответно, ако производната показва скоростта на промяна на функция, тогава двойната производна показва ускорение.
2080.1947