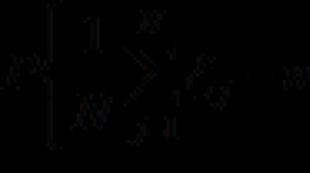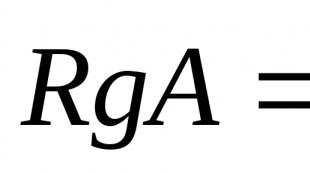إذا تم تحديد قاعدة يتم بموجبها ربط رقم معين u بكل نقطة M من المستوى (أو جزء من المستوى)، فسيقولون أنه على المستوى (أو على جزء من المستوى) "وظيفة النقطة هي محدد"؛ يتم التعبير عن مواصفات الوظيفة بشكل رمزي من خلال المساواة في النموذج u=f(M). الرقم u المرتبط بالنقطة M يسمى قيمة هذه الدالة عند النقطة M. على سبيل المثال، إذا كانت A نقطة ثابتة على المستوى، M هي نقطة عشوائية، فإن المسافة من A إلى M هي دالة للنقطة M في هذه الحالة، f(m)=AM .

دع بعض الوظائف u=f(M) تعطى وفي نفس الوقت يتم تقديم نظام الإحداثيات. ثم يتم تحديد النقطة التعسفية M بواسطة الإحداثيات x، y. وبناءً على ذلك، يتم تحديد قيمة هذه الدالة عند النقطة M بواسطة الإحداثيات x، y، أو كما يقولون أيضًا، u=f(M) هي دالة لمتغيرين x و y. يُشار إلى دالة مكونة من متغيرين x وy بالرمز f(x; y): إذا كانت f(M)=f(x;y)، فإن الصيغة u=f(x; y) تسمى التعبير عن هذا وظيفة في نظام الإحداثيات المحدد. لذلك، في المثال السابق f(M)=AM; إذا أدخلنا نظام إحداثيات ديكارتي مستطيل الأصل عند النقطة A، فسنحصل على التعبير الخاص بهذه الوظيفة:

ش = الجذر التربيعي (س ^ 2 + ص ^ 2)

مشكلة 3688 إعطاء دالة f (x, y)=x^2–y^2–16.

بالنظر إلى الدالة f (x, y)=x^2–y^2–16. حدد تعبير هذه الوظيفة في نظام الإحداثيات الجديد إذا تم تدوير محاور الإحداثيات بزاوية -45 درجة.

معادلات الخطوط البارامترية

دعونا نشير إلى إحداثيات نقطة معينة M بالحرفين x و y؛ دعونا نفكر في وظيفتين للوسيطة t:

س=φ(ر)، ص=ψ(ر) (1)

عندما يتغير t، ستتغير القيمتان x و y، بشكل عام، وبالتالي ستتحرك النقطة M. تسمى المساواة (1). معادلات الخطوط البارامتريةوهو مسار النقطة M؛ تسمى الوسيطة t معلمة. إذا كان من الممكن استبعاد المعلمة t من المساواة (1)، فإننا نحصل على معادلة مسار النقطة M في النموذج

المساواة في النموذج F (س، ص) = 0تسمى معادلة في متغيرين س، ذ،إذا لم يكن صحيحا لجميع أزواج الأرقام س، ص.يقولون رقمين س = س 0 , ص = ص 0, تلبية بعض معادلة النموذج و(س، ص)=0،إذا عند استبدال هذه الأرقام بدلا من المتغيرات Xو فيوفي المعادلة يختفي طرفها الأيسر.

معادلة خط معين (في نظام إحداثي معين) هي معادلة بمتغيرين تكون محققة لإحداثيات كل نقطة تقع على هذا الخط وغير محققة لإحداثيات كل نقطة لا تقع عليه.

وفيما يلي بدلا من عبارة "تعطى معادلة الخط و(س، y) = 0" غالبًا ما نقول باختصار: بالنظر إلى السطر و (س، ص) = 0.

إذا تم إعطاء معادلات خطين و(س، ص) = 0و Ф(س، ص) = س،ثم الحل المشترك للنظام

يعطي كل نقاط التقاطع الخاصة بهم. وبتعبير أدق، يحدد كل زوج من الأرقام التي تمثل حلاً مشتركًا لهذا النظام إحدى نقاط التقاطع.

*) في الحالات التي لا يتم فيها تسمية النظام الإحداثي، يفترض أنه مستطيل ديكارتي.

157. يتم منح النقاط *) م 1 (2; - 2), م 2 (2; 2), م 3 (2; - 1), م 4 (3; -3), م 5 (5; -5), م 6 (3؛ -2). تحديد النقاط المنشورة التي تقع على الخط المحدد بالمعادلة X+ ص = 0،وأيها لا تكذب عليه. ما الخط الذي تحدده هذه المعادلة؟ (ارسمه على الرسم.)

158. على الخط الذي تحدده المعادلة X 2 +y 2 =25، أوجد النقاط التي تساوي أحرفها الإحداثية الأرقام التالية: أ) 0، ب) - 3، ج) 5، د) 7؛ على نفس الخط، ابحث عن نقاط إحداثياتها تساوي الأعداد التالية: e) 3, f) - 5, g) - 8. أي خط تحدده هذه المعادلة؟ (ارسمه على الرسم.)

159. تحديد الخطوط التي يتم تحديدها بواسطة المعادلات التالية (قم بإنشائها على الرسم):

1) س - ص = 0؛ 2) س + ص = 0؛ 3) س- 2 = 0; 4) س+ 3 = 0;

5) ص - 5 = 0؛ 6) ذ+ 2 = 0; 7) س = 0; 8) ذ = 0;

9) س 2 - س ص = 0؛ 10) xy+ ص 2 = 0؛ أحد عشر) س 2 - ذ 2 = 0; 12) xy= 0;

13) ص 2 - 9 = 0؛ 14) xy 2 - 8xy+15 = 0; 15) ص 2 +5ص+4 = 0;

16) X 2 ص - 7س ص + 10ذ = 0; 17) ذ =|س|; 18) س =|في|; 19)ذ + |س|=0;

20) س +|في|= 0; 21)ص =|X- 1|; 22) ذ = |س+ 2|; 23) X 2 + في 2 = 16;

24) (س-2) 2 +(ذ-1) 2 =16; 25) (س+ 5) 2 +(ذ- 1) 2 = 9;

26) (X - 1) 2 + ذ 2 = 4; 27) س 2 +(ذ + 3) 2 = 1; 28) (س -3) 2 + ذ 2 = 0;

29) X 2 + 2ذ 2 = 0; 30) 2X 2 + 3ذ 2 + 5 = 0

31) (س- 2) 2 + (ذ + 3) 2 + 1=0.

160. الأسطر المعطاة:

1)X+ ص = 0; 2)س - ص = 0; 3) س 2 + ذ 2 - 36 = 0;

4) س 2 +ذ 2 -2س==0; 5) س 2 +ذ 2 + 4س-6ذ-1 =0.

تحديد أي منهم يمر عبر الأصل.

161.السطور المقدمة:

1) س 2 + ذ 2 = 49; 2) (س- 3) 2 + (ذ+ 4) 2 = 25;

3) (س+ 6) 2 + (ص - 3) 2 = 25؛ 4)( س + 5) 2 + (ص - 4) 2 = 9؛

5) س 2 +ذ 2 - 12س + 16ص = 0; 6) س 2 +ذ 2 - 2س + 8في+ 7 = 0;

7) س 2 +ذ 2 - 6س + 4ذ + 12 = 0.

أوجد نقاط التقاطع: أ) مع المحور أوه؛ب) مع المحور الوحدة التنظيمية.

162. العثور على نقاط تقاطع خطين.

1)X 2 +ص 2 = 8، س-ص = 0;

2) X 2 +ص 2 -16س+4في+18 = 0, س + ص= 0;

3) X 2 +ص 2 -2س+4في -3 = 0, X 2 + ص 2 = 25;

4) X 2 +ص 2 -8س+10u+40 = 0, X 2 + ص 2 = 4.

163. يتم إعطاء النقاط في نظام الإحداثيات القطبية

م 1 (1; ), م 2 (2; 0), م 3 (2; )

م 4 (
;) و م 5 (1; )

حدد أيًا من هذه النقاط تقع على الخط المحدد بالمعادلة في الإحداثيات القطبية  = 2 cos ، وأيها لا تقع عليه. ما الخط الذي تحدده هذه المعادلة؟ (ارسمه على الرسم :)

164. على الخط المحدد بالمعادلة  = , أوجد النقاط التي زواياها القطبية تساوي الأعداد التالية: أ) ،ب) - ، ج) 0، د) . ما الخط الذي تحدده هذه المعادلة؟

(قم ببنائه على الرسم.)

165.على الخط المحدد بالمعادلة  = ، ابحث عن النقاط التي يساوي نصف قطرها القطبي الأرقام التالية: أ) 1، ب) 2، ج)
. ما الخط الذي تحدده هذه المعادلة؟ (قم ببنائه على الرسم.)

166. حدد الخطوط التي يتم تحديدها في الإحداثيات القطبية بواسطة المعادلات التالية (قم بإنشائها على الرسم):

1)  = 5؛ 2)  = ; 3)  = ; 4)  كوس  = 2؛ 5)  الخطيئة  = 1;

6)  = 6 cos ; 7)  = 10 خطيئة ؛ 8) الخطيئة  = 9) الخطيئة  =

167. قم ببناء حلزونات أرخميدس التالية على الرسم:

1)  = 5، 2)  = 5؛ 3)  = ; 4)ع = -1.

168. قم ببناء اللوالب الزائدية التالية على الرسم:

1)  = ; 2) = ; 3)= ; 4) = - .

169. قم ببناء اللوالب اللوغاريتمية التالية على الرسم:

,
.

170. تحديد أطوال الأجزاء التي تقطع فيها دوامة أرخميدس

الشعاع الخارج من القطب ويميل إلى المحور القطبي بزاوية
. جعل الرسم.

171. في دوامة أرخميدس
نقطة اتخذت مع،الذي يبلغ نصف قطره القطبي 47. أوجد عدد أجزاء هذا الحلزون الذي يقطع نصف القطر القطبي للنقطة مع،جعل الرسم.

172. على دوامة الزائدي
العثور على نقطة ص،الذي يبلغ نصف قطره القطبي 12. ارسم رسمًا.

173. في دوامة لوغاريتمية
ابحث عن النقطة Q التي يبلغ نصف قطرها القطبي 81. ارسم رسمًا.

دع نظام الإحداثيات الديكارتي المستطيل Oxy وبعض الخطوط L معطى على المستوى .

تعريف. المعادلة و(س؛ص)=0 (1)مُسَمًّى معادلة الخطل(بالنسبة لنظام إحداثي معين)، إذا كانت هذه المعادلة تتحقق بإحداثيات x وy لأي نقطة تقع على الخط L، وليس بإحداثيات x وy لأي نقطة لا تقع على الخط L.

الذي - التي. خط على متن الطائرةهو موضع النقاط (M(x;y)) التي تلبي إحداثياتها المعادلة (1).

المعادلة (1) تحدد الخط L.

مثال. معادلة الدائرة.

دائرة- مجموعة من النقاط متساوية البعد عن نقطة معينة M 0 (x 0,y 0).

النقطة م 0 (س 0,ص 0) – مركز الدائرة.

لأي نقطة M(x;y) تقع على الدائرة، المسافة MM 0 =R (R=const)

مم 0 == ر

(س-س 0 ) 2 +(أوه 0 ) 2 = ر 2 –(2) – معادلة دائرة نصف قطرها R ومركزها عند النقطة M 0 (x 0,y 0).

المعادلة البارامترية للخط.

دع إحداثيات x و y للنقاط على السطر L يتم التعبير عنها باستخدام المعلمة t:

(3) - المعادلة البارامترية للخط في DSC

حيث تكون الدالتان (t) و(t) متصلتين بالنسبة إلى المعلمة t (في مدى معين من تغير هذه المعلمة).

وباستثناء المعلمة t من المعادلة (3)، نحصل على المعادلة (1).

لنعتبر الخط L بمثابة المسار الذي تعبره نقطة مادية تتحرك بشكل مستمر وفقًا لقانون معين. دع المتغير t يمثل الوقت المحسوب من لحظة أولية. إذن فإن تحديد قانون الحركة يمثل تحديد الإحداثيات x و y للنقطة المتحركة كبعض الدوال المستمرة x=(t) و y=(t) للزمن t.

مثال. دعونا نشتق معادلة بارامترية لدائرة نصف قطرها r>0 ومركزها عند نقطة الأصل. اجعل M(x,y) نقطة اعتباطية لهذه الدائرة، وt هي الزاوية بين ناقل نصف القطر ومحور الثور، محسوبًا عكس اتجاه عقارب الساعة.

ثم x=r cos x y=r sin t. (4)

المعادلات (4) هي معادلات بارامترية للدائرة قيد النظر. يمكن أن تأخذ المعلمة t أي قيمة، ولكن لكي تدور النقطة M(x,y) حول الدائرة مرة واحدة، يقتصر نطاق تغيير المعلمة على نصف القطعة 0t2.

وبتربيع وإضافة المعادلات (4) نحصل على المعادلة العامة للدائرة (2).

2. نظام الإحداثيات القطبية (psc).

دعونا نختار المحور L ( المحور القطبي) وتحديد نقطة هذا المحور O ( عمود). يتم تعريف أي نقطة على المستوى بشكل فريد من خلال الإحداثيات القطبية ρ وφ، حيث

ρ – نصف القطر القطبي، تساوي المسافة من النقطة M إلى القطب O (ρ≥0)؛

φ – ركنبين اتجاه المتجه أوموالمحور L ( الزاوية القطبية). م(ρ ; φ )

معادلة الخط في UCSيمكن أن تكون مكتوبة:

ρ=f(φ) (5) معادلة صريحة للخط في UCS

F = (ρ؛ φ) (6) معادلة الخط الضمني في UCS

العلاقة بين الإحداثيات الديكارتية والقطبية لنقطة ما.

(س؛ص) (ρ ; φ ) من المثلث OMA:

tan φ=(استعادة الزاويةφ بحسب المعروفيتم إنتاج الظلمع الأخذ في الاعتبار النقطة التي يقع فيها الربع M).(ρ ; φ )(س;ص). س = ρcosφ،ص = ρsinφ

مثال . أوجد الإحداثيات القطبية للنقطتين M(3;4) وP(1;-1).

بالنسبة إلى M:=5، φ=arctg (4/3). بالنسبة لـ P: ρ =؛ φ=Π+arctg(-1)=3Π/4.

تصنيف الخطوط المسطحة.

التعريف 1.الخط يسمى جبري،إذا كان في بعض أنظمة الإحداثيات المستطيلة الديكارتية، إذا تم تعريفه بالمعادلة F(x;y)=0 (1)، حيث تكون الدالة F(x;y) متعددة الحدود جبرية.

التعريف 2.كل خط غير جبري يسمى متسام.

التعريف 3. يسمى الخط الجبري خط النظامن، إذا تم تحديد هذا الخط في بعض أنظمة الإحداثيات الديكارتية المستطيلة بواسطة المعادلة (1)، حيث تكون الدالة F(x;y) متعددة الحدود جبرية من الدرجة n.

وبالتالي، فإن الخط من الرتبة n هو خط محدد في بعض الأنظمة الديكارتية المستطيلة بواسطة معادلة جبرية من الدرجة n مع مجهولين.

تساهم النظرية التالية في إثبات صحة التعريفات 1،2،3.

نظرية(الوثيقة ص١٠٧). إذا تم تحديد خط في بعض أنظمة الإحداثيات المستطيلة الديكارتية بواسطة معادلة جبرية من الدرجة n، فإن هذا الخط في أي نظام إحداثيات ديكارتي مستطيل آخر يتم تحديده بواسطة معادلة جبرية من نفس الدرجة n.

هدف:النظر في مفهوم الخط على المستوى، وإعطاء أمثلة. استنادا إلى تعريف الخط، قدم مفهوم معادلة الخط على المستوى. النظر في أنواع الخطوط المستقيمة، وإعطاء أمثلة وطرق تحديد الخط المستقيم. تعزيز القدرة على ترجمة معادلة الخط المستقيم من الصورة العامة إلى معادلة خط مستقيم "مقطع" بمعامل زاوي.

1. معادلة الخط على الطائرة.
2. معادلة الخط المستقيم على المستوى. أنواع المعادلات.
3. طرق تحديد الخط المستقيم.

1. دع x و y يكونان متغيرين عشوائيين.

تعريف: تسمى العلاقة بالصيغة F(x,y)=0 معادلة ، إذا لم يكن صحيحًا لأي أزواج من الأرقام x و y.

مثال: 2س + 7ص – 1 = 0، س 2 + ص 2 – 25 = 0.

إذا كانت المساواة F(x,y)=0 تنطبق على أي x, y، فإن F(x,y) = 0 هي هوية.

مثال: (س + ص) 2 - س 2 - 2 س ص - ص 2 = 0

يقولون أن الأرقام x هي 0 و y هي 0 إرضاء المعادلة ، إذا تحول عند استبدالهم في هذه المعادلة إلى مساواة حقيقية.

إن أهم مفهوم في الهندسة التحليلية هو مفهوم معادلة الخط.

تعريف: معادلة خط معين هي المعادلة F(x,y)=0، والتي تتحقق بإحداثيات جميع النقاط الواقعة على هذا الخط، ولا تتحقق بإحداثيات أي من النقاط غير الواقعة على هذا الخط.

الخط المحدد بالمعادلة y = f(x) يسمى الرسم البياني لـ f(x). يسمى المتغيران x وy بالإحداثيات الحالية، لأنهما إحداثيات نقطة متغيرة.

بعض أمثلةتعريفات الخط.

1) س – ص = 0 => س = ص. تحدد هذه المعادلة خطًا مستقيمًا:

2) x 2 - y 2 = 0 => (x-y)(x+y) = 0 => يجب أن تحقق النقاط إما المعادلة x - y = 0، أو المعادلة x + y = 0، والتي تتوافق على المستوى زوج من الخطوط المستقيمة المتقاطعة التي تعتبر منصفات للزوايا الإحداثية:

3) x 2 + y 2 = 0. تتحقق هذه المعادلة بنقطة واحدة فقط O(0,0).

2. تعريف: يمكن تحديد أي خط مستقيم على المستوى بمعادلة من الدرجة الأولى

الفأس + وو + C = 0،

علاوة على ذلك، فإن الثوابتين A وB لا يساويان الصفر في نفس الوقت، أي. أ 2 + ب 2 ¹ 0. هذه المعادلة من الدرجة الأولى تسمى المعادلة العامة للخط المستقيم.

اعتمادًا على قيم الثوابت A وB وC، من الممكن حدوث الحالات الخاصة التالية:

C = 0، A ¹ 0، B ¹ 0 – يمر الخط المستقيم عبر نقطة الأصل

A = 0، B ¹ 0، C ¹ 0 (بواسطة + C = 0) - خط مستقيم موازٍ لمحور الثور

B = 0، A ¹ 0، C ¹ 0 (Ax + C = 0) – خط مستقيم موازي لمحور Oy

B = C = 0، A ¹ 0 – يتطابق الخط المستقيم مع محور Oy

أ = ج = 0، ب ¹ 0 – الخط المستقيم يتطابق مع محور الثور

يمكن تقديم معادلة الخط المستقيم بأشكال مختلفة اعتمادًا على أي شروط أولية معينة.

معادلة الخط المستقيم بمعامل الزاوي.

إذا تم تخفيض المعادلة العامة للخط المستقيم Ax + By + C = 0 إلى الشكل:

وتدل على ذلك، ثم تسمى المعادلة الناتجة معادلة الخط المستقيم مع الميل ك.

معادلة الخط المستقيم في القطاعات.

إذا كان في المعادلة العامة للخط المستقيم Аh + Ву + С = 0 С ¹ 0، فبالقسمة على –С نحصل على: أو حيث

المعنى الهندسي للمعاملات هو المعامل أهي إحداثيات نقطة تقاطع الخط مع محور الثور و ب– إحداثيات نقطة تقاطع الخط المستقيم مع محور أوي.

المعادلة العادية للخط.

إذا كان طرفا المعادلة Ax + By + C = 0 مقسوما على رقم يسمى عامل التطبيع، ثم نحصل

xcosj + ysinj - p = 0 – المعادلة العادية للخط المستقيم.

يجب اختيار العلامة ± لعامل التطبيع بحيث تكون m×С< 0.

p هو طول العمودي المسقط من نقطة الأصل إلى الخط المستقيم، وj هي الزاوية التي يشكلها هذا العمود مع الاتجاه الموجب لمحور الثور.

3. معادلة الخط المستقيم باستخدام النقطة والمنحدر.

دع المعامل الزاوي للخط يساوي k، ويمر الخط عبر النقطة M(x 0, y 0). ثم يتم إيجاد معادلة الخط المستقيم بالصيغة: y – y 0 = k(x – x 0)

معادلة الخط الذي يمر بنقطتين.

دع النقطتين M 1 (x 1، y 1، z 1) و M 2 (x 2، y 2، z 2) معطاة في الفضاء، فإن معادلة الخط الذي يمر بهذه النقاط هي:

إذا كان أي من المقامات يساوي صفرًا، فيجب أن يكون البسط المقابل مساويًا للصفر.

على المستوى، تم تبسيط معادلة الخط المستقيم المكتوبة أعلاه:

إذا كان x 1 ¹ x 2 و x = x 1، إذا كان x 1 = x 2.

الكسر = k يسمى ميلمستقيم.

المساواة في الشكل F(x, y) = 0 تسمى معادلة ذات متغيرين x, y إذا لم تكن صحيحة لجميع أزواج الأرقام x, y. يقولون أن الرقمين x = x 0, y = y 0 يحققان بعض المعادلات بالشكل F(x, y) = 0 إذا، عند استبدال هذه الأرقام بدلاً من المتغيرين x وy في المعادلة، يصبح الجانب الأيسر صفرًا .

معادلة خط معين (في نظام إحداثي معين) هي معادلة بمتغيرين تكون محققة لإحداثيات كل نقطة تقع على هذا الخط وغير محققة لإحداثيات كل نقطة لا تقع عليه.

في ما يلي، بدلًا من التعبير "بالنظر إلى معادلة الخط F(x, y) = 0"، سنقول غالبًا بشكل أكثر إيجازًا: بالنظر إلى الخط F(x, y) = 0.

إذا تم إعطاء معادلات خطين: F(x, y) = 0 و Ф(x, y) = 0، فإن الحل المشترك للنظام

F(x,y) = 0, Ф(x, y) = 0

يعطي كل نقاط التقاطع الخاصة بهم. وبتعبير أدق فإن كل زوج من الأرقام التي تشكل حلاً مشتركاً لهذا النظام يحدد إحدى نقاط التقاطع،

157. النقاط المعطاة *) م 1 (2؛ -2)، م 2 (2؛ 2)، م 3 (2؛ - 1)، م 4 (3؛ -3)، م 5 (5؛ -5)، م 6 (3؛ -2). حدد أي النقاط المعطاة تقع على الخط المحدد بالمعادلة x + y = 0 وأيها لا تقع عليه. ما الخط الذي تحدده هذه المعادلة؟ (ارسمه على الرسم.)

158. على الخط المحدد بالمعادلة x 2 + y 2 = 25، ابحث عن النقاط التي تساوي حروفها الإحداثية الأرقام التالية: 1) 0، 2) -3، 3) 5، 4) 7؛ على نفس الخط، ابحث عن نقاط إحداثياتها تساوي الأرقام التالية: 5) 3، 6) -5، 7) -8. ما الخط الذي تحدده هذه المعادلة؟ (ارسمه على الرسم.)

159. حدد الخطوط التي يتم تحديدها بواسطة المعادلات التالية (قم بإنشائها على الرسم): 1)x - y = 0; 2) س + ص = 0؛ 3) س - 2 = 0؛ 4)س + 3 = 0؛ 5) ص - 5 = 0؛ 6) ص + 2 = 0؛ 7) س = 0؛ 8) ص = 0؛ 9) × 2 - س ص = 0؛ 10) س ص + ص 2 = 0؛ 11) × 2 - ص 2 = 0؛ 12) س ص = 0; 13) ص 2 - 9 = 0؛ 14) × 2 - 8س + 15 = 0؛ 15) ص 2 + بواسطة + 4 = 0؛ 16) × 2 ص - 7 س ص + 10 ص = 0؛ 17) ذ - |س|؛ 18) س - |ص|؛ 19) ذ + |س| = 0؛ 20) س + |ص| = 0؛ 21) ص = |س - 1|; 22) ص = |س + 2|; 23) × 2 + ص 2 = 16؛ 24) (س - 2) 2 + (ص - 1) 2 = 16؛ 25 (س + 5) 2 + (ص-1) 2 = 9؛ 26) (س - 1) 2 + ص 2 = 4؛ 27) × 2 + (ص + 3) 2 = 1؛ 28) (س - 3) 2 + ص 2 = 0؛ 29) × 2 + 2ص 2 = 0؛ 30) 2س 2 + 3ص 2 + 5 = 0؛ 31) (س - 2) 2 + (ص + 3) 2 + 1 = 0.

160. الأسطر المعطاة: l)x + y = 0; 2)س - ص = 0؛ 3)س 2 + ص 2 - 36 = 0؛ 4) س 2 + ص 2 - 2س + ص = 0؛ 5) x 2 + y 2 + 4x - 6y - 1 = 0. حدد أي منها يمر بنقطة الأصل.

161. الأسطر المعطاة: 1) × 2 + ص 2 = 49؛ 2) (س - 3) 2 + (ص + 4) 2 = 25؛ 3) (س + 6) 2 + (ص - ي) 2 = 25؛ 4) (س + 5) 2 + (ص - 4) 2 = 9؛ 5) س 2 + ص 2 - 12س + 16ص - 0؛ 6) س 2 + ص 2 - 2س + 8ص + 7 = 0؛ 7) x 2 + y 2 - 6x + 4y + 12 = 0. أوجد نقاط التقاطع: أ) مع محور الثور؛ ب) مع محور أوي.

162. أوجد نقاط تقاطع خطين:

1) س 2 + ص 2 - 8؛ س - ص =0؛

2) س 2 + ص 2 - 16س + 4ص + 18 = 0؛ س + ص = 0؛

3) س 2 + ص 2 - 2س + 4ص - 3 = 0؛ س 2 + ص 2 = 25؛

4) × 2 + ص 2 - 8ص + 10ص + 40 = 0؛ س 2 + ص 2 = 4.

163. في نظام الإحداثيات القطبية، النقاط M 1 (l؛ π/3)، M 2 (2؛ 0)، M 3 (2؛ π/4)، M 4 (√3؛ π/6) وM 5 ( 1; 2/3π). حدد أيًا من هذه النقاط تقع على الخط المحدد في الإحداثيات القطبية بالمعادلة p = 2cosΘ، وأيها لا تقع عليه. ما الخط الذي تحدده هذه المعادلة؟ (ارسمه على الرسم.)

164. على الخط المحدد بالمعادلة p = 3/cosΘ، ابحث عن النقاط التي تساوي زواياها القطبية الأعداد التالية: أ) π/3، ب) - π/3، ج) 0، د) π/6. ما الخط الذي تحدده هذه المعادلة؟ (قم ببنائه على الرسم.)

165. على الخط المحدد بالمعادلة p = 1/sinΘ، أوجد النقاط التي يساوي نصف قطرها القطبي الأعداد التالية: أ) 1 6) 2، ج) √2. ما الخط الذي تحدده هذه المعادلة؟ (قم ببنائه على الرسم.)

166. حدد الخطوط التي يتم تحديدها في الإحداثيات القطبية من خلال المعادلات التالية (قم بإنشائها على الرسم): 1) ع = 5؛ 2) Θ = π/2؛ 3) Θ = - π/4؛ 4) ص كوسΘ = 2؛ 5) ع الخطيئةΘ = 1؛ 6.) ع = 6cosΘ؛ 7) ع = 10 خطيئةΘ؛ 8) الخطيئةΘ = 1/2؛ 9) جيب = 1/2.

167. أنشئ حلزونات أرخميدس التالية على الرسم: 1) ع = 20؛ 2) ع = 50؛ 3) ع = Θ/π؛ 4) ع = -Θ/π.

168. قم ببناء اللوالب الزائدية التالية على الرسم: 1) p = 1/Θ؛ 2) ع = 5/Θ؛ 3) ع = π/Θ؛ 4) ع= - ط/Θ

169. قم ببناء اللوالب اللوغاريتمية التالية على الرسم: 1) p = 2 Θ؛ 2) ع = (1/2) Θ.

170. حدد أطوال المقاطع التي يتم فيها قطع دوامة أرخميدس p = 3Θ بواسطة شعاع يخرج من القطب ويميل إلى المحور القطبي بزاوية Θ = π/6. جعل الرسم.

171. في دوامة أرخميدس p = 5/πΘ، يتم أخذ النقطة C، ونصف القطر القطبي لها 47. حدد عدد الأجزاء التي تقطعها هذه الدوامة نصف القطر القطبي للنقطة C. ارسم رسمًا.

172. في دوامة زائدية P = 6/Θ، أوجد النقطة P التي يبلغ نصف قطرها القطبي 12. ارسم رسمًا.

173. في دوامة لوغاريتمية p = 3 Θ، أوجد النقطة P التي يبلغ نصف قطرها القطبي 81. ارسم رسمًا.