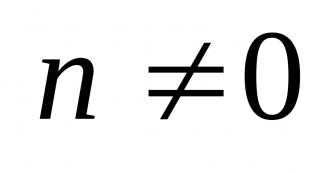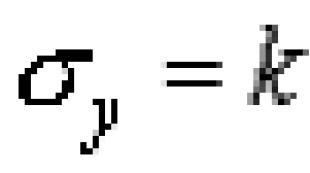hunarmandchilik

Elastiklik nazariyasidagi masalalar turlari. Elastiklik nazariyasining asosiy tenglamalari. Elastiklik nazariyasidagi muammolar turlari Elastiklikning klassik nazariyasi nimani o'rganadi.

Rossiya davlat universiteti

ularni neft va gaz. I.M.Gubkina

Texnik mexanika kafedrasi

ANTRACT

"Elastiklik nazariyasi"

To'ldiruvchi: Polyakov A. A.

Tekshirildi: Evdokimov A.P.

Moskva 2011 yil

elastiklik nazariyasi tenglamasi

1.Kirish

Tananing bir nuqtasida kuchlanish-deformatsiya holati nazariyasi

2.1 Stress nazariyasi

2 Deformatsiyalar nazariyasi

3 Elastik jismlar uchun kuchlanish va deformatsiyalangan holat o'rtasidagi bog'liqlik

Elastiklik nazariyasining asosiy tenglamalari. Elastiklik nazariyasidagi masalalar turlari

1 Elastiklik nazariyasining asosiy tenglamalari

2 Elastiklik nazariyasidagi masalalar turlari

4 Ko`chishlardagi elastiklik nazariyasi tenglamalari (cho`loq tenglamalar)

Elastiklik nazariyasining variatsion tamoyillari

1 Mumkin bo'lgan siljishlar printsipi (Lagrange printsipi)

2 Mumkin bo'lgan holatlar printsipi (Kastilyano printsipi)

3 Lagrange va Castigliano tamoyillari asosida aniq yechim va olingan yechimlar o'rtasidagi bog'liqlik

Foydalanilgan adabiyotlar ro'yxati

1.Kirish

Kuchlanish va deformatsiyalar nazariyalarini O. Koshi yaratgan. Ular 1822 yilda Parij Fanlar akademiyasiga taqdim etilgan ishda bayon etilgan, uning qisqacha mazmuni 1823 yilda nashr etilgan va bir qator keyingi maqolalar. O.Koshi elementar tetraedr muvozanatining uchta tenglamasini chiqardi, tangensial kuchlanishlarning juftlashuv qonunini isbotladi, bosh o‘qlar va bosh kuchlanishlar tushunchalarini kiritdi va differensial muvozanat tenglamalarini chiqardi (odatda ular kuchlilik jarayonida chiqarilmaydi). materiallar). U, shuningdek, radius vektorlarining uchlari joylashgan, yo'nalishlari normallarning maydonlarga yo'nalishi bilan mos keladigan va qiymati kvadrat ildizga teskari proportsional bo'lgan normal kuchlanishlar yuzasini (Koshi kvadrati) kiritdi. bu sohadagi normal kuchlanishning mutlaq qiymatiga teng bo'ldi va bu sirt koordinata boshida joylashgan ikkinchi tartibli sirt ekanligi isbotlandi. Oddiy kuchlanishlar sirtini asosiy o'qlarga aylantirish imkoniyati har bir nuqtada uchta o'zaro asosiy perpendikulyar maydon mavjudligini ko'rsatadi.

Xuddi shunday siljish kuchlanish yuzasi rossiyalik mexanik G.V. Kolosov 1933 yil

Kosmosdagi kuchlanish holatining kuchlanish ellipsoidi shaklida geometrik talqini G. Lame va B. Klapeyron tomonidan 1828 yilda Parij Fanlar akademiyasiga taqdim etilgan va 1833 yilda nashr etilgan xotiralarida berilgan.

Asosiy o'qdan o'tuvchi platformalarning bir qatori uchun tekislikda kuchlanish holatini, kuchlanishlar doirasi shaklida geometrik tasvirni K.Kulman 1866 yilda o'z kitobida taklif qilgan.

Stress holatining umumiy holati uchun uning tekislikda juda aniq geometrik talqini 1882 yilda O. Mohr (aylana Mohr diagrammasi deb ataladi) tomonidan berilgan. Undan bir qator muhim xulosalar chiqarish mumkin. asosiy kuchlanishlarning ekstremalligi, tangensial kuchlanishlar maksimal bo'lgan maydonlarning holati va ushbu maksimal kesish kuchlanishlarining qiymatlari haqida.

O. Koshi deformatsiyalarga ta’rif berdi, kichik deformatsiyalarning alohida holatida ularning siljishlarga bog‘liqligini chiqardi (bu bog‘liqliklar, qoida tariqasida, materiallarning mustahkamligi jarayonida kelib chiqmaydi), asosiy kuchlanish va asosiy kuchlanish tushunchalarini aniqladi. shtammlarni aniqladi va kuchlanish komponentlarining izotropik va anizotrop elastik jismga nisbatan deformatsiya komponentlariga bog'liqligini oldi. Materiallarning qarshiligida, odatda, izotrop jism uchun deformatsiya komponentlarining kuchlanish komponentlariga bog'liqligi aniqlanadi. Ular umumlashtirilgan Guk qonuni deb ataladi, garchi, albatta, bu nom shartli, chunki R.Guk stress tushunchasini bilmagan.

Ushbu bog'liqliklarda Koshi birinchi bo'lib ikkita konstantani kiritdi va kuchlanishlarning deformatsiyalarga bog'liqligini shaklda yozdi.

m, ,

Biroq, keyinchalik O. Koshi L. Navier kontseptsiyasini qabul qildi. Unga ko'ra, elastik jismlar molekulalardan iborat bo'lib, ular orasida deformatsiya paytida molekulalarni bog'laydigan to'g'ri chiziqlar yo'nalishi bo'yicha harakat qiladigan va molekulalar orasidagi masofalarning o'zgarishiga mutanosib bo'lgan kuchlar paydo bo'ladi. U holda anizotrop jismning umumiy holati uchun elastik konstantalar soni 15 ta, izotrop jism uchun esa bitta elastik konstantani olamiz. S. Puasson bu gipotezaga amal qildi va boshida - G. Lame va B. Klapeyron. Unga asoslanib, Puasson ko'ndalang deformatsiya koeffitsienti 1/4 ekanligini aniqladi.

D. Green 1839 yilda elastik jismlarning molekulyar tuzilishi haqidagi gipotezadan foydalanmasdan deformatsiyalar va kuchlanishlar o'rtasidagi bog'liqlikni keltirib chiqardi. U ularni energiyani saqlash tamoyiliga asoslanib, elastik potentsial tushunchasini kiritgan holda oldi va olti kuchlanish komponentiga olti deformatsiya komponentining chiziqli bog'liqligini qo'llashda 36 koeffitsientdan 21 tasi mustaqil, ya'ni umumiy holatda ekanligini ko'rsatdi. anizotrop jism, elastik konstantalar soni 21 Izotrop jism uchun elastik konstantalar soni ikkiga kamayadi. Anizotrop jism uchun elastik konstantalar soni 15 ga, izotrop jism uchun 1 ga teng bo'lgan nazariya ba'zan "rarik konstanta" yoki "uniconstant" deb ataladi va anizotrop jism uchun elastik konstantalar soni 21, va izotrop 2 uchun - "ko'p doimiy" .

Ushbu nazariyalar tarafdorlari o'rtasidagi tortishuv fiziklarni eksperimental tadqiqotlarga undadi.

G. Wertheim, eksenel taranglikda shisha va metall quvurlarning ichki hajmlarini o'lchashga asoslanib, 1848 yilda ko'ndalang deformatsiya koeffitsienti 1/4 ga teng emasligini aniqladi. U turli materiallar uchun uni boshqacha deb hisobladi, lekin ko'p materiallar uchun u 1/3 ga yaqin edi.

VA MEN. Kupffer 1853 yilda metall rodlarni kuchlanish va buralish uchun sinovdan o'tkazar ekan, shuningdek, siljish va kuchlanishdagi modullarning nisbati 1/4 ga teng bo'lgan ko'ndalang deformatsiyaga mos kelmasligini aniqladi.

1855 yilda F. Neumann to'rtburchaklar kesimning namunalarini bükme uchun sinovdan o'tkazdi va nurning ikki yuzining burilish burchaklarini o'lchadi (kesma trapezoidal shaklni oladi). Natijada, u ko'ndalang deformatsiya koeffitsienti 1/4 ga teng emasligini ko'rsatdi. F.Neymanning shogirdi G.Kirxgof 1859-yilda bir uchi muhrlangan va ikkinchi uchiga konsentrlangan kuch bilan yuklangan dumaloq guruch novdalarning qoʻshma egilishi va buralishi boʻyicha oʻtkazilgan sinovlar asosida shunday xulosaga keldi. novda burilish burchagi va bo'limning burilish burchagi o'lchovi.

Har xil turdagi po'latlar uchun ko'ndalang deformatsiya koeffitsientlarining katta eksperimental tadqiqoti G. Kirchhoffning talabalaridan biri M.F. Okatov 1865-1866 yillarda Natijalar uning doktorlik dissertatsiyasida keltirilgan.Monokristallardan kesilgan yupqa prizmalarning buralish va egilish sinovlari, shuningdek, kristallarning bir xilda teng siqilish sharoitida siqilish sinovlari V.Foygt tomonidan o‘tkazilgan va keyinchalik o‘zining ko‘plab maqolalarida bayon etilgan. 1910 yilda nashr etilgan kitobda birlashtirildi Ular ko'p doimiy nazariyaning to'g'riligini tasdiqladilar.

Anizotrop jismlar uchun Guk qonunining matematik tuzilishini chuqur o'rganish mexanik va muhandis Yan Rychlevskiy tomonidan 1984 yilda o'zi kiritgan elastik xos holat tushunchasi asosida amalga oshirildi. Xususan, u 21 elastik konstanta oltita haqiqiy qattiqlik modulini, 12 qattiqlik distribyutorini va uchta burchakni ifodalashini ko'rsatdi.

2. Jismning bir nuqtasida kuchlanish-deformatsiya holati nazariyasi

1 Stress nazariyasi

Elastik jism yuklanganda paydo bo'ladigan ichki kuch omillari tananing ma'lum bir qismining holatini tavsiflaydi, lekin kesmaning qaysi nuqtasi eng ko'p yuklangan yoki ular aytganidek, xavfli nuqta degan savolga javob bermaydi. Shuning uchun tananing ma'lum bir nuqtadagi holatini tavsiflovchi qo'shimcha miqdorni hisobga olish kerak.

Agar tashqi kuchlar qo'llaniladigan jism muvozanatda bo'lsa, uning biron bir qismida ichki qarshilik kuchlari paydo bo'ladi. Elementar maydonga ta'sir qiluvchi ichki kuch bilan belgilang va bu maydon uchun normal qiymatni keyin

to'liq kuchlanish deb ataladi.

Umumiy holda, umumiy kuchlanish oddiy elementar maydon yo'nalishiga to'g'ri kelmaydi, shuning uchun uning tarkibiy qismlari bilan koordinata o'qlari bo'ylab ishlash qulayroqdir -

Agar tashqi normal har qanday koordinata o'qiga, masalan, X o'qiga to'g'ri keladigan bo'lsa, unda kuchlanish komponentlari shaklni oladi, komponent esa kesmaga perpendikulyar bo'lib chiqadi va normal stress deb ataladi va komponentlar ichida yotadi. kesim tekisligi va siljish kuchlanishlari deyiladi.

Oddiy va kesish kuchlanishlarini osongina ajratish uchun odatda boshqa belgilar qo'llaniladi: - normal kuchlanish, - kesish.

Tashqi kuchlar ta'sirida yuzlari koordinata tekisliklariga parallel bo'lgan va qirralari uzunligi bo'lgan cheksiz kichik parallelepipedni tanadan ajratib olaylik. Bunday elementar parallelepipedning har bir yuzida koordinata o'qlariga parallel bo'lgan uchta kuchlanish komponenti mavjud. Hammasi bo'lib, biz oltita yuzda 18 ta stress komponentini olamiz.

Oddiy stresslar quyidagicha belgilanadi, bu erda indeks mos keladigan yuzga nisbatan normalni bildiradi (ya'ni qiymatlarni qabul qilishi mumkin). Kesish kuchlanishlari shaklga ega; bu erda birinchi indeks berilgan siljish kuchlanishi harakat qiladigan saytning normaliga mos keladi, ikkinchisi esa bu kuchlanish yo'naltirilgan parallel o'qni ko'rsatadi (1-rasm).

1-rasm. Oddiy va kesish kuchlanishlari

Ushbu kuchlanishlar uchun quyidagi belgi qoidasi qabul qilinadi. Oddiy stress kuchlanishda ijobiy yoki ekvivalent, u harakat qiladigan joyga tashqi normal yo'nalishga to'g'ri kelganda hisoblanadi. Tangensial kuchlanish, agar normal holat unga parallel bo'lgan koordinata o'qi yo'nalishiga to'g'ri keladigan joyda, ushbu kuchlanishga mos keladigan musbat koordinata o'qiga yo'naltirilgan bo'lsa, ijobiy hisoblanadi.

Stress komponentlari uchta koordinataning funktsiyalari. Masalan, koordinatali nuqtadagi normal kuchlanishni belgilash mumkin

Ko'rib chiqilayotgan nuqtadan cheksiz kichik masofada joylashgan nuqtada, kuchlanish birinchi tartibdagi cheksiz kichiklarga qadar Teylor qatorida kengaytirilishi mumkin:

Tekislikka parallel bo'lgan platformalar uchun faqat x koordinatasi va o'sishlar o'zgaradi, shuning uchun tekislikka to'g'ri keladigan parallelepipedning yuzida normal kuchlanish bo'ladi. Shuning uchun, 18 ta kuchlanish komponentidan faqat to'qqiztasi noma'lum.

Elastiklik nazariyasida kesishish kuchlanishlarining juftlashuv qonuni isbotlangan, unga ko'ra ikkita o'zaro perpendikulyar maydon bo'ylab, bu sohalarning kesishish chiziqlariga perpendikulyar bo'lgan kesishish kuchlanishlarining tarkibiy qismlari bir-biriga tengdir:

Tenglik (2) shuni anglatadiki, tananing bir nuqtasida stress holatini tavsiflovchi to'qqizta stress komponentidan faqat oltitasi qoladi:

Ko'rsatish mumkinki, stresslar (3) nafaqat ma'lum bir nuqtada tananing stress holatini tavsiflaydi, balki uni o'ziga xos tarzda belgilaydi. Ushbu kuchlanishlarning kombinatsiyasi kuchlanish tensori deb ataladigan nosimmetrik matritsani hosil qiladi:

(4)

Tensorni skalyar qiymatga ko'paytirishda barcha komponentlari dastlabki tensorning tarkibiy qismlaridan bir necha marta katta bo'lgan yangi tensor olinadi.

2 Deformatsiyalar nazariyasi

Tashqi yuklarning ta'siri ostida elastik tanasi shaklini o'zgartiradi va deformatsiyalanadi. Bunday holda, tananing nuqtalari qandaydir yangi pozitsiyani egallaydi. Elastik tananing deformatsiyasini aniqlash uchun biz yukni qo'llashdan oldin va keyin tananing nuqtalarining pozitsiyalarini taqqoslaymiz.

Yuklanmagan tananing nuqtasini va yuk qo'llanilgandan keyin uning yangi holatini ko'rib chiqing. Vektor nuqta siljishi vektori deb ataladi (2-rasm).

2-rasm. Nuqta harakatlanuvchi vektor

Ikki turdagi siljishlar mumkin: butun jismning deformatsiyasiz siljishi - bunday siljishlar nazariy mexanika tomonidan mutlaqo qattiq jismning siljishi va tananing deformatsiyasi bilan bog'liq bo'lgan siljishlar - bunday siljishlar nazariya tomonidan o'rganiladi. elastiklikdan.

Nuqtaning siljishi vektorining koordinata o'qlaridagi proyeksiyalarini mos ravishda belgilaymiz. Ular nuqtalarning mos keladigan koordinatalari orasidagi farqga teng va:

va koordinatalarning funktsiyalari:

Tananing deformatsiyasi uning turli nuqtalarining siljishlaridagi farq tufayli yuzaga keladi. Cheksiz kichik parallelepiped chetlari ixtiyoriy nuqtaga yaqin joylashgan elastik jismdan kesilgan , uning nuqtalarining turli xil siljishi tufayli shunday deformatsiyalanadiki, uning qirralari uzunligi o'zgaradi va yuzlar orasidagi dastlab to'g'ri burchaklar buziladi.

3.3-rasmda ushbu parallelepipedning ikkita qirrasi ko'rsatilgan: va qirrasining uzunligi teng va qirrasi

Deformatsiyadan so'ng nuqtalar o'z o'rnini egallaydi.Bu holda nuqta chizma tekisligidagi komponentlari teng bo'lgan siljishni oladi va cheksiz kichik masofada nuqtadan ajratilgan nuqta siljishni oladi. uning komponentlari koordinata o'zgarishi sababli nuqtaning siljishining tarkibiy qismlaridan cheksiz kichik qiymat bilan farq qiladi.

3-rasm. Chiziqli va burchakli deformatsiyalar

Nuqta siljishining komponentlari koordinataning o'zgarishi tufayli nuqta siljishining tarkibiy qismlaridan cheksiz kichik qiymat bilan farq qiladi.

Deformatsiyadan keyin qovurg'aning o'qdagi proektsiyasining uzunligi:

Qovurg'aning mutlaq cho'zilishining eksa bo'yicha proyeksiyasi

Eksa bo'ylab nisbiy cho'zilish

(6)

o'q yo'nalishidagi chiziqli deformatsiya deyiladi.

Xuddi shunday, o'qlarning yo'nalishlari bo'ylab chiziqli deformatsiyalar va

(7)

Parallelepipedning qirralari orasidagi burchaklarning o'zgarishini ko'rib chiqing (3-rasm). Qovurg'aning tekislikdagi burilish burchagi tangensi

Deformatsiyalarning kichikligi tufayli a, chiziqli deformatsiyani birlikka nisbatan kichikligi tufayli e'tiborsiz qoldirish mumkin, keyin esa

Xuddi shunday, siz bir xil tekislikda qovurg'aning burilish burchagini aniqlashingiz mumkin:

To'g'ri burchakning buzilishi burchak deformatsiyasi deb ataladi va qovurg'alarning burilish burchaklarining yig'indisi sifatida aniqlanadi va:

(8)

Xuddi shu tarzda, boshqa ikkita koordinata tekisligidagi burchak deformatsiyalari aniqlanadi:

(9)

Formulalar (6)-(9) siljish komponentlariga chiziqli va burchakli deformatsiyalar uchun oltita asosiy bog'liqlikni beradi. Ushbu bog'liqliklar Koshi tenglamalari deb ataladi:

(10)

Parallelepiped qirralarining uzunligi nolga moyil bo'lgan chegarada, Koshi munosabatlari nuqta yaqinidagi chiziqli va burchakli deformatsiyalarni aniqlaydi.

Ijobiy chiziqli deformatsiyalar cho'zilishlarga, manfiylar esa qisqarishlarga mos keladi. Tegishli koordinata o'qlarining musbat yo'nalishlari orasidagi burchak pasayganda va salbiy - aks holda, siljish burchagi ijobiy hisoblanadi.

Stress tensoriga o'xshab, ma'lum bir nuqtada tananing deformatsiyalangan holati deformatsiya tenzori bilan tavsiflanadi.

(11)

Stress tensori singari, kuchlanish tensori ham to'qqizta komponentni o'z ichiga olgan nosimmetrik matritsa bo'lib, ulardan oltitasi boshqacha.

2.3 Elastik jismlar uchun kuchlanish va deformatsiya o'rtasidagi bog'liqlik

Stress va kuchlanish o'rtasidagi munosabatlar jismoniy xususiyatga ega. Kichik shtammlar bilan cheklangan, kuchlanish va deformatsiyalar o'rtasidagi munosabatlar chiziqli deb hisoblanishi mumkin.

Tayoqni kuchlanishda sinab ko'rishda (materiallarni mexanik sinovdan o'tkazish keyingi bo'limda batafsil ko'rib chiqiladi) bir yo'nalishdagi normal kuchlanish va chiziqli deformatsiya o'rtasida mutanosib bog'liqlik o'rnatiladi, bu Huk qonuni deb ataladi:

bu yerda elastik konstanta uzunlamasına elastiklik moduli deyiladi.

Xuddi shu eksperimental tarzda, uzunlamasına va ko'ndalang yo'nalishdagi chiziqli deformatsiyalar o'rtasida bog'liqlik o'rnatildi:

bu erda - ko'ndalang yo'nalishdagi chiziqli deformatsiya, - ikkinchi elastik doimiy, Puasson nisbati deb ataladi.

Sof siljish uchun mexanik sinovlarda kesishish kuchlanishi va bu kuchlanishning harakat tekisligidagi burchak deformatsiyasi o'rtasida to'g'ridan-to'g'ri proportsional bog'liqlik o'rnatildi, bu kesishishdagi Guk qonuni deb nomlandi:

bu erda qiymat uchinchi elastik konstanta bo'lib, kesish moduli deb ataladi. Biroq, bu elastik doimiy mustaqil emas, chunki birinchi ikkitasi bilan bog'liq

Deformatsiyalar va kuchlanishlar o'rtasidagi munosabatni o'rnatish uchun biz tanadan cheksiz kichik parallelepipedni tanlaymiz (1-rasm) va faqat oddiy kuchlanishlarning ta'sirini ko'rib chiqamiz. kichiklikning yuqori tartibidagi deformatsiyalarga olib keladi.

Qovurg'aning kuchlanishga parallel bo'lgan cho'zilishi aniqlansin. Ushbu kuchlanish ta'sirida Guk qonuniga (3.12) ko'ra, qovurg'aning nisbiy cho'zilishi sodir bo'ladi.

Stress qovurg'aga perpendikulyar yo'nalishda xuddi shunday cho'zilishni keltirib chiqaradi

va qovurg'a yo'nalishi bo'yicha - qisqarish, (13) ga muvofiq

yoki deformatsiya ifodasini hisobga olgan holda

Xuddi shunday, stress ta'sirida qovurg'aning nisbiy qisqarishi aniqlanadi

Kuchlar ta'sirining mustaqilligi printsipiga asoslanib, qovurg'aning umumiy nisbiy cho'zilishi har bir kuchlanish ta'siridan cho'zilishlar yig'indisi sifatida aniqlanishi mumkin:

Xuddi shunday, boshqa ikkita o'qning yo'nalishlari bo'yicha chiziqli deformatsiyalarni aniqlash mumkin:

Siqilishdagi Guk qonuniga (14) muvofiq, burchak deformatsiyalari va siljish kuchlanishlari o'rtasidagi bog'liqlik koordinata tekisliklariga parallel bo'lgan uchta tekislikning har biri uchun mustaqil ravishda ifodalanishi mumkin:

Shunday qilib, izotropik elastik jismdagi deformatsiya va kuchlanish komponentlari orasidagi chiziqli munosabatni ifodalovchi oltita formula olindi va ular umumlashtirilgan Guk qonuni deb ataladi:

(16)

3. Elastiklik nazariyasining asosiy tenglamalari. Elastiklik nazariyasidagi masalalar turlari

Elastiklik nazariyasining asosiy vazifasi tanani yuklash va mahkamlashning berilgan shartlariga muvofiq kuchlanish-deformatsiya holatini aniqlashdir.

Stress-deformatsiya holati, agar kuchlanish tensorlari (lar) va siljish vektorining tarkibiy qismlari to'qqizta funktsiya topilsa, aniqlanadi.

3.1 Elastiklik nazariyasining asosiy tenglamalari

Ushbu to'qqiz funktsiyani topish uchun elastiklik nazariyasining asosiy tenglamalarini yozish kerak, yoki:

Differensial Cauchies

(17)

Koshi deformatsiyalarining chiziqli qismi tenzorining komponentlari qayerda;

radius bo'ylab siljish hosilasining tenzorining komponentlari.

Differensial muvozanat tenglamalari

stress tensor komponentlari qayerda; j o'qiga jism kuchining proyeksiyasi.

Chiziqli elastik izotrop jism uchun Guk qonuni

oqsoq konstantalar qayerda; izotrop tana uchun. Bu erda normal va kesish stresslari; navbati bilan deformatsiya va kesish burchaklari.

Yuqoridagi tenglamalar Sen-Venant bog'liqliklarini qondirishi kerak

Elastiklik nazariyasida barcha asosiy tenglamalar qanoatlansa, masala yechiladi.

2 Elastiklik nazariyasidagi masalalar turlari

Jism yuzasidagi chegaraviy shartlar qanoatlantirilishi kerak va chegaraviy shartlarning turiga qarab elastiklik nazariyasida uch xil masalalar mavjud.

Birinchi tur. Kuchlar tananing yuzasiga beriladi. Chegara shartlari

Ikkinchi tur. Tana yuzasida siljish ko'rsatilgan muammolar. Chegara shartlari

Uchinchi tur. Elastiklik nazariyasining aralash muammolari. Kuchlar tana yuzasining bir qismida, siljish tana yuzasining bir qismida beriladi. Chegara shartlari

Tana yuzasida kuchlar yoki siljishlar aniqlangan, lekin tananing ichidagi kuchlanish-deformatsiya holatini topish talab qilinadigan va sirtda aniqlanmagan masalalar to'g'ridan-to'g'ri masalalar deyiladi. Ammo, agar tananing ichida kuchlanishlar, deformatsiyalar, siljishlar va boshqalar ko'rsatilgan bo'lsa va tananing ichida ko'rsatilmagan narsalarni, shuningdek, tananing sirtidagi siljishlar va kuchlanishlarni aniqlash kerak bo'lsa (ya'ni, bunday stress-deformatsiya holatini keltirib chiqargan sabablar)), keyin bunday muammolar teskari deb ataladi.

4 Ko`chishlardagi elastiklik nazariyasi tenglamalari (cho`loq tenglamalar)

Ko'chishlardagi elastiklik nazariyasi tenglamalarini aniqlash uchun biz yozamiz: differensial muvozanat tenglamalari (18) Chiziqli elastik izotrop jism uchun Guk qonuni (19)

Agar deformatsiyalar siljishlar (17) bilan ifodalanishini hisobga olsak, yozamiz:

Shuni ham eslatib o'tish kerakki, kesish burchagi siljishlar bilan quyidagi bog'liqlik bilan bog'liq (17):

(23)

(22) ifodani (19) tengliklarning birinchi tenglamasiga qo'yib, biz normal stresslarni olamiz.

(24)

E'tibor bering, bu holda u belgisi i ustidan yig'indini bildirmaydi.

(23) ifodani ikkinchi tenglik (19) tenglamasiga qo'yib, biz kesishish kuchlanishlarini olamiz.

(25)

Muvozanat tenglamalarini (18) j = 1 uchun kengaytirilgan shaklda yozamiz

(26)

Oddiy (24) va tangensial (25) kuchlanishlarni (26) tenglamaga almashtirib, biz hosil bo'lamiz.

Bu erda l - oqsoqlangan doimiy, u quyidagi ifoda bilan aniqlanadi:

(28) ifodani (27) tenglamaga almashtiramiz va yozamiz:

bu yerda (22) ifoda bilan yoki kengaytirilgan shaklda aniqlanadi

Biz (29) ifodani G ga bo'lamiz va shunga o'xshash shartlarni qo'shamiz va birinchi Lame tenglamasini olamiz:

(30)

Bu erda Laplas operatori (garmonik operator), u sifatida aniqlanadi

(31)

Xuddi shunday, siz quyidagilarni olishingiz mumkin:

(32)

(30) va (32) tenglamalarni quyidagicha yozish mumkin:

(33)

(33) yoki (30) va (32) tenglamalar oqsoq tenglamalardir. Agar tana kuchlari nolga teng yoki doimiy bo'lsa, u holda

(34)

bundan tashqari, bu holda belgi i ustidan yig'indini bildirmaydi. Bu yerga

Ko'rsatish mumkinki, ko'chishlarning garmonik funktsiya nuqtai nazaridan bunday tasviri Lame tenglamalarni (33) o'ziga xoslikka aylantiradi. Ko'pincha ular Popkovich-Grodskiy sharoitlari deb ataladi. To'rt garmonik funktsiya shart emas, chunki ph0 ni nolga tenglashtirish mumkin.

4. Elastiklik nazariyasining variatsion tamoyillari.

1 Mumkin bo'lgan siljishlar printsipi (Lagrange printsipi)

Lagrange printsipi. Muvozanat holatidagi jism uchun tashqi va ichki kuchlarning har qanday mumkin bo'lgan cheksiz kichik siljishlar bo'yicha ishi nolga teng.

Klapeyron teoremasidan foydalanib, elastik deformatsiyalangan jism uchun siljishni o'zgartirib, biz Lagranj printsipini olamiz.

Deformatsiyalanadigan jismlar mexanikasida tanaga qo'yilgan tashqi va ichki cheklovlarni qondiradigan bunday siljishlar mumkin.

Tashqi ulanishlar - mahkamlash uchun shartlar, ichki ulanishlar - uzluksizlik sharti.

Ichki cheklovlarni qondirish uchun siljish o'sishlari koordinatalarning uzluksiz bir qiymatli funktsiyalari bo'lishi kerak.

Bu shaklda Lagranj printsipi har qanday deformatsiyalanuvchi jismlar uchun amal qiladi.

Elastik jismlar uchun shunday olingan

(41)

Keyin (41) ni hisobga olgan holda (40) sifatida yozish mumkin

(42)

bu erda W - o'ziga xos kuchlanish va

Bu erda U - tananing butun potensial energiyasining o'zgarishi.

(43) ifodani (42) o'rniga qo'yamiz va kuchlar o'zgarmasligi uchun shunday yozamiz.

(44)

(44) tenglama - variatsion Lagranj tenglamasi.

Agar kuchlar konservativ bo'lsa, unda dastlabki ikkita integral deformatsiyalanmagan holatdan deformatsiyalangan holatga o'tish paytida tashqi kuchlar potentsialining o'zgarishini ifodalaydi.

Tashqi kuchlarning potentsiali

(45)

bu erda - deformatsiyalanmagan holatdan deformatsiyalangan holatga o'tishda tashqi kuchlarning mumkin bo'lgan ishi tashqi kuchlar o'zgarishsiz qoladi degan faraz bilan hisoblanadi. Tizimning umumiy energiyasi

Keyin (44) - (46) iboralarni hisobga olgan holda Lagranj printsipi yoziladi:

ya'ni muvozanat holatidagi sistemaning umumiy energiyasining mumkin bo'lgan siljishlar bo'yicha o'zgarishi nolga teng. (47) ifoda faqat konservativ kuchlar ta'siridagi Lagranj variatsion tenglamasidir.

Barqaror muvozanat holatida umumiy energiya P minimal,

Lagrange printsipi - minimal energiya printsipi.

2 Mumkin bo'lgan holatlar printsipi (Kastilyano printsipi)

Biz tashqi va ichki kuchlarga mos keladigan, ya'ni muvozanat tenglamalarini qanoatlantiradigan holatlarni mumkin bo'lgan holatlar deb ataymiz.

Tenglama (57) Castigliano printsipini yozadi. Tananing kuchlanish holatidagi mumkin bo'lgan o'zgarishlar bilan, o'zgaruvchanlik mumkin bo'lgan sirt kuchlari va siljishlar mahsulotidan siljishlar berilgan tana yuzasining o'sha qismidagi integralga tengdir.

3 Lagrange va Castigliano tamoyillari asosida aniq yechim va olingan yechimlar o'rtasidagi bog'liqlik

Lagrange printsipiga asoslanib, ba'zi funktsiyalarni yoki ularning to'plamini tanlash va funktsiyalar to'plami cheklanganligi sababli, biz tizimning kamroq erkinlik darajalarini olamiz va shu bilan strukturaning erkinlik darajalarini kamaytiramiz. Ya'ni, energiya ma'nosida, yechim aniq bo'lganidan ko'ra qattiqroq bo'lib chiqadi.

Agar biz integral xarakteristikalarni oladigan bo'lsak, u holda taxminiy yechim yanada qat'iy integraldir.

Menteşali nurni oraliqning o'rtasiga ko'ndalang kuch bilan yuklash masalasini hal qilishda (1-rasm), taxminiy yechim aniq echimga qaraganda kuch ostida kichikroq siljishni beradi.

aniq yechim

Xuddi shu masalani Castigliano variatsion printsipi yordamida hal qilishda, uzluksizlik sharti bajarilmaganligi sababli, tizim haqiqatdan ko'ra ko'proq erkinlikka ega bo'ladi.

Aniq yechim bu ikki taxminiy usul (Lagrange va Castigliano) o'rtasida yotadi. Ba'zida olingan eritmalar orasidagi farq kichikdir.

5. Foydalanilgan adabiyotlar ro‘yxati

1. Aleksandrov A.V., Potapov V.D. Elastiklik va plastiklik nazariyasi asoslari. 400 bet.Oliy maktab.1990 yil.

2. Veretimus D.K. Elastiklik nazariyasi asoslari I qism. Stress nazariyasi “Elastiklik va plastiklik nazariyasi asoslari” kursi bo’yicha uslubiy qo’llanma. 2005.-37s.

Veretimus D.K. Elastiklik nazariyasi asoslari.II qism.Deformatsiyalar nazariyasi. Kuchlangan va deformatsiyalangan holatning munosabati.“Elastiklik va plastiklik nazariyasi asoslari” kursi boʻyicha uslubiy qoʻllanma, 2005.-53b.

Veretimus D.K. Elastiklik nazariyasi asoslari III qism.Elastiklik nazariyasining asosiy tenglamalari.Elastiklik nazariyasiga oid masalalar turlari.“Elastiklik va plastiklik nazariyasi asoslari” kursi boʻyicha uslubiy qoʻllanma, 2005.-45b.

Tinch holatda yoki yuklar ta'sirida harakatlanuvchi jismlarda.

1. Elastiklik nazariyasi muammosi

Ushbu nazariyaning vazifasi matematik tenglamalarni yozishdan iborat bo'lib, ularning echimi quyidagi savollarga javob berishga imkon beradi:

Agar ma'lum bir jismga ma'lum joylarda ma'lum qiymatdagi yuklar qo'llanilsa, uning deformatsiyalari qanday bo'ladi?
tanadagi kuchlanish qanday bo'ladi?

Savol shundaki, tana qulab tushadi, bu yuklarga bardosh beradi, elastiklik nazariyasi bilan chambarchas bog'liq, ammo, qat'iy aytganda, uning vakolatiga kirmaydi.

Ko'plab misollar mavjud - tayanchlarda yuklangan nurda deformatsiyalar va kuchlanishlarni aniqlashdan tortib, samolyot, raketa, suv osti kemasi tanasida, avtomobil g'ildiragida tank zirhidagi bir xil parametrlarni hisoblashgacha. snaryad, tog 'tizmasiga, adit yotqizayotganda, ko'p qavatli bino ramkasiga va hokazo.

Muhandislik muammolari uchun strukturalardagi kuchlanish va deformatsiyalar elastiklik nazariyasiga mantiqiy asoslanib, soddalashtirilgan nazariyalar bo'yicha hisoblanadi. Bu nazariyalarga quyidagilar kiradi: materiallarning mustahkamligi, uning vazifasi novdalar va nurlarni hisoblash, shuningdek, qattiq jismlarning kontaktli o'zaro ta'siri zonalarida paydo bo'ladigan kuchlanishlarni baholash; strukturaviy mexanika- bar tizimlarini loyihalash (masalan, ko'priklar) va qobiq nazariyasi- deformatsiya va kuchlanish fanining mustaqil va yaxshi rivojlangan tarmog'i bo'lib, uning predmeti ingichka devorli qobiqlar - silindrsimon, konussimon, sharsimon va murakkab shakllardir.

2. Elastiklik nazariyasining asosiy tushunchalari

Elastiklik nazariyasining asosiy tushunchalari - kichik tekisliklarga ta'sir etuvchi kuchlanish, berilgan P nuqta orqali tanada aqliy ravishda tortilishi mumkin bo'lgan kuchlanish, P nuqtaning kichik qo'shnisining deformatsiyasi va P nuqtaning o'zini siljishi. aniq, mexanik kuchlanish tensori, kichik deformatsiya tensori va siljish vektori kiritilgan. u i. Qisqacha belgi , Qayerda indekslar i, j 1, 2, 3 qiymatlarini oling (yoki x, y, z) shakldagi matritsa sifatida tushunilishi kerak:

Tensorning qisqacha yozuvini ham xuddi shunday tushunish kerak.

Agar deformatsiya tufayli M jismning fizik nuqtasi P fazoda yangi pozitsiyani egallagan bo'lsa, u holda siljish vektori komponentlar bilan vektordir. (u x, u y, u z), yoki qisqasi, u i. Kichik deformatsiyalar nazariyasida komponentlar u men va kichik miqdorlar (qat'iy aytganda, cheksiz kichik) hisoblanadi. Tenzorning komponentlari, bu ham deyiladi kuchlanish tensori Koshi yoki chiziqli kuchlanish tensori va vektor u men Tegishli bog'liqliklar:

Oxirgi yozuvdan ko'rinib turibdiki, , Demak, deformatsiya tenzori ta'rifi bo'yicha simmetrikdir.

Agar tashqi kuchlar ta'sirida elastik jism muvozanatda bo'lsa (ya'ni, uning barcha nuqtalarining tezligi nolga teng bo'lsa), u holda tananing undan aqliy ravishda ajratilishi mumkin bo'lgan har qanday qismi ham muvozanatda bo'ladi. Tanadan cheksiz kichik to'rtburchak parallelepiped chiqariladi, uning yuzlari Dekart tizimining koordinata tekisliklariga parallel. Kenar o'lchamlari bilan parallelepiped uchun muvozanat holatidan dx, dy, dz, Prognozlarda kuchlar muvozanati shartlarini ko'rib chiqib, biz quyidagilarni olishimiz mumkin:

Xuddi shunday, parallelepipedga ta'sir qiluvchi barcha kuchlarning asosiy momentining nolga tengligini ifodalovchi muvozanat tenglamalari olinadi, quyidagi ko'rinishga keltiriladi:

Bu tenglik stress tensorining nosimmetrik tensor ekanligini anglatadi va stress tensorining noma'lum komponentlari soni 6 ga kamayadi. Faqat uchta muvozanat tenglamalari mavjud, ya'ni. statika tenglamalari muammoni hal qilish uchun etarli emas. Chiqish yo'li - Guk qonuni tenglamalari yordamida kuchlanishlarni deformatsiyalar ko'rinishida ifodalash va keyin deformatsiyalarni siljishlar bo'yicha ifodalash. u men Koshi formulalaridan foydalanib, natijani muvozanat tenglamasiga almashtiring. Bunda uchta noma'lum funksiyaga nisbatan uchta differentsial muvozanat tenglamalari olinadi u x u y u z, bular. noma'lumlar soni tenglamalar soniga mos keladi. Bu tenglamalar Navye-Koshi tenglamalari deb ataladi.

3. Chegaraviy shartlar

Elastiklik nazariyasidagi muammolarni hal qilish elastik jismning ichki nuqtalarda harakatini aniqlaydigan qisman hosilalarda differensial tenglamalar tizimini integrallashga keltiriladi. Ushbu tenglamalar tanani bog'laydigan sirtdagi shartlar bilan to'ldiriladi. Bu shartlar tashqi sirt kuchlarining vazifalarini yoki tananing sirtidagi nuqtalarning siljishlarini belgilaydi. Bunga qarab odatda uch turdagi chegaraviy masalalardan biri tuziladi.

Birinchi chegaraviy masala- kinematik. Tananing hajmida siljishning tarkibiy qismlari topiladi, ular sirtda ma'lum qiymatlarni oladi. Tananing sirtidagi holatda, sirt tenglamalari va undagi siljishlar komponentlarining qiymatlari shunday o'rnatiladi.

Ikkinchi chegaraviy masala- statik. Bunday holda, tananing yuzasida harakatga hech qanday cheklovlar qo'yilmaydi va normal kosinuslarni sirtga va sirt yuk komponentlarining qiymatlariga yo'naltiruvchi sirt tenglamalari o'rnatiladi.

Agar tananing yuzasi koordinata tekisliklariga to'g'ri keladigan bo'lsa, chegara shartlari to'g'ridan-to'g'ri stresslar bo'yicha ifodalanishi mumkin. Keyin sirt tenglamasini ko'rsatish va unga kuchlanish komponentlarining qiymatlarini o'rnatish kifoya.

Uchinchi chegaraviy masala- aralashgan. Bunda tana yuzasining bir qismida kinematik sharoitlar, ikkinchisida esa statik sharoitlar o'rnatiladi.

Ushbu uchta muammo chegara shartlarining barcha turlarini tugatmaydi. Masalan, sirtning ba'zi joylarida uchta siljish komponenti yoki sirt yuki komponentlari ko'rsatilmasligi mumkin.

4. Shuningdek qarang

Manbalar

Timoshenko S.P., Goodyear J. Elastiklik nazariyasi. M.: Nauka, 1979. 560 b.

ELASTIKLIK NAZARIYASI- yuklar ta'sirida dam olayotgan yoki harakatlanuvchi jismlarning siljishlari, deformatsiyalari va kuchlanishlarini o'rganuvchi uzluksiz mexanikaning bo'limi. Ushbu nazariyaning maqsadi matematik tenglamalarni chiqarishdir, ularning yechimi quyidagi savollarga javob berishga imkon beradi: agar ma'lum joylarda unga ma'lum bir qiymatdagi yuklar qo'llanilsa, ushbu tananing deformatsiyasi qanday bo'ladi? Tanadagi kuchlanish qanday bo'ladi? Tananing qulashi yoki bu yuklarga bardosh berishi haqidagi savol elastiklik nazariyasi bilan chambarchas bog'liq, ammo qat'iy aytganda, bu nazariyaning vakolatiga kirmaydi.

Mumkin bo'lgan misollar soni cheksizdir - tayanchlarda yotgan va kuchlar yuklangan nurda deformatsiyalar va kuchlanishlarni aniqlashdan samolyot, kema, suv osti kemasi, vagon g'ildiragidagi bir xil qiymatlarni hisoblashgacha, snaryad tekkanda zirhda, tog' tizmasida aditdan o'tayotganda, ko'p qavatli bino ramkasida va hokazo. Bu erda rezervatsiya qilish kerak: yupqa devorli elementlardan tashkil topgan tuzilmalar elastiklik nazariyasiga mantiqiy asoslanib, soddalashtirilgan nazariyalar bo'yicha hisoblanadi; bunday nazariyalarga quyidagilar kiradi: materiallarning yuklarning ta'siriga chidamliligi nazariyasi (mashhur "sopromat"), uning vazifasi asosan rodlar va nurlarni hisoblashdir; strukturaviy mexanika - bar tizimlarini hisoblash (masalan, ko'priklar); va nihoyat, qobiqlar nazariyasi, aslida, deformatsiyalar va stresslar haqidagi fanning mustaqil va juda rivojlangan sohasi bo'lib, uning mavzusi eng muhim strukturaviy elementlar - yupqa devorli qobiqlar - silindrsimon, konussimon, sferoiddir. , va yanada murakkab shakllarga ega. Shuning uchun elastiklik nazariyasida odatda muhim o'lchamlari unchalik farq qilmaydigan jismlar ko'rib chiqiladi. Shunday qilib, ma'lum kuchlar ta'sir qiladigan ma'lum shakldagi elastik jism ko'rib chiqiladi.

Elastiklik nazariyasining asosiy tushunchalari ma'lum bir nuqta orqali tanada aqliy ravishda amalga oshirilishi mumkin bo'lgan kichik maydonlarga ta'sir qiluvchi stresslardir. M, nuqtaning kichik qo'shnisining deformatsiyalari M va nuqtani o'zi siljitadi M. Aniqroq aytganda, stress tensorlari s ij, kichik kuchlanish tensori e ij va siljish vektori u men.

Qisqacha belgilash s ij, bu erda indekslar i, j 1, 2, 3 qiymatlarini qabul qilish quyidagi shakl matritsasi sifatida tushunilishi kerak:

Tensorning qisqacha yozuvi e ij.

Agar tananing jismoniy nuqtasi bo'lsa M deformatsiya tufayli kosmosda yangi pozitsiyani egalladi M´, u holda siljish vektori komponentlarga ega vektor ( u x u y u z), yoki, qisqasi, u men. Kichik deformatsiyalar nazariyasida komponentlar u men va e i kichik miqdorlar (qat'iy aytganda, cheksiz) deb hisoblanadi. E tensorning komponentlari ij va vektor u ij Koshi formulalari bilan bog'langan bo'lib, ular quyidagi shaklga ega:

Ko'rinib turibdiki, e xy=e yx, va, umuman olganda, e ij=e ji, shuning uchun deformatsiya tensori ta'rifi bo'yicha simmetrikdir.

Agar tashqi kuchlar ta'sirida elastik jism muvozanatda bo'lsa (ya'ni, uning barcha nuqtalarining tezligi nolga teng bo'lsa), u holda tananing undan aqliy ravishda ajratilishi mumkin bo'lgan har qanday qismi ham muvozanatda bo'ladi. Kichkina (qat'iy aytganda, cheksiz kichik) to'rtburchaklar parallelepiped tanadan ajralib turadi, uning yuzlari Dekart tizimining koordinata tekisliklariga parallel. Oxyz(1-rasm).

Parallelepipedning chetlari uzunliklarga ega bo'lsin dx, dy, dz mos ravishda (bu erda, odatdagidek dx farq bor x, va hokazo.). Stress nazariyasiga ko'ra, kuchlanish tensorining tarkibiy qismlari parallelepipedning yuzlariga ta'sir qiladi, ular quyidagilar bilan belgilanadi:

yoqasida OADG:s xx, s xy, s xz

yoqasida OABC:s yx, s yy, s yz

yoqasida DABE:s zx, s zy, s zz

bir xil indekslarga ega bo'lgan komponentlar (masalan, s xx) yuzga perpendikulyar harakat qiladi, turli indekslarga ega bo'lganlar esa maydon tekisligida ishlaydi.

Qarama-qarshi tomonlarda bir xil nomdagi stress tensor komponentlarining qiymatlari bir oz farq qiladi, bu ularning koordinata funktsiyalari va nuqtadan nuqtaga o'zgarishi bilan bog'liq (har doim, ma'lum oddiy holatlar bundan mustasno), va o'zgarishning kichikligi parallelepipedning kichik o'lchamlari bilan bog'liq, shuning uchun biz taxmin qilishimiz mumkinki, agar yoqasida bo'lsa. OABC kuchlanish s yy, keyin yoqasida GDEF kuchlanish s yy+ds yy, va kichik qiymat ds yy aniq kichikligi tufayli uni Teylor seriyasidagi kengayish yordamida aniqlash mumkin:

(bu erda qisman hosilalar ishlatiladi, chunki stress tensorining tarkibiy qismlari bog'liq x, y, z).

Xuddi shunday, barcha yuzlardagi stresslarni s bilan ifodalash mumkin ij va ds ij. Bundan tashqari, kuchlanishdan kuchlarga o'tish uchun siz stressning kattaligini u harakat qiladigan sayt maydoniga ko'paytirishingiz kerak (masalan, s yy+ds yy ga ko'paytiring dx dz). Parallelepipedga ta'sir etuvchi barcha kuchlar aniqlanganda, statikada bo'lgani kabi, tananing muvozanat tenglamasini yozish mumkin, asosiy vektor uchun barcha tenglamalarda faqat hosilalari bo'lgan hadlar qoladi, chunki stresslarning o'zi. bir-birini va omillarni bekor qiladi dx dy dz kamayadi va natijada

Xuddi shunday, parallelepipedga ta'sir qiluvchi barcha kuchlarning asosiy momentining nolga tengligini ifodalovchi muvozanat tenglamalari olinadi, ular quyidagi ko'rinishga keltiriladi:

Bu tengliklar stress tensorining simmetrik tenzor ekanligini bildiradi. Shunday qilib, 6 ta noma'lum komponentlar uchun s ij uchta muvozanat tenglamasi mavjud, ya'ni. statika tenglamalari muammoni hal qilish uchun etarli emas. Chiqish yo'li - stresslarni ifodalash s ij deformatsiyalar orqali e ij Guk qonuni tenglamalaridan foydalanib, keyin deformatsiya e ij siljish bilan ifodalanadi u men Koshi formulalaridan foydalanib, natijani muvozanat tenglamalariga almashtiring. Bunda uchta noma'lum funksiyaga nisbatan uchta differentsial muvozanat tenglamalari olinadi u x u y u z, ya'ni. noma'lumlar soni tenglamalar soniga teng. Bu tenglamalar Lame tenglamalari deb ataladi

tana kuchlari (og'irlik va boshqalar) hisobga olinmaydi

D - Laplas operatori, ya'ni.

Endi biz tananing yuzasida chegara shartlarini o'rnatishimiz kerak;

Ushbu shartlarning asosiy turlari quyidagilardan iborat:

1. S 1 jismning sirtining ma'lum qismida siljishlar berilgan, ya'ni. siljish vektori komponentlar bilan ma'lum vektorga teng ( f x; f y; f z ):

u x = f(xyz)

u y= f(xyz)

u z= f(xyz)

(f x, f y, fz ma'lum koordinata funktsiyalari)

2. Sirtning qolgan qismida S 2 ga sirt kuchlari berilgan. Bu shuni anglatadiki, tanadagi stressning taqsimlanishi sirtning bevosita yaqinidagi kuchlanish qiymatlari va chegarada - har bir elementar sohada sirtda tarkibiy qismlar bilan ma'lum tashqi yuk vektoriga teng kuchlanish vektorini hosil qiladi. ( F x ;Fy ; Fz) sirt kuchlari. Matematik jihatdan bu quyidagicha yoziladi: agar bir nuqtada A sirt, bu sirtga birlik normal vektor komponentlarga ega n x, n y, nz keyin bu nuqtada (noma'lum) komponentlarga nisbatan tenglik s ij:e ij, keyin uchta noma'lum uchun biz oltita tenglamani olamiz, ya'ni ortiqcha aniqlangan tizim. Bu tizim e uchun qo'shimcha shartlar bajarilgan taqdirdagina yechimga ega bo'ladi ij. Bu shartlar moslik tenglamalaridir.

Bu tenglamalar ko'pincha uzluksizlik shartlari deb ataladi, ular deformatsiyadan keyin tananing uzluksizligini ta'minlaydi. Bu ibora majoziy, ammo noto'g'ri: bu shartlar, agar deformatsiyalarning (yoki kuchlanishlarning) tarkibiy qismlari noma'lum sifatida qabul qilinsa, doimiy siljish maydonining mavjudligini ta'minlaydi. Ushbu shartlarga rioya qilmaslik uzluksizlikning buzilishiga emas, balki muammoni hal qilishning yo'qligiga olib keladi.

Shunday qilib, egiluvchanlik nazariyasi chegaraviy masalalarni shakllantirishga imkon beruvchi differensial tenglamalar va chegaraviy shartlarni beradi, ularning yechimi ko'rib chiqilayotgan jismlardagi kuchlanishlar, deformatsiyalar va siljishlarning taqsimlanishi haqida to'liq ma'lumot beradi. Bunday masalalarni yechish usullari juda murakkab bo'lib, kuchli kompyuterlar yordamida analitik usullarni raqamli usullar bilan birlashtirish orqali eng yaxshi natijalarga erishiladi.

Vladimir Kuznetsov

ELASTIKLIK NAZARIYASI ASOSLARI

ELASTIKLIK NAZARIYASINING AKSIMMETRIK MASSALALARI

ELASTIKLIK NAZARIYASI ASOSLARI

Asosiy qoidalar, taxminlar va belgi. Elementar parallelepiped va elementar tetraedr uchun muvozanat tenglamalari. Eğimli platforma bo'ylab normal va kesish kuchlanishlari

Bir nuqtada asosiy kuchlanishlarni va eng katta siljish kuchlanishlarini aniqlash. Oktaedral maydonlardagi kuchlanishlar Siqilishlar haqida tushuncha. Deformatsiyalar va siljishlar o'rtasidagi munosabatlar. Qarindosh

ixtiyoriy yo'nalishdagi chiziqli deformatsiya Deformatsiyaning moslik tenglamalari. Izotrop jism uchun Guk qonuni To‘g‘ri to‘rtburchak koordinatadagi tekislik masalasi Qutb koordinatalaridagi tekislik masalasi

Elastiklik nazariyasi masalalarining mumkin bo'lgan yechimlari. Ko'chish va kuchlanishlardagi masalalarni yechish Harorat maydonining mavjudligi. ODDIY EKSIMMETRIK MASALALAR bo'limi bo'yicha qisqacha xulosalar Silindrsimon koordinatalardagi tenglamalar Silindrsimon koordinatalardagi tenglamalar (davomi)

Qalin devorli sharsimon idishning deformatsiyasi Tekislikda ta'sir qiluvchi konsentrlangan kuch

Elastik yarim bo'shliqni yuklashning alohida holatlari: aylananing maydoni bo'ylab bir xil yuklanish, "yarim shar bo'ylab aylana maydoniga yuklash", teskari muammo Mutlaq qattiq to'pni elastik yarmiga kiritish. bo'sh joy. To'plarning elastik qulashi muammosi QALIN DEVORLI QUVURLAR

Umumiy ma'lumot. Quvur elementining muvozanat tenglamasi Konturlardan birida bosim ostida kuchlanishlarni o'rganish. Elastik deformatsiya uchun mustahkamlik shartlari Kompozit quvurlardagi kuchlanishlar. Ko'p qatlamli quvurlarni hisoblash tushunchasi Hisoblash misollari

PLATALAR, MEMBRANLAR Asosiy ta'riflar va farazlar

To'rtburchaklar koordinatalarda plastinkaning egri o'rta yuzasining differentsial tenglamasi Plitaning silindrsimon va sferik egilishi

Dumaloq plastinkaning aksimetrik egilishi uchun egilish momentlari. Dumaloq plastinkaning egri o'rta yuzasining differentsial tenglamasi Dumaloq plitalardagi chegara shartlari. Eng katta stresslar va burilishlar. kuch sharoitlari. Plitalardagi termal stresslar

Membranada kuchlarni aniqlash. Zanjir kuchlari va tarangliklari. Dumaloq diafragmalarda egilish va kuchlanishlarni taxminiy aniqlash Hisoblash misollari Hisoblash misollari (davomi)

1.1 Asosiy qoidalar, taxminlar va belgilar

Elastiklik nazariyasi elastik jismning kuchlanish-deformatsiya holatini analitik o'rganishga qaratilgan. Elastiklik nazariyasi yordamida qarshilik taxminlari yordamida olingan yechimlarni tekshirish mumkin

materiallar va bu yechimlarning qo'llanilishi chegaralari belgilanadi. Ba'zida elastiklik nazariyasining bo'limlari bo'lib, ularda materiallarning qarshiligida bo'lgani kabi, qismning yaroqliligi masalasi ko'rib chiqiladi, lekin juda murakkab matematik apparatlar (plitalar, qobiqlar, massivlarni hisoblash) yordamida ular deyiladi. elastiklikning amaliy nazariyasi sifatida.

Bu bobda elastiklikning matematik chiziqli nazariyasining asosiy tushunchalari bayon etilgan. Fizik hodisalarni tavsiflashda matematikani qo'llash ularni sxematiklashtirishni talab qiladi. Elastiklikning matematik nazariyasida masalalar eng kichik taxminlar soni bilan echiladi, bu esa yechim uchun ishlatiladigan matematik usullarni murakkablashtiradi. Elastiklikning chiziqli nazariyasi komponentlarning kuchlanishlari va deformatsiyalari o'rtasida chiziqli bog'liqlik mavjudligini taxmin qiladi. Bir qator materiallar (kauchuk, quyma temirning ba'zi navlari) uchun bunday bog'liqlik, hatto kichik deformatsiyalar bilan ham qabul qilinishi mumkin emas: egiluvchanlik chegaralaridagi s - e diagrammasi yuklashda ham, tushirishda ham bir xil shaklga ega, ammo ikkala holatda ham egri chiziqli. Bunday materiallarni o'rganishda nochiziqli elastiklik nazariyasining bog'liqliklaridan foydalanish kerak.

IN Egiluvchanlikning matematik chiziqli nazariyasi quyidagi taxminlarga asoslanadi:

1. Muhitning uzluksizligi (uzluksizligi) haqida. Bunda moddaning atomistik tuzilishi yoki mavjudligi har qanday bo'shliqlar hisobga olinmaydi.

2. Tabiiy holat bo'yicha, uning asosida kuch ta'sirini qo'llashdan oldin vujudga kelgan tananing dastlabki kuchlanish (deformatsiyalangan) holati hisobga olinmaydi, ya'ni tanani yuklash paytida deformatsiyalar sodir bo'ladi deb taxmin qilinadi. va uning istalgan nuqtasidagi kuchlanishlar nolga teng. Dastlabki kuchlanishlar mavjud bo'lganda, bu taxmin haqiqiy bo'ladi, agar egiluvchanlikning chiziqli nazariyasining bog'liqliklari hosil bo'lgan kuchlanishlarga qo'llanilishi mumkin bo'lsa (dastlabki va ta'sirlardan kelib chiqadigan yig'indi).

3. Bir jinslilik bo'yicha, buning asosida tananing tarkibi barcha nuqtalarda bir xil bo'ladi deb taxmin qilinadi. Metalllar uchun bu taxmin katta xatoliklarni bermasa-da, beton uchun kichik hajmlarni hisobga olgan holda, bu muhim xatolarga olib kelishi mumkin.

4. Sferik izotropiya bo'yicha, buning asosida bunga ishoniladi materialning mexanik xususiyatlari barcha yo'nalishlarda bir xil. Metall kristallari bunday xususiyatga ega emas, lekin ko'p sonli mayda kristallardan tashkil topgan butun metall uchun bu gipotezani to'g'ri deb taxmin qilishimiz mumkin. Turli yo'nalishlarda turli xil mexanik xususiyatlarga ega bo'lgan materiallar uchun, masalan, laminatlangan plastmassalar uchun ortotrop va anizotrop materiallarning elastikligi nazariyasi ishlab chiqilgan.

5. Ideal elastiklik haqida, uning asosida yuk olib tashlanganidan keyin deformatsiyaning to'liq yo'qolishi taxmin qilinadi. Ma'lumki, har qanday yuk ostida haqiqiy jismlarda qoldiq deformatsiya sodir bo'ladi. Shuning uchun, taxmin

6. Komponent shtammlari o'rtasidagi chiziqli munosabat to'g'risida va stresslar.

7. Deformatsiyalarning kichikligi to'g'risida, buning asosida nisbiy chiziqli va burchakli deformatsiyalar birlikka nisbatan kichik deb hisoblanadi. Kauchuk kabi materiallar yoki spiral kamon kabi elementlar uchun katta elastik deformatsiyalar nazariyasi ishlab chiqilgan.

Elastiklik nazariyasi masalalarini yechishda ular yechimning yagonaligi haqidagi teoremadan foydalanadilar: agar berilgan tashqi sirt va tana kuchlari muvozanatda bo'lsa, ular kuchlanish va siljishlarning yagona tizimiga mos keladi. Yechimning o'ziga xosligi pozitsiyasi, agar tananing tabiiy holati to'g'risidagi faraz o'rinli bo'lsa (aks holda, cheksiz miqdordagi echimlar mumkin) va deformatsiyalar va tashqi kuchlar o'rtasidagi chiziqli bog'liqlik haqidagi faraz haqiqiy bo'ladi.

Elastiklik nazariyasidagi muammolarni hal qilishda ko'pincha Sent-Venant printsipi qo'llaniladi: Agar elastik jismning kichik qismiga tatbiq etilgan tashqi kuchlar bir xil kesimga ta'sir qiluvchi kuchlarning statik ekvivalent tizimi bilan almashtirilsa (bir xil asosiy vektor va bir xil asosiy momentga ega), u holda bu almashtirish faqat mahalliy deformatsiyalarning o'zgarishiga olib keladi. .

Tashqi yuklar qo'llaniladigan joylardan etarlicha uzoq bo'lgan nuqtalarda kuchlanishlar ularni qo'llash usuliga juda bog'liq emas. Materiallarning qarshiligi jarayonida Sent-Venant printsipi asosida sxematik ravishda kuch yoki kontsentrlangan moment shaklida ifodalangan yuk, aslida normal va kesish stresslari bo'ylab u yoki bu tarzda taqsimlanadi. tana yuzasining ma'lum bir maydoni. Bunday holda, turli xil kuchlanish taqsimotlari bir xil kuch yoki kuchlar juftligiga mos kelishi mumkin. Sen-Venant printsipiga asoslanib, tana sirtining bir qismidagi kuchlarning o'zgarishi ushbu kuchlar qo'llaniladigan joydan etarlicha katta masofada joylashgan nuqtalardagi kuchlanishlarga deyarli ta'sir qilmaydi, deb hisoblash mumkin. yuklangan maydonning chiziqli o'lchamlari).

Tadqiq qilinayotgan maydonning tanada tanlangan holati (1-rasm) x, y va z to'rtburchaklar koordinata o'qlarining tanlangan tizimidagi maydonga normal N ning yo'nalish kosinuslari bilan aniqlanadi.

Agar P A nuqtada tanlangan elementar maydonga ta'sir etuvchi ichki kuchlarning natijasi bo'lsa, u holda bu nuqtada normal N bilan maydon bo'ylab umumiy kuchlanish p N dagi nisbat chegarasi sifatida aniqlanadi.

quyidagi shakl:

P N vektorini fazoda uchta o'zaro perpendikulyar komponentlarga ajratish mumkin.

2. Komponentlarga s N , t N s va t N t saytga normal (normal kuchlanish) va sayt tekisligida yotgan ikkita o'zaro perpendikulyar o'q s va t (1b-rasm) (tangensial) yo'nalishlarida. stresslar). 1-rasmga ko'ra, b

Agar tananing kesimi yoki maydon koordinata tekisliklaridan biriga parallel bo'lsa, masalan, y0z (2-rasm), u holda uchinchi koordinata o'qi x bu maydon uchun normal bo'ladi va kuchlanish komponentlari s x belgilashga ega bo'ladi. t xy va t xz.

Oddiy kuchlanish, agar u cho'zilgan bo'lsa, ijobiy, agar u siqilgan bo'lsa, salbiy. Kesish kuchlanishining belgisi quyidagi qoida yordamida aniqlanadi: agar sayt bo'ylab ijobiy (tortishish) normal kuchlanish ijobiy proektsiyani bersa, u holda tangensial

bir xil maydon ustidagi kuchlanish, shuningdek, tegishli o'qda ijobiy proektsiyani berish sharti bilan ijobiy hisoblanadi; agar kuchlanishning normal kuchlanishi manfiy proyeksiyani bersa, u holda musbat siljish kuchlanishi ham mos keladigan o'qda manfiy proyeksiya berishi kerak.

Shaklda. 3, masalan, elementar parallelepipedning yuzlariga ta'sir qiluvchi, koordinata tekisliklari bilan mos keladigan barcha stress komponentlari ijobiydir.

Elastik jismning bir nuqtasida kuchlanish holatini aniqlash uchun ushbu nuqtadan o'tadigan uchta o'zaro perpendikulyar maydon uchun umumiy kuchlanishlarni p N bilish kerak. Har bir umumiy stress uchta komponentga bo'linishi mumkinligi sababli, to'qqizta stress komponenti ma'lum bo'lsa, stress holati aniqlanadi. Ushbu komponentlarni matritsa shaklida yozish mumkin

nuqtadagi kuchlanish tensor komponentlari matritsasi deb ataladi.

Matritsaning har bir gorizontal chizig'i bir xil maydonda ishlaydigan uchta stress komponentini o'z ichiga oladi, chunki birinchi piktogramma (normalning nomi) ular uchun bir xil. Tensorning har bir vertikal ustunida bir xil o'qga parallel bo'lgan uchta stress mavjud, chunki ikkinchi belgilar (stress ta'sir qiladigan o'qning parallel nomi) bir xil.

1.2 Elementar parallelepiped uchun muvozanat tenglamalari

va elementar tetraedr

Zorlangan elastik jismning o'rganilayotgan A nuqtasida (x, y va z koordinatalari bilan) chetlari dx, dy va dz bo'lgan elementar parallelepipedni uchta o'zaro perpendikulyar juft tekisliklar orqali ajratamiz (2-rasm). A nuqtasiga (koordinata tekisliklariga eng yaqin) ulashgan uchta o'zaro perpendikulyar yuzlarning har birida uchta stress komponenti ishlaydi - normal va ikkita tangensial. Biz ular A nuqtaga tutashgan yuzlar bo'ylab musbat deb taxmin qilamiz.

A nuqtadan o'tuvchi yuzdan parallel yuzga o'tishda kuchlanishlar o'zgaradi va o'sishlarni oladi. Masalan, agar stress komponentlari s x \u003d f 1 (x, y, z), t xy \u003d f 2 (x, y, z,), t xz \u003d f 3 (x, y, z,) , keyin parallel yuz bo'ylab, bir yuzdan ikkinchisiga o'tishda faqat bitta x koordinatasining ortishi tufayli,

kuchlanish komponentlari Rasmda ko'rsatilganidek, elementar parallelepipedning barcha yuzlaridagi kuchlanishlarni aniqlash mumkin. 3.

Elementar parallelepipedning yuzlariga qo'llaniladigan stresslardan tashqari, unga tana kuchlari ham ta'sir qiladi: og'irlik kuchlari, inertial kuchlar. Bu kuchlarning hajm birligiga proyeksiyalarini koordinata o‘qlari bo‘yicha X, Y va Z bilan belgilaymiz. Agar barcha normal, tangensial va hajmli kuchlarning x o‘qiga proyeksiyalari yig‘indisini nolga tenglashtirsak,

elementar parallelepipedga ta'sir etsa, u holda dxdydz ko'paytmasi bilan qisqartirilgandan so'ng biz tenglamani olamiz.

Y va z o'qlaridagi kuchlarning proyeksiyalari uchun shunga o'xshash tenglamalarni tuzib, biz Koshi tomonidan olingan elementar parallelepipedning muvozanati uchun uchta differentsial tenglama yozamiz,

Parallelepipedning o'lchamlari nolga kamaytirilganda, u nuqtaga aylanadi va s va t - A nuqtadan o'tadigan uchta o'zaro perpendikulyar maydon bo'ylab kuchlanish komponentlari.

Agar elementar parallelepipedga x c o'qiga nisbatan x o'qiga parallel va uning og'irlik markazidan o'tuvchi barcha kuchlarning momentlari yig'indisini nolga tenglashtirsak, tenglamani olamiz.

yoki tenglamaning ikkinchi va toʻrtinchi hadlari qolganlari bilan solishtirganda kattaroq kichiklik tartibida ekanligini hisobga olib, dxdydz ga qisqartirilgandan keyin

t yz - t zy = 0 yoki t yz = t zy.

Markaziy o'qlar y c va z c bo'yicha momentlarning o'xshash tenglamalarini tuzib, biz siljish kuchlanishlarining juftlashuv qonuni uchun uchta tenglamani olamiz.

t xy = t yx, t yx = t xy , t zx = t xz . (1.3)

Ushbu qonun quyidagicha tuzilgan: O'zaro perpendikulyar maydonlarga ta'sir etuvchi va maydonlarning kesishish chizig'iga perpendikulyar yo'naltirilgan tangensial kuchlanishlar kattaligi bo'yicha teng va belgisi bo'yicha bir xil.

Shunday qilib, T s tenzor matritsasining to'qqizta kuchlanish komponentidan oltitasi bir-biriga juft bo'lib teng bo'lib, bir nuqtadagi kuchlanish holatini aniqlash uchun faqat quyidagi oltita kuchlanish komponentlarini topish kifoya qiladi:

Ammo belgilangan muvozanat shartlari bizga faqat uchta tenglamani (1.2) berdi, ulardan oltita noma'lumni topib bo'lmaydi. Shunday qilib, bir nuqtada kuchlanish holatini aniqlashning bevosita muammosi, umumiy holatda, statik jihatdan noaniqdir. Ushbu statik noaniqlikni aniqlash uchun qo'shimcha geometrik va jismoniy bog'liqliklar kerak.

A nuqtadagi elementar parallelepipedni yuzlariga moyil tekislik bilan kesamiz; bu tekislikka normal N ning yo'nalish kosinuslari l, m va n bo'lsin.Olingan geometrik shakl (4-rasm) uchburchak asosli piramida - elementar tetraedrdir. Faraz qilamizki, A nuqta koordinatalarning kelib chiqishiga to'g'ri keladi va tetraedrning uchta o'zaro perpendikulyar yuzlari koordinata tekisliklariga to'g'ri keladi.

Tetraedrning bu yuzlariga ta'sir qiluvchi stress komponentlari ko'rib chiqiladi

ijobiy. Ular rasmda ko'rsatilgan. 4. BCD tetraedrining x, y va z o‘qlaridagi qiya yuziga ta’sir etuvchi to‘liq kuchlanish p N proyeksiyalari bilan belgilang. BCD ning moyil yuzining maydoni dF bilan belgilanadi. Keyin ABC yuzining maydoni dFp, yuz ACD - dFl va yuz ADB - dFt bo'ladi.

Tetraedrning yuziga taʼsir etuvchi barcha kuchlarni x oʻqiga proyeksiya qilib, uning muvozanat tenglamasini tuzamiz; tana kuchining proyeksiyasi proyeksiya tenglamasiga kiritilmagan, shuning uchun

sirt kuchlari proyeksiyalari bilan solishtirganda kichiklikning yuqori tartibining qiymati qanday?

Tetraedrga y va z o'qlarida ta'sir etuvchi kuchlar uchun proyeksiya tenglamalarini tuzib, yana ikkita o'xshash tenglamaga ega bo'lamiz. Natijada, biz elementar tetraedr uchun uchta muvozanat tenglamasiga ega bo'lamiz

Ixtiyoriy shakldagi fazoviy jismni oʻzaro perpendikulyar xOu, yOz va xOz tekisliklar tizimi orqali (5-rasm) bir qancha elementar parallelepipedlarga ajratamiz. Tananing yuzasida, elementar

tetraedra, (sirtning egri chiziqli qismlari, ularning kichikligi tufayli, tekisliklar bilan almashtirilishi mumkin). Bu holda p N sirtdagi yukni ifodalaydi va (1.4) tenglamalar bu yukni tanadagi s va t kuchlanishlarga bog'laydi, ya'ni ular elastiklik nazariyasi masalasining chegara shartlarini ifodalaydi. Ushbu tenglamalar bilan aniqlangan shartlar deyiladi sirt sharoitlari.

Shuni ta'kidlash kerakki, elastiklik nazariyasida tashqi yuklar tananing yuzasiga to'g'ri keladigan joylarga qandaydir qonunga muvofiq qo'llaniladigan normal va tangensial stresslar bilan ifodalanadi.

1.3 Nishab bo'ylab normal va siljish kuchlanishlari

sayt

ABCD elementar tetraedrini ko'rib chiqaylik, uning uchta yuzi koordinata tekisliklariga parallel, normal N to'rtinchi yuzi esa koordinata o'qlari bilan burchaklar hosil qiladi, kosinuslari l, m va n ga teng (6-rasm). . Faraz qilaylik, koordinata tekisliklarida yotgan maydonlarga ta’sir etuvchi normal va siljish kuchlanishlarining komponentlari berilgan va BCD maydonidagi kuchlanishlarni aniqlaymiz. Biz x 1, y 1 va z 1 to'rtburchaklar koordinata o'qlarining yangi tizimini tanlaymiz, shunda x 1 o'qi normal N ga to'g'ri keladi,

Elastiklik nazariyasining asosiy vazifasi tanani yuklash va mahkamlashning berilgan shartlariga muvofiq kuchlanish-deformatsiya holatini aniqlashdir.

Stress-deformatsiya holati, agar kuchlanish tensorining () komponentlari va to'qqiz funktsiyani almashtirish vektori topilgan bo'lsa, aniqlanadi.

Elastiklik nazariyasining asosiy tenglamalari

Ushbu to'qqiz funktsiyani topish uchun elastiklik nazariyasining asosiy tenglamalarini yozish kerak, yoki:

Differensial Cauchies

Koshi deformatsiyalarining chiziqli qismi tenzorining komponentlari qayerda;

Radius bo'ylab siljish hosilasi tenzorining komponentlari.

Differensial muvozanat tenglamalari

stress tensor komponentlari qayerda; j o'qiga jism kuchining proyeksiyasi.

Chiziqli elastik izotrop jism uchun Guk qonuni

oqsoq konstantalar qayerda; izotrop tana uchun. Bu erda normal va kesish stresslari; navbati bilan deformatsiya va kesish burchaklari.

Yuqoridagi tenglamalar Sen-Venant bog'liqliklarini qondirishi kerak

Elastiklik nazariyasida barcha asosiy tenglamalar qanoatlansa, masala yechiladi.

Elastiklik nazariyasidagi masalalar turlari

Jism yuzasidagi chegaraviy shartlar qanoatlantirilishi kerak va chegaraviy shartlarning turiga qarab elastiklik nazariyasida uch xil masalalar mavjud.

Birinchi tur. Kuchlar tananing yuzasiga beriladi. Chegara shartlari

Ikkinchi tur. Tana yuzasida siljish ko'rsatilgan muammolar. Chegara shartlari

Uchinchi tur. Elastiklik nazariyasining aralash muammolari. Kuchlar tana yuzasining bir qismida, siljish tana yuzasining bir qismida beriladi. Chegara shartlari

Elastiklik nazariyasining bevosita va teskari masalalari

Siqilishlardagi elastiklik nazariyasi tenglamalari (Choqsoq tenglamalari)

Ko'chishlardagi elastiklik nazariyasi tenglamalarini aniqlash uchun biz yozamiz: differensial muvozanat tenglamalari (18) chiziqli elastik izotrop jism uchun Guk qonuni (19)

Agar deformatsiyalar siljishlar (17) bilan ifodalanishini hisobga olsak, yozamiz:

Shuni ham eslatib o'tish kerakki, kesish burchagi siljishlar bilan quyidagi bog'liqlik bilan bog'liq (17):

(22) ifodani (19) tengliklarning birinchi tenglamasiga qo'yib, biz normal stresslarni olamiz.

E'tibor bering, bu holda u belgisi i ustidan yig'indini bildirmaydi.

(23) ifodani ikkinchi tenglik (19) tenglamasiga qo'yib, biz kesishish kuchlanishlarini olamiz.

Muvozanat tenglamalarini (18) j = 1 uchun kengaytirilgan shaklda yozamiz

Oddiy (24) va tangensial (25) kuchlanishlarni (26) tenglamaga almashtirib, biz hosil bo'lamiz.

Bu erda l - oqsoqlangan doimiy, u quyidagi ifoda bilan aniqlanadi:

(28) ifodani (27) tenglamaga almashtiramiz va yozamiz:

bu yerda (22) ifoda bilan yoki kengaytirilgan shaklda aniqlanadi

Biz (29) ifodani G ga bo'lamiz va shunga o'xshash shartlarni qo'shamiz va birinchi Lame tenglamasini olamiz:

Bu erda Laplas operatori (garmonik operator), u sifatida aniqlanadi

Xuddi shunday, siz quyidagilarni olishingiz mumkin:

(30) va (32) tenglamalarni quyidagicha yozish mumkin:

(33) yoki (30) va (32) tenglamalar oqsoq tenglamalardir. Agar tana kuchlari nolga teng yoki doimiy bo'lsa, u holda

bundan tashqari, bu holda belgi i ustidan yig'indini bildirmaydi. Bu yerga

yoki hisobga olgan holda (31)

(22) ni (34) ga almashtirib, o‘zgartirishlarni bajarib, hosil bo‘lamiz

va natijada

bu tenglikni qanoatlantiradigan funksiya qayerda. Agar

demak, f garmonik funktsiyadir. Demak, hajmli deformatsiya ham garmonik funktsiyadir.

Oldingi taxminni to'g'ri deb hisoblab, biz garmonik operatorni Lame tenglamasining i - qatoridan olamiz.

Agar tana kuchlari nolga teng yoki doimiy bo'lsa, u holda siljish komponentlari bigarmonik funktsiyalardir.

Bigarmonik funksiyalarni garmonik (Lame tenglamalarini qanoatlantiruvchi) nuqtai nazaridan ifodalashning turli shakllari mavjud.

Bu erda k = 1,2,3. Va