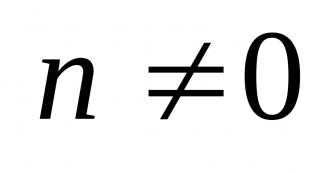Funksioni i analizës së Matit. Analiza matematikore. Shihni se çfarë është "analiza matematikore" në fjalorë të tjerë

Përpiluar nga Yu.V.Obrubov

Kaluga - 2012

Hyrje në analizën matematikore.

Numrat realë. Variablat dhe konstantet.

Një nga konceptet bazë të matematikës është numri. Quhen numrat pozitivë 1,2,3, ..., të cilët fitohen me numërim natyrore. Numrat ... -3, -2, -1,0,1,2,3, ... quhen numra të plotë. Numrat që mund të paraqiten si një raport i fundëm i dy numrave të plotë (
) quhen racionale. Këto përfshijnë numra të plotë dhe thyesorë, pozitivë dhe negativë. Numrat që mund të paraqiten si thyesa të pafundme që nuk përsëriten quhen irracionale. Shembuj të numrave irracionalë janë
,
. Në grupin e numrave irracionalë dallojnë transcendentale numrat. Këta janë numra që janë rezultat i veprimeve joalgjebrike. Më të famshmit prej tyre janë numri dhe numri jo-peer . Numrat racional dhe irracional quhen e vlefshme . Numrat realë përfaqësohen me pika në vijën numerike. Çdo pikë në boshtin e numrave korrespondon me një numër të vetëm real dhe, anasjelltas, për çdo numër real korrespondon një pikë e vetme në boshtin e numrave. Kështu, është krijuar një korrespodencë një me një midis numrave realë dhe pikave të vijës numerike. Kjo bën të mundur përdorimin e termave "numri a" dhe "pika a" në mënyrë të ndërsjellë.

Në procesin e studimit të proceseve të ndryshme fizike, ekonomike, sociale, shpesh duhet të merret me sasi që përfaqësojnë vlerat numerike të parametrave të dukurive në studim. Në të njëjtën kohë, disa prej tyre ndryshojnë, ndërsa të tjerët ruajnë vlerat e tyre.

e ndryshueshme Një sasi që merr vlera të ndryshme numerike quhet. Një sasi, vlera numerike e së cilës nuk ndryshon në një problem ose eksperiment të caktuar quhet konstante. Variablat zakonisht shënohen me shkronja latine
dhe të përhershme
.

e ndryshueshme konsiderohet e dhënë nëse dihet grupi i vlerave që mund të marrë. Ky grup quhet diapazoni i ndryshores.

Ekzistojnë lloje të ndryshme të grupeve të vlerave të një ndryshoreje numerike.

intervali është bashkësia e vlerave x e mbyllur midis numrave a dhe b, ndërsa numrat a dhe b nuk i përkasin grupit në shqyrtim. Intervali shënohet me: (a,b);a

segment quhet bashkësia e vlerave x e mbyllur midis numrave a dhe b, ndërsa numrat a dhe b i përkasin grupit në shqyrtim. Segmenti shënohet me ,a≤x≤b.

Bashkësia e të gjithë numrave realë është një interval i hapur. Shënohet: (- ∞,+ ∞), -∞<х <+∞, R.

Lagjja e pikës x 0 quhet një interval arbitrar (а, b) që përmban një pikë x 0, të gjitha pikat e këtij intervali plotësojnë pabarazinë a

ε - lagja e pikës a është një interval i përqendruar në pikën a që plotëson pabarazinë a–ε

Funksioni. Përkufizimet dhe konceptet bazë.

Funksioni është një nga konceptet bazë të analizës matematikore. Le të jenë X dhe Y bashkësi arbitrare të numrave realë.

Nëse çdo numri x X, sipas ndonjë rregulli ose ligji, i caktohet një numër real unik i mirëpërcaktuar yY, atëherë ata thonë se funksionin me domenin e përkufizimit X dhe grupin e vlerave Y. Përcaktoni y \u003d f (x). Ndryshorja x quhet argument funksione.

Në përkufizimin e një funksioni, dy pika janë thelbësore: një tregues i fushës së përkufizimit dhe krijimi i një ligji korrespondues.

Fusha e përkufizimit ose zona e ekzistencës Një funksion është një grup vlerash argumentesh për të cilat ekziston funksioni, domethënë ka kuptim.

Ndrysho zonën Funksioni quhet bashkësia e vlerave y që merr për vlerat e pranueshme të x.

Mënyrat për të vendosur një funksion.

Mënyra analitike e përcaktimit të një funksioni.

Me këtë metodë të vendosjes së funksionit, ligji i korrespondencës shkruhet si një formulë (shprehje analitike) që tregon se me çfarë transformimesh matematikore, duke përdorur vlerën e njohur të argumentit x, mund të gjeni vlerën përkatëse të y.

Një funksion mund të përcaktohet nga një shprehje e vetme analitike në të gjithë domenin e tij të përkufizimit ose të përfaqësojë një koleksion të disa shprehjeve analitike.

Për shembull: y \u003d mëkat (x 2 + 1)

2. Mënyra tabelare e vendosjes së një funksioni

Si rezultat i vëzhgimit të drejtpërdrejtë ose studimit eksperimental të një dukurie ose procesi, vlerat e argumentit x dhe vlerat përkatëse të y shkruhen në një rend të caktuar.

Kjo tabelë përcakton funksionin y të x.

Një shembull i një mënyre tabelare të specifikimit të një funksioni mund të jenë tabelat e funksioneve trigonometrike, tabelat e logaritmeve, datat dhe kurset e këmbimit, temperatura dhe lagështia, etj.

3. Mënyra grafike e vendosjes së funksionit.

Mënyra grafike për të vendosur funksionin është shfaqja e pikave (x, y) në planin koordinativ me anë të pajisjeve teknike. Metoda grafike e specifikimit të një funksioni në analizën matematikore nuk përdoret, por gjithmonë përdoret një ilustrim grafik i funksioneve të dhëna analitike.

Të ulesh në errësirë ​​dhe të lexosh artikujt e mi? Ruani shikimin tuaj. Nëse keni një vend të preferuar, ka shumë të ngjarë që është një shtrat, atëherë shakullat e murit me shpërndarje në të gjithë Ukrainën në vend mund të jenë një opsion i përshtatshëm. Lexoni në dritë dhe kujdesuni për shikimin tuaj.

Çdo gjë duhet thënë sa më thjeshtë, por jo më e thjeshtë.
Albert Einstein

Udhëtimi ynë fillon me një personazh imagjinar që do ta quajmë John Doe. Ai është një punëtor mesatar që mund të gjendet lehtësisht në çdo qytet të botës. Pothuajse çdo ditë, Gjoni zgjohet nga alarmet me zë të lartë dhe shkon në punë me makinën e tij. Ai ngjitet me ashensorin në zyrën e tij, ku ndez kompjuterin dhe fut emrin e përdoruesit dhe fjalëkalimin. Gjoni i bën të gjitha këto gjëra pa as idenë më të vogël se si funksionojnë.

Ndoshta ai do të ishte i interesuar të mësonte se si janë rregulluar dhe funksionojnë pajisjet dhe pajisjet që ai përdor çdo ditë, megjithatë, ai nuk ka as kohë dhe as forcë për ta bërë këtë. Ai i konsideron makinat, ashensorët, kompjuterët dhe orët e alarmit si mekanizma krejtësisht të ndryshëm dhe kompleks që nuk kanë asgjë të përbashkët. Sipas John, duhen vite studimi për të kuptuar se si funksionon secila prej tyre.

Disa njerëz i shohin gjërat pak më ndryshe se John Doe ynë. Ata e dinë se motorët elektrikë në instalimet e ashensorëve janë shumë të ngjashëm me alternatorët e makinave.

Ata e dinë se kontrolluesi logjik i programueshëm që kontrollon motorin elektrik që është përgjegjës për lëvizjen e ashensorit është shumë i ngjashëm me një kompjuter pune John Doe. Ata e dinë se në një nivel themelor, PLC, ora e ziles dhe kompjuteri bazohen në teorinë relativisht të thjeshtë të tranzistorit. Ajo që John Doe dhe personi mesatar e konsiderojnë tepër komplekse është përdorimi më i zakonshëm i parimeve të thjeshta mekanike dhe elektrike nga një haker. Problemi është se si zbatohen këto parime. Abstraktimi i parimeve themelore nga idetë komplekse na lejon t'i kuptojmë dhe thjeshtojmë ato në një mënyrë që i përgjigjet këshillave të improvizuara të Albert Ajnshtajnit të cituar më sipër.

Shumë prej nesh e shohin llogaritjen si diçka komplekse. (John Doe e konsideron të njëjtë parimin e pajisjes dhe funksionimin e mekanizmave të ndryshëm.) Ju shihni një grumbull gjërash komplekse dhe të ndërlikuara. Për t'i kuptuar ato, ju duhet shumë kohë dhe përpjekje. Po sikur t'ju thoshim se analiza matematikore (llogaritja) nuk është aq e komplikuar sa duket në shikim të parë, si dhe shumica e mekanizmave? Se ka disa parime bazë që të gjithë duhet t'i kuptojnë, dhe sapo ta bëni këtë, do të keni një perspektivë të re për botën dhe si funksionon ajo?

Një tekst tipik i llogaritjes përmban rreth një mijë faqe. Një John Doe tipik do të shohë në të një mijë gjëra të vështira për t'u kuptuar dhe studiuar, dhe një haker do të shohë dy parime bazë (derivativ dhe integral) dhe 998 shembuj të këtyre parimeve. Së bashku do të përpiqemi të kuptojmë se cilat janë këto parime. Bazuar në punën e bërë nga Michael Starbird, një profesor në Universitetin e Teksasit në Austin, ne do të përdorim shembuj të përditshëm që çdokush mund t'i kuptojë. Analiza matematikore zbulon bukurinë e veçantë të botës sonë - bukurinë që shfaqet kur jeni në gjendje ta vëzhgoni atë në mënyrë dinamike, jo statike. Shpresojmë që gjithçka të funksionojë për ju.

Para se të fillojmë, do të doja të kaloja shkurtimisht në historinë e shfaqjes së llogaritjes, rrënjët e së cilës qëndrojnë në një analizë shumë të kujdesshme të ndryshimit dhe lëvizjes.

Paradoksi i Zenonit

Zeno nga Elea është një filozof që jetoi në shekullin e IV para Krishtit. Ai ngriti disa paradokse delikate por të thella, dy prej të cilave përfundimisht çuan në lindjen e llogaritjes. Për të zgjidhur paradokset e Zenonit, njerëzimit iu deshën më shumë se dy mijë vjet. Siç mund ta imagjinoni, nuk ishte e lehtë. Vështirësitë lidheshin kryesisht me idenë e pafundësisë. Cili është problemi i pafundësisë nga pikëpamja matematikore? Në shekullin e 17-të, Isaac Newton dhe Gottfried Leibniz arritën të zgjidhnin paradokset e Zenoit dhe të krijonin analiza matematikore. Le t'i hedhim një vështrim më të afërt këtyre paradokseve për të kuptuar pse ka pasur kaq shumë zhurmë rreth tyre.

Shigjeta

Imagjinoni një shigjetë që fluturon në ajër. Mund të themi me shumë siguri se shigjeta është në lëvizje. Tani konsideroni shigjetën në një moment të caktuar kohor. Ajo nuk lëviz më, por është në pushim. Por ne e dimë me siguri që shigjeta është në lëvizje, atëherë si mund të jetë në qetësi?! Ky është thelbi i këtij paradoksi. Mund të duket budallallëk, por në realitet është një koncept shumë kompleks që duhet marrë në konsideratë nga pikëpamja matematikore.

Më vonë do të zbulojmë se kemi të bëjmë me konceptin e një shkalle ndryshimi të menjëhershëm, të cilin do ta lidhim me idenë e njërit prej dy parimeve të analizës matematikore (llogaritjes) - derivatit. Kjo do të na lejojë të llogarisim shpejtësinë e shigjetës në një moment të caktuar kohor - diçka që njerëzimi nuk ka mundur ta bëjë për më shumë se dy mijëvjeçarë.

Dikotomia

Le të shohim përsëri të njëjtën shigjetë. Këtë herë, imagjinoni se ai fluturon në drejtimin tonë. Zenoni argumentoi se ne nuk duhet të lëviznim, pasi shigjeta nuk mund të na godiste kurrë. Imagjinoni që pasi shigjeta të jetë në ajër, ajo duhet të mbulojë gjysmën e distancës midis harkut dhe objektivit. Pasi të arrijë një pikë të caktuar në gjysmë të rrugës, do t'i duhet përsëri të përshkojë gjysmën e distancës - këtë herë midis kësaj pike dhe objektivit. Imagjinoni nëse vazhdojmë ta bëjmë këtë. Kështu, shigjeta përshkon vazhdimisht gjysmën e distancës midis pikës së referencës dhe objektivit. Nisur nga kjo, mund të konkludojmë se shigjeta nuk do të mund të na godasë kurrë! Në jetën reale, shigjeta përfundimisht do të godasë objektivin e saj, duke na lënë të pyesim veten se çfarë do të thotë paradoksi.

Ashtu si në rastin e paradoksit të parë, më vonë do të shqyrtojmë se si ta zgjidhim këtë problem duke përdorur një nga parimet e analizës matematikore - integralin. Integrali na lejon të shohim konceptin e pafundësisë si një funksion matematikor. Është një mjet jashtëzakonisht i fuqishëm, sipas shkencëtarëve dhe inxhinierëve.

Dy parime themelore të llogaritjes

Thelbi i dy parimeve themelore të analizës matematikore mund të demonstrohet duke i zbatuar ato për të zgjidhur paradokset e Zenos.

Derivat. Derivati ​​është një metodë që do të na lejojë të llogarisim shpejtësinë e shigjetës në Paradoksin e Shigjetës. Ne e bëjmë këtë duke analizuar pozicionin e shigjetës në intervale kohore në rënie të njëpasnjëshme. Shpejtësia e saktë e shigjetës do të bëhet e njohur kur koha midis matjeve të rezultojë të jetë pafundësisht e vogël.

Integrale. Integrali është një metodë që do të na lejojë të llogarisim pozicionin e shigjetës në paradoksin e Dikotomisë. Ne do ta bëjmë këtë duke analizuar shpejtësinë e shigjetës përmes intervaleve kohore në rënie të njëpasnjëshme. Pozicionin e saktë të shigjetës do ta dimë kur koha ndërmjet matjeve të jetë pafundësisht e vogël.

Është e lehtë të shihen disa ngjashmëri midis derivatit dhe integralit. Të dyja vlerat llogariten gjatë analizës së pozicionit ose shpejtësisë së bumit në intervale kohore gradualisht në rënie. Më vonë do të zbulojmë se integrali dhe derivati ​​janë, në fakt, dy anë të të njëjtit kondensator qeramik.

Pse duhet të studiojmë bazat e llogaritjes?

Të gjithë e dimë Ligjin e Ohm-it, i cili lidh rrymën, tensionin dhe rezistencën në një ekuacion të thjeshtë. Tani le të shohim Ligjin e Ohmit duke përdorur shembullin e një kondensatori. Fuqia aktuale e një kondensatori varet nga voltazhi dhe koha. Koha në këtë rast është një variabël kritik dhe duhet të merret parasysh në çdo ngjarje dinamike. Analiza matematikore na lejon të kuptojmë dhe vlerësojmë se si gjërat ndryshojnë me kalimin e kohës. Në rastin e një kondensatori, rryma është e barabartë me kapacitetin herë volt për sekondë, ose i = C(dv/dt), ku:

i - forca aktuale (e menjëhershme);
C - kapaciteti, i cili matet në farad;
dv - ndryshimi i tensionit;
dt është ndryshimi në kohë.

Në këtë qark, nuk ka rrymë elektrike në kondensator. Voltmetri do të tregojë tensionin e baterisë, por ampermetri nuk do të tregojë asgjë. Tensioni nuk do të ndryshojë për sa kohë që potenciometri mbetet i paprekur. Në këtë rast, i = C(0/dt) = 0 amer. Por çfarë ndodh nëse fillojmë të rregullojmë potenciometrin? Duke gjykuar nga ekuacioni, forca aktuale që rezulton do të shfaqet në kondensator. Kjo rrymë do të varet nga ndryshimi i tensionit, i cili lidhet me shpejtësinë e lëvizjes së potenciometrit.

Këta grafikë tregojnë lidhjen ndërmjet tensionit në kondensator, rrymës dhe shpejtësisë me të cilën e rrotullojmë potenciometrin. Ne e bëjmë atë ngadalë në fillim. Një rritje e shpejtësisë çon në një ndryshim të tensionit, i cili, nga ana tjetër, provokon një rritje të mprehtë të rrymës. Në të gjitha fazat, rryma në kondensator është proporcionale me shkallën e ndryshimit të tensionit në të.

Analiza matematikore, ose më saktë, derivati, na jep mundësinë të përcaktojmë shpejtësinë e ndryshimit, në mënyrë që të dimë saktësisht vlerën e rrymës në kondensator në një moment të caktuar kohor. Në mënyrë të ngjashme, ne mund të llogarisim shpejtësinë e menjëhershme të shigjetës së Zenoit. Ky është një mjet tepër i fuqishëm që duhet të jetë në arsenalin tuaj.

Materiali u përgatit posaçërisht për sitin - sipas artikullit të faqes hackaday.com

P.S. Emri im është Aleksandër. Ky është projekti im personal, i pavarur. Më vjen shumë mirë nëse ju pëlqeu artikulli. Dëshironi të ndihmoni faqen? Thjesht shikoni më poshtë për një reklamë për atë që keni kërkuar kohët e fundit.

Faqja e autorit © - Ky lajm i përket faqes, dhe është pronë intelektuale e blogut, e mbrojtur nga ligji për të drejtat e autorit dhe nuk mund të përdoret askund pa një lidhje aktive me burimin. Lexo më shumë - "Rreth autorësisë"

A po kërkoni për këtë? Ndoshta kjo është ajo që nuk mund të gjenit për kaq shumë kohë?

ANALIZA MATEMATIKE

pjesë e matematikës, në të cilën funksione dhe përgjithësimet e tyre studiohen me metodë kufijtë. Koncepti i një kufiri është i lidhur ngushtë me konceptin e një sasie pafundësisht të vogël, prandaj mund të thuhet gjithashtu se M. a. studion funksionet dhe përgjithësimet e tyre me metodën infinitesimale.

Emri "M. a." - një modifikim i shkurtuar i emrit të vjetër të kësaj pjese të matematikës - "Analizë pafundësisht e vogël"; kjo e fundit e zbulon më të plotë përmbajtjen, por edhe shkurtohet (titulli “Analiza me anë të infinitezimaleve” do ta karakterizonte më saktë subjektin). Në M. klasike dhe. objektet e studimit (analizës) janë kryesisht funksione. "Para së gjithash" sepse zhvillimi i M. a. çoi në mundësinë e studimit me metodat e tij formacione më komplekse sesa - funksionalët, operatorët, etj.

Në natyrë dhe teknologji, lëvizjet dhe proceset gjenden kudo, to-thekra përshkruhen me funksione; ligjet e dukurive natyrore zakonisht përshkruhen edhe me funksione. Prandaj rëndësia objektive e M. a. si mjet për të mësuar funksionet.

M. a. në kuptimin e gjerë të termit, mbulon një pjesë shumë të madhe të matematikës. Ai përfshin llogaritja diferenciale, integrale, funksionet e një teorie të ndryshoreve komplekse, teori ekuacionet diferenciale të zakonshme, teori ekuacionet diferenciale të pjesshme, teori ekuacionet integrale, llogaritja e variacioneve, analiza funksionale dhe disa të tjera matematikore disiplinat. Moderne teoria e numrave Dhe teoria e probabilitetit zbatojnë dhe zhvillojnë metodat M. dhe.

Megjithatë, termi M. a. shpesh përdoret për të emërtuar vetëm bazat e analizës matematikore që kombinojnë teorinë numër real, teoria e kufijve, teoria rreshtave, llogaritja diferenciale dhe integrale dhe aplikimet e tyre të menjëhershme, të tilla si teoria e maksimumit dhe minimumit, teoria funksionet e nënkuptuara, seritë Furier, integralet Furier.

Funksioni. Në M. a. vazhdo nga përkufizimi i një funksioni sipas Lobachevsky dhe Dirichlet. Nëse për çdo numër xz të një grupi të caktuar numrash F, në bazë të k.-l. ligji renditet ndër y, atëherë kjo përcakton funksionin

nga një variabël X. Funksioni është përcaktuar në mënyrë të ngjashme

nga variablat, ku x=(x 1 , ..., x n) - pika e hapësirës n-dimensionale; merrni parasysh edhe funksionet

nga pikat x=(x 1 , X 2 , ...) të një hapësire me dimensione të pafundme, të cilat, megjithatë, më shpesh quhen funksionale.

funksionet elementare. Vlera themelore në M. dhe. Luaj funksionet elementare. Në praktikë, ato kryesisht funksionojnë me funksione elementare, përafrojnë funksione të një natyre më komplekse. Funksionet elementare mund të konsiderohen jo vetëm për x real, por edhe për x kompleks; atëherë idetë për këto funksione bëhen të plota në një kuptim të caktuar. Në këtë drejtim, një degë e rëndësishme e M. a., e quajtur. teoria e funksioneve të një ndryshoreje komplekse, ose teoria funksionet analitike.

Numri real. Koncepti i një funksioni bazohet në thelb në konceptin e një numri real (racional dhe irracional). Më në fund mori formë vetëm në fund të shekullit të 19-të. Në veçanti, është krijuar një lidhje logjikisht e përsosur midis numrave dhe pikave gjeometrike. vijë e drejtë, e cila çoi në vërtetimin formal të ideve të R. Descartes (R. Descartes, mesi i shekullit të 17-të), i cili futi sistemet e koordinatave drejtkëndore në matematikë dhe paraqitjen e funksioneve në to me grafikë.

Kufiri. Në M. a. metoda e studimit të funksioneve është . Të bëjë dallimin midis kufirit të një sekuence dhe kufirit të një funksioni. Këto koncepte u formuan përfundimisht vetëm në shekullin e 19-të, megjithëse grekët e tjerë kishin një ide për to. shkencëtarët. Mjafton të thuhet se Arkimedi (shek. III para Krishtit) ishte në gjendje të llogariste segmentin e një parabole me një proces që do ta quajmë kalimin në kufi (krh. metoda e shterimit).

Funksionet e vazhdueshme. Një funksion i rëndësishëm i studiuar në M. a., forma funksionet e vazhdueshme. Një nga përkufizimet e mundshme të këtij koncepti: funksioni y=f(x).nga një ndryshore X, dhënë në intervalin ( a, b), thirrur e vazhdueshme në një pikë X, Nëse

Funksioni është i vazhdueshëm në intervalin ( a, b), nëse është i vazhdueshëm në të gjitha pikat e tij; atëherë është një kurbë, e vazhdueshme në kuptimin e përditshëm të fjalës.

Derivat dhe . Ndër funksionet e vazhdueshme duhet të veçohen funksionet që kanë derivatore. Derivati ​​i funksionit

në një pikë ka shkallën e ndryshimit të saj në këtë pikë, d.m.th., kufirin

Nëse kemi koordinatën e një pike që lëviz përgjatë boshtit y në kohë X, atëherë f "(x) është shpejtësia e menjëhershme e një pike në një kohë X.

Me shenjën e derivatit f "(x) . gjykoni natyrën e ndryshimit në f (x): nëse f "(z)> 0 ( f"(x) <0 ). në intervalin ( c, d), atëherë funksioni / rritet (zvogëlohet) në këtë interval. Nëse funksioni / në pikën x arrin një ekstrem lokal (maksimum ose minimal) dhe ka një derivat në këtë pikë, atëherë ky i fundit është i barabartë me zero në këtë pikë f "(x 0) \u003d 0.

Barazia (1) mund të zëvendësohet nga barazia ekuivalente

ku është një infinitezimal kur, d.m.th., nëse funksioni f ka një derivat në pikë X, atëherë rritja e tij në këtë pikë zbërthehet në dy terma. Nga këto, i pari

është nga (proporcionale), e dyta - tenton në zero më shpejt se

Vlera (2) ref. diferencial funksionet që i korrespondojnë rritjes Në të vogla mund të konsiderohen afërsisht të barabarta me dy:

Arsyetimi i mësipërm për diferencialin është karakteristik për M. a. Ato shtrihen në funksione të shumë variablave dhe në funksionalë.

Për shembull, nëse funksioni

nga variablat ka të vazhdueshme derivatet e pjesshme në pikën x=(x 1 , ... , x n), pastaj rritja e saj që i përgjigjet rritjeve të variablave të pavarur mund të shkruhet si

ku në dmth nëse të gjitha

Këtu termi i parë në anën e djathtë të (3) është diferenciali dz funksionet f. Varet në mënyrë lineare dhe termi i dytë tenton në zero me më shpejt se

Le të jepet (shih Art. Llogaritja e variacioneve)

zgjeruar në klasat e funksionit x(t) , që ka një derivat të vazhdueshëm në interval dhe që plotëson kushtet kufitare x( t0)\u003d x 0, x( t1)=x l, Ku x 0, x 1 - numrat e dhënë; Le të jetë, më tej, klasa e funksionit h(t) , që ka një derivat të vazhdueshëm në dhe të tillë që h( t0)=h(t1)=0. Natyrisht nëse

Në llogaritjen e variacioneve, vërtetohet se, në kushte të caktuara në L, rritja e funksionit J(x) mund të shkruhet si

ku

dhe kështu termi i dytë në anën e djathtë të (4) tenton në zero më shpejt se ||h||, dhe termi i parë varet në mënyrë lineare nga Termi i parë në (4) quhet. variacion i funksionalit dhe shënohet me dJ( x, h).

Integrale. Së bashku me derivatin ka rëndësi themelore në M. a. Ka integrale të pacaktuar dhe të caktuar.

Integrali i pacaktuar është i lidhur ngushtë me funksionin antiderivativ. Funksioni F(x). antiderivativ i funksionit f në intervalin ( a, b) nëse në këtë interval F"(x) =f(x).

Integrali i caktuar (Riemann) i funksionit / në intervalin [ a, b] ka një kufi

Nëse funksioni f është pozitiv dhe i vazhdueshëm në intervalin [ a, b], atëherë integrali i tij në këtë segment është i barabartë me sipërfaqen e figurës së kufizuar nga kurba y=f(x), boshti Oh dhe të drejtpërdrejtë x=a, x=b.

Klasa e funksioneve të integrueshme nga Riemann përmban të gjitha të vazhdueshme në [ a, b]funksionet dhe disa funksione të ndërprera. Por të gjitha janë domosdoshmërisht të kufizuara. Për funksionet e pakufizuara që nuk rriten shumë shpejt, si dhe për funksione të caktuara të dhëna në intervale të pafundme, prezantohet i ashtuquajturi. integrale të pahijshme, duke kërkuar një kalim të dyfishtë në kufi për përcaktimin e tyre.

Koncepti i integralit të Riemann-it për një funksion të një ndryshoreje shtrihet në funksionet e shumë ndryshoreve (shih Integral i shumëfishtë).

Nga ana tjetër, nevojat e M. dhe. çoi në një përgjithësim të integralit në një drejtim, kuptim krejtësisht të ndryshëm integrali Lebesgue ose më e përgjithshme integrale Lebesgue-Stieltjes. Thelbësore në përcaktimin e këtyre integraleve është prezantimi për grupe të caktuara, të quajtura të matshme, i konceptit të masës së tyre dhe, mbi këtë bazë, i konceptit të një funksioni të matshëm. Për funksionet e matshme dhe futet integrali Lebesgue-Stieltjes. Në këtë rast, merren parasysh një gamë e gjerë masash të ndryshme dhe klasat përkatëse të grupeve dhe funksioneve të matshme. Kjo bën të mundur përshtatjen e këtij apo atij integrali ndaj një problemi të caktuar specifik.

Formula Njuton-Leibniz. Ekziston një lidhje midis derivatit dhe integralit, e shprehur me formulën (teoremën) e Njutonit - Leibniz.

Këtu f(x) është i vazhdueshëm në [ a, b] funksion, një F(x) - prototipi i saj.

Formula dhe Taylor. Së bashku me derivatin dhe integralin, koncepti më i rëndësishëm (mjet kërkimi) në analizën matematikore. janë Taylor p Seria Taylor. Nëse funksioni f(x) , a ka derivate të vazhdueshme deri në rendin p përfshirëse në një lagje të pikës x 0, atëherë ajo mund të përafrohet në këtë fqinjësi me një polinom

thirrur polinomi i tij Taylor (gradë n). x-x 0:

(Formula Taylor); ndërsa gabimi i përafrimit

tenton në zero në

Me shpejte se

Kështu, funksioni f (x) në afërsi të pikës x 0 mund të përafrohet me çdo shkallë saktësie me një funksion shumë të thjeshtë (polinom), që kërkon vetëm aritmetikë për llogaritjen e tij. veprimet - mbledhje, zbritje dhe shumëzim.

Rëndësi të veçantë kanë të ashtuquajturat funksionet që janë analitike në një lagje të caktuar x 0 dhe kanë një numër të pafund derivatesh, të tillë që për ta në këtë lagje at mund të përfaqësohen si një seri fuqie e pafundme Taylor:

Zgjerimet e Taylor në kushte të caktuara janë gjithashtu të mundshme për funksionet e shumë variablave, si dhe për funksionalët dhe operatorët.

Referencë historike. Deri në shekullin e 17-të M. a. ishte një grup zgjidhjesh për probleme të veçanta të ndryshme; për shembull, në llogaritjen integrale, këto janë detyra për llogaritjen e sipërfaqeve të figurave, vëllimet e trupave me kufij të lakuar, punën e një force të ndryshueshme, etj. Çdo detyrë ose problem i veçantë zgjidhej me metodën e vet, ndonjëherë komplekse dhe të rëndë. (për parahistorinë e M. a. shih. artikull Njehsimi infinitimal), M. a. si të vetme dhe sistematike. e tëra u formua në veprat e I. Newton (I. Newton), G. Leibniz (G. Leibniz), L. Euler (L. Euler), J. Lagrange (J. Lagrange) dhe shkencëtarë të tjerë të shekullit të 17-të. shekulli i 18-të, dhe e tij - teoria e kufijve - u zhvillua nga O. Komi (A. Cauchy) në fillim. Shekulli i 19 Analizë e thellë e koncepteve fillestare të M. a. u shoqërua me zhvillimin në shekujt XIX dhe XX. teoria e grupeve, teoria e masës, teoria e funksioneve të një ndryshoreje reale dhe çoi në përgjithësime të ndryshme.

Ndezur.: La V a l l e - P u s s e n S.-J. e, Një kurs në analizën e infinitesimals, përkth. nga frëngjishtja, vëll.1-2, Moskë, 1933; Ilyin V. A., Poznyak E. G., Fundamentals of Mathematical Analysis, 3rd ed., Pjesa 1, M., 1971; Botimi i dytë, pjesa 2, M., 1980; Dhe l dhe N V. A., Sadovnichiy V. A., Seidov B. Kh., Analiza matematikore, M., 1979; K u d r i v e në L. D., Analiza matematikore, botimi 2, vëll.1-2, M., 1973; Nikolsky S. M., Kursi i analizës matematikore, botimi i dytë, vëll.1-2, M., 1975; Uitteker E. T., W a t s o n J. N., Kursi i analizës moderne, përkth. nga anglishtja, pjesa 1-2, botimi i dytë, M., 1962-63; F dhe kht n o l ts G. M., Kursi i llogaritjes diferenciale dhe integrale, botimi i 7-të, vëll.1-2, M., 1970; Botimi i 5-të, vëll.3, M., 1970. S. M. Nikolsky.

Enciklopedi matematikore. - M.: Enciklopedia Sovjetike. I. M. Vinogradov. 1977-1985.

Shihni se çfarë është "ANALIZA MATEMATIKE" në fjalorë të tjerë:

ANALIZA MATEMATIKE, një grup degësh të matematikës kushtuar studimit të funksioneve me metoda të llogaritjes diferenciale dhe llogaritjes integrale ... Enciklopedia moderne

Një grup i degëve të matematikës kushtuar studimit të funksioneve me metoda të llogaritjes diferenciale dhe integrale. Termi është më shumë pedagogjik sesa shkencor: kurset në analizën matematikore mësohen në universitete dhe shkolla teknike ... Fjalori i madh enciklopedik

anglisht analiza matematikore; gjermane analiza matematikore. Degë e matematikës kushtuar studimit të funksioneve me metoda të llogaritjes diferenciale dhe integrale. Antinazi. Enciklopedia e Sociologjisë, 2009 ... Enciklopedia e Sociologjisë

Egzist., numri i sinonimeve: 2 matan (2) analiza matematikore (2) fjalor sinonimi ASIS. V.N. Trishin. 2013... Fjalor sinonimik

ANALIZA MATEMATIKE- ANALIZA MATEMATIKE. Një grup i degëve të matematikës kushtuar studimit të funksioneve matematikore me metoda të llogaritjes diferenciale dhe integrale. Përdorimi i metodave M. dhe. është një mjet efektiv për të zgjidhur çështjet më të rëndësishme ... ... Një fjalor i ri termash dhe konceptesh metodologjike (teoria dhe praktika e mësimdhënies së gjuhëve)

analiza matematikore- — SHQ analiza matematikore Dega e matematikës e lidhur më qartë me procesin e kufirit ose konceptin e konvergjencës; përfshin teoritë e diferencimit,…… Manuali i Përkthyesit Teknik

Analiza matematikore- ANALIZA MATEMATIKE, një grup seksionesh të matematikës kushtuar studimit të funksioneve me metoda të llogaritjes diferenciale dhe llogaritjes integrale. … Fjalor Enciklopedik i Ilustruar

“... nëse do të më duhej të krijoja një mekanizëm me qëllimin e vetëm për të shkatërruar kuriozitetin natyror të fëmijës dhe dashurinë e tij për modelimin, vështirë se do të kisha bërë më mirë se sa është zbatuar tashmë - thjesht nuk do të kisha imagjinatë të mjaftueshme për të. konkurrojnë me ide të tilla të pandjeshme, të mërzitshme që janë mishëruar në metodat moderne të studimit të matematikës.

Mendoni të studioni artin e bukur si kjo: Fëmijë, jo vizatim në kopsht. Në vend të kësaj, le të studiojmë kiminë e produkteve të bojës, fizikën e dritës dhe anatominë e syrit. Pas 12 vitesh studimi të këtyre aspekteve, nëse fëmijët (më saktë tashmë adoleshentët) nuk e urrejnë ende artin, ata mund të fillojnë të vizatojnë vetë. Në fund të fundit, ata tani kanë një themel të fortë në mënyrë që të fillojnë të respektojnë artin. E drejtë?

Edhe me poezi. Imagjinoni të studioni këtë citat (formula):

“Por gjëja kryesore: ji i vërtetë me veten; Atëherë, ashtu si nata pason ditën, Ti nuk do t'i tradhtosh të tjerët.” -William Shakespeare, Hamlet

Është një mënyrë elegante për të thënë "të jesh vetvetja" (dhe nëse kjo do të thotë të shkruash për matematikën me mungesë respekti, kështu qoftë). Por nëse do të kishim parasysh poezinë në një orë matematike, në vend që të kërkonim kuptimin, do të numëronim numrin e rrokjeve, do të analizonim pentametrin jambik, do të shënonim emrat, foljet dhe mbiemrat.

Matematika dhe poezia janë si mënyra të ndryshme për të shpjeguar, për të karakterizuar të njëjtën gjë. Formulat janë një mjet për të arritur një qëllim, një mënyrë për të shprehur të vërtetën matematikore.

Kemi harruar që matematika funksionon me ide, nuk është manipulimi mekanik i formulave që i shpreh këto ide.

Epo, gjithçka është e qartë, kështu që cila është ideja juaj e mrekullueshme?

Ja çfarë nuk do të bëj: nuk do t'i ritregoj librat që kam shkruar tashmë. Nëse keni nevojë për përgjigje këtu dhe tani, ka mijëra faqe interneti, video mësimore dhe 20 minuta te ndihmosh.

Në vend të kësaj, le të zotërojmë bazat e llogaritjes. Ekuacionet nuk janë të mjaftueshme - unë dua momente depërtimi në mënyrë që ju të shihni me të vërtetë kuptimin e tyre dhe të kuptoni gjuhën e matematikës.

Gjuha matematikore formale është thjesht një mënyrë komunikimi. Grafikët, animacionet informative dhe gjuha e thjeshtë mund të ofrojnë më shumë njohuri sesa një faqe me prova të pakuptimta.

Por matematika është e vështirë!

Unë mendoj se çdokush mund të kuptojë parimet bazë të llogaritjes. Ne nuk duhet të jemi poetë për të shijuar veprat e Shekspirit.

Do të jetë shumë më e lehtë për ju nëse dini algjebër dhe jeni të interesuar për matematikën. Jo shumë kohë më parë, leximi dhe shkrimi ishin punë e skribëve të trajnuar posaçërisht. Dhe sot çdo fëmijë 10-vjeçar mund ta bëjë këtë. Pse?

Sepse ne e presim. Pritjet luajnë një rol të madh në zhvillimin e mundësive. Pra, prisni që llogaritja të jetë vetëm një lëndë tjetër. Disa njerëz zbresin në detajet më të vogla (shkrimtarë/matematicienë). Por ne të tjerët mund të admirojmë atë që po ndodh dhe të përpiqemi ta kuptojmë atë. Do të doja që të gjithë të zotëronin konceptet bazë të analizës matematikore dhe të thoshin "Uau!".

Pra, çfarë është analiza e matematikës?

Ky ishte një shembull i thjeshtë, por a e morët idenë kryesore? Morëm diskun, e ndamë dhe i vendosëm pjesët së bashku në një mënyrë paksa të ndryshme. Analiza matematikore tregoi se disku dhe unaza janë të lidhura ngushtë me njëri-tjetrin: disku është në të vërtetë një grup unazash. Kjo është një temë shumë e njohur në llogaritje: gjërat e mëdha përbëhen nga gjëra më të vogla. Dhe ndonjëherë është më e lehtë dhe më e qartë të punosh me këto objekte të vogla.

Disa shembuj

Shumë shembuj në llogaritje bazohen në fizikë. Kjo, natyrisht, është e mrekullueshme, por mund të jetë e vështirë t'i perceptosh ato: sinqerisht, nuk është gjithmonë e mundur të mbash parasysh formula të ndryshme fizike, siç është formula për shpejtësinë e një objekti.

Më pëlqen të filloj me shembuj të thjeshtë vizualë sepse kështu funksionon truri ynë. Unaza/rrethi që kemi hetuar - ju mund të modeloni të njëjtën gjë me disa pjesë tubash me diametra të ndryshëm: t'i ndani, t'i rreshtoni dhe t'i vendosni në një trekëndësh të përafërt për t'u siguruar që matematika funksionon vërtet. Me një formulë të thjeshtë fizike, kjo nuk ka gjasa të bëhet.

Pak për ashpërsinë matematikore (për fanatikët e kësaj shkence)

Ndjej matematikanë pedantë që djegin tastierat e tyre. Prandaj, do të fus vetëm disa fjalë për "rreptësinë". A e dini se ne nuk e mësojmë llogaritjen ashtu siç e zbuluan Njutoni ose Leibniz? Ata përdorën idetë intuitive të "fluksit" dhe "pafundësisht të vogla" të cilat u zëvendësuan nga kufijtë sepse "Sigurisht që funksionon në praktikë. Por a funksionon në teori?

Ne kemi krijuar modele komplekse mekanike për të vërtetuar "saktësisht" llogaritjet, por ne kemi humbur intuitën tonë në procesin e provave të tilla.

Ne e shikojmë ëmbëlsinë e sheqerit në aspektin e kimisë së trurit, në vend që ta shpjegojmë me gjuhën e shkencës “Sheqeri ka shumë energji. Haje."

Unë nuk dua (dhe nuk mund) t'u mësoj llogaritje studentëve ose të trajnoj shkencëtarë. Por a do të ishte keq nëse të gjithë mund ta kuptonin llogaritjen në nivelin "të pasaktë" në të cilin Njutoni e kuptoi atë? Që edhe ajo të ndryshojë botën për ju, siç bëri dikur për të?

Përqendrimi i parakohshëm në saktësi i shpërndan studentët dhe e bën matematikën të vështirë për të mësuar. Ja një shembull i mirë: numri e përcaktohet teknikisht nga një kufi, por ai u zbulua pikërisht me ndihmën e një supozimi intuitiv për rritjen. Logaritmi natyror mund të duket si një integral, ose një kohë për t'u rritur. Cilat shpjegime janë më të mira për fillestarët?

Le të vizatojmë pak me dorë dhe të zhytemi në kimi gjatë rrugës. Gëzuar informatikë.

(P.S: Një lexues i sjellshëm krijoi një rrëshqitje të animuar në Powerpoint që ndihmon për ta paraqitur këtë ide më vizualisht (është më mirë ta shikoni në PowerPoint, animacionet do të jenë të dukshme atje). Faleminderit!)

9 tetor 2015

Sipas fjalorit të gjuhës ruse analiza- kjo është një metodë e kërkimit shkencor duke marrë parasysh aspektet individuale, vetitë, përbërësit e diçkaje. Një nga degët më të rëndësishme të matematikës quhet analiza matematikore dhe shpesh edhe vetëm analiza. Menjëherë lind pyetja: çfarë saktësisht analizohet nga analiza matematikore? Përgjigja është e qartë - analizohen funksionet. Funksioni(nga latinishtja "funksion" - zbatim) paraqet lidhjen ndërmjet vlerave numerike të variablave.

Meqenëse analiza është një metodë kërkimore, lind një pyetje e dytë: çfarë është kjo metodë? Përgjigja jep emrin e dytë të analizës matematikore - llogaritja diferenciale dhe integrale. Llogaritja është një degë e matematikës që përcakton rregullat për llogaritjen. fjala " diferencial" vjen nga fjala latine "diferencim", d.m.th. ndryshim. fjala " integrale” nuk ka një origjinë kaq të qartë (“integrator” - tërësi; "integro" - rivendos), por ka kuptimin e kombinimit të pjesëve në një tërësi, rikthimit të thyer në dallime. Ky rikuperim arrihet me përmbledhje.

Le të përmbledhim rezultatet e para:

· objektet kryesore studiuar në analizën matematikore janë funksionet.

· Funksionet janë varësi të llojeve të ndryshme midis vlerave numerike të ndryshueshme.

· Metoda e analizës matematikore është diferencimi– punë me diferencat e vlerave të funksionit, dhe integrimin- llogaritja e shumave.

Kështu, për të zotëruar analizën matematikore, para së gjithash, duhet të kuptoni konceptin e një funksioni. Funksioni është koncepti më i rëndësishëm matematik, sepse funksionet janë një mënyrë matematikore për të përshkruar lëvizjen dhe ndryshimin. Funksioni është një proces.

Lloji më i rëndësishëm i lëvizjes është lëvizja mekanike në vijë të drejtë. Kur lëvizni, maten distancat e përshkuara nga objekti, por kjo nuk mjafton qartë për të përshkruar plotësisht lëvizjen. Si Akili ashtu edhe breshka mund të lëvizin në të njëjtën distancë nga pika e fillimit, por lëvizja e tyre ndryshon në shpejtësi dhe shpejtësia nuk mund të matet pa matur kohën.

Tashmë nga shqyrtimi i këtij shembulli, bëhet e qartë se një variabël nuk mjafton për të përshkruar lëvizjen dhe ndryshimin. Është intuitivisht e qartë se koha ndryshon në mënyrë uniforme, ndërsa distanca mund të ndryshojë ose më shpejt ose më ngadalë. Lëvizja përshkruhet plotësisht nëse në çdo moment të kohës dihet se sa është larguar objekti nga pika e fillimit. Pra, gjatë lëvizjes mekanike, ekziston një korrespondencë midis vlerave të dy variablave - koha, e cila ndryshon në mënyrë të pavarur nga çdo gjë, dhe largësia, e cila varet nga koha. Ky fakt është baza për përcaktimin e funksionit. Dy variablat nuk quhen më kohë dhe distancë.

Përkufizimi i funksionit: funksionin – a është rregull apo ligj, duke vendosur çdo vlerë të ndryshores së pavarur X një vlerë të caktuar të ndryshores së varur në . Ndryshore e pavarur X quhet argument, dhe i varur në - funksion. Ndonjëherë thuhet se një funksion është një marrëdhënie midis dy ndryshoreve.

Si të imagjinoni se çfarë është një variabël? Një ndryshore është një vijë numerike (vizore ose shkallë) përgjatë së cilës lëviz një pikë (një termometër ose një gjilpërë me një rruazë). Një funksion është një mekanizëm ingranazhesh me dy dritare x dhe y. Ky mekanizëm ju lejon të instaloni në dritare X çdo vlerë, por në kuti në vlera e funksionit do të shfaqet automatikisht me ndihmën e ingranazheve.

Detyra 1. Temperatura e pacientit matet çdo orë. Ekziston një funksion - varësia e temperaturës nga koha. Si të paraqitet kjo veçori? Përgjigju: tabela dhe grafiku.

Funksioni është i vazhdueshëm, ashtu si lëvizja është e vazhdueshme, por në praktikë është e pamundur të rregullohet kjo vazhdimësi. Mund të kapni vetëm vlera të vetme të argumentit dhe funksionit. Megjithatë, është ende e mundur të përshkruhet teorikisht vazhdimësia.

Detyra 2. Galileo Galilei zbuloi se një trup që bie lirshëm përshkon një njësi distancë në sekondën e parë, 3 njësi në të dytën, 5 njësi në të tretën, etj. Përcaktoni varësinë e kohës nga distanca. tregues: Nxjerr formulën e përgjithshme për lidhjen ndërmjet distancës së përshkuar dhe numrit të distancës.

Mënyrat për të vendosur funksionet.

Probleme të analizës matematikore.

Kalimi nga një paraqitje e një funksioni në tjetrin (llogaritja e vlerave të funksionit, ndërtimi i funksioneve analitike të përafërta nga të dhënat eksperimentale numerike dhe grafike, hulumtimi i funksioneve dhe vizatimi).

Studimi matematikor i vetive të një funksioni si proces. Shembulli 1: kërkimi i shpejtësisë nga një funksion i njohur i rrugës së kohës (diferencimi). Shembulli 2: Gjetja e një shtegu duke përdorur një funksion të njohur të shpejtësisë kundrejt kohës (integrimi).

	|	ligjërata e radhës ==>
Kreativiteti: Fletoret kontrollohen nga x (kush?) mësues	|